1 Introduction

The Anti-de Sitter/conformal field theories (AdS/CFT) correspondence [1,2,3] has been proven to be a powerful tool in studying strongly coupled systems and quantum information properties. In recent years, it has been widely applied to study the holographic superconductor model [4,5,6]. The simple holographic superconductor model dual to gravity theories was constructed by applying a scalar field and a Maxwell field coupled in an AdS black hole background. The physical picture is that the AdS black hole becomes unstable and scalar hair condenses as one tunes the temperature of black hole. This condensation of the scalar hair induces the symmetry breaking, which results in the non-vanishing vacuum expectation value of the dual operator in the field theory side. In the past decade, a number of holographic superconductor models have been explored. These models have shown many characteristic properties exhibited in real superconductors, see [7, 8] for reviews.

In addition, two of the most important aspects that have received wide attention in the context of the AdS/CFT correspondence are holographic entanglement entropy (HEE), introduced in [9, 10], and holographic complexity, initiated by the works of [11,12,13,14]. In a strongly coupled system, the entanglement entropy is a powerful tool to keep track of the degrees of freedom. Especially, a simple and elegant method of calculating the entanglement entropy of CFTs from the minimal area surface in the gravity side was proposed by Ryu and Takayanagi. In this way, the HEE has been applied to disclose properties of phase transitions in various holographic superconductor models [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. It shows that the HEE is a good probe to explore the properties of holographic superconductors.

On the other hand, the quantum complexity describes how many simple elementary gates are needed to obtain a target state from a certain simple reference state. In the holographic framework, there have been two distinct proposals to evaluate the complexity of a holographic boundary state, which are referred to as the CV conjecture (complexity = volume) [11, 12] and the CA conjecture (complexity = action) [13, 14], respectively. The former relates the complexity of the CFT state to the size of the wormhole, while the latter relates the complexity of the CFT state to the bulk action evaluated in a particular spacetime region known as the Wheeler-DeWitt patch. It should be noted that the above two conjectures of holographic complexity are proposed for the global spacetime. Inspired by the HEE proposal, the CV conjecture for the whole boundary system is generalized for the subregion [33]. The complexity for a subsystem on the boundary equals the volume of the extremal codimensional-one hypersurface enclosed by Ryu–Takayanagi surface. This is usually referred to as the holographic subregion complexity (HSC) [34,35,36], which will be the focus of this paper.

More recently, several authors have studied the holographic complexity in different types of holographic superconductors and argued that it may be used as another independent probe to the physics of the phase transition [37,38,39,40,41,42]. However, there are still many ambiguities about the behavior of HSC in holographic superconductors. Especially for the behavior of HSC with temperature changes, it is different from the HEE in some models [38, 41], while it is similar to the behavior of HEE in some cases [42, 43]. As pointed out in [44], since the entanglement entropy grows in a very short time during the thermalization process of a strongly coupled system, it is usually not enough to describe the rich geometric structure. The time evolution of HSC after a thermal quench has been recent another interesting direction [45,46,47,48,49]. For holographic superconductors, we expect to use the HSC as a probe to capture the richer information of phase transition. Thus, it is meaningful to further analyze the behavior of HSC in other holographic superconductors, such as unbalanced holographic superconductors [50,51,52,53,54,55].

One motivation of selecting the unbalanced system is that it is quite interesting in the condensed matter framework. An unbalanced model is based on an emergence of superconducting state near a quantum critical point [56]. This is a relevant theme both in the condensed matter and finite density QCD contexts [57]. The mechanism of this model is that the superconducting state occurs where the two fermionic species contribute with unbalanced populations or unbalanced chemical potentials. The unbalanced chemical potential can be produced by the presence of magnetic impurities in the system or by an external magnetic field inducing Zeeman splitting of single-electron energy levels. In the holographic framework, Ref. [50] gives a holographic description of a 2+1-dimensional unbalanced superconductor by introducing a second U(1) gauge field in the bulk theory. This is discussed in more detail in next section.

In this paper, we would like to investigate the behavior of HSC and examine whether the HSC approach is still useful in the unbalanced holographic superconductors. We will focus on the time-independent HSC for a straight strip geometry at AdS boundary and compare it to the behavior of HEE. We will see that the HEE and HSC show similar linear growth behaviors with the change of width. The HSC can indeed respond to phase transitions as the HEE does. However, for different fixed widths, the HSC exhibits different behaviors, while the HEE remains consistent. In particular, we find that there are certain conditions that make it difficult to observe phase transitions through the HSC approach. Furthermore, the HSC and HEE also show different behaviors for the influence of unbalance parameter \(\beta \).

This work is organized as follows. In Sect. 2, we briefly review the unbalanced holographic superconductor model, and give the complete equations of motion to be solved. In Sect. 3, we present the fully back-reacted solution of the holographic system. In Sect. 4, we will present our results for both the HEE and HSC of this system. The conclusion and discussions are included in Sect. 5.

2 Unbalanced holographic superconductors

In this section, we begin with a brief review the holographic model for the minimal unbalanced superconductor in \(2 + 1\) dimensions. The dual gravity description of this unbalanced superconductor is defined by the following action [50]

$$\begin{aligned} S= & {} \frac{1}{2\kappa ^{2}_{4}}\int d x^{4}\sqrt{-g}\left[ {\mathcal {R}}+\frac{6}{L^{2}}-\frac{1}{4}F_{ab}F^{ab}\right. \nonumber \\&\left. -\frac{1}{4}Y_{ab}Y^{ab}-V(|\psi |) -|\partial \psi -i q A\psi |^2\right] , \end{aligned}$$
(1)

where \(F=d A\) and \(Y=d B\) are the two field strengths associated to the gauge fields U\((1)_{A}\) and U\((1)_{B}\), and \(\psi \) represents a scalar field with potential \(V(|\psi |)=m^{2}\psi ^{\dag }\psi \). Note that the scalar \(\psi \) is minimally coupled to gauge field A and uncharged with respect to gauge field B. When \(Y=0\), the system reduces to the model introduced in [5, 6].

In the holographic framework, the non-trivial charged field under the U\((1)_{A}\) gauge field in an asymptotically \(AdS_{4}\) black hole background leads to the breaking of a U\((1)_{A}\) “charge” symmetry, which characterizes the onset of superconductivity [4,5,6]. Turning on the temporal component of the gauge field U\((1)_{B}\) can make the system obtain the chemical potential mismatch, which can also be interpreted as the chemical potential for the U\((1)_{B}\) “spin” symmetry [58]. These two gauge fields correspond to two conserved currents in the boundary theory. Indeed, this extended holographic model can study many strong coupling physics of unbalanced mixtures, such as the strong-coupling generalization of the two-current model proposed by Mott [59, 60], the mixed spin-electric linear response, and Larkin–Ovchinnikov–Fulde–Ferrel (LOFF) phase [61, 62] in strongly coupled superconductors.

Including the backreaction, our ansatz for the metric and matter fields is given by

$$\begin{aligned}&ds^2=-f(r)e^{-\chi (r)}dt^{2}+\frac{dr^2}{f(r)}+\frac{r^{2}}{L^{2}} (dx^{2}+dy^{2}), \end{aligned}$$
(2)
$$\begin{aligned}&\psi =\psi (r),\quad A_{a}dx^{a}=\phi (r)dt,\quad B_{a}dx^{a}=v(r)dt. \end{aligned}$$
(3)

Then the Hawking temperature of such a black hole is expressed as

$$\begin{aligned} T=\frac{f^{\prime }(r_{H})e^{-\chi (r_{H})/2}}{4\pi }, \end{aligned}$$
(4)

where \(r_{H}\) corresponds to the event horizon of the black hole satisfying \(f(r_{H})=0\). From above assumptions, we can obtain the corresponding independent equations of motion as follows

$$\begin{aligned}&\psi ''+\psi '\left( \frac{f'}{f}+\frac{2}{r}-\frac{\chi '}{2} \right) +\frac{1}{f}\left( \frac{q^{2}e^{\chi }\phi ^2}{f}-m^2\right) \psi =0, \end{aligned}$$
(5)
$$\begin{aligned}&\quad \phi ''+\phi '\left( \frac{2}{r}+\frac{\chi '}{2}\right) -\frac{2q^{2}\psi ^{2}}{f}\phi =0, \end{aligned}$$
(6)
$$\begin{aligned}&\quad f'+f\left( \frac{1}{r}+\frac{r\psi '^{2}}{2}\right) +\frac{r\psi ^{2}}{2}\left( \frac{e^{\chi }q^{2}\phi ^{2}}{f} +m^{2}\right) \nonumber \\&\qquad +\frac{re^{\chi }(\phi '^{2}+v'^{2})}{4} -\frac{3r}{L^{2}}=0, \end{aligned}$$
(7)
$$\begin{aligned}&\quad \chi ^{\prime }+r\psi '^{2}+\frac{re^{\chi }q^{2}\phi ^{2}\psi ^{2}}{f^{2}}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\quad v''+v'\left( \frac{2}{r}+\frac{\chi '}{2}\right) =0, \end{aligned}$$
(9)

where the prime denotes the derivative with respect to r. In the following we will work in units \(L=1\) and \(2\kappa _{4}^{2}=1\). We also take the standard choice of mass and charge as \(m^{2}=-2\,,q=2\). For this case, in which \(m^{2}>-9/4\), the Breitenlohner-Freedman bound [63] is respected.

In order to solve the equations of this complex system, we have to specify the boundary conditions. At the horizon \(r_{H}\), the regularity condition gives the boundary conditions

$$\begin{aligned} \phi (r_{H})=v(r_{H})=0. \end{aligned}$$
(10)

Near the AdS boundary (\(r\rightarrow \infty \)), the asymptotic behaviors of the solutions are

$$\begin{aligned} \psi (r)&=\frac{\psi _{1}}{r}+\frac{\psi _{2}}{r^{2}}+\cdots , \end{aligned}$$
(11)
$$\begin{aligned} \phi (r)&=\mu -\frac{\rho }{r}+\cdots ,\quad v(r)=\delta \mu -\frac{\delta \rho }{r}+\cdots , \end{aligned}$$
(12)
$$\begin{aligned} f(r)&=r^{2}-\frac{\varpi }{2r}+\cdots ,\quad \chi (r)=0+\cdots , \end{aligned}$$
(13)

where \(\mu \) (\(\delta \mu \)) and \(\rho \) (\(\delta \rho \)) are the corresponding chemical potential (chemical potential mismatch) and charge density (charge density mismatch) in the dual boundary field theory, and \(\varpi \) is the mass of black hole interpreted as the energy density of the dual field theory, respectively. According to the AdS/CFT correspondence, \(\psi _{1}\) and \(\psi _{2}\) can be dual to the source while the other is the vacuum expectation value. Specifically we will choose \(\psi _{1}\) as the source and \(\psi _{2}\) corresponds to the vacuum expectation values \(\langle {\mathcal {O}}_{2}\rangle \). We turn off the source, i.e., \(\psi _{1}=0\) to describe a spontaneous symmetry breaking. Thus, if \(\psi _{2}\ne 0\) the state is superconducting while if \(\psi _{2}=0\) (or \(\psi =0\)) the state is normal. From the equations of motion for the system, we can get the useful scaling symmetries in the forms

$$\begin{aligned}&r\rightarrow \alpha r,\quad (x,y,t)\rightarrow (x,y,t)/\alpha ,\quad \phi \rightarrow \alpha \phi ,\quad v\rightarrow \alpha v,\quad f\rightarrow \alpha ^2f. \nonumber \\ \end{aligned}$$
(14)

Using above symmetries, we can set \(r_{H}=1\).

3 Condensation and phase transition

In this part, we are looking for the physical properties of phase transition in this model through the behaviors of the scalar condensation. For the normal phase, the metric becomes the \(U(1)^{2}\)-charged Reissner–Nordström-\(AdS_{4}\) black hole. Thus, we have

$$\begin{aligned} ds^{2}&=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}(dx^{2}+dy^{2}), \end{aligned}$$
(15)
$$\begin{aligned} f(r)&=r^{2}\left( 1-\frac{r_{H}^{3}}{r^{3}}\right) +\frac{\mu ^{2}r_{H}^{2}}{4r^{2}}\left( 1-\frac{r}{r_{H}}\right) (1+\beta ^{2}), \end{aligned}$$
(16)

where \(\beta =\delta \mu /\mu \) is the unbalance parameter, and the gauge fields are

$$\begin{aligned} \phi (r)= & {} \mu \left( 1-\frac{r_{H}}{r}\right) =\mu -\frac{\rho }{r}, \end{aligned}$$
(17)
$$\begin{aligned} v(r)= & {} \delta \mu \left( 1-\frac{r_{H}}{r}\right) =\delta \mu - \frac{\delta \rho }{r}. \end{aligned}$$
(18)

For purpose of getting the solutions in the superconducting phase where \(\psi (r)\ne 0\), we will first make a coordinate transformation from r-coordinate to z-coordinate by defining \(z=r_{H}/r\), then we will solve these equations by using the numerical shooting method. In the following we shall work in the grand-canonical ensemble with fixed chemical potentials \(\mu =1\).

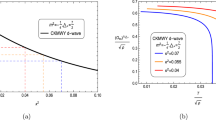
The condensate of the scalar operator as a function of temperature with different values of the unbalance parameter \(\beta \) is shown in Fig. 1. It can be seen clear from the Fig. 1 that the condensation of the operator emerges at the critical temperature \(T_{c}\), which implies the appearance of the phase transition. Obviously, this phase transition here is a typically second order transition in our choice of parameters. From Fig. 1, we can find that the critical temperature \(T_{c}\) decreases as the unbalance parameter \(\beta \) increases, which means that it is harder for the scalar condensation to form in highly unbalanced systems. This result corresponds to the fact that the unbalance hinders the condensation, which is consistent with Refs. [50, 51].

Fig. 1
figure 1

The condensate of the scalar operator \({\mathcal {O}}_{2}\) versus temperature for different values of the unbalance parameter \(\beta \). The colored curves correspond to \(\beta =0\) (red, \(T_{c}=0.09012\)), \(\beta =1\) (green, \(T_{c}=0.06909\)) and \(\beta =1.5\) (blue, \(T_{c}=0.05002\)), respectively.

Full size image

4 HEE and HSC of the holographic model

In this part, we will calculate the HEE and HSC in this holographic model. We consider a straight strip geometry \({\mathcal {A}}\) with a finite width along the x direction and infinitely extending in y direction as: \(-\frac{\ell }{2}\le x \le \frac{\ell }{2}\,,-\frac{R}{2}<y<\frac{R}{2}\), where \(\ell \) is defined as the size of region \({\mathcal {A}}\) and R is a regulator which can be set to infinity. The hypersurface \(\gamma _A\) in z-coordinate starts from \(z=\epsilon \) at \(x=\frac{\ell }{2}\), then extends into the bulk until it reaches \(z=z_{*}\), and returns back to the AdS boundary \(z=\epsilon \) at \(x=-\frac{\ell }{2}\), where \(\epsilon \) is UV cutoff. It is easy to obtain the induced metric on the hypersurface \(\gamma _A\) as follow

$$\begin{aligned} d s^{2}_{induced}=\frac{1}{z^{2}}\left\{ \left[ 1+\frac{1}{z^{2}f} \left( \frac{d z}{d x}\right) ^{2}\right] d x^{2}+d y^{2}\right\} . \end{aligned}$$
(19)

According to the Ryu–Takayanagi proposal [9], the entanglement entropy of \({\mathcal {A}}\) is given by the formula

$$\begin{aligned} {\mathcal {S}}=\frac{Area(\gamma _{{\mathcal {A}}})}{4G_{N}}, \end{aligned}$$
(20)

where \(G_{N}\) is the Newton’s constant in the dual gravity theory. By using the induced metric (19), the entanglement entropy in the strip geometry can be evaluated as

$$\begin{aligned} {\mathcal {S}}=\frac{R}{2G_{4}} \int _{-\ell / 2}^{\ell / 2} \frac{d x}{z^{2}} \sqrt{\frac{1}{z^{2}f}\left( \frac{d z}{d x}\right) ^{2}+1}, \end{aligned}$$
(21)

The minimality condition gives us

$$\begin{aligned} \frac{d z}{d x} = \frac{1}{z} \sqrt{\left( z_{*}^{4}-z^{4}\right) f}, \end{aligned}$$
(22)

with the turning point \(z=z_{*}\) for the minimal surface which satisfies the condition \(\frac{d z}{d x}|_{z=z_{*}}=0\). Integrating the condition, we have

$$\begin{aligned} x(z)=\int ^{z_{*}}_{z}dz\frac{z}{\sqrt{(z^{4}_{*}-z^{4})f(z)}}, \end{aligned}$$
(23)

which obeys, with a UV cutoff \(\epsilon \),

$$\begin{aligned} x(\epsilon \rightarrow 0)=\frac{\ell }{2}. \end{aligned}$$
(24)

Substituting Eq. (22) into Eq. (21), the HEE can be rewritten as

$$\begin{aligned} {\mathcal {S}}= \frac{R}{2G_{4}} \int _{\varepsilon }^{z_{*}} d z \frac{z_{*}^{2}}{z^{3}} \frac{1}{\sqrt{\left( z_{*}^{4}-z^{4}\right) f(z)}}=\frac{R}{2G_{4}}\left( s+\frac{1}{\epsilon }\right) ,\nonumber \\ \end{aligned}$$
(25)

where the first term s is the finite part of entanglement entropy and thus is physical important. While the second term is divergent (\(\epsilon \rightarrow 0\)) and represents the area law [9].

On the other hand, following the subregion CV conjecture [33], the subregion complexity of the system \({\mathcal {A}}\) is proportional to the volume surrounded by the minimal surface \(\gamma _A\) as follows

$$\begin{aligned} {\mathcal {C}}=\frac{Volume(\gamma _{{\mathcal {A}}})}{8\pi LG_{N}}. \end{aligned}$$
(26)

Thus, the HSC in the strip geometry is

$$\begin{aligned} {\mathcal {C}}=\frac{R}{4 \pi L G_{4}} \int _{\epsilon }^{z *} \frac{x(z) d z}{z^{4} \sqrt{f}}=\frac{R}{4 \pi L G_{4}}\left[ c+\frac{F(z_{*})}{\epsilon ^{2}}\right] , \end{aligned}$$
(27)

where the term c is a finite term, which is physically important. The term \(F(z_{*}) / \epsilon ^{2}\) is divergent and the value of \(F(z_{*})\) in different situations can be found numerically [38]. For more details on the regularization of HSC, see Refs. [64, 65].

Now we are in a position to study the behaviors of HSC and HEE of this system numerically. Figure 2 shows our results for the HEE and HSC as functions of the strip width \(\ell \) at a fixed temperature \(T=0.04\), which is below the transition temperature \(T_{c}\). From the left panel, we find that the curves go linearly with \(\ell \) for the large \(\ell \), which means that the area law holds in unbalanced holographic superconductors. It also can be seen from the left panel that the HEE in the superconducting phase is always less than the one in the normal case. This property holds for different values of the unbalance parameter \(\beta \). This is consistent with the expectation that in the superconducting phase the degrees of freedom decrease due to the formation of Cooper pairs [15]. From the right panel in Fig. 2, we also see the expected linear growth behavior for the large \(\ell \) and the HSC in the superconducting phase is less than the one in the normal case for the large \(\ell \). But different from the case of HEE, we observe that, for the small strip width \(\ell \), the HSC in the normal is less than the one in the superconducting phase case.

Fig. 2
figure 2

The HEE (left) and HSC (right) as functions of the stripe width \(\ell \) for various unbalance parameters \(\beta \) with a fixed temperature \(T=0.04\). The dashed and solid curves in each panel indicate the normal and surperconducting phases. The colored curves correspond to \(\beta =0\) (red), \(\beta =1\) (green) and \(\beta =1.5\) (blue), respectively

Full size image
Fig. 3
figure 3

The HEE (left) and HSC (right) as functions of the temperature T for a fixed \(\ell =2\). The dashed and solid curves in each panel indicate the normal and surperconducting phases. The colored curves correspond to the unbalance parameter \(\beta =0\) (red, \(T_{c}=0.09012\)), \(\beta =1\) (green, \(T_{c}=0.06909\)) and \(\beta =1.5\) (blue, \(T_{c}=0.05002\)), respectively

Full size image
Fig. 4
figure 4

The HEE (left) and HSC (right) as functions of the temperature T for a fixed \(\ell =8\). The dashed and solid curves in each panel indicate the normal and surperconducting phases. The colored curves correspond to unbalance parameter \(\beta =0\) (red, \(T_{c}=0.09012\)), \(\beta =1\) (green, \(T_{c}=0.06909\)) and \(\beta =1.5\) (blue, \(T_{c}=0.05002\)), respectively

Full size image

The behaviors of HEE and HSC as functions of the temperature T for different unbalance parameters \(\beta \) with \(\ell =2\) are presented in Fig. 3. The left panel is the case of HEE and right panel shows the case of HSC. In both cases, we can see clearly that the HEE and HSC have a discontinuous slop at the critical temperature \(T_{c}\), which implies the non-trivial reorganization of the degrees of freedom in the system. The discontinous change of the slop marks the phase transition point, which indicates that the system has undergone a phase transition from the normal state to the superconducting one. Moreover, we can also see that the critical temperature \(T_{c}\) of the phase transition decreases as the unbalance parameter \(\beta \) increases, which is completely consistent with the result of Fig. 1. As can be seen from the left panel of Fig. 3, the HEE in the superconducting phase is always less than the one in the normal case and drops as the temperature decreases. In contrast, as shown in the right panel of Fig. 3, when the temperature decreases to be lower than the critical value \(T_{c}\) , the values of HSC for the superconducting state is larger than that for the normal state and increases as the temperature decreases. This behavior of the HSC is similar to that found in the previous Refs. [38, 41].

We also give the HEE and HSC as functions of the temperature T for a large width \(\ell =8\) in Fig. 4. As shown in the picture, the slopes of HEE and HSC present again a discontinuous change at the critical temperatures \(T_{c}\). This means that both the HEE and HSC can be used to search for the critical phase transition temperature. Furthermore, for a large fixed width \(\ell \), the behavior of HSC as a function of the temperature is quite similar to the case of HEE, i.e., both the HEE and HSC in the superconducting phase are less than the ones in the normal case and drop as the temperature decreases. It should be noted that, this feature is consistent with the result of complexity for pure states in holographic superconductors discussed in Ref. [39].

The physical interpretations for behaviors of HEE are explicit, since the entanglement entropy is a measure of the degrees of freedom in the field theory, as the temperature decreases, the condensate turns on at the critical temperature and the formation of Cooper pairs suppresses of the degree of freedom of the system. The jump of the slop of HEE indicates that the system undergoes the second order phase transition. On the other hand, combining with the results of Figs. 3 and 4, we find that the HSC exhibits different behaviors as a function of the temperature for different fixed widths \(\ell \). It seems that the dependence of HSC on the temperature in holographic superconducting systems is not universal. In fact, for the HSC in two different operators, similar phenomena have also been found in the Refs. [42, 43], but the underlying mechanism is still unclear.

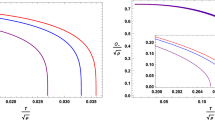
It should be noted that since the different behaviors of HSC for different fixed widths, and our choice of widths is arbitrary, a question arises: Are there certain specific parameter choices that make it difficult for us to observe the phase transition of this system through the HSC approach? With more calculations, we find that the behavior of HSC does indeed have a slow change process as the width \(\ell \) increases. For each selected unbalance parameter \(\beta \), we give the corresponding example and show the results in Fig. 5. As shown in the figure, for each set of parameters, we find that the HSC and its slope are continuous around the critical temperature. In particular, from the left panel of Fig. 5, we can see that the HSC in the superconducting phase has a non-monotonic behavior. This means that for some specific parameters, we cannot read the critical temperature of the phase transition directly form the plot of HSC. From this perspective, although both the HEE and HSC can be used as probes for holographic superconducting phase transitions, the HEE is the one that performs better.

Fig. 5
figure 5

The HSC as a function of the temperature T for various widths and different values of the unbalance parameter \(\beta \). The panels from left to right represent the cases: (1) \(\ell =4.1\,,\beta =0\) (left); (2) \(\ell =4.5\,,\beta =1\) (middle); (3) \(\ell =6\,,\beta =1.5\) (right)

Full size image

To get further understanding of the effect of the unbalance parameter on the HEE and HSC for different widths \(\ell \) , we plot the corresponding results in Figs. 6 and 7 with a fixed temperature \(T=0.04\), which is below the critical temperature \(T_{c}\). Correspondingly, we find that in Fig. 6, the HEE in the superconducting phase always increases with the increase of the unbalance parameter \(\beta \) for each fixed width \(\ell \). This is reasonable because as the chemical imbalance increases, the critical temperature of the system decreases and the scalar condensation is more difficult to form, which results in less Cooper pairs available. However, we find that for different widths, the effect of the unbalance parameter \(\beta \) on the HSC in the superconducting phase has three different behaviors. The specific examples are shown in Fig. 7. For small subregions (\(\ell =1\)), the HSC in the superconducting phase decreases monotonously with the increase of the unbalance parameter \(\beta \). When the subregion enlarges, the influence of the unbalance parameter \(\beta \) on HSC will exhibit a non-monotonic behavior, e.g., for a fixed width \(\ell =2\), the HSC in the superconducting phase first decreases and reaches its minimum at some threshold as the unbalance parameter \(\beta \) increases, then increases monotonically. For large enough subregions (\(\ell =8\)), we find that the effect of the unbalance parameter \(\beta \) on the HSC is quite similar to the case of HEE, i.e., the HSC monotonously increases as the unbalance parameter \(\beta \) increases.

Fig. 6
figure 6

The HEE as a function of the unbalance parameter \(\beta \) for different widths \(\ell \) at \(T=0.04\). The left plot (red) is for \(\ell =1\), the middle one (green) for \(\ell =2\), and the right one (blue) for \(\ell =8\)

Full size image
Fig. 7
figure 7

The HSC as a function of the unbalance parameter \(\beta \) for different widths \(\ell \) at \(T=0.04\). The left plot (red) is for \(\ell =1\), the middle one (green) for \(\ell =2\), and the right one (blue) for \(\ell =8\)

Full size image

5 Summary and discussion

By using the subregion CV conjecture, in this paper, we have investigated the HSC in unbalanced holographic superconductors. We calculated the HSC of a straight strip subregion and compared it with the behaviors of the HEE, which shows that, near the critical temperature \(T_{c}\), both the HEE and HSC are continuous and the slopes in terms of the temperature have a jump. This jump of slope could be thought of as a signature of the phase transition and corresponds to the second order phase transition of the unbalanced superconducting system. From the results of HSC and HEE, we observed that as the unbalance parameter \(\beta \) increases, the critical temperature of the phase transition decreases. Our results indicates that both the HEE and HSC precisely captures the information about the phase transitions, i.e., both of them can be used as good probes to the phase transition in unbalanced holographic superconductors.

We observed that HEE and HSC show similar linear growth behavior with the increase of width \(\ell \) when the size of the subregion was large. Furthermore, we found that the HEE in the superconducting phase is always less than the one in the normal case and drops as the temperature goes down. However, for different fixed widths, the HSC in the superconducting phase can exhibit completely different behaviors with the change of temperature. In particular, for given unbalance parameters, we have found the corresponding examples, which proves that there are certain specific parameter choices that make it difficult for us to see the obvious change in the slope of HSC near the critical temperature. Therefore, compared with HSC, HEE can be more efficient to probe the critical temperature of phase transition in unbalanced holographic superconductor. On the other hand, we found that the HEE is always monotonically increasing with the increase of the unbalance parameter, while the HSC displays more diverse behaviors on the influence of the unbalance parameter. This implies that, as another independent probe to phase transition in holographic superconductor models, the HSC has the potential to offer richer physical information. Thus, the physical origins of these phenomena and deep insight from the field theory side deserve further study.

It is worth noting here that only the second order phase transition is involved in this unbalanced holographic superconductor model. It is interesting to study HSC in other holographic superconductor models with first order phase transition. In addition, in this work, we focused on the subregion CV conjecture only, but it will be interesting to study the complexity of holographic superconductor by the CA conjecture, and compare the results form the two conjectures. We wish to report on the related works in future.