1 Introduction

There are different models for nonlinear electrodynamics. The first such model, known as Born-Infeld (BI) nonlinear electrodynamics, which is fully relativistic and gauge-invariant, was proposed by Max Born and Leopold Infeld in 1934 [1,2,3]. The initial idea was to modify Maxwell’s linear Lagrangian i.e., \(\mathcal {L}=-F_{\mu \nu }F^{\mu \nu }\) to construct a nonlinear Lagrangian with respect to Maxwell’s invariants \(\mathcal {S} =F_{\mu \nu }F^{\mu \nu }\) and \(\mathcal {P}=F_{\mu \nu }\tilde{F}^{\mu \nu }\) such that the self-energy and the fields of a point charge remain finite at the location of the charge. Furthermore, the vacuum polarization phenomena in quantum electrodynamics (QED) has been observed experimentally since the 1940s. It is the polarization of virtual electron-positron pairs in vacuum that is an indication for the nonlinear interaction of electromagnetic fields such as photon-photon scattering. The interaction between photons can be explained using the so-called Heisenburg–Euler (HE) effective-field theory. The HE model was proposed by W. Heisenburg and H. Euler in 1936 [4] and is valid in the weak-field limit and large wavelengths. There are other nonlinear electrodynamic models that have been introduced more recently. For instance, the Logarithmic [5], the Maxwell Power Law [6,7,8,9], the arcsin [10], the rational [11, 12], the exponential [13,14,15] and the double-Logarithmic [16] models are among them which all reproduce Maxwell’s linear model in the weak-field limit except the Maxwell Power Law. Furthermore, there are NED models that don’t reduce to the linear one in the weak-filed limit. Such models have been coupled to Einstein’s theory for constructing regular electric black holes [17, 18]. As it was proved by Bronnikov [19], unlike the existence of a regular magnetic black hole, a regular electric black hole solution doesn’t exist in the gravity coupled with a NED which yields Maxwell’s theory in the weak-field limit.

In general, a generic NED model does not admit the symmetries of Maxwell’s theory. Among them are preserving conformal and SO(2) duality-rotation invariance symmetries. In Ref. [20] a NED model has been introduced which respects these symmetries (see Eq. (1) below). In this interesting model, there is also a constant \(\gamma ,\) which is, in accordance with [20, 21], a positive parameter. In this study, we would like to apply the so-called causality and unitarity principles for making an estimation for the upper bound of the parameter \(\gamma \). We would also like to examine the effects of this parameter in the physical properties of the black hole solution in the context of gravity coupled with this specific NED model. Since the black hole is a dyonic solution, it is worth mentioning that such solutions have already been found in the literature. In [22,23,24,25], dyonic black holes (DBH) are found in string theory and in [26] DBH is found in gravity rainbow. Also, DBH in dilatonic gravity and in nonlinear electrodynamics coupled with gravity have been introduced in [27,28,29,30,31], respectively.

Finally, we would like to add that it is the conformal invariant symmetry of the Maxwell theory which results in a traceless energy-momentum tensor, i.e., \(T_{\mu }^{\mu }=0.\) The same symmetry in a NED field theory also yields a traceless energy-momentum tensor. This fact has been studied in [6] as well as in [32,33,34,35].

Our Letter is organized as follows. In Sect. 2 we present the NED model that admits conformal and SO(2) duality-rotation invariance symmetries. In Sect. 3 we find the black hole solution of the gravity minimally coupled with this NED. In Sect. 4 we study the thermal stability of the solution. We conclude our work in Sect. 5.

2 The Model

The nonlinear Maxwell’s Lagrangian is given by

$$\begin{aligned} \mathcal {L}\left( \mathcal {S},\mathcal {P}\right) =-\mathcal {S}\cosh \gamma + \sqrt{\mathcal {S}^{2}+\mathcal {P}^{2}}\sinh \gamma \end{aligned}$$
(1)

which has been first proposed in [20] and then re-proposed in [21]. Considering the electromagnetic two-form, given by

$$\begin{aligned} \mathbf {F}=\frac{1}{2}F_{\mu \nu }dx^{\mu }\wedge dx^{\nu } \end{aligned}$$
(2)

in which

$$\begin{aligned} F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu } \end{aligned}$$
(3)

is the electromagnetic field tensor and

$$\begin{aligned} \mathbf {A}=A_{\mu }dx^{\mu } \end{aligned}$$
(4)

is the gauge potential one-form, the Maxwell invariants are defined to be \( \mathcal {S}=F_{\mu \nu }F^{\mu \nu }\) and \(\mathcal {P}=F_{\mu \nu }\tilde{F} ^{\mu \nu }\) where

$$\begin{aligned} {\tilde{\mathbf {F}}}=\frac{1}{2}\tilde{F}_{\mu \nu }dx^{\mu }\wedge dx^{\nu } \end{aligned}$$
(5)

is the Hodge dual two-form of \(\mathbf {F}\) with \(\tilde{F}^{\mu \nu }=\frac{1 }{2}\epsilon ^{\mu \nu \alpha \beta }F_{\alpha \beta }.\) In accordance with [20] and [21], \(\gamma \) is a positive parameter, however, we would like to see its possible upper bound by applying the causality and unitarity conditions. Under the causality principle, the group velocity of the elementary electromagnetic excitations should be less than the speed of light in the vacuum and therefore there will be no tachyons in the theory spectrum. Also, the unitarity principle requires the positive definiteness of the norm of every elementary excitation of the vacuum upon which ghosts are avoided. To obtain the necessary conditions imposed on any NED due to the casualty and unitarity principles, basically one should study the propagation of an electromagnetic wave in a spacetime filled with a background electromagnetic field that is constant in time and space. In Ref. [36], the corresponding dispersion relation for a general NED Lagrangian has been found. In Ref. [37], a simplified version of the former reference has been considered where the background electromagnetic field was either purely electric or purely magnetic with \( \mathcal {P}=0\). In this configuration, due to the phenomenon known as birefringence, the propagating electromagnetic wave splits into two orthogonal propagating modes. The requirement constraints found in [37], are applied to each of these modes and are given in terms of some inequality relations as

$$\begin{aligned} \mathcal {L}_{\mathcal {S}}\le 0,\mathcal {L}_{\mathcal {SS}}\ge 0,\mathcal {L} _{\mathcal {PP}}\ge 0 \end{aligned}$$
(6)

and

$$\begin{aligned} \mathcal {L}_{\mathcal {S}}+2\mathcal {SL}_{\mathcal {SS}}\le 0,2\mathcal {SL}_{ \mathcal {PP}}-\mathcal {L}_{\mathcal {S}}\ge 0. \end{aligned}$$
(7)

Redefining \(\mathcal {L}\left( \mathcal {S},\mathcal {P}\right) =-\mathcal {S} y\left( z\right) \) with

$$\begin{aligned} y\left( z\right) =\cosh \gamma -sgn\left( \mathcal {S}\right) \sqrt{1+z^{2}} \sinh \gamma \end{aligned}$$
(8)

and \(z=\frac{\mathcal {P}}{\mathcal {S}},\) these inequalities reduce to

$$\begin{aligned} y-zy^{\prime }\ge 2y^{\prime \prime }\ge 0\text { } \end{aligned}$$
(9)

for \(\mathcal {S}<0\) and

$$\begin{aligned} y-zy^{\prime }\ge -2z^{2}y^{\prime \prime }\ge 0 \end{aligned}$$
(10)

for \(\mathcal {S}>0.\) Considering the explicit form of \(y\left( z\right) \) we find

$$\begin{aligned} y^{\prime }=-sgn\left( \mathcal {S}\right) \frac{z\sinh \gamma }{\sqrt{1+z^{2} }} \end{aligned}$$
(11)

and

$$\begin{aligned} y^{\prime \prime }=-sgn\left( \mathcal {S}\right) \frac{\sinh \gamma }{\left( 1+z^{2}\right) ^{3/2}}. \end{aligned}$$
(12)

Clearly, with \(\gamma >0,\) \(y^{\prime \prime }\) is definite-positive and definite-negative for \(\mathcal {S}<0\) and \(\mathcal {S}>0,\) respectively. Hence, (9) and (10) reduce to \(y-zy^{\prime }-2y^{\prime \prime }\ge 0\) for \(\mathcal {S}<0\) and \(y-zy^{\prime }+2z^{2}y^{\prime \prime }\ge 0\) for \( \mathcal {S}>0,\) respectively. In Fig. 1 we plot \(K=y-zy^{\prime }+2z^{2}y^{\prime \prime }\) in terms of z for different values of \(\gamma . \) Our numerical calculation shows that for \(\mathcal {S}>0\), (10) is satisfied provided \(0<\gamma <\gamma _{\max }=\tanh ^{-1}\left( \frac{\sqrt{2 }}{2}\right) .\) A similar numerical calculation reveals that for \(\mathcal {S} <0\), (9) is satisfied provided \(0<\gamma <\infty .\) Therefore, in order to satisfy all conditions with \(\mathcal {S}>0\) and \(\mathcal {S}<0\), we impose \(0<\gamma <\gamma _{\max },\) which is the intersection of the two individual intervals. It is worth mentioning that for systems with no magnetic charge/field such as the Hydrogen atom, \(\mathcal {P}=0\) upon which the Lagrangian reduces to the linear Maxwell’s theory provided \(\gamma =0\).

Finally, at the end of this section, we conclude that \(\gamma \) which is a dimensionless parameter of the theory has to be bounded from above as well as from below i.e., \(0<\gamma <\gamma _{\max }\). Therefore, through the rest of the paper, we shall consider \(\gamma \) to be in this interval.

Fig. 1
figure 1

Plot of \(K=y-zy^{\prime }+2z^{2}y^{\prime \prime }\) in terms of \(z=\frac{ \mathcal {P}}{\mathcal {S}}\) for \(\gamma =0.0000\) to \(\gamma =1.0000\) with equal steps (\(=0.1000\)) from top to bottom. K remains positive as long as \( \gamma <\tanh ^{-1}\left( \frac{\sqrt{2}}{2}\right) \)

Full size image

3 The field equations and the black hole solution

The action of Einstein-nonlinear-Maxwell theory is given by (\(8\pi G=1\))

$$\begin{aligned} I=\frac{1}{2}\int \sqrt{-g}d^{4}x\left( \mathcal {R}+\mathcal {L}\left( \mathcal {S},\mathcal {P}\right) \right) \end{aligned}$$
(13)

in which \(\mathcal {L}\left( \mathcal {S},\mathcal {P}\right) \) is given by Eq. (1). Upon applying the causality and unitarity conditions we have already obtained an upper limit for \(\gamma \) i.e., \(\gamma <\tanh ^{-1}\left( \frac{\sqrt{2}}{2}\right) .\) Moreover,

$$\begin{aligned} \lim _{\gamma \rightarrow 0}\mathcal {L}\left( \mathcal {S},\mathcal {P}\right) =-\mathcal {S}, \end{aligned}$$
(14)

which is the linear Maxwell theory, however, it isn’t the weak-field limit of the Lagrangian (1). The static spherically symmetric spacetime and the electromagnetic two-form are chosen to be

$$\begin{aligned} ds^{2}=-\psi \left( r\right) dt^{2}+\frac{dr^{2}}{\psi \left( r\right) } +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) \end{aligned}$$
(15)

and

$$\begin{aligned} \mathbf {F}=Edt\wedge dr+Br^{2}\sin \theta d\theta \wedge d\phi , \end{aligned}$$
(16)

respectively, in which E and B are the radial components of the static electric and magnetic fields indicating the presence of the electric and magnetic monopoles. Variation of the action with respect to the metric tensor implies the Einstein-nonlinear Maxwell equations given by

$$\begin{aligned} G_{\mu }^{\nu }=T_{\mu }^{\nu } \end{aligned}$$
(17)

in which

$$\begin{aligned} T_{\mu }^{\nu }=\frac{1}{2}\left( \left( \mathcal {L}-\mathcal {PL}_{\mathcal {P }}\right) \delta _{\mu }^{\nu }-4\mathcal {L}_{\mathcal {S}}F_{\mu \lambda }F^{\nu \lambda }\right) \end{aligned}$$
(18)

is the energy-momentum tensor and \(G_{\mu }^{\nu }\) is the standard Einstein’s tensor. We note that, \(\mathcal {L}_{\mathcal {S}}=\frac{\partial \mathcal {L}}{ \partial \mathcal {S}}\) and \(\mathcal {L}_{\mathcal {P}}=\frac{\partial \mathcal {L}}{\partial \mathcal {P}}.\) Furthermore, the variation of the action with respect to the four-potential yields the Maxell-nonlinear equations

$$\begin{aligned} d\left( \mathcal {L}_{\mathcal {S}}{\tilde{\mathbf {F}}}+\mathcal {L}_{\mathcal {P}} \mathbf {F}\right) =0 \end{aligned}$$
(19)

where \({\tilde{\mathbf {F}}}\) is the dual two-form of \(\mathbf {F}\) which is found to be

$$\begin{aligned} {\tilde{\mathbf {F}}}=-Bdt\wedge dr+Er^{2}\sin \theta d\theta \wedge d\phi . \end{aligned}$$
(20)

Having, \(\mathbf {F}\) and \({\tilde{\mathbf {F}}}\) given by (16) and (20) we obtain

$$\begin{aligned} \mathcal {S}=2\left( B^{2}-E^{2}\right) \end{aligned}$$
(21)

and

$$\begin{aligned} \mathcal {P}=4EB, \end{aligned}$$
(22)

upon which, the Maxell-nonlinear equations (19) reduce to the following two individual equations

$$\begin{aligned} d\left( \left( -\mathcal {L}_{\mathcal {S}}B+\mathcal {L}_{\mathcal {P}}E\right) dt\wedge dr\right) =0 \end{aligned}$$
(23)

and

$$\begin{aligned} d\left( \left( \mathcal {L}_{\mathcal {S}}E+\mathcal {L}_{\mathcal {P}}B\right) r^{2}\sin \theta d\theta \wedge d\phi \right) =0. \end{aligned}$$
(24)

From the Bianchi identity, i.e.,

$$\begin{aligned} d\mathbf {F=0} \end{aligned}$$
(25)

which implies

$$\begin{aligned} d\left( Edt\wedge dr+Br^{2}\sin \theta d\theta \wedge d\phi \right) =0, \end{aligned}$$

one finds that both radial fields i.e., E and B,  and consequently the invariants \(\mathcal {S}\) and \(\mathcal {P}\) should be only functions of r. Hence, (23) is trivially satisfied and (24) suggests

$$\begin{aligned} \left( \mathcal {L}_{\mathcal {S}}E+\mathcal {L}_{\mathcal {P}}B\right) r^{2}=c \end{aligned}$$
(26)

in which c is an integration constant. Furthermore, the Bianchi identity implies that,

$$\begin{aligned} B=\frac{Q_{m}}{r^{2}} \end{aligned}$$
(27)

where \(Q_{m}\) is an integration constant representing the magnetic charge. Considering, (27) and (26) together with the Maxwell’s invariants, one obtains

$$\begin{aligned} E=\frac{Q_{e}}{r^{2}} \end{aligned}$$
(28)

in which \(Q_{e}\) is a constant representing the electric charge, satisfying

$$\begin{aligned} \left( zQ_{e}-Q_{m}\right) y^{\prime }-Q_{e}y=c \end{aligned}$$
(29)

with

$$\begin{aligned} z=\frac{\mathcal {P}}{\mathcal {S}}=\frac{2Q_{e}Q_{m}}{Q_{m}^{2}-Q_{e}^{2}} \end{aligned}$$
(30)

which is a constant. The explicit form of Maxwell’s invariants are given by

$$\begin{aligned} \mathcal {S}=2\frac{Q_{m}^{2}-Q_{e}^{2}}{r^{4}} \end{aligned}$$
(31)

and

$$\begin{aligned} \mathcal {P}=\frac{4Q_{m}Q_{e}}{r^{4}}. \end{aligned}$$
(32)

Following the nonlinear-Maxwell equations, we shall solve the Einstein-nonlinear Maxwell equations. To do so, we find the nonzero components of the energy momentum-tensor given by

$$\begin{aligned} T_{t}^{t}= & {} T_{r}^{r}=\frac{1}{2}\left[ \left( \mathcal {L}-\mathcal {PL}_{ \mathcal {P}}\right) +4\mathcal {L}_{\mathcal {S}}E^{2}\right] \nonumber \\= & {} \left( y^{\prime }z-y\right) \frac{Q_{m}^{2}+Q_{e}^{2}}{r^{4}} \end{aligned}$$
(33)

and

$$\begin{aligned} T_{\theta }^{\theta }= & {} T_{\phi }^{\phi }=\frac{1}{2}\left[ \left( \mathcal {L}- \mathcal {PL}_{\mathcal {P}}\right) -4\mathcal {L}_{\mathcal {S}}B^{2}\right] \nonumber \\= & {} -\left( y^{\prime }z-y\right) \frac{Q_{m}^{2}+Q_{e}^{2}}{r^{4}}. \end{aligned}$$
(34)

Using a fluid model for the energy momentum tensor i.e., \(T_{\mu }^{\nu }=diag\left( -\rho ,p_{r},p_{\theta },p_{\phi }\right) \) one finds

$$\begin{aligned} \rho =\left( y-zy^{\prime }\right) \frac{Q_{m}^{2}+Q_{e}^{2}}{r^{4}} =-p_{r}=p_{\theta }=p_{\phi }. \end{aligned}$$
(35)

Having,

$$\begin{aligned} y-zy^{\prime }=\cosh \gamma \left( 1-\frac{sgn\left( \mathcal {S}\right) \tanh \gamma }{\sqrt{1+z^{2}}}\right) , \end{aligned}$$
(36)

which is definite-positive for all values of \(0<\gamma <\gamma _{\max },\) \( \mathcal {S}\) and z,  we obtain \(\rho \ge 0\) and \(\rho +p_{i}\ge 0\) which in turn imply that the weak energy conditions are satisfied. Furthermore, the strong energy conditions i.e., \(\rho +p_{i}\ge 0\) and \(\rho +\sum _{i}p_{i}\ge 0\) are also satisfied.

Next, we introduce

$$\begin{aligned} \omega ^{2}=y-zy^{\prime }=\cosh \gamma \left( 1-\frac{1-q^{2}}{1+q^{2}} \tanh \gamma \right) , \end{aligned}$$
(37)

which is definite-positive with \(q^{2}=\frac{Q_{e}^{2}}{Q_{m}^{2}}\). This is because of the causality and unitarity conditions upon which we imposed \( 0<\gamma <\gamma _{\max }\). Hence, the energy momentum-tensor simplifies as

$$\begin{aligned} T_{\mu }^{\nu }=\omega ^{2}\frac{Q_{m}^{2}+Q_{e}^{2}}{r^{4}}diag\left( -1,-1,1,1\right) . \end{aligned}$$
(38)

Finally, the Einstein-nonlinear-Maxwell equations admit

$$\begin{aligned} \psi \left( r\right) =1-\frac{2M}{r}+\omega ^{2}\frac{Q_{m}^{2}+Q_{e}^{2}}{ r^{2}} \end{aligned}$$
(39)

in which M is an integration constant, representing the mass of the black hole. This is a dyonic Reissner–Nordström-type [38, 39] charged black hole solution with an additional parameter \(\gamma .\) Hence, the general properties of (39), are similar to RN black hole. In the next section, we study the effects of the parameter \(\gamma \) in the thermal stability of the black hole. For the thermodynamic theory of black holes including RN, we refer to [40] while for the phase transition in RN black hole we refer to [41,42,43,44].

Fig. 2
figure 2

The Hawking temperature \(4\pi Q_{m}T_{H}\) in terms of \(x=\frac{r_{h}}{Q_{m}}\) for \(\gamma =0.0000\) to \(\gamma =\tanh ^{-1}\left( \frac{\sqrt{2}}{2}\right) \) with equal steps (from bottom to top) and \(\left( \frac{Q_{e}}{Q_{m}} \right) =0.2 \)

Full size image
Fig. 3
figure 3

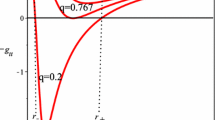
The heat capacity \(C_{Q}/Q_{m}^{2}\) in terms of \(x=\frac{r_{h}}{Q_{m}}\) for \( \gamma =0.0000\) to \(\gamma =\tanh ^{-1}\left( \frac{\sqrt{2}}{2}\right) \) with equal steps (from bottom to top) and \(\left( \frac{Q_{e}}{Q_{m}}\right) =0.2.\) Please note that, the second branch of the heat capacity is not depicted

Full size image

4 Thermal Stability of the black hole solution

To investigate the effects of the parameter \(\gamma \) in the thermal stability of the black hole solution (39) we start with the Hawking temperature which is given by

$$\begin{aligned} T_{H}=\frac{\psi ^{\prime }\left( r_{h}\right) }{4\pi }=\frac{1}{4\pi r_{h}} \left( 1-\frac{\omega ^{2}Q^{2}}{r_{h}^{2}}\right) \end{aligned}$$
(40)

in which \(r_{h}\) is the radius of the event horizon and \( Q^{2}=Q_{m}^{2}+Q_{e}^{2}\). In Fig. 2, we plot the \(4\pi Q_{m}T_{H}\) versus \( x=\frac{r_{h}}{Q_{m}}\) with \(\frac{Q_{e}}{Q_{m}}=0.2\) and \(\gamma =0\) to \( \gamma =\gamma _{\max }\) with equal steps. Increasing the value of \(\gamma ,\) for a given radius of the event horizon, increases the Hawking temperature. Furthermore, the heat capacity for constant Q is defined to be

$$\begin{aligned} C_{Q}=\left( T_{H}\frac{\partial S}{\partial T_{H}}\right) _{Q}=-\frac{2\pi r_{h}^{2}\left( r_{h}^{2}-\omega ^{2}Q^{2}\right) }{r_{h}^{2}-3\omega ^{2}Q^{2}} \end{aligned}$$
(41)

where \(S=\pi r_{h}^{2}\) is the entropy of the black hole. In Fig. 3 we plot \( C_{Q}/Q_{m}^{2}\) with respect to \(x=\frac{r_{h}}{Q_{m}}\) with \(\frac{Q_{e}}{ Q_{m}}=0.2\) and \(\gamma =0\) to \(\gamma =\gamma _{\max }\) with equal steps. The Type-1 (\(C_{Q}=0\)) and Type-2 (\(C_{Q}\rightarrow \pm \infty \)) transition points are emphasized. These points are given by

$$\begin{aligned} \left( r_{h}\right) _{Type-1}=\omega Q \end{aligned}$$
(42)

and

$$\begin{aligned} \left( r_{h}\right) _{Type-2}=\sqrt{3}\omega Q. \end{aligned}$$
(43)

Let’s add that the thermal stability region is defined to admit both \(T_{H}\) and \(C_{Q}\) positive. Therefore, the black hole is thermally stable if \( \left( r_{h}\right) _{Type-1}<r_{h}<\left( r_{h}\right) _{Type-2}.\) For the specific value of \(\frac{Q_{e}}{Q_{m}}=0.2\) it is observed from Fig. 3 that, the transition points are shifted to the smaller values for the larger \(\gamma \) which in turn yields a narrower stability region.

Fig. 4
figure 4

Plots of \(\omega \) with respect to \(\gamma \) for various value of \(q=\frac{ Q_{e}}{Q_{m}}=0\ldots 2\) with equal steps. The dashed curve is for the particular \(q=0.7\) and the three regions colored with green (left), white (middle), and light-blue (right) imply \(\omega \) decreasing and less than 1, increasing and less than 1, and increasing and greater than 1, respectively. For \(q\ge 1,\) the curve of \(\omega \) is increasing with respect to \(\gamma \). These curves are depicted above the sign of \(q=1 \)

Full size image

For the sake of completeness, we give a general overview of the stability region. In Figs. 2 and 3, the value of q was set to 0.2,  however, for larger q the configuration changes. Let’s define the width of the stability region to be

$$\begin{aligned} \triangle r_{h}=\left( r_{h}\right) _{Type-2}-\left( r_{h}\right) _{Type-1}=\left( \sqrt{3}-1\right) \omega Q. \end{aligned}$$
(44)

In Fig. 4 we plot \(\omega \) versus \(\gamma \) for the various value of \( q=0...2\). It can be seen from Fig. 4 that the width of the region of stability \(\triangle r_{h}\) depends not only on \(\gamma \) but also on q. For \(q=0.2,\) that we plot the corresponding \(T_{H}\) and \(C_{Q}\) in Figs. 2 and 3, \(\omega \) is a decreasing function in the interval \(0<\gamma <\gamma _{\max }.\) Hence, we concluded that the region of stability decreases with the increment of \(\gamma .\) Our detailed calculation reveals that \(\omega \) admits a minimum at \(\gamma _{crit}=\ln \frac{1}{q}\) and becomes zero at \( \gamma _{0}=2\gamma _{crit}.\) For \(q<\frac{1}{1+\sqrt{2}}\), both \(\gamma _{crit}\) and \(\gamma _{0}\) remain outside of the domain of \(\gamma \) such that with an increment in \(\gamma \) the width of stability becomes smaller. For \(\frac{1}{1+\sqrt{2}}<q<\frac{1}{\sqrt{1+\sqrt{2}}},\) only \(\gamma _{crit}\) falls in the domain of \(\gamma <\gamma _{\max }\) and consequently the width of the stability region first decreases and then increases, even though it remains less than the corresponding RN case. Finally, if \(\frac{1}{ \sqrt{1+\sqrt{2}}}<q<1\) then both \(\gamma _{crit}\) and \(\gamma _{0}\) remain in the domain of acceptable \(\gamma .\) Hence, \(\triangle r_{h}\) first decreases with \(\gamma<\) \(\gamma _{crit}\) then increases and remains less than one with \(\gamma <\gamma _{0}\) and finally increases to the values greater than the corresponding RN case with \(\gamma _{0}<\gamma <\gamma _{\max }.\) In Fig. 4, these three regions of \(\gamma \) are shown with different shaded colors for a particular \(q=0.7.\) Furthermore, for \(q\ge 1,\) the graph of \(\omega \) versus \(\gamma \) is an increasing function, which indicates that the width of the stability region increases. For this fact, we refer to the curves after \(q=1\) in Fig. 4.

5 Conclusion

We re-examined the recently introduced conformal and SO(2) duality-rotation invariance NED model, given in Eq. (1). The same model has also been used in two very recent papers [45, 46] to study NUT wormholes, Taub-Bolt instantons, black holes, and exact gravitational waves. We applied the unitarity and casualty conditions to find an upper bound for the arbitrarily dimensionless constant \(\gamma \) in the theory. Following our results, the domain of \(\gamma \) has been found to be \(0<\gamma <\gamma _{\max }=\tanh ^{-1}\left( \frac{\sqrt{2}}{2}\right) \). Furthermore, we minimally coupled this particular NED with Einstein’s gravity. From the field equations, we obtained a Reissner–Nordström-type charged black hole solution with a new extra parameter, i.e., \(\gamma \). Let’s note that \(\omega ^{2}=\cosh \gamma -\frac{1-q^{2}}{1+q^{2}}\sinh \gamma \) represents \(\gamma \) in our investigation. The effects of \(\gamma \) on the physical properties of the black hole solutions have been investigated. The thermal stability of the black hole, specifically, has been studied. The results have been demonstrated in Figs. 2, 3, and 4. In accordance with our analysis, for \(0<q<1\) the stability region may increase or decrease depending on the value of q and \(\gamma \). However, for \(q\ge 1,\) the stability region increase with \(\gamma \).