From oscillation dip to oscillation valley in atmospheric neutrino experiments

Abstract

Atmospheric neutrino experiments can show the “oscillation dip” feature in data, due to their sensitivity over a large L/E range. In experiments that can distinguish between neutrinos and antineutrinos, like INO, oscillation dips can be observed in both these channels separately. We present the dip-identification algorithm employing a data-driven approach – one that uses the asymmetry in the upward-going and downward-going events, binned in the reconstructed L/E of muons – to demonstrate the dip, which would confirm the oscillation hypothesis. We further propose, for the first time, the identification of an “oscillation valley” in the reconstructed ($E_\mu$,$\,\cos \theta _\mu$) plane, feasible for detectors like ICAL having excellent muon energy and direction resolutions. We illustrate how this two-dimensional valley would offer a clear visual representation and test of the L/E dependence, the alignment of the valley quantifying the atmospheric mass-squared difference. Owing to the charge identification capability of the ICAL detector at INO, we always present our results using $\mu ^{-}$ and $\mu ^{+}$ events separately. Taking into account the statistical fluctuations and systematic errors, and varying oscillation parameters over their currently allowed ranges, we estimate the precision to which atmospheric neutrino oscillation parameters would be determined with the 10-year simulated data at ICAL using our procedure.

1 Introduction and motivation

We have witnessed remarkable developments in neutrino physics over the last two decades, driven by the astonishing discovery of “neutrino mass-induced flavor oscillation” suggesting that neutrinos have non-degenerate mass and they mix with each other [1, 2]. Due to these two unique features, neutrinos change their flavor as they move in space and time implying that leptonic flavors are not symmetries of Nature [3]. Such a path-breaking discovery of fundamental significance, recently recognized with the Nobel Prize [4], has created enormous interest in the global neutrino community to measure the fundamental oscillation parameters with much better precision [5]. Such measurements of neutrino oscillations parameters are essential to provide a stringent test of the standard three-flavor neutrino oscillation framework, which has six fundamental parameters: (i) the solar mass-squared difference, $\Delta m^2_{21}$ ($\equiv m_2^2 - m_1^2 \approx 7.4 \times 10^{-5}$ $\hbox {eV}^2$), (ii) the solar mixing angle, $\theta _{12} \approx 34^\circ$, (iii) the atmospheric mass-squared difference, $|\Delta m^2_{32}|$ ($\equiv |m_3^2 - m_2^2| \approx 2.5 \times 10^{-3}$ $\hbox {eV}^2$), (iv) the atmospheric mixing angle, $\theta _{23} \approx 48^\circ$, (v) the reactor mixing angle, $\theta _{13} \approx 8.6^\circ$, and (vi) the Dirac CP phase, $\delta _{\mathrm{CP}}$, which at present lies in the third quadrant with large uncertainty.

It is quite remarkable to see that starting from almost no knowledge of the neutrino masses or lepton mixing parameters twenty years ago, we have been able to construct a robust, simple, three-flavor oscillation framework which successfully explains most of the data [6,7,8,9]. Atmospheric neutrino experiments have contributed significantly to achieve this milestone [10, 11] by providing an avenue to study neutrino oscillations over a wide range of energies ($E_\nu$ in the range of $\sim 100$ MeV to a few hundreds of GeV) and baselines ($L_\nu$ in the range of a few km to more than 12,000 km) in the presence of Earth’s matter with a density varying in the range of 0 to 10 $\hbox {g}/\hbox {cm}^3$.

An important breakthrough in the saga of atmospheric neutrinos came in 1998 when the pioneering Super-Kamiokande (Super-K) experiment reported convincing evidence for neutrino oscillations in atmospheric neutrinos by observing the zenith angle (this angle is zero for vertically downward-going events) dependence of $\mu$-like and e-like events [12]. The data accumulated by the Super-K experiment, based on an exposure of 33 kt$\cdot$yr, showed a clear deficit of upward-going events in the zenith angle distributions of $\mu$-like events with a statistical significance of more than $6\sigma$, while the zenith angle distribution of e-like events did not show any significant up–down asymmetry. These crucial observations by the Super-K experiment were successfully interpreted in a two-flavor scenario assuming oscillation between $\nu _\mu$ and $\nu _\tau$, leading to the disappearance of $\nu _\mu$. In this scenario, the survival probability of $\nu _\mu$ can be expressed in the following simple fashion:

$$\begin{aligned} P(\nu _\mu \rightarrow \nu _\mu )&= 1 - \sin ^2 2\theta _{23} \cdot \nonumber \\&\quad \sin ^2 \left( {1.27 \cdot |\Delta m^2_{32}| \left( \text{ eV}^2\right) \cdot {L_\nu \left( \text{ km }\right) \over E_\nu \left( \text{ GeV }\right) }}\right) .\nonumber \\ \end{aligned}$$

(1)

Due to the hierarchies in neutrino mass pattern ($\Delta m^2_{21} \ll |\Delta m^2_{32}|$) and in mixing angles ($\theta _{13} \ll \theta _{12}, \theta _{23}$), the above simple two-flavor $\nu _\mu$ survival probability expression was sufficient to explain the following broad features of the Super-K atmospheric data, providing a solution of the long-standing atmospheric neutrino anomaly in terms of “neutrino mass-induced flavor oscillations”.

• Around 50% of upward-going muon neutrinos disappear after traveling long distances. For very long baselines, the above $\nu _\mu$ survival probability expression (see Eq. 1) approaches $1 - (1/2)\sin ^22\theta _{23}$ and the observed survival probability becomes close to 0.5, suggesting that the mixing angles is close to the maximal value of 45$^\circ$.

• The disappearance of $\nu _\mu$ events starts for the zenith angle close to the horizon indicating that the oscillation length should be around $\sim$ 400 km for neutrinos having energies close to 1 GeV. This suggests that the atmospheric mass-squared difference, $|\Delta m^2_{32}|$ should be around $\simeq 10^{-3}$ $\hbox {eV}^2$.

• There is no visible excess or deficit of electron neutrinos. It suggests that the oscillations of muon neutrinos mainly occur due to $\nu _\mu \rightarrow \nu _\tau$ transitions.

• The Super-K experiment was also the first experiment to observe the sinusoidal L/E dependence of the $\nu _\mu$ survival probability [13]. A special analysis was performed by the Super-K collaboration, where they selected events with good resolution in L/E, largely excluding low-energy and near-horizon events. Using this high-resolution event sample, they took the ratio of the observed and expected event rates and the oscillation dip started to appear on the canvas around L/E $\sim$ 100 km/GeV, with the deepest location of the dip around L/E $\sim$ 500 km/GeV (see Fig. 4 in Ref. [13]). This study was quite useful to disfavor the other alternative models which showed different L/E behaviors. Note that the oscillation dip was also observed in the DeepCore data where the ratio of observed events to unoscillated Monte Carlo (MC) events is plotted against the reconstructed L/E of neutrino [14].

The proposed atmospheric neutrino detector Iron Calorimeter (ICAL) at the India-based Neutrino Observatory (INO) project aims to detect atmospheric neutrinos and antineutrinos separately over a wide range of energies and baselines. The performance of ICAL is optimized for the reconstructed muon energy ($E^{\mathrm{rec}}_\mu$) range of 1–25 GeV, and reconstructed baseline ($L^{\mathrm{rec}}_\mu$) from 15 to 12,000 km except around the horizon. Thus, the range of reconstructed $L^{\mathrm{rec}}_\mu /E^{\mathrm{rec}}_\mu$ of detected muon to which ICAL is sensitive, is from 1 km/GeV to around $10^4$ km/GeV. Therefore, we expect to see an oscillation dip (or two) as in Super-K. In this paper, we investigate the capability of the ICAL detector to reconstruct the oscillation dip in the reconstructed $L^{\mathrm{rec}}_\mu /E^{\mathrm{rec}}_\mu$ distribution of observed muon events. Moreover, it would be possible to identify the dip in $\mu ^-$ and $\mu ^+$ events separately, due to the muon charge identification capability of ICAL.

In contrast to the studies in [13, 14] where the ratio between data and unoscillated MC as a function of L/E was used, in this paper, we use the ratio between upward-going and downward-going events for the analysis. We exploit the fact that the downward-going atmospheric neutrinos and antineutrinos in multi-GeV energy range do not oscillate, and up-down asymmetry reflects the features mainly due to oscillations in upward-going events in these energies. The magnetic field in the ICAL detector enables us to study these distributions in neutrino and antineutrino oscillation channels separately. In this paper, we also discuss the procedure to measure the atmospheric mass-squared difference $|\Delta m^2_{32}|$ and the mixing angle $\theta _{23}$ using the information from the oscillation dip, and provide the results.

In this paper, we point out for the first time that there is an “oscillation valley” feature in the two-dimensional plane of reconstructed muon observables ($E_\mu ^\text {rec}$, $\cos \theta _\mu ^\text {rec}$) for $\mu ^-$ and $\mu ^+$ events separately at ICAL. The presence of valley-like feature in the oscillograms of survival probability of $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ in the plane of neutrino energy and direction is well known. But, it is not a priori obvious that the reconstructed energy and direction of muon will serve as a good proxy for the neutrino energy and direction, and will be able to reproduce this valley. In this work, we show that the reconstructed muon observables at ICAL preserve these features, which is a non-trivial statement about the fidelity of the detector.

The valley-like feature would be recognizable at ICAL due to its sensitivity to muons having energies in the wide range of 1 GeV to 25 GeV and excellent angular resolution at these energies (the muon energy resolution at ICAL is around $10\%$ to $15\%$, whereas the direction resolution is less than $1^\circ$ for multi-GeV muons with directions away from the horizon [15]). We show, using the complete migration matrices of ICAL for muon as obtained from GEANT4 simulation [15] that, due to the excellent energy and direction resolution, the oscillation valley in two-dimensional ($E_\mu ^\text {rec},\cos \theta _\mu ^\text {rec}$) plane would appear prominently at ICAL. We also demonstrate for the first time that the mass-squared difference may be determined using the alignment of the oscillation valley.

There are studies to measure the sensitivity of the ICAL detector for measuring the atmospheric oscillation parameters $|\Delta m^2_{32}|$ and $\theta _{23}$, see Refs.  [16,17,18,19,20,21]. ICAL would be able to determine these parameters separately in the neutrino and antineutrino channels [22, 23]. The difference between these analyses and our study is that Refs.  [16,17,18,19,20,21,22,23] employ the $\chi ^2$ method, while the focus of our study is to identify the oscillation dip and the oscillation valley, independently in $\mu ^-$ and $\mu ^+$ events, and determine the oscillation parameters from them. This is possible due to the wide range of energy and baselines reconstructed at ICAL with excellent detector properties. We also include statistical fluctuations, systematic uncertainties, and errors in other oscillation parameters while determining $|\Delta m^2_{32}|$ and $\theta _{23}$ with 10-year data at ICAL.

This paper is organized in the following fashion. In Sect. 2, we present the survival probabilities of neutrinos and antineutrinos as one-dimensional functions of $L_\nu /E_\nu$ and as two-dimensional oscillograms in $(E_\nu , \cos \theta _\nu )$ plane, to pinpoint the oscillation dips and the oscillation valley, respectively. For exploring these features in atmospheric neutrino and antineutrino data separately, we simulate $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ interactions at ICAL as discussed in Sect. 3. Next, in Sect. 4, we formulate a data-driven variable, the ratio between upward-going and downward-going events (U/D), to use it as an observable for all the analyses in this paper. We propose a novel algorithm to identify the oscillation dip and to measure its “location” in reconstructed $L^{\mathrm{rec}}_\mu /E^{\mathrm{rec}}_\mu$ distributions. We present the 90% C.L. range for $|\Delta m^2_{32}|$ expected with 500 kt$\cdot$yr exposure of ICAL using the calibration curve between the location of the dip and $|\Delta m^2_{32}|$. We also estimate the allowed range for $\sin ^2\theta _{23}$ at 90% C.L. using the ratio of upward-going and downward-going events (U/D). Section 5 is devoted to discuss our analysis of U/D distributions in reconstructed ($E^{\mathrm{rec}}_\mu , \cos \theta ^{\mathrm{rec}}_{\mu }$) plane. For identifying the oscillation valley in reconstructed ($E^{\mathrm{rec}}_\mu , \cos \theta ^{\mathrm{rec}}_{\mu }$) plane of these distributions and to measure the “alignment” of the valley, we suggest a unique algorithm and demonstrate its use. We present the 90% C.L. range of $|\Delta m^2_{32}|$ using 500 kt$\cdot$yr exposure of ICAL with the help of the calibration curve between the alignment of the valley and $|\Delta m^2_{32}|$. In Sect. 6, we summarize our findings and point out the utility of our novel approach in establishing the oscillation hypothesis in atmospheric neutrino experiments. In Appendix A, we explore the oscillation dip and oscillation valley with a relatively smaller exposure of 250 kt$\cdot$yr and show the 90% C.L. allowed ranges in $|\Delta m^2_{32}|$ from both the analysis procedures.

2 Neutrino oscillation probabilities

In this section, we discuss the survival probabilities of atmospheric $\nu _\mu$ and ${{\bar{\nu }}}_\mu$, reaching the detector after their propagation through the atmosphere and possibly the Earth. The oscillation probabilities are functions of energy ($E_\nu$) and zenith angle ($\theta _\nu$) of neutrino. The net distance $L_\nu$ traversed by a neutrino (its “baseline”) is related to its zenith angle via

$$\begin{aligned} L_\nu = \sqrt{(R+h)^2 - (R-d)^2\sin ^2\theta _\nu } \,-\, (R-d)\cos \theta _\nu \, ,\nonumber \\ \end{aligned}$$

(2)

where R, h, and d denote the radius of Earth, the average height from the surface at which neutrinos are produced, and the depth of the detector underground, respectively. In this study, we take $R = 6371$ km, $h = 15$ km, and $d=0$ km. Since $R \gg h \gg d$, the changes in the survival probabilities with small variations in h and d are negligible.

The survival probabilities may be represented in two ways: (i) as one-dimensional functions of $L_\nu /E_\nu$, and (ii) as two-dimensional oscillograms in the plane of energy and zenith angle. Below we discuss these two representations, and the major physics insights obtained via them.

2.1 $L_\nu /E_\nu$ dependence of $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ survival probabilities

Fig. 1

The survival probabilities of $\nu _\mu$ (left panel) and ${{\bar{\nu }}}_\mu$ (right panel) as functions of $L_\nu /E_\nu$, in the three-flavor neutrino oscillation framework in the presence of Earth matter (PREM profile [24]). Different colors represent different values of the neutrino zenith angle $\theta _\nu$ (or equivalently, the neutrino baseline $L_\nu$). We use the oscillation parameters given in Table 1

Figure 1 shows the survival probabilities for $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ as functions of $\log _{10}[L_\nu /E_\nu ]$ for different zenith angles for a benchmark set of oscillation parameters as shown in Table 1. It may be observed that at $\log _{10}[L_\nu /E_\nu ] \approx 2.7$, the first oscillation minimum appears for $\nu _\mu$ as well as for ${{\bar{\nu }}}_\mu$. For $L_\nu /E_\nu$ values smaller than the location of the first oscillation minimum, the survival probabilities for $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ are almost equal, and the overlapping nature of different $\cos \theta _\nu$ curves shows that there is no $\theta$-dependence beyond that coming from $L_\nu /E_\nu$. This is an indication that the survival probabilities are dominated by vacuum oscillations in this region. However for higher $L_\nu /E_\nu$ values, Earth matter effects introduce an additional $\theta$-dependence beyond that via $L_\nu /E_\nu$, which can be prominently seen for $\nu _\mu$ survival probability in the case of NO. Since matter effects on antineutrinos are not significant in NO, the ${{\bar{\nu }}}_\mu$ survival probability does not show this feature.

Table 1 The values of the benchmark oscillation parameters used in this analysis. These values are in good agreement with the current global fits [6,7,8,9]. Normal mass ordering corresponds to $m_1< m_2 < m_3$

Fig. 2

Oscillograms of survival probabilities of $\nu _\mu$ (left panel) and ${{\bar{\nu }}}_\mu$ (right panel) in the ($E_\nu$, $\cos \theta _\nu$) plane, using three-flavor neutrino oscillation framework in the presence of Earth matter (PREM profile [24]). We use the oscillation parameters given in Table 1

2.2 Oscillograms in ($E_\nu$, $\cos \theta _\nu$) plane

Figure 2 shows the survival probabilities of $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ in the ($E_\nu$, $\cos \theta _\nu$) plane, with NO as the neutrino mass ordering. In both the panels of Fig. 2, we can see the prominent dark diagonal band, which represents the minimum survival probability. This oscillation minimum region corresponds to the same “oscillation dip” as that earlier observed in Fig. 1 at $\log _{10}[L_\nu /E_\nu ] \approx 2.7$. Its nature in neutrino and antineutrino survival probabilities is almost identical, indicating that this region is dominated by vacuum oscillations. In this study, we will explore whether we can reconstruct this band of oscillation minima (an “oscillation valley”) from the atmospheric neutrino data. The part of the oscillogram below the blue band corresponds to lower energies and longer baselines, where the matter effects are significant for neutrinos (in the NO scenario considered here). For neutrinos, the MSW resonance [25,26,27,28] can be observed for $6 ~ \text {GeV}< E_{\nu } < 8 ~ \text {GeV}$ and $-0.7< \cos \theta _{\nu } < -0.5$. The parametric resonance [29, 30] or oscillation length resonance [31, 32] can be seen for $3 ~ \text {GeV}< E_{\nu } < 6 ~ \text {GeV}$ and $\cos \theta _{\nu } < -0.8$. The region above the blue band corresponds to vacuum oscillations, and is almost identical for $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ survival probabilities.

In the next sections, we demonstrate how these multi-GeV range features in the probability may be reflected in the expected event spectra of neutrinos and antineutrinos in an atmospheric neutrino experiment like ICAL.

3 Event generation at ICAL detector

While the analysis in this paper can in principle be performed with any atmospheric neutrino detector, we use the proposed ICAL detector at the India-based Neutrino Observatory [33, 34] for our simulations. There are two main reasons for this. (i) ICAL would be able to distinguish neutrinos from antineutrinos, and hence independent analyses for these two channels may be carried out. (ii) ICAL would be able to reconstruct the energy as well as the direction of $\mu ^-$ and $\mu ^+$ (produced in the charged-current interactions of $\nu _\mu$ and ${{\bar{\nu }}}_\mu$, respectively) with a good precision, which will be crucial for the analysis. These are also the reasons due to which ICAL would be able to provide a direct measurement of neutrino mass ordering by observing the Earth’s matter effects separately in neutrino and antineutrino channels in the multi-GeV energy range [34].

ICAL will be composed of 50 kt magnetized iron as the target, and glass resistive plate chambers (RPCs) as the sensitive detector elements. Iron plates of 5.6 cm thickness, and around 30,000 glass RPCs, will be stacked alternately in three modules, each of dimension 16 m (L) $\times$ 16 m (W) $\times$ 14.5 m (H). The magnetic field in the detector volume will be around 1.5 T. Charged particles passing through the RPCs will ionize the gas inside them, thereby inducing an electrical signal in the X- and Y-pickup strips and providing the X–Y coordinates of the charged particle. The layer number provides the Z coordinate. In the charged-current (CC) interactions of neutrinos, the muon, and hadrons in the final state will be distinguished from their track-like and shower-like features respectively. The time resolution of less than 1 ns for each RPC layer [35,36,37] would enable ICAL to distinguish between upward-going and downward-going events with a high confidence. The direction of bending of the charged muon track will enable the identification of its charge, and hence the identification of whether the original interacting particle was a neutrino or antineutrino.

To simulate the neutrino interactions in the ICAL detector, we use the MC neutrino generator NUANCE [38] and the neutrino flux calculated for the INO site [39, 40]. In this context, it is worthwhile mentioning that the studies of atmospheric neutrino oscillations [34] for the ICAL detector have been performed using the neutrino fluxes calculated for the Kamioka site. The neutrino fluxes vary from place to place due to the different geomagnetic field of the Earth, and there are important differences in the fluxes at Kamioka and at the proposed site of INO at Theni district of Tamil Nadu, India. Theni is close to the region having the largest horizontal component ($\approx 40 ~\upmu$T) of the Earth’s magnetic field. In comparison to this, the horizontal component of the geomagnetic field at Kamioka is $\approx 30 ~ \upmu$T. As a result, the neutrino flux at the INO site is smaller by approximately a factor of 3 at low energies. However, for neutrino energies around 10 GeV, the fluxes at INO and Kamioka sites are almost the same [40]. In this study, we use the neutrino fluxes given in [39, 40], taking into account the 1 km rock coverage of the mountain. Also, to take into account the effect of solar modulation on the neutrino fluxes, we use the fluxes with high solar activity (solar maximum) for half the exposure and the fluxes with low solar activity (solar minimum) for the remaining half. These fluxes are given in the website [41].

In this work, we focus on the CC interactions of muon neutrinos and antineutrinos at the ICAL detector. These may be a result of the unoscillated original $\nu _\mu / {{\bar{\nu }}}_\mu$, or original $\nu _e / {{\bar{\nu }}}_e$ which have oscillated to $\nu _\mu / {{\bar{\nu }}}_\mu$. The muon events from tau decay in the detector is small (around 2% of total upward going muons from $\nu _\mu$ interactions [42]), and these are mostly softer in energy and below the 1 GeV energy threshold of ICAL. In this work, we have not included this small contribution.

The three-flavor neutrino oscillations in the presence of matter (PREM profile [24]) are incorporated using the re-weighting algorithm as in [16, 17, 43]. The events are then folded with the detector properties as obtained from the GEANT4 simulation for muons at ICAL [15]. The reconstructed energies ($E_{\mu }^{\mathrm{rec}}$) and zenith angles ($\theta _{\mu }^{\mathrm{rec}}$) of the charged muons are considered to be the observable quantities, and we do not reconstruct neutrino energy or its direction. We also use the observable $L_\mu ^\text {rec}$, which is the effective baseline related to the reconstructed muon direction $\theta _\mu ^\text {rec}$ in the following fashion,

$$\begin{aligned} L_\mu ^{\mathrm{rec}} = \sqrt{(R+h)^2 - (R-d)^2\sin ^2\theta _\mu ^{\mathrm{rec}}} \,-\, (R-d)\cos \theta _\mu ^{\mathrm{rec}} \,. \end{aligned}$$

(3)

Note that $L_\mu ^{\mathrm{rec}}$ is an observable associated with the reconstructed muon direction, and not to be related directly with the neutrino direction.

In this paper, we use the ratios of upward-going and downward-going charged muons in various energy and direction bins. Note that the upward-going vs. downward-going events may lead to some ambiguity when the events are near-horizon, i.e., $-0.2< \cos \theta _{\mu }^{\mathrm{rec}} < 0.2$ (or $73 ~ \text {km}< L_\mu ^{\mathrm{rec}} < 2621 ~ \text {km}$). For these events, there is a significant change in the neutrino path length for a small variation in the estimated neutrino arrival direction. However, the detector response of ICAL to such events is anyway very poor, owing to the horizontally stacked structure, and it is observed that these events (corresponding to $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$ in the range of 1.5–2.0) do not affect the analysis.¹ Note that the Super-K collaboration selected only the “high-resolution” events in their L/E analysis [44, 45]. In particular, their analysis rejected neutrino events near the horizon, as well as low-energy events where the large scattering angles would have led to large errors in the reconstruction of neutrino direction. The low efficiency of ICAL for the near-horizontal event, and our analysis threshold of 1 GeV for muons, automatically incorporates both these filters. However, a difference between our analysis and the L/E analysis of Super-K [44] also needs to be pointed out. While the analysis in [44] is in terms of the inferred $L_\nu$ and $E_\nu$ of neutrinos, our analysis is in terms of the $L_\mu ^\text {rec}$ and $E_\mu ^\text {rec}$ of muons. The energy deposited at the detector by hadrons in the final state of neutrino interaction can be reconstructed at ICAL [46], but we do not use the hadron energy information in this study.

In Sects. 4 and 5, we discuss the event distributions as the one-dimensional functions of reconstructed $L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}$, and in the two-dimensional reconstructed ($E_\mu ^{\mathrm{rec}}$, $\cos \theta _\mu ^{\mathrm{rec}}$) plane, respectively.

4 Oscillation dip in the $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ distribution

In this section, we analyze the expected event distributions of $\mu ^-$ and $\mu ^+$ as functions of reconstructed $L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}$, with an MC event sample corresponding to 1000 years, and simulated event sample corresponding to 10 years, for ICAL. The 1000-year MC sample will correspond to the expected observations if an unlimited amount of data were available, and analysis using this sample will guide our algorithms. It will also lead to the calibrations of oscillation parameters like $|\Delta m^2_{32}|$ and $\sin ^2\theta _{23}$. On the other hand, the analysis with the 10-year sample would give an idea of the effects due to statistical fluctuations, an important consideration for low-statistics experiments like those with atmospheric neutrinos. To this end, we will analyze 100 independent sets of the 10-year samples.

Table 2 Total number of upward-going (U) and downward-going (D) $\mu ^-$ and $\mu ^+$ events expected at the 50 kt ICAL detector in 10 years (total exposure of 500 kt$\cdot$yr). We use the oscillation parameters given in Table 1

The number of events expected in 10 years at the 50 kt ICAL are shown in Table 2. Here, U is the number of upward-going muon events ($\cos \theta _\mu ^{\mathrm{rec}} <0$), while D is the number of downward-going muon events ($\cos \theta _\mu ^{\mathrm{rec}} >0$). The U/D ratio for reconstructed muons is defined as

$$\begin{aligned} \text {U/D} (E_\mu ^\text {rec}, \cos \theta _\mu ^{\mathrm{rec}}) \equiv \frac{N(E_\mu ^\text {rec}, -|\cos \theta _\mu ^{\mathrm{rec}}|)}{N(E_\mu ^\text {rec}, +|\cos \theta _\mu ^{\mathrm{rec}}|)} \; , \end{aligned}$$

(4)

where $N(E_\mu ^\text {rec}, \cos \theta _\mu ^{\mathrm{rec}})$ is the number of muon events with reconstructed energy $E_\mu ^\text {rec}$ and the reconstructed zenith angle $\theta _\mu ^{\mathrm{rec}}$. We associate the U/D ratio as a function of $\cos \theta _\mu ^\text {rec}$ with the upward-going events, i.e., with $\cos \theta _\mu ^\text {rec}<0$. We can also associate this U/D asymmetry with the $L_\mu ^\text {rec}$ corresponding to these upward-going events, which is related to $\cos \theta _\mu ^\text {rec}$ by Eq. (3).

The ratio U/D may be taken to be a proxy for the probability $P({\nu _\mu \rightarrow \nu _\mu })$ since in the ICAL detector, around 98% events are contributed from the oscillation channel $\nu _\mu \rightarrow \nu _\mu$, and only $\sim 2\%$ of total events come from the $\nu _e\rightarrow \nu _\mu$ channel for the benchmark values of the oscillation parameters shown in Table 1. With the use of this ratio, the analysis becomes less dependent on the uncertainties in the absolute neutrino flux values. Below, we shall analyze the event distributions and U/D ratios for $\mu ^-$ and $\mu ^+$ events separately, as the functions of $L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}$.

4.1 Events and U/D ratio using 1000-year Monte Carlo simulation

Fig. 3

Upper panels: the expected $\log _{10}[L_\mu ^\text {rec}/E_\mu ^\text {rec}]$ distributions of $\mu ^-$ (left panel) and $\mu ^+$ (right panel) events. The upward-going and downward-going events are represented with blue and red lines respectively. Lower panels: the U/D ratios as functions of $\log _{10}[L_\mu ^\text {rec}/E_\mu ^\text {rec}]$ of $\mu ^{-}$ (left panel) and $\mu ^{+}$ (right panel). All of these results are obtained with the 1000-year MC data sample. The $E_\mu ^{\mathrm{rec}}$ lies in the range of 1–25 GeV. We use the oscillation parameters given in Table 1

The upper panels of Fig. 3 present the distributions of $\mu ^-$ (left panel) and $\mu ^+$ (right panel) events for the 1000-year MC sample. We take events with the reconstructed muon energy in the range $(E_\mu ^{\mathrm{rec}})_{\mathrm{min}} = 1$ GeV to $(E_\mu ^{\mathrm{rec}})_{\mathrm{max}} = 25$ GeV. Since $L_\mu ^{\mathrm{rec}}$ is in the range of 15–12,757 km, the minimum and maximum values of $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ are $\log _{10}[(L_\mu ^{\mathrm{rec}})_{\mathrm{min}}/(E_\mu ^{\mathrm{rec}})_{\mathrm{max}}]$ = 0.22 and $\log _{10}[(L_\mu ^{\mathrm{rec}})_{\mathrm{max}}/(E_\mu ^{\mathrm{rec}})_{\mathrm{min}}] = 4.1$, respectively. Note that for upward-going events, the minimum value of $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ is 1.2, since $L_\mu ^\text {rec}(\text {min})$ for upward-going events is 437 km. We have binned the data in 100 bins, uniform in $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$. The number of upward-going events is clearly less than that of the downward-going events, since the upward-going $\nu _\mu$ have traveled larger distances and have had a larger chance of oscillating to the other neutrinos flavors. The number of $\mu ^+$ events is less than that of $\mu ^-$ events mainly because, at these energies, the cross-section of antineutrinos is smaller than that of neutrinos by a factor of approximately 2.

For the lower panels of Fig. 3, we divide the range of upward-going muons ($\cos \theta _\mu ^\text {rec} < 0$), i.e.  $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}] =$ 1.2–4.1, in 66 uniform bins. A downwarding event with a given $\cos \theta _\mu ^\text {rec} > 0$ value is then assigned to the bin corresponding to $-\cos \theta _\mu ^\text {rec}$. The U/D ratio in each bin is then calculated by dividing the number of upward-going events by the number of downward-going events, and plotted with the corresponding value of $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$. Two major dips in the U/D ratio may be observed in the figure, in both the $\mu ^-$ and $\mu ^+$ channels. These dips occur at $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}] \sim 2.75$ and $\sim$ 3.2, respectively. In this study, we focus on the observation of the first dip.

Note that, while the two dips discussed above correspond to the first two minima in the survival probability as shown in Fig. 1, they are not exactly at the same location. This is because of the crucial difference that, while Fig. 1 uses the actual values of energy and zenith angle of the atmospheric neutrino, Fig. 3 uses the reconstructed values of energy and zenith angle of the muon produced from the CC interaction of that neutrino. In CC deep inelastic scattering of neutrino, hadrons in the final state take away some energy of the incoming neutrino, resulting in $E_\mu ^\text {rec} < E_\nu$. As a result, the dips move towards higher values of $L_\mu ^\text {rec}/E_\mu ^\text {rec}$. Since the average inelasticities² in the antineutrino events ($\langle y_{{{\bar{\nu }}}} \rangle \approx 0.3$) are smaller than that in the neutrino events ($\langle y_{\nu } \rangle \approx 0.45$) in the multi-GeV energy range [17], the shift of the dip is smaller in the case of $\mu ^+$ than $\mu ^-$.

Note that the dips in Fig. 3 are shallower and broader than those in Fig. 1, where the dips reach all the way to the bottom, that is $P(\nu _\mu \rightarrow \nu _\mu ) \approx 0$, with $\sin ^2 \theta _{23}=0.5$. The reason for this smearing lies in the difference between the momenta of the neutrino and muon, as well as the limitations on the muon momentum reconstruction in the detector. It may also be observed that the smearing is more in $\mu ^-$ events as compared to the $\mu ^+$ events in Fig. 3. This difference is due to the broader spread in the inelasticities of neutrino interactions than that in antineutrino interactions [17]. As a result of this spread, the dips in $\mu ^-$ events get smeared more, and hence become shallower, as compared to the dips in $\mu ^+$ events.

4.2 Events and U/D ratio using 10-year simulated data

Table 3 The binning scheme adopted for $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ for $\mu ^-$ and $\mu ^+$ events of 10-year simulated data

Fig. 4

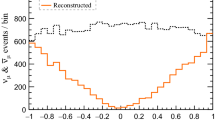
Upper panels: the expected $\log _{10} [L_\mu ^{\text {rec}}/ E_\mu ^{\text {rec}}]$ distributions for $\mu ^{-}$ (left panel) and $\mu ^{+}$ (right panel) events. The red and blue lines are for downward-going and upward-going events, respectively. The shaded boxes represent statistical uncertainties. Lower panels: the U/D ratios as functions of $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$. The height of shaded boxes represents expected uncertainties in the U/D ratio. The exposure is taken to be 10 years of 50 kt ICAL, i.e.  500 kt$\cdot$yr. We use the oscillation parameters given in Table 1

In this section, we discuss the expected event distributions as functions of reconstructed $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ at the ICAL detector, with an exposure of 500 kt$\cdot$yr. In order to take into account the statistical fluctuations, which are expected to have a significant impact on the accuracy of the results, we take 100 independent sets, and calculate the mean as well as root-mean-square (rms) deviations of relevant quantities.

We distribute the events in bins corresponding to the reconstructed $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ values, as described in Sect. 4.1. However, since the number of events available here is much smaller than that for 1000 years, we choose a non-uniform binning scheme shown in Table 3 such that typically, all the bins will have at least 10 down-going events. We have a total of 34 bins of $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ in the range of 0–4. The distribution of the number of events in these bins is shown in the top panels of Fig. 4. The uncertainties due to statistical fluctuations, calculated as the rms deviation obtained from 100 independent simulated data sets, are also shown.

The lower panels of Fig. 4 show the U/D ratio in reconstructed $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ bins, using the same procedure outlined in Sect. 4.1. We choose the range of $\log _{10}[L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}]$ to be in the range 2.0 – 4.0, which is the most interesting range. The fluctuations shown in the figure are the rms deviations obtained from the distributions of the U/D ratio in 100 independent simulated data sets. It is observed that, while the first dip is quite prominent, the second dip is lost in the statistical fluctuations, and due to the broad binning scheme that we have to employ owing to a small number of events. While this does not rule out the identification of the second dip using more efficient algorithms, in this work, we shall focus on the first dip. Henceforth, when we refer to the dip position, we refer to the position of the first dip. It may be observed that the dip in the $\mu ^+$ channel is deeper than that in the $\mu ^-$ channel similar to 1000-year MC sample as described in Sect. 4.1.

4.3 Identifying the dip with 10-year simulated data

Fig. 5

Left panel: the U/D ratios as functions of $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$ for five independent simulated data sets with 500 kt$\cdot$yr exposure of ICAL are shown by thin colored lines. The black solid line is the mean of 100 such data sets. Right panel: the red parabola represents the fit to the dip in one of the data sets (blue line), obtained after the dip-identification procedure described in the text. The black dashed line corresponds to the initial U/D ratio threshold for the algorithm, while the blue dashed line corresponds to the U/D ratio threshold once the dip has been identified

The left panel of Fig. 5 shows the U/D ratios as functions of reconstructed $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$ of muons for five independent simulated data sets with 500 kt$\cdot$yr exposure of ICAL. Clearly, the statistical fluctuations are significant, and may lead to the misidentification of the dip position. An identification of the dip position should not correspond simply to the lowest value of the U/D ratio, but also be guided by the values of the U/D ratios in surrounding bins. In order to achieve this, we use the dip-identification algorithm as described below.

To start with, we consider the region corresponding to the range $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$ = 3.2 – 4.0 as a single bin, since in this region, we expect the oscillations to be quite rapid, leading to the U/D ratio averaging out to a constant value. Let the measured value of the U/D ratio in this bin be $R_0$. From the simulations done with 100 independent sets, we have found that the statistical fluctuations in data sets give rise to a rms deviation of $\Delta R_0 \approx 0.02$ and 0.03 in this ratio for $\mu ^-$ and $\mu ^{+}$ respectively. We take this fluctuation into account, and start with an initial ratio threshold of $R_{\mathrm{th}} \equiv R_0 - 2 \Delta R_0$, shown by the black dashed line in the right panel of Fig. 5. All the bins with measured U/D ratio less than $R_{\mathrm{th}}$ form the initial candidates for the dip position. However, all these bins need not be a part of the actual dip, due to fluctuations. In order to identify the actual bins surrounding the dip, we try to find the cluster of consecutive bins, all of which have U/D ratio less than that in all the other bins. This is achieved by lowering the value of $R_{\mathrm{th}}$ till all the bins with U/D ratio less than $R_{\mathrm{th}}$ are contiguous. This final value of $R_{\mathrm{th}}$ is denoted by the blue dashed line in the right panel of Fig. 5.

Once the dip-identification algorithm has thus identified a cluster of contiguous bins as the dip region, we fit the U/D ratios in these bins with a parabola as shown in the right panel of Fig. 5. The value of $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]$ corresponding to the lowest U/D ratio obtained from this fit, denoted by $x_{\mathrm{min}}$, would be identified with the “location” of the dip.

4.4 $|\Delta m^2_{32}|$ and $\theta _{23}$ from the dip and the U/D ratio

The first dip in the survival probability $P(\nu _\mu \rightarrow \nu _\mu )$, in the approximation of two-flavor oscillations in vacuum, appears at $L_\nu (\text {km})/ E_\nu (\text {GeV})= \pi /(2.54\,|\Delta m^2_{32}|(\text {eV}^2))$ (see Eq. 1). However, as discussed in Sect. 4.1, the location of the dip $x_{\mathrm{min}}$ in the $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ distribution would have a complicated dependence on the three flavor neutrino oscillation, matter effect, neutrino fluxes, CC cross-sections, inelasticities of events, and detector response. However, we can obtain a calibration of $|\Delta m^2_{32}|$ with the location of the dip, using the 1000-year MC sample. The binning scheme used is the same as in Sect. 4.3. For obtaining the calibration curves, we keep the oscillation parameters (except for the one to be calibrated) fixed at benchmark values as given in Table 1. The blue points in the upper panels of Fig. 6 represent the values of $x_{\mathrm{min}}$ obtained from the U/D ratio distribution with different values of $|\Delta m^2_{32}|$. These points are observed to lie close to a straight line, and we can draw a calibration curve that would enable us to infer the actual value of $|\Delta m^2_{32}|$, given the $x_{\mathrm{min}}$ value determined from the data. Note that this calibration curve also has a dependence on the analysis procedure, including the binning scheme and bin-identification algorithm.

While the calibration curve allows a one-to-one correspondence between the actual $|\Delta m^2_{32}|$ value and the location of the dip for sufficiently large data (like 1000 years of exposure), practically speaking the data available is going to be limited. The statistical fluctuations introduced due to this will lead to uncertainties in the determination of $|\Delta m^2_{32}|$ via this method. To estimate these uncertainties, we generate 100 independent simulated data sets with an exposure of 500 kt$\cdot$yr each, and determine the location of the dip in each of them. The distribution of the dip locations thus obtained allows us to determine 90% C.L. allowed regions for the dip location, and hence the 90% C.L. allowed regions for the calibrated $|\Delta m^2_{32}|$ values. These allowed regions are represented in the upper panels of Fig. 6 by dark gray bands, where all the oscillation parameters are kept fixed at benchmark values as given in Table 1 and no systematics are taken into account. The figure indicates that the 90% C.L. allowed range for $|\Delta m^2_{32}|$ from $\mu ^-$ events is (2.14–2.67)$\times 10^{-3}$ $\hbox {eV}^2$, while that from $\mu ^+$ data is (2.22–2.79)$\times 10^{-3}$ $\hbox {eV}^2$.

Fig. 6

Upper panels: the blue points and the blue line correspond to the calibration of actual $|\Delta m^2_{32}|$ with the location of the dip, obtained by using the 1000-year MC data sample. The light (dark) gray bands represent the 90% C.L. regions of the location of the dip, and hence the inferred $|\Delta m^2_{32}|$ through calibration, for $|\Delta m^2_{32}| \,(\text{ true}) = 2.46\times 10^{-3}$ $\hbox {eV}^2$, with (without) systematic errors and uncertainties in the other oscillation parameters. Lower panels: The blue points and the blue line correspond to the calibration of actual $\sin ^2\theta _{23}$ with the total U/D ratio across all bins. The light (dark) gray bands represent the 90% C.L. allowed ranges of the U/D ratio, and hence the inferred $\sin ^2\theta _{23}$ through calibration, for $\sin ^2\theta _{23} \,(\text{ true}) = 0.5$, with (without) systematic errors and uncertainties in the other oscillation parameters. For all the confidence regions, we use 10 years exposure of ICAL. The results obtained from $\mu ^-$ and $\mu ^+$ events are shown in left and right panels, respectively. For the fixed-parameter analysis, we use the benchmark oscillation parameters given in Table 1, while for the inclusion of systematic uncertainties and variation of oscillation parameters, we use the procedure described in Sect. 4.4

We also investigate the effect on the measurements of $\Delta m^2_{32}$ and $\theta _{23}$ due to uncertainties in the other oscillation parameters. For this, we vary the values of the other oscillation parameters in 100 statistically independent unoscillated data sets. For each of these data sets, 20 random choices of oscillation parameters are taken following the Gaussian distributions:

$$\begin{aligned} \Delta m^2_{21}&= (7.4 \pm 0.2)\times 10^{-5} \,\text {eV}^2, ~ \nonumber \\ \Delta m^2_{32}&= (2.46\pm 0.03)\times 10^{-3} \,\text {eV}^2\,,\nonumber \\ \sin ^2 2\theta _{12}&= 0.855 \pm 0.020,~ \nonumber \\ \sin ^2 2\theta _{13}&= 0.0875 \pm 0.0026, ~ \nonumber \\ \sin ^2\theta _{23}&= 0.50\pm 0.03, \end{aligned}$$

(5)

which are in accordance with the present neutrino global fit results [7]. This way, the variations of the results over a large number (2000) of different combinations of values of the other oscillation parameters are effectively included. Note that the value of the oscillation parameter to be determined is kept fixed at benchmark value as given in Table 1. We keep $\delta _\text {CP}$ fixed at zero because its effect on $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ survival probabilities is negligible in the multi-GeV energy range.

We do not see any major changes in the measurement of $|\Delta m^2_{32}|$ caused by uncertainties in the other oscillation parameters, viz. $\theta _{12}$, $\theta _{23}$, $\theta _{13}$, and $\Delta m^2_{21}$. This is expected, since (a) the mixing angle $\theta _{23}$ does not change the dip-location of $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ survival probabilities, (b) the mixing angle $\theta _{13}$ is already precisely measured, (c) the solar oscillation parameters $\Delta m^2_{21}$ and $\theta _{12}$ have negligible impact on $\nu _\mu$ and ${{\bar{\nu }}}_\mu$ survival probabilities in the multi-GeV energy range.

We also check the impact of systematic uncertainties on the result. For this, we incorporate the standard systematic uncertainties used in $\chi ^2$ analyses of ICAL [34]. These are (i) 20% error in flux normalization, (ii) 10% error in cross-section, (iii) 5% error in energy dependence of flux, (iv) 5% error in zenith angle dependence of flux, and (v) 5% overall systematics. The event number in each ($E_\mu ^\text {rec}$, $\cos \theta _\mu ^\text {rec}$) bin is modified in each of the 2000 simulated data sets as

$$\begin{aligned} N = N^{0} (1+\delta _1)(1+\delta _2)(E_\mu ^\text {rec}/E_0)^{\delta _3} (1 + \delta _4 \cos \theta _\mu ^\text {rec}) (1+\delta _5)\,, \end{aligned}$$

(6)

with $E_0 = 2$ GeV and $N^0$ as the theoretically predicted event number. The parameters $\delta _1$, $\delta _2$, $\delta _3$, $\delta _4$, $\delta _5$ are random numbers generated following Gaussian distributions with mean zero and the $1\sigma$ widths as $20\%$, $10\%$, $5\%$, $5\%$, $5\%$, respectively, which correspond to the systematics mentioned above.

After incorporating systematic uncertainties and varying oscillation parameters, we get the 90% C.L. allowed range for $|\Delta m^2_{32}|$ from $\mu ^-$ events as (2.18–2.79)$\times 10^{-3}$ $\hbox {eV}^2$, and from $\mu ^+$ data as (2.22–2.80)$\times 10^{-3}$ $\hbox {eV}^2$, for $|\Delta m^2_{32}| \,(\text{ true}) = 2.46\times 10^{-3}$ $\hbox {eV}^2$. These results are shown with light gray bands in upper panels of Fig. 6. Note that the change in the measurement of $|\Delta m^2_{32}|$ from $\mu ^+$ events after inclusion of systematic uncertainties and errors in other oscillation parameters is quite small, whereas that from $\mu ^-$ events is larger. This is because the dip in $\mu ^+$ data is quite sharp, owing to the lower inelasticity in ${{\bar{\nu }}}_\mu$ CC interactions.

We can follow the same procedure to determine the value of the mixing angle $\theta _{23}$ from the data. In principle, this is related to the depth of the dip, and such a calibration could be obtained using the 1000-year MC events. However, the statistical fluctuations in the 500 kt$\cdot$yr simulated data are observed to give rise to large uncertainties. On the other hand, it is found that the total U/D ratio of all events with $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ in the range of 2.2 – 4.1 gives a much better estimate of $\theta _{23}$. In the lower panels of Fig. 6, we show in blue the calibration for $\sin ^2\theta _{23}$ with the measured total U/D ratio, obtained using the 1000-year MC sample for several $\sin ^2\theta _{23} \,(\text{ true})$ values. We also show the 90% C.L. allowed values of $\sin ^2\theta _{23}$ inferred using the 100 independent simulated data sets with 500 kt$\cdot$yr exposure each, keeping all the oscillation parameters fixed at benchmark values as given in Table 1, with dark gray bands. The expected allowed range for $\sin ^2\theta _{23}$ at 90% C.L. is (0.44–0.64) from $\mu ^-$ events, and (0.39–0.61) from $\mu ^+$ events. With the systematic uncertainties and the variation of oscillation parameters $|\Delta m^2_{32}|$, $\theta _{13}$, $\theta _{12}$, and $\Delta m^2_{21}$ as mentioned above, we get the 90% C.L. allowed range for $\sin ^2\theta _{23}$ from $\mu ^-$ events as (0.38–0.70), and from $\mu ^+$ data as (0.35–0.65), for $\sin ^2\theta _{23} \,(\text{ true}) = 0.5$. These results are shown with light gray bands in lower panels of Fig. 6.

Note that we do not claim or demand that our analysis gives better results than those obtained with the complete $\chi ^2$ analysis done for ICAL in Refs. [16, 17]. The $\chi ^2$ analyses take into account the complete event spectra, while our focus is on the identification of the dip, a feature that would reconfirm the oscillation paradigm for neutrinos. The observation that the inferred $|\Delta m^2_{32}|$ range is comparable to the range expected from the complete $\chi ^2$ analysis points to the conclusion that most of the information about the $|\Delta m^2_{32}|$ is concentrated in the location of the U/D dip.

5 Oscillation valley in the $(E_\mu ^{\mathrm{rec}}, \cos \theta _\mu ^{\mathrm{rec}})$ plane

The oscillation dip discussed in the last section was a dip in the U/D ratio as a function of $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$. The dependence on $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ was motivated from the approximate form of the neutrino oscillation probability (with two flavors in vacuum). However, if the detector can reconstruct both $L_\mu$ (hence $\cos \theta _\mu$) and $E_\mu$ accurately, then one can go a step ahead and look at the distribution of the U/D ratio in the $(E_\mu , \cos \theta _{\mu })$ plane. We perform such an analysis in this section, and find that such a distribution can have many interesting features with physical significance, which may be identifiable with sufficient data. In particular, we point out an “oscillation valley” corresponding to the dark diagonal band in Fig. 2, whose nature can provide stronger tests for the oscillation hypothesis, albeit only with a large amount of data. On the other hand, we show that the identification of the oscillation valley, and the determination of $|\Delta m^2_{32}|$ based on its “alignment”, is possible with 500 kt$\cdot$yr of simulated data at ICAL.

5.1 Events and U/D ratio using 1000-year Monte Carlo simulation

Fig. 7

The distribution of event density (upper panels) and U/D ratio (lower panels), for $\mu ^{-}$ (left panels) and $\mu ^{+}$ (right panels), in the ($E_\mu ^{\mathrm{rec}},\cos \theta _\mu ^{\mathrm{rec}}$) plane, obtained using the 1000-year MC sample. We use the oscillation parameters given in Table 1. Note that the event density in the upper panels has units of [$\hbox {GeV}^{-1} \hbox {sr}^{-1}$], and is obtained by dividing the number of events in each bin by ($2\pi ~\times$ the bin area), i.e.by ($2\pi \Delta E_{\mu }^{\mathrm{rec}} \Delta \cos \theta _{\mu }^{\mathrm{rec}}$). Here $\Delta E_{\mu }^{\mathrm{rec}}$ and $\Delta \cos \theta _{\mu }^{\mathrm{rec}}$ are the height and the width of the bin, respectively. Note that the U/D($E_\mu ^\text {rec}, \cos \theta _\mu ^\text {rec}$) is defined only for $\cos \theta _\mu ^\text {rec} < 0$ (see Eq. 4)

In this section, we discuss the distributions of events and the U/D ratio, in the plane of reconstructed energy $E_{\mu }^{\mathrm{rec}}$ and zenith angle $\cos \theta _{\mu }^{\mathrm{rec}}$ of the $\mu ^-$ and $\mu ^+$ events, for a 1000-year MC sample. The main reason for considering such a huge exposure here is not to miss those features, which survive in spite of our not using $E_\nu$ and $\cos \theta _\nu$ directly, but which may disappear due to the limitation of statistics.

The quantities shown in Fig. 7 are binned based on the reconstructed values of $E_{\mu }^{\mathrm{rec}}$ and $\cos \theta _{\mu }^{\mathrm{rec}}$. The $\cos \theta _\mu ^{\mathrm{rec}}$ range of -1.0 to 1.0 has been divided into 80 bins of equal width. We have a total of 84 bins in $E_{\mu }^{\mathrm{rec}}$ in the range of 1 GeV to 25 GeV. The bin width is not uniform in $E_\mu ^{\mathrm{rec}}$, since at higher energies the number of events decreases rapidly. The first 45 $E_\mu ^{\mathrm{rec}}$ bins, in the range of 1.0 – 5.5 GeV, have a width of 0.1 GeV each, and the last 39 bins, in the range of 5.5 – 25 GeV, have a width of 0.5 GeV each. The upper panels of Fig. 7 present the distributions of $\mu ^-$ (left panel) and $\mu ^+$ (right panel) event density. The abrupt lowering of the event density for $-0.2<\cos \theta _{\mu }^{\mathrm{rec}}<0.2$ is due to the poor reconstruction efficiency of the ICAL detector for the events coming near the horizontal direction. Note that this feature was absent in Fig. 3 since it was distributed over a large $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ range.

In lower panels of Fig. 7, we show the U/D ratio in each bin, in the ($E_\mu ^{\mathrm{rec}}, \cos \theta _\mu ^{\mathrm{rec}}$) plane. Note that the U/D($E_\mu ^\text {rec}, \cos \theta _\mu ^\text {rec}$) is defined only for $\cos \theta _\mu ^\text {rec} < 0$ (See Eq. 4). This also makes the features in Fig. 7 resemble those in Fig. 2, thus enabling their understanding in terms of the survival probabilities shown in the oscillograms. The lower panels may be observed to have many interesting features. The most prominent one is of course the light/ dark blue band, corresponding to U/D $\lesssim 0.25$, extending diagonally from $(E_\mu ^{\mathrm{rec}}, \cos \theta _{\mu }^{\mathrm{rec}}) \approx (5 ~\mathrm{GeV},-0.3)$ to $(E_\mu ^{\mathrm{rec}}, \cos \theta _{\mu }^{\mathrm{rec}}) \approx (25 ~\mathrm{GeV},-1.0)$. This is the band with the lowest values of U/D ratio in this plane, and we shall henceforth refer to it as the “oscillation valley”. Clearly, this valley is deeper for $\mu ^+$, since the number of dark blue bins with U/D $< 0.15$ is seen to be larger for $\mu ^+$. This is consistent with the observation of a deeper oscillation dip in $\mu ^+$, as discussed in Sect. 4.1. The main reason for this is the smaller inelasticity of antineutrino CC events. The differences observed between the left and right panel may be attributed to the Earth matter effects, which affect the survival probabilities of neutrinos and antineutrinos differently for a given neutrino mass ordering.

5.2 Events and U/D ratio using 10-year simulated data

Fig. 8

The distribution of mean number of events (upper panels) and mean U/D ratio (lower panels) for $\mu ^{-}$ (left panels) and $\mu ^{+}$ (right panels) in the plane of $\cos \theta _{\mu }^{\mathrm{rec}}$ and $E_{\mu }^{\mathrm{rec}}$. The mean is calculated from 100 independent data sets of exposure 500 kt$\cdot$yr each of ICAL. The number of events written in white are rounded to the nearest integer. We use the oscillation parameters given in Table 1. Note that the U/D($E_\mu ^\text {rec}, \cos \theta _\mu ^\text {rec}$) is defined only for $\cos \theta _\mu ^\text {rec} < 0$ (see Eq. 4)

In the upper panels of Fig. 8, we show the expected event distributions of $\mu ^-$ (left panel) and $\mu ^+$ (right panel) events, for 500 kt$\cdot$yr exposure of ICAL, in the plane of reconstructed muon energy ($E_{\mu }^{\mathrm{rec}}$) and reconstructed muon zenith angle ($\cos \theta _{\mu }^{\mathrm{rec}}$). The $\cos \theta _{\mu }^{\mathrm{rec}}$ range of -1.0 to 1.0 is divided into 20 uniform bins of width 0.1 each. The binning in $E_{\mu }^{\mathrm{rec}}$ is non-uniform, and is such that there are at least a few number of events in each bin (except in the largest energy bins, where this may not be possible due to the smaller neutrino flux at higher energies). The $E_{\mu }^{\mathrm{rec}}$ range of 1 – 25 GeV has been divided into 16 non-uniform bins, as given in Table 4.

Table 4 The binning scheme considered for $E_\mu ^{\mathrm{rec}}$ and $\cos \theta _\mu ^{\mathrm{rec}}$ for $\mu ^-$ and $\mu ^+$ events of 10-year simulated data while we show event distribution and U/D plots in the ($E_\mu ^\text {rec}$, $\cos \theta _\mu ^{\text {rec}}$) plane. This binning scheme is used in analysis of oscillation valley as well

In order to take care of the statistical fluctuations that will clearly be significant with 500 kt$\cdot$yr data, we generate 100 independent data sets, each with this exposure. In the upper panels of Fig. 8, we show the mean number of events obtained from these 100 data sets. Similarly, in the lower panels of Fig. 8, we calculate the U/D ratios in each bin for the above 100 sets, and present their mean values in the figure, using appropriate colors. Note that the U/D($E_\mu ^\text {rec}, \cos \theta _\mu ^\text {rec}$) is defined only for $\cos \theta _\mu ^\text {rec} < 0$ (see Eq. 4).

Clearly, while many of the features corresponding to matter effects seem to get diluted due to the coarser bins and statistical fluctuations, the oscillation valley along the diagonal survives. In the following sections, we shall provide a procedure for identifying this oscillation valley and extracting information about the oscillation parameters from it.

5.3 Identifying the valley with 10-year simulated data

Fig. 9

Demonstration of the algorithm for identifying the valley and determining its alignment. Left panel: the blue line represents the U/D ratio as a function of ($\cos \theta _\mu ^{\mathrm{rec}}$) for a fixed energy bin. The gray areas are those with $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}] < 2.2$ and $> 3.1$. The red curve represents the parabolic fit to the U/D ratios with $2.2< \log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}] < 3.1$. Right panel: the colored background shows the U/D ratios for each bin in the $(E_\mu ^{\mathrm{rec}}, \cos \theta _\mu ^{\mathrm{rec}})$ plane, for a particular 500 kt$\cdot$yr data set. The black dashed and solid lines show the cuts corresponding to $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}]= 2.2$ and 3.1, respectively. White points represent the locations of minima for the fitted parabolas corresponding to each horizontal energy “strip”. The white line is a fit to the white points with appropriate weights as described in the text. Note that the U/D($E_\mu ^\text {rec}, \cos \theta _\mu ^\text {rec}$) is defined only for $\cos \theta _\mu ^\text {rec} < 0$ (see Eq. 4)

We now describe the methodology adopted for the identification of the oscillation valley in the $(E_\mu ^{\mathrm{rec}}, \cos \theta _\mu ^{\mathrm{rec}})$ plane, and the determination of its alignment. To this end, we use the binning described in Sect. 5.2 for the 500 kt$\cdot$yr data set.

• Since the events with $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}] > 3.1$ are susceptible to significant matter effect and rapid oscillations, the information from these bins cannot be directly connected to the dip corresponding to the vacuum oscillations. As far as the region $\log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}] < 2.2$ is concerned, the oscillation are not developed yet. Therefore, we only choose the region $2.2< \log _{10} [L_\mu ^{\text {rec}}/E_\mu ^{\text {rec}}] < 3.1$ for our analysis, where vacuum oscillations are expected to dominate, and to be resolvable.

• We then analyze each horizontal “energy strip” in this region, i.e. the U/D ratio for all $\cos \theta _\mu ^{\mathrm{rec}}$, as shown in the left panel of Fig. 9. We perform a parabolic fit to the points in this strip that are in the allowed region as specified above. The equation of the parabola to be fitted is $y = y_E + a_E (x-x_E)^2$, where y is the U/D ratio while x is the value of $\cos \theta _\mu ^{\mathrm{rec}}$. The parameters $(x_E,y_E)$ correspond to coordinates ($\cos \theta _\mu ^\text {rec}$, U/D) at the bottom of the parabola, while the parameter $a_E$ describes the “width” of the parabola. Higher the value of $a_E$, more prominent the dip in that energy strip.

• Once the parabolic fits in all energy strips are obtained, all the points ($E_\mu ^\text {rec} = E,~\cos \theta _\mu ^\text {rec} = x_E$) are plotted on the $(E_\mu ^{\mathrm{rec}}, \cos \theta _\mu ^{\mathrm{rec}})$ plane, as shown in the right panel of Fig. 9. A straight line, passing through the origin $(E_\mu ^\text {rec}=0,~\cos \theta _\mu ^\text {rec} = 0)$, is fitted to these points. For this fitting, each of the points is given a weight of $\sqrt{a_E N_E}$, where $N_E$ is the number of downward-going events in the analysis region (between the solid and dashed black lines in the right panel Fig. 9) of the energy strip. The points lying outside the analysis region are not taken into account in the fit. The best-fit line is thus obtained of the form $y = m\cdot x$, where y represents $E_\mu ^{\mathrm{rec}}$, and x represents $\cos \theta _\mu ^{\mathrm{rec}}$. The slope m of this line quantifies the “alignment” of the valley.

Note that the above procedure is motivated by our expectation that the valley would correspond to the value of $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ which would correspond to the dip in the one-dimensional L/E analysis described in Sect. 4.3. Our analysis is rather simple, focused only on the identification of the valley and on determining its alignment. With more data and a refined analysis, one maybe able to use the goodness of the fit to the line, or the intercepts of the line on either axes, for testing the oscillation framework in more detail. We show here that 500 kt$\cdot$yr of exposure would be enough to locate the valley and quantify its alignment even with our simplified treatment. In the following section, we shall also show that the value of $|\Delta m^2_{32}|$ may be calibrated using the alignment of the valley.

Fig. 10

The blue points and the blue line correspond to the calibration of actual $|\Delta m^2_{32}|$ with the alignment of the valley, obtained by using the 1000-year MC data sample. The light (dark) gray bands represent the 90% C.L. regions of the alignment of the valley, and hence the inferred $|\Delta m^2_{32}|$ through calibration, with (without) systematic uncertainties and error in other oscillation parameters. Here, we take $|\Delta m^2_{32}| \,(\text{ true}) = 2.46\times 10^{-3}$ $\hbox {eV}^2$ and 10-year exposure of ICAL. The negative values of the alignments of the valley correspond to the negative slope of the best-fit line in the right panel of Fig. 9. The results obtained from $\mu ^-$ and $\mu ^+$ events are shown in left and right panels, respectively. For the fixed-parameter analysis, we use the benchmark oscillation parameters given in Table 1, while for the inclusion of systematic uncertainties and variation of oscillation parameters, we use the procedure described in Sect. 4.4

5.4 $|\Delta m^2_{32}|$ from the alignment of the valley

For the same reasons described in Sect. 4.4, we expect the alignment of the valley, as determined through the procedure outlined in the previous section, to lead to the value of $|\Delta m^2_{32}|$. Indeed, for upward-going events, $L_\mu ^{\mathrm{rec}}$ is approximately proportional to $\cos \theta _\mu ^{\mathrm{rec}}$, so that the alignment of the valley, i.e. $E_\mu ^{\mathrm{rec}} (\text {GeV})/\cos \theta _\mu ^{\mathrm{rec}}$, is approximately $(5.08/\pi )\,|\Delta m^2_{32}| (\text {eV}^2)\, R(\text {km})$.

We calibrate the actual value of $|\Delta m^2_{32}|$ with the alignment of the valley using the same procedure as in Sect. 4.4. The 1000-year MC samples, with different true values of $|\Delta m^2_{32}|$, are used to locate the blue calibration points, and hence the blue calibration curve, in Fig. 10. The statistical fluctuations with 500 kt$\cdot$yr data are taken into account by generating 100 independent data sets. The dark gray bands in Fig. 10 present the 90% C.L. allowed values for the alignment of the valley, and hence the 90% C.L. allowed values of the calibrated $|\Delta m^2_{32}|$, with all the oscillation parameters fixed at benchmark values as given in Table 1. The figure indicates that the 90% C.L. allowed range for $|\Delta m^2_{32}|$ from $\mu ^-$ events is (2.31–2.92)$\times 10^{-3}$ $\hbox {eV}^2$, while that from $\mu ^+$ data is (2.19–2.81)$\times 10^{-3}$ $\hbox {eV}^2$, for $|\Delta m^2_{32}| \,(\text{ true}) = 2.46\times 10^{-3}$ $\hbox {eV}^2$. After incorporating the systematics uncertainties and varying the oscillation parameters $\theta _{12}$, $\theta _{23}$, $\theta _{13}$, and $\Delta m^2_{21}$ as discussed in Sect. 4.4, we get the 90% C.L. allowed range for $|\Delta m^2_{32}|$ from $\mu ^-$ events as (2.26–2.94)$\times 10^{-3}$ $\hbox {eV}^2$, and from $\mu ^+$ data as (2.19–2.84)$\times 10^{-3} \hbox {eV}^2$. These results are shown with light gray bands in Fig. 10.

So far, our analysis has been based upon 500 kt$\cdot$yr of simulated data. However, ICAL should be able to identify the oscillation dip/oscillation valley even with half the exposure, and may provide some early measurement of $|\Delta m^2_{32}|$ with data in the multi-GeV range. We show some results with 250 kt$\cdot$yr exposure in Appendix A.

6 Summary and concluding remarks

Atmospheric neutrino experiments access a large range of energies and baselines for neutrino oscillations, hence they are capable of testing basic features of the neutrino flavor conversion framework over a large parameter space. In this work, we study the potential of the ICAL detector to visualize the L/E dependence of survival probabilities in neutrino and antineutrino channels separately, by distinguishing $\mu ^-$ and $\mu ^+$ events. For this, we use the reconstructed muon energy and zenith angle, as opposed to the inferred neutrino energy and zenith angle. Further, we consider the ratio of upward-going (U) and downward-going (D) events, instead of the ratio of observed oscillated events and simulated unoscillated events. The reconstructed $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ distributions of the U/D ratio for 1000-year MC indicate that the feature of the first oscillation dip in muon neutrinos (and antineutrinos) is still preserved in the detected $\mu ^-$ and $\mu ^+$. We demonstrate that this first oscillation dip can be clearly identified at ICAL with an exposure of 500 kt$\cdot$yr, i.e.10 years running of the 50 kt ICAL.

We develop a novel dip-identification algorithm to identify the oscillation dip and measure the value of $|\Delta m^2_{32}|$, using the information from the first oscillation dip in the $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ distributions of the U/D ratio, in $\mu ^-$ and $\mu ^+$ events separately. This algorithm finds a contiguous set of $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ bins with the lowest U/D values, and uses the combined information in all of them to determine the dip location precisely. The value of $|\Delta m^2_{32}|$ is then calibrated against the location of the dip using the 1000-year MC, and the statistical uncertainties expected with the 10-year data are estimated using simulations of 100 independent data sets. The expected 90% C.L. ranges of $|\Delta m^2_{32}|$ obtained after taking into account the systematic uncertainties and varying the other oscillation parameters over their currently allowed ranges, are summarized in Table 5. We also calibrate $\theta _{23}$, however, here simply the ratio of the total number of U and D events is found to be a better choice to calibrate against, rather than the depth of the dip. We find that, when the true value of $\sin ^2\theta _{23}$ is 0.50, the U/D ratio would determine the 90% C.L. range of its value to be (0.38–0.70) with $\mu ^-$ events, and (0.35–0.65) with $\mu ^+$ events, taking into account systematic uncertainties and errors in the other oscillation parameters.

Table 5 The expected 90% C.L. allowed ranges for $|\Delta m^2_{32}|$, from the analyses using $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ and $(E_\mu ^{\mathrm{rec}}, \, \cos \theta _\mu ^{\mathrm{rec}})$ distributions of the U/D ratio, with 500 kt$\cdot$yr exposure. The true value of $|\Delta m^2_{32}|$ is taken to be $2.46 \times 10^{-3}$ $\hbox {eV}^2$, and the other oscillation parameters $\theta _{12}$, $\theta _{23}$, $\theta _{13}$, and $\Delta m^2_{21}$ are varied over their currently allowed ranges, and systematics are taken into account

In this paper, we point out for the first time that the identification of an “oscillation valley” feature is possible, in the distribution of the U/D ratio in the plane of $(E_\mu ^{\mathrm{rec}}, \, \cos \theta _\mu ^{\mathrm{rec}}$). The oscillation dip observed in the one-dimensional $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ analysis above now appears as an oscillation valley in the two-dimensional $(E_\mu ^{\mathrm{rec}},\cos \theta _\mu ^{\mathrm{rec}}$) plane. We go on to develop an algorithm for finding the alignment of the valley, i.e. the slope of the best-fit line to the valley in the $(E_\mu ^{\mathrm{rec}},\cos \theta _\mu ^{\mathrm{rec}}$) plane, and show that it serves as a good proxy for $|\Delta m^2_{32}|$. As in the oscillation dip analysis, we calibrate $|\Delta m^2_{32}|$ against the alignment of the valley using 1000-year MC data, and estimate the uncertainties with 10-year data using 100 independent data sets. The expected 90% C. L. ranges of $|\Delta m^2_{32}|$ with systematic uncertainties and errors in other oscillation parameters are summarized in Table 5.

Fig. 11

Upper panels: the blue points and the blue line correspond to the calibration of actual $|\Delta m^2_{32}|$ with the location of the dip, obtained by using the 1000-year MC data sample. The gray bands represent the 90% C.L. regions of the location of the dip, and hence the inferred $|\Delta m^2_{32}|$ through calibration, for $|\Delta m^2_{32}| \,(\text{ true}) = 2.46\times 10^{-3}$ $\hbox {eV}^2$, with 5 years of exposure. Lower panels: the same results, by using the alignment of the valley. The results obtained from $\mu ^-$ and $\mu ^+$ events are shown in left and right panels of both the panels, respectively. The oscillation parameters have been kept fixed at the values given in Table 1, and no sytematics have been included

We also show the expected results for 90% C.L. ranges for $|\Delta m^2_{32}|$, obtained with half the data (5 years data, or an exposure of 250 kt$\cdot$yr), in Appendix A. This shows that preliminary results with the oscillation dip and oscillation valley analyses may already start appearing within the first few years of ICAL. Note that the aim of this exercise is not to compare the precisions achieved by different methods – indeed, this study does not aim to compete with the conventional $\chi ^2$ method for precision. Our aim is to present an approach (“oscillation dip”) that has proved useful in the past for establishing the oscillation hypothesis and rejecting some alternative hypotheses, and to go one step beyond it, by performing the “oscillation valley” analysis in the two-dimensional $(E_\mu ^{\mathrm{rec}}, \, \cos \theta _\mu ^{\mathrm{rec}}$) plane. An important feature of our analysis is that the reconstruction of dip and valley and their identification processes are data-driven. Of course, to retrieve the information on oscillation parameters using the calibration curve, we use MC simulations.

Note that the precisions on $|\Delta m^2_{32}|$, obtainable from our dip and valley analyses, are very similar to each other. This is expected, since the L/E dependence is assumed and the two-dimensional analysis offers no advantages for the determination of $|\Delta m^2_{32}|$ in the context of the SM. However, our focus has been on confirming that such two-dimensional reconstruction of the valley survives in the detector environment, i.e., the ICAL characteristics are sufficient to reconstruct the valley feature. This would also act as the fidelity test for the detector. The power of the valley analysis would become evident when L/E dependence is not assumed, where it would open up avenues for testing the oscillation framework from more angles – for example, by looking for effects of new physics on the shape, alignment, width, or depth of the valley. In the context of non-standard interactions (NSI) of neutrinos, this has been addressed in [47].

Though we have presented our results for ICAL, the same procedure can be used for any present or upcoming atmospheric neutrino experiment that has access to a large range of energies and baselines. An atmospheric neutrino experiment can perform the analysis based on the oscillation dip as well as the oscillation valley. Of course, if the detector cannot identify the muon charge, the data from neutrino and antineutrino channels will have to be combined, which may dilute some of the observable features. However, the principle of performing the oscillation valley analysis in the $(E_\mu ^{\mathrm{rec}}, \, \cos \theta _\mu ^{\mathrm{rec}}$) plane – going one step ahead of the $L_\mu ^{\mathrm{rec}}/E_\mu ^{\mathrm{rec}}$ analysis – may be adopted in any atmospheric neutrino experiment. Note that while the fixed-baseline experiments may in principle be able to identify the $L_\nu /E_\nu$ oscillation dip, they do not have access to the $(E_\nu , \, \cos \theta _\nu$) plane, and hence they cannot perform the oscillation valley analysis.

Even then, certain features of ICAL make it uniquely suited for such an analysis. It will likely be the first detector to identify the oscillation dip separately for the neutrino and antineutrino channels, which will also be a test for new physics that may affect the neutrino and antineutrino differently. Further, as far as the oscillation valley analysis goes, a crucial requirement for the capability to identify the alignment of the valley is enough number of points to determine the best-fit line as shown in the right panel of Fig. 9. This needs a large energy range to which the detector is sensitive (large number of y-bins), and an excellent angular resolution (large number of x-bins). ICAL is thus uniquely suited for the oscillation valley analysis, for providing an orthogonal approach to establish the nature of neutrino oscillations, and hence for making the neutrino oscillation picture more robust.

A Oscillation dip and valley using 5-year simulated data

While in this work we have presented the expected results with an exposure of 500 kt$\cdot$yr, i.e. with 10 years running of the 50 kt ICAL, it is worthwhile noticing that the identification of the oscillation dip and the oscillation valley, as well as the determination of the dip position and valley alignment, is possible even with half the data size. In this appendix, we show in Fig. 11 the results of the calibration of $|\Delta m^2_{32}|$ with the dip position and valley alignment, with 250 kt$\cdot$yr exposure of ICAL. We have adopted the same analysis as used for 500 kt$\cdot$yr with the same binning schemes as given in Tables 3 and 4. These could be some of the earliest significant neutrino oscillation results from ICAL.