Abstract
The next generation of water Cherenkov neutrino telescopes in the Mediterranean Sea are under construction offshore France (KM3NeT/ORCA) and Sicily (KM3NeT/ARCA). The KM3NeT/ORCA detector features an energy detection threshold which allows to collect atmospheric neutrinos to study flavour oscillation. This paper reports the KM3NeT/ORCA sensitivity to this phenomenon. The event reconstruction, selection and classification are described. The sensitivity to determine the neutrino mass ordering was evaluated and found to be 4.4\(\sigma \) if the true ordering is normal and 2.3\(\sigma \) if inverted, after 3 years of data taking. The precision to measure \(\varDelta m^2_{32}\) and \(\theta _{23}\) were also estimated and found to be \(85 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+1.9}_{-3.1})^{\circ }\) for normal neutrino mass ordering and, \(75 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+2.0}_{-7.0})^{\circ }\) for inverted ordering. Finally, a unitarity test of the leptonic mixing matrix by measuring the rate of tau neutrinos is described. Three years of data taking were found to be sufficient to exclude  event rate variations larger than 20% at \(3\sigma \) level.
event rate variations larger than 20% at \(3\sigma \) level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The standard framework of three neutrino flavour eigenstates (\(\nu _e\), \(\nu _\mu \), \(\nu _\tau \)), which are superpositions of the three mass eigenstates (\(\nu _1\), \(\nu _2\), \(\nu _3\)) with masses (\(m_1\), \(m_2\), \(m_3\)), has been established with more than two decades of neutrino oscillation physics research. By convention, \(\nu _1\) is the mass eigenstate with the largest \(\nu _e\) component, and \(\nu _3\) is the one with the smallest. The ordering of the neutrino mass eigenstates is not yet resolved, and it can be either \(m_1<m_2<m_3\) (‘normal ordering’, NO) or \(m_3<m_1<m_2\) (‘inverted ordering’, IO). The question of the neutrino mass ordering (NMO) is one of the main drivers of neutrino oscillation physics.
Neutrino mixing is described by the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix, U, [1,2,3] with
where \(\alpha = {e,\mu ,\tau }\) and \(i = {1,2,3}\). Under the assumption that the mixing matrix U is unitary, it is usually parametrised in terms of three mixing angles \(\theta _{12}\), \(\theta _{13}\) and \(\theta _{23}\), and a CP-violating phase \(\delta _{\text {CP}}\) [4]. Neutrino oscillations are sensitive to mass-squared differences \(\varDelta m_{ij}^2 = m^2_i - m^2_j ~ (i,j=1,2,3)\). From the three neutrino mass eigenstates two independent mass-squared differences can be constructed, which we choose as \(\varDelta m_{12}^2\) and \(\pm \left| \varDelta m_{23}^2 \right| \), where the sign of the latter is positive for NO and negative for IO.
Global fits of the available data form a coherent picture and provide values for \(\theta _{12}\), \(\theta _{13}\), \(\theta _{23}\), \(\varDelta m_{12}^2\) and \(\left| \varDelta m_{23}^2 \right| \) with few-percent level precision [5,6,7]. However, some questions remain: the determination of the value of \(\delta _{\mathrm{{CP}}}\), the octant of \(\theta _{23}\) (i.e. whether \(\theta _{23}\) is greater or smaller than \(\pi /4\)) and the neutrino mass ordering (i.e. the sign of \(\varDelta m_{23}^2\)). The current status is that global fits [8, 9] indicate a mild preference for NO over IO, second octant of \(\theta _{23}\) and \(\delta _{\mathrm{{CP}}} \approx \pi \) to \(\frac{3}{2} \pi \). The experiments driving the NMO sensitivity results are T2K [10], NOvA [11], MINOS [12], Super-Kamiokande [13] and IceCube/DeepCore [14]. Notably, the hints for NO tend to weaken in the light of combined analyses [8, 9] using the latest results from T2K [15] and NOvA [16].
Deriving strong experimental constraints on the unitarity of the \(3\times 3\) PMNS mixing matrix is challenging, as direct observations of  are difficult and the \(\tau \) rest-mass suppresses the
are difficult and the \(\tau \) rest-mass suppresses the  interaction cross section. Appearance of
interaction cross section. Appearance of  has been directly observed at the long baseline CNGS neutrino beam by OPERA [17, 18]. Evidence for
has been directly observed at the long baseline CNGS neutrino beam by OPERA [17, 18]. Evidence for  appearance has also been found on a statistical basis in the atmospheric neutrino flux by Super-Kamiokande [19] and IceCube [20]. However, the uncertainty on the normalisation of the
appearance has also been found on a statistical basis in the atmospheric neutrino flux by Super-Kamiokande [19] and IceCube [20]. However, the uncertainty on the normalisation of the  signal is currently too large to probe the unitarity of the PMNS mixing matrix. Non-unitarity would imply the incompleteness of the \(3\times 3\) flavour paradigm and could point to the existence of additional neutrino flavours. A statistically highly-significant detection of
signal is currently too large to probe the unitarity of the PMNS mixing matrix. Non-unitarity would imply the incompleteness of the \(3\times 3\) flavour paradigm and could point to the existence of additional neutrino flavours. A statistically highly-significant detection of  appearance from
appearance from  oscillations of atmospheric neutrinos could make an important contribution to further constrain the PMNS matrix elements involving
oscillations of atmospheric neutrinos could make an important contribution to further constrain the PMNS matrix elements involving  .
.
The NMO can be determined by measuring the energy and zenith angle dependent oscillation pattern of few-GeV atmospheric neutrinos that have traversed the Earth [21]. Matter-induced modifications [22, 23] of the oscillation probabilities lead to an enhancement of the  transition for neutrinos in the case of NO, and anti-neutrinos in the case of IO. Earth matter effects are due to coherent neutrino electron forward scattering. They arise mainly below \(E_\nu \lesssim 15\) GeV and depend on the electron density of the medium. The largest effects appear around 7 GeV for neutrinos passing through the Earth’s mantle and around 3 GeV for neutrinos passing through the Earth’s core. The oscillation pattern for neutrinos with respect to anti-neutrinos is flipped between the two mass orderings.
transition for neutrinos in the case of NO, and anti-neutrinos in the case of IO. Earth matter effects are due to coherent neutrino electron forward scattering. They arise mainly below \(E_\nu \lesssim 15\) GeV and depend on the electron density of the medium. The largest effects appear around 7 GeV for neutrinos passing through the Earth’s mantle and around 3 GeV for neutrinos passing through the Earth’s core. The oscillation pattern for neutrinos with respect to anti-neutrinos is flipped between the two mass orderings.
In case of detectors that cannot distinguish between neutrinos and anti-neutrinos on an event-by-event basis, the determination of the NMO can be based on the observation of a net difference in the event rates of atmospheric neutrinos, resulting from a higher interaction cross section (factor \(\sim 2\)) and the existing atmospheric flux difference (factor \(\sim 1.1\)) for neutrinos with respect to anti-neutrinos. Due to this event rate difference, the strength of the observed matter effects, i.e. the enhancement of the  transition, is larger for NO compared to IO. This is the experimental signature exploited by KM3NeT/ORCA and other atmospheric neutrino experiments to determine the NMO.
transition, is larger for NO compared to IO. This is the experimental signature exploited by KM3NeT/ORCA and other atmospheric neutrino experiments to determine the NMO.
KM3NeT is a large research infrastructure that will consist of a network of deep-sea neutrino detectors in the Mediterranean Sea. Two underwater neutrino telescopes, called ARCA and ORCA, are currently under construction [24]. ARCA (Astroparticle Research with Cosmics in the Abyss) is a sparsely instrumented gigaton-scale detector optimised for TeV–PeV neutrino astronomy. ORCA (Oscillation Research with Cosmics in the Abyss) is a more densely instrumented detector optimised for measuring the oscillation of few-GeV atmospheric neutrinos in order to determine the neutrino mass ordering.
With atmospheric neutrino data, ORCA can also perform a precise measurement of \(\theta _{23}\) and \(\varDelta m_{23}^2\) as well as a high-statistics measurement of  appearance in the atmospheric neutrino flux, which allows to probe deviations from the unitarity assumption of the 3-neutrino mixing. Sensitivity for tau-neutrino appearance mainly comes from atmospheric neutrinos with energy \(\gtrsim {15}\,{\mathrm{GeV}}\) and therefore has only a weak dependence on the still undetermined neutrino mass ordering.
appearance in the atmospheric neutrino flux, which allows to probe deviations from the unitarity assumption of the 3-neutrino mixing. Sensitivity for tau-neutrino appearance mainly comes from atmospheric neutrinos with energy \(\gtrsim {15}\,{\mathrm{GeV}}\) and therefore has only a weak dependence on the still undetermined neutrino mass ordering.
A first estimation of the sensitivity of ORCA to the NMO as well as to other oscillation parameters was published in the ‘Letter of Intent for KM3NeT 2.0’ (LoI) [24]. Since then, the detector and the analysis methods have been further optimised. First, the detector geometry has been updated. In addition, significant improvements in the neutrino detection efficiency as well as reconstruction performance have been achieved as illustrated in Sect. 2.4. The event classification procedure has been significantly improved as well. We use now three event classes and hit features are included, this is discussed in Sect. 2.5. At the same time the analysis has been refined. The detector response is modeled in greater detail and a more complete list of systematic effects is now considered. These effects partly compensate the expected gain in sensitivity from the improvements mentioned above but make them at the same time more realistic. The updated sensitivities are presented in this paper.
This paper is organised as follows. Section 2 describes the detector design and the simulations performed to obtain the detector response to atmospheric neutrinos, atmospheric muons as well as optical background noise. Then, the algorithms used for event reconstruction and for high flavour purity event classification are described. In Sect. 3, the methods used to analyse these samples and derive the sensitivity to the NMO, the atmospheric oscillation parameters and the  appearance are presented together with the results. Finally, Sect. 4 summarises the main detector and analysis updates and the expected sensitivity to neutrino oscillations.
appearance are presented together with the results. Finally, Sect. 4 summarises the main detector and analysis updates and the expected sensitivity to neutrino oscillations.
2 ORCA detector response
The ORCA detector design comprises a 3-dimensional array of photosensors that register the Cherenkov light produced by relativistic charged particles emerging from neutrino-induced interactions. The arrival time of the Cherenkov photons and the position of the sensors are used to reconstruct the energy and direction of the incoming neutrino as well as the event topology.
2.1 Detector design
The ORCA detector design consists of an array of 115 vertical detection units (DUs) featuring 18 digital optical modules (DOMs) each. Each DOM is a pressure-resistant glass sphere, housing 31 photomultiplier tubes (PMTs) of 3-inch diameter and the related electronics. The KM3NeT PMTs are characterised in [25].
The detector is located at the KM3NeT-France site and the base container of each DU is placed at about \({2450}\,{\mathrm{m}}\) depth. The DUs are arranged in a circular footprint with a radius of about \({115}\,{\mathrm{m}}\) with an average spacing between the DUs of \({20}\,{\mathrm{m}}\). Along a DU, the vertical spacing between the DOMs varies between \({8.7}\,{\mathrm{m}}\) to \({10.9}\,{\mathrm{m}}\) (due to technical constraints from the deployment procedure) with an average of \({9.3}\,{\mathrm{m}}\). The first DOM is at a distance of about \({30}\,{\mathrm{m}}\) from the seabed [26]. In total, a volume of about \({6.7\times 10^{6}}\,{\mathrm{m}^3}\) (equivalent to \({7.0}\,{\mathrm{Mt}}\) of sea water) is instrumented. This detector configuration is the outcome of an optimisation study using the sensitivity to the NMO as figure of merit.
2.2 Simulation
Detailed Monte Carlo (MC) simulations are used to evaluate the detector response to atmospheric neutrinos, atmospheric muons and optical background noise. The simulation chain used for the analysis presented in this paper is similar to the one described in [24].
Neutrino induced interactions in sea water are simulated with gSeaGen [27], a software package based on the widely used GENIE (version 2.12.10) code [28, 29]. Neutrinos and antineutrinos in the energy range from 1 to \({100}\,{\mathrm{GeV}}\) are simulated and weighted to reproduce the conventional atmospheric neutrino flux following the Honda model [30]. All particles emerging from neutrino interactions are propagated with the GEANT4-based software package KM3Sim [31]. Using this software, Cherenkov photons are generated from primary and secondary particles, tracked through the sea water taking into account absorption and scattering, and detected by the PMTs.
Atmospheric muon events are generated using the MUPAGE package [32]. The KM3 package [33, 34] is then used for tracking the muons in sea water and the subsequent Cherenkov light production.
The PMT response and the readout are simulated using custom KM3NeT software. The digitised PMT output signal is typically called a hit. In this step, the optical background due to Cherenkov light from \(\beta \)-decays of \(^{40}\)K in the sea water is also added: an uncorrelated hit rate of \({10}\,{\mathrm{kHz}}\) per PMT as well as time-correlated noise on multiple PMTs on each DOM (\({600}\,{\mathrm{Hz}}\) twofold, \({60}\,{\mathrm{Hz}}\) threefold, \({7}\,{\mathrm{Hz}}\) fourfold, \({0.8}\,{\mathrm{Hz}}\) fivefold and \({0.08}\,{\mathrm{Hz}}\) sixfold). The simulated time-correlated noise rate is taken from the data of the first deployed DUs [35]. Finally, the simulated data is filtered by dedicated trigger algorithms to identify events induced by energetic particles. The trigger algorithms are designed to search for large clusters of causally-connected hits. The same trigger algorithms are applied to both simulated and real data.
Compared to the LoI [24], significant improvements have been made in the triggering of faint events with only a few tens of detected photons [36]. A new trigger algorithm has been developed for the needs of ORCA. It is based on only one local coincidence (photons recorded on two or more PMTs of the same DOM within 10 ns) and a tunable number of causally-connected single hits on DOMs in the vicinity. A minimum of seven additional hits distributed over at least three different DOMs are required. This new algorithm significantly increases the trigger efficiency in the few-GeV neutrino energy range, while still satisfying the bandwidth requirements of the data acquisition system.
The total trigger rate due to atmospheric muons is about \({50}\,{\mathrm{Hz}}\) and noise events add about \({54}\,{\mathrm{Hz}}\), while atmospheric neutrinos are triggered with a rate of about \({8}\,{\mathrm{mHz}}\). In total, 1.4 days of noise events, 14 days of atmospheric muons and more than 15 years of atmospheric neutrinos are simulated. These event samples are sufficient to probe a percent-level background contamination (see Sect. 2.5). In future analysis of real data, the background will be included based on run-by-run simulations [34], accounting for the detector and data-taking conditions.
2.3 Event topologies
Two distinct event topologies can be distinguished in the detector: track-like and shower-like. In the few-GeV energy range, muons are the only particles that can be confidently identified, because they are the only particles that appear as tracks in the detector, with a track length proportional to the muon energy (\(\sim 4\) m/GeV). Electrons and hadrons initiate particle showers that develop over distances of a few metres. Compared to elongated muon tracks, these showers appear as localised light sources in the detector. All neutrino-induced events producing a muon with sufficient energy are called track-like, i.e.  charged-current (CC) events and
charged-current (CC) events and  events with muonic \(\tau \) decays. All other neutrino-induced events are called shower-like, i.e.
events with muonic \(\tau \) decays. All other neutrino-induced events are called shower-like, i.e.  neutral-current (NC) events,
neutral-current (NC) events,  events and
events and  events with non-muonic \(\tau \) decays.
events with non-muonic \(\tau \) decays.
2.4 Event reconstruction and event selection
Dedicated reconstruction algorithms are applied for track-like and shower-like events as well as an event topology classification algorithm. The track and shower reconstruction algorithms are described in [37, 38], respectively. Both reconstruction algorithms are maximum likelihood fits and reconstruct the energy and direction as well as interaction vertex position and time. Events reconstructed as upgoing, i.e. with a negative cosine zenith angle, are selected based on the reconstruction quality and containment. The containment criteria are based on the event position and direction inside the instrumented detector volume [36]. The goal of the event preselection is to fulfil two main purposes: suppress background events and select well-reconstructed events with a good reconstruction accuracy.
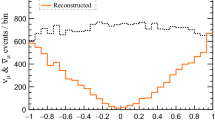
Effective detector volume as a function of true neutrino energy \(E_\nu \) for different neutrino flavours and interactions. Events are weighted according to the Honda atmospheric neutrino flux model and averaged over the zenith angle. Only events reconstructed and selected as upgoing are used. The dashed black line indicates the instrumented volume of the detector
Probability distribution of the reconstructed energy as a function of true neutrino energy for upgoing \(\nu _{\text {e}}\,\text {CC}\) and \(\overline{\nu }_{e}\,\text {CC}\) events classified as shower-like (left) as well as \(\nu _{\mu }\,\text {CC}\) and \(\overline{\nu }_{\mu }\,\text {CC}\) events classified as track-like (right). Solid and dashed black lines indicate 50, 15 and 85% quantiles. For a definition of shower- and track-like events see Eq. 2. The red diagonal line indicates perfect energy reconstruction
Median direction resolution as a function of true neutrino energy \(E_\nu \) for upgoing \(\nu _{\text {e}}\,\text {CC}\) and \(\overline{\nu }_{e}\,\text {CC}\) events classified as shower-like as well as \(\nu _{\mu }\,\text {CC}\) and \(\overline{\nu }_{\mu }\,\text {CC}\) events classified as track-like. For a definition of shower- and track-like events see Eq. 2
The effective detector volume after the event preselection is shown in Fig. 1 for upgoing neutrinos weighted according to the Honda atmospheric neutrino flux model [30]. The effective detector volume reaches a plateau and is nearly as large as the instrumented detector volume for  with \(E_\nu \gtrsim {15}\,{\mathrm{GeV}}\), while 50% efficiency is reached for \(E_\nu \sim {4}\,{\mathrm{GeV}}\). Compared to the LoI [24], the turn-on region of the effective detector volume is shifted by about 20% to lower energies due to improvements in event triggering and reconstruction. Indeed, as discussed in Sect. 2.2, additional methods have been developed to record events with a lower number of in-time hits from the same DOM but with extra hits causally connected on other DOMs and a similar method is applied at the prefit stage of the reconstruction. These refinements contribute to lower the detection energy threshold. In general, the effective volume is smaller for
with \(E_\nu \gtrsim {15}\,{\mathrm{GeV}}\), while 50% efficiency is reached for \(E_\nu \sim {4}\,{\mathrm{GeV}}\). Compared to the LoI [24], the turn-on region of the effective detector volume is shifted by about 20% to lower energies due to improvements in event triggering and reconstruction. Indeed, as discussed in Sect. 2.2, additional methods have been developed to record events with a lower number of in-time hits from the same DOM but with extra hits causally connected on other DOMs and a similar method is applied at the prefit stage of the reconstruction. These refinements contribute to lower the detection energy threshold. In general, the effective volume is smaller for  and
and  than for
than for  events as the outgoing neutrinos are invisible to the detector. For \(\overline{\nu }_{\text {e},\mu }\,\text {CC}\) events the effective volume is larger than for \(\nu _{\text {e},\mu }\,\text {CC}\) due to the lower average inelasticity and the resulting higher average light yield (at the considered energies hadronic showers have a smaller average light yield than electromagnetic showers). The difference between \(\nu _{\tau }\,\text {CC}\) and \(\overline{\nu }_{\tau }\,\text {CC}\) is diluted due to the effect of finite mass of the \(\tau \) lepton on the neutrino interaction cross sections [39]. Due to the KM3NeT DOM design, more PMTs are oriented downwards (housed in the lower hemisphere) compared to oriented upwards (housed in the upper hemisphere), resulting in a higher photon detection efficiency for upgoing compared to horizontal events.
events as the outgoing neutrinos are invisible to the detector. For \(\overline{\nu }_{\text {e},\mu }\,\text {CC}\) events the effective volume is larger than for \(\nu _{\text {e},\mu }\,\text {CC}\) due to the lower average inelasticity and the resulting higher average light yield (at the considered energies hadronic showers have a smaller average light yield than electromagnetic showers). The difference between \(\nu _{\tau }\,\text {CC}\) and \(\overline{\nu }_{\tau }\,\text {CC}\) is diluted due to the effect of finite mass of the \(\tau \) lepton on the neutrino interaction cross sections [39]. Due to the KM3NeT DOM design, more PMTs are oriented downwards (housed in the lower hemisphere) compared to oriented upwards (housed in the upper hemisphere), resulting in a higher photon detection efficiency for upgoing compared to horizontal events.
In total, a sample of about 66,000 upgoing neutrinos per year, corresponding to a rate of about 2 mHz, will be detected and can be used for further analysis. In addition, about 0.4 Hz of noise events and 0.1 Hz of atmospheric muon events pass the preselection criteria. To suppress the noise and atmospheric muon background, a more sophisticated event classification is performed, as detailed in Sect. 2.5.
The energy resolution for \(\nu _{\text {e}}\,\text {CC}\) and \(\overline{\nu }_{e}\,\text {CC}\) events classified as shower-like, as well as \(\nu _{\mu }\,\text {CC}\) and \(\overline{\nu }_{\mu }\,\text {CC}\) events classified as track-like are shown in Fig. 2. The energy resolution is Gaussian-like with \(\varDelta E / E \approx 25\)% for  events with \(E_\nu = {10}\,{\mathrm{GeV}}\), and it is dominated by the intrinsic light yield fluctuations in the hadronic shower [40]. For
events with \(E_\nu = {10}\,{\mathrm{GeV}}\), and it is dominated by the intrinsic light yield fluctuations in the hadronic shower [40]. For  , the resolution on the neutrino energy levels off at \(\varDelta E / E \approx 35\)% as the reconstructed muon track tends not to be fully contained inside the instrumented volume.
, the resolution on the neutrino energy levels off at \(\varDelta E / E \approx 35\)% as the reconstructed muon track tends not to be fully contained inside the instrumented volume.
Figure 3 shows the median resolution on the neutrino direction for the same set of simulated neutrino events. At \(E_\nu = {10}\,{\mathrm{GeV}}\), the median neutrino direction resolution is \(9.3^\circ \)/\(7.0^\circ \)/\(8.3^\circ \)/\(6.5^\circ \) for \(\nu _{\text {e}}\)/\(\overline{\nu }_{e}\)/\(\nu _{\mu }\)/\(\overline{\nu }_{\mu }\,\text {CC}\) events, respectively. The neutrino direction resolution is dominated by the intrinsic \(\nu \)–lepton scattering kinematics [40], resulting in better resolutions for \(\overline{\nu }\) CC than for \(\nu \) CC due to the smallerBjorken-y.
Left: Distribution of the atmospheric muon score variable for the RDF trained to separate between neutrinos and atmospheric muons, for the main classes of events. Right: Fraction of remaining neutrinos weighted with an oscillated atmospheric flux versus atmospheric muon contamination in the final sample
2.5 Event classification
For event classification, random decision forests (RDFs) [41] are used, which consist of an ensemble of binary decision trees.
Two RDFs are trained individually for selecting neutrino candidates against each of the two dominant classes of background – atmospheric muons and noise events – and a third one is trained to distinguish track-like from shower-like event topologies.
To train the classifiers,  events have been used to represent track-like event topologies. For showers
events have been used to represent track-like event topologies. For showers  and
and  events have been used. The neutrino event distributions were flattened in \(\log _{10}\) of neutrino energy and the numbers of events per class were balanced between tracks and showers. In contrast, background was fed with the expected true spectra.
events have been used. The neutrino event distributions were flattened in \(\log _{10}\) of neutrino energy and the numbers of events per class were balanced between tracks and showers. In contrast, background was fed with the expected true spectra.
Each trained classifier yields a score variable (atmospheric_muon_score, noise_score, track_score). These represent the fraction of trees voting for the respective result class. The individual score parameters allow to separately optimise the suppression of the atmospheric muon and noise components using selection cuts and to divide the remaining events into different classes for analysis.
Fractions of preselected neutrino events of different types that are classified in the track class, the intermediate class, and the shower class, as a function of true neutrino energy. The definition of the classes is given in Eq. 2. Coloured areas correspond to the composition of the atmospheric neutrino flux. Solid and dashed lines show individual fractions for neutrinos and anti-neutrinos, respectively
In the training, only events which pass the preselection requirements for either tracks or showers were used. The classifiers were trained independently of each other. Consequently, no further selection based on the resulting score from one of the other classifiers and none of the resulting score variables is used to train the RDFs. In the training, a forest size of 101 trees,Footnote 1 and 50,000 events per class (25,000 for noise suppression due to smaller available statistics after preselection) have been used. In the training process, five-fold cross validation was applied.
To ensure diversity of trees within the forest, each tree was trained on a randomly drawn 60% subset of the training variables and 40% of the available training events.
The training variables consist of the fitted event parameters and additional variables quantifying the reconstruction quality. These are provided by the track and shower algorithms [37, 38]. Additional sets of variables fed to the classifier are relative distances between the fitted track and shower hypothesis and variables quantifying how well the Cherenkov light signature is contained within the instrumented volume.
To separate between track- and shower-like signatures, further hit-based variables are added, which have not been used in [24] and exploit the distribution of detected photon hits in the detector. These are based on likelihood ratios of the time and position of the hits expected for the  and
and  event hypotheses with respect to the reconstructed position and direction of the shower reconstruction algorithm. More information on the classifier training can be found in [36].
event hypotheses with respect to the reconstructed position and direction of the shower reconstruction algorithm. More information on the classifier training can be found in [36].
The classifier performance in rejecting the atmospheric muon background is given in Fig. 4. The distribution of the atmospheric_muon_score (left panel) shows a clear separation between neutrinos weighted with an oscillated atmospheric flux and atmospheric muons. The increase of neutrino events with a \(track_score \approx 1\) comes from  CC and
CC and  CC events with \(\tau ^\pm \) decay to \(\mu ^\pm \) and is absent for other neutrino channels. Noise events have not been used in training the classifier and therefore are not clustered at the edges of the distributions. A relatively hard cut at atmospheric_muon_score \(< 0.05\) is used to reach a \(\sim 3\%\) contamination level, cf. Fig. 4 (right panel). The loss in neutrino efficiency for the atmospheric muon rejection does not strongly depend on the neutrino energy and is about \(\sim 5\%\).
CC events with \(\tau ^\pm \) decay to \(\mu ^\pm \) and is absent for other neutrino channels. Noise events have not been used in training the classifier and therefore are not clustered at the edges of the distributions. A relatively hard cut at atmospheric_muon_score \(< 0.05\) is used to reach a \(\sim 3\%\) contamination level, cf. Fig. 4 (right panel). The loss in neutrino efficiency for the atmospheric muon rejection does not strongly depend on the neutrino energy and is about \(\sim 5\%\).
Noise events are rejected sufficiently with a cut on noise_score \(< 0.1\). As can be seen from Fig. 5 (right panel), the rejection of noise events does not significantly reduce the number of neutrino events in the analysis sample. However, the reduction of neutrino events tends to increase for faint neutrino events with energies near the detection threshold. The proposed cuts on the atmospheric_muon_score and noise_score values reduce the muon and noise contamination of the selected event sample to a level which can be safely neglected in the sensitivity study.
The training of track- versus shower-like neutrino event signatures results in a \(\texttt {track\_score}\) variable, representing the fraction of trees voting for the candidate event to be track-like. Using this variable, events can be split in three event classes based on the following criteria:
Comparison of the classifier performance as a function of true neutrino energy in terms of the separation power metric as defined in Eq. 3. Separation power for training with (solid) and without (dashed) hit-based features is shown
The performance of the event type classifier for neutrinos is shown in Fig. 6, where the fractions of events ending up in the respective class are presented as a function of neutrino energy.
The fraction of correctly classified events increases steeply in the energy region up to \(\sim {15}\,{\mathrm{GeV}}\), where less than \(5\%\) of  and
and  are mis-classified as tracks. At \(\sim {15}\,{\mathrm{GeV}}\), 85% \(\overline{\nu }_{\mu }\,\text {CC}\) and 70% of \(\nu _{\mu }\,\text {CC}\) are correctly classified as tracks. The better classification performance for \(\overline{\nu }_{\mu }\,\text {CC}\) compared to \(\nu _{\mu }\,\text {CC}\) is due to the different Bjorken-y distribution resulting in longer tracks of the final state muon for \(\overline{\nu }_{\mu }\,\text {CC}\). The fraction of
are mis-classified as tracks. At \(\sim {15}\,{\mathrm{GeV}}\), 85% \(\overline{\nu }_{\mu }\,\text {CC}\) and 70% of \(\nu _{\mu }\,\text {CC}\) are correctly classified as tracks. The better classification performance for \(\overline{\nu }_{\mu }\,\text {CC}\) compared to \(\nu _{\mu }\,\text {CC}\) is due to the different Bjorken-y distribution resulting in longer tracks of the final state muon for \(\overline{\nu }_{\mu }\,\text {CC}\). The fraction of  events classified as tracks is higher compared to
events classified as tracks is higher compared to  and
and  reflecting the 17% branching ratio for muonic tau decays.
reflecting the 17% branching ratio for muonic tau decays.
To quantify the gain in classification performance when including the additional variables based on the expected hit distributions for  and
and  , the separation power, S, is used. It quantifies the overlap in the distribution of the track_score between
, the separation power, S, is used. It quantifies the overlap in the distribution of the track_score between  and
and  events by using the correlation coefficient, C, and is defined as:
events by using the correlation coefficient, C, and is defined as:

The separation power is calculated in slices of neutrino energy \(\varDelta E\) by summing over binned probabilities for the track_score values, \(P_{i,\text {score}}\). The resulting quantity is shown as a function of neutrino energy in Fig. 7. The event type classification reaches 50% separation power at 20% lower neutrino energies when including hit-based variables in the classifier.
3 Sensitivity calculation
3.1 Method
The neutrino oscillation parameters are studied by analysing the expected bi-dimensional distributions – reconstructed energy, reconstructed cosine zenith angle – of the neutrino candidates in the three event classes (track, intermediate and shower).
These distributions are obtained based on the true energy and cosine zenith angle event distributions split by neutrino interaction type (\(\nu _{\text {e}}\,\text {CC}\), \(\overline{\nu }_{e}\,\text {CC}\) , \(\nu _{\mu }\,\text {CC}\), \(\overline{\nu }_{\mu }\,\text {CC}\),\(\nu _{\tau }\,\text {CC}\), \(\overline{\nu }_{\tau }\,\text {CC}\), \(\nu \,\text {NC}\), \(\overline{\nu }\,\text {NC}\)). The true distributions are derived from the neutrino flux [30], the neutrino cross section [42], the probability for each neutrino flavour to oscillate while traversing the Earth computed with the OscProb software [43] and a bi-dimensional parametric description of the detector effective volume. The latter is obtained based on the simulations described in Sect. 2.2.
Each of the eight true energy and cosine zenith angle distributions are then split in the three event classes (track, intermediate and shower), resulting in 24 distributions. The fractions of the distribution classified in each category, given the true neutrino energy, is obtained using parametric functions, derived from simulations.
The distributions of the reconstructed quantities are obtained from these 24 distributions using two sets of parametric functions that describe, first, the probability for a neutrino to be reconstructed at any energy given the true neutrino energy and, second, the probability for a neutrino to be reconstructed at any zenith angle given the true neutrino energy and true zenith angle.
These 24 distributions are merged to form the three final distributions of observables (reconstructed energy and cosine zenith angle) for events classified as track, intermediate and shower.
These three final distributions are used as an Asimov data set [44] to derive the median sensitivity to the oscillation parameters under study. A distribution obtained with a given set of oscillation parameters, the null hypothesis, is confronted with other sets, the alternate hypotheses, using \(LL_0\), the Poisson likelihood \(\chi ^2\) [45], defined as:
where \(n^{\mathrm{null}}_i\) and \(n^{\mathrm{alt}}_i\) are the expected numbers of events under the null and alternate hypotheses, respectively, in the \(i^{th}\) region of the reconstructed energy – cosine zenith angle plane.
Relevant external information on the neutrino oscillation parameters [6] and model uncertainties are taken into account by adding to \(LL_0\) extra contributions measuring the discrepancy between the parameter value, \(p_i^{obs}\), and the one expected, \(p_i^{exp}\), in standard deviation unit, \(\sigma _i\):
The sensitivity to the parameters under study (described in the next sections) is obtained from the \(LL_{\mathrm{eff}}\), minimised over all remaining parameters, as \(\sqrt{LL_{\mathrm{{eff}},\mathrm {min}}}\).
A first set of model parameters reflecting the current knowledge on the neutrino flux are considered using the uncertainties reported in [46]:
-
1.
the spectral index of the neutrino flux energy distribution is allowed to vary without constraint,
-
2.
the ratio of upgoing to horizontally-going neutrinos,
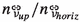 , is allowed to vary with a standard deviation of 2% of the parameter’s nominal value,
, is allowed to vary with a standard deviation of 2% of the parameter’s nominal value, -
3.
the ratio between the total number of
 and
and 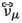 ,
, 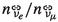 , is allowed to vary with a standard deviation of 2% of the parameter’s nominal value,
, is allowed to vary with a standard deviation of 2% of the parameter’s nominal value, -
4.
the ratio between the total number of \(\nu _{\text {e}}\) and \(\overline{\nu }_{e}\), \(n_{\nu _{\text {e}}} / n_{\overline{\nu }_{e}}\), is allowed to vary with a standard deviation of 7% of the parameter’s nominal value,
-
5.
the ratio between the total number of \(\nu _{\mu }\) and \(\overline{\nu }_{\mu }\), \(n_{\nu _{\mu }} / n_{\overline{\nu }_{\mu }}\), is allowed to vary with a standard deviation of 5% of the parameter’s nominal value.
In addition, two uncertainties on the neutrino cross section are considered:
-
6.
the number of NC events is scaled by a factor \(n_{NC}\) to which no constraint is applied,
-
7.
the number of
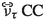 is scaled by a factor \(n_\tau ^{CC}\) to which no constraint is applied.
is scaled by a factor \(n_\tau ^{CC}\) to which no constraint is applied.
(Left) Expected event distributions for NO after 3 years of data taking for events classified as track (top), intermediate (middle), and shower (bottom). (right) Signed binned Poisson likelihood \(\chi ^2\) derived using these distributions and the ones obtained minimising \(LL_{\mathrm{eff}}\) with the IO hypothesis. If more events are expected for NO than for IO, the value plotted is \(LL_{0,i}\) which, as defined in Eq. 4, is positive. Otherwise, the value plotted is \(-LL_{0,i}\)
Then three uncertainties on the detector response are taken into account:
-
8.
the absolute energy scale of the detector depends on the knowledge of the PMT efficiencies and the water optical properties, as shown in [24] (section 3.4.6). The time dependent PMT efficiencies are monitored permanently with high fidelity, using coincidence signals from \(^{40}\)K decays, as demonstrated in ANTARES [47]. Several methods are under study to monitor in-situ the water optical properties, exploiting both Cherenkov light from atmospheric muons and \(^{40}\)K decays as well as signals from artificial light sources. The combination of these methods will allow to constrain the energy scale uncertainty to a few percent. In the study presented here, the energy scale of the detector is allowed to vary with a standard deviation of 5% around its nominal value,
-
9.
the light yield in hadronic showers, Had. Energy Scale is allowed to vary with a standard deviation of 6% of the parameter’s nominal value, as obtained while comparing two different simulation software packages Gheisha and Fluka [40],
-
10.
the number of events in the three classes is allowed to vary without constraints via three scaling factors \(n_{\mathrm{Tracks}}\), \(n_{\mathrm{Intermediate}}\), \(n_{\mathrm{Showers}}\).
Previous studies [24, 48] showed that the uncertainty on the Earth model had negligible effects on the NMO sensitivity and is thus ignored in this study. Systematics 2 and 4–10 were not included in the previous analysis [24]. Table 1 reports all the parameters and the external constraints applied to them.
3.2 NMO sensitivity
The sensitivity to the neutrino mass ordering is obtained as a function of \(\theta _{23}\) using the method described in Sect. 3.1. For every \(\theta _{23}\) value, each mass ordering hypothesis – the null hypothesis – is confronted with the reversed one – the alternate hypothesis. The oscillation parameters used for the null hypothesis are reported in Table 2 as well as the constraints applied to them in the minimisation procedure.
a Sensitivity to NMO after 3 years of data taking, as a function of the true \(\theta _{23}\) value, for both normal (red upward pointing triangles) and inverted ordering (blue downward pointing triangles) under three assumptions for the \(\delta _{\text {CP}}\) value: the world best fit point for NO, IO reported in Table 2 (plain line), \({0}^{\circ }\) (dotted line) or \({180}^{\circ }\) (dashed line). The coloured shaded areas represent the sensitivity that 68% of the experiment realisation would yield, according to the Asimov approach [44]. b Sensitivity to NMO as a function of data taking time for both normal (red upward pointing triangles) and inverted ordering (blue downward pointing triangles) and assuming the oscillation parameters reported in Table 2
The distributions of selected events after 3 years of data taking for the null hypothesis assuming NO, \(n^{\mathrm{null}}_i\), obtained with the parametric detector response are shown in Fig. 8 using a \(40\times 40\) grid of energy, equally logarithmically spaced between 2 and 100 GeV, and cosine zenith angle equally spaced between 0 and \(-1\). Around 51d3 events are expected for the track-class, 63d3 for the intermediate-class and 64d3 for the shower-class. Figure 8 shows also the \(LL_{0, i,\mathrm {min}}\) obtained confronting these distributions with the alternate hypothesis ones.
The sensitivity to the NMO after 3 years of data taking is reported as a function of \(\theta _{23}\) for both NMO in Fig. 9a. Assuming the current best estimates for \(\theta _{23}\) (see Table 2), the NMO sensitivity is 4.4\(\sigma \) if the true NMO is NO and 2.3\(\sigma \) if it is IO. Table 1 illustrates the fit results at one test point for oscillation parameters reported in Table 2. None of the systematic uncertainties exhibits a strong pull in this wrong-hierarchy fit, demonstrating that degeneracies between the NMO choice and systematic uncertainties are generally small.
Figure 9b shows the sensitivity for both NMO as a function of data taking time. The NMO can be determined at 3\(\sigma \) level after 1.3 years if the true NMO is NO, and after 5.0 years if it is IO.
3.3 Sensitivity to \(\varDelta m^2_{32}\) and \(\theta _{23}\)
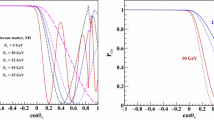
The sensitivity to \(\varDelta m^2_{32}\) and \(\theta _{23}\) is obtained using the method described in Sect. 3.1. The null hypothesis, assuming the latest oscillation parameter values, reported in Table 2, is confronted with a set of alternate hypotheses, one for each point in the \(\varDelta m^2_{32}\), \(\theta _{23}\) plane. The NMO is kept fixed in the \(LL_{\mathrm{eff}}\) minimisation. All (\(\varDelta m^2_{32}\), \(\theta _{23}\)) points for which the resulting \(LL_{\mathrm{{eff,min}}}\) exceeds by 4.61 [4] the \(LL_{\mathrm{eff}}\) minimum in the (\(\varDelta m^2_{32}\), \(\theta _{23}\)) plane are excluded with 90% confidence level. The oscillation parameters used and the constraints applied during the \(LL_{\mathrm{eff}}\) minimisation are reported in Table 2. The resulting 90% confidence level contours for both NMO are shown in Fig. 10. The 90% confidence level interval on \(\varDelta m^2_{32}\) and \(\theta _{23}\) are \(85 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+1.9}_{-3.1})^{\circ }\) for NO and, \(75 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+2.0}_{-7.0})^{\circ }\) for IO.
The same analysis allows to calculate the significance to determine the octant of \(\theta _{23}\). The alternate hypothesis is now the minimal \(LL_{\mathrm{eff}}\) for \(\theta _{23}\) in the opposite octant with respect to the true \(\theta _{23}\) value. The results are shown in Fig. 11, which illustrates the needed data taking time to reach a 1, 2 and 3\(\sigma \) octant significance as a function of the true value of \(\theta _{23}\). Dashed lines ignore the NMO, while for solid lines the NMO is assumed to be known. KM3NeT/ORCA can constrain the octant with better than 95% confidence level after 6 years of data taking for \(\left| {\text {sin}^2\theta _{23}}-0.5\right| < 0.05\).
Expected sensitivity to determine the \(\theta _{23}\) octant at 1 (blue), 2 (green) or 3\(\sigma \) (red) as a function of data taking time for both NO (a) and IO (b) assuming the true NMO is known (solid line) or unknown (dashed line). The dashed lines differ from the plain ones when the \(LL_{\mathrm{eff}}\) minimisation converges to the wrong NMO
3.4 Sensitivity to  appearance
appearance
The appearance of  is determined by measuring the normalisation factor
is determined by measuring the normalisation factor  of the
of the  contribution. For this study, NO is assumed. As in the analyses above, the oscillation parameter values are taken from Table 2 and the normalisation is fixed to
contribution. For this study, NO is assumed. As in the analyses above, the oscillation parameter values are taken from Table 2 and the normalisation is fixed to  for the null hypothesis. The latter is expected if the commonly accepted picture of unitary \(3\times 3\) neutrino mixing is complete and, in addition, the assumed standard model cross sections are correct. A measurement in tension with
for the null hypothesis. The latter is expected if the commonly accepted picture of unitary \(3\times 3\) neutrino mixing is complete and, in addition, the assumed standard model cross sections are correct. A measurement in tension with  would therefore provide a model-independent test for new physics. Two choices to scale the
would therefore provide a model-independent test for new physics. Two choices to scale the  contribution are possible for the alternate hypotheses. The first is to vary only the
contribution are possible for the alternate hypotheses. The first is to vary only the  CC contribution, leaving the NC contribution fixed to unity. The second allows for a combined CC+NC scaling of the
CC contribution, leaving the NC contribution fixed to unity. The second allows for a combined CC+NC scaling of the  flux. Note, that the CC-only case correlates directly with a scaling of the
flux. Note, that the CC-only case correlates directly with a scaling of the  CC cross section. Both choices, CC-only and CC+NC normalisation scaling, have been adopted in previous experiments ( [18, 19] and [20], respectively).
CC cross section. Both choices, CC-only and CC+NC normalisation scaling, have been adopted in previous experiments ( [18, 19] and [20], respectively).
The sensitivity is evaluated using the method described in Sect. 3.1 extended by the additional scaling parameter  , affecting the
, affecting the  CC flux and in case of CC + NC scaling also the NC fraction that has oscillated into the
CC flux and in case of CC + NC scaling also the NC fraction that has oscillated into the  channel. While oscillations of the NC do not need to be considered if the overall flux remains unchanged, this is different for
channel. While oscillations of the NC do not need to be considered if the overall flux remains unchanged, this is different for  . In this case the procedure to populate the event distributions is modified and includes the oscillated fractions of each flavour, which allows to scale the
. In this case the procedure to populate the event distributions is modified and includes the oscillated fractions of each flavour, which allows to scale the  contribution accordingly.
contribution accordingly.
The sensitivity to  appearance after 1 and 3 years of operation for CC and CC+NC normalisation scaling is shown for a scan in
appearance after 1 and 3 years of operation for CC and CC+NC normalisation scaling is shown for a scan in  in Fig. 12a. In Fig. 12b, the sensitivity for CC-only scaling is presented as a function of operation time.
in Fig. 12a. In Fig. 12b, the sensitivity for CC-only scaling is presented as a function of operation time.
KM3NeT/ORCA will already be able to confirm the exclusion of non-appearance with high statistical significance with few months of data-taking. For CC the normalisation can be constrained to \(\pm 30\%\) at \(3\sigma \)-level and to \(\pm 10\%\) at \(1\sigma \)-level after 1 year of data taking. After 3 years, the normalisation can be constrained to \(\pm 20\%\) at \(3\sigma \)-level, and to \(\pm 7\%\) at \(1\sigma \)-level. The measured  normalisation is robust against an incorrectly assumed sign of the still undetermined NMO. This enables KM3NeT/ORCA to measure
normalisation is robust against an incorrectly assumed sign of the still undetermined NMO. This enables KM3NeT/ORCA to measure  appearance already during an early phase of construction [49].
appearance already during an early phase of construction [49].
4 Conclusions
The importance of an independent study of neutrino oscillations, notably the determination of the NMO, has recently been reinforced as earlier hints, which favoured NO, are fading away in the light of latest combined results [8, 9].
The KM3NeT/ORCA sensitivity to atmospheric neutrino oscillation has been updated accounting for an optimised detector geometry and major improvements in neutrino trigger and reconstruction algorithms, and data analysis. The trigger algorithm has been improved allowing to more efficiently collect neutrinos in the few-GeV energy range. The algorithms to select neutrino flavour-enriched samples have been optimised using multivariate analysis techniques. Finally, the models used in the statistical analysis have been refined with a realistic description of the systematic uncertainties.
The sensitivity to determine the NMO after 3 years of data taking was found to be 4.4 (2.3) \(\sigma \) if the true NMO is NO (IO) and the other oscillation parameters are set to the current best estimates [6]. The measurement precision on \(\varDelta m^2_{32}\) and \(\theta _{23}\) are \(85 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+1.9}_{-3.1})^{\circ }\) for NO, and \(75 . 10^{-6}~{\mathrm{eV}^{2}}\) and \((^{+2.0}_{-7.0})^{\circ }\) for IO. Finally, the unitary \(3\times 3\) neutrino mixing paradigm can be assessed by confronting the  event rate to the expectation in this model. With 3 years of data taking,
event rate to the expectation in this model. With 3 years of data taking,  event rate variation larger than 20% can be excluded at the 3\(\sigma \) level.
event rate variation larger than 20% can be excluded at the 3\(\sigma \) level.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This study is based on simulations. The hypotheses used for the simulations are described in the article.]
Notes
The uneven number was chosen for practical purposes only and simplifies consistency of event selection across different analyses (> vs. \(\ge \)).
References
B. Maki, M. Nakagawa, S. Sakata, Prog. Theor. Phys. 28, 870 (1962). https://doi.org/10.1143/PTP.28.870
B. Pontecorvo, Sov. Phys. JETP 26, 984 (1968)
V. Gribov, B. Pontecorvo, Phys. Lett. B 28, 493 (1969). https://doi.org/10.1016/0370-2693(69)90525-5
M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98(3), 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
P.F. de Salas, D.V. Forero, C.A. Ternes, M. Tórtola, J.W.F. Valle, Phys. Lett. B 782, 633 (2018). https://doi.org/10.1016/j.physletb.2018.06.019
I. Esteban, M.C. Gonzalez-Garcia, A. Hernandez-Cabezudo, M. Maltoni, T. Schwetz, J. High Energy Phys. 01, 106 (2019). https://doi.org/10.1007/JHEP01(2019)106
F. Capozzi, E. Lisi, A. Marrone, A. Palazzo, Prog. Part. Nucl. Phys. 102, 48 (2018). https://doi.org/10.1016/j.ppnp.2018.05.005
I. Esteban, M.C. Gonzalez-Garcia, M. Maltoni, T. Schwetz, A. Zhou, JHEP 09, 178 (2020). https://doi.org/10.1007/JHEP09(2020)178
K.J. Kelly, P.A. Machado, S.J. Parke, Y.F. Perez Gonzalez, R. Zukanovich-Funchal, Phys. Rev. D 103(1), 013004 (2021). https://doi.org/10.1103/PhysRevD.103.013004
K. Abe et al. (T2K Collaboration), Nature 580(7803), 339 (2020). https://doi.org/10.1038/s41586-020-2177-0
M.A. Acero et al. (NOvA Collaboration), Phys. Rev. Lett. 123(15), 151803 (2019). https://doi.org/10.1103/PhysRevLett.123.151803
A. Aurisano, Recent results from MINOS and MINOS+, XXVIII International Conference on Neutrino Physics and Astrophysics (2018). https://doi.org/10.5281/zenodo.1286760
K. Abe et al. (Super-Kamiokande Collaboration), Phys. Rev. D 97(7), 072001 (2018). https://doi.org/10.1103/PhysRevD.97.072001
M.G. Aartsen et al. (IceCube Collaboration), Phys. Rev. Lett. 120(7), 071801 (2018). https://doi.org/10.1103/PhysRevLett.120.071801
P. Dunne, Latest neutrino oscillation results from T2K, XXIX International Conference on Neutrino Physics and Astrophysics (2020). https://doi.org/10.5281/zenodo.4154355
A. Himmel, New oscillation results from the NOvA experiment. XXIX International Conference on Neutrino Physics and Astrophysics (2020). https://doi.org/10.5281/zenodo.3959581
N. Agafonova et al. (OPERA Collaboration), Phys. Rev. Lett. 115(12), 121802 (2015). https://doi.org/10.1103/PhysRevLett.115.121802
N. Agafonova et al. (OPERA Collaboration), Phys. Rev. Lett. 120(21), 211801 (2018). https://doi.org/10.1103/PhysRevLett.120.211801 [Erratum: Phys. Rev. Lett. 121, 139901 (2018)]
Z. Li et al. (Super-Kamiokande Collaboration), Phys. Rev. D 98(5), 052006 (2018). https://doi.org/10.1103/PhysRevD.98.052006
M.G. Aartsen et al. (IceCube Collaboration), Phys. Rev. D 99(3), 032007 (2019). https://doi.org/10.1103/PhysRevD.99.032007
E.K. Akhmedov, S. Razzaque, A.Yu. Smirnov, J. High Energy Phys. 02, 82 (2013). https://doi.org/10.1007/JHEP02(2013)082
L. Wolfenstein, Phys. Rev. D 17, 2369 (1978). https://doi.org/10.1103/PhysRevD.17.2369
S.P. Mikheyev, A.Y. Smirnov, Sov. J. Nucl. Phys. 42, 913 (1985)
S. Adrián-Martínez et al., KM3NeT Collaboration. J. Phys. G 43(8), 084001 (2016). https://doi.org/10.1088/0954-3899/43/8/084001
S. Aiello et al. (KM3NeT Collaboration), JINST 13(05), P05035 (2018). https://doi.org/10.1088/1748-0221/13/05/P05035
S. Aiello et al. (KM3NeT Collaboration), JINST 15(11), P11027 (2020). https://doi.org/10.1088/1748-0221/15/11/P11027
S. Aiello (KM3NeT Collaboration), Comput. Phys. Commun. 256, 107477 (2020). https://doi.org/10.1016/j.cpc.2020.107477
C. Andreopoulos et al., Nucl. Instrum. Methods A 614, 87 (2010). https://doi.org/10.1016/j.nima.2009.12.009
C. Andreopoulos et al., The GENIE neutrino Monte Carlo generator: physics and user manual (2015). arXiv:1510.05494 [hep-ph]
M. Honda, M.S. Athar, T. Kajita, K. Kasahara, S. Midorikawa, Phys. Rev. D 92, 023004 (2015). https://doi.org/10.1103/PhysRevD.92.023004
A.G. Tsirigotis, A. Leisos, S.E. Tzamarias, Nucl. Instrum. Methods A 626–627, S185 (2011). https://doi.org/10.1016/j.nima.2010.06.258
G. Carminati, A. Margiotta, M. Spurio, Comput. Phys. Commun. 179, 915 (2008). https://doi.org/10.1016/j.cpc.2008.07.014
D. Bailey, Monte Carlo tools and analysis methods for understanding the ANTARES experiment and predicting its sensitivity to dark matter. Ph.D. thesis, University of Oxford (2002)
A. Albert et al. (ANTARES Collaboration), JCAP 01, 064 (2021). https://doi.org/10.1088/1475-7516/2021/01/064
M. Ageron et al. (KM3NeT Collaboration), Eur. Phys. J. C 80(2), 99 (2020). https://doi.org/10.1140/epjc/s10052-020-7629-z
S. Hallmann, Sensitivity to atmospheric tau-neutrino appearance and all-flavour search for neutrinos from the Fermi Bubbles with the deep-sea telescopes KM3NeT/ORCA and ANTARES. Ph.D. thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) (2021). https://nbn-resolving.org/urn:nbn:de:bvb:29-opus4-157495
L. Quinn, Neutrino mass hierarchy determination with KM3Net/ORCA. Ph.D. thesis, Aix-Marseille University (2018). http://hal.in2p3.fr/tel-02265297
J. Hofestädt, Measuring the neutrino mass hierarchy with the future KM3NeT/ORCA detector. Ph.D. thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) (2017). https://nbn-resolving.org/urn:nbn:de:bvb:29-opus4-82770
Y.S. Jeong, M.H. Reno, Phys. Rev. D 82, 033010 (2010). https://doi.org/10.1103/PhysRevD.82.033010
S. Adrián-Martínez et al. (KM3NeT Collaboration), JHEP 05, 008 (2017). https://doi.org/10.1007/JHEP05(2017)008
L. Breiman, Mach. Learn. 45(1), 5 (2001). https://doi.org/10.1023/A:1010933404324
J.A. Formaggio, G.P. Zeller, Rev. Mod. Phys. 84, 1307 (2012). https://doi.org/10.1103/RevModPhys.84.1307
J. Coelho, OscProb neutrino oscillation calculator. https://github.com/joaoabcoelho/OscProb
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Eur. Phys. J. C 71, 1554 (2011). https://doi.org/10.1140/epjc/s10052-011-1554-0 [Erratum: Eur. Phys. J. C 73, 2501 (2013)]
S. Baker, R.D. Cousins, Nucl. Instrum. Methods 221, 437 (1984). https://doi.org/10.1016/0167-5087(84)90016-4
G.D. Barr, T.K. Gaisser, S. Robbins, T. Stanev, Phys. Rev. D 74, 094009 (2006). https://doi.org/10.1103/PhysRevD.74.094009
A. Albert et al. (ANTARES Collaboration), Eur. Phys. J. C 78(8), 669 (2018). https://doi.org/10.1140/epjc/s10052-018-6132-2
A.M. Dziewonski, D.L. Anderson, Phys. Earth Planet. Inter. 25, 297 (1981). https://doi.org/10.1016/0031-9201(81)90046-7
B. Strandberg, S. Hallmann, PoS ICRC2019, 1019 (2019). https://doi.org/10.22323/1.358.1019
Acknowledgements
The authors acknowledge the financial support of the funding agencies: Agence Nationale de la Recherche (contract ANR-15-CE31-0020), Centre National de la Recherche Scientifique (CNRS), Commission Européenne (FEDER fund and Marie Curie Program), Institut Universitaire de France (IUF), LabEx UnivEarthS (ANR-10-LABX-0023 and ANR-18-IDEX-0001), Paris Île-de-France Region, France; Shota Rustaveli National Science Foundation of Georgia (SRNSFG, FR-18-1268), Georgia; Deutsche Forschungsgemeinschaft (DFG), Germany; The General Secretariat of Research and Technology (GSRT), Greece; Istituto Nazionale di Fisica Nucleare (INFN), Ministero dell’Università e della Ricerca (MIUR), PRIN 2017 program (Grant NAT-NET 2017W4HA7S) Italy; Ministry of Higher Education Scientific Research and Professional Training, ICTP through Grant AF-13, Morocco; Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO), the Netherlands; The National Science Centre, Poland (2015/18/E/ST2/00758); National Authority for Scientific Research (ANCS), Romania; Ministerio de Ciencia, Innovación, Investigación y Universidades (MCIU): Programa Estatal de Generación de Conocimiento (refs. PGC2018-096663-B-C41, -A-C42, -B-C43, -B-C44) (MCIU/FEDER), Severo Ochoa Centre of Excellence and MultiDark Consolider (MCIU), Junta de Andalucía (ref. SOMM17/6104/UGR), Generalitat Valenciana: Grisolía (ref. GRISOLIA/2018/119) and GenT (ref. CIDEGENT/2018/034 and CIDEGENT/2019/043) programs, La Caixa Foundation (ref. LCF/BQ/IN17/11620019), EU: MSC program (ref. 713673), Spain.
Author information
Authors and Affiliations
Consortia
Corresponding authors
Additional information
Deceased: Giorgos Androulakis.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Aiello, S., Albert, A., Alves Garre, S. et al. Determining the neutrino mass ordering and oscillation parameters with KM3NeT/ORCA. Eur. Phys. J. C 82, 26 (2022). https://doi.org/10.1140/epjc/s10052-021-09893-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09893-0










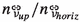 , is allowed to vary with a standard deviation of 2% of the parameter’s nominal value,
, is allowed to vary with a standard deviation of 2% of the parameter’s nominal value, and
and 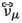 ,
, 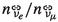 , is allowed to vary with a standard deviation of 2% of the parameter’s nominal value,
, is allowed to vary with a standard deviation of 2% of the parameter’s nominal value,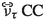 is scaled by a factor
is scaled by a factor 



 appearance
appearance
 appearance for CC and CC+NC normalisation scaling after 1 and 3 years of operation (a). Measurements from other experiments [
appearance for CC and CC+NC normalisation scaling after 1 and 3 years of operation (a). Measurements from other experiments [ appearance sensitivity for CC scaling is presented as a function of data taking period
appearance sensitivity for CC scaling is presented as a function of data taking period