1 Introduction

The Dirac oscillator has been introduced in terms of a new type interaction in the Dirac equation [1,2,3] (also see [4]) and it has been shown that this interaction has a great potential for many theoretical and experimental applications [5,6,7,8,9,10,11,12,13]. This form of the Dirac equation is linear in both momentum and spatial coordinate [1, 2] and solution of this instance of the Dirac equation gives a simple quantum oscillator solution with a strong spin-orbit coupling term in the non-relativistic limit [3, 5]. This is why it has been called as Dirac oscillator (DO) [3, 6]. The electromagnetic potential associated with this interaction has been obtained [7] and it has been shown that the DO interaction is a physical system due to the fact that it corresponds to the interaction of the anomalous (chromo) magnetic moment with a linearly growing electric field [7]. The DO interaction is regarded as an alternative confinement potential for heavy quarks in quantum chromodynamics (QCD) [7, 8] and the DO system can describe the relativistic dynamics of quarks in mesons and baryons [7,8,9,10,11] since the DO interaction is normally utilized in the context of many-body theory [2, 9]. Therefore, a well-established mathematical model for a tight-binding fermion-antifermion system can be useful to better understand the physics of composite systems such as mesons [9]. The potential of applications of the DO system has been enhanced after achieving the first experimental microwave realization of the one-dimensional DO system [12]. This experiment has been relied on a relation of the DO system to a tight-binding system (coupled dielectric disks) [12] and the obtained results are in good agreement with the theoretical predictions [12, 13]. Two-dimensional DO has been used to describe the relativistic dynamics of charge carriers in monolayer graphene [14,15,16] and one of the most important aspects of the DO is that it has found many application areas in various branches of physics such as mathematical physics [17,18,19,20,21,22,23], nuclear (or subnuclear) physics [24,25,26] (also see [27, 28]) and quantum optics [18, 29,30,31,32]. The DO has been also studied in the context of minimal length uncertainty [33, 34]. The DO is an exactly solvable system and this important fact makes the DO is a useful system to determine the influence of spacetime topology on the dynamics of the corresponding systems [5, 35,36,37,38,39,40]. However, in many areas of the modern physics, a quantum oscillator is used to determine the dynamics of the interacting particles [6].

On the other hand, a phenomenological way to describe the dynamics of many-body systems is to use one-time equations including free Hamiltonians for each particle plus interparticle interaction potentials [41, 42]. In the relativistic quantum theory, the history of such equations goes long way back [43, 44] but there are still different relativistic many-body equations in use today in the literature [43,44,45,46,47,48]. In this study, we will use the corresponding form of a fully-covariant two-body Dirac equation (FCTBE) [9, 48,49,50,51,52,53,54], derived from quantum electrodynamics (QED) with the help of action principle [47], in order to obtain relativistic Landau levels for a composite system formed by a fermion-antifermion (\(\mathbf{f} \overline{\mathbf{f }}\)) pair interacting via DO coupling. The FCTBE is a one-time equation including the most general electric and magnetic potentials [48,49,50,51,52,53,54]. This equation leads a \(16\times 16\) matrix equation in 4-dimensions [52,53,54] and the separation of angular and radial variables requires group theoretical methods [52,53,54,55]. It has been announced that the well-known energy spectrum for one-electron atoms or some \(\mathbf{f} \overline{\mathbf{f }}\) systems can be obtained via perturbative solution of the FCTBE [9, 52,53,54] in 4-dimensions. Recently, it has been shown that the FCTBE can be exactly solvable for low dimensional systems [48] and some systems that have dynamical symmetries [49,50,51], without considering any group theoretical method. The FCTBE has been used to describe the dynamics of an exciton (electron-hole pair) in a monolayer free standing medium and the lifetime of the exciton has been obtained simultaneously besides its binding energy [48]. Moreover, this equation has been solved exactly for an electron-hole pair that they interact via attractive Coulomb potential in a monolayer dielectric medium and the results show that, in principle, one can actively tune both binding energy and decaytime of an exciton during photo-excitation experiments by adjusting the dielectric substrates [51]. The FCTBE is also appropriate to study in curved spacetime backgrounds. Recently, this equation has been used to determine the effects of cosmic strings on the unstable composite systems such as ortho-positronium (spin symmetric quantum state of an electron-positron pair) and it has been shown that an ortho-positronium system has a great potential to prove the existence of the cosmic strings in the universe [49]. In the relativistic quantum theory, two-body systems have been studied for a very long time [43,44,45,46,47,48], however there is a few investigation about the dynamics of \(\mathbf{f} {} \mathbf{f} \) (or \(\mathbf{f} \overline{\mathbf{f }}\)) systems with DO couplings [9, 56,57,58]. Moreover, we could not find exact results for the relativistic dynamics of a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling in the literature. On the other hand, exact results for the dynamics of matter-antimatter systems in the presence of an external magnetic field are very important in the context of relativistic quantum theory [50], since we know that the magnetic fields exist at almost every point in the universe [50] (but we do not know the origin of the magnetic field in the universe [50]). Therefore, determination of the influence of external magnetic fields on the dynamics of an interacting \(\mathbf{f} \overline{\mathbf{f }}\) system is very important in QCD and QED [50].

In this manuscript, we introduce a well established model to determine the relativistic Landau levels of a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling. In order to acquire this, we write the FCTBE for arbitrary two Dirac particles (massive) with DO couplings. We investigate the relativistic dynamics of such a composite system in 3-dimensional flat spacetime background by choosing the interaction of the particles with the external uniform magnetic field in the symmetric gauge, since this system has translational symmetry [50]. We separate center of mass motion coordinates and relative motion coordinates. Then, we arrive at a \(4\times 4\) dimensional matrix equation, resulting a set of coupled equations for a static \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling under the influence of an external uniform magnetic field. We solve this set of coupled equations for spin antisymmetric state (\(s=0\)) of such a pair and obtain an energy spectrum in closed-form. The results show that such a \(\mathbf{f} \overline{\mathbf{f }}\) pair behaves like a single relativistic quantum oscillator carrying total rest mass of the particles. We discuss several interesting features of this system by comparing the results and their limits with the previously announced results for related one-body systems. We show that the obtained results agree well with the previously announced theoretical and experimental results for DO (one-body). Therefore, we think that our results can provide a suitable basis for many new theoretical and experimental applications.

2 Mathematical model

In this part of the present manuscript we introduce a model Hamiltonian for a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting through DO interaction in the presence of an external uniform magnetic field in \(2+1\) dimensional flat spacetime background, without considering Coulomb type charge-charge interaction. To acquire this, we start with the generalized form of the FCTBE written for arbitrary of two Dirac particles [48,49,50,51,52,53,54],

$$\begin{aligned}&\left\{ H^{\left( 1\right) }\otimes \gamma ^{0^{\left( 2\right) }}+\gamma ^{0^{\left( 1\right) }}\otimes H^{\left( 2\right) } \right\} \chi \left( \mathbf{x} _{1},\mathbf{x} _{2}\right) =0,\nonumber \\&{H^{\left( 1\right) }=\left[ \gamma ^{\mu ^{\left( 1\right) }}\pi ^{\left( 1\right) }_{\mu }+ib_{1}{} \mathbf{I} _{2}\right] ,\quad H^{\left( 2\right) }=\left[ \gamma ^{\mu ^{\left( 2\right) }}\pi ^{\left( 2\right) }_{\mu }+ib_{2}{} \mathbf{I} _{2}\right] },\nonumber \\&{\pi ^{\left( 1\right) }_{\mu }=\left( \partial ^{\left( 1\right) }_{\mu }+i\frac{e_{1}A^{\left( 1\right) }_{\mu }}{\hbar c}-\Gamma _{\mu }^{\left( 1\right) }\right) ,\quad \pi ^{\left( 2\right) }_{\mu }=\left( \partial ^{\left( 2\right) }_{\mu }+i\frac{e_{2}A^{\left( 2\right) }_{\mu }}{\hbar c}-\Gamma _{\mu }^{\left( 2\right) }\right) },\nonumber \\&b_{1}=\frac{m_{1}c}{\hbar },\quad b_{2}=\frac{m_{2}c}{\hbar },\quad \left( \mu =0,1,2.\right) ,\nonumber \\&\partial _{\mu }=(\partial _{0}, \partial _{1}, \partial _{2}.), \end{aligned}$$
(1)

here, the superscripts (1) and (2) refer to the first fermion with mass \(m_{1}\) and second fermion with mass \(m_{2}\), respectively, \(\mathbf{I} _{2}\) is the 2-dimensional unit matrix, \(\chi \left( \mathbf {x}_{1},\mathbf {x}_{2}\right) \) is the bi-local composite field that is constructed by Kronocker product \((\otimes )\) of arbitrary massive of two Dirac fields as in the following,

$$\begin{aligned} \chi \left( \mathbf {x}_{1},\mathbf {x}_{2}\right) =\chi _{1} \left( \mathbf {x}_{1}\right) \otimes \chi _{2} \left( \mathbf {x}_{2}\right) , \end{aligned}$$
(2)

\(\hbar \) is the reduced Planck constant, c is the speed of light, \(e_{1}\) and \(e_{2}\) represent to the charges of the particles, \(\Gamma _{\mu }\) and \(A_{\mu }\) stand for the spinor connections and vector potentials, respectively. Here, it is important to underline that the \(\gamma ^{0}\) means \(\gamma ^{\mu }\lambda _{\mu }\) in everywhere in Eq. (1) and the \(\lambda _{\mu }\) is a timelike vector \(\lambda _{\mu }=(1,0,0)\) [59] (normal vector of the two-dimensional spacelike subspace). This equation includes spin algebra spanned by Kronocker product of the Dirac matrices [47]. Dynamic symmetry of the system that under consideration allows to study in \(2+1\) dimensional spacetime background. In terms of cartesian coordinates, this spacetime background is represented by the following line element [50],

$$\begin{aligned} ds^{2}=c^{2}dt^{2}-(dx^{2}+dy^{2}), \end{aligned}$$
(3)

for which the spinor connections in Eq. (1) vanish [60]. We can choose the interaction of the arbitrary charged of two Dirac particles with the external uniform magnetic field in the symmetric gauge [50], for which the vector potentials in Eq. (1) become as in the following,

$$\begin{aligned}&A^{\left( 1\right) }_{t}=0,\quad A^{\left( 1\right) }_{x}=-\frac{B_{0}y_{1}}{2}, \quad A^{\left( 1\right) }_{y}=\frac{B_{0}x_{1}}{2},\nonumber \\&A^{\left( 2\right) }_{t}=0,\quad A^{\left( 2\right) }_{x}=-\frac{B_{0}y_{2}}{2}, \quad A^{\left( 2\right) }_{y}=\frac{B_{0}x_{2}}{2}. \end{aligned}$$
(4)

Here, \(B_{0}\) is the amplitude of the external uniform magnetic field and spatial coordinate pairs (\(x_{i},y_{i} \left( i=1,2.\right) \)) correspond to the spatial coordinates of the particles confined on a spatial plain. According to the signature \((+,-,-)\) in Eq. (3) we can choose the Dirac matrices in terms of the Pauli spin matrices (\(\sigma ^{x}, \sigma ^{y}, \sigma ^{z}\)) as in the following [48, 50, 51],

$$\begin{aligned} \gamma ^{t^{\left( 1,2\right) }}= & {} \sigma ^{z},\quad \gamma ^{x^{\left( 1,2\right) }}=i\sigma ^{x},\quad \gamma ^{y^{\left( 1,2\right) }}=i\sigma ^{y},\nonumber \\ \sigma ^{x}= & {} \left( \begin{array}{cc} 0 &{} 1 \\ 1 &{}0\\ \end{array} \right) ,\quad \sigma ^{y}=\left( \begin{array}{cc} 0 &{} -i \\ i &{}0\\ \end{array} \right) ,\quad \sigma ^{z}=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{}-1\\ \end{array} \right) , \end{aligned}$$
(5)

since they are independent from the coordinates of the particles (see also [49]). Now, we can introduce two dimensional of two DOs (arbitrary massive) via the non-minimal substitution terms as follows [3],

$$\begin{aligned}&{\partial _{x}^{\left( 1\right) }\rightarrow \partial _{x}^{\left( 1\right) }+\frac{m_{1}\omega _{1}}{\hbar } \gamma ^{0^{\left( 1\right) }}x_{1},\quad \partial _{y}^{\left( 1\right) } \rightarrow \partial _{y}^{\left( 1\right) }+\frac{m_{1}\omega _{1}}{\hbar } \gamma ^{0^{\left( 1\right) }}y_{1}},\nonumber \\&{\partial _{x}^{\left( 2\right) }\rightarrow \partial _{x}^{\left( 2\right) }+\frac{m_{2}\omega _{2}}{\hbar } \gamma ^{0^{\left( 2\right) }}x_{2},\quad \partial _{y}^{\left( 2\right) }\rightarrow \partial _{y}^{\left( 2\right) }+\frac{m_{2} \omega _{2}}{\hbar }\gamma ^{0^{\left( 2\right) }}y_{2}},\nonumber \\ \end{aligned}$$
(6)

here, \(\omega _{1(2)}\) is the frequency of the oscillator with mass \(m_{1(2)}\). Then, we separate the center of mass motion coordinates and relative motion coordinates via the following expressions [48],

$$\begin{aligned} R_{\mu }= & {} \frac{1}{M}\left( m_{1}x_{\mu }^{\left( 1\right) } +m_{2}x_{\mu }^{\left( 2\right) }\right) ,\quad r_{\mu }= x_{\mu }^{\left( 1\right) }-x_{\mu }^{\left( 2\right) },\nonumber \\ x_{\mu }^{\left( 1\right) }= & {} \frac{m_{2}}{M}r_{\mu }+R_{\mu }, \quad x_{\mu }^{\left( 2\right) }=-\frac{m_{1}}{M}r_{\mu }+R_{\mu },\nonumber \\ \partial _{x_{\mu }}^{\left( 1\right) }= & {} \partial _{r_{\mu }} +\frac{m_{1}}{M}\partial _{R_{\mu }},\quad \partial _{x_{\mu }}^{\left( 2\right) }= -\partial _{r_{\mu }}+\frac{m_{2}}{M}\partial _{R_{\mu }},\quad \partial _{x_{\mu }}^{\left( 1\right) }+\partial _{x_{\mu }}^{\left( 2\right) } =\partial _{R_{\mu }}.\nonumber \\ \end{aligned}$$
(7)

3 Coupled equations for the components of bi-spinor

In this section, we obtain a set of coupled equations in terms of the relative radial coordinate for a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling in the presence of an external uniform magnetic field. Provided that the interaction is time-independent and momentum of the center of mass is a constant of motion we can define the bi-spinor \(\chi \) as follows,

$$\begin{aligned}&\chi \left( R_{0},\mathbf{R} ,\mathbf{r} \right) =e^{-iwt}e^{i\mathbf{k} .\mathbf{R} } \psi \left( \mathbf{r} \right) , \psi \left( \mathbf{r} \right) =\left( \begin{array}{c} \varphi _{1}\left( \mathbf{r} \right) \\ \varphi _{2}\left( \mathbf{r} \right) \\ \varphi _{3}\left( \mathbf{r} \right) \\ \varphi _{4}\left( \mathbf{r} \right) \end{array} \right) , \end{aligned}$$
(8)

here, w is the total frequency that determined according to the proper time (\(R_{0}\)) of the system [47], \(\mathbf{k} \) relates with the center of mass momentum as \(\hbar \mathbf{k} \), \(\mathbf{R} \) is the spatial position vector of the center of mass and \(\mathbf{r} \) is the relative spatial vector between the \(\mathbf{f} \overline{\mathbf{f }}\) pair. By assuming the center of mass is rest (\(\hbar \mathbf{k} =0\)) at the origin (\(R_{1}=R_{2}=0\)) of the background, we obtain the following matrix equation for a \(\mathbf{f} \overline{\mathbf{f }}\) pair (\(e_{1}=e,e_{2}=-e\))Footnote 1 interacting through DO coupling in the presence of an external uniform magnetic field,

$$\begin{aligned}&-\left( \gamma ^{t}\otimes \gamma ^{t}\right) i\varepsilon \psi +i \frac{mc}{\hbar }\left( \mathbf{I} _{2}\otimes \gamma ^{t}+\gamma ^{t}\otimes \mathbf{I} _{2}\right) \psi \nonumber \\&\quad +\left( \gamma ^{x}\otimes \gamma ^{t}-\gamma ^{t}\otimes \gamma ^{x}\right) \partial _{x}\psi \nonumber \\&\quad +\left( \gamma ^{y}\otimes \gamma ^{t}-\gamma ^{t}\otimes \gamma ^{y}\right) \partial _{y}\psi \nonumber \\&\quad +i\kappa x\left( \gamma ^{y}\otimes \gamma ^{t}+\gamma ^{t}\otimes \gamma ^{y}\right) -i\kappa y\left( \gamma ^{x}\otimes \gamma ^{t}+\gamma ^{t}\otimes \gamma ^{x}\right) \psi \nonumber \\&\quad +\xi x\left( \left( \gamma ^{x}\gamma ^{t}\right) \otimes \gamma ^{t}+\gamma ^{t}\otimes \left( \gamma ^{x} \gamma ^{t}\right) \right) \psi \nonumber \\&\quad +\xi y\left( \left( \gamma ^{y}\gamma ^{t}\right) \otimes \gamma ^{t}+\gamma ^{t}\otimes \left( \gamma ^{y}\gamma ^{t}\right) \right) \psi =0,\nonumber \\&\varepsilon =\frac{w}{c},\quad \kappa =\frac{eB_{0}}{2\hbar c},\quad \xi = \frac{m\omega }{2\hbar },\nonumber \\ \end{aligned}$$
(9)

with the help of Eqs. (4), (5), (6), (7), (8) and (1). In Eq.  (9), x and y are the spatial coordinates for the relative motion of the \(\mathbf{f} \overline{\mathbf{f }}\) pair confined on a spatial plain. By multiplying the Eq. (9) with \(\gamma ^{t}\otimes \gamma ^{t}\) from left (note that \(\left( \gamma ^{t}\otimes \gamma ^{t}\right) ^{2}\) gives \(4\times 4\) dimensional unit matrix), one can obtain the following \(4\times 4\) dimensional matrix equation,

$$\begin{aligned}&\left( \begin{array}{cccc} \varepsilon -M &{}\partial _{-} &{} -\partial _{-} &{} 0 \\ -\partial _{+}&{} \varepsilon &{} 0 &{} -\partial _{-} \\ \partial _{+} &{} 0 &{} \varepsilon &{} \partial _{-} \\ 0 &{} \partial _{+} &{} -\partial _{+} &{} \varepsilon +M \end{array} \right) \psi \left( \mathbf{r} \right) +\left( \xi -\kappa \right) \left( \begin{array}{cccc} 0 &{} r_{-} &{} r_{-} &{} 0 \\ r_{+} &{} 0 &{} 0 &{}r_{-} \\ r_{+} &{} 0 &{} 0 &{} r_{-} \\ 0 &{} r_{+} &{}r_{+} &{} 0 \end{array} \right) \psi \left( \mathbf{r} \right) =0,\nonumber \\&M=\frac{2mc}{\hbar },\quad \partial _{\pm }=\partial _{x}\pm i\partial _{y},\quad r_{\pm }=x\pm iy. \nonumber \\ \end{aligned}$$
(10)

Now, we can construct to possible spin states of such a \(\mathbf{f} \overline{\mathbf{f }}\) pair. To end this, we can use the following expressions [48, 50],

$$\begin{aligned} \partial _{\mp } = e^{\mp i\phi }\left( \mp \frac{i}{r}\partial _{\phi }+\partial _{r}\right) ,\quad r_{\mp }=re^{\mp i\phi }, \end{aligned}$$

here, \(\partial _{+}\) and \(\partial _{-}\) stand for the spin raising and spin lowering operators, respectively, and r is the relative radial distance between the particles. Afterwards, we can obtain a set of coupled equations for the components of the transformed spinor,

$$\begin{aligned} {\psi \left( \mathbf{r} \right) \Longrightarrow \left( \varphi _{1}\left( r\right) e^{i\left( s-1\right) \phi },\varphi _{2}\left( r\right) e^{is\phi },\varphi _{3} \left( r\right) e^{is\phi },\varphi _{4}\left( r\right) e^{i\left( s+1\right) \phi }\right) ^\mathbf{T }},\nonumber \\ \end{aligned}$$

as follows,

$$\begin{aligned}&\varepsilon \psi _{1}\left( r\right) -M\psi _{2}\left( r\right) +2\partial _{r}\psi _{3}\left( r\right) +2\Omega r\psi _{4}\left( r\right) =0,\nonumber \\&\varepsilon \psi _{2}\left( r\right) -M\psi _{1}\left( r\right) +\frac{2s}{r}\psi _{3}\left( r\right) =0,\nonumber \\&\varepsilon \psi _{3}\left( r\right) +\frac{2s}{r}\psi _{2} \left( r\right) -2\left( \frac{1}{r}+\partial _{r}\right) \psi _{1}\left( r\right) =0,\nonumber \\&\varepsilon \psi _{4}\left( r\right) -2\Omega r\psi _{1}\left( r\right) =0,\nonumber \\&\Omega =\left( \xi -\kappa \right) , \end{aligned}$$
(11)

two of which becomes algebraic for the following definitions,

$$\begin{aligned} \psi _{1}\left( r\right)= & {} \varphi _{1}\left( r\right) +\varphi _{4}\left( r\right) ,\quad \psi _{2}\left( r\right) = \varphi _{1}\left( r\right) -\varphi _{4}\left( r\right) ,\nonumber \\ \psi _{3}\left( r\right)= & {} \varphi _{2}\left( r\right) -\varphi _{3}\left( r\right) ,\quad \psi _{4}\left( r\right) =\varphi _{2}\left( r\right) +\varphi _{3}\left( r\right) . \end{aligned}$$

In Eq. (11), s represents to total spin of the composite system formed by a \(\mathbf{f} \overline{\mathbf{f }}\) pair. It is known that one of the mathematical difficulties in the many-body problems is the total angular momentum of the corresponding composite systems [44, 50]. As can be seen in Eq. (11), we can obtain a complete and analytical solution of this set of equations when \(s=0\). For antisymmetric spin state (\(s=0\)) of such a \(\mathbf{f} \overline{\mathbf{f }}\) pair, we can introduce a dimensionless independent variable that reads \(z=\Omega r^{2}\). In terms of the variable z, the equation system in Eq. (11) becomes as follows,

$$\begin{aligned}&{\varepsilon \psi _{1}\left( z\right) -M\psi _{2}\left( z\right) +4\Omega \sqrt{\frac{z}{\Omega }} \partial _{z}\psi _{3}\left( z\right) -2\Omega \sqrt{\frac{z}{\Omega }}\psi _{4}\left( z\right) =0},\nonumber \\ \nonumber \\&\varepsilon \psi _{2}\left( z\right) -M\psi _{1}\left( z\right) =0,\nonumber \\ \nonumber \\&\varepsilon \psi _{3}\left( z\right) -\frac{2}{\sqrt{\frac{z}{\Omega }}} \psi _{1}\left( z\right) -4\Omega \sqrt{\frac{z}{\Omega }}\partial _{z} \psi _{1}\left( z\right) =0,\nonumber \\ \nonumber \\&\varepsilon \psi _{4}\left( z\right) -2\Omega \sqrt{\frac{z}{\Omega }} \psi _{1}\left( z\right) =0;\nonumber \\ \end{aligned}$$
(12)

in which, all of the other spinor components can be expressed in terms of the \(\psi _{1}\left( z\right) \).

4 Non-perturbative energy spectrum

In this part of calculations, we obtain relativistic Landau levels of a spinless composite system consisting of a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO interaction, without considering any approximation. By solving the equation system in Eq. (12) for \(\psi _{1}\left( z\right) \) we obtain the following wave equation,

$$\begin{aligned} {\partial ^{2}_{z}\psi _{1}\left( z\right) +\frac{1}{z}\partial _{z}\psi _{1}\left( z\right) +\left( \frac{\varepsilon ^{2}-M^{2}}{16\Omega z}-\frac{1}{4 z^{2}}-\frac{1}{4}\right) \psi _{1}\left( z\right) =0}.\nonumber \\ \end{aligned}$$

Via an ansatz that reads \(\psi _{1}\left( z\right) =\frac{1}{\sqrt{z}}\Psi \left( z\right) \), this wave equation can be reduced into the well-known shape of the Whittaker differential equation,

$$\begin{aligned} \partial ^{2}_{z}\Psi \left( z\right) +\left( \frac{\varepsilon ^{2}-M^{2}}{16\Omega z}-\frac{1}{4}\right) \Psi \left( z\right) =0. \end{aligned}$$
(13)

Solution function of Eq. (13) is obtained as follows [50, 62, 63],

$$\begin{aligned} \Psi \left( z\right) =NW_{\varpi ,\tau }(z ),\quad \varpi = \frac{\varepsilon ^{2}-M^{2}}{16\Omega z},\quad \tau =\frac{1}{2}, \end{aligned}$$
(14)

here, N is the normalization constant and \(W_{\varpi ,\tau }(z )\) is the Whittaker function [50, 62, 63]. However, this solution function can only be reduced to polynomial of degree n with respect to the variable z provided that the following condition is satisfied [50, 62, 63],

$$\begin{aligned} \frac{1}{2}+\tau -\varpi =-n, \end{aligned}$$
(15)

in which, n is the principal quantum number (non-negative integer). Eq. (15) leads to the quantization condition for the formation of the composite system that under consideration. Now, one can obtain a non-perturbative energy spectrum with the help of the parameters in Eq. (9), Eq. (10), Eq. (11) and Eq. (14),

$$\begin{aligned} E_{n}= & {} \pm m^{*}c^{2}\sqrt{1+\frac{\overline{\omega }\hbar }{m^{*}c^{2}}n^{*}},\quad m^{*}=2m,\nonumber \\ \overline{\omega }= & {} 4\left( \omega -\frac{\omega _{c}}{2}\right) ,\quad \omega _{c}=\frac{|e|B_{0}}{m c},\quad n^{*}=\left( n+1\right) , \end{aligned}$$
(16)

here, \(\omega _{c}\) is the cyclotron frequency [30, 50]. Also, the spinor components can be obtained, in terms of the variable z, as in the following,

$$\begin{aligned} \psi _{1}\left( z\right)= & {} N\frac{W_{\varpi ,\tau }(z )}{\sqrt{z}},\nonumber \\ \psi _{2}\left( z\right)= & {} N\frac{M}{\varepsilon \sqrt{z}}W_{\varpi ,\tau }(z ),\nonumber \\ \psi _{3}\left( z\right)= & {} N\left[ \frac{2}{\varepsilon \sqrt{\frac{1}{\Omega }}}+\frac{4\sqrt{\Omega z}}{\varepsilon }\left( \frac{1}{2}-\frac{\varpi }{z}\right) \right] W_{\varpi ,\tau }(z )\nonumber \\&-N\frac{4\sqrt{\Omega }}{\varepsilon z}W_{\varpi +1 ,\tau }(z ),\nonumber \\ \psi _{4}\left( z\right)= & {} -N\frac{2\sqrt{\Omega }}{\varepsilon }W_{\varpi ,\tau }(z ), \end{aligned}$$

which satisfy the coupled equations in Eq. (12). The Eq. (16) gives relativistic Landau levels of a static and spinless composite system formed by a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling and shows that such a pair behaves like a single relativistic quantum oscillator carrying total rest mass of the particles (\(m^{*}\)). In Eq. (16), one can see that the second term in square root does not vanish even for \(n=0\) quantum state of such a pair. In Eq. (16), we see that the influence of external uniform magnetic field on this \(\mathbf{f} \overline{\mathbf{f }}\) pair is to decrease the oscillation frequency by half of the cyclotron frequency (see [64]). Also, Eq. (16) shows that the dynamics of such a \(\mathbf{f} \overline{\mathbf{f }}\) pair remains unchanged except for a special value of the strength of external uniform magnetic field, \(B_{0}=\frac{m^{*}\omega c}{|e|}\), since the result oscillator stops oscillating for this special strength of the external uniform magnetic field. This means that the total energy of such a \(\mathbf{f} \overline{\mathbf{f }}\) pair closes to the total rest mass energy (\(m^{*}c^{2}\)) of the \(\mathbf{f} \overline{\mathbf{f }}\) pair when \(\omega \approx \omega _{c}/2\) for any physically possible quantum state of this system. Also, it is clear that such a composite system (in the external uniform magnetic field) is mapped onto a single relativistic oscillator oscillating with a different oscillation frequency without magnetic field. The energy spectrum given in Eq. (16) can be reduced into the previously obtained results for relativistic Landau levels of a \(2+1\) dimensional DO provided that \(m^{*}\rightarrow m\) and \(n^{*}\rightarrow n\). Therefore, we think that the suggested model in this manuscript is appropriate for many different theoretical and experimental applications (for more details see [64]). Here, it is important to underline that the introduced model in this manuscript is appropriate only for massive \(\mathbf{f} \overline{\mathbf{f }}\) systems (see Eq. (7)). A \(\mathbf{f} \overline{\mathbf{f }}\) system with DO interaction was studied firstly by Moshinsky and his collaborators [9, 56, 57] and they obtained perturbative energy expressions. However, it has been shown that these energy expressions can give the mass spectrum for mesons. Therefore, the obtained exact spectrum in Eq. (16) can be very useful to determine the mass spectrum of mesons [9, 56, 57].

Fig. 1
figure 1

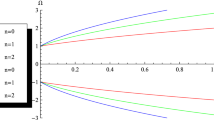
Dependence of the total energy of a spinless composite system formed by a fermion-antifermion pair interacting via Dirac oscillator interaction (\(\propto \omega \)) in the presence of an external uniform magnetic field on the effective coupling strength (\(\overline{\omega }\)) that holds such a pair together. Here, \(\overline{\omega }= 4\left( \omega -\frac{\omega _{c}}{2}\right) , \omega _{c}=\frac{|e|B_{0}}{m c}\) and \(m=c=\hbar =1\)

Full size image

5 Results and discussion

In this manuscript, we introduce a unique model for a \(\mathbf{f} \overline{\mathbf{f }}\) pair interacting via DO coupling in the presence of an external uniform magnetic field. This model is based on an exact solution of the corresponding form of a fully-covariant two-body Dirac equation (one-time). This equation includes spin algebra spanned by Kronocker product of Dirac matrices. The translational symmetry (see [50]) of the system that under consideration allows to study in \(2+1\) dimensional spacetime background. The considered composite system consists of an interacting \(\mathbf{f} \overline{\mathbf{f }}\) pair and as is usual with two-body problems we separate the center of motion coordinates and relative motion coordinates. Afterwards, we construct possible spin eigenstates of such a static \(\mathbf{f} \overline{\mathbf{f }}\) pair by exploiting the angular symmetry of the polar space. As we mentioned before, one of the main difficulties in the solution of many-body quantum systems is total angular momentum of the corresponding composite systems [44] (this problem may not appear for some topologies [49]). In Eq. (11), it can be seen that an exact solution of this set of coupled equations may not be possible if \(s\ne 0\). We solve this set of equations for spin antisymmetric state (\(s=0\)) of such a \(\mathbf{f} \overline{\mathbf{f }}\) pair and we obtain an energy spectrum in closed-form. The obtained spectrum is given in Eq. (16) and it shows that such a composite system behaves like a single relativistic oscillator carrying total rest mass \((m^{*})\) of the \(\mathbf{f} \overline{\mathbf{f }}\) pair. In Eq. (16), one can see that the total energy (\(E_{n}\)) of the composite system closes to the total rest mass energy (\(m^{*}c^{2}\)) of the particles when external magnetic field and oscillator frequency (coupling strength between the particles) are very weak. In Eq. (16), it is also clear that the coupling terms do not vanish for such a \(\mathbf{f} \overline{\mathbf{f }}\) pair in the ground state (\(n=0\)). We can also see that, the obtained total energy value closes to the total rest mass energy of the system when the strength of external uniform magnetic field closes to \(\frac{m^{*}\omega c}{|e|}\). Therefore, the dynamics of this interacting \(\mathbf{f} \overline{\mathbf{f }}\) pair remains unchanged except for the \(B_{0}=\frac{m^{*}\omega c}{|e|}\) value. Also, our results can be reduced into the previously announced results for the relativistic Landau levels of a \(2+1\) dimensional DO provided that \(m^{*}\rightarrow m\) and \(n^{*}\rightarrow n\) (see Eq. (16) and see [64]). Eq. (16) shows that a composite system formed by a \(\mathbf{f} \overline{\mathbf{f }}\) pair under the influence of an external uniform magnetic field maps into a DO oscillating with a different frequency (\(\omega \)) in the absence of the external uniform magnetic field (\(\omega _{c}=0\)), since this external field decreases the coupling strength between \(\mathbf{f} \overline{\mathbf{f }}\) pair by half of the cyclotron frequency (\(\frac{\omega _{c}}{2}\)). This property of the obtained energy spectrum agrees well with the results obtained for the relativistic Landau levels of a \(2+1\) dimensional DO (see [64]). The obtained energy spectrum (Eq. (16) agrees well with the results of the first experimental microwave realization of the one-dimensional DO (see Eq. (16) and [12]) and theoretical predictions for one-dimensional DO (see Eq. (16 and [13]) when \(m^{*}\rightarrow m\). Here, it is important to remember that our result (Eq. (16)) does not include spin coupling. Due to the this fact, it may not be very useful to discuss the similarities between the obtained results in this manuscript and the quantum optical models such as Jaynes-Cummings (or anti-Jaynes-Cummings) model, since the entanglement of the spin with the orbital motion is very important in these models of quantum optics. On the other hand, the thermodynamics properties of one-dimensional DO has been studied in [13] and such a discussion is also valid for our results (by substituting \(m^{*}\rightarrow m\)) in the absence of the external uniform magnetic field. Now, we can discuss the dependence of the total energy of such a pair on the coupling strength between the particles and the strength of the external uniform magnetic field. In Eq. (16), the \(\overline{\omega }\) can be considered as an effective coupling strength between \(\mathbf{f} \overline{\mathbf{f }}\) pair in the presence of an external uniform magnetic field since we have obtained that the presence of this external field decreases the strength of the coupling between the \(\mathbf{f} \overline{\mathbf{f }}\) pair. The dependence of the total energy (\(E_{n}\)) on the \(\overline{\omega }\) can be seen in Fig. 1, in which total energy of such a composite system increases when \(\overline{\omega }\) increases. It is also clear that the energy of this composite system decreases when the strength of the external uniform magnetic field increases. According to the our results, \(\omega _{c}>2\omega \) case can be possible if the external magnetic field (uniform) is very strong. This case may also be possible if the strength of coupling between the particles is very weak. In both cases, especially, the excited states of such a composite system cannot be steady states and hence the corresponding modes can decay exponentially in time [48,49,50,51, 65] if \(|\overline{\omega }|\hbar >m^{*}c^{2}\).