1 Introduction

The intriguingly physical phenomena of neutrino oscillations were proposed over half a century ago [1,2,3]. Subsequently, some experimental collaboration groups achieved the convincing evidences of the transitions among various neutrino flavors from the various neutrino sources, including solar neutrinos [4,5,6], atmospheric neutrinos [7, 8], reactor neutrinos [9, 10] and accelerator neutrinos [11,12,13,14]. In the regime of three generation neutrinos, neutrinos and antineutrinos can be simultaneously generated and they are available in the different kinds of flavors, namely, the electron e, muon \(\mu \) and tau \(\tau \) neutrinos [15]. The interestingly physical details of neutrinos have been revealed on measuring and analyzing the refined oscillations parameters [16,17,18,19].

Generally, the so-called neutrino oscillation is a physical process that one flavor can transform to another flavor in the course of the propagation due to the nonzero mass and mixing. Vast numbers of promising experiments have verified such behaviors by utilizing the natural neutrino and man-made neutrino. Fundamentally, the neutrino oscillations are the three-flavor oscillations [20]. The three-flavor oscillations can map into the neutrino states, treating them as the three-mode systems, i.e., the three-qubit quantum systems [21, 22]. For the special cases, the neutrino oscillations can be also simplified into the effective two-flavor oscillations. Likewise, the two-flavor oscillations can be considered as a two-mode system, to that the two-qubit system [23,24,25,26,27]. According to the normal ordering of the neutrino mass spectrum \(\left( {{m_1}< {m_2} < {m_3}} \right) \), the best fit values of neutrino oscillations parameters are \(\varDelta m_{21}^2 = 7.50 \times {10^{ - 5}}{\mathrm {e}}{{\mathrm {V}}^{\mathrm {2}}}\), \(\varDelta m_{31}^2 = 2.457 \) \(\times {10^{ - 3}}{\mathrm {e}}{{\mathrm {V}}^{\mathrm {2}}}\), \(\varDelta m_{32}^2 = 2.382 \times {10^{ - 3}}{\mathrm {e}}{{\mathrm {V}}^{\mathrm {2}}}\), \({\theta _{12}} = {33.48^\circ }\), \({\theta _{23}} = {42.3^\circ }\) and \({\theta _{13}} = {8.50^\circ }\) [28, 29].

Neutrinos interact only via weak processes. Hence, compared to other particles widely exploited in quantum information processing, neutrinos exhibit smaller decoherence and can sustain the coherence over astrophysical length scales. There could be many importantly potential applications in the domain of quantum information science. Motivated by this, various attempts have been made to explore the quantumness of neutrino system by means of flavor transition probabilities, including Leggett–Garg inequality [24, 30,31,32], Svetlichny inequalities [29], quantum discord [23], quantum entanglement [33], and quantum coherence [26]. Moreover, the quantum information theoretic tools are capable of addressing some intractable issues in neutrino oscillations, which are the distinct problem of the neutrinos nature between Dirac and Majorana fermions [34], and the mass-degeneracy problem [35]. However, so far, there have been no observations on entropic uncertainty relations in neutrino systems. Entropic uncertainty relation gives rise to many potential applications in the course of quantum information processing [36], including entanglement witness, quantum randomness, quantum metrology, quantum steering, quantum key distribution, and so on. Exploring the entropic uncertainty relations of neutrino systems may be open an exciting window to utilize neutrinos in the domain of quantum information science.

Uncertainty principle is originally put forward by Heisenberg, and is viewed as one of the backbones in quantum mechanics [37]. Importantly, the uncertainty principle virtually provides a threshold of our ability to accurately predict the measurement outcomes for a pair of incompatible observables on a given quantum system. Whereafter, Kennard [38] and Robertson [39] derived the uncertainty principle \(\varDelta P \cdot \varDelta R \ge \frac{1}{2}\left\langle \Phi \right| \left[ {P,\ R} \right] \left| \Phi \right\rangle \) by utilizing the standard deviation with respect to two arbitrary non-commuting observables P and R for the state \(\left| \Phi \right\rangle \). Later, Deutsch conjectured the celebrated entropic uncertainty relation (EUR) in terms of Shannon entropy [40], which was improved by Kraus [41] and subsequently proved by Maassen and Uffink [42]. EUR is generalized to the new version in the presence of a quantum memory, viz., quantum-memory-assisted entropic uncertainty relation (QMA-EUR) [36, 43, 44]. Soon afterwards, many works have made some efforts to improve and generalize QMA-EUR [45,46,47,48,49,50,51,52,53]. Furthermore, some promising experiments have been achieved to demonstrate the entropic uncertainty relation [54,55,56,57,58,59].

In this paper, we pay attention to investigate QMA-EUR in experimentally observed neutrino oscillations. It can be obtained that the entropic uncertainty for neutrino-flavor states and the lower bound of uncertainty are non-monotonic as the energy increases. Quantum correlation for neutrino-flavor states exhibits strong robustness in the order of km and is a dependent factor of the lower bound. The result shows that entropic uncertainty relations can be used as a credible criterion for quantum entanglement of neutrino-flavor states.

The outline of the paper is organized as follows. In Sect. 2, we first review the fundamental characteristics of neutrino oscillations and use the tools of quantum information theory to illuminate the two-flavor mode entangled states. In Sect. 3, we explore QMA-EUR and quantum correlation in experimentally observed neutrino oscillations, and further reveal the intrinsic relationship between both of them. Finally, we end up our paper with conclusions and discussions in Sect. 4.

2 Two-flavor neutrino oscillations

The standard neutrinos model is composed of three distinct neutrino flavors. However, we mainly focus on the energy and distance on oscillations between two-flavor states with a two-state approximation [60]. Therefore, in the limit of relativity, we can analyze the oscillations between two-flavor states by means of the Bloch sphere formalism [61], which geometrically corresponds to the space of pure states of a generic two-level system.

In the limit of two-flavor, the Hamiltonian for neutrino propagation reads (setting \({\hbar }= c = 1\)) [31, 62, 63]

$$\begin{aligned} {\hat{H}}= & {} \left( {\frac{{m_1^2 + m_2^2}}{{4p}} +\frac{{{V_C}}}{2} + {V_N} + p} \right) {{\mathbb {I}}}_{2 \times 2}\nonumber \\&+\frac{1}{2}\left( \begin{array}{*{20}{c}} {{V_C} - \omega \cos 2\theta }&{}{\omega \sin 2\theta }\\ {\omega \sin 2\theta }&{}{\omega \cos 2\theta -{V_C}} \end{array}\right) \nonumber \\= & {} \frac{{\mathbf {r}} \cdot {\mathbf {\sigma }}}{2} + {r_0}{{{\mathbb {I}}}_{2 \times 2}}, \end{aligned}$$
(1)

where \(\theta \) denotes the mixing angle of neutrino vacuum, \(m_1\) and \(m_2\) stand for the different mass states, respectively. \(\omega = ( {m_2^2 - m_1^2} )/2p\) stands for the oscillation frequency and \(p \simeq E\) is the relativistic neutrino momentum-energy. Owing to the coherent forward scattering of neutrinos with electrons (neutrons) in matter, the charged (neutral) current potential can be expressed by \({V_{C\left( N \right) }} = \sqrt{2} {G_F}{n_{e\left( n \right) }}\) with the Fermi coupling constant term \(G_F\). \(\mathbf{{\sigma }} = \left( {{\sigma _x},{\sigma _{y,}}{\sigma _z}} \right) \) denotes a two-dimension Pauli matrices vector, \({\mathbb {I}}_{2 \times 2}\) represents the \(2 \times 2\) identity matrix. The term \(r_{0}{\mathbb {I}}_{2 \times 2}\) is proportional to \({\mathbb {I}}_{2 \times 2}\) and can identically affect all flavor states, and thus it almost entirely never contributes to the oscillations of the different flavors. For the neutrino with an energy \(E_n\), the time evolution of the flavor states can be controlled by an unitary operator \({\hat{U}}\) related to \({\hat{H}_{osc}} \equiv {\mathbf {r}} \cdot {\mathbf {\sigma }}/2\) expressed as

$$\begin{aligned} {\hat{U}}\left( {{\omega _n};{t_i};{t_j}} \right)&\equiv {\hat{U}} \left( {{\psi _{n;ij}}} \right) = \exp \left( { - i\int _{{t_j}}^{{t_i}} {{{\hat{H}}_{osc}}\left( {{\omega _n}} \right) dt} } \right) \nonumber \\&= \cos \left( {{\psi _{n;ij}}} \right) {{\mathbb {I}}_{2 \times 2}}\nonumber \\&\quad - i\sin \left( {{\psi _{n;ij}}} \right) \left( {\hat{r}\left( {{\omega _n}} \right) \cdot {\mathbf {\sigma }}} \right) , \end{aligned}$$
(2)

where \(\omega _n\) denotes the oscillation frequency in regard to the energy \(E_n\) and \({\psi _{n;ij}} \equiv \left| {{\mathbf {r}}\left( {{\omega _n}} \right) } \right| \left( {{t_i} - {t_j}} \right) /2\) stands for the accumulated phase in the propagating period from \(t_i\) to \(t_j\) with the energy \(E_n\). In the limit of neglecting the matter effects, the accumulated phase \({\psi _{n;ij}}\) is written as

$$\begin{aligned} {\psi _{n;ij}} \simeq \frac{{{\omega _n}}}{2}\left( {{t_j} - {t_i}} \right) = \frac{1}{{4{E_n}}}\left( {m_2^2 - m_1^2} \right) \left( {{t_j} - {t_i}} \right) . \end{aligned}$$
(3)

The evolution of the neutrino is only dependent on the accumulated phase \({\psi _{n;ij}}\), not the individual times \(t_i\) and \(t_j\). As a result, the flavor neutrino states will evolve as

$$\begin{aligned} \left| {{\nu _\alpha }\left( t \right) } \right\rangle&= {\hat{U}} \left( {{\omega _n};{t_i};{t_j}} \right) \left| {{\nu _\alpha }} \right\rangle = {a_{\alpha \alpha }}\left( t \right) \left| {{\nu _\alpha }} \right\rangle \nonumber \\&\quad + {a_{\alpha \beta }}\left( t \right) \left| {{\nu _\beta }} \right\rangle \end{aligned}$$
(4)

in the flavor basis, where \(\alpha ,\beta = e,\mu \) being associated with electron- and muon-flavor neutrino states. \(\left| {{\nu _\alpha }} \right\rangle \) denotes the flavor state with respect to the initial time \(t=0\). The probabilities of detecting the neutrino in states \(\left| {{\nu _\alpha }} \right\rangle \) and \(\left| {{\nu _\beta }} \right\rangle \) are \({P_{\alpha \alpha }} = {\left| {{a_{\alpha \alpha }}\left( t \right) } \right| ^2}\) and \({P_{\alpha \beta }} = {\left| {{a_{\alpha \beta }}\left( t \right) } \right| ^2}\), respectively, i.e., the survival probability \({\nu _\alpha } \rightarrow {\nu _\alpha }\) and the oscillation probability \({\nu _\alpha } \rightarrow {\nu _\beta }\). And they satisfy \({P_{\alpha \alpha }} + {P_{\alpha \beta }} = 1\). The occupation number states of neutrinos are imposed by taking advantage of the following correspondence [23]

$$\begin{aligned} \left| {{\nu _\alpha }} \right\rangle \equiv {\left| 1 \right\rangle _\alpha } \otimes {\left| 0 \right\rangle _\beta } \equiv \left| {10} \right\rangle , \nonumber \\ \left| {{\nu _\beta }} \right\rangle \equiv {\left| 0 \right\rangle _\alpha } \otimes {\left| 1 \right\rangle _\beta } \equiv \left| {01} \right\rangle . \end{aligned}$$
(5)

From the above statements, the flavor states of the neutrino in principle can be considered as a two-qubit state with form of

$$\begin{aligned} \left| {{\nu _\alpha }\left( t \right) } \right\rangle = {a_{\alpha \alpha }}\left( t \right) \left| {10} \right\rangle + {a_{\alpha \beta }}\left( t \right) \left| {01} \right\rangle . \end{aligned}$$
(6)

3 QMA-EUR and quantum correlation in the experimentally observed neutrino oscillations

Basically, the QMA-EUR may be clearly explained based on a guessing game (the uncertainty game). To be explicit, there exists a pair of legitimate participants (say, Alice and Bob) in this game. Bob prepares two particles (A and B), and sends particle A entangled with his quantum memory B to Alice. After receiving A, Alice measures it by randomly choosing measurement P or R, and then tells Bob her measuring choice. Based on Alice’s measurement choice, Bob is able to guess Alice’s measurement results with minimal deviation limited by the uncertainty’s lower bound.

In the following, let us briefly recall the entropic uncertainty relation with quantum memory (i.e., QMA-EUR), which can be written by

$$\begin{aligned} S\left( {P|B} \right) + S\left( {R|B} \right) \ge - {\log _2}c\left( {P,R} \right) + S\left( {A|B} \right) , \end{aligned}$$
(7)

where \(S\left( {P|B} \right) = S\left( {{{\hat{\rho }}_{PB}}} \right) - S\left( {{{\hat{\rho }}_B}} \right) \) is the conditional von Neumann entropy of the post-measurement state with \({\hat{\rho }_{PB}} = \sum \nolimits _i {\left( {{{\left| {\varphi _i^P} \right\rangle }_A}\left\langle {\varphi _i^P} \right| {\mathbb {I}}_B} \right) } {\hat{\rho } _{AB}}\left( {{{\left| {\varphi _i^P} \right\rangle }_A}\left\langle {\varphi _i^P} \right| {\mathbb {I}}_B} \right) \) after performing the measurement on particle A by the observable P with the eigenstates \(\left| {\varphi _i^P} \right\rangle \). \({\mathbb {I}}_B\) represents an identical operator in the Hilbert space of B. \(c\left( {P,R} \right) = {\max _{j,k}}{\left| {\left\langle {\varphi _j^P|\psi _k^R} \right\rangle } \right| ^2}\) represents the maximal overlap.

And \(S\left( {A|B} \right) = S\left( {{{\hat{\rho }}_{AB}}} \right) - S\left( {{{\hat{\rho }}_B}} \right) \) denotes the conditional von Neumann entropy of systemic state \({\hat{\rho }}_{AB}\) with \(S\left( {{{\hat{\rho }}_{AB}}} \right) = - {\mathrm {tr}}\left( {{{\hat{\rho }}_{AB}} {{\log }_2}{{\hat{\rho }}_{AB}}} \right) \) and \({\hat{\rho }} _B = {\mathrm {t}}{{\mathrm {r}}_A}\left( {{{\hat{\rho }}_{AB}}} \right) \) [64].

Next, we recall quantum correlation for a bipartite system. Here, quantum correlation is measured by quantum discord (QD), which is given by [65]

$$\begin{aligned} QD\left( {{{\hat{\rho }}_{AB}}} \right) = I\left( {{{\hat{\rho } }_{AB}}} \right) - CC\left( {{{\hat{\rho }}_{AB}}} \right) , \end{aligned}$$
(8)

where \(I\left( {{{\hat{\rho }}_{AB}}} \right) = S\left( {{{\hat{\rho } }_A}} \right) + S\left( {{{\hat{\rho }}_B}} \right) - S\left( {{{\hat{ \rho }}_{AB}}} \right) \) is the systemic total correlation, representing the mutual information between two subsystems A and B. The quantum mutual information consists of two different parts (the classical part and the quantum part). The classical part (classical correlation) is described as \(CC\left( {{{\hat{\rho } }_{AB}}} \right) = {\max _{\left\{ {\prod _i^B} \right\} }}\left( {S\left( {{{\hat{\rho }}_B}} \right) - {S_{\left\{ {\prod _i^B} \right\} }}\left( {{{\hat{\rho }}_{A|B}}} \right) } \right) \). The maximum is taken over the set of all possible positive operator-valued measures (POVMs) \(\left\{ {\prod _i^B} \right\} \) on the subsystem B and \({S_{\left\{ {\prod _i^B} \right\} }}\left( {{{\hat{\rho }}_{A|B}}} \right) = \sum \nolimits _i {{p_i}S\left( {\hat{ \rho } _A^i} \right) }\) stands for the averaged conditional entropy of \(\hat{\rho }_A^i = \frac{1}{{{p_i}}}{\mathrm {t}}{{\mathrm {r}}_{AB}}\left( {\prod _i^B{{\hat{\rho }}_{AB}}\prod _i^B} \right) \) is the post-measurement state with the corresponding probability \({p_i} = {\mathrm {t}}{{\mathrm {r}}_{AB}}\left( {{{\hat{\rho } }_{AB}}\prod _i^B} \right) \). Therefore, the quantum part (quantum correlation) is easily obtained

$$\begin{aligned} QD\left( {{{\hat{\rho }}_{AB}}} \right)&= S\left( {{{\hat{\rho }}_B}} \right) - S\left( {{{\hat{\rho }}_{AB}}} \right) \nonumber \\&\quad + {\min _{\left\{ {\prod _i^B} \right\} }}{S_{\left\{ {\prod _i^B} \right\} }}\left( {{{\hat{\rho }}_{A|B}}} \right) . \end{aligned}$$
(9)

3.1 QMA-EUR and quantum correlation in the muon neutrino oscillations

Considering the muon neutrino in the initial time \(t=0\), the evolutive states for two-flavor neutrino oscillations are written as

$$\begin{aligned} \left| {{\nu _\mu }\left( t \right) } \right\rangle = {a_{\mu \tau }}\left( t \right) \left| {{\nu _\tau }} \right\rangle + {a_{\mu \mu }}\left( t \right) \left| {{\nu _\mu }} \right\rangle , \end{aligned}$$
(10)

where the oscillation probabilities for the tau flavor state \(\nu _\tau \) corresponds to \({P_{\mu \tau }}\left( t \right) = {\left| {{a_{\mu \tau }}\left( t \right) } \right| ^2}\),

and the survival probabilities for the muon flavor state \({\nu _\mu }\) is \({P_{\mu \mu }}\left( t \right) = {\left| {{a_{\mu \mu }}\left( t \right) } \right| ^2}\), respectively. The effective atmospheric \(\varDelta m_{\mu \mu }^2\) measured in \(\nu _\mu \) disappearance experiments is \(\varDelta m_{\mu \mu }^2 = {\sin ^2}{\theta _{12}}\varDelta m_{31}^2 +{\cos ^2}{\theta _{12}}\varDelta m_{32}^2 +\sin {\theta _{13}}\sin 2{\theta _{12}}\tan {\theta _{23}}\varDelta m_{21}^2\cos \varDelta \) [66].

In MINOS and MINOS+ Collaborations, the muon (anti)neutrino production is based on the proton beams of accelerators, and the length of baseline is 735 km and it covers the energy of \(0.5\sim 50\) GeV. It is clear that the ratio L/E ranges from 15 km/GeV to 1500 km/GeV. In particular, the MINOS+ data provide significant additional statistical power integrated in the range from 4 to 8 GeV energy over the lower energy MINOS data. The evolutions of probabilities (survival probabilities of the muon neutrino oscillation) is plotted as a function of L/E shown as Fig. 1. In the figure, the experimental result based on the data of MINOS and MINOS+ Collaborations [17, 18] and the theoretical result are offered.

Fig. 1
figure 1

The Long-range survival probabilities \({\nu _\mu } \rightarrow {\nu _\mu }\) (solid line, blue) as a function of the distance traveled per energy L/E with the initial muon flavor state. The solid line is theoretical value and the data of MINOS and MINOS+ Collaborations (blue square) are addressed from Refs. [17, 18]

Full size image

To further explore the QMA-EUR and the quantum correlation in experimentally observed muon neutrino oscillations, the evolutive states for two-flavor neutrino are

$$\begin{aligned} {\hat{\rho }} _{AB}^\mu \left( t \right)&= {\left| {{a_{\mu \mu }} \left( t \right) } \right| ^2}\left| {10} \right\rangle \left\langle {10} \right| + {a_{\mu \tau }}\left( t \right) a_{\mu \mu }^ * \left( t \right) \left| {01} \right\rangle \left\langle {10} \right| \nonumber \\&\quad + {\left| {{a_{\mu \tau }}\left( t \right) } \right| ^2}\left| {01} \right\rangle \left\langle {01} \right| \nonumber \\&\quad + {a_{\mu \mu }}\left( t \right) a_{\mu \tau }^ * \left( t \right) \left| {10} \right\rangle \left\langle {01} \right| \end{aligned}$$
(11)

in the orthonormal basis \(\left\{ {\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle ,\left| {11} \right\rangle } \right\} \). Herein, we choose a pair of spin\(-1/2\) Pauli observables \((P,R) = (\sigma _x,\sigma _y)\) as the incompatibility. By some calculations, one can obtain that the maximal overlap \(c\left( {P,R} \right) =1/2\). By combining Eq. (7), the entropic uncertainty (\(U^\mu \)) and the uncertainty’s lower bound of (\(U_b^\mu \)) are the left-hand side (LHS) and right-hand side (RHS) of Eq. (7), which can be described as

$$\begin{aligned} U^\mu&= S\left( {\hat{\rho }_{PB}^\mu \left( t \right) } \right) + S\left( {\hat{\rho }_{RB}^\mu \left( t \right) } \right) - 2S\left( {\hat{\rho }_B^\mu \left( t \right) } \right) \nonumber \\&= 2\left( {{P_{\mu \mu }}{{\log }_2}{P_{\mu \mu }} + {P_{\mu \tau }}{{\log }_2}{P_{\mu \tau }} + 1} \right) , \end{aligned}$$
(12)
$$\begin{aligned} {U_b^\mu }&= S\left( {\hat{\rho }_{AB}^\mu \left( t \right) } \right) - S\left( {\hat{\rho }_B^\mu \left( t \right) } \right) - {\log _2}c\left( {P,R} \right) \nonumber \\&= {P_{\mu \mu }}{\log _2}{P_{\mu \mu }} + {P_{\mu \tau }}{\log _2}{P_{\mu \tau }} + 1, \end{aligned}$$
(13)
$$\begin{aligned} QD \left( {\hat{\rho }_{AB}^\mu \left( t \right) } \right) = - {P_{\mu \mu }}{\log _2}{P_{\mu \mu }} - {P_{\mu \tau }}{\log _2}{P_{\mu \tau }} \end{aligned}$$
(14)

in terms of the transition probabilities, respectively. As a result, an interesting and nontrivial result can be obtained as

$$\begin{aligned} U^\mu =2U_b^\mu =2-2QD\left( {\hat{\rho }_{AB}^\mu \left( t \right) } \right) . \end{aligned}$$
(15)

This equality states that the quantum correlation quantified by QD is completely responsible for the dynamics of the entropy-based uncertainty and its lower bound in the physical process of muon neutrino oscillations. Specifically, the uncertainty is completely anti-correlated with the quantum correlation of two-flavor neutrino states \(\hat{\rho }_{AB}^\mu \left( t \right) \), i.e., the stronger quantum correlation will lead to the smaller entropic uncertainty in the current architecture.

Fig. 2
figure 2

a The entropic uncertainty and the uncertainty’s lower bound in Eq. (7) in theory (solid line) and experiment (square) with the error bars in regard to the distance traveled per energy L/E for the initial \(\mu \)-flavor state; b The quantum discord quantified by Eq. (9) in theory and experiment with the error bars in regard to L/E for the initial \(\mu \)-flavor state. LHS (solid line, red) denotes the entropic uncertainty [the left-hand side of Eq. (7)]; RHS (solid line, green) represents the uncertainty’s lower bound [the right-hand side of Eq. (7)]; QD (solid line, violet) corresponds to the quantum discord

Full size image

In Fig. 2, the QMA-EUR and the quantum discord are drawn with respect to the ratios L/E for both theoretical and experimental results. It is seen that the theoretical lines are periodically oscillating with the same period \(T = 513.215\). When the ratio at the points \(L/E = \left( {2n + 1} \right) 256.608\) with integers \(n \in \left[ {0,2} \right] \), yielding the maximal entangled state \((| 01\rangle + | 10\rangle )/{\sqrt{2}}\), the entropic uncertainty and the uncertainty’s lower bound coincide, and reach the minimum value \({\hbox {LHS}} = {\hbox {RHS}} = 0\). In the contrary, the quantum discord is maximized with the value \(QD=1\). From viewpoint of quantum resource theory, it implies that more quantum resources could be harvested with regard to the neutrinos propagation in the MINOS/MINOS+ experiments. For the ratio at the points \(L/E = n \times 513.215\) with positive integers \(n \in \left[ {1,2} \right] \), generating the product state \(\left| {01} \right\rangle \), the entropic uncertainty and the lower bound reach the maximum value LHS=RHS=2. However, the quantum discord is minimized with the value of QD.

Fig. 3
figure 3

Experimental results for the entanglement witness with respect to the ratio L/E for the initial muon flavor state. The entropy (solid line, red) \(S\left( {P|B} \right) + S\left( {R|B} \right) + {\log _2}c\left( {P,R} \right) \), and the concurrence (solid line, blue) of neutrino-flavor state in theory and experiment with the error bars. The magenta solid line denotes the entropy limit (zero value)

Full size image

Moreover, we explore the application of QMA-EUR as entanglement witness. Quantum entanglement is a vital quantum resource and the basis of many protocols in quantum information processing. Here, we use the concurrence \(C\left( {{{\hat{\rho }}_{AB}}} \right) = \max \left\{ {0,\sqrt{{\lambda _1}} - \sqrt{{\lambda _2}} - \sqrt{{\lambda _3}} - \sqrt{{\lambda _4}} } \right\} \) as a measurement of two-flavor neutrino state’s entanglement [67], and \({\lambda _i}\) represent the eigenvalues of the non-Hermitian matrix \({\hat{\rho }_{AB}}( {{\sigma _y} \otimes {\sigma _y}} )\) \(\hat{\rho }_{AB}^ * ( {{\sigma _y} \otimes {\sigma _y}} )\) in the decreasing order. In fact, there exists a criterion as to entanglement detection that the system consisting of A and B must be entangled when its conditional von Neumann entropy \(S\left( {A|B} \right) <0\). In connection with QMA-EUR in Eq. (7), if the entropy satisfies

$$\begin{aligned}&S\left( {P|B} \right) + S\left( {R|B} \right) + {\log _2}c\left( {P,R} \right) \nonumber \\&= 2(P_{\mu \mu }\log _2P_{\mu \mu } + P_{\mu \tau }\log _2P_{\mu \tau })+1< 0, \end{aligned}$$
(16)

we can deduce \(S\left( {A|B} \right) <0\), which is regarded as an indicator that the bipartite neutrino-flavor state is entangled definitely.

Consequently, we make use of the sufficient condition of judging quantum entanglement expressed in Eq. (16) to detect the muon neutrino-flavor state’s entanglement, while its concurrence has been provided in Fig. 3. From the figure, it is obvious that the theoretical line of entropy is periodically oscillating with the period \(T=513.215\). By some numerical calculations, it can be obtained that the amount of entropy is less than zero, i.e., \(S\left( {P|B} \right) + S\left( {R|B} \right) + {\log _2}c\left( {P,R} \right) <0\) in regions of \(L/E \in (110.468 + n \times 513.215,\) \(\ 402.746 + n \times 513.215)\) with the integers \(n \in \left[ {0,2} \right] \). It shows that the entropic estimation can witness the neutrino-flavor state’s entanglement in muon neutrinos, and the corresponding region of the concurrence \(\left( {0.626,1} \right] \) can be numerically obtained, which supports the criterion based on QMA-EUR can be effectively used to detect the quantum entanglement in the processing of the muon neutrino oscillations. Due to the fact that if the entanglement criterion based on QMA-EUR satisfies, and then the concurrence must be non-zero, this manifests that the proposed entropy-based criterion is stronger than the concurrence-based one, and can be viewed as a reliable tool to detect the entanglement.

3.2 QMA-EUR and quantum correlation in the electron antineutrino oscillations

We firstly prepare an electron neutrino in the initial time \(t=0\), the time evolution of states for the two-flavor neutrino oscillations are

$$\begin{aligned} \left| {{\nu _e}\left( t \right) } \right\rangle = {a_{ee}}\left( t \right) \left| {{\nu _e}} \right\rangle + {a_{e\mu }}\left( t \right) \left| {{\nu _\mu }} \right\rangle \end{aligned}$$
(17)

with the probabilities \({P_{ee}}\left( t \right) = {\left| {{a_{ee}}\left( t \right) } \right| ^2}\) and \({P_{e\mu }}\left( t \right) = {\left| {{a_{e\mu }}\left( t \right) } \right| ^2}\) for detecting the neutrino in the electron flavor state \({\nu _e}\) and the muon flavor state \({\nu _\mu }\), respectively. In Ref. [66], the effective atmospheric \(\varDelta m_{ee}^2\) measured in \({\nu _e}\) disappearance experiments is given by \(\varDelta m_{ee}^2 = {\cos ^2}{\theta _{12}}\varDelta m_{31}^2 + {\sin ^2}{\theta _{12}}\varDelta m_{32}^2\).

Fig. 4
figure 4

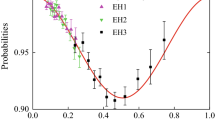
The survival probabilities \({\nu _e} \rightarrow {\nu _e}\) (solid line, blue) versus the distance traveled per energy L/E with the initial electron flavor state. The solid line is theoretical value and the data of Daya Bay Collaboration in three different underground experimental halls (EH1: square; EH2: upper triangle; EH3: circle) are taken from Ref. [19]

Full size image

In Fig. 4, we provide the evolution relation of survival probabilities versus the ratio L/E, with the experimental results and the theoretical predictions. Therein, the experimental data we adopted is from the Daya Bay neutrino experiments [19], and explicitly EH1, EH2 and EH3 stand for all the measurement positions of the Daya Bay collaboration, where they take advantage of \(\beta \) decay to generate the electron antineutrino source with different baselines and energies. They utilized the Daya Bay Reactor Neutrino Experiment to detect the electron antineutrino disappearance, the energy in the experiment ranges from 1 MeV to 8 MeV. It shows that the effective L/E is with \(\left[ {0,1} \right] \) km/MeV. As can be seen in Fig. 4, for the short-range oscillations (with the current ratios L/E) in the Daya Bay experiment, the survival probabilities of finding the electron flavor state \({\nu _e}\) is more than 0.9 all the time. For \(L/E\approx 0.5\), the survival probability comes to the minimum value. Correspondingly, the oscillation probability of detecting other flavor state reaches the maximum value.

In order to investigate the QMA-EUR and the quantum correlation in experimentally observed electron neutrino oscillations, the time evolutive states for the initial electron flavor state are given by

$$\begin{aligned} {\hat{\rho }}_{AB}^e\left( t \right)&= {\left| {{a_{ee}}\left( t \right) } \right| ^2} \left| {10} \right\rangle \left\langle {10} \right| + {a_{ee}}\left( t \right) a_{e\mu }^ * \left( t \right) \left| {10} \right\rangle \left\langle {01} \right| \nonumber \\&\quad + {\left| {{a_{e\mu }}\left( t \right) } \right| ^2}\left| {01} \right\rangle \left\langle {01} \right| \nonumber \\&\quad + {a_{e\mu }}\left( t \right) a_{ee}^ * \left( t \right) \left| {01} \right\rangle \left\langle {10} \right| \end{aligned}$$
(18)

in the orthonormal basis \(\left\{ {\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle ,\left| {11} \right\rangle } \right\} \). According to Eqs. (7) and (9), the entropic uncertainty, the uncertainty’s lower bound and quantum correlation are analytically derived as

$$\begin{aligned} U^e&= S\left( {\hat{\rho }_{PB}^e\left( t \right) } \right) + S\left( {\hat{\rho }_{RB}^e\left( t \right) } \right) - 2S\left( {\hat{\rho }_B^e\left( t \right) } \right) \nonumber \\&= 2\left( {{P_{ee}}{{\log }_2}{P_{ee}} + {P_{e\mu }}{{\log }_2}{P_{e\mu }} + 1} \right) ,\end{aligned}$$
(19)
$$\begin{aligned} {U_b^e}&= S\left( {\hat{\rho }_{AB}^e\left( t \right) } \right) - S\left( {\hat{\rho }_B^e\left( t \right) } \right) - {\log _2}c\left( {P,R} \right) \nonumber \\&= {P_{ee}}{\log _2}{P_{ee}} + {P_{e\mu }}{\log _2}{P_{e\mu }} + 1, \end{aligned}$$
(20)

and

$$\begin{aligned} QD\left( {\hat{\rho }_{AB}^e\left( t \right) } \right) = - {P_{ee}}{\log _2}{P_{ee}} - {P_{e\mu }}{\log _2}{P_{e\mu }}. \end{aligned}$$
(21)

Upon the above equations, it is easy to obtain

$$\begin{aligned} U^e=2U_b^e=2-2QD\left( {\hat{\rho }_{AB}^e \left( t \right) } \right) \end{aligned}$$
(22)

for the electron neutrino oscillations. In terms of this relation, we attain that the entropic uncertainty and its bound are fully opposite to the systemic quantum correlation, which is essentially the same as that statement previously concluded in the \(\mu \) neutrino oscillations.

Fig. 5
figure 5

The entropic uncertainty in Eq. (7), the uncertainty’s lower bound in Eq. (7) and the quantum discord in Eq. (9) in theory and experiment with the error bars in regard to the distance traveled per energy L/E for the initial electron flavor state. LHS (solid line, red) denotes the entropic uncertainty [the left-hand side of Eq. (7)]; RHS (solid line, green) is the uncertainty’s lower bound [the right-hand side of Eq. (7)]; QD (solid line, violet) is the quantum discord

Full size image

In Fig. 5a, we observe the QMA-EUR when performing the measurements \({\sigma _x}\) and \({\sigma _y}\) in experimental electron neutrino oscillations by the data adopted from the Daya Bay neutrino experiment. From the figure, it shows that the experimental results are well consistent with the theoretical predictions within the error bars, and we compute that the goodness of fit is \(\chi ^2 / {\hbox {NDF}}=25.17 / 33\) with respect to the entropic uncertainty, which corresponds to that p-value is equal to 0.83. The time evolution of the entropic uncertainty always keeps in step with the lower bound of uncertainty, which first increases and then decreases with the growing ratio L/E. With respect to the ratio at the point \(L/E=0\) and \(L/E=1\), the neutrino-flavor states are the maximally mixed states without entanglement. Consequently, the entropic uncertainty and the lower bound become the maximum value LHS=2 and RHS=1, respectively. The neutrino-flavor state at around the point \(L/E=0.5\), the uncertainty and the lower bound reach the minimum value 1.1274 and 0.5637, respectively. The small entropic uncertainty implies that the prediction of the measuring outcomes is relatively precise. Whereas, it displays that the quantum discord first increases and subsequently reduces with the ratio. It is obvious that the entropy-based uncertainty is oppositely associated with quantum correlation (i.e., QD), which supports our derivation in Eq. (15).

Moreover, we explore the application of QMA-EUR as entanglement witness. According to the criterion of entanglement detection \(S\left( {A|B} \right) <0\), the entropy satisfies

$$\begin{aligned} 2(P_{ee}\log _2P_{ee} + P_{e\mu }\log _2P_{e\mu })+1< 0, \end{aligned}$$
(23)

then we can conclude that the bipartite neutrino-flavor state is entangled definitely in the current architecture.

Fig. 6
figure 6

Experimental results for the entanglement witness with respect to the ratio L/E for the initial electron flavor state. The entropy (solid line, red) \(S\left( {P|B} \right) + S\left( {R|B} \right) + {\log _2}c\left( {P,R} \right) \), the concurrence (solid line, blue) of neutrino-flavor state in theory and experiment with the error bars

Full size image

We draw the entropy \(S\left( {P|B} \right) + S\left( {R|B} \right) + {\log _2}c\left( {P,R} \right) \) and the electron neutrino-flavor state’s concurrence as a function of the ratio L/E in Fig. 6. From the figure, it is apparent that the experimental results are compatible with the theoretical predictions within the error bars, by calculating \(\chi ^2 / {\hbox {NDF}}=21.80 / 33\) and the corresponding p-value of 0.93. As to the ratio L/E in the region \(\left[ {0,1} \right] \), the neutrino-flavor state’s concurrence can be always detected except for the points \(L/E=0\), however, the entropy is larger than zero. It shows that the entropy estimation is ineffective to detect the entanglement in electron antineutrino oscillations. This result can be interpreted as that the large survival probabilities of finding the electron flavor states lead to the relatively small concurrence. Thus, it is difficult to detect entanglement by using the entropic uncertainty relations.

4 Conclusions

In this paper, quantum-memory-assisted entropic uncertainty relation and quantum correlation have been investigated in neutrino oscillations with an initial muon or electron neutrino. To be specific, the entropic uncertainty, the lower bound of uncertainty and the systemic quantum correlation have been analyzed in experimentally observed neutrino oscillations from two different neutrino sources, i.e., MINOS/MINOS+ and Daya Bay collaborations. It is found that the uncertainty and the lower bound is non-monotonic as the energy increases. Notably, they exhibit the periodically oscillating evolutions in muon neutrino oscillations. Remarkably, we have disclosed the intrinsic relationships among the entropic uncertainty, its lower bound and quantum correlation, and proved that the quantum correlation is uniquely responsible for the dynamics of both the entropic uncertainty and its lower bound in neutrino systems, obtaining that the uncertainty and its bound are fully anti-correlated with QD.

Moreover, we explore the application of the entropic uncertainty relations on entanglement witness, it can witness the neutrino-flavor state’s entanglement in muon neutrino oscillations in the regions of \(L/E \in (110.468 + n \times 513.215,\) \(\ 402.746 + n \times 513.215)\) with \(n \in \left[ {0,2} \right] \), and this never occurs in antielectron neutrino oscillations. The survival probabilities of finding the electron flavor state is more than 0.9 all the time, which leads to relatively small entanglement compared to the muon neutrino oscillations. Therefore, the entropic uncertainty relation is ineffective to detect the entanglement in electron antineutrino oscillations within the current framework. It is obtained that the entropic uncertainty relations can be treated as the reliable entanglement witness for the muon neutrino oscillations in the practical experiments of neutrino oscillations. Therefore, we argue that our investigations could shed light on quantum measurement estimation and be applicable in the further quantum information science with neutrinos.