Anisotropic neutron stars with hyperons: implication of the recent nuclear matter data and observations of neutron stars

Abstract

Motivated by a recent report by Biwas and Bose (Phys Rev D 99:104002, 2019) that the observations of GW170817 to constrain the extent of pressure anisotropy in neutron stars within Bower–Liang anisotropic model, we systematically study the effects of anisotropic pressure on properties of the neutron stars with hyperons. The equation of state is calculated using the relativistic mean-field model with a BSP parameter set to determine nucleonic coupling constants and by using SU(6) and hyperon potential depths to determine hyperonic coupling constants. We investigate three models of anisotropic pressure known in literature namely Bowers and Liang (Astrophys J 88:657, 1974), Horvat et al. (Class Quant Grav 28:025009, 2011), and Cosenza et al. (J Math Phys (NY) 22:118, 1981). The reliability of the equation of state used is checked by comparing the parameters of the corresponding EOS to recent experimental data. The mass–radius, moment of inertia, and tidal deformability results of Bowers–Liang, Horvat et al., and Cosenza et al. anisotropic models are compared to the corresponding recent results extracted from the analysis of some NS observation data. We have found that the radii predicted by anisotropic NS are sensitive to the anisotropic model used and the results obtained by using the model proposed by Horvat et al. with anisotropic free parameter $\varUpsilon ~\approx -$ 1.15 are relative compatible with all taken constraints.

1 Introduction

Neutron stars (NSs) are the perfect compact objects to study the matter at high densities and strong-field gravity simultaneously. However, both of the matter and the gravity of NSs still are not fully understood.

There is tremendous progress related to NS properties observations such as mass, radius, and tidal deformation have been reported. Here we discuss shortly only some crucial ones. The accurate measurements of massive pulsars [1,2,3,4,5] provide maximum mass limit of NS around 2.0 $M_\odot$. There are also many studies reported the maximum mass of NSs from analyzing data extracted from gravitational wave (GW) events (see the recent review in Refs. [6, 7], and the references therein). Note that Lim and Holt [7] discussed the Bayesian modeling of the nuclear equation of state (EOS) systematically, assuming a minimal model at high-density and neglect the possibility of phase transition for NS tidal deformability and GW170817 by generating 300000 NS EOSs by sampling from Bayesian posterior probability distributions. The obtained tidal deformability and the radius range of the canonical NS are consistent with observational constraints from GW170817, but 30% of the EOS fail to generate 2.0 $M_\odot$ maximum mass constraint. The results are also indicated that improved microscopic constraints from chiral effective field theory are necessary. The maximum mass of pulsar observed provides an impact on the allowed stiffness of the EOS of an NS. Other consequences of NS maximum mass have been discussed in recent studies (see Ref. [6] and the references therein). We also note that the authors of Ref. [6] concluded that the predicted absolute maximum mass of NS is less than 2.4 $M_\odot$ independent to EOS. These results can pin down the mass boundary between NSs and black holes. Accurately measured NS radii are also important to constraint the EOS of NSs. However, we still have challenges that come from the systematic error to extract NS radii from observational data [8]. However, it is interesting to note that the X-ray burst from accreting NSs in low mass binary (LMXB) provides possibilities to constrain the NS mass and radius simultaneously. It is shown in Ref. [6], several constraints of NSs radii reported up to the recent years. If the radii constraint from LMXB is compared to the one predicted by using EOS constrained by the nuclear laboratory data and the ones obtained by the majority of post-GW170817 analysis, the radius constraints of LMXB data are mostly smaller than those of the nuclear laboratory data and from the post-GW170817 (Please see the detail discussions in Ref.  [6] and the references therein).

The X-ray measurements of emission from the hot-spots on the NS surface with NICER [9, 10] can offer information about the mass and radius of selected pulsars. Recently, NICER reports mass and radius constraints for its first target PSR J0030 + 0451 [11,12,13]. GW observations of coalescence NSs with LIGO and VIGO can measure the tidal deformability of NSs. This novel probe can investigate a wide range of NS mass and the corresponding central density [9, 14,15,16,17]. Two GW signals from the coalescence of binary NSs have been recently reported, GW170817 [14, 15], and GW190425 [17]. These results provide a stringent constraint to the NS EOS. Note also that moment inertia is measured through pulsar timing as one of the other future probes for NS properties. Moment inertia measurements become crucial and attract much attention recently. Many works concerning the analysis of NS moment of inertia and the NS crust properties have been reported, e.g.,  [18,19,20,21,22,23,24,25,26,27,28,29]. Furthermore, some studies have been performed by examining systematically the latest astronomical measurements or and nuclear properties to extract the accurate information of the properties of the EOS of NSs [9, 30, 33, 34].

As of today, there is no comprehensive description of NS matter. The matter in an NS is usually considered as an isotropic fluid because astrophysical observations so far favor this choice [35]. However, NSs as compact objects with a density larger than twice nuclear saturation density and composed with many interacting particles have indeed quite complex structures. Therefore, one can expect that the appearance of unequal pressures or known as anisotropic pressure in NSs matter, is natural. Many factors can cause the appearance of anisotropic pressure. Due to the novel properties of matter such as the presences of strong magnetic and electric fields, different kinds of phase transition, superfluidity, boson condensations, anisotropic momentum distribution in matter [35,36,37,38,39] and or due to the impact of modified gravity [40,41,42,43,44]. The anisotropic pressure has impacts on NS properties such as mass–radius relation, a moment of inertia, tidal deformability, universal relation, instability due to cracking or overturning, energy conditions [35, 37, 38, 45,46,47,48,49,50,51]. Moreover, there are also some analytically models to study anisotropic stars for examples one can see in Refs. [35, 52].

To describe NS core EOS theoretically, one uses non-relativistic or relativistic models. There are hundreds of EOS models are already proposed up to now. The relativistic mean-field (RMF) belongs to the relativistic models. Note that the authors of Ref. [53] analyzed 263 RMF parameter sets with different kinds. They have found only 34 RMF parameter sets that satisfy nuclear matter constraints. Furthermore, in the case of isotropic NS without hyperons, from 35, only 15 parameter sets predict NS maximum mass around 2.0 $M_\odot$. However, if hyperons and other exotic particles are included, none of them satisfy the later constraint (See Ref.  [54] and the references therein for details.). The later is known in the literature as “hyperons puzzle”. Note that BKA22 [55] and BSR12 [56] RMF parameter sets are the ones that belong to 15 well-tested parameter sets. The recent reports on the role of hyperons and other exotics and how to deal with the “hyperon puzzle” can be found, e.g., in Refs. [57,58,59,60,61,62,63,64,65,66,67,68] and also see the references therein.

It is also important to note that the LIGO/Virgo collaboration recently reported the GW190814 observation of the merger of a black hole of mass (22.2–24.3) $M_\odot$ and a secondary massive compact object with mass (2.50–2.67) $M_\odot$ [17]. It is already much discussions exist about the nature the corresponding secondary compact object whether it is black hole, neutron star or other exotic objects [17, 69,70,71,72,73,74,75]. For standard static isotropic NS the mass around 2.6 $M_\odot$ is impossible to reach except the NS rotates very fast [17, 74]. Therefore, it is also interesting to check the role anisotropic pressure of NS for reaching this extreme maximum mass limit.

In this work, we study the properties of NS with hyperons systematically, such as mass-radius relation, a moment of inertia, and tidal deformability of predicted by three models of anisotropic pressure proposed by Bowers–Liang, Horvat et al., and Cosenza et al. [76,77,78,79,80]. We use BSP parameter set of RMF model [60, 81]. The hyperon coupling constant is determined by using the standard SU(6) prescription and hyperon potential depths [82]. For the inner and outer crusts, we use the crust EOS that proposed by Miyatsu et al. [83]. The compatibility of the nuclear matter properties predicted by the BSP parameter is tested by comparing them to other calculations and experimental and observations data. The corresponding NS mass–radius relation, moment of inertia, and tidal deformability results are confronted with the corresponding recent extracted results from the combination of some observation data in Refs. [1,2,3,4, 9, 15, 17, 18, 20,21,22, 30,31,32]. The aim is to check whether the anisotropic pressure NSs with hyperons compatible with the recent experimental and observational data.

We organize the paper as follows: In Sect. 2, we briefly discuss the model used to calculate the EOS of NSs. In Sect. 3, we discuss the anisotropic pressure and the effect in NS moment of Inertia is discussed in Sect. 4. In Sect. 5, we discuss the effect of anisotropic pressure on the tidal deformability of NS. Section 6 is devoted to numerical details. Finally, we conclude in Sect. 7.

2 Model for neutron star matter

In this section we briefly review the EOS model used in this work.

We use relativistic mean field (RMF) model to describe homogeneous matter of the NS core. The RMF Lagrangian density can be expressed as [60]:

$$\begin{aligned} {\mathcal {L}} = {\mathcal {L}}_{B} + {\mathcal {L}}_{BM} + {\mathcal {L}}_{M} +{\mathcal {L}}_{L}, \end{aligned}$$

(1)

where the free Lagrangian density for baryons (B = N, $\Lambda$, $\varSigma$, $\varXi$) is

$$\begin{aligned} {\mathcal {L}}_{B}=\sum _{B}\overline{\varPsi }_B[i\gamma ^{\mu }\partial _{\mu }-M_B]\varPsi _B, \end{aligned}$$

(2)

with $M_B$ is baryon mass and the Lagrangian density for meson–baryon couplings is given by

$$\begin{aligned} {\mathcal {L}}_{BM}= & {} \sum _{B}\overline{\varPsi }_B[g_{\sigma B} \sigma -\gamma _\mu g_{\omega B} \omega ^\mu \nonumber \\&-\frac{1}{2}\gamma _\mu g_{\rho B}{\tau _B}\cdot {\rho } ^\mu -\gamma _\mu g_{\phi B}\phi ^\mu ]\varPsi _B, \end{aligned}$$

(3)

where the non-strange mesons which are coupled to all baryons are $\sigma$, $\omega$, $\rho$. However, the hidden-strangeness meson $\phi$ is only coupled to hyperons (H = $\Lambda$, $\varSigma$, $\varXi$). The free and self interaction meson Lagrangian density can be expressed as

$$\begin{aligned} {\mathcal {L}}_{M}= & {} \frac{1}{2}(\partial _{\mu }\sigma \partial ^{\mu }\sigma -m_{\sigma }^2\sigma ^2)+\frac{1}{2}(\partial _{\mu }\sigma ^*\partial ^{\mu } \sigma ^*-m_{\sigma ^*}^2\sigma ^{*2})\nonumber \\&-\frac{1}{4}\omega _{\mu \nu }\omega ^{\mu \nu }+\frac{1}{2}m_{\omega }^2\omega _{\mu } \omega ^{\mu }-\frac{1}{4}\phi _{\mu \nu }\phi ^{\mu \nu }+\frac{1}{2}m_{\phi }^2\phi _{\mu }\phi ^{\mu }\nonumber \\&-\frac{1}{4}{\rho }_{\mu \nu }{\rho }^{\mu \nu }+\frac{1}{2}m_{\rho }^2{\rho }_{\mu } {\rho }^{\mu }+{\mathcal {L}}^{NL}_{M}, \end{aligned}$$

(4)

the $\omega ^{\mu \nu }$, $\phi ^{\mu \nu }$ and ${\rho }^{\mu \nu }$ are meson tensor fields of the $\omega$, $\phi$ and $\rho$ mesons. They are be defined as $\omega ^{\mu \nu }=\partial ^{\mu }\omega ^{\nu }-\partial ^{\nu }\omega ^{\mu }$, $\phi ^{\mu \nu }=\partial ^{\mu }\phi ^{\nu }-\partial ^{\nu }\phi ^{\mu }$, and ${\rho }^{\mu \nu }=\partial ^{\mu }{\rho }^{\nu }- \partial ^{\nu }{\rho }^{\mu }$. The explicit form of Lagrangian density for meson self interactions ${\mathcal {L}}^{NL}_{M}$ can be written as

$$\begin{aligned} {\mathcal {L}}^{NL}_{M}= & {} - \frac{\kappa _3 g_{\sigma N} m_{\sigma }^2}{6 m_{ N} } \sigma ^{3} - \frac{\kappa _4 g_{\sigma N}^2 m_{\sigma }^2}{24 m_{ N}^2 } \sigma ^{4}+\frac{\zeta _0 g_{\omega N}^2}{24} {(\omega _{\mu } \omega ^{\mu })}^2\nonumber \\&+ \frac{\eta _1 g_{\sigma N} m_{\omega }^2}{2 m_{ N} } \sigma \omega _{\mu } \omega ^{\mu }+\frac{\eta _2 g_{\sigma N}^2 m_{\omega }^2}{4 m_{ N}^2 }\sigma ^{2} \omega _{\mu } \omega ^{\mu } \nonumber \\&+\frac{\eta _{\rho } g_{\sigma N} m_{\rho }^2}{2 m_{ N} } \sigma {\rho }_{\mu } \cdot {\rho }^{\mu } +\frac{\eta _{1\rho }g_{\sigma N}^2m_{\rho }^{2}}{4m_N^2} \sigma ^2{\rho }_{\mu } \cdot {\rho }^{\mu } \nonumber \\&+\frac{\eta _{2 \rho } g_{\omega N}^2 m_{\rho }^2}{4 m_{ N}^2 } \omega _{\mu } \omega ^{\mu } {\rho }_{\mu } \cdot {\rho }^{\mu }. \end{aligned}$$

(5)

Eq. (5) includes contribution from the standard RMF nonlinear self-interaction for $\sigma$ and $\omega$ mesons as well as additional cross interaction terms for $\sigma$, $\omega$, and $\rho$ mesons. For the nucleon sector, we use the BSP parameter set. The value of nucleon–meson coupling constants and the parameters of the Lagrangian density for mesons self-interactions of the BSP parameter set can be seen in Refs. [60, 81]. Note that the finite nuclei, pure neutron matter (PNM), and symmetric nuclear matter (SNM) properties predicted by the BSP parameter set quite compatible with experimental and other theoretical results (See more details about the BSP predictions in Refs. [60, 81]). Here we show the nuclear-matter and core-crust transition properties predicted by BSP parameter set due to their relations to NS properties in Table  1, Figs. 1, and 2. We also compare the results with those from other works. Note that the most crucial SNM property is the binding energy at saturation density (E/N). Other nuclear-matter isoscalar properties at saturation density can be derived from the binding energy $E (\rho )$ as follows:

$$\begin{aligned} K_0= & {} 9 \rho _0^2 \frac{d^2 E(\rho )}{d\rho ^2} |_{\rho =\rho _0},\nonumber \\ J_0= & {} 27 \rho _0^3 \frac{d^3 E(\rho )}{d\rho ^3} |_{\rho =\rho _0}, \end{aligned}$$

(6)

in the isovector sector, the role of symmetry energy at saturation density J is similar to that of the binding energy. Other nuclear-matter isovector properties at saturation density can be derived from $E_\mathrm{sym} (\rho )$ and are given by the following:

$$\begin{aligned} L= & {} 3 \rho _0 \frac{d E_\mathrm{sym}(\rho )}{d\rho } |_{\rho =\rho _0},\nonumber \\ K_\mathrm{sym}= & {} 9 \rho _0^2 {\frac{d^2 E_\mathrm{sym}(\rho )}{d^2\rho } |_{\rho =\rho _0}}, \end{aligned}$$

(7)

Table 1 Nuclear-matter properties at the saturation density $\rho _0$ and NS core-crust transition properties predicted by BSP [60, 81], BKA22 [55], and BSR12 [56] parameter sets, respectively. The binding energy E, incompressibility coefficient for SNM $K_0$, symmetry energy $E_\mathrm{sym}$, and other quantities are defined in Eqs. (6) and (7)

Fig. 1

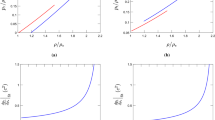
a Pressure as a function of the ratio of the nucleon to nuclear saturation densities. b Energy per particle as a function of the density around the saturation density for SNM using BSP, BSR12, and BKA22 parameter sets. The Grey shaded areas on a is the results extracted from heavy-ion experimental data [96], whereas the yellow shaded area in b is the constraint imposed by the SNM binding energy near twice the saturation density extracted from the FOPI experimental data [97] and the boxed area around saturation density in b is the acceptable range of the SNM binding energy around the saturation density which is extracted from the Bethe–Weizäcker mass formula. For comparison, we also show the SNM binding energy at the saturation density of Refs. [84, 98]

Fig. 2

Similar to Fig. 1 but for PNM. The shaded areas in a are the results extracted from heavy-ion experimental data [96], while the yellow shaded area in b is the theoretical binding energy for PNM at low densities obtained from the chiral effective field theory calculations [102, 103]

Table 1 shows the parameters of nuclear matter at saturation predicted by the BSP parameter set. The results are quite compatible with the ones predicted by BKA22 [55] and BSR12 [56] as well as from the latest constraints of nuclear matter. We need to note that constraining nuclear matter parameters with GW 170817  [93] yields the incompressibility $K_0$, its slope $M_0$ which is defined as $J_0+12K_0$, and the curvature of symmetry energy $K_\mathrm{sym}$ at nuclear saturation density to be (81 $\le K_0 \le$ 362) MeV, (1556 $\le M_0 \le$ 4971) MeV, and (− 259 $\le K_\mathrm{sym} \le$ 32) MeV. Here we use a relativistic random phase approximation to calculate the core-crust transition density $\rho _t$ and the corresponding pressure $P_t$ [94, 95]. It is known that $\rho _t$ and $P_t$ are the key factors determining the core-crust properties of NSs. The core-crust transition properties significantly affected by the slope of symmetry energy L. The consistent or unified treatment of the EOS of crust and core, and the method used to calculate $\rho _t$ also affect core-crust properties [21, 23,24,25,26,27,28]. The most recent comprehensive study about the relation of nuclear matter properties with $\rho _t$ and $P_t$ can be found in Ref. [21].

Furthermore, it can be seen in Figs. 1 and 2 that the BSP parameter set yields compatible SNM and PNM EOSs with heavy-ion experimental data [96] and by the SNM binding energy near twice the saturation density extracted from the FOPI experimental data [97]. Moreover, if we compare them with the ones predicted by BKA22 [55] and BSR12 [56] parameter sets, the SNM and PNM EOS stiffnesses predicted by BSP parameter set are relatively similar. Only at relatively high density ($\rho _N > 4 \rho _0$), SNM EOS of BSP becomes stiffer than those of BKA22 and BSR12. We also compare the binding energy predicted by the BSP parameter with the recent results obtained by the authors of Refs. [84, 98]. It is also evident that the BSP result is also compatible with their results. Furthermore, in SNM binding energy constraint in Fig. 1 we also use SNM binding energy around the saturation density data, which is extracted from simple Bethe–Weizäcker mass formula. This constraint can also be extracted from a better model, such as a droplet or liquid-drop model [99, 100]. The recent discussion of the relation between the droplet parameter with EOS can be found in Ref. [101]. The binding energy for PNM predicted by BSP at low and intermediate densities is shown in the lower panel of Fig. 2. It can be seen that the BSP result is more compatible with the ones predicted by the current chiral many-body results [102, 103] than those predicted by BKA22 and BSR12 parameter sets. Detail discussions about the progress and current state of the art of chiral many-body perturbation theory (MBPT) can be found e.g., in Refs. [98, 103,104,105,106]. It is important to note that theoretical uncertainties of nuclear matter are significantly reduced when going to higher order in chiral MBPT, and up to next-to-next-to-leading order, the uncertainties are already small [106]. Therefore, chiral MBPT can be used to improve the isovector sector predictions of RMF models by fitting the isovector parameters of RMF models using PNS EOS predicted by chiral MBPT results. Note that BSR12 and BKA22 parameter sets are ones of the small number of RMF parameter sets that satisfy all adapted nuclear matter experimental constraints performed in Ref. [53]. Therefore, both parameter sets have relatively acceptable finite nuclei and nuclear matter predictions. It can be seen here that the quality of nuclear matter prediction of the BSP parameter set [60, 81] is not too far from those parameter sets. Therefore, we use the BSP parameter set as a representative RMF parameter set for our study here. Note that a recent review of nuclear matter properties related to NS properties can be found in Ref. [6] and see also a nice discussion of more consistent nuclear matter calculations in Ref. [7].

Even though many progress up to now, in the strange sectors, the corresponding EOS is still not too certain due to the uncertainty in hyperons and other exotic particle coupling constants. In general, hyperons and other exotic particles tend to soften the corresponding EOS of NS core. Therefore, in the case NS with hyperons and other exotics, the predicted maximum mass is always smaller than that without hyperons and other exotics. This situation is known in litterateur as “Hyperon puzzle”. Here, we do not go deep into the hyperon puzzle discussion. We take the most conservative or standard way to determine the hyperon coupling constants, i.e., by using SU(6) prescription and experimental value of potential depths at nuclear matter saturation density and neglect the contribution of the exotics. Other novel prescriptions to determine hyperon coupling constants tend to stiffer the corresponding EOS or milder the role of hyperons.

Here to determine the vector part of hyperons coupling constant $g_{\omega H}$ and $g_{\phi H}$, we consider standard prescription based on SU(6) symmetry [82]. The hyperon coupling constant relations are

$$\begin{aligned} \frac{1}{3}g_{\omega N}= & {} \frac{1}{2}g_{\omega \Lambda }=\frac{1}{2}g_{\omega \varSigma }=g_{\omega \varXi },\nonumber \\ g_{\rho N}= & {} \frac{1}{2}g_{\rho \varSigma }=g_{\rho \varXi },~ ~ ~ ~ ~ ~ g_{\rho \Lambda }=0, \nonumber \\ 2 g_{\phi \Lambda }= & {} 2 g_{\phi \varSigma }=g_{\phi \varXi }=\frac{2 \sqrt{2}}{3}g_{\omega N},~ ~ ~ ~ ~ ~ g_{\phi N}=0. \end{aligned}$$

(8)

For the given values of $g_{\omega H}$, the scalar hyperons coupling constants $g_{\sigma H}$ are obtained using the potential depth of hyperons in the symmetric nuclear matter which is evaluated at the symmetric nuclear matter saturation density $\rho _0$ as,

$$\begin{aligned} U_{H}^{(N)}(\rho _0) = -g_{\sigma H}\sigma (\rho _0)+g_{\omega H}\omega (\rho _0). \end{aligned}$$

(9)

The values of the experimentally potential depth $U_H^{(N)}$ at $\rho _0$ are  taken from Ref. [82] :

$$\begin{aligned} U_{\Lambda }^{(N)}= & {} -28 \mathrm{~MeV}, \quad U_{\varSigma }^{(N)} = +30 \mathrm{~MeV} \nonumber \\&\mathrm{and}&\quad U_{\varXi }^{(N)} = -18 { \mathrm ~MeV}, \end{aligned}$$

(10)

For lepton (L=e and $\mu$), the free Lagrangian density is employed. The corresponding Lagrangian density takes following form

$$\begin{aligned} {\mathcal {L}}_{L}=\sum _{L}\overline{\varPsi }_L[i\gamma ^{\mu }\partial _{\mu }-M_L]\varPsi _L, \end{aligned}$$

(11)

where $M_L$ is lepton mass.

To describe the NS crusts’ inhomogeneous matter, we use the inner and outer crust EOSs based on the Hartree–Fock Thomas–Fermi model used by Miyatsu et al. [83]. The NS matter is assumed in $\beta$-stability. Therefore, the potential chemical balance, charge neutrality, and baryon density conservation conditions can be used to determine the composition of the constituents in NS. Note that the main impacts of crust EOSs are in the radius of low mass NS and the crust properties. It is reported that the uncertainties in NS radii and crust properties due to the uncertainties of EOS used can be as large as 30 $\%$ for the NS crust thickness and 4 $\%$ for the NS radius [26]. Consequently, the unified description of core and inner crust is essential to pin down the uncertainties in crust properties. Baym, Bethe, and Pethick (BBP)  [107] and by Baym, Pethick, and Sutherland (BPS) [108], respectively did the benchmark works on the calculation of inner and outer crust EOSs. Both EOSs based on the droplet model to generate the corresponding nuclear properties. The systematic study of outer crust for updating BPS EOS by using current nuclear data and relativistic and non-relativistic theoretical nuclear models and also considering nuclear pairing and deformation can be found in Ref. [109]. Please see also the references therein for detailed developments. Compared to the BPS, the impacts of using more recent data and the different theoretical models are the order of a few percent for the outer crust thicknesses [110]. Furthermore, it is reported that the location of the drip line and the sequence of nuclei in the outer crust of cold nonaccreting neutron stars seem to be rather robust predictions, being nearly insensitive to the parameter set, to the approximation scheme, and even to the triaxial deformations for most of the state-of-the-art nuclear models [111]. Note that the recent report of the statistical uncertainties impact on the composition of NS outer crust has been discussed in Ref. [112] while the new analytical determination of the structure of the outer crust of a cold nonaccreted neutron star can be found in Ref. [113]. The inner crust EOS is less certain than the outer crust EOS. The inner EOS is rather sensitive to the nuclear model and the method to calculate the EOS while it is shown that the crucial role of inner crust EOS on the crust thickness. Please see the detail discussions in Refs. [26, 114,115,116,117]. For examples, in the case of 1. $M_\odot$ NS, the unified core-crust EOS for RMF NL3 parameter set yield R=14.547 and $\varDelta R_\mathrm{crust}$ 1.956, while if we use NL3 for core and BBP for inner crust EOS, R=14.870 and $\varDelta R_\mathrm{crust}$ 2.230, It means the difference in R is about 2 $\%$ while $\varDelta R_\mathrm{crust}$ is about 12 $\%$. The differences of radius and crust thickness results for other RMF parameter sets are not exactly the same compared to those of NL3, but the values are around the same order as those of NL3. Note, in general, a unified core-crust model predicts a smaller radius and crust thickness than those with BBP inner crust EOS (See table. IV in Ref. [115] for details). It can be seen in Fig. 7 of Ref. [83] the outer crust EOS of Miyatsu is coincide with the one of BPS and has a tiny difference with the one of BBP in the region of near the core-crust transition region. Consequently, the difference in radius between the mass–radius results calculated using the same core EOS but different crust EOSs, i.e., Miyatsu EOS and BSP+BBP EOS, appears at low mass. In general, for each NS mass, Miyatsu EOS yields a smaller radius than that of BSP+BBP with a difference of around 1 $\%$ (see Fig. 8 of Ref. [83] and the corresponding discussions). For crust thickness, the trend is similar, Miyatsu EOS yields smaller crust thickness than that of BSP+BBP with the difference around 10 $\%$ (see Fig. 10 of Ref. [83] and the corresponding discussions). Therefore, we could estimate roughly that for a particular model of core EOS, the differences in radius and crust thickness between the EOS predicted by the unified core-crust model and the one used in this work in average could be less than 1 $\%$ and 10 $\%$, respectively.

Fig. 3

EOS of NSs with and without hyperons. a Pressure as a function of the ratio of density to saturation density and b energy density as a function of pressure. For comparison, some NS pressures constraints are given. First, from GW170817 [15], second, from recent non-parametric analysis [9] while the third is the constraint from the joint of PSR J0030+0451, GW170817, and the nuclear data analysis [30]. The horizontal line in a and the vertical line in b are a marker $P\approx$ 48 $\mathrm MeV fm^{-3}$ when the hyperons start to appear

The NS EOS is presented by (a) pressure as a function of the ratio of density to nuclear matter saturation density and (b) energy density as a function of pressure for the cases with and without hyperons predicted by BSP, is depicted in Fig. 3. For comparison, we also show NS EOS without hyperon predicted by the BKA22 parameter set. It can be seen that the Hyperons start to appear in $P \approx$ 48 $\mathrm{MeV fm}^{-3}$ i.e. $P>$ P(3 $\rho _{\mathrm{nuc}}$). It can be seen in panel (a) of Fig. 3 that the uncertainty due to the role of hyperons are larger in the region $P>$ 48 $\mathrm MeV fm^{-3}$ or $\rho > 3 \rho _\mathrm{nuc}$ than that due to the difference RMF model used as long as the corresponding RMF parameter sets compatible with nuclear matter experimental data. Note that NS pressure constraint P(2 $\mathrm \rho _{nuc}$) is taken from GW170817 data analysis from Ref. [15]. Recent non-parametric analysis [9] provides constraints for P($\mathrm \rho _{nuc}$), P(2 $\mathrm \rho _{nuc}$), and P(6 $\mathrm \rho _{nuc}$). We also take P(2 $\mathrm \rho _{nuc}$) constraint from the joint of PSR J0030+0451, GW170817, and the nuclear data analysis from Ref. [30]. Rather detailed discussion of the constraints obtained of non-parametric analysis will provide in Sect. 6. It can be seen that the constraints from Refs. [9, 15, 30] at P(2 $\mathrm \rho _{nuc}$) are consistent each other. It can be seen in Fig. 3 that the corresponding EOS is quite compatible to the ones of Refs. [9, 15, 30] and it seems that the P(6 $\rho _{\mathrm{nuc}}$) results of Ref. [9] tends to favor EOS without hyperons or at least with hyperons but only with a small number of hyperons existed in NSs.

3 Anisotropic pressure models

The local pressure anisotropy means that the radial pressure differs from the tangential pressure. Note that the difference between radial and tangential pressure $\sigma$ generates an additional force in a standard isotropic Tolman–Oppenheimer–Volkoff (TOV) equation. This force can be directed outward or inward of the star center, depending on the sign of $\sigma$. The strength and the distribution of this force depend on the $\sigma$ model used [37]. The discussion-based on anisotropic pressure and the physical conditions for anisotropic stars can be consulted in Refs. [37, 38], and further details can be seen in an anisotropic pressure review paper [36]. In this work, we will examine the impacts on NS properties of the three forms of the local anisotropic pressure parameter $\sigma$ model existed in literature. The anisotropic term $\sigma$ of Bowers and Liang [76] denoted here by $\sigma _{BL}$, while the $\sigma$ of Horvat et al. [77] denoted here by $\sigma _{DY}$, and the $\sigma$ of Cosenza et al. [78] denoted here by $\sigma _{HB}$. The explicit forms of the $\sigma$ of these models are [76,77,78,79,80]

$$\begin{aligned} \sigma _{BL}\equiv & {} -\frac{\lambda _{BL} G \epsilon r^2 }{3}(1+ \frac{3 p}{\epsilon }) \frac{(1+ \frac{p}{\epsilon })}{(1-\frac{2 M G}{r })}, \end{aligned}$$

(12)

$$\begin{aligned} \sigma _{DY}\equiv & {} \varUpsilon (\frac{2 M G}{r }) p , \end{aligned}$$

(13)

$$\begin{aligned} \sigma _{HB}\equiv & {} -\frac{r}{2}\frac{(1-h)}{h}(\frac{dp}{dr}), \end{aligned}$$

(14)

respectively. Free parameters $\lambda _{BL}$, $\varUpsilon$, and h are defined as the strength of anisotropic terms of the Bowers and Liang (BL), Horvat (DY), and Cosenza (HB) models, respectively.

Fig. 4

Impact of anisotropic pressure on constituent composition profiles for 1.4 M$_\odot$ NS with hyperons. a For DY anisotropic model, b for the isotropic case, c for BL anisotropic model, and d for HB anisotropic model

We need to note that the BH model was constructed by using the following assumptions: the $\sigma _{BL}$ should vanish quadratically at the center, depend non-linearly on p. Therefore, the $\sigma _{BL}$ is gravitationally induced. Furthermore, it was explicitly constructed to solve the modified TOV equation analytically for an incompressible anisotropic star with $\epsilon$ constant [76]. The $\sigma _{BL}$ becomes discontinuous at the surface if the energy density is also discontinuous. The DY model  [77] is constructed, such that the $\sigma _{DY}$ vanishes in the center.

Furthermore, $\sigma _{DY}$ is continuous at the surface even if the tangential pressure vanishes at low energy densities. The heuristic procedure obtains the HB model  [78]. The heuristic procedure has the purpose of obtaining solutions for anisotropic matter from known solutions for isotropic matter. More detailed discussions about the heuristic procedure to obtain the HB model can be seen in Ref. [78]. Different from the cases of BL and DY models, $\sigma _{HB}$ of HB is not zero in the non-relativistic limit of the hydrostatic equilibrium equation. We also need to note that the slow rotating NS within anisotropic pressure using BL and DY models of pressure anisotropy also discuss in Ref. [45]. Note that it is reported  [46] that the gravitational wave (GW) and electromagnetic observations of GW can constrain the extent of pressure anisotropy in neutron star without hyperons within BL model. The study suggested that certain EOSs that are ruled out by GW 170817 data, under isotropic pressure assumption, becomes viable, and the inference radius by GW 170817 data can rule out certain EOSs even for high anisotropic pressure.

In Figs. 4 and 5, we show the profiles of the constituent composition in NS with M=1.4 $M_\odot$ and M=2.0 $M_\odot$ for a certain free parameter value of each anisotropic pressure model. Here we can see the impact of pressure anisotropy on the composition of particles in NSs. The free parameter value of each model is chosen in order, and the corresponding can reproduce a similar value of maximum mass. It is obvious for M=1.4 $M_\odot$ that all anisotropic models the hyperons have not yet appeared in that NS. The latter fact is quite contrasting to what happens in the isotropic model. For all models, the fractions of protons, neutrons, electrons, and muons d not show significant differences. While in the case of M=2.0 $M_\odot$, $\Lambda$, $\varSigma ^-$, and $\varXi ^-$ have already appeared in the core of NS with anisotropic pressure. The hyperons are existed up around R=8 km. The fractions of all constituents in M=2.0 $M_\odot$ case also does not significantly affect by the difference in the anisotropic model used.

Fig. 5

Impact of anisotropic pressure on constituent composition profiles for 2 $M_\odot$ NS with hyperons. a For HB anisotropic model, b for DY anisotropic model, and c for BL anisotropic model

Fig. 6

Impact of anisotropic pressure for all models used on a radius and b mass profiles of NS with hyperons as a function of NS central pressure. The Vertical line in $P_c$=48 MeV fm$^{-3}$ is a marker when the hyperons start to appear

Figure 6 shows the NS mass and radius as a function center pressure of NS for all anisotropic pressure models used. In general, the role of anisotropic pressure is for increasing or decreasing NS mass and radius. However, the increasing radius depends significantly on the anisotropic model, while the trend of increasing mass is almost independent of the anisotropic model used. We can see that the DY model can yield a more easily relatively short NS radius compared to ones of other anisotropic models. In all models that anisotropic NSs with the mass around M $\lesssim$ (1.6–1.7) $M_\odot$, hyperons do not yet play a role. It means that in the region $P\lesssim$ 48 $\mathrm MeV fm^{-3}$, the trend of the mass and radius profiles is purely determined by the role of anisotropic pressure. However, for the ones in the region $P\gtrsim$ 48 $\mathrm MeV fm^{-3}$, it is also influenced by hyperons’ role. In consequence that the trend of radius profiles in both regions are different and the role of NS EOS for region with $M \lesssim$ (1.6–1.7) $M_\odot$ is relative more certain than that of M $\gtrsim$ (1.6–1.7) $M_\odot$.

4 Slow rotating neutron stars

In this section, the main properties for slow rotating NS with anisotropic matter pressure are briefly discussed.

The equilibrium solution for a rotating star is obtained by solving Einstein equation $G_{\mu \nu }= 8 \pi G T_{\mu \nu }$. The explicit form of the components of $G_{\mu \nu }$ is derived from the line element as follow

$$\begin{aligned} ds^2= & {} -e^{2 \nu } dt^2 +e^{2 \lambda } dr+ r^2 (d \theta ^2 + sin^2 \theta ~d\phi ^2) \nonumber \\&- 2 \omega (r)~r^2~sin^2 ~\theta ~dt ~d\phi . \end{aligned}$$

(15)

$\omega (r)\equiv (d\phi /dt)_{ZAMO}$, is the Lenze–Thirring angular velocity of a zero momentum angular momentum (ZAMO). It means $\omega (r)$ accounts for the frame-dragging effect. Note that if $\Omega$ is the angular velocity of a uniform rotating NS, and if $\Omega _k$ is Kepler angular velocity, the slow rotating approximation means $\Omega /\Omega _k <<$ 1. Therefore, the line element in Eq. (15) is only correct up to first order $\Omega$, and the NS retains its spherical geometry since the centrifugal deformation is considered in order $\Omega ^2$ [118]. The matter stress–energy tensor with anisotropic pressure can be written as [76, 79, 80]:

$$\begin{aligned} T_{\mu \nu }=\epsilon u_{\mu } u_{\nu }+p k_{\mu } k_{\nu } + q [g_{\mu \nu }+u_{\mu } u_{\nu }- k_{\mu } k_{\nu }], \end{aligned}$$

(16)

where $g_{\mu \nu }$ is the space–time metric used, $u_{\mu }$ is the fluid 4-velocity, $\epsilon$ is the total energy density, $k_{\mu }$ is the unit radial vector orthogonal to $u^{\mu }$. Therefore, $u^{\mu }k_{\mu }$ is equal to zero. At the center of symmetry, the anisotropic pressure must vanish since here, $k_{\mu }$ is no longer defined. Note that $g_{\mu \nu }+u_{\mu } u_{\nu }- k_{\mu } k_{\nu }$ is the projection tensor onto the 2-surface orthogonal to $k_{\mu }$ and $u_{\mu }$. The anisotropic pressure parameter is defined as $\sigma$ $\equiv$ $p-q$. If we set $\sigma$=0, all expressions below correspond to one of the isotropic stars. Following the standard procedure, we can obtain three first-order ordinary differential equations from the diagonal componets of Einstein field equation as:

$$\begin{aligned} \frac{dM}{dr}= & {} 4 \pi \epsilon r^2,\nonumber \\ \frac{dp}{dr}= & {} -G \frac{\epsilon M}{r^2}\left( 1+\frac{p}{\epsilon }\right) \frac{(1+\frac{4 \pi r^3 p}{M})}{(1-\frac{2GM}{r})} - \frac{2\sigma }{r}, \end{aligned}$$

(17)

and

$$\begin{aligned} \frac{d\nu }{dr} = G \frac{M +4 \pi r^3 p}{r(r-2 G M)}. \end{aligned}$$

(18)

Given pressure of the NS center $p_c$ and the corresponding energy density $\epsilon _c$, as well as center mass $M_c \approx 0$ and radius $r_c\approx 0$. Both equations in Eq. (17) are integrated numerically outwards using Runge–Kutta method from the center $r_c$ until the integration reaches the surface of NS defined by p(R)=0. The mass of NS is simply m(R)=M. Different from the ones of Eq. (17) where the mass and pressure values at $r_c$ are given, for the differential equation in Eq. (18), the given boundary condition is $\nu$ value at R i.e., $e^{\nu (R)}=\frac{1}{2}(1-\frac{2 G M}{R}$). Therefore, to solve this differential equation we simply guess some particular value of $\nu$ at $r_c$ and repeat the integration several times until the $\nu$ value at R fulfills the required boundary value of $\nu$ at R. And we also have one second order ordinary differential equation for $\bar{\omega }$ from $t \phi$ component of Einstein field equation for the matric in Eq. 15 as

$$\begin{aligned} \frac{1}{r^4}\frac{d}{dr}(r^4 J \bar{\omega })+\frac{4}{r^4}\frac{d J}{dr}(1+\frac{\sigma }{\epsilon +p})\bar{\omega }=0, \end{aligned}$$

(19)

where

$$\begin{aligned} J\equiv e^{-\nu } {\left( 1-\frac{2 G M}{r}\right) }^{1/2}, \end{aligned}$$

(20)

with

$$\begin{aligned} \bar{\omega }(r) \equiv \Omega -\omega (r). \end{aligned}$$

(21)

Note that by using Eq. (19) and the fact that around R, $J\approx 1$ and $\frac{d\bar{\omega }}{dr} \approx \frac{ 6 G I \Omega }{R^4}$, where I is inertia moment than we can write the inertia moment in an integral representation as

$$\begin{aligned} I= \frac{8 \pi }{3} \int _{r_c}^{R} \frac{ r^5 J \tilde{\omega }}{r-2 G M}(\epsilon +p) \left[ 1+\frac{\sigma }{\epsilon +p}\right] dr, \end{aligned}$$

(22)

where $\tilde{\omega }=\bar{\omega }/\Omega$. Instead, solve integral equation Eq. (22), we also can obtain the inertia moment directly from Eq. (19) by transforming this second-order differential into two first-order differential equations such as

$$\begin{aligned} \frac{d \tilde{\omega }}{dr}= & {} \frac{6}{r^4} e^{\nu } {\left( 1-\frac{2 G M}{r}\right) }^{-1/2} \tilde{\kappa }\nonumber \\ \frac{d \tilde{\kappa }}{dr}= & {} \frac{8 \pi G}{3} \frac{r^4 e^{-\nu }(\epsilon +p)}{{\left( 1-\frac{2 G M}{r}\right) }^{1/2}} \left( 1 +\frac{\sigma }{\epsilon +p}\right) \tilde{\omega }, \end{aligned}$$

(23)

with boundary conditions:

$$\begin{aligned} \tilde{\omega }(R)= & {} 1-\frac{2 G R}{R^3},\nonumber \\ \tilde{\kappa } (R)= & {} G I. \end{aligned}$$

(24)

To solve equations in Eq. (23), we start by defining trial boundary conditions in the center $\tilde{\omega }^T(r_c)$ and $\tilde{\kappa }^T (r_c)$ and integrate both equations outwards using Runge–Kutta method from the center of NS until R, respectively. Then we obtain $\tilde{\omega }^T(r)$ and $\tilde{\kappa }^T (r)$. Because the Eq. (19) is scale invariant then we can define that $\tilde{\omega }(r)=\zeta \tilde{\omega }^T(r)$ and $\tilde{\kappa } (r)= \zeta \tilde{\kappa }^T (r)$, respectively. Therefore, form Eq. (24), we can obtain $\zeta =1/(\tilde{\omega }^T(R)+2\frac{\tilde{\kappa }^T (R)}{R^3})$ and the inertia moment is simply $I=\frac{\tilde{\kappa }(r)}{G}$. The differential equation form is more efficient in calculation than that of integration. Therefore, we use it in this work. Note that for NS with the masses greater than 1$M_\odot$ the moment of inertia can be approximated very well [18, 19] as

$$\begin{aligned}&I \approx (0.237\pm 0.008)M R^2\nonumber \\&\quad \times \left[ 1 + 4.2 \frac{M~\mathrm{km}}{M_\odot ~R}+90 {(\frac{M ~\mathrm{km}}{M_\odot ~R})}^4 \right] . \end{aligned}$$

(25)

We have checked that our moment inertia numerical calculation results are entirely consistent with that of the approximation in Eq. (25).

5 Tidal deformability

In this section, the tidal deformability for NS with an- isotropic matter pressure is briefly discussed.

The presence of external gravitation tidal field $\left( \epsilon _{ij}\right)$ causes NS deformed. The deformability of NS can be observed from gravitation quadrupole moment $\left( Q_{ij}\right)$. The relation between the external gravitational tidal field with the quadrupole is [119]

$$\begin{aligned} Q_{ij} = -\lambda \epsilon _{ij}, \end{aligned}$$

(26)

where the “inertia of deformation” $\lambda$ is known as tidal deformability parameter. $\lambda$ can be expressed as

$$\begin{aligned} \lambda = \frac{2}{3}k_{2}R^{5}, \end{aligned}$$

(27)

where $k_{2}$ is electric-tidal Love number. A valuable property which can be extracted from GW170817 data is dimensionless tidal deformability $\Lambda$ which is defined as  [120]

$$\begin{aligned} \Lambda = \frac{2k_{2}}{3C^{5}}, \end{aligned}$$

(28)

where $C=\frac{2GM}{R}$ is a compactness of NS.

To calculate $k_{2}$, we start from the perturbed line element. The corresponding line element to induce the tidal deformability[121]. The perturbed metric can be expressed as

$$\begin{aligned} ds^{2}= & {} -e^{2\nu } \left[ 1 + H\left( r\right) Y_{20} \left( \theta , \phi \right) \right] dt^{2} \nonumber \\&+ e^{2\lambda } \left[ 1 - H\left( r\right) Y_{20} \left( \theta , \phi \right) \right] dr^{2} \nonumber \\&+ r^{2} \left[ 1 + K\left( r\right) Y_{20}\left( \theta , \phi \right) \right] d\theta ^{2} \nonumber \\&+ r^{2} \sin ^{2}\theta \left[ 1 + K\left( r\right) Y_{20}\left( \theta , \phi \right) \right] d\phi ^{2}, \end{aligned}$$

(29)

where $Y_{20}\left( \theta , \phi \right)$ is spherical harmonics function with $l = 2$ and $m = 0$. From perturbed stress–energy–momentum tensor, we obtain the following relations: $\delta T^{t}_{t} = -\delta \epsilon = -\frac{d\epsilon }{dp}\delta p$, $\delta T^{r}_{r} = \delta p$, and $\delta T^{\theta }_{\theta } = \delta T^{\phi }_{\phi } = \delta q = \left( 1 - \frac{d\sigma }{dp}\right) \delta p$. From Eq. (29), we obtain perturbed Einstein equation $\left( \delta G^{\mu }_{\nu } = 8 \pi \delta T^{\mu }_{\nu }\right)$. From $\delta G^{r}_{\theta } = 0$, we obtain equations

$$\begin{aligned} K' \left( r\right)= & {} - H' \left( r\right) - H \left( r\right) \nu ' \left( r\right) , \end{aligned}$$

(30)

$$\begin{aligned} K'' \left( r\right)= & {} - H'' \left( r\right) - H' \left( r\right) \nu ' \left( r\right) - H \left( r\right) \nu '' \left( r\right) . \end{aligned}$$

(31)

By inserting Eq.  (30) and Eq.  (31) into $\delta G^{t}_{t} - \delta G^{r}_{r} = 8 \pi \left( \delta T^{t}_{t} - \delta T^{r}_{r}\right)$, we obtain

$$\begin{aligned} H''\left( r\right) + AH'\left( r\right) + BH \left( r\right) = 0, \end{aligned}$$

(32)

where

$$\begin{aligned} A= & {} \frac{2}{r} + e^{2\lambda } \left( \frac{2M}{r^{2}} + 4\pi r \left( p - \epsilon \right) \right) , \end{aligned}$$

(33)

$$\begin{aligned} B= & {} e^{2\lambda } \left( - \frac{6}{r^{2}} + \frac{4\pi \left( p + \epsilon \right) \left( 1 + \frac{d\epsilon }{dp}\right) }{1 - \frac{d\sigma }{dp}} + 4 \pi \left( 4 \epsilon + 8p\right) \right) \nonumber \\&+ 16 \pi \sigma e^{2 \lambda } - \left( \nu '\right) ^{2}. \end{aligned}$$

(34)

Note that we obtain almost exactly the same result as the one of Ref. [46] except the term $16 \pi \sigma e^{2 \lambda }$ in Eq. (34) is not present in their result. However, we agree well with the one obtained in Ref.  [122]. If we set $y \equiv \frac{r H' \left( r\right) }{H \left( r\right) }$, then we obtain a first order differential equation that is

$$\begin{aligned} ry' + y^{2} + yF + r^{2}Q = 0, \end{aligned}$$

(35)

where

$$\begin{aligned} F= & {} \frac{r - 4 \pi r^{3} \left( \epsilon - p\right) }{r - 2M}, \end{aligned}$$

(36)

$$\begin{aligned} Q= & {} \frac{4 \pi r \left[ 4\epsilon + 8P + \frac{\left( \epsilon + P\right) \left[ 1 + \frac{d \epsilon }{dP}\right] }{1 - \frac{d \sigma }{dP}} + 4 \sigma \right] }{r - 2m} \nonumber \\&- 4 \left[ \frac{m + 4 \pi r^{3} P}{r^{2} \left( 1 - \frac{2m}{r}\right) }\right] ^{2}. \end{aligned}$$

(37)

After solving Eq. (35) and TOV equations simultaneously with Runge Kutta method where the initial value of y is y(0) = 2. We can calculate $k_{2}$ using the following equation

$$\begin{aligned} k_{2} = \frac{8}{5} \left( 1 - 2C\right) ^{2} C^{5} \left[ 2C\left( y - 1\right) - y + 2\right] /X \end{aligned}$$

(38)

with

$$\begin{aligned} X= & {} 2C\left[ 4\left( y + 1\right) C^{4} + \left( 6y - 4\right) C^{3}\right] \nonumber \\&+ 2C\left[ \left( 26 - 22 y\right) C^{2} + 3\left( 5y - 8\right) C - 3y + 6\right] \nonumber \\&- 3\left( 1 - 2C\right) ^{2}\left( 2C\left( y - 1\right) - y + 2\right) \log \left( \frac{1}{1 - 2C}\right) , \end{aligned}$$

(39)

Here y = y(R). Finally, we can obtain $\Lambda$ from $k_{2}$ as an important property that can be compared to the one predicted by GW 170817 and GW190425 data.

6 Numerical details

To this end, we have discussed in this work that the EOS as the input to obtain the properties of NSs is restricted by two uncertainties at high densities, i.e., the due RMF parameter set used and due to the uncertainty of hyperon coupling constants. The impact of the first one on NS’s global properties is not too significant as long as we use the parameter set with acceptable nuclear matter predictions. However, the second one could provide an impact on NS properties prediction. The following fact leads to the uncertainty of the value of the free parameter of the anisotropic model obtained, consistent with the selected constraints. Therefore, we might not take too seriously the exact value of the obtained free parameter. However, the estimation value of the free parameter of the anisotropic model obtained is in order. It means we still can check which anisotropic pressure model that more compatible with observations of NSs.

In mass–radius constraints, we take the recent accurate measured of NS mass of J0740+6620 to constraint the maximum mass and also the mass of J1614−2230 with lower mass and lower error-bar for comparison [1,2,3,4] where the corresponding masses of both pulsars are M = $2.14^{0.10}_{0.09}~M_\odot$ and M = $1.928^{0.0017}_{0.0017}~M_\odot$, respectively. Note that another accurate measure mass of massive NS is J0348+0432 is reported in Ref. [5], whose the mass is M = $2.01^{0.04}_{0.04}~M_\odot$. The corresponding mass value is in between the masses of J1614−2230 and J0740+6620. Compared to the NSs mass, the measurements of the radius of NSs are less precise. The recent review about the status of observation or measurement masses and radii of NSs and the corresponding constraints with a variety basis, including from observation from GW170817, can be seen, e.g., in Refs.  [6, 8], and please see also the references therein for further discussion related to the methods used to extract the radius constraints. To constrain the canonical mass–radius, we use the constraints from the recent non-parametric study from Landry et al. [9]. Note that the authors of Ref. [9] used non-parametric EOS representation method proposed in Refs. [123, 124] to obtain their constraints based on three classes of astronomical observations, i.e.,

• 1. The masses of pulsars J1614−2230, J0740+6620, and J0348+0432,

• 2. Data from GW 170817 and GW190425,

• 3. Data mass and radius of J0030+0451 from NICER.

For comparison, we also use the radius of canonical NS constraint from joint analysis of PSR J0030+0451, GW170817, and the nuclear data from Ref. [30]. It can be seen that both canonical mass constraints are consistent with each other, but the one of Ref. [30] is more restricted. Note that both canonical mass–radius constraints are also compatible with the ones obtained from systematically study using the GW170817 basis in Refs. [33]. Note there is also interesting finding reported in Ref. [22] about the NS masses and radii results, which are inferred from GW178087 with universal relation. The inferring masses and radii obtained from Ref. [22] are the ones of double neutron stars (DNS), millisecond pulsars (MSP), and low-mass X-ray binaries (LMXB) (please see the numerical values in Table II, III, and IV in Ref. [22]). The later results actually should be useful for constraining mass and radius of NSs, respectively. Unfortunately, the corresponding error-bars are still too large to provide a meaningful conclusion. Therefore, we do not show them in Fig.  7.

Fig. 7

Impact of anisotropic pressure on the mass–radius relation of NSs with hyperons. a For HB anisotropic model, b for DY anisotropic model, and c for BL anisotropic model. We include the constraint from the recent non-parametric study from Ref. [9], and the constraint from joint analysis of PSR J0030+0451, GW170817, and the nuclear data from Ref. [30] as well as the recent observed maximum masses of NSs, J1614−2230, and J0740+6620 from Refs. [1,2,3,4]. As benchmark’s, we also include the result of isotropic (ISO) case

Fig. 8

Impact of anisotropic pressure on inertia moment of NS with hyperons (a, b). For comparison, we also include in b, new non-parametric constraint on inertia moment of canonical NS from Ref. [9], and the one from joint PSR J0030+0451, GW170817, the nuclear data analysis constraints from Ref. [30]. The predicting the moment inertia of pulsar J0737−3039A from Bayesian modeling of nuclear EOS of Ref. [21] also is given. While in a, we include the inferring moment inertia of DNS, MSP, and LMXB obtained from GW178087 with universal relations [22]. For dimensionless inertia moment as a function of compactness case (c), we include the results of Refs. [18, 20] for comparison

Figure 7 has shown that the role of the values of free parameters $\varUpsilon$, h and $\lambda _{BL}$ of DY, HB, and BL models, respectively in increasing maximum mass and radius of NS. It can be seen for isotropic NS with hyperons using SU(6) prescription to determine hyperon coupling constants, and the corresponding maximum mass does not reach 2 $M_\odot$ constraint. It is interesting to see that the used constraints here are very restricted. It can be seen in Fig.  7 that compared to other models, the DY model has more flexibility to fit together by the used maximum mass and canonical mass–radius constraints. Since the form of $\sigma$ in the DY model, making the predicted maximum mass is sensitive, but the predicted radius is not to decrease or increase the free parameter value of the anisotropic model. In consequence, only the DY model that compatible with all constraints used, i.e., for the free parameter value in the range − 2 $\le$ $\varUpsilon$ $\le$ − 1.15. However, if we make the constraint requirements rather loose by only using the constraints of Landry et al. and the mass of J1614−2230, they allow free parameter value for HB model is exist, i.e., with h=0.85, and for BL model is also exist within 1 $\le$ $\lambda _{BL}$ $\le$ 1.82, while for DY model the constraint range is wider. It becomes in the range of − 2.5 $\le$ $\varUpsilon$ $\le$ − 1.15. Note that these obtained ranges of the corresponding free parameter will slightly change if we use other prescriptions to determine the hyperon coupling constants to obtain the EOS at high density, as discussed above.

A measurement of NS moment inertia is crucial because its inherent capability to constrain quite restricted the EOS of NSs at high density is insensitive to EOS, and it has a universal relation with compactness and tidal deformability. Panel (a) and panel (b) of Fig. 8 show the impact of anisotropic pressure on inertia moment of NS with hyperons. Here, we use $\lambda _{BL}$= 1.82, $\varUpsilon$= − 1.15, and h=0.8. The results are confronted with the ones obtained by the new non-parametric constraints on inertia moment from Ref. [9], the one obtained from joint PSR J0030+0451, GW170817, and the nuclear data analysis constraints from Ref. [30], the predicting the moment inertia of pulsar J0737−3039A from Ref. [21], and the one obtained by inferring moment inertia of DNS, MSP, and LMXB obtained from GW178087 with universal relations [22]. Note that the moment of inertia results of some NS obtained by the author of Ref. [22] have more data compared to others, but on average, the corresponding moment inertia values are systematically smaller and the corresponding error-bars are larger than those of Refs. [9, 21, 30]. It is obvious from Panel (a) and Panel (b) of Fig. 8 that moment inertia results from anisotropic NS with hyperons predict relative larger than those of Refs. [9, 21, 22, 30]. It can also be seen that only model NS with hyperons by using the DY anisotropic model with $\varUpsilon ~\approx$ − 1.15 and the case isotropic NS with hyperons which are compatible with those of Refs. [9, 21, 30]. For completeness, we also provide the dimensionless inertia moment as a function of compactness results in Panel (c). We include the results of Refs. [18, 20] for comparison. Note that the constraint from Ref. [20] is relative more accurate than that of Ref. [18]. It can be seen that all anisotropic pressure models compatible with constraint from Ref. [18], but some parts of the one of the BL model is located outside the constraint from Ref. [20]. Note that the most recent analysis of moment of inertia from the speed of sound model using EOS constraints from nuclear physics, NS masses and future moment inertia measurements can be seen in Ref. [29].

For isotropic NS, the structure of the crust, as well as some related dynamical processes, happen affected only by the core-crust interface. E.g., the values transition density is related to the existence of the nuclear pasta, the pulsar glitches related to the crustal fraction of the moment of inertia. At the same time, the dynamical process of the NSs cooling, thermal relaxation of the crust is sensitive to crust radius (see Ref. [28] and the references therein for further detail discussion.). In Fig.  9, we show that the anisotropic factor also affects the crust properties. It can be seen that for the same transition density value, the crust radius and the crust mass of anisotropic NS are relatively larger than that of isotropic NS. How large the impact of anisotropic pressure on the corresponding crustal fraction of the radius and mass depends on the anisotropic model used. Compared to the ones of isotropic, the HB model predicts the larger crustal fraction of the mass and radius. DY model predicts the smaller crustal fraction of mass and radius to those of other anisotropic models. Panel (c) displays the crustal fraction of moment inertia. It can be seen that the anisotropic factor increases the allowed region of the crustal fraction of moment inertia. Like the mass and radius of the crust cases, the HB model predicts the larger crustal fraction of the moment of inertia compared to the one of the isotropic case, while DY model predicts a closer value of crustal fraction to that of isotropic case. If we use unified core-crust EOSs, we would obtain the trends of the relation between anisotropic parameter with crust properties not change much qualitatively from what we have done. However, employing the unified or consistent description of core and crust EOSs is necessary for the study that the quantitave results are essential because the low uncertainties in the predictions are a requirement. For example, the study of the correlation between nuclear parameters and crust properties yields more meaningful results if we use unified core-crust EOSs. The corresponding study has been done recently, and the results are reported in Ref. [21].

Fig. 9

Impact of anisotropic pressure on the crust properties. a The ratio of the crust to core radius as a function of NS mass, b the ratio of crust to core mass as a function of NS mass, and c the ratio of crust to core inertia moment of NS with hyperons as a function of NS mass. For comparison, we include the horizontal lines in c $I_{cr}/I$ constraint deduced from Vela pulsar with canonical mass (see Ref. [28] and the references therein)

Fig. 10

Impact of anisotropic pressure for all anisotropic pressure models on compactness profiles of NS with a 2 $M_{\odot }$, b 1.4 $M_{\odot }$, and c compactness on maximum mass. In b, we include the compactness of one recently measured isolated NS [125], while in c, we include the NS maximum compactness results of Refs. [8, 126] for comparisons.

Fig. 11

Impact of anisotropic pressure for all anisotropic pressure models on dimensionless tidal deformability as a function of NS radius (a) and as a function of mass (b). For comparison, we also include the new non-parametric constraint on dimensionless tidal deformability from Ref. [9], and the one from joint of PSR J0030+0451, GW170817, and the nuclear data analysis constraints from Ref. [30] as well as the inferring tidal deformability of DNS, MSP, and LMXB obtained from GW170817 with universal relations [22]

Fig. 12

Impact of anisotropic pressure for all anisotropic pressure models on dimensionless tidal deformability for M = 1.4 $M_{\odot }$. a $\Lambda _{1.4}$ as a function of radius and b as a function anisotropic pressure parameters. For comparison, we also include the new non-parametric constraint on dimensionless tidal deformability from Ref. [9] and the constraint from joint of PSR J0030+0451, GW170817, and the nuclear data analysis constraints from Ref. [30], Constraints on EOS from experiments and chiral effective theory using Bayesian framework [31], empirical formula from Ref. [32] as well as the results from GW170817 (a) [14, 16], GW170817 (b) [15] and GW190425 [17]

The detection of GWs from the coalescence of binary NSs has been reported [14,15,16,17]. In the inspiralling stage of the, both NS orbits can be extracted a quantity known as tidal deformation on GW signals that informing about the related composition and EOS of the NS. In Figs. 11 and 12 we show the impact of anisotropic pressure for the three anisotropic pressure models used on dimensionless tidal deformability as a function of NS radius and mass as well as the ones for specific mass, i.e., for canonical mass as the function of the corresponding radius and the anisotropic free parameter values. We check the compatibility of tidal deformability of anisotropic NS results with data by comparing the results with those of Refs. [9, 22, 30] as well as the results from GW170817 and GW190425 [15, 17]. We discuss first the impact of anisotropic pressure for all anisotropic pressure models on compactness profiles for NS with a mass equal to 2 $M_{\odot }$ and 1.4 $M_{\odot }$, and the corresponding compactness on maximum mass because the tidal deformability depends on the compactness C of the stars and the compactness of anisotropic NS also depends on the anisotropic pressure model. For comparisons, in Panel (b) of Fig. 10, we include the compactness of one recently measured isolated NS [125] while in Panel (c), we include the NS maximum compactness results of Refs. [8, 126].

Note recent study [54] has shown that within isotropic NSs, the RMF models are consistent with the experimental observed nuclear matter properties [53] also are compatible with the recent data from binary neutron star merger event GW170817. They also confirm the strong correlation between $\Lambda _{1.4}$ and the radius of canonical stars. They have also found that RMF parameter sets belonging to the same families present very similar compactness both for the maximum mass case and the canonical one. It can be seen in Fig. 10 that the impact of the anisotropic NS model on the compactness profiles for NS with a mass equal to 2 $M_{\odot }$ and 1.4 $M_{\odot }$ are not too significantly different and for the later, the maximum value is quite compatible with the observed one of Ref. [125]. The impact of the value of the free parameter of the corresponding anisotropic model has been shown in Panel (c). It can be seen that the different parameter values of each model are still in the range of the maximum compactness constraints from Refs. [8, 126]. It is depicted in Fig. 11 that for a specific value of a free parameter of the anisotropic models, which are consistent with maximum mass constraints, it can be seen that only DY model with $\varUpsilon$ = − 1.15 is compatible with the ones obtained in Refs. [9, 30]. Note that the data from Table II, III, and IV of Ref. [22] yield quite large error-bar both for $\Lambda$ is a function of mass and radius. While the ones of $\Lambda$ as a function of radius yield systematically smaller radius for the same $\Lambda$ compared to other data[9, 30] and $\Lambda$ calculation results in this work.

$\Lambda _{1.4}$ as a function of the corresponding radius for some varied free parameters of each anisotropic model used are shown in panel (a) of Fig. 12. Some free parameter results lie on the outside of the grey box constraint from GW170817 result [15], and the only the results of isotropic and anisotropic with DY model lie inside the green box of Ref. [31]. However, not all of the results inside the grey and green boxes, also compatible with the maximum mass constraints. The results from isotropic and from anisotropic with HB and DY models are closer to those of Refs. [9, 30]. It can also be seen in panel (a) that the results of all models are quite compatible with the empirical formula of Annala et al.  [32]. The latter fact is more explicit seen if we observe from Panel (b) of Fig. 12, $\Lambda _{1.4}$ as a function of a free parameter of each anisotropic models. The light grey box and orange box constraints of Refs. [15, 17] are tightly limit the allow free parameter value, i.e., for the DY model with $\varUpsilon =-$ 1.15, HB model with h = 0.95, and isotropic case. It is evident that only for DY model with $\varUpsilon =-$ 1.15 is also simultaneously in agreement with the maximum mass constraints.

7 Conclusions

In conclusion, we have systematically investigated the mass–radius relation, the moment of inertia, and the tidal deformability predicted by three models of anisotropic pressure of NS with hyperons, namely DY, HB, and BL models [76,77,78,79,80]. The EOS of the core of NS is calculated using the RMF model with the BSP parameter set [60, 81] under which the standard SU(6) prescription and hyperon potential depths [82] are utilized to determine the hyperon coupling constants. For the inner and outer crusts, we use the crust EOS that obtained from Miyatsu et al. [83]. The compatibility of the nuclear matter properties is discussed. They are also compared to other calculations as well as experimental and observations data. We have found that as far as the nuclear matter predicted by the corresponding parameter set compatible with experimental nuclear data, the uncertainty of EOS and the corresponding parameters in the nucleon sector is not too significant. However, the uncertainty of EOS in the hyperon sector due to uncertainty of hyperon coupling constant values wherein the case of the BSP parameter set starts to appear at $\rho \approx 3 \rho _\mathrm{nuc}$, is relatively significant. Hopefully, future progress in hyper-nuclei physics will pin down this uncertainty significantly. We have shown that the effect of anisotropic pressure on NSs is mainly to increase the stiffness of the NS EOS. This effect can compensate for the EOS softening due to hyperons and or other exotic particles by delaying the appearance of hyperons or other exotic particles at relatively higher critical density. It means the role of anisotropic pressure is to increase or decrease the NS mass and radius. However, the trend of increasing radius depends significantly on the anisotropic model, while the trend of increasing mass almost does not depend on the model used.

Furthermore, it is interesting to observe that the DY model can yield a relatively short NS radius easily compared to one of the other anisotropic models. We also have confronted the corresponding NS mass–radius relation, moment of inertia, and tidal deformability results with the corresponding recent extracted results from the combination of some observation data [1,2,3,4, 9, 15,16,17,18, 20,21,22, 30,31,32]. As we expected, we have found that the results obtained by using DY model with $\varUpsilon ~\approx -$ 1.15 are compatible with all constraints used. This result also confirms the previous finding [37].