Eikonal model analysis of elastic proton–proton collisions at 52.8 GeV and 8 TeV

Abstract

Under the influence of standardly used description of Coulomb-hadronic interference proposed by West and Yennie the protons have been interpreted as transparent objects; elastic events have been interpreted as more central than inelastic ones. It will be shown that using eikonal model the protons may be interpreted in agreement with usual ontological conception; elastic processes being more peripheral than inelastic ones. The corresponding results (differing fundamentally from the suggested hitherto models) will be presented by analyzing the most ample elastic data set measured at the ISR energy of 52.8 GeV and the LHC energy of 8 TeV. Detailed analysis of measured differential cross section will be performed and possibility of peripheral behavior on the basis of eikonal model will be presented. The impact of recently established electromagnetic form factors on determination of quantities specifying hadron interaction determined from the fits of experimental elastic data in the broadest region of momentum transfers will be analyzed.

1 Introduction

Elastic differential cross section $\text {d}\sigma /\text {d}t$ represents basic experimental characteristic established in elastic collisions of hadrons. If the influence of spins is not considered, the t (four momentum transfer squared) dependence exhibits a very similar structure in all cases of elastic scattering of charged hadrons at contemporary high energies: there is a peak at very low values of |t|, followed by a (nearly) exponential region and then there is a dip-bump or shoulder structure at even higher values of |t| practically for all colliding hadrons [1]. Figures 1 and 7 show measured $\text {d}\sigma /\text {d}t$ of pp scattering at the ISR energy of 52.8 GeV and at much higher LHC energy of 8 TeV as examples.

The elastic differential cross section is standardly defined using elastic scattering amplitude $F_{}^{\text {}}(s,t)$ as (common units $\hbar = c = 1$ used)

$$\begin{aligned} \frac{\text {d} \sigma }{\text {d}t} = \frac{\pi }{s p^2} \left| {F_{}^{\text {}}(s,t)} \right| ^2 \end{aligned}$$

(1)

where s is the square of the total center-of-mass energy and p is the value of momentum of one incident hadron in the center-of-mass system; $t = - 4p^2 \sin ^2 \frac{\theta }{2}$ where $\theta$ is scattering angle.

Two fundamental interactions, i.e., the Coulomb and hadronic ones being described by phenomenologically constructed amplitudes $F_{}^{\text {C}}(s,t)$ and $F_{}^{\text {N}}(s,t)$, have been commonly used for description of measured elastic differential cross section of charged hadrons. Only some phenomenological models of elastic complete amplitude $F_{}^{\text {C+N}}(s,t)$, describing effect of both the Coulomb and hadron interactions, have been applied to in interpreting experimental data represented by elastic differential cross sections until now.

One of the first attempts to determine the t-dependence of $F_{}^{\text {C+N}}(s,t)$ was done by West and Yennie (WY) in 1968 [2] who used Bethe’s [3] formula for corresponding complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$. However, the formula has been derived under very simplified and limited conditions. The approach of WY has not allowed to study shape of t-dependence of hadronic amplitude on the basis of experimental data as the shape has been, without any justification, strongly limited by the used assumptions.

It has been almost generally assumed (under the influence of the WY approach) that the imaginary part of $F_{}^{\text {N}}(s,t)$ is dominant in a broad region of t around $t=0$ and that it is vanishing around the region of diffractive minimum. It has concerned nearly all contemporary models of elastic (hadronic) scattering including the most recently published papers, see, e.g. [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] (in some papers the t-dependence of the phase of $F_{}^{\text {N}}(s,t)$ has not been discussed at all). These additional assumptions constraining hadronic amplitude $F_{}^{\text {N}}(s,t)$ have never been sufficiently reasoned (up to our knowledge) in the literature. They have led to some unusual physical properties of protons - to some kind of proton transparency in head-on collisions, i.e., to central behavior of elastic collisions.

The centrality of elastic collisions has been recently “rediscovered” by some authors under the term hollowness, see, e.g., [16,17,18, 23]. The result has followed mainly from the requirement of the dominance of the imaginary part of $F_{}^{\text {N}}(s,t)$ in quite broad interval of t around $t=0$ in the given models, see Sect. 5 in [24] and useful comments related to the hollowness in [25]. The fact that t-dependence of the phase of $F_{}^{\text {N}}(s,t)$ matters for determination of characteristics of collisions in impact parameter space has been recently admitted in [26]. The question of peripheral behavior of elastic collisions has been recognized as an interesting question in [27]. It has been summarized in [28] that protons cannot be taken as point-like particles during collisions and that it is necessary to take into account sizes of colliding particles in a description of the physical process. In other words, some even basic questions and problems concerning description of pp scattering have not been satisfactorily understood and solved up to know.

In order to overcome the mentioned deficiencies convenient approach based on the eikonal model has been proposed in [29]. In this case the used complete eikonal elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ describes the influence of both Coulomb and hadronic scattering with the help of only one formula in the whole measured region of momentum transfers in a unique and consistent way. It is based on additivity of individual eikonals of the Coulomb and hadron interactions. The formula for complete amplitude $F_{}^{\text {C+N}}(s,t)$ has been derived with the aim not to impose any strong assumptions concerning t-dependence of elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$.

It has been shown already in 1981 in [30] that the central behavior has followed as direct consequence of the mentioned t-dependence of the dominant imaginary part of $F_{}^{\text {N}}(s,t)$. It has been found in [30] that the high-energy elastic hadronic scattering may be described with the help of eikonal model as a fully peripheral process if the phase of $F_{}^{\text {N}}(s,t)$ has been allowed to change rather quickly with changing t already at small values of |t| (for more details see [29, 31,32,33,34,35]).

We have revisited possibilities of basically all historical as well as more recent approaches (models) trying to describe elastic scattering data and determine some properties of protons (see also [36]). The eikonal model is currently the only one which is widely used at high energies and allows to take into account consistently both the Coulomb-hadronic interference at all measured values of t and dependence of collisions on impact parameter.

This paper is structured as follows. The simplified description of Coulomb and hadron interference proposed by WY, which influenced directly or indirectly many contemporary models of elastic (hadronic) scattering, is summarized in Sect. 2.

In Sect. 3 one may find formula for complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ derived within the eikonal model which allows to take into account the influence of Coulomb interaction described with the help of both the electric and magnetic form factors in elastic scattering of charged hadrons (originally only electric form factors have been used in [29]).

Elastic hadronic amplitude constrained similarly as it has been done in majority of widely used models and leading to central behaviour of elastic collisions was fitted to experimental data of elastic pp scattering at the ISR energy of 52.8 GeV and at much higher LHC energy of 8 TeV. The same data were fitted without the strong limitations and a peripheral solution has been obtained. The results corresponding to the two fundamentally different alternatives are compared and discussed in Sect. 4 in a greater detail than it was done in the past. The impact of choice of form factors on the determined results is discussed also in Sect. 4; it represents another new result. Concluding remarks are given in Sect. 5.

Formalism of impact parameter representation of the elastic hadron scattering amplitude in the eikonal model is summarized briefly in appendix A.

Electromagnetic form factors needed in description of elastic pp collisions are discussed in appendix B. There are several formulas or parameterizations which have been used recently by several (group of) authors for determination of t-dependences of electric and magnetic form factors. However, it seems that there is no comparative study between them showing how much the t-dependences differ (if at all). In appendix B new plots comparing several alternatives available in the literature are, therefore, shown.

2 Simplified description of Coulomb and hadron interference proposed by West and Yennie

According to Bethe [3] the complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ of two charged hadrons (neglecting spins) has been commonly decomposed into the sum of the Coulomb scattering amplitude $F_{}^{\text {C}}(s,t)$ and the hadronic amplitude $F_{}^{\text {N}}(s,t)$ bound mutually with the help of relative phase $\alpha \phi (s,t)$

$$\begin{aligned} F_{}^{\text {C+N}}(s,t) = F_{}^{\text {C}}(s,t){{\,\mathrm{e}\,}}^{\text {i}\alpha \phi (s,t)}+F_{}^{\text {N}}(s,t); \end{aligned}$$

(2)

$\alpha =1/137.036$ being the fine structure constant. The t-dependence of the relative phase factor $\alpha \phi (s,t)$ has been determined on various levels of sophistication. The dependence having been commonly accepted in the past was proposed by West and Yennie (WY) [2] within the framework of Feynman diagram technique (one-photon exchange) in the case of charged point-like particles and for $s \gg m^2$ (m standing for nucleon mass) as

$$\begin{aligned}&\alpha \phi (s,t) = {\mp } \alpha \left[ \ln \left( \frac{-t}{s}\right) \nonumber \right. \\&\left. \quad + \int _{-4p^2}^0 \frac{\text {d}t'}{\left| {t-t'} \right| } \left( 1-\frac{F^\text {N}(s,t')}{F^\text {N}(s,t)}\right) \right] . \end{aligned}$$

(3)

The upper (lower) sign corresponds to the scattering of particles with the same (opposite) electric charges.

Formula (3) containing the integration over all admissible values of four-momentum transfer squared $t'$ seemed to be complicated when it was proposed. It has been simplified for practical use to perform the analytical integration. The t-dependencies of modulus and phase of the hadronic amplitude $F_{}^{\text {N}}(s,t)$ defined as

$$\begin{aligned} F_{}^{\text {N}}(s,t) = \text {i}\left| {F_{}^{\text {N}}(s,t)} \right| {{\,\mathrm{e}\,}}^{-\text {i}\zeta ^\text {N}_{}(s,t)} \end{aligned}$$

(4)

have been strongly limited. It has been assumed:

• (i) the modulus $\left| {F_{}^{\text {N}}(s,t)} \right|$ has had purely exponential t-dependence at all kinematically allowed t values;

• (ii) the phase $\zeta ^\text {N}_{}(s,t)$ has been t-independent for all kinematically allowed t values (see [2, 37] and [34, 35]).

As analyzed in [38] some other high energy approximations and simplifications were added, too (see also [36]).

For the relative phase between the Coulomb and elastic hadronic amplitude the following simplified expression has been then obtained:

$$\begin{aligned} \alpha \phi (s,t) = {\mp } \alpha \left[ \ln {\left( \frac{-B(s)t}{2}\right) }+\gamma \right] \end{aligned}$$

(5)

where $\gamma =0.577215$ is Euler constant and B(s) is the value of diffractive slope B(s, t) at $t=0$ generally defined as

$$\begin{aligned} B(s,t) = \frac{\text {d}}{\text {d} t} \left[ \ln \frac{\text {d}\sigma ^{\text {N}}{}}{\text {d}t} (s,t)\right] = \frac{2}{\left| {F_{}^{\text {N}}(s,t)} \right| } \frac{\text {d}}{\text {d}t}\left| {F_{}^{\text {N}}(s,t)} \right| \; . \nonumber \\ \end{aligned}$$

(6)

The t-independence of B(t) is equivalent to the requirement of purely exponential t-dependence of $\left| {F_{}^{\text {N}}(s,t)} \right|$.

One may further define quantity $\rho (s,t)$ as ratio of the real to imaginary parts of elastic hadronic amplitude

$$\begin{aligned} \rho (s,t) = \frac{{\text {Re}}\,F_{}^{\text {N}}(s,t)}{{\text {Im}}\,F_{}^{\text {N}}(s,t)}. \end{aligned}$$

(7)

It follows from Eqs. (4) and (7) that

$$\begin{aligned} \tan {\zeta ^\text {N}_{}(s,t)} = \rho (s,t) \; . \end{aligned}$$

(8)

The following simplified formula for complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ has been then derived in [2]

$$\begin{aligned} \begin{aligned} F_{\text {WY}}^{\text {C+N}}(s,t) =&\pm \frac{\alpha s}{t}G_1(t)G_2(t) {{\,\mathrm{e}\,}}^{\text {i}\alpha \phi (s,t)} \\&+ \frac{\sigma ^{\text {tot,N}}(s)}{4\pi }p \sqrt{s}(\rho (s)+\text {i}){{\,\mathrm{e}\,}}^{B(s)t/2} \, . \end{aligned} \end{aligned}$$

(9)

Here the first term corresponds to the Coulomb scattering amplitude (relative phase included) while the second term represents the elastic hadronic amplitude in which the quantity $\sigma ^{\text {tot,N}}(s)$ is the total cross section given by optical theorem

$$\begin{aligned} \sigma ^{\text {tot,N}}(s) = \frac{4 \pi }{p\sqrt{s}} {\text {Im}}\,F^{\text {N}}(s,t=0) \end{aligned}$$

(10)

and the quantity $\rho (s)$ is value of the assumed t-independent quantity $\rho (s,t)$.

The two quantities $G_1(t)$ and $G_2(t)$ in Eq. (9) stand for the electric form factors taken commonly in standard dipole form (see, e.g., [39]) as

$$\begin{aligned} G_{\text {E}}^{\text {D}}(t) = \left( 1 - \frac{t}{\varLambda ^2}\right) ^{-2} \end{aligned}$$

(11)

where $\varLambda ^2 = 0.71\; \text {GeV}^2$. The electric form factors as Fourier-Bessel (FB) transform of electric charge distribution of colliding hadrons have been put into formula (9) by hand.

The Coulomb differential cross section (including form factors) has been, therefore, taken as

$$\begin{aligned} \frac{\text {d}\sigma ^{\text {C}}(s,t)}{\text {d}t} = \frac{\pi s}{p^2} \frac{\alpha ^2}{t^2} G_1^2(t)G_2^2(t) \, , \end{aligned}$$

(12)

i.e., diverging at $t\!=\!0$. Integrated elastic hadronic cross section may be calculated as

$$\begin{aligned} \sigma ^{\text {el,N}}(s) = \int _t \frac{\text {d}\sigma ^{\text {el,N}}}{\text {d}t} = \int _t \frac{\pi }{sp^2}\left| {F_{}^{\text {N}}(s,t)} \right| ^2 \,. \end{aligned}$$

(13)

The optical theorem then allows to determine integrated inelastic cross section

$$\begin{aligned} \sigma ^{\text {inel}}(s) = \sigma ^{\text {tot,N}}(s) - \sigma ^{\text {el,N}}(s) \, . \end{aligned}$$

(14)

As to Eqs. (5) and (9) they were derived also by Locher [40] one year earlier than Eq. (3) proposed by WY [2]. Locher assumed from the very beginning the validity of both the mentioned assumptions (i) and (ii) limiting the general t-dependence of the elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$. He, therefore, avoided the misleading idea that WY integral formula (3) may be correctly used for determination of the relative phase for any t-dependent elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$. The high-energy approximations used in the given approach might be regarded as acceptable at that time when nothing was known about actual structure of elastic differential cross section data. However, the questions have arisen when experimental data have shown not to be in agreement with the mentioned assumptions (for details see [35, 41]).

Simplified formula of WY given by eqs. (5) and (9) has been used in the majority of analyses of all hitherto elastic scattering data of charged hadrons in the forward region, i.e., for $|t|\lesssim 0.05$ $\hbox {GeV}^2$ (see, e.g., [37, 39, 42,43,44,45,46,47,48,49,50,51,52,53]); contrary to the fact that both the mentioned theoretical assumptions (i) and (ii) justifying the validity of both Eqs. (9) and (5) have not been fulfilled in the analyzed experimental data. At higher values of |t| the influence of Coulomb scattering has been then fully neglected and the elastic scattering of charged hadrons has been described only with the help of the elastic hadronic amplitude being constructed on a phenomenological basis with completely different t-dependence. Such type of fundamentally inconsistent description of elastic scattering by two different approaches in diverse regions of t has been pointed out and further analyzed in, e.g., [35, 54,55,56].

The relative WY phase specified by Eq. (3) should be a real quantity. According to a mathematical theorem derived in [58] this is fulfilled if the phase of elastic hadronic amplitude is a t-independent quantity for all kinematically allowed values of t. Thus it has turned out that the specification of the complete Bethe elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ with the help of WY phase according to Eq. (2) contains fundamental limitation from the very beginning.

The values of $\sigma ^{\text {tot,N}}$ and $\rho$ determined with the help of the WY approach at different energies have often been used also in connection with dispersion relations (see, e.g., [57]). These approaches have been, therefore, based on all problems and limitations involved in the WY approach; neither one of these models has provided precise and consistent description of elastic differential cross section at all energies.

3 Eikonal model description of Coulomb and hadron interference

3.1 Eikonal complete amplitude with effective electromagnetic form factors

Instead of the limited approach of WY (see Sects. 1 and 2) it is necessary to give the preference to a more suitable eikonal approach concerning description of Coulomb-hadronic interference, based on impact parameter representation which has been proved to be mathematically consistent and valid at any s and t [59]. In the eikonal model the complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ has been introduced as the function of common eikonal being equal to the sum of individual (Coulomb and hadronic) eikonals [60, 61]. This approach has been used by Cahn [62] who has rederived the West and Yennie simplified formula (9) using several approximations similar to the ones used by WY.

However, the eikonal model approach can be used in a more general way as it has been shown in [29]. The complete elastic scattering amplitude in this approach may be written as

$$\begin{aligned} F_{}^{\text {C+N}}(s,t) = \pm \frac{\alpha s}{t} G^2_{\text {eff}}(t) + F_{}^{\text {N}}(s,t)[1 {\mp } \text {i} \alpha \bar{G}(s,t)], \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{aligned} \bar{G}(s,t)&= \int \limits _{t_{\text {min}}}^0 \text {d}t' \left\{ \ln \left( \frac{t'}{t} \right) \frac{\text {d}}{\text {d}t'} \left[ { G^2_{\text {eff}}(t') }\right] \right. \\&\quad - \left. \frac{1}{2\pi } \left[ \frac{F^{\text {N}}(s,t')}{F_{}^{\text {N}}(s,t)} - 1 \right] I(t,t')\right\} , \end{aligned} \end{aligned}$$

(16)

and

$$\begin{aligned} I(t,t')=\int \limits _0^{2\pi }\text {d}{\varPhi ''} \frac{G^2_{\text {eff}}(t'')}{t''}; \end{aligned}$$

(17)

here $G^2_{\text {eff}}$ is effective form factor squared given by (51) reflecting the electromagnetic structure of colliding charged hadrons and $t'' = t+t'+2\sqrt{tt'}\cos {\varPhi ''}$. The lowest value of t is limited by kinematical limit

$$\begin{aligned} t_{\text {min}}= -s+4m^2 \end{aligned}$$

(18)

where m is rest mass of hadron in the case of elastic hadron-hadron scattering. The upper (lower) sign in Eq. (15) corresponds to the scattering of particles with the same (opposite) electric charges.

Comparing the t-dependence of the complete eikonal scattering amplitude given by Eq. (15) with the standardly used complete WY scattering amplitude (9) one may see the substantial difference between these two approaches. Instead of calculating the relative phase between the Coulomb and elastic hadron components the shape of the whole complete elastic amplitude has been derived in the eikonal model approach. More detailed analysis [54, 63] shows that the function $\bar{G}(s,t)$ represents the convolution between the Coulomb and hadronic amplitudes and it is in general a complex function.

At difference to the previous approaches one complete amplitude $F_{}^{\text {C+N}}(s,t)$ describes the influence of both the Coulomb and elastic hadron collisions at any finite s in the whole interval of $t\in \langle t_{\text {min}},0 \rangle$ up to the terms linear in $\alpha$. Formulas (15), (16) and (17) may be used in two ways: either for establishing the elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ from the analysis of measured corresponding differential cross section data provided the hadronic amplitude is conveniently parametrized as it has been done in [29]. Or for a consistent inclusion of the influence of Coulomb scattering if the elastic hadronic amplitude is phenomenologically established as it has been done in [64] in the case of predictions of pp elastic differential cross sections at the LHC.

The use of electromagnetic form factors reflects the influence of both the electric and magnetic charge structures of colliding nucleons. Only the electric form factors given by Eq. (49) have been used originally in [29] to calculate $F_{}^{\text {C+N}}(s,t)$ according to Eq. (15) for analysis of experimental data. It has enabled to include in the elastic scattering the influence of electric space structure of colliding protons. Such an approach can be generalized by taking into account also the influence of the proton magnetic form factor, i.e., the interaction of magnetic moment of the proton with Coulomb field of the other colliding proton.

The influence of the magnetic form factors in the case of elastic pp scattering at high energies have been theoretically studied by Block [53, 65]. However, this approach has been based on the application of standard WY complete elastic amplitude containing originally only the dipole electric proton form factors given by Eq. (11) which have been replaced by effective electromagnetic form factor (51) containing also dipole magnetic form factor (48). Such an approach, however, contains many limitations and deficiencies as it has been discussed in Sects. 1 and 2.

Unlike the approach of WY the electromagnetic form factors form the part of Coulomb amplitude from the very beginning in the eikonal model. Due to the integration over all kinematically allowed region of $t'$ in Eq. (16) the $t'$-dependence of effective electromagnetic form factors should describe the charge distributions in the largest possible interval of momentum transfers $t'$. For some suitable t-dependent parameterizations of electromagnetic proton form factor the integral $I(t,t')$ may be analytically calculated (see appendix C) which helps in numerical calculations in application of the eikonal model to experimental data. The elaborated approach then enables to study either the influence of individual effective electric or magnetic form factor or the common influence of both of them.

In [66] one may find a recent review of calculations concerning Coulomb-nuclear interference at high energies within the eikonal model framework. It confirmed that the Bethe’s formula Eq. (2) and the simplified description of Coulomb-hadronic interference proposed by West and Yennie (see Sect. 2) can be hardly used for reliable analysis of contemporary experimental data. The approach in [66], however, did not sufficiently distinguish between kinematically allowed and forbidden values of t variable in the calculations, see Sect. 7 in [24] for further details.

The eikonal model approach allows to study behavior of hadron collisions in impact parameter space, see the main formulae in appendix A (see also [67]). Dependence of elastic hadron collisions on the value of impact parameter will be analyzed with the help of experimental data and under different assumptions in the next section.

4 Analysis of elastic pp scattering data

4.1 Fitting procedure

Main unknown function in the eikonal interference formula given by Eqs. (15) and (16) is elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$. It may be, therefore, parametrized and one may try to determine it from experimental data under different assumptions (constrains). Conveniently parameterized elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ has been fitted to the measured pp elastic differential cross section at given energy in broad interval of t values including both peak at very low values of |t| and dip-bump structure at higher values of |t| with the help of Eq. (1) and complete amplitude $F_{}^{\text {C+N}}(s,t)$ given by Eqs. (15) and (16).

The recent analyses of both electric and magnetic proton form factors has showed some deviations from standardly used dipole formulas (see appendix B). One may see in Fig. 15 that the effective electromagnetic form factor has quite different values than the widely used electric one for analysis of pp experimental data represented by measured elastic differential cross section. Details and valuable comments concerning measurement of elastic pp scattering data at high energies may be found, e.g., in TOTEM papers [68,69,70] (see also review of TOTEM results in chapter 2 in [36]). It is clear that the inclusion of magnetic form factor might have an impact also on the results of analysis of elastic pp scattering data at high energies.

This was one of the reasons why we have performed new analysis of pp elastic scattering data (at the ISR energy of 52.8 GeV and the LHC energy of 8 TeV) with the help of the eikonal model (see Sect. 3) similarly as it has been done in [29] but now with the help of effective electric form factor (52) and effective electromagnetic form factor (51). Form factors $G_{\text {E}}^{\text {BN}}(t)$ and $G_{\text {M}}^{\text {BN}}(t)$ (i.e., Borkowski’s et al. parameterizations (49) and (50) specified by parameters taken from table 2) have been used for this purpose. However, impact of the choice of form factor on determination of $F_{}^{\text {N}}(s,t)$ and corresponding hadronic quantities has been found to be very small or negligible (see [36] for numerical details). In the following results corresponding to only effective electromagnetic form factors will be, therefore, shown.

The integral $I(t,t')$ in Eq. (16) has been analytically calculated using Eqs. (54) to (64) and parameters from table 2, and compared to corresponding numerical integration (17). The result of numerical integration of the complete amplitude performed for the measured t values should be finite. The formulas (both analytical and numerical) for the integral $I(t,t')$ contain singularity at $t=t'$. However, this singularity is canceled by the factor $\left[ \frac{F^{\text {N}}(s,t')}{F_{}^{\text {N}}(s,t)} - 1 \right]$ in Eq. (16). The integration in Eq. (16) needs to be treated with care at $t'$ equal to t and 0 (for both numerically and analytically calculated function $I(t,t')$).¹ The integrals in the regions $(t_{\text {min}}, t -\epsilon )$ and $(t+\epsilon , -\epsilon )$ where $\epsilon$ is small and positive, should be convergent. Also the integrand leading to the different improper integrals should be convergent in all the regions. Using the theorems valid for the values of improper integrals (see, e.g., [71]) their values can be easily calculated in the limiting case when $\epsilon \rightarrow 0$.

All the fits of experimental data under different assumptions have been performed by minimizing the corresponding $\chi ^2$ function with the help of program MINUIT [72]. Quoted uncertainties of free parameters have been estimated with the help of HESSE procedure in MINUIT. Uncertainty $\sigma _{f}$ of a function f depending on free parameters $x_i$ has been calculated with the help of

$$\begin{aligned} \sigma _{f} = \sqrt{\sum _i \left( \frac{\partial f(x)}{\partial x_i}\right) ^2 (\sigma _{x_i})^2} \end{aligned}$$

(19)

where $\sigma _{x_i}$ stands for uncertainty of the i-th parameter.

For each performed fit of data the following consistency tests were performed. Values of integrated cross section $\sigma ^{\text {tot,N}}$ determined with the help of Eq. (10) and $\sigma ^{\text {el,N}}$ determined with the help of Eq. (13) were compared to values obtained on the basis of integrating corresponding b-dependent profile functions $D^{\text {X}}(b)$ with the help of Eq. (39). Similarly, mean impact parameters $\sqrt{\langle b^{2} \rangle ^{\text {X}}}$ calculated on the basis of Eqs. (41) to (43) have been compared to values obtained with the help of Eq. (40). In all cases good numerical agreement was obtained.

4.2 Parameterization of hadronic amplitude

The analysis of experimental data with the help of Eqs. (15) and (16) requires a convenient parameterization of the complex elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$, e.g., its modulus and its phase. The modulus may be parameterized very generally as

$$\begin{aligned} \begin{aligned} \left| {F_{}^{\text {N}}(s,t)} \right| \; = \;\;\;&(a_1 + a_2t){{\,\mathrm{e}\,}}^{b_1t+b_2t^2+b_3t^3} \\ +&(c_1 + c_2t){{\,\mathrm{e}\,}}^{d_1t} \;. \end{aligned} \end{aligned}$$

(20)

The integration limit $t_{\text {min}}$ in Eq. (16) is lesser than the lower limit of measured data. The t-dependence of the modulus parametrization given by Eq. (20) can be used for extrapolation to the higher values of |t| if the modulus is strongly decreasing with increasing value of |t| in this region. The care needs to be devoted to the allowed fitted values of free parameters specifying the modulus in order to guarantee its vanishing when |t| tends to infinity as required by validity of corresponding dispersion relations.

In [73] (and even earlier in [74, 75]) the following parameterization of hadronic phase has been used

$$\begin{aligned} \zeta ^\text {N}_{}(s,t)= \arctan {\frac{\rho _0}{1-\frac{t}{t_{\text {dip}}}}} \end{aligned}$$

(21)

where $t_{\text {dip}}$ is the position of the dip in data and $\rho _0 = \rho (t\!=\!0)$. This parameterization a priori restricts allowed t-dependences and reproduces the widely assumed dominance of the imaginary part of $F_{}^{\text {N}}(s,t)$ and vanishing of the imaginary part at $t=t_{\text {dip}}$, see Sect. 1. The parameterization of the phase has been used later in several other analyses of experimental data, including [29] where it has been shown that it leads to central behavior of elastic collisions in impact parameter space. However, this parameterization of the phase is not analytic in t; not only due to the pole at $t\!=\!t_{\text {dip}}$ but also due to the fact that the complex function $\arctan (z)$ is not analytic at the points $z=\pm i$ (i being complex unit) [76]. Moreover, the parameterization of the phase (21) cannot fulfill conclusion of Martin’s asymptotic theorem [77] (derived in 1997) requiring, under certain assumptions, the real part of elastic hadronic amplitude to change sign at some low value of |t|.

In [29] different and more general parameterization of hadronic phase has been used for analysis of experimental data ($t_0=-1$ $\hbox {GeV}^2$)

$$\begin{aligned} \zeta ^\text {N}_{}(s,t)= \zeta _0 + \zeta _1 \left( \frac{t}{t_0}\right) ^\kappa {{\,\mathrm{e}\,}}^{\nu t} \end{aligned}$$

(22)

enabling to include a fast increase of $\zeta ^\text {N}_{}(s,t)$ with increasing |t| and, consequently, a peripheral behavior of elastic hadronic scattering.

Natural question arises under which conditions both the parameterizations of the modulus given by Eq. (20) and of the phase Eq. (22) represent analytic function of complex variable t as standardly required (see [78, 79] and review [80]). The parameterized modulus in Eq. (20) forms the real analytic function and its analytic properties are preserved also in the case of complex variable t. However, the same statement is not valid for the phase introduced by Eq. (22) due to the power $t^\kappa$ in it. For complex variable t this power is analytic at the point $t\!=\!0$ only if parameter $\kappa$ is positive integer [76]. Thus the analyticity of the elastic hadron phase for complex t is guaranteed only for positive integer values of parameter $\kappa$. As the complex goniometric functions $\sin (x)$ and $\cos (x)$ are analytic for complex variable x, both the real and imaginary parts of elastic hadron amplitude are analytic, too. It means that the positive integer value of parameter $\kappa$ guarantees that the parameterization of elastic hadronic amplitude given by Eqs. (20) and (22) is analytic for complex t. In [29] this parameter was fitted.

The parameterization (22) is much more general and flexible than (21) as it may reproduce very broad class of t-dependent phases which may all fit measured data and lead to either central or peripheral behavior depending on the values of the free parameters - according to additional assumptions constraining $F_{}^{\text {N}}(s,t)$ as it will be explicitly shown in Sects. 4.3.2 and 4.3.3 (at 52.8 GeV) and Sect. 4.4 (at 8 TeV).

When $F_{}^{\text {N}}(s,t)$ is not constrained only by the measured differential cross section but also by some other constrains one needs to solve in general the problem of bounded extrema of the $\chi ^2$ function, i.e., of the function of the n free parameters $x=(x_1, ..., x_n)$ which may be solved with the help of penalty functions technique. If at the minimum of the $\chi ^2$ the values of the free parameters x are limited at point $x_0$ by some condition $g(x\!=\!x_0)$ then one may add to the minimized $\chi ^2$ function additional function $[g(x) - g(x\!=\!x_0)]^2 * C_p$, where $C_p$ is some conveniently chosen constant value (weight of the penalty function). In the case of several limiting conditions the resulting penalty function is given by the sum of all individual penalty functions which is added to the original $\chi ^2$ during minimization. Performing the minimization procedure one can significantly influence the way how the position of the minimum can be achieved. When performing several successive minimizations one has to decrease successively the values of all the penalty constants $C_p$ in such a way that the position of the minimum is being preserved. Using this approach the added value of total penalty function $\varDelta {\chi }^2$ may become finally very small compared to the value of the original $\chi ^2$.

Fig. 1

Eikonal model of Coulomb-hadronic interaction fitted to measured elastic pp differential cross section at energy of 52.8 GeV in the interval $|t| \in \langle 0.00126, 7.75 \rangle$ $\hbox {GeV}^2$ corresponding to Fit 1, i.e., central picture of elastic pp scattering. Fit 2 leading to peripheral picture of elastic scattering gives similar graphs

4.3 Energy of 52.8 GeV

4.3.1 Data

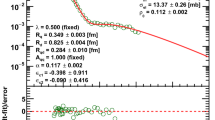
At the energy of 52.8 GeV experimental data in broad region of $|t| \in \langle 0.00126, 7.75 \rangle$ $\hbox {GeV}^2$ taken from [81] have been used, see the data points in Fig. 1.

4.3.2 Elastic hadronic amplitude as constrained in many contemporary models and leading to central behavior of elastic collisions

Table 1 Comparison of several hadronic quantities characterizing pp elastic scattering at energy of 52.8 GeV and 8 TeV. Values of free parameters specifying elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ have been obtained by fitting experimental data under different assumptions using the eikonal model approach

The first Fit 1 of data at 52.8 GeV has been performed with the help of parameterization of $F_{}^{\text {N}}(s,t)$ given by Eqs. (20) and (22). The parameter $\kappa =3$ has been taken to fit data at 52.8 GeV to keep analyticity of elastic hadronic amplitude at all kinematically allowed values of t, see Sect. 4.2. To obtain t-dependence of hadronic amplitude roughly corresponding to many contemporary hadronic models of elastic scattering we have required (as it is often assumed without sufficient reasoning, see Sect. 5 in [24] and fig. 14 in [70]):

• 1. dominance of the imaginary part of $F_{}^{\text {N}}(s,t)$ at broad interval of t values in the forward region

• 2. vanishing of the imaginary part of $F_{}^{\text {N}}(s,t)$ at (or around) $t=t_{\text {dip}}$

• 3. change of sign of the real part of $F_{}^{\text {N}}(s,t)$ at $|t|<|t_{\text {dip}}|$ (motivated by the asymptotic theorem of Martin [77])

These constrains of hadronic amplitude may be fulfilled if the phase $\zeta ^\text {N}_{}(s,t)$ given by (22) passes through, e.g., the two following points

$$\begin{aligned} {[}t_1&=t_{\text {dip}}, y_1=-\pi /2] \end{aligned}$$

(23)

$$\begin{aligned} {[}t_2&=-3 \text { GeV}^2, y_2=-\pi ] \; . \end{aligned}$$

(24)

In this case values of $\nu$ and $\zeta _1$ in Eq. (22) may be calculated as follows

$$\begin{aligned} \nu =&\ln \left[ \frac{y_2 - \zeta _0}{y_1 - \zeta _0} \left( \frac{t_1}{t_2}\right) ^\kappa \right] \frac{1}{t_2-t_1} \end{aligned}$$

(25)

$$\begin{aligned} \zeta _1 =&\frac{y_1-\zeta _0}{\left( \frac{t_1}{t_0}\right) ^\kappa {{\,\mathrm{e}\,}}^{\nu t_1}} \, . \end{aligned}$$

(26)

It means that the hadronic phase given by Eq. (22) is strongly constrained under the given conditions and it has only one free parameter $\zeta _0$ which may be fitted to experimental data together with other free parameters specifying the modulus of $F_{}^{\text {N}}(s,t)$.

Fit 1 has been quite straight forward (due to the fact that t-dependence of the “standard” phase is strongly constrained). Fitted values of all the free parameters specifying the elastic hadronic amplitude at 52.8 GeV are in Table 1. Figure 1 shows fitted elastic pp differential cross section $\frac{\text {d}\sigma ^{\text {C+N}}{}}{\text {d}t}$ together with corresponding Coulomb $\frac{\text {d}\sigma ^{\text {C}}{}}{\text {d}t}$ and hadronic $\frac{\text {d}\sigma ^{\text {N}}{}}{\text {d}t}$ differential cross sections. The phase $\zeta ^\text {N}_{}(s,t)$ corresponding to the amplitude is pictured in Fig. 2 (dotted line). The diffractive slope B(t) calculated with the help of Eq. (6) is shown in Fig. 3 (dotted line).

The corresponding elastic hadronic amplitudes for both the fits have dominant imaginary parts in the large region of t around forward direction which decrease with increasing |t| and vanish in the diffraction dip (as commonly assumed), see Fit 1 in Fig. 4b. The corresponding real parts of $F_{}^{\text {N}}(s,t)$ change sign at $|t| \approx 0.35$ $\hbox {GeV}^2$ as motivated by the asymptotic theorem of Martin, see Fit 1 in Fig. 4a.

Determined values of several physically interesting quantities calculated from the fitted hadronic amplitude corresponding to Fit 1 may be found in Table 1. The total hadronic cross section $\sigma ^{\text {tot,N}}$ has been calculated using the optical theorem (10), integrated elastic hadron cross section $\sigma ^{\text {el,N}}$ using Eq. (13) and inelastic $\sigma ^{\text {inel}}$ as their difference (14).

Root-mean-squares of impact parameter values $\sqrt{\langle b^{2} \rangle ^{\text {tot}}}$, $\sqrt{\langle b^{2} \rangle ^{\text {el}}}$, $\sqrt{\langle b^{2} \rangle ^{\text {inel}}}$ determined with the help of Eqs. (42) to (43) (see Sect. A.2) may be found also in Table 1. It holds $\sqrt{\langle b^{2} \rangle ^{\text {el}}} < \sqrt{\langle b^{2} \rangle ^{\text {inel}}}$, i.e., elastic collisions according to this description should correspond in average to lower impact parameters than average impact parameter corresponding to inelastic collisions ($\sim 0.68$ fm against $\sim 1.09$ fm). Fit 1 will be, therefore, labeled as “central”. This centrality of elastic collisions may be further seen from the profile functions $D^{\text {X}}(b)$ (X=tot, el, inel) calculated at finite collision energy $\sqrt{s}$ as explained in Sect. A.2, see Fig. 5a corresponding to Fit 1. The elastic profile function $D^{\text {el}}(b)$ has Gaussian shape with a maximum at $b=0$. Some other b-dependent functions corresponding to Fit 1 and characterizing hadron collisions in b-space, see Sect. A.2, are shown in Fig. 6a.

Fig. 2

Elastic hadronic phases $\zeta ^\text {N}_{}(s,t)$ for central and peripheral pictures of elastic pp scattering (Fits 1 and 2) at energy of 52.8 GeV

Fig. 3

t-dependence of elastic hadronic diffractive slopes B(t) calculated with the help of Eq. (6) and corresponding to Fits 1 and 2 at energy of 52.8 GeV

Fig. 4

The real and imaginary parts of elastic hadron scattering amplitude corresponding to Fits 1 and 2 at 52.8 GeV

4.3.3 Possibility of peripheral behavior of elastic scattering

The second Fit 2 of the same differential cross section data have been performed similarly as in Sect. 4.3.2, with the help of the same parameterization of $F_{}^{\text {N}}(s,t)$ given by Eqs. (20) and (22) but without the additional, unjustified and widely used constrains on hadronic amplitude expressed by conditions (25) and (26) (and leading to central behavior of elastic collisions).

To obtain peripheral behavior of elastic collisions, to demonstrate this possibility, it has been required for the corresponding root-mean-square impact parameter values to hold $\sqrt{\langle b^{2} \rangle ^{\text {el}}} > \sqrt{\langle b^{2} \rangle ^{\text {inel}}}$ and $D^{\text {el}}(b)$ to have its maximum at some non-zero impact parameter b. However, the fit has not been unique. We have, therefore, further required value of $\sqrt{\langle b^{2} \rangle ^{\text {el}}}$ to be around 1.95 fm. If all these additional conditions bounding the values of fitted free parameters have been added then unambiguous fit has been obtained. In this case it has been necessary to solve non-trivial problem of bounded extrema as explained at the end of Sect. 4.2. Table 1 contains the results of Fit 2. It holds $\sqrt{\langle b^{2} \rangle ^{\text {el}}} > \sqrt{\langle b^{2} \rangle ^{\text {inel}}}$ as required. The table contains also the final values of penalty functions $\varDelta {\chi }^2$ which are small compared to the $\chi ^2$ values.

Differential cross sections $\frac{\text {d}\sigma ^{\text {N}}{}}{\text {d}t}$ , $\frac{\text {d}\sigma ^{\text {C}}{}}{\text {d}t}$ and $\frac{\text {d}\sigma ^{\text {C+N}}{}}{\text {d}t}$ corresponding to the peripheral Fit 2 are very similar to those shown in Fig. 1. The diffractive slope B(t) for the Fit 2 calculated with the help of Eq. (6) is shown in Fig. 3; its t-dependence is very similar to diffractive slope corresponding to Fit 1 (i.e., central pictures of elastic pp scattering). However, t-dependence of the phase $\zeta ^\text {N}_{}(s,t)$ obtained in the Fit 2 is very different from the dependence corresponding to Fit 1 already at small values of |t|, see Fig. 2.

It may be interesting to note that the peripheral Fit 2 fulfill conclusion of Martin’s asymptotic theorem [77], even if it has not been explicitly required. Figure 4 contains the t-dependences of fitted real and imaginary parts of elastic hadronic amplitudes corresponding to Fits 1 and 2. In the peripheral case the corresponding real part changes its sign at $|t| \approx 0.2$ $\hbox {GeV}^2$ and the imaginary parts at $|t| \approx 0.1$ $\hbox {GeV}^2$.

Fig. 5

Proton-proton profile functions $D^{\text {}}(b)$ at energy of 52.8 GeV determined on the basis of Eqs. (38), (35) and (44). Full line corresponds to total profile function, dashed line to elastic one and dotted line to inelastic one

Fig. 6

Function c(s, b) and several other functions characterizing pp collisions in dependence on impact parameter at the energy of 52.8 GeV corresponding to the central and peripheral fits

For the total mean impact parameter $\sqrt{\langle b^{2} \rangle ^{\text {tot}}}$ value of $\sim 1.02$ fm has been obtained. As to the numerically greater value $\sim 1.96$ fm of $\sqrt{\langle b^{2} \rangle ^{\text {el}}}$ in the peripheral case it is given by the second term in Eq. (41) representing the influence of the phase; inelastic $\sqrt{\langle b^{2} \rangle ^{\text {inel}}}$ being correspondingly lower.

The profile functions $D^{\text {X}}(b)$ for the peripheral Fit 2 is shown in Fig. 5b. Additional b-dependent functions corresponding to the Fit 2 and further characterizing hadron collisions in dependence on impact parameter are shown in Fig. 6b. It may look like that functions ${\text {Im}}\,h_1(b)=0$ and $g_1(b)=0$ at the same b-values around 2.5 fm, 4 fm and at even higher values, see Fig. 6b. This would lead to violation of the unitarity given by Eq. (34) (if function K(s, b) is neglected). The two functions are equal to zero in these regions but not at the same value of b; the unitarity is conserved at all values of b. Given that the function $g_1(b)$ at any value of b in any of the performed fits is calculated on the basis of Eq. (34) there is no reason to violate the unitarity.

It may be seen from Table 1 and Figs. 5 and 6 that even if data may be fitted in the central and peripheral cases equally well in terms of ${\chi }^2/$ndf value the corresponding behavior of proton collisions in impact parameter space is completely different. In the discussed peripheral case one may obtain elastic profile function $D^{\text {el}}(b)$ having its maximum at some $b>0$. The non-zero function c(s, b) discussed in details in Sect. A.2 and shown in Fig. 6 enables to define non-oscillating and non-negative profile functions. In the central case the function c(s, b) plays much less significant role.

4.3.4 Comparison to the simplified model of WY

The results obtained in Sects. 4.3.2 and 4.3.3 may be now compared to the results obtained earlier on the basis of the simplified WY formula (9) also at the energy of 52.8 GeV. The values of quantities $\sigma ^{\text {tot,N}}$, $\rho (t\!=\!0)$ and $B(t\!=\!0)$ in Table 1 may be compared to similar values

$$\begin{aligned} \begin{aligned} \sigma ^{\text {tot,N}} =&\; (42.38 \pm 0.27) \; \text {mb}, \\ \rho (t\!=\!0) =&\; (0.078 \pm 0.010), \\ B(t\!=\!0) =&\; (13.1 \pm 0.2) \; \text {GeV}^{-2}; \end{aligned} \end{aligned}$$

(27)

determined in [82] (see also [83]). However, the simplified WY complete amplitude (9) has been applied to only in the very narrow region $|t| \in \langle 0.00126, 0.01)\;\; \text {GeV}^{-2}$, while the Fits 1 and 2 have been performed in much broader measured region of $|t| \in \langle 0.00126, 7.75 \rangle$ $\hbox {GeV}^2$ including also the dip-bump structure. While in Eq. (9) it has been assumed that $\zeta ^\text {N}_{}(s,t)$ and B(t) are t-independent these quantities are t-dependent in the Fits 1 and 2, see the graps in Figs. 2 and 3.

Figure 3 clearly shows that diffractive slope is not constant in the analyzed region of t; therefore one of the assumptions used in derivation of simplified WY complete amplitude (9) is not fulfilled, see Sect. 2. It may be interesting to note that in the case of elastic hadronic amplitude in the model of WY with t-independent hadronic phase the real part of $F_{}^{\text {N}}(s,t)$ does not change sign at any value of t; the conclusion of the asymptotic theorem of Martin is not fulfilled.

The simplified WY approach can be hardly used for the correct analysis of experimental $\frac{\text {d} \sigma }{\text {d}t}$ data and studying t-dependence of elastic hadronic amplitude and corresponding b-dependent characteristics of hadrons on the basis of experimental data.

4.4 Energy of 8 TeV

4.4.1 Data

Elastic pp differential cross section has been recently measured at the LHC by TOTEM at 8 TeV in the region $0.000741 \le |t| \le 0.2010$ $\hbox {GeV}^2$ [70] which contains Coulomb-hadronic interference region. Nearly exponential elastic pp differential cross section at the same energy has been measured by TOTEM [69] in the region $0.027< |t| < 0.2$ $\hbox {GeV}^2$. These two data sets may be combined and continuously extended by renormalized 7 TeV TOTEM data corresponding to the region $0.2< |t| < 2.5$ $\hbox {GeV}^2$ [68] which contains dip-bump structure. This compilation of data will be denoted as “8 TeV data” in the following (only statistical errors will be taken into account), see Fig. 7. The extension by the renormalized 7 TeV data is only an approximation (may be improved when measured data at 8 TeV in this region are available). This is also one of the reason why we have been more interested in overall character of an elastic collision model fitted to data rather than in discussion of “precise” numerical values of some quantities. Measured elastic pp differential cross section at 52.8 GeV and 8 TeV may be found in Figs. 1 and 7. There is clearly visible energy difference and one may ask what we can learn from it.

4.4.2 The eikonal model

Fig. 7

Eikonal model of Coulomb-hadronic interaction fitted to measured elastic pp differential cross section at energy of 8 TeV in the interval $|t| \in \langle 0.000741, 2.5 )$ $\hbox {GeV}^2$ corresponding to Fit 1, i.e., central picture of elastic pp scattering. Fit 2 leading to peripheral picture of elastic scattering gives similar graphs

Fig. 8

Elastic hadronic phases $\zeta ^\text {N}_{}(s,t)$ for central and peripheral pictures of elastic pp scattering (Fits 1 and 2) at energy of 8 TeV

Fig. 9

t-dependence of elastic hadronic diffractive slopes B(t) calculated with the help of Eq. (6) and corresponding to Fits 1 and 2 at energy of 8 TeV

The pp data at 8 TeV have been analysed in very similar way, using the eikonal model, as it has been done in Sect. 4.3 in the case of pp data at 52.8 GeV. Two fits of data under different constrains have been performed.

In Fit 1 at 8 TeV reproducing similar t-dependence of elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ as it is assumed in many contemporary models of elastic hadronic scattering, the phase $\zeta ^\text {N}_{}(s,t)$ has been required to pass through point

$$\begin{aligned}{}[t_2&=-1 \text { GeV}^2, y_2=-\pi ] \end{aligned}$$

(28)

instead of (24). To obtain a stable fit at 8 TeV leading to peripherality of elastic collisions (Fit 2) we have required $\sqrt{\langle b^{2} \rangle ^{\text {el}}}$ to be around 1.85. The parameter $\kappa =2$ has been used at 8 TeV to keep analyticity of elastic hadronic amplitude, see Sect. 4.2. Values of free fitted parameters, together with corresponding values of several hadronic quantities, may be found in Table 1 for both the Fits 1 and 2.

Hadronic phase $\zeta ^\text {N}_{}(s,t)$ and diffractive slope B(t) fitted to experimental data under different conditions are shown in Figs. 8 and 9. It may be seen from Table 1 that quantities $B(t\!=\!0)$ and $\rho (t\!=\!0)$ at 8 TeV are higher than at 52.8 GeV.

The real and imaginary parts of elastic hadronic amplitude determined in each fit may be found in Fig. 10. Both the Fits 1 and 2 at 8 TeV fulfill conclusion of the Martin’s asymptotic theorem [77], similarly as at lower energy of 52.8 GeV.

b-dependent profile functions corresponding to effective electromagnetic form factors at 8 TeV are shown in Fig. 11; other b-dependent functions further characterizing pp collisions in dependence on impact parameter are pictured in Fig. 12. One may see big differences between the central case and the peripheral case shown in Figs. 11 and 12.

The eikonal model analysis of experimental data explained and performed in this paper has been prepared and already used for analysis of pp elastic scattering data by the whole TOTEM collaboration, see the very first results of similar analysis of 8 TeV data in the Coulomb-hadronic interference region measured by TOTEM in [70]. Numerical values of some quantities such as $\sigma ^{\text {tot,N}}$, $\sigma ^{\text {el,N}}$, $\sigma ^{\text {inel}}$, $B(t\!=\!0)$ or $\rho (t\!=\!0)$ determined in this section are slightly different from those published in [70]. There are several subtle differences between both the analyses. First of all we have fitted (approximate) data in broad region of |t| values including the dip-bump structure as our aim was to determine, at least approximately, t-dependences of elastic hadronic amplitude in the widest possible t-range and corresponding b-dependences of profile functions - full physical picture under given set of assumptions. In [70] the data were fitted in much narrower t-region without the dip-bump structure with focus on determination of only some quantities (see [70] for details). Our parameterization of hadronic modulus differs, therefore, from the one used in [70]. As to t-dependence of hadronic phase in peripheral case we have used technique of penalty functions in order to find a few different solutions under given constrains while in [70] the t-dependence was chosen in quite fixed form (an ansatz) and then it was demonstrated that the corresponding elastic hadronic amplitude has given properties (leads to peripheral interpretation of elastic collisions in b-space). In our analysis only statistical errors of data points were taken into account while in [70] also systematical errors were considered.

It is evident that describing in one model the Coulomb-hadronic interference region together with the dip-bump structure in measured data (i.e., non-trivial t-dependence) is more difficult than fitting, e.g., only (quasi)exponential part of data. Fit of data in broader region of t-values typically leads to higher values of reduced $\chi ^2$. One may expect that lower values of reduced $\chi ^2$ then shown in Table 1 may be obtained by using more flexible parameterization of mainly the modulus of hadronic amplitude. The purpose of the fits performed in this paper has been to study mainly conceptual questions related to different interpretation possibilities of (elastic) pp collisions and corresponding assumptions.

4.4.3 Comparison to the simplified model of WY

The values of quantities $\sigma ^{\text {tot,N}}$, $\rho (t\!=\!0)$, and $B(t\!=\!0)$ at 8 TeV in Table 1 determined on the basis of the eikonal model (under different assumptions) may be compared to the values obtained on the basis of the simplified WY formula (9)

$$\begin{aligned} \begin{aligned} \sigma ^{\text {tot,N}} =&\; (102.0 \pm 2.2) \; \text {mb}, \\ \rho (t\!=\!0) =&\; (0.05 \pm 0.02), \\ B(t\!=\!0) =&\; (19.42 \pm 0.05) \; \text {GeV}^{-2}; \end{aligned} \end{aligned}$$

(29)

discussed in [70]. Hadronic phase $\zeta ^\text {N}_{}(s,t)$ and diffractive slope B(t) in the simplified approach of WY are t-independent at all values of t. In the performed fits they are strongly t-dependent, see Figs. 8 and 9. In the simplified model of WY the real and imaginary parts of elastic hadronic amplitude are purely exponential in t while in the eikonal model describing full measured region of t-values they have different t-dependence, see Fig. 10.

Fig. 10

The real and imaginary parts of elastic hadron scattering amplitude corresponding to Fits 1 and 2 at 8 TeV

Fig. 11

Proton-proton profile functions $D^{\text {}}(b)$ at energy of 8 TeV corresponding to Fits 1 and 2 and determined on the basis of Eqs. (38), (35) and (44). Full line corresponds to total profile function, dashed line to elastic one and dotted line to inelastic one

Fig. 12

Function c(s, b) and several other functions characterizing pp collisions in dependence on impact parameter at energy of 8 GeV corresponding to the central (Fit 1) and the peripheral (Fit 2) picture of elastic scattering

5 Conclusion

The measurement of elastic pp differential cross section $\frac{\text {d}\sigma }{\text {d}t}$ represents main source of experimental data for the analysis of elastic processes of protons. The goal of contemporary theoretical description consists in separation of the Coulomb effect from data to determine elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ from which conclusions concerning structure and interactions of colliding hadrons should be derived and further tested. There has not been any actual theory until now which would consistently determine its corresponding t-dependence on the basis of measured elastic differential cross section at all measured values of |t| (including both the Coulomb-hadronic region at very low values of |t| and the dip-bump region at higher values of |t|) - except the eikonal model approach.

In the past the simplified approach of West and Yennie has been made use of for separation of Coulomb and hadron interactions. However, this method is not theoretically consistent and is not in sufficient agreement with the measured data. It contains many limitations as it has been discussed in Sect. 1. It has been applied to the analysis of the data only in a very narrow region of momentum transfers in forward direction and the influence of Coulomb scattering at higher values of momentum transfers has been always neglected by definition. The elastic scattering at higher values of momentum transfer has been always described phenomenologically as purely hadronic scattering on the basis of assumptions not consistent with the ones used in the approach of WY. Such an inconsistent dual description of data in the description of elastic hadron collisions can be hardly justified.

It is assumed in the approach of WY that the relative phase $\alpha \phi (s,t)$ is a real quantity (it is defined as imaginary part of another complex function). It has been proved mathematically in [58] the relative phase $\alpha \phi (s,t)$ given by the integral formula (3) is a real quantity only if the elastic hadronic phase is t-independent at all kinematically allowed t values. Otherwise the relative phase becomes a complex quantity and WY formula looses its physical sense. The WY approach cannot be, therefore, used for analysis of experimental data with arbitrary t-dependence of hadronic phase.

The eikonal model approach, based on the complete elastic scattering amplitude $F_{}^{\text {C+N}}(s,t)$ fulfilling Eqs. (15) to (17), provides more reliable basis for analysis of elastic collisions of (charged) hadrons. In principle it is established on the fact that the common influence of the Coulomb and hadronic elastic scattering can be reliably described by the sum of the Coulomb and elastic hadronic potentials (eikonals) and without any a priori limitation on t-dependence of the elastic hadronic amplitude. However, analyses of experimental data have shown that the complex hadronic component $F_{}^{\text {N}}(s,t)$ cannot be uniquely established. Only its modulus is strongly determined on the basis of measured elastic differential cross section. The t-dependence of its phase has been only partially constrained when Coulomb-hadronic interference (the region of very small |t|) has been taken into account.

In the majority of published analyses of experimental data the corresponding freedom has been, however, strongly limited by the choice of amplitude parameterization. The imaginary part has been usually assumed to be dominant in a great interval of t and vanishing in the region around diffractive minimum; with the real part determining the non-zero value of differential cross section in the diffractive minimum; see, e.g., the earlier papers [73, 75, 84,85,86,87,88,89,90,91,92] and also recent papers [5,6,7,8,9,10, 12,13,14,15,16,17,18,19, 22, 93, 94]. Description of elastic hadronic amplitude corresponding to these widely used assumptions has been fitted to experimental data at energy of 52.8 GeV and 8 TeV in Sects. 4.3.2 and 4.4. The so-called central behavior in impact parameter space has been then obtained in such a constrained case; elastic processes being more central (i.e., existing for very small b even at $b=0$) than inelastic ones. Transparent protons during elastic processes may be, however, hardly brought to agreement with the existence of inelastic processes in which many particles may be formed.

Much more general parameterization of the hadronic amplitude $F_{}^{\text {N}}(s,t)$ has been used in Sects. 4.3.3 and 4.4. A rather steep rise of phase $\zeta ^\text {N}_{}(s,t)$ with increasing |t| already at very small values of |t| has been allowed. It has been possible to obtain strongly peripheral impact parameter profile for elastic processes; the imaginary part (dominant at $t=0$) going quickly to zero with rising |t| (${\text {Im}}\,F_{}^{\text {N}}(s,t) = 0$ at $t \simeq -0.1$ $\hbox {GeV}^2$, at 52.8 GeV and 8 TeV).

Similar analysis of experimental data with the help of the eikonal model (see Eqs. (15) to (17)) has been done already earlier in [29]. In [29] only electric form factors have been taken into account. It has been shown in the present paper that addition of magnetic form factors does not lead to significant change of determined amplitude $F_{}^{\text {N}}(s,t)$. For the purpose of this analysis integral $I(t,t')$ defined by Eq. (17) has been calculated analytically for one suitable parameterization of the form factors, see appendix C. In Sect. 4 we have determined t-dependences of elastic hadronic amplitude under different constrains and showed that all the solutions may be constructed as analytic, while in [29] used parameterizations have not been analytic. All the performed fits at older energy of 52.8 GeV and newer energy of 8 TeV discussed in detail in Sect. 4 are analytic, satisfy condition of unitarity and the real parts of all elastic hadronic amplitudes change sign at low value of |t| as motivated by the asymptotic theorem of Martin [77].

Analysis of data presented in this paper with the help of the eikonal model has been prepared and already used for analysis of pp elastic scattering at the LHC energies, see the very first results of similar analysis of 8 TeV data in the Coulomb-hadronic interference region measured by TOTEM in [70]. Similar analysis of experimental data under different assumptions may be performed at any other (high) energy and the results further studied. It is possible to say (against earlier conviction) that there is not any reason against more realistic interpretation of elastic processes when protons are regarded as compact (non-transparent) objects.

The results presented in this paper have helped to identify and better understand several open questions and problems in description of elastic pp collisions. They are discussed in Sect. 7 in [24], see also Sect. 6 in [67].

Appendices

Appendix: Impact parameter representation of elastic scattering amplitude

1.1 Infinite collision energy

Elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ is standardly transformed into impact parameter representation of elastic scattering amplitude $h_{\text {el}}(s,b)$ introduced with the help of Fourier-Bessel (FB) transform:

$$\begin{aligned} h_{\text {el}}(s,b) =\frac{1}{4p\sqrt{s}}\int \limits _{-\infty }^0 F_{}^{\text {N}}(s,t) J_0(b\sqrt{-t})\text {d}t; \end{aligned}$$

(30)

$J_0(x)$ being the Bessel function of the zeroth order. The elastic scattering amplitude $h_{\text {el}}(s,b)$ has been then required to fulfill the unitarity equation

$$\begin{aligned} {\text {Im}}\,h_{\text {el}}(s,b) = |h_{\text {el}}(s,b)|^2+g_{\text {inel}}(s,b) \end{aligned}$$

(31)

with the inelastic impact parameter profile $g_{\text {inel}}(s,b)$ being defined similarly as the FB transform of the inelastic overlap function $G_{\text {inel}}(s,t)$ fulfilling the unitarity relation [95, 96] (see also [97])

$$\begin{aligned} {\text {Im}}\,F_{}^{\text {N}}(s,t)= & {} \frac{p}{4\pi \sqrt{s}} \int \text {d} \varOmega ' F^{\text {N}^*}(s,t') F^{\text {N}}(s,t'')\nonumber \\&+ G_{\text {inel}}(s,t), \end{aligned}$$

(32)

being valid at any s and kinematically allowed value of t. The function $G_{\text {inel}}(s,t)$ represents summation of all possible inelastic states including integration over all remaining kinematical variables specifying corresponding production amplitude; $\text {d}\varOmega ' = \sin \vartheta '\text {d}\vartheta ' \text {d}\varPhi '$, $t = -4p^2 \sin ^2{\frac{\vartheta }{2}}$, $t' = -4p^2 \sin ^2{\frac{\vartheta '}{2}}$, $t'' = -4p^2 \sin ^2{\frac{\vartheta ''}{2}}$ and $\cos \vartheta '' = \cos \vartheta \cos \vartheta ' +\sin \vartheta \sin \vartheta ' \cos \varPhi '$. Variables $\vartheta$, $\vartheta '$ and $\vartheta ''$ are angles connected with the variables t, $t'$ and $t''$ in the center of mass system.

Formulas (30) and (31) have represented the starting basis practically in all phenomenological model analyses at finite energies where the impact parameter representation of elastic hadronic scattering amplitudes has been made use of, in spite of the fact that the formulas have been derived at infinite (asymptotic) energies only (see, e.g., [73, 75, 84,85,86,87,88,89]).

1.2 Finite collision energy

Consistent mathematical formalism of the elastic scattering amplitude in the impact parameter representation at finite energies has been studied by several authors, for more details see appendix A in [24] where mainly work of Islam [97] has been discussed in greater detail. In the following only the main points and formulas, which are needed for data analysis in Sect. 4, are summarized.

Elastic scattering amplitude $h_{\text {el}}(s,b)$ at finite energies may be deffined using the FB transform

$$\begin{aligned} \begin{aligned} h_{\text {el}}(s,b) =\;&h_1(s,b) + h_2(s,b) \\ =\;&\frac{1}{4p\sqrt{s}}\int \limits _{t_{\text {min}}}^0 F_{}^{\text {N}}(s,t) J_0(b\sqrt{-t})\text {d}t \\&+\frac{1}{4p\sqrt{s}}\int \limits _{-\infty }^{t_{\text {min}}}\lambda (s,t)J_0(b\sqrt{-t})\text {d}t \end{aligned} \end{aligned}$$

(33)

where first term $h_1(s,b)$ corresponds to integration over kinematically allowed values of t, see Eq. (18). Similarly, one may introduce inelastic b-dependent amplitude $g_{\text {inel}}(s,b) = g_1(s,b) + g_2(s,b)$ using FB transform of $G_{\text {inel}}(s,t)$ at finite energies.

According to [41, 54,55,56, 63] non-negative (non-oscillating) total and inelastic profile functions at finite energies may be defined if a convenient real function c(s, b) is introduced and unitarity equation is written in the form

$$\begin{aligned} {\text {Im}}\,h_1(s,b) + c(s,b) =&|h_1(s,b)|^2+g_1(s,b)\nonumber \\&+ K(s,b) + c(s,b) \, . \end{aligned}$$

(34)

Function K(s, b) appearing at finite energies in unitarity equation represents only small correction, it may be evaluated at any energy for given $F_{}^{\text {N}}(s,t)$. It is then possible to define at finite energies total, elastic and inelastic profile functions $D^{\text {X}}(s,b)$

$$\begin{aligned} D^{\text {el}}(s,b)&\equiv 4\,|h_1(s,b)|^2, \end{aligned}$$

(35)

$$\begin{aligned} D^{\text {tot}}(s,b)&\equiv 4\,({\text {Im}}\,h_1(s,b) + c(s,b)), \end{aligned}$$

(36)

$$\begin{aligned} D^{\text {inel}}(s,b)&\equiv 4\,(g_1(s,b) + K(s,b)+c(s,b)). \end{aligned}$$

(37)

and rewrite the unitarity condition in b-space in the form

$$\begin{aligned} D^{\text {tot}}(s,b) = D^{\text {el}}(s,b) + D^{\text {inel}}(s,b). \end{aligned}$$

(38)

The shape of $D^{\text {tot}}(s,b)$ and $D^{\text {inel}}(s,b)$ might be then modified by the function c(s, b) to become non-negative; the shape of elastic profile remains the same. The function c(s, b) should, however, fulfill some additional conditions. Values of the total and inelastic cross section given by

$$\begin{aligned} \sigma ^{\text {X}}(s) = 2\pi \int \limits _0^{\infty } b \text {d}b\;D^{\text {X}}(s,b) \end{aligned}$$

(39)

should be preserved. The other physical quantities which should be preserved are the mean squared values of the total and inelastic impact parameters, i.e., function c(s, b) should not change the quantities $\langle b^{2} \rangle ^{\text {tot}}$ and $\langle b^{2} \rangle ^{\text {inel}}$ defined as

$$\begin{aligned} \langle b^{2} \rangle ^{\text {X}} = \frac{\int \nolimits _0^{\infty } b^2 \; 2 \pi bD^{\text {X}}(s,b) \text {d}b}{\int \nolimits _0^{\infty } 2 \pi b D^{\text {X}}(s,b) \text {d}b}. \end{aligned}$$

(40)

According to [63] the mean squares of total, elastic and inelastic impact parameter defined by Eq. (40) may be determined directly from the hadronic amplitude $F_{}^{\text {N}}(s,t)$ in t variable without being necessary to know the corresponding profile function or the function c(s, b). It is possible to write for the mean squared value of elastic impact parameters

$$\begin{aligned} \begin{aligned} \langle b^{2} \rangle ^{\text {el}} =&\langle b^{2} \rangle ^{\text {mod}}+\langle b^{2} \rangle ^{\text {ph}}\\ =&\frac{4 \int \nolimits _{t_{\text {min}}}^0 \text {d} t |t| \left( \frac{\text {d}}{\text {d} t} \left| {F_{}^{\text {N}}(s,t)} \right| \right) ^2}{\int \limits _{t_{\text {min}}}^0 \text {d} t {} \left| {F_{}^{\text {N}}(s,t)} \right| ^2} \\&+ \frac{4 \int \limits _{t_{\text {min}}}^0 \text {d} t {} \left| {F_{}^{\text {N}}(s,t)} \right| ^2{|t|}\left( \frac{\text {d}}{\text {d} t} \zeta ^\text {N}_{}(s,t)\right) ^2}{\int \limits _{t_{\text {min}}}^0 \text {d} t {} \left| {F_{}^{\text {N}}(s,t)} \right| ^2} \end{aligned} \end{aligned}$$

(41)

and for the total mean squared value

$$\begin{aligned}&\langle b^{2} \rangle ^{\text {tot}} \nonumber \\&\quad = \left. 4\left( \frac{\frac{\text {d}}{\text {d}t}\left| {F_{}^{\text {N}}(s,t)} \right| }{\left| {F_{}^{\text {N}}(s,t)} \right| } -\tan {\zeta ^\text {N}_{}(s,t)}{\frac{\text {d}}{\text {d}t} \zeta ^\text {N}_{}(s,t)}\right) \right| _{t=0}. \nonumber \\ \end{aligned}$$

(42)

The inelastic mean squared value is then given by

$$\begin{aligned} \langle b^{2} \rangle ^{\text {inel}} = \frac{\sigma ^{\text {tot,N}}(s) \langle b^{2} \rangle ^{\text {tot}} - \sigma ^{\text {el,N}}(s) \langle b^{2} \rangle ^{\text {el}}}{\sigma ^{\text {inel}}(s)} \end{aligned}$$

(43)

if the cross sections are determined using the optical theorem (10) and Eqs. (13) and (14).

The b-dependent profile functions may be determined in the following way. We may chose Gaussian shape of total profile function $D^{\text {tot}}(b)$ corresponding to the commonly assumed one [55]

$$\begin{aligned} D^{\text {tot}}(b) = \tilde{a}_2 {{\,\mathrm{e}\,}}^{-\tilde{a}_1 b^2} \end{aligned}$$

(44)

where $\tilde{a}_1$ and $\tilde{a}_2$ are some parameters which may be expressed using Eqs. (39) and (40) as (see integral formulas 3.461 in [98])

$$\begin{aligned} \tilde{a}_1&= \frac{1}{\langle b^{2} \rangle ^{\text {tot}}}, \end{aligned}$$

(45)

$$\begin{aligned} \tilde{a}_2&= \frac{\sigma ^{\text {tot,N}}}{\pi \langle b^{2} \rangle ^{\text {tot}}}. \end{aligned}$$

(46)

The total profile function $D^{\text {tot}}$ given by Eq. (44) may be, therefore, determined from values of $\sigma ^{\text {tot,N}}$ and $\langle b^{2} \rangle ^{\text {tot}}$ using optical theorem (10) and Eq. (42), i.e., from t-dependent elastic amplitude $F_{}^{\text {N}}(s,t)$. It means that using FB transform (33) of $F_{}^{\text {N}}(s,t)$ and Eq. (38) the total, elastic and inelastic profile functions (and also the corresponding c(s, b) function) may be determined for a given $F_{}^{\text {N}}(s,t)$. This approach is used in Sect. 4 where the hadronic amplitude $F_{}^{\text {N}}(s,t)$ is determined on the basis of experimental data using the eikonal model description of Coulomb-hadronic interference discussed in Sect. 3.1.

Electromagnetic proton form factors determined from elastic ep scattering

The proton cannot be taken as point-like object, which represents a modification of the simple Coulomb interaction as its charge is distributed in a larger space. The shape of this distribution and its influence on the corresponding interactions is commonly characterized by elastic electromagnetic form factors. They have been standardly determined from elastic electron-proton scattering on the basis of Rosenbluth formula [99] describing measured differential cross section. The formula contains electric form factor $G_{\text {E}}(t)$ and magnetic form factor $G_{\text {M}}(t)$ which depend only on the square of exchanged momentum transfer and which should satisfy the initial conditions

$$\begin{aligned} G_{\text {E}}(0) \;= \; {{G_\text {M}(0)}/{\mu _p}} \;=\;1; \end{aligned}$$

(47)

here $\mu _p \approx 2.793$ is the proton magnetic moment divided by nuclear magneton.

From early measurements of the elastic ep scattering at lower energies it has been deduced that electric $G_{\text {E}}(t)$ proton form factor can be described by the dipole formula (11) and the magnetic one by

$$\begin{aligned} G_{\text {M}}^{\text {D}}(t) \approx \mu _p G_{\text {E}}^{\text {D}}(t) \; . \end{aligned}$$

(48)

Borkowski et al. [100, 101] analyzed elastic ep scattering data at several energies with the help of the Rosenbluth formula where the t-dependencies of both the electric and magnetic form factors have been parametrized by the formulas

$$\begin{aligned} G_{\text {E}}^{\text {B}}(t)&= \sum _{j=1}^4 \frac{g_k^{\text {E}}}{w_k^{\text {E}} - t}, \;\;\; \end{aligned}$$

(49)

$$\begin{aligned} G_{\text {M}}^{\text {B}}(t)&= \mu _p \; \sum _{j=1}^4 \frac{g_k^{\text {M}}}{w_k^{\text {M}} - t} \end{aligned}$$

(50)

inspired by the vector dominance model. The original values of the parameters $g_k^{\text {E,M}}$ and $w_k^{\text {E,M}}$ (being different for both the electric and magnetic form factors) may be found in [101]; the corresponding electric and magnetic form factors may be denoted as $G_{\text {E}}^{\text {BO}}(t)$ and $G_{\text {M}}^{\text {BO}}(t)$. Different shapes of electromagnetic form factor parametrizations have been proposed by Arrington et al. [102, 103] (denoted as $G_{\text {E}}^{\text {AR}}(t)$ and $G_{\text {M}}^{\text {AR}}(t)$) and Kelly [104] which has been applied by Puckett [105] (denoted as $G_{\text {E}}^{\text {PU}}(t)$ and $G_{\text {M}}^{\text {PU}}(t)$), too.

Extending the measurements of the proton electric and magnetic form factors to higher values of |t| has offered a chance for a better description of the influence of electromagnetic proton structure in the elastic pp collisions at high energies. However, this approach may be considered as fully entitled assuming that the electric and magnetic form factors determined from an analysis of elastic ep scattering are identical with the form factors involved in a description of pp elastic scattering. This assumption should be tested in the future.

Table 2 New values of refitted parameters specifying electromagnetic proton form factors in Borkowski’s parameterization, see Eqs. (49) to (51). The parameters are expressed in units of $\hbox {GeV}^{2}$

Fig. 13

Proton electric form factors $G_{\text {E}}(t)$

The relatively recent determination of t-dependent electric and magnetic form factors has been done by Arrington et al. [103] (see also [102, 106]) in the relatively broad region of $-t \in (0.007, 5.85)$ $\hbox {GeV}^2$. In this region we may express (refit) the form factors using the parameterizations of Borkowski given by Eqs. (49) and (50). The refitted parameters are in Table 2; the corresponding electric and magnetic form factors may be denoted as $G_{\text {E}}^{\text {BN}}(t)$ and $G_{\text {M}}^{\text {BN}}(t)$; they allow to perform some analytical calculations and are used for data analysis in Sect. 4. The mentioned electric and magnetic form factors (in different parameterizations) $G_{\text {E,M}}^{\text {AR}}(t)$, $G_{\text {E,M}}^{\text {PU}}(t)$, $G_{\text {E,M}}^{\text {BO}}(t)$, $G_{\text {E,M}}^{\text {BN}}(t)$ and $G_{\text {E,M}}^{\text {D}}(t)$ are shown for comparison in Figs. 13 and 14.

Fig. 14

Proton magnetic form factors $G_{\text {M}}(t)/\mu _p$ having very similar t-dependences

The effective electromagnetic form factor squared ($\tau = \frac{-t}{4 m^2}$)

$$\begin{aligned} G_{e\!f\!f}^2 (t) = \frac{1}{1 + \tau } \left[ G_{\text {E}}^2(t) + \tau \; G_{\text {M}}^2(t) \right] \end{aligned}$$

(51)

appearing in the Rosenbluth formula has been introduced in [65] for analysis of elastic pp scattering. One may define effective electric form factor squared as

$$\begin{aligned} G_{\text {E},e\!f\!f}^2 (t) = \frac{1}{1 + \tau } G_{\text {E}}^2(t) \end{aligned}$$

(52)

and effective magnetic form factor as

$$\begin{aligned} G_{\text {M},e\!f\!f}^2 (t) = \frac{\tau }{1 + \tau } \; G_{\text {M}}^2(t) \, . \end{aligned}$$

(53)

The graphs of the effective electric form factor $G_{\text {E},e\!f\!f}^2(t)$, the effective magnetic form factor $G_{\text {M},e\!f\!f}^2(t)$ and effective electromagnetic form factor $G_{e\!f\!f}^2(t)$ corresponding to the $G_{\text {E}}^{\text {BN}}(t)$ and $G_{\text {M}}^{\text {BN}}(t)$ (i.e., Borkowski’s parameterization with the newly determined values of free parameters) are shown in Fig. 15. For the comparison also the electric form factor $(G_{\text {E}}^{\text {BO}}(t))^2$ used in [29] is shown.

Fig. 15 shows that the t-dependence of the effective electromagnetic form factor $G_{e\!f\!f}^2 (t)$ in Eq. (51) is different from that one appearing in original Borkowski’s et al. parameterization (49) which has been used in analysis of experimental elastic pp data in [29]. One may ask what the difference in the result is if magnetic form factor is included. In next section it will be, therefore, shown how to generalize the approach in [29] to take into account either the effective electric or the effective electromagnetic form factor in the eikonal model description of elastic pp collisions.

Analytical expression of integral $I(t,t')$

It has been mentioned in Sect. 3.1 that the integral involving the electromagnetic proton form factors (17) may be calculated analytically for conveniently parameterized form factors. It is sufficient to integrate only over a finite region of momentum transfers in formula (15) since the whole integral is multiplied by the elastic hadronic amplitude $F_{}^{\text {N}}(s,t)$ the modulus of which decreases very strongly at high |t| (see Figs. 1 and 7). The used limited integration region of momentum transfers allows us to use some simpler formulas for the ep form factors enabling us much simpler analytical calculation.

In [29] the integral $I(t,t')$ was analytically calculated only for electric form factor parameterized according to (49). The same analytical formulas for this integral have been used in [64]. The integral may be analytically calculated for effective electromagnetic form factor given by Eq. (51) if the corresponding electric and magnetic form factors are given by Eqs. (49) to (50). Due to the fact that both the effective form factors have more complicated t-dependences the corresponding formulas will be a little bit more complicated than that ones in [29].

The analytical calculation of the new form of the integral $I(t,t')$ in Eq. (17) has been calculated with the program Mathematica [107] and equals to the sum of two contributions coming from the electric and magnetic form factors which contain now some kinematical factors ($r_p=-\tau /t=1/(4m^2)$)

$$\begin{aligned} \begin{aligned} I(t,t')\; =\;-&\left[ \sum _{j,k=1}^4 g_j^{\text {E}} g_k^{\text {E}} \; W_{jk}^{\text {E}}(t,t')\;I_{jk}^{\text {E}}(t,t') \right. \\ \;&+ \left. \; r_p {\mu _p}^2 \sum _{m,n=1}^4 g_m^{\text {M}} g_n^{\text {M}} \; W_{mn}^{\text {M}}(t,t')\;I_{mn}^{\text {M}}(t,t') \right] . \end{aligned} \end{aligned}$$

(54)

The contribution of electric form factor in this equation is given as follows. For $j \ne k$ it holds

$$\begin{aligned} \begin{aligned} I_{jk}^{\text {E}}(t,t') =&2 \pi \left[ \frac{(U-1)^3}{\sqrt{U}(U-R)(U-P^{\text {E}}_{j})(U-P^{\text {E}}_{k})} \right. \\&+ \frac{(R-1)^3}{\sqrt{R}(R-U)(R-P^{\text {E}}_{j})(R-P^{\text {E}}_{k})} \\&+ \frac{(P^{\text {E}}_{j}-1)^3}{\sqrt{P^{\text {E}}_{j}}(P^{\text {E}}_{j}-U)(P^{\text {E}}_{j}-R)(P^{\text {E}}_{j}-P^{\text {E}}_{k})} \\&+ \left. \frac{(P^{\text {E}}_{k}-1)^3}{\sqrt{P^{\text {E}}_{k}}(P^{\text {E}}_{k}-U)(P^{\text {E}}_{k}-R)(P^{\text {E}}_{k}-P^{\text {E}}_{j})} \right] \; , \end{aligned} \end{aligned}$$

(55)

while for $j=k$ one has

$$\begin{aligned} I_{jj}^{\text {E}}(t,t')= & {} 2 \pi \left[ \frac{(U-1)^3}{\sqrt{U}(U-R) (U-P^{\text {E}}_{j})^2} \right. \nonumber \\&+ \frac{(R-1)^3}{\sqrt{R}(R-U) (R-P^{\text {E}}_{j})^2} \nonumber \\&+ \frac{(P^{\text {E}}_{j}-1)^2}{2 (U-P^{\text {E}}_{j})^2 (R - P^{\text {E}}_{j})^2 (P^{\text {E}}_{j})^{3/2}} \nonumber \\&\;\;\; \left[ U\left( R+5 R P^{\text {E}}_{j}-3 P^{\text {E}}_{j}(P^{\text {E}}_{j}+1)\right) \right. \nonumber \\&\;\;\; \left. + P^{\text {E}}_{j}\left( -3 R (P^{\text {E}}_{j}+1) + P^{\text {E}}_{j} (5+P^{\text {E}}_{j})\right) \right] \Bigg ]\; . \nonumber \\ \end{aligned}$$

(56)

The quantities U, R and $P^{\text {E}}_{j}$ are the functions of t and $t'$ variables defined as

$$\begin{aligned} U =&\frac{(\sqrt{-t}+\sqrt{-t'})^2}{(\sqrt{-t}-\sqrt{-t'})^2}, \end{aligned}$$

(57)

$$\begin{aligned} R =&\frac{1 + r_p(\sqrt{-t} + \sqrt{-t'})^2}{1 + r_p (\sqrt{-t}-\sqrt{-t'})^2}, \end{aligned}$$

(58)

$$\begin{aligned} P^{\text {E}}_{j} =&\frac{w_j^{\text {E}} + (\sqrt{-t} + \sqrt{-t'})^2}{w_j^{\text {E}} + (\sqrt{-t} - \sqrt{-t'})^2}. \end{aligned}$$

(59)

Similarly the quantity $W_{jk}^{\text {E}}$ is also the function of t and $t'$ variables and equals

$$\begin{aligned} \begin{aligned} W_{jk}^{\text {E}}(t, t') =&\left[ [w_j^{\text {E}} + (\sqrt{-t}-\sqrt{-t'})^2] [w_k^{\text {E}}+ (\sqrt{-t}-\sqrt{-t'})^2] \right. \\&\left. \times [\sqrt{-t} - \sqrt{-t'}]^2 [1 + r_p(\sqrt{-t} - \sqrt{-t'})^2] \right] ^{-1}\; . \end{aligned} \end{aligned}$$

(60)

Fig. 15

Effective form factors squared corresponding to $G_{\text {E}}^{\text {BN}}(t)$ and $G_{\text {M}}^{\text {BN}}(t)$ (see Eqs. (51) to (53)) and compared to $(G_{\text {E}}^{\text {BO}}(t))^2$

The contribution of magnetic form factor is represented by the second term in Eq. (54). The integral for $m \ne n$ equals to

$$\begin{aligned} I_{mn}^{\text {M}}(t,t')= & {} 2 \pi \left[ \frac{(P^{\text {M}}_{m}-1)^2}{\sqrt{P^{\text {M}}_{m}}(P^{\text {M}}_{m}-R)(P^{\text {M}}_{m}-P^{\text {M}}_{n})} \right. \nonumber \\&+ \frac{(R-1)^2}{\sqrt{R}(R-P^{\text {M}}_{m})(R-P^{\text {M}}_{n})} \nonumber \\&+ \left. \frac{(P^{\text {M}}_{n} - 1)^2}{\sqrt{P^{\text {M}}_{n}}(P^{\text {M}}_{n} - R)(P^{\text {M}}_{n} - P^{\text {M}}_{m})} \right] \end{aligned}$$

(61)

and for $m=n$ it equals

$$\begin{aligned} \begin{aligned} I_{mm}^{\text {M}}(t,t') =&2 \pi \left[ \frac{(R-1)^2}{\sqrt{R}(R-P^{\text {M}}_{m})^2} \right. \\&+ \left. \frac{(P^{\text {M}}_{m}-1)\left[ P^{\text {M}}_{m}(P^{\text {M}}_{m}+3)-R(3P^{\text {M}}_{m}+1)\right] }{2 \; (P^{\text {M}}_{m})^{3/2}(R-P^{\text {M}}_{m})^2}\right] \; .\\ \end{aligned}\nonumber \\ \end{aligned}$$

(62)

The quantities $P^{\text {M}}_{m}$ and $W_{mn}^{\text {M}}$ are the functions of t and $t'$ variables and equal

$$\begin{aligned} P^{\text {M}}_{m} = \frac{w_m^{\text {M}}+(\sqrt{-t}+\sqrt{-t'})^2}{{w_m^{\text {M}}}+(\sqrt{-t}-\sqrt{-t'})^2} \end{aligned}$$

(63)

and

$$\begin{aligned} \begin{aligned} W_{mn}^{\text {M}} =&\left[ [w_m^{\text {M}}+(\sqrt{-t}-\sqrt{-t'})^2] [w_n^{\text {M}}+(\sqrt{-t}-\sqrt{-t'})^2] \right. \\&\;\left. [1 + r_p(\sqrt{-t} - \sqrt{-t'})^2] \right] ^{-1}\; . \end{aligned} \end{aligned}$$

(64)

Then the complete elastic scattering amplitude in the eikonal model describing the common influence of Coulomb and hadron scattering in one-photon exchange approach which is valid up to the terms linear in $\alpha$ is generally given by Eqs. (15) to (17) with the quantity $I(t,t')$ given by Eqs. (54) to (64). This newly derived form of the complete elastic scattering amplitude, enabling to study influence of different form factors, will be used for the analysis of pp elastic scattering data at given energy at all measured values of t in a consistent way in Sect. 4.