1 Introduction

Finding new solutions of physical interest to the Einstein field equations is not an easy task due to the highly nonlinear behavior of its equations. In this regard, in (2017) was proposed the Gravitational Decoupling Method [1], which represents an easy algorithm to decouple gravitational sources in General Relativity. This algorithm involves a Minimal Geometric Deformation (MGD) to the metric tensor together with a decoupling of sources. One interesting extension of the method was showed in reference [2]. The method was described in reference [3] as follows: “given two gravitational sources: a source A and an extra source B, standard Einstein’s equations are first solved for A, and then a simpler set of quasi-Einstein equations are solved for B. Finally, the two solutions can be combined in order to derive the complete solution for the total system”. The source A represents to the seed sector and the source B represents to the extra sector. Since its appearance, this method has served to find several new solution of physical interest, as for example well behaved solutions that could represent stellar distributions [3,4,5,6,7,8,9,10,11], black hole solutions [12,13,14], \(f({{\mathcal {G}}})\) gravity [15], Einstein Klein Gordon System [16], Pure Lovelock gravity [17], f(R, T) gravity [18], f(R) gravity [19]. See other applications [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

On the other hand, the fact that the black holes, due to quantum fluctuations, emit as black bodies where its temperature is related to its surface gravity [43,44,45,46], shows that in these objects the geometry and thermodynamics are directly connected. In this regard, the simplest version of the first law of thermodynamics is (see for example [47]):

$$\begin{aligned} dM=TdS+\Omega dJ+ \phi dQ, \end{aligned}$$
(1)

where M, T, S, J and Q represent the mass, temperature, entropy, angular momentum and electric charge, respectively. In Eq. (1) one can notice the absence of the terms of pressure and volume. In that respect, one way to address this problem was showed in reference [48], where the cosmological constant was associated with the thermodynamics pressure of the system, \(P=-\frac{\Lambda }{8\pi }\), whereas the thermodynamics volume corresponds to the thermodynamic variable conjugate to P. So, the mass parameter is interpreted as the enthalpy. However, other way to address this problem was showed in reference [49], identifying the thermodynamics pressure with the radial pressure of the energy momentum tensor. As indicates this reference, it is showed an interesting “ analogy between the gravitational dynamics of the horizons and thermodynamics, specifically, it is showed that it is possible to interpret the field equations near any spherically symmetric horizon as a thermodynamic identity \(dU=TdS-PdV\)” for the non rotating and non charged case. In this way, the term \(-PdV\) can represent the macroscopic work done by the system. This analogy has been used for example for the study of the evolution of the regular black holes with a cosmological horizon in theories of Lovelock with a unique ground state [50], the study of regular black hole thermodynamics in Einstein Hilbert theory [51], stationary axis-symmetric space time and time dependent evolving horizons [49], generic Lovelock theory [52] . See also [53,54,55].

In this work, inspired by the gravitational decoupling method, where the equations of motion are characterized by the standard Einstein’s equations and the quasi Einstein equations, we write the equations of motion as a thermodynamics identity \(dU=TdS-PdV\), which, in analogous way to the mentioned method, will be characterized by two sectors, namely, the standard first law and the quasi first law. We will determine, as consequence of the application of the algorithm, which thermodynamics quantities are shared for both sectors and which quantities of the total system correspond to a simple sum of the quantities of each sector. Furthermore, by mean of an example, where the energy density of the seed sector correspond to the Hayward model [56] and the energy density of the extra sector correspond to the Dymnikova model [57], we will test the thermodynamics behavior of each sector and the total system.

2 The Einstein field equations for multiple sources

In this section, we will show the Einstein field equations for multiple sources. The seed energy momentum tensor \({\bar{T}}_{\mu \nu }\) is coupled to an additional source \(\theta _{\mu \nu }\), whose coupling is proportional to the constant \(\alpha \) and causes anisotropic effects on the self gravitating system [10]. As indicates reference [3], this additional source can contain new fields, like scalar, vector and tensor fields. So, the energy momentum is:

$$\begin{aligned} T_{\mu \nu } = {\bar{T}}_{\mu \nu } + \alpha \theta _{\mu \nu }, \end{aligned}$$
(2)

where the conservation law is:

$$\begin{aligned} \nabla _\nu T^{\mu \nu } =0. \end{aligned}$$
(3)

Taken account an energy momentum tensor of the form \(T^\mu _\nu =\text{ diag }(-\rho ,p_r,p_\theta ,p_\theta ,...)\) and a seed energy momentum tensor of the form \({\bar{T}}^\mu _\nu = \text{ diag }(-{\bar{\rho }},{\bar{p}}_r,{\bar{p}}_\theta ,{\bar{p}}_\theta ,...)\), from Eq. (2) it is straightforward to note that:

$$\begin{aligned} \rho&={\bar{\rho }}-\alpha \theta ^0_0 \end{aligned}$$
(4)
$$\begin{aligned} p_r&= {\bar{p}}_r +\alpha \theta ^1_1 \end{aligned}$$
(5)
$$\begin{aligned} p_\theta&= {\bar{p}}_{\theta } +\alpha \theta ^2_2 \end{aligned}$$
(6)

The Einstein field equations, in natural units, correspond to

$$\begin{aligned} G^\mu _\nu = 8 \pi T^\mu _\nu . \end{aligned}$$
(7)

We will study the following spherically symmetric space time:

$$\begin{aligned} ds^2=-\mu (r)dt^2+\mu (r)^{-1} dr^2+r^2 d\Omega ^2_{2}. \end{aligned}$$
(8)

It is worth to mention that the form of this metric has the two following consequences on the energy momentum tensor through the Einstein field equations :

$$\begin{aligned} T^t_t&=T^r_r \end{aligned}$$
(9)
$$\begin{aligned} T^\theta _\theta&=T^\phi _\phi , \end{aligned}$$
(10)

which implies that

$$\begin{aligned} \rho&=-p_r \end{aligned}$$
(11)
$$\begin{aligned} p_\theta&=p_\phi . \end{aligned}$$
(12)

To accomplish the condition (11) it is imposed in arbitrarily way that

$$\begin{aligned} {\bar{\rho }}&=-{\bar{p}}_r \text{,and } \end{aligned}$$
(13)
$$\begin{aligned} \theta ^0_0&=\theta ^1_1 . \end{aligned}$$
(14)

In this way, the \((t-t)\) and \((r-r)\) components of the Einstein field equations are similar and are given by:

$$\begin{aligned} 8\pi {\bar{\rho }}-8 \pi \alpha \theta ^0_0 = \dfrac{1-\mu }{r^2}-\dfrac{\mu '}{r}, \end{aligned}$$
(15)

where \('\) denotes derivation respect to the radial coordinate.

On the other hand, the conservation law has the form:

$$\begin{aligned}&{\bar{p}}_r'+ \frac{2}{r}({\bar{p}}_r-{\bar{p}}_t ) \nonumber \\&+ \alpha \Big ( (\theta ^1_1)'+\frac{2}{r}(\theta ^1_1-\theta ^2_2 ) \Big )=0 . \end{aligned}$$
(16)

As indicates the reference [1], due that, in the limit \(\alpha \rightarrow 0\), the geometry of the line element (8) is associate with the geometry of the seed perfect fluid, and its respective Bianchi identities are satisfied, the seed energy momentum tensor is conserved, i.e. : \(\nabla _\nu {\bar{T}}^{\mu \nu } =0\):

$$\begin{aligned} {\bar{p}}_r'+ \frac{2}{r}({\bar{p}}_r-{\bar{p}}_t ) =0 , \end{aligned}$$
(17)

and, by inserting Eq. (17) into Eq. (16) , it is easily to see that the extra source is also conserved, i.e. \(\nabla _\nu \theta ^{\mu \nu } =0\):

$$\begin{aligned} (\theta ^1_1)'+\frac{2}{r}(\theta ^1_1-\theta ^2_2 ) =0, \end{aligned}$$
(18)

thus, each source is separately conserved.

3 A brief review of the gravitational decoupling method

As was said in the introduction, the gravitational decoupling method applies a decoupling of the gravitational sources, Eq. (2), together with the Minimal Geometric Deformation (MGD) of the space time (explained below).

We will call seed solution to the solution of the Einstein field Eq. (7) with \(\alpha =0\). In our case the seed solution is written as the following spherically symmetric and static line element

$$\begin{aligned} ds^2=-{\bar{\mu }}(r)dt^2+{\bar{\mu }}(r)^{-1} dr^2+r^2 d\Omega ^2_{2}. \end{aligned}$$
(19)

It is easy to check that the equations of motion are given by the Eq. (15) with \(\alpha =0\) and \(\mu ={\bar{\mu }}\), whereas, the conservation equation is given by the Eq. (17). A complete analysis of the gravitational decoupling method when de metric components \(g_{tt} \ne g_{rr}^{-1}\) can be found in references [1, 3].

Turning on the parameter \(\alpha \), the effects of the source \(\theta _{\mu \nu }\) appear on the seed solution. These effects are encoded in the geometric deformation undergone by the seed fluid geometry in Eq. (19) as follows:

$$\begin{aligned} \mu (r) \rightarrow {\bar{\mu }} (r) + \alpha g(r). \end{aligned}$$
(20)

This last is known as the Minimal Geometric Deformation. MGD was initially proposed in references [58, 59] for the study of brane world models [60,61,62] and was extended to the study of black hole solutions [63]. Other applications in references [64,65,66].

Replacing Eq. (20) into the Eq. (15), under the assumptions (11), (12), (13) and (14), the system splits into two sets of equations:

  • The standard Einstein equations for a seed solution (with \(\alpha =0\)) given by:

    $$\begin{aligned} 8\pi {\bar{\rho }} = \dfrac{1-{\bar{\mu }}}{r^2}-\dfrac{{\bar{\mu }}'}{r}, \end{aligned}$$
    (21)

    and the respective conservation equation (17).

  • The terms of order \(\alpha \) give rise to the following quasi-Einstein equations [1], which include the source \(\theta _{\mu \nu }\):

    $$\begin{aligned} -8 \pi \theta ^0_0 = \dfrac{-g}{r^2}-\dfrac{g'}{r}, \end{aligned}$$
    (22)

    and the respective conservation equation (18).

4 Decoupling the first law of thermodynamics

In order to analyse the thermodynamics, we will follow one scheme analogous to the above mentioned method, but, unlike the previous case, following the idea of the references [49, 54], we will study the behavior of the equations of motion at the black hole horizon, and thus, these equations will be write as two sectors analogous to the first law of thermodynamics. Will call \(r=a\) to the generic horizon, where \(\mu (a)=0\). The first step, following reference [49], is, identify the thermodynamics pressure with the radial pressure of the fluid perfect,

$$\begin{aligned} P_{tot}=p_r=&{\bar{p}}_r + \alpha \theta ^1_1 \nonumber \\ P_{tot}=&P_s+ \alpha P_q, \end{aligned}$$
(23)

where \({\bar{p}}_r=P_s\) and \(\theta ^0_0=P_q\), and, using the conditions (13) and (14), evaluating the equations of motion (15) at \(r=a\):

$$\begin{aligned} 4\pi a^2 \left( P_s + \alpha P_q \right) = \dfrac{u'}{2}a- \frac{1}{2}. \end{aligned}$$
(24)

Next, also following [49], we consider two horizons whose values are a and \(a+da\), thus, multiplying Eq. (24) by da:

$$\begin{aligned} (P_s+ \alpha P_q) d \left( \frac{4}{3}\pi a^3 \right) = \left( \dfrac{\mu '}{4\pi } \right) d \left( \dfrac{4\pi a^2}{4} \right) - d \left( \dfrac{a}{2} \right) .\nonumber \\ \end{aligned}$$
(25)

To test the role of the constant \(\alpha \), we will apply the MGD to the geometry. Turning on \(\alpha \), the effects of the source \(\theta _{\mu \nu }\) appear on the seed solution. These effects are encoded in the geometric deformation undergone by the seed fluid by the Eq. (20).

Thus, it is direct to see that the Eq. (15) can be written as:

$$\begin{aligned} \mu = {\bar{\mu }} + \alpha g =1 - \dfrac{2}{r} \Big ( m_s(r) + \alpha \cdot m_q(r) \Big ), \end{aligned}$$
(26)

where

$$\begin{aligned} m_s(r)=&\int 4 \pi r^2 {\bar{\rho }} dr, \end{aligned}$$
(27)
$$\begin{aligned} m_q(r)=&-\int 4 \pi r^2 \theta ^0_0 dr , \end{aligned}$$
(28)

and

$$\begin{aligned} {\bar{\mu }}(r)=&1 - \dfrac{2}{r}m_s(r) \end{aligned}$$
(29)
$$\begin{aligned} g(r)=&- \dfrac{2}{r}m_q(r). \end{aligned}$$
(30)

To ensure an asymptotically flat behavior, must be imposed that:

$$\begin{aligned} \displaystyle&\lim _{r \rightarrow \infty } m_s(r) =M_s \end{aligned}$$
(31)
$$\begin{aligned} \displaystyle&\lim _{r \rightarrow \infty } m_q(r) =M_q , \end{aligned}$$
(32)

also

$$\begin{aligned} \displaystyle&\lim _{r \rightarrow \infty } \frac{d}{dr} m_s(r) =0 \end{aligned}$$
(33)
$$\begin{aligned} \displaystyle&\lim _{r \rightarrow \infty } \frac{d}{dr} m_q(r) =0 , \end{aligned}$$
(34)

Thus, replacing (26) at \(r=a\), where \(\mu (a)=0\):

$$\begin{aligned} \dfrac{a}{2}= m_s(a) + \alpha \cdot m_q(a). \end{aligned}$$
(35)

Thus, inserting Eqs. (20) and (35) into Eq. (25), the system splits into the following sets of equations:

  • The standard firs law of thermodynamics of order \(\alpha ^0\), which is analogous to the standard Einstein equations:

    $$\begin{aligned} P_s d \left( \frac{4}{3}\pi a^3 \right) = \left( \dfrac{{\bar{\mu }}'}{4\pi } \right) d \left( \dfrac{4\pi a^2}{4} \right) - d \Big ( m_s(a) \Big ). \end{aligned}$$
    (36)

    This equation has the form of the first law of thermodynamics \(PdV=TdS-dU\), where each term is identified as:

    $$\begin{aligned} \text{ Thermodynamics } \text{ Pressure }=&P_s \end{aligned}$$
    (37)
    $$\begin{aligned} \text{ Volume }=&\frac{4}{3}\pi a^3 \end{aligned}$$
    (38)
    $$\begin{aligned} \text{ Temperature }=&T_s=\frac{{\bar{\mu }}'}{4\pi } \end{aligned}$$
    (39)
    $$\begin{aligned} \text{ Entropy }=&\dfrac{4\pi a^2}{4}=\dfrac{Area}{4} \end{aligned}$$
    (40)
    $$\begin{aligned} \text{ Local } \text{ Energy }=&U_s^{loc}= m_s(a) \end{aligned}$$
    (41)

    It is worth to mention that our thermodynamics variables obtained coincide with the previously known in literature. The thermodynamics volume coincide with the geometric volume, the temperature is the well known expression and the entropy follows the area’s law. The energy \(m_s(a)\) corresponds to a local definition of energy, at \(r=a\), given by reference [50]. In the vacuum case, where \({\bar{\rho }}=\theta ^\mu _\nu =0\), the solution (26) has the form \(\mu =1-2M/r\) and the local energy coincide with the energy of the Schwarzschild black hole, \(a/2=M\). These thermodynamics variables \(P_s\),\(T_s\) and \(U_s^{loc}\) represent the contribution of the standard sector to the total pressure, total temperature and total local energy of the black hole. These ones do not represent the pressure, temperature and local energy of an independent black hole.

  • The quasi first law of thermodynamics of order \(\alpha \), which is analogous to the quasi Einstein equations:

    $$\begin{aligned} P_q d \left( \frac{4}{3}\pi a^3 \right) = \left( \dfrac{g'}{4\pi } \right) d \left( \dfrac{4\pi a^2}{4} \right) - d \Big ( m_q(a) \Big ). \end{aligned}$$
    (42)

    This equation also has the form of the first law of thermodynamics, \(PdV=TdS-dU\), and each term is identified as:

    $$\begin{aligned} \text{ Thermodynamics } \text{ Pressure }=&P_q \end{aligned}$$
    (43)
    $$\begin{aligned} \text{ Volume }=&\frac{4}{3}\pi a^3 \end{aligned}$$
    (44)
    $$\begin{aligned} \text{ Temperature }=&T_q=\frac{g'}{4\pi } \end{aligned}$$
    (45)
    $$\begin{aligned} \text{ Entropy }=&\dfrac{4\pi a^2}{4}=\dfrac{Area}{4} \end{aligned}$$
    (46)
    $$\begin{aligned} \text{ Local } \text{ Energy }=&U_q^{loc}= m_q(a), \end{aligned}$$
    (47)

    where, in a similar way to the previous case, all the thermodynamics variables coincide with the previously known in the literature.

Also, these thermodynamics variables \(P_q\),\(T_q\) and \(U_q^{loc}\) represent the contribution of the quasi sector to the total pressure, total temperature and total local energy of the black hole. These ones do not represent the pressure, temperature and local energy of an independent black hole.

4.1 Some remarks

From the previous analysis one can remark some properties:

  • The total thermodynamics pressure, total temperature and total local energy correspond to a simple sum of the thermodynamics contributions of each sector

    $$\begin{aligned} P_{tot}&=P_s+\alpha P_q \end{aligned}$$
    (48)
    $$\begin{aligned} T_{tot}&=T_s+\alpha T_q \end{aligned}$$
    (49)
    $$\begin{aligned} U_{tot}^{loc}&=U_s^{loc}+\alpha U_q^{loc} \end{aligned}$$
    (50)

    So, as was said above, it is worth to mention that the temperatures \(T_s\) and \(T_q\) represent the contribution of each sector (standard and quasi) to the total temperature of black hole and, do not represent the temperature of one independent black hole. The same occurs with the pressure and energy.

  • Both sectors share the same thermodynamics volume and entropy.

As was said above, \(U_{tot}^{loc}\) corresponds to a local definition of energy, located at \(r=a\) [50]. However, the total energy of the system must be computed by the Noether charge [67], by mean of the Komar formula [68].

$$\begin{aligned} E \propto&\displaystyle \lim _{r \rightarrow \infty } K(\xi )= \nonumber \\ =&\lim _{r \rightarrow \infty } \frac{1}{8\pi } \frac{d}{dr} \mu (r) r^{2} \int d\Omega _{2} \nonumber \\ =&\dfrac{1}{2} \Big (M_s+ \alpha \cdot M_q \Big ), \end{aligned}$$
(51)

where \(\xi \) is a timelike Killing vector. Thus, the total energy is proportional to the Komar formula [68]. After a regularization, based on the inclusion of the boundary terms in the action [67], can be obtained that:

$$\begin{aligned} E= M_s+ \alpha \cdot M_q. \end{aligned}$$
(52)

At infinity, our local definitions of energy coincide with the total energy. Thus, other important result of our decoupling of the first law of thermodynamics is that: The total energy corresponds to the contribution of the Noether charge of each sector. So, turning on the coupling constant \(\alpha \), the total energy increases proportionally to this constant.

5 A simple example

As a simple example, we choose a seed and a extra source, such that, near the origin, the mass functions behave as:

$$\begin{aligned}&m_s(r) \Big |_{r \approx 0} \approx C_1 r^3 \end{aligned}$$
(53)
$$\begin{aligned}&m_q(r) \Big |_{r \approx 0} \approx C_2 r^3. \end{aligned}$$
(54)

This one implies that near the origin the geometry behaves as a de Sitter space time, where the invariants of curvature have finite values, and thus, unlike the singular Schwarzschild solution, the geometry is regular near the origin. These models are called regular black holes [69, 70].

The seed source is given by the Hayward model [56]:

$$\begin{aligned} \rho (r) = \frac{1}{2\pi } \frac{3Q^2M_s^2}{(2Q^2M_s+r^3)^2}, \end{aligned}$$
(55)

where Q is a constant. The mass function is:

$$\begin{aligned} m_s(r)=\frac{M_sr^3}{r^3+2M_sQ^2}. \end{aligned}$$
(56)

On the other hand, the extra source is given by the Dymnikova model [51]:

$$\begin{aligned} \theta ^0_0(r) = -\frac{M_q \exp (-r^3/R^3)}{(4/3)\pi R^3}, \end{aligned}$$
(57)

where R is a constant. The mass function is:

$$\begin{aligned} m_q(r)=M_q \Big (1-\exp (-r^3/R^3) \Big ). \end{aligned}$$
(58)

It is direct to check that the conditions (53) and (54) are fulfilled, an thus, this model is suited to represent a regular black hole. It is worth to mention that the combination of both energy density models, (55) and (57), provides a new model of regular black holes, inserting Eqs. (56) and (58) into Eq. (26)

$$\begin{aligned} \mu = 1 {-} \dfrac{2}{r} \left( \frac{M_sr^3}{r^3{+}2M_sQ^2} {+} \alpha \cdot M_q \left( 1{-}\exp (-r^3/R^3) \right) \right) .\nonumber \\ \end{aligned}$$
(59)

On the other hand, also it is direct to check that the conditions (31) and (32) are fulfilled. This one ensures that the total energy corresponds to the contribution of the Noether charge of each sector, equation (52).

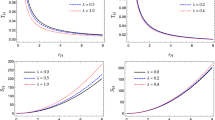
In the figure 1 one can check the existence of one critical value of \(M_s=M_*\), which corresponds to the minimum value on the curve, where there is an extremal black hole, where the internal horizon \(a=r_-\) and black hole horizon \(a=r_+\) coincide. On the other hand, for \(M_s>M_*\) there are two horizons, namely, the internal horizon \(r_-\) and the black hole horizon \(r_+\). This behavior is generic for other values of the parameters.

Fig. 1
figure 1

Behavior of \(M_s\) parameter for \(\alpha =Q=R=1\), \(M_q=0.7\)

Full size image
Fig. 2
figure 2

Behavior of \(T_s\),\(T_q\) and \(T_{tot}\) for \(\alpha =Q=R=1\),\(M_q=0.7\)

Full size image

Figures 2 (a), 2(b) and 2(c) display the behavior of the contributions \(T_s\) and \(T_q\) and the total temperature \(T_{tot}\), respectively. This behavior is generic for other values of the parameters. One can check that the temperature vanishes at the extremal case [71]. \(T_s\) and \(T_q\) are contributions to the total temperature \(T_{tot}\), where, this last is always positive. The total temperature has a local maximum, located at \(r_+=r_{max}\). One can check that this inflection point is due to the behavior of the contribution of the quasi sector, \(T_q\), which vanishes after this point. Using the standard definition of the heat capacity:

$$\begin{aligned} C= T_{tot} \frac{\partial S}{\partial r_+} \left( \frac{\partial T_{tot}}{\partial r_+} \right) ^{-1} , \end{aligned}$$
(60)

it is direct to see that the sign of the specific heat depend only on the factor \(\dfrac{\partial T_{tot}}{\partial r_+}\). So in the point \(r_+=r_{max}\), where this derivative vanishes, there is a phase transition. At the left side of \(r_+=r_{max}\) this derivative is positive and the heat capacity is positive, i.e the black hole is stable. However, at the right side of \(r_+=r_{max}\) this derivative is negative and the heat capacity is negative, i.e the black hole is unstable.

6 Conclusion and discussion

In this work is showed that, a direct consequence of the splitting of the equations of motion of one spherically symmetric space time, in an analogue way to the gravitational decoupling method, is the decoupling of the first law of thermodynamics in two sectors, called, the standard first law of thermodynamics, and the quasi first law of thermodynamics. This is achieved, following the approximation of the reference [49], where the equations of motion are evaluated at the horizon \(r=a\).

Each sector is written as a thermodynamics identity \(PdV=TdS-dU\). In this respect, both sectors share the same thermodynamics volume and the same entropy. The total thermodynamics pressure, total temperature and total local energy correspond to a simple sum of the thermodynamics contributions of each sector, Eqs. (48), (49) and (50). Other interesting result is that the total energy corresponds to the contribution of the Noether charge of each sector, Eq. (52). Thus, turning on the coupling constant \(\alpha \), the total energy increases proportionally to this constant.

In both sectors, the terms corresponding to the identity \(PdV=TdS-dU \) coincide with the previously known in literature. The thermodynamics volume coincide with the geometric volume, the temperature is the well known expression and the entropy follows the area’s law. The local definition of energy coincide with the definition of the reference [50].

Finally, it is provided one example, where the seed source and the extra sources correspond to the Hayward model [56] and the Dymnikova model [57], respectively. It is worth to mention that this combination provides a new model of regular black hole. It is showed that the total temperature has an inflection point where there is a phase transition between stable/unstable black hole. Thus, due to the application of the decoupling, it is possible to determinate that this phase transition occurs due to the behavior of the temperature contribution at the quasi sector.