1 Introduction

Due to the clear strong/weak dual dictionary, the AdS/CFT correspondence provides a powerful tool to study \((d+1)\) dimensional strongly coupled systems by means of its d-dimensional weak AdS gravity [1, 2]. In the recent years, the AdS/CFT correspondence and its generalized version (gauge/gravity duality) have been widely applied in many strong correlated systems [3,4,5,6], especially the holographic construction of the high critical temperature superconductor [7, 8].

In contrast with the conventional superconductor, the high critical temperature superconductor is believed to involve strong interaction and thus its pair mechanism is one of the most challenges in condensed matter physics. The AdS/CFT correspondence obviously opens a new window to understand the properties of superconductors. In 2008, by using the Einstein-Abelian-Higgs system, the authors in Ref. [7] built numerically a holographic description of the s-wave conductor/superconductor model in the probe limit, and produced the main characters of the superconductor, such as the appearance of the scalar condensate accompanied by spontaneous breaking of the U(1) symmetry below the critical temperature as well as the infinite DC conductivity on top of the hairy gravitational background. Soon after, the Meissner effect and the vortex lattice solution about the superconductor were managed to realize via the holographic duality [9], following which the numerical results about holographic superconductor model were upheld by the analytical Sturm-Liouville (S-L) eigenvalue method [10].

The above works showed that the main properties of superconductors have been disclosed successfully by the the gauge/gravity duality. Since then, holographic superconductor models were studied from various perspectives [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], which greatly promoted the development of holographic superconductor model. One important developing direction of holographic superconductor is to build the holographic model which is more close to the real superconducting materials in condensed-matter physics [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Following this line, the superconductor model were generalized to the SU(2) Yang-Mills p-wave model [11], the d-wave model [12, 13], Maxwell-complex-vector (MCV) p wave model [14, 15], the backreaction of the matter field to the gravitational background [15,16,17], the superfluid model [18,19,20], the coexistence and competition of multiple order parameter [21,22,23,24], the superconductor model with momentum relaxation [25,26,27,28], their corresponding insulator/superconductor phase transition model [29], complexity of superconductors [30], the ones with the anisotropic scaling [31,32,33,34,35] and Kibble-Zurek Scaling [36] as well as impurity [37].

The other direction of the development for holographic superconductor model is to improve the basic framework of the gauge/gravity by investigating the influences of the \(1/\lambda \)(\(\lambda \) is the ’t Hooft coupling) corrections on the holographic superconductor models [38,39,40,41,42,43,44,45,46,47,48,49,50]. In particular, the related works involve high curvature corrections such as the Gauss-Bonnet gravity [38, 39], Quasi-topological gravity [40], nonlinear electrodynamics, for example, Born-Infeld correction [41], exponential correction [42], Logarithmic correction [43] as well as gravity-gauge field coupled correction, for instance, \(RF^2\) term [44, 45] and \(CF^2\) correction [46, 47] and \(C^2F^2\) correction [48,49,50] with R and C representing the curvature scalar (tensor) and Weyl tensor. It follows that the first kind of corrections inhibit both the conductor/superconductor and insulator/superconductor phase transition [38,39,40], while second kind of corrections inhibit the conductor/superconductor phase transition but do not affect the critical value of insulator/superconductor phase transition [41,42,43]. Meanwhile, the third kind of corrections enhance the conductor/superconductor and do not influence the s-wave and p-wave insulator/superconductor phase transition while inhibit the SU(2) p-wave insulator/superconductor phase transition [44,45,46,47,48, 50].

Of course, there are also many works which took into account simultaneously the effects of both directions of development on the holographic superconductors, for example, the superconductor model with backreaction in Gauss-Bonnet gravity [38], the superconductor with momentum relaxation and Weyl correction [51] and the MCV p-wave model with Weyl correction [47] or \(RF^2\) correction [45] and the MCV p-wave superfluid in AdS soliton [44] as well as superfluid with vortex lattice [52]. In addition, there is a more natural gravity theory worthy of attention for the construction of holographic superconductor, i.e., the Horndeski gravity [53]. The Horndeski gravity has a series of advantages. First of all, although its lagrangian contain high order derivative about the metric and scalar field, the equations of motion and the energy-momentum tensor involve less than second order derivative of the fields which is similar to the Lovelock gravity. Secondly, as one constructs the s-wave superconductor model by means of the scalar field of the present theory, the coupled term between the Einsten tensor and the scalar provide a new kind of interaction compared with the above corrections. Furthermore, the s-wave conductor/superconductor phase transition in the Horndeski gravity showed that the increasing Horndeski coupling makes the condensate more difficult [54,55,56]. Meanwhile, the Horndeski coupling was argued to play the role of a high concentration of impurities in a material [54, 57]. In terms of other investigations of the Horndeski coupling in holography and cosmology, see, for example, Refs. [58,59,60,61,62,63]. Based on the above works, it is interesting to ask how the Horndeski coupling parameter affects the insulator/superconductor phase transition. Therefore, we will generalized the insulator/superconductor model from the minimal coupling between the gravity and scalar field to the nonminimal case by introducing the Horndeski correction and study the effects of the Horndeski coupling parameter on the critical value as well as the conductivity. It follows that the increasing Horndeski coupling inhibits the scalar condensate to appear and suppresses the growth of the scalar condensate.

This paper is planed as follows. In Sect. 2, we will numerically build the s-wave insulator/superconductor phase transition and thus calculate the conductivity, following which we restudy the critical value and the critical behavior by the analytical S-L method. To testify numerical results of the s-wave conductor/superconductor model with the Horndeski correction, we study the corresponding superconductor model by the S-L method. The final section is devoted to the conclusions and discussions.

2 Insulator/superconductor phase transition

In this section, we firstly construct the holographic s-wave insulator/superconductor phase transition in the five-dimensional AdS soliton with the Maxwell complex scalar field coupled to the Einstein tensor (i.e., the Horndeski correction) via the numerical method. To verify that above the critical chemical potential the state with scalar hair is indeed stable, we define the grand potential of the system density and then compare the grand potential of the hairy state with the one of no hairy state, following which the frequency dependent conductivity is studied. In order to check the reasonability of the model, we reconstruct the holographic superconductor model by the analytical S-L method to back up the above numerical results.

As a preparation, we start with the review of the five-dimensional AdS soliton, the action of which consists of the Ricci scalar and a cosmological constant as [64, 65]

$$\begin{aligned} {\mathcal {S}}=\frac{1}{16\pi G_5}\int d x^5 \sqrt{-g} \left( R-2\Lambda \right) , \end{aligned}$$
(1)

where \(\Lambda =-\,\frac{6}{l^2}\) with l the radius of the AdS spacetime. For simplicity, we will set \(l=1\) throughout the paper. Varying the action (1) yields the Einstein equation of motion, by solving which we can obtain the five-dimensional AdS soliton solution as [29, 64,65,66,67,68,69]

$$\begin{aligned} ds^2= & {} -r^2dt^2+\frac{dr^2}{r^2f(r)}+r^2(dx^2+dy^2)+r^{2}f(r)d\eta ^2,\nonumber \\ f(r)= & {} 1-\frac{r_0^4}{r^4}. \end{aligned}$$
(2)

Some remarks about the soliton solution (2) are as follows: firstly, the parameter \(r_0\) denotes the tip of the soliton geometry. To avoid the conical singularity at \(r=r_0\), we impose a periodicity for the Scherk-Schwarz circle on the spatial direction \(\eta \), i.e., \(\eta \sim \eta +\frac{\pi }{r_0}\), which thus suggests that the present five-dimensional solition corresponds to a three-dimensional CFT. Secondly, different from the black hole, the soliton solution has no event horizon, and thus no the Hawking temperature defined from the horizon, of course the associated entropy vanishes. Thirdly, for the boundary topology (\(R\times S^1\times R^{2}\)) to the soliton solution, there exist other two kinds of bulk solutions as for the action (1), i.e., the Ricci flat AdS black hole and the AdS space [64, 65]. In fact, the soliton solution can be obtained from the double Wick rotation to the Ricci flat AdS black hole solution. Meanwhile, Horowitz and Myers have conjectured that the soliton solution is not only a negative energy solution but also the minimum energy solution compared with the AdS vacuum and the Ricci flat AdS black hole with the same boundary topology [67]. Choosing the AdS soliton as a reference background, the authors in Ref. [66] found that there exists a Hawking-Page phase transition between the Ricci flat AdS black hole and the AdS soliton if at least one of black hole horizon coordinate is compact, which corresponds to the confinement/deconfinement phase transition in the dual CFT [70]. Fourthly, due to the soliton’s lower energy than the one of the AdS vacuum, the soliton gravitational background corresponds to the field theory with a “mass gap”, which is similar to the insulator in the condensed physics and is thus believed to provide a gravitational background for modeling the holographic insulator/superconductor phase transition [29, 35, 68, 69].

Subsequently, we take the Lagrangian density consisting of a Maxwell field and a complex scalar field coupled to the Einstein tensor as [54, 55]

$$\begin{aligned} {\mathcal {L}}_m= & {} -\,\frac{1}{4}F_{\mu \nu }F^{\mu \nu }-(g^{\mu \nu }+kG^{\mu \nu }) D_\mu \psi (D_\nu \psi )^*\nonumber \\&-m^2 |\psi |^2, \end{aligned}$$
(3)

where \(F_{\mu \nu }=\nabla _\mu A_\nu -\nabla _\nu A_\mu \) is the field strength of the gauge field \(A_\mu \), the symmetric tensor \(G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}g_{\mu \nu } R\) is the Einstein tensor with the Ricci scalar R, \(D_\mu =\nabla _\mu -iq A_\mu \), and m (q) is the mass (charge) of the scalar field \(\psi \). Obviously, the parameter k characterizes the strength of the Horndeski correction. In particular, as \(k=0\), the above Lagrangian density restores to the case in Refs. [7, 8, 16, 68, 69]. Besides, to simplify the calculation, we regarded the matter field as the probe to the soliton, where the equations of motion for both the scalar and the gauge field decouple from the Einstein field equation and the main physics of the system is believed to be grasped at the same time. From Eq. (3), we can read off the equations of motion of scalar field and gauge field as

$$\begin{aligned}&D_\mu \left( (g^{\mu \nu }+kG^{\mu \nu })D_\nu \psi \right) -m^2\psi = 0, \end{aligned}$$
(4)
$$\begin{aligned}&\nabla _\mu F^{\mu \nu }+iq(g^{\mu \nu }+kG^{\mu \nu })(\psi ^*D_\mu \psi -\psi (D_\mu \psi )^*) =0.\nonumber \\ \end{aligned}$$
(5)

Throughout the paper, we will set \(L=1\) and \(q=1\) without loss of generality.

Fig. 1
figure 1

The condensate (left) and the charge density (right) versus chemical potential with \(\Delta =\frac{9}{4},\frac{5}{2},3,\frac{7}{2}\) (from left to right)

Full size image
Table 1 The critical chemical potential and the fitted coefficient of the condensate (\({\mathcal {C}}_4\)) and the charge density (\({\mathcal {C}}_5\)) for various \(\Delta \)
Full size table

Following the works in Refs. [7, 8, 29, 54, 55, 68, 69], we take the complex scalar field to be real and only turn on the time component of the Maxwell field, which are

$$\begin{aligned} \psi =\psi (r), \ \ \ A_\mu dx^\mu =\phi (r) dt. \end{aligned}$$
(6)

Combining the ansatz (6) with the soliton background (2), the concrete equations of motion in term of \(\psi (r)\) and \(\phi \) read

$$\begin{aligned}&\psi ''(r)+\frac{{\mathcal {C}}_1 }{ r f{\mathcal {C}}_2}\psi '(r)+\left( \frac{ q{\mathcal {C}}_3 \phi ^2(r)}{r^4 f{\mathcal {C}}_2 }-\frac{2 m^2 }{ r^2 f{\mathcal {C}}_2}\right) \psi (r)=0, \nonumber \\\end{aligned}$$
(7)
$$\begin{aligned}&\phi ''(r)+\left( \frac{3}{r}+\frac{f'}{f}\right) \phi '(r)-\frac{{\mathcal {C}}_3\psi (r)^2}{r^2f}\phi (r) = 0. \end{aligned}$$
(8)

where \({\mathcal {C}}_1=r f'(r) \left( 2+3 k r f'(r)\right) +f(r) \left( 10+42 k r f'(r)+3 k r^2 f''(r)\right) +60 k f(r)^2\), \({\mathcal {C}}_2=2+12 k f(r)+3 k r f'(r)\), \({\mathcal {C}}_3=2+12 k f(r)+8 k r f'(r)+k r^2 f''(r)\), the prime stands for the derivative with respect to r. Obviously, as \(k=0\), Eqs. (7) and (8) restore to the standard case in Refs. [29, 35, 68, 69].

2.1 Numerical part

To solve the above coupled differential equations by the shooting method, we have to specify the boundary conditions for \(\psi (r)\) and \(\phi (r)\). It should be noted that the constant \(\mu \) is a trial solution of Eq. (8) which is obviously different from the AdS black holes requiring the gauge field vanishing [7, 8, 54]. Here, we only impose the Neumann-like boundary condition [29] to remove the logarithm term in order for both \(\psi (r_0)\) and \(\phi (r_0)\) to be finite at the tip \(r=r_0\).

At the boundary \(r\rightarrow \infty \), \(\psi (r)\) and \(\phi (r)\) behave as

$$\begin{aligned} \psi (r)= & {} \frac{\psi _1}{r^{\Delta _-}}+\frac{\psi _2}{r^{\Delta _+}}+\cdots , \end{aligned}$$
(9)
$$\begin{aligned} \phi (r)= & {} \mu -\frac{\rho }{ r^{2}}+\cdots , \end{aligned}$$
(10)

where \(\Delta _\pm =2 \pm \sqrt{4+\frac{m^2}{1+6k}}\), \(\psi _1\), \(\psi _2\), \(\mu \) and \(\rho \) are all constants. According to the gauge/gravity duality, \(\psi _1\) (\(\psi _2\)) can be regarded as the source (the vacuum expectation value) of the dual operator \({\mathcal {O}}\), and \(\mu \)(\(\rho \)) is chemical potential (charge density) of the dual field theory. Since the U(1) symmetry is expected to be broken spontaneously, we impose the source-free condition \(\psi _1=0\). Hereafter, we denote \(\Delta =\Delta _+\) for simplicity. The mass squared \(m^2\) of the scalar field has a lower bound as \(m^2=-4-24k\). In the present paper, we choose \(m^2=-\frac{63}{16}\) and mainly consider the effects of the Horndeski correction with the range \(0\le k\le 1\).

We still take \(r_0=1\) in the numerical calculation. Thus the period of the spatial coordinate \(\chi \) is \(\Gamma =\pi \). In order for the insulator/superconductor model with different Horndeski correction to be comparable, we fix the period of the spatial coordinate \(\chi \), which is another difference from the case of the black holes requiring either the charge density or the chemical potential to be fixed.Footnote 1 Fortunately, different from the Lifshitz case in Ref. [35], the period \(\Gamma \) is independent of the Horndeski correction, which implies that the present work does not need rescale the numerical result if we fix \(\Gamma =\pi \).

After series of calculation, we plot the scalar condensate \(\langle {\mathcal {O}}\rangle \) and the charge density \(\rho \) versus chemical potential with \(\Delta =\frac{9}{4}\) (black solid), \(\frac{5}{2}\) (red dashed), 3 (blue dotted) and \(\frac{7}{2}\) (purple dotdashed) in Fig. 1, from which we have the following remarks. As for the curves of scalar condensate, first of all, for all cases there always exists a critical chemical potential, above which the scalar hair starts to condense. Meanwhile, the critical chemical potential increases with the larger Horndeski parameter k, which means that the larger Horndeski correction hinders the insulator/superconductor phase transition. It should be mentioned that we have also listed critical chemical potential in Table 1 and plotted the value of \(\mu _c\) versus the Horndeski parameter k in the form the black solid points in the left panel of Fig. 2. It follows that when \(\Delta =\frac{5}{2},~3\), the results return to the ones in Refs. [29, 35, 68, 69]. What is more, near the critical point, we have \(\langle {\mathcal {O}}\rangle \sim {\mathcal {C}}_4\sqrt{\mu -\mu _c}\) by fitting the numerical curves. The critical exponent of the condensate \(\left( \frac{1}{2}\right) \) indicates that the system undergoes a second-order phase transition at the critical point. Meanwhile, we read off the coefficient \({\mathcal {C}}_4\) in Table 1 and find it decreases with the increasing Horndeski parameter, which suggests that the larger correction suppresses the growth of the condensate and is consistent with the phenomenon that the critical chemical potential increases with the larger Horndeski correction. In term of the curves for the charge density, we observe that above the critical point, the charge density appears and increases with the chemical potential. By fitting the numerical results, we find the charge density has the linear dependent on the chemical potential as \(\rho \sim {\mathcal {C}}_5(\mu -\mu _c)\), which agrees with the meaning field theory. Besides, the coefficient \({\mathcal {C}}_5\) listed in Table 1 decreases with the improving Horndeski parameter, which agrees with the fact from the condensate curve that the increasing Horndeski correction makes the phase transition more difficult.

Fig. 2
figure 2

The left panel represents the critical chemical potential versus the Horndeski parameter k and the right panel shows the grand potential as a function of the chemical potential about the normal state (horizontal) and the superconducting state (curved) in the case of \(\Delta =\frac{9}{4},\frac{5}{2},3,\frac{7}{2}\) (from right to left)

Full size image

To check that above the critical chemical potential, the superconducting state with scalar hairy is indeed thermodynamically favored in contrast with the normal state, we define the ‘temperature’Footnote 2 of the soliton as \(\int dt=\frac{1}{T}\), upon which the grand potential of the system is defined by the Euclidean on-shell action \(S_E\) timing the ‘temperature’ of the soliton, i.e., \(\Omega =T S_E\). Integrating the Minkowski action (3) by parts yields the on-shell part of action as

$$\begin{aligned} S_{os}= & {} \int \sqrt{-g}d^5x\big (-\nabla _\mu \left( \psi ^*(g^{\mu \nu }+kG^{\mu \nu }) D_\nu \psi +\frac{1}{2}A_\nu F^{\mu \nu }\right) \\&-\frac{iq}{2}\int \sqrt{-g}d^5xA_\nu (g^{\mu \nu }+kG^{\mu \nu })\\&(\psi (D_\mu \psi )^*-\psi ^*D_\mu \psi ) \big ) \\= & {} -\frac{V_3}{T} \sqrt{h} n_r\left( \psi ^*(g^{\mu r}+kG^{\mu r}) D_\mu \psi +\frac{1}{2}A_\mu F^{r\mu }\right) \Big |_{r\rightarrow \infty } \\&-\frac{V_3}{T}\frac{iq}{2}\int \sqrt{-g}A_\nu (g^{\mu \nu }+kG^{\mu \nu })\\&(\psi (D_\mu \psi )^*-\psi ^*D_\mu \psi )dr, \end{aligned}$$

where we have taken into account \(\int d^3x=V_3\), and also Eqs. (4) and (5). Keep in mind that \(S_E=-S_{os}\), the density of the grand potential reads

$$\begin{aligned} \frac{\Omega }{V_3}=\frac{-TS_{os}}{V_3}=-\mu \rho +\frac{1}{2}q^2\int ^\infty _{r_+}r{\mathcal {C}}_3\phi ^2\psi ^2 dr. \end{aligned}$$
(11)

Due to the existence of the coefficient \({\mathcal {C}}_3\), it is clear that the Horndeski parameter k will affect the grand potential. Especially, in the case of \(k=0\), Eq. (11) returns to the standard AdS case [29]. Next, we typically display the grand potential with respect to the chemical potential for the case of \(\Delta =\frac{9}{4},\frac{5}{2},3,\frac{7}{2}\) in the right panel of Fig. 2, from which we can observe that near the critical point, the superconducting curve stretches out from the insulator horizontal line smoothly with the increasing chemical potential, which means that the system indeed suffers from a second-order phase transition at the critical chemical potential, and thus agrees with the behavior of the condensate in Fig. 1. What is more, the value of the grand potential of the superconducting state is always lower than the one of the normal state, which means that above the critical point, the superconducting state is indeed thermodynamically stable. In addition, the behaviors of the other values of the Horndeski parameter in \(0\le k\le 1\) are similar to the case in Fig. 2. The above results uphold clearly the numerical results about the condensate and charge density.

Fig. 3
figure 3

The left panel represents the imaginal part of frequency dependent conductivity with \(\Delta =3\) and \(\frac{\mu }{\mu _c}\approx 1,~1.5,~2\) (from left to right), while the right panel represents the one with \(\frac{\mu }{\mu _c}\approx 2\) and \(\Delta =\frac{9}{4},~\frac{5}{2},~\frac{7}{2}\) (from right to left)

Full size image

As we all know, the infinite DC conductivity is a typical character of the superconductor. So it is meaningful to study the conductivity to check whether the hairy state is indeed superconducting state. According to the gauge/gravity duality, we should calculate an electromagnetic perturbation in the hairy soliton to obtain the retarded current-current two-point function. Concretely, we turn on the perturbation \(\delta A=A_x(r)e^{-i \omega t}\), and thus obtain the linear equation as

$$\begin{aligned} A_x''+\left( \frac{3}{r}+\frac{f'}{f}\right) A_x'+\frac{\omega ^2}{r^4f}A_x-\frac{{\mathcal {C}}_3\psi ^2}{r^2f}A_x=0. \end{aligned}$$
(12)

In order for \(A_x\) to be finite at the tip, we take the ansatz of \(A_x\) near the tip

$$\begin{aligned} A_x(r)= & {} 1+A_{x1} (r-r_0)+A_{x2} (r-r_0)^2\nonumber \\&+A_{x3}(r-r_0)^3+\cdots . \end{aligned}$$
(13)

where \(A_{x1}\), \(A_{x2}\) and \(A_{x3}\) are all constants and the leading term is taken to be unity due to the linearity of the equation for \(A_x\). At the boundary \(r\rightarrow \infty \), the asymptotical expansion of \(A_x\) is of the form

$$\begin{aligned} A_x(r)= A^{(0)}+\frac{ A^{(2)}}{r^2}+\frac{ A^{(0)} \omega ^2}{2r^2}\ln {\xi r}+\cdots , \end{aligned}$$
(14)

where \(A^{(i)}\), and \(\xi \) are all constants. From the gauge field perturbation we can then obtain the Green function as

$$\begin{aligned} G^R(\omega )=-\lim _{r\rightarrow \infty }fr^3 \frac{A'_x}{ A_x}=2\frac{A^{(2)}}{A^{(0)}}-\frac{\omega ^2}{2}. \end{aligned}$$
(15)

It should be noted that we have removed the logarithmic divergence by the holographic renormalization [8]. Hence, the AC conductivity reads

$$\begin{aligned} \sigma (\omega )= & {} \frac{1}{i \omega }G^R(\omega )=\frac{1}{i \omega }\left( 2\frac{A^{(2)}}{A^{(0)}}-\frac{\omega ^2}{2}\right) . \end{aligned}$$
(16)

In Fig. 3, we typically show the imaginal part of conductivity as a function of the frequency for different values of chemical potential and \(\Delta \), from which some remarks are in order. In term of the left panel, the imaginal part of the conductivity vanishes at the critical chemical potential, which corresponds to the finite conductivity. However, when the chemical potential increases away from the critical point, such as \(\frac{\mu }{\mu _c}\approx \frac{3}{2},~2\), a clear pole appears in the low frequency region, which suggests the infinite DC conductivity as expected from the superconducting state. Meanwhile, the value of the location for the second pole of conductivity increases with the larger chemical potential, which implies that the larger chemical potential increases the energy of quasiparticle excitation. As for the right panel, due to the fact that all curves are from superconducting state, it is reasonable that there always exists a pole in the low frequency. Furthermore, for the fixed ratio of the chemical to the critical value, the location of the second pole moves toward left when one increases the value of \(\Delta \). In addition, for all cases, we find the behavior of the conductivity is independent of the Horndeski correction.

2.2 Analytical part

To back up the above numerical results, especially, the effects of the Horndeski correction on the critical chemical potential and the condensate, we construct the s-wave insulator/superconductor model by the analytical S-L method. Concretely, we need resolve analytically the coupled differential equations (7) and (8) with the same boundary conditions as the ones in Sect.  2.1. For simplicity, by introducing a new variable \(z=\frac{r_0}{r}\), Eqs. (7) and (8) can be rewritten as

$$\begin{aligned}&\psi ''(z)-\frac{3+z^4}{z-z^5}\psi '(z)+\left( \frac{\phi (z)^2}{1-z^4}-\frac{m^2}{(1+6 k) z^2 \left( 1-z^4\right) }\right) \nonumber \\&\psi (z)=0, \end{aligned}$$
(17)
$$\begin{aligned}&\phi ''(z)-\frac{1+3 z^4}{z-z^5}\phi '(z)-\frac{2 (1+6 k) \psi ^2}{z^2 \left( 1-z^4\right) } \phi (z)=0, \end{aligned}$$
(18)

where the prime represents the derivative with respect to the new variable z.

In the normal phase, \(\psi (r)= 0\), the general solution \(\phi (r)\) from Eq. (18) is of the form

$$\begin{aligned} \phi (u)={\mathcal {C}}_6 +{\mathcal {C}}_7\log \frac{1+z^2}{1-z^2}, \end{aligned}$$
(19)

where \({\mathcal {C}}_6\) and \({\mathcal {C}}_7\) are two constants. As we have analyzed in Sect. 2.1, we take \({\mathcal {C}}_7=0\) in order for the gauge field to be finite at the tip via the Neumann-like boundary condition [29, 68, 69]. Hence, the constant \({\mathcal {C}}_6=\mu \) is regarded as the chemical potential in the dual field theory. Obviously, the charge density vanishes in the normal phase, which agrees well with the numerical results in Fig. 1.

When the chemical potential goes slightly beyond the critical point, the scalar condensate begins to condense and can be expressed as

$$\begin{aligned} \psi = \langle {\mathcal {O}}\rangle z^\Delta F(z), \end{aligned}$$
(20)

where F(z) is a function to be determined with the boundary condition \(F(0)=1\). Plugging Eq. (20) in to Eq. (17) yields the equation of F(z) as

$$\begin{aligned}&F''(z)+\frac{1}{z}\left( 2 \Delta -\frac{3+z^4}{1-z^4}\right) F'(z) \nonumber \\&\quad +\left( \frac{\Delta (1+6 k) \left( \Delta \left( z^4-1\right) +4\right) +m^2}{(1+6 k) z^3 \left( z^4-1\right) }+\frac{\mu _c ^2}{1-z^4}\right) F(z)=0\nonumber \\\ \end{aligned}$$
(21)

Multiplying the factor \({\mathcal {T}}=z^{2\Delta -3}(1-z^4)\) to the above equation reads the S-L eigenvalue equation as

$$\begin{aligned} \frac{d}{dz}({\mathcal {T}} F')-{\mathcal {P}}F +\mu _c^2 {\mathcal {Q}}F=0, \end{aligned}$$
(22)

where \({\mathcal {P}}\) and \({\mathcal {Q}}\) are given by

$$\begin{aligned} {\mathcal {P}}= & {} \frac{z^{2 \Delta -6} \left( \Delta (1+6 k) \left( \Delta \left( z^4-1\right) +4\right) +m^2\right) }{1+6 k},\nonumber \\ {\mathcal {Q}}= & {} z^{2 \Delta -3}. \end{aligned}$$
(23)

The minimal eigenvalue \(\mu _c^2\) is obtained by minimizing the following expression with respect to the coefficient \(\alpha \)

$$\begin{aligned} \mu _c^2=\frac{\int _0^1 ({\mathcal {T}} {F'}^2-{\mathcal {P}}F^2)dz}{\int ^1_0 {\mathcal {Q}} F^2 dz} \end{aligned}$$
(24)

with the boundary condition \(F'(0)=0\) [68, 69]. According to the boundary conditions for F(z), i.e., \(F(0)=1\) and \(F'(0)=0\), we introduce a trial function

$$\begin{aligned} F=F_\alpha (z)\equiv 1-\alpha z^2, \end{aligned}$$
(25)

by substituting which into Eq. (24) we can read off the critical chemical potential. In order to compare the analytical results with the numerical ones, we plot the critical chemical potential \(\mu _c\) versus the Horndeski parameter k in the form of curve in the left plot of Fig. 2 and list the results in Table 1. It is observed that the analytical results agree well with the numerical ones, which means that S-L method is still powerful in the superconductor with Horndeski correction.

When the chemical potential is slightly above the critical point, the condensate \(\langle {\mathcal {O}}\rangle \) is small, so we can expand the gauge field \(\phi (z)\) in the form of the small parameter \(\langle {\mathcal {O}}\rangle \) as

$$\begin{aligned} \phi (z)=\mu _c+\langle {\mathcal {O}}\rangle \chi (z)+\cdots . \end{aligned}$$
(26)

Combining with Eq. (20), we have the equation of \(\chi (z)\) as

$$\begin{aligned} \chi ''-\frac{1+3 z^4}{z-z^5}\chi '-\frac{2 (1+6 k) \mu _c \langle {\mathcal {O}}\rangle \left( 1-\alpha z^2\right) ^2 z^{2 \Delta -2}}{1-z^4}=0.\nonumber \\ \end{aligned}$$
(27)

Defining \(T(z)= \frac{1-z^4}{z}\), Eq. (27) can be rewritten as

$$\begin{aligned} (T\chi ')'=2 (1+6 k) \mu _c \langle {\mathcal {O}}\rangle \left( 1-\alpha z^2\right) ^2 z^{2 \Delta -3}. \end{aligned}$$
(28)

At the boundary \(z\rightarrow 0\), the function \(\chi (z)\) can be further expanded as

$$\begin{aligned} \chi (z)=\chi (0)+\chi ^\prime (0)z+\frac{1}{2}\chi ^{\prime \prime }(0) z^2+\frac{1}{6}\chi ^{\prime \prime \prime }(0)z^3+\cdots \end{aligned}$$
(29)

Substituting Eq. (29) into Eq. (26) and thus comparing it with Eq. (10), we can get

$$\begin{aligned} \langle {\mathcal {O}}\rangle= & {} \frac{1}{\chi (0)}(\mu -\mu _c), \end{aligned}$$
(30)
$$\begin{aligned} \rho= & {} -\frac{\chi ''(0)}{2}\langle {\mathcal {O}}\rangle =-\frac{1}{2}\frac{\chi ''(0)}{\chi (0)}(\mu -\mu _c), \end{aligned}$$
(31)

Obviously, the following main task is to calculate the values of \(\chi ''(0)\) and \(\chi (0)\). By using the boundary condition \(\chi '(0)=0\) [68, 69], integrating Eq. (28) reads

$$\begin{aligned} (T\chi ')|^z_1= & {} (1+6 k)\mu _c \langle {\mathcal {O}}\rangle \int ^{u=z}_{u=1}2\left( \alpha u^2-1\right) ^2 u^{2 \Delta -3}\nonumber \\= & {} (1+6 k)\mu _c \langle {\mathcal {O}}\rangle {\mathcal {M}}(\alpha ,\Delta , z). \end{aligned}$$
(32)

Further integrating the above equation, we can obtain the value of \(\chi (0)\) as

$$\begin{aligned} \chi (0)= & {} (1+6 k)\mu _c \langle {\mathcal {O}}\rangle \int ^0_1\frac{{\mathcal {M}}(\alpha ,\Delta , z)}{T}dz\nonumber \\= & {} (1+6 k)\mu _c \langle {\mathcal {O}}\rangle {\mathcal {N}}(\alpha ,\Delta ). \end{aligned}$$
(33)

Combining Eq. (33) with Eq. (30), we can obtain the scalar condensate

$$\begin{aligned} \langle {\mathcal {O}}\rangle =\frac{1}{\sqrt{(1+6k)\mu _c{\mathcal {N}}}}\sqrt{\mu -\mu _c}. \end{aligned}$$
(34)

Considering Eq. (27) up to the zero order of \(\langle {\mathcal {O}}\rangle \), we can obtain

$$\begin{aligned} \chi ''(0)= & {} \frac{1+3 z^4}{z-z^5}\chi '|_{z\rightarrow 0}\approx \frac{\chi '}{z}|_{z\rightarrow 0}=(T\chi ')(0)\nonumber \\= & {} (1+6 k)\mu _c \langle {\mathcal {O}}\rangle {\mathcal {M}}(\alpha ,\Delta , 0). \end{aligned}$$
(35)

Thus we can rewrite the charge density as

$$\begin{aligned} \rho =-\frac{1}{2}\frac{\chi ''(0)}{\chi (0)}(\mu -\mu _c)=-\frac{1}{2}\frac{ {\mathcal {M}}(\alpha ,\Delta , 0)}{{\mathcal {N}}(\alpha ,\Delta )}(\mu -\mu _c). \end{aligned}$$
(36)

We calculate and list the values of \(\frac{1}{\sqrt{(1+6k)\mu _c{\mathcal {N}}}}\) for Eq. (34) and \(-\frac{1}{2}\frac{{\mathcal {M}}(\alpha ,\Delta , 0)}{{\mathcal {N}}(\alpha ,\Delta )}\) for Eq. (36) in Table 1 to compare with the numerical results.

It is obvious that the analytical results agree with the numerical ones at the same order, especially, the trend of the effect for Horndeski parameter on the coefficient is consistent with each other. What is more, the results in the case of \(m^2=-\frac{15}{4}\) recover the ones in Refs. [29, 35, 68, 69].

3 Conductor/superconductor phase transition

The authors in Ref. [54] studied the s-wave conductor/superconductor phase transition model with Horndeski correction in the probe limit by the numerical method and found that the increasing Horndeski parameter decreases the critical temperature and the phase transition is always second order. To check the reasonability of the numerical results, we will restudy the s-wave model by the analytical S-L method in this section.

Firstly, we give the four-dimensional Schwarzshild AdS planer black hole as

$$\begin{aligned} ds^2= & {} -r^2f(r)dt^2+\frac{dr^2}{r^2f(r)}+r^2(dx^2+dy^2),\nonumber \\ f(r)= & {} 1-\frac{r_+^3}{r^3} \end{aligned}$$
(37)

where \(r_+\) denotes the location of event horizon corresponding to the Hawking temperature \(T=\frac{3r_+}{4\pi }\). Considering the Lagrangian density (3) and the ansatz in terms of the scalar field and the gauge field (6), we can derive the equations of motion as

$$\begin{aligned}&\psi ''+\frac{{\mathcal {C}}_8 }{ r f{\mathcal {C}}_9}\psi '+\left( \frac{ q\phi ^2}{r^4 f}-\frac{m^2 }{ r^2 f{\mathcal {C}}_9}\right) \psi =0,\end{aligned}$$
(38)
$$\begin{aligned}&\phi ''+\left( \frac{2}{r}+\frac{f'}{f}\right) \phi '-\frac{2q^2{\mathcal {C}}_9\psi ^2}{r^2f}\phi = 0. \end{aligned}$$
(39)

where \({\mathcal {C}}_8=r f'(r) \left( k r f'(r)+1\right) +f(r) \left( k r^2 f''(r)\right. \left. +11 k r f'(r)+4\right) +12 k f(r)^2\), \({\mathcal {C}}_9=1+3 k f(r)+ k r f'(r)\), a prime stands for the derivative with respect to r. Obviously, Eqs. (38) and (39) are the same to Eqs. (13) and (14) with \(\kappa =0,~c_1=0,~c_2=0,~\xi =0\) in Ref. [56]. It should be noted that by redefining \(g(r)=r^2f(r)\), Eqs. (38) and (39) restore to Eqs. (23) and (24) in Ref. [54] and Eqs. (14) and (15) with \(\tau =0\) in Ref. [57].

At the boundary \(r\rightarrow \infty \), \(\psi (r)\) and \(\phi (r)\) behave as

$$\begin{aligned} \psi (r)=\frac{\psi _1}{r^{\Delta _-}}+\frac{\psi _2}{r^{\Delta _+}}+\cdots , \ \ \ \phi (r)=\mu -\frac{\rho }{r}+\cdots , \end{aligned}$$
(40)

where \(\Delta _\pm =\frac{3}{2} \pm \frac{1}{2}\sqrt{9+\frac{4m^2}{1+3k}}\) consistent with Eq. (17) in Refs. [56, 57], \(\psi _1\), \(\psi _2\), \(\mu \) and \(\rho \) are all constants. According to the gauge/gravity duality, the explanations of the constants (\(\psi _1\), \(\psi _2\), \(\mu \) and \(\rho \)) are the same with the ones for the insulator/superconductor model in section 2. In order to compare the current model with the ones in Ref. [54], we choose \(m^2=-2\) and restrict the Horndeski parameter in the range \(-0.01\le k\le 1\).

By means of the new variable \(z=\frac{r_+}{r}\), Eqs. (38) and (39) can be rewritten as

$$\begin{aligned}&\psi ''(z)-\frac{2+z^3}{z-z^4}\psi '(z)\nonumber \\&\quad +\left( \frac{\phi (z)^2}{\left( z^3-1\right) ^2}-\frac{m^2}{(3 k+1) z^2\left( 1-z^3\right) }\right) \psi (z)=0, \end{aligned}$$
(41)
$$\begin{aligned}&\phi ''(z)-\frac{2 (3 k+1) \psi (z)^2}{z^2\left( 1-z^3\right) }\phi (z) = 0, \end{aligned}$$
(42)

where the prime represents the derivative with respect to the variable z.

At the critical point, the scalar condensate vanishes, we can thus read off the solution of the gauge field as

$$\begin{aligned} \phi (z)=\lambda r_+(1-z), \lambda =\frac{\rho }{r^2_{+c}}, \end{aligned}$$
(43)

where \(r_{+c}\) represents the location of the horizon at the critical temperature.

Near the critical point, similar to the soliton case (20), we can express the scalar field \(\psi (z)\) as

$$\begin{aligned} \psi (z)= \frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta } z^\Delta F(z). \end{aligned}$$
(44)

Combining Eqs. (43) and (44), Eq. (41) can be written as the S-L eigenvalue equation

$$\begin{aligned} \frac{d}{dz}({\mathcal {T}} F')-{\mathcal {P}}F +\lambda ^2 {\mathcal {Q}}F=0, \end{aligned}$$
(45)

where the coefficients \({\mathcal {T}}\), \({\mathcal {P}}\) and \({\mathcal {Q}}\) are as follows

$$\begin{aligned} {\mathcal {T}}= & {} \left( 1-z^3\right) z^{2 (\Delta -1)},{\mathcal {P}}=\frac{ \Delta (1+3 k) \left( 3-\Delta \left( 1-z^3\right) \right) +m^2}{z^{4-2 \Delta }(1+3k)},\nonumber \\ {\mathcal {Q}}= & {} \frac{(1-z) z^{2 \Delta -2}}{1+z+z^2}. \end{aligned}$$
(46)

Thus \(\lambda ^2\) is obtained by minimizing the following expression as

$$\begin{aligned} \lambda ^2=\frac{\int _0^1 ({\mathcal {T}} {F'}^2-{\mathcal {P}}F^2)dz}{\int ^1_0 {\mathcal {Q}} F^2 dz}. \end{aligned}$$
(47)

Given the boundary conditions \(F(0)=1,~F'(0)=0\) [10, 35, 49], we take also the form of trial function (25) and obtain the value of \(\lambda \). Thus the critical temperature can be written as

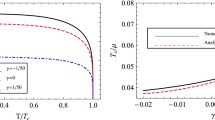
$$\begin{aligned} T_c=\frac{3}{4\pi }r_{+c}=\frac{3}{4\pi }\sqrt{\frac{\rho }{\lambda }}. \end{aligned}$$
(48)

The concrete results of the critical temperature are listed in Table 2,

Table 2 The critical temperature and the coefficient \({\mathcal {C}}_{10}\) of the critical behavior for the condensate from the analytical S-L method
Full size table
Table 3 The critical temperature and the coefficient \({\mathcal {C}}_{11}\) of the critical behavior for the condensate with \(\Delta _+\) from the analytical S-L method
Full size table

from which we can see clearly that the critical temperature decreases with the increasing Horndeski parameter k, which means that the larger Horndeski correction makes the conductor/superconductor phase transition more difficult to occur. Meanwhile, the analytical results agree well with the numerical ones in Ref. [54]. In particular, as \(k=0\), the result restores to the standard case in Refs. [7, 8, 10, 35, 49]

Below (but close to) the critical temperature, the condensate \(\frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta }\) is very small, by using which we expand the gauge field (43) in the form of the small parameter as

$$\begin{aligned} \frac{\phi (z)}{r_+}=\lambda (1-z)+\frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta }\chi (z). \end{aligned}$$
(49)

Substituting Eq. (49) into Eq. (42) yields the equation of \(\chi (z)\) at the linear order of \(\langle {\mathcal {O}}\rangle \) as

$$\begin{aligned} \chi ''(z)=2 (3 k+1) \lambda \frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta } \frac{\left( 1-\alpha z^2\right) ^2 z^{2 \Delta -2}}{z^2+z+1} \end{aligned}$$
(50)

with the boundary condition \(\chi (1)=0=\chi '(1)\). Integrating Eq. (50), we can obtain

$$\begin{aligned} \chi '(0)= & {} -2 (3 k+1) \lambda \frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta } \int ^1_0\frac{\left( 1-\alpha z^2\right) ^2 z^{2 \Delta -2}}{z^2+z+1}\nonumber \\= & {} -2 (3 k+1) \lambda \frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta } {\mathcal {W}}(\alpha , \Delta ). \end{aligned}$$
(51)

By further expanding Eq. (49) at the infinite boundary (\(z\rightarrow 0\)) and comparing the linear order of z with Eq. (40), we can

$$\begin{aligned} \frac{\langle {\mathcal {O}}\rangle }{r_+^\Delta }=\frac{1}{\chi '(0)}\left( \lambda -\frac{\rho }{r_+^2}\right) . \end{aligned}$$
(52)

Take notice of the value of \(\chi '(0)\) in Eq. (52), the condensate can be expressed as

$$\begin{aligned} \frac{\langle {\mathcal {O}}\rangle }{{\sqrt{\rho }}^\Delta }\approx \frac{1}{\sqrt{(1+3k){\mathcal {W}}(\alpha , \Delta )\lambda ^\Delta }}\sqrt{1-\frac{T}{T_c}}={\mathcal {C}}_{10}T_c^\Delta \sqrt{1-\frac{T}{T_c}}.\nonumber \\ \end{aligned}$$
(53)

The coefficient \({\mathcal {C}}_{10}\) are listed in Table 2, from which we can find that the coefficient agrees with the numerical results in Ref. [54] at the same order, especially, the monotone decreasing trend as a function of the Horndeski parameter k.

For completeness, we also calculate the critical temperature of the conductor/superconductor phase transition in the five-dimensional AdS black hole with the Horndeski correction by the S-L method in the probe limit. Concretely, in order for our results to be comparable with the ones in the previous literature, we take the mass squared of the scalar field as \(m^2=-3\), and thus the scaling dimension of the scalar operator reads \(\Delta _\pm =2 \pm \sqrt{4+\frac{m^2}{1+6k}}=2 \pm \sqrt{4-\frac{3}{1+6k}}\). The critical temperature for various value of the Horndeski parameter k is listed in Table 3.

It is shown that the critical temperature decreases with the increasing Horndeski correction, which is similar to the four-dimensional case. In particular, the critical value for the vanishing Horndeski parameter k restores to the one in Refs. [8, 35]. Meanwhile, we also consider the critical behavior of the scalar condensate. It is found that the critical exponent of the condensate is still \(\frac{1}{2}\), which means the second order phase transition at the critical point. What is more, we derive the coefficient (\({\mathcal {C}}_{11}\)) of the condensate near the critical temperature (\( \frac{\langle {\mathcal {O}}\rangle }{{\rho }^{\Delta /3}}\approx {\mathcal {C}}_{11}T_c^\Delta \sqrt{1-\frac{T}{T_c}}\)) and also list the value of \({\mathcal {C}}_{11}\) in Table 3. It is observed that the coefficient increases with the Horndeski correction on the whole, which is different from the case in the four-dimensional black hole. Even though, the value with \(k=0\) agrees well with the analytical one in Ref. [35] and at the same order with the numerical one in Ref. [8].

4 Conclusions and discussions

In this paper, at the probe approximation, we have constructed the holographic s-wave insulator/superconductor model in the five-dimensional AdS soliton with the Horndeski correction via both numerical and analytical methods. Then, we realized analytically the corresponding conductor/superconductor model in the four- and five-dimensional AdS black hole. The effects of the Horndeski parameter k on the superconductor models were studied and the main conclusions of which are as follows.

In term of the insulator/superconducotor model, when the mass squared is fixed, the critical chemical potential increases with the larger Horndeski parameter k, which means that the increasing Horndeski correction hinders the superconductor phase transition. Meanwhile, the critical exponent of the condensate is \(\frac{1}{2}\), which suggests that the system suffers from a second-order phase transition at the critical point, and thus be upheld by the behavior of the grand potential. What is more, near the critical point, the charge density increases linearly with the chemical potential, which is the university of holographic insulator/superconductor model. Furthermore, beyond the critical point, the imaginal part of conductivity displays an obvious pole at the low frequency, which implies that the system is indeed at superconducting state above the critical chemical potential. In addition, the stability of the hairy state is checked by the comparison of the grand potential with the no hair state. The analytical results such as the value of the critical chemical potential, the critical exponents of condensate \(\langle {\mathcal {O}}\rangle \) and charge density \(\rho \) agree with the numerical results, and the coefficients of \(\langle {\mathcal {O}}\rangle \) and \(\rho \) are qualitatively the same with the numerical ones near the critical point. As for the conductor/superconductor model, our analytical results showed that the increasing Horndeski parameter k hinders the superconductor phase transition. Especially, the analytical results in the four-dimensional case are consistent with the previous numerical results in Ref. [54]. Even though the present calculation is restricted to some special cases of the parameter space of mass squared and Horndeski correction, we can obtain the qualitatively same results for other values of Horndeski parameter k.

Comprehensively speaking, the increasing Horndeski correction hinders both superconducting phase transition models for fixed mass squared of scalar field, which is reasonable, because in this case the larger k will increases the effective mass of the scalar field and the scaling dimension \(\Delta \) of the operator \( {\mathcal {O}}\) and thus prevent the instability occurring. On the contrary, if we do not fix the mass squared \(m^2\) but the scaling dimension \(\Delta \) during the calculation (i.e., the \(\frac{m^2}{1+6k}\) is constant), by rescaling \((1+6k)\psi ^2\rightarrow {\bar{\psi }}^2\), we can see clearly that the equations of motion for our insulator/superconductor model do not depend on the Horndeski correction, and thus the critical value and grand potential as well as the conductivity are independent of Horndeski correction. However, it should be noted that the phenonemon with fixed scaling dimension \(\Delta \) might only occur in the probe limit. In the near future, we will try to generalize the insulator/superconductor model from the probe limit to the backreaction case, and further study the effect of the Horndeski correction on the phase transition for fixed mass squared and scaling dimension \(\Delta \), respectively, which will shed light on the understanding of the effect of Horndeski correction on our superconductor model.