Abstract
We consider the presence of odd powers of the speed of light c in the covariant nonrelativistic expansion of General Relativity (GR). The term of order c in the relativistic metric is a vector potential that contributes at leading order in this expansion and describes strong gravitational effects outside the (post-)Newtonian regime. The nonrelativistic theory of the leading order potentials contains the full non-linear dynamics of the stationary sector of GR.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The covariant nonrelativistic approximation to GR as introduced by Dautcourt [1] has recently been revisited [2,3,4,5,6,7,8,9]. The approximation amounts to an expansion of the relativistic metric in inverse powers of the speed of light c and for this reason we will refer to it as the large c expansion. Originally [1, 2] the aim was simply to provide a manifestly coordinate invariant version of the post-Newtonian expansion. But in [3] it was pointed out that the large c expansion naturally allows the inclusion of strong gravitational effects which are not capturedFootnote 1 in the post-Newtonian setup. That the large c expansion extends the post-Newtonian expansion is no surprise, since the latter is not only a nonrelativistic, but also a weak field expansion [10]. This feature of effectively describing some strong gravitational effects suggests the large c expansion could have interesting phenomenological applications. This remains largely unexplored, but we make a few initial observations in Sect. 4.4. Still this approach has already led to some interesting theoretical progress, such as the formulation of a variational principle for Newtonian gravity [5] and a better understanding of the geometry underlying nonrelativistic gravity [3, 4]. Furthermore it has some conceptual value, in that it clearly separates relativistic effects from strong gravity effects [8]. The work on the large c expansion, which by construction provides a nonrelativistic gravity theory descendant from GR, is also of value to the recent explorations of more general theories of nonrelativistic gravity. In that context we can mention for example recent work on 3d nonrelativistic gravity [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], Lifshitz Holography [28,29,30,31], nonrelativistic string theory [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] and condensed matter and fluid mechanics applications [48,49,50,51,52,53,54,55,56,57]. In parallel the symmetries underlying such theories have been further investigated [58,59,60,61,62,63,64,65,66,67].
Previous work on the large c expansion has focused on an expansion of the metric in inverse powers of \(c^2\). This is a self-consistent assumption in the gravitational sector since gravitational potentials of even power in c can not source potentials of odd power in c. Under an additional weak field assumption, together with consideration of some physical constraints on energy-momentum and an appropriate coordinate choice, one can show that odd terms in the relativistic metric can appear only at subleading order [1, 10]. In case one does not make the weak field assumption the presence of terms with an odd power of c has to date remained unexplored and in this work we initiate its study. This is motivated by the observation that energy-momentum that sources the strong time dilation potential – the twistless torsion of [3] – will also source the leading order odd term in the metric when it is dynamic [4, 68].
The main result of this paper is the set of equations presented in Table 4. These are the Einstein and conservation equations, at leading order in an expansion of inverse powers of c, with the only assumption made that the relativistic metric and the energy-momentum tensor are of the form \(g_{\mu \nu }\sim c^2\tau _\mu \tau _\nu +{\mathcal {O}}(c)\,,\) \(T_{\mu \nu }\sim c^{6}\tau _\mu \tau _\nu +{\mathcal {O}}(c^{5})\). The physical fields at the leading order are a scalar potential \(\Psi \), a vector potential \(C_{\dot{\mu }}\) and a spatial metric \(k^{\mu \nu }\), which in appropriate coordinates correspond to a relativistic metric
In case the fields \((\Psi , C_{\dot{\mu }}, k^{\mu \nu })\) are time independent the leading part of the metric above describes a generic stationary metric and indeed the leading order nonrelativistic equations in Table 4 can be identified with the Einstein equations for stationary metrics. Absence of time derivatives in the leading order equations in Table 4 implies that more generally at leading order in the large c expansion any solution to Einstein equations will be of the form of a stationary metric, but with integration constants replaced by an arbitrary function of time. This extra time dependence will lead to source terms in the subleading equations. This observation gives the large c expansion the interpretation of an expansion around the stationary sector of GR. This generalizes the observation of [7] that the large \(c^2\)-expansion has the interpretation of an expansion around the static sector of GR.
If one chooses the leading order stationary metric to be Minkowski space the large c expansion reduces to the standard post-Newtonian one. But more generally one can choose any stationary metric (with time-dependent integration constants) as the starting point for the expansion, extending it into the strong gravitational regime. We illustrate this explicitly using the example of the Kerr metric.
In our derivation of the leading order equations we make use of the Newton–Cartan formalism. We make a number of comments and observations that are new with respect to [1,2,3,4]. One main novelty is that we leave the leading time-like component of the relativistic metric – denoted \({\overset{\,{(-2)}}{A}}{}\) – free, rather than choosing it to be \(-1\) as was done previously. This clarifies the structure of the various potentials and equations appearing at arbitrary order, see Table 2. Additionaly there now appears an extra local scaling symmetry under which \({\overset{\,{(-2)}}{A}}{}=-1\) is a particular choice of gauge. We point out that there is another appealing choice of gauge, namely one where the torsion of the Newton–Cartan structure vanishes.
In addition to this new scaling symmetry we also consider the Milne boost symmetry inherent to the Newton–Cartan formalism and in particular carefully analyze the diffeomorphism symmetry at various orders. This leads us to introduce a new set of variables and to reorganize the equations, see Table 3, simplifying them greatly. This suggests that, especially if one would attempt to go to higher orders, the large c expansion can be formulated more efficiently in an alternative set of variables rather then those used in [1,2,3,4].
The paper is organized as follows. In Sect. 2 we review some of the Newton–Cartan formalism we need, introduce a convenient dotted index notation and prepare GR towards a covariant nonrelativistic expansion. Section 3 concerns itself with this expansion: we define it precisely, discuss its symmetries and present the leading order equations upon the inclusion of odd terms, our main result. We then comment on various properties of these equations in Sect. 4. We present an example, discuss various gauge choices and provide a variational principle. Appendices A and B contain some technicalities, while appendix C contains a three parameter generalization of the nonrelativistic algebra of [4, 5], which we believe is new. We take the non-uniqueness of the nonrelativistic local translation algebra as an indication that the large c expansion is most naturally expressed in terms of metric variables transforming under expanded diffeomorphism symmetries rather than vielbein variables transforming under expanded Poincaré symmetries.
2 GR in Newton–Cartan split form
A diffeomorphism invariant formulation of the nonrelativistic approximation to GR – the large c expansion – is naturally formulated using the language of Newton–Cartan geometry [1,2,3,4]. One feature of Newton–Cartan geometry is that it provides a local split of time versus space, something expected in a nonrelativistic theory.
Anticipating these facts we choose to ’prepare’ GR towards this expansion by performing this split in space vs time already at the relativistic level. We do this by introducing an arbitrary Newton–Cartan structure \((\tau _\mu , h^{\mu \nu })\) in addition to the relativistic metric \(g_{\mu \nu }\). Later, once we perform the expansion, this artificial Newton–Cartan structure will be given a natural interpretation by equating it to some of the leading order components of \(g_{\mu \nu }\). Our approach is similar in spirit to that of [4, 9], but differs in that the Newton–Cartan structure we introduce will be chosen to be c independent.
In this section we first discuss how any tensorial quantity can be split along temporal and spatial directions using a Newton–Cartan structure and introduce a dotted index notation to represent this split in a convenient way. In the second part of the section we apply such a split to the main ingredients of GR: the metric, energy-momentum tensor and their equations of motion.
2.1 Newton–Cartan split: generalities
We will restrict the discussion in this paper to 1+3 dimensions – a generalization to arbitrary dimensions is straightforward – and work with coordinates \(x^\mu \), \(\mu =0,1,2,3\).
We’ll define a Newton–Cartan structure \((\tau _\mu , h^{\mu \nu })\) as a positive semi-definite, symmetric 2-tensor \(h^{\mu \nu }\) together with a zero eigencovector \(\tau _\mu \) that is unique up to rescaling, i.e.
The one-form \(\tau _\mu \) is often referred to as the clock form as it sets the direction of time, while \(h^{\mu \nu }\) encodes a purely spatial metric [69, 70].
Given a Newton–Cartan structure one can introduce additional fields \(\tau ^\mu \) and \(h_{\mu \nu }\) such that
Note that \(\tau ^\mu \) and \(h_{\mu \nu }\) are not unique for a given Newton–Cartan structure. This non-uniqueness can be interpreted as a gauge invariance of the formalism, the Milne boosts that we will discuss below. The equations (2) can also be read as the definition of two complementary projectors:
Using these, any tensor index can be decomposed into a temporal and spatial part, something we will refer to as a ’Newton–Cartan split’. For an arbitrary one-form \(U_\mu \) for example, such decomposition reads
Since we will perform such a Newton–Cartan split on essentially any tensor we will encounter it will be useful to introduce some more compact notation. We’ll write the temporal part of \(U_\mu \) as
and we will indicate the spatial projection by putting a dot on the projected index:
In this notation the decomposition (4) then simplifies to
Note that dotted indices contracted with \(\tau \) vanish, while the spatial components can be lowered and raised by h
This notation can be safely extended to higher rank tensors as long as they are either fully symmetric or anti-symmetric. For example for a (1,2)-tensor that is symmetric in its upper indices we get
We will reserve the raising and lowering of dotted indices with h as in (8) only for tensors where there will be no ambiguity in the notation. For example, note that in the split of \(V_\mu {}^{\nu \rho }\) above we have \(V^{{\dot{\mu }}{\dot{\nu }}}=\tau ^\rho h^\mu _\sigma h^\nu _\lambda V_\rho {}^{\sigma \lambda }\) and \(V_{{\dot{\mu }}}{}^{{\dot{\nu }}}=\tau _\rho h_{\mu }^\sigma h^\nu _\lambda V_\sigma {}^{\rho \lambda }\) and thus \(V^{{\dot{\mu }}{\dot{\nu }}}\ne h^{\mu \rho }V_{{\dot{\rho }}}{}^{{\dot{\nu }}}\).
Finally it is important to point out that we will not work with the most general type of Newton–Cartan structure, but rather assume that the clock form satisfies \(\partial _{[{\dot{\mu }}}\tau _{{\dot{\nu }}]}=0\). This condition can be expressed in three equivalent ways:
Geometrically these conditions guarantee the existence of a foliation by spatial hypersurfaces. Another interpretation is that this condition restricts the torsion of any connection compatible with the Newton–Cartan structure and for this reason (10) also goes under the name of twistless torsion [28]. We make this assumption on the Newton–Cartan structure from the beginning, anticipating compatibility with the expanded Einstein equations [3].
Note that from (10) it follows that
where furthermore
so that locally
The derivation of (10) and the other formulae above is shortly reviewed in appendix A.
2.2 Newton–Cartan split: GR
We take as our dynamical variables for GR a Lorentzian metric \(g_{\mu \nu }\) and the trace-reversed energy-momentum tensor \({\mathcal {T}}_{\mu \nu }\):
The dynamics is then provided by the Einstein equations, which we write as
The Bianchi identity satisfied by the Ricci tensor \(R_{\mu \nu }\) guarantees the conservation of energy-momentum, which is equivalent to
We then apply a Newton–Cartan split to each of these ingredients:
We will use a separate notation for the split of the metric and its inverse:
This A vs B notation is introduced to indicate that we will treat the A variables as independent fields, while the B fields are interpreted as fully determined in terms of the A’s through the condition that \(g^{\mu \rho }g_{\rho \nu }=\delta _\nu ^\mu \) :
with \(A_{{\dot{\mu }}{\dot{\nu }}}\) is the uniqueFootnote 2 solution to
The upshot of this Newton–Cartan split of GR can be found in Table 1.
3 The large c expansion
A manifestly diffeomorphism invariant approximation to GR can be constructed by expanding the relativistic metric and its inverse in inverse powers of the speed of light [1,2,3,4]:
Although it is consistent to assume all coefficients of odd powers to vanish – as was done in [1,2,3,4] – we will explore in this work the consequences of relaxing this assumption. The presence of non-vanishing coefficients for odd powers of c is motivated by the fact that these coefficients can be sourced in the equations of motion by certain types of energy-momentum [4, 68].
We will first discuss some generalities and then focus on the leading order, working out explicitly the dynamical equations to this order. Symmetries will play an important role in an appropriate organization of the result.
3.1 Setup and general observations
We will take a slightly different – but equivalent – approach than the one that was previously taken in [1,2,3,4]. We will perform the expansion not directly in terms of the relativistic metric as in (23), but rather expand the components as obtained after a Newton–Cartan split as in (20), see also Table 1. It should be stressed that the Newton–Cartan structure \(\tau _\mu \,, h^{\mu \nu }\) is taken to be independent of c.
Our expansion ansatz for the dynamical fields is then
This ansatz is based on a number of starting assumptions, equivalent to those of [1,2,3,4] with the exception that odd powers are allowed to be non-vanishing. In those previous works [1,2,3,4] the choice \({\overset{\,{(-2)}}{A}}{}=-1\) was made, but as we will explain below that is simply a choice of gauge for a local scaling symmetry in our formulation. Leaving \({\overset{\,{(-2)}}{A}}{}\) free has some advantages. In particular it makes manifest the fact that at each order in the expansion there appear two new triplets of fields, (\({\overset{\,{(k)}}{A}}{}\,, {\overset{\,{(k+1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(k+2)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}\)) and (\({\overset{\,{(k)}}{{\mathcal {T}}}}{}\,, {\overset{\,{(k+1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\,, {\overset{\,{(k+2)}}{{\mathcal {T}}}}{}_{{\dot{\mu }}{\dot{\nu }}}\)), all of which are a priori free to vary. In Table 2 we compare the potentials as we define them here, to the potentials as previously considered in [1,2,3,4]. In the formulation using the Newton–Cartan split it also becomes clear that the proper organization of the orders is not just by counting inverse powers of c, but rather that at a given order the powers of c depend on the number of spatial indices the field carries. The triplet (\({\overset{\,{(k)}}{A}}{}\,, {\overset{\,{(k+1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(k+2)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}\)) for example consists of coefficients of the powers \((c^{-k},c^{-k-1},c^{-k-2})\). This is something which was not properly appreciated in [1,2,3], but suggested by the results of [4, 5]. That this is indeed the more appropriate point of view is supported by the fact that the equations of motion – which we will further work out below – organize themselves in the following formFootnote 3:
One sees that if the expansion is truncated at order n, i.e. keeping only triplets of the form (\({\overset{\,{(k)}}{A}}{}\,, {\overset{\,{(k+1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(k+2)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}\)) and (\({\overset{\,{(k)}}{{\mathcal {T}}}}{}\,, {\overset{\,{(k+1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\,, {\overset{\,{(k+2)}}{{\mathcal {T}}}}{}_{{\dot{\mu }}{\dot{\nu }}}\)) with \(k\le n\), then the above set of equations for \(k\le n\) is consistent. Furthermore the set of equations has a hierarchic structure, in that one can solve them recursively in the order. The leading order corresponds to \(n=-2\) and will be worked out fully below.
Finally we should point out that since \(\tau _\mu {\overset{\,{(0)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}=0\) we can choose to identify the spatial part of the Newton–Cartan structure introduced in section (2.1) with it:
Translated back to the more familiar relativistic metric variables this amounts to
So once we start considering the large c expansion, we identify the Newton–Cartan structure that was artificially introduced in Sect. 2.1 with the leading coefficients of the relativistic metric and its inverse.
3.2 Symmetries
The relativistic theory we start from, GR, has as its symmetries simply the diffeomorphismsFootnote 4. These diffeomorphisms are however allowed to depend on the speed of light c, which implies that they will generate a new independent set of symmetries at each order of the expansion [2, 3]. In addition to the diffeomorphisms – and their descendants – there are two additional symmetries that appear into the expansion simply because the Newton–Cartan structure and decomposition we introduced in Sect. 2 have some redundancy: a nonrelativistic local boost symmetry and a local scaling symmetry. We now discuss the various symmetries in turn, in the next subsection they will be used to organize the LO equations.
3.2.1 Milne Boosts
Given a Newton–Cartan structure \((\tau _\mu ,h^{\mu \nu })\) the ’inverse’ fields \(\tau ^\mu \) and \(h_{\mu \nu }\) – defined to satisfy (2) – are not unique. An equivalent set of solutions to (2) is generated through the infinitesimal transformations
Note that this impliesFootnote 5 via (11, 13) that
Since the relativistic metric \(g_{\mu \nu }\) is independent of our choice of \(\tau ^\mu \) and \(h_{\mu \nu }\) used to split it, it follows that the components as defined in (20) must transform as
Since we choose \(\tau _\mu \,, \tau ^\mu \,, h^{\mu \nu }\) and \(h_{\mu \nu }\) to be c independent it follows that the parameter \(\chi _{\dot{\mu }}\) will be c independent and thus the action of the boost symmetry on the expanded fields is immediate:
Still, these are rather complicated transformations due to the rather lengthy expressions for the B’s in terms of the A’s once the order increases, see appendix B. On the leading triplet the action is very simple however:
The boost transformations of the leading order energy-momentum triplet are found to be
3.2.2 Scaling
A re-scaling of the clock form can be absorbed in the definitions of the A fields, while leaving \(g_{\mu \nu }\) invariant. Infinitesimally these scaling transformations that leave (20) and (2) invariant are
Let us point out that this implies that
Because of (13) this reveals that the twistless torsion degree of freedom in \(\tau _\mu \) is pure gauge, something which we’ll discuss further below.
Due to the c independence of \(\lambda \) it follows that the scaling acts straightforwardly on the expansion coefficients:
Similarly
3.2.3 Diffeomorphisms
One of the key features of GR is its invariance under diffeomorphisms. A priori they can depend arbitrarily on the speed of light c. Compatibility with the expansion ansatz (23) requires however that the generating vector field satisfies [2, 3]
The zeroth order coefficients \({\overset{\,{(0)}}{\xi }}{}^\mu \) generate the diffeomorphisms of the nonrelativistic theory obtained by the expansion, while the higher order coefficients generate additional gauge transformations. The action on the coefficients of an arbitrary relativistic tensor \(U_{\mu _1\ldots \mu _n}^{\nu _1\ldots \nu _m}(c)\) is
We define the Newton–Cartan structure \(\tau _\mu \), \(h^{\mu \nu }\) and \(\tau ^\mu \), \(h_{\mu \nu }\) to transform as tensors under \({\overset{\,{(0)}}{\xi }}{}{}^\mu \) but to be invariant under all subleading diffeomorphisms \({\overset{\,{(k)}}{\xi }}{}{}^\mu \), \(k>0\). We stress that although such definition is consistent, it implies that the components A, \(A_{{\dot{\mu }}}\) and \(A^{{\dot{\mu }}{\dot{\nu }}}\) do not transform as tensors under c dependent diffeomorphisms. Rather their transformations are defined as the respective components of the transformed relativistic metric:
This is equivalent to
which in turn can be rewritten via (20) as
Note that because \({\overset{\,{(k)}}{A}}{}={\overset{\,{(k+1)}}{A}}{}_{\dot{\nu }}={\overset{\,{(k+2)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}=0\) when \(k<-2\) it follows that the subleading diffeomorphism \({\overset{\,{(k)}}{\xi }}{}\) acts non-trivially only on the triplets \(({\overset{\,{(l)}}{A}}{},{\overset{\,{(l+1)}}{A}}{}_{\dot{\nu }},{\overset{\,{(l+2)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}})\) for which \(l\ge k-2\). In particular, at leading order only \({\overset{\,{(1)}}{\xi }}{}\) acts non-trivially, in the simple fashion
Note that the transformation of \({\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\) resembles a U(1) transformation, and indeed we will recast it as such below. Furthermore, the spatial part \({\overset{\,{(1)}}{\xi }}{}{}^{\dot{\mu }}\) acts trivially at this order. Let us point out that this simple structure repeats itself at all orders, when one considers only the action of the highest order diffeomorphisms on the highest order triplet:
A similar analysis reveals the transformations of the leading order energy-momentum triplet to be
3.3 Leading Order
At leading order in the large c expansion we have the dynamical fields (\({\overset{\,{(-2)}}{A}}{}\,, {\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(0)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}\)) and (\({\overset{\,{(-2)}}{{\mathcal {T}}}}{}\,, {\overset{\,{(-1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\,, {\overset{\,{(0)}}{{\mathcal {T}}}}{}_{{\dot{\mu }}{\dot{\nu }}}\)). The leading order in the expansion of the equations in Table 1 provides a consistent set of equations for these fields that we will now compute. Although similar in spirit to [1,2,3,4], this is the first such calculation keeping \({\overset{\,{(-1)}}{A}}{}_{{\dot{\mu }}}\) arbitrary.
3.3.1 Field redefinitions
A brute force calculation – using (73), see footnote 3 – reveals that the leading coefficients of the Einstein and conservation equations are
Although these equations can in principle be expressed as equations for the variables (\({\overset{\,{(-2)}}{A}}{}\,, {\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(0)}}{A}}{}{}^{{\dot{\mu }}{\dot{\nu }}}\)) and (\({\overset{\,{(-2)}}{{\mathcal {T}}}}{}\,, {\overset{\,{(-1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\,, {\overset{\,{(0)}}{{\mathcal {T}}}}{}_{{\dot{\mu }}{\dot{\nu }}}\)) they can be much more efficiently formulated in terms of an equivalent set of equations expressed in terms of redefined variables that are more adapted to the symmetries. Schematically we replace
and
The detailed redefinitions behind the above schematic are collected in Table 3.
We start our motivation for these redefinitions by considering the scaling symmetry. Since all variables and equations scale homogeneously with a respective weight we can make them scale invariant by multiplication with an appropriate power \({\overset{\,{(-2)}}{A}}{}\), which scales with weight \(-2\). In particular one can check that the following objects are scale invariant: \((-{\overset{\,{(-2)}}{A}}{})^{-1/2}{\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\,, {\overset{\,{(-2)}}{A}}{}^{-1}{\overset{\,{(-2)}}{{\mathcal {T}}}}{}\,, (-{\overset{\,{(-2)}}{A}}{})^{-1/2}{\overset{\,{(-1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\) and \({\overset{\,{(-2)}}{A}}{}^{-1}{\overset{\,{(-2)}}{{\mathcal {E}}}}{}\,, (-{\overset{\,{(-2)}}{A}}{})^{-1/2}{\overset{\,{(-1)}}{{\mathcal {E}}}}{}_{\dot{\mu }}\,, (-{\overset{\,{(-2)}}{A}}{})^{-1/2}{\overset{\,{(-1)}}{{\mathcal {C}}}}{}_{\dot{\mu }}\). Since after such a reformulation all equations and all variables – except one – are scale invariant, it follows that \({\overset{\,{(-2)}}{A}}{}\), which scales non-trivially has to disappear. There is one subtlety to this observation, in that derivatives of \({\overset{\,{(-2)}}{A}}{}\) will transform non-homogeneously, with the transformation including an extra \(\partial _\mu \lambda \). But remembering that the one-form \(a_{\dot{\mu }}\) transforms in the same way – see (36) – we can define an invariant one-form:
Additionally, due to (13), we can furthermore write
The upshot of this observation is that the torsion one-form \(a_{\dot{\mu }}\) and the field \({\overset{\,{(-2)}}{A}}{}\) can only appear in the scale invariant equations through the scale invariant field \(\Psi \), or its derivatives.
Further simplification can be obtained by considering invariance under the subleading diffeomorphisms \({\overset{\,{(1)}}{\xi }}{}^\mu \). The scale invariant version of \({\overset{\,{(-1)}}{A}}{}_{{\dot{\mu }}}\), \((-{\overset{\,{(-2)}}{A}}{})^{-1/2}{\overset{\,{(-1)}}{A}}{}_{{\dot{\mu }}}\), transforms under subleading diffeomorphisms (43) as
The definition (52) then suggests to define
so that this appropriately rescaled version of \({\overset{\,{(-1)}}{A}}{}_{{\dot{\mu }}}\) transforms as a U(1) gauge field under subleading diffeomorphisms:
If one can make the other variables and equations manifestly invariant under these subleading diffeomorphisms then it will follow that \(C_{\dot{\mu }}\) can only appear through its gauge invariant curvature. Let us illustrate how one can indeed make the other variables invariant under \({\overset{\,{(1)}}{\xi }}{}^\mu \) transformations, by considering the transformation (45) of \({\overset{\,{(1)}}{{\mathcal {T}}}}{}_{\dot{\mu }}\) and using the transformation (43) of \({\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\) one can make the invariant combination:
Similar invariant combinations can be made for \({\overset{\,{(0)}}{{\mathcal {T}}}}{}_{{\dot{\mu }}{\dot{\nu }}}\) and the equations, see Table 3.
Finally we should point out that in addition to scale and subleading diffeomorphism invariant combinations, the field redefinitions in Table 3 contain also particular conformal rescalings by powers of \(e^\Psi \). Except for the definition of \(C_{\dot{\mu }}\), where this is related to making the U(1) gauge invariance manifest, these powers in the definitions of the other fields are chosen to simplify the equations. In particular the choice to redefine the spatial metric with such a factor is related to putting the equations in a form that can naturally be obtained from a variational principle.
3.3.2 LO equations
Finally we are ready to present the leading order Einstein and conservation equations. After the redefinitions (48, 50) – see Table 3 for details – one finds that each of \(\mathfrak {E}=0\,, \mathfrak {E}_{\dot{\mu }}=0\,, \mathfrak {E}_{{\dot{\mu }}{\dot{\nu }}}=0\) and \(\mathfrak {C}=0\,, \mathfrak {C}_{\dot{\mu }}=0\) is equivalent to the corresponding equation in the list of equations in Table 4. Note that in those equations all upper indices are indices raised with \(k^{\mu \nu }\) and the connection  is one preserving the Newton–Cartan structure \((\tau _\mu , k^{\mu \nu })\). There are various such connections, see e.g.
[71, 72] for a discussion of the possibilities, but in Table 4 we used the connectionFootnote 6
is one preserving the Newton–Cartan structure \((\tau _\mu , k^{\mu \nu })\). There are various such connections, see e.g.
[71, 72] for a discussion of the possibilities, but in Table 4 we used the connectionFootnote 6

Note that this connection has the torsion  . In the equations of 4 also the “Einstein tensor” of this connection appears,
. In the equations of 4 also the “Einstein tensor” of this connection appears,
as well as the field strength of the gauge potential \(C_{\dot{\mu }}\)Footnote 7
An important consistency check on the equations in Table 4 is that last two equations – the conservation equations – follow from the first three equations – the ’Einstein’ equations – through the Bianchi identityFootnote 8  .
.
4 Discussion
We conclude the paper with a number of remarks and observations about the equations in Table 4.
4.1 Invariance
Due to the introduction of scale invariant variables – see Table 3 – invariance under the scale symmetry has become trivial. The tensorial nature of the equations guarantees invariance under c independent diffeomorphisms \({\overset{\,{(0)}}{\xi }}{}\). Furthermore, in these new variables the subleading diffeomorphisms only act on \(C_{\dot{\mu }}\) and precisely as a U(1) transformation. The equations are invariant since \(C_{\dot{\mu }}\) only appears through its gauge invariant curvature \(F_{{\dot{\mu }}{\dot{\nu }}}\). So of the symmetries listed above only Milne boost invariance remains to be considered.
Because some of the variables do transform non-trivially under boosts it might appear as if boost invariance is not manifest. However, only objects with lower indices have a non-zero transformation under the Milne boosts and this will furthermore be proportional to \(\tau _\mu \). It follows that all objects that either have all indices raised or contracted with some other raised indices will automatically be boost invariant. As this is exactly the case for the equations in Table 4, these are actually manifestly boost invariant. Let us illustrate this argument with the example of \(\partial _{\dot{\mu }}\Psi \). By (33, 30) it follows that \(\Psi \) is boost invariant so that \(\delta _\chi (\partial _{\dot{\mu }}\Psi )=\tau _\mu \chi ^{\dot{\rho }}\partial _{\dot{\rho }}\Psi \). But then observe that
Similarly  .
.
Note that invariance under Milne boosts as above is possible due to absence of time-like derivatives. At higher order such derivatives will be present. In that case boost invariant variables can be introduced [3, 4], but the construction of these variables requires fields that are not present at leading order.
4.2 Gauge choices
As we mentioned in Sect. 3.1, our approach differs from some of the earlier literature [1,2,3,4] in that we leave the potential \({\overset{\,{(-2)}}{A}}{}\) free, rather than choosing it to be \(-1\). This does not amount to the introduction of a new degree of freedom, since upon freeing \({\overset{\,{(-2)}}{A}}{}\) there appears a local scaling symmetry that in turn removes one scalar degree of freedom. The gauge invariant scalar degree of freedom \(\Psi \) – defined in (52) – is a combination of \({\overset{\,{(-2)}}{A}}{}\) and the torsion potential \(\psi \) defined in (13).
4.2.1 Dautcourt gauge
By a scale transformation (37) one can always make \({\overset{\,{(-2)}}{A}}{}=-1\), fixing the scaling symmetry. In this choice of gauge our setup reduces to that originally introduced by Dautcourt [1] and followed in [2,3,4]. In this case the variable \(\Psi \) can be identified with the torsion potential \(\psi \), or in other words:
In this gauge the physical degree of freedom \(\Psi \) – describing a nonrelativistic but strong gravitational time dilation – finds itself thus in the (twistless) torsion of the Newton–Cartan structure, as was first emphasized in [3].
4.2.2 Torsion free gauge
Alternatively, via (36), one can also use a scale transformation to put \(\psi =0\), again fixing this gauge symmetry. In this gauge the vector \(a_{\dot{\mu }}\) vanishes and hence the Newton–Cartan structure is torsionless:
This gauge has the advantage that the nonrelativistic geometry used to express the large c expansion is simpler and that the potentials \({\overset{\,{(k)}}{A}}{}\) are treated equally at all orders. The field redefinitions for the leading order triplet, see Table 3, reduce in this gauge to those in Table 5.
4.2.3 Galilean gauge
The main motivation behind the Newton–Cartan formalism is to express nonrelativistic gravity in manifestly 4-diffeomorphism invariant form. Still, it turns out that the dynamics restrict \(\tau _\mu \) to be twistless [3] which means that there is an inherent direction of time in the theory that all observers can agree upon. Furthermore it is clear from Table 4, the equations obtained from the large c expansion take their simplest form in terms of a time vs space split. This all suggests that it might be quite natural to gauge-fix some of the diffeomorphism invariance by working with an adapted time coordinate. As reviewed in appendix A, the twistless torsion condition guarantees that there exists a function \(t(x^\mu )\) such that locally \(\tau _\mu =e^{-\psi }\partial _\mu t\). One can thus choose coordinates \(x^\mu =(t,x^i)\) such that \(\tau _\mu =e^{-\psi }\delta _\mu ^0\). Together with a choice of \(\tau ^\mu =e^{\psi }\delta ^\mu _0\) these conditions are left invariant by a particular combination of Milne boosts (29) and time-dependent spatial diffeomorphisms [7, 73]. This gauge condition can be summarized as
The LO equations in Table 4 remain essentially form invariant under this gauge fixing: one simply replaces \({\dot{\mu }}\rightarrow i\) and finds that the covariant derivatives and Einstein tensor become those with respect to the Levi-Civita connection of the 3-metric \(k_{ij}\). Note that in this gauge the relativistic metric becomesFootnote 9
If one additionally observes that there are no time derivatives in the LO equations in Table (4), one recognizes these equations as those for an arbitrary stationary relativistic 4-metric. The key crucial difference is that in the large c expansion we performed we did not assume time independence of the fields. But we can conclude that any stationary metric will solve the LO equations exactly. Conversely it follows that at leading order in the large c expansion any solution to the relativistic Einstein equations takes the form of a solution to the stationary Einstein equations but with time-dependent integration constants. We can conclude that the large c expansion is an expansion around the stationary sector of GR. If one makes the coefficients of odd powers vanish – i.e. take \(C_i=0\) above – the leading order reduces to the static sector, as was already observed in [7].
Finally we point out that the (vacuum) LO equations, just like those for stationary metrics, can be obtained from a Lagrangian, which follows from a time-like Kaluza-Klein reduction of the Einstein-Hilbert Lagrangian:
4.3 Example
Here we illustrate the expansion procedure and how stationary relativistic metrics provide exact solutions to the LO equations. Starting with the relativistic Kerr metric as in [74] one finds for the potentials defined through the Newton–CartanFootnote 10 split (20)
where
Depending on how one assumes the mass m and angular momentum J to scale with the speed of light c one gets different expansions.
4.3.1 Weakly massive, weakly rotating Kerr metric
First let us consider the standard Newtonian regime where \(\frac{Gm}{r}\ll c^2\) and \(\frac{J}{mr}\ll c\), expanding (66) and expressing the fields in terms of the variables of Table 3 gives
In this case at leading order the fields simply provide a nonrelativistic description of Minkowski space, the starting point of a weak gravity approximation to GR. The first correction comes in the form of the Newtonian potential \({\overset{\,{(0)}}{A}}{}=2\Phi =\frac{2GM}{r}\), and then follow further subleading post-Newtonian corrections.
4.3.2 Strongly massive, weakly rotating Kerr metric
Another regime is where \(\frac{Gm}{r}\approx c^2\) but \(\frac{J}{mr}\ll c\). We can formally implement this regime by defining \(m=Mc^2\) and keeping M rather than m fixed as \(c\rightarrow \infty \). In this way of expanding the Kerr metric the leading order fields become
In this regime we see that the LO fields contain a spatial metric that is not flat and that translates to a relativistic metric which is not approximately Minkowski. This is an example where the large c expansion extends beyond the regime of weak gravity captured by the post-Minkowski/Newtonian expansion. Note that up to the leading order written here, the Kerr solution coincides with that of Schwarzschild [3, 4]. Again there is an infinite series of further subleading corrections. Interestingly the Newtonian potential \({\overset{\,{(0)}}{A}}{}\) vanishes.
4.3.3 Strongly massive, strongly rotating Kerr metric
The previous expansions of the Kerr solution are free of odd powers of c and as such fall inside the treatment of [3, 4]. If we however consider a regime where \(\frac{Gm}{r}\approx c^2\) and \(\frac{Jm}{r}\approx c\) we will see the odd powers appear already at leading order. To set up an expansion around this regime we keep \(M=m/c^2\) and \(a=J/mc\) fixed as \(c\rightarrow \infty \). In this case one finds at leading order
where
We see here an explicit example of the situation discussed in this paper, namely one where the whole leading order triplet of fields is non-trivial.
Finally let us point out that an analogous weakly massive, strongly rotating regime would be unphysical as it violates the extremality bound.
4.4 On phenomenological applications
The example of the Kerr black hole in the previous subsection shows that there are real world gravitational phenomena that find themselves in the strong field non-relativistic regime that is well approximated by the large c expansion. Still, the expansion is only of real practical use for phenomena that – contrary to the Kerr black hole – are too complicated to describe analytically in GR and at the same time require high orders, or a break down, in the post-Minkowski/Newtonian approximation. For such phenomena the large c expansion would an efficient, and possibly unique, analytic tool to compete with numerical GR. What phenomena would qualify as such? The main result of this paper was to identify the large c expansion as an expansion around the stationary sector of GR, and as we pointed out it generalizes the post-Newtonian expansion to include metrics that are not nearly flat. One concludes that possible practical applications of the large c expansion concern phenomena where gravity is strong and that are almost stationary.
An actual computation of practical value in the large c expansion would hence go at least one order beyond the leading one we worked out, and falls for this reason outside the scope of this paper. Still, to motivate why a further study of the large c expansion might be relevant also to gravitational modeling, we point out two phenomena where an improvement on current techniques might be made.
Dense rotating stars In the interior, or close to, massive dense stars, such as neutron stars or white dwarfs, gravity is strong. When the star is rotating at a small, constant angular velocity it is well described by a stationary space-time that approximately solves Einstein’s equations, known as the Hartle-Thorn metric [75]. As we showed in this paper this stationary metric can be taken as a starting point at leading order for the large c-expansion and non-stationary corrections can be computed at the next to leading order. This provides an example where one improves on post-Minkowskian/post-Newtonian methods almost by definition, since reproducing the Hartle-Thorn metric itself would already amount to a re-summation of an infinite number of terms of those series.
Black hole binaries In the current exciting new era of gravitational wave astronomy [76] an outstanding question is of course if the large c expansion could help improving models of black hole inspiral. For well separated black holes the initial phase of inspiral is well described by post-Newtonian methods, see e.g. [77] for an introduction. Close to merger, when gravity becomes strong, this expansion reaches its limits and we currently need to rely on numerical methods. The merging of two black holes is of course not an almost stationary setting either, which suggests that this phenomenon will fall outside the reach of the large c-expansion as well. Still, we expect that there exists a regime, at least for certain types of inspiral and for short enough time-scales, where the centers are close enough in orbit that gravity is already strong but motion is not too far from stationarity such that the large c-expansion, possibly at a few orders, will give accurate results while post-Newtonian methods would be much less efficient or even break down. It is interesting to recall that stationary solutions describing orbiting black holes have been well studied [78, 79]. These solutions are typically disqualified as unphysical since they exhibit a conical excess singularity between the holes. It is tempting to speculate however that such a singularity might be an artifact that can be resolved by including non-stationary corrections such as described by the large c-expansion. In more basic terms a concrete problem/challenge can be posed as follows. Where the two-body problem in GR is currently out of reach of analytic treatment, its (post-)Newtonian version was solved a long time ago. Can this problem still be solve/addressed analytically in the large c-expansion? This expansion has the advantage that it removes radiation, just as the Newtonian version, but gets us closer to GR by including various strong field effects, such as time dilation.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data sharing not applicable to this article as no datasets were generated or analysed during the current study.]
Change history
22 July 2020
In the original version of this article, the last name of the second author missed its last letter.
Notes
To be precise, the strong gravitational effects present at leading order in the large c expansion can not be fully reproduced at any finite order of the post-Newtonian expansion.
Note that the structure of (26) follows upon assuming that \({\overset{\,{(-4)}}{R}}{}_{\mu \nu }=0\) which amounts to the twistless torsion condition (10), see [3]. But since this is equivalent to the assumption that \({\overset{\,{(-4)}}{{\mathcal {T}}}}{}_{\mu \nu }={\overset{\,{(-3)}}{{\mathcal {T}}}}{}_{\mu \nu }=0\), one sees that this condition is already encoded in (25).
In a frame formulation one can introduce local Poincare symmetries. These symmetries are however not compatible with the large c expansion ansatz. This is related to the appearance of exotic nonrelativistic algebras that have no relativistic origin, see appendix C. For this reason we refrain from using a frame formulation in this work.
One computes \(\delta _\chi (\partial _{\dot{\mu }}\psi )=\tau _\mu \chi ^{\dot{\rho }}\partial _{\dot{\rho }}\psi +\partial _{\dot{\mu }}\delta _\chi \psi \).
Note that actually any connection of the form
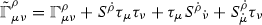 would leave the equations in Table 4 invariant. In that sense (57) is the minimal choice. It is related to the boost invariant connections of
[3, 4] by an appropriate choice S’s in terms of the higher order fields and a conformal transformation \(h^{\mu \nu }=e^{-\Psi }k^{\mu \nu }\).
would leave the equations in Table 4 invariant. In that sense (57) is the minimal choice. It is related to the boost invariant connections of
[3, 4] by an appropriate choice S’s in terms of the higher order fields and a conformal transformation \(h^{\mu \nu }=e^{-\Psi }k^{\mu \nu }\).Note that \(C_\mu =C \tau _\mu +C_{\dot{\mu }}\). The scalar C does actually not appear in (59) as one can check that \(F_{{\dot{\mu }}{\dot{\nu }}}=h^{\rho }_\mu h_{\nu }^\sigma (\partial _\rho C_{\dot{\sigma }}-\partial _\sigma C_{\dot{\rho }})\). Note that this expression is subtly different from \(\partial _{\dot{\mu }}C_{\dot{\nu }}-\partial _{\dot{\mu }}C_{\dot{\nu }}=h^{\rho }_\mu \partial _\rho C_{\dot{\nu }}-h^{\rho }_\nu \partial _\rho C_{\dot{\mu }}=F_{{\dot{\mu }}{\dot{\nu }}}+2\tau _{[\mu }h_{\nu ]}^\rho C_{\dot{\sigma }}\partial _\rho \tau ^\sigma \).
See [4] for a comprehensive discussion of various curvature identities of Newton–Cartan connections.
We made the choice \(\tau _\mu dx^\mu =dt\).
References
G. Dautcourt, Post-Newtonian extension of the Newton-Cartan theory. Class. Quant. Grav. 14, A109–A118 (1997). https://doi.org/10.1088/0264-9381/14/1A/009. arXiv:gr-qc/9610036 [gr-qc]
W. Tichy, E.E. Flanagan, Covariant formulation of the post-1-Newtonian approximation to General Relativity. Phys. Rev. D 84, 044038 (2011). https://doi.org/10.1103/PhysRevD.84.044038. arXiv:1101.0588 [gr-qc]
D. Van den Bleeken, Torsional Newton–Cartan gravity from the large c expansion of general relativity. Class. Quant. Grav. 34(18), 185004 (2017). https://doi.org/10.1088/1361-6382/aa83d4. arXiv:1703.03459 [gr-qc]
D. Hansen, J. Hartong, N.A. Obers, Non-Relativistic Gravity and its Coupling to Matter, arXiv:2001.10277 [gr-qc]
D. Hansen, J. Hartong, N.A. Obers, Action principle for Newtonian gravity. Phys. Rev. Lett. 122(6), 061106 (2019). https://doi.org/10.1103/PhysRevLett.122.061106. arXiv:1807.04765 [hep-th]
M. Cariglia, General theory of Galilean gravity. Phys. Rev. D 98(8), 084057 (2018). https://doi.org/10.1103/PhysRevD.98.084057. arXiv:1811.03446 [gr-qc]
D. Van den Bleeken, Torsional Newton-Cartan gravity and strong gravitational fields, in 15th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (MG15) Rome, Italy, July 1–7, 2018. (2019). arXiv:1903.10682 [gr-qc]
D. Hansen, J. Hartong, N.A. Obers, Gravity between Newton and Einstein. Int. J. Mod. Phys. D 28(14), 1944010 (2019). https://doi.org/10.1142/S0218271819440103. arXiv:1904.05706 [gr-qc]
D. Hansen, J. Hartong, N.A. Obers, Non-relativistic expansion of the Einstein-Hilbert Lagrangian, in 15th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (MG15) Rome, Italy, July 1–7, 2018. (2019). arXiv:1905.13723 [gr-qc]
E. Poisson, C. Will, Gravity: Newtonian, post-Newtonian (Cambridge University Press, Relativistic, 2014)
G. Papageorgiou, B.J. Schroers, A Chern–Simons approach to Galilean quantum gravity in 2+1 dimensions. JHEP 11, 009 (2009). https://doi.org/10.1088/1126-6708/2009/11/009. arXiv:0907.2880 [hep-th]
R. Andringa, E.A. Bergshoeff, J. Rosseel, E. Sezgin, 3D Newton–Cartan supergravity. Class. Quant. Grav. 30, 205005 (2013). https://doi.org/10.1088/0264-9381/30/20/205005. arXiv:1305.6737 [hep-th]
E. Bergshoeff, J. Rosseel, T. Zojer, Newton–Cartan (super)gravity as a non-relativistic limit. Class. Quant. Grav. 32(20), 205003 (2015). https://doi.org/10.1088/0264-9381/32/20/205003. arXiv:1505.02095 [hep-th]
E.A. Bergshoeff, J. Rosseel, Three-dimensional extended bargmann supergravity. Phys. Rev. Lett. 116(25), 251601 (2016). https://doi.org/10.1103/PhysRevLett.116.251601. arXiv:1604.08042 [hep-th]
J. Hartong, Y. Lei, N.A. Obers, Nonrelativistic Chern–Simons theories and three-dimensional HoV̂ava-Lifshitz gravity. Phys. Rev. D 94(6), 065027 (2016). https://doi.org/10.1103/PhysRevD.94.065027. arXiv:1604.08054 [hep-th]
J. Hartong, Y. Lei, N.A. Obers, G. Oling, Zooming in on \(\text{ AdS}_{{3}}\)/\(\text{ CFT}_{{2}}\) near a BPS bound. JHEP 05, 016 (2018). https://doi.org/10.1007/JHEP05(2018)016. arXiv:1712.05794 [hep-th]
E. Bergshoeff, A. Chatzistavrakidis, L. Romano, J. Rosseel, Newton–Cartan Gravity and Torsion. JHEP 10, 194 (2017). https://doi.org/10.1007/JHEP10(2017)194. arXiv:1708.05414 [hep-th]
J. Matulich, S. Prohazka, J. Salzer, Limits of three-dimensional gravity and metric kinematical Lie algebras in any dimension. JHEP 07, 118 (2019). https://doi.org/10.1007/JHEP07(2019)118. arXiv:1903.09165 [hep-th]
N. Ozdemir, M. Ozkan, O. Tunca, U. Zorba, Three-Dimensional extended Newtonian (super)gravity. JHEP 05, 130 (2019). https://doi.org/10.1007/JHEP05(2019)130. arXiv:1903.09377 [hep-th]
L. Avilés, J. Gomis, D. Hidalgo, Stringy (Galilei) Newton–Hooke Chern–Simons gravities. JHEP 09, 015 (2019). https://doi.org/10.1007/JHEP09(2019)015. arXiv:1905.13091 [hep-th]
D. Chernyavsky, D. Sorokin, Three-dimensional (higher-spin) gravities with extended Schrödinger and \(l\)-conformal Galilean symmetries. JHEP 07, 156 (2019). https://doi.org/10.1007/JHEP07(2019)156. arXiv:1905.13154 [hep-th]
D.M. Peãafiel, P. Salgado-Rebolledo, Non-relativistic symmetries in three space-time dimensions and the Nappi–Witten algebra. Phys. Lett. B 798, 135005 (2019). https://doi.org/10.1016/j.physletb.2019.135005. arXiv:1906.02161 [hep-th]
N. Ozdemir, M. Ozkan, U. Zorba, Three-dimensional extended Lifshitz, Schrödinger and Newton–Hooke supergravity. JHEP 11, 052 (2019). https://doi.org/10.1007/JHEP11(2019)052. arXiv:1909.10745 [hep-th]
P. Concha, L. Ravera, E. Rodríguez, Three-dimensional exotic Newtonian gravity with cosmological constant, arXiv:1912.02836 [hep-th]
P. Concha, E. Rodríguez, Non-relativistic gravity theory based on an enlargement of the extended Bargmann algebra. JHEP 07, 085 (2019). https://doi.org/10.1007/JHEP07(2019)085. arXiv:1906.00086 [hep-th]
P. Concha, L. Ravera, E. Rodríguez, Three-dimensional Maxwellian extended Bargmann supergravity, arXiv:1912.09477 [hep-th]
E. Bergshoeff, J. Gomis, P. Salgado-Rebolledo, Non-relativistic limits and three-dimensional coadjoint Poincare gravity, arXiv:2001.11790 [hep-th]
M.H. Christensen, J. Hartong, N.A. Obers, B. Rollier, Torsional Newton–Cartan geometry and Lifshitz holography. Phys. Rev. D 89, 061901 (2014). https://doi.org/10.1103/PhysRevD.89.061901. arXiv:1311.4794 [hep-th]
M.H. Christensen, J. Hartong, N.A. Obers, B. Rollier, Boundary stress-energy tensor and Newton–Cartan geometry in lifshitz holography. JHEP 01, 057 (2014). https://doi.org/10.1007/JHEP01(2014)057. arXiv:1311.6471 [hep-th]
J. Hartong, E. Kiritsis, N.A. Obers, Lifshitz space-times for Schrödinger holography. Phys. Lett. B 746, 318–324 (2015). https://doi.org/10.1016/j.physletb.2015.05.010. arXiv:1409.1519 [hep-th]
J. Hartong, N.A. Obers, Hořava–Lifshitz gravity from dynamical Newton–Cartan geometry. JHEP 07, 155 (2015). https://doi.org/10.1007/JHEP07(2015)155. arXiv:1504.07461 [hep-th]
J. Gomis, H. Ooguri, Nonrelativistic closed string theory. J. Math. Phys. 42, 3127–3151 (2001). https://doi.org/10.1063/1.1372697. arXiv:hep-th/0009181 [hep-th]
R. Andringa, E. Bergshoeff, J. Gomis, M. de Roo, ’Stringy’ Newton–Cartan gravity. Class. Quant. Grav. 29, 235020 (2012). https://doi.org/10.1088/0264-9381/29/23/235020. arXiv:1206.5176 [hep-th]
T. Harmark, J. Hartong, N.A. Obers, Nonrelativistic strings and limits of the AdS/CFT correspondence. Phys. Rev. D 96(8), 086019 (2017). https://doi.org/10.1103/PhysRevD.96.086019. arXiv:1705.03535 [hep-th]
J. Kluson, Remark about non-relativistic string in Newton–Cartan background and null reduction. JHEP 05, 041 (2018). https://doi.org/10.1007/JHEP05(2018)041. arXiv:1803.07336 [hep-th]
J. Kluson, Nonrelativistic string theory sigma model and its canonical formulation. Eur. Phys. J. C 79(2), 108 (2019). https://doi.org/10.1140/epjc/s10052-019-6623-9. arXiv:1809.10411 [hep-th]
T. Harmark, J. Hartong, L. Menculini, N.A. Obers, Z. Yan, Strings with non-relativistic conformal symmetry and limits of the AdS/CFT correspondence. JHEP 11, 190 (2018). https://doi.org/10.1007/JHEP11(2018)190. arXiv:1810.05560 [hep-th]
E. Bergshoeff, J. Gomis, Z. Yan, Nonrelativistic string theory and T-duality. JHEP 11, 133 (2018). https://doi.org/10.1007/JHEP11(2018)133. arXiv:1806.06071 [hep-th]
E.A. Bergshoeff, K.T. Grosvenor, C. Simsek, Z. Yan, An action for extended string Newton-Cartan gravity. JHEP 01, 178 (2019). https://doi.org/10.1007/JHEP01(2019)178. arXiv:1810.09387 [hep-th]
J. Gomis, J. Oh, Z. Yan, Nonrelativistic String Theory in Background Fields, arXiv:1905.07315 [hep-th]
E.A. Bergshoeff, J. Gomis, J. Rosseel, C. Simsek, Z. Yan, String Theory and String Newton-Cartan Geometry, arXiv:1907.10668 [hep-th]
A.D. Gallegos, U. Gürsoy, N. Zinnato, Torsional Newton Cartan gravity from non-relativistic strings, arXiv:1906.01607 [hep-th]
T. Harmark, J. Hartong, L. Menculini, N.A. Obers, G. Oling, Relating non-relativistic string theories, arXiv:1907.01663 [hep-th]
J. Kluson, \((m, n)\)-string and D1-brane in stringy Newton–Cartan background. JHEP 04, 163 (2019). https://doi.org/10.1007/JHEP04(2019)163. arXiv:1901.11292 [hep-th]
J. Kluson, T-duality of Non-Relativistic String in Torsional Newton-Cartan Background, arXiv:1909.13508 [hep-th]
C.D.A. Blair, A worldsheet supersymmetric Newton-Cartan string, arXiv:1908.00074 [hep-th]
J. Kluson, Unstable D-brane in Torsional Newton-Cartan Background, arXiv:2001.11543 [hep-th]
D.T. Son, Newton-Cartan Geometry and the Quantum Hall Effect, arXiv:1306.0638 [cond-mat.mes-hall]
K. Jensen, On the coupling of Galilean-invariant field theories to curved spacetime, arXiv:1408.6855 [hep-th]
M. Geracie, D.T. Son, C. Wu, S.-F. Wu, Spacetime symmetries of the quantum hall effect. Phys. Rev. D 91, 045030 (2015). https://doi.org/10.1103/PhysRevD.91.045030. arXiv:1407.1252 [cond-mat.mes-hall]
K. Jensen, Aspects of hot Galilean field theory. JHEP 04, 123 (2015). https://doi.org/10.1007/JHEP04(2015)123. arXiv:1411.7024 [hep-th]
M. Geracie, K. Prabhu, M.M. Roberts, Fields and fluids on curved non-relativistic spacetimes. JHEP 08, 042 (2015). https://doi.org/10.1007/JHEP08(2015)042. arXiv:1503.02680 [hep-th]
M. Geracie, K. Prabhu, M.M. Roberts, Curved non-relativistic spacetimes, Newtonian gravitation and massive matter. J. Math. Phys. 56(10), 103505 (2015). https://doi.org/10.1063/1.4932967. arXiv:1503.02682 [hep-th]
J. de Boer, J. Hartong, N.A. Obers, W. Sybesma, S. Vandoren, Hydrodynamic modes of homogeneous and isotropic fluids. SciPost Phys. 5(2), 014 (2018). https://doi.org/10.21468/SciPostPhys.5.2.014. arXiv:1710.06885 [hep-th]
J. de Boer, J. Hartong, N.A. Obers, W. Sybesma, S. Vandoren, Perfect fluids. SciPost Phys. 5(1), 003 (2018). https://doi.org/10.21468/SciPostPhys.5.1.003. arXiv:1710.04708 [hep-th]
J. Armas, J. Hartong, E. Have, B.F. Nielsen, N.A. Obers, Newton-Cartan Submanifolds and Fluid Membranes, arXiv:1912.01613 [hep-th]
A. Bagchi, R. Basu, A. Mehra, P. Nandi, Field Theories on Null Manifolds, arXiv:1912.09388 [hep-th]
R. Andringa, E. Bergshoeff, S. Panda, M. de Roo, Newtonian gravity and the bargmann algebra. Class. Quant. Grav. 28, 105011 (2011). https://doi.org/10.1088/0264-9381/28/10/105011. arXiv:1011.1145 [hep-th]
H.R. Afshar, E.A. Bergshoeff, A. Mehra, P. Parekh, B. Rollier, A Schrödinger approach to Newton–Cartan and Hořava–Lifshitz gravities. JHEP 04, 145 (2016). https://doi.org/10.1007/JHEP04(2016)145. arXiv:1512.06277 [hep-th]
J. Figueroa-O’Farrill, Classification of kinematical Lie algebras, arXiv:1711.05676 [hep-th]
J. Figueroa-O’Farrill, S. Prohazka, Spatially isotropic homogeneous spacetimes. JHEP 01, 229 (2019). https://doi.org/10.1007/JHEP01(2019)229. arXiv:1809.01224 [hep-th]
E. Bergshoeff, J. M. Izquierdo, T. Ortín, L. Romano, Lie Algebra Expansions and Actions for Non-Relativistic Gravity, arXiv:1904.08304 [hep-th]
J. Gomis, A. Kleinschmidt, J. Palmkvist, Galilean free Lie algebras. JHEP 09, 109 (2019). https://doi.org/10.1007/JHEP09(2019)109. arXiv:1907.00410 [hep-th]
J. Figueroa-O’Farrill, R. Grassie, S. Prohazka, Geometry and BMS Lie algebras of spatially isotropic homogeneous spacetimes. JHEP 08, 119 (2019). https://doi.org/10.1007/JHEP08(2019)119. arXiv:1905.00034 [hep-th]
J.A. de Azcárraga, D. Gútiez, J.M. Izquierdo, Extended \(D=3\) Bargmann supergravity from a Lie algebra expansion, arXiv:1904.12786 [hep-th]
M. Abedini, H.R. Afshar, A. Ghodsi, Covariant Poisson’s equation in torsional Newton–Cartan gravity. JHEP 04, 117 (2019). https://doi.org/10.1007/JHEP04(2019)117. arXiv:1903.04206 [hep-th]
J. Gomis, A. Kleinschmidt, J. Palmkvist, P. Salgado-Rebolledo, Symmetries of post-Newtonian expansions, arXiv:1910.13560 [hep-th]
J. Raeymaekers, B. Vercnocke, D. Van den Bleeken Unpublished
E. Cartan, Sur les variétés à connexion affine et la théorie de la rélativité généralisée (première partie). Ann. Éc. Norm. Super. 40, 325 (1923)
E. Cartan, Sur les variétés à connexion affine et la théorie de la rélativité généralisée (première partie)(suite). Ann. Éc. Norm. Super. 41, 1 (1924)
X. Bekaert, K. Morand, Connections and dynamical trajectories in generalised Newton–Cartan gravity I. An intrinsic view. J. Math. Phys. 57(2), 022507 (2016). https://doi.org/10.1063/1.4937445. arXiv:1412.8212 [hep-th]
G. Festuccia, D. Hansen, J. Hartong, N.A. Obers, Torsional Newton–Cartan geometry from the noether procedure. Phys. Rev. D 94(10), 105023 (2016). https://doi.org/10.1103/PhysRevD.94.105023. arXiv:1607.01926 [hep-th]
D. Van den Bleeken, C. Yunus, Newton–Cartan, Galileo–Maxwell and Kaluza–Klein. Class. Quant. Grav. 33(13), 137002 (2016). https://doi.org/10.1088/0264-9381/33/13/137002. arXiv:1512.03799 [hep-th]
R. M. Wald, General Relativity. Chicago Univ. Pr., Chicago, USA, 1984. https://doi.org/10.7208/chicago/9780226870373.001.0001
J.B. Hartle, K.S. Thorne, Slowly rotating relativistic stars. II. models for neutron stars and supermassive stars. Astrophys. J. 153, 807 (1968). https://doi.org/10.1086/149707
B.P. Abbott et al., Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116(6), 061102 (2016). https://doi.org/10.1103/PhysRevLett.116.061102. arXiv:1602.03837 [gr-qc]
J.D. Creighton, W.G. Anderson, Gravitational-wave physics and astronomy: An introduction to theory, experiment and data analysis. 11. Wiley-VCH Verlag (2011)
G. Weinstein, The stationary axisymmetric two body problem in general relativity. Comm. Pure Appl. Math. 45, 1183–1203 (1992)
G. Weinstein, Harmonic maps with prescribed singularities and applications in general relativity, arXiv:1902.01576 [gr-qc]
O. Khasanov, S. Kuperstein, (In)finite extensions of algebras from their Inonu–Wigner contractions. J. Phys. A 44, 475202 (2011). https://doi.org/10.1088/1751-8113/44/47/475202. arXiv:1103.3447 [hep-th]
Acknowledgements
It is a pleasure to thank E. Bergshoeff, D. Hansen, J. Hartong, N. Obers, M. Özkan, S. Prohazka, J. Raeymaekers and B. Vercnocke for valuable discussions. The work of DVdB is partially supported by the Boğaziçi University Research Fund under grant number 17B03P1 and TÜBITAK Grant 117F376.
Author information
Authors and Affiliations
Corresponding author
Appendices
Some technicalities behind twistless torsion.
A first technical result is that for any two-form \(\phi _{\mu \nu }\) one has the following equivalences
The equivalence of the very left and very right follow directly from a decomposition as in Sect. 2.1:
Note that the middle equality in (70) is a direct consequence of the equality on the far right. Furthermore observe that via the decomposition above
This then establishes (70), which by taking \(\phi _{\mu \nu }=\partial _{[{\dot{\mu }}}\tau _{{\dot{\nu }}]}\) becomes (10).
Given that
one can then additionally observe that
Combining this with (70) for \(\phi _{\mu \nu }=\partial _{[\mu }a_{\nu ]}\) then leads to (12), which for convenience we reproduce here:
It follows from a simple calculation that this is satisfied if \(a_\mu =\partial _{{\dot{\mu }}}\psi \):
We need a more geometric argument to show that (75) actually always implies that (locally) \(a_\mu =\partial _{{\dot{\mu }}}\psi \). First note that the condition (73) is actually equivalent to the definition of a foliation by hypersurfaces. Consider two purely spatial vectors, i.e. \(v^\mu =v^{\dot{\mu }}\) and \(w^\mu =w^{\dot{\mu }}\), then their commutator will also be purely spatial:
By Frobenius theorem there thus exists a corresponding foliation and, because the kernel of \(h^{\mu }_\nu \) is one dimensional, the leaves are hypersurfaces. We can now argue for \(a_\mu =\partial _{{\dot{\mu }}}\psi \) in two separate but equivalent ways. One could consider the hypersurfaces to be defined as those surfaces for which the function t(x) is constant. It then follows that because \(\tau _\mu v^\mu =0\) for any vector \(v^\mu =v^{\dot{\mu }}\) tangent to the hypersurface that
It then follows that
An alternative route to the same conclusion is to introduce coordinates \(y^a\) along a given hypersurface, it follows that
because the \(\partial _a\) form a basis for the hypersurface’s tangent space. Furthermore, because a coordinate basis commutes it follows that
Then observe that
Via the Poincare lemma on the hypersurface we conclude that
Finally we use the fact that (80) is invertible, i.e. since also the \(\partial _{{\dot{\mu }}}\) form a basis of the tangent space of the hypersurface we can conclude that there exists a matrix \(e_a^{\dot{\mu }}\) such that \(e_a^{\dot{\mu }}e^a_{\dot{\nu }}=h^\mu _\nu \). Multiplying both sides of (83) with this matrix we again find \(a_{{\dot{\mu }}}=\partial _{{\dot{\mu }}}\psi \).
From A to B
The relativistic metric \(g_{\mu \nu }\) and its inverse \(g^{\mu \nu }\) are determined in terms of \((A,A_{\dot{\mu }},A^{{\dot{\mu }}{\dot{\nu }}})\) through the fields \((B,B^{\dot{\mu }},B_{{\dot{\mu }}{\dot{\nu }}})\) as in (20, 21). If one wants to carry out the large c expansion in practice then one will need the expression of the coefficients of the B’s in terms of the coefficients of the A’s. Expanding the equations (21) results in the following recurrence relations:
To illustrate the use of these recursion relations we work out the first orders of the B fields:
LO (\(k=-2\)):
$$\begin{aligned} {\overset{\,{(0)}}{B}}{}=0\qquad {\overset{\,{(0)}}{B}}{}^\mu =0\qquad {\overset{\,{(-2)}}{B}}{}_{{\dot{\mu }}{\dot{\nu }}}=0 \end{aligned}$$(85)Which is equivalent to
$$\begin{aligned} {\overset{\,{(-2)}}{g}}{}_{\mu \nu }={\overset{\,{(-2)}}{A}}{}\tau _\mu \tau _\nu \qquad {\overset{\,{(0)}}{g}}{}^{\mu \nu }=h^{\mu \nu } \end{aligned}$$(86)\(\hbox {N}^{1/2}\)LO (\(k=-1\)):
$$\begin{aligned} {\overset{\,{(1)}}{B}}{}=0\qquad {\overset{\,{(1)}}{B}}{}^{\dot{\mu }}={\overset{\,{(-2)}}{A}}{}^{-1}{\overset{\,{(-1)}}{A}}{}^{\dot{\mu }}\qquad {\overset{\,{(-1)}}{B}}{}_{{\dot{\mu }}{\dot{\nu }}}=0 \end{aligned}$$(87)Which is equivalent to
$$\begin{aligned} {\overset{\,{(-1)}}{g}}{}_{\mu \nu }= & {} {\overset{\,{(-1)}}{A}}{}\tau _\mu \tau _\nu +{\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}\tau _\nu +{\overset{\,{(-1)}}{A}}{}_{\dot{\nu }}\tau _\mu \end{aligned}$$(88)$$\begin{aligned} {\overset{\,{(1)}}{g}}{}^{\mu \nu }= & {} -{\overset{\,{(-2)}}{A}}{}^{-1}({\overset{\,{(-1)}}{A}}{}^{\dot{\mu }}\tau ^\nu +{\overset{\,{(-1)}}{A}}{}^{\dot{\nu }}\tau ^\mu )+{\overset{\,{(1)}}{A}}{}^{{\dot{\mu }}{\dot{\nu }}} \end{aligned}$$(89)NLO (\(k=0\)):
$$\begin{aligned} {\overset{\,{(2)}}{B}}{}= & {} {\overset{\,{(-2)}}{A}}{}^{-2}{\overset{\,{(-1)}}{A}}{}_{\dot{\rho }}{\overset{\,{(-1)}}{A}}{}^{\dot{\rho }}+ {\overset{\,{(-2)}}{A}}{}^{-1} \end{aligned}$$(90)$$\begin{aligned} {\overset{\,{(2)}}{B}}{}^{\dot{\mu }}= & {} {\overset{\,{(-2)}}{A}}{}^{-2}{\overset{\,{(-1)}}{A}}{}{\overset{\,{(-1)}}{A}}{}^{\dot{\mu }}-{\overset{\,{(-2)}}{A}}{}^{-1}({\overset{\,{(1)}}{A}}{}^{{\dot{\mu }}{\dot{\nu }}}{\overset{\,{(-1)}}{A}}{}_{\dot{\nu }}+h^{\mu \nu }{\overset{\,{(0)}}{A}}{}_{\dot{\nu }}) \end{aligned}$$(91)$$\begin{aligned} {\overset{\,{(0)}}{B}}{}_{{\dot{\mu }}{\dot{\nu }}}= & {} h_{\mu \nu }+ {\overset{\,{(-2)}}{A}}{}^{-1}{\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}{\overset{\,{(-1)}}{A}}{}_{\dot{\nu }}\end{aligned}$$(92)Which is equivalent to
$$\begin{aligned} {\overset{\,{(0)}}{g}}{}_{\mu \nu }= & {} {\overset{\,{(0)}}{A}}{}\tau _\mu \tau _\nu +{\overset{\,{(0)}}{A}}{}_\mu \tau _\nu +{\overset{\,{(0)}}{A}}{}_\nu \tau _\mu +h_{\mu \nu }\nonumber \\&+ {\overset{\,{(-2)}}{A}}{}^{-1}{\overset{\,{(-1)}}{A}}{}_{\dot{\mu }}{\overset{\,{(-1)}}{A}}{}_{\dot{\nu }}\nonumber \\ {\overset{\,{(2)}}{g}}{}^{\mu \nu }= & {} ({\overset{\,{(-2)}}{A}}{}^{-2}{\overset{\,{(-1)}}{A}}{}_{\dot{\rho }}{\overset{\,{(-1)}}{A}}{}^{\dot{\rho }}+ {\overset{\,{(-2)}}{A}}{}^{-1} )\tau ^\mu \tau ^\nu \nonumber \\&+{\overset{\,{(-2)}}{A}}{}^{-2}\tau ^\nu {\overset{\,{(-1)}}{A}}{}_{\dot{\rho }}({\overset{\,{(-1)}}{A}}{}h^{\rho \mu }-{\overset{\,{(-2)}}{A}}{}{\overset{\,{(1)}}{A}}{}^{{\dot{\rho }}{\dot{\mu }}})\nonumber \\&+{\overset{\,{(-2)}}{A}}{}^{-2}\tau ^\mu {\overset{\,{(-1)}}{A}}{}_{\dot{\rho }}({\overset{\,{(-1)}}{A}}{}h^{\rho \nu }\nonumber \\&-{\overset{\,{(-2)}}{A}}{}{\overset{\,{(1)}}{A}}{}^{{\dot{\rho }}{\dot{\nu }}})-{\overset{\,{(-2)}}{A}}{}^{-1}(h^{\mu \nu }+2{\overset{\,{(0)}}{A}}{}^{({\dot{\mu }}}\tau ^{\nu )}) \end{aligned}$$(93)
A comment on local translations
The content of this appendix is somewhat independent of the main text, it served however as an important motivation for the choice of formalism used there. We point out that the link between diffeomorphims and local translations in the nonrelativistic case is more degenerate than in the relativistic case. Where in the relativistic case this degeneracy can be lifted by expressing the Einstein equations in terms of curvatures only, this seems not to be the case in the nonrelativistic setting.
Consider a Lie-algebra valued one form A, and a gauge parameter \(\Lambda \), which is a zero-form valued in the same algebra. Then we can define the adjoint transformation and curvature as
The Lie derivative of the gauge field is defined as
It follows that
Since the Lie derivative generates an infinitesimal diffeomorphism the above equality can be used to translate an adjoint transformation into a diffeomorphism at the cost of an extra curvature contribution. This procedure is very natural if the curvature vanishes by a combination of constraints and dynamic equations, as for example in a frame formulation to general relativity, but less so when this is not the case, as for example in the nonrelativistic approximation to general relativity. Nonetheless this approach remains valid and in [4, 5] an algebra was introduced whose translational part reproduces the diffeomorphism symmetries on the gauge field
This Lie-algebra is however not the unique one with this feature since in (96) a modification of the adjoint action can be canceled by a modification of the curvature contribution, leading to identical transformations under diffeomorphisms. Demanding that the Lie-algebra is consistent and that the boost and rotational part remains unchanged one can classify all possibilities:
This is a family of algebra’s parameterized by the real numbers \(\alpha ,\beta \) and \(\gamma \), that reproduces the algebra of [4, 5] when \(\alpha =\beta =\gamma =0\). Just as that algebra can be obtained by an expansion procedure from the Poincare algebra [4, 80], the algebras with non-trivial \(\alpha \) but \(\beta =\gamma =0\) can be obtained by expansion from the (A)dS algebra. For other values of the parameters there doesn’t seem to exist any relativistic algebra that they descent from, making them similar to some of the exotic nonrelativistic algebras found in [64].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Ergen, M., Hamamcı, E. & Van den Bleeken, D. Oddity in nonrelativistic, strong gravity. Eur. Phys. J. C 80, 563 (2020). https://doi.org/10.1140/epjc/s10052-020-8112-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8112-6




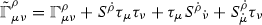 would leave the equations in Table
would leave the equations in Table