Extended gravitational decoupling (GD) solution for charged compact star model

Abstract

In the present article, we have obtained a new solution for the charged compact star model through the gravitational decoupling (GD) by using a complete geometric deformation (CGD) approach (Ovalle, Phys Lett B 788:213, 2019). In this approach, the initial decoupled system is separated into two subsystems namely Einstein–Maxwell’s system and quasi-Einstein system. We solve Einstein–Maxwell’s system by taking well known Tolman–Kuchowicz spacetime geometry in the context of the perfect fluid matter distribution. On the other hand, the second system introduce the anisotropy inside the matter distribution which is solved by taking an EOS in $\theta$ components. The boundary conditions have been derived to determine the constants parameter. To support the mathematical and physical analysis of the present GD solution, we have plotted all the graphs for the compact objects PSR J1614-2230, 4U1608-52 and Cen X-3 corresponding to the constant $\alpha =0.001$, 0.0012 and 0.0014, respectively. Moreover, we also studied the equilibrium and stability of the solution. The present study shows that the GD technique is a very significant tool to generalize the solution in a more complex form or one matter distribution to another matter distribution.

1 Introduction

It is a great challenge to find the exact solutions of Einstein’s field equation (EFE) due to its non-linearity. Last 100 years, many exact solutions for EFE have been obtained in the context of perfect fluid matter distribution [1]. But only few of them are well behaved that describe astrophysical compact objects. Therefore, still, the researchers are busy to find the exact solution of EFE in different contexts. Usually, there are two methodologies that have great interests among all the researchers for solving the field equations. Fist procedure is that consider one metric function or decreasing energy density in order to solve the system. This approach leads an equation with other unknowns which is determined by using the pressure isotropy condition. But this process does not provide always an admissible exact solution. In a second way, we can solve the EFE by specifying an equation of state (EOS) that relates the pressure and density. In this way, we also did not get an exact solution easily for perfect fluid matter distribution due to its complicated integral from. On the other hand, it is not necessary that the matter distribution should be perfect fluid. This was proved by a theoretical investigation that the stellar configuration may contain the anisotropic pressure ($p_r\ne p_t$) when the matter density is very high, in particular, if it is more than the nuclear density [2,3,4,5,6,7]. This anistropic pressure introduce an anisotropy inside stellar configuration. Then the solution of Einstein’s field equation in the presence of anisotropy can be determined easily as compared to perfect fluid matter distribution. In this connection, Many pioneering works have been done by several authors in different context [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. The several authors have been also obtained anisotropic and charged solution using embedding class one condition which is a much popular methodology from last few years [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. The presence of the electric charge in the static charged fluid compact object creates a repulsive force that averts the gravitational collapse [61, 62]. Therefore, we can avoid the singularities by introducing the electric field inside the matter distribution. This repulsive force, due to the electric charge, balances the equilibrium for the dust distribution against the gravitational collapse. Recently, several authors have discovered the solution of the Einstein–Maxwell equations in a different framework which describe strange quark stars, charged black hole, and other astrophysical compact objects [63,64,65,66,67,68,69,70,71]. Varela et al. [72] studied self-gravitating, charged, anisotropic fluid in solving Einstein–Maxwell equations. In doing so they considered Krori and Barua’s [73] metric potentials and linear or nonlinear equation of state. Arbanil et al. [74] studied a class of charged compact fluid spheres obeying the polytropic equation of state. They studied the Oppenheimer–Volkoff limit, Buchdahl limit for the charged polytropic spheres, and they found that the limit is extremal as it is a quasi black hole. So, as a result, we can say that the study of the charged fluid sphere is very interesting. That’s why many researchers obtained exact solutions of Einstein–Maxwell field equations by electrifying some well- known uncharged fluid spheres e.g. Heintzmann’s [75] solution by Pant et al. [76], Durgapal IV [77] by Pant and Rajasekhara [78], Durgapal V [77] by Gupta and Maurya [79], Pant I [80] solution by Maurya and Gupta [81]. The positive values of the charge parameter K describe completely the interior of the charged super-dense astrophysical object. One may consult the following works of literature [82,83,84,85,86,87,88] to study the relativistic compact stellar system more precisely with an electric charge. In this connection, recently the anisotropic charged and uncharged models in modified $f(R, {\mathcal {T}})$ theory gravity have been studied [89,90,91,92]. On the other hand, last few years the gravitational decoupling using minimal geometric deformation (MGD) approach has attracted the researchers. In this directions, few well recognize solutions of the Einstein field equations have been investigated in the framework of charged, uncharged and anisotropic matter distribution by using MGD [93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113]. This MGD technique was developed to deform Schwarzschild space-time [114, 115] into the Randall–Sundrum framework [116, 117]. Ovelle et al. [118] and Contreras and Bargueno [119] have extended the black hole in $3+1$ (Schwarzschild outer space-time) and BTZ black hole in $2+1$ dimensions using the MGD, respectively. The technique for determining an anisotropic solution from any isotropic solution and inverse problem in the black hole context using the MGD is investigated by Contreras and his collaborators [120, 121]. Recently, Ovelle [122] has proposed the extended case of MGD to solve the Einstein–Maxwell equations. In this connection, the extended gravitational decoupling in $2+1$ dimensional space-time with cosmological context was discovered in [128]. This MGD approach has been also applied in other areas like Klein–Gordon scalar fields as an extra matter content [125], in cloud of strings [124], an extension of isotropic coordinates [126], ultra-compact Schwarzschild star or gravastar [127], as well as extended Durgapal isotropic model in the context of class one space-time for charged anisotropic matter distribution [129]. More recently MGD approach was used to discover the higher dimensional compact objects [130] and extent in the context of Lovelock [131] and modified f(R, T) [91] gravity theories as well as in cosmological problems [132]. Moreover, through this GD approach, we can extend any well behaved isotropic solution (as discussed above) of the Einstein field equation into anisotropic or charged, as well as both anisotropic-charged domains by adding extra source $\theta _{ij}$ in the original energy-momentum tensor $T_{ij}$ or by defining the action for total energy tensor. The presence of this extra source $\theta _{ij}$ in the system can create an anisotropy or electric charge inside the matter distribution.

In the present article, we have applied the CGD approach by defining the modified action for total energy momentum tensor for the charged matter distribution which includes the extra source $\theta _{ij}$. In this situation, the field equations for complete or original system will contain ten unknown functions for charged perfect fluid matter distribution. By taking this into account, in the present article we solve these field equations using gravitational decoupling via complete geometric deformation (CGD) approach by transforming the metric potentials as: ${{\xi }}~\mapsto ~ \nu = \xi +\alpha \, h(r)$ and $\mu ~ \mapsto ~ e^{-\lambda } = \mu +\alpha \,f(r)$. In this way, we arrive two systems of equations namely Einstein–Maxwell’s system for perfect fluid and quasi-Einstein system corresponding to the source $T_{ij}$ and $\theta _{ij}$, respectively. However, we suppose this $\theta _{ij}$ will produce anisotropy inside the stellar structure. Then, we need to solve the Einstein–Maxwell’s system of equations for anisotropic matter distribution. To do this, first, we solve Einstein-Maxwell’s system by using well known Tolman–Kuchowicz gravitational potentials in the context of perfect fluid matter distribution. Then for finding the solution of a second system (quasi-Einstein system) we use the an equation of state (EOS), that relates the $\theta$ components, and specific physically motivated ansatz for deformation function f(r). In this way, we obtain a well-behaved expression for the deformation function h(r). After solving both systems individually, we combine both solutions and discussed several physical analysis in order to get the viability of this methodology.

The structure of the article is organized as follows: The Sect. 2 is the Einstein’s-Maxwell field equations for the gravitationally decoupled system. This section is divided into three sections namely as: (2.1) the action for gravitational decoupling system, (2.2) basic stellar equation for the decoupled system, and (2.3) the gravitational decoupling approach and stellar field equations for $T_{ij}$ and $\theta _{ij}$. The matching conditions are performed to determine all the constants in Sect. 3. In the Sect. 4, we obtain a gravitational decoupling solution for the charged anisotropic compact star model by using CGD approach. The physical analysis has been done in Sect. 5 where we discussed regularity condition and causality condition in order to put the bound on the constants. The Sect. 6 contains the detailed discussion on the compactness and redshift. We have performed the equilibrium and stability analysis of the solution in Sect. 7. The physical feasibilty of the energy conditions have been verified in Sect. 8. The final Sect. 9 has been made for discussion and conclusion.

2 The Einstein–Maxwell field equations for gravitationally decoupled system

2.1 The action for gravitational decoupled system

The modified action for gravitational decoupled system can be defined by introducing an extra Lagrangian density for an extra source as [122],

$$\begin{aligned} S=S_{EH}+S_{\theta }=\int \left[ {\frac{R}{16\pi }}+{\mathcal {L}}_M+{\mathcal {L}}_e+{\mathcal {L}}_\theta \right] \sqrt{-g}~ d^4x.~~ \nonumber \\ \end{aligned}$$

(1)

where ${\mathcal {L}}_M$ and ${\mathcal {L}}_e$ denote the Lagrangian for matter field and electromagnetic field, respectively, while ${\mathcal {L}}_\theta$ is a Lagrangian density corresponding to additional source. However, the symbols R and g has their usual meanings.

Now we define $T_{ij}$ as a energy-momentum tensor for Lagrangian matter field ${\mathcal {L}}_M$ which can be written as,

$$\begin{aligned} {T}_{ij}=-\frac{2}{\sqrt{-g}}\,\frac{\delta \left( \sqrt{-g}\,{\mathcal {L}}_M\right) }{\delta g^{ij}}, \end{aligned}$$

(2)

As we know that matter Lagrangian ${\mathcal {L}}_M$ depends on only the components of metric tensor $g_{ij}$ and not on their derivatives, so we obtain

$$\begin{aligned} {T}_{ij}=-\frac{2\,\partial ({\mathcal {L}}_M)}{\partial g^{ij}}+g_{ij} {\mathcal {L}}_M, \end{aligned}$$

(3)

On the other hand, we denoted $E_{ij}$ and $\theta _{ij}$ as electromagnetic field tensor and extra source corresponding to Lagrangian density ${\mathcal {L}}_e$ and ${\mathcal {L}}_\theta$, respectively, which can be given by,

$$\begin{aligned}&E_{ij}=-g_{ij}{L}_e+2\frac{\partial {L}_e}{\partial g^{ij}}, \end{aligned}$$

(4)

$$\begin{aligned}&\theta _{\mu \nu } =-2{\delta {\mathcal {L}}_\theta \over \delta g^{\mu \nu }}+g_{\mu \nu } {\mathcal {L}}_\theta . \end{aligned}$$

(5)

Now by varying the action (1) with respect to the metric tensor $g^{ij}$ we obtain the general equations of motion for the decoupled charged system as,

$$\begin{aligned} G_{ij}=-8\pi \,\left( T^{\text {tot}}_{ij}+E_{ij}\right) , \end{aligned}$$

(6)

where,

$$\begin{aligned} T^{\text {tot}}_{ij} =T_{ij}+\,\theta _{ij}. \end{aligned}$$

(7)

Here, $G_{ij}$ denotes the Einstein tensor and the relativistic units are to be taken $G=c=1$. We define $T_{ij}$ (corresponding to perfect fluid matter distribution) and $E_{ij}$ as,

$$\begin{aligned} {T}_{ij}= & {} ({\rho }+{p})u_\mu u_\nu -{p}g_{ij} \end{aligned}$$

(8)

$$\begin{aligned} E_{ij}= & {} \frac{1}{4 \pi }\left( -F^{m}_{\mu }F_{\nu \,m} + \frac{1}{4}{g_{ij}} F_{\gamma \,n}F^{\gamma \,n}\right) . \end{aligned}$$

(9)

Here ${\rho }$ and p represent the matter density and pressure for charged matter distribution while ${u _{\nu }}$ is a covariant component for the 4-velocity which fulfil $u_{\mu }u^{\mu }= 1$ and $u^{\mu }\nabla ^{\mu }u_{\mu }=0$. On the other hand, the anti-symmetric electromagnetic field tensor $F_{\mu \nu }$ satisfies the Maxwell’s field equations,

$$\begin{aligned} \nabla _{v}\left[ (-g)^{1/2}\,F^{ij}\right]= & {} 4\pi \, (-g)^{1/2}\,j^{\mu }, \end{aligned}$$

(10)

$$\begin{aligned} F_{\mu \nu ,\gamma } + F_{\nu \gamma ,\mu }+F_{\gamma \mu , \nu }= & {} 0, \end{aligned}$$

(11)

where $j^i$, denotes the electromagnetic four current vector, is given by,

$$\begin{aligned} J^{i}=\frac{\sigma }{\sqrt{g_{44}}}\,\frac{dx^i}{dx^4}=\sigma \,v^i, \end{aligned}$$

(12)

where $\sigma$ denotes the charge density and defined as $\sigma =e^{\nu /2}\,J^{0}(r)$. Moreover, the non-vanishing component for the four-current static fluid matter distribution is $J^4$. Therefore, the four-current component acts only along radial direction due to the spherical symmetry. Then the corresponding non-zero components for electromagnetic field tensor are $F^{01}$ and $F^{10}$ that are related as $F^{01}=-F^{10}$. Then the electric field along the radial direction r can be defined by these components $F^{01}$ and $F^{10}$ only.

2.2 Basic stellar equation for decoupled system

In order to describe interior spacetime for the spherically symmetric static stellar system, we take the following line element as,

$$\begin{aligned} ds^{2} = -e^{\lambda (r)} dr^{2} -r^{2}(d\theta ^{2} -\sin ^{2} \theta \, d\phi ^{2})+e^{\nu (r) } \, dt^{2},\nonumber \\ \end{aligned}$$

(13)

where the metric potentials $\nu$ and $\lambda$ are depend on the radial coordinate r only. Then the Einstein’s field equations for the static spherically symmetric spacetime (13) corresponding to decoupling system (6) can be written as,

$$\begin{aligned}&\frac{\mathrm{e}^{-\lambda }}{8\pi }\left( {\frac{\lambda ^{{\prime }}}{r}}-\frac{1}{r^2}+\frac{\mathrm{e}^{\lambda }}{r^2}\right) =(T^0_0)^{\text {tot}}+E^0_0, \end{aligned}$$

(14)

$$\begin{aligned}&\quad -\frac{\mathrm{e}^{-\lambda }}{8\pi } \left( {\frac{\nu ^{{\prime }}}{r}}+\frac{1}{r^2}-\frac{\mathrm{e}^{\lambda }}{r^2}\right) +\frac{1}{r^2}=(T^1_1)^{\text {tot}}+E^1_1, \end{aligned}$$

(15)

$$\begin{aligned}&\quad -\frac{\mathrm{e}^{-\lambda }}{32\pi } \left( 2 \nu ^{{\prime \prime }}+\nu ^{\prime 2}+2{\frac{\nu ^{{\prime }}-\lambda ^{{\prime }}}{r}}-\nu ^{\prime }\lambda ^{\prime } \right) =(T^2_2)^{\text {tot}}+E^2_2.\nonumber \\ \end{aligned}$$

(16)

where,

$$\begin{aligned}&(T^0_0)^{\text {tot}}=T^0_0+\theta ^0_0, \end{aligned}$$

(17)

$$\begin{aligned}&(T^1_1)^{\text {tot}}=T^1_1+\theta ^1_1,\end{aligned}$$

(18)

$$\begin{aligned}&(T^2_2)^{\text {tot}}=T^2_2+\theta ^2_2. \end{aligned}$$

(19)

Then the linear combination of equations (14) -(16) yields the following conservation equation,

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}\,\left( {T}^0_{0}-{T}^1_{1}+E^0_0-E^1_1\right) +\left( {T}^1_{1}+E^1_1\right) ^{\prime }-\frac{2}{r}\,\left( {T}^2_{2}-{T}^1_{1}\right) \nonumber \\ -\frac{2}{r}\left( {E}^2_{2}-{E}^1_{1}\right) -\frac{\nu ^{\prime }}{2} \left( \theta ^{0}_{0}-\theta ^{1}_{1}\right) +\left( \theta ^{1}_{1}\right) ^{\prime } -\frac{2}{r}\,\left( \theta ^{2}_{2}-\theta ^{1}_{1}\right) =0,~~~~ \end{aligned}$$

(20)

However for the spherically symmetric line element (13), the non-vanishing anti-symmetric electric field components $F^{01}$ and $F^{10}$ can be given in terms of the electric charge as,

$$\begin{aligned} F^{01} = - F^{10}=\frac{q}{r^2}\,e^{-(\nu +\lambda )/2} \end{aligned}$$

(21)

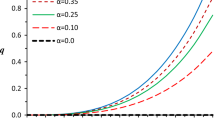
where q(r) denotes the electric charge contained within the compact star of radius r. By using relativistic Gauss law, the electric charge q(r) as well as electric field E can be defined as,

$$\begin{aligned} q(r)= & {} 4\,\pi \int ^{r}_{0}{\sigma \,r^2\,e^{\lambda /2} dr}=r^2\,\sqrt{-F_{10}\,F^{10}}, \end{aligned}$$

(22)

$$\begin{aligned} E^2= & {} -F_{10}\,F^{10}=\frac{q^2}{r^4}. \end{aligned}$$

(23)

Then the components for $T^{i}_{j}$ and $E^{i}_{j}$ can be expressed as,

$$\begin{aligned}&T^{0}_{0}=\rho (r),~~~T^{1}_{1}=-p(r),~~~T^{2}_{2}=-p(r),\end{aligned}$$

(24)

$$\begin{aligned}&E^{0}_{0}=E^{1}_{1}=- E^{2}_{2}=\frac{1}{8\pi }\,\frac{q^2(r)}{r^4}. \end{aligned}$$

(25)

Then the conservation equation (20) will take the following form as,

$$\begin{aligned}&-p^{\prime }-\frac{\nu ^{\prime }}{2}\,(\rho +p)+\frac{qq^{\prime }}{4\,\pi r^4}-\frac{\nu ^{\prime }}{2}\left( \theta ^{0}_{0}-\theta ^{1}_{1}\right) +(\theta ^{1}_{1})^{\prime }\nonumber \\&\quad -\frac{2}{r}\,\left( \theta ^{2}_{2}-\theta ^{1}_{1}\right) =0. \end{aligned}$$

(26)

On the other hand, it is clearly noted that the inclusion of new source $\theta _{ij}$ in the system introduced the anisotropy inside the matter distribution, if $\theta ^2_2\ne \theta ^1_1$. In this situation, the total energy tensor $T^{\text {tot}}$, given in Eq. (7), can be described as,

$$\begin{aligned} (T^0_0)^{\text {tot}}= & {} \rho ^{\text {tot}}(r)=\rho (r)+\theta ^0_0(r),\end{aligned}$$

(27)

$$\begin{aligned} - (T^1_1)^{\text {tot}}= & {} p^{\text {tot}}_r(r)=p(r)-\theta ^1_1(r),\end{aligned}$$

(28)

$$\begin{aligned} - (T^2_2)^{\text {tot}}= & {} p^{\text {tot}}_t(r)=p(r)-\theta ^2_2(r). \end{aligned}$$

(29)

Hence, the anisotropy factor is given as,

$$\begin{aligned} \Delta (r)=p^{\text {tot}}_t(r)-p^{\text {tot}}_r(r)=\theta ^1_1(r)-\theta ^2_2(r) \end{aligned}$$

(30)

2.3 The gravitational decoupling approach and stellar field equations corresponding to $T_{ij}$ (for charge matter distribution) and extra source $\theta _{ij}$

In this section, we will see that how the extended gravitational decoupling converts the field equations (14)–(16) in two separate systems which are known as the Einstein–Maxwell system and quasi-Einstein system, respectively. As the previous discussion, we take the Einstein–Maxwell system with the perfect matter distribution for $T_{ij}$ while the quasi-Einstein system corresponding to extra source $\theta _{ij}$. Now we apply the Ovalle [122] transformation in metric potentials as,

$$\begin{aligned}&{{\xi }}~\mapsto ~ \nu = \xi +\alpha \, h(r)\end{aligned}$$

(31)

$$\begin{aligned}&\mu ~ \mapsto ~ e^{-\lambda } = \mu +\alpha \,f(r). \end{aligned}$$

(32)

where h(r) and f(r) represents the geometric deformation functions corresponding to the temporal and radial metric component. The coupling constant $\alpha$ is a real number. Moreover, the above transformation is the extended case of minimal geometric deformation (MGD) which is called a complete geometric deformation (CGD) or extended geometric deformation along with both radial and temporal components of the line element. By substituting the deformed metric functions (31) and (32) in the field equations of decoupled system (14)–(16) with Eqs. (24) and (25), we arrive at the following set of equations:

• (I) The Einstein’s equations of the charged perfect fluid matter distribution for energy momentum tensor $T_{ij}$ are given as (corresponds to $\alpha =0$),

  $$\begin{aligned}&\frac{1-\mu }{r^{2}}-\frac{\mu ^{\prime }}{r}=8\pi \rho +\frac{q^2}{r^4}, \end{aligned}$$

  (33)
  $$\begin{aligned}&\frac{\mu -1}{r^{2}}+\frac{\mu \,{\xi }'}{r} = 8\pi p-\frac{q^2}{r^4} , \end{aligned}$$

  (34)
  $$\begin{aligned}&\mu \,\left( \frac{{\xi }''}{2}+\frac{{\xi }'^{2}}{4}+\frac{\xi ^{\prime }}{2r}\right) +\left( \frac{{\xi }'{\mu }'}{4}+\frac{{\mu }^{\prime }}{2r} \right) = 8\pi p+\frac{q^2}{r^4}. ~~~~~\nonumber \\ \end{aligned}$$

  (35)

  along the conservation equation,

  $$\begin{aligned} -p^{\prime }-\frac{\nu ^{\prime }}{2}\,(\rho +p)+\frac{qq^{\prime }}{4\,\pi r^4}= & {} 0. \end{aligned}$$

  (36)

  The solution of the field equations (33)–(35), satisfies conservation equation (36) that can describe the internal structure of the compact object for the charged perfect fluid matter distribution. The corresponding solution can be given by the following line element,

  $$\begin{aligned} ds^2= - \mu \, dr^2-r^2(d\theta ^2-\sin ^2\theta \,d\phi ^2)+e^{\xi }\,dt^2 \end{aligned}$$

  (37)

  where the interior mass function $m_0$ is a mass function of the charged matter distribution for the standard GR expressions (33)–(35), which can be given as

  $$\begin{aligned} \frac{2\,m_0}{r} {\equiv } 1{-}\mu {+}\frac{q^2}{r^2}\, {\equiv } \frac{8\pi }{r}\,\int ^r_0{\bigg (\rho {+}\frac{q^2}{8\pi \,r^2}\bigg ) r^2\,dr}{+}\frac{q^2}{r^2}.~~ \nonumber \\ \end{aligned}$$

  (38)

• (II) Now let us go on the parameter $\alpha$ to see the effects of the extra source $\theta _{ij}$ on the charged perfect fluid solution $\{\xi ,\mu \,\rho ,p,\}$. For this purpose we write the field equations for the quasi-Einstein system associated with the source $\theta _{ij}$ as ,

  $$\begin{aligned}&-\alpha \bigg ({f' \over r}+{f\over r^2}\bigg )=8\,\pi \,\theta _0^0, \end{aligned}$$

  (39)
  $$\begin{aligned}&-\alpha \,f\left( {{\nu }' \over r}+{1\over r^2}\right) -\alpha F_1 = 8\,\pi \,\theta _1^1,~~~~ ~~ \end{aligned}$$

  (40)
  $$\begin{aligned}&- {\alpha \,f \over 2}\left( {\nu }''+{{\nu }'^2 \over 2}+{{\nu }' \over r}\right) -{\alpha \,f' \over 2}\left( {{\nu }' \over 2}+{1\over r}\right) = 8\,\pi \,\theta _2^2+\,\alpha F_2.\nonumber \\ \end{aligned}$$

  (41)

  and the linear combination of quasi-Einstein equations (39)–(41) yields the following conservation equation,

  $$\begin{aligned} -\frac{\nu ^{\prime }}{2}\left( \theta ^{0}_{0}{-}\theta ^{1}_{1}\right) {+}\,\left( \theta ^{1}_{1}\right) ^{\prime }{-}\frac{2\,}{r}\,\left( \theta ^{2}_{2} -\theta ^{1}_{1}\right) =\frac{h^{\prime }}{2}\,({p}{+}{\rho }).\nonumber \\ \end{aligned}$$

  (42)

  where, $F_1$ and $F_2$ are given as,

  $$\begin{aligned} F_1=\frac{\mu \,h^{\prime }}{r},~~ F_2=\frac{\mu }{4}\,\left( 2\,h^{\prime \prime }+\alpha \,h^{{\prime }\,2} +\frac{2\,h^{\prime }}{r}+2\,\xi ^{\prime }\,h^{\prime }\right) +\frac{\mu ^{\prime }\,h^{\prime }}{4}. \end{aligned}$$

  It is clearly noted that the presence of $\theta$-sector in the system will introduce the anisotropy inside the stellar structure.

3 Matching conditions for the stellar structure

The matching condition is a critical part in the study of the stellar distributions at the surface of the star ($r=R$) between interior ($r<R$) and exterior ($r>R$) spacetime geometries. In the present study, the interior stellar geometry is given by the extended geometric deformation line element,

$$\begin{aligned} ds^2= & {} - \bigg (1-\frac{2\,{\tilde{m}}(r)}{r}+\frac{q^2}{r^2}\bigg )^{-1} dr^2-r^2(d\theta ^2-\sin ^2\theta \,d\phi ^2)\nonumber \\&+e^{\xi (r)}e^{\alpha \,h(r)}\,dt^2,~~~ \end{aligned}$$

(43)

where ${\tilde{m}}(r)$ is internal mass of the stellar structure for total energy tensor $T^{\text {tot}}_{ij}$. Now the inner metric (43) should be smoothly matched with an exterior spacetime geometry. In his regard, Ovalle [122] has proposed that the exterior spacetime for the extended gravitational decoupling corresponding to “Maxwell version” of the vacuum solution $T_{ij}=0$ can be given by the well-known Reissner–Nordstrom solution as,

$$\begin{aligned} ds^2= & {} - \bigg (1-\frac{2{\tilde{M}}}{r}+\frac{Q^2}{r^2}\bigg )^{-1} dr^2-r^2(d\theta ^2-\sin ^2\theta \,d\phi ^2)\nonumber \\&+\bigg (1-\frac{2{\tilde{M}}}{r}+\frac{Q^2}{r^2}\bigg )\,dt^2,~~~~~ \end{aligned}$$

(44)

where ${\tilde{m}}(R)={\tilde{M}}$ and $q(R)=Q$ is the total mass and total charge for the compact object of the radius R, respectively. For smooth joining we apply the Israel–Darmois junction conditions procedure [133, 134] to match the inner manifold ${\mathcal {M}}^{-}$ with the external one ${\mathcal {M}}^{+}$ at the boundary $\Sigma$. The procedure of joining both space-time at the boundary is known as the continuity of the first and second fundamental forms across the surface $\Sigma$. The first fundamental form says that the intrinsic geometry described by the metric tensor $g_{ij}$ induced by ${\mathcal {M}}^{-}$ and ${\mathcal {M}}^{+}$ on the interface meets

$$\begin{aligned} g^{-}_{tt}|_{r=R}=g^{+}_{tt}|_{r=R}, \end{aligned}$$

(45)

$$\begin{aligned} \quad g^{-}_{rr}|_{r=R}=g^{+}_{rr}|_{r=R}. \end{aligned}$$

(46)

By writing the first fundamental in the explicit form as,

$$\begin{aligned}&e^{-\lambda (R)}=\bigg (1-{\frac{2{\tilde{M}}}{R}}+\frac{Q^2}{R^2}\bigg ),~~~~ \end{aligned}$$

(47)

$$\begin{aligned}&e^{\nu (R)} =\bigg (1-{\frac{2{\tilde{M}}}{R}}+\frac{Q^2}{R^2} \bigg ).~~~~~~ \end{aligned}$$

(48)

While the continuity of the second fundamental can be described as,

$$\begin{aligned}{}[G_{ij}\,r^j]_\Sigma =0 \end{aligned}$$

(49)

here $r_j$ is a unit vector. Using Eqs. (6) and (49) we can find

$$\begin{aligned}{}[T^{\text {tot}}_{ij}\,r^j]_\Sigma =0, \end{aligned}$$

(50)

which gives,

$$\begin{aligned} \big [p^{\text {tot}}_{r}\big ]_\Sigma = \left[ p_r-\theta ^1_1(r)\right] _\Sigma =0 \end{aligned}$$

(51)

Now we will explain by simple way, for the standard GR case the $T_{ij}=0$ is the vacuum solution for the region $r>R$. Here $r=R$ is the boundary of the stellar structure. But the exterior spacetime ($r>R$) may not be a vacuum anymore due to presence of new fields which is coming from the $\theta$ sector. This extra field introduce the anisotropy inside the self-gravitating system. Then the above boundary condition (51) will take the following final form,

$$\begin{aligned} p_r(R)-(\theta ^1_1)^{-}(R)=-(\theta ^1_1)^{+}(R) \end{aligned}$$

(52)

where $p_r(R)=p_r^{-}(R)$. The condition given by Eq. (52) is called the general expression for the second fundamental form connected with the Einstein field equations described by Eq. (6). Now we substitute the value of $(\theta ^1_1)^{-}(R)$ for the interior geometry from Eq. (40) into the condition (52). Then the second fundamental form (52) can be written as,

$$\begin{aligned}&p_r(R)+\frac{\alpha }{8\pi }\,\left[ f(R)\bigg (\frac{\nu ^{\prime }(R)}{R} +\frac{1}{R^2}\bigg )-\frac{\mu (R)\,h^{\prime }(R)}{R}\right] \nonumber \\&\quad =-(\theta ^1_1)^{+}(R), \end{aligned}$$

(53)

here $\nu ^{\prime }(R)\equiv \partial _r\,\nu ^{-}|_{r=R}$. To obtain $(\theta ^1_1)^{+}(R)$, we use the Eqs. (38) and (48) for the outer geometry in Eq. (53) which gives,

$$\begin{aligned}&p_r(R)+\frac{\alpha \,f(R)}{8\pi }\,\bigg (\frac{\nu ^{\prime }(R)}{R} +\frac{1}{R^2}\bigg )-\frac{\alpha \,\mu (R)\,h^{\prime }(R)}{8\pi R}\nonumber \\&\quad =\frac{\alpha \,f^{*}(R)}{8\pi }\left[ \frac{2}{R^2}\bigg (\frac{{\tilde{M}}}{R} {-}\frac{Q^2}{R^2}\bigg )\,\frac{1}{\bigg (1-\frac{2{\tilde{M}}}{R} +\frac{Q^2}{R^2}\bigg )}+\frac{1}{R^2}\right] \nonumber \\&\qquad -\frac{\alpha \,\big (h^{*}(R)\big )^{\prime }}{8\pi R}\,\bigg (1-\frac{2{M_0}}{R}{+}\frac{Q^2}{R^2}\bigg ),~~~ \end{aligned}$$

(54)

where, $f^{*}(R)$ and $h^{*}(R)$ are geometric deformation functions for the outer Reissner–Nordstrom solution (44) due to the extra source $\theta _{\mu \nu }$. It is a important remark that if the exterior solution is given by the Reissner-Nordstrom solution (44) then we must have $f^{*}(r)=0$ and $h^{*}(r)=0$. Now from Eq. (54) we get,

$$\begin{aligned} p_r(R)+\frac{\alpha \,f(R)}{8\pi }\,\bigg (\frac{\nu ^{\prime }(R)}{R} +\frac{1}{R^2}\bigg )-\frac{\mu (R)\,h^{\prime }(R)}{8\pi R} =0~~~ \end{aligned}$$

(55)

which can also read as,

$$\begin{aligned} p^{\text {tot}}_r(R)= p_{r}(R)-\theta ^1_1(R)=0. \end{aligned}$$

(56)

The conditions (47), (48) and (56) are the necessary and sufficient conditions for determining the arbitrary constants involve in the system.

4 Gravitational decoupling solution

As we see that system of equations (33)–(35) and (39)–(41) contains ten unknowns. Therefore, in order to solve the first system of equations (33)–(35) we consider the seed space-time (37) corresponding to well-known Tolman–Kuchowicz solution as,

$$\begin{aligned}&\mu =\frac{1}{(1+a\,r^2+b\,r^4)}, \end{aligned}$$

(57)

$$\begin{aligned}&\xi = B\,r^2+C. \end{aligned}$$

(58)

here, a, b, B are the parameters of dimension $l^{-2}$, $l^{-4}$, and $l^{-2}$, respectively while C is a dimensionless constant. As we observe that both $\mu$ and $\xi$ are non-singular and well behaved throughout within the stellar model. These forms of the gravitational potential yield a physically viable solution. From the Eqs. (33) and (34) together with pressure isotropy condition (using in Eqs. (34) and (35)), we obtain the expressions for $\rho$, p and $q^2/r^4$ as,

$$\begin{aligned}&\rho =\frac{a^2\,r^2 + b\, r^2\, (5 + b\, r^4) + a\, (3 + 2 \,b\, r^4)}{8\pi \,(1 + a\, r^2 + b\, r^4)^2}-\frac{q^2}{8\pi \,r^4}, \end{aligned}$$

(59)

$$\begin{aligned}&p=\frac{(2\,B-a + b\, r^2)}{8\pi \,(1 + a\, r^2 + b\, r^4)}+\frac{q^2}{8\pi \,r^4}, \end{aligned}$$

(60)

$$\begin{aligned}&\frac{q^2}{r^4}=\frac{r^2 [a^2 + B^2 + b^2 r^4 - a (B - 2 b r^2 - B^2 r^2) + \psi _1(r)]}{2\,(1 + a r^2 + b r^4)^2}.~~~~~ \end{aligned}$$

(61)

where, $\psi _1(r)= b (B^2 r^4-1 - 2 B r^2 )$.

Now we focus on the second system of equations (39)–(41). As we see that this system involes five unknown function namely $\theta ^0_0$, $\theta _1^1$, $\theta ^2_2$, and two deformation functions f(r) and h(r). For solving of this system, we propose a linear equation of state (EOS) in $\theta$ along with the one deformation function f(r). But It is important to note that the choice of f(r) should depend upon the following points:

• 1. For positive $\alpha$ together with positive and increasing function f(r), the growth of $\mu (r)$ must be faster than the the deformation function $\alpha . f(r)$ in order to preserve $e^{\lambda (r)}$ and mass function to be positive and increasing.

• 2. For positive $\alpha$, and negative decreasing function f(r), the metric function $e^{\lambda (r)}$ and mass function will increase throughout automtically.

Based on above discussions we take,

$$\begin{aligned}&\theta ^0_0=\beta \,\theta ^1_1+\gamma , \end{aligned}$$

(62)

$$\begin{aligned}&f(r)= -a\,r^2\,(1+a\,r^2+b\,r^4) . \end{aligned}$$

(63)

Now using (39), (40) together with EOS (62) and (63), we obtain other deformation function h(r) as,

$$\begin{aligned} h(r)=\frac{r^2\,[h_1(r)+h_2(r)+h_3(r)+h_4(r)]}{60\, \alpha \,\beta } \end{aligned}$$

(64)

with

$$\begin{aligned} h_1(r)= & {} 30 [a \alpha (\beta -3) + \gamma ] + 15 a [2 a \alpha (\beta -4) \\&\quad + 2 B \alpha \,\beta + \gamma ] r^2,\\ h_2(r)= & {} 10\,[a^3 \alpha \, (\beta -5) + 2 a b \alpha (\beta -5) \\&\quad + 4 a^2 B \alpha \beta + b\, \gamma ] r^4,\\ h_3(r)= & {} 15\, a\, \alpha \, [a \,b\, (\beta -6) + a^2 \,B \,\beta + 2 \,b\, B\, \beta ]\, r^6,\\ h_4(r)= & {} 6\, a \,b\, \alpha \, [b \,(\beta -7) + 4\, a\, B\, \beta ]\, r^8 + 10 a\, b^2 B \,\alpha \, \beta r^{10}.\\ \end{aligned}$$

Now we have completely determined the deformation functions f(r) and h(r), which are physically viable (Fig. 1). Then the gravitational decoupling solution for the total energy momentum tensor $T^{\text {tot}}_{ij}$ can be given by following line element,

$$\begin{aligned} ds^2= & {} \frac{- (1+a\,r^2+b\,r^4)}{1+\alpha \,(1+a\,r^2+b\,r^4)f(r)} dr^2-r^2(d\theta ^2 \nonumber \\&+ \sin ^2 \theta ~d\phi ^2)+ e^{B\,r^2+C}\,e^{\alpha \,h(r)}\, dt^2.~ \end{aligned}$$

(65)

Hence, the explicit form of the deformed gravitational potentials read as,

$$\begin{aligned}&e^{\lambda (r)}=\frac{ (1+a\,r^2+b\,r^4)}{1+\alpha \,(1+a\,r^2+b\,r^4)f(r)}, \end{aligned}$$

(66)

$$\begin{aligned}&e^{\nu (r)}=e^{B\,r^2+C}\,e^{\alpha \,h(r)}. \end{aligned}$$

(67)

where the interior mass function ${\tilde{m}}(r)$ for decoupled system (14)–(16) can be given by,

$$\begin{aligned}&\frac{2{\tilde{m}}(r)}{r}=1{-}e^{-\lambda (r)}{+}\frac{q^2}{r^2} {=}\frac{8\pi }{r}\,\int ^r_0{\bigg (\rho ^{\text {tot}}\,{+}\frac{q^2}{8\pi \,r^2}\bigg ) r^2\,dr}\nonumber \\&\quad +\frac{q^2}{r^2}.~~~ \end{aligned}$$

(68)

Then from Eqs. (27), (38) and (68), we get the following relation,

$$\begin{aligned} {\tilde{m}}(r)\equiv m_0(r)-\frac{\alpha \,r}{2}f(r)= 4\pi \,\int ^r_0{\rho \,r^2\,dr}-\frac{\alpha \,r}{2}f(r).\nonumber \\ \end{aligned}$$

(69)

It is noted that the masses ${\tilde{m}}(r)$ and $m_0$ will be equal and describe the mass function for the standard GR case when $\alpha =0$.

Fig. 1

The behavior of electric charge, q(r) (top left), deformation functions, |f(r)| (top right) and h(r) (bottom left), and bottom right figure for gravitational potentials $e^{\lambda }$ (solid lines) and $e^{\nu }$ (dashed lines) have been plotted against the radial coordinate r/R of different compact objects as PSR J1614-2230 (black curve for $\alpha =0.001$), 4U1608-52 (green curve for $\alpha =0.0012$), and Cen X-3 (red curve for $\alpha =0.0014$). For plotting of these figures for each object, we have used the values of free parameters as: $a=0.00509$, $b=0.00002$, $\beta =1.8$ and $\gamma =0.0001$

Now the expressions for the components of $\theta$-sector are determined as,

$$\begin{aligned}&\theta _0^0(r)=\frac{a\,\alpha \, (3 + 5\, a\, r^2 + 7\, b\, r^4)}{8\,\pi }, \end{aligned}$$

(70)

$$\begin{aligned}&\theta _1^1(r)=\frac{ 5\, a^2\, \alpha \, r^2 + a\, \alpha \, (3 + 7\, b\, r^4)-\gamma }{8\,\pi \,\beta }, \end{aligned}$$

(71)

$$\begin{aligned}&\theta ^2_2(r){=}\frac{\theta _{11}(r){+}\theta _{12}(r){+}\theta _{13}(r){+}a^2 r^2[\theta _{14}(r){+}\theta _{15}(r)]}{-32\,\pi \,\alpha \,\beta ^2\, (1 + a r^2 + b r^4)}.\nonumber \\ \end{aligned}$$

(72)

where the used coefficients in $\theta _2^2(r)$ are given in appendix due to long expressions.

Fig. 2

The behavior of total radial pressure $p^{\text {tot}}_r$ (top left), total tangential pressure $p^{\text {tot}}_t$ (top right), total energy density $\rho ^{\text {tot}}_r$ (bottom left), and anisotropy factor $\Delta$ (bottom right) verses radial coordinate r/R. The used numerical values for plotting these figures along with the same description of the curve for each compact object are same as used in Fig. (1)

By substituting the Eqs. (59)–(60) together with Eqs. (70)–(72) into Eqs. (27)–(29), we find the expressions for the total density ($\rho ^{\text {tot}}$) and total radial pressure ($p^{\text {tot}}_r$) and total tangential pressure ($p^{\text {tot}}_t$) as,

$$\begin{aligned}&\rho ^{\text {tot}}(r)=\frac{a (6 + B r^2 + 2 b r^4 - B^2 r^4) + \psi _2 (r)}{2 (1 + a r^2 + b r^4)^2}+\theta ^0_0(r), \end{aligned}$$

(73)

$$\begin{aligned}&p^{\text {tot}}_r(r) =\frac{a\, (3 B r^2 - 2 b r^4 + B^2 r^4 - 2) +\psi _3 (r)}{2 (1 + a r^2 + b r^4)^2}-\theta ^1_1(r),~~~~ \end{aligned}$$

(74)

$$\begin{aligned}&p^{\text {tot}}_t(r)=\frac{a\, (3 B r^2 - 2 b r^4 + B^2 r^4 - 2) +\psi _3 (r)}{2 (1 + a r^2 + b r^4)^2}-\theta ^2_2(r)~~~~~~ \end{aligned}$$

(75)

and anisotropy factor $\Delta$ can be calculated by the formula:    $\Delta (r)=p^{\text {tot}}_t(r)-p^{\text {tot}}_r(r)$.

where,

$$\begin{aligned} \psi _ 2 (r)= & {} a^2 r^2 {+} r^2 [b^2 r^4 {+} b (11 {+} 2 B r^2 - B^2 r^4) - B^2] ,\\ \psi _ 3 (r)= & {} B^2 (r^2 {+} b r^6) {-} a^2 r^2 + 2 B (2 {+} b r^4) - b r^2 (3 + b r^4) . \end{aligned}$$

5 Physical analysis

To be a regular model, it requires that the spacetime should be free from any mathematical and geometrical as well as physical singularity. For this purpose, we need to check the variation of the deformed metric potentials within the stellar interior. From Eqs. (66) and (67) we obtain: $e^{\lambda (0)}=1$ and $e^{\nu (0)}=e^{C}$. The variation of the metric potentials is presented in Fig. 1 (bottom right) which shows metric potentials are regular and positive throughout the model.

On the other hand the central values of total pressure ($p^{\text {tot}}_0$) and total density ($\rho ^{\text {tot}}_0$) can be given ,

$$\begin{aligned}&\big (p^{\text {tot}}_r\big )_{r=0} =\big (p^{\text {tot}}_t\big )_{r=0}=\frac{2\,B\,\beta - a (3 \alpha + \beta ) + \gamma }{8\,\pi \,\beta }\,>\,0,~~~~~~ \end{aligned}$$

(76)

$$\begin{aligned}&\Longrightarrow ~~~~~~~~~ B > \frac{a \,(3 \,\alpha + \beta ) - \gamma }{2\, \beta },~~~~~~ \end{aligned}$$

(77)

$$\begin{aligned}&\big (\rho ^{\text {tot}}_r\big )_{r=0}=\frac{3\,a \,(1 + \alpha )}{8\,\pi }~>~0~ \Longrightarrow ~a ~\text {is positive}.~~ \end{aligned}$$

(78)

Now, the solution should satisfy the Zeldovich condition i.e. the ratio of pressure-density should be less than unity, then

$$\begin{aligned} \bigg (\frac{p^{\text {tot}}_r}{\rho ^{\text {tot}}}\bigg )_{r=0}= & {} \bigg (\frac{p^{\text {tot}}_t}{\rho ^{\text {tot}}}\bigg )_{r=0} {=}\frac{2\,B\,\beta - a (3 \alpha {+} \beta ) {+} \gamma }{3 a\,\beta \, (1+\alpha ) }~\le 1, \nonumber \\&\Longrightarrow&B\le \frac{a\,(3\alpha +4\beta +3\alpha \,\beta )-\gamma }{2\,\beta }.~~ \end{aligned}$$

(79)

In addition to above, the causality condition must satisfy everywhere within the star i.e. $0<\text {v}^2_r<1$ and $0<\text {v}^2_t<1$. Then we obtain the central values $(\text {v}^2_r)_{r=0}$ and $(\text {v}^2_t)_{r=0}$ and together with causality condition, we obtain

$$\begin{aligned}&0< (\text {v}_r^2)_{r=0}=\frac{5a B \beta -( B^2-3 b)\beta - a^2 (3 \beta -10 \alpha )}{[B^2-11 b - a B - a^2 (10\alpha -11)]\,\beta } < 1,~~ \end{aligned}$$

(80)

$$\begin{aligned}&0< (\text {v}^2_t)_{r=0}=\frac{b (6 \alpha \beta ^2 - \gamma ^2)-2\,B\, \alpha \, \beta \,(B\,\beta + 2\,\gamma ) -\delta _1}{2\,\alpha \,\beta ^2\,[B^2-11\,b - a\,B + a^2 (11 - 10\,\alpha )]}< 1.~~ \end{aligned}$$

(81)

Then the inequality (80) gives,

$$\begin{aligned}&\frac{5a}{2} -\frac{\sqrt{12\,b\,\beta + a^2\,(40\,\alpha + 13\,\beta )}}{(2 \sqrt{\beta }}<B\nonumber \\&\quad <\frac{3 a \sqrt{\beta } - \sqrt{28 b \beta + a^2\,[20\,\alpha \, (1 + \beta )-19 \beta ]\,}}{2\,\sqrt{\beta }},~~~~ \end{aligned}$$

(82)

while inequality (81) yields,

$$\begin{aligned}&\frac{2\,a\,\alpha \,\beta \,[\alpha \,(6-4 \beta ) + 5\,\beta ] - 4\,\alpha \,\beta \,\gamma - \digamma _1}{4\, \alpha \,\beta ^2}<B\nonumber \\&\quad <\frac{a\,\alpha \, \beta (3\alpha +3\beta -2\alpha \, \beta )- \alpha \, \beta \,\gamma -\digamma _2}{2 \alpha \,\beta ^2}.~~~ \end{aligned}$$

(83)

Where $\digamma _1$ and $\digamma _2$ are given in the appendix. Now combine all the inequalities (77), (79), (82) and (83), we obtain an inequality that restricts B as,

$$\begin{aligned}&\frac{a \,(3 \,\alpha + \beta ) - \gamma }{2\, \beta }< B \nonumber \\&\quad < \frac{3 a \sqrt{\beta } - \sqrt{28 b \beta + a^2\,[20\,\alpha \, (1 + \beta )-19 \beta ]\,}}{2\,\sqrt{\beta }}. \end{aligned}$$

(84)

Also, the variation of total density ($\rho ^{\text {tot}}$) and total radial and tangential pressures ($p^{\text {tot}}_r$ and $p^{\text {tot}}_t$ ) are shown in Fig. 2, which shows that those are positive and decreasing away from centre. However the maximum values attain at the centre of the compact object. The numerical values of the physical quantities and constant parameters are given in Table 1.¹

6 Mass-radius ratio and surface redshift

It is required to discuss the maximum limit of the mass-radius ratio to describe the compactness of the stellar model. In the case of isotropic matter distribution, the maximum limit of the mass-radius ratio was proposed by Buchdahl’s [139] in the framework of perfect fluid having decreasing energy density towards to boundary. This maximum limit for mass-radius is given as,

$$\begin{aligned}&\frac{M}{R}\le \frac{4}{9}, \end{aligned}$$

(85)

where $m(R)=M$ describes the total mass of the object in perfect fluid matter distribution, while the R represents the radius of the model which is obtained by taking the pressure to be zero on the surface. Moreover, the presence of an electric charge in the solution modifies Buchdahl’s limit. In this case, Andreasson [140], and Bohmer and Harko [141] have provided the maximum and minimum limit for the mass-radius ratio, respectively as,

Table 1 The numerical values of mass, radius, central pressure, central density, surface density, electric charge at surface and constants B and C of the different compact objects, namely PSRJ1614-2230 [135, 136], 4U1608-52 [136, 137], Cen X-3 [136, 138] for fixed value of $a=0.00509 \mathrm {km^{-2}}$, $b=0.00002 \mathrm {km^{-4}}$, $\beta =1.8$, and $\gamma =0.0001$ with different values of $\alpha$

Table 2 Comparative study of lower bound, Mass-radius ratio, upper bound, compactness $(u=M_{\text {eff}}/R)$ and surface red-shift of the star for different values of $\alpha$

$$\begin{aligned} \frac{Q^{2}\left( 18R^{2}+Q^{2}\right) }{2R^{2}\left( 12R^{2}+Q^{2}\right) }{\le } \frac{M_0}{R}{\le } \frac{2R^{2}+3Q^{2}+2R\sqrt{R^{2}+3Q^{2}}}{9R^{2}}.\nonumber \\ \end{aligned}$$

(86)

where $m_0(R)=M_0$ is the total mass of the compact object for the charged perfect fluid matter distribution. It is noted that the mass $M_0$ present in the Eq. (86) is not equal as the total mass appears in (85). This can be defined as,

$$\begin{aligned} M_0= & {} m_0(R){=}4\pi \int ^{R}_{0}r^{2}\rho (r)dr{+}\frac{1}{2}\int ^{R}_{0} \frac{q^{2}(r)}{r^{2}}dr{+}\frac{Q^{2}(R)}{2R}\nonumber \\= & {} \frac{R}{2}\left[ 1-\mu (R){+}\frac{Q^{2}(R)}{R^{2}}\right] . \end{aligned}$$

(87)

On the other hand, the gravitational mass (appears in Eq. (85)) and effective mass both will be same in the context of perfect fluid or anisotropic fluid matter distribution, which can written as,

$$\begin{aligned} M = m(R)= 4\pi \int ^{R}_{0}r^{2}\rho (r)dr{=}\frac{R}{2}\left[ 1{-}\mu (R)\right] = \big [M\big ]_{\text {eff}}.\nonumber \\ \end{aligned}$$

(88)

But the above situation is not same for the charged matter distribution. In this case, the effective mass for charged matter distribution can be given as,

$$\begin{aligned} \big [M_0\big ]_{\text {eff}}= & {} \big [m_0(R)\big ]_{\text {eff}} =4\pi \int _{0}^{R}\left( {\rho }+\frac{q^{2}}{8\pi \,r^4}\right) r^{2}dr\nonumber \\= & {} \frac{R}{2}\left[ 1-\mu (R)\right] .~~ \end{aligned}$$

(89)

Now from the equations (87), (88) and (89), we observed the followings: (i) the total mass $M_{0}$ for charged stellar object will be more than the total mass M of the compact object corresponding to the prefect or anisotropic fluid matter distribution, (ii) the effective mass $[M_0]_{\text {eff}}$ of the charged compact stellar model will be same as the total mass M in context of prefect fluid or anisotropic fluid matter distribution. Of course, the gravitational mass for the electrically charged stellar object has more value than the uncharged perfect fluid stellar model. Moreover, the same scenario will happen for the present gravitational decoupling models². Now our aim is to see that whether the compactness i.e. mass-radius ratio in the presence of gravitational decoupling will take more value than the without gravitational decoupling, and also it will go beyond to the above standard bounds or not?. Then from the Table 2, we see that the mass-radius ratio ($\frac{{\tilde{M}}}{R}$) for GD model is also lying within the range given in Eq. (86). But It has more value than the mass-radius ratio ($\frac{{M_0}}{R}$) in absence of anisotropy (means when $\alpha =0)$. Then it can be concluded that the presence of $\theta$-sector i.e. anistropy, in the system can produce more compact objects. On the other hand, we would like to mention here that the effective mass plays an important role to define the upper bound of the surface redshift $z_s$ for the compact object. As we have already discussed that the mass-radius ratio gives a significant bound to observe the surface redshift $z_s$ value. This bound can be determined by the following formula,

$$\begin{aligned}&\text {z}_s=\left( 1-2u\right) ^{-1/2}-1=e^{\lambda (R)/2}-1, ~\nonumber \\&\quad \text{ where }~~~~u\equiv \frac{{\tilde{M}}_{\text {eff}}}{R} =\frac{1}{R}\bigg (\big [{M_0}\big ]_{\text {eff}} -\frac{\alpha \,R}{2}f(R)\bigg ).~~~~ \end{aligned}$$

(90)

On the other hand the gravitational redshift inside the compact object for GD solution can be obtained as,

$$\begin{aligned}&\text {z}={e^{-\nu (r)/2}}-1=\sqrt{e^{-(B\,r^2+C)}\,e^{-\alpha \,h(r)}}-1. \end{aligned}$$

(91)

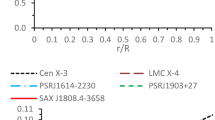
We have shown the behavior of the gravitational redshift inside the star in Fig. 3. From this figure, we can see that the gravitational redshift is maximum at the centre and decreasing outward. Table 2 demonstrated the numerical values of the surface redshift for different values of coupling constant $\alpha$.

Fig. 3

The variation of gravitational redshift (z) verses radial coordinate r/R. The same values are taken for plotting of this figure as in Fig. 2

7 Equilibrium and stability for the gravitational decoupling model

It is very important to investigate the stable equilibrium for the gravitational decoupling solution. For doing this investigation, we need to find the generalized Tolman-Oppenheimer-Volkoff (TOV) equation for the charged anisotropic matter distribution in the presence of extra gravitational source $\theta _{ij}$. This generalized TOV equation can be obtained from the the conservation equation of $T^{\text {tot}}_{ij}$ i.e. by taking covariant derivative of $T^{\text {tot}}_{ij}$ to be zero, which yields: $\nabla ^{\mu }T^{\text {tot}}_{ij}=0$. The explicit form of this conservation can be expressed as,

$$\begin{aligned} -(p^{\text {tot}}_r)^{\prime }-\frac{\nu ^{\prime }}{2}\,\left( \rho ^{\text {tot}} {+}p^{\text {tot}}_r\right) {+}\frac{qq^{\prime }}{4\,\pi r^4}{-}\frac{2}{r}\,\left( \theta ^{2}_{2}{-}\theta ^{1}_{1}\right) =0.\nonumber \\ \end{aligned}$$

(92)

which is same as Eq.  (26). Also, the above Eq. (92) can be divided in different forces whose linear combination will balance the system and achieve a stable equilibrium of the solution. These forces can be written as: (i). gravitational force: $F_g=-\frac{\nu ^{\prime }}{2}\,(\rho ^{\text {tot}}+p^{\text {tot}}_r)$, (ii). hydrostatic force: $F_h=-(p^{\text {tot}}_r)^{\prime }$,   (iii). electric force: $F_e=\frac{2\,q\,q^{\prime }}{8\,\pi \,r^4}$,  and (iv). anisotropic force: $F_{a}=\frac{2}{r}\,(\theta ^{2}_{2}-\theta ^{1}_{1})$.

Fig. 4

The behavior of different forces: $F_g$ (solid lines), $F_h$ (long dashed-dot), $F_e$ (long dashed), and $F_a$ (small dashed-dot) verses radial coordinate r/R. The description of the figure is as follows: (i) red color curves corresponding to the star PSR J1614-2230 for $\alpha =0.001$; (ii) green color curves corresponding to the star 4U1608-52 for $\alpha =0.0012$ and (iii) green color curves corresponding to the star Cen X-3 for $\alpha =0.0014$. The numerical values of free parameters are: $a=0.00509$, $b=0.00002$, $\beta =1.8$ and $\gamma =0.0001$.

To find the variations of these forces we plot the Fig. 4 for modified TOV equation (92) for different values of $\alpha$. From Fig. 4 we observe that gravitational force (solid lines) and hydrostatic force (long dashed-dot lines), and like anisotropic force (small dashed-dot lines) are increasing and achieve its maximum value at the point within the stellar interior and then start decreases in each case. while other forces like electric force (long dashed lines) are monotonically increasing for throughout within the stellar interior. Another important point is that the electric force ($F_e$) plays a major role to balance the system near to surface of the objects while ansitropic force introduces a less impact on the system. As we see that the gravitational forces can be balanced by joint action of all other forces like hydrostatic force, electric force and anisotropic force such that $F_g+F_h+F_e+F_a=0$. In this way, we achieved the stable equilibrium of the obtained each stellar model.

After analyzing the hydrostatic equilibrium under different forces, it is also required to check the stability analysis of the stellar model. To check this analysis, we use Abreu’s criteria [38] which has been initiated by Herrera’s cracking concept [142]. According to the Abreu’s criterion, the stellar model will be stable if the subliminal radial and tangential sound speeds satisfy the following inequalities (Fig. 5),

$$\begin{aligned}&0\le |v^{2}_{t}-v^{2}_{r}|\le 1 \nonumber \\&\quad = \left\{ \begin{array}{ll} (v^{2}_{t}-v^{2}_{r})\in [0, 1], ~&{}~ \mathrm {Potentially\ unstable}, \\ (v^{2}_{t}-v^{2}_{r}) \in [-1, 0] ~&{}~ \mathrm {Potentially\ stable\ } \end{array} \right\} .~~~~~ \end{aligned}$$

(93)

Fig. 5

The left panel has been plotted for radial speed ($\text {v}^2_r$) and right panel for the tangential speed ($\text {v}^2_t$) verses radial coordinate r/R of different compact objects as PSR J1614-2230 (black curve for $\alpha =0.001$), 4U1608-52 (green curve for $\alpha =0.0012$), and Cen X-3 (red curve for $\alpha =0.0014$). The numerical values of the free parameters a, b, $\beta$ and $\gamma$ are same as used in Fig. 4

Fig. 6

The trend of stability factors corresponding to $v^2_r-v^2_t$ (solid lines) and $v^2_t-v^2_r$ (dashed lines) verses the radial coordinate r/R. The description of the compact objects are as follows: PSR J1614-2230 (black curve) for $\alpha =0.001$, 4U1608-52 (green curve) for $\alpha =0.0012$, and Cen X-3 (red curve) for $\alpha =0.0014$. The numerical values of the free parameters a, b, $\beta$ and $\gamma$ are same as used in Fig. 4

In order to verify these above inequalities, first, we need to check whether the stellar model is satisfying causality condition or not?. Then from Fig. 5, we see that the radial and tangential subliminal speed of sounds are satisfying the causality conditions i.e. $v^{2}_{r}<1$ (top figure) and $v^{2}_{t}<1$ (bottom figure) throughout within stellar object (where the speed of light is taken as unity i.e. $c=1$). But we mention an interesting point that both radial and tangential velocities of sound are decreasing monotonically and radial velocity ($v^2_r$) is always greater than the tangential velocity ($v^2_r$) throughout within the stellar compact object for each chosen value of $\alpha$, which can be analyzed from Fig. (5). After verifying the causality condition, we check the stability condition of the stellar compact model through the Eq. (93). Form Fig. 6, we observe that stability factors $\text {v}^2_t-\text {v}^2_r$ (dashed lines) and $\text {v}^2_t-\text {v}^2_r$ (solid lines) are lying within the intervals $[-1, 0]$ and [0, 1]. This implies that the radial velocity dominates the tangential velocity everywhere inside the stellar interior. Also, there is no cracking within the star. Therefore, we conclude that the obtained self-gravitating charged compact star models are stable.

8 Energy conditions

It is very important to check the feasibility of some inequalities corresponding to the stress-energy tensor. For this purpose, we study these inequalities so-called energy conditions for representing physically realistic matter configuration. The respective energy conditions viz., the null energy condition (NEC), strong energy condition (SEC) and weak energy condition (WEC) are defined as

$$\begin{aligned} \text {WEC}&:&T_{\mu \nu }l^\mu l^\nu \ge 0~\text{ or }~{\rho ^{\text {tot}}} \ge 0,~{\rho }^{\text {(tot)}}+{p}^{\text {(tot)}}_i \ge 0 \end{aligned}$$

(94)

$$\begin{aligned} \text {NEC}&:&T_{\mu \nu }t^\mu t^\nu \ge 0~\text{ or }~~~~~~~ {\rho }^{\text {(tot)}}+{p}^{\text {(tot)}}_i \ge 0 \end{aligned}$$

(95)

$$\begin{aligned}&\text{ where }~~T_{\mu \nu }l^{\mu } \in \text{ nonspace-like } \text{ vector } \nonumber \\ \text {SEC}&:T_{\mu \nu }l^\mu l^\nu - \frac{1}{ 2} T^\lambda _\lambda l^\sigma l_\sigma \ge 0 ~\text{ or }~ {\rho }^{\text {(tot)}} +\sum _i {p}^{\text {(tot)}}_i \ge 0.\nonumber \\ \end{aligned}$$

(96)

where $i\equiv (radial~r, transverse ~t),~l^\mu$ and $t^\mu$ are time-like vector and null vector respectively. In order to verify the viable feasibility of the stress-energy tensor, we need to study whether the compact stellar structure is consistent with the inequalities (94)–(96) or not? For this purpose, we plot the Fig. 7 for the above energy conditions and we observe that our stellar compact objects are consistent with all the energy conditions and hence ratifies that the physical acceptability of gravitational decoupling solution for compact objects.

Fig. 7

The behavior of energy condition verses radial coordinate r/R. The description of the figures as follows: the solid line for $\rho ^{\text {tot}}$, dotted line for $\rho ^{\text {tot}}+p^{\text {tot}}_r$, small dashed lines for $\rho ^{\text {tot}}+p^{\text {tot}}_t$, and long dashed-dotted lines for $\rho ^{\text {tot}}+p^{\text {tot}}_t+2p^{\text {tot}}_t$ for different compact objects PSR J1614-2230 (black color), 4U1608-52 (green color), and Cen X-3 (red color)

9 Discussion and conclusions

In this article, a completely deformed anisotropic charged fluid solution for the compact star model has been investigated by applying gravitational decoupling by means of a geometric deformation approach. To find the gravitational decoupling solution for the compact star model, first, we write the modified action for the gravitational decoupling system. Then we define the equation of motion by varying this action along with the metric tensor $g^{ij}$. In this way, we arrive the Einstein’s field equation for the coupled system which corresponds to the total energy-momentum tensor $T^{\text {tot}}_{ij}$ in the context of spherically symmetric spacetime. The corresponding Einstein’s field equations for coupled system will be solved by using the gravitational decoupling (GD) using a complete geometric deformation approach (CGD) in which both gravitational potentials have bee deformed as ${{\xi }}~\mapsto ~ \nu = \xi +\alpha \ h(r)$ and $\mu ~ \mapsto ~ e^{-\lambda } = \mu +\alpha \,f(r)$, as proposed by Ovalle [122]. This GD approach transforms the original Einstein’s field equations for coupled system into two individual subsystems corresponding to the new sources $T_{ij}$ and $\theta _{ij}$. Here we would like to mention that the energy tensor $T_{ij}$ is considered for the charged perfect fluid matter distribution while $\theta _{ij}$ introduce the anisotropy in the system (quasi-Einstein system). To solve the system for $T_{ij}$, we use well-defined spacetime given by Tolman–Kuchowicz and find the solution for the first system, which provides the gravitational potentials $\mu$ and $\xi$ and electric field $E^2$. Now still five unknowns namely $\theta ^0_0$, $\theta ^1_1$ and $\theta ^2_2$, h(r) and f(r) are remaining in order to describe the complete structure of the stellar structure. Since it is clear that we have three independent equations for determining these five unknown which implies that we have two degree of freedom. To find this, we solve the quasi-Einstein system of Eqs. (39)–(41) corresponding to $\theta$-sector by specifying the linear equation of state (EOS), $\theta ^0_0=\beta \,\theta ^1_1+\gamma$, and well motivated ansatz for f(r). After solving of this EOS, we obtain another deformation function h(r). In this process, we achieved a complete deformed charged anisotropic solution for the compact star model. Moreover, we use the well known Isrial–Dormois junction condition for determining the constant parameters. The physical properties of the solution are described through the graphical analysis. We would like to mention that all the plots have been made for the same values of $a=0.00509$, $b=0.00002$, $\beta =1.8$ and $\gamma =0.0001$ with different $\alpha$. In this way we obtained three different compact stars: (i) PSR J1614-2230 for $\alpha =0.001$, $R=11.0143$km, (ii) 4U1608-52 for $\alpha =0.0012$ and $R=10.514$ km, and (iii) Cen X-3 with $\alpha =0.0014$ and $R=9.922$km. Here, we would like to mention that Demorest et al.  [135] have predicted the radius corresponding to the differential neutron star EOS. They found that the radius of the compact objects with 1.97 solar mass lies between 11 and 15 km. But for strange quark matter (SS EOS), the radius will be less for this compact object with the same 1.97 solar mass. Later on, Gangopadhyay and his collaborators [136] have predicted the radii corresponding to 12 different stars and fitted the refined mass measurement of 12 pulsars using strange star equation of state (SS EOS) and they found that the star PSR J1614-2230 with solar mass 1.97 solar has the radius, approx. 9.69 km. In the present paper, By varying $\alpha$ we have predicted the radius of the realistic compact objects, as above, for fixed mass value. Then we observe the following points: if $\alpha$ increases then we will get less compact object as well lower masses stars. But for higher values of $\alpha \approx 0.15$ either causality will violates or cracking will appears in the system.

The Fig. 1 shows the behavior of the deformation functions h(r), |f(r)|, electric charge q(r) and gravitational potentials $e^{\nu (r)}$ and $e^{\lambda (r)}$. From this figure, we observe that the functions |f(r)| (as f(r) is negative and monotonic decreasing throughout the star) and h(r) are zero at the centre and increasing towards the boundary of the stellar object and the same scenario happens in q(r) also. The amount of charge on the surface of the star in Coulomb unit as: (i) $Q=2.8578\times 10^{20} \text {C}$ for PSR J1614-2230 with $\alpha =0.0001$, (ii) $Q=2.4628\times 10^{20} \text {C}$ for 4U1608-52 with $\alpha =0.0012$, and (iii) $Q=2.0361\times 10^{20} \text {C}$ for Cen X-3 with $\alpha =0.0014$. However, the $e^{\nu }$ and $e^{\lambda }$ both are positive and increasing monotonically for all values of $\alpha$ and free from singularity. The above well-defined regular gravitational potentials describe a well behaved physically viable gravitational decoupling solution for compact objects. On the other hand the Fig. 2 also shows the behavior of total radial and tangential pressures, ($p^{\text {tot}}_r$ and ($p^{\text {tot}}_t$), total density ($\rho ^{\text {tot}}$), and the anisotropy ($\Delta$) against the radial coordinate r/R. As we can see in this Fig. 2 that the total pressures and density are maximum at centre and decreasing monotonically away from centre, while the anisotropy is zero at centre and increasing monotonically towards the boundary. The radial pressure is vanishes of the boundary of star which decide the size of the compact model i.e. radius R while tangential pressure is not. We determined the total mass (${\tilde{M}}$), and surface redshift ($z_s$) of each obtained compact object which are the most important physical features of the model. It was proposed that the mass ${\tilde{M}}$ has larger value as compared to the total mass ${M}_0$, which means that anisotropy introduce more massive objects. We have presented the numerical values of the compactness $\big (\frac{{\tilde{M}}}{R}\big )$ and $\big (\frac{{M}_0}{R}\big )$ for fixed values of $a=0.00509$, $b=0.00002$, $\beta =1.8$ and $\gamma =0.0001$ for the different compact objects as PSR J1614-2230 for $\alpha =0.001$, $R=11.0143\,\mathrm {km}$, 4U1608-52 for $\alpha =0.1$, $R=10.5146\,\mathrm {km}$, and Cen X-3 for $\alpha =0.15$, $R=9.922\,\mathrm {km}$. Apart from this we have also calculated the lower and upper bound for the same values of a, b, $\alpha$, $\beta$ and $\gamma$ which shows that the each compactness factor (mass-radius ratio) lies between the lower and upper bound. Through the compactness, we have evaluated the surface redshift of the each different compact star model which are given as follows: (1) $\text {z}_s=0.38425$ for PSR J1614-2230, (2) $\text {z}_s=0.34576$ for 4U1608-52, (3) $\text {z}_s=0.30321$ forCen X-3. These obtained values for surface redshift are compatible with the values proposed by Ivanov [63] and Bowers and Liang [8]. Moreover, the variation of gravitational redshift within the charged ansitropic compact stellar models are shown in Fig. 4. The gravitational redshift is maximum at centre and decreasing towards the surface boundary, and attains minimum at surface. On the other hand, we verified the stable equilibrium of the gravitational decoupling solution via different forces. To do so, we need to study the modified Tolman–Oppenheimer–Volkoff (TOV) equation for anisotropic charged matter distribution. We have presented distributions of all forces $F_g$, $F_h$, $F_a$, and $F_e$ in Fig. 4. From this Fig. 4, we found that the anisotroic force $F_{\alpha }$ and electric force $F_e$ acts along an outward direction. However, the combined impact of the hydrostatic force $F_h$, anisotropic force $F_a$ and electric force $F_e$ will balance the gravitational force $F_{g}$ such that $F_g+F_h+F_a+F_e=0$, which yields the stable equilibrium for the matter distribution $T^{\text {tot}}_{ij}$. Therefore, our obtained GD solution is in the equilibrium stage. Finally, we discussed the causality and stability of the GD solution. The Fig. 5 shows that the speed of sounds is decreasing throughout the stellar interior and less than the speed of light. Moreover, the radial velocity is always greater than the tangential one which can be predicted from Fig. 5. On the other hand, from Fig. 6, we also see that the values of the stability factors $\text {v}^2_t-\text {v}^2_r$ (dashed lines) and $\text {v}^2_r-\text {v}^2_t$ (solid lines) belong to the intervals $[-1, 0]$ and [0, 1], respectively. Also, The anisotropic model satisfies all the energy conditions (see Fig. 7). Finally, we would like to mention that the obtained charged anisotropic solution satisfies all the mathematical and physical requirements which shows that the extended gravitational decoupling by means of a complete geometric deformation approach is very effective and significant tool for generalizing or finding the new solution of the Einstein’s equations.

The used coefficients in the above expressions

$$\begin{aligned} \theta _{11}(r)= & {} a^6 b \alpha ^2 r^10 (-5 + \beta + 2 B \beta r^2)^2 + 4 a^5 b \alpha ^2 r^8 \\&(-5 + \beta + 2 B \beta r^2) (-4 - 6 b r^4\\&+\beta (1 + 2 B r^2) (1 + b r^4))+\gamma (b \gamma (r + b r^5)^2\\&+ 4\alpha \beta (1 + 2 b r^4 + B (r^2 + b r^6)))\\&+ 2 a^4 b \alpha r^6 [\gamma r^2 (-5 + \beta + 2 B \beta r^2) \\&+ \alpha \{47 + 146 b r^4 + 107 b^2 r^8 \\&+ 3 \beta ^2 (1 + 2 B r^2)^2 (1 + b r^4)^2 \\&- 12 \beta (1 + 2 B r^2) (2 + 5 b r^4 + 3 b^2 r^8)\}],\\ \theta _{12}(r)= & {} 2 a^3 \alpha r^4 [\alpha \beta (-25 + \beta - 10 B r^2 + 8 B \beta r^2 \\&+ 2 B^2 \beta r^4) + 2 b^4 \alpha r^12 (42 - 13 \beta (1 + 2 B r^2) \\&+ (\beta + 2 B \beta r^2)^2) + 2 b^3 \alpha r^8 \{88 - 33 \beta (1 + 2 B r^2) \\&+ 3 (\beta + 2 B \beta r^2)^2\} + b \{\gamma r^2 (-13 + \beta (3 + 6 B r^2)) \\&+ 2 \alpha (12 - 7 \beta (1 + 2 B r^2) + (\beta + 2 B \beta r^2)^2)\} \\&+ b^2 r^4 \{\gamma r^2 (-17 + \beta (3 + 6 B r^2)) \\&+ 2 \alpha (58 - 27 \beta (1 + 2 B r^2) + 3 (\beta + 2 B \beta r^2)^2)\}], \\ \theta _{13}(r)= & {} 2 a [b \gamma ^2 r^4 (1 + b r^4) \\&+ \alpha \gamma r^2 \{\beta (3 + 2 B r^2) + b^4 r^12 (-7 + \beta + 2 B \beta r^2) \\&+ b (-3 + \beta + 2 B \beta r^2)\\&+ b^3 r^8 (-17 + \beta (3 + 6 B r^2)) + b^2 r^4 (-13 \\&+ \beta (3 + 6 B r^2))\} + 2 \alpha ^2 \beta \{-3 + b (-27 + \beta ) r^4 \\&+ b^2 (-28 + \beta ) r^8 \\&+ \beta r^4 (B + b B r^4)^2 \\&+B r^2 (1 + b r^4) (-3 - 7 b r^4 + \beta (2 + 6 b r^4))\}],\\ \theta _{14}(r)= & {} b^5 \alpha ^2 r^16 (-7 + \beta + 2 B \beta r^2)^2 \\&+ 2 \alpha ^2 \beta (-29 + \beta - 16 B r^2 \\&+ 12 B \beta r^2 + 4 B^2 \beta r^4) + 4 b^2 \alpha r^4 (-5 + \beta \\&+ 2 B \beta r^2) [3 \gamma r^2 +\alpha (-3 + \beta + 2 B \beta r^2)] \\&+ 4 b^4 \alpha ^2 r^12 [35 - 12 \beta (1 + 2 B r^2) \\&+ (\beta {+} 2 B \beta r^2)^2] {+} 2 b^3 \alpha r^8 [\gamma r^2 (-19 {+} \beta (3 {+} 6 B r^2)) \\&+ \alpha (71 - 30 \beta (1 + 2 B r^2) + 3 (\beta + 2 B \beta r^2)^2)],\\ \theta _{15}(r)= & {} b [\gamma ^2 r^4 + 2 \alpha \gamma r^2 (-11 + \beta (3 + 6 B r^2))\\&+\alpha ^2 \{9 - 2 \beta (3 + 79 r^4 \\&+ 6 B (r^2 + 4 r^6)) + \beta ^2 (1 + 6 r^4 + 4 B (r^2 + 10 r^6) \\&+ 4 B^2 (r^4 + 2 r^8))\}],\\ \digamma _1= & {} \sqrt{\digamma _{11} - 8\,\alpha \,\beta ^2\,(a^2\, \alpha \, \digamma _{12} + \digamma _{13})},\\ \digamma _2= & {} \sqrt{\alpha \,\beta ^2 (28\, b\,\alpha \, \beta ^2 + a^2\, \alpha \,\digamma _{21} - \digamma _{22})},\\ \digamma _{11}= & {} [2 a \alpha \beta (-5 \beta + \alpha (4 \beta -6)) + 4 \alpha \beta \gamma ]^2,\\ \digamma _{12}= & {} b\,\alpha \,(\beta -3)^2 + 2 \beta [\alpha (\beta -23) + 3 \beta ],\\ \digamma _{13}= & {} 2\, a\, \alpha \, [b\,(\beta -3 ) {+} \beta ]\,\gamma {+} b (6 \alpha \beta ^2 {-} \gamma )^2,\\ \digamma _{21}= & {} \alpha ^2 (3 {-} 2 \beta )^2 {-} b \alpha \, (\beta -3)^2 {-} 19\,\beta ^2 {+} 2 \alpha \, \beta (32 + 3 \beta )\\ \digamma _{22}= & {} 2\,a\, \alpha \, [\alpha \, (3 {-} 2 \beta ) {+} b (\beta -3) {+} 4 \beta ]\,\gamma - b\,\gamma ^2 {+} \alpha \, \gamma ^2. \end{aligned}$$

with,

$$\begin{aligned} \delta _1= & {} a^2 \alpha [b \alpha (-3 + \beta )^2 + 2 \beta (\alpha (-23 + \beta ) + 3 \beta )]\\&+2\, a\,\alpha \,[B\,\beta (-5 \beta + \alpha (-6 + 4 \beta )) {+} (b (-3 {+} \beta ) {+} \beta ) \gamma ]. \end{aligned}$$