Testing the origin of the “$f_1(1420)$” with the ${\bar{K}} p \rightarrow \Lambda (\Sigma ) K{\bar{K}} \pi$ reaction

Abstract

We study the ${\bar{K}} p \rightarrow Y K{\bar{K}} \pi$ reactions with ${\bar{K}} = {\bar{K}}^0, K^-$ and $Y=\Sigma ^0, \Sigma ^+, \Lambda$, in the region of $K{\bar{K}} \pi$ invariant masses of $1200-1550$ MeV. The strong coupling of the $f_1(1285)$ resonance to $K^* {\bar{K}}$ makes the mechanism based on $K^*$ exchange very efficient to produce this resonance observed in the $K{\bar{K}} \pi$ invariant mass distribution. In addition, in all these reactions one observes an associated peak at 1420 MeV which comes from the $K^* {\bar{K}}$ decay mode of the $f_1(1285)$ when the $K^*$ is placed on shell at higher invariant masses. We call the attention to the possibility that the peaks observed in other reactions where the “$f_1(1420)$” is observed have a similar origin.

1 Introduction

Kaon beams are called to play a relevant role in studies of hadron dynamics. So far kaon beams in the GeV range are available at the Japan Proton Accelerator Research Complex (J-PARC) [1, 2]. Kaon beams of low energy from $\phi$ decay are available in the Phi-Factory at Frascati [3, 4]. The COMPASS collaboration at CERN can also select events coming from kaon induced reactions [5,6,7]. In addition the planned $K_L$ factory at Jefferson Lab has passed the first steps for approval [8, 9]. The main aim of this latter factory is the study of strange hadron spectroscopy, but its potential for non-strange hadron studies is also relevant. In this sense, having this facility in mind, a proposal was made in Ref. [10] to produce the $f_0(980)$ and $a_0(980)$ resonances in ${\bar{K}}$ induced reactions on protons, which should shed light on the much debated nature of these resonances.

In the present work we make a proposal that shows the usefulness of such facilities to provide relevant information on the nature of the “$f_1(1420)$” resonance, which is catalogued in the PDG [11] as a standard resonance. This resonance has been observed in many very high energy reactions, as proton or pion induced, $e^+e^-$, $\gamma \gamma$ and $J/\psi$ decays, and exceptionally in one experiment with a $K^-$ induced reaction at $32.5 ~\mathrm{GeV}/c$ in Serpukhov [12, 13]. One of the peculiar properties of this resonance is that it is only seen in the $K{\bar{K}}\pi$ decay mode, supposed to be $K^* {\bar{K}} +c.c.$, with a small fraction seen in the $a_0(980) \pi$ channel and a very small fraction to $\phi \gamma$. However, the right to be catalogued as a standard resonance was challenged in Ref. [14], where it was proved that in such reactions a peak appeared naturally at 1420 MeV as the $K^* {\bar{K}} +c.c.$ decay mode of the $f_1(1285)$ resonance, which showed two peaks in the $K{\bar{K}} \pi$ decay channel, one at the nominal $f_1(1285)$ mass and another one around 1420 MeV, where the $K^* {\bar{K}}$ channel with $K^*$ on shell becomes open. The small fraction of $a_0(980)\pi$ decay was also shown in Ref. [14] to correspond to a triangle singularity decay mode of the $f_1(1285)$.

It is interesting to mention how the $\pi ^0 a_0(980)$ mode is generated in Ref. [14]. A triangle mechanism is considered where the $f_1(1285)$ decays to $K^* {\bar{K}}$, $K^*$ decays to $\pi ^0 K$ and then the $\bar{K}K$ fuse to give the $a_0(980)$ resonance. This mechanism was shown to have a triangle singularity peaking at $M_\mathrm{inv} (\pi ^0 a_0)\simeq 1412$ MeV, and it explained the $\pi ^0 a_0$ spectrum observed in the experiment of Ref. [15]. In the same experiment [15], a $\gamma \phi$ decay mode of the $f_1(1420)$ is also reported, albeit with small statistics since the branching ratio is around $0.3 \%$, about an order of magnitude smaller than the branching ratio for $\pi ^0 a_0(980)$ ($4 \%$). It is not our purpose to study this process here, but it is pertinent to mention that, similarly to the $\pi ^0 a_0(980)$ decay mode, one can get a $\gamma \phi$ decay mode with a similar triangle mechanism, $f_1(1285) \rightarrow K^* {\bar{K}}$, followed by $K^* \rightarrow K \gamma$ and then $K{\bar{K}}$ fusing to give the $\phi$. The mechanism develops a triangle singularity, at $M_\mathrm{inv}(\gamma \phi ) \simeq 1384$ MeV (see Eq. (18) of Ref. [16]), which is converted into a broad bump because of the width of the $K^*$. Provided one can get improved statistics in the future, such an idea would be worth pursuing, but for the moment we note the fact that such a decay mode is unavoidable with the dynamics of the $f_1(1285)$ coupling strongly to $K^*{\bar{K}}$.

In the present work we show that the peak at 1420 MeV can also be produced in the present and future lower energy Kaon Facilities with reactions that one has under control theoretically, such that their experimental search and comparison with the theoretical predictions can shed much valuable light on the origin and nature of the “$f_1(1420)$” peak. For this purpose we propose several reactions, all tied among themselves, $K^- p \rightarrow \Lambda (\Sigma ^0) K^0 K^- \pi ^+$, and ${\bar{K}}^0 p \rightarrow \Sigma ^+ K^0 K^- \pi ^+$, for which we make evaluations of the cross section, with the assumption that the $f_1(1420)$ is only a manifestation of the $K^* {\bar{K}} + c.c.$ decay mode of the $f_1(1285)$. We make absolute predictions of the cross section for the three reactions, and the strength of this cross section around the $f_1(1285)$ and $f_1(1420)$ peaks results as a consequence of the coupling of the $f_1(1285)$ to $K^*{\bar{K}}+c.c.$ and dynamical details of the production mechanisms in the ${\bar{K}}$-induced reaction. We should note that a strong coupling of the $f_1(1285)$ to $K^*{\bar{K}}+c.c.$ components emerges in pictures where this resonance is dynamically generated from the pseudoscalar-vector meson interaction [17,18,19,20]. However, independent of this information, the strong coupling of the $f_1(1285)$ to $K^*{\bar{K}}+c.c.$ has experimental backing from the explicit experimental ${\bar{K}} K\pi$ decay mode of the $f_1(1285)$ (see a theoretical description of this decay mode in Ref. [21]).

2 Formalism

The $f_1(1285)$ axial vector meson has the quantum numbers $I^G (J^{PC})=0^+ (1^{++})$. Using chiral Lagrangians for pseudoscalar-vector interaction [22] and a chiral unitary approach in coupled channels, the axial vector mesons emerge as a consequence of the interaction [17,18,19,20]. In particular the $f_1(1285)$ is the cleanest example, appearing in a single channel $K^* {\bar{K}} - c.c.$, with the mass at the right position using a cut off to regularize the loops that provides masses for the other resonances in agreement with experiment as an average. The masses of the other resonances are not provided as accurately as the one for the $f_1(1285)$ in that approach. On the other hand, the important partial decay widths of this resonance have been studied and are described successfully in this approach, the $\pi ^0 a_0(980)$ and $\pi ^0 f_0(980)$ decays in Ref. [23] and the $K{\bar{K}} \pi$ decay in Ref. [21].

The $f_1(1285)$ state is given, with the isospin convention $(K^+, K^0)$, $({\bar{K}}^0, K^0)$ and $C (K^{*+})= -K^{*-}$, etc., by

$$\begin{aligned} | f_1(1285) \rangle = - \frac{1}{2} \, | K^{*+} K^- + K^{*0} {\bar{K}}^0 - K^{*-} K^+ - {\bar{K}}^{*0} K^0 \rangle . \end{aligned}$$

(1)

The coupling of the state to this $K^* {\bar{K}} -c.c.$ combination in s-wave obtained from the residues of the $t_{f_1, f_1}$ amplitude at the pole

$$\begin{aligned} t_{f_1, f_1}= \frac{g^2_{f_1, K^*{\bar{K}}}}{z-z_R}, \end{aligned}$$

(2)

with z the complex energy, and $z_R$ the complex pole position, is given by

$$\begin{aligned} g_{f_1, K^{*} {\bar{K}}} =7219 ~ {\mathrm{MeV}} ~[18]; ~~~~ g_{f_1, K^{*} {\bar{K}}} =7230 ~ {\mathrm{MeV}} ~[17]. \end{aligned}$$

(3)

We shall take the second value in our calculations. The $t_{f_1, K^{*+} K^-}$ amplitude is then given by

$$\begin{aligned} -\frac{1}{2} \, g_{f_1, K^* {\bar{K}}} \ \vec \epsilon \;(f_1) \cdot \vec \epsilon \;(K^*), \end{aligned}$$

(4)

with $\vec \epsilon$ the polarization vector, similarly with the other components.

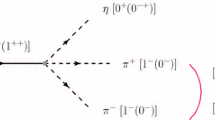
In view of this, the $K^-p \rightarrow Y f_1 \rightarrow Y K\pi {\bar{K}}$ decay proceeds via the mechanism shown in Fig. 1.

Fig. 1

The mechanism for $K^- p \rightarrow \Lambda (\Sigma ^0) f_1 \rightarrow \Lambda (\Sigma ^0) K \pi {\bar{K}}$ reactions

We should note that this mechanism is the same one used in Ref. [24] to study the $K^- p \rightarrow \Lambda f_1(1285)$ reaction, but in that work the process stops in the $f_1$ production of Fig. 1 without looking into the specific decay channel of $K \pi {\bar{K}}$, hence, the $f_1(1420)$ excitation was not addressed in that work.

We shall specify the $K^0 \pi ^+ K^-$ decay channel of $f_1$, and, hence, only the (b) and (g) diagrams of Fig. 1 contribute.

Apart from the $f_1$ coupling to $K^* {\bar{K}}$, we need the coupling of $K^*$ to $K\pi$ which is given by the standard Lagrangian

$$\begin{aligned} \mathcal {L}_{VPP}= -ig\, \langle [P, \partial _\mu P]\, V^\mu \rangle , \end{aligned}$$

(5)

with P, V the standard SU(3) pseudoscalar and vector meson matrices

$$\begin{aligned} P= & {} \left( \begin{array}{ccc} \frac{1}{\sqrt{2}} \pi ^0 + \frac{1}{\sqrt{6}} \eta &{} \pi ^+ &{} K^+ \\ \pi ^- &{} - \frac{1}{\sqrt{2}} \pi ^0 + \frac{1}{\sqrt{6}} \eta &{} K^0\\ K^- &{} \bar{K}^0 &{} -\frac{2}{\sqrt{6}} \eta \\ \end{array} \right) , \end{aligned}$$

(6)

$$\begin{aligned} V= & {} \left( \begin{array}{ccc} \frac{1}{\sqrt{2}} \rho ^0 + \frac{1}{\sqrt{2}} \omega &{} \rho ^+ &{} K^{* +} \\ \rho ^- &{} -\frac{1}{\sqrt{2}} \rho ^0 + \frac{1}{\sqrt{2}} \omega &{} K^{* 0} \\ K^{* -} &{} \bar{K}^{* 0} &{} \phi \\ \end{array} \right) , \end{aligned}$$

(7)

with $g=M_V/2f_\pi$ ($M_V=800$ MeV, $f_\pi =93~$ MeV).

On the other hand, we need the $K^* BB$ vertex. This vertex is given in terms of the Lagrangian [25, 26]¹

$$\begin{aligned} \mathcal {L}_{BBV} = g\, \left( \langle \bar{B} \gamma _{\mu } [V^{\mu },B] \,\rangle + \langle \bar{B} \gamma _{\mu } B \rangle \langle V^{\mu } \rangle \right) \, , \end{aligned}$$

(8)

with the SU(3) baryon matrix B given by

$$\begin{aligned} B = \left( \begin{array}{ccc} \frac{1}{\sqrt{2}} \Sigma ^0 + \frac{1}{\sqrt{6}} \Lambda &{} \Sigma ^+ &{} p \\ \Sigma ^- &{} - \frac{1}{\sqrt{2}} \Sigma ^0 + \frac{1}{\sqrt{6}} \Lambda &{} n \\ \Xi ^- &{} \Xi ^0 &{} - \frac{2}{\sqrt{6}} \Lambda \end{array} \right) . \end{aligned}$$

(9)

It is worth noting that while Eq. (8) is not provided by chiral Lagrangians, the combination of this Lagrangian together with Eq. (5) and vector exchange between mesons and baryons gives rise exactly to the lowest order meson-baryon chiral Lagrangians [27] when $q^2 \rightarrow 0$ in the propagator of the exchanged vector [28, 29].

Since we will work with relatively low ${\bar{K}}$ energies, we will take the spatial components of the $K^*$, $\epsilon ^i$, neglecting the $\epsilon ^0$ component, which has been shown to be a very good approximation even for relatively large $K^*$ momenta [30]. The relevant couplings are then given by

$$\begin{aligned} V_{{\bar{K}}^{*0},\; K^- \pi ^+}= & {} g \; \vec \epsilon \,({\bar{K}}^{*0}) \cdot (\vec p_{K^-}- \vec p_{\pi ^+}), \nonumber \\ V_{K^{*+}, \;K^0 \pi ^+}= & {} -g \; \vec \epsilon \,(K^{*+}) \cdot (\vec p_{K^0}- \vec p_{\pi ^+}), \nonumber \\ V_{BBV}= & {} g\; \langle \bar{u} | \gamma ^\mu | u \rangle \; C_B, \end{aligned}$$

(10)

with

$$\begin{aligned} C_B=\left\{ \begin{array}{cl} \frac{1}{\sqrt{2}}, &{} \mathrm{for}~ pK^{*-} \rightarrow \Sigma ^0; \\ \frac{1}{\sqrt{6}}, &{} \mathrm{for}~ pK^{*-} \rightarrow \Lambda ;\\ 1, &{} \mathrm{for}~ pK^{*0} \rightarrow \Sigma ^+. \end{array} \right. \end{aligned}$$

(11)

A different BBV vertex is used in Ref. [24] following Refs. [31, 32], given by

$$\begin{aligned} V'_{BBV}= g\, (1+2\alpha )\,\langle \bar{u} | \left[ \gamma ^\mu + i \dfrac{\kappa }{M+M'}\, \sigma ^{\mu \nu }\, (p'-p)_\nu \right] | u \rangle , \end{aligned}$$

(12)

where $M, M', p, p'$ are the masses and momenta of the incoming and outgoing baryons, with $\alpha =1.15$ and $\kappa =2.77$ according to Refs. [33, 34] and a slightly different value of g. The magnetic $\sigma ^{\mu \nu }$ term of Eq. (12) is usually neglected in chiral dynamics calculations since the momentum transfer is small, but in this case it is not negligible and we shall take it into account. The coupling of Eq. (12) seems much bigger than that of Eqs. (10), (11) but they are accompanied with form factors which are normalized differently. In the formalism of Eq. (12) the form factor is normalized to unity when $q^2=(p'-p)^2 =m^2_{K^*}$, while in Eqs. (10), (11) it is normalized to unity for $q^2=0$. We shall take a form factor of the type

$$\begin{aligned} \dfrac{\Lambda ^2}{\Lambda ^2-q^2}~~\mathrm{for~Eqs.}~, (10), (11);~~~~ \dfrac{\Lambda ^2-m^2_{K^*}}{\Lambda ^2-q^2}~~\mathrm{for~Eq.}~(12), \end{aligned}$$

(13)

and we shall see the difference between the results with the two approaches, which we will accept as uncertainties of our results.

With the ingredients discussed above, the amplitude for the diagram of Fig. 1b is given by

$$\begin{aligned} \tilde{t}= & {} - \dfrac{1}{4}\, g^2\, g^2_{f_1, K^* {\bar{K}}} \, C_B \nonumber \\&\quad \times \langle {\bar{u}} | \left[ \gamma ^i + i \dfrac{\kappa }{M+M'}\, \sigma ^{i\nu }\, (p'-p)_\nu \right] | u \rangle \, \left( p_{K^0}-p_{\pi ^+}\right) ^i \nonumber \\&\qquad \times \dfrac{1}{M_\mathrm{inv}^2 (K^0 \pi ^+)-m^2_{K^*}+i\, m_{K^*} \,\Gamma _{K^*}}\nonumber \\&\qquad \times \dfrac{1}{M_\mathrm{inv}^2 (K^0 \pi ^+ K^-)-M^2_{f_1}+i\, M_{f_1} \,\Gamma _{f_1}} \nonumber \\&\qquad \times \dfrac{1}{q^2-m^2_{K^*} +i\, m_{K^*} \,\Gamma _{K^*}} \; \dfrac{\Lambda ^2-m^2_{K^*}}{\Lambda ^2-q^2}. \end{aligned}$$

(14)

We should also sum coherently the contribution of the diagram of Fig. 1g. Since $K^{*+}$ and ${\bar{K}}^{*0}$ are different particles, in the limit of small $K^*$ width these diagrams do not interfere. However, with the finite $K^*$ width there is an interference and we take it into account. As a consequence, and evaluating explicitly the $\langle \bar{u} | \gamma ^i | u \rangle$, $\langle \bar{u} | \sigma ^{i\nu } | u \rangle$ matrix elements we obtain at the end, for angles close to the forward direction,

$$\begin{aligned}&\overline{\sum } \sum |\tilde{t}|^2 = \dfrac{1}{16}\, \left[ g\, g(1+2\alpha )\, g^2_{f_1, K^* {\bar{K}}} \, C_B \right] ^2 \nonumber \\&\quad \times \left( \dfrac{\Lambda ^2-m^2_{K^*}}{\Lambda ^2-q^2}\right) ^2 \nonumber \\&\quad \times \left\{ \dfrac{1+2(1+\kappa )^2}{3} \, \left( \dfrac{\vec p^{\;2}}{4M^2} + \dfrac{\vec p^{\; \prime 2}}{4M^{\prime 2}} \right) \right. \nonumber \\&\quad \left. -\dfrac{2}{3} \dfrac{|\vec p\,| \, |\vec p\,'|}{4MM'}\,[2(1+\kappa )^2 -1]\right\} \nonumber \\&\quad \times \left| \dfrac{1}{M_\mathrm{inv}^2 (K^0 \pi ^+ K^-)-M^2_{f_1}+i\, M_{f_1} \,\Gamma _{f_1}} \right| ^2\nonumber \\&\quad \times \left| \dfrac{1}{q^2-m^2_{K^*} +i\, m_{K^*} \,\Gamma _{K^*}} \right| ^2 \nonumber \\&\quad \times \left\{ \dfrac{\lambda (M_\mathrm{inv}^2(K^0 \pi ^+), m^2_{K^0}, m^2_{\pi ^+})}{M_\mathrm{inv}^2 (K^0 \pi ^+)}\,\right. \nonumber \\&\quad \left. \times \left| \dfrac{1}{M_\mathrm{inv}^2 (K^0 \pi ^+)-m^2_{K^*}+i\, m_{K^*} \,\Gamma _{K^*}}\right| ^2 \right. \nonumber \\&\quad + \left. \dfrac{\lambda (M_\mathrm{inv}^2(K^- \pi ^+), m^2_{K^-}, m^2_{\pi ^+})}{M_\mathrm{inv}^2 (K^- \pi ^+)}\,\right. \nonumber \\&\quad \times \left| \dfrac{1}{M_\mathrm{inv}^2 (K^- \pi ^+)-m^2_{K^*}+i\, m_{K^*} \,\Gamma _{K^*}}\right| ^2 \nonumber \\&\quad +\, 2\, p^2_\pi \, \mathrm{Re} \left[ \left( \dfrac{1}{M_\mathrm{inv}^2 (K^0 \pi ^+)-m^2_{K^*}+i\, m_{K^*} \,\Gamma _{K^*}} \right) \right. \nonumber \\&\quad \left. \left. \cdot \left( \dfrac{1}{M_\mathrm{inv}^2 (K^- \pi ^+)-m^2_{K^*}+i\, m_{K^*} \,\Gamma _{K^*}} \right) ^* \right] \right\} , \end{aligned}$$

(15)

where an angular average in $[(\vec p_K - \vec p_\pi ) \cdot \vec p\,]^2$ and $[(\vec p_K - \vec p_\pi ) \cdot \vec p\,']^2$ has been done, and linear terms in cosines of angles are neglected in the interference term. The magnitude $p_\pi$ in the interference term of Eq. (15) is the pion momentum in the $f_1(1285)$ rest frame, given by

$$\begin{aligned} p^2_\pi= & {} E^2_\pi -m^2_\pi ; \\ E_\pi= & {} \dfrac{1}{2\,M_\mathrm{inv}(K^0 \pi ^+ K^-)}\nonumber \\&\;\times \left[ M_\mathrm{inv}^2 (K^- \pi ^+) + M_\mathrm{inv}^2 (K^0 \pi ^+) -2m^2_K \right] . \end{aligned}$$

The cross section for the reaction is given by

$$\begin{aligned}&\dfrac{\mathrm{d} \sigma }{\mathrm{d}\! \cos \!\theta \; \mathrm{d} \!M_\mathrm{inv}(K^0 \pi ^+ K^-)} \nonumber \\&= \dfrac{MM'}{s}\, \dfrac{p'}{p_{{\bar{K}}}} \, \dfrac{1}{(2\pi )^5} \, \dfrac{1}{32\, M_\mathrm{inv}(K^0 \pi ^+ K^-)}\nonumber \\&\qquad \times \int \mathrm{d} M_\mathrm{inv}(K^- \pi ^+)\, 2\,M_\mathrm{inv}(K^- \pi ^+)\nonumber \\&\qquad \times \int \mathrm{d} M_\mathrm{inv}(K^0 \pi ^+)\, 2\,M_\mathrm{inv}(K^0 \pi ^+)\; \overline{\sum } \sum |\tilde{t}|^2, \end{aligned}$$

(16)

where the angle $\theta$ is defined between $K^-$ and $f_1$ in the $K^- p$ rest frame. The limits of the integration for $M_\mathrm{inv}(K^0 \pi ^+)$ with fixed $M_\mathrm{inv}(K^- \pi ^+)$ are given in the PDG [11], and $p_{{\bar{K}}}$ is the initial ${\bar{K}}$ momentum.

Since the peak of the $M_\mathrm{inv}(K^0 \pi ^+ K^-)$ distribution around 1420 MeV is sensitive to the tail of the $f_1(1285)$ resonance, we do a more refined picture for the $f_1(1285)$ width than taking the nominal width as a constant. We take the important $\pi ^0 a_0(980)$ decay channel explicitly, with a $38\%$ branching ratio, and also the $K^* {\bar{K}}$ decay width, which is relevant around 1420 MeV. Hence we take

$$\begin{aligned} \Gamma _{f_1} = 0.38\, \Gamma _{f_1, \,\pi ^0 a_0} + 0.62 \, \Gamma _{f_1, \mathrm{on}} + \Gamma _{f_1, \,K^* {\bar{K}}}, \end{aligned}$$

(17)

with

$$\begin{aligned} \Gamma _{f_1,\,\pi ^0 a_0}= & {} \dfrac{M^2_{f_1}}{M_\mathrm{inv}^2 (f_1)} \; \dfrac{p_\pi }{p_{\pi ,\mathrm{on}}}\; \Gamma _{f_1, \mathrm{on}}, \end{aligned}$$

(18)

$$\begin{aligned} \Gamma _{f_1, \mathrm{on}}= & {} 22.7 \; \mathrm{MeV}, ~~~~ p_\pi = \dfrac{\lambda ^{1/2}(M_\mathrm{inv}^2(f_1), m^2_\pi , m^2_{a_0})}{2\, M_\mathrm{inv}(f_1)},\nonumber \\ p_{\pi ,\mathrm{on}}= & {} \dfrac{\lambda ^{1/2}(M^2_{f_1}, m^2_\pi , m^2_{a_0})}{2\, M_{f_1}},\nonumber \\ \Gamma _{f_1, \,K^* {\bar{K}}}= & {} \dfrac{1}{N}\, \int _{(m_{K^*}-2\Gamma _{K^*})^2}^{(m_{K^*}+2\Gamma _{K^*})^2} \mathrm{d} s_v \;S(s_v) \; \tilde{\Gamma }_{f_1,\, K^* {\bar{K}}} (s_v),\nonumber \\ N= & {} \int _{(m_{K^*}-2\Gamma _{K^*})^2}^{(m_{K^*}+2\Gamma _{K^*})^2} \mathrm{d} s_v \;S(s_v), \end{aligned}$$

(19)

where $S(s_v)$ is the $K^*$ spectral function

$$\begin{aligned} S(s_v)=-\dfrac{1}{\pi }\, \mathrm{Im}\, \dfrac{1}{s_v -m^2_{K^*}+i m_{K^*} \Gamma _{K^*}} \end{aligned}$$

(20)

with $m_{K^*}$ and $\Gamma _{K^*}$ the nominal $K^*$ mass and width [11], and $\tilde{\Gamma }_{f_1,\, K^* {\bar{K}}} (s_v)$ the $K^* {\bar{K}}$ decay width of the $f_1$ with $K^*$ mass $\sqrt{s_v}$ given by

$$\begin{aligned}&\tilde{\Gamma }_{f_1,\, K^* {\bar{K}}}=\dfrac{1}{8\pi }\; \dfrac{1}{M_\mathrm{inv}^2 (f_1)}\nonumber \\&\quad \times g^2_{f_1, K^* {\bar{K}}}\; \tilde{p}_K \;\theta (M_\mathrm{inv}(f_1)-\sqrt{s_v}-m_K), \end{aligned}$$

(21)

with

$$\begin{aligned} \tilde{p}_K = \dfrac{\lambda ^{1/2} (M_\mathrm{inv}^2(f_1), s_v, m^2_K)}{2\,M_\mathrm{inv}(f_1)}. \end{aligned}$$

In addition, we also take $\Gamma _{K^*}$ in Eq. (15) as energy dependent, with

$$\begin{aligned} \Gamma _{K^*} = \Gamma _{K^*,\mathrm{on}} \; \dfrac{m^2_{K^*}}{M_\mathrm{inv}^2 (\pi K)} \; \left( \dfrac{p'_\pi }{p'_{\pi , \mathrm{on}}} \right) ^3, \end{aligned}$$

(22)

where

$$\begin{aligned} p'_\pi= & {} \dfrac{\lambda ^{1/2}(M_\mathrm{inv}^2 (\pi K), m^2_\pi , m^2_K)}{2\, M_\mathrm{inv}(\pi K)}, \\ p'_{\pi ,\mathrm{on}}= & {} \dfrac{\lambda ^{1/2}(m^2_{K^*}, m^2_\pi , m^2_K)}{2\, m_{K^*}}, \end{aligned}$$

with $\pi K$ standing for $K^0 \pi ^+$ or $K^- \pi ^+$ depending on the term in Eq. (15).

We can tune the $\Lambda$ parameter to get an important datum which is the integrated cross section for $f_1(1285)$ production in the $K^-p \rightarrow \Lambda f_1(1285)$ at $\sqrt{s}=3010$ MeV, $\sigma = 11\pm 3 \,\mu b$ [35]. The process can be described by the diagram of Fig. 2.

Fig. 2

Mechanism for $f_1$ production in the $K^- p \rightarrow \Lambda f_1$ reaction

Proceeding as before, we find now

$$\begin{aligned} \dfrac{\mathrm{d}\sigma }{\mathrm{d}\!\cos \!\theta }=\dfrac{M_p\, M_\Lambda }{8\pi }\, \dfrac{1}{s}\, \dfrac{p_{f_1}}{p_{{\bar{K}}}}\, \overline{\sum } \sum |t'|^2, \end{aligned}$$

(23)

where $p_{f_1}, p_{{\bar{K}}}$ are the $f_1$ and ${\bar{K}}$ momenta, and now ($C_B=\frac{1}{\sqrt{6}}$)

$$\begin{aligned} \overline{\sum } \sum |t'|^2= & {} \dfrac{1}{24}\, g^2_{f_1, K^* {\bar{K}}} \, g^2 (1+2\alpha ) \, \left( \dfrac{\Lambda ^2 - m^2_{K^*}}{\Lambda ^2 -q^2}\right) ^2\nonumber \\&\times \left| \dfrac{1}{q^2-m^2_{K^*} +i\, m_{K^*} \,\Gamma _{K^*}} \right| ^2 \nonumber \\&\times \left\{ [1+2(1+\kappa )^2] \left( \dfrac{\vec p^{\,2}}{4M_p^2} + \dfrac{\vec p^{\, \prime 2}}{4M_\Lambda ^{2}} \right) \right. \nonumber \\&\left. -\dfrac{2\,|\vec p\,| \, |\vec p\,'|}{4M_p M_\Lambda '}\,\cos \!\theta \,[2(1+\kappa )^2 -1]\right\} . \end{aligned}$$

(24)

3 Results

The first step is to use Eq. (23) to obtain the cross section for $K^- p \rightarrow \Lambda f_1(1285)$. By using Eq. (12) for the BBV coupling and a value of $\Lambda =1250$ MeV, we find $\sigma =11.07 \,\mu b$. This result is compatible with those of Ref. [24] where a bigger $\Lambda$ is demanded because extra powers of $\frac{\Lambda ^2 - m^2_{K^*}}{\Lambda ^2 -q^2}$ are used in the form factor. If we use Eq. (23) together with Eqs. (10), (11) and the form factor of Eq. (13) normalized to 1 at $q^2=0$, then we need a value $\Lambda =1900$ MeV and we get $\sigma =11.24 \,\mu b$. We shall use these two versions of the BBV vertex and evaluate the cross section for $K^0 \pi ^+ K^-$ production of Eq. (16), accepting the differences as uncertainties. The results will be given with the coupling of Eq. (12).

In Fig. 3 we show $\frac{\mathrm{d} \sigma }{\mathrm{d}\! \cos \!\theta \; \mathrm{d} \!M_\mathrm{inv}(K^0 \pi ^+ K^-)}$ for $\cos \!\theta =1$ as a function of $M_\mathrm{inv}(K^0 \pi ^+ K^-)$ for the ${\bar{K}}^0 p \rightarrow \Sigma ^+ K^0 \pi ^+ K^-$ at two ${\bar{K}}^0$ energies corresponding to $\sqrt{s}=2850$ MeV and $\sqrt{s}=3010$ MeV.

Fig. 3

Differential cross section $\frac{\mathrm{d} \sigma }{\mathrm{d}\! \cos \!\theta \; \mathrm{d} \!M_\mathrm{inv}(K^0 \pi ^+ K^-)}$ (with $\cos \!\theta =1$) for the ${\bar{K}}^0 p \rightarrow \Sigma ^+ K^0 \pi ^+ K^-$ reaction at ${\bar{K}}^0$ energy $\sqrt{s}=2850$ MeV or 3010 MeV

We observe a clear peak at the $f_1(1285)$ nominal mass, corresponding to the $K\pi {\bar{K}}$ decay of the $f_1$ [11], but interestingly we find also a peak around $M_\mathrm{inv}(K^0 \pi ^+ K^-)$ of 1420 MeV. This peak comes from the $f_1(1285)\rightarrow K^* {\bar{K}}$ when the $K^*$ becomes on shell. We should see this peak as a combination of two factors: The increasing of $M_\mathrm{inv}(K^0 \pi ^+ K^-)$ allows the intermediate $K^*$ to get on shell, increasing the cross section, but the tail of the $f_1(1285)$ tends to reduce the cross section with increasing $M_\mathrm{inv}$. The result of it is the peak seen at 1420 MeV which is hence the manifestation of the $K^* {\bar{K}}$ decay mode of the $f_1(1285)$ and does not come from any new resonance. We can make an estimate of the width of the 1420 MeV peak by taking a background below the curve, as an experimental analysis would do. A rough estimate can be done drawing a straight line between the minimum at 1350 MeV and the last point of the distribution. We find a width of about 75 MeV, a bit bigger than the average PDG value of 55 MeV [11], but in qualitative agreement considering the approximations done in the model, and the dispersion of values between different experiments tabulated in the PDG [11].

There is no need to show results for the $K^- p \rightarrow \Sigma ^0 K^0 \pi ^+ K^-$ reaction, since neglecting the $\Sigma ^0, \Sigma ^+$ mass difference the cross section is just $\frac{1}{2}$ of the former one (see Eq. (11)). At this point, it is interesting to see what happens if we use the BBV coupling of Eq. (11). The results are very similar but about a factor of two smaller. We accept this as uncertainty in our results. Yet, the important thing is that the shape of the cross section is practically identical, with about the same ratio of the strength at the 1420 MeV and 1285 MeV peaks.

In Fig. 4 we show the cross section for the $K^- p \rightarrow \Lambda K^0 \pi ^+ K^-$ reaction for $\cos \!\theta =1$ and $\sqrt{s}=2850$ MeV, 3010 MeV.

Fig. 4

Differential cross section for the $K^- p \rightarrow \Lambda K^0 \pi ^+ K^-$ reaction for $\cos \!\theta =1$ and $\sqrt{s}=2850$ MeV, 3010 MeV

The results are very similar to those shown before except that they are about a factor of 6 smaller in size, according to Eq. (11). Once again, the peak at 1420 MeV appears as before and the ratio of the strengths at the peaks is also very similar to that found before. We have also evaluated the results with the BBV input of Eqs. (10), (11) and the form factor normalized to 1 at $q^2=0$ and, as before, we find the same shape for the cross section and a size about $\frac{1}{2}$ the former one.

The size of the cross sections obtained is relatively large, and the fact that there are results in Ref. [35] guarantees its measurability in present facilities.

It is worth making some observation about possible contamination of background from other sources. In order to minimize this potential contribution, one should bear in mind that the characteristics of the peak at 1420 MeV that we obtain is that it corresponds to $K^* {\bar{K}}$, concretely $K^{*+} K^-$ and ${\bar{K}}^{*0} K^0$ since, as discussed above, the peak comes from placing the $K^*$ on shell in the diagrams of Fig. 1b, g. The other important feature is that the $K^*{\bar{K}}$ are produced in relative s-wave. These two conditions can serve as a fitter of other possible background contributions that could distort the picture that we have obtained.

When arriving to this point it is worth making some observations. In all cases we observe that the peak of the $f_1(1285)$ is always bigger than for the 1420 MeV peak. This is not a universal feature independent of the reaction. Indeed, the main ingredients are the width of the $f_1(1285)$ and the phase space for $K\pi {\bar{K}}$ production mediated by a $K^*$. However, in $\mathrm{d} \sigma / [\mathrm{d} \cos \!\theta \; \mathrm{d} M_\mathrm{inv}(f_1)]$, for fixed $\cos \!\theta$, as we have done, the ${\bar{K}}^*$ propagator depends on $M_\mathrm{inv}(f_1)$ and becomes weaker as $M_\mathrm{inv}(f_1)$ increases. We have then taken a different magnitude $\mathrm{d} \sigma / [\mathrm{d} t\; \mathrm{d} M_\mathrm{inv}(f_1)]$ ($\mathrm{d}t = 2 \,p_{K^-, \mathrm{ini}}\; p_\Sigma \;\mathrm{d} \cos \! \theta$) and have fixed t at the value of the maximum $M_\mathrm{inv}$ in Fig. 3 for $\sqrt{s}=3010$ MeV. The results are shown in Fig. 5.

Fig. 5

$\mathrm{d} \sigma / [\mathrm{d} t\; \mathrm{d} M_\mathrm{inv}(K^0 \pi ^+ K^-)]$ for $\sqrt{s}=3010$ MeV, with t fixed at $M_\mathrm{inv}= 1550$ MeV

What we see in Fig. 5 is that while the ratio of strengths in the peaks in $\mathrm{d} \sigma / [\mathrm{d} \cos \!\theta \; \mathrm{d} M_\mathrm{inv}(f_1)]$ is about 3.7 in Fig. 3, this ratio is 2.6 in Fig. 5. We simply want to draw the lesson that the relative strength of the peaks depends on the reaction and the quantity chosen to see the peaks. In this sense, the investigation of different reactions, and the present work shows one such example, is most useful to settle the issue of the meaning of the 1420 MeV peak seen in different reactions.

In this context it is worth making a survey of the different works from where the $f_1(1420)$ resonance has been claimed. The different works look at the mass distribution of the $K {\bar{K}} \pi$ channel to see the $f_1(1420)$ peak. Many of the old experiments have poor statistics and some of them do not see a signal for the $f_1(1285)$. This is not the case in more modern experiments. In general the experiments based in $\pi p$ scattering at very high energy tend to see similar strength for the $f_1(1285)$ and $f_1(1420)$ peaks [36,37,38]. However, there are exceptions. In Ref. [39] the signal for $f_1(1285)$ is bigger than for $f_1(1420)$, and with some cuts the $f_1(1420)$ signal becomes clearer and a bit magnified. In Ref. [40, 41] the strength of the $f_1(1285)$ is significantly bigger than the one of the $f_1(1420)$, and in Ref. [42] the $f_1(1285)$ signal is also magnified with some cuts. In pp induced reactions the situation is similar, many of them show a similar strength for the two peaks [43,44,45,46,47]. But, again, there are exceptions. In Ref. [48] the signal for the $f_1(1420)$ is a bit larger than for the $f_1(1285)$. In Ref. [49] the signal for the $f_1(1285)$ is bigger than for $f_1(1420)$ for a range of the chosen longitudinal momentum, while for another range the strengths are similar. There are also data in $p \bar{p}$ annihilation. In Ref. [50], producing $K {\bar{K}} \pi \pi \pi$, a similar strength for the two peaks is seen for some $K{\bar{K}} \pi$ spectra, but in the $K^0_S K^0_S \pi ^0$ channel the $f_1(1285)$ signal is clearly seen but the $f_1(1420)$ disappears if a cut of $\pi ^+ \pi ^- \pi ^0$ is made in the $\omega$ region. In $\gamma \gamma$ collisions in Ref. [51] the strength of the $f_1(1285)$ is about one third from the one of the $f_1(1420)$, but one must note that the $f_1(1285)$ falls at the beginning of the acceptance region. Another example is the Z decay studied in Ref. [52]. The bare data do not show any signal of either resonance, but when a cut is made in the $K {\bar{K}}$ invariant mass the two peaks appear with about the same strength, a bit larger for the $f_1(1420)$.

It is not clear what to conclude about the shape and strength of the two peaks, except that they depend much on the reaction and cuts made in certain observables, which means that this issue is very much tied to the dynamics of each process and each of them would deserve a separate study.

In our reaction we found the strength of the $f_1(1285)$ larger than the one of the $f_1(1420)$. We have tried to see if this is due to uncertainties of the model and for this we have investigated two sources of possible modifications. The first one is to allow the two kaons in Fig. 1 rescatter, giving rise to a triangle diagram that according to Ref. [16] develops a triangle singularity at 1420 MeV (see Eq. (18) of Ref. [16]). Technically this is implemented using the same formalism as in Ref. [14], where rescattering of the $K{\bar{K}}$ to give $\pi \eta$ was considered, substituting the $K{\bar{K}} \rightarrow \pi \eta$ amplitude by the $K{\bar{K}} \rightarrow K{\bar{K}}$ one. We find very small corrections, of the order of $10 \sim 20 \%$. This might be surprising in the presence of the triangle singularity, but without entering into further details, we should blame for it the memory that the process has of the Schmid theorem [53] (see Ref. [54] for a detailed discussion of the theorem and implications). Another aspect that we investigated was possible modifications of the $f_1(1285)$ amplitude in the region of 1420 MeV. For this we used directly the amplitude generated in Ref. [18] from the chiral unitary approach in the 1420 MeV region and, again, we found small changes of the same order of magnitude. In summary, the relative strength that we get from the $f_1(1285)$ peak to the peak at 1420 MeV does not change qualitatively.

While, without studying in detail the different reactions where the $f_1(1420)$ resonance has been claimed, we cannot dismiss it from the findings of our work, yet, the unavoidable peak that we get at 1420 MeV related to the $K^* {\bar{K}}$ decay width of the $f_1(1285)$ should be taken into account in any work aiming at describing these experiments. On the other hand, we propose some reactions where, with moderate uncertainties, we can get the cross sections and predict the strength for these two peaks. Performance of the experiment and comparison with the predictions will be an important step to learn more about the $f_1(1420)$ peak and its possible origin as we have described in this work, or a consequence of a different dynamics, including its possible nature as an ordinary mesonic resonance.

4 Conclusions

We have evaluated the cross section for the ${\bar{K}} p\rightarrow Y K^0 \pi ^+ K^-$ reactions, with ${\bar{K}}= {\bar{K}}^0, K^-$ and $Y=\Lambda , \Sigma ^0, \Sigma ^+$ in the region of invariant masses around $M_\mathrm{inv}(K^0 \pi ^+ K^-) \in [1200, 1550]$ MeV. The fact that the $f_1(1285)$ couples very strongly to the $K^* {\bar{K}}$ components has as a consequence that the mechanism with $K^*$ exchange leads to the production of that resonance in these reactions, which has been already observed in the $K^- p \rightarrow \Lambda f_1(1285)$ reaction. The novelty presented here is that, together with the $f_1(1285)$ excitation, the reaction shows a peak at 1420 MeV in all these reactions, which would be very interesting to observe experimentally. We state that such a mechanism should be taken into account in any study trying to understand the peak at 1420 MeV in the different reactions where the $f_1(1420)$ resonance has been claimed, to see if by itself it can explain the experimental features observed, in which case the arguments to advocate a new resonance would disappear. On the other hand, it is interesting to propose new reactions, prior to experiment, making predictions along the lines discussed here. The reactions proposed here go in this direction and their experimental implementation and comparison with the predictions done here certainly will help unveiling the nature of the $f_1(1420)$.