$f_0(500)$, $f_0(980)$, and $a_0(980)$ production in the $\chi _{c1} \rightarrow \eta \pi ^+\pi ^-$ reaction

Abstract

We study the $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ decay, paying attention to the production of $f_0(500)$, $f_0(980)$, and $a_0(980)$ from the final state interaction of pairs of mesons that can lead to these three mesons in the final state, which is implemented using the chiral unitary approach. Very clean and strong signals are obtained for the $a_0(980)$ excitation in the $\eta \pi$ invariant mass distribution and for the $f_0(500)$ in the $\pi ^+ \pi ^-$ mass distribution. A smaller, but also clear signal for the $f_0(980)$ excitation is obtained. The results are contrasted with experimental data and the agreement found is good, providing yet one more test in support of the picture where these resonances are dynamically generated from the meson–meson interaction.

1 Introduction

The $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ reaction has been measured by the CLEO collaboration in Ref. [1] and is presented as the reaction where a cleanest signal for the $a_0(980)$ resonance is seen. Indeed, a neat and strong peak is observed in the $\eta \pi$ invariant mass distribution, peaking around the $K \bar{K}$ threshold and with the characteristic strong cusp structure of this resonance, as observed in other high statistics experiments [2]. What makes this experiment singular is that the strength of the peak is much bigger than the rest of the distribution at other $\eta \pi$ invariant masses. The complementary $\pi ^+ \pi ^-$ mass distribution shows a clear contribution from the $f_0(500)$ resonance at lower invariant masses, a dip in the region of the $f_0(980)$ and also a strong peak for the $f_2(1270)$ resonance and of the $f_4(2050)$ at larger invariant masses. The reaction has been remeasured with much more statistics by the BESIII collaboration and is presently under internal discussion. A preliminary view of the results is available in Ref. [3], where in the region of the $f_0(980)$ a small peak seems to show up followed by a dip around $1070 \,\mathrm{MeV}$. This hence constitutes a clear case for a test of the ideas of the unitarized chiral perturbation theory. In this approach the input from chiral Lagrangians [4] for the meson–meson interaction is used in a coupled channels Bethe–Salpeter equation, from which the $f_0(500)$, $f_0(980)$, and $a_0(980)$ resonances emerge [5,6,7,8,9]. They are dynamically generated from the meson–meson interaction and would qualify as meson–meson molecular states. The same results are obtained using an equivalent unitarizing method, the inverse amplitude method, in Refs. [10,11,12,13].

The nature of the low energy scalar mesons has generated a long controversy [14]. Yet, other different approaches which start from a seed of $q \bar{q}$ for these resonances, also get a large meson–meson component for these states as soon as this seed is coupled to two mesons and the mesons are allowed to interact in a realistic scheme fulfilling unitarity [15,16,17,18]. A thorough recent review on these issues can be found in Ref. [19], presenting theoretical arguments and abundant experimental information that support the picture of the dynamical generation of these resonances and its clear difference from $q \bar{q}$ states.

The chiral unitary approach not only provides a picture for these resonances, it also allows one to make clean predictions for any reaction where these resonances are produced, providing, in the worse of the cases, when not enough dynamical information is available for the process studied, ratios for the production of the different resonances. This is a remarkable property of this approach that is not shared by other theoretical approaches trying to interpret the data. Hence experimental data could easily disprove the model, but so far this has not been the case in spite of the many reactions studied (see a recent review of B and D decays where many such reactions are analyzed and discussed [20]). Two of the most recent cases are the $B^0$ and $B^0_s$ decays into $J/\psi \pi ^+ \pi ^-$ measured in Ref. [21] and analyzed in Ref. [22] (see Refs. [23, 24] for a different approach based on the use of form factors) and the $D^0$ decay into $K^0$ and the $f_0(500)$, $f_0(980)$, and $a_0(980)$ measured in Refs. [25, 26] and analyzed in Ref. [27] (see Ref. [28] for also an approach based on form factors). Yet, the present reaction, with its spectacular signal for $a_0(980)$ production, a large signal for $f_0(500)$ and the small signal for the $f_0(980)$, all seen in the same reaction, is a case that should not be missed to challenge this theoretical approach. The purpose of the present paper is to make the theoretical study of the process along the lines of the chiral unitary approach, to confront the results with the relevant data already existing and eventually predict some features that could also be detected with the coming analysis from the BESIII large statistics experiment.

2 Formalism

The $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ decay is depicted in Fig. 1 with the quantum numbers of the different particles. The $\chi _{c1}$ has $I^G(J^{PC})\equiv 0^+(1^{++})$ and the $\eta$, $0^+(0^{-+})$. The conservation of quantum numbers indicates that the $\pi ^+ \pi ^-$ pair must have isospin $I=0$, C-parity positive, and G-parity positive. In addition, since the $\chi _{c1}$ has spin 1 we need one unity of spin or angular momentum in the final state. Since neither of the final $\eta$, $\pi ^+$, $\pi ^-$ has spin, we need to form a scalar with the polarization vector of the $\chi _{c1}$ and a momentum of one of the mesons. We can have a structure like

Fig. 1

$\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ process with the quantum numbers of the particles produced. The $\pi ^+ \pi ^-$ pair combines to $f_0(500), f_0(980)$, and $f_2(1270)$

$$\begin{aligned} V_1&= A \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\eta }, \nonumber \\ V_2&= B \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^{+}}, \\ V_3&= C \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^{-}}. \nonumber \end{aligned}$$

(1)

Let us take the first structure of $V_1$. The $\vec {p}_{\eta }$ coupling introduces $L=1$ and forces the $\pi ^+ \pi ^-$ pair to also have positive parity. With these quantum numbers, the $\pi ^+ \pi ^-$ pair can be $0^+ (0^{++})$, $0^+ (2^{++})$, and then can produce the resonance $f_0(500)$, $f_0(980)$, and $f_2(1270)$, which are well known resonances.

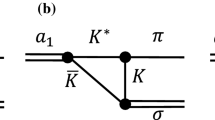
Let us single out the term of $V_2$ in Eq. (1). Now it is the $\pi ^+$ that carries $L=1$. We write for this term another diagram in Fig. 2.

Fig. 2

$\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ process with the quantum numbers of the particles produced. The $\pi ^- \eta$ pair combines to $a_0(980)$ and $a_2(1320)$

Now the $\eta \pi ^-$ system must have $I=1$ and positive parity. The angular momentum of $\pi ^- \eta$ can be $L'= 0,2$ and then we can have as primary choice $a_0(980)$ production and in the analysis of Ref. [1] they also allow $a_2(1320)$ formation.

As we can see, we can produce $f_0(500)$, $f_0(980)$, and $a_0(980)$ in the same reaction and there is still one more symmetry that we must consider and which, together with the ingredients of the chiral unitary approach, will allow us to establish the connection between the production of any of them in this reaction. The symmetry that we invoke is SU(3) symmetry. Since the $\chi _{c1}$ is a $c\bar{c}$ state, with respect to the u, d, s quarks, it behaves as a neutral system, it is a scalar of SU(3). Thus, we must construct a scalar of SU(3) with three pseudoscalar mesons. This means that we will inevitably mix the $\eta \pi ^+ \pi ^-$ with the other three meson states that can appear in the $\chi _{c1}$ decay. This will occur at a primary step of the $\chi _{c1}$ decay, but then the mesons will interact in coupled channels and finally produce the $\eta \pi ^+ \pi ^-$ in a final step.

In order to see the proper combination of three mesons that lead to a SU(3) scalar, we introduce the $q\bar{q}$ matrix M

$$\begin{aligned} M=\left( \begin{array}{ccc} u\bar{u} &{} u \bar{d} &{} u\bar{s} \\ d\bar{u} &{} d\bar{d} &{} d\bar{s} \\ s\bar{u} &{} s\bar{d} &{} s\bar{s} \\ \end{array} \right) = \left( \begin{array}{c} u \\ d \\ s \end{array}\right) \left( \begin{array}{ccc} \bar{u}&\bar{d}&\bar{s} \end{array}\right) . \end{aligned}$$

(2)

This matrix has the property

$$\begin{aligned} MMM&= \left( \begin{array}{c} u \\ d \\ s \end{array}\right) \left( \begin{array}{ccc} \bar{u}&\bar{d}&\bar{s} \end{array}\right) \left( \begin{array}{c} u \\ d \\ s \end{array}\right) \left( \begin{array}{ccc} \bar{u}&\bar{d}&\bar{s} \end{array}\right) \left( \begin{array}{c} u \\ d \\ s \end{array}\right) \left( \begin{array}{ccc} \bar{u}&\bar{d}&\bar{s} \end{array}\right) \nonumber \\&= \left( \begin{array}{c} u \\ d \\ s \end{array}\right) \left( \begin{array}{ccc} \bar{u}&\bar{d}&\bar{s} \end{array}\right) (\bar{u} u +\bar{d} d +\bar{s} s)^2 \nonumber \\&=M (\bar{u} u +\bar{d} d +\bar{s} s)^2. \end{aligned}$$

(3)

Since $(\bar{u} u +\bar{d} d +\bar{s} s)$ is a SU(3) scalar, the scalar that we form with the combination of Eq. (3) is

$$\begin{aligned} \mathrm{Trace} [M (\bar{u} u +\bar{d} d +\bar{s} s)^2] = (\bar{u} u +\bar{d} d +\bar{s} s)^3= \mathrm{Trace} [MMM]. \end{aligned}$$

Next we write the matrix M in terms of the pseudoscalar mesons, taking into account the $\eta$-$\eta '$ mixing [29] and we obtain [30]

$$\begin{aligned}&M \rightarrow \phi \nonumber \\&\quad \equiv \left( \begin{array}{c@{\quad }c@{\quad }c} \frac{1}{\sqrt{2}}\pi ^0 + \frac{1}{\sqrt{3}}\eta + \frac{1}{\sqrt{6}}\eta ' &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{1}{\sqrt{2}}\pi ^0 + \frac{1}{\sqrt{3}}\eta + \frac{1}{\sqrt{6}}\eta ' &{} K^0 \\ K^- &{} \bar{K}^0 &{} -\frac{1}{\sqrt{3}}\eta + \sqrt{\frac{2}{3}}\eta ' \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(4)

Then the combination of three mesons that behaves as a SU(3) scalar is given by¹

$$\begin{aligned} \mathrm{SU(3)[scalar]} \equiv \mathrm{Trace} (\phi \phi \phi ). \end{aligned}$$

(5)

By performing the algebra involved in Eq. (5) and isolating the $\eta$ term we find the combination

$$\begin{aligned} C_1 :~~ \eta \left( \frac{6}{\sqrt{3}} \pi ^+ \pi ^- + \frac{3}{\sqrt{3}} \pi ^0 \pi ^0 + \frac{1}{3 \sqrt{3}} \eta \eta \right) . \end{aligned}$$

(6)

Thus, when taking the structure of $V_1$ of Eq. (1), apart from a $\eta$ in P-wave we shall have a $\pi ^+ \pi ^-$, $\pi ^0 \pi ^0$ or $\eta \eta$ produced in the primary step which will undergo final state interaction to produce a $\pi ^+ \pi ^-$ pair. The $\eta$ will in principle interact with the pions but this would involve a P-wave, where the interaction is very weak and negligible in the energy region of interest to us [32]. We shall explicitly take into account the $\pi \pi$ or $\eta \eta$ interaction in S-wave [5], which will give rise to the $f_0(500)$, $f_0(980)$ resonances. We shall take into account the contribution of the $f_2(1270)$ empirically. $f_2(1270)$ appears within the local hidden gauge approach as a bound state of $\rho \rho$ in S-wave [33, 34] and decays into $\pi \pi$ in D-wave. This resonance gives a small contribution in the $\pi ^+ \pi ^-$ distribution in the region of the $f_0(500)$ and $f_0(980)$ that we are concerned about, and we take it into account to allow for a proper comparison with the data.

Similarly, if we isolate one pion to carry the P-wave, taking for instance the term $V_2$ in Eq. (1), then we find the combination

$$\begin{aligned} C_2 :~~ \pi ^+ \left( \frac{6}{\sqrt{3}} \pi ^- \eta +3 K^0 K^- \right) \end{aligned}$$

(7)

and equivalently the term with $V_3$ in Eq. (1) comes with the combination

$$\begin{aligned} C_3 :~~ \pi ^- \left( \frac{6}{\sqrt{3}} \pi ^+ \eta +3 K^+ \bar{K}^0 \right) . \end{aligned}$$

(8)

Once again, we shall now allow the $\pi \eta$ in each of these combinations to interact in S-wave, which will give rise to a big signal of the $a_0(980)$. Note that in the $C_2$ and $C_3$ combinations, the $\pi \eta$ interaction in P-wave is negligible, and since the $\pi \pi$ system is necessarily produced in $I=0$, then it cannot interact in P-wave either (in fact there is no trace of $\rho$ production in the experiment).

In the present process, we shall have the combination of the three structures of Eq. (1) and then the primary amplitude will be of the type

$$\begin{aligned} t= A~ \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\eta } + B~ \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^{+}} + C~ \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^{-}}, \end{aligned}$$

(9)

and the first thing to note is that there is no interference between these terms. Indeed, the crossed terms in $|t|^2$ after averaging over the polarization of the massive $\chi _{c1}$ state go as

$$\begin{aligned}&{\overline{ \sum }} 2 \mathrm{Re}(A B^*)\vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\eta }~\vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^{+}} \nonumber \\&\quad = 2 \mathrm{Re}(A B^*) \frac{1}{3} \delta _{ij} p_{\eta i} p_{\pi ^{+} j} = \frac{2}{3} \mathrm{Re}(A B^*) \vec {p}_{\eta } \cdot \vec {p}_{\pi ^{+}}, \end{aligned}$$

(10)

which will vanish upon integration over angles in phase space. Thus, for $|t|^2$ we shall have the sum of the squares of each amplitude in Eq. (9) which are described below.

We should note that at the tree level (Fig. 3a), the factors A, B, C in Eq. (9) stand for the basic dynamics in the $\chi _{c1} \rightarrow 3M$(M denotes meson) transition up to the flavor factors that we have evaluated. For symmetry reasons, the probability that the P-wave is in either of the mesons should be the same, and thus we should take $A=B=C$ at tree level.

Next, we must take into account the final state interaction. For the process corresponding to $V_1$ of Eq. (1) we can have $\eta \pi ^+ \pi ^-$ in the final state by considering the $C_1$ combination of Eq. (6) as depicted in Fig. 3.

Fig. 3

Production of $\eta \pi ^+ \pi ^-$ through tree level (a) and rescattering (b) of $\pi ^+ \pi ^-$ pair

We will have

$$\begin{aligned} t_{\eta }=(\vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\eta }) \tilde{t}_{\eta }, \end{aligned}$$

(11)

with

$$\begin{aligned} \tilde{t}_{\eta }=V_\mathrm{P} \left( h_{\pi ^+ \pi ^-}+\sum _i h_i S_i G_i(M_\mathrm{inv}) t_{i,\pi ^+ \pi ^-} \right) , \end{aligned}$$

(12)

where

$$\begin{aligned} h_{\pi ^+ \pi ^-}=\frac{6}{\sqrt{3}},\quad h_{\pi ^0 \pi ^0}=\frac{3}{\sqrt{3}},\quad h_{\eta \eta }=\frac{1}{3\sqrt{3}} \end{aligned}$$

(13)

are the weights of Eq. (6) and $S_i$ are symmetry and combination factors for the identical particles,

$$\begin{aligned} S_{\pi ^0 \pi ^0}=2\!\times \!\frac{1}{2} \;(\mathrm{for~ two}~ \pi ^0);\quad S_{\eta \eta }=3! \frac{1}{2} \;(\mathrm{for~ three} ~\eta ). \end{aligned}$$

The functions $G_i$ and $t_{i, \pi ^+ \pi ^-}$ are the meson–meson loop functions and scattering amplitudes, which we take from Ref. [5] updated in Refs. [22, 27].

Similarly, corresponding to $V_2$ of Eq. (1), we would have the mechanism depicted in Fig. 4.

Fig. 4

Production of $\pi ^+ \eta \pi ^-$ through tree level (a) and rescattering (b) of $\eta \pi ^-$ pair

The amplitude corresponding to the diagrams of Fig. 4 is given by

$$\begin{aligned} t_{\pi ^+}=( \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^+}) \tilde{t}_{\pi ^+}, \end{aligned}$$

(14)

with

$$\begin{aligned} \tilde{t}_{\pi ^+}= V_\mathrm{P} \left( h_{\pi ^- \eta }+\sum _i h_i G_i(M_\mathrm{inv}) t_{i,\pi ^- \eta } \right) , \end{aligned}$$

(15)

and

$$\begin{aligned} h_{\pi ^- \eta }=\frac{6}{\sqrt{3}},\quad h_{K^0 K^-}=3. \end{aligned}$$

(16)

For the process associated to $V_3$ of Eq. (1), we would have²

$$\begin{aligned} t_{\pi ^-}=( \vec {\epsilon }_{\chi _{c1}} \cdot \vec {p}_{\pi ^-}) \tilde{t}_{\pi ^-}, \end{aligned}$$

(17)

with

$$\begin{aligned} \tilde{t}_{\pi ^-}=V_\mathrm{P} \left( h_{\pi ^+ \eta }+\sum _i h_i G_i(M_\mathrm{inv}) t_{i,\pi ^+ \eta } \right) , \end{aligned}$$

(18)

and

$$\begin{aligned} h_{\pi ^+ \eta }=\frac{6}{\sqrt{3}},\quad h_{\bar{K}^0 K^+}=3. \end{aligned}$$

(19)

As mentioned before, the interaction of the meson that comes with the P-wave with any of the other two, should proceed in P-wave, which is negligible for $\pi \eta$ and zero for $\pi \pi$ which have been created in $I=0$. This makes the interpretation of the signals particularly easy in this case, since they come from either the $\pi \pi$ or $\eta \pi$ interaction in S-wave.

We can see from Eqs. (12), (13), and (15)–(18) that at tree level, prior to the final state interaction [first term in Eqs. (12), (15), and (18)], the values of $\tilde{t}_i$ are the same by taking a unique value of $V_\mathrm{P}$ in accordance with the previous conclusion that A, B, C should be equal for the tree level terms.

The amplitudes for $\pi \pi , K\bar{K}, \pi \eta$ interaction are taken from Refs. [22, 27], where only the neutral components are considered. Here we also need the charged components, which can easily be obtained using isospin symmetry and we find [35]

$$\begin{aligned} t_{K^0 K^-, \pi ^- \eta }&= \sqrt{2} t_{K^+ K^-, \pi ^0 \eta }, \nonumber \\ t_{K^+ \bar{K}^0, \pi ^+ \eta }&= \sqrt{2} t_{K^+ K^-, \pi ^0 \eta }, \\ t_{\pi ^+ \eta , \pi ^+ \eta }&= t_{\pi ^- \eta , \pi ^- \eta }=t_{\pi ^0 \eta , \pi ^0 \eta }. \nonumber \end{aligned}$$

(20)

With all these ingredients we can write the differential mass distribution for $\pi ^+ \pi ^-$ as

$$\begin{aligned} \frac{\mathrm{d} \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \pi )}=\frac{1}{(2\pi )^3}\frac{1}{4M_{\chi _{c1}}^2}\frac{1}{3}p_{\eta }^2 p_{\eta } \tilde{p}_{\pi } \left| \tilde{t}_{\eta } \right| ^2, \end{aligned}$$

(21)

where $p_{\eta }$ is the $\eta$ momentum in the $\chi _{c1}$ rest frame

$$\begin{aligned} p_{\eta }=\frac{\lambda ^{1/2}(M_{\chi _{c1}}^2, m_{\eta }^2, M_\mathrm{inv}^2(\pi \pi ))}{2M_{\chi _{c1}}}, \end{aligned}$$

(22)

and $\tilde{p}_{\pi }$ is the pion momentum in the $\pi ^+ \pi ^-$ rest frame

$$\begin{aligned} \tilde{p}_{\pi }=\frac{\lambda ^{1/2}(M_\mathrm{inv}^2(\pi \pi ), m_{\pi }^2, m_{\pi }^2)}{2M_\mathrm{inv}(\pi \pi )}. \end{aligned}$$

(23)

For the case of $\pi \eta$ invariant mass we would sum the contributions of $\pi ^+ \eta$ and $\pi ^- \eta$, which would give the same contribution, hence, the formula for $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \eta )}$, to be compared with experiment, will be

$$\begin{aligned} \frac{\mathrm{d} \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \eta )}=\frac{2}{(2\pi )^3}\frac{1}{4M_{\chi _{c1}}^2}\frac{1}{3}p_{\pi }^2 p_{\pi } \tilde{p}_{\eta } \left| \tilde{t}_{\pi ^+} \right| ^2, \end{aligned}$$

(24)

where now

$$\begin{aligned} p_{\pi }= & {} \frac{\lambda ^{1/2}(M_{\chi _{c1}}^2, m_{\pi }^2, M_\mathrm{inv}^2(\pi \eta ))}{2M_{\chi _{c1}}},\end{aligned}$$

(25)

$$\begin{aligned} \tilde{p}_{\eta }= & {} \frac{\lambda ^{1/2}(M_\mathrm{inv}^2(\pi \eta ), m_{\pi }^2, m_{\eta }^2)}{2M_\mathrm{inv}(\pi \eta )}. \end{aligned}$$

(26)

The factor $V_\mathrm{P}$ is the only unknown quantity in our approach, which provides a global normalization, and it is fitted to the data. Note that the factors A, B, and C in Eq. (1) are absorbed in factor $V_\mathrm{P}$.

In principle we could have summed all the amplitudes and use the general $\frac{\mathrm{d}^2 \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \pi )~\mathrm{d} M_\mathrm{inv}(\pi \eta )}$ formula, integrating over each of them to find the invariant mass distribution of the other pair. In practice, we find it unnecessary for the comparison of our results with data in the relevant region of invariant masses. The reason can be seen in the Dalitz plot that we show in Fig. 5.

Fig. 5

Dalitz plot for the $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ decay

If we consider $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \eta )}$ in the region of the $a_0(980)$, the $\pi \pi$ invariant mass has a range between $500 \,\mathrm{MeV}$ and $2800 \,\mathrm{MeV}$. So its strength is divided over a large range of $\pi \pi$ invariant masses, providing a smooth background in the $\pi \pi$ mass distribution. We will take this into account empirically, following the analysis of Ref. [3].

There is another element to consider. We have taken the $\pi \eta$ invariant mass from the interacting pair of Fig. 4b. Since one is summing $\pi ^+ \eta$ and $\pi ^- \eta$ distributions, one would also have to account for the invariant mass distribution of the $\eta$ with the odd pion carrying the P-wave. Yet, it is easy to see where this mass distribution goes. Indeed, using the property

$$\begin{aligned} m^2_{12} + m^2_{13} +m^2_{23} = M^2_{\chi _{c1}} + m^2_{\pi }+m^2_{\pi }+m^2_{\eta }, \end{aligned}$$

taking $m_{23}=980 \, \mathrm{MeV}$ and $m_{12}\simeq 1200 \, \mathrm{MeV}$ (in the middle of the phase space allowed in the Dalitz plot), we find $m_{13} \simeq 2968 \, \mathrm{MeV}$, which is very far away from the region of the $a_0(980)$ and does not disturb the shape and strength of the $a_0(980)$.

Similarly, we will find a large contribution in the $\pi \pi$ invariant mass distribution from the $f_0(500)$. Once again, by looking at the Dalitz plot, we see the strength is distributed in a region of $\pi \eta$ invariant masses from $1200\,\mathrm{MeV}$ to $3400\,\mathrm{MeV}$, again a large region of invariant masses, but the most important for our discussion is that it does not contribute below the peak of the $a_0(980)$. Thus, the signal for the $a_0(980)$ is clean and easy to interpret, coming basically from the $\pi \eta$ interaction.

3 Results

In Fig. 6, we show our results for the $\pi \eta$ invariant mass distribution.

Fig. 6

$\pi \eta$ invariant mass distribution for the $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ decay. Preliminary BESIII data from Ref. [3]. Black solid line $q_\mathrm{max}=600 \,\mathrm{MeV}$; green dashed line $q_\mathrm{max}=630 \,\mathrm{MeV}$; red dotted line $q_\mathrm{max}=580 \,\mathrm{MeV}$

The parameter $V_\mathrm{P}$ has been adjusted to the strength of the experimental preliminary data of BESIII at its peak [3]. As we can see, both theory and experiment show the typical huge cusp form of the $a_0(980)$. The agreement of our results with experiment is quite good, but one can see that the theoretical results are a bit higher than experiment below $980\,\mathrm{MeV}$ and a bit lower above that energy. In order to see if these discrepancies are due to uncertainties of the model or another source, we have changed a bit the cut off ($q_\mathrm{max}$), from the central value of $600\,\mathrm{MeV}$ to $580\,\mathrm{MeV}$ and $630\,\mathrm{MeV}$.³ We see that the changes are small. With $q_\mathrm{max}=630 \,\mathrm{MeV}$, one finds a small improvement at higher energies and not much change at lower energies. We tentatively conclude that the discrepancies are due to the effect of background from other contributions not explicitly considered in our approach and which appear in the experiment [3]. One might think that the background should further increase the mass distribution, but this is not necessarily the case because there can be interference of terms. In fact, we have a good example that this can be the case in the study of the $\eta _c \rightarrow \eta \pi ^+\pi ^-$ decay in Ref. [31]. There the coherent sum of the different terms contributing to the reaction has the effect of reducing $\mathrm{d} \Gamma / \mathrm{d} M_{\pi \eta }$ below the peak of the $a_0(980)$ and increasing it above this energy, with respect to the mechanism of Fig. 4 considered here, in an amount of the order of the discrepancies seen in Fig. 6. Although the S-wave case in Ref. [31] is different from the P-wave case that we have here, the results of Ref. [31] can serve to give an idea of possible effects of background in this channel and energy region.

In Fig. 7 we plot the invariant mass distribution for the $\pi ^+ \pi ^-$, using the same $V_\mathrm{P}$ factor determined before.

Fig. 7

$\pi \pi$ invariant mass distribution for the $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ decay. Preliminary BESIII data from Ref. [3]. The purple short dashed line is the theoretical prediction with $q_\mathrm{max}=600 \,\mathrm{MeV}$. The black solid line, the green dashed line and the red dotted line add an empirical background (see text), corresponding the results with $q_\mathrm{max}=600 \,\mathrm{MeV}$, $630 \,\mathrm{MeV}$, and $580 \,\mathrm{MeV}$, respectively

What we see is a relatively large strength for the production of the $f_0(500)$ and a small contribution from the $f_0(980)$. The experiment reflects both, a broad peak in the $f_0(500)$ region, and a rapid increase of the distribution in the region of $980 \,\mathrm{MeV}$. Our contribution of the $f_0(980)$ is rather sharp, while the experiment has a resolution of $20 \,\mathrm{MeV}$, and the raise of $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_\mathrm{inv}(\pi \pi )}$ around $980 \,\mathrm{MeV}$ is not so sharp. We should note that the strength of the $f_0(500)$ at its peak is about 110 events/10 MeV, compared to 560 events/10 MeV of the $a_0(980)$ at its peak. The signal for the $a_0(980)$ is thus quite big. Even integrating the strength of the $a_0(980)$ up to $1200 \,\mathrm{MeV}$ and the one of the $f_0(500)$ up to $1000 \,\mathrm{MeV}$, we find a strength for the $a_0(980)$ almost 2.7 times bigger than that of the $f_0(500)$.

It is interesting to recall that the features of the $\pi \pi$ mass distribution are remarkably similar to those of the $J/\psi \rightarrow \omega \pi \pi$ reaction measured in Refs. [36, 37], which was studied along similar lines as here in Refs. [38, 39].

The features observed here are also similar to those observed in the $\bar{B}^0$ decay into $D^0$ and $f_0(500)$, $f_0(980)$, and $a_0(980)$ [40], yet the relative strength of the structures found is different and is related to the weight of the different meson–meson components prior to the final state interaction. The fact that one describes all these reactions with this picture, and the chiral unitary approach for the meson–meson interaction, offers support for the picture of these resonances as dynamically generated from the meson–meson interaction. Together with other reactions mentioned in the Introduction, the support for this picture is, indeed, remarkable.

To facilitate the comparison with the data, we have added a background, very similar to the one of Ref. [3] coming from the $a_0(980)$ peak, and which we have taken linear in the invariant mass for simplicity. In addition, to account for the tail of the $f_2(1270)$, which shows up in Fig. 7 at high invariant masses, we have taken a Breit–Wigner shape, with physical mass and width, and adjusted the strength to reproduce the data around 1100–$1200\,\mathrm{MeV}$. The agreement with the $\pi \pi$ mass distribution is quite good, with some discrepancy around 1000–$1040\, \mathrm{MeV}$. As mentioned above, the data shows a fast raise around $980 \,\mathrm{MeV}$ as our theory predicts, only that the theoretical raise is sharper than experiment, where data are collected in bins of $20 \,\mathrm{MeV}$. On the other hand, the data shows a peak around $1040 \,\mathrm{MeV}$, which the theory cannot reproduce, even if we convolute the $f_0(980)$ signal with the experimental resolution. The discrepancy is in two experimental points and it would be worth checking whether this is just a fluctuation or a genuine peak. We should note that in Ref. [1], the data, with admittedly smaller statistics, one does not see a structure around 1000–$1060 \,\mathrm{MeV}$ like in Ref. [3].

In Fig. 7, as in Fig. 6, we also show the results increasing or decreasing a bit $q_\mathrm{max}$ with respect to the central value of $q_\mathrm{max}=600 \,\mathrm{MeV}$. As in the case of Fig. 6, we see that the changes are small, and smaller than the effects of the background from other sources.

In any case, the data of Ref. [3] is also telling us that the strength of the $f_0(980)$ is far smaller than the one of the $f_0(500)$, as the theory predicts. It would be interesting to see what comes out from the final analysis of Ref. [3], which motivated our work. A partial wave analysis can separate the contribution of the different structures, allowing for a more quantitative comparison with our results.

4 Conclusions

We have made a study of the $\chi _{c1} \rightarrow \eta \pi ^+ \pi ^-$ reaction, looking at the $\pi ^+ \pi ^-$ and $\eta \pi$ invariant mass distributions. We have used a simple picture to combine the mesons to give a singlet of SU(3), which corresponds to the $c \bar{c}$ nature of the $\chi _{c1}$. This gives us the relative weights of three mesons at a primary production step, which can revert into the $\eta \pi ^+ \pi ^-$ in the final state upon interaction of pairs of mesons in coupled channels. We have used the chiral unitary approach to describe this interaction, which generates the $f_0(500)$, $f_0(980)$, and $a_0(980)$ scalar mesons. The interesting feature of the approach is that, up to a global normalization constant, we are able to construct the $\pi \pi$ and $\eta \pi$ invariant mass distributions and compare with the experimental data available. We observed a prominent signal of the $a_0(980)$ production with a relative strength to the other two resonances much bigger than in other reactions studied previously. We also observed a clear signal for $f_0(500)$ production in the $\pi ^+ \pi ^-$ mass distribution and also a clear signal for $f_0(980)$ production, but with much smaller strength. The agreement with experiment is quite good in the two invariant mass distributions up to about $1040 \,\mathrm{MeV}$, once a background borrowed from the experiment is implemented in the $\pi \pi$ distribution. We also justified that no background for the $\eta \pi$ distribution was needed in that energy range.

We noted some small discrepancy with the data around $1040 \,\mathrm{MeV}$, which could be given extra attention in the final analysis of the work of Ref. [3].

The agreement found in general lines for the shapes and strengths of the $f_0(500)$, $f_0(980)$, and $a_0(980)$ excitation in this reaction adds to the long list of reactions that give support to these resonances as being dynamically generated from the interaction of pseudoscalar mesons.