Entanglement dynamics for static two-level atoms in cosmic string spacetime

Abstract

We study the entanglement dynamics of two static atoms coupled with a bath of fluctuating scalar fields in vacuum in the cosmic string spacetime. Three different alignments of atoms, i.e. parallel, vertical, and symmetric alignments with respect to the cosmic string are considered. We focus on how entanglement degradation and generation are influenced by the cosmic string, and find that they are crucially dependent on the atom-string distance r, the interatomic separation L, and the parameter $\nu$ that characterizes the nontrivial topology of the cosmic string. For two atoms initially in a maximally entangled state, the destroyed entanglement can be revived when the atoms are aligned vertically to the string, which cannot happen in the Minkowski spacetime. When the symmetrically aligned two-atom system is initially in the antisymmetric state, the lifetime of entanglement can be significantly enhanced as $\nu$ increases. For two atoms which are initially in the excited state, when the interatomic separation is large compared to the transition wavelength, entanglement generation cannot happen in the Minkowski spacetime, while it can be achieved in the cosmic string spacetime when the position of the two atoms is appropriate with respect to the cosmic string and $\nu$ is large enough.

1 Introduction

Quantum entanglement is one of the most intriguing properties in quantum mechanics [1], and it plays a key role in quantum information and quantum computing [2, 3]. However, entanglement degrades due to the inevitable interactions between quantum systems and environment [4], which is one of the main obstacles to the realization of quantum information technologies. In particular, a pair of initially entangled atoms can become separable within a finite time, which is referred to as entanglement sudden death [5, 6]. However, in certain circumstances, entanglement can be generated rather than destroyed due to indirect interactions between atoms provided by the common bath they immersed in [7,8,9,10,11]. Meanwhile, the destroyed entanglement can also be recreated, depending on the initial state of the two atoms as well as the environment, known as entanglement revival [12].

In recent years, there is increasing interest in the study of entanglement generation in non-inertial frames and in curved spactime [13,14,15,16,17,18,19,20,21,22,23,24], focusing on the effects of acceleration and spacetime curvature on entanglement dynamics. In this paper, we are concerned with how the entanglement dynamics of a two-atom system is influenced if the atoms are placed in a locally flat spacetime but with nontrivial topology. In particular, we consider two static two-level atoms in cosmic string spacetime. Cosmic strings are topological defects that may have been created in the early Universe during phase transitions [25]. The simplest cosmic string spacetime is that of a static, straight and infinitely thin cosmic string, which can be regarded as a flat spacetime with a planar angle deficit. Quantum fields propagating in the cosmic string spacetime are inevitably influenced by the nontrivial topology, and many quantum effects, such as the vacuum expectations of stress-energy tensor [26,27,28,29,30,31], the Casimir–Polder effect [32], atomic transition rate [33,34,35,36], resonance interaction [37], and lightcone fluctuations [38, 39] have been studied, which exhibit behaviors similar to those in a flat spacetime with a boundary. Therefore, it is also of interest to investigate the entanglement dynamics of two static atoms coupled with the vacuum fluctuations of massless scalar fields in the cosmic string spacetime, and compare the result with that in the Minkowski spacetime with a reflecting boundary [10, 17, 24].

In this paper, we study the entanglement dynamics of two mutually independent, static two-level atoms coupled with a bath of fluctuating massless scalar fields in vacuum in the cosmic string spacetime. We consider three different alignments of atoms, i.e. parallel, vertical, and symmetric alignments with respect to the cosmic string. In particular, we investigate how the entanglement degradation and generation are influenced by the cosmic string, and compared the results with those in the free Minkowski spacetime case, as well as those in the case of a Minkowski spacetime with a reflecting boundary.

2 The master equation

We study the entanglement dynamics of a two-atom system coupled with a bath of fluctuating scalar fields in vacuum in the cosmic string spacetime. The total Hamiltonian of the system can be expressed in the following form,

$$\begin{aligned} H=H_{S}+H_{F}+H_{I}. \end{aligned}$$

(1)

Here $H_{S}$ is the Hamiltonian of the two-atom system,

$$\begin{aligned} H_{S}=\frac{\omega }{2}\sigma _3^{(1)}+\frac{\omega }{2}\sigma _3^{(2)}, \end{aligned}$$

(2)

where $\sigma _i^{(1)}=\sigma _i\otimes \sigma _0$, $\sigma _i^{(2)}=\sigma _0\otimes \sigma _i$, with $\sigma _i~(i=1,2,3)$ being the Pauli matrices, $\sigma _0$ is the $2\times 2$ unit matrix, and $\omega$ denotes the energy level spacing of the atoms. $H_{F}$ is the Hamiltonian of the scalar field. $H_{I}$ denotes the interaction between the atoms and the scalar field, which can be written as

$$\begin{aligned} H_{I}=\mu [\sigma _2^{(1)} \phi (t,\vec {x}_{1})+\sigma _2^{(2)} \phi (t,\vec {x}_{2})], \end{aligned}$$

(3)

where $\mu$ is the coupling constant which is assumed to be small.

At first, we assume that the two-atom system and the quantum fields are decoupled, so the initial state of the total system takes the form $\rho _{tot}(0)=\rho (0)\otimes |0\rangle \langle 0|$, where $\rho (0)$ is the initial state of the two-atom system, and $|0\rangle$ denotes vacuum state of the scalar fields. In the weak-coupling limit, the reduced density matrix of the two-atom system takes the Kossakowski–Lindblad form [40, 41]

$$\begin{aligned} \frac{\partial \rho (t)}{\partial t}=-i[H_{eff},\rho (t)]+\mathcal {D}[\rho (t)], \end{aligned}$$

(4)

where

$$\begin{aligned} H_{eff}=H_{S}-\frac{i}{2}\sum _{\alpha ,\beta =1}^{2}\sum _{i,j=1}^{3}H_{ij}^{(\alpha \beta )}\sigma _{i}^{(\alpha )} \sigma _{j}^{(\beta )}, \end{aligned}$$

(5)

and

$$\begin{aligned} \mathcal {D}[\rho (t)]=\frac{1}{2}\sum _{\alpha ,\beta =1}^{2}\sum _{i,j=1}^{3}C^{(\alpha \beta )}_{ij}[2\sigma ^{(\beta )}_{j}\rho \sigma ^{(\alpha )}_{i}-\sigma ^{(\alpha )}_{i}\sigma ^{(\beta )}_{j}\rho -\rho \sigma ^{(\alpha )}_{i}\sigma ^{(\beta )} _{j}]. \end{aligned}$$

(6)

Here $C^{(\alpha \beta )}_{ij}$ and $H^{(\alpha \beta )}_{ij}$ are related to the Fourier and Hilbert transforms, $\mathcal {G}^{(\alpha \beta )}(\lambda )$ and $\mathcal {K}^{(\alpha \beta )}(\lambda )$, of the scalar field correlation functions,

$$\begin{aligned} G^{(\alpha \beta )}(\Delta t)=\langle \phi (t,\vec {x}_{\alpha })\phi (t^{\prime },\vec {x}_{\beta })\rangle , \end{aligned}$$

(7)

where $\Delta t=t-t^{\prime }$, which can be expressed as

$$\begin{aligned}&\mathcal {G}^{(\alpha \beta )}(\lambda )=\int ^\infty _{-\infty }\,d\Delta t e^{i\lambda \Delta t}G^{(\alpha \beta )}(\Delta t), \end{aligned}$$

(8)

$$\begin{aligned}&\mathcal {K}^{(\alpha \beta )}(\lambda )=\frac{P}{\pi i}\int ^\infty _{-\infty }\,d\omega \frac{\mathcal {G}^{(\alpha \beta )}(\omega )}{\omega -\lambda }, \end{aligned}$$

(9)

where P denotes principal value. Then $C^{(\alpha \beta )}_{ij}$ can be represented as

$$\begin{aligned} C^{(\alpha \beta )}_{ij}=A^{(\alpha \beta )}\delta _{ij}-iB^{(\alpha \beta )}\epsilon _{ijk}\delta _{3k}-A^{(\alpha \beta )}\delta _{3i}\delta _{3j}, \end{aligned}$$

(10)

where

$$\begin{aligned} A^{(\alpha \beta )}=\frac{\mu ^2}{4}[\mathcal {G}^{(\alpha \beta )}(\omega )+\mathcal {G}^{(\alpha \beta )}(-\omega )],\nonumber \\ B^{(\alpha \beta )}=\frac{\mu ^2}{4}[\mathcal {G}^{(\alpha \beta )}(\omega )-\mathcal {G}^{(\alpha \beta )}(-\omega )]. \end{aligned}$$

(11)

To study the time evolution of the reduced density matrix, we choose the coupled basis $\{|G\rangle =|00\rangle ,|A\rangle =\frac{1}{\sqrt{2}}(|10\rangle -|01\rangle ),|S\rangle =\frac{1}{\sqrt{2}}(|10\rangle + |01\rangle ),|E\rangle =|11\rangle \ \}$. Rewriting Eq. (10) as

$$\begin{aligned}&C^{(11)}_{ij}=A_{1}\delta _{ij}-iB_{1}\epsilon _{ijk}\delta _{3k}-A_{1}\delta _{3i}\delta _{3j},\nonumber \\&C^{(22)}_{ij}=A_{2}\delta _{ij}-iB_{2}\epsilon _{ijk}\delta _{3k}-A_{2}\delta _{3i}\delta _{3j},\nonumber \\&C^{(12)}_{ij}=C^{(21)}_{ij}=A_{3}\delta _{ij}-iB_{3}\epsilon _{ijk}\delta _{3k}-A_{3}\delta _{3i}\delta _{3j}, \end{aligned}$$

(12)

then a series of equations describing the evolution of the two-atom system can be written as

$$\begin{aligned} \dot{\rho }_{GG}= & {} -2(A_{1}-B_{1}+A_{2}-B_{2})\rho _{GG}\nonumber \\&+\,(A_{1}+B_{1}+A_{2}+B_{2}-2A_{3}-2B_{3})\rho _{AA}\nonumber \\&+\,(A_{1}+B_{1}+A_{2}+B_{2}+2A_{3}\nonumber \\&+\,2B_{3})\rho _{SS}+(A_{1}+B_{1}-A_{2}-B_{2})(\rho _{AS}+\rho _{SA}),\nonumber \\ \dot{\rho }_{EE}= & {} -2(A_{1}+B_{1}+A_{2}+B_{2})\rho _{EE}+(A_{1}-B_{1}\nonumber \\&+\,A_{2}-B_{2}-2A_{3}+2B_{3})\rho _{AA} \nonumber \\&+\,(A_{1}-B_{1}+A_{2}-B_{2}+2A_{3}-2B_{3})\rho _{SS}\nonumber \\&+\,(-A_{1}+B_{1}+A_{2}-B_{2})(\rho _{AS}+\rho _{SA}),\nonumber \\ \dot{\rho }_{SS}= & {} -2(A_{1}+A_{2}+2A_{3})\rho _{SS}+(A_{1}-B_{1}\nonumber \\&+\,A_{2}-B_{2}+2A_{3}-2B_{3})\rho _{GG}\nonumber \\&+\,(A_{1}+B_{1}+A_{2}+B_{2}+2A_{3}+2B_{3})\rho _{EE}\nonumber \\&+\,(-B_{1}+B_{2})(\rho _{AS}+\rho _{SA}),\nonumber \\ \dot{\rho }_{AA}= & {} -2(A_{1}+A_{2}-2A_{3})\rho _{AA}+(A_{1}-B_{1}+A_{2}\nonumber \\&-\,B_{2}-2A_{3}+2B_{3})\rho _{GG}\nonumber \\&+\,(A_{1}+B_{1}+A_{2}+B_{2}-2A_{3}-2B_{3})\rho _{EE}\nonumber \\&+\,(-B_{1}+B_{2})(\rho _{AS}+\rho _{SA}),\nonumber \\ \dot{\rho }_{AS}= & {} -2(A_{1}+A_{2})\rho _{AS}+(A_{1}-B_{1}-A_{2}+B_{2})\rho _{GG}\nonumber \\&+\,(-A_{1}-B_{1}+A_{2}+B_{2})\rho _{EE}\nonumber \\&+\,(-B_{1}+B_{2})(\rho _{SS}+\rho _{AA}),\nonumber \\ \dot{\rho }_{SA}= & {} -2(A_{1}+A_{2})\rho _{SA}+(A_{1}-B_{1}-A_{2}+B_{2})\rho _{GG}\nonumber \\&+\,(-A_{1}-B_{1}+A_{2}+B_{2})\rho _{EE}\nonumber \\&+\,(-B_{1}+B_{2})(\rho _{SS}+\rho _{AA}),\nonumber \\ \dot{\rho }_{GE}= & {} -2(A_{1}+A_{2})\rho _{GE},\nonumber \\ \dot{\rho }_{EG}= & {} -2(A_{1}+A_{2})\rho _{EG}, \end{aligned}$$

(13)

where $\rho _{IJ}=\langle I|\rho | J\rangle \,,I,J\in \{G,E,A,S\}$. The differential equations above can be solved analytically, and the explicit expressions are given in Appendix A.

We take concurrence [42] as a measurement of quantum entanglement, which is 1 for maximally entangled states and 0 for separable states. For the X states, the concurrence can be calculated as [43]

$$\begin{aligned} C[\rho (t)]= \mathrm {max} \{0,K_1(t),K_2(t)\}, \end{aligned}$$

(14)

where

$$\begin{aligned} K_1(t)= & {} \sqrt{[\rho _{AA}(t)-\rho _{SS}(t)]^2-[\rho _{AS}(t)-\rho _{SA}(t)]^2}\nonumber \\&-\,2\sqrt{\rho _{GG}(t) \rho _{EE}(t)}, \end{aligned}$$

(15)

$$\begin{aligned} K_2(t)= & {} 2 \left| \rho _{GE}(t)\right| \nonumber \\&-\,\sqrt{[\rho _{AA}(t)+\rho _{SS}(t)]^2-[\rho _{AS}(t)+\rho _{SA}(t)]^2}.\nonumber \\ \end{aligned}$$

(16)

3 Quantum scalar field in the cosmic string spacetime

The line element in the spacetime of a static, straight cosmic string can be written as

$$\begin{aligned} ds^2=dt^2-dr^2-r^2d\theta ^2-dz^2, \end{aligned}$$

(17)

where $0\le \theta <\frac{2\pi }{\nu }$. Here $\nu =(1-4G\mu )^{-1}$, with $\mu$ being the mass per unit length of the string, and G the Newtonian constant. The spacetime described by the metric above is locally flat but with a nontrivial global topology characterized by a deficit angle $8\pi G \mu$.¹ In the cosmic string spacetime, the Klein–Gordon equation of scalar field can be expressed as

$$\begin{aligned} \left( \partial ^2_t-\frac{1}{r}\partial _r(r \partial _r)-\frac{1}{r^2}\partial ^2_\theta -\partial ^2_z \right) \phi (t,\vec {x})=0. \end{aligned}$$

(18)

Solving the equation above, one obtains a complete set of normal field modes [33]

$$\begin{aligned} u_{j}(t,\vec {x})=u_{j}(\vec {x}) e^{-i\omega t}, \end{aligned}$$

(19)

with

$$\begin{aligned} u_{j}(\vec {x})=\frac{1}{2\pi }\sqrt{\frac{\nu }{2\omega }}J_{\left| \nu m\right| }(k_\bot r)e^{i(\nu m\theta +k_3z)}. \end{aligned}$$

(20)

where J is the Bessel J function, the subscript $j=(k_3,k_\perp ,m)$, with m being an integer. Here $\omega =\sqrt{k^2_3+k^2_\perp }$, with $k_3\in (-\infty ,+\infty )$, and $k_\perp \in (0,+\infty )$. The modes are normalized according to

$$\begin{aligned} -i \int \;d^3x\,u_{j}(t,\vec {x})\overleftrightarrow {\partial _t} u^*_{j^\prime }(t,\vec {x})=\delta _{j,j^\prime }. \end{aligned}$$

(21)

Now the field operator can be expanded with the complete set of normal modes as

$$\begin{aligned} \phi (t,\vec {x})=\int \,d\mu _j[c_{j}(t)u_{j}(\vec {x})+c_{j}^\dagger (t)u^*_{j}(\vec {x})], \end{aligned}$$

(22)

in which

$$\begin{aligned} \int \,d\mu _j\equiv \sum _{m=-\infty }^\infty \,\int _{-\infty }^\infty \,dk_3\,\int _0^\infty dk_\perp k_\perp , \end{aligned}$$

(23)

and $c_{j}(t)=c_{j}(0)e^{-i\omega t}$ and $c_{j}^\dagger (t)=c_{j}^\dagger (0)e^{i\omega t}$ express respectively the annihilation and creation operators. The commutation relations of the annihilation and creation operators show that

$$\begin{aligned} {[}c_{j}(t,\vec {x}),c_{j^{'}}^\dagger (t,\vec {x})]=\delta _{j,j^{'}}. \end{aligned}$$

(24)

Then, the correlation function can be written as

$$\begin{aligned}&\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle =\frac{\nu }{8\pi ^2}\sum _{m=-\infty }^{\infty }\int ^\infty _0 dk_\perp \int ^\infty _{-\infty }dk\frac{k_\perp }{\omega }\nonumber \\&\times \, J_{\nu \left| m\right| }(k_\perp r)J_{\nu \left| m\right| }(k_\perp r^{\prime })e^{ik_3 \Delta z}e^{-i\omega \Delta t} e^{i \nu m \Delta \theta }, \end{aligned}$$

(25)

where $\Delta t=t-t^\prime$, $\Delta \theta =\theta -\theta ^{\prime }$, and $\Delta z=z-z^{\prime }$. Let

$$\begin{aligned} k_3=\omega \cos \varphi ,\qquad k_\perp =\omega \sin \varphi , \end{aligned}$$

(26)

then the correlation function can be rewritten as

$$\begin{aligned}&\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle \nonumber \\&\quad =\frac{\nu }{8\pi ^2}\sum _{m=-\infty }^{\infty } \int ^\pi _0 d\varphi \int ^\infty _0 d\omega \omega \sin \varphi \nonumber \\&\quad \times \, J_{\left| \nu m\right| }(\omega r \sin \varphi )J_{\left| \nu m\right| }(\omega r^{\prime } \sin \varphi ) e^{-i \omega \Delta t} e^{i \omega \Delta z \cos \varphi } e^{i \nu m \Delta \theta },\nonumber \\ \end{aligned}$$

(27)

and the Fourier transform takes the form

$$\begin{aligned} \mathcal {G}^{(\alpha \beta )}(\omega )=\left\{ \begin{aligned}&\frac{\nu \,\omega }{4 \pi }\sum _{m=-\infty }^{\infty }\int ^\pi _0 d\varphi \sin \varphi \times J_{\nu \left| m\right| }(\omega r \sin \varphi )\\&J_{\nu \left| m\right| }(\omega r^{\prime } \sin \varphi )e^{i \omega \Delta z \cos \varphi }e^{i \nu m \Delta \theta }, ~~\;\omega >0\;,\\&0,\qquad \qquad \quad \qquad \qquad \qquad \qquad \qquad \quad ~~~~ \omega <0\;.\\ \end{aligned} \right. \end{aligned}$$

(28)

4 Entanglement dynamics of two-atom system

In this section, we investigate the entanglement dynamics of two static atoms coupled with a bath of fluctuating scalar fields in vacuum in the cosmic string spacetime. We assume that the separation between the two atoms is L, and consider three different alignments of atoms, i.e. parallel, vertical, and symmetric alignments with respect to the cosmic string, as shown in Fig. 1. In particular, we will study the entanglement degradation and generation for atoms placed at different distances to the cosmic string, and compared the results with those in the free Minkowski spacetime, and in the case of the Minkowski spacetime with a reflecting boundary. For simplicity, in the following, we assume $\nu$ is an integer.

Fig. 1

The parallel (left), vertical (middle) and symmetric (right) alignments of atoms with respect to the cosmic string

4.1 Entanglement degradation

We begin our discussion with the entanglement degradation of two-atom systems initially prepared in the symmetric state $|S\rangle$ and the antisymmetric state $|A\rangle$, both of which are maximally entangled.

4.1.1 Two-atom system placed extremely close to the cosmic string

I. Parallel alignment When the two atoms are aligned parallel to the cosmic string, the concurrence takes the form

$$\begin{aligned} C[\rho (t)]=e^{-4(A_1\pm A_3) t}, \end{aligned}$$

(29)

where the ± sign refers to the symmetric state and the antisymmetric state respectively. It is obvious that the concurrence always decays monotonically in this case.

When the distance between the two-atom system and the string is extremely small, the corresponding coefficients take the form $A_1=\frac{\nu \Gamma _0}{4}, A_3=\frac{\nu \Gamma _0}{4} \frac{\sin (\omega \, L)}{\omega \, L}$, which can be derived from Eqs. (B4)–(B5) in Appendix B by taking the limit $\omega r\rightarrow 0$. When the interatomic separation is vanishingly small ($\omega L\rightarrow 0$), $A_1=A_3=\frac{\nu \Gamma _0}{4}$. For atoms initially in the antisymmetric state $|A\rangle$, the two atoms remain maximally entangled during evolution as if it were a closed system. When the interatomic separation is very large ($\omega L\rightarrow \infty$), we have $A_3=0$, so the evolution of concurrence is the same whether the initial state is the symmetric state $|S\rangle$ or the antisymmetric state $|A\rangle$. Now we compare the result with those in the Minkowski spacetime, and in the case of a Minkowski spacetime with a reflecting boundary. Note that the concurrence in the latter two cases take the same form as Eq. (29), but with different coefficients. For the Minkowski spacetime case, the coefficients are $A_1=\frac{\Gamma _0}{4}, A_3=\frac{\Gamma _0}{4} \frac{\sin (\omega \, L)}{\omega \, L}$. So when the two atoms are placed extremely close to the string, the concurrence evolves $\nu$ times as fast as that in the Minkowski spacetime. For the case of the Minkowski spacetime with a reflecting boundary, one gets $A_1=A_3=0$ when the atoms are extremely close to the boundary, c.f. Eqs. (B17)–(B18). Therefore, the two-atom system will remain maximally entangled as if it were a closed system, regardless of the interatomic separation and the initial state, which is different from the cosmic string case.

II. Vertical alignment In the vertical case, the expression of concurrence can be calculated as

$$\begin{aligned}&C[\rho (t)]\nonumber \\&\;=\frac{e^{-2(A_1+A_2) t}\left[ (A_1-A_2)^2+4 {A_3}^2\cosh (2 \gamma t)\mp 2 A_3 \gamma \sinh (2 \gamma t)\right] }{\gamma ^2}, \end{aligned}$$

(30)

where $\gamma =\sqrt{(A_1-A_2)^2+4{A_3}^2}$, and the $\mp$ sign refers to the symmetric state $|S\rangle$ and the antisymmetric state $|A\rangle$ respectively. In this case, since the coefficients $A_1\ne A_2$ (see Eqs. (B9)–(B11) in Appendix B), the expression is rather complicated. In particular, it is not monotonous, so entanglement revival may happen in certain cases.

Fig. 2

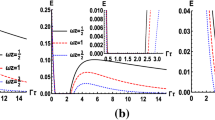
Entanglement dynamics for vertically aligned atoms initially prepared in $|S\rangle$. On the left, the black, green, and red lines correspond to $\omega L=1/4,1,4$, respectively, with $\nu =2$. On the right, the dot-dashed blue, real red, green, and black lines correspond to $\nu =1,2,5,8$, respectively, with $\omega L=1$. Note that $\nu =1$ corresponds to the Minkowski spacetime

Fig. 3

Entanglement dynamics for vertically aligned atoms initially prepared in $|A\rangle$. On the left, the black, green, and red lines correspond to $\omega L=2,4,8$, respectively, with $\nu =2$. On the right, the dot-dashed blue, real red, green, and black lines correspond to $\nu =1,2,5,8$, respectively, with $\omega L=4$

When the separation between the two atoms is extremely small ($\omega L\rightarrow 0$), the entanglement dynamics is the same as that in the parallel case, as expected. When the separation is very large ($\omega L\rightarrow \infty$), the concurrence takes the form $C[\rho (t)]=e^{-2 (A_1+A_2) t}$, where $A_1=\frac{\nu \Gamma _0}{4}$, $A_2=\frac{\Gamma _0}{4}$, no matter the initial state of the two-atom system is $|S\rangle$ or $|A\rangle$. So in these limiting cases, concurrence decays monotonically. When the separation between the atoms is comparable to the transition wavelength ($\omega L\sim 1$), we study the entanglement dynamics numerically. Here and after we plot the time evolution of concurrence as a function of dimensionless time $\Gamma _0 t$. To better illustrate the results, we use a logarithmic time scale in this paper. From Fig. 2 (left) and Fig. 3 (left), we observe that when the interatomic separation is appropriate, entanglement revival can be achieved, which is different from the parallel case in which concurrence always decreases monotonically. In Fig. 2 (right) and Fig. 3 (right), it has been shown that as the parameter characterizing the nontrivial topology $\nu$ gets larger, the entanglement revival happens earlier, and the maximal value of the revived concurrence is larger. For comparison, we note that in the case of the Minkowski spacetime with a reflecting boundary, the concurrence is $C[\rho (t)]=e^{-2 A_2 t}$ whether the initial state is symmetric or antisymmetric, where $A_2=\frac{\Gamma _0}{4} \left( 1-\frac{\sin (\omega \, L \,)}{\omega \, L}\right)$. So entanglement revival can not occur.

III. Symmetrical alignment When the two atoms are symmetrically aligned with respect to the cosmic string, i.e. $\Delta r=0$, $\Delta \theta =\frac{\pi }{\nu }$, and $\Delta z=0$, the concurrence takes the same form as Eq. (29), with $A_1=A_3=\frac{\nu \Gamma _0}{4}$. So entanglement revival cannot happen. When the initial state is $|S\rangle$, the concurrence evolves $\nu$ times as fast as that in the Minkowski spacetime, which is similar to the parallel case. When the initial state is $|A\rangle$, the concurrence can be protected as if it were an isolated system, which is different from the parallel case.

4.1.2 Two-atom system placed at a distance comparable to the atomic transition wavelength

In the following, we discuss the entanglement degradation when the two-atom system is at a distance comparable to the atomic transition wavelength, i.e, $r \sim {\omega }^{-1}$.

a. Distance effects In this part, we focus on how entanglement dynamics is influenced by the atom-string distance r, so we fix the interatomic separation at $\omega L\sim 1$. We assume that the two atoms are initially in $|S\rangle$. However, when the initial state is $|A\rangle$, the results are essentially the same.

I. Parallel alignment As have been discussed, when two atoms are parallel to the cosmic string, the concurrence takes the form of Eq. (29), which decays monotonically as time grows. Here we can define a relative decay rate as

$$\begin{aligned} \Omega =-\frac{1}{C[\rho (t)]}\frac{d C[\rho (t)]}{dt}. \end{aligned}$$

(31)

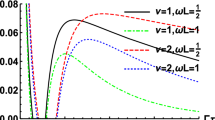
When the initial state of the two atoms is symmetric state, we can get the relative decay rate of concurrence as $\Omega = 4(A_1+A_3)$. In Fig. 4, we show how the decay rate varies with the atom-string distance. It is shown that the relative decay rate is the largest when two atoms are placed on the string. As the distance increases, it oscillates with a damping amplitude. However, in the boundary case, as the atoms are approaching to the boundary, the relative decay rate becomes zero.

Fig. 4

Relative decay rate of concurrence when the atoms are parallel to the cosmic string, with initial state $|S\rangle$, $\nu =2$, and $\omega L=1$. The real line describes the case in the cosmic string spacetime, and the dashed line describes the corresponding case in the Minkowski spacetime with a boundary

II. Vertical alignment In the following, we numerically study the entanglement degradation for atoms aligned vertically to the cosmic string, and compare the result with that in the case with a reflecting boundary. As shown in Fig. 5 (left), when the two atoms are vertically aligned to the string, entanglement revival can be achieved, and the revival time of entanglement oscillates as the atom-string distance increases. Similar to the cosmic string case, entanglement revival happens when the two atoms are vertically aligned to the boundary, see Fig. 5 (right).

Fig. 5

Entanglement dynamics for atoms aligned vertically to the cosmic string initially prepared in $|S\rangle$, with $\nu =2$. On the left, the black, green, red, orange, and blue lines correspond to $\omega r=1/2, 1, 2, 4, 8$, respectively. On the right, the black, green, and red lines correspond to $\omega r=1/2, 5/2, 7/2$, respectively. The real lines describe the cases in the cosmic string spacetime, and the dashed lines describe the corresponding cases in the presence of a reflecting boundary

III. Symmetrical alignment When the two atoms are symmetrically aligned with respect to the cosmic string, the concurrence takes the same form as Eq. (29). So the result is similar to that of the parallel case and we do not discuss it in detail here.

b. Topological effects In this part, we consider the effects of the parameter $\nu$ that describes the nontrivial topology of the cosmic string spacetime on the entanglement dynamics, so we fix the interatomic separation and the distance at the order of the transition wavelength.

I. Parallel alignment In Fig. 6 (left), we show the entanglement dynamics of two atoms aligned parallel to the cosmic string. As the parameter $\nu$ gets larger, the decay rate becomes larger, and the lifetime of entanglement becomes shorter.

II. Vertical alignment In contrast to the parallel case, when the two atoms are placed vertically to the cosmic string, entanglement revival occurs, see Fig. 6 (right). The larger the parameter $\nu$ is, the earlier the entanglement revival occurs. Here we note that for the parallel and vertical alignments, we assume the two-atom system is initially prepared in $|S\rangle$. However, when the initial state is $|A\rangle$, the results are essentially the same.

Fig. 6

Entanglement dynamics for atoms aligned parallel to (left), and vertically to (right) the cosmic string initially prepared in $|S\rangle$, with $\omega L=2, \omega r=1$. The dot-dashed blue, real red, green, and black lines correspond to $\nu =1, 2, 5,8$, respectively

III. Symmetrical alignment In Fig. 7, we plot the entanglement dynamics for atoms symmetrically aligned with respect to the cosmic string. The decay rate of concurrence increases as $\nu$ increases when the initial state of the two-atom system is the symmetric state $|S\rangle$. However, when the initial state of the two-atom system is the antisymmetric state $|A\rangle$, as $\nu$ increases, the decay rate of concurrence significantly decreases, and the lifetime of entanglement is significantly enhanced.

Fig. 7

Entanglement dynamics for atoms aligned symmetrically to the cosmic string initially prepared in $|S\rangle$ (left) and $|A\rangle$ (right), with $\omega r=1$. The dot-dashed blue, real red, green, and black lines correspond to $\nu =1, 2, 5, 8$, respectively

4.1.3 Two-atom system placed far from the cosmic string

When the two-atom system is placed far from the cosmic string, i.e. $\omega r \rightarrow \infty$, the coefficients of the master equation can be calculated as $A_1=A_2=B_1=B_2= \frac{\Gamma _0}{4}$, $A_3=B_3=\frac{\Gamma _0 \sin (\omega L)}{4 \omega L}$, and the entanglement dynamics is the same as that in the Minksowski spacetime.

4.2 Entanglement generation

Now, we turn our attention to the phenomenon of entanglement generation when the initial state of the two-atom system is $|E\rangle$, which is separable. From Eqs. (14)–(16), we can see that entanglement generation can occur as long as the value $\sqrt{[\rho _{AA}(\tau )-\rho _{SS}(\tau )]^2-[\rho _{AS}(\tau )-\rho _{SA}(\tau )]^2}$ is larger than $2\sqrt{\rho _{GG}(\tau ) \rho _{EE}(\tau )}$, which takes a finite time of evolution via spontaneous emission.

4.2.1 Two-atom system placed extremely close to the cosmic string

I. Parallel alignment In the parallel case, when the interatomic separation is vanishingly small ($\omega L\rightarrow 0$), or extremely large ($\omega L\rightarrow \infty$), it can be shown that entanglement cannot be created. When the separation of the two atoms is of the order of the transition wavelength ($\omega L\sim 1$), we investigate the entanglement dynamics numerically and show the result in Fig. 8, which suggests that the birth time of entanglement becomes earlier as $\nu$ increases (see Fig. 8 (left)).

Fig. 8

Entanglement dynamics for atoms aligned parallel to (left), and vertically to (right) the cosmic string initially prepared in $|S\rangle$, with $\omega L=1$. The dot-dashed blue, real red, green, and black lines correspond to $\nu =1, 2, 5,8$, respectively

Fig. 9

Entanglement dynamics for atoms aligned parallel to (left, with $\omega L=1$), vertically to (middle, with $\omega L=1$), and symmetrically to (right) the cosmic string initially prepared in $|E\rangle$, with $\nu =2$. The real black, green, and red lines correspond to $\omega r=1, 2, 3$, respectively. The real lines describe the cases in the cosmic string spacetime, and the dashed lines describe the corresponding boundary case (left, middle), and the Minkowski spacetime case (right)

II. Vertical alignment In the vertically aligned case, when the interatomic separation is extremely small ($\omega L\rightarrow 0$), the situation is essentially the same as the parallel case, so entanglement cannot be generated. When the interatomic separation is very large ($\omega L\rightarrow \infty$), we have $C[\rho (t)]=0$ since $A_1=A_3=0$, so entanglement cannot be created either. In Fig. 8 (right), we show the time evolution of concurrence when the separation of the two atoms is of the order of the transition wavelength ($\omega L\sim 1$). Similar to the parallel case, the larger the parameter $\nu$ is, the earlier the birth time of entanglement is.

III. Symmetrical alignment When the two atoms are symmetrically aligned with respect to the cosmic string, the situation is similar to the parallel case when $\omega r$ and $\omega L$ approach to zero simultaneously. Thus, similarly, entanglement generation cannot happen in this case.

4.2.2 Two-atom system placed at a distance comparable to the atomic transition wavelength

In this part, we investigate the entanglement generation when the two-atom system is at a distance comparable to the atomic transition wavelength.

a. Distance effects

I. Parallel alignment As shown in Fig. 9 (left), when the two-atom system is aligned parallel to the string, the birth time of entanglement oscillates as the atom-string distance increases. However, the maximal concurrence during evolution remains nearly unchanged.

II. Vertical alignment When the two-atom system is placed vertically to the string, the birth time of entanglement also oscillates as the atom-string distance increases, as shown in Fig. 9 (middle). Compared with the parallel case, the maximal concurrence shows a notable change as the atom-string distance increases. In contrast to the corresponding boundary case, the birth time of entanglement is more sensitive to the atom-string distance in the cosmic string case.

III. Symmetrical alignment Similar to the parallel case, when the two-atom system is symmetrically aligned with respect to the string, entanglement generation can occur only when the distance between the two-atom system and the string is neither too far nor too close. In certain cases, e.g. when $\omega r=3$ in the symmetrical case as shown in Fig. 9 (right), entanglement can be generated, but it cannot in the corresponding Minkowski spacetime.

b. Topological effects

I. Parallel alignment When the two-atom system is aligned parallel to the cosmic string, as $\nu$ increases, the birth time of entanglement becomes earlier, while the maximal entanglement during evolution is almost unchanged, as shown in Fig. 10 (left).

II. Vertical alignment When the two-atom system is aligned vertically to the cosmic string, similar to the parallel case, the birth time of entanglement also becomes earlier as $\nu$ increases. However, in contrast to the parallel case, the maximal entanglement during evolution is also enhanced as $\nu$ increases, see Fig. 10 (middle).

III. Symmetrical alignment When the two-atom is symmetrically aligned with respect to the cosmic string, as shown in Fig. 10 (right), the birth time of entanglement oscillates as $\nu$ increases, in contrast to the parallel and vertical cases.

Fig. 10

Entanglement dynamics for atoms aligned parallel to (left, with $\omega L=1, \omega r=1$), vertically to (middle, with $\omega L=1, \omega r=1$), and symmetrically to (right, with $\omega r=6$) the cosmic string initially prepared in $|E\rangle$. The dot-dashed blue, real red, green, and black lines correspond to $\nu =1, 2, 5, 8$, respectively

4.2.3 Two-atom system aligned far from the cosmic string

When the two-atom system is placed far from the cosmic string, i.e. $\omega r \rightarrow \infty$, we have $(\omega r \rightarrow \infty )$, $A_1=A_2=B_1=B_2= \frac{\Gamma _0}{4}$, $A_3=B_3=\frac{\Gamma _0 \sin (\omega L)}{4 \omega L}$, the entanglement dynamics is the same as that in the Minksowski vacuum.

5 The maximal concurrence during evolution

In the previous section, we have shown that entanglement can be generated for a pair of atoms initially in a separable state in certain conditions. The concurrence starts from zero, reaching its maximum, and then decreases to zero. In the following, we study how the maximal entanglement during evolution is influenced by the cosmic string. We will show that the maximal entanglement during evolution can either be enhanced or weakened, depending on the distance between the two-atom system and the string, the interatomic separation, and the parameter characterizing the nontrivial topology.

5.1 Parallel alignment

In the following, we investigate the situation when the atoms are parallel to the cosmic string. First, we fix the atom-string distance and see how the maximal concurrence varies with the interatomic separation. When the atoms are placed extremely close to the cosmic string, the corresponding coefficients are $\nu$ times those in the Minkowski spacetime as mentioned before. Thus the concurrence evolves $\nu$ times as fast as that in the free space, but the maximal concurrence during evolution remains the same. In Fig. 11 (left), we observe that when the atom-string distance is small compared to the transition wavelength, the maximal concurrence during evolution in the cosmic string spacetime with different $\nu$ is almost the same as that in the Minkowski spacetime as expected. When the atom-string distance is comparable to the transition wavelength, as $\nu$ increases, the range of the atomic separation within which entanglement can be created is broadened, see Fig. 11 (middle). Furthermore, when $\nu$ gets large enough, the maximal entanglement during evolution does not change with $\nu$ any more. When the two atoms get farther from the string, the maximal entanglement during evolution approaches that in the Minkowski spacetime, see Fig. 11 (right).

Now we investigate how the maximal concurrence varies with the atom-string distance with a fixed interatomic separation. In Fig. 12, it has been shown that the maximal concurrence can be significantly enhanced or weakened in the presence of the string. In particular, when the separation between the two atoms is very large, entanglement cannot be generated in the Minkowski spacetime. However, it can be generated in the presence of the cosmic string when the two atoms are placed at an appropriate distance to the string and the parameter $\nu$ is large enough, see Fig. 12 (right).

Fig. 11

Entanglement dynamics for atoms aligned parallel to the cosmic string initially prepared in $|E\rangle$, with $\omega r=2/10$ (left), $\omega r=2$ (middle), and $\omega r=20$ (right). The dot-dashed blue, real red, dashed green, and real black lines correspond to $\nu =1, 2, 5,8$, respectively

Fig. 12

Entanglement dynamics for atoms aligned parallel to the cosmic string initially prepared in $|E\rangle$, with $\omega L=2/10$ (left), $\omega L=2$ (middle), and $\omega L=20$ (right). The dot-dashed blue, real red, dashed green, and real black lines correspond to $\nu =1, 2, 5,8$, respectively

Fig. 13

Entanglement dynamics for atoms aligned vertically to the cosmic string initially prepared in $|E\rangle$, with $\omega r=2/10$ (left), $\omega r=2$ (middle), and $\omega r=20$ (right). The dot-dashed blue, real red, dashed green, and real black lines correspond to $\nu =1, 2, 5,8$, respectively

Fig. 14

Entanglement dynamics for atoms aligned vertically to the cosmic string initially prepared in $|E\rangle$, with $\omega L=2/10$ (left), $\omega L=2$ (middle), and $\omega L=20$ (right). The dot-dashed blue, real red, dashed green, and real black lines correspond to $\nu =1, 2, 5,8$, respectively

5.2 Vertical alignment

As before, first we study how the maximal concurrence varies with interatomic separation with a fixed atom-string distance. In contrast to the parallel case, the maximal concurrence is significantly affected by the cosmic string when the atoms is placed close to the string, see Fig. 13 (left). The range of the atomic separation within which entanglement created can be broadened in the presence of a cosmic string. Also, the larger $\nu$ is, the wider the range is. When the two atoms get farther from the string, the maximal entanglement during evolution approaches that of the Minkowski spacetime, see Fig. 13 (right).

Now we investigate effect of the atom-string distance on the maximal concurrence with a fixed interatomic separation. When the interatomic separation L is small compared with the transition wavelength of the atoms $\omega ^{-1}$, entanglement creation cannot happen when the two-atom system is placed extremely close to the cosmic string, see Fig. 14 (left). When the distance between the two atoms is large compared to the transition wavelength, entanglement generation cannot happen in the Minkowski spacetime, while it happens in the cosmic string spacetime with a large $\nu$ when the atom-string distance is small or comparable with the transition wavelength, see Fig. 14 (right).

5.3 Symmetrical alignment

Now we come to the symmetrical case. As shown in Fig. 15, entanglement can be generated only when the atom-string distance is appropriate. The range of the distance that entanglement can be generated is broadening as $\nu$ increases. Also, the larger $\nu$ is, the more peaks there exist. In particular, there is an interval of distance within which entanglement generation can not happen in the presence of a cosmic string when atoms are close to the string.

Fig. 15

Entanglement dynamics for atoms aligned symmetrically to the cosmic string initially prepared in $|E\rangle$. The dot-dashed blue, real red, green, and black lines correspond to $\nu =1, 2, 5,8$, respectively

6 Conclusion

In conclusion, we have investigated the dynamics of two static atoms in the cosmic string space in the framework of open quantum systems. We consider three situations, i.e. parallel, vertical and symmetric alignments of atoms with respect to the cosmic string. In particular, we focus on how the phenomena of entanglement degradation and generation are influenced by the cosmic string.

For atoms initially in the symmetric state $| S \rangle$ and the antisymmetric state $|A\rangle$, both of which are maximally entangled, the concurrence decays monotonically when the atoms are aligned parallel to or symmetrically to the cosmic string, while the destroyed entanglement can be revived when the two atoms are aligned vertically to the string, which cannot happen in the Minkowski spacetime. In the parallel case, when the atoms are placed extremely close to the string, the decay rate of concurrence is $\nu$ times that in the Minkowski spacetime, no matter the initial states is $|S\rangle$ or $|A\rangle$. When the two atoms are symmetrically aligned with respect to the cosmic string, the situation is the same when the initial state is $|S\rangle$, but concurrence can be protected as if the two-atom system were isolated from its environment when the initial state is $|A\rangle$. Even if the atom-string distance is comparable to the transition wavelength, the lifetime of entanglement can be significantly enhanced as $\nu$ increases when the symmetrically aligned two-atom system is initially in $|A\rangle$.

For two initially separable atoms, entanglement can be generated when the separation between the two atoms is comparable to the transition wavelength. For the parallel two-atom system, the atom-string distance mainly affects the birth time of entanglement, while for the vertical two-atom system, the maximal concurrence during evolution is also sensitive to the atom-string distance. When the distance between two atoms is large compared with the transition wavelength, entanglement generation cannot happen in the Minkowski spacetime, while it happens in the cosmic string spacetime at some appropriate positions.

Appendices

Appendix A: The matrix elements for the density matrix

In this section, we give the time-dependent matrix elements of the density matrix by solving Eq. (13).

1.1 1. Parallel and symmetrical alignments

As we will show in Appendix B, in these two cases, we have $A_1=A_2=B_1=B_2$, and $A_3=B_3$, so their matrix elements for the density matrix are the same, except that the explicit forms of the coefficient $A_3$ are different.

a. When the two-atom system is initially in $|A\rangle$, we have

$$\begin{aligned}&\rho _{AA}(t)=e^{-4(A_1-A_3) t},\nonumber \\&\rho _{GG}(t)=1-e^{-4(A_1-A_3) t}, \end{aligned}$$

(A1)

and all the other components are zero.

b. When the two-atom system is initially in $|S\rangle$, we have

$$\begin{aligned}&\rho _{SS}(t)=e^{-4(A_1+A_3) t},\nonumber \\&\rho _{GG}(t)=1-e^{-4(A_1+A_3) t}, \end{aligned}$$

(A2)

and all the other components are zero.

c. When the two-atom system is initially in $|E\rangle$, we have

$$\begin{aligned} \rho _{AA}(t)&=\frac{A_1-A_3}{A_1+A_3} \left[ e^{-8 A_1 t}(e^{4 (A_1+A_3 )t}-1)\right] ,\nonumber \\ \rho _{SS}(t)&=\frac{A_1+A_3}{A_1-A_3} \left[ e^{-8 A_1 t}(e^{4 (A_1-A_3 )t}-1)\right] ,\nonumber \\ \rho _{GG}(t)&=1-\left[ \frac{A_1-A_3}{A_1+A_3} \left[ e^{-8 A_1 t}(e^{4 (A_1+A_3 )t}-1)\right] \right. \nonumber \\&\quad \left. +\,\frac{A_1+A_3}{A_1-A_3} \left[ e^{-8 A_1 t}(e^{4 (A_1-A_3 )t}-1)\right] +e^{-8 A_1 t}\right] ,\nonumber \\ \rho _{EE}(t)&= e^{-8 A_1 t}, \end{aligned}$$

(A3)

and all the other components are zero.

1.2 2. Vertical alignment

In this case, since $A_1\ne A_2$, the results are more complicated. In the following results, for brevity, we let $\xi =A_1A_2(A_1+A_2)+4A_1A_2A_3+(A_1+A_2)A_3^2$, $\eta =A_1A_2(A_1+A_2)-4A_1A_2A_3+(A_1+A_2)A_3^2$, $\chi _1=A_1+A_2$, $\chi _2=A_1-A_2$, and $\gamma =\sqrt{(A_1-A_2)^2+4A_3^2}$.

a. When the two-atom system is initially in $|A\rangle$, we have

$$\begin{aligned} \rho _{AA}(t)&=\frac{ e^{-2 \chi _1 t}}{2{\gamma }^2 } \left[ \chi _2^2 +({\gamma }^2+\,4 {A_3}^2) \cosh (2 \gamma t )\right. \nonumber \\&\quad \left. +4 A_3 {\gamma } \sinh (2 \gamma t )\right] ,\nonumber \\ \rho _{SS}(t)&=\frac{\chi _2^2}{{\gamma }^2 } e^{-2 \chi _1 t} \sinh ({\gamma }^2 t^2 ) ,\nonumber \\ \rho _{GG}(t)&=\frac{ e^{-2 (\chi _1+\gamma ) t}}{2{\gamma } } \left[ 2 A_3(1-e^{4 \gamma t})\right. \nonumber \\&\quad \left. -\,\gamma (1+e^{4 \gamma t}- 2 e^{2 (\chi _1+\gamma ) t} ) \right] ,\nonumber \\ \rho _{AS}(t)&=\rho _{SA}(t)\nonumber \\&=-\frac{\chi _2\, e^{-2 \chi _1 t} \sinh (\gamma t) }{{\gamma }^2 }\left[ 2 A_3 \sinh (\gamma t)+ {\gamma }\cosh (\gamma t) \right] ,\nonumber \\ \rho _{EE}(t)&=0. \end{aligned}$$

(A4)

b. When the two-atom system is initially in $|S\rangle$, we have

$$\begin{aligned} \rho _{AA}(t)&=\frac{\chi _2^2}{{\gamma }^2 } e^{-2 \chi _1 t} \sinh ({\gamma }^2 t^2 ) ,\nonumber \\ \rho _{ss}(t)&=\frac{ e^{-2 \chi _1 t}}{2{\gamma }^2 } \left[ \chi _2^2 + ({\gamma }^2+4 {A_3}^2) \cosh (2 \gamma t )\right. \left. -\,4 A_3 {\gamma } \sinh (2 \gamma t )\right] ,\nonumber \\ \rho _{GG}(t)&=\frac{ e^{-2 (\chi _1+\gamma ) t}}{2{\gamma } } \left[ 2 A_3(e^{4 \gamma t}-1) -\,\gamma (1+e^{4 \gamma t}- 2 e^{2 (\chi _1+\gamma ) t} ) \right] ,\nonumber \\ \rho _{AS}(t)&=\rho _{SA}(t)=\frac{\chi _2\,e^{-2 \chi _1 t} \sinh (\gamma t) }{{\gamma }^2 }\nonumber \\&\quad \left[ 2 A_3 \sinh (\gamma t)- {\gamma }\cosh (\gamma t) \right] , \rho _{EE}(t)=0. \end{aligned}$$

(A5)

c. When the two-atom system is initially in $|E\rangle$, we have

$$\begin{aligned} \rho _{AA}(t)= & {} \frac{e^{-2 \chi _1 t}}{\chi _1 (A_1 A_2-A_3^2)\gamma ^2 }\nonumber \\&\Bigg \{ 4 A_3 \chi _2^2 (A_3^2-A_1 A_2) -\gamma ^2 \eta \cosh \left( 2\chi _1t\right) \nonumber \\&+\,\chi _1 \left( A_1 \chi _2^2 A_2+ \chi _1^2 A_3^2- 4\chi _1 A_3^3+4 A_3^4 \right) \cosh (2 \gamma t)\nonumber \\&+\,\gamma \left[ 2 A_3 \chi _1 (A_1-A_3) (A_2-A_3)\sinh (2\gamma t)\right. \nonumber \\&\quad \left. +\,\gamma \eta \sinh \left( 2\chi _1 t\right) \right] \Bigg \},\nonumber \\ \rho _{SS}(t)= & {} \frac{-e^{-2 \chi _1 t}}{\chi _1 (A_1 A_2-A_3^2)\gamma ^2 }\nonumber \\&\Bigg \{ 4 A_3 \chi _2^2 (A_3^2-A_1 A_2)\nonumber \\&+\,\gamma ^2 \xi \cosh \left( 2\chi _1t\right) \nonumber \\&-\,\chi _1 \left( A_1 \chi _2^2 A_2+ \chi _1^2 A_3^2+ 4\chi _1A_3^3+4 A_3^4 \right) \cosh (2 \gamma t)\nonumber \\&+\,\gamma \left[ 2 A_3 \chi _1 (A_1+A_3) (A_2+A_3)\sinh (2\gamma t)\right. \nonumber \\&\left. \left. -\,\gamma \xi \sinh \left( 2\chi _1 t\right) \right] \Bigg \},\right. \nonumber \\ \rho _{GG}(t)= & {} \frac{e^{-2 ( 2 \chi _1+\gamma ) t}}{(A_1 A_2-A_3^2) \gamma } \left\{ A_1\left[ 2A_3^2 e^{2\chi _1t }(e^{4 \gamma t}-1)\right. \right. \nonumber \\&\left. -\,A_2 \gamma \left( e^{2 \chi _1 t}(e^{4 \gamma t}+1)-e^{2 \gamma t}(1+e^{4 \chi _1t}) \right) \right] \nonumber \\&-\,A_3^2\left[ 2 A_2 e^{2\chi _1 t}(1-e^{4 \gamma t})\right. \nonumber \\&\left. \left. +\,\gamma \left( e^{2\chi _1t }(e^{4 \gamma t}+1)-e^{2 \gamma t}(3-e^{4 \chi _1t})\right) \right] \right\} ,\nonumber \\ \rho _{AS}(t)= & {} \rho _{AS}(t)=\frac{-\chi _2 e^{-2 \chi _1t}}{\chi _1 (A_1 A_2-A_3^2)\gamma ^2 }\nonumber \\&\left\{ \gamma \left[ \chi _1 (A_1 A_2+A_3^2)\sin (2 \gamma t)-2 A_3^2\gamma \sinh \left( 2 \chi _1 t\right) \right] \right. \nonumber \\&+\,8 A_3^2(A_1A_2-A_3^2)+2 A_3^2\gamma ^2 \cosh (2 \chi _1t)\nonumber \\&\left. -\,2 A_3^2\chi _1^2\cosh (2\gamma t) \right\} ,\nonumber \\ \rho _{EE}(t)= & {} e^{-4\chi _1 t}. \end{aligned}$$

(A6)

Appendix B: Calculations of the coefficients $A_i$ and $B_i$

In this Appendix we show the details of the calculations of the coefficients $A_i$ and $B_i$ in Eqs. (13) for different alignments of the two-atom system in the cosmic string spacetime, in the Minkowski spacetime with a boundary, and in the free Minkowski spacetime.

1.1 1. In the cosmic string spacetime

To get the coefficients $A_i$ and $B_i$, we need the Fourier transform of the field correlation function (28). In order to calculate the result explicitly, we use the property of Bessel function [46]

$$\begin{aligned} \sum _{m=-\infty }^{\infty }J_{\nu \left| m \right| }(k_\perp r)J_{\nu \left| m \right| }(k_\perp r^{\prime })e^{i \nu m \Delta \theta }=\frac{1}{\nu }\sum _{n=0}^{\nu -1}J_0(k_{\perp } L_{n,\nu }),\; \end{aligned}$$

(B1)

where $\nu$ is integer, and $L_{n,\nu }=\sqrt{r^2+{r^{\prime }}^2-2 r r^{\prime } \cos (\Delta \theta +\frac{2 \pi n}{\nu })}$.

1.1.1 a. Parallel alignment

When the two-atom system is aligned parallel to the string, taking Eqs. (B1) and $\Delta \theta =0, \Delta z=L, \Delta r=0$ into Eq. (28), we obtain

$$\begin{aligned} \mathcal {G}^{(11)}(\omega )&=\mathcal {G}^{(22)}(\omega ){=} \frac{\omega }{2 \pi }\int ^1_0\,dx\,\sum _{n=0}^{\nu -1}J_{0}(\omega r \,R_{n,\nu } \sqrt{1{-}x^2}),\end{aligned}$$

(B2)

$$\begin{aligned} \mathcal {G}^{(12)}(\omega )&=\mathcal {G}^{(21)}(\omega )\nonumber \\&= \frac{\omega }{2 \pi }\int ^1_0\,dx\,\cos (\omega \,x\,\Delta z) \sum _{n=0}^{\nu -1}J_{0}(\omega r \,R_{n,\nu } \sqrt{1{-}x^2}), \end{aligned}$$

(B3)

with $R_{n,\nu }=\sqrt{2-2 \cos \left( \frac{2 \pi n}{\nu }\right) }$. With the help of the formulas (6.677) in Ref. [47], the integration above can be calculated, and we get

$$\begin{aligned}&A_1=A_2=B_1=B_2=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega r \,R_{n,\nu })}{\omega r \,R_{n,\nu }},\end{aligned}$$

(B4)

$$\begin{aligned}&A_3=B_3=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin \sqrt{(\omega L)^2+(\omega r \,R_{n,\nu })^2}\;}{\sqrt{(\omega L)^2+(\omega r \,R_{n,\nu })^2}}, \end{aligned}$$

(B5)

where $\Gamma _0=\mu ^2 \omega /2 \pi$ denotes spontaneous emission rate in the Minkowski spacetime.

1.1.2 b. Vertical alignment

When the two-atom system is aligned vertically to the string, we have $\Delta \theta =0, \Delta z=0, \Delta r=L$. Similarly, we obtain

$$\begin{aligned}&\mathcal {G}^{(11)}(\omega )=\frac{\omega }{2 \pi }\int ^1_0\,dx\,\sum _{n=0}^{\nu -1}J_{0}( \omega r \, R_{n,\nu }\sqrt{1-x^2}), \end{aligned}$$

(B6)

$$\begin{aligned}&\mathcal {G}^{(22)}(\omega )=\frac{\omega }{2 \pi }\int ^1_0\,dx\,\sum _{n=0}^{\nu -1}J_{0}( \omega r^{\prime } \, R_{n,\nu }\sqrt{1-x^2}), \end{aligned}$$

(B7)

$$\begin{aligned}&\mathcal {G}^{(12)}(\omega )=\mathcal {G}^{(21)}(\omega )=\frac{\omega }{2 \pi }\int ^1_0\,dx\,\sum _{n=0}^{\nu -1}J_{0}( \omega \, L_{n,\nu }\sqrt{1-x^2}). \end{aligned}$$

(B8)

So we can get

$$\begin{aligned}&A_1=B_1=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega \, r \,R_{n,\nu })}{\omega \, r \,R_{n,\nu }},\end{aligned}$$

(B9)

$$\begin{aligned}&A_2=B_2=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega \, r^{\prime } \,R_{n,\nu })}{\omega \, r^{\prime } \,R_{n,\nu }},\end{aligned}$$

(B10)

$$\begin{aligned}&A_3=B_3=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega \, L_{n,\nu })}{\omega \,L_{n,\nu }}.\;\; \end{aligned}$$

(B11)

1.1.3 c. Symmetrical alignment

When the two atoms are symmetric alignment with respect to the cosmic string, i.e. $\Delta \theta =\pi /\nu , \Delta z=0, \Delta r=0$, we obtain

$$\begin{aligned} A_1&=A_2=B_1=B_2\nonumber \\&=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega \, r \,R_{n,\nu })}{\omega \, r \,R_{n,\nu }},\end{aligned}$$

(B12)

$$\begin{aligned} A_3&=B_3=\frac{\Gamma _0}{4} \sum _{n=0}^{\nu -1} \frac{\sin (\omega \, r \,H_{n,\nu })}{\omega \, r \,H_{n,\nu }}, \end{aligned}$$

(B13)

with $H_{n,\nu }=\sqrt{2-2 \cos \left[ \frac{(2n+1) \pi }{\nu }\right] }.$

1.2 2. In the Minkowski spacetime with a reflecting boundary

We assume that a conducting boundary is placed at $y=0$. The two-point function takes the following form

$$\begin{aligned}&\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle \nonumber \\&\quad =\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle _{free}{+}\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle _{bnd},\nonumber \\ \end{aligned}$$

(B14)

where

$$\begin{aligned}&\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle _{free}\nonumber \\&\quad =\frac{1}{4\pi }\frac{1}{(x-x^{'})^2+(y-y^{'})^2+(z-z^{'})^2-(t-t^{'}-i\epsilon )^2},\nonumber \\ \end{aligned}$$

(B15)

$$\begin{aligned}&\langle 0|\phi (t,\vec {x})\phi (t^{\prime },\vec {x}\;^{\prime })|0\rangle _{bnd}\nonumber \\&\quad =-\frac{1}{4\pi }\frac{1}{(x-x^{'})^2+(y+y^{'})^2+(z-z^{'})^2-(t-t^{'}-i\epsilon )^2},\nonumber \\ \end{aligned}$$

(B16)

and $\epsilon \rightarrow +0$.

1.2.1 a. Parallel alignment

When two atoms are aligned parallel to the boundary, the corresponding coefficients are

$$\begin{aligned}&A_1=A_2=B_1=B_2=\frac{\Gamma _0}{4}\left( 1-\frac{ \sin (2 \, \omega \,r)}{2 \, \omega \,r}\right) ,\end{aligned}$$

(B17)

$$\begin{aligned}&A_3=B_3=\frac{\Gamma _0}{4}\left( \frac{\sin (\omega \, L)}{\omega \,L}-\frac{ \sin (\sqrt{(\omega \,L)^2+(2\omega \,r)^2}\,)}{\sqrt{(\omega \,L)^2+(2\omega \,r)^2}}\right) . \end{aligned}$$

(B18)

1.2.2 b. Vertical alignment

When the two-atom system are aligned vertically to the boundary, we have

$$\begin{aligned}&A_1=B_1=\frac{\Gamma _0}{4}\left( 1-\frac{ \sin (2 \, \omega \,r)}{2 \, \omega \,r}\right) ,\end{aligned}$$

(B19)

$$\begin{aligned}&A_2=B_2=\frac{\Gamma _0}{4}\left( 1-\frac{ \sin (2 \, \omega \,r^{\prime })}{2 \, \omega \,r^{\prime }}\right) ,\end{aligned}$$

(B20)

$$\begin{aligned}&A_3=B_3=\frac{\Gamma _0}{4}\left( \frac{\sin (\omega \, L)}{\omega \,L}-\frac{ \sin (\omega \,r+\omega \,r^{\prime })}{\omega \,r+\omega \,r^{\prime }}\right) . \end{aligned}$$

(B21)

1.3 3. In the Minkowski spacetime

  In the free Minkowski spacetime, we have

$$\begin{aligned}&A_1=B_1= A_2=B_2=\frac{\Gamma _0}{4},\end{aligned}$$

(B22)

$$\begin{aligned}&A_3=B_3=\frac{\Gamma _0}{4} \frac{\sin (\omega \, L)}{\omega \, L}. \end{aligned}$$

(B23)