Constraints on a special running vacuum model

Abstract

We study a special running vacuum model (RVM) with $\Lambda = 3 \alpha H^2+3\beta H_0^4 H^{-2}+\Lambda _0$, where $\alpha$, $\beta$ and $\Lambda _0$ are the model parameters and H is the Hubble one. This RVM has non-analytic background solutions for the energy densities of matter and radiation, which can only be evaluated numerically. From the analysis of the CMB power spectrum and baryon acoustic oscillation along with the prior of $\alpha >0$ to avoid having a negative dark energy density, we find that $\alpha <2.83\times 10^{-4}$ and $\beta =(-0.2^{+3.9}_{-4.5})\times 10^{-4}$ (95$\%$ C.L.). We show that the RVM fits the cosmological data comparably to the $\Lambda \hbox {CDM}$. In addition, we relate the fluctuation amplitude $\sigma _8$ to the neutrino mass sum $\Sigma m_\nu$.

1 Introduction

Since the discovery of the accelerated expanding universe in 1998 [1, 2], dark energy has been the most popular scenario to explain this phenomenon [3]. Among the various theories, the Lambda Cold Dark Matter ($\Lambda \hbox {CDM}$) model is the simplest one to reveal the nature of our universe, which also fits well with all cosmological observational data. Unfortunately, the $\Lambda \hbox {CDM}$ model has some theoretical unsatisfactories, such as “fine-tuning” [4, 5] and “coincidence” [6, 7] problems.

In order to resolve the “coincidence” problem, people have proposed various models to improve the cosmological constant of $\Lambda$ in the Einstein’s equation, such as the running vacuum models (RVMs) [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. In this kind of the models, $\Lambda$, instead of being a constant, is a function of the Hubble parameter H, and decays to matter and radiation  [8]. It has been shown that the RVMs are suitable in describing the cosmological evolutions on both background and linear perturbation levels in the literature [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. In these studies, the Hubble parameter H has been used to compose many forms of $\Lambda = \sum A_n H^{2n}$ with a non-negative integer n, where $A_n$ is a mass dimension $2(1-n)$ constant. In this paper, we consider the specific extension of RVM from Ref. [22], in which a negative power term is proposed, $\Lambda = 3 \alpha H^2+3\beta H_0^4 H^{-2}+\Lambda _0$, where $\alpha$ and $\beta$ are the model parameters. Clearly, this RVM goes back to $\Lambda \hbox {CDM}$ when $\alpha =\beta =0$. Only in this case, $\Lambda _0$ plays the role of the cosmological constant. Naively, it is expected that the values of $\alpha$ and $\beta$ should be close to zero in order to fit the current cosmological observations. However, in some of the RVMs, the model parameters have been shown to be non-zero and sizable [15,16,17,18,19,20,21]. It is interesting to explore if our special form of the RVMs also has this peculiar feature.

In this study, we plan to fit this RVM by using the most recent observational data. In particular, we use the CAMB [34] and CosmoMC [35] packages with the Markov chain Monte Carlo (MCMC) method. Since this model has no analytical solution for the energy density of matter or radiation, we modify the CAMB program to get the background evolution.

This paper is organized as follows. In Sect. 2, we introduce our special RVM. We also derive the evolution equations for matter and radiation in the linear perturbation theory. In Sect. 3, we present our numerical calculations. In particular, we show the CMB and matter power spectra and the constraints on the model-parameters from several cosmological observation datasets. Finally, our conclusions are given in Sect. 4.

2 Running vacuum model

We start with the Einstein equation, written as

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }+\Lambda g_{\mu \nu } = 8\pi G T^{M}_{\mu \nu }, \end{aligned}$$

(1)

where $R=g^{\mu \nu }R_{\mu \nu }$ is the Ricci scalar, $\Lambda$ is the cosmological constant, G is the gravitational constant and $T^{M}_{\mu \nu }$ is the energy-momentum tensor of matter and radiation. For the homogeneous and isotropic universe, we use the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric, given by

$$\begin{aligned} ds^{2}= -dt^{2}+ a^{2}(t) \delta _{ij}dx^{i}dx^{j}. \end{aligned}$$

(2)

Consequently, the Friedmann equations are found to be

$$\begin{aligned}&H^{2}=\frac{8\pi G}{3}(\rho _m + \rho _r +\rho _{\Lambda }), \end{aligned}$$

(3)

$$\begin{aligned}&\dot{H}=- 4\pi G(\rho _m + \rho _r +\rho _{\Lambda } + P_m+ P_r + P_{\Lambda }), \, \end{aligned}$$

(4)

where $H=da/(adt)$ is the Hubble parameter and $\rho _{m,r,\Lambda }$ ($P_{m,r,\Lambda }$) represent the energy densities (pressures) of matter, radiation and dark energy, respectively. In this work, we consider $\Lambda$ to be the specific function of the Hubble parameter, given by

$$\begin{aligned} \Lambda = 3 \alpha H^2+3\beta H_0^4 H^{-2}+\Lambda _0. \end{aligned}$$

(5)

Here, $\alpha$ and $\beta$ are dimensionless model-parameters. It is clear that the $\Lambda \hbox {CDM}$ model is recovered by taking $\alpha =0$ and $\beta =0$. This special model is inspired by the studies of $\Lambda = c_0+c_1H^2+c_2 H^{-n}$ in Refs. [22, 23]. It is convenient to define the equations of state for matter, radiation and dark energy by

$$\begin{aligned} w_{m,r,\Lambda }=\frac{P_{m,r,\Lambda }}{\rho _{m,r,\Lambda }}= 0, \frac{1}{3}, -1, \end{aligned}$$

(6)

respectively.

In the RVM, dark energy decays to radiation and matter in the evolution of the universe, so that the continuity equations can be written as,

$$\begin{aligned}&\dot{\rho }_M+3 H(1+w_M)\rho _M = Q, \end{aligned}$$

(7)

$$\begin{aligned}&\dot{\rho }_\Lambda +3 H(1+w_\Lambda )\rho _\Lambda = - Q, \end{aligned}$$

(8)

where $\rho _\Lambda = \Lambda /(8\pi G)$, $\rho _M = \rho _m + \rho _r$, $w_M = (P_m + P_r) / \rho _M$ and $Q = Q_m+Q_r$ with $Q_{m(r)}$ the decay rate of dark energy to matter (radiation). By combining Eqs. (5) and (78), the coupling $Q_\mu$ with $\mu$ = m or r is given by

$$\begin{aligned} Q_\mu= & {} -\frac{\dot{\rho }_{\Lambda }(\rho _\mu +P_\mu )}{\rho _{M}+P_M}\nonumber \\= & {} 3 H \left( \alpha -\beta \frac{H_0^4}{H^4}\right) (1+w_\mu )\rho _\mu , \end{aligned}$$

(9)

with $P_M = P_m + P_r$.

The energy densities of matter and radiation can be evaluated from

$$\begin{aligned} \frac{\rho _\mu ^\prime }{\rho _\mu }= 3(1+w_\mu )\left( \alpha -\beta \frac{H_0^4}{H^4}-1 \right) , \end{aligned}$$

(10)

derived from Eq. (78), where “$\prime$” stands for the derivative with respective to $\ln a$ and $\rho _\mu ^\prime = \dot{\rho }_\mu /H$. However, there are no analytical solutions for $\rho _{m,r}$ in Eq. (10). From the modified $\mathbf{CAMB}$ program, we can solve Eq. (10) numerically. Note that $\alpha \ge 0$ is chosen to avoid the negative dark energy density in the early universe.

In our calculation, we use the conformal time $\tau$ in order to perform the perturbation theory in the synchronous gauge. From the standard linear perturbation theory [36], we can derive the growth equation of the density perturbation in the RVM. In the synchronous gauge, the metric is given by

$$\begin{aligned} ds^{2}=a^{2}(\tau )[-d\tau ^{2}+(\delta _{ij}+h_{ij})dx^{i}dx^{j}], \end{aligned}$$

(11)

where $i,j=1,2,3$ and

$$\begin{aligned} h_{ij}{=} \int d^3 k e^{i{\vec {k}}\vec {x}}\left[ \hat{k}_i \hat{k}_j h({\vec {k}},\tau ){+}6\left( \hat{k}_i\hat{k}_j{-}frac{1}{3}\delta _{ij}\right) \eta ({\vec {k}},\tau )\right] ,\nonumber \\ \end{aligned}$$

(12)

with the k-space unit vector of $\hat{k}= {\vec {k}}/k$ and two scalar perturbations of $h({\vec {k}},\tau )$ and $\eta ({\vec {k}},\tau )$. The conservation equation is given by $\nabla ^{\nu }( T^{M}_{\mu \nu }+T^{\Lambda }_{\mu \nu })=0$ with $\delta T^{0}_{0}=-\delta \rho _{m}$, $\delta T^{0}_{i}=-T^{i}_{0}=(\rho _{M}+P_{M})v^i_M$ and $\delta T^{i}_{j}=\delta P_{M}\delta ^{i}_{j}$.

As shown in Refs. [37, 38], there are two basic perturbation equations, given by

$$\begin{aligned}&\sum _{i = \Lambda , M} \delta \rho _i+3\delta \frac{\dot{a}}{a}(\rho _i+P_i)+3\mathcal {H}\left( \delta \rho _i+\delta P_i\right) = 0, \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{i = \Lambda , M}\dot{\theta }_i(\rho _i+P_i)+\theta _i (\dot{\rho }_i+\dot{P}_i+5\frac{\dot{a}}{a}(\rho _i+P_i)) = \frac{k^2}{a}\sum _{i = \Lambda , M}\delta P_i,\nonumber \\ \end{aligned}$$

(14)

where $\delta \rho _i$ represent the density fluctuations, and $\theta _i$ are the corresponding velocities. As there is no peculiar velocity for dark energy, we take $\theta _\Lambda =0$. In addition, we assume that $\delta \rho _M\gg \delta \rho _\Lambda$ and $\delta \dot{\rho }_M \gg \delta \dot{\rho }_\Lambda$ in our model. As a result, we can ignore the discussion for the dark energy perturbation. For the matter perturbation, the growth equations are given by

$$\begin{aligned} \dot{\delta }_\mu= & {} {-}(1+w_\mu )\left( \theta _{\mu }{+}\frac{\dot{h}}{2}\right) {-}3\frac{\dot{a}}{a}\left( \frac{\delta P_{\mu }}{\delta \rho _{\mu }}{-}w_{\mu }\right) \delta _{\mu }{-}\frac{Q_\mu }{\rho _{\mu }}\delta _{\mu } \,,\nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} \dot{\theta }_\mu= & {} -\frac{\dot{a}}{a}(1-3w_{\mu })\theta _{\mu }{-}\frac{\dot{w}_{\mu }}{1+w_{\mu }}\theta _{\mu }{+}\frac{\delta P_{\mu }/\delta \rho _{\mu }}{1{+}w_\mu }k^{2}\delta _\mu {-}\frac{Q_\mu }{\rho _{\mu }}\theta _{\mu },\nonumber \\ \end{aligned}$$

(16)

where $\delta _\mu \equiv \delta \rho _\mu /\rho _\mu$ and $\mu$ = m, r.

3 Numerical calculations

As mentioned in the previous section, we modify the $\mathbf{CAMB}$ program to solve Eq. (10). In our calculation, $\rho _m$ and $\rho _r$ are evaluated in terms of $\log a$ from the current universe to the past. By performing the CosmoMC program [35], we fit the RVM from the observational data with the MCMC method. The dataset includes those of the CMB temperature fluctuation from Planck 2015 with TT, TE, EE and low-l polarization [39,40,41], the baryon acoustic oscillation (BAO) data from 6dF Galaxy Survey [42, 43], the WiggleZ Dark Energy Survey [44] and BOSS [45,46,47] and the redshift space distortion (RSD) data from SDSS-III BOSS[48]. The BAO data points are shown in Table 1.

In addition, the $\chi ^2$ fit is given by

$$\begin{aligned} {\chi ^2}={\chi ^2_{BAO}}+{\chi ^2_{CMB}}+{\chi ^2_{RSD}}. \end{aligned}$$

(17)

For the BAO, the observation measures the distance ratio of $d_{z}\equiv r_{s}(z_{d})/D_{V}(z)$, where $D_{V}$ is the volume-averaged distance and $r_{s}(z_d)$ is the comoving sound horizon with $z_{d}$ the redshift at the drag epoch [49]. Here, $D_{V}(z)$ is defined as [50]

$$\begin{aligned} D_{V}(z)\equiv \left[ (1+z)^{2}D_{A}^{2}(z)\frac{z}{H(z)}\right] ^{1/3}, \end{aligned}$$

(18)

where $D_{A}(z)$ is the proper angular diameter distance, given by

$$\begin{aligned} D_{A}(z)=\frac{1}{1+z}\int _{0}^{z}\frac{dz'}{H(z')}, \end{aligned}$$

(19)

while $r_{s}(z)$ is described by

$$\begin{aligned} r_{s}(z)=\frac{1}{\sqrt{3}}\int _{0}^{1/(1+z)}\frac{da}{a^{2}H({\scriptstyle z'=\frac{1}{a}-1})\sqrt{1+(3\Omega _{b}^{0}/4\Omega _{\gamma }^{0})a}},\nonumber \\ \end{aligned}$$

(20)

where $\Omega _{b}^{0}$ and $\Omega _{\gamma }^{0}$ are the present values of baryon and photon density parameters, respectively. The $\chi ^2$ value for the BAO data is given by

$$\begin{aligned} {\chi ^2_{BAO}}= \sum _{i=1}^n \frac{({D_V/r_s}^{th}(z_i) - {D_V/r_s}^{obs}(z_i))^2}{\sigma ^2_i}, \end{aligned}$$

(21)

where n is the number of the BAO data points and $\sigma _i$ correspond to the errors of the data, given by Table 1. Here, the subscripts of “th” and “obs” represent the theoretical and observational values of the volume-averaged distance, respectively.

The CMB is sensitive to the distance to the decoupling epoch $z_{*}$. It constrains the model in the high redshift region of $z\sim 1000$. The $\chi ^{2}$ value of the CMB data can be calculated by

$$\begin{aligned} \chi _{CMB}^{2}=\left( x_{i,CMB}^{th}{-}x_{i,CMB}^{obs}\right) \left( C_{CMB}^{-1}\right) _{ij}\left( x_{j,CMB}^{th}{-}x_{j,CMB}^{obs}\right) ,\nonumber \\ \end{aligned}$$

(22)

where $C_{CMB}^{-1}$ is the inverse covariance matrix and $x_{i,CMB}\equiv \left( l_{A}(z_{*}),R(z_{*}),z_{*}\right)$ with the acoustic scale $l_{A}$ and shift parameter R, defined by

$$\begin{aligned} l_{A}(z_{*})\equiv (1+z_{*})\frac{\pi D_{A}(z_{*})}{r_{S}(z_{*})} \end{aligned}$$

(23)

and

$$\begin{aligned} R(z_{*})\equiv \sqrt{\Omega _{m}^{0}}H_{0}(1+z_{*})D_{A}(z_{*}), \end{aligned}$$

(24)

respectively.

For the RSD measurements, we use

$$\begin{aligned} {\chi ^2_{RSD}}= & {} \sum _{i=1}^n \left( D^{obs}_{z_i} - D^{th}_{z_i}\right) ^\mathrm {T} C^{-1}_{z_i}\left( D^{obs}_{z_i} - D^{th}_{z_i}\right) , \end{aligned}$$

(25)

$$\begin{aligned} D_{z}= & {} \left( \begin{array}{c} f(z)\sigma _8(z) \\ H(z)r_s(z_d) \\ D_A(z)/{r_s({z_d})} \end{array} \right) \end{aligned}$$

(26)

where $\sigma _8$ is the amplitude of the over-density at the comoving 8$h^{-1}$ Mpc scale and f(z)=$\delta ^{\prime }/\delta$ with $\delta$ the evolution of the matter density contrast.

The data points in RSD are given by

$$\begin{aligned} D^{obs}_{0.32}=\left( \begin{array}{c} 0.45960 \\ 11.753 \\ 6.7443 \end{array} \right) \quad \text {and}\quad D^{obs}_{0.57}=\left( \begin{array}{c} 0.41750 \\ 13.781 \\ 9.3276 \end{array} \right) , \end{aligned}$$

(27)

with the covariance matrices being

$$\begin{aligned} C^{-1}_{0.32}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 406.87 &{} -16.551 &{} -64.272\\ -16.551 &{} 6.0291 &{} -5.6683\\ -64.272 &{} -5.6683 &{} 44.018 \end{array} \right) ~\text {and}\nonumber \\ C^{-1}_{0.57}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 1402.2 &{} -24.384 &{} -202.70\\ -24.384 &{} 19.007 &{} -15.976\\ -202.70 &{} -15.976 &{} 95.850 \end{array} \right) , \end{aligned}$$

(28)

respectively.

Table 1 BAO data points

The priors of the various cosmological parameters are listed in Table 2. Here, we have set $\alpha$ to be a positive number to avoid having a negative dark energy density.

Table 2 Priors for cosmological parameters with $\Lambda = 3\alpha H^2 + 3\beta H_0^4/H^2 + \Lambda _0$

Fig. 1

CMB power spectra for the $\Lambda \hbox {CDM}$ and RVM with different sets of $\alpha$ and $\beta$, where $\alpha =0.0001$ and $\beta =0.0001$ in the RVM are illustrated by the blue line, which almost coincides with the black one from $\Lambda \hbox {CDM}$, while the green and red lines with $\alpha =0.01$ are also almost in the same line

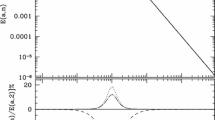
In Fig. 1, we show the CMB power spectra in the $\Lambda \hbox {CDM}$ and RVM with several different sets of $\alpha$ and $\beta$. In the figure, we see that both model parameters $\alpha$ and $\beta$ in Eq. (5) are expected to be smaller than 0.0001 as illustrated by the blue line, which almost coincides with the $\Lambda \hbox {CDM}$ one (black). In the green and red lines with $\alpha =0.01$, the first acoustic peaks are reduced, which could result from too much contribution from dark energy to the total energy density to suppress the baryon part [51]. In this case, the overall shift of the Doppler peaks towards lower multipoles as a consequence of the increased sound speed of the plasma [51]. Compared with $\alpha$, the effect of $\beta$ in the CMB is not obvious, because H(z) is very large due to the $H^2$ term in the early universe. In Fig. 2, we give the ratio of $\Delta C_{\ell }/C_{\ell }$, where $\Delta C_{\ell }$ is the change between the RVM and $\Lambda \hbox {CDM}$ for the TT mode of the CMB power spectra, while $C_{\ell }$ corresponds to the one in $\Lambda \hbox {CDM}$. This figure illustrates the effects from the model-parameter of $\beta$ from $-0.01$ to 0.01. It is clear that the changes in the CMB power spectra due to $\beta$ are small, so that the results in the RVM will be only slightly different from those in $\Lambda \hbox {CDM}$ in the early universe. We present the matter power spectra of the RVM in Fig. 3, which behavior similar to those in Figs. 1 and 2. In addition, we demonstrate that the matter power spectra for the RVM and $\Lambda \hbox {CDM}$ do not have similar evolution paths in the early universe until k $\approx$ 5.

Fig. 2

Ratio of $\Delta C_{\ell }/C_{\ell }$, where $\Delta C_{\ell }$ is the change between the RVM and $\Lambda \hbox {CDM}$ for the TT mode of the CMB power spectra, while $C_{\ell }$ corresponds to the one in $\Lambda \hbox {CDM}$

Fig. 3

Matter power spectra for the $\Lambda \hbox {CDM}$ and RVM, where the legend is the same as Fig. 1

In Fig. 4 and Table 3, we present our results of the global fits from several datasets, where the values in the brackets correspond to the best-fit values in the $\Lambda \hbox {CDM}$ model. In particular, we find that ($\alpha$, $\beta$) = $(<2.83, -0.2^{+3.9}_{-4.5})\times 10^{-4}$ and $(<1.57, -0.2\pm 2.6)\times 10^{-4}$ with 95$\%$ and 68$\%$ C.L., respectively. Here, $\Omega _{\Lambda }=( \rho _{\Lambda }/\rho _C)|_{z=0} = \alpha +\beta +\Lambda _0/(3H_0^2)$ is the fractional dark energy density with $\rho _{\Lambda }\equiv \Lambda /(8\pi G)$ and $\rho _{C}= 3H^2/(8\pi G)$. It is interesting to note that the value of $\sigma _8$=$0.835\pm {0.038}$ (95$\%$ C.L.) in the RVM is smaller than that of $0.838^{+0.038}_{-0.040}$ (95$\%$ C.L.) in $\Lambda \hbox {CDM}$. As shown in Table 3, the best fitted $\chi ^2$ value in the RVM is 2543.259, which is smaller than 2546.662 in the $\Lambda \hbox {CDM}$ model. Although the cosmological observables for the best $\chi ^2$ fit in the RVM do not significantly deviate from those in $\Lambda \hbox {CDM}$, they look better in all datasets. It implies that the RVM is favored by the cosmological observations. However, we remark that our results can only be viewed as comparable to those in $\Lambda \hbox {CDM}$ due to the extra parameters in the RVM. In addition, it should be noted that $\alpha \sim \mathcal {O}(10^{-4})$ in our RVM is about one to two orders of magnitude lower than those of $\alpha \sim \mathcal {O}(10^{-3})- \mathcal {O}(10^{-2})$ of the corresponding $H^2$ term in the other RVMs in the

literature [15,16,17,18,19]. However, this difference may be due to the fact that the models are actually different as there is no term proportional to negative powers of H in the cases of the other authors.

Fig. 4

One and two-dimensional distributions of $\Omega _b h^2$, $\Omega _c h^2$, $\tau$, $\sum m_\nu$, $\alpha$, $\beta$, $\sigma _8$, where the contour lines represent 68$\%$  and 95$\%$  C.L., respectively

Table 3 Fitting results for the RVM and $\Lambda \hbox {CDM}$, where the limits are given at 68$\%$ and 95$\%$ C.L., respectively

Fig. 5

One and two-dimensional distributions of $\Sigma m_\nu$ and $\sigma _8$, where the contour lines represent 68$\%$  and 95$\%$  C.L., respectively

Another interesting result is about the correlation between the fluctuation amplitude $\sigma _8$ and the neutrino mass sum $\Sigma m_\nu$ shown in Fig. 5. Many local observations [52,53,54] have claimed that the value of $\sigma _8$ should be smaller than the one given by the Planck measurement [55, 56]. We remark that our fitted value of $\sigma _8$ is much higher than those in Refs. [55, 56] due to the different data set. It is known that the cosmic shear data are important as well and several surveys usually provide values of $\sigma _8$ much smaller than those from the Planck data [57]. Nevertheless, we would examine the tendency of $\sigma _8$ in our model. In order to reduce $\sigma _8$, we should have a smaller matter amplitude, which is consistent with our fitting result in Fig. 4, in which the RVM has lower values of $\Omega _b$ and $\sigma _8$ than those in the $\Lambda \hbox {CDM}$ model. In Fig. 5 we focus on the relationship between $\sigma _8$ and $\Sigma m_\nu$, where the red to blue points represent different values of $\sigma _8$ form 0.9 to 0.76. It is clear that a smaller value of $\sigma _8$ allows of a larger $\Sigma m_\nu$.

Finally, it is interesting to discuss a specific case with $\Lambda _0 = 0$, which might give us a late-time accelerating epoch at the present time and leads our universe to end up with the de-Sitter space in the far future. Such a future dark energy dominated universe can be discussed by substituting Eq. (5) into Eq. (3) with $\rho _m = \rho _r =0$, that is

$$\begin{aligned} H^2 = \alpha H^2 + \beta H_0^4 H^{-2}, \end{aligned}$$

(29)

which leads to $H^2 = H_0^2 \sqrt{\beta / (1-\alpha )}$, pointing out that the existence of the de-Sitter space appears only if $\beta /(1-\alpha ) > 0$. As we have discussed [20, 21], $\alpha \sim 1$ gives us a large abundance of the dark energy density in the early universe, so that the observations require the value of $\alpha$ to be small. On the other hand, the negative value of $\alpha$ induces $\rho _{\Lambda }<0$ at a high z, which should be avoided. Thus, the allowed window for $\alpha$ is tiny with $1 \gg \alpha \ge 0$. As a result, the de-Sitter space can exist if we have a suitable positive value of $\beta \sim \mathcal {O}(1)$. This special case not only keeps the late-time accelerating universe but also further reduces the model parameters by one, i.e., $\Lambda _0 =0$. We show the evolution of $f \sigma _8$ in Fig. 6 with $\alpha =0$ and different values of $\Lambda _0$ and $\beta$. Here, to illustrate the behavior of $f\sigma _8$, we have fixed $\Omega _{\Lambda }$ to be the best fitted value of 0.68 shown in Table 3. As we can see, the smaller value for $\Lambda _0$ is, the more significant deviation from that of the $\Lambda \hbox {CDM}$ prediction behaves, indicating that the vanishment of the $\Lambda _0$ term in the specific RVM does not work well at the linear perturbation level. This result is clearly due to the strong interaction between matter and dark energy in the late time of the universe. A bunch of relativistic and non-relativistic matter decay into dark energy, which further enhance the matter density perturbation $\delta _M$ and change $f \sigma _8$ in our universe. Therefore, this specific case with $\Lambda _0=0$ is available in the background evolution history but, of course, unacceptable at linear perturbation observations.

Fig. 6

$f\sigma _8$ as a function of z in our model and $\Lambda \hbox {CDM}$, where $\Omega _{\Lambda }$ is fixed to be 0.68

4 Conclusions

We have studied the RVM with $\Lambda = 3 \alpha H^2+3\beta H_0^4 H^{-2}+\Lambda _0$ . By modifying the program in $\mathbf{CAMB}$, we have solved the equations for the energy densities of matter and radiation and obtain the numerical solutions. In the CMB and matter power spectra, we have used several different sets of $\alpha$ and $\beta$ to show the cosmological evolutions of the model in the early universe. With the data of BAO, RSD and CMB, we have found that $\alpha$ and $\beta$ are $(<2.83, -0.2^{+3.9}_{-4.5})\times 10^{-4}$ (95$\%$ C.L.) and $(<1.57, -0.2\pm 2.6)\times 10^{-4}$ (68$\%$ C.L.), respectively. The best fitted $\chi ^2$ value is 2543.259 in the RVM, which is in the same order but a little smaller than 2546.662 in the $\Lambda \hbox {CDM}$ model. In addition, the fitting result of $\sigma _8$ has been found to be also smaller than that in $\Lambda \hbox {CDM}$. The results in the RVM are comparable to those in $\Lambda \hbox {CDM}$ to explain the observational data, especially consistent with the local data in the $\sigma _8$ problem.