Constraints on running vacuum models with the baryon-to-photon ratio

Abstract

We study the influence of running vacuum on the baryon-to-photon ratio in running vacuum models (RVMs). The photon and baryon number densities, from photon decoupling to the present day, are obtained in the context of RVMs by assuming that photons and baryons can be coupled to running vacuum, respectively. Both cases lead to a time-evolving baryon-to-photon ratio, whose values at different epochs of the universe are strictly constrained by observations. It is found that if the dominant dynamical term of running vacuum is indeed coupled to photons or baryons, the corresponding coefficient must be far less than the upper limit given by previous research, and so it is difficult to distinguish RVMs from the standard ${\varLambda }$CDM model. Such RVMs which are barely distinguishable from the ${\varLambda }$CDM model seem to be unconvincing. Therefore, if RVMs are reliable cosmological models, running vacuum is unlikely to be coupled to photons or baryons, and then the coefficient of the dominant dynamical term of running vacuum no longer needs to be extremely small.

1 Introduction

The Big Bang theory is by far the most accepted theory explaining the birth, evolution and future of the universe. The measurements of the hydrogen abundance and helium abundance in the universe are exactly consistent with the predictions given by the standard Big Bang nucleosynthesis (BBN) model, which is regarded as one of the strongest evidences¹ supporting the Big Bang theory (see Refs. [1,2,3,4,5,6] for a review). Since the Big Bang theory proposes that the abundances of most of the light elements in the universe are closely related to one basic parameter, i.e., the baryon-to-photon ratio $\eta$, the photon and baryon number densities are of interest and significant for cosmology. In the standard ${\varLambda }$CDM model, as the universe expands, they seem to dilute at the same dilution rate after BBN. Therefore, the value of the baryon-to-photon ratio is regarded as a constant from the end of BBN to the present day [5, 7,8,9].

At different epochs of the universe, $\eta$ can be determined independently from different perspectives. For the BBN epoch one can derive $\eta ^{BBN}$ based on the abundances of primordial chemical elements [5,6,7,8,9,10,11], and for the recombination epoch one can get $\eta ^{re}$ by analysing the anisotropy of the cosmic microwave background (CMB) radiation [12,13,14,15]. If these independent $\eta$’s are in line with the current observed $\eta _0$ [6, 16,17,18,19], the hypotheses and calculations of cosmological processes in the ${\varLambda }$CDM model are reasonable and well-founded. In practice, the photon and baryon number densities are affected by many factors related to particle physics, nuclear physics and cosmology (especially the theory of gravity and the components of the universe). If dark matter could annihilate or decay (see Refs. [20,21,22,23,24,25,26] and references therein), then the baryon-to-photon ratio will deviate from the constant predicted in the ${\varLambda }$CDM model. But from the end of BBN to the present day, the deviation is almost negligible ($\frac{{\varDelta } \eta }{\eta }\le 10^{-5}$) [27, 28]. The impact of dark energy on $\eta$ is mainly due to the possibility that dark energy could decay into CMB, but the decay rate of dark energy must be sufficiently small to be in accordance with observations [29,30,31,32,33]. Considering low-amplitude and large-scale fluctuations, $\eta$ may change with the region of the universe, which could provide a new limit on the graininess of the early universe [34]. In addition, $\eta$ is influenced by varying fundamental “constants” as well [35,36,37,38,39]. The variation of Newton’s constant could modify nucleosynthesis codes, which can be used for restraining Brans–Dicke theory and scalar-tensor theories [39, 40]. A time-varying cosmological “constant” is also able to affect the primordial nucleosynthesis [2, 41, 42]. Although most of these works do not specify the extent of the influence of varying fundamental “constants” on $\eta$, it is not hard to infer that, in these cosmological models, either $\eta$ is a constant different from the one in the ${\varLambda }$CDM model, or it will inevitably evolve over time. Overall, the prediction of $\eta$ at different epochs of the universe is one of the keys to verifying the feasibility of various cosmological models.

In this work, we study the effect of varying vacuum on $\eta$ in a class of cosmological models, which are so called running vacuum models (RVMs), see Refs. [43,44,45,46] and references therein. Assuming that running vacuum is coupled to photons or baryons, the estimation on $\eta$ can be used to constrain the coefficient of the dominant dynamical term of running vacuum. Since the constraints are independent of the ones given by previous research [47,48,49,50,51], comparing our results with the existing results, we can infer whether it is reasonable for running vacuum to be coupled to photons or baryons.

There is a long history of investigations of dynamical vacuum [52,53,54,55,56,57,58], but most dynamical vacuum models lack theoretical support and motivation. The proposal of RVMs is attempting to connect the vacuum energy density with the quantum field theory in curved space-time [47, 59, 60]. In recent years, the research and development of RVMs have shown that running vacuum is better than a single cosmological constant in some respects, such as describing cosmology global picture [45, 46, 61, 62] and matching observation data [48, 49, 57, 63, 64]. Recently, it is found that RVMs, comparing with the ${\varLambda }$CDM model, even exhibit more superior thermodynamic characteristics [65,66,67].

In RVMs, according to the (contracted) Bianchi identities ($\nabla _{\mu }G^{\nu \mu }=0$), one still has $\nabla _{\mu }(T_m^{\nu \mu }+T_{\text {vac}}^{\nu \mu })=0$, where $T_m^{\mu \nu }$ is the energy-momentum tensor of all matter fields and $T_{\text {vac}}$ indicates the energy-momentum tensor of running vacuum. However, it can be found that $\nabla _{\mu }T_m^{\nu \mu }\ne 0$ because the vacuum energy density is not a constant in RVMs.² According to the viewpoint of Tiberiu Harko et al., if the energy-momentum tensor of a matter field is not conserved, using the formalism of open thermodynamic systems, it can be interpreted as describing irreversible particle annihilation (or production) processes, which could be validated by fundamental particle physics [68, 69]. If photons are coupled to running vacuum, the redshift of a single photon in the expanding universe will deviate from the result given by the ${\varLambda }$CDM model (see Refs. [70, 71] and references therein). It can be predicted that the impact of running vacuum on CMB will lead to a time-varying baryon-to-photon ratio. Combining with the values of $\eta$ at different epochs, we can constrain the RVMs with a coupling between running vacuum and photons. Similarly, if running vacuum is coupled to baryons and the interaction is a baryon number non-conserving process, there could be baryon annihilation (or production) even after the Hadron epoch. The influence of the baryon annihilation (or production) on $\eta$ also needs to be limited by observations. Since it is not entirely clear whether baryon number non-conserving processes can occur in the context of low energy and weak gravitational field, in order not to contradict the existing experiments and observations on the baryon decay, the occurrence rate of baryons decaying into running vacuum (or the contrary process) must be very low. Therefore, it could impose strict constraints on the RVMs with a coupling between running vacuum and baryons.

It is worth noting that the influence of running vacuum on the baryon-to-photon ratio actually includes two aspects: indirect influence and direct influence. A typical case of the former is that running vacuum has more or less effect on the primordial nucleosynthesis, so it indirectly alters the baryon-to-photon ratio during the BBN epoch [42]. The indirect influence usually lasts for a short time throughout the evolution of the universe. For more relevant literature on the indirect influence of dynamical “constants” on the baryon-to-photon ratio, one can refer to Refs. [42, 72, 73]. The latter is derived from the possible coupling between running vacuum and photons (or baryons), which can directly affect the number of photons (or baryons) per comoving volume via particle annihilation (or production). Such direct influence may start accumulating from the early universe and bring about observable effects. In this work we only consider the latter case. According to the current value of the baryon-to-photon ratio $\eta _0$ [17,18,19], theoretically we can derive the value of $\eta$ at any epoch if we know what running vacuum is coupled to. However, before photon decoupling (which is close to the end of recombination), photons are coupled to electrons and baryon nuclei, which makes our research on the impact of running vacuum on the baryon-to-photon ratio complicated. Therefore, this work only involves the period from photon decoupling to the present day.

The paper is organized as follows: Sect. 2 is devoted to the review of RVMs. Next, in Sect. 3, we calculate the particle number density of photons in RVMs, and the similar calculations on the particle number density of baryons are presented in Sect. 4. Then, based on Sects. 3 and 4, we study the effect of running vacuum on the baryon-to-photon ratio in Sect. 5. The last part, Sect. 6, is a summary and discussion on our results and possible future work.

2 Running vacuum models

The background space-time of the homogeneous and isotropic universe can be described by Friedmann–Robertson–Walker metric:

$$\begin{aligned} ds^2=-dt^2+a(t)^2 (dx^2+dy^2+dz^2), \end{aligned}$$

(1)

where a(t) is the scale factor and we employ natural units $c=\hbar =1$. For simplicity, here we only consider flat three-dimensional geometry and so the density parameter ${\varOmega }$ is equal to 1.

In the framework of RVMs, the Friedmann equations are similar to the ones in the ${\varLambda }$CDM model:

$$\begin{aligned}&3H^2=\kappa ^2\rho _t, \end{aligned}$$

(2)

$$\begin{aligned}&3H^2+2\dot{H}=-\kappa ^2p_t, \end{aligned}$$

(3)

where $\kappa ^2=8\pi G$ (G is Newton’s constant), $H=\dot{a}/a$ is the Hubble rate, and the dot means time derivative. The parameters $\rho _t$ and $p_t$ represent the total energy density and pressure of all components of the universe, respectively. Since the dominant component is unfixed throughout the evolution of the universe and some of the components can be ignored at particular epochs, the specific forms of $\rho _t$ and $p_t$ rely on the accuracy requirement and the epoch of the universe.

In this work, we consider a class of well described and extensively studied RVMs, in which the vacuum energy density $\rho _{\varLambda }$ “runs” in the form of a function of the Hubble rate based on a renormalization group equation:

$$\begin{aligned} \rho _{\varLambda }(H)=\frac{{\varLambda }(H)}{\kappa ^2}=\frac{3}{\kappa ^2}\left( c_0+\nu H^2+\alpha \frac{H^4}{H_I^2}\right) . \end{aligned}$$

(4)

Hereafter, we just set $\kappa ^2=1$ for simplicity. Note that $c_0$ is a constant with the dimension of energy squared in natural units. Since the current observed value of the Hubble rate is so small, to be consistent with observations, $c_0$ should approximately equal $\frac{1}{3}{\varLambda }_0$ (${\varLambda }_0$ is the value of the cosmological constant in the ${\varLambda }$CDM model [18, 74]). The argument $H_I$ can be chosen as the Planck scale or at least below the Planck scale. The dimensionless coefficients $\nu$ and $\alpha$ have been confined to a narrow range by considering various cosmological phenomena. If the vacuum energy decays into cold dark matter, the density fluctuation spectrum obtained from the CMB data could limit strongly the decay rate of the vacuum energy [75], which is closely related to the magnitude of $\nu$ in RVMs. The possible time variation of the fundamental constants (such as the fine structure “constant”, the ratio of the proton mass to the electron mass, the strong coupling “constant” and Newton’s “constant”) could also provide limits on the parameter $\nu$ from multiple phenomenological perspectives [76, 77]. According to previous research [47,48,49,50,51, 75,76,77], the appropriate values for $\nu$ and $\alpha$ should be $|\nu |<10^{-3}$ and $\alpha \ll 1$, respectively. Actually, based on the structure of RVMs, the parameter $\nu$ can be obtained from explicit quantum field theory calculations in curved space-time. Therefore, $\nu$ is connected with the renormalization-group arguments and one could prove that it is a naturally small parameter [49].

It is worth noting that there are three reasons why we choose running vacuum in the form of Eq. (4) as our model. Firstly, $\rho _{\varLambda }$ as a function of the Hubble rate, is based on a renormalization group equation, and so all coefficients can be expressed as the renormalization-group arguments. For example, the parameter $\nu$ is formally given in quantum field theory as [49]

$$\begin{aligned} \nu =\frac{1}{48\pi ^2}\sum _{i}a_i\frac{M_i^2}{M_{Pl}^2}, \end{aligned}$$

(5)

where $M_{Pl}$ is the reduced Planck mass, $M_i$ is the heavy particle mass from the Grand Unified Theories, and $a_i$ is a dimensionless coefficient associated with $M_i$ (more detail about the coefficients in RVMs can be found in Refs. [44, 46, 78] and references therein). Therefore, compared with the dynamical vacuum model in which $\rho (t)$ is an arbitrary function, RVMs have clear physical significance. Secondly, the energy density of running vacuum could include terms related to odd powers of H and $\dot{H}$, but if the general covariance of the theory is a prerequisite in our model, only powers $\sim H^2, \dot{H}, H^4, \dot{H}^2, H^2\dot{H}\ldots$ (the first two would count as $\sim H^2$ and others would count as $H^4$) can appear [44]. Therefore, the energy density of running vacuum is expected to have the following general form

$$\begin{aligned} \rho _{\varLambda }(H)= a_0+ a_2 H^2+a_4H^4+{\mathcal {O}}(H^{2n})\,\ldots , \end{aligned}$$

(6)

where ${\mathcal {O}}(H^{2n})$ denotes higher order invariant (even) powers. Finally, the reason why we do not consider ${\mathcal {O}}(H^{2n})$ is that such terms have a prominent effect on cosmology only at the epoch of inflation. When one studies the period after inflation, it is practicable to ignore the higher order terms, which is also helpful to solve Friedmann equations analytically.

For our model, it is demonstrable that $\nu H^2$ has been much larger than $\alpha \frac{H^4}{H_I^2}$ after BBN [61], and so the dynamical characteristics of the vacuum energy is mainly manifested in $\nu H^2$. Since our following study does not involve BBN and prior epochs, it is reasonable to discard the subordinate term $\alpha \frac{H^4}{H_I^2}$ in Eq. (4). Now it is easy to get analytical solutions of Eqs. (2) and (3) for the radiation-dominated universe by assuming that the main components of the universe are photons and running vacuum. For such a simplified cosmological model, Eqs. (2) and (3) are rewritten as

$$\begin{aligned} 3H^2= & {} \rho _{\varLambda }+\rho _r, \end{aligned}$$

(7)

$$\begin{aligned} 3H^2+2\dot{H}= & {} -(p_{\varLambda }+p_r). \end{aligned}$$

(8)

Since we have reduced the vacuum energy density (4) as $\rho _{\varLambda }=3\nu H^2+3c_0$, it is found from Eq. (7) that the energy density of photons can be written as an explicit function of the Hubble rate. And also if we express the energy density of photons as a function of the scale factor, we have

$$\begin{aligned} \rho _r(a)=3(H^2-\nu H^2-c_0)=\rho _{r}(t_0) a^{-4(1-\nu )}, \end{aligned}$$

(9)

where the equations of state of the corresponding components are $p_r=1/3\rho _r$ and $p_{\varLambda }=-\rho _{\varLambda }$, respectively. Note that the integration constant $\rho _r(t_0)$ is not necessarily equal to the current power density of CMB radiation. This solution is only applicable to the radiation-dominated epoch, so the value of $\rho _{r}(t_0)$ should be decided by other cosmological processes in the early universe. Obviously, when $\nu =0$, Eq. (9) degenerates into the formula that CMB radiation satisfies in the ${\varLambda }$CDM model.

As for the matter-dominated epoch, one can assume that the universe consists of dark matter, ordinary (baryonic) matter, and running vacuum. So, the Friedmann equations (2) and (3) are given as

$$\begin{aligned} 3H^2= & {} \rho _{\varLambda }+\rho _{dm}+\rho _b, \end{aligned}$$

(10)

$$\begin{aligned} 3H^2+2\dot{H}= & {} -(p_{\varLambda }+p_{dm}+p_b). \end{aligned}$$

(11)

For the sake of simplicity, we set the equations of state of baryonic matter and dark matter as $p_b=p_{dm}=0$. In view of the fact that baryonic matter and dark matter have the same equation of state and similar energy-momentum tensor (which has only one non-zero component, i.e., energy density), we can regard them as a whole when solving the equations above. From Eqs. (10) and (11), it is clear that the total energy density of baryonic matter and dark matter satisfies

$$\begin{aligned} \rho _{dm}+\rho _b= & {} 3(H^2-\nu H^2-c_0)\nonumber \\= & {} [\rho _{dm}(t_0)+\rho _{b}(t_0)]a^{-3(1-\nu )}. \end{aligned}$$

(12)

Here, $\rho _{b}(t_0)$ and $\rho _{dm}(t_0)$ are the current values of the baryon density and the dark matter density, respectively. Apparently, Eq. (12) can also degenerate into the standard one in the ${\varLambda }$CDM model when $\nu =0$. More properties of RVMs can be referred to the literature mentioned above (see Refs. [44, 46] for a review).

3 Photons in RVMs

CMB is a powerful tool and indicator for studying the evolution of the universe. In the ${\varLambda }$CDM model, photons in the universe travel freely after photon decoupling and the energy-momentum tensor of photons is conserved. Therefore, the number of photons inside a comoving volume remains as a constant after photon decoupling. Since the baryon number inside a comoving volume is also conserved after BBN, one can draw a significant conclusion about the ${\varLambda }$CDM model, i.e., the baryon-to-photon ratio is fixed after photon decoupling.³

In different cosmological models, the properties of CMB may be completely different. Combining observations and reasonable inferences, one can put forward effective constraints on cosmological models and even eliminate fallacious cosmological models. In RVMs, running vacuum can influence the evolution of certain components of the universe by a non-minimal coupling. If running vacuum could be coupled to CMB, after photons are decoupled from other matter, the energy density of CMB will be only controlled by the scale factor and running vacuum. In this section, we study the properties of CMB in the context of the RVMs with a coupling between running vacuum and photons. To study explicitly the interaction between running vacuum and photons and exclude the interaction between photons and other substances, we only consider the period of the universe after recombination. Note that to some extent the tail end of recombination can be approximated to the epoch of photon decoupling.

From the end of recombination to the current day, the universe is no longer dominated by radiation, but baryonic matter (or dust), dark matter, and vacuum (or dark energy). Here the radiation is usually a combination of photons and neutrinos. Since the latter is not the dominant component, we usually do not consider neutrinos during the period after photon decoupling. Then, the Friedmann equations can be given as

$$\begin{aligned} 3H^2= & {} \rho _{\varLambda }+\rho _{dm}+\rho _b+\rho _{r}, \end{aligned}$$

(13)

$$\begin{aligned} 3H^2+2\dot{H}= & {} -(p_{\varLambda }+p_{dm}+p_b+p_r). \end{aligned}$$

(14)

For dust and dark matter with a vanishing pressure, energy conservation is equivalent to energy-momentum tensor conservation ($\nabla _{\mu \nu }T^{\nu }_{(b,dm)}=0\longrightarrow \dot{\rho }_{(b,dm)}+3H \rho _{(b,dm)}=0\longrightarrow V\rho _{(b,dm)}\equiv \text {Const}$). The conservation of the total energy-momentum tensor of photons and running vacuum yields

$$\begin{aligned}&{\dot{\rho }}_{{\varLambda }}+{\dot{\rho }}_r+3H(p_{{\varLambda }}+p_r+ \rho _{{\varLambda }}+\rho _r)\nonumber \\&\quad ={\dot{\rho }}_{{\varLambda }}+{\dot{\rho }}_r+4H\rho _r=0. \end{aligned}$$

(15)

So, the energy density of photons is given as

$$\begin{aligned} \rho _r(a)= & {} \rho _r({t_0}) a^{-3}+\frac{3\rho _{bdm}(t_0)}{4}a^{-3}\log a\ \ \left( \nu =\frac{1}{4}\right) \nonumber \\ \rho _r(a)= & {} \rho _{r0} a^{-4(1-\nu )}+\frac{3\nu \rho _{bdm}(t_0) }{1-4\nu } a^{-3}\ \ \left( \nu \ne \frac{1}{4}\right) , \end{aligned}$$

(16)

where $\rho _{bdm}(t_0)=\rho _b(t_0)+\rho _{dm}(t_0)$. $\rho _r({t_0})$ is the current energy density of CMB, but $\rho _{r0}\ne \rho _r(t_0)$, which is decided by $\rho _r({t_0})$:

$$\begin{aligned} \rho _{r0}=\rho _r(t_0)-\frac{3\nu \rho _{bdm}(t_0) }{1-4\nu }. \end{aligned}$$

(17)

The solution of the vacuum density can be expressed as

$$\begin{aligned} \rho _{{\varLambda }}(a)= & {} \frac{\nu }{1-\nu }\rho _{r0}a^{-4(1-\nu )}+ \frac{\nu \rho _{bdm}(t_0)}{1-4\nu }a^{-3}\nonumber \\&+\frac{3}{1-\nu }c_0\ \ \left( \nu \ne \frac{1}{4}\ \ \text {and}\ \ \nu \ne 1\right) \nonumber \\ \rho _{{\varLambda }}(a)= & {} H^2_0a^{-3}+ \frac{1}{4}\rho _{bdm}(t_0)a^{-3}\log a+ 4c_0\ \ \left( \nu =\frac{1}{4}\right) \nonumber \\ \rho _{{\varLambda }}(a)= & {} -\frac{\rho _{bdm}(t_0)}{3}a^{-3} -4\rho _{r0} \log a \ \ (\nu =1), \end{aligned}$$

(18)

where $H^2_0=\frac{1}{3}[\rho _{bdm}(t_0) +\rho _r(t_0)]$. For the solution with $\nu =1$, we have $\rho _{r0}=-3 c_0$. Because we already know that the reasonable value of $\nu$ is $|\nu |<10^{-3}$ [47,48,49,50,51], our following discussion no longer involves the solutions corresponding to $|\nu |>10^{-3}$.

In order to make our discussion more clear and reasonable, let us sort out the known facts about CMB and the observable universe in advance. First of all, the current CMB temperature ($T_0=2.73$ K) and the radius of the observable universe ($R_{0}\sim$ 46 billion light-years) are given by precise observations, which can not be violated in any model of the universe. Secondly, according to the theory of scattering describing the collision between photons and atoms (electrons), the decoupling temperature of CMB is determined around 3000 K [6, 79], which is almost irrelevant to the model of the universe. Finally, the size of the observable universe at the epoch of photon decoupling is indistinct (i.e., the value of the scale factor is indistinct). This argument will affect our evaluation on the age of the universe⁴ and the value of the baryon-to-photon ratio at the epoch of photon decoupling. Based on these facts, we can calculate and analyze the impact of running vacuum on CMB in the RVMs with a coupling between running vacuum and photons.

The number of photons per unit comoving volume (not unit volume) is the most concerned issue in this section. Taking $\rho _{r0}$ [see Eq. (17)] into Eq. (16), since the energy of photons per unit volume satisfies

$$\begin{aligned} \rho _r(t_1)=\frac{\pi ^2 k^4}{15c^3\hbar ^3} T_1^4, \end{aligned}$$

(19)

the correlation between the CMB temperature and the scale factor in our RVMs is given as

$$\begin{aligned}&\left[ \rho _r(t_0)-\frac{3\nu \rho _{bdm}(t_0) }{1-4\nu }\right] a^{-4(1-\nu )}+\frac{3\nu \rho _{bdm}(t_0) }{1-4\nu } a^{-3}\nonumber \\&\quad =\frac{\pi ^2 k^4}{15c^3\hbar ^3} T^4. \end{aligned}$$

(20)

When $T=T_0=2.73$ K and $a(t_0)=1$, $\rho _r(t_0)\sim 4.0\times 10^{-14}~\text {J/m}^3$ is not related to $\nu$. When $\nu =0$ (the ${\varLambda }$CDM model), $a(t_{re})$ is approximately given as $9.1\times 10^{-4}$ with redshift $z\sim 1100$.

Fig. 1

Both of the upper panels are the CMB temperature evolving with the scale factor. The under left panel is the number of photons per unit comoving volume. The under right panel is the energy density of running vacuum, which has been plotted in a dimensionless manner. In a, c, d, seven cases of the parameter $\nu$ are presented: $\nu =-10^{-3}$ (orange-solid), $\nu =-10^{-4}$ (green-solid), $\nu =-10^{-5}$ (blue-solid), $\nu =0$ (red-solid), $\nu =8\times 10^{-6}$ (blue-dashed), $\nu =4\times 10^{-5}$ (green-dashed), and $\nu =5.2\times 10^{-5}$ (orange-dashed). In b, three cases of the parameter $\nu$ are presented: $\nu =10^{-3}$ (red), $\nu =10^{-4}$ (green), and $\nu =5.3\times 10^{-5}$ (orange). For all plots, the proportions of the current universe are $26.8\%$ dark matter, $4.9\%$ dust, $0.005\%$ CMB, and $68.295\%$ vacuum

Table 1 Scale factor and photon number per unit comoving volume at the end of recombination

With Eq. (20), it is found that the sign of $\nu$ has decisive influence on the value of the scale factor. Noting that in Fig. 1a, in which we have selected seven cases of the parameter $\nu$ as samples, all temperature lines will converge to the point ($a=1$, $T=2.73$ K). All intersections of the temperature lines with the horizontal line $T=3000$ K represent the value of the scale factor at the end of recombination (see Table 1 for detail). When $\nu >0$, the value of the scale factor at the end of recombination is less than the value predicted by the ${\varLambda }$CDM model ($\nu =0$). And $\nu <0$ has exactly reverse effects. Overall, the value of the scale factor at the end of recombination increases with $\nu$.

Our research finds that within the reference range of $|\nu |<10^{-3}$, the evolution of CMB provides unexpectedly an extra constraint on the parameter $\nu$ if running vacuum is coupled to photons. In order to guarantee that the CMB temperature evolves normally, the upper limit of $\nu$ is about $5.25\times 10^{-5}$ (see Fig. 1a, b), which is more strict than $\nu <10^{-3}$.

The number of photons per unit comoving volume is given as

$$\begin{aligned} N_{rc}= r_A\left[ \frac{T_0^4[a^{4\nu }(1-19024\nu )+19020\nu a]}{a^4(1-4\nu )}\right] ^{\frac{3}{4}}\ a^3, \end{aligned}$$

(21)

where $r_A=\frac{2k^3\zeta (3)}{\pi ^2c^3\hbar ^3}\sim 2.02\times 10^7$ (K $\cdot$ m)$^{-3}$. For some special values of the parameter $\nu$, the evolution of $N_{rc}$ is shown in Fig. 1c. Only when $\nu =0$, $N_{rc}$ does not evolve with the CMB temperature (see the red-solid line in Fig. 1c), which is exactly what happens in the ${\varLambda }$CDM model. Since the current energy density of photons is given directly by observations, it should be independent of the value of $\nu$. Therefore, when $a=1$, the number density of photons is always $4.1\times 10^{8}~\text {m}^{-3}$ (see Fig. 1c), which exactly corresponds to the current CMB temperature ($T_0=2.73$ K). We also note that although the number density of photons at the end of recombination is independent of $\nu$ and the scale factor, the number of photons per unit comoving volume can differ more than two orders of magnitude due to the parameter $\nu$. Even for $\nu \sim -10^{-5}$, comparing with the ${\varLambda }$CDM model, the gap could be close to $15\%$ (see more detail in Table 1).

The effect of running vacuum on the temperature and particle number of CMB can also be interpreted as photon creation induced by running vacuum [80]. According to the thermodynamic state functions for a black-body photon gas, the number of photons per unit comoving volume is proportional to the cube of the CMB temperature:

$$\begin{aligned} N_{rc}\sim a^3\, T^3. \end{aligned}$$

(22)

The energy of photons per unit volume is proportional to the fourth power of temperature [see Eq. (19)]. When photons are coupled to running vacuum, the energy density of photons as a function of the scale factor is given by Eq. (16). Combining Eqs. (19) and (16), the relation between the CMB temperature and the scale factor satisfies Eq. (20), which reverts to the result ($T\sim a^{-1}$) in the ${\varLambda }$CDM model as $\nu =0$. It is obviously that when $\nu =0$ ($T\sim a^{-1}$), the number of photons is conserved. When $\nu \ne 0$, the number of photons changes with the scale factor (temperature). Such a phenomenon can be interpreted as photons being created by running vacuum. The relation between the creation rate of photons and the scale factor (temperature or redshift) can be given by Eq. (21). Since similar calculations and discussions have been presented in Ref. [80], we will not repeat them in detail here.

Finally, the energy density of running vacuum is shown in Fig. 1d, which evolves monotonously with the scale factor (monotone decreasing for $\nu >0$ and monotone increasing for $\nu <0$).

4 Baryons in RVMs

In this section, we discuss the possible impact of running vacuum on baryons in the RVMs with a coupling between running vacuum and baryons. Similar to the previous approach, when baryons are coupled to vacuum, we assume that the energy-momentum tensor of CMB maintains independently conservation.

For the coupling between running vacuum and baryons, the corresponding Friedmann equations are still Eqs. (13) and (14). Since the solution of the energy density of photons with respect to the scale factor is the same as the one in the ${\varLambda }$CDM model, we can immediately get the energy density of baryons, which satisfies

$$\begin{aligned}&\frac{d\rho _{{\varLambda }}}{da}+\frac{d\rho _{b}}{da}+ 3\frac{\rho _{b}}{a}\nonumber \\&\quad =-\frac{3\nu }{a}\left[ \frac{4}{3}\rho _r(t_0)a^{-4}+\rho _{dm}(t_0)a^{-3}+\rho _b\right] \nonumber \\&\qquad +\frac{d \rho _b}{d a}+\frac{3\rho _b}{a}=0. \end{aligned}$$

(23)

The corresponding solution is given as

$$\begin{aligned} \rho _b(a)= & {} \rho _{b0}a^{-3(1-\nu )}-\rho _{dm}(t_0)a^{-3}\nonumber \\&-\frac{4\nu \rho _r(t_0)}{1+3\nu }a^{-4}\ \ \ \ \left( \nu \ne -\frac{1}{3}\right) \nonumber \\ \rho _b(a)= & {} \rho _{bdm}(t_0)a^{-4}-\rho _{dm}(t_0)a^{-3}\nonumber \\&-\frac{4\rho _r(t_0)}{3}a^{-4}\log a\ \ \ \ \ \ \left( \nu =-\frac{1}{3}\right) . \end{aligned}$$

(24)

Noth that $\rho _{b0}=\rho _{bdm}(t_0)+ \frac{4\nu \rho _r(t_0)}{1+3\nu }$, which insures that when $\nu =0$, $\rho _b(a)$ could revert to the solution in the ${\varLambda }$CDM model. And the solution of the energy density of running vacuum with respect to the scale factor can be written as

$$\begin{aligned} \rho _{{\varLambda }}(a)= & {} \frac{\nu \rho _r(t_0)}{1+3\nu }a^{-4}+\frac{\nu \rho _{b0}}{1-\nu }a^{-3(1-\nu )}\nonumber \\&+\frac{3}{1-\nu }c_0\ \ \left( \nu \ne -\frac{1}{3}\ \ \text {and}\ \ \nu \ne 1\right) \nonumber \\ \rho _{{\varLambda }}(a)= & {} -\frac{1}{4}[\rho _r(t_0)+\rho _{bdm}(t_0)]a^{-4}+ \frac{1}{3}\rho _r(t_0)a^{-4}\log a\nonumber \\&+\frac{9}{4}c_0\ \ \left( \nu =-\frac{1}{3}\right) \nonumber \\ \rho _{{\varLambda }}(a)= & {} 4\rho _r(t_0)a^{-4}-3\rho _{b0}\log a\ \ (\nu =1), \end{aligned}$$

(25)

where $\rho _{b0}=-3c_0$ and the corresponding integration constant has been set to 0. With these solutions, we can study the evolution of the number density of baryons after recombination. Also, since Joan Solà et al. have pointed out, based on multiple observations in cosmology, $|\nu |<10^{-3}$ [47,48,49,50,51], we only discuss the impact of running vacuum on the number density of baryons within the scope of $|\nu |<10^{-3}$.

Fig. 2

The upper left panel is the energy density of baryons. The upper right panel is the number of baryons per unit comoving volume. The under panel is the energy density of running vacuum. All plots have been plotted in a dimensionless manner. Five cases of the parameter $\nu$ are presented in all plots: $\nu =-10^{-3}$ (orange-solid), $\nu =10^{-4}$ (green-solid), $\nu =0$ (red-solid), $\nu =10^{-3}$ (orange-dashed), and $\nu =10^{-4}$ (green-dashed). The current number of baryons per unit comoving volume is about 0.2. The proportions of the current universe are $26.8\%$ dark matter, $4.9\%$ dust, $0.005\%$ CMB, and $68.295\%$ vacuum

Table 2 Baryon density and baryon number per unit comoving volume at the end of recombination

Suppose there exists a baryon-annihilation (or production) process throughout the universe and the energy sink (or source) is running vacuum.⁵ According to the above analysis on the freely expanding photons ($\nu =0$), the approximate value of the scale factor is 0.00091 at the end of recombination. The baryon density of the current universe is approximately $4.2\times 10^{-28}\ \text {kg}/\text{m}^3$. Therefore, the baryon density at the end of recombination can be obtained from Eq. (24), which is plotted in Fig. 2a. When $|\nu |<10^{-5}$, it is hard to distinguish between the RVMs ($\nu \ne 0$) and the ${\varLambda }$CDM model ($\nu =0$) from the perspective of the baryon density. Even if $\nu$ takes the maximum (or minimum) value of the feasible range $|\nu |<10^{-3}$, the corresponding baryon density can not deviate significantly from the result in the ${\varLambda }$CDM model. At the end of recombination, the maximum deviation is about $14\%$ (see Table 2).

It is worth mentioning that in Fig. 2c, when $\nu <0$ and $a(t)\ll 1$, running vacuum presents a state of negative energy. Such state actually also appears in Fig. 1d when $\nu <0$ and $a(t)\ll 1$. It is an obvious consequence according to the structure of running vacuum [see Eq. (4)]. Therefore, in practice, as we discuss the RVMs with $\nu <0$, we must be very careful to insure that the vacuum energy is positive in the early universe.

Unlike baryons, the energy density of running vacuum at the end of recombination is sensitive to the value of $\nu$. Even if $\nu$ deviates a little bit from $\nu =0$, there can be an order of magnitude difference in the vacuum energy density (see Fig. 2c). When $\nu =0$, $\rho _{\varLambda }=3c_0\sim 6.3\times 10^{-10}\ \text {kg}/(\text {m} \cdot \text {s}^{2})$ is the current vacuum energy density (see the red-solid line in Fig. 2c).

Now we analyse the number density of baryons, which can be expressed as

$$\begin{aligned} \rho _b(a)=n_b(a) m_0 c^2, \end{aligned}$$

(26)

where $m_0$ is the mass of a single baryon, $n_b(a)$ is the number density of baryons, and c is the speed of light. According to the latest observations, we take $n_b(t_0)\sim 2.5\times 10^{-7}$ atoms$\cdot$cm$^{-3}$ [17]. If $m_0$ is a constant, $n_b(t_{re})=\frac{\rho _b(t_{re})}{\rho _b(t_0)}n_b(t_0)$. The number of baryons per unit comoving volume satisfies

$$\begin{aligned} N_{bc}(a)=n_b(a) a^3=\frac{\rho _b(a)}{\rho _b(t_0)}n_b(t_0)a^3, \end{aligned}$$

(27)

where $\rho _b(a)$ refers to Eq. (24). The evolution of $N_{bc}(a)$ with respect to the scale factor is presented in Fig. 2b. When $\nu =0$, it is a constant and consistent with the ${\varLambda }$CDM model. The value of $\nu$ has no significant impact on the baryon number per comoving volume at the end of recombination (see Table 2).

5 The effect of running vacuum on the baryon-to-photon ratio

From the previous sections, it is found that running vacuum can indeed influence the particle number densities of photons and baryons by assuming that running vacuum is non-minimally coupled to them, respectively. In this section, we will estimate the value of the baryon-to-photon ratio at the end of recombination in the RVMs with these two kinds of couplings, and get some new constraints on the parameter $\nu$. If running vacuum is minimally coupled to baryons and photons, the influence of running vacuum on the baryon-to-photon ratio could be weaker. Therefore, this kind of RVMs are not discussed in this paper.

In the ${\varLambda }$CDM model, the baryon-to-photon ratio is close to a constant after recombination because the particle number densities of photons and baryons have the same decay rate, and it can even be traced back to the BBN epoch. However, if there exists a non-minimal coupling between running vacuum and photons (or baryons) in RVMs, the particle number density of photons (or baryons) could evolve. Therefore, the baryon-to-photon ratio in such RVMs is not a constant even after recombination. For general RVMs, the dynamical term of running vacuum evolves slowly after inflation, so the influence of running vacuum on BBN and recombination may not be significant.⁶ However, the time period from photon decoupling to the present day is almost the age of the universe. The influence of running vacuum on photon number (or baryon number) is an accumulated effect if there exists a coupling between running vacuum and photons (or baryons) [30, 31], which may cause the baryon-to-photon ratio to diverge significantly from the result in the ${\varLambda }$CDM model. Here, we study the influence of such an accumulated effect on the evolution of the baryon-to-photon ratio. As we mentioned earlier, in our RVMs, the vacuum energy density could be negative when $\nu <0$ and $a\ll 1$. So to avoid non-physical situations in the process of studying the baryon-to-photon ratio, next we will only study the RVMs with $0\le \nu <10^{-3}$.

Table 3 $\eta _{\nu }^{re}$ with running vacuum coupled to photons

Fig. 3

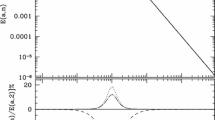
Plots of the baryon-to-photon ratio from recombination to the present day. The upper panel is for the case of running vacuum coupled to photons [$\nu =5.2\times 10^{-5}$ (orange), $\nu =4\times 10^{-5}$ (green), $\nu =8\times 10^{-6}$ (blue), and $\nu =0$ (red)]. The under panel is for running vacuum coupled to baryons [$\nu =10^{-3}$ (orange), $\nu =10^{-4}$ (green), $\nu =10^{-5}$ (blue), and $\nu =0$ (red)]. The current baryon-to-photon ratio is $\eta _0\sim 6.11\times 10^{-10}$

5.1 Running vacuum coupled to photons

If running vacuum is only coupled to photons, the range of $\nu$ is about $0\le \nu \le 5.25\times 10^{-5}$, which could insure that the energy densities of CMB and running vacuum are normal. In this case, the baryon-to-photon ratio is given by

$$\begin{aligned} \eta (a)\!\!&=\frac{n_b(a)}{n_r(a)}=\frac{n_{b}(a)a^3}{N_{rc}(a)}\nonumber \\&=\frac{N_{bc}(a)}{r_A a^{3}}\!\!\left[ \frac{T_0^4[a^{4\nu }(1\!-\!19024\nu )\!+\!19020\nu a]}{a^4(1-4\nu )}\right] ^{-\frac{3}{4}}\!\!, \end{aligned}$$

(28)

where $N_{rc}(a)$ [see Eq. (21)] is the number of photons per unit comoving volume and $N_{bc}(a)=n_{b}(a)a^3$ is the number of baryons per unit comoving volume, respectively. Since running vacuum is only coupled to photons, the total number of baryons inside the observable universe is a constant after BBN and $N_{bc}(a)=n_{b}(a)a^3=n_{b}(t_0)\sim 2.5\times 10^{-7}$ atoms $\cdot$ cm$^{-3}$. The evolution of Eq. (28) is presented in Fig. 3a and the value of the baryon-to-photon ratio at the end of recombination is given in Table 3. For convenience, we set $\eta (a_{re})=\eta _{\nu }^{re}$. One can find that when photons are coupled to running vacuum, $\eta (a)$ always decreases with the increase of the scale factor and $\eta _{\nu }^{re}$ increases with $\nu$. The deviation of $\eta _{\nu }^{re}$ from the constant in the ${\varLambda }$CDM model (when $\nu =0$, $\eta _{\nu }^{re}\sim \eta _0\sim 6.11\times 10^{-10}$) is limited by the upper limit of $\nu$. When $\nu =5.2\times 10^{-5}$, $\eta _{\nu }^{re}\sim 1.80\times 10^{-8}$, which is almost 30 times as large as the constant in the ${\varLambda }$CDM model.

As we know that the value of $\eta$ at different epochs has significant influence on the processes of the universe and so $\eta$ at some epochs can be calculated according to the current observations. There are four epochs at which $\eta$ can be estimated based on observations: BBN ($\eta ^{BBN}$, $z\sim 10^9$), recombination ($\eta ^{re}$, $z\sim 1100$), the period of time associated with the Ly$\alpha$ forest ($\eta ^{\text {Ly}\alpha }$, $z\sim 2{-}3$) [81], and the present epoch ($\eta _{0}$, $z=0$). If we are clear about the values of $\eta$ at any two epochs of the universe, we can use them to constrain the cosmological models in which $\eta$ is related to some parameters. Therefore, it also applies to the RVMs in which photons (or baryons) are coupled to running vacuum. Considering the following aspects, it is more reasonable to use $\eta ^{re}$ and $\eta _0$ to constrain such RVMs:

Table 4 ${\hat{\eta }}_{\nu }^{re}$ with running vacuum coupled to baryons

1. First of all, $\eta _0$ must be considered because it is given directly by observations, which therefore is the most credible and accurate. According to multiple recent observations, the value of $\eta _0$ can be approximated as $\eta _0\sim 6.11\times 10^{-10}$ [17, 18], whose error has been ignored in our study.

2. Since $\eta _0$ has been chosen, $\eta ^{\text {Ly}\alpha }$ will be eliminated. The reason is that these two epochs are too close. Since the influence of running vacuum on $\eta$ is an accumulated effect in our study, it may be hard to inspect such an effect if the period is short.

3. At present, the lithium problem in BBN has not been solved [82, 83], so the estimation on $\eta ^{BBN}$ is questionable. Moreover, $\eta ^{BBN}$ relies heavily on the expansion rate of the universe. Since the influence of running vacuum on the expansion rate of the universe could be prominent during the early universe, if we use $\eta ^{BBN}$ in RVMs, we have to re-estimate $\eta ^{BBN}$. It is beyond the scope of this work. Moreover, during the period from BBN to recombination, the collision of photons with electrons and atomic nuclei may lead to a change in photon number density. Therefore, the change in $\eta$ after BBN is not only dependent on running vacuum, which makes our discussion complicated and ambiguous. These facts are all the reasons why we do not employ $\eta ^{BBN}$.

4. According to the latest observations on the CMB anisotropy, we have $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$ [19], and from the abundances of the light elements, it is estimated that $\eta ^{BBN}\sim (6.084\pm 0.230)\times 10^{-10}$ [19]. It is obvious that the former has higher accuracy. But most importantly, photons and baryons can only be coupled to running vacuum after recombination, which is the main reason why we employ $\eta ^{re}$.

Reviewing $\eta ^{re}$ and $\eta _0$ in the ${\varLambda }$CDM model, we notice that $\eta _0\sim 6.11\times 10^{-10}$ is almost in the middle of the range of $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$, that is to say, from the end of recombination to the present day, the value of $\eta$ can be reduced or increased on a small scale. We set the current baryon-to-photon ratio in RVMs to equal $\eta _0$ due to the current observations, and $\eta _{\nu }^{re}$ presents the baryon-to-photon ratio in RVMs at the end of recombination. Once again, since we only focus on the cumulative effect of running vacuum on the evolution of the baryon-to-photon ratio after photon decoupling, here we ignore the impact of running vacuum on the CMB anisotropy, that is, we assume that $\eta _{\nu }^{re}$ derived from the CMB anisotropy in RVMs is roughly equal to the estimated value $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$ in the ${\varLambda }$CDM model. In the RVMs with a coupling between running vacuum and photons, $\eta _{\nu }^{re}$ can also be obtained independently by Eq. (28), which is closely related to the evolution of running vacuum. In principle, these two independent results should be consistent, which is the basic idea that we can use the baryon-to-photon ratio to constrain the RVMs with a coupling between running vacuum and photons. Since the error of $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$ is small, the dynamical term in the RVMs must evolve very slowly to ensure that $\eta _{\nu }^{re}$ obtained from Eq. (28) in the RVMs is not in contradiction with $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$.

We list some results of $\eta _{\nu }^{re}$ in Table 3. It is seen that when $\nu \ge 0$, $\eta _{\nu }^{re}$ is always larger than $\eta _0$, and also $\eta _{\nu }^{re}$ increases with the parameter $\nu$. To be consistent with the observations, i.e., $\eta _{\nu }^{re}=\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$, we find that the parameter $\nu$ has to satisfy $0\le \nu <5\times 10^{-7}$. Comparing with the results $0\le \nu <10^{-3}$ obtained by a large string SNIa+BAO+H(z)+LSS+CMB of modern cosmological data [47,48,49,50,51], $0\le \nu <5\times 10^{-7}$ is obviously compatible with it and even much more accurate than it. Such a tiny $\nu$ signifies that it is difficult to distinguish the RVMs from the ${\varLambda }$CDM model. Even if $\nu =8\times 10^{-6}$ (which is larger than $5\times 10^{-7}$ and so the corresponding $\eta _{\nu }^{re}$ does not satisfies the observations on the CMB anisotropy), we can find from Fig. 3a that the evolution of $\eta$ almost overlaps with the result in the ${\varLambda }$CDM model ($\nu =0$).

To sum up, if there exits a coupling between photons and running vacuum in RVMs, according to the data on the baryon-to-photon ratio, the coefficient $\nu$ of the dominant dynamical term of running vacuum must be extremely small ($0\le \nu <5\times 10^{-7}$). Comparing with $0\le \nu <10^{-3}$ given by Solà et al. [47,48,49,50,51], the accuracy of the new constraint is several orders of magnitude higher than it. For such a tiny $\nu$, it is so difficult to distinguish the RVMs from the ${\varLambda }$CDM model.

5.2 Running vacuum coupled to baryons

Now, we study the second case, that is, running vacuum is only coupled to baryons. The pre-given range of the parameter $\nu$ is also $0\le \nu <10^{-3}$ [47,48,49,50,51]. In this case, the baryon-to-photon ratio is given as

$$\begin{aligned} {\hat{\eta }}(a)= & {} \frac{N_{bc}(a)}{n_r(a)a^3}= \Bigg [\left( \frac{317}{49}+\frac{\nu }{245(1+3\nu )}\right) a^{3\nu } -\frac{268}{49}\nonumber \\&-\frac{\nu }{245(1+3\nu )}a^{-1}\Bigg ]\frac{n_b(t_0)}{n_r(a)a^3}, \end{aligned}$$

(29)

where $N_{bc}(a)$ is given by Eq. (27). Note that $\frac{n_b(t_0)}{n_r(a)a^3}=\frac{n_b(t_0)}{n_r(t_0)} \sim 6.11\times 10^{-10}$ is the current baryon-to-photon ratio for $n_b(t_0)\sim 2.5\times 10^{-7}$ atoms $\cdot$ cm$^{-3}$ and $n_r(t_0)\sim 4.1\times 10^{8}~\text {m}^{-3}$.

The evolution of ${\hat{\eta }}(a)$ with the scale factor is presented in Fig. 3b. When the parameter $\nu$ increases, ${\hat{\eta }}_{\nu }^{re}$ decreases (see Table 4). We can see that ${\hat{\eta }}_{\nu }^{re}$ is not sensitive to the change in $\nu$. Similar to the previous subsection, the observations on the CMB anisotropy require ${\hat{\eta }}_{\nu }^{re}$ to be consistent with $\eta ^{re}\sim (6.090\pm 0.060)\times 10^{-10}$, so one can get a new constraint on the parameter $\nu$: $0\le \nu <10^{-4}$. The new constraint is slightly stronger than $0\le \nu <10^{-3}$. It seems to be a satisfactory result because there is the possibility of distinguishing the RVMs from the ${\varLambda }$CDM model under the new constraint.

Unfortunately, here the baryon decay rate⁷ is, in fact, rather fast if $\nu$ is not extremely small. One can simply make a following estimation. From recombination to the present day, the average particle number of decaying baryons per year within the observable universe can be estimated as

$$\begin{aligned} {\bar{N}}=\frac{N_0-N_{re}}{{\mathfrak {T}}}, \end{aligned}$$

(30)

where $N_0$ is the total number of baryons inside the observable universe at present and $N_{re}$ indicates the total number of baryons inside the observable universe at the end of recombination. Here, ${\mathfrak {T}}\sim 1.38\times 10^{10}$ years is the age of the universe (the period before recombination is negligible). We can assume that the baryon decay occurs everywhere in the universe with equal probability, because running vacuum is evenly distributed throughout the universe. At such decay rate, the number of baryons decaying into running vacuum on the entire earth per year (for the present day) should be

$$\begin{aligned} {\bar{N}}_{\text {earth}}={\bar{N}}\frac{N_{\text {earth}}}{N_0}, \end{aligned}$$

(31)

where $N_{\text {earth}}$ is the total number of baryons on the earth. In rough, we take the mass of the earth as $6\times 10^{24}$ kg and the average mass of a baryon as $2\times 10^{-27}$ kg, so $N_{\text {earth}}\sim 10^{51}$. The total number of baryons in the current observable universe can be given by the current baryon number density [$n_b(t_0)\sim 2.5\times 10^{-7}$ atoms $\cdot$ cm$^{-3}$] and the current volume of the observable universe ($V\sim 4\times 10^{80}$ m$^3$). Given any value of $\nu$, we can obtain a corresponding $N_{re}$ and ${\bar{N}}_{\text {earth}}$. Some results are presented in Table 5. When $\nu =10^{-5}$, $\bar{N}_{\text {earth}}\sim 10^{38}\sim 10^{-13}N_{\text {earth}}$, which indicates the earth will lose $10^{11}$ kg per year due to the decay of baryons into running vacuum. Such mass is insignificant compared to the total mass of the earth, but with the current measurement precision, we may have observed the phenomenon that baryons decay into running vacuum in the laboratory. Obviously, in order not to contradict observations and experiments, $\nu$ has to be re-estimated. Let us take the half-life of protons as an example, which is at least $1.67\times 10^{34}$ years [84]. For $\nu =10^{-5}$, if the decay rate of protons is equal to the decay rate of baryons and it is constant in the RVMs, the half-life of protons in the RVMs is given as $\sim 7\times 10^{12}$ years, which is much less than $1.67\times 10^{34}$ years. According to Table 5, $\nu$ is approximately proportional to the decay rate of baryons. Therefore, to prolong the half-life of protons in the RVMs, the value of $\nu$ should be smaller. We finally find $\nu$ should satisfy $0\le \nu <10^{-8}$ to match the half-life of protons in the laboratory. This constraint is stronger than $0\le \nu <10^{-4}$, and so it is our final result.

In summary, when baryons are coupled to running vacuum, based on the baryon-to-photon ratio, one can obtain a new constraint ($0\le \nu <10^{-4}$) on the coefficient $\nu$ of the dominant dynamical term of running vacuum, which basically fits the existing constraint ($0\le \nu <10^{-3}$). But considering the half-life of protons, the constraint will be strengthened to $0\le \nu <10^{-8}$. When $0\le \nu <10^{-8}$, it is difficult to distinguish between the RVMs and the ${\varLambda }$CDM model.

Table 5 The number of baryons decaying into running vacuum on the entire earth per year

6 Discussions and conclusions

The study on the baryon-to-photon ratio in BBN explains the current abundances of most of the light elements in the universe [1,2,3,4,5,6], which is an important basis for BBN and the ${\varLambda }$CDM model to be accepted by most physicists. However, the difference between the estimation and observation on lithium abundance is like a dark cloud hanging over BBN and the ${\varLambda }$CDM model [82, 83]. Although varying physical “constants” could bring about a turning point to the problem of lithium abundance [85], we do not know if varying physical “constants” will bring about new problems. In this work, we study the baryon-to-photon ratio in the context of RVMs, which have a special dynamical vacuum evolving in the form of a function of the Hubble rate.

Since there exists a non-minimal coupling between matter fields and running vacuum in RVMs, at least there exists a matter field whose evolution is different with the ${\varLambda }$CDM model due to running vacuum. If the matter field is photons or baryons, the baryon-to-photon ratio will evolve with running vacuum. Considering that the photon density may be affected by a variety of factors before the end of recombination, in order to analyze and study the influence of running vacuum on the baryon-to-photon ratio without other distractions, our study only involves the period from the end of recombination to the present day. If photons are coupled to running vacuum, the CMB temperature at the end of recombination still needs to meet the requirement of photon decoupling, and it is almost independent of cosmological models. According to the current CMB temperature, we can inversely deduce the size of the scale factor at the end of recombination, which is dependent on the coefficient $\nu$ of the dominant dynamical term of running vacuum (see Table 1). The photon number per unit comoving volume at the end of recombination is also related to $\nu$ (see Fig. 1c). To avoid non-physical results of CMB, the upper limit of $\nu$ is approximately equal to $5.25\times 10^{-5}$. Combining the current observations on the baryon-to-photon ratio and the corresponding value at the end of recombination predicted by the CMB anisotropy, it is found that $\nu$ must be tiny, i.e., $0\le \nu <5\times 10^{-7}$. Comparing this result with $0\le \nu <10^{-3}$ [47,48,49,50,51], the new constraint has a large improvement in accuracy. Similarly, if baryons are coupled to running vacuum, we obtain the energy density of baryons (see Fig. 2a) and the number of baryons per unit comoving volume (see Fig. 2b) for different values of $\nu$. We find that the constraint of the baryon-to-photon ratio on $\nu$ is $0\le \nu <10^{-4}$, which agrees very well with $0\le \nu <10^{-3}$ [47,48,49,50,51]. However, the decay rate of baryons decaying into running vacuum is too fast when $\nu \rightarrow 10^{-4}$. Taking the earth as an example, when $\nu =10^{-5}$, ${\bar{N}}_{\text {earth}}\sim 10^{-38}\sim 10^{-13}N_{\text {earth}}$, which means that the lost mass of the earth is about $10^{11}$ kg every year due to the baryon decay (see Table 5). On the other hand, according to the lower limit of the half-life of protons (which is about $7\times 10^{12}$ years), such a rapid decay rate is also unconvincing. Our rough calculations show that unless $\nu$ satisfies $0\le \nu <10^{-8}$, the half-life of protons in the RVMs will contradict existing observations and experiments. Therefore, when baryons are coupled to running vacuum, the constraint on the parameter $\nu$ should be $0\le \nu <10^{-8}$, which comparing with $0\le \nu <10^{-3}$ also has a large improvement in accuracy.

For the above results, our analysis is as follows. In RVMs, running vacuum must be coupled to other substances due to the “running” of vacuum. If we assume running vacuum is coupled to photons or baryons, based on the observations on the baryon-to-photon ratio and the proton decay one can obtain new constraints on the coefficient $\nu$ of the dominant dynamical term of running vacuum. The new constraints are all far more strict than the constraint given by Refs. [47,48,49,50,51]. However, since the upper limit of the coefficient $\nu$ obtained in this case is extremely small, it is difficult to distinguish between RVMs and the ${\varLambda }$CDM model. If they can not be distinguished, then RVMs would be meaningless and worthless. In other words, our research shows that if RVMs are reliable models of the universe, the results above make us believe that running vacuum is unlikely to coupled to photons and baryons (unless the coefficient of the dominant dynamical term of running vacuum is extremely small), but other matter (such as dark matter). Therefore, our research to a large extent excludes the possibility that running vacuum is coupled to photons and baryons.

At present, there have been some studies on dark matter in RVMs or dynamical vacuum models [27, 46, 49, 51, 56, 58, 75, 86, 87]. As far as we know, there is currently no research on the evolution of the baryon-to-photon ratio in the RVMs with a coupling between running vacuum and dark matter. According to the research in this work, we believe that the coupling has no much influence on the baryon-to-photon ratio, because the coupling is unlikely to directly affect the number of baryons and photons. If so, it will not change the bounds on $\nu$ in a significant way. Undoubtedly, it is a question worthy of further discussion. In the end, it is worth mentioning that in Ref. [88] the authors studied the gravitational baryogenesis mechanism and baryon asymmetry in RVMs. They found that there exists non-zero baryon-to-entropy ratio in RVMs, which is compatible with the observational data. Using the gravitational baryogenesis mechanism and the observed value of the baryon-to-entropy ratio, one can also constrain RVMs. For more details on their methodology and results, one can refer to Ref. [88].