1 Introduction

The wormhole is a solution to Einstein’s field equation which provides a possible way to connect different spacetime regions or different universe [1]. As early as 1935, Einstein and Rosen first obtained the famous Einstein–Rosen bridge (ERB) by solving the Einstein field equation. But such a wormhole solution turns out to be unworkable [2,3,4,5]. Therefore, finding a traversable wormhole has became an interesting research subject. Many traversable wormhole models have been proposed in the framework of the general relativity. For instance, Ellis pointed out that the traversable wormhole can be supported by a phantom scalar field [4, 5], Thorne found the famous Morris–Thorne (MT) traversable wormhole solution [6], which requires a kind of exotic matter to keep the wormhole’s throat open. In fact, the exotic matter has a positive energy density and a negative pressure, producing a repulsive effect, preventing the wormhole from closing. Generally speaking, such exotic matter usually violates the energy condition [7]. It is interesting to note that Kanti et al. constructed traversable wormholes in the context of quadratic gravitational theories, where gravity itself keeps the wormhole throat open without the need for any exotic matter [8, 9].

According to the standard cosmology model and the recent observation results, our universe is made up of about 4\(\%\) atomic matter, 29.6\(\%\) dark matter and 67.4\(\%\) dark energy [10,11,12]. On a galactic scale, dark matter plays an important role in the formation and evolution of galaxies (see e.g., [13]). Given the ubiquity of dark matter halos and galaxies, it is important to consider the formation of traversable wormholes in the dark matter halo and galaxy (see e.g., [14,15,16]). Some work has been done in this regard, such as [14], showing that based on the Navarro–Frenk–White (NFW) profile traversable wormholes may form in the outer halo of galaxies. Recently, [17] pointed out the possibility of traversable wormhole formation in a Bose–Einstein condensation dark matter halo, however, one only obtained the approximate solution. In this paper, we study the exact solutions of spherical symmetry traversable wormhole in the dark matter halos under the isotropic pressure condition, and we obtain the axisymmetric traversable wormhole by the Newman–Janis (NJ) algorithm. We also analyze the energy conditions of these traversable wormhole solutions near the wormhole throat with a radius \(r_{0}\). Furthermore, we discuss the dark matter density profile properties around the axisymmetric traversable wormhole.

The paper is organized as follows: In Sect. 2, we introduce several typical dark matter profile. In Sect. 3, we derive the spherical symmetry traversable wormholes in the dark matter halos under the isotropic pressure condition. In Sect. 4, we derive axisymmetric traversable wormholes by the NJ algorithm. In Sect. 5, we study the energy conditions near the wormhole throat. A summary is presented in Sect. 6.

2 The dark matter density profile

2.1 Navarro–Frenk–White (NFW) profile

An approximate analytical expression of the NFW density profile is derived based on the theory of the cosmological constant Cold Dark Matter (\(\Lambda \)CDM) and numerical simulation [18,19,20]. For galaxies and clusters, the dark matter halo can be determined by the NFW density profile, which is given by the analytical expression as

$$\begin{aligned} \rho _{\mathrm{NFW}}=\dfrac{\rho _{s}}{\dfrac{r}{R_{s}}\left( 1+\dfrac{r}{R_{s}}\right) ^{2}}, \end{aligned}$$
(1)

where \(\rho _{s}\) is the dark matter density when the dark matter halo collapses, and \(R_{s}\) is the scale radius. It is well known that the NFW density profile represents a broad category of dark matter models in which the collision effects between dark matter particles are so weak.

2.2 Thomas–Fermi (TF) profile

The Bose–Einstein Condensation dark matter (BEC-DM) model shows more advantages on the small scales of galaxies compared to the CDM model. For instance, the interactions between dark matter particles are very strong in the inner regions of galaxies, and thus the dark matter will no longer be cold. For the BEC-DM model, the dark matter density profile can be described by the TF profile [21]

$$\begin{aligned} \rho _{\mathrm{TF}}=\rho _{s}\dfrac{\sin (kr)}{kr}, \end{aligned}$$
(2)

where \(\rho _{s}\) is the center density of BEC-DM halo, \(k=\pi /R\) is the radius where the dark matter pressure and density vanish. The BEC-DM model predicts much less dark matter density in the center regions of galaxies than the NFW profile.

2.3 Pseudo isothermal (PI) profile

In addition to the CDM model and the BEC-DM model, there is an important class of dark matter models associated with modified gravity, such as Modified Newtonian Dynamics (MOND) [22]. In the MOND model, the dark matter density profile is described by the PI profile

$$\begin{aligned} \rho _{\mathrm{PI}}=\dfrac{\rho _{0}}{1+\left( \dfrac{r}{R_{c}}\right) ^{2}}, \end{aligned}$$
(3)

where \(\rho _{0}\) is the central dark matter density and \(R_{c}\) is the scale radius.

3 Traversable wormhole with isotropic pressure

In Schwarzschild-like coordinates, the spacetime metric of spherical symmetry traversable wormhole can be expressed as

$$\begin{aligned} \mathrm{d}s^{2}= & {} -e^{2\Phi (r)}\mathrm{d}t^{2}+\dfrac{1}{1-\dfrac{b(r)}{r}}\mathrm{d}r^{2}\nonumber \\&+r^{2} (\mathrm{d}\theta ^{2}+ \sin ^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$
(4)

where \(\Phi (r)\) is the redshift function and b(r) is the shape function. In order to ensure a wormhole to be traversable, there should be no event horizon. Therefore, \(\Phi (r)\) should be finite and tend to zero when \(r\rightarrow \infty \). The geometry of the wormhole is determined by the shape function b(r), which should satisfy the boundary condition \(b(r_{0})=r_{0}\), where \(r_{0}\) is the wormhole’s throat radius. Moreover, to keep the wormhole’s throat open, the shape function b(r) should also satisfy the flare-out condition \((b(r)-rb^{'}(r))/b^{2}(r)>0\) and \(b^{'}(r)<1\).

In order to obtain the wormhole metric under the general dark matter profile, we need to solve the Einstein field equation \(R_{\mu \nu }-g_{\mu \nu }R/2=8\pi T_{\mu \nu }\), where \(T_{\mu \nu }\) is the energy-momentum tensor, which can be determined by dark matter profile and be written as \(T_{\mu \nu }=\mathrm{{diag}}(-\rho ,P_{r},P_{\theta },P_{\phi })\). Therefore, the Einstein field equations can be simplified to

$$\begin{aligned} 8\pi \rho (r)= & {} \dfrac{b^{'}(r)}{r^{2}}, \end{aligned}$$
(5)
$$\begin{aligned} 8\pi P_{r}(r)= & {} -\dfrac{b(r)}{r^{3}}+2\left( 1-\dfrac{b(r)}{r}\right) \dfrac{\Phi ^{'}(r)}{r}, \end{aligned}$$
(6)
$$\begin{aligned} 8\pi P_{\theta }(r)= & {} 8\pi P_{\phi }(r)=\left( 1-\dfrac{b(r)}{r}\right) \bigg [\Phi ^{''}(r)+\Phi ^{'2}(r) \nonumber \\&\quad -\dfrac{rb^{'}(r)-b(r)}{2r(r-b(r))}\Phi ^{'}(r) -\dfrac{rb^{'}(r)-b(r)}{2r^{2}(r-b(r))}+\dfrac{\Phi ^{'}(r)}{r}\bigg ],\nonumber \\ \end{aligned}$$
(7)

where \(\rho (r)\) is the energy density for dark matter, \(P_{r}(r)\) is the radial pressures, \(P_{\theta }(r)\) and \(P_{\phi }(r)\) is the tangential pressures. According to the energy-momentum tensor conversation law \(T^{\mu \nu }_{~~;\nu }=0\), we can obtain the hydrostatic equation of dark matter,

$$\begin{aligned} P^{'}_{r}=-(P_{r}+\rho )\Phi ^{'}+\dfrac{2(P_{\theta }-P_{r})}{r}. \end{aligned}$$
(8)

Assuming the dark matter pressure is isotropic \(P_{\theta }=P_{r}=P\), Eq. (8) becomes

$$\begin{aligned} P^{'}=-(P+\rho )\Phi ^{'}. \end{aligned}$$
(9)

From Eq. (9), the redshift function \(\Phi (r)\) can be obtained with the state equation \(P=\omega \rho \),

$$\begin{aligned} \Phi (r)=-\dfrac{\omega }{1+\omega }\ln \left[ -\omega b^{'}(r)\left( \dfrac{r}{r_{0}}\right) ^{2}\right] , \end{aligned}$$
(10)

where the shape function b(r) can be determined by the boundary condition \(\Phi (r_{0})=0\). Consequently, if we know the expression for b(r), then we know the expression for the function \(\Phi (r)\).

Here, we derive the traversable wormhole’s metric based on the NFW, TF and PI dark matter density profile. Using Eqs. (1)–(3), (5) and the boundary condition \(b(r_{0})=r_{0}\), we can obtain the shape functions

$$\begin{aligned} b(r)=\left\{ \begin{array}{l} r_{0}+8\pi \rho _{s}R^{3}_{s}\\ \left[ \ln \dfrac{r+R_{s}}{r_{0}+R_{s}}+R_{s}\left( \dfrac{1}{r+R_{s}}-\dfrac{1}{r_{0}+R_{s}}\right) \right] , \, \, \quad \mathrm{for \, NFW \, profile;} \\ r_{0}+\dfrac{8\rho _{0}R^{3}}{\pi ^{2}}\left[ \sin \left( \dfrac{\pi r}{R}\right) -\sin \left( \dfrac{\pi r_{0}}{R}\right) \right] \\ -\dfrac{8\rho _{0}R^{3}}{\pi }\left[ \dfrac{r}{R}\cos \left( \dfrac{\pi r}{R}\right) -\dfrac{r_{0}}{R}\cos \left( \dfrac{\pi r_{0}}{R}\right) \right] , \, \, \, \, \, \,\, \mathrm{for\, TF \, profile;} \\ r_{0}+8\pi \rho _{0}R^{2}_{c}\left[ r-r_{0}-R^{2}_{c}\ln \dfrac{r+R^{2}_{c}}{r_{0}+R^{2}_{c}}\right] , \, \, \, \, \, \, \quad \, \mathrm{for\, PI \, profile.} \end{array} \right. \end{aligned}$$
(11)

Using Eqs. (4), (10) and the boundary condition \(\Phi (r_{0})=0\), we can obtain the expressions for the redshift function,

$$\begin{aligned} e^{2\Phi (r)}=\left\{ \begin{array}{l} \left( \dfrac{r+R_{s}}{r_{0}+R_{s}}\right) ^{\dfrac{4\omega }{1+\omega }}\times \left( \dfrac{r}{r_{0}}\right) ^{\dfrac{2\omega }{1+\omega }} , \, \, \, \, \, \mathrm{for \, NFW \, profile;}\\ \left( \dfrac{r}{r_{0}}\dfrac{\sin \left( \dfrac{\pi r_{0}}{R}\right) }{\sin \left( \dfrac{\pi r}{R}\right) }\right) ^{\dfrac{2\omega }{1+\omega }}, \, \, \, \, \, \qquad \qquad \quad \mathrm{for\, TF \, profile;}\\ \left( \dfrac{r^{2}+R^{2}_{c}}{r^{2}_{0}+R^{2}_{c}}\right) ^{\dfrac{2\omega }{1+\omega }}, \, \, \, \, \, \qquad \qquad \qquad \qquad \mathrm{for\, PI \, profile.} \end{array} \right. \end{aligned}$$
(12)

We find that if the equation of state satisfies k, the redshift function disappears at the asymptotic infinity, and the wormhole solution is asymptotically flat.

We present some discussions on the derived wormhole solutions below. From Eq. (12), we find that if the equation of state satisfies \(-1<\omega <0\), the redshift functions vanish at asymptotic infinity, and the wormhole solutions are asymptotically flat. In order to make the derived wormhole solutions better link with the external vacuum solutions (for further discussions, see [23]), we need to give the conditions of the pressure

$$\begin{aligned}&P(r)=\omega \rho \nonumber \\&\quad =\left\{ \begin{array}{l} -\dfrac{1}{8\pi r^{2}_{0}}\dfrac{r_{0}}{r}\left( \dfrac{r_{0}+R_{s}}{r+R_{s}}\right) ^{2}, \, \, \, \, \, \mathrm{for \, NFW \, profile;}\\ -\dfrac{1}{8\pi r^{2}_{0}}\dfrac{r_{0}}{r}\dfrac{\sin \left( \dfrac{\pi r}{R}\right) }{\sin \left( \dfrac{\pi r_{0}}{R}\right) }, \, \, \, \, \, \quad \mathrm{for\, TF \, profile;}\\ -\dfrac{1}{8\pi r^{2}_{0}}\dfrac{r^{2}_{0}+R^{2}_{c}}{r^{2}+R^{2}_{c}}, \, \, \, \, \, \qquad \quad \, \, \mathrm{for\, PI \, profile.} \end{array} \right. \end{aligned}$$
(13)

On the other hand, we discuss an interesting question. If these wormholes in the dark matter halos are traversable, what condition should the parameters of these wormholes satisfy? First, if an astronaut were to travel through these wormholes, the gravity that the astronaut felt in wormholes would not be greater than on the earth. Similar to the discussions of [6], we can obtain the inequality

$$\begin{aligned} \mid \dfrac{1}{\sqrt{-g_{rr}g_{tt}}}\dfrac{d\gamma \sqrt{g_{tt}}}{dr}\mid \le 9.8 \,\,\mathrm{m/s^{2}}, \end{aligned}$$
(14)

where \(\gamma =1/\sqrt{1+v^{2}/c^{2}}\), v is the velocity of astronaut and c is the speed of light. Second, the tidal acceleration that the astronaut felt in wormholes would not be greater than on the earth (see [6] for a detailed discussion). This condition should satisfy the inequalities

$$\begin{aligned} \mid R_{rtrt}\mid \le \dfrac{1}{(10^{10}\,\,\mathrm{cm})^{2}} \end{aligned}$$
(15)

and

$$\begin{aligned} \mid \gamma ^{2}R_{\theta t\theta t}+\gamma ^{2}\left( \dfrac{v}{c}\right) ^{2}R_{\theta r\theta r}\mid \le \dfrac{1}{(10^{10}\,\,\mathrm{cm})^{2}}, \end{aligned}$$
(16)

where \(R_{rtrt},R_{\theta t\theta t}\) and \(R_{\theta r\theta r}\) are tidal tensors from wormhole metric. Finally, assume an observer is on a space station located just outside the junction radius h at \(l=-l_{1}\) and \(l=-l_{2}\), where the proper distance is \(\mathrm{d}l=\sqrt{g_{rr}}\mathrm{d}r\). The traversal time measured by the astronaut is \(\Delta \tau =\int ^{+l_{2}}_{-l_{1}}1/(v\gamma ) \mathrm{d}l\), and the traversal time measured by the observer in the space stations is \(\Delta t=\int ^{+l_{2}}_{-l_{1}}(1/v\sqrt{g_{tt}})\mathrm{d}l\).

Next, for wormholes in NFW, TF and PI profile, we verify the above conditions. For simplicity, we consider only non-relativistic case, that is to say \(\gamma \approx 1\). Through calculation, we find that these wormholes satisfy inequalities (14) and (15). For inequality (16), near a wormhole’s throat, this inequality becomes

$$\begin{aligned}&v\le r_{0}\sqrt{\dfrac{2\times 9.8\,\,\mathrm{m}/\mathrm{s}^{2} }{2{m}\times \mid 1-b^{'}(r_{0})\mid }}\nonumber \\&\quad =\left\{ \begin{array}{l} r_{0}\sqrt{\dfrac{2}{\times } 9.8\,\, \mathrm{m}/\mathrm{s}^{2} \,{2{m}}}\left( 1+\dfrac{r_{0}}{R_{s}}\right) \\ \quad \times \left( 8\pi \rho _{s}r_{0}R_{s}-\left( 1+\dfrac{r_{0}}{R_{s}}\right) ^{2}\right) ^{-\dfrac{1}{2}}, \, \, \, \, \, \quad \qquad \qquad \,\,\, \mathrm{for \, NFW \, profile;}\\ r_{0}\sqrt{\dfrac{2\times 9.8 \,\, \mathrm{m}/\mathrm{s}^{2} }{2{m}}}\left( 1-8r_{0}\rho _{s}R\sin \left( \dfrac{\pi r_{0}}{R}\right) \right) ^{-\dfrac{1}{2}}, \, \quad \mathrm{for\, TF \, profile;}\\ r_{0}\sqrt{\dfrac{2\times 9.8\,\, \mathrm{m}/\mathrm{s}^{2}}{2{m}}}\sqrt{1+\left( \dfrac{r_{0}}{R_{s}}\right) ^{2}}\\ \quad \times \left( 1+\left( \dfrac{r_{0}}{R_{s}}\right) ^{2}-8\pi \rho _{0}r^{2}_{0}\right) ^{-\dfrac{1}{2}}, \, \, \, \, \, \quad \qquad \qquad \qquad \,\mathrm{for\, PI \, profile.} \end{array} \right. \nonumber \\ \end{aligned}$$
(17)

In order to compute the traversal time \(\Delta t (\approx \Delta \tau )\), we consider the equality case in inequality (17). At the same time, if we consider that the wormhole throat \(r_{0}\approx 100\) m and the junction radius \(h\approx 10000\) m, then the traversal time is given by \(\Delta t\approx \Delta \tau \approx 2h/v\). For the Milky Way (MW) [24], \(\rho _{s}=1.936\times 10^{7}M_{\odot }\mathrm{kpc}^{-3}=0.13\times 10^{-20}\) \(\mathrm{kg/m^{3}}\) and \(R_{s}=17.46\,\mathrm{kpc} = 5.4\times 10^{20}\) \(\mathrm{m}\) for NFW profile, \(\rho _{s}=3.43\times 10^{7}M_{\odot }\) \(\mathrm{kpc^{-3}} = 0.23\times 10^{-20}\) \(\mathrm{kg/m^{3}}\) and \(R=15.7\) \(\mathrm{kpc} = 4.84\times 10^{20}\) \(\mathrm{m}\) for TF profile. \(\rho _{0}=2\times 10^{7}M_{\odot }\) \(\mathrm{kpc^{-3}}=0.14\times 10^{-20}\) \(\mathrm{kg/m^{3}}\) and \(R_{s}=15\) \(\mathrm{kpc}=4.6\times 10^{20}\) m for the PI profile (for the PI profile, we did not find the corresponding fitting parameter value of MW, therefore we choose a value arbitrarily). We find that \(\Delta t \approx \Delta \tau \approx 261\) s for NFW profile, \(\Delta t \approx \Delta \tau \approx 64\) s for TF and PI profile.

4 Axisymmetric traversable wormhole by NJ algorithm

In this section, we generalize the spacetime metrics of a traversable wormhole to the axisymmetric ones by the NJ algorithm. Based on the isotropy pressure condition, according to the NJ algorithm in [25] and [26], the details of the derivation are as follows.

In order to derive the spacetime metric of the rotational wormhole, we rewrite the spherical symmetry wormhole spacetime metric as follows:

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+\dfrac{1}{g(r)}\mathrm{d}r^{2}+r^{2}(\mathrm{d}\theta ^{2}+sin^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$
(18)

where the metric coefficients are \(f(r)=e^{2\Phi (r)} \) and \(g(r)=1-\dfrac{b(r)}{r}\). For the first step of the NJ algorithm, we transform the wormhole metric (18) to advanced null coordinates \((u,r,\theta ,\phi )\) by the transformation \(\mathrm{d}u=\mathrm{d}t-\dfrac{1}{f(r)g(r)}\mathrm{d}r\). In the null trade, the inverse metric can be written as \(g^{\mu \nu }=-l^{\mu }n^{\nu }-l^{\nu }n^{\mu }+m^{\mu }{\overline{m}}^{\nu }+m^{\nu }{\overline{m}}^{\mu }\), where the base vectors satisfy \(l_{\mu }l^{\mu }=n_{\mu }n^{\mu }=m_{\mu }m^{\mu }=l_{\mu }m^{\mu }=n_{\mu }m^{\mu }=0\), \(l_{\mu }n^{\mu }=-m_{\mu }{\overline{m}}^{\mu }=1\), and they can be expressed as

$$\begin{aligned} l^{\mu }= & {} \delta ^{\mu }_{r},\nonumber \\ n^{\mu }= & {} \sqrt{\dfrac{f(r)}{g(r)}}\delta ^{\mu }_{\mu }-\dfrac{f(r)}{2}\delta ^{\mu }_{r},\nonumber \\ m^{\mu }= & {} \dfrac{1}{\sqrt{2}r}\delta ^{\mu }_{\theta }+\dfrac{i}{\sqrt{2}r \sin \theta }\delta ^{\mu }_{\phi },\nonumber \\ {\overline{m}}^{\mu }= & {} \dfrac{1}{\sqrt{2}r}\delta ^{\mu }_{\theta }-\dfrac{i}{\sqrt{2}r \sin \theta }\delta ^{\mu }_{\phi }. \end{aligned}$$
(19)

Now, in order to transform the metric from spherical symmetry to axisymmetry, we perform the following complex transformation:

$$\begin{aligned}&u\longrightarrow u-ia\cos \theta ,\nonumber \\&r\longrightarrow r+ia\cos \theta . \end{aligned}$$
(20)

In this case, the metric coefficients are changed like this \(f(r)\rightarrow F(r,\theta ,a)\), \(g(r)\rightarrow G(r,\theta ,a)\) and \(h(r)(=r^{2})\rightarrow \Psi (r,\theta ,a)\). So the basis vectors become

$$\begin{aligned} l^{\mu }= & {} \delta ^{\mu }_{r},\nonumber \\ n^{\mu }= & {} \sqrt{\dfrac{G}{F}}\delta ^{\mu }_{\mu }-\dfrac{F}{2}\delta ^{\mu }_{r},\nonumber \\ m^{\mu }= & {} \dfrac{1}{\sqrt{2\Psi }}\left( \delta ^{\mu }_{\theta }+ia \sin \theta \left( \delta ^{\mu }_{\mu }-\delta ^{\mu }_{r}\right) +\dfrac{i}{\sin \theta }\delta ^{\mu }_{\phi }\right) ,\nonumber \\ {\overline{m}}^{\mu }= & {} \dfrac{1}{\sqrt{2\Psi }}\left( \delta ^{\mu }_{\theta }-ia \sin \theta \left( \delta ^{\mu }_{\mu }-\delta ^{\mu }_{r}\right) -\dfrac{i}{\sin \theta }\delta ^{\mu }_{\phi }\right) . \end{aligned}$$
(21)

According to Eq. (21), we obtain the expression of the inverse metric \(g^{\mu \nu }\),

$$\begin{aligned} g^{uu}= & {} \dfrac{a^{2}\sin ^{2}\theta }{\Psi }, \quad g^{\theta \theta } = \dfrac{1}{\Psi },\nonumber \\ g^{ur}= & {} g^{ru}=\sqrt{\dfrac{G}{F}}-\dfrac{a^{2}\sin ^{2}\theta }{\Psi },\nonumber \\ g^{\phi \phi }= & {} \dfrac{1}{\Psi \sin ^{2}\theta }, \quad g^{u\phi } = g^{\phi u}=\dfrac{a}{\Psi },\nonumber \\ g^{r\phi }= & {} g^{\phi r}=\dfrac{a}{\Psi }, \quad g^{rr} = G+\dfrac{a^{2}\sin ^{2}\theta }{\Psi }. \end{aligned}$$
(22)

As a result, the line element of rotation wormhole metric in Eddington–Finkelstein coordinates (EFC) is

$$\begin{aligned} \mathrm{d}s^{2}= & {} -F\mathrm{d}u^{2}+2\sqrt{\dfrac{F}{G}}\mathrm{d}u\mathrm{d}r+2a\sin ^{2}\theta \left( \sqrt{\dfrac{F}{G}}+F \right) \mathrm{d}u\mathrm{d}\phi \nonumber \\&-2a\sin ^{2}\theta \sqrt{\dfrac{F}{G}}\mathrm{d}r\mathrm{d}\phi +\Psi \mathrm{d}\theta ^{2}\nonumber \\&-\sin ^{2}\theta \left[ -\Psi +a^{2}\sin ^{2}\theta \left( 2\sqrt{\dfrac{F}{G}}+F \right) \right] \mathrm{d}\phi ^{2}. \end{aligned}$$
(23)

Here we set \(k(r)=r^{2}\sqrt{f(r)/g(r)}\). In order to obtain the rotation wormhole in the Boyer–Lindquist coordinates (BLCs), we need the transform

$$\begin{aligned} \mathrm{d}u= & {} \mathrm{d}t-\dfrac{k+a^{2}}{r^{2}f(r)+a^{2}}\mathrm{d}r,\nonumber \\ \mathrm{d}\phi= & {} \mathrm{d}\phi -\dfrac{a}{r^{2}f(r)+a^{2}}\mathrm{d}r, \end{aligned}$$
(24)

where

$$\begin{aligned} F(r,\theta )= & {} -\dfrac{r^{2}f(r)+a^{2}\cos ^{2}\theta }{k(r)+a^{2}\cos ^{2}\theta }\Psi ,\nonumber \\ G(r,\theta )= & {} -\dfrac{r^{2}f(r)+a^{2}\cos ^{2}\theta }{\Psi }. \end{aligned}$$
(25)

Next, we set \(\Sigma ^{2}=k(r)+a^{2}\cos ^{2}\theta \), \(2{\overline{f}}=k(r)-r^{2}f(r)\), \(\Delta (r)=r^{2}f(r)+a^{2}\) and \(A=(k(r)+a^{2})^{2}-a^{2}\Delta \sin ^{2}\theta \), and then we obtain the useful rotation metric

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\dfrac{\Psi }{\Sigma ^{2}}\left( 1-\dfrac{2{\overline{f}}}{\Sigma ^{2}} \right) \mathrm{d}t^{2}+\dfrac{\Psi }{\Delta }\mathrm{d}r^{2}-\dfrac{4a{\overline{f}}\sin ^{2}\theta \Psi }{\Sigma ^{4}}\mathrm{d}t\mathrm{d}\phi \nonumber \\&\qquad +\Psi \mathrm{d}\theta ^{2}+\dfrac{\Psi A \sin ^{2}\theta }{\Sigma ^{4}}\mathrm{d}\phi ^{2}. \end{aligned}$$
(26)

According to [26], we need to define a new radial coordinate \({\bar{r}}\),

$$\begin{aligned} \mathrm{d}{\bar{r}}^{2}=\dfrac{f(r)}{1-\dfrac{b(r)}{r}}\mathrm{d}r^{2}, \end{aligned}$$
(27)

therefore, the second term of the metric in Eq. (26) is replaced by

$$\begin{aligned} \dfrac{\Psi }{\Delta }\mathrm{d}{\bar{r}}^{2}. \end{aligned}$$
(28)

Changing back to r, the general rotation wormhole metric is

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\dfrac{\Psi }{\Sigma ^{2}}\left( 1-\dfrac{2{\overline{f}}}{\Sigma ^{2}} \right) \mathrm{d}t^{2}+\dfrac{\Psi }{\Delta }\dfrac{f(r)}{1-\dfrac{b(r)}{r}}\mathrm{d}r^{2}\nonumber \\&- \dfrac{4a{\overline{f}}\sin ^{2}\theta \Psi }{\Sigma ^{4}}\mathrm{d}t\mathrm{d}\phi +\Psi \mathrm{d}\theta ^{2}+\dfrac{\Psi A \sin ^{2}\theta }{\Sigma ^{4}}\mathrm{d}\phi ^{2}. \nonumber \\ \end{aligned}$$
(29)

In this metric, \(\Psi \) is an unknown function determined by the rotational symmetric condition \(G_{r\theta }=0\) and the Einstein field equation \(G_{\mu \nu }=8\pi T_{\mu \nu }\). For a rotation wormhole the metric (29), \(\Psi \), satisfies

$$\begin{aligned} (k+a^{2}y^{2})^{2}(3\Psi _{,r}\Psi _{,y^{2}}-2\Psi \Psi _{,ry^{2}})=3a^{2}k_{,r}\Psi ^{2} \end{aligned}$$
(30)

and

$$\begin{aligned}&\Psi [k^{2}_{,r}+k(2-k_{,rr})-a^{2}y^{2}(2+k_{,rr})]\nonumber \\&\quad +(k+a^{2}y^{2})(4y^{2}\Psi _{,y^{2}}-k_{,r}\Psi _{,r})=0. \end{aligned}$$
(31)

Here \(y=\cos \theta \), \(\Psi _{,ry^{2}}=\partial ^{2}\Psi /\partial r \partial y^{2}\) and \(k_{,r}=\partial k(r)/\partial r\). According to [25], to Eqs. (30) and (31) there exists a simple solution, \(\Psi =r^{2}+p^{2}+a^{2}\cos ^{2}\theta \), where \(p^{2}\) is a real constant. If \(f(r)\approx g(r)\), the real constant \(p^{2}\) equals 0 and \(k(r)\approx r^{2}\). If f(r) is replaced by H, the axisymmetric wormhole metrics for three dark matter halos can be obtained:

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1-\dfrac{2{\overline{f}}}{\Sigma ^{2}}\right) \mathrm{d}t^{2}+\dfrac{\Sigma ^{2}H}{\Delta }\dfrac{1}{1-\dfrac{b(r)}{r}}\mathrm{d}r^{2}\nonumber \\&-\dfrac{4a {\overline{f}}\sin ^{2}\theta }{\Sigma ^{2}}\mathrm{d}\phi \mathrm{d}t+\Sigma ^{2}\mathrm{d}\theta ^{2}+\dfrac{A\sin ^{2}\theta }{\Sigma ^{2}}\mathrm{d}\phi ^{2}, \end{aligned}$$
(32)

where

$$\begin{aligned} \Sigma ^{2}= & {} r^{2}+a^{2}\sin ^{2}\theta , \quad 2{\overline{f}}=r^{2}(1-H), \end{aligned}$$
(33)
$$\begin{aligned} \Delta= & {} r^{2}H+a^{2},\quad A=(r^{2}+a^{2})^{2}-a^{2}\Delta \sin ^{2}\theta , \nonumber \\ H= & {} e^{2\Phi (r)}, \end{aligned}$$
(34)

where a is the spin of a traversable wormhole.

5 Energy condition

In this section, we check the weak energy condition (WEC) and the null energy condition (NEC) by calculating the energy-momentum tensor of axisymmetric traversable wormholes in different dark matter halos. To calculate the energy-momentum tensor of dark matter halos by the wormhole spacetime (32), we adopt the following frame system:

Fig. 1
figure 1

The behavior of dark matter density \(\rho \) with radial distance r. The modeling parameters are \(\theta =\pi /2\), \(\omega =0\), \(R_{s}(\mathrm{or} R \,\, \mathrm{and} \,\, R_{c}) \, = \, 10\), \(r_{0}=1\), \(\rho _{s}(\mathrm{or} \rho _{0}) \,= \, 0.05\) and \(a=0.5\)

Full size image
$$\begin{aligned} e^{\mu }_{t}= & {} \dfrac{1}{\sqrt{\Sigma ^{2}\Delta }}(r^{2}+a^{2},0,0,0),\nonumber \\ e^{\mu }_{r}= & {} \sqrt{\dfrac{\Delta }{\Sigma ^{2}}}\sqrt{\dfrac{r-b(r)}{rH}}(0,1,0,0),\nonumber \\ e^{\mu }_{\theta }= & {} \dfrac{1}{\sqrt{\Sigma ^{2}}}(0,0,1,0),\nonumber \\ e^{\mu }_{\phi }= & {} \dfrac{1}{\sqrt{\Sigma ^{2}}\sin \theta }(a\sin ^{2}\theta ,0,0,1). \end{aligned}$$
(35)

The energy-momentum tensor for a traversable wormhole in spherical symmetry is assumed to be isotropic with \(P_{r}=P_{\theta }=P_{\phi }=P\). However, the energy-momentum tensor for the axisymmetric traversable wormhole does not satisfy the isotropic pressure condition. In general, we can write it as \(T^{\mu \nu }=\rho e^{\mu }_{t}e^{\nu }_{t}+P_{r}e^{\mu }_{r}e^{\nu }_{r}+P_{\theta }e^{\mu }_{\theta }e^{\nu }_{\theta }+P_{\phi }e^{\mu }_{\phi }e^{\nu }_{\phi }\), with the components \(P_{r}\ne P_{\theta }\ne P_{\phi }\). The calculation results are given by

$$\begin{aligned} \rho= & {} \dfrac{r^{2}b^{'}(r)+a^{2}r^{2}_{0}[(3H-1)\cos ^{2}\theta -2]}{8\pi \Sigma ^{4}}, \end{aligned}$$
(36)
$$\begin{aligned} P_{r}= & {} -\dfrac{r^{2}b^{'}(r)+a^{2}r^{2}_{0}[(3H-1)\cos ^{2}\theta -2]}{8\pi \Sigma ^{4}}-\dfrac{r^{2}_{0}\Delta }{4\pi \Sigma ^{6}}, \nonumber \\ \end{aligned}$$
(37)
$$\begin{aligned} P_{\theta }= & {} \dfrac{2H^{2}+H(rH^{'}-2)+(r-b(r))(3H^{'}+rH^{''})}{16\pi \Sigma ^{2}H}\nonumber \\&+\dfrac{r^{2}b^{'}(r)+a^{2}r^{2}_{0}[(3H-1)\cos ^{2}\theta -2]}{8\pi \Sigma ^{4}}+\dfrac{r^{2}_{0}\Delta }{4\pi \Sigma ^{6}}, \nonumber \\ \end{aligned}$$
(38)
$$\begin{aligned} P_{\phi }= & {} \dfrac{2H^{2}+H(rH^{'}-2)+(r-b(r))(3H^{'}+rH^{''})}{16\pi \Sigma ^{2}H}\nonumber \\&+ \dfrac{r^{2}b^{'}(r)+a^{2}r^{2}_{0}[(3H-1)\cos ^{2}\theta -2]}{8\pi \Sigma ^{4}}\nonumber \\&+ \dfrac{r^{2}_{0}\Delta +a^{2}r^{2}_{0}\sin ^{2}\theta }{4\pi \Sigma ^{6}}. \end{aligned}$$
(39)
Fig. 2
figure 2

The behavior of dark matter’s \(\rho +p\) with radial distance r. The modeling parameters are \(\theta =\pi /2\), \(\omega =0\), \(R_{s}\) (or R and \(R_{c}\)) \(=\) 10, \(r_{0}=1\), \(\rho _{s}\) (or \(\rho _{0}\)) \(=\) 0.05 and \(a=0.5\)

Full size image
Fig. 3
figure 3

The dark matter density \(\rho \) as a function of the radial distance r with different wormhole’s spins a for the NFW profile. The modeling parameters are \(\theta =\pi /2\), \(\omega =-0.33\), \(R_{s}=10^{10}\), \(r_{0}=1\) and \(\rho _{s}=5\times 10^{-3}\)

Full size image

Next, we analyze the energy condition of the energy-momentum tensor for a axisymmetric traversable wormhole. In the standard locally non-rotating frame (LNRF) [27], the WEC and NEC are defined by \(T_{\mu \nu }u^{\mu }u^{\nu }\geqslant 0\), where \(u^{\mu }\) is the time-like vector. For a traversable wormhole spacetime (32), the above condition would reduce to \(\rho \geqslant 0\) and \(\rho +P_{r}\geqslant 0\). From Eqs. (36) to (37), we can obtain

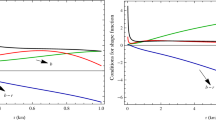
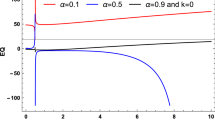
$$\begin{aligned} \rho (r)+P_{r}=-\dfrac{r^{2}_{0}\Delta }{4\pi \Sigma ^{6}}. \end{aligned}$$
(40)

We show the sign of \(\rho \) and \(\rho +P_{r}\) for axisymmetric traversable wormholes in Figs. 1 and 2. From Fig. 1, we find that the WEC is satisfied everywhere for axisymmetric traversable wormholes with the NFW profile and PI profile. However, the WEC is not satisfied everywhere, which depends on the radial distance r and dark matter parameters with the TF profile. From Fig. 2, we can find the NEC is not satisfied for axisymmetric traversable wormholes with the NFW profile, TF profile and PI profile.

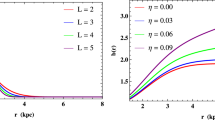
On the other hand, we show the dark matter density \(\rho \) as a function of the radial distancer with different wormhole spins a, and find that the behavior is similar to a black hole spike [28, 29]. Taking the NFW profile as an example, the dark matter profile has been altered by wormholes and makes it look like a spike shape (see Fig. 3 for details). We can also find that the dark matter density decreases with increasing wormhole’s spin, and this behavior is opposite to a black hole spike [30]. We suggest that the dark matter around traversable wormhole may be more easily detected.

6 Summary

In this work, we studied the traversable wormhole metrics in different dark matter halos with the NFW, TF and PI density profile. We obtained the exact solutions of the traversable wormhole for three dark matter halos under the isotropic pressure condition. We generalized the traversable wormhole solutions to the axisymmetric ones by the NJ algorithm. The energy conditions for the derived traversable wormhole solutions are then checked. Our results show that the dark matter density for axisymmetric traversable wormhole is similar to a black hole spike. However, the dark matter density varies with the wormhole’s spin in the opposite direction.