1 Introduction

The description of bound states, fully taking into account the general principles of the relativistic quantum field theory (QFT) and the needed non-perturbative regimes, is a longstanding and highly challenging problem. As it is well-known, the formal solution of the problem can be traced back to the birth of relativistic QFT, with the seminal paper by Salpeter and Bethe [1]. Starting from the analysis of the pole contributions to the Green’s function relevant for the bound state under scrutiny (e.g., the four-points Green’s function for investigating two-body bound states), they introduced an integral equation, known as the Bethe–Salpeter equation (BSE) for the bound-state amplitude, where the kernel is obtained from the two-particle irreducible diagrams, describing the dynamics inside the system. The systematic evaluation of the interaction kernel needs in turn the knowledge of other key ingredients: (i) self-energies of both intermediate particles and quanta and (ii) vertex functions, as pointed out by Gell–Mann and Low [2]. Unfortunately, those 2- and 3-point functions are quantities to be determined through the infinite tower of Dyson–Schwinger equations (DSEs) [3,4,5] (see for introductory reviews, e.g., Refs. [6,7,8,9,10,11], and references quoted therein) that govern the whole set of N-point functions. Therefore, in order to make feasible the construction of more and more realistic interaction kernels, model builders have to elaborate strategies for truncating the DSEs infinite tower, as much self-consistently as possible, while retaining the dynamical effects, at the greatest extent (see, e.g., Ref. [12] for a closed-form of the BSE kernel, obtained by using the acting symmetries). Finally, it is worth mentioning that within the Hamiltonian framework (suitable for the studies in Minkowski space), other relevant non-perturbative approaches, have been developed, like (i) the discretized light-cone quantization [13], e.g. recently applied to positronium, pion and kaon by using the so-called Basis Light-front Quantization and a suitable truncation of the Fock space (see, e.g., Refs. [14,15,16]); and (ii) the Hamiltonian formulation of the lattice gauge theories that preserves the evolution of the states with a continuous real time [17], (see, e.g., Ref. [18] and references quoted therein for a recent QCD study and Ref. [19] for interesting quantum simulations of lattice gauge theories).

In the last decades, significant progresses have been done for implementing the approach based on BSE plus truncated DSEs,Footnote 1 and a high degree of sophistication has been achieved, mainly in Euclidean space (see Refs. [6,7,8,9,10,11, 20] and also Refs. [21,22,23,24,25,26,27]). Moreover, as it is well-known, DSEs can be obtained in a very efficient way by using the path-integral formalism, that in turn acquires a rigorous mathematical meaning in the Euclidean space (see e.g. Ref. [28, 29]).Footnote 2 In particular, the most widely investigated field is the continuum QCD, with an impressive wealth of applications in hadron physics, ranging from baryon and meson spectra to elastic electromagnetic (em) form factors and transition ones (see, e.g., [6,7,8,9,10,11, 20]). Notice that also some timelike observables can be studied, e.g. by exploiting (i) analytic models for the running coupling (see the seminal Ref. [31]); (ii) the evaluation of a finite number of moments of proper Euclidean correlation functions (see, e.g., Ref. [32] for a recent approach on lattice QCD and Refs. [33, 34] for continuum QCD results); (iii) integral representations of the quantities primarily evaluated in Euclidean space or algebraic Ansätze, properly tuned through spacelike data (see, e.g., [35,36,37,38,39]).

Furthermore, also applications to QED have been pursued at large extent (see, e.g., Refs. [40,41,42,43] and for a recent study in Minkowski space Ref. [44]). The interest in investigating the QED, in the whole dynamical range, may be surprising, given the extraordinary accuracy achieved in the comparison with the data by using perturbative tools (see, e.g., the case of the muon anomalous magnetic moment [45]). Indeed, a close study of the non-perturbative regime on the one side is relevant for shedding light on QED at very short distances, as suggested, e.g., in Refs. [46, 47] for Euclidean studies of the critical coupling, below which chiral symmetry breaks down in quenched QED, and in Ref. [48] for an Euclidean investigation on how to escape the triviality fate of QED by adding a relevant four-fermion operator. On the other side, a non-perturbative exploration of QED represents a needed step for approaches played in Minkowski space, and eventually aiming to compare the calculated outcomes with experimental results for hadrons, as it has been already done by using approaches in Euclidean space.

Our investigation will focus on the study of the charged fermion and photon gap-equations below the critical coupling, \(\alpha _c \le \pi /3\), (see, e.g., Refs. [46, 47, 49]), and in order to help the reader to better appreciate the differences with other approaches it is useful to indicate, even in a simplistic way, the directions along which we will move in what follows. For this reason, let us immediately mention the two key ingredients we will adopt: (i) the Minkowski space, where the physical processes take place and (ii) the structure of the vertex function.

The vertex has a prominent role, and in our approach it is composed of two contributions. The first term is the well-known part introduced by Ball and Chiu in Ref. [50], that fulfills the Ward–Takahashi identities (WTIs) (both the differential form and the finite-difference one). The second term is a transverse contribution (see, e.g., Refs. [40, 42, 44, 51,52,53,54] for a wide discussion), based on a minimal Ansätz proposed in Ref. [22]. Such a transverse term is able to restore the full multiplicative renormalization of both fermion and photon propagators (solutions of suitably truncated DSEs), and in turn gracefully implements a workable, self-consistent truncation scheme. Indeed, although the knowledge of the full content of the vertex requires the one of the full off-shell scattering matrix, the longitudinal WTI and its transverse counterparts relate respectively the divergence and the curl of the vertex in terms of the fermion 2-points function. These relations are exact for the divergence and truncated for the curl, allowing for a viable closed system [12, 22].

Another important ingredient, though more technical, is represented by the so-called Nakanishi integral representation (NIR) of a generic n-leg transition amplitude [55,56,57]. Indeed, such a tool has allowed one to undertake new efforts for developing methods for solving in Minkowski space both truncated DSEs (see, e.g., Refs. [44, 58,59,60,61,62,63]) and BSE (see, e.g., Refs. [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78], where systems with and without spin degrees of freedom are investigated).

The main motivation for adopting the NIR, closely related to the Stieltjes transform (see an application in Ref. [79]), is given by the possibility to express the n-leg transition amplitudes through their all-order perturbative form. The freedom needed for exploring a non-perturbative regime is assured via the unknown Nakanishi weight functions (NWFs), that are real functions fulfilling a uniqueness theorem, within the Feynman diagrammatic framework [57]. Such a freedom has shown all its relevance in the numerical studies of the bound states (by using both ladder and cross-ladder interaction kernels), that are the main instance where the realistic description of the non-perturbative regime is necessary. Furthermore, the NWFs to be used for the self-energies do not depend upon the external momenta, greatly simplifying our formal elaboration, as shown in what follows. The advantage of the NIR is that the four-momentum dependence is made explicit, allowing direct algebraic manipulations, and eventually making affordable analytic integrations. This is an important virtue of the NIR approach, since it simplifies the treatment of the expected singularities. On the phenomenology side, when light-cone observables have to be evaluated, e.g. for describing the partonic structure of hadrons [35, 80,81,82,83,84,85,86,87,88], the explicit dependence upon the momenta facilitates the needed projection onto the light-cone. However, in the NIR context, the dynamical assumptions are still much simpler than the one made in Euclidean calculations. For instance, in the above mentioned works when solving Minkowskian BSE for mesons, the constituent fermions are most of the time considered perturbative-like, i.e. omitting the running of the dressed quark mass (with the exception of Ref. [76] where it has been proposed to import the running mass of the quarks from the Euclidean lattice into the BSE framework).

Our present effort aims at formally developing a method based on NIR for solving a coupled system composed by the gap-equations for both fermion and gauge boson, directly in Minkowski space. It should be pointed out that the final goal (to be presented elsewhere) of the program we are pursuing is to provide both implementation and quantitative solutions of the BSE with dressed propagators, in order to achieve a more and more realistic description of an interacting system within the QFT framework, directly in the physical space. The integral-equation system, we arrive at, is obtained by using a self-consistent truncation scheme of DSEs, valid in the whole dynamical range of QED, and by adopting both dimensional regularization and momentum-subtraction procedure for the renormalization. Moreover, to pragmatically remove the well-known IR divergences, a tiny mass-regulator has been introduced for the gauge boson, (see, e.g., Ref. [89] for a more general discussion and Ref. [90] for a recent analysis). In general, we share the same spirit of works as: (i) Ref. [44] where, within a quenched approximation, a spectral representation of the fermion propagator was adopted, in combination with its Källén–Lehman (KL) representation, and, importantly, a vertex function was constructed by exploiting the form suggested by the Gauge Technique [91] plus transverse terms, added for matching the perturbative expressions of the renormalized fermion self-energy (see also Refs. [77, 92] for further Minkowskian exploration of a massive QED, in quenched approximation); (ii) Refs. [58, 60, 61] (see also Ref. [93] for a first study of the transverse vertex contribution), where a more direct link to the NIR technique (with different sets of approximations) can be found. Simplifying, the main difference with the previous works is a fully dressing of fermion and photon self-energies, by introducing a vertex function composed by the standard Ball–Chiu component [50] and a minimal Ansätz for the purely transverse contribution [22], able to ensure the multiplicative renormalizability of the whole approach.

The paper is organized as follows. In Sect. 2, the general formalism is introduced for fermion and photon propagators and self-energies, in terms of the KL representations and the NIR, respectively. In Sect. 3, the adopted vertex function is discussed. In Sect. 4, the gap-equations are introduced and the main result of our formal analysis, i.e. the coupled system of integral equations for determining the NWFs, of both electron and photon self-energies, is illustrated. In Sect. 5 an initial application of the coupled system, based on its first iteration, is shown. In Sect. 6, the conclusions of our analysis of the truncated DSEs within the NIR framework are drawn and the perspectives of the future numerical studies are presented. Finally, it has to be emphasized that the Appendices have been written in a detailed form for making as simple as possible a check of the whole formalism, and therefore they have to be considered an essential part of the work.

2 General formalism

In this section, we summarize the general formalism that will be used in our investigation of QED in Minkowski space (see the review in Ref. [6] for the Euclidean version). We introduce first the expression of the self-energy (2-leg transition amplitude in the Nakanishi language [57], that emphasizes the set of external momenta) in terms of NIR, for both fermion and photon. Then, the KL representations of the corresponding propagators are given. The main goal of this initial step is the relations between KL weights and NWFs (see Refs. [60, 61], for an analogous approach, but with renormalization constants \(Z_1=Z_2=1\) and with a bare vertex function or the Ball–Chiu one, respectively).

The suitable renormalization scheme we adopt is the momentum subtraction one, applied on the mass-shell (MOM), as discussed in what follows. This scheme is suitable when asymptotic states exist, and this property is actually needed for the KL representation we have adopted. Clearly, when a confined phase of the QED establishes, likely for large values of photon running mass, the KL representation becomes unproved (see, e.g., Ref. [47] and references quoted therein for the analysis of the confining phase in QED within the gap-equation formalism in Euclidean space, and Ref. [94] for a more recent investigation in Minkowski space). It should be anticipated that both electron and photon self-energies can be nicely renormalized by applying such a scheme, given the benefit from the presence of the transverse component of the vertex function.

2.1 The renormalized propagator of a fermion

By adapting the notations in Ref. [6], one can write the following relations involving the renormalized propagator of a fermion and the regularized self-energy.

The renormalized fermion propagator is given by

(1)

with \(\zeta \) the renormalization point and \(\varSigma _R(\zeta ;p)\) the renormalized self-energy. From Lorentz invariance, one can write

(2)

with \({{\mathcal {A}}}_R(\zeta ;p)\) and \({{\mathcal {B}}}_R(\zeta ;p)\) suitable scalar functions. In terms of the expression in Eq. (2), the renormalized propagator reads

(3)

Noteworthy, by requesting that the renormalized propagator for \(p^2\rightarrow \zeta ^2\) has a pole at the mass \(m(\zeta )=m_{phys}\)Footnote 3 and the same residue of the free propagator, one finds the constraints to be fulfilled by the two scalar functions, at the renormalization point. Needless to say, those constraints are crucial for establishing the relations between the regularized self-energy and the two renormalization constants \(\delta m\) and \(Z_2(\zeta ,\varLambda )\) (see what follows). As a matter of fact, from the well-known general approach illustrated, e.g., in Ref. [89] (or adopting Eq. (3) and imposing for \(p\rightarrow p_{on}\), with \(p^2_{on}=m^2(\zeta )\)) one gets

$$\begin{aligned}&m(\zeta )~{{\mathcal {A}}}_R(\zeta ;\zeta )+{{\mathcal {B}}}_R(\zeta ;\zeta )= 0, \nonumber \\&{{\mathcal {A}}}_R(\zeta ;\zeta )+2m(\zeta ) \nonumber \\&\quad \times \left[ m(\zeta )~{\partial {{\mathcal {A}}}_R(\zeta ;p)\over \partial p^2}+ {\partial {{\mathcal {B}}}_R(\zeta ;p)\over \partial p^2}\right] _{p^2=\zeta ^2}=0. \end{aligned}$$
(4)

These two equations define the standard on-shell QED renormalization scheme. Bringing in mind that the natural outcome of our formal elaboration will be a system of integral equations, needed for determining \({{\mathcal {A}}}_R\) and \({{\mathcal {B}}}_R\), we adopt the following renormalization conditions defining the RI’/MOM scheme (see Ref. [95], for the renormalization independent method in the unquenched QED)

$$\begin{aligned} {{\mathcal {A}}}_R(\zeta ;\zeta )=0, \quad {{\mathcal {B}}}_R(\zeta ;\zeta )=0. \end{aligned}$$
(5)

It is worth noticing the following remarks about this choice: (i) it preserves the pole at the physical mass of the fermion; (ii) it allows a numerical simplification, avoiding to implement boundary conditions where there is an interplay between \({{\mathcal {A}}}_R\) and \({{\mathcal {B}}}_R\); and last but not least (iii) exchanging the physical mass for the current mass evaluated at a space-like momentum, it is formally similar to the RI’/MOM scheme exploited in the literature devoted to the non-perturbative studies of QFT, e.g. in the context of the investigation on the lattice (see the discussions on the RI’/MOM scheme e.g., in Refs. [96, 97]) as well as in continuous approaches (see, e.g., Refs. [6, 95]). Since at the present stage of the novel approach we are exploring, the two boundary conditions in Eq. (5) turn out to simplify the determination of the two renormalization constants, we will leave the study of QED in the standard renormalization scheme, Eq. (4), for further investigation.

The propagator \(S_R\) can be expressed in terms of the regularized quantity, \(\varSigma (\zeta ,\varLambda ;p)\), where \(\varLambda \) stands for a Poincaré invariant regulator, e.g. \(\varLambda =1/\epsilon \) within a dimensional regularization framework with \(d=4-\epsilon \). To make the mathematical notation less heavy, in what follows it is understood that the relations involving renormalized quantities hold only in the limit \(\varLambda \rightarrow \infty \) (notice that above the critical coupling, one expects to meet well-known difficulties for QED, as illustrated e.g., in Refs. [48, 95]). Hence, one writes

(6)

where \(Z_2(\zeta ,\varLambda )\) is the renormalization factor affecting the fermionic field and \(\delta m= m(\zeta )- m_0\), with \(m_0\) the bare mass. The analogous form of Eq. (2), for the regularized self-energy reads (it is useful to include the renormalization constant \(Z_2\) in the definition)

(7)

with \({{\mathcal {A}}}_Z(\zeta ,\varLambda ;p)\) and \({{\mathcal {B}}}_Z(\zeta ,\varLambda ;p)\) suitable scalar functions. In particular, comparing Eq. (1) and Eq. (6), one obtains

$$\begin{aligned} {{\mathcal {A}}}_R(\zeta ;p)= & {} {{\mathcal {A}}}_Z(\zeta ,\varLambda ;p) - \Bigl (Z_2(\zeta ,\varLambda )-1\Bigr ), \nonumber \\ {{\mathcal {B}}}_R(\zeta ;p)= & {} {{\mathcal {B}}}_Z(\zeta ,\varLambda ;p) - \Bigl [ m(\zeta )~ (1-Z_2(\zeta ,\varLambda )) \nonumber \\&+Z_2(\zeta ,\varLambda ) ~\delta m\Bigr ]. \end{aligned}$$
(8)

Indeed, those relations amount to the outcomes of the subtraction scheme for the renormalization of each scalar function. Moreover, by taking into account Eq. (5), one has

$$\begin{aligned}&{{\mathcal {A}}}_Z(\zeta ,\varLambda ;\zeta )= Z_2(\zeta ,\varLambda )-1, \nonumber \\&{{\mathcal {B}}}_Z(\zeta ,\varLambda ;\zeta )= m(\zeta ) (1-Z_2(\zeta ,\varLambda ))+Z_2(\zeta ,\varLambda ) ~\delta m, \end{aligned}$$
(9)

and therefore in the limit \(\varLambda \rightarrow \infty \):

(10)

Pursuing our goal of establishing a formal framework where one can get actual solutions of the gap equation, and eventually describe the renormalized propagator, we usefully introduce the NIR for the fermionic self-energy. This can be achieved by starting from the approach proposed for a scalar case by Nakanishi (see Ref. [57]), for summing up the infinite contributions to a given n-leg amplitude, and generalizing in two respects. One is the transition from scalars to fermions, and the second one, more important, from a perturbative to a non-perturbative regime. Those steps have been explored for the BSEs in Refs. [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]. For the fermion self-energy, it is necessary to introduce two NWFs, since one has to deal with two scalar functions. Hence, the regularized self-energy can be written in terms of the following scalar functions

$$\begin{aligned}&{{\mathcal {A}}}_Z(\zeta ,\varLambda ;p)= \int _{s_{th}}^\infty ds ~\frac{\rho _A(s,\zeta ,\varLambda )}{p^2-s+i\epsilon }, \nonumber \\&{{\mathcal {B}}}_Z(\zeta ,\varLambda ;p) = \int _{s_{th}}^\infty ds~ \frac{\rho _B(s,\zeta ,\varLambda )}{p^2-s+i\epsilon }, \end{aligned}$$
(11)

with \(s_{th}\) the multiparticle threshold and \(\rho _{A(B)}\) the NWFs. It should be recalled that the NWFs are real functions, and do not depend upon the external momenta. This last remark will be useful for simplifying the formal elaboration aiming to get the suitable integral equations for \(\rho _{A(B)}\).

Moreover, the NWFs have to fulfill the relation entailed by Eq. (9), i.e.

$$\begin{aligned}&Z_2(\zeta ,\varLambda )= 1 +\int _{s_{th}}^\infty ds ~\frac{\rho _A(s,\zeta ,\varLambda )}{\zeta ^2-s+i\epsilon }, \nonumber \\&Z_2(\zeta ,\varLambda ) ~\delta m= \int _{s_{th}}^\infty ds ~\frac{m(\zeta )~\rho _A(s,\zeta ,\varLambda )+ \rho _B(s,\zeta ,\varLambda )}{\zeta ^2-s+i\epsilon }. \nonumber \\ \end{aligned}$$
(12)

It is easily seen that NWFs with a constant behavior for \(s \rightarrow \infty \) generate an expected logarithmic divergence.

By using Eqs. (8), (9) and (11) one can write

$$\begin{aligned} {{\mathcal {A}}}_R(\zeta ;p)= & {} \lim _{\varLambda \rightarrow \infty }\left[ {{\mathcal {A}}}_Z(\zeta ,\varLambda ;p)-\left. \mathcal{A}_Z(\zeta ,\varLambda ;p)\right| _{p^2=\zeta ^2}\right] \nonumber \\= & {} (\zeta ^2-p^2) ~\int _{s_{th}}^\infty ds \frac{\rho _A(s,\zeta )}{(p^2-s+i\epsilon )~(\zeta ^2-s+i\epsilon )} ,\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} {{\mathcal {B}}}_R(\zeta ;p)= & {} \lim _{\varLambda \rightarrow \infty }\left[ {{\mathcal {B}}}_Z(\zeta ,\varLambda ;p)- \left. {{\mathcal {B}}}_Z(\zeta ,\varLambda ;p)\right| _{p^2=\zeta ^2}\right] \nonumber \\= & {} (\zeta ^2-p^2)~\int _{s_{th}}^\infty ds \frac{\rho _B(s,\zeta )}{(p^2-s+i\epsilon )~(\zeta ^2-s+i\epsilon )},\nonumber \\ \end{aligned}$$
(14)

where the notation \(\rho _{A(B)}(s,\zeta ) = \rho _{A(B)}(s,\zeta ,\varLambda \rightarrow \infty )\) is adopted from now on.

It should be pointed out that the actual form of the NFWs will follow from the solution of the coupled system of integral equations we are going to elaborate. Anticipating on the next sections, a possible constant behavior of the NWFs \(\rho _{A(B)}\) for \(s \rightarrow \infty \) would be regularized by the quadratic dependence upon s in the denominator, allowing to safely take \(\varLambda \rightarrow \infty \). A situation in which \(\rho _{A(B)}\) is not bounded at infinity would create regulator dependent results, and may appear above the critical coupling in QED as already mentioned.

Dealing with the gap-equations, it is fruitful to use the KL representation of the renormalized propagators, and therefore one has to establish the relation between KL weights and NWFs of the corresponding self-energy (see also Ref. [58] for the scalar case and Refs. [60, 61] for \(QED_{3+1}\)). Recalling the following KL representation

(15)

where \(\mathcal {R}_S\) is the fermion propagator residue, controlled by the choice of the renormalization scheme (here we have adopted RI’/MOM). Using \( \varSigma _R(\zeta ,p)\) from Eq. (2), one gets

(16)

with

$$\begin{aligned}&{{\mathcal {D}}}(p;\zeta )=p^2 \Bigl (1-{{\mathcal {A}}}_R(\zeta ;p)\Bigr )^2-\Bigl (m(\zeta )+\mathcal{B}_R(\zeta ;p)\Bigr )^2 \nonumber \\ \end{aligned}$$
(17)

By evaluating the needed traces, one can obtain the following relations

$$\begin{aligned} \int _{s_{th}}^\infty ds \frac{\sigma _V(s,\zeta ) }{p^2-s +i\epsilon }= & {} { 1-{{\mathcal {A}}}_R(\zeta ;p) \over {{\mathcal {D}}}(p;\zeta ) +i\epsilon }-{{{\mathcal {R}}}_S\over p^2 -m^2(\zeta ) +i\epsilon } \nonumber \\ \int _{s_{th}}^\infty ds \frac{ \sigma _S(s,\zeta )}{p^2-s +i\epsilon }= & {} { m(\zeta )+{{\mathcal {B}}}_R(\zeta ;p) \over {{\mathcal {D}}}(p;\zeta ) +i\epsilon }\nonumber \\&-{{{\mathcal {R}}}_S~m(\zeta )\over p^2 -m^2(\zeta ) +i\epsilon } \end{aligned}$$
(18)

If one assumes that both KL weights and NWFs match the hypotheses for applying the Sokhotski–Plemelj formula, that reads

$$\begin{aligned}&\int _{-\infty }^\infty ds \frac{ f(s) }{\omega -s +i\epsilon } = \text {PV}\left[ {f(s)\over \omega -s}\right] -i \pi f(\omega ), \end{aligned}$$
(19)

with an understood \( \theta (s-s_{th})\) inside f(s), then one can manipulate the singular integrals in the lhs of Eq. (18) and the rhs of Eqs. (13) and (14) as follows

$$\begin{aligned}&\int _{s_{th}}^\infty ds~{\sigma _{V(S)}(s',\zeta )\over (\omega -s' +i\epsilon )} \nonumber \\&\quad = \text {PV}\left[ {\sigma _{V(S)}(s',\zeta )\over (\omega -s')}\right] -i\pi \sigma _{V(S)}(\omega ,\zeta ), \end{aligned}$$
(20)
$$\begin{aligned}&\int _{s_{th}}^\infty ds ~ \frac{\rho _{A(B)}(s,\zeta )}{(\omega -s+i\epsilon )~(\zeta ^2-s+i\epsilon )} \nonumber \\&\quad = \text {PV}\left[ \frac{\rho _{A(B)}(s,\zeta )}{(\omega -s)~(\zeta ^2-s)}\right] -i\pi ~{\rho _{A(B)}(\omega ,\zeta )\over (\zeta ^2-\omega )}. \end{aligned}$$
(21)

Let us recall that \(\rho _{A(B)}(s=\zeta ^2,\zeta )=0\) and values \(\omega \ge s_{th}\) are relevant in what follows. By inserting Eqs. (21) in (13) and (14), the real and the imaginary parts of \({{\mathcal {A}}}_R(\zeta ;\omega )\) become

$$\begin{aligned} \mathfrak {R}e \Bigl \{{{\mathcal {A}}}_R(\zeta ;\omega )\Bigr \}= & {} (\zeta ^2-\omega )~ \langle \rho _A \rangle ,\nonumber \\ \mathfrak {I}m \Bigl \{\mathcal{A}_R(\zeta ;\omega )\Bigr \}= & {} -\pi \rho _{A}(\omega ,\zeta ), \end{aligned}$$
(22)

with the notation \(\langle \rho _A \rangle \) indicating the principal value in Eq. (21). Analogous expressions hold for \({{\mathcal {B}}}_R(\zeta ;\omega )\). Hence, one can formally gets the following relations between KL weights and NWFs for \(\omega >\omega _{th}=s_{th}\)

$$\begin{aligned}&\sigma _V(\omega ,\zeta ) = \frac{D_I\Bigl [1-(\zeta ^2-\omega )\langle \rho _A \rangle \Bigr ]-\rho _A(\omega ,\zeta )D_R}{D_R^2+\pi ^2 D_I^2} \nonumber \\&\sigma _S(\omega ,\zeta ) = \frac{D_I\Bigl [m(\zeta )+(\zeta ^2-\omega )\langle \rho _B \rangle \Bigr ]+\rho _B(\omega ,\zeta )D_R}{D_R^2+\pi ^2 D_I^2}, \nonumber \\ \end{aligned}$$
(23)

where

$$\begin{aligned} D_R= & {} \omega \Bigl [(1-(\zeta ^2-\omega )\langle \rho _A \rangle )^2-\pi ^2 \rho ^2_A(\omega ,\zeta ) \Bigr ] \nonumber \\&- \Bigl [(m(\zeta )+(\zeta ^2-\omega )\langle \rho _B \rangle )^2-\pi ^2 \rho _B^2(\omega ,\zeta )\Bigr ] , \nonumber \\ D_I= & {} 2 \omega \rho _A(\omega ,\zeta )\Bigl [1-(\zeta ^2-\omega )\langle \rho _A \rangle \Bigr ] \nonumber \\&+ 2\rho _B(\omega ,\zeta )\Bigl [m(\zeta )+ (\zeta ^2-\omega )\langle \rho _B \rangle \Bigr ]. \end{aligned}$$
(24)

It has to be pointed out that the knowledge of the KL weights \(\sigma _{S(V)}(\omega ,\zeta )\) for \(\omega >\omega _{th}\) is enough for determining the fermion propagator for all the possible values of \(p^2\).

2.2 The renormalized propagator of a photon

In the Landau gauge, the free propagator of the photon reads

$$\begin{aligned}&D^{\mu \nu }(q)=-i~{T^{\mu \nu }(q)\over q^2 -\zeta ^2_p+i\epsilon }, \end{aligned}$$
(25)

where \(T^{\mu \nu }(q)\) is the standard transverse projector

$$\begin{aligned}&T^{\mu \nu }(q) = g^{\mu \nu }-{q^\mu q^\nu \over q^2}, \end{aligned}$$
(26)

with its useful properties,

$$\begin{aligned} T_{\mu \nu }(q)= & {} g_{\mu \nu }-{q_\mu q_\nu \over q^2}, \quad T_{\mu \alpha }(q)~T^\alpha _{~\nu }(q)=T_{\mu \nu }(q) \nonumber \\ T_{\mu \nu }(q)~ g^{\nu \mu }= & {} T^\mu _{~\mu }(q)=~3 \end{aligned}$$
(27)

and \(\zeta _p\) is a IR-regulator, (see, e.g., Ref. [89]). For the sake of light notation, the dependence upon \(\zeta _p\) will be understood in the renormalized quantities. Hence, the renormalized photon propagator reads

$$\begin{aligned}&D_R^{\mu \nu }(\zeta ,q)=-i{T^{\mu \nu }\over (q^2-\zeta ^2_p+i\epsilon )~\Bigl [ 1 + \varPi _R(\zeta ;q)\Bigr ]}, \end{aligned}$$
(28)

where \(\varPi _R(\zeta ;q)\) can be called the photon self-energy, fulfilling the following condition, able to lead to the correct residue at photon pole

$$\begin{aligned}&\varPi _R(\zeta ;\zeta _p)=0. \end{aligned}$$
(29)

Notice that the photon propagator would present a problematic pole if there exists a critical value, \(q_{sing}\), such that \(1 + \varPi _R(\zeta ;q_{sing}) = 0\). Interestingly, the IR pole in (28) could be removed if also \(\varPi _R(q^2)\) develops an IR pole, i.e. the so-called Schwinger mechanism [98], that leads to a massive photon (see, e.g., Ref. [99] for the absence of this phenomenon in QED\(_3\) and Ref. [100] for a comprehensive review in the case of QCD).

The relation between \(D_R^{\mu \nu }(\zeta ;q)\) and both the regularized self-energy and the renormalization constant \(Z_3(\zeta ,\varLambda )\) is

$$\begin{aligned}&D_R^{\mu \nu }(\zeta ;q) \nonumber \\&\quad =-i{T^{\mu \nu }\over Z_3(\zeta ,\varLambda )~(q^2-\zeta ^2_p+i\epsilon )~ \Bigl [ 1 + \varPi (\zeta ,\varLambda ,q)\Bigr ]}. \end{aligned}$$
(30)

Comparing the denominators in Eqs. (28) and (30) one has for \(\varLambda \rightarrow \infty \)

$$\begin{aligned}&\varPi _R(\zeta ,q)= \varPi _Z(\zeta ,\varLambda ;q)+Z_3(\zeta ,\varLambda )-1, \end{aligned}$$
(31)

with

$$\begin{aligned} \varPi _Z(\zeta ,\varLambda ;q)=Z_3(\zeta ,\varLambda )\varPi (\zeta ,\varLambda ;q). \end{aligned}$$

By imposing the condition in Eq. (29), one gets the following normalization

$$\begin{aligned}&\varPi _Z(\zeta ,\varLambda ;\zeta _p)=1-Z_3(\zeta ,\varLambda ), \end{aligned}$$
(32)

and writes for \(\varLambda \rightarrow \infty \)

$$\begin{aligned}&\varPi _R(\zeta ;q)= \varPi _Z(\zeta ,\varLambda ;q)-\varPi _Z(\zeta ,\varLambda ;\zeta _p), \end{aligned}$$
(33)

It is also useful to recall that the renormalized propagator fulfills the well-known integral equation, given by

$$\begin{aligned} D_R^{\mu \nu }(\zeta ,q)= & {} D^{\mu \nu }(q)+D^{\mu \alpha }(q) \nonumber \\&\times ~\Bigl [i\varPi _{\alpha \beta }^R(\zeta ,q)\Bigr ] D_R^{\beta \nu }(\zeta ,q), \end{aligned}$$
(34)

where \(\varPi ^{\mu \nu }_R(\zeta ,q^2)\) is the renormalized vacuum polarization tensor, defined by

$$\begin{aligned}&\varPi ^{\mu \nu }_R(\zeta ,q)= -q^2~T^{\mu \nu }(q)~\varPi _R(\zeta ;q). \end{aligned}$$
(35)

This quantity is involved in the gap-equation for the photon (see Sect. 4 for more details).

Analogously to the fermion case, one introduces the following NIR for \(\varPi _Z(\zeta ,\varLambda ;q)\)

$$\begin{aligned}&\varPi _Z(\zeta ,\varLambda ;q)=\int _{s^p_{th}}^\infty ds ~ {\rho _\gamma (s,\zeta ,\varLambda )\over (q^2-s+i\epsilon )}, \end{aligned}$$
(36)

where the real function \( \rho _\gamma (s,\zeta ,\varLambda )\) is the NWF for the regularized photon self-energy, and \(s^p_{th}\) the multiparticle threshold, i.e. \(s^p_{th}=4m^2(\zeta )\).

Using Eqs. (32) and (36), one gets the following expression for \(Z_3(\zeta ,\varLambda )\)

$$\begin{aligned}&Z_3(\zeta ,\varLambda )= 1-\int _{s^p_{th}}^\infty ds ~ {\rho _\gamma (s,\zeta ,\varLambda )\over (\zeta ^2_p-s+i\epsilon )}. \end{aligned}$$
(37)

The same observation below Eq. (12) is relevant also for Eq. (37).

By exploiting Eqs. (32) and (36) in (33), \(\varPi _R(\zeta ;q)\) can be written in terms of NWFs, viz

$$\begin{aligned} \varPi _R(\zeta ;q)= & {} (\zeta ^2_p-q^2) \nonumber \\&\times ~ \int _{s^p_{th}}^\infty ds ~ \frac{\rho _\gamma (s,\zeta )}{(\zeta ^2_p-s+i\epsilon )~(q^2-s+i\epsilon )}, \end{aligned}$$
(38)

where \(\rho _\gamma (s,\zeta )=\rho _\gamma (s,\zeta ,\varLambda \rightarrow \infty )\).

The KL representation of \( D^R_{\mu \nu }(\zeta ,q)\) reads

$$\begin{aligned} D^R_{\mu \nu }(\zeta ,q)= & {} -i T_{\mu \nu }(q) \nonumber \\&\times ~\left( \frac{1}{q^2-\zeta ^2_p+i\epsilon }+ \int _{s^p_{th}}^\infty ds \frac{\sigma _\gamma (\omega ,\zeta )}{q^2-s+i\epsilon }\right) ,\nonumber \\ \end{aligned}$$
(39)

and has to be compared with the following expression obtained from Eq. (28)

$$\begin{aligned} D^{\mu \nu }_R(\zeta ,q)= & {} -iT_{\mu \nu }(q) ~\Biggl [{1\over q^2-\zeta ^2_p+i\epsilon } \nonumber \\&- {\varPi _R(\zeta ;q)\over (q^2-\zeta ^2_p+i\epsilon )~\Bigl (1 + \varPi _R(\zeta ;q)\Bigr )}\Biggr ]. \end{aligned}$$
(40)

Hence one gets

$$\begin{aligned}&\int _{s^p_{th}}^\infty ds \frac{\sigma _\gamma (s,\zeta )}{q^2-s+i\epsilon } =~-{\varPi _R(\zeta ;q)\over (q^2-\zeta ^2_p+i\epsilon )~\Bigl (1 + \varPi _R(\zeta ;q)\Bigr )}. \nonumber \\ \end{aligned}$$
(41)

By using Eqs. (19) and (38), the real and imaginary parts of \(\varPi _R(\zeta ;q)\) can be easily written in terms of the NWF \(\rho _\gamma (\omega ,\zeta )\) as follows (recall that \(q^2\ge s^p_{th}\))

$$\begin{aligned} \mathfrak {R}e \Bigl \{\varPi _R(\zeta ;q^2)\Bigr \}= & {} (q^2 -\zeta ^2_p)~\text {PV}\left[ \frac{\rho _\gamma (s,\zeta )}{(q^2-s)~(\zeta ^2_p-s)}\right] , \nonumber \\ \mathfrak {I}m \Bigl \{\varPi _R(\zeta ;q^2)\Bigr \}= & {} -\pi \rho _\gamma (q^2,\zeta ). \end{aligned}$$
(42)

Finally, by using once more Eq. (19), one obtains the desired relation between \(\rho _\gamma \) and \(\sigma _\gamma \), given by

$$\begin{aligned} \sigma _\gamma (\omega ,\zeta )= & {} -~{1\over (\omega -\zeta ^2_p)} \nonumber \\&\times ~{\rho _\gamma (\omega ,\zeta )\over \Bigl [(1+(\zeta ^2_p-\omega )\langle \rho _\gamma \rangle )^2+\pi ^2 \rho ^2_\gamma (\omega ,\zeta )\Bigr ]}, \end{aligned}$$
(43)

with \(\omega \ge s^p_{th}\) and \(\langle \rho _\gamma \rangle \) the principal value in Eq. (42).

3 The renormalized vertex function

The amputated three-leg transition amplitude, or vertex function, is the basic ingredient for any dynamical approach that aims at determining the self-energies of particle and quanta, involved in a given theory. Unfortunately, the fully dressed vertex function can be formally obtained only through the proper DSE where, in turn, the four-leg transition amplitude (i.e. the fully off-shell fermion-antifermion scattering kernel in the case of QED) is present. This fact makes clear the structure of the infinite tower of DSEs, where each n-leg transition amplitude fulfills an integral equation containing transition amplitudes with a number of legs greater than n. In spite of this, by using general principles, one can devise an overall form of the vertex, in terms of the Dirac structures allowed by both the Lorentz covariance, the parity conservation and time reversal (see, e.g., Refs [50, 101]), when QED is investigated. Following well-known steps, one decomposes the vertex into two parts: (i) the standard component introduced in the early eighties by Ball and Chiu [50], in order to fulfill WTIs and to avoid any kinematical singularity, and (ii) a contribution purely transverse, i.e. containing the possible Dirac structures orthogonal to the momentum transfer \(q=p_f-p_i\) (see Fig. 1. for the pictorial representation and the kinematics). As a matter of fact, one writes the renormalized vertex (or the regularized one, with the proper modification in the notations) as follows

$$\begin{aligned} \varGamma ^\mu _R(\zeta ,p_f,p_i)=\varGamma ^\mu _{R,BC}(\zeta ,p_f,p_i)+\varGamma ^\mu _{R,T}(\zeta ,p_f,p_i)\nonumber \\ \end{aligned}$$
(44)

where \(q\cdot \varGamma _{R,T}(\zeta ,p_f,p_i)=0\) and \(\varGamma ^\mu _{R,BC}(\zeta ,p_f,p_i)\) is the Ball–Chiu vertex dictated by the WTI i.e.

(45)

The actual expression of \(\varGamma ^\mu _{R;BC}\) [50], is given by

(46)

where

$$\begin{aligned}&F_{{{\mathcal {A}}}_+}(p_f,p_i,\zeta )=2-{{\mathcal {A}}}_R(\zeta ;p_f)-{{\mathcal {A}}}_R(\zeta ;p_i) \nonumber \\&\quad =2 + \int _{s_{th}}^\infty ds ~{\rho _A(s,\zeta )\over (\zeta ^2-s+i\epsilon )} \nonumber \\&\qquad \times ~\left[ {(p^2_f-\zeta ^2)\over (p^2_f-s+i\epsilon )} +{(p^2_i-\zeta ^2) \over (p^2_i-s+i\epsilon )}\right] , \nonumber \\&F_{{{\mathcal {A}}}_-}(p_f,p_i,\zeta )=~{{{\mathcal {A}}}_R(\zeta ;p_f)-{{\mathcal {A}}}_R(\zeta ;p_i)\over (p^2_f-p^2_i)} \nonumber \\&\quad = -\int _{s_{th}}^\infty ds ~{\rho _A(s,\zeta )\over (p^2_f-s+i\epsilon )~(p^2_i-s+i\epsilon )}, \nonumber \\&F_{{\mathcal {B}}}(p_f,p_i,\zeta )=~{{{\mathcal {B}}}_R(\zeta ;p_f)-{{\mathcal {B}}}_R(\zeta ;p_i)\over (p^2_f-p^2_i)}\nonumber \\&\quad = - \int _{s_{th}}^\infty ds ~{\rho _B(s,\zeta )\over (p^2_f-s+i\epsilon )~(p^2_i-s+i\epsilon )}. \end{aligned}$$
(47)

While \(\varGamma ^\mu _{R;BC}\) is elaborated starting from WTIs and the crucial request of avoiding kinematical singularities, the transverse part \(\varGamma ^\mu _{R;T}\) has to fulfill the constraint imposed by the curl of the current, \(q^\mu \varGamma ^\nu _{R}- q^\nu \varGamma ^\mu _{R}\) [51] (see also the analysis in Ref. [22]), and it can be expressed in terms of eight Dirac structures, \(T^\mu _i\), such that \(q\cdot T_i=0\) (see Ref. [50] for the complete list) and eight scalar functions, \({{\mathcal {F}}}_i\), viz

$$\begin{aligned}&\varGamma ^\mu _{R;T} (\zeta , p_f,p_i) = \sum _{i=1,8} {{\mathcal {F}}}_i(p_f,p_i,\zeta )~T^\mu _i(p_f,p_i) \end{aligned}$$
(48)

In general the functions \({{\mathcal {F}}}_i(p_f,p_i,\zeta )\) cannot be written only in terms of \({{\mathcal {A}}}_R\) and \({{\mathcal {B}}}_R\) [22], but the whole set of functions has to cooperate for ensuring another fundamental property: the multiplicative renormalizability of both self-energies (see Eqs. (6) and (30)) and vertex, viz

$$\begin{aligned}&\varGamma ^\mu _R(\zeta ,p_f,p_i)= Z_1(\zeta ,\varLambda )~\varGamma ^\mu (\zeta , \varLambda ;p_f,p_i) \end{aligned}$$
(49)

with the constraint \(Z_1(\zeta ,\varLambda )=Z_2(\zeta ,\varLambda )\). It is fundamental to notice that, given the DSEs, the multiplicative renormalizability of both two-leg and three-leg functions are intimately related. This has been elucidated by a vast literature, in different frameworks. In particular, in Refs. [40, 42,43,44, 52, 54] (and references quoted therein) a close analysis, ranging from a first perturbative study to non-perturbative ones, was carried out, pointing to the role played by leading logarithms in determining the aforementioned property, through an unavoidable cooperation between the scalar functions present in \(\varGamma ^\mu _{R;BC}\) and \(\varGamma ^\mu _{R;T}\). Differently, in Refs. [40, 53, 102], within a quenched approximation, the requirement of multiplicative renormalization is implemented by looking for solutions of the fermion gap-equation with a power-law behavior.

In our unquenched approach, we take into account the transverse vertex, retaining only some contributions, as it will be explained in what follows. Indeed, this is a distinctive feature of our work, in comparison with approaches sharing the same spirit, i.e. exploiting spectral representations of both propagators and self-energies (see Refs. [44, 58, 60,61,62,63]). In particular we consider the following two Dirac structures, of the eight identified in Ref. [101],

(50)

with \(\sigma _{\nu \rho }=i[\gamma _\nu ,\gamma _\rho ]/2\) and \(\epsilon ^{0123}=+1\). Notice that there is an overall different sign with respect to Ref. [50].

It is worth mentioning that in the fermion massless case (relevant for studying the dynamical generation of the mass) only the Dirac structures with \(i=2,~3,~5,~8\) contribute [42], and moreover, in the same limiting case, \(T^\mu _3\) and \(T^\mu _8\) allow one to implement the gauge covariance of the fermion propagator [103]. Finally, as pointed out in Ref. [22] the contribution \(T^\mu _8\) is able to generate an anomalous magnetic moment term, within a perturbative framework [21].

Fig. 1
figure 1

The pictorial representation of the regularized fermion-photon vertex, with a fermion absorbing a photon

Full size image

The adopted expressions of \({{\mathcal {F}}}_3\) and \({{\mathcal {F}}}_8\) are the ones given in [22] (see also [53]), where a very detailed formal analysis of \(\varGamma ^\mu _T\) was carried out (adopting a Euclidean metric) and general expression were found. In particular, due to the curl of the current, it turns out that \({{\mathcal {F}}}_3\) and \({{\mathcal {F}}}_8\) can be minimally chosen as linear combinations of \({{\mathcal {A}}}\) and \({{\mathcal {B}}}\) (see Sect. 2.1). In this way, one has a workable Ansätz for \(\varGamma ^\mu _{R;T} \), that has the virtue of closing the equations involving the fermion and photon self-energies. The actual \({{\mathcal {F}}}_3\) and \({{\mathcal {F}}}_8\) are given by (see also Ref. [53])

$$\begin{aligned}&{{\mathcal {F}}}_3( p_f,p_i,\zeta )= -{1\over 2} F_{{{\mathcal {A}}}_-}(p_f,p_i,\zeta ) \nonumber \\&{{\mathcal {F}}}_8( p_f,p_i,\zeta )= F_{{{\mathcal {A}}}_-}(p_f,p_i,\zeta ) \end{aligned}$$
(51)

that match the expected perturbative behavior for \(p^2_f>>p^2_i\) (see the discussion in Ref. [53]). Hence, one can write

(52)

In conclusion, we use \(\varGamma ^\mu _{R}\) given by the sum of the Ball-Chiu vertex [50] and one of the minimal Ansätze for \(\varGamma ^\mu _{R;T}\), proposed in Ref. [22]. In particular, by using Eq. (52) one can (i) fulfill the multiplicative renormalizability, (ii) establish a non-perturbative framework, where a closed coupled system of integral equations allows one to investigate the self-energies of both fermion and photon.

4 Coupled gap equations

This section, in particular Sects. 4.1 and 4.2, contains the main outcomes of our formal elaboration that aims to get a mathematical tool for determining the fermion and photon NWFs and eventually yield the fermion and photon self-energies. In order to accomplish such a task, it is necessary to proceed by writing down the DSEs for the self-energies (see, e.g., Ref. [6] for a general introduction), and insert the results obtained in Sect. 2 (see details in Appendix A and Appendix B).

The DSE for the regularized fermion self-energy, defined in Eq. (7), is given by

$$\begin{aligned} \varSigma _Z(\zeta ,\varLambda ;p)= & {} -iZ_1(\zeta ,\varLambda )~e^2_R \int _{\varLambda } {d^4k\over (2\pi )^4} \nonumber \\&\times ~ \gamma ^\beta ~ D^R_{\beta \alpha }(\zeta , p-k)~ S_R(\zeta ,k)~ \varGamma ^\alpha _R(\zeta ;k,p), \nonumber \\ \end{aligned}$$
(53)

where it is important to emphasize that the dependence upon \(\varLambda \) means that the rhs can have singular contributions (indeed this is the case). But such terms become finite after introducing a suitable regularization procedure, that in our case it turns out to be the dimensional one with \(d=4-\epsilon \) and \(\varLambda =1/\epsilon \) (see the details in Appendix A). Then, the renormalized self-energy fulfills

$$\begin{aligned} \varSigma _R(\zeta ;p)= & {} -iZ_1(\zeta ,\varLambda )~e^2_R ~\int _{\varLambda } {d^4k\over (2\pi )^4}~ \gamma ^\beta ~ S_R(\zeta ,k) \nonumber \\&\times ~\Bigl \{D^R_{\beta \alpha }(\zeta , p-k)~ \varGamma ^\alpha _R(\zeta ;k,p) \nonumber \\&-\left[ D^R_{\beta \alpha }(\zeta , p-k)~ \varGamma ^\alpha _R(\zeta ;k,p) \right] _{p^2=\zeta ^2}\Bigr \}. \end{aligned}$$
(54)

The two scalar functions describing \(\varSigma _R(\zeta ;p)\) (see Eq. (2)) can be obtained by evaluating the suitable traces, i.e.

(55)

In Sect. 4.1 the results of the traces will be presented and the relation with the NWFs established.

In the Landau gauge we are adopting (recall that the polarization tensor is transverse in this gauge), one can start from the following expression of the regularized polarization tensor (see Appendix B for details) in terms of the renormalized quantities

$$\begin{aligned}&\varPi ^{\mu \nu } (\zeta ,\varLambda ;q)\nonumber \\&= -q^2~T^{\mu \nu }~\varPi (\zeta ,\varLambda ;q) -i {Z_1(\zeta ,\varLambda )\over Z_3(\zeta ,\varLambda )}~e_R^2 \int _{\varLambda } \frac{d^4k}{(2\pi )^4} \nonumber \\&\quad \times \text {Tr}\Bigl \{\gamma ^\mu S_R(\zeta ,k)~\varGamma ^\nu _{R}(\zeta ;k,k-q)~S_R(\zeta ,k-q)\Bigr \} . \end{aligned}$$
(56)

Notice that \(T^{\mu \nu }\) is a symmetric tensor, and therefore also the rightmost term it has to be. One can convince himself by recalling that one has at disposal only one four-vector, \(q^\mu \) for constructing antisymmetric contributions. It is understood that \(\varPi ^{\mu \nu }\), microscopically described by the second line in Eq. (56), must satisfy the transversity property, i.e \( q_\mu \varPi ^{\mu \nu }=0,~~ \varPi ^{\mu \nu } q_\nu =0\). Hence, one has to verify that

(57)

Since, we are adopting a vertex that automatically fulfills the WTI, the second line in Eq. (56) can be easily demonstrated by using the WTI itself and the dimensional regularization, in order to make formally allowed a shift in the integrand. As a matter of fact, one gets

$$\begin{aligned}&\int \frac{d^dk}{(2\pi )^4} \text {Tr} \Bigl \{\gamma ^\mu S_R(\zeta ,k)\nonumber \\&\qquad \times ~\varGamma _{R}(\zeta ;k,k-q)\cdot q~S_R(\zeta ,k-q)\Bigr \} \nonumber \\&\quad = \int \frac{d^dk}{(2\pi )^4} \text {Tr}\Bigl \{\gamma ^\mu \left[ S_R(\zeta ,k-q)-~S_R(\zeta ,k)\right] \Bigr \} =0\nonumber \\ \end{aligned}$$
(58)

The equality in the first line of Eq. (57) is more involved, but for ensuring that the microscopic calculation of \(\varPi ^{\mu \nu }\) be proportional to \(T^{\mu \nu }\) one should recover the structure

$$\begin{aligned} g^{\mu \nu } A+ {q^\mu q^\nu \over q^2} B \end{aligned}$$

with the needed relations \(A=-B\). This is guaranteed by Eq. (58), that follow from the fulfillment of WTI.

In order to single out the photon self-energy, \(\varPi (\zeta ,\varLambda ;q)\), one can proceed by saturating the polarization tensor with any combination of \(g^{\mu \nu }\) and \(q^\mu q^\nu /q^2\), but it is extremely useful to take full advantage and guidance from the analyses carried out in perturbative regime, (see, e.g., Refs. [6, 42]). Hence, one can saturate both sides in Eq. (56) with the tensor \(\mathcal {P}^{\mu \nu }\) given by

$$\begin{aligned}&{{\mathcal {P}}}^{\mu \nu }=g^{\mu \nu } - 4 {q^\mu q^\nu \over q^2}. \end{aligned}$$
(59)

This tensor has been introduced in previous works (see Refs. [42, 104, 105]) in order to project \(T^{\mu \nu }\) on its \(q^\mu q^\nu \) part, avoiding to deal with quadratic singularities proportional to \(g^{\mu \nu }\) present in \(\varPi ^{\mu \nu }\). We emphasize that such a projector is adopted for convenience reasons. As a matter of fact, apparent quadratic singularities are met in the following elaboration, but the choice of the vertex presented in Sect. 3 (see also Appendix B) ensures their cancellations. These apparent singularities are easily bypassed by exploiting \({{\mathcal {P}}}^{\mu \nu }\), without carrying out a lengthy algebra (see also Refs. [104, 105]). As a final remark, it should be pointed out that the formal manipulation shown in Appendix B needs a dimensional regularization of some terms and therefore one should substitute 4 with a generic dimension d in the expression of \({{\mathcal {P}}}^{\mu \nu }\).

In conclusion, one gets the following expressions for the regularized self-energy

$$\begin{aligned}&q^2~\varPi _Z(\zeta ,\varLambda ;q)=-i {Z_1(\zeta ,\varLambda )\over 3}~e_R^2 \int _{\varLambda } \frac{d^4k}{(2\pi )^4} ~{{\mathcal {P}}}_{\mu \nu } \nonumber \\&\quad \times \text {Tr} \left[ \gamma ^\mu S_R(\zeta ,k)\varGamma _R^\nu (\zeta ,k,q)~S_R(k-q)\right] , \end{aligned}$$
(60)

where \(\varPi _Z(\zeta ,\varLambda ;q)=Z_3(\zeta ,\varLambda )~\varPi (\zeta ,\varLambda ;q)\). This entails for the renormalized self-energy, Eq. (33),

$$\begin{aligned}&\varPi _R(\zeta ;q)=-i Z_1(\zeta ,\varLambda )~{4\over 3}~e_R^2 \int _{\varLambda } \frac{d^4k}{(2\pi )^4} ~{{\mathcal {P}}}_{\mu \nu } \nonumber \\&\quad \times \Bigl \{{1\over 4q^2}\text {Tr}\left[ \gamma ^\mu S_R(\zeta ,k)\varGamma _R^\nu (\zeta ,k,q)~S_R(\zeta ,k-q)\right] \nonumber \\&\quad -{1\over 4\zeta ^2_p}\text {Tr}\left[ \gamma ^\mu S_R(\zeta ,k)\varGamma _R^\nu (\zeta ,k,q)~S_R(\zeta ,k-q)\right] _{q^2=\zeta ^2_p}\Bigr \}. \nonumber \\ \end{aligned}$$
(61)

4.1 The fermion gap equation and the NWFs

As it is shown in details in Appendix A, one can exploit the NIR of \({{\mathcal {A}}}_R(\zeta ;p)\) and \({{\mathcal {B}}}_R(\zeta ;p)\), Eq. (55), and the KL representations of both fermion and photon propagators, Eqs. (15) and (39) respectively, for obtaining the following relations

$$\begin{aligned} {{\mathcal {A}}}_R(\zeta ;p)= & {} \int _{s_{th}}^\infty ds ~\frac{(\zeta ^2-p^2)~\rho _A(s,\zeta )}{(p^2-s+i\epsilon )~(\zeta ^2-s+i\epsilon )} \nonumber \\= & {} {{\mathcal {T}}}_A(\zeta ,\varLambda ;p) - \left. {{\mathcal {T}}}_A(\zeta ,\varLambda ;p)\right| _{p^2=\zeta ^2} \nonumber \\ \end{aligned}$$
(62)

and

$$\begin{aligned} {{\mathcal {B}}}_R(\zeta ;p)= & {} \int _{s_{th}}^\infty ds ~\frac{(\zeta ^2-p^2)~\rho _B(s,\zeta )}{(p^2-s+i\epsilon )~(\zeta ^2-s+i\epsilon )} \nonumber \\= & {} {{\mathcal {T}}}_B(\zeta ,\varLambda ;p) - \left. {{\mathcal {T}}}_B(\zeta ,\varLambda ;p)\right| _{p^2=\zeta ^2}\nonumber \\ \end{aligned}$$
(63)

where

(64)

and

(65)

In Eqs. (64) and (65), we have

(66)

with \(\gamma _T^\nu = \gamma ^\nu - q^\nu q\cdot \gamma /q^2\) and \(p^\mu _T = p^\mu - q^\mu q\cdot p /q^2\).

In both \(F_{{{\mathcal {A}}}_+}\) and \(F_{{{\mathcal {A}}}_-}\), a term \(\mathcal {A}_R(\zeta ;p)\) is present. The one in \(F_{{{\mathcal {A}}}_+}\) generates a severe divergent behavior in k (see Eqs. (64) and (65)) that cannot be regularized by subtraction, since the corresponding term in \({{\mathcal {T}}}_{A(B)}\), being evaluated at \(p^2=\zeta ^2\), yields \(\mathcal {A}_R(\zeta ;\zeta )=0\), by definition. A simple power counting in \(k^2\) reveals that in \({{\mathcal {T}}}_A\) and \({{\mathcal {T}}}_B\), only the combination proportional to \( F_{{{\mathcal {A}}}_+}-(k^2-p^2)F_{{{\mathcal {A}}}_-}\) allows one to mitigate the divergent behavior due to \(\mathcal {A}_R(\zeta ;p)\) in \(F_{{{\mathcal {A}}}_+}\), leading to a logarithmic divergence that can be regularized by the subtraction in Eqs.(62) and (63) (see details in Appendix A). In fact, one has

$$\begin{aligned} F_{{{\mathcal {A}}}_+}(k,p,\zeta )-(k^2-p^2)F_{{{\mathcal {A}}}_-}(k,p,\zeta )=2\left( 1-\mathcal {A}_R(\zeta ;k) \right) .\nonumber \\ \end{aligned}$$
(67)

This cancellation highlights the intrinsic limitation of the BC vertex, since it is necessary to go beyond such a contribution for restoring the multiplicative renormalizability. This has been known from a long time (see, e.g. Ref. [52]), but it is relatively more recent the suggestion that the constraints coming from the curl of the vertex allow one to elaborate transverse contributions suitable for ensuring the multiplicative renormalizability (see, e.g., Ref. [22]). In Appendix A it is explicitly shown how non-multiplicatively renormalizable contributions, from the BC term, Eq. (46), and the transverse ones, Eq. (52), cancel each other.

Once the explicit expressions of the relations in Eqs. (62) and (63), are obtained as in Eqs. (A.63) and (A.50), respectively, by using a spacelike external momentum p in order to avoid unnecessary formal complexities (recall that the NWFs are real functions that do not depend upon the external momenta as one can also assess a posteriori), one can extract the integral equations fulfilled by the corresponding NWFs \(\rho _A\) and \(\rho _B\), after assuming that the uniqueness theorem by Nakanishi [57] can be applicable to the non-perturbative regime.

In particular comparing Eq. (A.63) and the lhs of Eq. (62), one gets the desired relation for \(\rho _A\) (see Appendix A)

$$\begin{aligned}&\varTheta \Bigl (y-s_{th}\Bigr )~ \rho _A(y,\zeta ) = {3\over (4\pi )^2}~e^2_R \lim _{\varLambda \rightarrow \infty }~Z_1(\zeta ,\varLambda ) \nonumber \\&\quad \times ~\int _{0}^\infty ~d\omega ~{\bar{\sigma }}_\gamma (\omega ,\zeta ,\zeta _p,\varLambda ) ~\int _0^1 d\xi ~\int _{0}^\infty ~ds' \nonumber \\&\quad \times \Biggl \{ {\bar{\sigma }}_V(s',\zeta ,s'_{th},\varLambda ) ~ \Biggl [\xi ~ \varTheta \Bigl (y\xi (1-\xi ) - \xi \omega -(1-\xi ) s'\Bigr ) \nonumber \\&\quad - \int _0^{1-\xi }dt \varTheta \Bigl ( yt (1-t) - \xi \omega -t s'\Bigr ) \Biggr ] + {\bar{\sigma }}_V(s',\zeta ,s'_{th},\varLambda ) \nonumber \\&\quad \times \Biggl [~\int _{s_{th}}^\infty ~ds~ ~\rho _A(s,\zeta ,\varLambda )~{{\mathcal {C}}}^{(0)}_{AV}(\zeta ,\omega ,s,s',\xi ,y) \nonumber \\&\quad + y~\int _{s_{th}}^\infty ~ds~ ~\rho _A(s,\zeta ,\varLambda )~{{\mathcal {C}}}^{(1)}_{AV}(\zeta ,\omega ,s,s',\xi ,y)\Biggr ] \nonumber \\&\quad - y{\bar{\sigma }}_S(s',\zeta ,s'_{th},\varLambda ) \int _0^{1-\xi }dt\int ^{1-\xi -t}_0 {dw} \nonumber \\&\quad \times ~\int _{s_{th}}^\infty ds ~\rho _B(s,\zeta ,\varLambda ) \nonumber \\&\quad \times ~ \varDelta ' \Bigl [y -s+ {s {{\mathcal {A}}}_4(t,w)-\xi \omega -t s' -ws\over {{\mathcal {A}}}_4(t,w)}\Bigr ]\Biggr \} , \end{aligned}$$
(68)

with \({{\mathcal {A}}}_4(t,w)=(t+w)~(1-t-w)\),

$$\begin{aligned}&\varDelta '\Bigl [y-s+(sA-B)/A\Bigr ] \nonumber \\&\quad = {\delta [y-s + (sA-B)/A] - \delta (y-s) \over (sA-B)}, \end{aligned}$$
(69)
$$\begin{aligned}&{{\mathcal {C}}}^{(0)}_{AV}(\zeta ,\omega ,s,s',\xi ,y)= ~{1\over (\zeta ^2-s+i\epsilon )}~ \nonumber \\&\quad \times ~\Biggl \{\xi ~ \varTheta \Bigl [y\xi (1-\xi ) - \xi \omega -(1-\xi ) s'\Bigr ] \nonumber \\&\quad - \int _0^{1-\xi }dt~ \varTheta \Bigl [ yt (1-t) - \xi \omega -t s'\Bigr ] \Biggr \} \nonumber \\&\quad + \int _0^{1-\xi }dt \Biggl \{{1\over (1-\xi )} ~\delta \Bigl [y -{\xi \omega +t s' +(1-\xi -t) s\over \xi (1-\xi )}\Bigr ] \nonumber \\&\quad -\int ^{1-\xi -t}_0 {dw\over {{\mathcal {A}}}_4(t,w)} \delta \Bigl [ y -{\xi \omega +t s' +w s\over {{\mathcal {A}}}_4(t,w)}\Bigr ] \Biggr \} ,\nonumber \\ \end{aligned}$$
(70)

and

$$\begin{aligned}&{{\mathcal {C}}}^{(1)}_{AV}(\zeta ,\omega ,s,s',\xi ,y)= \int _0^{1-\xi }dt ~\Biggl \{{ (1+\xi )\xi } \nonumber \\&\quad \times ~ \varDelta '\Bigl [y -s+{s \xi (1-\xi )-\xi \omega -t s' -(1-\xi -t) s\over \xi (1-\xi )}\Bigr ] \nonumber \\&\quad -\int ^{1-\xi -t}_0 \,{dw} ~ \varDelta '\Bigl [y -s+{s{{\mathcal {A}}}_4(t,w) -\xi \omega -t s' -ws \over {{\mathcal {A}}}_4(t,w)}\Bigr ] \Biggr \} ~. \nonumber \\ \end{aligned}$$
(71)

It has to be pointed out that the presence of the function \(\varDelta '\) does not prevent a quantitative investigation (to be presented elsewhere) once an integration with a function smooth enough is carried out. Indeed, the existence of NWFs fulfilling a suitable smoothness property will be the target of future numerical investigations. In the meanwhile, we should consider as an encouraging hint the results of the first quantitative check discussed in Sect. 5 since the obtained first-order NWFs lead to well-defined integrals in Eq. (68) when iterating further.

As to \(\rho _B\), after comparing Eq. (A.50) and the lhs of Eq. (63), one extracts

$$\begin{aligned}&\varTheta \Bigl (y-s_{th}\Bigr )~\rho _B(y,\zeta ) = -~{3 \over (4\pi )^2}~e^2_R~\lim _{\varLambda \rightarrow \infty }~ Z_1(\zeta ,\varLambda ) \nonumber \\&\quad \times ~\int _{0}^\infty ~d\omega ~{\bar{\sigma }}_\gamma (\omega ,\zeta ,\zeta _p,\varLambda ) ~\int _0^1 d\xi \int _{0}^\infty ~ds' \nonumber \\&\quad \times ~\Bigg \{ {\bar{\sigma }}_S(s',\zeta ,s'_{th},\varLambda )~ ~ \varTheta \Bigl [ y\xi (1-\xi ) - \xi \omega -(1-\xi ) s'\Bigr ] \nonumber \\&\quad + {\bar{\sigma }}_S(s',\zeta ,s'_{th},\varLambda )~ \nonumber \\&\quad \times \Biggl [~\int _{s_{th}}^\infty ~ds~ {\rho _A(s,\zeta ,\varLambda )}~{{\mathcal {C}}}^{(0)}_{AS}(\zeta ,\omega ,s,s',\xi ,y) \nonumber \\&\quad +y~ ~\int _{s_{th}}^\infty ~ds~ {\rho _A(s,\zeta ,\varLambda )}~{{\mathcal {C}}}^{(1)}_{AS}(\zeta ,\omega ,s,s',\xi ,y)\Biggr ] \nonumber \\&\quad +y~ {\bar{\sigma }}_V(s',\zeta ,s'_{th},\varLambda )~ \int _0^{1-\xi }dt\int ^{1-\xi -t}_0 {dw} \nonumber \\&\quad \times ~ \int _{s_{th}}^\infty ~ds~ \rho _B(s,\zeta ,\varLambda )\nonumber \\&\quad \times ~\varDelta ' \Bigl [y -s +{s {{\mathcal {A}}}_4(t,w) -\xi \omega -t s' -ws\over {{\mathcal {A}}}_4(t,w)}\Bigr ] \Biggr \}, \end{aligned}$$
(72)

with

$$\begin{aligned}&{{\mathcal {C}}}^{(0)}_{AS}(\zeta ,\omega ,s,s',\xi ,y)= {1\over \zeta ^2-s+i\epsilon } \nonumber \\&\quad \times ~ \varTheta \Bigl [ y \xi (1-\xi )- \xi \omega -(1-\xi ) s' \Bigr ] + {1\over \xi (1-\xi )} \nonumber \\&\quad \times ~\int _0^{1-\xi }dz ~\delta \Bigl [ y -{\xi \omega +z s' +(1-\xi -z) s\over \xi (1-\xi )}\Bigr ] , \end{aligned}$$
(73)

and

$$\begin{aligned}&{{\mathcal {C}}}^{(1)}_{AS}(\zeta ,\omega ,s,s',\xi ,y)= {1\over \zeta ^2-s+i\epsilon }~ \int _0^{1-\xi }dt ~ \Biggl \{ (1-\xi ) \nonumber \\&\quad \times ~ \varDelta ' \Bigl [y -s + {s \xi (1-\xi ) -\xi \omega -t s' -(1-\xi -t) s \over \xi (1-\xi )}\Bigr ] \nonumber \\&\quad + \int ^{1-\xi -t}_0 {dw} \nonumber \\&\quad \times ~ ~\varDelta ' \Bigl [y -s+{s {{\mathcal {A}}}_4(t,w) -\xi \omega -t s' -ws\over {{\mathcal {A}}}_4(t,w)}\Bigr ] \Biggr \}. \end{aligned}$$
(74)

4.2 The photon gap equation and the NWF

In Appendix B, the details are given for obtaining the integral equation fulfilled by the NWF \(\rho _\gamma \) (see Eq. (38)), exploiting both the integral equation that determines the renormalized photon self-energy, Eq. (61) and the uniqueness theorem [57]. One can write

$$\begin{aligned} \varPi _R(\zeta ;q)= & {} \int _{\zeta ^2_p}^\infty ds ~ \frac{(\zeta ^2_p-q^2)~\rho _\gamma (s,\zeta )}{(\zeta ^2_p-s+i\epsilon )~(q^2-s+i\epsilon )} \nonumber \\= & {} \Bigl [{{\mathcal {T}}}_P(\zeta ,\varLambda ;q) - \left. {{\mathcal {T}}}_P(\zeta ,\varLambda ;q)\right| _{q^2=\zeta ^2_p}\Bigr ], \end{aligned}$$
(75)

where

$$\begin{aligned} {{\mathcal {T}}}_P(\zeta ,\varLambda ;q)= & {} -i Z_1(\zeta ,\varLambda )~{4\over 3}~e_R^2 \int _{\varLambda } \frac{d^4k}{(2\pi )^4} ~{{\mathcal {P}}}_{\mu \nu } {1\over 4q^2} \nonumber \\&\times ~\text {Tr}\left[ \gamma ^\mu S_R(\zeta ,k)\varGamma _R^\nu (\zeta ,k,q)~S_R(\zeta ,k-q)\right] . \nonumber \\ \end{aligned}$$
(76)

Then, following the formal steps in Appendix B, where a spacelike \(q^2\) has been adopted for a straightforward elaboration without loss of generality (as in the fermionic case), one gets

$$\begin{aligned}&{ \varTheta (y-s^p_{th})~\rho _\gamma (y,\zeta )=} -{e_R^2\over (2\pi )^2}~ \lim _{\varLambda \rightarrow \infty }~Z_1(\zeta ,\varLambda )\int _{0}^\infty ds \nonumber \\&\quad \times ~ \int _{0}^\infty ds'~ \int _0^1 d\xi ~ \Biggl \{ {\bar{\sigma }}_V(s',\zeta ,s'_{th},\varLambda ) ~ {\bar{\sigma }}_V(s,\zeta ,s_{th},\varLambda ) \nonumber \\&\quad \times ~ 2 \xi (1-\xi ) \varTheta \Bigl [ y \xi (1-\xi )- \xi s'-(1-\xi )s) \Bigr ] \nonumber \\&\quad \times ~\left( 1 + \int _{s_{th}}^\infty d\omega ~ {\rho _A(\omega ,\zeta ,\varLambda )\over (\zeta ^2-\omega +i\epsilon )} \right) \nonumber \\&\quad +\int _{s_{th}}^\infty d\omega ~\rho _A(\omega ,\zeta ,\varLambda )~{{\mathcal {C}}}_\gamma (s,s',\xi ,\omega ) \nonumber \\&\quad + 2{\bar{\sigma }}_S(s',\zeta ,s'_{th},\varLambda ) ~ {\bar{\sigma }}_V(s,\zeta ,s_{th},\varLambda )~ \nonumber \\&\quad \times ~\int _{s_{th}}^\infty d\omega ~\rho _B(\omega ,\zeta ,\varLambda )~ ~ \int _0^{1-\xi } dv\int _0^{1-\xi -v} dw ~(v+w)\nonumber \\&\quad \times ~{1 -2 (v+w)\over {{\mathcal {A}}}_4^2(v,w)} ~{\partial \over \partial y}\delta \Bigl [y -{{\mathcal {A}}}_7(s,s',\omega ,v,\xi ,w) \Bigr ] \Biggr \}, \end{aligned}$$
(77)

with

$$\begin{aligned}&{{\mathcal {A}}}_7(s,s',\omega ,v,\xi ,w) \nonumber \\&\quad = {vs'+(\xi +w)\omega +(1-\xi -v-w)s\over (v+w)~(1-v-w)}, \nonumber \\&{{\mathcal {C}}}_\gamma (s,s',\xi ,\omega )=\int _0^{1-\xi } dv\int _0^{1-\xi -v} {dw\over {{\mathcal {A}}}_4(v,w)} \nonumber \\&\quad \times ~ \Biggl \{ 2~{\bar{\sigma }}_V(s',\zeta ,s'_{th}) ~ {\bar{\sigma }}_V(s,\zeta ,s_{th}) \nonumber \\&\quad \times ~\Biggl (\omega ~ ~{\partial \over \partial y}\delta \Bigl [ y-{{\mathcal {A}}}_7(s,s',\omega ,v,\xi ,w)\Bigr ] \nonumber \\&\quad + \delta \Bigl [y -{{\mathcal {A}}}_7(s,s',\omega ,v,\xi ,w)\Bigr ]\Biggr ) \nonumber \\&\quad +~{\bar{\sigma }}_S(s',\zeta ,s'_{th}) ~ {\bar{\sigma }}_S(s,s'_{th},\zeta ) \nonumber \\&\quad \times ~{\partial \over \partial y}\delta \Bigl [ y-{{\mathcal {A}}}_7(s,s',\omega ,v,\xi ,w)\Bigr ] \Biggr \}, \end{aligned}$$
(78)

and \({{\mathcal {A}}}_4(v,w)=(t+w)~(1-t-w)\). In order to obtain numerical solutions, the derivatives of the Dirac \(\delta \) can be traded for the derivative of the \(\rho \) functions, which, contrary to the \(\bar{\sigma }\), does not contain itself any Dirac \(\delta \). Just like in the fermion case, the first check performed in Sect. 5 yields results compatible with well defined integrals in (77). One can also note that in the right-hand side of Eq. (77), the dependence upon \(\rho _\gamma \) is not explicit, but buried into the fermionic quantities.

4.3 Some remarks

Concluding this section, that presents our formal results, some remarks are in order. The coupled systems for determining \(\rho _A\), \(\rho _B\) and \(\rho _\gamma \) is composed by the set of Eqs. (68), (72) and (77), supplemented with Eqs. (23) and (43). The fact that the NWFs do not depend on external momenta has been extensively used to build the system of equations. Indeed, Eqs. (23) and (43) are obtained from timelike (above threshold) momenta, taking advantage of the real and imaginary part decomposition, while Eqs. (68), (72) and (77) are derived for spacelike external momenta to avoid complications coming from singularities. Beside the above feature, the uniqueness theorem allows one to finalize the formal steps. Interestingly, derivatives of Dirac delta distribution naturally appear in our derivations. In summary, (i) the NWFs are real functions that do not depend upon the external momentum, as a posteriori can be checked by a direct inspection of the coupled system; (ii) once the NWFs are numerically evaluated, the scalar functions \({{\mathcal {A}}}_R(\zeta ;p)\), \({{\mathcal {B}}}_R(\zeta ;p)\) and \(\varPi _R(\zeta ;q)\) are known for any value of any momenta; (iii) the presence of the derivative of the delta-function is not an issue from the numerical point of view, as already observed when the NIR approach has been applied to the numerical solution of BSE (see, e.g., Refs. [70, 72]).

5 A first application

After establishing the formal results, i.e. the system of integral equations that the NWFs \(\rho _A\), \(\rho _B\) and \(\rho _\gamma \) have to fulfill, it is important to test the consistency. Following the same spirit of the first applications of the NIR approach to the two-scalar system, where the Wick–Cutokski model had to stem from the formal elaboration (see, e.g., Refs. [106, 107]), we have performed the first iteration of the coupled system, as an initial step, in view of the quantitative investigation in full, to be presented elsewhere. It should be pointed out that the first iteration offers the possibility to partly check our results, as it corresponds to the standard one-loop computation. Once the analytical expressions of \(\rho ^{(1)}_A\), \(\rho ^{(1)}_B\) and \(\rho ^{(1)}_\gamma \) have been obtained, we have carried out the evaluations of (i) the KL weights for both fermion and photon propagators, (ii) the fermionic running mass and iii) the charge renormalization function, and eventually compared with one-loop results (see, e.g., Ref. [89], but noting the different renormalization scheme).

The numerical investigation, aimed at establishing the validity of our approach by assessing the convergence of the iterative method, will be presented elsewhere. We stress that, generally speaking, the result of the iterative procedure may differ significantly from the first iteration one (see, e.g., Refs. [108, 109] and Ref. [110] for QCD studies), and that we perform here a basic test of consistency. In Appendix C all the details for obtaining the aforementioned first iteration, Eqs. (C.116), (C.120) and (C.122) respectively, are illustrated with also some of their features, while in Appendix D, the full expressions of the coupled system is summarized for the convenience of the interested reader.

In Fig. 2, the first-order Källén-Lehman weights for the fermionic propagator, Eq. (15), are presented for different values of the IR regulator \(\zeta _p\). They can be easily obtained from Eq. (23) after inserting \(\rho ^{(1)}_A\) and \(\rho ^{(1)}_B\) given by (see Eqs. (C.116), with its careful discussion, and (C.120))

$$\begin{aligned}&\varTheta \Bigl (y-s_{th}\Bigr )~ \rho ^{(1)}_A(y,\zeta ) = -{e^2_R\over 2(4\pi )^2}~{1\over \zeta ^2_py^2} \nonumber \\&\quad \times ~\varTheta (y-m^2(\zeta ))\Biggr \{\varTheta \Bigl [[m(\zeta )+ \zeta _p]^2- y\Bigr ]~\Bigl (y-m^2(\zeta )\Bigr )^3 \nonumber \\&\quad + \varTheta \Bigl [y-[m(\zeta )+ \zeta _p]^2\Bigr ]~\Bigl (y-m^2(\zeta )\Bigr )^3 \nonumber \\&\quad \times ~ \Bigl [1- f(y,\zeta ,\zeta _p^2)\Bigr ] \Biggr \}, \nonumber \\ \end{aligned}$$
(79)

with

$$\begin{aligned} f(y,\zeta ^2,\zeta _p^2)= & {} \sqrt{1 -\zeta ^2_p~{2y+2m^2(\zeta )-\zeta ^2_p\over (y-m^2(\zeta ))^2}}~ \nonumber \\&\times \Biggl [ 1+\zeta ^2_p~{y+m^2(\zeta )-2 \zeta ^2_p\over \Bigl (y-m^2(\zeta )\Bigr )^2} \Biggr ], \end{aligned}$$
(80)

and

$$\begin{aligned}&\varTheta \Bigl (y-s_{th}\Bigr )~\rho ^{(1)}_B(y,\zeta ) \nonumber \\&\quad = -~ \frac{3e_R^2}{(4\pi )^2} ~ m(\zeta ) ~ \varTheta \Bigl [y-[m(\zeta )+\zeta _p]^2\Bigr ] \nonumber \\&\quad \times ~ \frac{1}{y}\sqrt{[y-m^2(\zeta )-\zeta _p^2]^2-4m^2(\zeta )\zeta _p^2} \end{aligned}$$
(81)

Qualitatively \(\sigma _V\) and \(\sigma _S\) are quite similar, though width and tail of \(\sigma _S\) are slightly larger than the \(\sigma _V\) ones. The common features are (i) the negative values (in Ref. [44] the scalar weight is also negative), that is a consequence of our choice of the renormalization scheme, and (ii) the sharp peaks for \(\zeta _p\rightarrow 0\). The latter are very close to the threshold and clearly depend upon the IR-regulator \(\zeta _p\), while the tails are unaffected, as expected. To complete the discussion it is useful to recall that the residue at the pole of the renormalized fermion propagator, \({{\mathcal {R}}}_S\), is not equal to 1, as expected in the RI’/MOM scheme [96, 97]. Table 1 summarizes the different values of the residues associated with our curves in Fig. 2.

Table 1 Values of the fermion propagator residue \({{\mathcal {R}}}_S\) for different \(\zeta _p\)
Full size table
Fig. 2
figure 2

The first iteration of the Källén–Lehman weights for the fermionic propagator, Eq. (15), for different values of the IR-regulator, \(\zeta _p\). The threshold is given by \(\omega _{th}=m^2(\zeta )\). Upper panel the vector weight, \(\sigma _V(\omega ,\zeta )\). Lower panel: scalar weight \(\sigma _S(\omega ,\zeta )\). Solid line: \(\zeta _p=0.01~m(\zeta )\). Dotted line: \(\zeta _p=0.02~m(\zeta )\). Dashed line: \(\zeta _p=0.03~m(\zeta )\). Dash-dotted line: \(\zeta _p=0.04~m(\zeta )\)

Full size image

Another simple check is the formal comparison between the expression of \(\rho ^{(1)}_B(y,\zeta )\) for vanishing values of \(\zeta _p\), with the expression one can extract from standard one-loop computations of \({{\mathcal {B}}}_R(\zeta ;p)\) (see e.g. [89]), but within the RI’/MOM scheme. In the limit \(\zeta _p\rightarrow 0\), one has from Eq. (81)

$$\begin{aligned} \lim _{\zeta _p\rightarrow 0}\varTheta \Bigl (y-s_{th}\Bigr )~\rho ^{(1)}_B(y,\zeta )= & {} -3 ~ {\alpha _{em}\over 4\pi }~\varTheta \Bigl (y-m^2(\zeta )\Bigr )~ \nonumber \\&\times ~m(\zeta )~\left[ 1 -{m^2(\zeta )\over y}\right] \end{aligned}$$
(82)

with \(\alpha _{em}=e^2_R/4\pi \). Moreover from the definition in Eq. (14) one writes

$$\begin{aligned} \mathfrak {I}m\Bigl \{{{\mathcal {B}}}_R(\zeta ,p)\Bigr \} = -\pi \varTheta \Bigl (p^2-s_{th}\Bigr )~\rho ^{(1)}_B(p^2,\zeta ). \end{aligned}$$
(83)

After imposing \({{\mathcal {B}}}_R(\zeta ,\zeta )=0\), perturbative computations yield (see e.g. [89])

$$\begin{aligned} {{\mathcal {B}}}^{1\text {-loop}}_R(\zeta ,p)= & {} m(\zeta )~{\alpha _{em}\over 4\pi }~3~{m^2-p^2\over p^2} \nonumber \\&\times ~\ln \Bigl (1 -{p^2\over m^2(\zeta )}\Bigr ), \end{aligned}$$
(84)

Hence, for \(p^2>m^2(\zeta )\) the logarithm becomes complex, and adopting the same analytic continuation as in Ref. [89] (i.e. \(\ln (-\rho )=\ln \rho -i\pi \)), eventually one has

$$\begin{aligned} \mathfrak {I}m\Bigl \{{{\mathcal {B}}}^{IZ}_R(\zeta ,p\Bigr \} = \pi ~m(\zeta )~3~{\alpha _{em}\over 4\pi }~ \left[ 1-{m^2(\zeta )\over p^2}\right] . \end{aligned}$$
(85)

that coincides with the result one gets from Eqs. (81) and (83). As a final remark, one should point out that in the same limit \(\mathcal{A}_R(\zeta ,p)\) vanishes both in our case (see Eq. (C.119)) as well as in Ref. [89].

Fig. 3
figure 3

The first iteration of the Källén–Lehman weight for the photon propagator, Eq. (39). N.B. in this case there is no dependence upon the IR-regulator, \(\zeta _p\), as shown in Eq. (86). The threshold is given by \(\omega _{th}^p=[2m(\zeta )]^2\)

Full size image
Fig. 4
figure 4

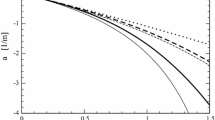
The invariant mass \(M(\zeta ;p)\), Eq. (87), below the threshold \(s_{th}=m(\zeta )^2\), vs \(p^2\)

Full size image

Figure 3 shows the Källén–Lehman weight for the photon propagator, Eq. (43), obtained from \(\rho ^{(1)}_\gamma \) given by (see also Eq. (C.122))

$$\begin{aligned} \varTheta (y-s^p_{th})~\rho ^{(1)}_\gamma (y,\zeta )= & {} - \frac{e_R^2}{3(2\pi )^2}\varTheta (y)\varTheta (y-4m^2(\zeta )) \nonumber \\&\times \Bigl (1+2{m^2(\zeta ) \over y}\Bigr )~\sqrt{1-4\frac{m^2(\zeta )}{y}} .\nonumber \\ \end{aligned}$$
(86)

The independence from the IR-regulator \(\zeta _p\), as shown in the expression of \(\rho ^{(1)}_\gamma \), is the standard feature of the one-loop calculation, and only the higher-order contributions will make apparent such a dependence. Differently from the fermion case, the KL weight of the photon is positive, as expected. This bosonic result points to the highly non trivial interplay of the two scalar functions \({{\mathcal {A}}}_R\) and \({{\mathcal {B}}}_R\), in order to obtain positive KL weights for the fermionic source. We have also calculated the running mass (see Eq. (4) for the value at the renormalization point)

$$\begin{aligned} M(\zeta ;p)= & {} {m(\zeta )+{{\mathcal {B}}}_R(\zeta ;p)\over 1-{{\mathcal {A}}}_R(\zeta ;p)} \nonumber \\= & {} m(\zeta ) +{m(\zeta ){{\mathcal {A}}}_R(\zeta ;p)+{{\mathcal {B}}}_R(\zeta ;p)\over 1-{{\mathcal {A}}}_R(\zeta ;p)} , \end{aligned}$$
(87)

and the charge renormalization function (Eq. (29) for the value at the renormalization point)

$$\begin{aligned} G(\zeta ;q^2)={\alpha _R(\zeta ;q^2)\over \alpha _{em}}= {1\over 1+\varPi _R(\zeta ;q)}. \end{aligned}$$
(88)

In Fig. 4, the running mass is shown for values of the four-momentum below the threshold, \(s_{th}=m^2(\zeta )\), adopting a tiny \(\zeta _p\) up to \(\zeta _p/m(\zeta )=10^{-4}\), while in Fig. 5 both real and imaginary terms, generated for \(p^2\ge s_{th}\), are presented. Notice that the positive sign of the imaginary part is a consequence of the first-order calculation (see. Eq. (85) and the vanishing of \({{\mathcal {A}}}_R\) for \(\zeta _p\rightarrow 0\)).

Fig. 5
figure 5

The same as in Fig. 4, but in the timelike region. Upper panel: real part of the running mass. Lower panel: imaginary part of the running mass

Full size image
Fig. 6
figure 6

The running charge \(G(\zeta ;q^2)\), Eq. (88), below the threshold vs \(q^2\), with \(s^p_{th}=4m^2(\zeta )\)

Full size image
Fig. 7
figure 7

The same as in Fig. 6, but for the timelike region. Upper panel: the real part. Lower panel: the imaginary part

Full size image

In Figs. 6 and 7, the running charge defined in Eq. (88) is shown for values below and above the threshold, that in this case holds \(s^p_{th}= 4m^2(\zeta )\). The comparison with the results of Ref. [61] (where \(\mathfrak {I}m\{M(\zeta ,p)\}\) has a negative sign) can be be performed only at the qualitative level, since the quantitative one is too early for our numerical efforts. In any case, one can recognize quite similar pattern, in particular, for the case of small values of the coupling constant \(\alpha _{em}\). It should be pointed out that the first-order self-energies (both fermion and photon ones) depend linearly upon the coupling constant and therefore, the values of the running mass and the relative running charge are not affected by such a dependence.

We would like to conclude this section by shortly anticipating a remark stemming from the detailed numerical investigations to be presented elsewhere. Indeed, in the quenched approximation, one can verify that the integrals relevant for the second iteration are all converging, even the ones including the function \(\varDelta ^\prime \) (see Eq. (69)). Of course, when extending the calculations to large values of the coupling constant, extra care on the convergence of the above quantities is requested, as one should expect additional singularity issues from Minkowski and Euclidean calculations focusing on the strong-coupling regime, both below and above the critical value (see, e.g., Refs. [47, 61, 94, 111] for the challenges beyond the critical value).

6 Conclusions and perspectives

This work belongs to the set of the early attempts (not too much numerous) to explore the non-perturbative regime of \(QED_{3+1}\) directly in Minkowski space, by exploiting the framework based on the so-called Nakanishi integral representation for describing the self-energies of both fermion and photon.

The originality of this work, elaborated within the RI’/MOM scheme, lies in the choice of the fermion-photon vertex, able to fulfill constraints coming from both the Ward–Takashi identity and the multiplicative renormalizability, that calls for purely transverse contributions. We have shown that despite the apparent complexity, it is possible to derive a well-defined system of equations for the Nakanishi weight functions, that we recall are real functions fulfilling a uniqueness theorem, within the Feynman diagrammatic framework [57]. In addition, we have presented an initial check based on the evaluation of the first iteration of the coupled system. In particular, we have initiated the comparison with known results of (i) the Källén–Lehmann weights for both fermion and photon, (ii) the running mass and (iii) the charge renormalization function. Beyond this, we have also verified that numerical stability remains under control, encouraging toward a more vast numerical investigation.

It has to be pointed out that the present results readily calls for two natural extensions on a short-time scale. First, complete numerical studies should be performed, allowing one to assess the convergence of the whole approach and to move the comparison to a quantitative level, e.g. with the results in Refs. [44, 61]. Second, the expected residue equal to one at the mass pole should be implemented at the level of the NWFs, i.e. going from the RI’/MOM scheme to the standard on-shell renormalization scheme.

On a longer time-scale, the third desirable extension would be to move from QED to QCD. An educated reader might object that many ingredients we used are not available or available in a much more complicated way for QCD. For instance, there is no formal proof that the propagators of confined particles should have Källén–Lehmann-like representation (positive definite). Nonetheless, lattice-QCD computations seem to be consistent with a spectral representation (although not a positive one) [112]. Furthermore, the Ward–Takahashi identities must be replaced by the Slavnov–Taylor ones, forcing deep modifications of the quark-gluon vertex function, playing an important role in realizing a dynamical breakdown of chiral symmetry. Also for this issue, progresses have been recently done in that direction, with the definition of the non-Abelian generalization of the Ball–Chiu vertex [27]. Therefore, despite the technical difficulties to jump from QED to QCD, we believe that such a possibility should deserve a careful investigation.

As a final remark, it is appropriate to recall that, for a given interacting system, our final goal is to implement and solve the BSE with dressed propagators for both particles and quanta, directly in Minkowski space, i.e. where the physical processes take place. In view of this, our present elaboration, that belongs to the phenomenological realm, should be considered a step forward for setting up a viable tool for the actual investigation of strong-coupling regimes (first below the critical value), within a QFT framework where the dynamical ingredients are made transparent and under control.