1 Introduction

The study of semi-leptonic decay \(\Lambda _{b}\rightarrow \Lambda _{c}\ell \nu \) is of great phenomenological significance as it provides an ideal place to constrain the CKM matrix element \(V_{cb}\). Furthermore, this process can also play an important role to test the lepton universality. The measured branching ratio is given by [1]

$$\begin{aligned} {{{\mathcal {B}}}}(\Lambda _{b}^{0}\rightarrow \Lambda _{c}^{+} e^{-}{\bar{\nu }}_{e}) =(6.2_{-1.3}^{+1.4})\times 10^{-2}. \end{aligned}$$
(1)

To extract \(V_{cb}\) or test the lepton universality, one must have the knowledge of \(\Lambda _b \rightarrow \Lambda _c\) transition form factors, which are defined as

$$\begin{aligned}&\langle \Lambda _{c}(p_{2},s_{2})|{\bar{c}} \gamma _{\mu }(1-\gamma _{5}) b|{\Lambda _{b}}(p_{1},s_{1})\rangle \nonumber \\&\quad = {\bar{u}}_{\Lambda _{c}}(p_{2},s_{2})\left[ \gamma _{\mu }f_{1} (q^{2})+i\sigma _{\mu \nu }\frac{q^{\nu }}{M_{1}}f_{2} (q^{2})\right. \nonumber \\&\qquad \left. +\frac{q_{\mu }}{M_{1}}f_{3}(q^{2}) \right] u_{\Lambda _{b}}(p_{1},s_{1})\nonumber \\&\qquad - {\bar{u}}_{\Lambda _{c}}(p_{2},s_{2})\left[ \gamma _{\mu } g_{1}(q^{2})+i\sigma _{\mu \nu }\frac{q^{\nu }}{M_{1}}g_{2}(q^{2})\right. \nonumber \\&\qquad \left. +\frac{q_{\mu }}{M_{1}}g_{3} (q^{2})\right] \gamma _{5}u_{\Lambda _{b}} (p_{1},s_{1}). \end{aligned}$$
(2)

In the heavy quark limit, the form factors \(f_1\) and \(g_1\) reduce to one unique Isgur–Wise function \(\zeta (w)\) , where \(w=v\cdot v'\), and \(f_2=f_3=g_2=g_3=0\). At zero recoil, we have \(\zeta (1)=1\). The heavy quark effective theory (HQET) provides a systemical framework to study the power corrections to the predictions in the heavy quark limit.

When the recoil energy is small, lattice QCD simulation works well and there already exist predictions of the \(\Lambda _b \rightarrow \Lambda _c\) form factors [2], while one has to employ phenomenological models to extrapolate the result to the whole momentum region. It makes great sense to evaluate the form factors in the large recoil region as the model dependence will be effectively reduced. Some works based on various quark models have been done [3,4,5,6,7,8,9,10], they being highly model dependent. Perturbative QCD approach (PQCD) is adopted in [11], but a relative small branching fraction of about 2% is obtained for \(\Lambda _b \rightarrow \Lambda _c \ell {\bar{\nu }}\). In [12], HQET and PQCD are adopted at small recoil and large recoil region, respectively, and the diquark picture is used for u, d quarks.

The QCD sum rules method is a time-honored QCD-based approach to dealing with hadronic parameters. It reveals a direct connection between hadron phenomenology and QCD vacuum structure via a few universal parameters such as quark condensates and gluon condensates. The method has been successfully applied to various problems relevant to the hadron structures. The three-point QCD sum rules have been widely used in the study on the transition form factors. For the heavy-to-light form factors such as \(B \rightarrow \pi \) form factors, the light-cone sum rules is more appropriate because the light-cone dominance of the correlation functions is proved at the large recoil region. Meanwhile for the heavy-to-heavy case, the three-point QCD sum rules are applicable if the virtuality of the momentum of the interpolating current is sufficient large (LCSRs are also applicable at appropriate virtuality region). In [13], we derived the form factors of doubly heavy baryons to singly heavy baryons using QCD sum rules for the first time, but so far our results are hard to test for the lack of experimental data. For the singly heavy baryon decays more data are accumulated which can help to check the theoretical predictions. In this work we will calculate the \(\Lambda _{b}\rightarrow \Lambda _{c}\) and \(\Xi _{b}\rightarrow \Xi _{c}\) transition form factors with three-point QCD sum rules so that the validity of the three-point sum rules can be checked.

Most studies on the heavy-to-heavy or heavy-to-light transition form factors are based on HQET (for the \(\Lambda _b \rightarrow \Lambda _c\) form factors, some of them can be found in [14,15,16,17], while [18] is based on the light-cone QCD sum rules), thus the power suppressed contributions are neglected. In this paper, we will employ the heavy quark field in full QCD. In this respect two studies have already been performed [19, 20], however, there are large discrepancies between these two references. The form factors obtained in [20] seem not to be reasonable because the form factors at the small recoil do not meet the predictions of HQET. For [19], there are some places to be improved, one is the two Borel parameters are not taken as free parameters, and the other is the following predictions for the form factors defined in Eq. (2),

$$\begin{aligned} f_{1}=g_{1},\quad f_{2}=f_{3}=g_{2}=g_{3}=0, \end{aligned}$$
(3)

is too rough. For the latter, the authors have only adopted the coefficients of the Dirac structures with the highest dimension to extract the vector and axial-vector form factors. In fact, at the next-to-leading power (NLP) of \(1/m_{Q}\) in HQET, \(f_{2}\) and \(g_{3}\) are fairly large rather than zero. Therefore, a more careful study on the \(\Lambda _b \rightarrow \Lambda _c\) transition is required. In addition, when [19] was done, there was no mature lattice QCD calculation available. In this work, we will make close comparisons with the predictions of lattice QCD.

In our method there are two points that need to be emphasized [13]. The first one is to obtain the spectral densities of double dispersion relations using cutting rules. As can be seen in Fig. 1, all the propagators perpendicular to \(p_{1}\) are to be cut if we intend to take discontinuity with respect to \(p_{1}^{2}\), and the same is true for the case of \(p_{2}\). This is readily justified using numerical integration for the situation of scalar quarks, and it can be evidently proved with the approach provided in [21]. The other one is to deal with the superfluous Dirac structures by taking into account the contributions from the negative-parity baryons. Because we are interested in the process of \(1/2^{+}\rightarrow 1/2^{+}\), once the other three processes including \(1/2^{-}\) baryons are considered, all the coefficients of Dirac structures will find their places in the final expressions for the form factors. Cutting rules were also adopted in [19], but only the coefficients of the Dirac structures with the highest dimension were used to extract the form factors.

For the processes of \(\Lambda _{b}\rightarrow \Lambda _{c}\) and \(\Xi _{b}\rightarrow \Xi _{c}\), the leading order contributions from dimension-3 and dimension-5 operators are, respectively, proportional to the mass of the light quark and the mass of the strange quark. For the former, these contributions can be neglected. Therefore, we will set the process \(\Xi _{b}\rightarrow \Xi _{c}\) as default in the following analysis. The corresponding results of \(\Lambda _{b}\rightarrow \Lambda _{c}\) will also be shown when appropriate. When performing the numerical analysis, the Wilson coefficients are calculated with perturbative QCD, thus we will employ the \(\overline{{\mathrm{MS}}}\) scheme for the quark masses. If we take the heavy quark limit the HQET sum rules results can be reproduced, as can be seen in [19, 22, 23].

The rest of this paper is arranged as follows. In Sect. 2, we will discuss the two-point correlation functions to evaluate the pole residues of \(\Xi _{Q}\) and \(\Lambda _{Q}\) for completeness. In Sect. 3, we will investigate the three-point correlation functions to arrive at the analytical results of the form factors. Numerical results for the form factors and their phenomenological applications will be shown in Sect. 4. In this section, we will also compare our results with other theoretical predictions and the experimental data to test the validity of our calculation. We conclude this paper in the last section.

Fig. 1
figure 1

Cutting rules for the spectral density of the double dispersion relation in Eq. (20)

Full size image

2 The two-point correlation functions and pole residues

The pole residues of heavy baryons have also been investigated in the literature [24, 25]. For completeness, we still briefly describe the calculation of the two-point correlation functions in this section.

To construct the correlation function, one should choose the appropriate interpolating currents for \(\Lambda _{Q}\) and \(\Xi _{Q}\). As the isospin of the diquark [ud] in the baryon \(\Lambda _{(c,b)}\) is 0, we adopt the following interpolating currents in our calculation:

$$\begin{aligned} J_{\Lambda _{Q}}&=\epsilon _{abc}(u_{a}^{T}C \gamma _{5}d_{b})Q_{c},\nonumber \\ J_{\Xi _{Q}}&=\epsilon _{abc}(q_{a}^{T}C\gamma _{5}s_{b})Q_{c}, \end{aligned}$$
(4)

where \(Q=b\) or c, \(q=u\) or d, the color indices are denoted by a, b, c and C is the charge conjugate matrix. The two-point correlation function is defined by

$$\begin{aligned} \Pi (p)=i\int \mathrm{d}^{4}x\ e^{ip\cdot x} \langle 0|T\{J(x){\bar{J}}(0)\}|0\rangle . \end{aligned}$$
(5)

On the hadronic side, one can insert the complete set of hadronic states to write the above correlation function as

(6)

where we have also considered the contribution from the negative-parity baryon, \(M_{\pm }\) (\(\lambda _{\pm }\)) stand for the masses (the pole residues) of the positive- and negative-parity baryons.

On the QCD side, we evaluate the correlation function in Eq. (5) following the OPE technique. Since the contributions from gluon condensate are small [23], one can only consider the contributions from dimension-0,3,5 operators and the corresponding nonzero diagrams can be found in Fig. 2. The result can be formally written as

(7)

where the coefficients A and B can be written in terms of the dispersion integrals,

$$\begin{aligned} A(p^{2})=\int \mathrm{d}s\ \frac{\rho ^{A}(s)}{s-p^{2}}, \quad B(p^{2})=\int \mathrm{d}s\ \frac{\rho ^{B}(s)}{s-p^{2}}. \end{aligned}$$
(8)
Fig. 2
figure 2

Only three nonzero diagrams survive for the two-point correlation function of \(\Xi _{Q}\), if we consider the contributions up to dimension-5 and neglect those from dimension-4. The double lines denote the heavy quarks and the dots stand for the condensates

Full size image

Taking advantage of the quark–hadron duality assumption and employing the Borel transform, the QCD sum rule for the pole residue of \(1/2^{+}\) baryon is given by

$$\begin{aligned}&(M_{+}+M_{-})\lambda _{+}^{2}\exp (-M_{+}^{2}/T_{+}^{2}) \nonumber \\&\quad =\int _{m_{Q}^{2}}^{s_{+}}\mathrm{d}s\ (M_{-}\rho ^{A}+\rho ^{B})\exp (-s/T_{+}^{2}), \end{aligned}$$
(9)

where \(T_{+}^{2}\) is the Borel parameters and \(s_{+}\) is the continuum threshold parameters. Differentiating Eq. (9) with respect to \(-1/T_{+}^{2}\), one can arrive at the sum rule for the mass of \(1/2^{+}\) baryon

$$\begin{aligned} M_{+}^{2}=\frac{\int _{m_{Q}^{2}}^{s_{+}}\mathrm{d}s\ (M_{-}\rho ^{A}+\rho ^{B})\ s\ \exp (-s/T_{+}^{2})}{\int _{m_{Q}^{2}}^{s_{+}}\mathrm{d}s\ (M_{-}\rho ^{A}+\rho ^{B})\ \exp (-s/T_{+}^{2})}. \end{aligned}$$
(10)

In practice, Eq. (10) is used to test the sum rule in Eq. (9).

3 Three-point correlation functions and form factors

For the \(\Lambda _{b}\rightarrow \Lambda _{c}\) and \(\Xi _{b}\rightarrow \Xi _{c}\) transition form factors, we take advantage of the following simpler parametrization in this section:

$$\begin{aligned}&\langle {{{\mathcal {B}}}}_{2}(p_{2},s_{2})|{\bar{c}}\gamma _{\mu }(1 -\gamma _{5})b|{{{\mathcal {B}}}}_{1}(p_{1},s_{1})\rangle \nonumber \\&\quad = {\bar{u}}_{{{{\mathcal {B}}}}_{2}}(p_{2},s_{2}) \left[ \frac{p_{1\mu }}{M_{1}}F_{1}(q^{2})+\frac{p_{2\mu }}{M_{2}}F_{2} (q^{2})\right. \nonumber \\&\qquad \left. +\gamma _{\mu }F_{3}(q^{2})\right] u_{{{{\mathcal {B}}}}_{1}}(p_{1},s_{1})\nonumber \\&\qquad - {\bar{u}}_{{{{\mathcal {B}}}}_{2}}(p_{2},s_{2}) \left[ \frac{p_{1\mu }}{M_{1}}G_{1}(q^{2})+\frac{p_{2\mu }}{M_{2}}G_{2}(q^{2})\right. \nonumber \\&\qquad \left. +\gamma _{\mu }G_{3}(q^{2})\right] \gamma _{5}u_{{{{\mathcal {B}}}}_{1}}(p_{1},s_{1}), \end{aligned}$$
(11)

where \({{{\mathcal {B}}}}_{1,2}\) are for \((\Lambda ,\Xi )_{b,c}\). The form factors \(F_{i},G_{i}\) are related to \(f_{i},g_{i}\) defined in (2) through

$$\begin{aligned} F_{1}&=f_{2}+f_{3},\quad F_{2}= \frac{M_{2}}{M_{1}}(f_{2}-f_{3}),\nonumber \\ F_{3}&=f_{1}-\frac{M_{1}+M_{2}}{M_{1}}f_{2};\nonumber \\ G_{1}&=g_{2}+g_{3},\quad G_{2}=\frac{M_{2}}{M_{1}}(g_{2}-g_{3}),\nonumber \\ G_{3}&=g_{1}+\frac{M_{1}-M_{2}}{M_{1}}g_{2}. \end{aligned}$$
(12)

Thus at the leading power of \(1/m_{Q}\) in HQET, the form factors defined in Eq. (11) satisfy [26]

$$\begin{aligned} F_{1}=F_{2}=G_{1}=G_{2}=0,\quad F_{3}= G_{3}=\zeta (\omega ),\nonumber \\ \end{aligned}$$
(13)

with

$$\begin{aligned} \zeta (\omega =1)=1, \end{aligned}$$
(14)

where \(\omega \equiv v_{1}\cdot v_{2}=(p_{1}\cdot p_{2})/(M_{1}M_{2})\).

As mentioned before, we will take the \(\Xi _{b}\rightarrow \Xi _{c}\) transition as the default process to illustrate our method. The correlation function for \(\Xi _{b}\rightarrow \Xi _{c}\) transition is defined as

$$\begin{aligned}&\Pi _{\mu }^{V,A}(p_{1}^{2},p_{2}^{2},q^{2})\nonumber \\&\quad =i^{2}\int \mathrm{d}^{4}x\mathrm{d}^{4}y\ e^{-ip_{1}\cdot x+ip_{2}\cdot y}\nonumber \\&\qquad \times \langle 0|T\{J_{\Xi _{c}}(y) (V_{\mu },A_{\mu })(0){\bar{J}}_{\Xi _{b}}(x)\}|0\rangle , \end{aligned}$$
(15)

where \(V_{\mu }(A_{\mu })={\bar{c}}\gamma _{\mu }(\gamma _{\mu }\gamma _{5})b\) is the vector (axial-vector) current for \(b\rightarrow c\) weak decay. The interpolating currents for initial and final states can be found in Eqs. (4).

Following the standard steps of QCD sum rules, the correlation function will be calculated at hadronic level and QCD level. At the hadronic level, after inserting the complete set of initial and final states, the vector current correlation function can be written as

(16)

where \(\lambda _{i(f)}=\lambda _{\Xi _{b(c)}}\), \(F_{i}\) are form factors defined in Eq. (11), \(M_{1,2}\) are the masses of initial and final states and the ellipsis stands for the contribution from higher resonances and continuum spectra. It is clear that there are 12 Dirac structures, but only three form factors to be determined in Eq. (16). For each form factor, there are four Dirac structures available. Furthermore, it is very likely that these different Dirac structures give rise to very different results since only the LO results are considered. To eliminate these ambiguities, we consider again the contributions from the negative-parity baryons, which have been swept into the ellipsis in Eq. (16). After that, the vector current correlation function can be rewritten as

(17)
Fig. 3
figure 3

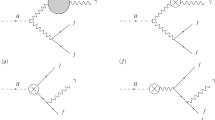
Only three nonzero diagrams survive for the three-point correlation function of \(\Xi _{b}\) decaying into \(\Xi _{c}\), if we consider the contributions up to dimension-5 and neglect those from dimension-4. The double lines denote the heavy quarks, the dots stand for the condensates, and the cross marks are vertices of weak interaction

Full size image

In Eq. (17), \(M_{1(2)}^{+(-)}\) denotes the masses of initial (final) positive (negative) parity baryons, and \(F_{1}^{-+}\) is the form factor \(F_{1}\) with the negative-parity final state and the positive-parity initial state, and so forth. To arrive at Eq. (17), we have also adopted the definitions of the pole residues for positive- and negative-parity baryons,

$$\begin{aligned} \langle 0|J_{+}|{{{\mathcal {B}}}}_{+}(p,s)\rangle&=\lambda _{+}u(p,s),\nonumber \\ \langle 0|J_{+}|{{{\mathcal {B}}}}_{-}(p,s)\rangle&=(i\gamma _{5})\lambda _{-}u(p,s), \end{aligned}$$
(18)

and the following conventions for the form factors \(F_{i}^{\pm \pm }\):

$$\begin{aligned}&\langle {{{\mathcal {B}}}}_{f}^{+}(p_{2},s_{2})|V_{\mu } |{{{\mathcal {B}}}}_{i}^{+}(p_{1},s_{1})\rangle \nonumber \\&\quad ={\bar{u}}_{{{{\mathcal {B}}}}_{f}^{+}}(p_{2},s_{2}) \left[ \frac{p_{1\mu }}{M_{1}^{+}}F_{1}^{++}+\frac{p_{2\mu }}{M_{2}^{+}} F_{2}^{++}+\gamma _{\mu }F_{3}^{++}\right] \nonumber \\&\qquad \times u_{{{{\mathcal {B}}}}_{i}^{+}}(p_{1},s_{1}),\nonumber \\&\langle {{{\mathcal {B}}}}_{f}^{+}(p_{2},s_{2})|V_{\mu } |{{{\mathcal {B}}}}_{i}^{-}(p_{1},s_{1})\rangle \nonumber \\&\quad ={\bar{u}}_{{{{\mathcal {B}}}}_{f}^{+}}(p_{2},s_{2}) \left[ \frac{p_{1\mu }}{M_{1}^{-}}F_{1}^{+-}+\frac{p_{2\mu }}{M_{2}^{+}} F_{2}^{+-} +\gamma _{\mu }F_{3}^{+-}\right] \nonumber \\&\qquad \times (i\gamma _{5})u_{{{{\mathcal {B}}}}_{i}^{-}} (p_{1},s_{1}),\nonumber \\&\langle {{{\mathcal {B}}}}_{f}^{-}(p_{2},s_{2})|V_{\mu } |{{{\mathcal {B}}}}_{i}^{+}(p_{1},s_{1})\rangle \nonumber \\&\quad ={\bar{u}}_{{{{\mathcal {B}}}}_{f}^{-}}(p_{2},s_{2})(i\gamma _{5}) \left[ \frac{p_{1\mu }}{M_{1}^{+}}F_{1}^{-+}+\frac{p_{2\mu }}{M_{2}^{-}} F_{2}^{-+}+\gamma _{\mu }F_{3}^{-+}\right] \nonumber \\&\qquad \times u_{{{{\mathcal {B}}}}_{i}^{+}}(p_{1},s_{1}),\nonumber \\&\langle {{{\mathcal {B}}}}_{f}^{-}(p_{2},s_{2})|V_{\mu } |{{{\mathcal {B}}}}_{i}^{-}(p_{1},s_{1})\rangle \nonumber \\&\quad ={\bar{u}}_{{{{\mathcal {B}}}}_{f}^{-}}(p_{2},s_{2})(i\gamma _{5}) \left[ \frac{p_{1\mu }}{M_{1}^{-}}F_{1}^{--}+\frac{p_{2\mu }}{M_{2}^{-}} F_{2}^{--}+\gamma _{\mu }F_{3}^{--}\right] \nonumber \\&\qquad \times (i\gamma _{5})u_{{{{\mathcal {B}}}}_{i}^{-}}(p_{1},s_{1}). \end{aligned}$$
(19)

In Eq. (18), \(J_{+}\) can be found in Eqs. (4), and \(\lambda _{+(-)}\) is the pole residue for the positive- (negative-) parity baryon.

At the QCD level, there are three diagrams to be considered up to dimension-5, as can be seen in Fig. 3.Footnote 1 For practical purpose, the correlation function is expressed as a double dispersion relation

$$\begin{aligned}&\Pi _{\mu }^{V,{\mathrm{QCD}}}(p_{1}^{2},p_{2}^{2},q^{2})\nonumber \\&\quad =\int ^{\infty }\mathrm{d}s_{1} \int ^{\infty }\mathrm{d}s_{2}\frac{\rho _{\mu }^{V,{\mathrm{QCD}}}(s_{1},s_{2},q^{2})}{(s_{1}-p_{1}^{2})(s_{2}-p_{2}^{2})}, \end{aligned}$$
(20)

with \(\rho _{\mu }^{V,{\mathrm{QCD}}}(s_{1},s_{2},q^{2})\) being the spectral function, which can be obtained by applying Cutkosky cutting rules. Based on the assumption of quark–hadron duality, the sum of the four pole terms in Eq. (17) should be equal to

$$\begin{aligned} \int ^{s_{1}^{0}}\mathrm{d}s_{1}\int ^{s_{2}^{0}}\mathrm{d}s_{2}\frac{\rho _{\mu }^{V,\mathrm{QCD}}(s_{1},s_{2},q^{2})}{(s_{1}-p_{1}^{2}) (s_{2}-p_{2}^{2})}\equiv \Pi _{\mu }^{V,\mathrm{pole}}, \end{aligned}$$
(21)

where \(s_{1(2)}^{0}\) is the continuum threshold parameter for the initial (final) baryon. \(\Pi _{\mu }^{V,{\mathrm{pole}}}\) can be formally written as

$$\begin{aligned} \Pi _{\mu }^{V,{\mathrm{pole}}}=\sum _{i=1}^{12}A_{i}e_{i\mu }, \end{aligned}$$
(22)

where we have defined

(23)

By equating Eq. (17) with Eq. (22), one can obtain 12 equations. Solving these equations, one can obtain these 12 form factors \(F_{i}^{\pm ,\pm }\), including the following three expressions for \(F_{i}^{++}\):

$$\begin{aligned}&\frac{\lambda _{i}^{+}\lambda _{f}^{+}(F_{1}^{++}/M_{1}^{+})}{(p_{1}^{2}-M_{1}^{+2})(p_{2}^{2}-M_{2}^{+2})} \nonumber \\&\quad = \frac{\{M_{1}^{-}M_{2}^{-},M_{2}^{-},M_{1}^{-},1\}\cdot \{A_{1},A_{2},A_{3}, A_{4}\}}{(M_{1}^{+}+M_{1}^{-})(M_{2}^{+}+M_{2}^{-})},\nonumber \\&\frac{\lambda _{i}^{+}\lambda _{f}^{+}(F_{2}^{++}/M_{2}^{+})}{(p_{1}^{2} -M_{1}^{+2})(p_{2}^{2}-M_{2}^{+2})} \nonumber \\&\quad = \frac{\{M_{1}^{-}M_{2}^{-}, M_{2}^{-},M_{1}^{-},1\}\cdot \{A_{5},A_{6},A_{7},A_{8}\}}{(M_{1}^{+}+M_{1}^{-}) (M_{2}^{+}+M_{2}^{-})},\nonumber \\&\frac{\lambda _{i}^{+}\lambda _{f}^{+}F_{3}^{++}}{(p_{1}^{2}-M_{1}^{+2}) (p_{2}^{2}-M_{2}^{+2})}\nonumber \\&\quad = \frac{\{M_{1}^{-}M_{2}^{-},M_{2}^{-}, M_{1}^{-},1\}\cdot \{A_{9},A_{10},A_{11},A_{12}\}}{(M_{1}^{+}+M_{1}^{-})(M_{2}^{+}+M_{2}^{-})}. \end{aligned}$$
(24)

Borel transforming the above equations to suppress the contributions from higher resonances and continuum spectra we arrive at

$$\begin{aligned}&\lambda _{i}^{+}\lambda _{f}^{+}(F_{1}^{++}/M_{1}^{+}) \exp \left( -\frac{M_{1}^{+2}}{T_{1}^{2}}-\frac{M_{2}^{+2}}{T_{2}^{2}}\right) \nonumber \\&\quad =\frac{\{M_{1}^{-}M_{2}^{-},M_{2}^{-},M_{1}^{-}, 1\}\cdot \{{{{\mathcal {B}}}}A_{1},{{{\mathcal {B}}}}A_{2}, {{{\mathcal {B}}}}A_{3},{{{\mathcal {B}}}}A_{4}\}}{(M_{1}^{+} +M_{1}^{-})(M_{2}^{+}+M_{2}^{-})},\nonumber \\&\lambda _{i}^{+}\lambda _{f}^{+}(F_{2}^{++}/M_{2}^{+}) \exp \left( -\frac{M_{1}^{+2}}{T_{1}^{2}}-\frac{M_{2}^{+2}}{T_{2}^{2}} \right) \nonumber \\&\quad =\frac{\{M_{1}^{-}M_{2}^{-},M_{2}^{-},M_{1}^{-},1\}\cdot \{{{{\mathcal {B}}}}A_{5},{{{\mathcal {B}}}}A_{6},{{{\mathcal {B}}}}A_{7}, {{{\mathcal {B}}}}A_{8}\}}{(M_{1}^{+}+M_{1}^{-})(M_{2}^{+}+M_{2}^{-})},\nonumber \\&\lambda _{i}^{+}\lambda _{f}^{+}F_{3}^{++}\exp \left( -\frac{M_{1}^{+2}}{T_{1}^{2}}-\frac{M_{2}^{+2}}{T_{2}^{2}}\right) \nonumber \\&\quad =\frac{\{M_{1}^{-}M_{2}^{-},M_{2}^{-},M_{1}^{-},1\}\cdot \{{{{\mathcal {B}}}}A_{9},{{{\mathcal {B}}}}A_{10},{{{\mathcal {B}}}}A_{11}, {{{\mathcal {B}}}}A_{12}\}}{(M_{1}^{+}+M_{1}^{-})(M_{2}^{+}+M_{2}^{-})}, \end{aligned}$$
(25)

where \({{{\mathcal {B}}}}A_{i}\equiv {{{\mathcal {B}}}}_{T_{1}^{2},T_{2}^{2}}A_{i}\) are doubly Borel transformed coefficients, and \(T_{1,2}^{2}\) are the Borel mass parameters.

To obtain the coefficients \(A_{i}\) in Eq. (22), one can project Eq. (22) onto 12 Dirac structures. Specifically, multiplying by \(e_{j}^{\mu }\) and then taking traces on both sides of Eq. (22), one can arrive at the following 12 linear equations:

$$\begin{aligned} B_{j}\equiv & {} {\mathrm{Tr}}[\Pi _{\mu }^{V,{\mathrm{pole}}}e_{j}^{\mu }]\nonumber \\= & {} {\mathrm{Tr}}\left[ \left( \sum _{i=1}^{12}A_{i}e_{i\mu }\right) e_{j}^{\mu }\right] ,\quad j=1,\ldots ,12. \end{aligned}$$
(26)

Solving these equations, one can obtain the expressions of \(A_{i}\) given that it is easy to write down \(\Pi _{\mu }^{V,{\mathrm{pole}}}\).

4 Numerical results and phenomenological applications

In our numerical calculations, the condensate parameters are taken as [27] \(\langle {\bar{q}}q\rangle =-(0.24\pm 0.01\ {\mathrm{GeV}})^{3}\), \(\langle {\bar{q}}g_{s}\sigma Gq\rangle =m_{0}^{2}\langle {\bar{q}}q\rangle \), \(m_{0}^{2}=(0.8\pm 0.2)~{\mathrm{GeV}}^{2}\), where the renormalization scale is taken at \(\mu =1\) GeV. In this work, we will use \(\overline{{\mathrm{MS}}}\) masses for quarks unless otherwise stated. When dealing with the two-point correction functions for bottom baryons, we take the renormalization scale at \(\mu =m_{b}\), while for charmed baryons, \(\mu =m_{c}\). For the three-point correction functions of a bottom baryon decaying into a charmed baryon, we take \(\mu =m_{b}\). The following quark masses are used [1]:

$$\begin{aligned} m_{b}(m_{b})&=4.18\pm 0.03~{\mathrm{GeV}},\quad m_{c}(m_{b})=1.02\pm 0.02~{\mathrm{GeV}},\nonumber \\ m_{s}(m_{b})&=(0.082\pm 0.010)~{\mathrm{GeV}},\nonumber \\ m_{c}(m_{c})&=1.27\pm 0.02~{\mathrm{GeV}},\quad m_{s}(m_{c})=0.103\pm 0.012~{\mathrm{GeV}}. \end{aligned}$$
(27)

Since we are considering the LO calculation of QCDSR, when arriving at the above masses, it would be enough to adopt the following one-loop evolution equation:

$$\begin{aligned} m_{q}(\mu _{0})\left( \frac{\log (\mu _{0}/\Lambda _{{\mathrm{QCD}}}^{(n_{f})})}{\log (\mu /\Lambda _{{\mathrm{QCD}}}^{(n_{f})})}\right) ^{4/\beta _{0}} \end{aligned}$$
(28)

for \(m_{c}(m_{b})\), \(m_{s}(m_{b})\) and \(m_{s}(m_{c})\). In the above equation, \(\beta _{0}=11-(2/3)n_{f}\) with \(n_{f}\) the number of active flavors, and \(\Lambda _{{\mathrm{QCD}}}^{(4)}=170\ {\mathrm{MeV}}\) has been used in Eqs. (27). In the following, \(\Lambda _{{\mathrm{QCD}}}^{(3)}=223~{\mathrm{MeV}}\) will also be used. These two values for \(\Lambda _{{\mathrm{QCD}}}\) are obtained by requiring the results for \(\alpha _{s}\) at the LO to reproduce the corresponding results at the NLO [28].Footnote 2

4.1 The two-point correlation function

In this work, we will also consider the leading logarithm (LL) approximation for the pole residues and masses of baryons. According to [29], the Wilson coefficients of the local operators that we derived in Sect. 2 should be multiplied by an evolution factor,

$$\begin{aligned} \left( \frac{\log (\mu _{0}/\Lambda _{{\mathrm{QCD}}}^{(n_{f})})}{\log (\mu /\Lambda _{{\mathrm{QCD}}}^{(n_{f})})}\right) ^{2\gamma _{J}-\gamma _{O}}, \end{aligned}$$
(29)

where \(\gamma _{J}\) is the anomalous dimension of the current J in Eq. (4), and \(\gamma _{O}\) is that of the local operator in the OPE. Following [29], we will also only consider the LL corrections for the perturbative and quark condensate contributions. \(\mu _{0}\) is the renormalization scale of the low-energy limit [29], which is roughly at \(1~{\mathrm{GeV}}\), and \(\mu \sim m_{Q}\) is the renormalization scale that we choose for the physical quantities of interest. For the interpolating current given in Eq. (4), the corresponding anomalous dimension is \(\gamma _{J}=-1/\beta _{0}\) [30]. The anomalous dimension for \({\bar{\psi }}\psi \) is given by \(\gamma _{{\bar{\psi }}\psi }=4/\beta _{0}\).

Fig. 4
figure 4

The pole residues of \(\Xi _{b}\) (top left), \(\Lambda _{b}\) (top right), \(\Xi _{c}\) (bottom left) and \(\Lambda _{c}\) (bottom right) as functions of the Borel parameters \(T_{+}^{2}\). The blue and red curves correspond to optimal and suboptimal choices for \(s_{+}\). The extreme points of these curves correspond to the optimal choices of \(T_{+}^{2}\) on these curves. The explicit values for these \(s_{+}\) and \(T_{+}^{2}\) can be found in Table 1. In practice, \(T_{+}^{2}\) is taken in the range of \([1,16]~{\mathrm{GeV}}^{2}\) with step length \(1~{\mathrm{GeV}}^{2}\) for \({{{\mathcal {B}}}}_{b}\), and \([0.5,5]~{\mathrm{GeV}}^{2}\) with step length \(0.5~{\mathrm{GeV}}^{2}\) for \({{{\mathcal {B}}}}_{c}\). It can be seen that our predictions for pole residues depend little on such sampling

Full size image
Table 1 The predictions of the pole residues and masses. For comparison, the experimental values of heavy baryons are also shown. Optimal and suboptimal \(s_{+}\) and \(T_{+}^{2}\) are given simultaneously. The central values for the pole residues and masses are taken at optimal \(s_{+}\) and \(T_{+}^{2}\), and the values at suboptimal \(s_{+}\) and \(T_{+}^{2}\) provide the error estimates. The results of bottom and charmed baryons are, respectively, obtained at the renormalization scale \(\mu =m_{b}\) and \(\mu =m_{c}\), respectively
Full size table

Using the sum rule in Eq. (9), we can determine the pole residues for \((\Lambda ,\Xi )_{b,c}\). The pole residues as functions of the Borel parameter \(T_{+}^{2}\) are given in Fig. 4, from which we arrive at our predictions of the pole residues and masses for \((\Lambda ,\Xi )_{b,c}\) in Table 1. Some comments are in order.

  • It can be seen that our predictions for the masses of \((\Lambda ,\Xi )_{b,c}\) are in very good agreement with the experimental results. Presumably it is due to the overwhelming contribution from perturbative diagram, since the second and third diagrams in Fig. 2 are proportional to the mass of light quark.

  • It turns out that the LL corrections for dimension-0,3 are, respectively, 16, \(54\%\) for the bottom baryons, and 3, \(10\%\) for the charmed baryons. Although the corrections for dimension-3 are large, they do not play an important role because of the fact stated in the last item.

4.2 The three-point correlation function

To access the numerical results for the form factors of \(\Xi _{b}\rightarrow \Xi _{c}\), firstly we need to find the optimal choices for the threshold parameters \(s_{1,2}^{0}\) and the Borel masses \(T_{1,2}^{2}\). For the former, we just borrow them from the corresponding two-point correlation functions. The optimal values for \(s_{1}^{0}\) and \(s_{2}^{0}\) are, respectively, \((6.20~{\mathrm{GeV}})^{2}\) and \((2.85~{\mathrm{GeV}})^{2}\), as can be seen from Table 1. Then we scan the \(T_{1}^{2}\)–\(T_{2}^{2}\) plane to determine the optimal Borel region.

Note that we also consider the LL resummation for the form factors. Since the anomalous dimensions for the vector current and axial-vector current vanish, the Wilson coefficients of the local operators that we derived in Sect. 3 should be multiplied by the same evolution factor as in Eq. (29). One more thing should be addressed: the pole residue for \(\Xi _{c}\) (\(\Lambda _{c}\)) in Table 1, which is evaluated at \(\mu =m_{c}\), should be evolved to the scale of \(\mu =m_{b}\).

However, we fail to find stable regions like the cases of the two-point correlation functions. To find relatively optimal regions on \(T_{1}^{2}\)–\(T_{2}^{2}\) plane, the following criteria are to be employed:

  • Pole dominance. We require

    $$\begin{aligned} r_{1}&\equiv \frac{\int ^{s_{1}^{0}}\mathrm{d}s_{1}\int ^{s_{2}^{0}}\mathrm{d}s_{2}}{\int ^{\infty }\mathrm{d}s_{1}\int ^{s_{2}^{0}}\mathrm{d}s_{2}}\gtrsim 0.5,\nonumber \\ r_{2}&\equiv \frac{\int ^{s_{1}^{0}}\mathrm{d}s_{1}\int ^{s_{2}^{0}}\mathrm{d}s_{2} }{\int ^{s_{1}^{0}}\mathrm{d}s_{1}\int ^{\infty }\mathrm{d}s_{2}}\gtrsim 0.5, \end{aligned}$$
    (30)

    which can be viewed as the pole dominance criteria for the \(\Xi _{b}\) (\(\Lambda _{b}\)) channel and the \(\Xi _{c}\) (\(\Lambda _{c}\)) channel, respectively.

  • OPE convergence. It can be achieved by requiring that the ratio dimension-5/Total should be small enough.

Complying with the above criteria, we arrive at the relatively optimal regions on the \(T_{1}^{2}\)–\(T_{2}^{2}\) plane for \(\Xi _{b}\rightarrow \Xi _{c}\), which are enclosed by the dashed contours, as plotted in Fig. 5. The specific values of \(r_{1,2}\) and dimension-5/Total in these regions can be found in Table 2. Since \(F_{1,2}\) is small, the definitions in Eqs. (30) may be ill-defined, so we only give the selected regions for \(F_{3}\), and just assume that the same regions are also applied to \(F_{1,2}\). Similar regions can be obtained for \(G_{3}\) and same assumption is applied to \(G_{1,2}\).

For \(\Lambda _{b}\rightarrow \Lambda _{c}\), the contributions from dimension-3,5 are neglected because they are proportional to the mass of the light quark, thereby the second criterion does not work. However, one can see that in the selected regions for \(\Xi _{b}\rightarrow \Xi _{c}\), \(T_{1}^{2}\sim {{{\mathcal {O}}}}(m_{b}^{2})\) and \(T_{2}^{2}\sim {{{\mathcal {O}}}}(m_{c}^{2})\), so it is plausible that similar pattern should also hold for \(\Lambda _{b}\rightarrow \Lambda _{c}\). By constraining \(T_{1}^{2}\in [15,25]~{\mathrm{GeV}}^{2}\), \(T_{2}^{2}\in [2,4]~{\mathrm{GeV}}^{2}\) and also considering the first criterion above, the Borel region for \(\Lambda _{b}\rightarrow \Lambda _{c}\) can also be determined, as can be seen in Fig. 5.

Fig. 5
figure 5

\(F_{3}^{\Xi _{b}\rightarrow \Xi _{c}}\) and \(F_{3}^{\Lambda _{b}\rightarrow \Lambda _{c}}\) at \(q^{2}=0\) as functions of the Borel parameters \(T_{1}^{2}\) and \(T_{2}^{2}\), where \(T_{1}^{2}\) and \(T_{2}^{2}\) are taken as free parameters. The larger the form factors, the darker the color. The preferred Borel regions are enclosed by the dashed contours

Full size image
Table 2 The quantitative criteria of the pole dominance and OPE convergence
Full size table

After all the parameters are fixed, central values and uncertainties of the form factors \(F_{i}\) and \(G_{i}\) at \(q^{2}=0\) for the processes of \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\) are then given in Table 3. In this table, central values of the Borel parameters \((T_{1}^{2},T_{2}^{2})\) are, respectively, taken as \((25,3)\ {\mathrm{GeV}}^{2}\) and \((20,3)\ {\mathrm{GeV}}^{2}\) for \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\). The three uncertainties are from the Borel region, and the threshold parameters \(s_{1}^{0}\) and \(s_{2}^{0}\), respectively. When determining the uncertainties from the threshold parameters, the suboptimal values in Table 1 are used as references.

Table 3 Central values and uncertainties of the form factors \(F_{i}\) and \(G_{i}\) at \(q^{2}=0\)
Full size table

To access the \(q^{2}\) dependence of the form factors, we calculate the form factors in a small interval \(q^{2}\in [0.0,0.5]~{\mathrm{GeV}}^{2}\), and fit the values with the following simplified z-expansion [2]:

$$\begin{aligned} f(q^{2})=\frac{a+b\ z(q^{2})}{1-q^{2}/m_{{\mathrm{pole}}}^{2}}, \end{aligned}$$
(31)

where \(m_{{\mathrm{pole}}}= m_{B_{c}}\),

$$\begin{aligned} z(q^{2})=\frac{\sqrt{t_{+}-q^{2}}-\sqrt{t_{+}-q_{{\mathrm{max}}}^{2}}}{\sqrt{t_{+}-q^{2}}+\sqrt{t_{+}-q_{{\mathrm{max}}}^{2}}} \end{aligned}$$
(32)

with \(t_{+}=m_{{\mathrm{pole}}}^{2}\) and \(q_{{\mathrm{max}}}^{2}=(M_{1}-M_{2})^{2}\), \(M_{1}=m_{\Xi _{b}}\) (\(m_{\Lambda _{b}}\)), \(M_{2}=m_{\Xi _{c}}\) (\(m_{\Lambda _{c}}\)). The fitted results of (a, b) for the form factors of \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\) are given in Table 4. In Table 5, our results are compared with those of lattice QCD [2] and those of HQET at the next-to-leading power (NLP) of \(1/m_{Q}\) [26]. Some comments are in order.

  • For the results of HQET at the NLP in Table 5, we have used

    $$\begin{aligned}&\zeta (1)=1,\quad {\bar{\Lambda }}_{\Lambda }=0.9\ {\mathrm{GeV}},\quad m_{c}=1.4~{\mathrm{GeV}},\nonumber \\&m_{b}=4.8~{\mathrm{GeV}}. \end{aligned}$$
    (33)

    The evaluation of nonperturbative constant \({\bar{\Lambda }}_{\Lambda }\) can be found in [23].

  • As can be seen in Table 3 about 10–20% uncertainties are introduced for the form factors of \(\Xi _{b}\rightarrow \Xi _{c}\) at \(q^{2}=0\), and about 20% for \(\Lambda _{b}\rightarrow \Lambda _{c}\). As a rough estimate, we assume that similar uncertainties are implicit in our predictions for the form factors at \(q^{2}=q_{{\mathrm{max}}}^{2}\) in Table 5. Considering these uncertainties, one can see that our results are very close to those of the Lattice QCD and HQET at NLP, especially for \(F_{3}\) and \(G_{3}\).

  • As stated above, the form factors of \(\Lambda _{b}\rightarrow \Lambda _{c}\) at the LP of HQET is

    $$\begin{aligned} F_{1}=F_{2}=G_{1}=G_{2}=0,\quad F_{3}=G_{3}=1. \end{aligned}$$
    (34)

    To be compared with this, about 10–40% corrections are introduced for the NLP results. Since the mass of the charm quark is not high enough, both HQET and HQET sum rules may receive sizable power corrections.

Table 4 The fitted results of (a, b) for the form factors
Full size table
Table 5 Our predictions for the form factors at \(q^{2}=0\) and \(q^{2}=q_{{\mathrm{max}}}^{2}\) are compared with those from the Lattice QCD and the next-to-leading power of \(1/m_{Q}\) in HQET [26]. For the latter, only \(F(q_{{\mathrm{max}}}^{2})\) are shown, the choices for the parameter values can be found in the text. As can be seen in Table 3, about 10–20\(\%\) uncertainties can be introduced in our results for \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\)
Full size table

The predictions for the form factors are then applied to the semi-leptonic processes. The polarized decay widths for \({{{\mathcal {B}}}}_{1}\rightarrow {{{\mathcal {B}}}}_{2}l\nu \) are given as

$$\begin{aligned} \frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^{2}}&= \frac{G_{F}^{2}|V_{{\mathrm{CKM}}}|^{2}q^{2}\ p\ (1-{\hat{m}}_{l}^{2})^{2}}{384\pi ^{3}M_{1}^{2}}\nonumber \\&\quad \times \left( (2+{\hat{m}}_{l}^{2}) (|H_{-\frac{1}{2},0}|^{2}+|H_{\frac{1}{2},0}|^{2})\right. \nonumber \\&\quad \left. +3{\hat{m}}_{l}^{2} (|H_{-\frac{1}{2},t}|^{2}+|H_{\frac{1}{2},t}|^{2})\right) , \end{aligned}$$
(35)
$$\begin{aligned} \frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^{2}}&= \frac{G_{F}^{2}|V_{{\mathrm{CKM}}}|^{2}q^{2}\ p\ (1-{\hat{m}}_{l}^{2})^{2}(2+{\hat{m}}_{l}^{2})}{384\pi ^{3}M_{1}^{2}}\nonumber \\&\quad \times \left( |H_{\frac{1}{2},1}|^{2} +|H_{-\frac{1}{2},-1}|^{2}\right) , \end{aligned}$$
(36)

where \({\hat{m}}_{l}\equiv m_{l}/\sqrt{q^{2}}\), and \(p=\sqrt{Q_{+}Q_{-}}/(2M_{1})\) with \(Q_{\pm }=(M_{1}\pm M_{2})^{2}-q^{2}\) is the magnitude of the three-momentum of \({{{\mathcal {B}}}}_{2}\) in the rest frame of \({{{\mathcal {B}}}}_{1}\). The helicity amplitudes \(H_{\lambda _{2},\lambda _{W}}\) in Eqs. (35) and (36), which are written in terms of the form factors, can be found in [13]. Integrating out the momentum transfer \(q^{2}\), one can obtain the total decay width:

$$\begin{aligned} \Gamma =\int _{m_{l}^{2}}^{(M_{1}-M_{2})^{2}}\mathrm{d}q^{2} \frac{\mathrm{d}\Gamma }{\mathrm{d}q^{2}}, \end{aligned}$$
(37)

where

$$\begin{aligned} \frac{\mathrm{d}\Gamma }{\mathrm{d}q^{2}}=\frac{\mathrm{d}\Gamma _{L}}{\mathrm{d}q^{2}}+\frac{\mathrm{d}\Gamma _{T}}{\mathrm{d}q^{2}}. \end{aligned}$$
(38)

We arrive at

$$\begin{aligned} \Gamma&=(3.80\pm 0.33)\times 10^{-14}~{\mathrm{GeV}},\nonumber \\ {{{\mathcal {B}}}}&=(9.02\pm 0.79)\%,\nonumber \\ \Gamma _{L}/\Gamma _{T}&=1.29\pm 0.06 \end{aligned}$$
(39)

for \(\Xi _{b}\rightarrow \Xi _{c}e^{-}{\bar{\nu }}_{e}\), and

$$\begin{aligned} \Gamma&=(2.96\pm 0.48)\times 10^{-14}~{\mathrm{GeV}},\nonumber \\ {{{\mathcal {B}}}}&=(6.61\pm 1.08)\%,\nonumber \\ \Gamma _{L}/\Gamma _{T}&=1.28\pm 0.12 \end{aligned}$$
(40)

for \(\Lambda _{b}\rightarrow \Lambda _{c}e^{-}{\bar{\nu }}_{e}\). The uncertainties come from those of the form factors. Our predictions for the branching fractions are compared with those from lattice QCD [2] and experimental data [1], as can be seen in Table 6. It can be seen that our prediction for \(\Lambda _{b}\rightarrow \Lambda _{c}e^{-}{\bar{\nu }}_{e}\) is consistent with that of lattice QCD and experiment. In addition, the SU(3) symmetry breaking between \(\Xi _{b}\rightarrow \Xi _{c}e^{-}{\bar{\nu }}_{e}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}e^{-}{\bar{\nu }}_{e}\) is about 30%.

Table 6 Our predictions for the semi-leptonic branching fractions (in units of \(\%\)) are compared with those from lattice QCD [2] and experimental data [1]
Full size table

5 Conclusions

In this work, the full LO results of the form factors for the processes \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\) are obtained in QCD sum rules. For completeness, we also study the two-point correlation functions to obtain the pole residues of \(\Xi _{Q}\) and \(\Lambda _{Q}\). Contributions from up to dimension-5 operators have been considered. We have also included the leading logarithm approximation. For the two-point correlation function, since the perturbative contribution dominates and a stable Borel window for the pole residue can be found, higher accuracy is achieved both for the pole residue and the mass. However, although the perturbative contribution also dominates for the three-point correlation function, a stable Borel region can hardly be found. Somewhat artificial criteria have to be adopted to select the relatively optimal region, and about 20% uncertainties are introduced for the form factors of \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\). Our results of the form factors are consistent with those of lattice QCD within errors. It is worth noting that, starting from our full LO results, one can arrive at the results of HQET sum rules, when \(m_{b,c}\) are taken to be infinity [22, 23]. Similar arguments have been performed in [19].

In [13], we derived the form factors of doubly heavy baryons to singly heavy baryons using QCD sum rules for the first time, but so far our results are hard to be tested for the lack of experimental data. For the singly heavy baryon decays more data are accumulated which can help to check the theoretical predictions. In this work reliable results are obtained for the form factors of \(\Xi _{b}\rightarrow \Xi _{c}\) and \(\Lambda _{b}\rightarrow \Lambda _{c}\) so that the validity of the three-point sum rules is checked. A potential application is to calculate the matrix elements for the lifetimes of weakly-decay heavy baryons. Our forthcoming works will focus on this problem.