Neutral physical compact spherically symmetric stars with non-exotic matters in Einstein’s cluster model using Weitzenböck geometry

Abstract

We revisit the neutral (uncharged) solutions that describe Einstein’s clusters with matters in the frame of Weitzenböck geometry. To this end, we use a tetrad field with non-diagonal spherical symmetry which gives vanishing of the off-diagonal components of the gravitational field equations. The cluster solutions are calculated by using an anisotropic energy–momentum tensor. We solve the field equations using two novel assumptions. First, we use an equation of state that relates density with tangential pressure, and then we assume a specific form of one of the metric potentials in addition to the assumption of the vanishing of radial pressure to make the system of differential equations in a closed-form. The resulting solutions are coincide with the literature $however \, \,in\, \,this\, \,study\, \,we\, \,constrain\,\, the\,\, constants \, \,of\, \, integration\, \, from\, \, \,the\, \, matching\,\, of\, \,boundary$ $condition\, \, in a\,\, way \,\,different\,\, from\,\, that\,\, presented \,\,in \,\,the\,\, literature.$ Among many things presented in this study, we investigate the static stability specification and show that our model is consistent with a real compact start except that the tangential pressure has a vanishing value at the center of the star which is not accepted from the physical viewpoint of a real compact star. We conclude that the model that has vanishing radial pressure in the frame of Einstein’s theory is not a physical model. Therefore, we extend this study and derive a new compact star without assuming the vanishing of the redial pressure but instead we assume new form of the metric potentials. We repeat our procedure done in the case of vanishing radial pressure and show in details that the new compact star is more realistic from different physical viewpoints of real compact stellar.

1 Introduction

To investigate the importance of astrophysics or astronomy with gravitational waves, the theory of general relativity (GR) plays an essential role in astrophysical systems like compact objects and radiation with high energy usually from strong gravity field around neutron stars and black holes [1].

Recently, observations show that our universe is experiencing cosmic acceleration. The existence of a peculiar energy component called dark energy (DE) controlling the universe is validated by many observations including type Ia supernovae (SNeIa), the Wilkinson Microwave Anisotropy Probe (WMAP) and the Planck in terms of the cosmic microwave background (CMB) radiation, the surveys of the large-scale structure (LSS) [2,3,4,5,6]. In terms of an equation of state for dark energy, $p=\omega \rho$, when $\omega <-1/3$ the accelerated expansion is realized, when $-1/3<\omega <-1$ we have quintessence regime, when $\omega <-1$ we have a phantom regime, and when $p=-\rho$ we have a gravastar (gravitational vacuum condensate star) [7,8,9,10,11,12,13]. Explanations for the properties of DE have proposed among those are: 1) Modifications of the cosmic energy by involving novel components of DE like a scalar field including quintessence [14, 15]. 2) Modifications of GR action to derive different kinds of amendment theories of gravity like f(T) gravity [16,17,18,19,20,21,22,23], where T is the torsion scalar in teleparallelism; f(R) gravity [24,25,26,27,28,29,30] with R the scalar curvature; f(G) gravity with G the Gauss-Bonnet invariant [31]; $f(R,{\mathcal {T}})$ gravity, where ${\mathcal T}$ the trace of the energy–momentum tensor of matter [32, 33]; $f(T,{\mathcal T})$ gravity, where T is the torsion scalar in teleparallelism and ${\mathcal T}$ the trace of the energy–momentum tensor of matter [34] etc. The Weitzenböck geometry is another formulation of GR whose dynamical variables are the tetrad fields defined as ${l^i}_\mu$. Here, at each point $x^\mu$ on a manifold, i is the orthonormal basis of the tangent space, and $\mu$ denotes the coordinate basis and both of the indices run from $0\cdots 3$. In Einstein’s GR the torsion is absent, and the gravitational field is described by curvature while in Weitzenböck geometry theory, the curvature is vanishing identically, and the gravitational field is described by torsion [35,36,37,38,39,40,41]. Fortunately, the two theories describe the gravitational field equivalently on the background of the Lagrangian up to a total divergence term [42,43,44,45].

Einstein’s cluster [46] is a spherically symmetric astrophysical solution discovered by Einstein to discuss stationary gravitating particles, each of which moves in a circular track around a common center under the effect of the gravitational field. When such particles rotate on the common track and have the same phases, they constitute a shell that is named “Einstein’s shell”. The construction layers of Einstein’s shell form Einstein’s cluster. The distribution of such a particle has spherical symmetry and it is continuous and random. These particles have collisionless geodesics. When the gravitational field is balanced by the centrifugal force, i.e., the radial pressure has a vanishing value, the above systems are said to be static and are in equilibrium form. A thick matter shell with spherical symmetry is constituted by the procedure described above. The resultant configuration has no radial pressure and there exists only its stress in the tangential direction. There are many studies of Einstein’s clusters in the literature [47,48,49,50]. For the spherically symmetric case the energy–momentum tensor has anisotropic form, i.e. ${T^0}_0=-\rho$, ${T^r}_r=p_r$, and ${T^\theta }_\theta ={T^\phi }_\phi =p_t$, where ${T^\mu }_\nu$ is the matter energy–momentum tensor, $\rho$ is the energy density, $p_r$ and $p_t$ are the radial and tangential pressures, respectively. By using the junction condition it can be found that the pressure in the radial direction vanishes for Einstein’s clusters. Recently, the compact objects filled with fluids with their anisotropy have been attracted many researchers and their structure and evolutional processes have been studied [51,52,53,54,55,56,57,58,59,60,61,62,63,64]. It is the aim of this study to apply a non-diagonal tetrad field that possesses spherical symmetry to the non-vacuum equation of motions of Weitzenböck geometry theory using some physically-motivated assumptions and try to derive novel models in this theory that are different from the unphysical models presented in the literature. We discuss the physical contents of our models and compare the results to the true stellar models.

The arrangement of this paper is as follows. In Sect. 2 we explain the basic formulae in terms of Weitzenböck geometry. In Sect. 3 the gravitational field equations for the Weitzenböck geometry theory in the non-vacuum background are applied to a non-diagonal tetrad and the non-zero components in terms of these differential equations are derived. The number of the differential equations with their non-linearity is found to be less than the number of unknowns. Therefore, we postulate two different assumptions and derive two novel solutions in this section. In Sect. 4 we discuss the physical contents of these two solutions and show that the second solution possesses many merits that make it physically acceptable. Among these things that make the second solution physically acceptable is that it satisfies the energy conditions, the TOV equation is satisfied, it has static stability and its adiabatic index is satisfied. However, this model has a vanishing value of the tangential pressure at the center of the star which makes it inconsistent with a real compact star. Therefore, in Sect. 5 we construct a new compact star abandoning the constrain of vanishing radial pressure and instead assume a new form of the metric potentials. We follow the same procedure done in the previous sections we derive a new model that is consistent with a real compact star in Sect. 5.

2 Basic formulae of Weitzenböck geometry

In this section, we describe the basic formulae of Weitzenböck geometry. The tetrad field ${l^i}_\mu$, covariant, and its inverse one $l_i{}^\mu$, contravariant, play a role of the fundamental variables for Weitzenböck geometry. These quantities satisfy the following relation In Sect. 6 discussions and conclusions of the present considerations are given.

$$\begin{aligned} \varvec{l_\nu } = l^i{}_\nu \varvec{l_i}, \quad \varvec{l_i} = l_i{}^\nu \varvec{l_\nu }. \end{aligned}$$

(1)

Based on the tetrads the metric tensor is defined by

$$\begin{aligned} g_{_{_{\mu \nu }}} = \eta _{ij} l^i{}_\mu l^j{}_\nu = \vec {l}_\mu \cdot \vec {l}_\nu . \end{aligned}$$

(2)

Here $\eta _{a b}$ denotes the Minkowski spacetime and it is given by $\eta _{a b}=diag(-1,+1,+1,+1)$. Moreover, $\vec {l}_\mu$ is the co-frame.

Using the above equations, one can easily prove the following identities:

$$\begin{aligned} \eta _{ij}&= g_{\mu \nu } l_i{}^\mu l_j{}^\nu =\vec {l}_i \cdot \vec {l}_j,&\eta ^{ij}&= g^{\mu \nu } l^i{}_\mu l^j{}_\nu , \end{aligned}$$

(3a)

$$\begin{aligned} g^{\mu \nu }&= \eta ^{ij} l_i{}^\mu l_j^{\nu },&l&= \sqrt{|g|}, \end{aligned}$$

(3b)

$$\begin{aligned} l^i{}_\mu l_i{}^\nu&= \delta ^\nu _\mu ,&l^i{}_\mu l_j{}^\mu&= \delta ^i_j . \end{aligned}$$

(3c)

With the spin connection the curvature quantity and the torsion one can be written as

$$\begin{aligned} R^{ij}{}_{\mu \nu }:= & {} \partial _\mu \omega ^{ij}{}_\nu -\partial _\nu \omega ^{ij}{}_\mu + \omega ^i{}_{s\mu } \omega ^{sj}{}_\nu - \omega ^i{}_{s\nu } \omega ^{sj}{}_\mu , \end{aligned}$$

(4)

$$\begin{aligned} T^i{}_{\mu \nu }:= & {} \partial _\mu l^i{}_\nu - \partial _\nu b^i{}_\mu + \omega ^i{}_{k\mu } l^k{}_\nu - \omega ^i{}_{k\nu }l^k{}_\mu , \end{aligned}$$

(5)

where $\omega ^{ij}{}_\nu$ is the spin connection. The matrices with the local Lorentz symmetry, $\Lambda ^a{}_b$, generates the spin connection as

$$\begin{aligned} \omega ^a{}_{b\mu } = \omega ^a{}_{b\mu }(\Lambda ) = \Lambda ^a{}_c \partial _\mu (\Lambda ^{-1})^c{}_{b},\quad \eta _{ab}\Lambda ^a{}_c\Lambda ^b{}_d = \eta _{cd} . \end{aligned}$$

(6)

The tensors $R^\mu {}_{\nu \rho \sigma }$ and $T^i{}_{\mu \nu }$ are defined as follows:

• (i) $R^\mu {}_{\nu \rho \sigma } = l_i{}^\mu l_{j\nu } R^{ij}{}_{\rho \sigma },$

• (ii) $l^i{}_\sigma T^\sigma {}_{\mu \nu } = T^i{}_{\mu \nu } .$

Using the above data one can define the torsion in terms of the derivative of tetrad and spin connection as

$$\begin{aligned} T^a{}_{\mu \nu } = 2 (\partial _{[\mu }l^a{}_{\nu ]} + \omega ^a{}_{b[\mu } l^b{}_{\nu ]} ) , \end{aligned}$$

(7)

where square brackets denote that the pair of indices are skew-symmetric and $\partial _\mu =\frac{\partial }{\partial x^\mu }$. In the Weitzenböck geometry theory, the spin connection is set to be zero ($\omega ^a{}_{b\mu }=0$). Therefore, the torsion tensor takes the form

$$\begin{aligned} T^a{}_{\mu \nu } = \partial _{[\mu }l^a{}_{\nu ]}. \end{aligned}$$

The Weitzenböck geometry theory is constructed by using the Lagrangian

$$\begin{aligned} L_{\mathrm{Weitzenb}\ddot{\mathrm{o}}\mathrm{ck geometry}}= \int \mathrm {d}^4x\ |l| \left( \frac{1}{2\kappa ^2} T + {\mathcal {L}}_\mathrm{m}(g,\Psi ) \right) , \end{aligned}$$

(8)

with $\kappa ^2=8\pi$. Here ${\mathcal {L}}_\mathrm{m}(g,\Psi )$ is the Lagrangian of matter with minimal coupling to gravitation through the metric tensor written with the tetrad fields. In addition, T is the torsion scalar and it is defined as

$$\begin{aligned} T&= T^a{}_{\mu \nu }S_a{}^{\mu \nu }n\nonumber \\&=\frac{1}{2} \Bigg (l_a{}^\sigma g^{\rho \mu } l_b{}^\nu + 2 l_b{}^\rho g^{\sigma \mu } l_a{}^\nu \nonumber \\&\quad + \frac{1}{2} \eta _{ab} g^{\mu \rho } g ^{\nu \sigma } \Bigg ) T^a{}_{\mu \nu } T^b{}_{\rho \sigma } . \end{aligned}$$

(9)

The superpotential $S_a{}^{\mu \nu }$ is defined as

$$\begin{aligned} S_a{}^{\mu \nu } = \frac{1}{2}(K^{\mu \nu }{}_a - h_a{}^\mu T_\lambda {}^{\lambda \nu } + h_a{}^\nu T_\lambda {}^{\lambda \mu }), \end{aligned}$$

with $K^{\mu \nu }{}_a$ the contortion tensor, expressed by

$$\begin{aligned} K^{\mu \nu }{}_a = \frac{1}{2}(T^{\nu \mu }{}_a + T_a{}^{\mu \nu } - T^{\mu \nu }{}_a) . \end{aligned}$$

Variation of the Lagrangian (8) with respect to a tetrad $l^a{}_\mu$ yields [65, 66]

$$\begin{aligned} \frac{1}{4}T l_a{}^\mu + T^b{}_{\nu a} S_b{}^{\mu \nu } + \frac{1}{l}\partial _{\nu }(l S_a{}^{\mu \nu })&= \frac{1}{2}\kappa ^2 \Theta _a{}^\mu . \end{aligned}$$

(10)

The stress-energy tensor, $\Theta _a{}^\mu$, is the energy–momentum tensor for fluids whose configuration has anisotropy and it is represented by

$$\begin{aligned}&\Theta _a{}^\mu {}=(p_t+\rho )u^\mu u_a+p_t\delta _a{}^\mu +(p_r-p_t)\xi _a \xi ^\mu , \end{aligned}$$

(11)

with $u_\mu$ the time-like vector defined as $u^\mu =[1,0,0,0]$ and $\xi _\mu$ the unit radial vector with its space-like property, defined by $\xi ^\mu =[0,1,0,0]$ such that $u^\mu u_\mu =-\,1$ and $\xi ^\mu \xi _\mu =1$. Here $\rho$ means the energy density, $p_r$ and $p_t$ are the radial and tangential pressures, respectively.

3 Neutral compact stars

In this section, we adopt the gravitational field equation (10) to the tetrad with its spherical symmetry, which represents a dense compact relativistic star.

Based on the spherical coordinates $(t,r,\theta , \phi )$, the metric with its spherical symmetry is given by

$$\begin{aligned} ds^2= & {} -e^{\mu (r)} \,dt^2+e^{\nu (r)}dr^2+r^2d\Omega ^2 , \nonumber \\ d\Omega ^2= & {} (d\theta ^2+\sin ^2\theta d\phi ^2) , \end{aligned}$$

(12)

where $\mu (r)$ and $\nu (r)$ are the functions of r in the radial direction. This line element in Eq. (12) can be reproduced from the following tetrad field  [67]:

$$\begin{aligned}&l^a{}_{\mu }\nonumber \\&\quad =\left( \begin{array}{cccc} e^{\mu (r)/2} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\nu (r)/2} \cos (\phi ) \sin (\theta ) &{} r \cos (\phi ) \cos (\theta ) &{} -r \sin (\phi ) \sin (\theta ) \\ 0 &{} e^{\nu (r)/2} \sin (\phi ) \sin (\theta ) &{} r \sin (\phi ) \cos (\theta ) &{} r \cos (\phi ) \sin (\theta ) \\ 0 &{} e^{\nu (r)/2} \cos (\theta ) &{} -r \sin (\theta ) &{} 0 \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(13)

We mention that the tetrad (13) is an output product of a diagonal tetrad and local Lorentz transformation, i.e., one can write it as

$$\begin{aligned}&l^a{}_{\mu }=\Lambda ^a{}_b l^b{}_{\mu _{diag}}\nonumber \\&\quad \Rightarrow \left( \begin{array}{cccc} e^{\mu (r)/2} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\nu (r)/2} \cos (\phi ) \sin (\theta ) &{} r \cos (\phi ) \cos (\theta ) &{} -r \sin (\phi ) \sin (\theta ) \\ 0 &{} e^{\nu (r)/2}\sin (\phi ) \sin (\theta ) &{} r \sin (\phi ) \cos (\theta ) &{} r \cos (\phi ) \sin (\theta ) \\ 0 &{} e^{\nu (r)/2} \cos (\theta ) &{} -r \sin (\theta ) &{} 0 \\ \end{array} \right) \nonumber \\&\quad \equiv \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} \cos (\phi ) \sin (\theta ) &{} \cos (\phi ) \cos (\theta ) &{} - \sin (\phi ) \\ 0 &{} \sin (\phi ) \sin (\theta ) &{} \sin (\phi ) \cos (\theta ) &{} \cos (\phi ) \\ 0 &{}\cos (\theta ) &{} -\sin (\theta ) &{} 0 \\ \end{array} \right) \nonumber \\&\qquad \times \left( \begin{array}{cccc} e^{\mu (r)/2} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\nu (r)/2} &{} 0 &{} 0 \\ 0 &{} 0 &{} r &{} 0 \\ 0 &{}0 &{} 0 &{} r \sin (\theta ) \\ \end{array} \right) . \end{aligned}$$

(14)

Using Eq. (13) in Eq. (9) the torsion scalar takes the form

$$\begin{aligned} T= \frac{2e^{-\nu } [e^{\nu }-e^{\nu /2}(2+r\mu ')+1+r\mu ' ]}{r^2} . \end{aligned}$$

(15)

It follows from Eq. (15) that T vanishes in the limit $\mu =\nu \rightarrow 0$ unlike what has been studied before in the literature [67].¹ Using Eq. (15) in the field equations (10) we get

$$\begin{aligned} 8\pi \rho= & {} \frac{1-e^{-\nu }(1-r\nu ')}{r^2} ,\nonumber \\ 8\pi p_r= & {} \frac{e^{-\nu }(1+r\mu ')-1}{r^2} ,\nonumber \\ 8\pi p_t= & {} \frac{e^{-\nu } [2r\mu ''+(r\mu '+2)(\mu '-\nu ')]}{4r} , \end{aligned}$$

(16)

where $'$ denotes derivatives w.r.t. r. These differential equations are three independent equations in five unknowns: $\mu$, $\nu$ and $\rho$, $p_r$ and $p_t$. Therefore, we need extra conditions to be able to solve the above system. The extra conditions are the zero radial pressure, namely, $p_r=0$ [68, 69], and assuming the equation of state (EoS) in terms of the energy density and the tangential pressure. We can represent these conditions as

$$\begin{aligned} p_r=0, \quad p_t=\omega _t \rho , \end{aligned}$$

(17)

where $\omega _t$ is the EoS parameter for anisotropic fluids.

Substituting Eq. (17) into (16) we obtain

$$\begin{aligned}&\rho =\frac{\omega _t}{2\pi r^2(1+4\omega _t)}, \quad \mu =4\omega _t\ln (r)+c_1, \nonumber \\&\nu =\ln (4\omega _t+1), \quad p_t=\omega _t \rho , \nonumber \\&\rho =0, \quad \mu =\ln \Bigg (\frac{c_3r-c_2}{r}\Bigg ), \nonumber \\&\nu =\ln \Bigg (\frac{rc_3}{c_3r-c_2}\Bigg ), \quad p_t=0 . \end{aligned}$$

(18)

The main reason why the tangential pressure, as well as the energy density, vanish as in the second set of Eq. (18) is due to the composition of the two unknown functions $\mu$ and $\nu$ that give the Schwarzschild solution.

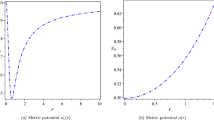
Another solution that can be derived from Eq. (16) is through the assumption on the unknown function $\mu$ to have the form [69]

$$\begin{aligned} \mu (r)=\ln (b_0+b_1r^2+b_2r^4) . \end{aligned}$$

(19)

This assumption together with the vanishing of the radial pressure give new solution in the framework of Weitzenböck geometry theory. Using Eq. (19) in (16) we get the remaining unknown functions in the form

$$\begin{aligned}&\rho =\frac{(3b_1+10b_2r^2)(b_0+b_1r^2+b_2r^4)}{4\pi (b_0+3b_1r^2+5b_2r^4)^2}, \nonumber \\&\nu =\ln \Bigg (\frac{b_0+3b_1r^2+5b_2r^4}{b_0+b_1r^2+b_2r^4}\Bigg ) , \nonumber \\&p_t=\frac{r^2(b_1[3b_1+16b_2r^2]+20b_2{}^2r^4)}{8\pi (b_0+3b_1r^2+5b_2r^4)^2} . \end{aligned}$$

(20)

The authors of Ref. [69] applied tetrad (13) to the field equations of pure GR. Our results are coincide with their results but when they interpretable the physics of tangential pressure they find that it increase forever however, in this study and according to the suitable choice of the constants $b_0$, $b_1$ and $b_2$ we show that the tangential pressure is increase in a short distance and then turn to decrease.

The EoS of the first and second solutions given by Eqs. (18) and (20) takes the form

$$\begin{aligned} \omega _{t_{1}}=1 , \quad \omega _{t_{2}}=\frac{r^2(b_1+2b_2r^2)}{2(b_0+b_1r^2+b_2r^4)} . \end{aligned}$$

(21)

The first EoS shows that we have a stiff matter while the behavior of the second EoS is shown in Fig. 2c below which shows behavior less than a unit which describes a physical matter.

The behavior of the density and tangential pressure of the first and second solutions are drawn in Fig. 1. Figure 1a, b which show that energy and pressure decrease as the radial coordinate r increases. For the second solution, Fig. 2a–c show that the energy density and pressure decrease as the radial coordinate r increases.² The dominator of Eq. (21) has only two real solutions that have the form

$$\begin{aligned} \pm \frac{\sqrt{\sqrt{b_1{}^2-4b_0b_2}-b_1}}{\sqrt{2b_2}}, \quad b_2>0.\end{aligned}$$

(22)

Equation (22) ensures that the parameter $b_2\ne 0$, must be positive and $b_1>\pm 2\sqrt{b_0b_2}$ which are consistent with the values given in Fig. 2c and through the whole of the present study.

Fig. 1

Schematic plot of the radial coordinate r in the unit of km versus the energy density and pressure of the solution (18)

Fig. 2

Schematic plot of the radial coordinate r in the unit of km versus the energy density, pressure and the EoS of the solution (20) when $b_0=0.0001$ and $b_1=0.01$

We consider the physical contents for the first and second solutions. To this end, we are going to calculate the following quantities. The surface red-shift of the first and second solutions takes the form:

$$\begin{aligned} z_{s_{1}}=e^{\nu _s}-1=4\omega _{t_{1}} , \quad z_{s_{2}}=\frac{2r^2(b_1+2b_2r^2)}{b_0+b_1r^2+b_2r^4} . \end{aligned}$$

(23)

The behavior of the surface red-shift of the second solution is identical with the behavior of the EoS, as shown in Fig. 2c, because the two forms are identical up to some constant.

The gravitational mass of a spherically symmetric source with the radial dependence r is expressed by [69]

$$\begin{aligned}&m(r)=4\pi {\int _0}^r \rho (\xi ) \xi ^2 d\xi , \end{aligned}$$

(24)

which gives for solutions (18) and (20) the form

$$\begin{aligned}&m_1(r)=\frac{2\omega _{t_{1}} r}{4\omega _{t{1}}+1} ,\nonumber \\&m_2(r)=\frac{20b_2r^3(b_1+2b_2 r^2)}{(3b_1+10b_2r^2)^2-9b_1{}^2+20b_0b_2} . \end{aligned}$$

(25)

The behavior of the gravitational mass of solutions (18) and (20) are drawn in Fig. 3a, b. These figures show the gravitational mass increases with the radial coordinate. The compactness parameter of a source with its spherical symmetry in terms of the radius, r takes the form [69]

$$\begin{aligned}&u(r)=\frac{2m(r)}{r} ,\nonumber \\&\text {that gives for solutions}\, (18)\, \text {and}\, (20)\, \text {the form} \nonumber \\&u_1(r)=\frac{4\omega _{t_{1}}}{4\omega _{t_{1}}+1} ,\nonumber \\&u_2(r)=\frac{20r^2(b_1+2b_2 r^2)}{(3b_0+10b_2r^2)^2-9b1^2+20b_0b_2}. \end{aligned}$$

(26)

Fig. 3

Schematic plot of the gravitational mass of solutions (18) and (20) and compactness parameter versus the radial coordinate r in km when $b_0=0.0001$ and $b_1=0.01$

We show the behavior of compactness parameter of solution (20), we did not draw solution (18) because it gives a constant value, in Fig. 3c. As Fig. 3b, c show that solution (20) is a regular well-behaved because both mass function and compactness vanishes at r = 0.

The gradient of density and pressure of (18) and (20) take the form [69]

$$\begin{aligned}&d\rho _1=-\frac{\omega _t}{2\pi r^3(1+4\omega _t)} ,\quad dp_{{t_1}}=-\frac{\omega ^2_t}{2\pi r^3(1+4\omega _t)} ,\nonumber \\&d\rho _2=-\frac{r(8b_0b_2r^2[8b_1+15b_2r^2]-10b_0^2b_2+5b_1b_2r^4[9b_1+20b_2r^2]+15b_0b_2^2+r^2[9b_1^3+50b_2^3r^6])}{2\pi (b_0+3b_1r^2+5b_2r^4)^3} ,\nonumber \\&dp_{{t_2}}=\frac{r(3b_0[b_1^2+20b_2^2r^4]-9b_1^2r^2[b_1+5b_2r^2]-100b_2{}^2r^6[b_1+b_2r^2]+32b_0b_1b_2r^2)}{4\pi (b_0+3b_1r^2+5b_2r^4)^3} . \end{aligned}$$

(27)

The derivative of the tangential pressure of Eq. (27), $dp_{{t_2}}$, is different from the one given in [69] because the tangential pressures themselves are different.

Fig. 4

Variation of the gradient of density and pressure of (18) and (20) against r in km when $b_0=0.0001$ and $b_1=0.01$

Figure 4, shows that for solutions (18) and (20) we have always negative gradient for density and pressure.

Finally, the speed of sound of (18) and (20) take the form [69]

$$\begin{aligned}&v_t^2=\frac{dp_{{t}}}{d\rho } , \quad \text {that gives for solutions}\, (18)\, \text {and}\, (20)\, \text {the form} \nonumber \\&v_{{t_1}}^2=\omega _t ,\quad v_{{t_2}}^2=\frac{3b_0[b_1^2+20b_2^2r^4]-9b_1^2r^2[b_1+5b_2r^2]-100b_2{}^2r^6[b_1+b_2r^2]+32b_0b_1b_2r^2}{10b_0^2b_2-8b_0b_2r^2[8b_1+15b_2r^2]-5b_1b_2r^4[9b_1+20b_2r^2]-15b_0b_2^2-r^2[9b_1^3+50b_2^3r^6]} .\nonumber \\ \end{aligned}$$

(28)

We discuss the property of the speed of the sound of the second solution because the first one gives a constant, which depends on the EoS parameter. Usually, the sound velocity must be less than the light speed [69]. Hence, in relativistic units, the sound speed must be less than or equal to unity. Thus, for the first solution, to give the sound speed less than or equal to unity, we must have $\omega _t \le 1$. As Fig. 5 shows for solution (20), we have speed of sound less than 1 when the parameters $b_1=10^{-4}$ and $b_1=10^{-2}$.

4 Physics of the compact stars (18) and (20)

In this section, we explore the physical consequences for the first and second solutions given by Eqs. (18) and (20). To this end, first, we are going to determine the values of the constants appearing in these solutions.

4.1 Matching of boundary

We compare the solution within the compact objects with the Schwarzschild vacuum solution outside it. We use the first solution in Eq. (18) with the Schwarzschild one, i.e.,

$$\begin{aligned} ds^2= -\Big (1-\frac{2M}{r}\Big )dt^2+\Big (1-\frac{2M}{r}\Big )^{-1}dr^2+r^2d\Omega ^2.\nonumber \\ \end{aligned}$$

(29)

This yields the following matching conditions:

$$\begin{aligned}&1-\frac{2M}{{\mathcal {R}}}=4\omega _t\ln ({\mathcal {R}})+c_1 ,\nonumber \\&\frac{1}{1-\frac{2M}{{\mathcal {R}}}}=\ln (4\omega _t+1) , \end{aligned}$$

(30)

where ${\mathcal {R}}$ is the radius at the boundary, i.e., at the boundary $r ={\mathcal {R}}$. Solving for $\omega _t$ and $c_1$ from Eq. (30), we obtain

$$\begin{aligned}&\omega _t = \frac{e^{\frac{1}{1-\frac{2M}{{\mathcal {R}}}}}-1}{4}\, ,\quad \text {and } \nonumber \\&c_1=\frac{{{\mathcal {R}}}-2M+{\mathcal {R}}\ln \,{{\mathcal {R}}} -{{\mathcal {R}}}\ln \, {{\mathcal {R}}} {e^{\frac{1}{(1-\frac{2M}{{\mathcal {R}}})}}}}{\mathcal {R}}. \end{aligned}$$

(31)

Here M and ${\mathcal {R}}$ are determined by the observations of the compact objects. Applying the same procedure to the second solution (20) we get

$$\begin{aligned}&b_0 = \frac{{\mathcal {R}}(1+b_2{\mathcal {R}}^4)-3M}{{\mathcal {R}}} ,\quad b_1= \frac{M-2b_2{\mathcal {R}}^5}{{\mathcal {R}}^3} , \end{aligned}$$

(32)

where $b_2$ is tackled by the data fitting and the values of M and ${\mathcal {R}}$ are selected from the observations of the compact objects. The matching condition given by Eq. (32) is different from the one presented in [69] because in this study the constant $b_2$ is left arbitrary while in [69] they leave $b_1$ as an arbitrary.

Fig. 5

Speed of sound of (20) against r in km when $b_0=0.0001$ and $b_1=0.01$

4.2 Energy conditions for compact stars

In general, for perfect fluid models, the energy conditions described by the relation between the energy density and pressure can be satisfied. We check strong (SEC), weak (WEC), dominant (DEC), and finally null (NEC) energy conditions, given by

$$\begin{aligned}&\text {SEC:} \rho +2p_t\ge 0 , \quad \text {NEC:} \rho +p_t\ge 0 ,\nonumber \\&\text {WEC:} \rho \ge 0, \quad \rho +p_t\ge 0 , \quad \text {DEC:} \rho \ge \mid p_t\mid . \end{aligned}$$

(33)

By using Eqs. (18) and (20), one can easily show that the above conditions are satisfied as indicated in Fig. 6a, b.

Fig. 6

The energy conditions of solutions (18) and (20) against r in km when $b_0=0.0001$ and $b_1=0.01$

4.3 Tolman–Oppenheimer–Volkoff equation and the analyses of the equilibrium

In this subsection, we investigate how stable the models of Einstein’s clusters are. We assume the equilibrium of the hydrostatic state. Through the TOV equation [70, 71] as that presented in [72], we acquire the equation

$$\begin{aligned} \frac{2p_t(r)}{r}-\frac{M_g(r)\rho (r)e^{(\mu -\nu )/2}}{r}=0 , \end{aligned}$$

(34)

where $M_g(r)$ is the gravitational mass as a function of r, which is defined by the Tolman-Whittaker mass formula as

$$\begin{aligned} M_g(r)= & {} 4\pi {\int _0}^r ({T_t}^t-{T_r}^r-{T_\theta }^\theta -{T_\phi }^\phi )r^2e^{(\mu +\nu )/2}dr\nonumber \\= & {} \frac{re^{(\nu -\mu )/2}\mu '}{2} . \end{aligned}$$

(35)

Using Eq. (35) in (34) we get

$$\begin{aligned} \frac{2p_t(r)}{r}-\frac{\mu '\rho (r)}{2}=F_g+F_a=0 , \end{aligned}$$

(36)

with $F_g=-\frac{\mu '\rho (r)}{2}$ being the gravitational force and $F_a=\frac{2p_t(r)}{r}$ is the anisotropic force. The behaviors of the TOV equations of solutions (18) and (20) are shown in Fig. 7a, b, respectively.

Fig. 7

TOV solutions (18) and (20) against r in km when $b_0=0.0001$ and $b_1=0.01$

4.4 Relativistic adiabatic index and stability analysis

Our particular interest is to study the stable equilibrium configuration of a spherically symmetric cluster and the adiabatic index which is a basic ingredient of the stable/unstable criterion. Now considering an adiabatic perturbation, the adiabatic index $\Gamma$ is defined as [73,74,75]

$$\begin{aligned} \Gamma =\frac{\rho +p_t}{p_t}\frac{dp_t}{d\rho } , \end{aligned}$$

(37)

with $\frac{dp_t}{d\rho }$ being the speed of sound. Using Eq. (37) we get the adiabatic index of the two solutions (18) and (20) in the form:

$$\begin{aligned}&\Gamma _1=1+\omega _{t1} , \nonumber \\&\Gamma _2=\frac{(2b_0+3b_1r^2+4b_2r^4)(3b_0b_1{}^2-45b_1{}^2b_2r^4-100b_1b_2{}^2r^6+32b_0b_1b_2r^2-100b_2{}^3r^8+ 60b_0b_2{}^2r^4-9b_1{}^3r^2)}{2r^2(b_1+2b_2r^2)(10b_0{}^2b_2-64b_0b_1b_2r^2-120b_0b_2{}^2r^4-45b_1{}^2b_2r^4-100b_1b_2{}^2r^6 -50b_2{}^3r^8-15b_0b_1{}^2-9b_1{}^3r^2)} .\nonumber \\ \end{aligned}$$

(38)

The first set of Eq. (38) is always larger than or equal to unity, depending on the value of EoS of $\omega _{t1}$. The behavior of the second set of Eq. (38) is shown in Fig. 8. From this figure, we can see that the adiabatic index is always larger than unity and its value depends on the parameters $b_0$, $b_1$ and $b_2$.

Fig. 8

Adiabatic index of (20) against r in km when $b_0=0.0001$, $b_1=0.01$ for different values of the $b_2$ parameter. Note that the larger the value of $b_0$, the bigger the amplitude of adiabatic index

It has been found by Bondi [76] that in the case of non-charged equilibrium, $\Gamma = 4/3$ for the stable Newtonian sphere which is satisfied for the second solution given by Eq. (20).

4.5 Stability in the static state

For stable compact stars, in terms of the mass-central as well as mass-radius relations for the energy density, Harrison, Zeldovich and Novikov [77,78,79] claimed that the gradient of the central density with respect to mass must be positive, i.e., $\frac{\partial M}{\partial \rho _{r_0}}> 0$. If this condition is satisfied then we have stable configurations. To be more specific, stable or unstable region is satisfied for constant mass i.e. $\frac{\partial M}{\partial \rho _{r_0}}= 0$ [69]. Let us apply this procedure to our solutions (18) and (20). To this end, we calculate the central density for both solutions. For solution (18) the central density is undefined so we will exclude this case from our consideration because it may represent an unstable configuration. As for the second solution, the central density has the form

$$\begin{aligned}&\rho _{r_0}=\frac{3b_1}{4\pi b_0} \Rightarrow b_1=\frac{4 \pi b_0 \rho _{r_0}}{3},\nonumber \\&M(\rho _{r_0})=\frac{2 R^3 (3b_2R^2+2b_0\pi \rho _{r_0})}{3(b_0+4\pi b_0R^2\rho _{r_0}+5 b_2 R^4)} . \end{aligned}$$

(39)

With Eq. (39) we have

$$\begin{aligned} \frac{\partial M}{\partial \rho _{r_0}}=\frac{4\pi b_0R^3(b_0-b_2 R^4)}{3(b_0+4\pi b_0R^2\rho _{r_0}+5 b_2 R^4)^2} . \end{aligned}$$

(40)

From Eq. (40), it is seen that the solution (20) has a stable configuration since $\frac{\partial M}{\partial \rho _{r_0}}> 0$ [69]. The behavior of (39) and (40) are shown in Fig. 9. It follows from this figure that the mass increases as the energy density become larger and the gradient of mass decreases as energy density becomes larger. All the above discussion of solution (20) shows that we have a good model except the defect of vanishing tangential pressure at the center of the star. Therefore, we can say that in the frame of Einstein’s theory we can not get a real compact star when we assume the vanishing of the radial pressure. In the next section, we will leave the condition of vanishing radial coordinate and try to assume another physical constrain and study if the born model is physically acceptable or it has some defects.

Fig. 9

Static stability of (20) against $\rho _{r_0}$ in $\mathrm {km}^{-3}$ when $b_0=b_2=0.0001, R=0.1$

5 Real compact star

In Sect. (3) we solved the differential equations (16) by assuming the vanishing of the radial pressure and got a model that is not consistent with a real compact star because the tangential pressure has a vanishing value at the center. In this section, we are going to solve the system of differential equations (16) abandoning the vanishing of radial pressure and assume instead the metric potentials to have the form

$$\begin{aligned} \mu =-2\ln (a_1-r^2a_0), \quad \nu =-2\ln (1+a_0r^2) , \end{aligned}$$

(41)

with $a_0$ and $a_1$ are constants that will determined from the matching condition. Using Eq. (41) in (16) we get

$$\begin{aligned}&\rho =-\frac{a_0(6+5a_1r^2)}{8\pi }, \nonumber \\&p_r=\frac{a_0(4+6a_0r^2+3a_0{}^2r^4+2a_1+a_0a_1r^2)}{8\pi (a_1-a_0r^2)} ,\nonumber \\&p_t=\frac{a_0(2a_0r^2+a_0{}^2r^4+2a_1+2a_0a_1r^2+a_1{}^2)}{8\pi (a_1-a_0r^2)^2} . \end{aligned}$$

(42)

The behavior of density, radial and tangential pressures of Eq. (42) is draw in Fig. 10a which shows a physical content of compact star. The EoS of solution (42) takes the form

$$\begin{aligned} \omega _{r}&=\frac{4+6a_0r^2+3a_0{}^2r^4+2a_1+a_0a_1r^2}{(a_0r^2-a_1)(6+5a_0r^2)} ,\nonumber \\ \omega _{t}&=\frac{2(1+a_0r^2)(a_1{}^2+2a_0a_1r^2+2a_1+a_0{}^2r^4+2a_0r^2)}{(a_1-a_0r^2)^2(6+5a_0r^2)} . \end{aligned}$$

(43)

The behavior of the EoS (42) is shown in Fig. 10b which shows a positive EoS within a range of 1 which describes a physical well-known matter.

Fig. 10

Schematic plot of the radial coordinate r in the unit of km versus: a the energy density, (a)of solution (42), b the EoS (43) which shows a physical content of matter for the stellar 4U1608–52 whose mass $1.74\pm 0.14$ and its radius $9.52\pm 0.15$

Using Eq. (23) we calculate the surface red-shift of solution (42) and get:

$$\begin{aligned} Z_s=-\frac{a_0r^2(2+a_0r^2)}{(1+a_0r^2)^2} . \end{aligned}$$

(44)

The behavior of the surface red-shift of Eq. (44) is draw in Fig. 11a which indicates that it is consistent with the constrain of Böhmer and Harko that $Z_s< 5$ [80]. The surface red-shift of this model is calculated according to the stellar 4U1608–52 and found to have 0.6362098138. Using Eq. (26) we get the gravitational mass as

$$\begin{aligned} m(r)=-\frac{a_0r^3(2+a_0r^2)}{2}. \end{aligned}$$

(45)

The behavior of the gravitational mass of Eq. (45) and the compactness $u(r)=2m(r)/r$ are draw in Fig. 11b which shows that solution (42) is a regular well-behaved because both mass function and compactness vanishes at $r=0$ [69].

Fig. 11

Schematic plot of the radial coordinate r in the unit of km versus: a surface red-shift of Eq. (44), b mass and compactness using the stellar 4U1608–52

The gradient of density and pressure of (42) take the form [69]

$$\begin{aligned}&d\rho _2=-\frac{5a_0{}^2r}{4\pi },dp_{r}=-\frac{a_0{}^2r(3a_0{}^2r^4-a_1{}^2-4-8a_1-6a_0a_1r^2)}{4\pi (a_1-a_0{}^2r^2)^2} ,\nonumber \\&dp_{t}=-\frac{a_0{}^2r(6a_1+2a_0r^2+10a_0a_1r^2+6a_1{}^2+5a_0a_1{}^2r^2+3a_1a_0{}^2r^4+a_1{}^3-a_0{}^3r^6)}{2\pi (a_0{}^2r^2-a_1)^3}\, . \end{aligned}$$

(46)

Fig. 12

Schematic plot of the radial coordinate r in the unit of km versus: a the gradient of density, radial and tangential pressures of (42) which ensure that all of them have negative values, b the radial and tangential sound speed which have values less than one in the relativistic unit, c the SEC, WEC, NEC and DEC, d the gravitational, the anisotropic and the hydrostatic forces

Figure 12a shows that for solutions (42) we have always negative gradient for density, radial and tangential pressures as is required for any real stellar.

The speed of sound of solution (42) takes the form [69]

$$\begin{aligned} v_{{r}}^2= & {} \frac{dp_{{r}}}{d\rho }=\frac{3a_0{}^2r^4-4-a_1{}^2-8a_1-6a_0a_1r^2}{5(a_1-a_0{}^2r^2)^2} , \nonumber \\ v_{{t}}^2= & {} \frac{dp_{{t}}}{d\rho }=\frac{2(a_0{}^3r^6-6a_1{}^2-5a_0a_1{}^2r^2-3a_0{}^2a_1r^4-a_1{}^3-6a_1-2a_0r^2-10a_0a_1r^2)}{5(a_1-a_0{}^2r^2)^3} . \end{aligned}$$

(47)

It is well known that the sound velocity must be less than the light speed [69]. Hence, in relativistic units, the sound speed must be less than or equal to unity which is satisfied for solution (42) as Fig. 12b shows.

5.1 Matching of boundary of solution (42)

Comparing solution (42) with the Schwarzschild vacuum solution outside which yields the following matching conditions:

$$\begin{aligned} 1-\frac{2M}{{\mathcal {R}}}= & {} \frac{1}{(a_1-a_0r^2)^2} ,\nonumber \\ \frac{1}{1-\frac{2M}{{\mathcal {R}}}}= & {} \frac{1}{(1+a_0r^2)^2}\, , \end{aligned}$$

(48)

where ${\mathcal {R}}$ is the radius at the boundary, i.e., at the boundary. Solving Eq. (48) for $a_0$ and $a_1$ we obtain

$$\begin{aligned} a_0= & {} \frac{\sqrt{{\mathcal {R}}^2-2M{\mathcal {R}}}-{\mathcal {R}}}{{\mathcal {R}}^3} ,\quad \text {and }\nonumber \\ a_1= & {} \frac{[{\mathcal {R}}-{\mathcal { R}}^2-2M]-\sqrt{{\mathcal {R}}^2-2M{\mathcal {R}}}}{\sqrt{{\mathcal {R}}^2-2M{\mathcal {R}}}}. \end{aligned}$$

(49)

Here M and ${\mathcal {R}}$ are determined by the observations of the compact objects. Now we are going to test if solution (42) satisfies the energy conditions list in Eq. (33). For this aim we use Eq. (42) in Eq. (33) and draw the behavior of these conditions in 12c which ensures that it satisfied these conditions for the stellar 4U1608–52.

Using the TOV equation [70, 71] as that presented in [72], we get the following form

$$\begin{aligned} \frac{2[p_t-p_r]}{r}-\frac{M_g(r)[\rho (r)+p_r]e^{(\mu -\nu )/2}}{r}-\frac{dp_r}{r}=0, \end{aligned}$$

(50)

with $M_g(r)$ being the gravitational mass at radius r, as defined by the Tolman-Whittaker mass formula which gives

$$\begin{aligned} M_g(r)= & {} 4\pi {\int _0}^r ({T_t}^t-{T_r}^r-{T_\theta }^\theta -{T_\phi }^\phi )r^2e^{(\mu +\nu )/2}dr\nonumber \\= & {} \frac{r\mu 'e^{\nu /2-\mu }}{2} , \end{aligned}$$

(51)

Inserting Eq. (51) into (50), we get

$$\begin{aligned} \frac{2(p_t-p_r)}{r}-\frac{dp_r}{dr}-\frac{\mu 'e^{\mu /2}[\rho (r)+p_r]}{2\sqrt{G}}= & {} F_g+F_a+F_h\nonumber \\= & {} 0 , \end{aligned}$$

(52)

where $F_g=-\frac{\mu 'e^{\mu /2}[\rho (r)+p_r]}{2}$, $F_a=\frac{2(p_t-p_r)}{r}$ and $F_h=-\frac{dp_r}{dr}$ are the gravitational, the anisotropic and the hydrostatic forces respectively. The behavior of the TOV equation for the model (42) is shown in Fig. 12d for the stellar 4U1608–52.

Now considering an adiabatic perturbation, the adiabatic index $\Gamma$ is defined by Eq. (37) which gives the adiabatic index of solution (42) in the form:

$$\begin{aligned} \Gamma= & {} \frac{1}{5} \{(6a_1+2a_0r^2+10a_0a_1r^2-a_0{}^3r^6\nonumber \\&+6a_1{}^2+5a_0a_1{}^2r^2+3a_1a_0{}^2r^4+a_1{}^3)\nonumber \\&(4a_1{}^2+3a_0a_1{}^2r^2-20a_0a_1r^2 -14a_1a_0{}^2r^4\nonumber \\&+3a_0{}^3r^6-4a_0r^2-4a_1 )[(1+a_0r^2)(a_1-a_0r^2)^3\nonumber \\&(2a_0r^2+a_0{}^2r^4+2a_1+2a_0a_1r^2+a_1{}^2)]^{-1} \} . \end{aligned}$$

(53)

The behavior of Eq. (53) is shown in Fig. 13a. From this figure, we can see that the adiabatic index is always larger than 4/3 as required by by Bondi [76].

Fig. 13

Schematic plot of the radial coordinate r in the unit of km versus: a the adiabatic index of Eq. (42) which ensure that $\Gamma >3/4$, b the mass as a function of central density and its gradient w.r.t. central density for stellar 4U1608–52

Finally, we are going to check if the gradient of the central density concerning mass is positive or not, i.e., $\frac{\partial M}{\partial \rho _{r_0}}> 0$ [69]. For this aim, we calculate the central density of solution (42) and get

$$\begin{aligned}&\rho _{r_0}=-\frac{3a_0}{4\pi } \Rightarrow a_0=-\frac{4 \pi \rho _{r_0}}{3},\nonumber \\&M(\rho _{r_0})=\frac{4\pi \rho _{r_0} R^3 (3-2\pi R^2 \rho _{r_0})}{9} . \end{aligned}$$

(54)

With Eq. (54) we get

$$\begin{aligned} \frac{\partial M}{\partial \rho _{r_0}}=\frac{4\pi R^3(3-4\pi \rho _{r_0} R^2)}{9} . \end{aligned}$$

(55)

From Eq. (55), it is seen that the solution (42) has a stable configuration since $\frac{\partial M}{\partial \rho _{r_0}}> 0$ [69]. The behavior of Eqs. (54) and (55) are shown in Fig. 13b. It follows from this figure that the mass increases as the energy density becomes larger and the gradient of mass is always positive.

6 Discussions and conclusions

In this study, we have explored and discussed the model of compact stars which mimic clusters of Weitzenböck geometry. The non-vacuum gravitational field equations have been applied to a tetrad field having non-diagonal components and has two unknown functions, $\mu$ and $\nu$. We have derived a set of three differential equations having five unknown quantities: $\mu$, $\nu$, $\rho$, $p_r$, and $p_t$. To be able to solve this system, we have put the radial pressure equal to zero [68, 69] in addition to two different assumptions:

• In our first assumption we have taken an EoS between the density and the tangential pressure in the form $p_t=\omega _{{t_1}} \rho$. By using the vanishing of the pressure in the radial direction and the EoS parameter, we have solved the set of differential equations and obtained two different solutions. One of these solutions is just the Schwarzschild exterior solution and we excluded it and the other one gave the unknown functions $\mu$, $\nu$, $\rho$ depending on the radial coordinate r, the parameter of EoS $\omega _{{t_1}}$ and on a constant of integration. We have studied the physics of this solution and shown that it has a positive density and pressure and a positive gravitational mass as shown in Figs. 1a, b and 3a. We have found that the speed of sound depends on the parameter of EoS, $\omega _t$ which should be less than one, i.e., $\omega _t\le 1$ [69]. We have also studied the boundary condition, i.e., matching our solution on the boundary with the exterior Schwarzschild solution, we derived the relations between the EoS parameter, the constant of integration, and the gravitational mass of Schwarzschild and its radius at the boundary. Moreover, we showed that this solution satisfies all the energy conditions, i.e., SEC, WEC, DEC, and NEC. As shown in Fig. 7a, this solution satisfies the TOV equation. Finally, we have demonstrated that the adiabatic index of this solution is satisfied provided that $\omega _t\ge 1/3$ has $\Gamma \ge 4/3$ [69]. The problem of this model is that it depends on the tangential EoS $\omega _t$ and this is not familiar in the literature.

• In the second assumption, we have used a specific form of the metric potential, $\mu$, that has three constants and derived the other unknown functions $\nu$, $\rho$ ad $p_t$. our results for the functions $\nu$, $\partial _t$ and $\rho$ are coincide with the results given in the literature. As a result, many aspects like the derivative of the tangential pressure, the matching conditions, the energy conditions, TOV equation and the adiabatic index, are novel results of our model due to the constraints of the constants from the matching boundary condition. We have repeated the above procedure and shown that this solution has a positive density, a positive tangential pressure and a positive gravitational mass as shown in Figs. 2a, b and 3b. Also we have found that the sound speed depends on the radial coordinate and is always less than 1 as indicated in Fig. 5. The energy conditions of this solution are satisfied as shown in Fig. 6b. We have matched our solution with the Schwarzschild exterior and derived a relation between two constants that characterize the unknown function $\mu$ with the gravitational mass and boundary radius of Schwarzschild and dealt with the third constant as a fitting parameter. Moreover, we showed that this solution satisfies the TOV equation as shown in Fig. 7d. We have illustrated that the adiabatic index of this solution is satisfied and always has $\Gamma \ge 4/3$ as drawn in Fig. 8. Finally, we have demonstrated that the static stability is always satisfied because the derivative of the gravitational mass w.r.t. central density is always positive, indicating the gravitational mass increases with the central density as shown in Fig. 9. From the above discussion we see that our model is satisfactory with the results of realistic stellar models except that the tangential pressure has a vanishing value at the center of the star as shown in Fig. 2b. Therefore, this study and the study done in [69] ensure that the assumption of vanishing radial pressure in the frame of Einstein theory is not a physical assumption. Therefore, we abandon this assumption.

Finally, we construct a compact star model assuming a new form of the metric potentials and derive the form of the density, radial, and tangential pressures. We repeat the same procedure done for the solution (20) and show in detail that this model is a physical model because it has positive density, radial and tangential pressures positive gravitational mass, and compactness as shown in Figs. 10 and 11. Also, this model has no vanishing value of density, radial, and tangential pressures at the center of the star in contrast to the model (20). Also, we show that the tangential pressure is greater from the radial pressure, $p_t>p_r$ as shown in Figs. 10a which means that we have a repulsive force [81]. Moreover, we study the issue of stability and show in detail that our model is stable against the gravitational, hydrostatic, and anisotropic forces as Fig. 12d shows. We calculate the sound speed and show that it is consistent with a real compact star in contrast to the Einstein study done in [69] which gave imaginary value. Also, we calculate the adiabatic index and show that it satisfies the condition given by Bondi [76].

To summarize, in the present paper we have used a non-diagonal form of tetrad field that gives null values of the off-diagonal components of the field equations unlike what has been studied in the literature [82,83,84,85,86,87,88]. We show that solution (18) depends on the tangential EoS which is not familiar for compact star and solution (20) has infinite central pressure as shown in Fig. 2b, which is not the case in compact stars which means that the system has central singularity and therefore unstable. However the results of solution (42) give physically-motivated compact star solution as shown in Figs. 10, 11, 12 and 13.