1 Introduction

It is a widely accepted concept that the n dimensional manifold \(V_n\) can be embedded in a pseudo-Euclidean space of \(m = n (n+1)/2\) dimensions. The minimum extra dimensions, \(m-n = n(n-1)/2\) of the pseudo-Euclidean space needed are called the embedding class of \(V_n\). In the case of the 4 dimensional relativistic space-time, the embedding class is obviously 6. The well-known cosmological metric of Friedmann–Lemaître–Robertson–Walker (FLRW) [1] is of class 1, whereas the Schwarzschild interior and exterior solutions are of class 1 and 2, respectively. The Kerr space-time metric has been shown to be of class 5 [2]. However, in the present paper we limit ourselves to the static spherically symmetric metric of embedding class 1 space-time.

It is seen that the above mentioned metric is compatible only with two perfect fluid distributions, viz. (i) the Schwarzschild solution [3] and (ii) the Kohler and Chao [4] solution. We would like to exploit this metric to construct electromagnetic mass models under the Einstein–Maxwell framework by considering a charged perfect fluid distribution. In general, when the charge is zero in a charged distribution of matter, the subsequent distribution becomes the neutral counterpart of the charged distribution. This neutral counterpart may belong to either a Schwarzschild interior solution [3] or a Kohler–Chao interior solution [4].

However, every charged fluid distribution indeed does not possess its neutral counterpart and consequently if the charge is set to zero then the describing metric turns out to be flat and the corresponding energy density and fluid pressure will vanish identically. This special type of charged fluid distribution is said to provide an electromagnetic mass model. In connection with his model for an extended electron, Lorentz [5] conjectured that “there is no other, no ‘true’ or ‘material’ mass”, and thus he proposed the ‘electromagnetic mass of the electron’. Later on Wheeler [6] and Wilczek [7] pointed out that the electron has a “mass without mass”. Feynman et al. [8] actually termed this type of models “electromagnetic mass models”. For further reading on historical notes and technical works on the electromagnetic mass, see Ref. [9] and Refs. [10–19] respectively, under the framework of Einstein–Maxwell theory.

Unfortunately, the electromagnetic mass models proposed by most of the above investigators [11–19] suffer from a negative pressure or density of the fluid due to the equation of state (EOS) of the form

$$\begin{aligned} \rho + p = 0, \end{aligned}$$
(1)

where \(\rho \) is the density and p is the pressure. This type of EOS in the literature is known as a ‘false vacuum’ or ‘degenerate vacuum’ or ‘\(\rho \)-vacuum’ [20–23]. It has been argued that, though in general this EOS leads to negative pressure, it provides easier junction conditions and a realistic expression for the mass [12–14, 24]. Although the junction conditions do not require the density to vanish at the boundary as is true for gaseous spheres, such a model is available in the literature for both the uncharged and the charged cases [25, 26]. However, we also note that the classical models of electron should contain regions of negative density [27, 28]. It would be interesting to mention that a Weyl-type character of the field has been considered which forms an electromagnetic mass model [29].

In the present study we have attempted to obtain a charged fluid with a metric of class 1 by choosing specific metric potentials such that they do not form a sub-set of the metric potentials of Schwarzschild’s interior metric (inclusive de Sitter and Einstein universe) and Kohler–Chao metric [4]. We argue here that the static spherically symmetric metric of embedding class 1 is more suitable to construct an electromagnetic mass model, as it possesses a smaller number of neutral counterparts of the charged fluids in comparison to the general static spherically symmetric metric. Now, if the charge would be zero in the charged fluid, the describing metric will turn into a flat one by virtue of the structure of the metric. In the past, several alternatives were used by several investigators to obtain electromagnetic mass models [12–16] by employing the EOS (1) as a pure charge condition [13], which takes the equivalent form \(g_{11}g_{44} = -1\) [12]. On the other hand, Ponce de Leon [16] has utilized the charged Einstein clusters [30, 31] to get the electromagnetic mass models. For further studies on different aspects of electromagnetic mass models, see Refs. [32–38].

However, for the construction of electromagnetic mass models we invoke a different method by adopting an algorithm which is very efficient to generate solutions of the desired form and physics, as no such ad hoc assumptions are required to obtain electromagnetic mass models. The main motivation of the present paper, therefore, is to obtain a set of solutions for the electromagnetic mass model with the help of a charged fluid distribution of a spherically symmetric class 1 metric. The logic behind considering the class 1 metric is that if one removes the charge from the solutions then either the Schwarzschild solution [3] or the Kohler–Chao solution [4] will emerge from the metric, which turns out eventually to be flat; and all the physical parameters—pressure, density etc.—become zero.

Our scheme of investigations is as follows: in Sect. 2 we provide the class 1 metric and fit the metric potentials into the Einstein–Maxwell field equations for the spherically symmetric matter distribution. In the next part (Sect. 3) we provide an algorithm to construct the electromagnetic mass models for stellar systems. Consequently by exploiting the mathematical formalism we generate three new set of Solutions I, II, and III in connection with the electromagnetic mass model (Sect. 4) and systematically analyze these solutions as regards the stellar models for a suitable functional relation of \(\nu (r)\). However, unfortunately we find that the Solution I only provides a physically valid and well-behaved situation and thus the other two set of Solutions II and III are not included in the present investigation. We now discuss the boundary conditions regarding the solutions and determine the constants of integration (Sect. 5). As till now we do not know the exact nature of the solutions set, we adopt in Sect. 6 some specific techniques to explore the different features and properties of the electromagnetic mass models for the physical acceptability of the anisotropic stellar models. In Sect. 7 we try to validate the solutions set related to the electromagnetic mass models with some of the observed compact star candidates. We discuss our results in the concluding Sect. 8.

2 The class 1 metric and the Einstein–Maxwell field equations

Let us consider the static spherically symmetric metric

$$\begin{aligned} \mathrm{d}s^2 = - e^{\lambda } \mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2) + e^{\nu } \mathrm{d}t^2, \end{aligned}$$
(2)

which may represent the space-time of embedding class 1, if it satisfies the Karmarkar condition [39]

$$\begin{aligned} R_{1414}=\frac{R_{1212}R_{3434} + R_{1224}R_{1334}}{R_{2323}}, \end{aligned}$$
(3)

with \(R_{2323} \ne 0\) [40].

The above condition along with (2) yields the following differential equation:

$$\begin{aligned} \frac{\lambda ' \nu '}{\left( 1-e^\lambda \right) }=-2\left( \nu ''+\nu '^2 \right) +\nu '^2+\lambda ' \nu ', \end{aligned}$$
(4)

with the constraint \(e^{\lambda (r)}\ne 1\) for \(r \ne 0\), where \(\lambda \) and \(\nu \) are metric potentials of the line element (2) which are functions of the radial coordinate r only.

The solution of the above differential Eq. (4) can be obtained as

$$\begin{aligned} e^\lambda =\left( 1 + K \frac{\nu '^2 e^\nu }{4}\right) , \end{aligned}$$
(5)

where K is a non-zero arbitrary constant, \(\nu '(r)\ne 0\), \(\nu '(0)=0\), and \(e^{\lambda (0)}=1\).

If Eqs. (2) and (5) describe a charge perfect fluid distribution then the functions \(\lambda (r)\) and \(\nu (r)\) must satisfy the Einstein–Maxwell field equations,

$$\begin{aligned} {G^i}_j = {R^i}_j - \frac{1}{2} R {g^i}_j = \kappa ({T^i}_j + {E^i}_j), \end{aligned}$$
(6)

where \(\kappa = 8\pi \) is the Einstein constant with \(G=c=1\) in the relativistic geometrized units.

The matter within the star is assumed to be locally a perfect fluid and consequently \(T^i_j\) and \(E^i_j\), the energy-momentum tensors for the fluid distribution and the electromagnetic field tensors, are, respectively, defined by

$$\begin{aligned} {T^i}_j = [(\rho + p)v^iv_j - p{\delta ^i}_j], \end{aligned}$$
(7)
$$\begin{aligned} {E^i}_j = \frac{1}{4 \pi }\left( -F^{im}F_{jm} + \frac{1}{4}{\delta ^i}_jF^{mn}F_{mn}\right) , \end{aligned}$$
(8)

where \(v^i\) is the four-velocity as \(e^{-\nu (r)/2}v^i={\delta ^i}_4\), \(\rho \) is the matter-energy density and p is the fluid pressure.

The above anti-symmetric electromagnetic field tensor \(F_{ij}\) in Eq. (8) denotes the field strength tensor and can be defined as

$$\begin{aligned} F_{ij} = \frac{\partial A_j}{\partial A_i} - \frac{\partial A_i}{\partial A_j}. \end{aligned}$$
(9)

This should satisfy the Maxwell equations,

$$\begin{aligned} F_{ik,j} + F_{kj,i} + F_{ji,k} = 0, \end{aligned}$$
(10)

and

$$\begin{aligned} \frac{\partial }{\partial x^k}\left( {\sqrt{-}g} F^{ik}\right) = -4\pi {\sqrt{-}g} J^i, \end{aligned}$$
(11)

where g is the determinant of quantities \(g_{ij}\) in Eq. (11) and is given by

$$\begin{aligned} g = \left( \begin{array}{cccc} e^{\nu } &{} 0 &{} 0 &{} 0\\ 0 &{}-e^{\lambda } &{} 0 &{} 0\\ 0 &{} 0 &{} -r^2 &{} 0\\ 0 &{} 0 &{} 0 &{} -r^2\sin ^2\theta \end{array} \right) = - e^{(\nu +\lambda )}r^4 sin^2\theta , \end{aligned}$$

where \(A_j=(\phi (r), 0, 0, 0)\) is the four-potential and \(J^i\) is the four-current vector defined by

$$\begin{aligned} J^i = \frac{\sigma }{\sqrt{g}_{44}} \frac{\mathrm{d}x^i}{\mathrm{d}x^0} = \sigma v^i, \end{aligned}$$

where \(\sigma \) is the charged density.

For a static matter distribution the only non-zero component of the four-current is \(J^4\); because of the spherical symmetry this has only a functional relation with the radial coordinate r. The only non-vanishing component of the electromagnetic field tensor (\(F^{41} = - F^{14}\)) describes the radial component of the electric field. Hence, from Eq. (11), one can easily get the expression for the electric field,

$$\begin{aligned} F^{41} = e^{-(\nu +\lambda )/2} \left[ \frac{q(r)}{r^2}\right] , \end{aligned}$$
(12)

where q(r) represents the electric charge contained within the sphere of radius r is defined by

$$\begin{aligned} q(r) = 4\pi \int _0^r \sigma r^2 e^{\lambda /2} \mathrm{d}r = r^2 \sqrt{-F_{14}F^{14}} = r^2 F^{41} e^{(\nu +\lambda )/2}. \end{aligned}$$
(13)

Equation (13) can be treated as the relativistic version of Gauss’ law, which, due to Eqs. (2) and (11), reduces to the following form:

$$\begin{aligned} \frac{\partial }{\partial r}(r^2 F^{41} e^{(\nu +\lambda )/2}) = - 4\pi r^2 e^{(\nu +\lambda )/2} J^4. \end{aligned}$$
(14)

For the spherically symmetric metric (2), the Einstein–Maxwell field equations can be expressed by the following ordinary differential equations:

$$\begin{aligned} -\kappa {T^1}_1 = \frac{{\nu }^{\prime }}{r} e^{-\lambda } - \frac{(1 - e^{-\lambda })}{r^2} = \kappa p - \frac{q^2}{r^4}, \end{aligned}$$
(15)
$$\begin{aligned} -\kappa {T^2}_2&= -\kappa {T^3}_3 = \left[ \frac{{\nu }^{\prime \prime }}{2} - \frac{{\lambda }^{\prime }{\nu }^{\prime }}{4} + \frac{{{\nu }^{\prime }}^2}{4} + \frac{{\nu }^{\prime } - {\lambda }^{\prime }}{2r}\right] e^{-\lambda }\nonumber \\&= \kappa p + \frac{q^2}{r^4}, \end{aligned}$$
(16)
$$\begin{aligned} \kappa {T^4}_4 = \frac{{\lambda }^{\prime }}{r} e^{-\lambda } + \frac{(1 - e^{-\lambda })}{r^2} = \kappa \rho + \frac{q^2}{r^4}, \end{aligned}$$
(17)

where the prime denotes differentiation with respect to the radial coordinate r.

By using Eqs. (15)–(17) and also (5), we obtain

$$\begin{aligned} \frac{\nu '}{r^2 \left( 4 + K \nu '^2 e^\nu \right) }(4r-K \nu ')=\kappa p - \frac{q^2}{r^4}, \end{aligned}$$
(18)
$$\begin{aligned}&\frac{4}{\left( 4 + K \nu '^2 e^\nu \right) }\left[ \frac{\nu '}{2r} - \frac{\left( K \nu ' e^\nu -2r \right) \left( 2\nu ''+\nu '^2 \right) }{2r \left( 4 + K \nu '^2 e^\nu \right) } \right] = \kappa p + \frac{q^2}{r^4}, \end{aligned}$$
(19)
$$\begin{aligned} \frac{K \nu ' e^\nu }{\left( 4 + K \nu '^2 e^\nu \right) }\left[ \frac{4(2\nu ''+\nu '^2)}{\left( 4 + K \nu '^2 e^\nu \right) }+\frac{\nu '}{r}\right] = \kappa \rho + \frac{q^2}{r^4}. \end{aligned}$$
(20)

On the other hand, the pressure isotropy condition can be given by

$$\begin{aligned} \left( \frac{k\nu ' e^\nu }{2r}-1\right) \left[ \frac{2\nu '}{r\left( 4 + K \nu '^2 e^\nu \right) }-\frac{4(2\nu ''+\nu '^2)}{\left( 4 + K \nu '^2 e^\nu \right) ^2}\right] =\frac{2q^2}{r^4}. \end{aligned}$$
(21)

A closer observation of the above set of differential equations easily indicates that if charge vanishes in a charged fluid of embedding class 1, then the remaining neutral counterpart will only be either the Schwarzschild [3] interior solution (or its special cases of the de Sitter universe or the Einstein universe) or the Kohler and Chao [4] solution, otherwise either the charge cannot be zero or the surviving space-time metric will become flat.

Now, one can look at Eq. (21) which immediately indicates that in the absence of charge either of the two factors on the left hand side has to be zero. Consequently, it can be shown that if the first factor of Eq. (21) is zero then it gives rise to the Kohler–Chao [4] solution in the form:

$$\begin{aligned} \mathrm{d}s^2&= -\frac{(A+2Br^2)}{(A+Br^2)} \mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2)\nonumber \\&\quad + (A+Br^2) \mathrm{d}t^2, \end{aligned}$$
(22)

where A and B are two non-zero constants.

The pressure and density, in this model, are

$$\begin{aligned} \kappa p&= \frac{B}{(A+2Br^2)}, \end{aligned}$$
(23)
$$\begin{aligned} \kappa \rho&= B\frac{(3A+2Br^2)}{(A+Br^2)}. \end{aligned}$$
(24)

One can observe from Eqs. (23) and (24) that, since it does not possess zero pressure as well as density for any finite radius on the surface, it cannot represent a compact star.

Let us now consider the second factor of Eq. (21), which in its vanishing form provides the Schwarzschild [3] interior solution

$$\begin{aligned} \mathrm{d}s^2&= -\left( 1-\frac{r^2}{R^2}\right) ^{-1} -r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2)\nonumber \\&\quad + \left( A+B\sqrt{1-\frac{r^2}{R^2}} \right) ^2 \mathrm{d}t^2, \end{aligned}$$
(25)

with its pressure and density as follows:

$$\begin{aligned} \kappa p = - \frac{A+3B\sqrt{1-\frac{r^2}{R^2} }}{R^2\left( A+B\sqrt{1-\frac{r^2}{R^2} }\right) }, \end{aligned}$$
(26)
$$\begin{aligned} \kappa \rho = \frac{3}{R^2}, \end{aligned}$$
(27)

where A and R are non-zero constant quantities and \(B > 0\).

If the mass function for the electrically charged fluid sphere is denoted by m(r), then it can be defined in terms of the metric function \(e^{\lambda (r)}\) as

$$\begin{aligned} e^{-\lambda (r)} = 1 - \frac{2m(r)}{r} + \frac{q^2}{r^2}, \end{aligned}$$
(28)

where the function m(r) represents the gravitational mass of the matter contained in a sphere of radius r. Now, if R represents the radius of the fluid sphere, then it can be shown that m is a constant with \(m(r = R) = M\) outside the fluid distribution where M is the gravitational mass. Following the work of Florides [30] this can be defined as

$$\begin{aligned} M = \mu (R) + \xi (R), \end{aligned}$$
(29)

where \(\mu (R) = \frac{\kappa }{2} \int _0^R\rho r^2 \mathrm{d}r\) is the mass inside the sphere, \(\xi (R) = \frac{\kappa }{2} \int _0^R \sigma r q e^{\lambda /2}\mathrm{d}r\) is the mass equivalence of the electromagnetic energy of distribution, and \(Q = q(R)\) is the total charge inside the fluid sphere.

By using Eq. (29) one can write the mass, in terms of energy density and charge function, as follows:

$$\begin{aligned} m(r)= \frac{\kappa }{2} \int \rho r^2 \mathrm{d}r +\frac{1}{2} \int \frac{q^2}{r^2}\mathrm{d}r + \frac{q^2}{2r}. \end{aligned}$$
(30)

Again from Eqs. (15) and (18) we obtain the expression for metric potential,

$$\begin{aligned} \nu ^{\prime } = \frac{\left( \kappa r p + \frac{2m}{r^2} - \frac{2q^2}{r^3}\right) }{\left( 1 - \frac{2m}{r} + \frac{q^2}{r^2}\right) }. \end{aligned}$$
(31)

Also, the expression for the pressure, in its gradient form, can be obtained by using Eqs. (15) and (18)–(20) as follows:

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r} = -\frac{M_\mathrm{G}(r)\left( p + \rho \right) }{r^2}e^{\left( \lambda -\nu \right) /2} + \frac{q}{4 \pi r^4}\frac{\mathrm{d}q}{\mathrm{d}r}, \end{aligned}$$
(32)

where \(M_\mathrm{G}\) is the gravitational mass within the sphere of radius r, given by

$$\begin{aligned} M_\mathrm{G}(r)=\frac{1}{2}r^2\nu 'e^{\left( \nu -\lambda \right) /2}. \end{aligned}$$
(33)

Equation (32) represents the charged generalization of the Tolman–Oppenheimer–Volkoff (TOV) equation of continuity for a perfect fluid stellar system [41, 42].

3 Algorithm for stellar models

We are now in a position to construct models of stellar systems for class 1 metric by using an algorithm given by Maurya et al. [43].

Equations (15)–(17) in terms of the mass function reduce to

$$\begin{aligned} -\frac{2m(1+r\nu ')}{r^3} + \frac{\nu '}{r}+\frac{q^2(1+r\nu ')}{r^4}+ \frac{q^2}{r^4}=\kappa p, \end{aligned}$$
(34)
$$\begin{aligned}&-\frac{m'(2+r{\nu '})}{2r^2} - \frac{m(2r^2\nu '' +r^2{\nu '}^2 +r\nu ' -2)}{2r^3} \nonumber \\&\quad + \frac{2rqq'\nu '-2q^2\nu '+4qq' +(r^2+q^2)(2r\nu '' +r\nu '^2+2\nu )}{4r^3} \nonumber \\&\quad - \frac{2q^2}{r^4}=\kappa p , \end{aligned}$$
(35)
$$\begin{aligned} \frac{2m'}{r^2} - \frac{2qq'}{r^3}= \kappa \rho . \end{aligned}$$
(36)

From Eqs. (34) and (35), the first order linear differential equation for m(r) in terms of \(\nu (r)\) and electric charge function q(r) can be provided as follows:

$$\begin{aligned}&m'+ \frac{(2r^2\nu '' + r^2\nu '^2 - 3\nu 'r -6)}{r(r\nu ' + 2)}m\nonumber \\&\quad = \frac{r(2r\nu '' + r\nu '^2 - 2\nu ')}{2(r\nu ' + 2)} + f(r), \end{aligned}$$
(37)

where

$$\begin{aligned} f(r)&=\frac{q^2\left[ 2r^2\nu '' + r\nu '(r\nu ' - 4) -16\right] }{2r^2(r\nu ' + 2)}+ \frac{qq'(r\nu ' + 2)}{r(r\nu ' + 2)}.\nonumber \\ \end{aligned}$$
(38)

Hence the mass function m(r) can be given by

$$\begin{aligned} m(r)= e^{-\int g(r) \mathrm{d}r} \left[ \int \left\{ h(r) + f(r)\right\} \left( e^{\int g(r)\mathrm{d}r}\right) \mathrm{d}r + A \right] , \end{aligned}$$
(39)

where

$$\begin{aligned} g(r) = \frac{(2r^2\nu '' + r^2\nu '^2 - 3r\nu ' -6)}{r(r\nu ' + 2)} \end{aligned}$$
(40)

and

$$\begin{aligned} h(r) = \frac{r(2r^2\nu '' + r\nu '^2 - 2\nu ')}{2(r\nu ' + 2)}. \end{aligned}$$
(41)

4 New class of models for stellar systems

To construct a new class of models for stellar systems we have considered three different forms of \(\nu \), viz. (I) \(\nu (r) = 2Ar^2+ \ln B\), (II) \(\nu (r) = 2\ln (1+ \sinh Ar^2)+ \ln B\), and (III) \(\nu (r) = 2\ln (1+ \sin Ar^2)+ \ln B\). However, we observe that all the solutions are physically valid, though the forms of \(\nu \) corresponding to Solutions II and III i.e. \(\nu (r) = 2\ln (1+ \sinh Ar^2)+ \ln B\) and \(\nu (r) = 2\ln (1+ \sin Ar^2)+ \ln B\) are not well behaved as the velocity of sound is not decreasing, as usual. Therefore, we have not included the solutions (II) and (III) in the present work.

Let us now consider the form I of \(\nu \), as mentioned above, as follows:

$$\begin{aligned} \nu (r) = 2Ar^2+ \ln B, \end{aligned}$$
(42)

along with another suitable function

$$\begin{aligned} \lambda (r) = \ln \left( 1 + K \frac{\nu '^2 e^\nu }{4}\right) , \end{aligned}$$
(43)

where A and B are positive constants as mentioned earlier.

The expressions for the mass and the electric charge are, respectively,

$$\begin{aligned}&\frac{2m(r)}{r}=Ar^2\nonumber \\&\quad \times \left[ \frac{De^{2Ar^2}}{1+DAr^2e^{2Ar^2}}+\frac{Ar^2(D^2e^{4Ar^2} + 4 - 4De^{2Ar^2})}{2(1+DAr^2e^{2Ar^2})^2}\right] , \end{aligned}$$
(44)
$$\begin{aligned} \frac{q^2}{r^4} = E^2 = A^2r^2\left[ \frac{D^2e^{2Ar^2} +4-4De^{2Ar^2}}{2(1+DAr^2e^{2Ar^2})^2}\right] , \end{aligned}$$
(45)

where \(D=4ABK\) is a pure constant.

Again, the expression for the energy density and the pressure are given by

$$\begin{aligned}&\kappa \rho =A\nonumber \\&\quad \times \left[ \frac{D^2Ar^2e^{4Ar^2} -4Ar^2+6De^{2Ar^2}(2Ar^2+1)}{2(1+DAr^2e^{2Ar^2})^2}\right] , \end{aligned}$$
(46)
$$\begin{aligned} \kappa p =A\left[ \frac{-D^2Ar^2e^{4Ar^2}+4(2+Ar^2)+2De^{2Ar^2}(2Ar^2-1)}{2(1+DAr^2e^{2Ar^2})^2}\right] . \end{aligned}$$
(47)

The respective gradients of the above physical parameters are

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r}&= -\frac{2A^2r}{\kappa }\left[ \frac{-D^3Ar^2e^{6Ar^2}+D^2e^{4Ar^2}(-3+4Ar^2+8A^2r^4)+4De^{2Ar^2}(4+7Ar^2+4A^2r^4)-4}{2(1+DAr^2e^{2Ar^2})^3}\right] , \end{aligned}$$
(48)
$$\begin{aligned} \frac{\mathrm{d}\rho }{\mathrm{d}r}&=-\frac{2A^2r}{\kappa }\left[ \frac{D^3Ar^2e^{6Ar^2}+D^2e^{4Ar^2}(11+20Ar^2+28A^2r^4)-4De^{2Ar^2}(6+7Ar^2+4A^2r^4)+4}{2(1+DAr^2e^{2Ar^2})^3}\right] . \end{aligned}$$
(49)
Fig. 1
figure 1

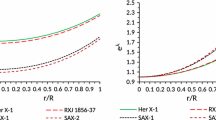
\(e^{\nu }\) are plotted with continuous line for Solution I, small dashed line for Solution II and long dashed line for Solution III. For plotting this figure the following values of the arbitrary constants A, D, B, and K are used where for Solution I: \(B=0.5189\), \(A= 5.0962 \times 10^{-13}\), \(D= 2.9540\), \(K=2.7925 \times 10^{12}\), for Solution II: \(B=0.4351\), \(A=1.0288 \times 10^{-12}\), \(D=3.7290\), \(K=2.0829 \times 10^{12}\), and for Solution III: \(B=0.4446\), \(A=1.0024 \times 10^{-12}\), \(D=3.9468\), \(K=2.2140 \times 10^{12}\)

Full size image

Let us look at Figs. 1 and 2 regarding the desirable features on the basis of their respective solution. It is expected that the solution should be free from physical and geometrical singularities, i.e. the fluid pressure and the energy density at the center should be finite, and the metric potentials \(e^{\lambda (r)}\) and \(e^{\nu (r)}\) should have non-zero positive values in the range \(0 \le r \le R\). At the center one must have \(e^{\lambda (0)}=1\) and \(e^{\nu (0)}=B\) for each solution. Interestingly, both Figs. 1 and 2 show that the metric potentials are positive and finite at the center.

Similarly, the density \(\rho \) should be positive and the pressure p must be positive inside the star and it should be zero at the boundary of the fluid sphere. All these features are quite available from Figs. 3 and 4.

Fig. 2
figure 2

\(e^{\lambda }\) are plotted with a continuous line for Solution I, a small dashed line for Solution II and a long dashed line for Solution III. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Fig. 1

Full size image
Fig. 3
figure 3

Pressure is plotted with a long dashed line for Solution I, a continuous line for Solution II, and a small dashed line for Solution III. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Figs. 1 and 2

Full size image
Fig. 4
figure 4

Density is plotted with a long dashed line for Solution I, a small dashed line for Solution II, and a continuous line for Solution III. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Figs. 1, 2, and 3

Full size image

Let us summarize and consider the above results. We would like to mention here that for \(A=0\) the corresponding metric at once turns out to be a flat space-time and also the expressions for the electric charge, the pressure, and the energy density automatically vanish. Therefore, the charged fluid distributions obtained above depict an electromagnetic mass model. This is also true for the other two cases of solutions for different forms of \(\nu \).

5 Boundary conditions for the spherical system

The above system of equations has to be solved under the condition that the radial pressure \(p=0\) at \(r=a\) (where \(r=a\) is the outer boundary of the fluid sphere). The interior metric (2) can join smoothly at the surface of spheres to the Reissner–Nordström metric [44],

$$\begin{aligned} \mathrm{d}s^2&=-\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) ^{-1}\mathrm{d}r^2 -r^2(\mathrm{d}\theta ^2 +\sin ^2 \theta \mathrm{d}\phi ^2)\nonumber \\&\quad +\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) \mathrm{d}t^2. \end{aligned}$$
(50)

This requires the continuity of \(e^{\lambda (r)}\), \(e^{\nu (r)}\), and q(r) across the boundary \(r=R\),

$$\begin{aligned}&e^{-\lambda (R)} = \left( 1-\frac{2M}{R}+\frac{Q^2}{R^2}\right) ,\end{aligned}$$
(51)
$$\begin{aligned}&e^{\nu (R)} = \left( 1-\frac{2M}{R}+\frac{Q^2}{R^2}\right) ,\end{aligned}$$
(52)
$$\begin{aligned}&q(R)=Q,\end{aligned}$$
(53)
$$\begin{aligned}&p_{(r=R)}=0. \end{aligned}$$
(54)

By using all the above boundary conditions we are able to find expressions for various constants as can be seen below.

The pressure p at \((r=R)=0\) gives

$$\begin{aligned} D=\frac{(2AR^2-1) {^+_-} \sqrt{(8A^2R^4+4AR^2+1)}}{AR^2e^{2AR^2}}, \end{aligned}$$
(55)

however, the \(+\) sign is only applicable in the above equation.

At the boundary,

$$\begin{aligned} e^{-\lambda (R)} =e^{\nu (R)}, \end{aligned}$$
(56)

gives

$$\begin{aligned} B=\frac{1}{e^{2AR^2}(1+DAR^2e^{2AR^2})}. \end{aligned}$$
(57)
Fig. 5
figure 5

The sound velocity is plotted with continuous line for Solution I, long dashed line for Solution II and small dashed line for Solution III. For the purpose of plotting this figure, we have employed the same data set for arbitrary constants A, D, B, and K as in Figs. 1, 2, 3, and 4

Full size image

Again, \(\rho (r=R) = \rho _R\) gives

$$\begin{aligned} A=\frac{\kappa \rho _R [2(1+DAR^2 e^{2AR^2})^2]}{[D^2AR^2 e^{4AR^2} - 4AR^2 + 6De^{2AR^2} (1+2AR^2)]}. \end{aligned}$$
(58)

6 Physical features of the models for stellar systems

In Sect. 4 we have analyzed some of the physical parameters, potentials, density, pressure etc., through their graphical plots. They exhibited desirable physical features regarding stellar configuration. However, in Sect. 6 we are interested in performing a few rigorous tests for the other physical parameters, velocity and charge, and also we prepare a check list for energy conditions and stability issues (such as the TOV equation and the Buchdahl condition).

6.1 Sound velocity for Solutions I, II, and III

The velocity of sound within the matter distribution should monotonically decrease away from the center and increase with the increase of density, i.e. \(\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{\mathrm{d}p}{\mathrm{d}\rho }\right) <0\) or \(\frac{\mathrm{d}^2p}{\mathrm{d}\rho ^2}>0\) for \(0 \le r \le R\). It is argued by Canuto [45] that for the EOS with an ultra-high distribution of matter the sound speed decreases outwards.

In the present model, from Fig. 5, it is clear that the velocity is decreasing for Solution I and increasing for Solution II and III throughout the star. Therefore, the solutions for solution II and III are not suitable at all as far as a compact star is concerned. This is because the EOS for nuclear matter shows a regular behavior of \(\frac{\mathrm{d}p}{\mathrm{d}\rho } \) for these solutions [46].

The above discussions, based on the demonstration of the figures, immediately restrain us to the study henceforth of only the solution of a type I electromagnetic mass model.

From Fig. 5, as the sound velocity is less than 1, the present star in this model is stable.

6.2 Electric charge for Solution I

From the present model it is observed that in the unit of Coulomb, the charge on the boundary is \(1.15295 \times 10^{20}\) C and at the center it is zero (as the charge on the boundary is 0.9889 so we have to multiply this by the number \(1.1659 \times 10^{20}\) to obtain the resultant numerical value).

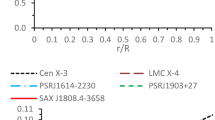
One can observe from Fig. 6 that the charge profile starts from a minimum and acquires the maximum value at the boundary. This figure has been drawn for the compact star \(RX~J~1856-37\) with the constant values \(CR^2=0.1836\), \(D=2.9540\).

Fig. 6
figure 6

Electric charge is plotted with long dashed line for Solution I. For plotting this figure the following data set of arbitrary constants \(B=0.5189\), \(A= 5.0962 \times 10^{-13}\), \(D=2.9540\), and \(K=2.7925 \times 10^{12}\) are used related to the compact star \(RX J 1856 - 37\) (see Table 1)

Full size image

6.3 Energy conditions for Solution I

For the physical validity the energy-momentum tensor has to obey the following energy conditions:

  1. 1.

    null energy condition (NEC): \(\rho +\frac{E^2}{4\pi } \ge 0\),

  2. 2.

    weak energy condition (WEC): \(\rho -p+\frac{E^2}{4\pi } \ge 0\),

  3. 3.

    strong energy condition (SEC): \(\rho -3p+\frac{E^2}{4\pi } \ge 0\).

We have plotted the feature of different energy conditions in Fig. 7 for the values of different physical parameters connected to energy conditions for the constants: \(CR^2=0.1836\), \(M=0.9041~M_{\odot }\), \(R=6.006\) Km, and \(\frac{M}{R}=0.222\). The figure indicates that all the energy conditions are satisfied throughout the interior region of the stellar system.

Fig. 7
figure 7

NEC is plotted with a long dashed line, WEC is plotted with a continuous line and SEC is plotted with a small dashed line for Solution I. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Fig. 6

Full size image

6.4 Generalized TOV equation for Solution I

We write the generalized TOV equation [47] in the following form:

$$\begin{aligned} -\frac{M_\mathrm{G}(\rho +p_r)}{r^2}e^{(\lambda -\nu )/2}-\frac{\mathrm{d}p}{\mathrm{d}r}+ \sigma \frac{q}{r^2}e^{\lambda /2} =0, \end{aligned}$$
(59)

where \(M_\mathrm{G}\) is the effective gravitational mass within the radius r and can be written

$$\begin{aligned} M_\mathrm{G}(r)=\frac{1}{2}r^2 \nu ^{\prime }e^{(\nu - \lambda )/2}. \end{aligned}$$
(60)

The above TOV equation describes the equilibrium condition for a charged fluid subject to gravitational (\(F_g\)), hydrostatic (\(F_h\)) and electric (\(F_e\)) forces. Therefore, one can write it in the more suitable form

$$\begin{aligned} F_g+F_h+F_e=0, \end{aligned}$$
(61)

where

$$\begin{aligned} F_g&=-\frac{1}{2} \nu '(\rho +p)\nonumber \\&=-\frac{2A^2r}{8\pi }\left[ \frac{2De^{2Ar^2}(1+4Ar^2)+4}{(1+DAr^2e^{2Ar^2})^2}\right] , \end{aligned}$$
(62)
$$\begin{aligned} F_h=-\frac{\mathrm{d}p}{\mathrm{d}r}=\frac{2A^2r}{8\pi }\left[ \frac{-D^3Ar^2e^{6Ar^2}+D^2e^{4Ar^2}(-3+4Ar^2+8A^2r^4)+4De^{2Ar^2}(4+7Ar^2+4A^2r^4)-4}{2(1+DAr^2e^{2Ar^2})^3}\right] , \end{aligned}$$
(63)

and

$$\begin{aligned} F_e=\sigma \frac{q}{r^2}e^{\lambda /2}=\frac{A^2r}{4\pi }\left[ \frac{(-2+De^{Ar^2}) \left[ -6+D^2Ar^2e^{4Ar^2}+De^{2Ar^2}(3+2Ar^2+8A^2r^4)\right] }{2(1+DAr^2e^{2Ar^2})^3}\right] . \end{aligned}$$
(64)

The plot for the TOV equation is shown in Fig. 8. We observe from this figure that the system is under the joint balancing action of the different forces, e.g. gravitational, hydrostatic, and electric forces, to attain an overall static equilibrium. However, from Fig. 8 it is also clear that the gravitational force has a dominant role over the hydrostatic force whereas the electric force has a negligible contribution to the equilibrium. This feature seems quite reasonable in the case of the compact stellar system.

Fig. 8
figure 8

\(F_g\) is plotted with a long dashed line, \(F_h\) is plotted with a continuous line, and \(F_e\) is plotted with a small dashed line for Solution I. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Figs. 6 and 7

Full size image

6.5 Effective mass–radius relation and surface redshift for Solution I

Buchdahl [48] has proposed an absolute constraint of the maximally allowable mass-to-radius ratio \((M/R)\) for isotropic fluid spheres in the form \(2M/R \le 8/9\). However, Böhmer and Harko [49] have shown that for a compact object with charge, \(Q (<M)\), there is a lower bound for the mass–radius ratio,

$$\begin{aligned} \frac{3Q^2}{2R^2} \left( \frac{1+\frac{Q^2}{18R^2}}{1+\frac{Q^2}{12R^2}}\right) \le \frac{2M}{R}, \end{aligned}$$
(65)

whereas the upper bound of the mass–radius of a charged sphere was generalized by Andréasson [50] as follows:

$$\begin{aligned} \sqrt{M} \le \frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9} + \frac{Q^2}{3R}}. \end{aligned}$$
(66)
Fig. 9
figure 9

Redshift, plotted with a long dashed line for Solution I. For the purpose of plotting this figure, we have employed the same data set for the arbitrary constants A, D, B, and K as in Figs. 6, 7, and 8

Full size image
Table 1 Values of the model parameters A, B, D, and K for different strange stars
Full size table
Table 2 Energy densities and pressure for different strange star candidates for the above parameter values of Table 1
Full size table

In the present model, the total effective gravitational mass is given by

$$\begin{aligned} M_{\mathrm{eff}}&=4\pi \int _{0}^{R}\left( \rho +\frac{E^2}{8\pi }\right) r^2 \mathrm{d}r\nonumber \\&= \frac{1}{2}R[1-e^{-\lambda (R)}]= \frac{1}{2}R\left[ \frac{DAR^2e^{2AR^2}}{1+DAR^2e^{2AR^2}}\right] . \end{aligned}$$
(67)

Therefore, the compactness factor can be written as

$$\begin{aligned} u= \frac{M_{\mathrm{eff}}}{R}= \frac{1}{2}\left[ \frac{DAR^2e^{2AR^2}}{1+DAR^2e^{2AR^2}}\right] . \end{aligned}$$
(68)

The surface redshift in connection with the above compactness is given by

$$\begin{aligned} Z&= (1-2u)^{-1/2} - 1 = e^{\lambda (R)/2} - 1\nonumber \\&=\sqrt{1+DAR^2e^{2AR^2}} -1. \end{aligned}$$
(69)

The plot of the surface redshift is shown in Fig. 9 for the compact star \(RX~J~1856-37\) with the constant values \(CR^2=0.1836\), \(D=2.9540\). It can be observed that there is a gradual increase in the redshift, which is an acceptable physical feature. The maximum surface redshift for the present stellar configuration of radius \(R = 6.006\) Km turns out to be \(Z = 0.3882\), which seems well within the limit \(Z \le 2\) [48, 51, 52].

7 Validating the model with compact star candidates

In Sect. 6 we have studied several physical behaviors of a stellar system in connection with the electromagnetic mass models. In some of the subsections, e.g. Sects. 6.2 (electric charge) and 6.5 (surface redshift), we have also shown graphical plots specifically for the compact star \(RX~J~1856-37\) with the mass \(M=0.9041~M_{\odot }\) and the radius \(R=6.006\) Km. We note that the star \(RX~J~1856-37\) represents a strange quark star obeying the bag model EOS.

However, it seems that more investigations are needed to show the validity of our models for other compact stars which have definite observed physical features. In Tables 1 and 2 we, therefore, produce a data set for the purpose of comparison between the present model stars and the observed compact stars.

For our model we particularly note that for the compact star \(RXJ~1856-37\) with mass \(M=0.9041~M_{\odot }\) and radius \(R=6.006\) Km the surface redshift turns out to be \(Z = 0.3882\), which seems to fall within the range \(Z \le 2\) [48, 51, 52] and \(0 < Z \le 1\) [53–57]. However, one may figure out the surface redshifts for other compact stars also as provided in Tables 1 and 2, and we expect those values will be within the above specified range. On the other hand, the surface density is of the order of \(10^{14}\)–\(10^{15}\) gm/cc (as can be seen from Table 2). This very high density indicates that the model mentioned under ‘electromagnetic mass’ represents an ultra-compact star [58–60].

Therefore, we would like to make the general remark that our models in connection with an ‘electromagnetic mass’ represent compact stars of several categories.

8 Conclusion

We have considered the static spherically symmetric space-time metric of embedding class 1 in the present investigation. Is has been possible to show the existence of electromagnetic mass models specifically in connection with compact stars. Three new electromagnetic mass models are discussed where the solutions are entirely originating from the electromagnetic field, such that the physical parameters like the density and pressure do vanish for the vanishing charge alone. However, a meticulous analysis reveals that among these three sets of solutions not all are equally interesting as far as several astrophysical aspects are concerned. To validate these special types of solutions related to electromagnetic mass models, we have also conducted a comparison between our proposed model and the observed compact stars which shows satisfactory results in favor of the present theoretical modeling.

However, an obvious question may arise as to the study of the compact stellar configuration in an Einstein–Maxwell space-time, especially as regards how the charge should be considered for such a kind of systems. Brief historical notes on the issues of the stability of static spherically symmetric stellar systems and of the effective measure for averting singularity, and why one should include charge and what the process is of holding a huge amount of charge inside the bodies are available exhaustively in Ref. [35] and the references therein. As a continuation of this discussion, we feel that an outline on the charged bodies, which follows in the next paragraph, may be helpful to the readers.

In the history of general relativity the first ever exact solutions of the Einstein field equations, the well-known Schwarzschild interior solutions, suffer from the problem of a singularity due to gravitational collapsing of a spherically symmetric matter distribution. One way to overcome this singularity is to include electrical charge to the neutral bodies. It has been suggested that gravitational collapse can be avoided in the presence of charge where the gravitational attraction is counter-balanced by the electrical repulsion in addition to the pressure gradient [61–63]. To this end questions came up regarding the stability of the charged sphere and also about the amount of charge of the star. A good amount of work has been done by several authors on the stability issue [64–69]. On the other hand, in some recent studies [47, 70, 71] we find an estimate of the electric charge in compact stars, which amounts to a huge charge of the order of \(10^{19} \)–\( 10^{20}\) Coulomb.

We emphasize the following point: that the solutions in the present work have been obtained under a strong assumption of the embedding in a higher dimensional space-time. However, it seems that at this stage a discussion is needed to highlight all the physical implications of such an assumption as follows: the postulates of general relativity do not provide any physical meaning to a higher-dimensional embedding space. However, it provides new characterizations of gravitational fields, which hopefully can be connected to physics. Some researchers are trying to link the group of motions of flat embedding space to the internal symmetries of elementary particle physics [72]. Some have utilized the higher dimensions to study the singularity of the space-time. Recently, Pavsic and Tapia [73] have published an article where many references regarding the applications of embedding to general relativity, extrinsic gravity, strings and membranes, and the new brane world are mentioned. Also Treibergs [74] has discussed the embedding diagrams of Schwarzschild space and Misner’s wormhole manifold to study the evolution problem for Einstein’s equations of gravity.

As a final point, we note the very recent claim by Corne et al. [75] that ‘pure electromagnetic mass cannot exist’. This result seems very puzzling as it raises a question regarding the validity of several classic as well as the seminal work in [5–8, 11–19, 33, 35, 76–78]. In this connection we would specially like to mention the study of Arnowitt et al. [79] where by considering the same self-energy they conclusively constructed ‘pure electromagnetic mass’ in the form \(m = 2|e|\), where e is the electric charge. Therefore, we strongly feel that the result of Corne et al. [75] needs further investigation with a proper and rigorous methodology.