Two-body charmed baryon decays involving decuplet baryon in the quark-diagram scheme

Abstract

In the quark-diagram scheme, we study the charmed baryon decays of $\mathbf{B}_c\rightarrow \mathbf{B}^* M$, where $\mathbf{B}_c$ is $\Lambda _c^+$ or $\Xi _c^{+(0)}$, together with $\mathbf{B}^*$ (M) the decuplet baryon (pseudoscalar meson). It is found that only two W-exchange processes are allowed to contribute to $\mathbf{B}_c\rightarrow \mathbf{B}^* M$. Particularly, we predict ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*0(+)} \pi ^{+(0)})=(2.8\pm 0.4)\times 10^{-3}$, which respects the isospin symmetry. Besides, we take into account the SU(3) flavor symmetry breaking, in order to explain the observation of ${\mathcal {B}}(\Lambda _c^+\rightarrow \Sigma ^{*+}\eta )$. For the decays involving $\Delta ^{++}(uuu)$, we predict ${\mathcal {B}}(\Lambda _c^+\rightarrow \Delta ^{++} \pi ^-,\Xi _c^+ \rightarrow \Delta ^{++} K^-) =(7.0\pm 1.4,13.5\pm 2.7)\times 10^{-4}$ as the largest branching fractions in the singly Cabibbo-suppressed $\Lambda _c^+,\Xi _c^+\rightarrow \mathbf{B}^*M$ decay channels, respectively, which are accessible to the LHCb, BELLEII and BESIII experiments.

1 Introduction

To determine the mass and lifetime of the $\Lambda _b$ baryon, $\Lambda _c^+$ is often taken as the final state in the $\Lambda _b$ decays [1], which involves the favored Cabibbo–Kobayashi–Maskawa (CKM) matrix elements for bigger branching fractions. With the higher precision in the recent years [2, 3], the subsequent $\Lambda _c^+\rightarrow p K^-\pi ^+$ decay has helped to make more accurate observations for the $\Lambda _b$ decays, which receives the significant contribution from $\Lambda _c^+\rightarrow \Delta ^{++}K^-,\Delta ^{++}\rightarrow p \pi ^+$. Similarly, one uses $\Xi _b^0\rightarrow \Xi _c^+\pi ^-$ to determine the $\Xi _b^0$ lifetime, whereas we find that the subsequent process $\Xi _c^+\rightarrow pK^-\pi ^+$ and its resonant contribution from $\Xi _c^+\rightarrow \Delta ^{++}K^-,\Delta ^{++}\rightarrow p \pi ^+$ have not been well studied yet [1]. Therefore, $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ plays the key role in the precision measurements for the multi-body decays of beauty and charm baryons, where $\mathbf{B}_c=(\Lambda _c^+,\Xi _c^{+(0)})$, $\mathbf{B}^*$ the decouplet baryon and M the meson state, such as $\Lambda _c^+(\Xi _c^+)\rightarrow \Delta ^{++}K^-$.

The $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays are not richly observed. Therefore, it is still unclear how the $\mathbf{B}_c\rightarrow \mathbf{B}^* M,\mathbf{B}^*\rightarrow \mathbf{B}M'$ decays mix with the non-resonant contributions to $\mathbf{B}_c\rightarrow \mathbf{B}MM'$. In addition, $\mathbf{B}_c\rightarrow \mathbf{B}V,V\rightarrow MM'$ with V the vector meson causes more complicated mixtures [1]. The SU(3) flavor ($SU(3)_f$) symmetry has been widely applied to the charmed baryon decays [4,5,6,7,8,9,10,11,12,13,14,15,16]. By well explaining the data, the flavor symmetry does not appear to be severely broken in $\mathbf{B}_c\rightarrow \mathbf{B}M$ [17], where $\mathbf{B}$ denotes the octet baryon. By contrast, ${\mathcal {B}}(\Lambda _c^+\rightarrow \Sigma ^{*+} \eta )$ not well interpreted by the $SU(3)_f$ symmetry might hint the broken effect in $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ [7], which could be as large as that in the D meson decays [18,19,20,21].

For a better understanding of the hadronization in $\mathbf{B}_c\rightarrow \mathbf{B}^* M$, there have been some theoretical attempts, which are in terms of the pole model, quark model and irreducible SU(3) flavor ($SU(3)_f$) symmetry [4,5,6,7, 22,23,24]. Particularly, the quark-diagram scheme with the topological $SU(3)_f$ symmetry provides a clear picture for the decay processes [17, 25,26,27]. Due to the fact that $\mathbf{B}^*$ is a spin-3/2 baryon with totally symmetric quark contents, it can be shown that the topological diagrams involving the flavor anti-symmetric quark pair in $\mathbf{B}^*$ are forbidden or suppressed. Therefore, we purpose to use the quark-diagram scheme to relate all possible $\mathbf{B}_c\rightarrow \mathbf{B}^*M$ decay channels. With the existing data, we will perform the numerical analysis, and determine different topological contributions. We can hence test the validity of the topological scheme, which involves the $SU(3)_f$ symmetry and its broken effect. Furthermore, we will give predictions for ${\mathcal {B}}(\mathbf{B}_c\rightarrow \mathbf{B}^* M)$ to be compared to the future measurements, which can help to clarify how $\mathbf{B}_c\rightarrow \mathbf{B}^*M,\mathbf{B}^*\rightarrow \mathbf{B}M'$ mixes with $\mathbf{B}_c\rightarrow \mathbf{B}V,V\rightarrow MM'$ and the non-resonant configuration in $\mathbf{B}_c\rightarrow \mathbf{B}MM'$.

2 Formalism

2.1 Effective Hamiltonian in the flavor symmetry

To study the two-body charmed baryon decays, the corresponding quark-level effective Hamiltonian is given by [28]

$$\begin{aligned} {\mathcal {H}}_{eff}= & {} \frac{G_F}{\sqrt{2}}\sum _{i=1,2} c_i (\lambda _a O_i^a+\lambda _p O_i^p+\lambda _c O_i^c ) , \end{aligned}$$

(1)

with $\lambda _{(a,p,c)}\equiv (V_{cs}^*V_{ud},V_{cp}^*V_{up},V_{cd}^*V_{us})$ and $p=(d,s)$, where $G_F$ is the Fermi constant, and $c_i$ the Wilson coefficients. The current–current operators $O_i^{(a,p,c)}$ are written as

$$\begin{aligned}&O_1^a=(\bar{u} d)(\bar{s} c) ,\quad O_2^a=(\bar{u}_\beta d_\alpha )(\bar{s}_\alpha c_\beta ) ,\nonumber \\&O_1^p=(\bar{u} p)(\bar{p} c) ,\quad O_2^p=(\bar{u}_\beta p_\alpha )(\bar{p}_\alpha c_\beta ) ,\nonumber \\&O_1^c=(\bar{u} s)(\bar{d} c) ,\quad O_2^c=(\bar{u}_\beta s_\alpha )(\bar{d}_\alpha c_\beta ) , \end{aligned}$$

(2)

where $(\bar{q}_1 q_2)=\bar{q}_1\gamma _\mu (1-\gamma _5)q_2$, and the subscripts $(\alpha ,\beta )$ denote the color indices. With $s_c\equiv \sin \theta _c\simeq 0.22$, where $\theta _c$ denotes the Cabibbo angle for the quark-mixing in the weak interaction, the decays with $|\lambda _{(a,p,c)}|\simeq (1,s_c,s_c^2)$ are regarded as the Cabibbo-allowed (CA), singly Cabibbo-suppressed (SCS) and doubly Cabibbo-suppressed (DCS) processes, respectively.

For the lowest-lying anti-triplet charmed baryon states $\Xi _c^0$, $\Xi _c^+$ and $\Lambda _c^+$ that consist of $(ds-sd)c$, $(su-us)c$ and $(ud-du)c$, respectively, we present them as

$$\begin{aligned} \mathbf{B}_c= & {} \left( \begin{array}{ccc} 0&{} \Lambda _c^+ &{} \Xi _c^+\\ -\Lambda _c^+&{}0&{}\Xi _c^0 \\ -\Xi _c^+&{}-\Xi _c^0&{}0 \end{array}\right) . \end{aligned}$$

(3)

The pseudoscalar meson states are given by

$$\begin{aligned} M=\left( \begin{array}{ccc} \frac{1}{\sqrt{2}}(\pi ^0+ c\phi \eta +s\phi \eta ' ) &{} \pi ^- &{} K^-\\ \pi ^+ &{} \frac{-1}{\sqrt{2}}(\pi ^0- c\phi \eta -s\phi \eta ') &{} \bar{K}^0\\ K^+ &{} K^0&{} -s\phi \eta +c\phi \eta ' \end{array}\right) ,\nonumber \\ \end{aligned}$$

(4)

where $(\eta ,\eta ')$ mix with $\eta _q=\sqrt{1/2}(u\bar{u}+d\bar{d})$ and $\eta _s=s\bar{s}$. The mixing angle $\phi =(39.3\pm 1.0)^\circ$ in $(s\phi ,c\phi )\equiv (\sin \phi ,\cos \phi )$ comes from the mixing matrix, given by [29, 30]

$$\begin{aligned} \left( \begin{array}{c} \eta \\ \eta ^\prime \end{array}\right) = \left( \begin{array}{cc} \cos \phi &{} -\sin \phi \\ \sin \phi &{} \cos \phi \end{array}\right) \left( \begin{array}{c} \eta _q \\ \eta _s \end{array}\right) . \end{aligned}$$

(5)

The decuplet baryons are written as

$$\begin{aligned}&\mathbf{B}^*=\frac{1}{\sqrt{3}} \left( \begin{array}{ccc} \left( \begin{array}{ccc} \sqrt{3}\Delta ^{++}&{}\Delta ^+ &{} \Sigma ^{* +}\\ \Delta ^+ &{}\Delta ^0 &{} \frac{\Sigma ^{* 0}}{\sqrt{2}}\\ \Sigma ^{* +}&{} \frac{\Sigma ^{* 0}}{\sqrt{2}}&{} \Xi ^{* 0} \end{array}\right) , \left( \begin{array}{ccc} \Delta ^+ &{}\Delta ^0 &{} \frac{\Sigma ^{* 0}}{\sqrt{2}}\\ \Delta ^0 &{}\sqrt{3}\Delta ^-&{} \Sigma ^{* -}\\ \frac{\Sigma ^{* 0}}{\sqrt{2}}&{}\Sigma ^{* -}&{}\Xi ^{* -} \end{array}\right) , \left( \begin{array}{ccc} \Sigma ^{* +}&{} \frac{\Sigma ^{* 0}}{\sqrt{2}}&{}\Xi ^{* 0}\\ \frac{\Sigma ^{* 0}}{\sqrt{2}}&{}\Sigma ^{* -}&{}\Xi ^{* -}\\ \Xi ^{* 0}&{}\Xi ^{* -}&{}\sqrt{3}\Omega ^- \end{array}\right) \end{array}\right) . \end{aligned}$$

(6)

By neglecting the Lorentz indices, ${\mathcal {H}}_{eff}$ for the $c\rightarrow q_i\bar{q}_j q_k$ transition can be presented with the tensor notation, $H^{ki}_j$, and the nonzero entries are given by [27]

$$\begin{aligned} H^{31}_2=\lambda _a,\quad H^{21}_2=\lambda _d,\quad H^{31}_3=\lambda _s,\quad H^{21}_3=\lambda _c . \end{aligned}$$

(7)

2.2 The quark-diagram scheme

Fig. 1

Topological diagrams for the $\mathbf{B}_c\rightarrow \mathbf{B}^{(*)} M$ decays

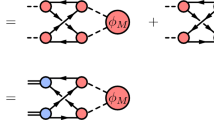
In the quark-diagram scheme, there exist six different topological diagrams for the $\mathbf{B}_c\rightarrow \mathbf{B}^{(*)}M$ decays, as drawn in Fig. 1a–f, parameterized as the topological amplitudes $(T,C,C')$ and $(E',E_\mathbf{B},E_M)$, respectively [17]. More explicitly, T and $C^{(\prime )}$ proceed with the W-boson emission ($W_{\text {EM}}$). By exchanging the W boson ($W_{\text {EX}}$), it gives rise to $E'$ and $E_{\mathbf{B}(M)}$. Since only (T, C) can be decomposed of two separate matrix elements based on the factorization, that is, $(T,C)\propto \langle M|\bar{q}_1 q_2|0\rangle \langle \mathbf{B}^{(*)}|\bar{q}_3 c|\mathbf{B}_c\rangle$ [31], one classifies (T, C) and $(C',E',E_{M,\mathbf{B}})$ as the factorizable and non-factorizable amplitudes, respectively.

Furthermore, it is found in Fig. 1a, b that $\mathbf{B}_c$ with $(q_a q_b-q_b q_a)c$ cannot be turned into $\mathbf{B}^*(q_a q_b q_{k(i)})$, where $q_a q_b q_{k(i)}$ are totally symmetric, such that (T, C) give no contributions to $\mathbf{B}_c\rightarrow \mathbf{B}^* M$. Thus, the $\mathbf{B}_c\rightarrow \mathbf{B}^*M$ decays are purely non-factorizable processes. In addition, $C'$ and $E'$ are suppressed in $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ [25], which is in accordance with the K$\ddot{\text {o}}$rner–Pati–Woo theorem [32,33,34]. With the current–current structure of $(\bar{q}_i q_j)_{V-A}(\bar{q}_k c)_{V-A}$ in Eq. (2), $q_i$ and $q_k$ are color anti-symmetric. When combined as the constituents of the baryon, $q_{i,k}$ are flavor anti-symmetric, such that the topological diagrams $(C',E')$ in Fig. 1c, d contribute to $\mathbf{B}_c\rightarrow \mathbf{B}M$, instead of $\mathbf{B}_c\rightarrow \mathbf{B}^* M$. Consequently, we are left with the $W_{\text {EX}}$ topological diagrams $(E_\mathbf{B},E_M)$ in Fig. 1e, f for $\mathbf{B}_c\rightarrow \mathbf{B}^* M$.

To proceed, we derive the amplitudes as ${\mathcal {A}}(\mathbf{B}_c\rightarrow \mathbf{B}^*M)=({G_F}/{\sqrt{2}}) T(\mathbf{B}_c\rightarrow \mathbf{B}^*M)$. Explicitly, the T amplitudes (T-amps) read [17, 25, 27]

$$\begin{aligned} T(\mathbf{B}_c\rightarrow \mathbf{B}^*M)= & {} E_\mathbf{B}^{(s)} ({\mathbf{B}_c})^{ja} H^{ki}_j(\mathbf{B}^*)_{kab}(M)_i^b \nonumber \\&+E_M^{(s)} ({\mathbf{B}_c})^{ja} H^{ki}_j(\mathbf{B}^*)_{iab}(M)_k^b , \end{aligned}$$

(8)

where the parameters $E_{\mathbf{B},M}^{(s)}$ correspond to the topological diagrams in Fig. 1e, f, respectively. The $W_{\text {EX}}$ decay process needs an additional quark pair from $g\rightarrow q\bar{q}$, where $q\bar{q}$ could be $u\bar{u}$, $d\bar{d}$ or $s\bar{s}$. To take into account the broken $SU(3)_f$ symmetry, $E_{\mathbf{B}(M)}$ with $g\rightarrow s\bar{s}$ can be more specifically denoted by $E_{\mathbf{B}(M)}^s$. Under the exact $SU(3)_f$ symmetry, it leads to $E_{\mathbf{B}(M)}^s=E_{\mathbf{B}(M)}$ [26]. In Tables 1, 2 and 3, we present the full expansions of $T(\mathbf{B}_c\rightarrow \mathbf{B}^*M)$ for the CA, SCS and DCS decay modes, respectively. For the branching fractions, we use the equation for the two-body decays, given by [1]

$$\begin{aligned}&{\mathcal {B}}(\mathbf{B}_c\rightarrow \mathbf{B}^* M)= \frac{G_F^2|\vec {p}_{\mathbf{B}^*}|\tau _{\mathbf{B}_c}}{16\pi m_{\mathbf{B}_c}^2 } |T(\mathbf{B}_c\rightarrow \mathbf{B}^* M)|^2 ,\nonumber \\&|\vec {p}_{\mathbf{B}^*}|=\frac{ \sqrt{(m_{\mathbf{B}_c}^2-m_+^2)(m_{\mathbf{B}_c}^2-m_-^2)}}{2 m_{\mathbf{B}_c}} , \end{aligned}$$

(9)

with $m_\pm =m_{\mathbf{B}^*}\pm m_M$, where $\tau _{\mathbf{B}_c}$ stands for the $\mathbf{B}_c$ baryon lifetime.

3 Numerical analysis and discussions

Table 1 Cabibbo-allowed $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays

In the numerical analysis, we adopt the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements as [1]

$$\begin{aligned}&(V_{cs},V_{ud},V_{us},V_{cd})= (1-\lambda ^2/2,1-\lambda ^2/2,\lambda ,-\lambda ) , \end{aligned}$$

(10)

with $\lambda =s_c=0.22453\pm 0.00044$ in the Wolfenstein parameterization. Besides, the $\mathbf{B}_c$ and $\mathbf{B}^*$ masses, together with the lifetime for $\mathbf{B}_c$, are adopted from the PDG [1]. We perform a minimum $\chi ^2$-fit with $\chi ^2=\sum ({\mathcal {B}}_{th}-{\mathcal {B}}_{ex})^2/\sigma _{ex}^{2}$, where ${\mathcal {B}}_{th(ex)}$ represents the theoretical (experimental) input of the branching ratio, and $\sigma _{ex}$ the experimental error. We calculate ${\mathcal {B}}_{th}$ with the equation in Eq. (9), together with $({\mathcal {B}}_{ex},\sigma _{ex})$ from Table 1. Note that ${\mathcal {B}}(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0,\Xi ^{*0} \pi ^+)$ are not involved in the fit.

We use two scenarios for the global fit. In the first scenario (S1), we take $E_{\mathbf{B}(M)}^s=E_{\mathbf{B}(M)}$ under the exact $SU(3)_f$ symmetry. Since $E_\mathbf{B}$ and $E_{M}$ are complex numbers, it leads to three independent parameters, given by

$$\begin{aligned} |E_\mathbf{B}|,\,|E_{M}| e^{i\delta _{E_M}} , \end{aligned}$$

(11)

where $E_\mathbf{B}$ is set to be real, and $\delta _{E_{M}}$ is a relative strong phase. Using the $\chi ^2$-fit, we extract that

$$\begin{aligned}&(|E_\mathbf{B}|,|E_{M}|)=(0.41\pm 0.03,0.34\pm 0.03)\,\text {GeV}^3 ,\nonumber \\&\delta _{E_M}=(180.0\pm 35.8)^\circ , \end{aligned}$$

(12)

with $\chi ^2/n.d.f=4.5$, where $n.d.f=1$ is the number of the degrees of freedom. For $\delta _{E_M}$, its information is from ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta )$. Although $\delta _{E_M}=180^\circ$ has induced the largest positive interference between $E_\mathbf{B}$ and $E_M$, our result of ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta )=(5.3\pm 0.7)\times 10^{-3}$ is still shown to be in tension with the observation of $(9.1\pm 2.0)\times 10^{-3}$. Sizeably, it adds 3.6 to the total $\chi ^2$ value.

Since $\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta$ is in association with $|E_M^s|$, the tension hints the broken $SU(3)_f$ symmetry, where $|E_M^s|$ is not equal to $|E_M|$. On the other hand, ${\mathcal {B}}(\Xi _c^0 \rightarrow \Omega ^- K^+)$ is fitted to agree with the data, indicating that $|E_\mathbf{B}^s|$ is not deviating from $|E_\mathbf{B}|$. Currently, the data points are not sufficient for an independent extraction of $|E_M^s|$. We hence adopt the numerical results from the two-body D meson decays, where the similar $W_{\text {EX}}$ contributions have been found to induce the severe $SU(3)_f$ symmetry breaking [18,19,20,21]. In the second scenario (S2), we take $|E_M^s|=n_q\times |E_M|$ and $|E_\mathbf{B}^s|\simeq |E_\mathbf{B}|$, with $n_q=1.4$ adopted from [21]. Consequently, we obtain

$$\begin{aligned}&(|E_\mathbf{B}|,|E_{M}|)=(0.40\pm 0.03,0.34\pm 0.03)\,\text {GeV}^3 ,\nonumber \\&\delta _{E_M}=(180.0\pm 46.8)^\circ , \end{aligned}$$

(13)

where $\chi ^2/n.d.f$ is reduced as 1.3. As the demonstration, we obtain ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta )=(7.3\pm 1.5)\times 10^{-3}$, which alleviates the deviation from the observation. With the fit values of $(|E_\mathbf{B}|,|E_{M}|,\delta _{E_M})$ in S1 and S2, we present the branching ratios of the $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays in Tables 1, 2 and 3, along with the recent theoretical results for comparison.

Table 2 Singly Cabibbo-suppressed $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays

We get some useful relations in the quark-diagram scheme. For example, we find out three triangle sum rules for $\mathbf{B}_c\rightarrow \Delta \pi$, given by

$$\begin{aligned}&T(\Lambda _c^+\rightarrow \Delta ^0\pi ^+)-T(\Lambda _c^+\rightarrow \Delta ^{++}\pi ^-) \nonumber \\&\quad -\sqrt{6} T(\Lambda _c^+\rightarrow \Delta ^+\pi ^0)=0 , \nonumber \\&T(\Xi _c^+\rightarrow \Delta ^0\pi ^+)-T(\Xi _c^+\rightarrow \Delta ^{++}\pi ^-) \nonumber \\&\quad -\sqrt{6} T(\Xi _c^+\rightarrow \Delta ^+\pi ^0)=0 , \nonumber \\&T(\Xi _c^0\rightarrow \Delta ^+\pi ^-)-T(\Xi _c^0\rightarrow \Delta ^{-}\pi ^+) \nonumber \\&\quad -\sqrt{6} T(\Xi _c^0\rightarrow \Delta ^0\pi ^0)=0 . \end{aligned}$$

(14)

Besides, we obtain

$$\begin{aligned}&T(\Lambda _c^+ \rightarrow \Delta ^+ K^0,\Delta ^0 K^+)=0 ,\nonumber \\&T(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0,\Xi ^{*0} \pi ^+)=0 , \end{aligned}$$

(15)

as the consequence of $C'$ being set to give no contribution to $\mathbf{B}_c\rightarrow \mathbf{B}^* M$. Indeed, $C'$ is the only topology that takes part in the decays in Eq. (15), but suppressed due to the K$\ddot{\text {o}}$rner–Pati–Woo theorem [32,33,34]. According to the other theoretical calculations [6, 7, 22,23,24], ${\mathcal {B}}(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0,\Xi ^{*0} \pi ^+)=0$ is also predicted, which supports that $C'=0$. Experimentally, ${\mathcal {B}}_{ex}(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0,\Xi ^{*0} \pi ^+)$ in Table 2 can be used to test the suppression. With ${\mathcal {B}}(\Xi _c^+ \rightarrow \Xi ^{*0} \pi ^+)/{\mathcal {B}}(\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+)<0.1$ and ${\mathcal {B}}(\Xi _c^+\rightarrow \Xi ^-\pi ^+\pi ^+) =(2.86\pm 1.21\pm 0.38)\times 10^{-2}$ [1, 35], we determine ${\mathcal {B}}_{ex}(\Xi _c^+ \rightarrow \Xi ^{*0} \pi ^+)<4.0\times 10^{-3}$, which can be seen as the non-observation to agree with $T(\Xi _c^+ \rightarrow \Xi ^{*0} \pi ^+)=0$. However, ${\mathcal {B}}_{ex}(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0)=(2.9\pm 1.7)\times 10^{-2}$ seems to disagree with the prediction of ${\mathcal {B}}(\Xi _c^+ \rightarrow \Sigma ^{*+} \bar{K}^0)=0$, despite of the large uncertainty. While the K$\ddot{\text {o}}$rner–Pati–Woo theorem is regarded as a tree-level approximation, allowing possible corrections to $C'$ and $E'$, we need more accurate observations to test if $C'(E')=0$.

Table 3 Doubly Cabibbo-suppressed $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays

Uniquely, the decuplet baryon can contain three identical quarks, denoted by $\mathbf{B}^*(qqq)$, which leads to an additional weight factor of $\sqrt{3}$ among the decuplet baryons in Eq. (6). The factor can be considered as the main reason why $\Lambda _c^+ \rightarrow \Delta ^{++} K^-$ and $\Xi _c^0 \rightarrow \Omega ^- K^+$ are measured with the largest branching fractions in the CA decay channels of $\Lambda _c^+,\Xi _c^0\rightarrow \mathbf{B}^*M$, respectively. Accordingly, the T-amps with $\mathbf{B}^*(qqq)$ are listed as

$$\begin{aligned}&T(\Lambda _c^+\rightarrow \Delta ^{++} K^-,\Delta ^{++} \pi ^-)=-(\lambda _a,\lambda _d)\,E_M ,\nonumber \\&T(\Xi _c^+ \rightarrow \Delta ^{++} K^-,\Delta ^{++} \pi ^-)=-(\lambda _s,\lambda _c)\,E_M ,\nonumber \\&T(\Xi _c^0 \rightarrow \Omega ^- K^+,\Delta ^- \pi ^+)=(\lambda _a,-\lambda _c)\,E_\mathbf{B} . \end{aligned}$$

(16)

While ${\mathcal {B}}(\Lambda _c^+\rightarrow \Delta ^{++} K^-)$ and ${\mathcal {B}}(\Xi _c^0 \rightarrow \Omega ^- K^+)$ have been observed, the other branching fractions are given by

$$\begin{aligned}&{\mathcal {B}}(\Lambda _c^+\rightarrow \Delta ^{++} \pi ^-,\Xi _c^+ \rightarrow \Delta ^{++} K^-) \nonumber \\&\quad =(7.0\pm 1.4,13.5\pm 2.7)\times 10^{-4} ,\nonumber \\&{\mathcal {B}}(\Xi _c^+ \rightarrow \Delta ^{++} \pi ^-,\Xi _c^0 \rightarrow \Delta ^- \pi ^+) \nonumber \\&\quad =(7.8\pm 1.6,2.5\pm 0.4)\times 10^{-5} , \end{aligned}$$

(17)

which are predicted as the largest branching fractions in the SCS $\Lambda _c^+(\Xi _c^+)$ and DCS $\Xi _c^{+(0)}$ decay channels, respectively. Here, we present our predictions of S2, which is favored by the $\chi ^2$-fit. The equality of $T(\Lambda _c^+ \rightarrow \Sigma ^{*0} \pi ^+)=T(\Lambda _c^+ \rightarrow \Sigma ^{*+} \pi ^0)$ corresponds to the isospin symmetry. The branching fraction, given by

$$\begin{aligned} {\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*0(+)} \pi ^{+(0)})= & {} (2.8\pm 0.4)\times 10^{-3} , \end{aligned}$$

(18)

can be used to test the broken effect. The decays $\mathbf{B}_c\rightarrow \mathbf{B}^*\eta ^{(\prime )}$, $\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta$, $\Xi _c^0 \rightarrow \Xi ^{*0} \eta$ and $\Xi _c^+ \rightarrow \Sigma ^{*+}\eta$ have sizeable branching fractions, which is due to the constructive interferences between $E_\mathbf{B}$ and $E_M$. However, the other branching fractions of $\mathbf{B}_c\rightarrow \mathbf{B}^*\eta ^{(\prime )}$ are typically small with the destructive interferences. Moreover, we find that ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta ^\prime )=0$ with $m_{\Lambda _c^+}<m_{\Sigma ^{*+}}+m_{\eta ^\prime }$.

The approach of the irreducible $SU(3)_f$ symmetry has been widely used in the hadron weak decays [4,5,6,7,8,9,10,11,12,13,14,15,16]. For $\mathbf{B}_c\rightarrow \mathbf{B}^*M$, there exist four parameters $a_8$ and $a_{9,10,11}$ [4, 6], which correspond to the decomposition of ${\mathcal {H}}_{eff}=H(6)+H(\overline{15})$ in the $SU(3)_f$ representation of 6 and $\overline{15}$, respectively. By comparison, we derive that

$$\begin{aligned} (E_{\mathbf{B}},E_{M})&=(-2 a_8+a_9,2a_8+a_9),\;(E',C')\nonumber \\&=(-2a_9-2a_{10},-2a_{11})\,, \end{aligned}$$

(19)

such that $a_i$ are found to correspond to the topologies. Since $(E',C')$ have been the vanishing topological parameters, one has $a_9=-a_{10}$ and $a_{11}=0$. Moreover, our global fits for $E_{\mathbf{B},M}$ indicate that $a_{9(10)}$ from $H(\overline{15})$ has a non-zero value. By contrast, the numerical analysis performed with the irreducible $SU(3)_f$ symmetry neglects the contributions from $H(\overline{15})$ [7], whose results are given in the tables. In the physical mass scenario ($S_{pm}$) for the global fit in Ref. [7], where $m_{\mathbf{B}_c}$, $m_{\mathbf{B}^*}$ and $m_M$ are taken from the physical values in Ref. [1], ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta ,\Xi ^{*0} K^+)$ and ${\mathcal {B}}(\Xi _c^0 \rightarrow \Omega ^- K^+)$ are fitted to be a few times smaller than the observations. Instead of considering the $SU(3)_f$ symmetry breaking, one performs another fit in the equal mass scenario ($S_{em}$), where $m_{\Lambda _c}=m_{\Xi _c}$, $m_\Delta =m_{\Sigma ^*}=m_{\Omega }$ and $m_\pi =m_\eta =m_K$, resulting in the raised values of the above branching fractions.

4 Conclusions

In summary, we have studied the $\mathbf{B}_c\rightarrow \mathbf{B}^* M$ decays in the quark-diagram scheme. We have found that only two W-exchange diagrams, $E_\mathbf{B}$ and $E_M$, could give contributions to the observed branching fractions of $\Lambda _c^+ \rightarrow (\Delta ^{++} K^-$, $\Sigma ^{*+} \eta$, $\Xi ^{*0} K^+)$ and $\Xi _c^0 \rightarrow \Omega ^- K^+$. In addition, we have predicted ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*0(+)} \pi ^{+(0)})=(2.8\pm 0.4)\times 10^{-3}$, which respects the isospin symmetry. To interpret the observation of ${\mathcal {B}}(\Lambda _c^+ \rightarrow \Sigma ^{*+} \eta )$, we have taken into account the $SU(3)_f$ symmetry breaking. In particular, ${\mathcal {B}}(\Lambda _c^+\rightarrow \Delta ^{++} \pi ^-,\Xi _c^+ \rightarrow \Delta ^{++} K^-) =(7.0\pm 1.4,13.5\pm 2.7)\times 10^{-4}$ and ${\mathcal {B}}(\Xi _c^+ \rightarrow \Delta ^{++} \pi ^-,\Xi _c^0 \rightarrow \Delta ^- \pi ^+) =(7.8\pm 1.6,2.5\pm 0.4)\times 10^{-5}$ have been predicted as the largest branching fractions in the SCS $\Lambda _c^+(\Xi _c^+)$ and DSC $\Xi _c^{+(0)}$ decay channels, respectively.