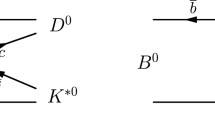Strong decays of ${\bar{D}}^{*}K^{*}$ molecules and the newly observed $X_{0,1}$ states

Abstract

Lately, the LHCb Collaboration reported the discovery of two new states in the $B^+\rightarrow D^+D^- K^+$ decay, i.e., $X_0(2866)$ and $X_1(2904)$. In the present work, we study whether these states can be understood as ${\bar{D}}^*K^*$ molecules from the perspective of their two-body strong decays into $D^-K^+$ via triangle diagrams and three-body decays into ${\bar{D}}^*K\pi$. The coupling of the two states to ${\bar{D}}^*K^*$ are determined from the Weinberg compositeness condition, while the other relevant couplings are well known. The obtained strong decay width for the $X_0(2866)$ state, in marginal agreement with the experimental value within the uncertainty of the model, hints at a large ${\bar{D}}^*K^*$ component in its wave function. On the other hand, the strong decay width for the $X_1(2904)$ state, much smaller than its experimental counterpart, effectively rules out its assignment as a ${\bar{D}}^*K^*$ molecule.

1 Introduction

Ever since the experimental discovery of X(3872) and $D_{s0}^*(2317)$, many hadrons that cannot be simply classified into conventional mesons of $q{\bar{q}}$ and baryons of qqq have been discovered, with the latest addition being the $cc{\bar{c}}{\bar{c}}$ states discovered by the LHCb Collaboration [1]. See, e.g., Refs. [2,3,4,5] for recent reviews. It should be noted that most of the so-called exotic hadrons mix with conventional hadrons or can be understood as hadron–hadron molecules or threshold effects such that they are not that “exotic”. Curiously, two of the truly exotic candidates, $\theta ^+(1540)$ [6] and X(5568) [7] seem to fade away with time. In such a context, the latest LHCb announcement of two structures observed in the $D^-K^+$ invariant mass of the $B^+ \rightarrow D^+D^-K^+$ decay points to the likely existence of genuinely exotic mesonic states with a minimum quark content of ${\bar{c}}{\bar{s}}ud$ [8, 9]. Their spin-parities, masses, and widths (in units of MeV) are, respectively¹

$$\begin{aligned}&X_0(2866):\quad 0^+, \quad M=2866\pm 7\pm 2, \quad \nonumber \\&\quad \text{ and }\quad \Gamma =57\pm 12\pm 4, \end{aligned}$$

(1)

$$\begin{aligned}&X_1(2904):\quad 1^-,\quad M=2904\pm 5\pm 1, \quad \nonumber \\&\quad \text{ and }\quad \Gamma =110\pm 11\pm 4. \end{aligned}$$

(2)

Fig. 1

Diagrams representing the decay of the $X_{J=0,1}$ states to $D^{-}K^{+}$

Fig. 2

Diagrams representing the decay of the $X_{J=0,1}$ states to ${\bar{D}}^{*}K\pi$

The existence of compact tetraquark states in this energy region has been predicted in either quark models [10,11,12,13], or QCD sum rules [14, 15]. However, the lattice QCD study found no compact tetraquark state of ${\bar{c}}{\bar{s}}ud$ with $I=0$ and spin-parity $0^+$ and $1^+$ [16]. The $X_J$ states might be ${\bar{D}}^{*}K^*$ hadronic molecules, since their masses are just below ($X_0$) or close to ($X_1$) the ${\bar{D}}^{*}K^*$ threshold. Indeed, in one earlier study [17], a molecular $X_0$ state with a narrow width and a mass around 2848 MeV was predicted in the unitary coupled channels approach. This state may be related to the newly observed $X_0(2866)$ state. Following the discovery of the $X_{J=0,1}$ states, a study within the one-boson-exchange model [18] found that $X_0$ can be interpreted as a hadronic molecule composed of ${\bar{D}}^{*} K^{*}$. On the other hand, it is shown that the $D^{*-}K^{*+}$ rescattering via the $\chi _{c1}D^{*-}K^{*+}$ loop or the ${\bar{D}}_{1}^{0}K^{0}$ rescattering via the $D_{sJ}^{+}{\bar{D}}_{1}^{0}K^{0}$ loop may contribute to the observed two peaks as discussed in Ref. [19]. So far, the support for the ${\bar{D}}^{*}K^*$ bound state nature of the $X_J$ states is getting more consensus, especially for $X_0(2866)$. In this context it is worth studying their two-body and three-body strong decays, based on the molecular picture.

In the present work, we examine the possibility whether they can be understood as ${\bar{D}}^*K^*$ molecules. For such a purpose, we first assume that they are bound states of ${\bar{D}}^*K^*$, and then employ the Weinberg compositeness rule to determine their couplings to ${\bar{D}}^*K^*$. The two-body strong decays then follow from the exchange of a pseudoscalar meson between the ${\bar{D}}^*K^*$ pair, which then transforms into $D^-K^+$. Such a process is depicted in Fig. 1. In addition, the ${\bar{D}}^*K^*$ molecules can also decay into a three-body final state ${\bar{D}}^*K\pi$, as shown in Fig. 2. If within the uncertainties of the model, the so-obtained strong decay widths are consistent with data, then it is possible to assign the state under study as a molecular state, otherwise, the possibility is excluded. Such an approach has been widely applied to study newly observed (exotic) hadrons, see, e.g., Refs. [20,21,22,23,24,25,26,27] for a partial list.

This work is organized as follows. In Sect. 2, we explain the theoretical formalism. Results and discussions are provided in Sect. 3, followed by a short summary in Sect. 4.

2 Theoretical framework

In the following, we explain how the strong decays into ${\bar{D}}K$, Fig. 1, and ${\bar{D}}^*K\pi$, Fig. 2, are computed. We take advantage of the fact that ${\bar{D}}^*$ is very narrow (with a width of less than 100 keV) and therefore can be treated as a stable particle for our purpose.

We shall construct the amplitudes using the isospin formalism, where the ${\bar{D}}^{*}K^*$ isospin doublet reads

$$\begin{aligned} |{\bar{D}}^{*}K^{*},I=0\rangle&=\frac{1}{\sqrt{2}}(D^{*-}K^{*+}+{\bar{D}}^{*0}K^{*0}), \end{aligned}$$

(3)

$$\begin{aligned} |{\bar{D}}^{*}K^{*},I=1\rangle&=-\frac{1}{\sqrt{2}}(D^{*-}K^{*+}-{\bar{D}}^{*0}K^{*0}), \end{aligned}$$

(4)

with the following isospin assignments for the ${\bar{D}}^*$ and $K^*$ states:

$$\begin{aligned} \left( \begin{array}{c} {\bar{D}}^{*0} \\ D^{*-} \\ \end{array} \right) \thicksim \left( \begin{array}{c} \big |\frac{1}{2},\frac{1}{2}\big \rangle \\ -\big |\frac{1}{2},-\frac{1}{2}\big \rangle \\ \end{array} \right) ,~~~~~ \left( \begin{array}{c} K^{*+} \\ K^{*0} \\ \end{array} \right) \thicksim \left( \begin{array}{c} \big |\frac{1}{2},\frac{1}{2}\big \rangle \\ \big |\frac{1}{2},-\frac{1}{2}\big \rangle \\ \end{array} \right) . \end{aligned}$$

(5)

Considering quantum numbers and phase space, the two-body strong decay modes of $X_J$ are $X_J\rightarrow {}D^{-}K^{+}$ and $X_J\rightarrow {}{\bar{D}}^{0}K^{0}$. In this work, we only explicitly compute the partial decay width of $X_J\rightarrow {}D^{-}K^{+}$, and that of $X_J\rightarrow {}{\bar{D}}^{0}K^{0}$ can be obtained by isospin symmetry $\Gamma _{X_J\rightarrow {}D^{-}K^{+}}=\Gamma _{X_J\rightarrow {}{\bar{D}}^{0}K^{0}}$. The sum of the two parts is the total decay width of the $X_J\rightarrow {\bar{D}}K$.

Fig. 3

Mass operators of the $X_J$ states

In order to calculate the Feynman diagrams shown in Fig. 1, we need to determine the relevant vertices. For the vertex of $X_J{\bar{D}}^{*}K^{*}$, since the $X_J$ states are considered as bound states of ${\bar{D}}^*K^{*}$, this coupling can be determined by the Weinberg compositeness condition. In the present work, we adopt the method developed in Refs. [20,21,22,23,24,25,26,27]. In this framework, the relevant Lagrangians for $X_0(2866)$ can be written as [21]

$$\begin{aligned} \mathcal{{L}}_{X_0}(x)=&g_{X_0{\bar{D}}^{*}K^{*}}X_J(x)\int {}dy\Phi (y^2){\bar{D}}^{*\mu }(x+\omega _{K^{*}}y)\nonumber \\&\times K^{*}_{\mu }(x-\omega _{{\bar{D}}^{*}}y)+H.c., \end{aligned}$$

(6)

while for $X_1(2904)$ the Lagrangian has the form [28]

$$\begin{aligned} \mathcal{{L}}_{X_1}(x)&=g_{X_1{\bar{D}}^{*}K^{*}}X_J^{\alpha }(x)\int {}dy\Phi (y^2){\bar{D}}^{*}_{\mu }(x+\omega _{K^{*}}y) \overleftrightarrow {\partial }_{\alpha }\nonumber \\&\times K^{*\mu }(x-\omega _{{\bar{D}}^{*}}y), \end{aligned}$$

(7)

where $\omega _{i}=m_{i}/(m_i+m_j)$ is a kinematical parameter with $m_i$ and $m_j$ being the masses of the involved mesons. In the Lagrangians, an effective correlation function $\Phi (y^2)$ is introduced to describe the distribution of the two constituents, ${\bar{D}}^{*}$ and $K^{*}$, in the hadronic molecular $X_J$ states. The introduced correlation function also serves the purpose of making the Feynman diagrams ultraviolate finite. Here we choose the Fourier transformation of the correlation function to have a Gaussian form,

$$\begin{aligned} \Phi (-p_E^2)\doteq \exp (-p_E^2/\alpha ^2), \end{aligned}$$

(8)

with $\alpha$ being the size parameter which characterizes the distribution of the constituents inside the molecule. The value of $\alpha$ has to be determined by fitting to data. It is found that the experimental total decay widths of some states that can be considered as molecules (see, e.g., Refs. [20,21,22,23,24,25,26,27] and references therein) can be well explained with $\alpha \approx 1.0$ GeV. Therefore we take $\alpha =1.0\pm 0.1$ GeV in this work to study whether the $X_J$ states can be interpreted as molecules composed of ${\bar{D}}^{*}K^{*}$.

The coupling constant $g_{X_J{\bar{D}}^*K^{*}}$ is determined by the compositeness condition [20,21,22,23,24,25,26,27]. It implies that the renormalization constant of the hadron wave function is set to zero, i.e.,

$$\begin{aligned} Z_{X_J}=1-\frac{d\Sigma ^{~~T}_{0,1}}{dk\!\!\!/_0}|_{k\!\!\!/_0=m_{X_J}}=0, \end{aligned}$$

(9)

where $\Sigma _0$ is the self-energy operator of $X_0$, and $\Sigma ^T_{1}$ is the transverse part of the self-energy operator $\Sigma ^{\mu \nu }_{1}$ of $X_1$, related to $\Sigma ^{\mu \nu }_{1}$ via

$$\begin{aligned} \Sigma ^{\mu \nu }_{1}(k_0)=\bigg (g_{\mu \nu }-\frac{k_0^{\mu }k_0^{\nu }}{k_0^2}\bigg )\Sigma ^{T}_{1}+\cdots . \end{aligned}$$

(10)

The concrete form of the mass operator $\Sigma _0$ of $X_0$ corresponding to Fig. 3 is

$$\begin{aligned} \Sigma _0(k_0)&=\frac{g^2_{X_0{\bar{D}}^{*}K^{*}}}{16\pi ^2m^2_{K^{*}}m^2_{{\bar{D}}^*}}\int _0^{\infty }d\eta \int _0^{\infty }d\beta \sum _{Y={\bar{D}}^{*0}K^{*0},D^{*-}K^{*+}}(\mathcal{{C}}^I_{Y})^2\nonumber \\&\quad \times \bigg \{-\frac{k_0^2\Delta _Y[(m^2_{K^{*}}+m^2_{{\bar{D}}^{*}})z\Delta _Y+4z^2m^2_{{\bar{D}}^{*}}+6\alpha ^2(\Delta _Y+2z)]}{4z^2}\nonumber \\&\quad +2\bigg [m^2_{K^{*}}(2zm^2_{{\bar{D}}^*}+\alpha ^2)+\alpha ^2(m^2_{{\bar{D}}^*}+3\alpha ^2)\bigg ]+\frac{k_0^4\Delta ^2_{Y}(\Delta _Y+2z)^2}{16z^3}\bigg \}\nonumber \\&\quad \times {}\frac{1}{z^3}\exp \bigg \{-\frac{1}{\alpha ^2}\bigg [-2k_0^2\omega ^2_{{\bar{D}}^{*}}+\eta {}m^2_{{\bar{D}}^*}+\beta (-k_0^2+m^2_{K^{*}})+\frac{\Delta _Y^2}{4z}k_0^2\bigg ]\bigg \}, \end{aligned}$$

(11)

and that of the transverse part of the self-energy operator of $X_1$ is

$$\begin{aligned} \Sigma ^T_{1}(k_0)&=\frac{\alpha ^2g^2_{X_1{\bar{D}}^{*}K^{*}}}{16\pi ^2m^2_{K^{*}}m^2_{{\bar{D}}^*}}\int _0^{\infty }d\eta \int _0^{\infty }d\beta \sum _{Y={\bar{D}}^{0}K^{0},D^{*-}K^{*+}}(\mathcal{{C}}^I_{Y})^2\nonumber \\&\quad \times \bigg \{-\frac{k_0^2\Delta _Y[(m^2_{K^{*}}+m^2_{{\bar{D}}^{*}})z\Delta _Y+4z^2m^2_{{\bar{D}}^{*}}+8\alpha ^2(\Delta _Y+2z)]}{2z}\nonumber \\&\quad +2[3\alpha ^2z(m^2_{K^{*}}+m^2_{{\bar{D}}^{*}})+12\alpha ^4+4m^2_{K^{*}}m^2_{{\bar{D}}^*}z^2]+\frac{k_0^4\Delta _Y^2(\Delta _Y+2z)^2}{8z^2}\bigg \}\nonumber \\&\quad \times {}\frac{1}{z^5}\exp \bigg \{-\frac{1}{\alpha ^2}\bigg [-2k_0^2\omega ^2_{{\bar{D}}^{*}}+\eta {}m^2_{{\bar{D}}^*}+\beta (-k_0^2+m^2_{K^{*}})+\frac{\Delta _Y^2}{4z}k_0^2\bigg ]\bigg \}, \end{aligned}$$

(12)

where $z=2+\eta +\beta$, $\Delta _Y=-4\omega _{{\bar{D}}^{*}}-2\beta {}$, and $k_0^2=m^2_{X}$ with $k_0$, $m_{X}$ denoting the four-momenta and mass of $X_J$, respectively. Here, we set $m_{X_J}=m_{{\bar{D}}^{*}}+m_{K^{*}}-E_b$ with $E_b$ the binding energy of $X_J$, $k_1$, and $m_{{\bar{D}}^{*}}$ are the four-momenta and mass of ${\bar{D}}^{*}$, and $m_{K^{*}}$ is the mass of $K^{*}$, respectively. I is isospin and isospin symmetry implies that

$$\begin{aligned} \begin{aligned} \mathcal{{C}}^{I=0}_Y= \left\{ \begin{array}{ll} 1/\sqrt{2}, &{} Y={\bar{D}}^{*0}K^{*0}\\ 1/\sqrt{2}, &{} Y=D^{*-}K^{*+} \end{array} \right. , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mathcal{{C}}^{I=1}_Y= \left\{ \begin{array}{ll} 1/\sqrt{2}, &{} Y={\bar{D}}^{*0}K^{*0}\\ -1/\sqrt{2}, &{} Y=D^{*-}K^{*+} \end{array} \right. . \end{aligned} \end{aligned}$$

To evaluate the diagrams of Figs. 1 and 2, in addition to the Lagrangians in Eqs. (6, 7), the following effective Lagrangians, responsible for the interaction between a vector meson and a pseudoscalar meson, are needed as well [29]

$$\begin{aligned} \mathcal{{L}}_{PPV}=\frac{i}{4}g_{h}\langle [\partial ^{\mu }P,P]V_{\mu }\rangle , \end{aligned}$$

(13)

where P is the SU(4) pseudoscalar meson matrix, and $V_{\mu }$ is the matrix of vector fields. The $\langle \cdots \rangle$ denotes trace in the SU(4) flavor space. The meson matrices are [29]

$$\begin{aligned} P=\sqrt{2} \left( \begin{array}{cccc} \frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}+\frac{\eta ^{'}}{\sqrt{3}} &{}\pi ^{+} &{}K^{+} &{} {\bar{D}}^0 \\ \pi ^{-} &{} -\frac{\pi ^{0}}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}+\frac{\eta ^{'}}{\sqrt{3}} &{}K^{0} &{}-D^{-} \\ K^{-} &{} {\bar{K}}^{0} &{} -\sqrt{\frac{2}{3}}\eta +\frac{\eta ^{'}}{\sqrt{3}} &{} D^{-}_s\\ D^0 &{} -D^{+} &{}D_s^{+} &{}\eta _c \\ \end{array} \right) \nonumber \\ \end{aligned}$$

(14)

and

$$\begin{aligned} V_{\mu }= \left( \begin{array}{cccc} \frac{1}{\sqrt{2}}(\rho ^{0}+\omega ) &{} \rho ^{+} &{} K^{*+} &{} {\bar{D}}^{*0} \\ \rho ^{-} &{} \frac{1}{\sqrt{2}}(-\rho ^{0}+\omega ) &{} K^{*0} &{} -D^{*-} \\ K^{*-} &{} {\bar{K}}^{*0} &{} \phi &{} D^{*-}_s \\ D^{*0} &{} -D^{*+} &{} D^{*+}_{s} &{} J/\psi \\ \end{array} \right) _{\mu }. \end{aligned}$$

(15)

Then we obtain

$$\begin{aligned} \mathcal{{L}}_{\pi {}DD^{*}}&=-\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }D^{+}-D^{+}\partial ^{\mu }\pi ^0){\bar{D}}^{*-}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(\pi ^{-}\partial ^{\mu }D^{+}-D^{+}\partial ^{\mu }\pi ^{-}){\bar{D}}^{*0}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}(\pi ^{+}\partial ^{\mu }D^{0}-D^{0}\partial ^{\mu }\pi ^+){\bar{D}}^{*-}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }D^{0}-D^{0}\partial ^{\mu }\pi ^0){\bar{D}}^{*0}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }{\bar{D}}^{-}-{\bar{D}}^{-}\partial ^{\mu }\pi ^0)D^{*+}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}(\pi ^{+}\partial ^{\mu }{\bar{D}}^{-}-{\bar{D}}^{-}\partial ^{\mu }\pi ^+)D^{*0}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(\pi ^{-}\partial ^{\mu }{\bar{D}}^{0}-{\bar{D}}^{0}\partial ^{\mu }\pi ^-)D^{*+}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }{\bar{D}}^{0}-{\bar{D}}^{0}\partial ^{\mu }\pi ^0)D^{*0}_{\mu }, \end{aligned}$$

(16)

$$\begin{aligned} \mathcal{{L}}_{\eta {}DD^{*}}&=+\frac{ig_h}{2\sqrt{6}}(\eta \partial ^{\mu }D^{+}-D^{+}\partial ^{\mu }\eta ){\bar{D}}^{*-}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2\sqrt{6}}(\eta \partial ^{\mu }D^{0}-D^{0}\partial ^{\mu }\eta ){\bar{D}}^{*0}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2\sqrt{6}}(\eta \partial ^{\mu }{\bar{D}}^{-}-{\bar{D}}^{-}\partial ^{\mu }\eta )D^{*+}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2\sqrt{6}}(\eta \partial ^{\mu }{\bar{D}}^{0}-{\bar{D}}^{0}\partial ^{\mu }\eta )D^{*0}_{\mu }, \end{aligned}$$

(17)

$$\begin{aligned} \mathcal{{L}}_{\pi {}KK^{*}}&=-\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }K^{+}-K^{+}\partial ^{\mu }\pi ^0){\bar{K}}^{*-}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}(\pi ^{-}\partial ^{\mu }K^{+}-K^{+}\partial ^{\mu }\pi ^{-}){\bar{K}}^{*0}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}(\pi ^{+}\partial ^{\mu }K^{0}-K^{0}\partial ^{\mu }\pi ^+){\bar{K}}^{*-}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }K^{0}-K^{0}\partial ^{\mu }\pi ^0){\bar{K}}^{*0}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }{\bar{K}}^{-}-{\bar{K}}^{-}\partial ^{\mu }\pi ^0)K^{*+}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(\pi ^{+}\partial ^{\mu }{\bar{K}}^{-}-{\bar{K}}^{-}\partial ^{\mu }\pi ^+)K^{*0}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(\pi ^{-}\partial ^{\mu }{\bar{K}}^{0}-{\bar{K}}^{0}\partial ^{\mu }\pi ^-)K^{*+}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2\sqrt{2}}(\pi ^{0}\partial ^{\mu }{\bar{K}}^{0}-{\bar{K}}^{0}\partial ^{\mu }\pi ^0)K^{*0}_{\mu }, \end{aligned}$$

(18)

$$\begin{aligned} \mathcal{{L}}_{\eta {}KK^{*}}&=-i\frac{\sqrt{6}g_h}{4}(\eta \partial ^{\mu }K^{+}-K^{+}\partial ^{\mu }\eta ){\bar{K}}^{*-}_{\mu }\nonumber \\&\quad -i\frac{\sqrt{6}g_h}{4}(\eta \partial ^{\mu }K^{0}-K^{0}\partial ^{\mu }\eta ){\bar{K}}^{*0}_{\mu }\nonumber \\&\quad +i\frac{\sqrt{6}g_h}{4}(\eta \partial ^{\mu }{\bar{K}}^{-}-{\bar{K}}^{-}\partial ^{\mu }\eta )K^{*+}_{\mu }\nonumber \\&\quad +i\frac{\sqrt{6}g_h}{4}(\eta \partial ^{\mu }{\bar{K}}^{0}-{\bar{K}}^{0}\partial ^{\mu }\eta )K^{*0}_{\mu },\end{aligned}$$

(19)

$$\begin{aligned} \mathcal{{L}}_{D^{*}D_sK}&=+\frac{ig_h}{2}(K^0\partial ^{\mu }D_s^{-}-D_s^{-}\partial ^{\mu }K^0)D^{*+}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(K^+\partial ^{\mu }D_s^{-}-D_s^{-}\partial ^{\mu }K^+)D^{*0}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}({\bar{K}}^0\partial ^{\mu }D_s^{+}-D_s^{+}\partial ^{\mu }{\bar{K}}^0){\bar{D}}^{*-}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}(K^-\partial ^{\mu }D_s^{+}-D_s^{+}\partial ^{\mu }K^-){\bar{D}}^{*0}_{\mu }, \end{aligned}$$

(20)

$$\begin{aligned} \mathcal{{L}}_{DD_sK^*}&=-\frac{ig_h}{2}(D^+\partial ^{\mu }D_s^{-}-D_s^{-}\partial ^{\mu }D^+)K^{*0}_{\mu }\nonumber \\&\quad -\frac{ig_h}{2}({\bar{D}}^0\partial ^{\mu }D_s^{+}-D_s^{+}\partial ^{\mu }{\bar{D}}^0)K^{*-}_{\mu }\nonumber \\&\quad +\frac{ig_h}{2}(D^0\partial ^{\mu }D_s^{-}-D_s^{-}\partial ^{\mu }D^0)K^{*+}_{\mu } \nonumber \\&\quad +\frac{ig_h}{2}(D^-\partial ^{\mu }D_s^{+}-D_s^{+}\partial ^{\mu }D^-){\bar{K}}^{*0}_{\mu }. \end{aligned}$$

(21)

The coupling $g_h$ is fixed from the strong decay width of $K^{*}\rightarrow {}K\pi$. With the help of Eq. (18), the two-body decay width $\Gamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})$ is related to $g_h$ as

$$\begin{aligned} \Gamma (K^{*+}\rightarrow {}K^{0}\pi ^{+})=\frac{g_h^2}{24\pi {}m^2_{K^{*+}}}\mathcal{{P}}^3_{\pi {}K^{*}}=\frac{2}{3}\Gamma _{K^{*+}}, \end{aligned}$$

(22)

where $\mathcal{{P}}_{\pi {}K^{*}}$ is the three-momentum of $\pi$ in the rest frame of $K^{*}$. Using the experimental strong decay width ($\Gamma _{K^{*+}}=50.3\pm 0.8$ MeV) and the masses of the particles listed in Table 1 [30], we obtain $g_h=9.11$.

Table 1 Masses of the particles needed in the present work (in units of MeV)

2.1 Two-body decay width

With the above formalism, the decay amplitudes of the triangle diagrams of Fig. 1, evaluated in the final state center of mass frame, are

$$\begin{aligned} \mathcal{{M}}^{X_J}_{a}&=\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{a}=i^3\frac{g_h^2g_{X_J{\bar{D}}^{*}K^{*}}}{4}\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\nonumber \\&\quad \times \int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{K^{*0}}-k_2\omega _{{\bar{D}}^{*0}})^2]\nonumber \\&\quad \times (p_1^{\mu }+q^{\mu })(q^{\eta }-p^{\eta }_{2})\{1,i(k_2^{\alpha }-k_1^{\alpha })\epsilon ^{X}_{\alpha }\}\nonumber \\&\quad \times \frac{-g^{\mu \nu }+k^{\mu }_{1}k^{\nu }_{1}/m^2_{{\bar{D}}^{*0}}}{k_1^2-m^2_{{\bar{D}}^{*0}}}\frac{-g^{\nu \eta }+k^{\nu }_{2}k^{\eta }_{2}/m^2_{K^{*0}}}{k_2^2-m^2_{K^{*0}}}\frac{1}{q^2-m^2_{\pi ^{-}}}, \end{aligned}$$

(23)

$$\begin{aligned}&\mathcal{{M}}^{X_J}_{b}\nonumber \\&\quad =\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{b}=-i^3\frac{g_h^2g_{X_J{\bar{D}}^{*}K^{*}}}{8}\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\nonumber \\&\quad \quad \times \int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{K^{*+}}-k_2\omega _{D^{*-}})^2]\nonumber \\&\quad \quad \times (p_1^{\mu }+q^{\mu })(q^{\eta }-p^{\eta }_{2})\{1,i(k_2^{\alpha }-k_1^{\alpha })\epsilon ^{X}_{\alpha }\}\nonumber \\&\quad \quad \times \frac{-g^{\mu \nu }+k^{\mu }_{1}k^{\nu }_{1}/m^2_{D^{*-}}}{k_1^2-m^2_{D^{*-}}}\frac{-g^{\nu \eta }+k^{\nu }_{2}k^{\eta }_{2}/m^2_{K^{*+}}}{k_2^2-m^2_{K^{*+}}}\frac{1}{q^2-m^2_{\pi ^{0}}}, \end{aligned}$$

(24)

$$\begin{aligned}&\mathcal{{M}}^{X_J}_{c} \nonumber \\&\quad =\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{c}=i^3\frac{g_h^2g_{X_J{\bar{D}}^{*}K^{*}}}{8}\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\nonumber \\&\quad \quad \times \int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{K^{*+}}-k_2\omega _{D^{*-}})^2]\nonumber \\&\quad \quad \times (p_1^{\mu }+q^{\mu })(q^{\eta }-p^{\eta }_{2})\{1,i(k_2^{\alpha }-k_1^{\alpha })\epsilon ^{X}_{\alpha }\}\nonumber \\&\quad \quad \times \frac{-g^{\mu \nu }+k^{\mu }_{1}k^{\nu }_{1}/m^2_{D^{*-}}}{k_1^2-m^2_{D^{*-}}}\frac{-g^{\nu \eta }+k^{\nu }_{2}k^{\eta }_{2}/m^2_{K^{*+}}}{k_2^2-m^2_{K^{*+}}}\frac{1}{q^2-m^2_{\eta }}, \end{aligned}$$

(25)

$$\begin{aligned}&\mathcal{{M}}^{X_J}_{d} \nonumber \\&\quad =\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{d}=i^3\frac{g_h^2g_{X_J{\bar{D}}^{*}K^{*}}}{4}\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\nonumber \\&\quad \quad \times \int \frac{d^4q}{(2\pi )^4}\Phi [(k_1\omega _{K^{*0}}-k_2\omega _{{\bar{D}}^{*0}})^2]\nonumber \\&\quad \quad \times (p_2^{\eta }+q^{\eta })(q^{\mu }-p^{\mu }_{1})\{1,i(k_2^{\alpha }-k_1^{\alpha })\epsilon ^{X}_{\alpha }\}\nonumber \\&\quad \quad \times \frac{-g^{\nu \eta }+k^{\nu }_{1}k^{\eta }_{1}/m^2_{{\bar{D}}^{*0}}}{k_1^2-m^2_{{\bar{D}}^{*0}}}\frac{-g^{\mu \nu }+k^{\mu }_{2}k^{\nu }_{2}/m^2_{K^{*0}}}{k_2^2-m^2_{K^{*0}}}\frac{1}{q^2-m^2_{D_s^{+}}}, \end{aligned}$$

(26)

where the expressions in the curly brackets, $\{1$, $i(k_2^{\alpha }-k_1^{\alpha })\epsilon ^{X}_{\alpha }\}$, are for $X_0$ and $X_1$, respectively. The $\mathcal{{F}}^{X_J}$ is the residual part of the amplitude with the isospin factor $\mathcal{{C}}_Y^{I}$ explicitly separated.

2.2 Three-body decay width

Similarly, the decay amplitudes of Fig. 2, evaluated in the initial state center of mass frame, are

$$\begin{aligned}&\mathcal{{M}}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{0}\pi ^0)\nonumber \\&\quad =\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{0}\pi ^0)\nonumber \\&\quad =\frac{ig_hg_{X_J{\bar{D}}^{*}K^{*}}}{2\sqrt{2}}\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\Phi [(p_2\omega _{K^{*0}}-q\omega _{{\bar{D}}^{*0}})^2]\nonumber \\&\quad \quad \times (p_3-p_1)^{\mu }\{1,i(q-p_2)^{\alpha }\epsilon _{\alpha }(p)\}\nonumber \\&\quad \quad \times \frac{-g_{\mu \nu }+q_{\mu }q_{\nu }/m^2_{K^{*0}}}{q^2-m^2_{K^{*0}}+im_{K^{*0}}\Gamma _{K^{*0}}}\epsilon ^{*\nu }(p_2), \end{aligned}$$

(27)

$$\begin{aligned}&\mathcal{{M}}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{+}\pi ^-) \nonumber \\&\quad =\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{+}\pi ^-)\nonumber \\&\quad =\frac{ig_hg_{X_J{\bar{D}}^{*}K^{*}}}{2}\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\Phi [(p_2\omega _{K^{*0}}-q\omega _{{\bar{D}}^{*0}})^2]\nonumber \\&\quad \quad \times (p_3-p_1)^{\mu }\{1,i(q-p_2)^{\alpha }\epsilon _{\alpha }(p)\}\nonumber \\&\quad \quad \times \frac{-g_{\mu \nu }+q_{\mu }q_{\nu }/m^2_{K^{*0}}}{q^2-m^2_{K^{*0}}+im_{K^{*0}}\Gamma _{K^{*0}}}\epsilon ^{*\nu }(p_2), \end{aligned}$$

(28)

$$\begin{aligned}&\mathcal{{M}}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{+}\pi ^0) \nonumber \\&\quad =\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{+}\pi ^0)\nonumber \\&\quad =\frac{ig_hg_{X_J{\bar{D}}^{*}K^{*}}}{2\sqrt{2}}\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\Phi [(p_2\omega _{K^{*+}}-q\omega _{{\bar{D}}^{*-}})^2]\nonumber \\&\quad \quad \times (p_3-p_1)^{\mu }\{1,i(q-p_2)^{\alpha }\epsilon _{\alpha }(p)\}\nonumber \\&\quad \quad \times \frac{-g_{\mu \nu }+q_{\mu }q_{\nu }/m^2_{K^{*+}}}{q^2-m^2_{K^{*+}}+im_{K^{*+}}\Gamma _{K^{*+}}}\epsilon ^{*\nu }(p_2), \end{aligned}$$

(29)

$$\begin{aligned}&\mathcal{{M}}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{0}\pi ^+)\nonumber \\&=\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{0}\pi ^+)\nonumber \\&\quad =\frac{ig_hg_{X_J{\bar{D}}^{*}K^{*}}}{2}\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\Phi [(p_2\omega _{K^{*+}}-q\omega _{{\bar{D}}^{*-}})^2]\nonumber \\&\quad \quad \times (p_3-p_1)^{\mu }\{1,i(q-p_2)^{\alpha }\epsilon _{\alpha }(p)\}\nonumber \\&\quad \quad \times \frac{-g_{\mu \nu }+q_{\mu }q_{\nu }/m^2_{K^{*+}}}{q^2-m^2_{K^{*+}}+im_{K^{*+}}\Gamma _{K^{*+}}}\epsilon ^{*\nu }(p_2), \end{aligned}$$

(30)

where the expressions in the curly brackets, $\{1$, $i(q-p_2)^{\alpha }\epsilon _{\alpha }(p)\}$, are for $X_0$ and $X_1$, respectively.

Once the amplitudes are determined, the corresponding partial decay widths can be easily obtained, which read as,

$$\begin{aligned} d\Gamma (X_J\rightarrow {\bar{D}}K)&=\frac{1}{2J+1}\frac{1}{32\pi ^2}\frac{|\vec {p}_1|}{m^2_{X_J}}\bar{|\mathcal{{M}}|^2}d\Omega , \end{aligned}$$

(31)

$$\begin{aligned} d\Gamma (X_J\rightarrow {\bar{D}}^{*}K\pi )&=\frac{1}{2J+1}\frac{1}{(2\pi )^5}\frac{1}{16m_{X_J}^2}\bar{|\mathcal{{M}}|^2}|\vec {p}^{*}_3|\nonumber \\&\quad \times {}|\vec {p}_2|dm_{K{}\pi {}}d\Omega ^{*}_{p_3}d\Omega _{p_2}, \end{aligned}$$

(32)

where J is the total angular momentum of $X_J$, $|\vec {p}_1|$ is the three-momenta of the decay products in the center of mass frame, and the overline indicates the sum over the polarization vectors of the final hadrons. The ($\vec {p}^{*}_3,\Omega ^{*}_{p_3}$) is the momentum and angle of the particle K in the rest frame of K and $\pi$, and $\Omega _{p_2}$ is the angle of ${\bar{D}}^{*}$ in the rest frame of the decaying particle. The $m_{K{}\pi {}}$ is the invariant mass for K and $\pi$ and $m_{K}+m_{\pi }\le {}m_{K{}\pi }\le {}M-m_{{\bar{D}}^{*}}$. The total decay width of $X_J$ is the sum of $\Gamma (X_J\rightarrow {}{\bar{D}}K)$ and $\Gamma (X_J\rightarrow {\bar{D}}^{*}K{}\pi )$. The amplitude and its modulus squared are then

$$\begin{aligned} \mathcal{{M}}_{X_J\rightarrow {}D^{-}K^{+}}&=\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{a}+\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{b}\nonumber \\&\quad +\mathcal{{C}}_{D^{*-}K^{*+}}^{I}\mathcal{{F}}^{X_J}_{c}+\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I}\mathcal{{F}}^{X_J}_{d}, \end{aligned}$$

(33)

$$\begin{aligned} |\mathcal{{M}}|^2_{X_J\rightarrow {}{\bar{D}}^{*}K\pi }&=(\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I})^2|\mathcal{{F}}^{X_J}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{0}\pi ^0)|^2\nonumber \\&\quad +(\mathcal{{C}}_{{\bar{D}}^{*0}K^{*0}}^{I})^2|\mathcal{{F}}^{X_J}_{a}(X_J\rightarrow {\bar{D}}^{*0}K^{+}\pi ^-)|^2\nonumber \\&\quad +(\mathcal{{C}}_{D^{*-}K^{*+}}^{I})^2|\mathcal{{F}}^{X_J}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{+}\pi ^0)|^2\nonumber \\&\quad +(\mathcal{{C}}_{D^{*-}K^{*+}}^{I})^2|\mathcal{{F}}^{X_J}_{b}(X_J\rightarrow {\bar{D}}^{*-}K^{0}\pi ^+)|^2. \end{aligned}$$

(34)

It is obvious from Eq. (34) that the width of the three-body decay for $I=0$ and $I=1$ only differs by the isospin factor. However, for the two-body decay, one has

$$\begin{aligned} \mathcal{{M}}^{I=0}_{X_J\rightarrow {}D^{-}K^{+}}&=\frac{1}{\sqrt{2}}(\mathcal{{F}}^{X_J}_{a}+\mathcal{{F}}^{X_J}_{b}+\mathcal{{F}}^{X_J}_{c}+\mathcal{{F}}^{X_J}_{d}), \end{aligned}$$

(35)

$$\begin{aligned} \mathcal{{M}}^{I=1}_{X_J\rightarrow {}D^{-}K^{+}}&=\frac{1}{\sqrt{2}}(-\mathcal{{F}}^{X_J}_{a}+\mathcal{{F}}^{X_J}_{b}+\mathcal{{F}}^{X_J}_{c}-\mathcal{{F}}^{X_J}_{d}). \end{aligned}$$

(36)

Therefore, the decay width of $X_J \rightarrow {\bar{D}}K$ for $I=0$ is different from that for $I=1$.

3 Results and discussions

In order to obtain the allowed two-body decay widths through the triangle diagrams shown in Fig. 1 and three-body decay widths in Fig. 2, we first compute the coupling constant $g_{X_J{\bar{D}}^{*}K^{*}}$($\equiv {g_{X_J}}$). With a value of the cutoff $\alpha =0.9-1.1$ GeV, these coupling constants are shown in Fig 4. We note that they decrease very slowly with the increase of the cutoff. The different $\alpha$ dependencies for $J^P=0^+$ and $1^-$ reflect the different distribution of the two constituents, ${\bar{D}}^{*}$ and $K^{*}$, in the hadronic molecular $X_J$ states.

Fig. 4

Dependencies of the coupling constant of vertex $X_J{\bar{D}}^{*}K^{*}$ on the parameter $\alpha$ for different spin-parity assignments. The coupling constant $g_{X_J}$ for the case of $J^P=0^+$ is in units of GeV and for the case of $J^P=1^-$ is dimensionless

We show the dependence of the total decay width on the cutoff $\alpha$ in Fig. 5. In the present study, we vary $\alpha$ from 0.9 to 1.1 GeV. In this $\alpha$ range, the total decay width increases for the case of $J^P=0^{+}$, while it decreases for the $J^P=1^{-}$ case. The three-body decay widths for both $J^P=0^+,1^-$ and $I=0,1$ are in the range of 2 to 3 MeV, while the two-body decay width for $J^P=0^+$ is at the order of a few tens of MeV, but that for the $J^P=1^-$ is less than 1 MeV (see also Table 2). Because of the p-wave coupling of the $X_1(2904)$ state to the ${\bar{D}}^*K^*$ channel, the numerical results for its decay are always much smaller than the ones for the $X_0(2866)$ state, which is in s-wave.

From Fig. 5, we find that the calculated total decay width for the case of $I(J^P)=1(0^{+})$ is comparable with that of the experimental total width in the range of $\alpha =1.04-1.1$ GeV, while an even larger $\alpha$ is needed for $I(J^P)=0(0^+)$. Although a value of $\alpha =1.0$ GeV is preferred based on previous studies [20,21,22,23,24,25,26,27], considering the fact that our results should be considered as the lower limits because it is possible that other decay modes exist, our study does indicate a sizeable ${\bar{D}}^*K^*$ component in the $X_0$ wave function. The corresponding partial decay widths of $X_J\rightarrow {\bar{D}}K$, ${\bar{D}}^*K^*$, and the total decay widths for different spin-parity and isospin assignments of $X_J$ are listed in Table 2. For comparison, we show the results from the LHCb Collaboration as well [8]. The results show that $X_0(2866)$ might have a sizeable ${\bar{D}}^*K^*$ component while $X_1(2904)$ cannot be explained as a ${\bar{D}}^*K^*$ molecule. We note that in Ref. [31], $X_0(2866)$ is found to be compatible with a compact tetraquark state.

Fig. 5

Partial decay widths of $X_J\rightarrow {}{\bar{D}}K$ (red dashed lines), $X_J\rightarrow {}{\bar{D}}^{*}K{}\pi$ (blue dash dotted lines), and the total decay width (black solid lines) with different spin-parity and isospin assignments for $X_J$ as a function of the parameter $\alpha$. The cyan error bands correspond to the experimental total decay width [8]

Table 2 Partial decay widths of $X_J\rightarrow {\bar{D}}K$, ${\bar{D}}^{*}K{}\pi$, and the total decay widths for different spin-parity and isospin assignments of $X_J$, in comparison with the LHCb results [8]. Results for the preferred value of $\alpha =1$ GeV are given as central values and the uncertainties originated from the variation of $\alpha$ from 0.9 to 1.1 GeV. All widths are in units of MeV

4 Summary

We studied the two-body and three-body strong decays of the two $X_0(2866)$ and $X_1(2904)$ states assuming that they are bound states of ${\bar{D}}^*K^*$. The couplings of these states to their components are fixed by the Weinberg compositeness condition. The two-body decays are via triangle diagrams with exchanges of a pseudoscalar meson $\pi$, $\eta$, or $D_s$, where the three-body decays happen at tree level. With all the other couplings fixed from relevant experimental data, the only remaining parameter is the cutoff $\alpha$. We showed that with the well accepted range of $0.9\sim 1.1$ GeV, the so-obtained decay width for $X_0(2866)$ is in marginal agreement with the LHCb measurement but that for $X_1(2904)$ is much smaller. As a result, we conclude that $X_0(2866)$ may have a large ${\bar{D}}^*K^*$ component (also a non-negligible compact tetraquark component) but $X_1(2904)$ cannot be of molecular nature.

Such a conclusion is consistent with the OBE model of Ref. [18]. We note that a recent study by Karliner and Rosner favors the explanation of $X_0$ as a compact tetraquark state [31], while the lattice QCD study of Ref. [16] found no tetraquark candidate in this channel. As a result, more works are urgently needed to clarify the nature of these latest additions to the family of exotic mesons.