Abstract
Viewing the negative cosmological constant as a dynamical quantity derived from the matter field, we study the weak cosmic censorship conjecture for the higher-dimensional asymptotically AdS Reissner–Nordström black hole. To this end, using the stability assumption of the matter field perturbation and the null energy condition of the matter field, we first derive the first-order and second-order perturbation inequalities containing the variable cosmological constant and its conjugate quantity for the black hole. We prove that the higher-dimensional RN-AdS black hole cannot be destroyed under a second-order approximation of the matter field perturbation process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The weak cosmic censorship conjecture means that the singularity behind the horizon of the black hole formed by gravitational collapse cannot be exposed by any physical process. It also means that the event horizon of the black hole cannot be destroyed by particle matter or general matter. According to the conjecture, to ensure the existence of the event horizon of a black hole with mass M, electric charge Q and angular momentum J, there must be an inequality
It was shown in [1] that the cosmic censorship inequality cannot be violated by simply adding particle matter with energy E, charge q and angular momentum l, even for extreme black holes. That is, we still have
with the particle matter thrown into the black hole.
For a slightly non-extreme black hole, it was pointed out in [2] that the inequality (1) may be violated by fine-tuning the parameters of the particle matter. However, this Hubeny type violation originates from the neglect of the electromagnetic self-energy and self-force effects. In fact, one must calculate the quadratic-order contribution of the involved parameters of the particle to the energy. Later, by numerical calculations, though not analytical ones, this type of violation for the nearly extreme black hole was proved to be impossible [3,4,5,6].
To test the weak cosmic censorship conjecture for the black hole against any matter perturbation (rather than the particle matter perturbation [7,8,9,10,11,12,13,14,15,16]), a new version of gedanken experiment, where the self-force effects or finite size effects to the energy are regarded, was proposed recently [17]. Assuming that the nearly extreme Kerr–Newman black hole can still be stable against linear perturbations of the matter field and the null energy condition of the non-electromagnetic contribution to the matter’s stress–energy tensor is not violated, it was explicitly proved that the conjectured inequality (1) cannot be violated for the black hole. This new kind of gedanken experiment has been used to test (1) for other black holes; see, e.g., [18,19,20,21,22,23,24,25,26,27]. Furthermore, the new gedanken experiment was recently extended from asymptotically flat black hole to asymptotically AdS black hole with a negative cosmological constant [28], completing the investigation of the weak cosmic censorship conjecture for the AdS black hole via a particle absorbing process (see, e.g., [9, 29]). The philosophy is one of viewing the cosmological constant as a dynamical variable due to the evolution of the system composed of the black hole and arbitrary matter.
In [30], it was shown that the weak cosmic censorship conjecture cannot be violated for the nearly extreme higher-dimensional RN black hole with the new gedanken experiment. In this brief article, wondering whether the Hubeny type violation could occur in the AdS spacetime, we will use the new gedanken experiment to test the weak cosmic censorship conjecture for an asymptotically AdS higher-dimensional RN black hole. We will derive the first-order and second-order perturbation inequalities in Sect. 2. Then in Sect. 3 we will prove that the higher-dimensional RN-AdS black hole cannot be destroyed by arbitrary matter and the weak cosmic censorship conjecture is respected. Section 4 is devoted to our conclusion.
2 First-order and second-order perturbation inequalities
We provide some preliminaries of the RN-AdS black hole in Einstein–Maxwell gravity in Appendix A. The first-order variation of the Einstein–Maxwell Lagrangian \(\varvec{L}\) is
where we use \(\delta \) to denote a derivative valued at 0 point of the variation parameter \(\lambda \) for the field configurations \(\phi \). We have
where
The symplectic potential can be decomposed into a gravity part and an electromagnetic part,
where
with
Associated with a smooth vector field \(\zeta ^a\) and the field configuration \(\phi \) on the spacetime manifold, there is a Noether current \((D-1)\)-form,
It has been proved in [31] that the Noether current can also be expressed as
where \(\varvec{Q}_{\zeta }\) is the Noether charge \((D-2)\)-form
with
\(\varvec{C}_\zeta = \zeta \cdot \varvec{C}\) are constraints of the gravity theory, with
We have \(\varvec{C}=0\) and \(d\varvec{J}=0\) if \({\varvec{E}}(\phi )=0\).
The symplectic current can be defined as
the symplectic current can be conserved under the condition that \(\delta _{1}\varvec{E}_{\phi }=\delta _{2}\varvec{E}_{\phi }=0\). According to (10), we have the first-order variation of the Noether current \(\varvec{J}_{\zeta }\) as
Next we choose the vector field \(\zeta \) to be a Killing field in the background spacetime. By choosing a proper gauge condition, we can set \(\delta \zeta ^a=0\). Then we get the first-order perturbation identitiy
and the second-order perturbation identity
We now consider that the higher-dimensional RN-AdS black hole is perturbed by the spherically symmetric charged matter field with one-parameter family of field configurations \(\phi (\lambda )\). This corresponds to the \(\lambda \)-dependent perturbation equations of motion
where
is the stress–energy tensor of the electromagnetic field, and \(T_{ab}(\lambda )\) is the stress–energy tensor of the non-electromagnetic matter source. In this paper, we assume that the cosmological constant is a dynamical quantity and therefore it should come from the matter source, i.e., we have
for the background geometry. Here we denote \(\eta =\eta (\lambda =0)\) for the background quantity \(\eta \). The spacetime in this case can be generally described by
where \(\mu (r,v,0)=1\) and
for the background geometry. We suppose that the spacetime can still be described by the higher-dimensional RN-AdS solution at sufficiently late times after the original black hole being perturbed by general spherically symmetric matter source. It indicates that
at sufficiently late times. This supposition is dubbed the stability assumption [17]. Moreover, we also assume that the perturbation vanishes on the bifurcation surface B. i.e., \(\phi (\lambda )=\phi \) on B.
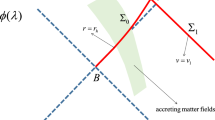
We can choose a hyper-surface \(\Sigma \) which starts from a perturbation-vanishing future event horizon of the nearly extreme higher-dimensional RN-AdS black hole, continues up through the non-vanishing matter source region, and finally becomes space-like as it extends to infinity. Let \({\mathcal {H}}\) and \(\Sigma _1\) individually be the horizon portion and space-like portion of the Cauchy surface \(\Sigma \); we have
The globally hyperbolic hyper-surface \(\Sigma \) terminates at the \((D-2)\)-dimensional bifurcation surface B of the near extreme D-dimensional RN-AdS black hole.
After using the Killing vector \(\xi ^{a}=(\partial /\partial v)^{a}\) for the background fields, (17) can be evaluated at \(\lambda =0\) and integrated over \(\Sigma \),
For the first term on the left side of (26), we have
where we denote \(V_c= \Omega _{D-2}\pi r_c^{D-1}/(D-1)\). To avoid the divergence taken by the cosmological constant as a dynamical quantity, \(S_c\) is a sphere with radius \(r_c\) replacing the asymptotic infinity boundary of a isochronous surface \(\Sigma _1\) that can be described by the late time line element of the higher-dimensional RN-AdS black hole. Above we have used the condition that the perturbations vanish on the bifurcation surface B. For the second term, we have
where we have used \(\xi \cdot \varvec{\epsilon }=0\) on \({\mathcal {H}}\) as well as \(j^a(\lambda )=0\) and \(g^{ab}\delta g_{ab}=0\) on \(\Sigma _1\). For the third term, we have
where we have used \(j^{a}|_{\Sigma }=0\) and denoted \(V_H= \Omega _{D-2}\pi r_H^{D-1}/(D-1)\). As a result, we can write the first-order perturbation equality as
where we have used the condition that the future-directed vector \(k^a\) be normal to the horizon and proportional to the Killing vector \(\xi ^{a}\). The volume element on the horizon \(\varvec{{\tilde{\epsilon }}}\) is defined via the relation \(\epsilon _{aa_{2}\cdots a_{D}}=k_{a}\wedge {\tilde{\epsilon }}_{a_{2}\cdots a_{D}}\). Provided that the null energy condition is respected by the non-electromagnetic stress–energy tensor \(\delta T^{ba}\), i.e., \(\int _\mathcal {H}\delta T^{ab} k_ak_b\geqslant 0\), we have the first-order perturbation inequality for the higher-dimensional RN-AdS black hole
When the stree-energy flux of the non-electromagnetic matter vanishes, we can have the optimal perturbation process for the horizon-corruption of the higher-dimensional RN-AdS black hole at first order.
Like the first-order case, the second-order perturbation identity (18) can also be evaluated at \(\lambda =0\) over \(\Sigma \) after choosing the Killing vector \(\xi ^{a}\),
Similar to the first-order case, for the first term on the left side, we have
It is evident that the second term vanishes. For the third term, we have
For the fourth term, resorting to a similar result in [17], we get
In order to calculate the last term, we need to use an indirect method. We may choose the one-parameter family \(\phi ^{\text {RA}}(\lambda )\), whose perturbations satisfy
It is natural that \(\delta ^{2}{\mathcal {M}}=\delta ^{2}{\mathcal {Q}}=\delta ^{2}\Lambda =0\). Integrating (18) over \(\Sigma _{1}\) yields
As the second and third terms vanish in (37), fortunately, we have
Then we obtain
So we can express the second-order perturbation equality as
Finally, we can get the second-order inequality for the perturbation
if the null energy condition for the matter fields
is fulfilled.
3 New gedanken experiment to destroy a nearly extreme higher-dimensional RN-AdS black hole
The key of testing the weak cosmic censorship conjecture for the nearly extreme higher-dimensional RN-AdS black hole under the perturbation is to verdict the sign of the perturbed metric function \(f(r,\lambda )\), which, for convenience, can be used to define a perturbation function
where \(r_{m}(\lambda )\) is the extreme value of \(f\left(r,\lambda \right)\) and it can be obtained from
so that (43) gives the minimal value of the metric function at late time. We can obtain the mass parameter of the black hole M in terms of the minimal radius \(r_{m}\):
Then we have the differential relation
Expanding \(h(\lambda )\) in terms of \(\lambda \) to second-order level, we have
where
Following a similar setup to [17], we consider the black hole to approach the extreme geometry, with
where \(\epsilon \rightarrow 0\) is in agreement with the extra matter fields’ first-order perturbation, i.e., it is of the same order as \(\lambda \). Note that \(\epsilon \) is defined in the background geometry and therefore it is independent of \(\lambda \). Without loss of generality, it is not difficult to deduce
and
Moreover, considering the zero-order approximation of \(\epsilon \), we have
which can be derived from \(f((1+\epsilon )r_m)=0\) and \(f'(r_m)=0\). After using the first-order perturbation inequality (31) and the second-order perturbation inequality (41), (47) can be further reduced,
where \({\mathcal {X}}(\lambda )\) is a tedious normal expression; we here will not explicitly show it. As \(f(r_{m})\leqslant f(r)\), or, in other words, \(f(r_{m})\) is the minimum value of the metric function f(r) for the higher-dimensional RN-AdS black hole, we have \(f^{\prime \prime }(r_{m})>0\). Then (56) implies
This result tells us that, to the level of second-order approximation of the perturbation from the extra spherically symmetric matter field, which affects the mass, electric charge and the cosmological constant of the higher-dimensional RN-AdS black hole, the event horizon of the nearly extreme black hole cannot be ignored and the weak cosmic censorship conjecture is straightforwardly respected.
4 Conclusion
In this article, assuming that the stress–energy tensors of the non-electromagnetic matters do not violate the null energy condition, and the nearly extreme higher-dimensional RN-AdS black hole comes to be linearly stable at late times under the perturbation of the matter, we derived the first-order perturbation and the second-order perturbation inequalities. We then proved that the weak cosmic censorship conjecture for the higher-dimensional RN-AdS black hole cannot be violated.
There are two kinds of investigations we can do further. The first one is to study whether the weak cosmic censorship conjecture can be violated by considering higher-order approximations, though this is highly unlikely [32]. The second one is to consider the new gedanken experiment addressing an asymptotically AdS rotating black hole.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All relevant mathematical calculations and data are explicitly presented in this paper and no external data has been used in this paper.]
References
R. Wald, Ann. Phys. 82, 548 (1974)
V.E. Hubeny, Phys. Rev. D 59, 064013 (1999). arXiv:grqc/9808043 [gr-qc]
P. Zimmerman, I. Vega, E. Poisson, R. Haas, Phys. Rev. D 87, 041501 (2013). arXiv:1211.3889 [gr-qc]
E. Barausse, V. Cardoso, G. Khanna, Phys. Rev. Lett. 105, 261102 (2010). arXiv:1008.5159 [gr-qc]
M. Colleoni, L. Barack, A.G. Shah, M. van de Meent, Phys. Rev. D 92, 084044 (2015). arXiv:1508.04031 [gr-qc]
E. Barausse, V. Cardoso, G. Khanna, Phys. Rev. D 84, 104006 (2011). arXiv:1106.1692 [gr-qc]
Y. Gim, B. Gwak, Phys. Lett. B 794, 122 (2019). arXiv:1808.05943 [gr-qc]
B. Gwak, JHEP 11, 129 (2017). arXiv:1709.08665 [gr-qc]
X.-X. Zeng, Y.-W. Han, D.-Y. Chen, Chin. Phys. C 43, 105104 (2019). arXiv:1901.08915 [gr-qc]
D. Chen, Eur. Phys. J. C 79, 353 (2019). arXiv:1902.06489 [hep-th]
S. Shaymatov, N. Dadhich, B. Ahmedov, Eur. Phys. J. C 79, 585 (2019). arXiv:1809.10457 [gr-qc]
P. Wang, H. Wu, H. Yang, Eur. Phys. J. C 79, 572 (2019)
S.-Q. Hu, B. Liu, X.-M. Kuang, R.-H. Yue, arXiv:1910.04437 [gr-qc] (2019)
Y.-W. Han, X.-X. Zeng, Y. Hong, Eur. Phys. J. C 79, 252 (2019). arXiv:1901.10660 [hep-th]
S.-J. Yang, J. Chen, J.-J. Wan, S.-W. Wei, Y.-X. Liu, Phys. Rev. D 101, 064048 (2020). arXiv:2001.03106 [gr-qc]
K.-J. He, G.-P. Li, X.-Y. Hu, Eur. Phys. J. C 80, 209 (2020). arXiv:1909.09956 [hep-th]
J. Sorce, R.M. Wald, Phys. Rev. D 96, 104014 (2017). arXiv:1707.05862 [gr-qc]
J. Jiang, B. Deng, Z. Chen, Phys. Rev. D 100, 066024 (2019). arXiv:1909.02219 [hep-th]
J. Jiang, X. Liu, M. Zhang, Phys. Rev. D 100, 084059 (2019). arXiv:1910.04060 [hep-th]
J. Jiang, (2019). arXiv:1912.10826 [gr-qc]
Y.-L. He, J. Jiang, Phys. Rev. D 100, 124060 (2019). arXiv:1912.05217 [hep-th]
J. Jiang ,M. Zhang, arXiv:2008.04906 [gr-qc] (2020)
X.-Y. Wang, J. Jiang, JHEP 05, 161 (2020). arXiv:2004.12120 [hep-th]
C. Liu, S. Gao, Phys. Rev. D 101, 124067 (2020). arXiv:2003.12999 [gr-qc]
S. Shaymatov, N. Dadhich, B. Ahmedov, M. Jamil, Eur. Phys. J. C 80, 481 (2020). arXiv:1908.01195 [gr-qc]
J. Jiang, M. Zhang, Eur. Phys. J. C 80, 196 (2020)
J. Jiang, Y. Gao, Phys. Rev. D 101, 084005 (2020). arXiv:2003.07501 [hep-th]
X.-Y.Wang ,J. Jiang, arXiv:1911.03938 [hepth] (2019)
X.-X. Zeng, X.-Y. Hu, K.-J. He, Nucl. Phys. B 949, 114823 (2019). arXiv:1905.07750 [hep-th]
B. Ge, Y. Mo, S. Zhao, J. Zheng, Phys. Lett. B 783, 440 (2018). arXiv:1712.07342 [hep-th]
V. Iyer, R.M. Wald, Phys. Rev. D 52, 4430 (1995). arXiv:gr-qc/9503052 [gr-qc]
P. Figueras, M. Kunesch, L. Lehner, S. Tunyasuvunakool, Phys. Rev. Lett. 118, 151103 (2017). arXiv:1702.01755 [hep-th]
D. Kastor, S. Ray, J. Traschen, Class. Quant. Grav. 26, 195011 (2009). arXiv:0904.2765 [hep-th]
D. Kubiznak, R.B. Mann, JHEP 07, 033 (2012). arXiv:1205.0559 [hep-th]
Acknowledgements
This work is supported by the Initial Research Foundation of Jiangxi Normal University with Grant no. 12020023 and the National Natural Science Foundation of China with Grant nos. 11675015, 11775022, 11873044.
Author information
Authors and Affiliations
Corresponding author
Appendix A: A brief review of higher-dimensional Reissner–Nordström black hole in anti-de Sitter background
Appendix A: A brief review of higher-dimensional Reissner–Nordström black hole in anti-de Sitter background
The action of the Einstein–Maxwell gravity with a cosmological constant is
where \(\varvec{\epsilon }\) is the volume element, R is the Ricci scalar, \(\Lambda \) is the negative cosmological constant, \(\varvec{F}\) is electromagnetic field strength. The equation of motion is
where
is the stress–energy tensor for the electromagnetic field,
is the stress–energy tensor for the matter field, \(G_{ab}\) is the Einstein tensor and \(j^{a}\) is the electric current for the matter field.
The D-dimensional RN-AdS black hole solution corresponding to the equations of motion is
where
We can introduce the Eddington–Finkelstein coordinate
then the solution can be written as
The mass, electric charge, electric potential, cosmological constant, thermodynamic pressure are [33, 34]
where \(\Omega _{D-2}=2\pi ^{(D-1)/2}/\Gamma [(D-1)/2]\) is the volume of the \((D-2)\)-dimensional sphere.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Zhang, M., Jiang, J. New gedanken experiment on higher-dimensional asymptotically AdS Reissner–Nordström black hole. Eur. Phys. J. C 80, 890 (2020). https://doi.org/10.1140/epjc/s10052-020-08475-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08475-w