1 Introduction

Since the observation of X(3872) in 2003 [1], the searching for hadrons beyond the conventional mesons and baryons have become one of intriguing topics in the past decades. On the experimental side, a growing number of new hadron states have been observed experimentally. Some of these states cannot be accommodated into the traditional mesons or baryons, which can be good candidates of molecular or tetraquark states. Recent experimental and theoretical status can be found in the literature reviews [2,3,4,5,6,7,8,9,10].

Among the observed new hadron states, those with heavy quark components are particularly interesting, since the spectroscopy of traditional mesons and baryons with heavy quarks are much clear than the light hadrons. Moreover, the interactions involved heavy quarks are supposed to be dominated by the short range potential generated by one gluon exchange rather than the long range potential resulted from light meson exchanges. Thus, the new hadron states composed by four heavy quarks should be good candidates of compact tetraquark states rather than deuteron-like molecular states.

A possible excess at \(18.4\pm 0.1 (\mathrm {stat.}) \pm 0.2 (\mathrm {syst.}) \mathrm {GeV}/c^2\) in four lepton channel was reported, which may be a \(bb {\bar{b}} {\bar{b}}\) tetraquark state [11, 12]. This structure is below the threshold of bottomonium meson pair, which demonstrates that the decays into bottomonium meson pair through quark rearrangement should be hindered. However, the LHCb and CMS Collaborations analyzed the invariant mass distributions of \(\Upsilon (1S) \mu ^+ \mu ^-\) subsequently, and no evident structure was observed [13, 14].

On the theoretical side, the compact tetraquark states composed of \(bb\bar{b}\bar{b}\) have been investigated extensively, but the conclusions are model dependent. In Refs. [15,16,17,18,19,20,21,22,23,24,25,26], the lowest \(bb\bar{b}\bar{b}\) tetraquark state is estimated to be below the threshold of bottomonium meson pair, while in Refs. [27,28,29,30,31,32,33,34,35], all the \(bb\bar{b}\bar{b}\) tetraquark states are above the threshold. To further distinguish different model and reveal the underlying dynamics of fully heavy tetraquark states, more efforts are needed, especially from the experimental side.

Very recently, the LHCb Collaboration reported their measurement of the \(J/\psi \) pair invariant mass spectrum and a structure near 6.9 GeV/\(c^2\) was observed with the significance greater than \(5\sigma \) [36]. The resonance parameters are fitted to be

$$\begin{aligned} m= & {} 6905 \pm 11(\mathrm {stat.}) \pm 7 (\mathrm {syst.}) \ \mathrm {MeV}/c^2 \nonumber \\ \Gamma= & {} 80 \pm 19(\mathrm {stat.}) \pm 33(\mathrm {syst.}) \ \mathrm {MeV}/c^2, \end{aligned}$$
(1)

in a no-interference scenario, or

$$\begin{aligned} m= & {} 6886 \pm 11 (\mathrm {stat.}) \pm 11(\mathrm {syst.}) \ \mathrm {MeV}/c^2 \nonumber \\ \Gamma= & {} 168 \pm 33(\mathrm {stat.}) \pm \mathrm {69}(\mathrm {syst.})\ \mathrm {MeV}/c^2, \end{aligned}$$
(2)

in an interference scenario. Besides the structure near 6.9 GeV, the experimental data also indicated another two structures in the vicinity of 6.4 GeV and 7.2 GeV, respectively [36]. These structures may be the evidence of compact tetraquark state composed by \(cc\bar{c}\bar{c}\), which can be a criterion for different models.

After the observation of the LHCb Collaboration, the state around 6.9 GeV has been investigated in different models. In Ref. [37], this state was interpreted as a \(P-\)wave tetraquark state in a nonrelativistic quark model, while the estimations with QCD sum rule indicated that it could be a second radial excited S-wave tetraquark state [38]. The results in Refs. [39, 40] suggested that the resonances with \(J^P=0^+\) and \(1^+\) are about \(6.4 \sim 6.6\) GeV, while the \(2^+\) state is about 7.0 GeV, which are consistent with the structures reported by LHCb Collaboration [36].

In Ref. [41], we extended the relativized quark model proposed by Godfrey and Isgur to investigate the doubly heavy tetraquarks with the same model parameters. With such an extension, the tetraquaks and conventional mesons can be described in a uniform frame. In the present work, we further study the full heavy tetraquarks \(QQ\bar{Q}\bar{Q}\) in the extended relativized quark model and give possible interpretation of the newly observed state around 6.9 GeV. Moreover, the newly observed structures are above the threshold of heavy quarkonium pair, thus, these states can decay into heavy quarkonium pair by quark rearrangement. For simplicity, the decay amplitude should be proportional to the overlap of wave functions of the initial and final states, thus, we can qualitatively discuss the decay behaviors of tetraquarks with the wave functions estimated from the relativized quark model.

This work is organized as follows. In Sect. 2, we present a review of the extended relativized quark model used in the present work. The numerical results of the masses and decays for the tetraquarks are given in Sect. 3. The last section is devoted to a brief summary.

2 Extended relativized quark model

To investigate the masses of fully heavy tetraquarks \(Q_1 Q_2 \bar{Q}_3\)\( {\bar{Q}}_4\), we employ an extended relativized quark model, which has been developed very recently for the tetraquark states [41]. It is an extension of the relativized quark model to deal with the four-body systems. The Hamiltonian for a \(Q_1 Q_2 {\bar{Q}}_3 {\bar{Q}}_4\) state can be expressed as

$$\begin{aligned} H = H_0+\sum _{i<j}V_{ij}^\mathrm{oge}+\sum _{i<j}V_{ij}^\mathrm{conf}, \end{aligned}$$
(3)

where

$$\begin{aligned} H_0 = \sum _{i=1}^{4}(p_i^2+m_i^2)^{1/2} \end{aligned}$$
(4)

is the relativistic kinetic energy, \(V_{ij}^\mathrm{oge}\) is the one gluon exchange potential including the spin-spin interaction, and \(V_{ij}^\mathrm{conf}\) stands for the confining part.

Fig. 1
figure 1

The \(Q_1Q_2 {\bar{Q}}_3 {\bar{Q}}_4\) tetraquark state in Jacobi coordinates

Full size image

In present work, only the S-wave fully heavy tetraquarks are calculated, and the spin-orbit and tensor interactions are not included. The potential \(V_{ij}^\mathrm{oge}\) can be written as

$$\begin{aligned} V_{ij}^\mathrm{{oge}} {=} \beta _{ij}^{1/2}{\tilde{G}}(r_{ij})\beta _{ij}^{1/2} {+} \delta _{ij}^{1/2+\epsilon _c}\frac{2\varvec{S_i} \cdot \varvec{S_j}}{3m_im_j} \nabla ^2\tilde{G}(r_{ij})\delta _{ij}^{1/2+\epsilon _c},\nonumber \\ \end{aligned}$$
(5)

with

$$\begin{aligned} \beta _{ij} = 1+\frac{p_{ij}^2}{(p_{ij}^2+m_i^2)^{1/2}(p_{ij}^2+m_j^2)^{1/2}}, \end{aligned}$$
(6)

and

$$\begin{aligned} \delta _{ij} = \frac{m_im_j}{(p_{ij}^2+m_i^2)^{1/2}(p_{ij}^2+m_j^2)^{1/2}}. \end{aligned}$$
(7)

The \(p_{ij}\) is the magnitude of the momentum of either of the quarks in the center-of-mass frame of ij quark subsystem, and the \(\epsilon _c\) is a parameter reflecting the momentum dependence. The smeared Coulomb potential \({\tilde{G}}(r_{ij})\) is

$$\begin{aligned} {\tilde{G}}(r_{ij}) = {\varvec{F}}_i \cdot {\varvec{F}}_j \sum _{k=1}^3\frac{\alpha _k}{r_{ij}}\mathrm{erf}(\tau _{kij}r_{ij}), \end{aligned}$$
(8)

with

$$\begin{aligned} \frac{1}{\tau _{kij}^2} = \frac{1}{\gamma _k^2}+\frac{1}{\sigma _{ij}^2}, \end{aligned}$$
(9)

and

$$\begin{aligned} \sigma _{ij}^2 = \sigma _0^2 \left[ \frac{1}{2}+\frac{1}{2}\left( \frac{4m_im_j}{(m_i+m_j)^2}\right) ^4\right] +s^2\left( \frac{2m_im_j}{m_i+m_j}\right) ^2.\nonumber \\ \end{aligned}$$
(10)

The \({\varvec{F}}_i \cdot {\varvec{F}}_j\) are the color matrix and reads

$$\begin{aligned} {\varvec{F}}_i = \left\{ \begin{aligned}&\frac{\lambda _i}{2}~~~\mathrm{for~quarks,} \\&-\frac{\lambda _i^*}{2}~\mathrm{for~antiquarks.} \\ \end{aligned} \right. \end{aligned}$$
(11)

Similarly, the confining interaction \(V_{ij}^\mathrm{conf}\) can be expressed as

$$\begin{aligned} V_{ij}^\mathrm{{conf}}= & {} -\frac{3}{4}{\varvec{F}}_i \cdot \varvec{F}_j \left\{ br \left[ \frac{e^{-\sigma _{ij}^2r^2}}{\sqrt{\pi }\sigma _{ij}r}\right. \right. \nonumber \\&\left. \left. +\left( 1+\frac{1}{2\sigma _{ij}^2r^2}\right) \mathrm{erf}(\sigma _{ij}r)\right] +c\right\} . \end{aligned}$$
(12)

The explicit parameters and relativization scheme can be found in Refs. [41, 42].

Table 1 Possible configurations for the \(cc {\bar{c}} {\bar{c}}\) and \(bb {\bar{b}} {\bar{b}}\) systems. The subscripts and superscripts denote the spin and color quantum numbers, respectively
Full size table

The wave function of a \(Q_1 Q_2 {\bar{Q}}_3 {\bar{Q}}_4\) state is composed of color, flavor, spin, and spatial parts. In the color space, two types of colorless states with determinate permutation properties exist

$$\begin{aligned} |{\bar{3}} 3\rangle= & {} |(Q_1 Q_2)^{{\bar{3}}} ({\bar{Q}}_3 {\bar{Q}}_4)^3\rangle , \end{aligned}$$
(13)
$$\begin{aligned} |6 {\bar{6}}\rangle= & {} |(Q_1 Q_2)^{6} ({\bar{Q}}_3 {\bar{Q}}_4)^{\bar{6}}\rangle , \end{aligned}$$
(14)

where the \(|{\bar{3}} 3\rangle \) and \(|6 {\bar{6}} \rangle \) are antisymmetric and symmetric under the exchange of \(Q_1Q_2\) or \(\bar{Q}_3 {\bar{Q}}_4\), respectively. In the flavor space, the combinations of \(\{ c c \}\), \(\{ {\bar{c}} {\bar{c}} \}\), \(\{b b \}\), and \(\{ {\bar{b}} {\bar{b}} \}\) are always symmetric, where the braces \(\{ ~ \}\) are adopted to stand for symmetric flavor wave functions.

For the spin part, the six spin bases can be written as,

$$\begin{aligned} \chi ^{00}_0= & {} |(Q_1 Q_2)_0 ({\bar{Q}}_3 {\bar{Q}}_4)_0\rangle _0, \end{aligned}$$
(15)
$$\begin{aligned} \chi ^{11}_0= & {} |(Q_1 Q_2)_1 ({\bar{Q}}_3 {\bar{Q}}_4)_1\rangle _0, \end{aligned}$$
(16)
$$\begin{aligned} \chi ^{01}_1= & {} |(Q_1 Q_2)_0 ({\bar{Q}}_3 {\bar{Q}}_4)_1\rangle _1, \end{aligned}$$
(17)
$$\begin{aligned} \chi ^{10}_1= & {} |(Q_1 Q_2)_1 ({\bar{Q}}_3 {\bar{Q}}_4)_0\rangle _1, \end{aligned}$$
(18)
$$\begin{aligned} \chi ^{11}_1= & {} |(Q_1 Q_2)_1 ({\bar{Q}}_3 {\bar{Q}}_4)_1\rangle _1, \end{aligned}$$
(19)
$$\begin{aligned} \chi ^{11}_2= & {} |(Q_1 Q_2)_1 ({\bar{Q}}_3 {\bar{Q}}_4)_1\rangle _2, \end{aligned}$$
(20)

where \((Q_1 Q_2)_0\) and \(({\bar{Q}}_3 {\bar{Q}}_4)_0\) are antisymmetric and the \((Q_1 Q_2)_1\) and \(({\bar{Q}}_3 {\bar{Q}}_4)_1\) are symmetric for the two fermions under permutations. The matrix elements of the color and spin parts are same as the doubly heavy tetraquarks [41].

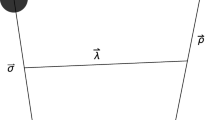
In the spatial space, the Jacobi coordinates are presented in Fig. 1. For the \(cc {\bar{c}} {\bar{c}}\) and \(bb {\bar{b}} \bar{b}\) systems, we can define

$$\begin{aligned}&{\varvec{r}}_{12}= {\varvec{r}}_1 - {\varvec{r}}_2, \end{aligned}$$
(21)
$$\begin{aligned}&{\varvec{r}}_{34}= {\varvec{r}}_3 - {\varvec{r}}_4, \end{aligned}$$
(22)
$$\begin{aligned}&{\varvec{r}} = \frac{{\varvec{r}}_1 + {\varvec{r}}_2}{2} - \frac{{\varvec{r}}_3 + {\varvec{r}}_4}{2}, \end{aligned}$$
(23)

and

$$\begin{aligned} {\varvec{R}} = \frac{{\varvec{r}}_1 + {\varvec{r}}_2 + {\varvec{r}}_3 + {\varvec{r}}_4}{4}. \end{aligned}$$
(24)

Then, other relevant coordinates of this system can be obtained in terms of \({\varvec{r}}_{12}\), \({\varvec{r}}_{34}\), and \({\varvec{r}}\). For a S-wave state, we adopt a set of Gaussian functions to approach its realistic spatial wave function [43]:

$$\begin{aligned} \Psi ({\varvec{r}}_{12},{\varvec{r}}_{34},{\varvec{r}}) {=} \sum _{n_{12},n_{34},n} C_{n_{12}n_{34}n} \psi _{n_{12}}(\varvec{r}_{12}) \psi _{n_{34}}({\varvec{r}}_{34}) \psi _n({\varvec{r}}),\nonumber \\ \end{aligned}$$
(25)

where \(C_{n_{12}n_{34}n}\) are the expansion coefficients. The \(\psi _{n_{12}}({\varvec{r}}_{12})\)\( \psi _{n_{34}}({\varvec{r}}_{34}) \psi _n({\varvec{r}})\) is the position representation of the basis \(|n_{12}n_{34}n\rangle \), where

$$\begin{aligned}&\psi _n({\varvec{r}}) = \frac{2^{7/4}\nu _n^{3/4}}{\pi ^{1/4}} e^{-\nu _n r^2} Y_{00}(\hat{{\varvec{r}}}) = \Bigg (\frac{2 \nu _n}{\pi } \Bigg )^{3/4} e^{-\nu _n r^2}, \end{aligned}$$
(26)
$$\begin{aligned}&\nu _n = \frac{1}{r_1^2a^{2(n-1)}},~~~~ (n=1-N_{max}). \end{aligned}$$
(27)

It should be stressed that our final results are independent on geometric Gaussian size parameters \(r_1\), a, and \(N_{max}\) when sufficiently large bases are chosen [43]. The \(\psi _{n_{12}}({\varvec{r}}_{12})\) and \(\psi _{n_{34}}(\varvec{r}_{34})\) can be written in a similar way, and the momentum representation the basis \( |n_{12}n_{34}n\rangle \) can be obtained by the Fourier transformation.

According to the Pauli exclusion principle, the total wave function of a tetraquark should be antisymmetric, and possible configurations for \(cc {\bar{c}} {\bar{c}}\) and \(bb {\bar{b}} {\bar{b}}\) systems are presented in Table 1. With the full wave functions, all the matrix elements of the Hamiltonian can be worked out. Then, the masses can be obtained by solving the following generalized eigenvalue problem

$$\begin{aligned} \sum _{j=1}^{N_{max}^3}(H_{ij}-EN_{ij})C_j=0,~~~~ (i=1-N_{max}^3), \end{aligned}$$
(28)

where the \(H_{ij}\) are the matrix elements in the total bases, \(N_{ij}\) is the overlap matrix elements of the Gaussian functions arising form the nonorthogonality of bases, E stands for the mass, and \(C_j\) are the eigenvector corresponding to the coefficients \(C_{n_{12}n_{34}n}\) of spatial wave function. Moreover, for a given system, different configurations with same \(J^{PC}\) can mix with each other. The mixing effects are taken into account by diagonalizing the mass matrix of these configurations.

Table 2 Predicted masses of the ground states for \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems
Full size table
Table 3 The color proportions and the root mean square radii of the ground states for \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} \bar{b}\) systems. The units of masses and root mean square radii are in MeV and fm, respectively
Full size table
Table 4 Predicted masses of radial excitations for \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems
Full size table

3 Results and discussions

In present work, we adopt \(N^3_{max} = 10^3\) Gaussian bases to estimate the S-wave \(QQ{\bar{Q}} {\bar{Q}}\) spectra. With these large bases, the numerical results are stable enough for our quark model calculations. The predicted masses of ground states for \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems are presented in Table 2. For the \(cc{\bar{c}} {\bar{c}}\) system, the masses of four ground states lie in the range 6435–6543 MeV, which are higher than the \(J/\psi J/\psi \) threshold. Compared with the experimental data, we expect that these states should correspond to the broad structure in the vicinity of 6.4 GeV. This broad structure may be one state or an overlap of several states from current data, and more experimental information are needed to clarify its nature. For the \(bb{\bar{b}} {\bar{b}}\) system, the masses are also above the relevant \(\Upsilon \Upsilon \) thresholds. These results for the ground states are consistent with nonrelativistic quark model calculations where the pairwise potentials are adopted properly [32,33,34,35, 44].

Besides the masses, we can also calculate the proportions of hidden color components and the root mean square radii. In addition to \(|\bar{3}3 \rangle \) and \(|6 \bar{6}\rangle \), other sets of color representations can be defined as

$$\begin{aligned} |11\rangle= & {} |(Q_1 {\bar{Q}}_3)^1 (Q_2 {\bar{Q}}_4)^1\rangle , \end{aligned}$$
(29)
$$\begin{aligned} |88\rangle= & {} |(Q_1 {\bar{Q}}_3)^8 (Q_2 {\bar{Q}}_4)^8\rangle , \end{aligned}$$
(30)

and

$$\begin{aligned} |1^\prime 1^\prime \rangle= & {} |(Q_1 {\bar{Q}}_4)^1 (Q_2 \bar{Q}_3)^1\rangle , \end{aligned}$$
(31)
$$\begin{aligned} |8^\prime 8^\prime \rangle= & {} |(Q_1 {\bar{Q}}_4)^8 (Q_2 \bar{Q}_3)^8\rangle . \end{aligned}$$
(32)

Then, the relations among three sets of color representations can be expressed as follows,

$$\begin{aligned}&|11\rangle = \sqrt{\frac{1}{3}}|{\bar{3}} 3\rangle + \sqrt{\frac{2}{3}}|6 {\bar{6}}\rangle , \end{aligned}$$
(33)
$$\begin{aligned}&|88\rangle = - \sqrt{\frac{2}{3}}|{\bar{3}} 3\rangle + \sqrt{\frac{1}{3}}|6 {\bar{6}}\rangle , \end{aligned}$$
(34)

and

$$\begin{aligned} |1^\prime 1^\prime \rangle= & {} - \sqrt{\frac{1}{3}}|{\bar{3}} 3\rangle + \sqrt{\frac{2}{3}}|6 {\bar{6}}\rangle , \end{aligned}$$
(35)
$$\begin{aligned} |8^\prime 8^\prime \rangle= & {} \sqrt{\frac{2}{3}}|{\bar{3}} 3\rangle + \sqrt{\frac{1}{3}}|6 {\bar{6}}\rangle . \end{aligned}$$
(36)

In present work, we adopt the \(|11\rangle \) and \(|88\rangle \) representations to stand for the neutral color and hidden color components, respectively. The color proportions and root mean square radii of the calculated ground states are displayed in Table 3. For the \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems, the expectations satisfy the following relations

$$\begin{aligned} \langle {\varvec{r}}_{12}^2 \rangle ^{1/2}= & {} \langle \varvec{r}_{34}^2 \rangle ^{1/2}, \end{aligned}$$
(37)
$$\begin{aligned} \langle {\varvec{r}}^{\prime 2} \rangle ^{1/2}= & {} \langle {\varvec{r}}^{\prime \prime 2} \rangle ^{1/2}, \end{aligned}$$
(38)
$$\begin{aligned} \langle {\varvec{r}}_{13}^2 \rangle ^{1/2}= & {} \langle \varvec{r}_{14}^2 \rangle ^{1/2} = \langle {\varvec{r}}_{23}^2 \rangle ^{1/2} = \langle {\varvec{r}}_{24}^2 \rangle ^{1/2}. \end{aligned}$$
(39)

From Table 3, it can be seen that these states have significant hidden color components and small root mean square radii, and this phenomena indicates that all of them can be regarded as compact tetraquarks.

The low-lying radial excitations of \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems are also calculated in our approach and the results are presented in Table 4. Theoretically, there are two types of radial excitations, the QQ or \({\bar{Q}} {\bar{Q}}\) mode, and the one between QQ and \({\bar{Q}} {\bar{Q}}\) subsystems. The physical states should correspond to the mixture of these two modes. Our results show that the first excitations for the \(cc{\bar{c}} {\bar{c}}\) states lie around 6900 MeV, which should correspond to the observed structure near 6.9 GeV by LHCb Collaboration. Given the \(J/\psi J/\psi \) decay mode, the \(J^{PC}\) of this structure should equal to \(0^{++}\) or \(2^{++}\). Current information is insufficient to determine its spin-parity, and more theoretical and experimental efforts are needed. Moreover, we find that another set of excitations are around 7050 MeV, which have not been observed by LHCb Collaboration. In addition, the predicted excitations for the \(bb {\bar{b}} {\bar{b}}\) systems are around 19600 and 19730 MeV, respectively, which can easily fall apart into the bottomonium pairs. It is claimed that there is no signal in the \(\Upsilon \mu ^+ \mu ^-\) channels by previous LHCb and CMS experiments [13, 14]. We expect that it is due to the small \(\Upsilon \mu ^+ \mu ^-\) branching ratio or lower \(bb{\bar{b}} {\bar{b}}\) production rates relative to the charm sector. Finally, the S-wave spectra for \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems are plotted in Fig. 2 for reference.

Fig. 2
figure 2

The predicted masses of \(cc{\bar{c}} {\bar{c}}\) and \(bb{\bar{b}} {\bar{b}}\) systems

Full size image

The proportions of the hidden color components and root mean square radii for excited \(QQ{\bar{Q}} {\bar{Q}}\) states are listed in Table 5. The small root mean square radii for these states suggest that they are compact tetraquarks, and the sketch of the \(cc {\bar{c}} {\bar{c}}\) structure near 6.9 GeV is presented in Fig. 3. For the excited states, besides the \(J/\psi J/\psi \) and \(\Upsilon \Upsilon \) final states, lots of fall-apart channels are also open. The possible decay modes via S-wave and \(P-\)wave are listed in Table 6.

Table 5 The color proportions and root mean square radii of the radial excited states for \(cc{\bar{c}} {\bar{c}}\) and \(bb\bar{b} {\bar{b}}\) systems. The units of masses and root mean square radii are in MeV and fm, respectively
Full size table
Fig. 3
figure 3

The narrow \(cc {\bar{c}} {\bar{c}}\) structure near 6.9 GeV

Full size image
Table 6 The decay channels of the \(cc{\bar{c}}{\bar{c}}\) and \(bb{\bar{b}}{\bar{b}}\) tetraquarks via fall-apart mechanism
Full size table

In our present work, we do not calculate the tetraquark masses with orbital excitations. Fortunately, one can estimate the typical intervals by considering the similarity among heavy quarkonium, triply heavy baryons, and fully heavy tetraquarks. For the low-lying heavy quarkonium spectra, it can be noticed that the average masses of the first radial excitations are about \(120\sim 150~\mathrm {MeV}\) higher than the orbital ones, while both of them are much higher than the ground states. These behaviors also exist in the predicted triply heavy baryon spectra [45]. Thus, one can expect these patterns and mass gaps also hold for the fully heavy tetraquarks. The average masses of the first orbital excitations are estimated to be approximate 300 MeV higher than the ground states for both \(cc {\bar{c}} {\bar{c}}\) and \(bb {\bar{b}} {\bar{b}}\) systems.

Since the structure near 6.9 GeV corresponds to a radial excited state in our calculation, the \(\psi (2S) J/\psi \) channel is expected to be significant. The ratios

$$\begin{aligned} R=\frac{\Gamma [cc{\bar{c}} {\bar{c}} \rightarrow J/\psi J/\psi ]}{\Gamma [cc{\bar{c}} {\bar{c}} \rightarrow \psi (2S) J/\psi ]} \end{aligned}$$
(40)

can be adopted to describe the relative magnitudes between \(J/\psi J/\psi \) and \(\psi (2S) J/\psi \) final states. For simplicity, one can assume the decay amplitudes are proportional to the overlap of wave functions of the initial and final states, and the proportional coefficient can be canceled in the final ratios. Here, the wave functions for initial tetraquarks have been obtained by solving the generalized eigenvalue problem, and the wave functions of \(J/\psi \), \(\psi (2S)\), \(\Upsilon \), and \(\Upsilon (2S)\) can be got within the relativized quark model as well. With these wave functions, the ratios for \(0^{++}\) and \(2^{++}\) states can be estimated to be

$$\begin{aligned} R[cc{\bar{c}} {\bar{c}}(6849)]= & {} 0.113, \end{aligned}$$
(41)
$$\begin{aligned} R[cc{\bar{c}} {\bar{c}}(6940)]= & {} 0.122, \end{aligned}$$
(42)
$$\begin{aligned} R[cc{\bar{c}} {\bar{c}}(6948)]= & {} 0.075. \end{aligned}$$
(43)

Combined with the branching ratios of \(J/\psi \rightarrow \mu ^+ \mu ^-\) and \(\psi (2S) \rightarrow \mu ^+ \mu ^-\), one can further define

$$\begin{aligned} R_{4\mu } = \frac{\Gamma [cc{\bar{c}} {\bar{c}} \rightarrow J/\psi J/\psi \rightarrow \mu ^+ \mu ^- \mu ^+ \mu ^-]}{\Gamma [cc{\bar{c}} {\bar{c}} \rightarrow \psi (2S) J/\psi \rightarrow \mu ^+ \mu ^- \mu ^+ \mu ^- ]}. \end{aligned}$$
(44)

Then, the ratios \(R_{4\mu }\) are predicted to be

$$\begin{aligned} R_{4\mu }[cc{\bar{c}} {\bar{c}}(6849)]= & {} 0.843, \end{aligned}$$
(45)
$$\begin{aligned} R_{4\mu }[cc{\bar{c}} {\bar{c}}(6940)]= & {} 0.910, \end{aligned}$$
(46)
$$\begin{aligned} R_{4\mu }[cc{\bar{c}} {\bar{c}}(6948)]= & {} 0.559. \end{aligned}$$
(47)

It can be found that the \(\psi (2S) J/\psi \) channel for the excited states is important even though the phase spaces are smaller. The similar situation occurs for the lower excited \(bb{\bar{b}} {\bar{b}}\) states, where the \(R_{4\mu }\) of \(bb{\bar{b}} {\bar{b}}(19567)\), \(bb{\bar{b}} {\bar{b}}(19625)\), and \(bb{\bar{b}} {\bar{b}}(19633)\) states are 0.113, 0.111, and 0.084, respectively. These ratios indicate that the lower excited \(bb{\bar{b}} {\bar{b}}\) states can decay to \(\mu ^+ \mu ^- \mu ^+ \mu ^-\) final states through \(\Upsilon (2S) \Upsilon \) more easily than \(\Upsilon \Upsilon \) mode. Future experiments can search for these states in \(\psi (2S) J/\psi \) and \(\Upsilon (2S) \Upsilon \) final states.

Besides the two-body fall apart process, the three-body decay mode \(J/\psi D {\bar{D}}\) may be also important for the excited \(cc {\bar{c}} {\bar{c}}\) states. It can be assumed that the \(cc {\bar{c}} {\bar{c}} \rightarrow J/\psi D {\bar{D}}\) process occurs through virtual charmonium. Given the phase space, three states \(\psi (2S)\), \(\psi (3770)\), and \(\psi (4040)\) lie in this energy region. Since the initial tetraquarks have no orbital excitation, the decay chain \(cc {\bar{c}} {\bar{c}} \rightarrow \psi (3770) J/\psi \rightarrow J/\psi D {\bar{D}}\) should be highly suppressed and the contributions from the virtual \(\psi (2S)\) and \(\psi (4040)\) states may be essential. Future theoretical and experimental investigations are needed to clarify this problem. The sophisticated study of various decay processes will be given in our future work elsewhere.

4 Summary

In this work, we investigate the masses of fully heavy tetraquarks \(cc {\bar{c}} {\bar{c}}\) and \(bb {\bar{b}} {\bar{b}}\) in an extended relativized quark model. The four-body Hamiltonian including the Coulomb potential, confining potential, spin-spin interactions, and relativistic corrections are solved within the variational method. Our estimations indicate that the broad structure around 6.4 GeV should contain one or more ground states for \(cc {\bar{c}} {\bar{c}}\) tetraquarks, while the narrow structure near 6.9 GeV can be categorized as the first radial excitation of \(cc {\bar{c}} {\bar{c}}\) system. The significant hidden color component and small root mean square radii demonstrate that these states are compact tetraquarks. For the radial excited states, the decay ratios between the \(J/\psi J/\psi \) and \(\psi (2S) J/\psi \) [or \(\Upsilon \Upsilon \) and \(\Upsilon (2S) \Upsilon \)] modes are also qualitatively discussed with the wave functions of the tetraquarks and mesons. Our results show that the \(\psi (2S) J/\psi \) or \(\Upsilon (2S) \Upsilon \) channel is significant for these excited tetraquarks. We hope our sophisticated calculations of the fully heavy tetraquarks may provide valuable information for future experimental searches.