Full-heavy tetraquarks in constituent quark models

Abstract

The full-heavy tetraquarks $bb{\bar{b}}{\bar{b}}$ and $cc{\bar{c}}{\bar{c}}$ are systematically investigated within the chiral quark model and the quark delocalization color screening model. Two structures, meson–meson and diquark–antidiquark, are considered. For the full-beauty $bb{\bar{b}}{\bar{b}}$ systems, there is no any bound state or resonance state in two structures in the chiral quark model, while the wide resonances with masses around $19.1-19.4$ GeV and the quantum numbers $J^{P}=0^{+}$, $1^{+}$, and $2^{+}$ are possible in the quark delocalization color screening model. For the full-charm $cc{\bar{c}}{\bar{c}}$ systems, the results are qualitative consistent in two quark models. No bound state can be found in the meson–meson configuration, while in the diquark–antidiquark configuration there may exist the resonance states, with masses range between 6.2 to 7.4 GeV, and the quantum numbers $J^{P}=0^{+}$, $1^{+}$, and $2^{+}$. And the separation between the diquark and the antidiquark indicates that these states may be the compact resonance states. The reported state X(6900) is possible to be explained as a compact resonance state with $IJ^{P}=00^{+}$ in present calculation. All these full-charm resonance states are worth searching in the experiments further.

1 Introduction

Multiquark states have been proposed in the early stage of quark models, which are invented by Gell-Man and Zweig [1, 2]. No one paid attention to the multiquark states at that time. In 1977, Jaffe did a calculation of the spectra and dominant decay couplings of $QQ{\bar{Q}}{\bar{Q}}$ mesons, which were named as tetrquark states, in the quark-bag model [3, 4]. However, the tetraquarks state became a hot topic only after the observation of exotic state X(3872) by Belle collaboration in 2003 [5]. Since then, more and more exotic states were observed and proposed, such as Y(4260), $Z_c(3900)$, X(5568), and so on. The study of exotic states can help us to understand the hadron structures and the hadron–hadron interactions better.

The full-heavy tetraquark states $(QQ{\bar{Q}}{\bar{Q}}, Q=c,b)$ attracted extensive attention for the last few years, since such states with very large energy can be accessed experimentally and easily distinguished from other states. In the experiments, the CMS collaboration measured pair production of $\Upsilon (1S)$ [6]. There was also a claim of the existence of a full-bottom tetraquark states $bb{\bar{b}}{\bar{b}}$ [7], with a global significance of $3.6 \sigma$ and a mass around 18.4 GeV, almost 500 MeV below the threshold of $\Upsilon \Upsilon$. However, the LHCb collaboration searched for the exotic state $bb{\bar{b}}{\bar{b}}$ in the $\Upsilon (1S)\mu ^{+}\mu ^{-}$ final state [8], and no significant results was found. For full-charm system, $J/\psi$ pair production [9,10,11] and double $c{\bar{c}}$ production [12] have also been measured experimentally, which may be helpful in seeking the exotic state $cc{\bar{c}}{\bar{c}}$. Very recently, the LHCb collaboration observed the structure in the $J/\psi -$pair mass spectrum, and found a narrow structure X(6900), matching the lineshape of a resonance and a broad structure next to the $di-J/\psi$ mass threshold [13]. Such a breakthrough offers more information for the searching of the tetraquark consisting of four charm quarks.

In fact, the possible existence of these full-heavy tetraquark states has already been considered in a number of theoretical work. Some researches pointed out that these full-heavy tetraquark states are stable under strong interaction decays [14,15,16,17,18,19,20,21,22]. Iwasaki first proposed that $cc{\bar{c}}{\bar{c}}$ is a stable bound state with the mass of about 6.0 GeV or 6.2 GeV in 1975 [14]. Chao predicted that there existed full-charm diquark–antidiquark states with masses in the range 6.4–6.8 GeV [15]. Heller et al. used the potential energy coming from the MIT bag model and found that the dimesons $cc{\bar{c}}{\bar{c}}$ and $bb{\bar{b}}{\bar{b}}$ are bound, and the binding energy are in the range of $0.16-0.22$ GeV, which depends on the parameters [16]. Lloyd et al. used a parametrized Hamiltonian to compute the spectrum of all-charm tetraquark states and obtained several close-lying bound states [17]. Berezhnoy et al. took diquark and antidiquark as point particles and employed hyperfine interaction between them, the masses of $cc{\bar{c}}{\bar{c}}$ and $bb{\bar{b}}{\bar{b}}$ states are under the thresholds for $J=1,2$ [18]. Debastiani et al. used a non-relativistic model to study the spectroscopy of a tetraquark composed of $cc{\bar{c}}{\bar{c}}$ in a diquark–antidiquark configuration, and they found that the lowest S-wave tetraquarks might be below their thresholds of spontaneous dissociation into low-lying charmonium pairs [19]. Yang Bai et al. also calculated the mass of $bb{\bar{b}}{\bar{b}}$ state in a diffusion Monte Carlo method and found it was around 100 MeV below the threshold of $\eta _{b}\eta _{b}$ [20]. Esposito et al. showed that the energy of $bb{\bar{b}}{\bar{b}}$ tetraquark is 18.8 GeV, approximately 100 MeV below the threshold [21]. Wei Chen et al. studied the existence of exotic doubly hidden-charm/bottom tetraquark states made of four heavy quarks in a moment QCD sum rule method and discovered that the masses of the $bb{\bar{b}}{\bar{b}}$ tetraquarks are all below or very close to the thresholds of $\Upsilon (1S)\Upsilon (1S)$ and $\eta _{b}(1S)\eta _{b}(1S)$, except one current of $J^{PC}=0^{++}$ and the masses of the $cc{\bar{c}}{\bar{c}}$ tetraquarks are all above the threshold [22].

However, there are also some researches, which disapproved the existence of the full-heavy tetraquark states [23,24,25,26,27,28,29,30,31]. Karliner et al. estimated the masses of the lowest-lying $cc{\bar{c}}{\bar{c}}$ and $bb{\bar{b}}{\bar{b}}$ tetraquarks by using the color-magnetic interaction model, and found they were 6192$\pm 25$ MeV and $18826\pm 25$ MeV, respectively, which were higher than the corresponding thresholds [24]. Hughes et al. searched for the beauty-fully bound tetraquarks by using the lattice nonrelativistic QCD method, and found no evidence of a QCD bound tetraquark below the lowest noninteracting thresholds in the channels studied [25]. Mingsheng Liu et al. studied the mass spectra of the all-heavy tetraquark systems within a potential model, and suggested that no bound state can be formed [27]. Chen studied the ground states of the beauty-full and charm-full systems in a nonrelativistic chiral quark model with the help of Gaussian expansion method [29, 30], and Deng employed three quark models by using the same method [31], neither of them found the $cc{\bar{c}}{\bar{c}}$ and $bb{\bar{b}}{\bar{b}}$ bound states.

Quantum chromodynamics (QCD) is widely accepted as a fundamental theory of strong interaction. However, it is difficult to study hadron–hadron interactions and multiquark states directly because of nonperturbtive properties of QCD in the low energy region. Many quark models based on QCD theory have been developed to get physical insights into the multiquark systems. A common approach is the chiral quark model (ChQM) [32], in which the constituent quarks interact with each other through colorless Goldstone bosons exchange in addition to the colorful one-gluon-exchange and confinement, and the chiral partner $\sigma$ meson exchange is introduced to give the immediate-range attraction of nucleon–nucleon interaction. An alternative approach to study the hadron–hadron interactions is the quark delocalization color screening model (QDCSM), which was developed in the 1990s with the aim of explaining the similarities between nuclear and molecular forces [33]. The quark delocalization and color screening in QDCSM work together to provide the short-range repulsion and the intermediate-range attraction. Both of these two models can give a good description of the properties of deuteron, nucleon–nucleon and hyperon–nucleon interactions [34, 35]. Recently, QDCSM has been used to study the pentaquarks with hidden strange [36], hidden-charm and hidden-bottom [37]. Besides, this model was also applied to the tetraquarks composed of $us{\bar{d}}{\bar{b}}$ and $ud{\bar{s}}{\bar{b}}$ to investigate the existence of X(5568) [38]. Therefore, it is interesting to extend this model to the full-heavy tetraquarks. In addition, to check the model dependence of the full-heavy tetraquarks and explore the hadron–hadron interactions in different quark models, the ChQM is also used in this work. The resonating-group method (RGM) [39], which has been widely used in the nuclear physics, is employed to do the calculation.

The structure of this paper is as follows. Section 2 gives a brief introduction of two quark models, and the construction of wave functions. The numerical results and discussions are given in Sect. 3. The summary is presented in the last section.

2 Models and wavefunctions

In this work, we investigate the full-heavy tetraquarks within two quark models: ChQM and QDCSM. Two structures, meson–meson and diquark–antidiquark, are considered. In this sector, we will introduce these two models and the wave functions of the tetraquarks for two structures.

2.1 The chiral quark model (ChQM)

The ChQM has been successfully applied to describe the properties of hadrons and hadron–hadron interactions [32, 39], and has been extended to the study of multiquark states. The model details can be found in Refs. [32, 40]. We only show the Hamiltonian of the model here.

$$\begin{aligned} H=\sum _{i=1}^{4}\left( m_i+\frac{p_i^2}{2m_i}\right) -T_{cm}+\sum _{i=1<j}^{4}( V^{CON}_{ij}+V^{OGE}_{ij})\nonumber \\ \end{aligned}$$

(1)

where $T_{cm}$ is the kinetic energy of the center of mass; $V^{CON}_{ij}$ and $V^{OGE}_{ij}$ are the interactions of the confinement and the one-gluon-exchange, respectively. For the full-heavy system, there is no $\sigma$-exchange and the Goldstone boson exchange. The central part of $V^{CON}_{ij}$ and $V^{OGE}_{ij}$ are shown below:

$$\begin{aligned} V^{CON}_{ij}= & {} -\varvec{\lambda }^c_i \cdot \varvec{\lambda }^c_j (a_c r^2_{ij}+V_{0})\end{aligned}$$

(2)

$$\begin{aligned} V^{OGE}_{ij}= & {} \frac{\alpha _s}{4} \varvec{\lambda }^c_i \cdot \varvec{\lambda }^c_j \left[ \frac{1}{r_{ij}}-\frac{\pi }{2}\delta ({\mathbf {r}}_{ij})\left( \frac{1}{m_{i}^{2}}+\frac{1}{m_{j}^{2}} \right. \right. \nonumber \\&\left. \left. +\frac{4\varvec{\sigma }_{i}\cdot \varvec{\sigma }_{j}}{3m_{i}m_{j}} \right) \right] \end{aligned}$$

(3)

where $\alpha _{s}$ is the running quark–gluon coupling constant.

2.2 The quark delocalization color screening model (QDCSM)

Generally, the Hamiltonian of QDCSM is almost the same as that of ChQM, but with two modifications [33]. The one is that there is no $\sigma$-meson exchange in QDCSM, and another one is that the screened color confinement is used between quark pairs reside in different clusters, aimed to take into account the QCD effect which has not yet been included in the two-body confinement and effective one gluon exchange. Since there is no $\sigma$-meson exchange interaction between the heavy quarks (c or b), the only difference here is the confinement interaction. The confining potential in QDCSM was modified as follows:

$$\begin{aligned} V^{CON}_{ij}=\left\{ \begin{array}{ll} -\varvec{\lambda }^c_i \cdot \varvec{\lambda }^c_j (a_c r^2_{ij}+V_{0}),&{}\text {i,j in the same cluster}\\ - \varvec{\lambda }^c_i \cdot \varvec{\lambda }^c_j a_c\frac{1 - e^{-\mu _{ij} r^2_{ij}}}{\mu _{ij}},&{}\text {otherwise}\\ \end{array}\right. \end{aligned}$$

(4)

where $\mu _{ij}$ is the color screening parameter, which is determined by fitting the deuteron properties, nucleon–nucleon scattering phase shifts, and hyperon–nucleon scattering phase shifts, respectively, with $\mu _{uu}=0.45~ \hbox {fm}^{-2}$, $\mu _{us}=0.19~ \hbox {fm}^{-2}$ and $\mu _{ss}=0.08~ \hbox {fm}^{-2}$, satisfying the relation, $\mu _{us}^{2}=\mu _{uu}\mu _{ss}$ [35]. When extending to the heavy quark case, there is no experimental data available, so we take it as a adjustable parameter $\mu _{cc}=0.01 \sim 0.001~ \hbox {fm}^{-2}$ and $\mu _{bb}=0.001 \sim 0.0001~ \hbox {fm}^{-2}$. We find the results are insensitive to the value of $\mu _{cc}$ and $\mu _{bb}$. So in the present work, we take $\mu _{cc}=0.01~ \hbox {fm}^{-2}$ and $\mu _{bb}=0.001~$ $\hbox {fm}^{-2}$.

The single particle orbital wave functions in the ordinary quark cluster model are the left and right centered single Gaussian functions:

$$\begin{aligned} \phi _\alpha ({\mathbf {S}}_{i})=\left( \frac{1}{\pi b^2}\right) ^{\frac{3}{4}}e^ {-\frac{({\mathbf {r}}-{\mathbf {S}}_i/2)^2}{2b^2}}, \nonumber \\ \phi _\beta (-{\mathbf {S}}_{i})=\left( \frac{1}{\pi b^2}\right) ^{\frac{3}{4}}e^ {-\frac{({\mathbf {r}}+{\mathbf {S}}_i/2)^2}{2b^2}}. \end{aligned}$$

(5)

The quark delocalization in QDCSM is realized by writing the single particle orbital wave function as a linear combination of the left and right Gaussians:

$$\begin{aligned} {\psi }_{\alpha }({\mathbf {S}}_{i},\epsilon )= & {} \left( {\phi }_{\alpha }({\mathbf {S}}_{i}) +\epsilon {\phi }_{\alpha }(-{\mathbf {S}}_{i})\right) /N(\epsilon ), \nonumber \\ {\psi }_{\beta }(-{\mathbf {S}}_{i},\epsilon )= & {} \left( {\phi }_{\beta }(-{\mathbf {S}}_{i}) +\epsilon {\phi }_{\beta }({\mathbf {S}}_{i})\right) /N(\epsilon ), \nonumber \\ N(\epsilon )= & {} \sqrt{1+\epsilon ^2+2\epsilon e^{{-S}_i^2/4b^2}}. \end{aligned}$$

(6)

where $\epsilon ({\mathbf {S}}_i)$ is the delocalization parameter determined by the dynamics of the quark system rather than adjusted parameters. In this way, the system can choose its most favorable configuration through its own dynamics in a larger Hilbert space.

The parameters used in our previous work are determined by fitting the mass spectrum of mesons and baryons including light quarks (u,  d,  s), but the meson composed of heavy quarks like $\eta _{b}$($\eta _{c}$) or $\Upsilon$($J/\psi$) do not fit well. To give the right mass of the mesons we used in this work, we adjust the parameters by fitting the masses of $\eta _{b}$, $\Upsilon$, $\eta _{c}$ and $J/\psi$. In order to give ranges of the model parameters, three sets of parameters of both two quark models are used in the calculation, which are listed in Table 1. The running coupling constant $\alpha _s$ and the constant $V_0$ take different values for charm quark pair and bottom quark pair to have a better fitting. The calculated masses of the mesons are $m_{\eta _{b}}=9399$ MeV, $m_{\Upsilon }=9460$ MeV, $m_{\eta _{c}}=2979$ MeV and $m_{J/\psi }=3097$ MeV within these model parameters.

Table 1 Model parameters

2.3 The wave function

In this work, the resonating group method (RGM) [40], a well-established method for studying a bound-state or a scattering problem, is employed to calculate the energy of the full-heavy systems. The wave function of the four-quark system is of the form

$$\begin{aligned} \varPsi ={\mathcal {A}}[[\psi ^{L}\chi ^{\sigma }]_{JM}\chi ^{f}\chi ^{c}]. \end{aligned}$$

(7)

where $\psi ^{L},\chi ^{\sigma },\chi ^{f}$ and $\chi ^{c}$ are the orbital, spin, flavor and color wave functions, respectively, which are given below. The symbol ${\mathcal {A}}$ is the anti-symmetrization operator. For the meson–meson configuration, ${\mathcal {A}}$ is defined as

$$\begin{aligned} {\mathcal {A}}=1-P_{13}-P_{24}+P_{13}P_{24}. \end{aligned}$$

(8)

For the diquark–antidiquark configuration,

$$\begin{aligned} {\mathcal {A}}=1-P_{12}-P_{34}+P_{12}P_{34}. \end{aligned}$$

(9)

2.3.1 The orbital wave function

The total orbital wave function is composed of two internal cluster orbital wave functions ($\psi _{1}({\mathbf {R}}_{1})$ and $\psi _{2}({\mathbf {R}}_{2})$), and one relative motion wave function ($\chi _{L}({\mathbf {R}})$) between two clusters.

$$\begin{aligned} \psi ^{L}=\psi _{1}({\mathbf {R}}_{1})\psi _{2}({\mathbf {R}}_{2})\chi _{L}({\mathbf {R}}), \end{aligned}$$

(10)

where ${\mathbf {R}}_{1}$ and ${\mathbf {R}}_{2}$ are the internal coordinates for the cluster 1 and cluster 2, respectively. ${\mathbf {R}}={\mathbf {R}}_{1}-{\mathbf {R}}_{2}$ is the relative coordinate between the two clusters 1 and 2. $\chi _{L}({\mathbf {R}})$ is expanded by gaussian bases

$$\begin{aligned} \chi _{L}({\mathbf {R}})= & {} \frac{1}{\sqrt{4\pi }}\left( \frac{3}{2\pi b^{2}}\right) \sum _{i=1}^{n}C_{i}\nonumber \\&\times \int \exp \left[ -\frac{3}{4b^{2}}({\mathbf {R}}-{\mathbf {S}}_{i})^{2}\right] Y_{LM}({\hat{S}}_{i})d\hat{S_{i}}, \end{aligned}$$

(11)

where ${\mathbf {s}}_{i}$ is the generate coordinate, n is the number of the gaussian bases, which is determined by the stability of the results. By doing this is expansion, we can simplify the integro-differential equation to an algebraic equation, solve this generalized eigen-equation to get the energy of the system more easily. The details of solving the RGM equation can be found in Ref. [40].

2.3.2 The flavor wave function

The flavor wave function for the full-heavy system is very simple. For the meson–meson structure,

$$\begin{aligned} \chi _{00}^{fm1}= & {} b{\bar{b}}b{\bar{b}} \end{aligned}$$

(12)

$$\begin{aligned} \chi _{00}^{fm2}= & {} c{\bar{c}}c{\bar{c}} \end{aligned}$$

(13)

where the superscript of the $\chi$ is the index of the flavor wave function for meson–meson structure, and the subscripts stand for the isospin and its third component $II_{z}$.

For the diquark–antidiquark structure,

$$\begin{aligned} \chi _{00}^{fd1}= & {} bb{\bar{b}}{\bar{b}} \end{aligned}$$

(14)

$$\begin{aligned} \chi _{00}^{fd2}= & {} cc{\bar{c}}{\bar{c}} \end{aligned}$$

(15)

The upper and lower indices are similar to those of the meson–meson structure.

2.3.3 The spin wave function

The total spin wave functions for the four-quark system can be obtained by coupling the wave functions of two clusters.

$$\begin{aligned} \chi ^{\sigma 1}_{00}= & {} \frac{1}{2}(\alpha \beta \alpha \beta -\beta \alpha \alpha \beta -\beta \beta \alpha +\beta \alpha \beta \alpha ) \end{aligned}$$

(16)

$$\begin{aligned} \chi ^{\sigma 2}_{00}= & {} \sqrt{\frac{1}{12}}(2\alpha \alpha \beta \beta +2\beta \beta \alpha \alpha \nonumber \\&~~~~~~~ -\alpha \beta \alpha \beta -\beta \alpha \alpha \beta -\beta \beta \alpha -\beta \alpha \beta \alpha ) \end{aligned}$$

(17)

$$\begin{aligned} \chi ^{\sigma 3}_{11}= & {} \sqrt{\frac{1}{2}}(\alpha \beta \alpha \alpha -\beta \alpha \alpha \alpha ) \end{aligned}$$

(18)

$$\begin{aligned} \chi ^{\sigma 4}_{11}= & {} \sqrt{\frac{1}{2}}(\alpha \alpha \alpha \beta -\alpha \alpha \beta \alpha ) \end{aligned}$$

(19)

$$\begin{aligned} \chi ^{\sigma 5}_{11}= & {} \frac{1}{2}(\alpha \alpha \alpha \beta +\alpha \alpha \beta \alpha -\alpha \beta \alpha \alpha -\beta \alpha \alpha \alpha ) \end{aligned}$$

(20)

$$\begin{aligned} \chi ^{\sigma 6}_{22}= & {} \alpha \alpha \alpha \alpha \end{aligned}$$

(21)

The spin wave function of two structures is the same.

2.3.4 The color wave function

For the meson–meson structure, we give the wave functions for the two-body clusters ($Q{\bar{Q}}$) first, which are

$$\begin{aligned}&\chi ^{1}_{c[111]}=\sqrt{\frac{1}{3}}(r{\bar{r}}+g{\bar{g}}+b{\bar{b}}) \end{aligned}$$

(22)

$$\begin{aligned}&\chi ^{2}_{c[21]}=r{\bar{b}} \qquad \chi ^{3}_{c[21]}=-r{\bar{g}}\nonumber \\&\chi ^{4}_{c[21]}=g{\bar{b}} \qquad \chi ^{5}_{c[21]}=-b{\bar{g}}\nonumber \\&\chi ^{6}_{c[21]}=g{\bar{r}} \qquad \chi ^{7}_{c[21]}=b{\bar{r}}\nonumber \\&\chi ^{8}_{c[21]}=\sqrt{\frac{1}{2}}(r{\bar{r}}-g{\bar{g}})\nonumber \\&\chi ^{9}_{c[21]}=\sqrt{\frac{1}{6}}(-r{\bar{r}}-g{\bar{g}}+2b{\bar{b}}) \end{aligned}$$

(23)

where the subscript [111] and [21] stand for the color singlet and color octet cluster respectively.

Then, the total color wave functions for the four-quark system with the meson–meson structure can be obtained by coupling the wave functions of two clusters.

$$\begin{aligned} \chi ^{cm1}&=\chi ^{1}_{c[111]}\chi ^{1}_{c[111]} \end{aligned}$$

(24)

$$\begin{aligned} \chi ^{cm2}&=\sqrt{\frac{1}{8}}(\chi ^{2}_{c[21]}\chi ^{7}_{c[21]}-\chi ^{4}_{c[21]}\chi ^{5}_{c[21]}-\chi ^{3}_{c[21]}\chi ^{6}_{c[21]}\nonumber \\ {}&\quad +\chi ^{8}_{c[21]}\chi ^{8}_{c[21]}-\chi ^{6}_{c[21]}\chi ^{3}_{c[21]}+\chi ^{9}_{c[21]}\chi ^{9}_{c[21]}\nonumber \\ {}&\quad -\chi ^{5}_{c[21]}\chi ^{4}_{c[21]}+\chi ^{7}_{c[21]}\chi ^{2}_{c[21]}) \end{aligned}$$

(25)

where $\chi ^{c1}_{m}$ and $\chi ^{c2}_{m}$ represent the color wave function for the color-singlet channel ($1\times 1$) and the hidden-color channel ($8\times 8$), respectively.

For the diquark–antidiquark structure, we firstly give the color wave functions of the diquark clusters,

$$\begin{aligned} \chi ^{1}_{c[2]}= & {} rr \qquad \chi ^{2}_{c[2]}=\sqrt{\frac{1}{2}}(rg+gr) \qquad \chi ^{3}_{c[2]}=gg\nonumber \\ \chi ^{4}_{c[2]}= & {} \sqrt{\frac{1}{2}}(rb+br) \qquad \chi ^{5}_{c[2]}=\sqrt{\frac{1}{2}}(gb+bg)\nonumber \\ \chi ^{6}_{c[2]}= & {} bb \qquad \chi ^{7}_{c[11]}=\sqrt{\frac{1}{2}}(rg-gr)\nonumber \\ \chi ^{8}_{c[11]}= & {} \sqrt{\frac{1}{2}}(rb-br) \qquad \chi ^{9}_{c[11]}=\sqrt{\frac{1}{2}}(gb-bg) \end{aligned}$$

(26)

and the color wave functions of the antidiquark clusters,

$$\begin{aligned} \chi ^{1}_{c[22]}= & {} {\bar{r}}{\bar{r}} \qquad \chi ^{2}_{c[22]}=\sqrt{\frac{1}{2}}({\bar{r}}{\bar{g}}+{\bar{g}}{\bar{r}}) \qquad \chi ^{3}_{c[22]}={\bar{g}}{\bar{g}}\nonumber \\ \chi ^{4}_{c[22]}= & {} \sqrt{\frac{1}{2}}({\bar{r}}{\bar{b}}+{\bar{b}}{\bar{r}}) \qquad \chi ^{5}_{c[22]}=\sqrt{\frac{1}{2}}({\bar{g}}{\bar{b}}+{\bar{b}}{\bar{g}})\nonumber \\ \chi ^{6}_{c[22]}= & {} {\bar{b}}{\bar{b}} \qquad \chi ^{7}_{c[211]}=\sqrt{\frac{1}{2}}({\bar{r}}{\bar{g}}-{\bar{g}}{\bar{r}})\nonumber \\ \chi ^{8}_{c[211]}= & {} \sqrt{\frac{1}{2}}({\bar{r}}{\bar{b}}-{\bar{b}}{\bar{r}}) \qquad \chi ^{9}_{c[211]}=\sqrt{\frac{1}{2}}({\bar{g}}{\bar{b}}-{\bar{b}}{\bar{g}}) \end{aligned}$$

(27)

After that, the total wave functions for the four-quark system with the diquark–antidiquark structure are obtained as below,

$$\begin{aligned} \chi ^{cd1}&=\sqrt{\frac{1}{6}}[\chi ^{1}_{c[2]}\chi ^{1}_{c[22]}-\chi ^{2}_{c[2]}\chi ^{2}_{c[22]}+\chi ^{3}_{c[2]}\chi ^{3}_{c[22]}\nonumber \\ {}&\quad +\chi ^{4}_{c[2]}\chi ^{4}_{c[22]}-\chi ^{5}_{c[2]}\chi ^{5}_{c[22]}+\chi ^{5}_{c[2]}\chi ^{5}_{c[22]}] \end{aligned}$$

(28)

$$\begin{aligned} \chi ^{cd2}&=\sqrt{\frac{1}{3}}[\chi ^{7}_{c[11]}\chi ^{7}_{c[211]}-\chi ^{8}_{c[11]}\chi ^{8}_{c[211]}+\chi ^{9}_{c[11]}\chi ^{9}_{c[211]}] \end{aligned}$$

(29)

Finally, we can acquire the total wave functions by substituting the wave functions of the orbital, the spin, the flavor and the color parts into the Eq.(7) according to the given quantum number of the system.

3 Numerical results and discussions

In the framework of two quark models, ChQM and QDCSM, we investigate the full-heavy tetraquarks $bb{\bar{b}}{\bar{b}}$ and $cc{\bar{c}}{\bar{c}}$ in two structures, meson–meson and diquark–antidiquark. The quantum numbers of the teraquarks we study here are $IJ^{P}=00^{+}$, $01^{+}$, and $02^{+}$. For the meson–meson structure ($Q{\bar{Q}}-Q{\bar{Q}}$), we take into account of two color configurations in the ChQM, which are the color singlet–singlet ($1\times 1$) and color octet–octet ($8\times 8$) configurations. Since the QDCSM considers the effect of the hidden color channel to some extent [41], only the color singlet–singlet is calculated in this model. For the diquark–antidiquark structure ($QQ-{\bar{Q}}{\bar{Q}}$), two color configurations, antitriplet-triplet (${\bar{3}}\times 3$) and sextet-antisextet ($6\times {\bar{6}}$), are considered in both models.

Table 2 The energies of $bb{\bar{b}}{\bar{b}}$ systems with meson–meson structure in ChQM and QDCSM. [ijk] stand for the indices of spin, flavor and color wave functions $\chi ^{\sigma {i}}$, $\chi ^{fm {j}}$, $\chi ^{cm {k}}$ (unit: MeV). The thresholds of $\eta _{b}\eta _{b}$, $\Upsilon \Upsilon$, $\eta _{b}\Upsilon$, $\Upsilon \eta _{b}$ are 18799 MeV, 18920 MeV, 18860 MeV and 18860 MeV, respectively

Table 3 The energies of $bb{\bar{b}}{\bar{b}}$ systems with diquark–antidiquark structure in ChQM and QDCSM. [ijk] stand for the indices of spin, flavor and color wave functions $\chi ^{\sigma {i}}$, $\chi ^{fd {j}}$, $\chi ^{cd {k}}$ (unit: MeV)

Table 4 The energies of $cc{\bar{c}}{\bar{c}}$ systems with meson–meson structure in ChQM and QDCSM. [ijk] stand for the indices of spin, flavor and color wave functions $\chi ^{\sigma _{i}}$, $\chi ^{fm {j}}$, $\chi ^{cm {k}}$ (unit: MeV). The thresholds of $\eta _{c}\eta _{c}$, $J/\psi J/\psi$, $\eta _{c}J/\psi$, $J/\psi \eta _{c}$ are 5958 MeV, 6195 MeV, 6076 MeV and 6076 MeV, respectively

Table 5 The energies of $cc{\bar{c}}{\bar{c}}$ systems with diquark–antidiquark structure in ChQM and QDCSM. [ijk] stand for the indices of spin, flavor and color wave functions $\chi ^{\sigma _{i}}$, $\chi ^{fd {j}}$, $\chi ^{cd {k}}$ (unit: MeV)

To find out if there is any bound state in such full-heavy tetraquark systems, we do a dynamic bound-state calculation here. The single-channel calculation, as well as the channel-coupling are carried out. All the results for $bb{\bar{b}}{\bar{b}}$ and $cc{\bar{c}}{\bar{c}}$ systems in two structures are listed in Tables 2, 3, 4, 5 and 6, respectively. In the tables, ChQM (or QDCSM) I, ChQM (or QDCSM) II, and ChQM (or QDCSM) III stand for the results of the ChQM (or QDCSM) with three sets of parameters respectively. The second column shows the combination in spin ($\chi ^{\sigma _{i}}$), flavor ($\chi ^{f_{j}}$), and color ($\chi ^{c_{k}}$) degrees of freedom for each channel. The columns headed with $E_{th}$ denotes the theoretical threshold of each channel and $E_{sc}$ represents the lowest energies in the single channel calculation. For meson–meson structure, $E_{cc1}$ and $E_{cc2}$ denote the lowest energies of the coupling of the color-singlet channels and the coupling of all channels, respectively. An additional column headed with “Channel” denotes the physical contents of the channel. For diquark–antidiquark structure, $E_{cc}$ means the energies of the coupling of all channels. All the general features of the calculated results are as follows.

3.1 Full-beauty tetraquarks $bb{\bar{b}}{\bar{b}}$

For the tetraquarks composed of $bb{\bar{b}}{\bar{b}}$, the energies of the possible quantum numbers with two structures in both ChQM and QDCSM are listed in Tables 2 and 3, respectively. The $\eta _{b8}\eta _{b8}$ in the Table 2 represents the molecular state $\eta _{b}\eta _{b}$ with the color octet–octet ($8\times 8$) configuration. For meson–meson structure, the energies of every single channel are above the corresponding theoretical threshold in both two models with different sets of parameters. The channel-coupling effect is very small and cannot help much, and the energies are still higher than the theoretical thresholds, which means that there is no any bound states with the meson–meson structure in both two models. Besides, we also find the results in both two models are almost the same, this is because that the quarks are too heavy to run, resulting in the value of the quark delocalization parameter $\epsilon$ in QDCSM is close to 0. The color screening parameter in QDCSM is also very small because of the heavy quarks, which makes the difference of the confinement between two models is very small. So both the effect of the quark delocalization and the color screening in QDCSM is very small in such full-heavy system with meson–meson structure, and the $\sigma$ meson exchange is also inoperative in ChQM, which make the coincident results of two models.

Table 6 The energies of $cc{\bar{c}}{\bar{c}}$ excited states with the diquark–antidiquark structure in the ChQM and QDCSM (unit: MeV)

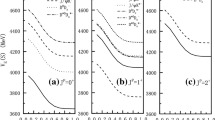
For the diquark–antidiquark structure, the energies of both ChQM and QDCSM are shown in Table 3, from which we can see that the energies of this configuration are higher than that of meson–meson configuration. Besides, the energies in QDCSM are generally lower than that in ChQM. Since the color symmetry of the diquark and antidiquark are color octet, the color screening will make the quark delocalization work in QDCSM, which leads to lower energy in this model. Comparing with the results of three different sets of parameters, we find that the energies of the color-singlet channels are very close to each other, while those of the hidden-color channels are different. However, the energy of every single channel is still above the corresponding theoretical threshold. Moreover, the effect of the channel-coupling is also very small in both two models. So none of these states listed in Table 3 is a bound state. However, it is possible for them to be resonance states, because the colorful subclusters diquark (QQ) and antidiquark (${\bar{Q}}{\bar{Q}}$) cannot fall apart directly due to the color confinement. To check the possibility, we carry out an adiabatic calculation of the effective potentials for the $bb{\bar{b}}{\bar{b}}$ system with diquark–antidiquark structure, the results of which are shown in Fig. 1. The variation tendency of the effective potentials with different sets of parameters are similar. To save space, we only show the results of one set of parameters here.

From the Fig. 1a we can see that the effective potential of each channel is increasing when the two subclusters fall apart, which means that the diquark and antidiquark tend to clump together without hinderance. This behavior indicates that the odds for the states being diquark–antidiquark configuration, meson–meson configuration, or other configurations are the same. Moreover, from the Tables 2 and 3, the energy of the each channel with the diquark–antidiquark structure is higher than the one of the meson–meson structure. So the state prefers to be two free mesons. Therefore, none of these state is a observable resonance state in ChQM. It is different in QDCSM (see Fig. 1b), where the energy of the state will rise when the two subclusters are too close, so there is a hinderance for the states change structure to meson–meson even if the energy of the state is lower in meson–meson structure. It is possible to form a wide resonance. The resonance energies are $19122 \sim 19344$ MeV for $IJ^P=00^+$, $19184 \sim 19354$ MeV for $IJ^P=01^+$, and $19236 \sim 19374$ MeV for $IJ^P=02^+$, respectively.

The effective potentials for the meson–meson $bb{\bar{b}}{\bar{b}}$ systems are also calculated and shown in Figs. 2 and 3, corresponding to the color singlet channels and the hidden color channels respectively. From Fig. 2 we find that the effective potentials for the color singlet channels are all repulsive except for the $IJ^{P}=00^{+}$ $\Upsilon \Upsilon$ channel, which has very weak attractions. That’s why we cannot obtain any bound state in the dynamical calculation. Figure 3 only gives the potential for the hidden color channels in ChQM, because the QDCSM considers the effect of the hidden color channel to some extent, only the color singlet channels are calculated in this model. It is obvious in Fig. 3 that the behavior of the potential for the hidden color channels is similar to that of the diquark–antidiquark configuration, where the effective potential of each channel is increasing when the two meson subclusters fall apart. So there is no any observable resonance state for the meson–meson $bb{\bar{b}}{\bar{b}}$ systems.

To investigate the interaction between two subclusters, we continue to study the contribution of each interaction term to the energy of the system. Here, to save space, we take the results of the $IJ^{P}=00^{+}$ $\Upsilon \Upsilon$ channel in meson–meson structure as an example. The total effective potential, as well as each interaction term to the effective potential, including the kinetic energy ($V_{VK}$), the confinement ($V_{CON}$), the Coulomb interaction ($V_{Coul}$) and the color-magnetic interaction ($V_{CMI}$), are shown in Fig. 4. We can see that the kinetic energy term in both ChQM and QDCSM provides attractive interactions, and the attraction in QDCSM is stronger than the one in ChQM. In the ChQM, the confinement does not contribute to the effective potential between $b{\bar{b}}$ and $b{\bar{b}}$, but it provides a slight repulsion in QDCSM. Both the Coulomb term and the color-magnetic term provide repulsion, which decrease the attraction of the kinetic energy term, and make the total weak attraction of this channel.

3.2 Full-charm tetraquarks $cc{\bar{c}}{\bar{c}}$

The full-charm systems $cc{\bar{c}}{\bar{c}}$ are investigated here and the energies of three sets of parameters in two quark models with two configurations are listed in Tables 4 and 5, respectively. The results are similar to the full-beauty systems $bb{\bar{b}}{\bar{b}}$. For meson–meson structure, the energy of each single channel is above the corresponding theoretical threshold in both two models. The energy is almost unchanged by the channel-coupling calculation, indicating that the effect of the channel-coupling is very small. This is because the mass difference between each channel is very large. So there is no any bound state with the meson–meson structure in both models. The results of three sets of parameters in both ChQM and QDCSM are similar.

To study the interaction between two mesons, we also carry out the adiabatic calculation of the effective potentials for the $cc{\bar{c}}{\bar{c}}$ systems, and the results are similar to those of the $bb{\bar{b}}{\bar{b}}$ systems. Besides, since the results of three sets of parameters in both ChQM and QDCSM are similar, we show the potentials of one set of them here. For the color singlet channels, the effective potentials in both two quark models are shown in Fig. 5a, b, respectively. In ChQM, although the effective potential of the $IJ=00$ $J/\psi J/\psi$ is attractive, the attraction is very weak. The potentials of other four channels are all repulsive. So none of these color singlet state is bound in the dynamical calculation. In QDCSM, although the attraction of the $IJ=00$ $J/\psi J/\psi$ channel is a little stronger than the one in ChQM, it is still not large enough to form a bound state. Besides, the potential of the $IJ=02$ $J/\psi J/\psi$ channel is attractive too, but it is very weak. The potential of other three channels are all repulsive. Therefore, there is still no any bound state in QDCSM for the meson–meson structure. Besides, to investigate if there is any resonance state, we also calculate the effective potential of the hidden color channels in ChQM, which are shown in Fig. 6. Clearly, the behavior of the potential is similar to that of the full-beauty systems, where the effective potential of each channel is increasing when the two meson subclusters fall apart. So there is no any observable resonance state for the $cc{\bar{c}}{\bar{c}}$ systems in meson–meson configuration.

Fig. 1

The effective potentials for the diquark–antidiquark $bb{\bar{b}}{\bar{b}}$ systems in two quark models

Fig. 2

The effective potentials of the color singlet channels for the meson–meson $bb{\bar{b}}{\bar{b}}$ systems in two quark models

Fig. 3

The effective potentials of the hidden color channels for the meson–meson $bb{\bar{b}}{\bar{b}}$ systems in ChQM

Fig. 4

The contributions to the effective potential of the $IJ^{P}=00^{+}$ $\Upsilon \Upsilon$ channel from various terms of interactions in the ChQM and QDCSM

Fig. 5

The effective potentials of the color singlet channels for the meson–meson $cc{\bar{c}}{\bar{c}}$ systems in two quark models

Fig. 6

The effective potentials of the hidden color channels for the meson–meson $cc{\bar{c}}{\bar{c}}$ systems in ChQM III

Towards to the diquark–antidiquark configuration, the energies with three sets of parameters in both ChQM and QDCSM are listed in Table 5. It is clear in Table 5 that the energy of every single channel is above the theoretical threshold of the corresponding channel in both models. The channel-coupling pushes the lowest energy down a little, but the effect is not large enough to lower the energy below the threshold. So there is no any bound state in this diquark–antidiquark structure, which is similar to the results of the full beauty systems. To check that if there is any resonance state, we also carry out the adiabatic calculation of the effective potentials for the $cc{\bar{c}}{\bar{c}}$ systems, as we do for the $bb{\bar{b}}{\bar{b}}$ systems.

Fig. 7

The effective potentials for the diquark–antidiquark $cc{\bar{c}}{\bar{c}}$ systems in two quark models

The effective potentials for the $cc{\bar{c}}{\bar{c}}$ system in the diquark–antidiquark structure are shown in Fig.7, from which we find the behavior of the potential is different from that of the diquark–antidiquark $bb{\bar{b}}{\bar{b}}$ systems. In ChQM, the minimum potential of each channel (except the first channel of $IJ=00$) appears at the separation of 0.3 fm, which indicates that two subclusters are not willing to huddle together or fall apart. Besides, the energy of each channel is higher than the corresponding threshold according to Table 5. So each state is possible to be a resonance state. We also find that the channel coupling of the $IJ=00$ system makes the energy a little lower. In QDCSM, the results are similar. The minimum potential of each channel appears at the separation of 0.5 fm, and the energy of each channel is higher than the corresponding threshold. So it is also possible for each channel to be a resonance state in QDCSM. From the Table 5, we can see that the resonance energy in QDCSM is lower than the one in ChQM. Besides, the minimum potential appears at the separation of 0.3 fm in ChQM and 0.5 fm in QDCSM, indicating that these two subclusters are close to each other. Therefore, these resonance states may be the compact resonance states.

To check whether these resonance states can be survived by coupling to the open channels, we do a channel-coupling calculation of all channels with both meson–meson and diquark–antidiquark structures. A stabilization method, which has proven to be a valuable tool for estimating the energies of the metastable states of electron-atom, electron-molecule, and atom-diatom complexes [42], is employed to find the genuine resonances. This method was also applied to the pentaquark systems in the quark model calculation recently [43, 44], and it was named as the real scaling method. In this work, the distance between two clusters ($Q{\bar{Q}}-Q{\bar{Q}}$ or $QQ-{\bar{Q}}{\bar{Q}}$) is labeled as $S_{i}$, and the largest one is $S_{m}$. With the increasing of $S_{m}$, an unbound state will fall off toward its threshold, but a resonance state will tend to be stable. So we calculate the energy eigenvalues of the full-heavy systems by taking the value of $S_{m}$ from 4.8 fm to 8.5 fm to see if there is any stable state. The stabilization plots of the energies of the $cc{\bar{c}}{\bar{c}}$ systems in ChQM III with possible quantum numbers are shown in Figs. 8, 9 and 10.

Fig. 8

The stabilization plots of the energies of the $cc{\bar{c}}{\bar{c}}$ system with $IJ^{P}=00^{+}$ in ChQM III

Fig. 9

The stabilization plots of the energies of the $cc{\bar{c}}{\bar{c}}$ system with $IJ^{P}=01^{+}$ in ChQM III

Fig. 10

The stabilization plots of the energies of the $cc{\bar{c}}{\bar{c}}$ system with $IJ^{P}=02^{+}$ in ChQM III

Figure 8 represents the results for the $cc{\bar{c}}{\bar{c}}$ system with $IJ^{P}=00^{+}$ in ChQM III. The first two horizontal lines stand for two thresholds of $\eta _{c}\eta _{c}$ and $J/\psi J/\psi$, respectively. The horizontal line around 6270 MeV is on behalf of a resonance state, and its energy is stable against the variation of range. Besides, another three horizontal lines appear in Fig. 8, corresponding to three resonance states with the energy around 6900 MeV, 7150 MeV, and 7260 MeV, respectively. For the $cc{\bar{c}}{\bar{c}}$ system with $IJ^{P}=01^{+}$ (see Fig. 9), a threshold of $J/\psi \eta _{c}$ is clearly showed, and two resonance states around 6960 MeV and 7250 MeV are obtained. From Fig. 10, it is obvious that the first horizontal line is the threshold of $J/\psi J/\psi$, and another horizontal line is possible to be a resonance state with $IJ^{P}=02^{+}$, and the energy around 6970 MeV. We do the same calculation for the $cc{\bar{c}}{\bar{c}}$ system with another two sets of parameters in ChQM, as well as in the QDCSM with three different sets of parameters. All possible resonance states with corresponding energies are listed in Table 6.

From the Table 6 we can see that the results are qualitatively consistent in different quark models with different parameters. There are four possible resonance states with $IJ^{P}=00^{+}$, among which the state with energy range between $6825-6975$ MeV is close to the reported state X(6900). Combining the above analysis, the observed X(6900) is possible to be a compact resonance state with $IJ^{P}=00^{+}$ in present calculation. Besides, another three resonance states with energies $6205-6270$ MeV, $7140-7170$ MeV, and $7210-7260$ MeV are also possible to be existent. For the $IJ^{P}=01^{+}$ system, two resonance states are obtained, with energies $6740 \sim 7150$ MeV and $7250-7280$ MeV. For the $IJ^{P}=02^{+}$ system, there is only one resonance state, the energy range of which is $6725-7050$ MeV. We suggest the experimental tests to check the existence of all these possible resonance states.

4 Summary

In this work, we systematically investigate the low-lying full-heavy systems $bb{\bar{b}}{\bar{b}}$ and $cc{\bar{c}}{\bar{c}}$ in two quark models ChQM and QDCSM with three different sets of parameters. Two structures, meson–meson and diquark–antidiquark, are considered. The dynamic bound-state calculation is carried out to search for any bound state in the full-heavy systems. To explore the effect of the multi-channel coupling, both the single channel and the channel coupling calculation are performed. Meanwhile, an adiabatic calculation of the effective potentials is added to study the interactions of the systems and a stabilization calculation is carried out to find any resonance state.

The numerical results show that: (1) For the full-beauty $bb{\bar{b}}{\bar{b}}$ systems, there is no any bound state or resonance state in two structures in ChQM. While in QDCSM, the wide resonances are possible in the diquark–antidiquark structure, and the resonance energies are $19122-19344$ MeV for $IJ^P=00^+$, $19184-19354$ MeV for $IJ^P=01^+$, and $19236-19374$ MeV for $IJ^P=02^+$, respectively. (2) For the full-charm $cc{\bar{c}}{\bar{c}}$ systems, there are four possible resonance states with $IJ^{P}=00^{+}$, and the energy ranges are $6205-6270$ MeV, $6825-6975$ MeV, $7140-7170$ MeV, and $7210-7260$ MeV, respectively. The reported state X(6900) can be explained as a compact resonance state with $IJ^{P}=00^{+}$ in present calculation. Besides, we also obtain two resonance states with $IJ^{P}=01^{+}$ and energies $6740-7150$ MeV and $7250- 7280$ MeV, and a resonance state with $IJ^{P}=02^{+}$ and energy $6725 \sim 7050$ MeV. All these full-heavy resonance states are worth searching in the future experiments. (3) The effective potentials show that for most channels, the interaction between two mesons are repulsive, that’s why it is difficult for these states to form bound states. The contribution of each interaction term to the potential of the system shows that the kinetic energy term provides attractive interactions, while the Coulomb term and the color-magnetic term provide repulsion, which decrease the attraction of the kinetic energy term, and make the total weak attraction or repulsion of the system. (4) By comparing the results of two quark models, the energy of the meson–meson configuration is almost the same in ChQM and QDCSM, because the $\sigma$ meson exchange of the ChQM is inoperative and the quark delocalization of QDCSM is close to 0 in the systems of full-heavy quarks. In the diquark–antidiquark configuration, the energy of QDCSM is smaller than that of ChQM, due to the color octet symmetry of the diquark and antidiquark, which makes the quark delocalization work in QDCSM, and leads to lower energy in this model. Nevertheless, the conclusions are consistent in these two quark models.

We study the full-heavy tetraquarks in two structures in this work. To find out more bound states or resonance states, we will explore the systems with other structures and do the coupling of the different structures. In addition, to confirm the existence of the full-heavy resonances, the study of the scattering process of the corresponding open channels is needed in future work.