Constraints on $\sigma _8$ and degeneracies from linear Nash-Greene perturbations in subhorizon scale

Abstract

Using a joint statistical analysis, we test a four-dimensional FLRW model embedded in a five-dimensional bulk based on the Nash-Greene embedding theorem. Performing a Markov Chain Monte Carlo (MCMC) modelling, we combine observational data sets as those of the recent growth data, the best-fit Planck2018/$\varLambda$CDM parameters on the Cosmic Microwave Background (CMB), the Baryon Acoustic Oscillations (BAO) measurements, the Pantheon Supernovae type Ia and the Hubble parameter data. From linear Nash-Greene fluctuations of the metric, we show the related perturbed equations in longitudinal Newtonian gauge to obtain the evolution of growth matter. A mild alleviation may be obtained from the degeneracies on the model parameter analyzing the $\sigma$ tension between the growth amplitude factor and the matter content in the plane $(\sigma _8$-$\varOmega _m)$ on the observations from CMB and Large Scale Structure (LSS) probes. The Akaike Information Criterion (AIC) is also applied and we find a relative statistical consistence of the present model with both $\varLambda$CDM and wCDM models lower than 1$\%$ of percentage difference at early times on the evolution of the Hubble function H(z). We also apply the Om(z) diagnosis to distinguish the present model from $\varLambda$CDM and wCDM models.

1 Introduction

The true mechanism behind the accelerated phase of the universe still remains an open question. After more than 20 years since the very first evidences of the cosmic accelerated expansion, one of the pivotal directions of investigation is about to unravel whether the dark energy equation of state (EoS), with the main fluid parameter w(z), is restricted to the value $w_0=-1$, as suggested by observations [1], in conformity with the very popular $\varLambda$CDM model in the context of general relativity (GR), or if there exists any deviations from that value leading to dynamical dark energy models. Even though its success, the $\varLambda$CDM model lacks of an underlying physical understanding, since the Cosmological constant $\varLambda$ and the Cold dark matter (CDM) are problems of their own nature [2,3,4,5,6,7,8].

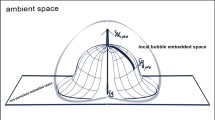
The theoretical background of this paper relies on the possibility that the universe may be embedded in a larger space and the dark energy problem may be explained as a geometric outcome from the extrinsic curvature to amplify the gravitational strength of Einstein’s gravity. Most of these extra dimensional models have been Kaluza–Klein or/and string inspired, such as, for instance, the Arkani–Hamed, Dvali and Dimopolous (ADD) model [9], the Randall–Sundrum model [10, 11] and the Dvali–Gabadadze–Porrati model (DPG) [12] commonly referred as braneworld models. Differently from these models and variants, we investigate how the embedding can be regarded as a prior mathematical structure well suited for construction of a physical theory, keeping no relation with brane or string proposals. Several authors have been explored this possibility in many contexts [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Moreover, a cosmological model is proposed based on previous works at background level [15, 19, 22, 23] and in this paper we proceed further to obtain the related cosmological perturbed equations.

This paper aims at investigating the $\sigma _8$ tension revealed by the notorious cryptic discrepancy of the data inferred from Planck CMB radiation probe and the Large Scale Structure (LSS) observations with the $\varLambda$CDM model as a background, and possible explanations may come from modified gravity [30,31,32,33,34,35,36]. The $\sigma _8$ denotes the r.m.s amplitude of matter density at a scale of a radius $R\sim 8$h.Mpc$^{-1}$ within a enclosed mass of a sphere.

We perform the Markov Chain Monte Carlo (MCMC) sample technique with a modified version of the available publicly code [37, 38] written in Mathematica$^{\mathrm{TM}}$ software using the joint likelihood of kinematical probes as of the Cosmic Microwave Background (CMB) Planck 2018 [1] datasets of TT,TE,EE+lowE on 68$\%$ interval of the related cosmological parameters, the largest dataset Pantheon SnIa [39] with redshift ranging from $0.01< z < 2.3$, the Hubble parameter a function of redshift H(z) [40] and Baryonic Acoustic Oscillations (BAO) from points of the joint surveys 6dFGS [41], BOSS DR12 [42], SDSS DR7 MGS [43], eBOSS DR14 [44], BOSS DR12 Ly$\alpha$ forest [45] and BOSS DR11 Ly$\alpha$ forest [46]. A comparison with the $\varLambda$CDM and wCDM [47, 48] models is presented with analysis on the growth density evolution and Om(z) diagnosis [49]. In addition, we apply the Akaike Information Criterion [50] on the resulting contours confidence regions. In the final section, we conclude with our final remarks and prospects.

2 The theoretical framework

2.1 The D-dimensional equations

We start with a summary of the main elements of a gravitational model based on the mathematical background of the theory of dynamical embeddings [14,15,16]. The first mechanism is defined by the gravitational action functional. Thus, in the presence of confined matter fields on a four-dimensional space with thickness l embedded in a D-dimensional ambient space (bulk), we define

$$\begin{aligned} S= -\frac{1}{2\kappa ^2_D} \int \sqrt{|\mathscr {G}|}\mathscr {R}d^{D}x - \int \sqrt{|\mathscr {G}|}\mathscr {L}^{*}_{m}d^{D}x\;, \end{aligned}$$

(1)

where $\kappa ^2_D$ is the fundamental energy scale on the embedded space, $\mathscr {R}$ denotes the Ricci scalar of the bulk and $\mathscr {L}^{*}_{m}$ is the confined matter lagrangian. The normal radii l are the smallest values of the curvature radii obtained from the relation

$$\begin{aligned} det(g_{\mu \nu }- l^ak_{\mu \nu a})=0\;. \end{aligned}$$

(2)

In a geometrical sense, the term $l^a$ represents a displacement of the embedded space along the extra-dimensions. The matter energy momentum tensor occupies a finite hypervolume with constant radius l along the extra-dimensions. The variation of Einstein–Hilbert action in Eq. (1) with respect to the bulk metric $\mathscr {G}_{AB}$ leads to the Einstein equations for the bulk

$$\begin{aligned} \mathscr {R}_{AB} - \frac{1}{2} \mathscr {G}_{AB}= \alpha ^{\star }\mathscr {T}_{AB}\;, \end{aligned}$$

(3)

where $\alpha ^{\star }=8\pi G^{*}$ is energy scale parameter and $G^{*}$ is the bulk “gravitational constant”. The tensor $\mathscr {T}_{AB}$ is the energy-momentum tensor for the bulk [15, 16, 19]. To generate a thick embedded space-time is important to perturb the related background. It can be done using the confinement hypothesis that depends only on the experimentally founded four-dimensionality of the space-time [51,52,53], even though any gauge theory can be mathematically constructed in a higher dimensional space.

In order to obtain a more general theory based on embeddings to elaborate a physical model, Nash’s original embedding theorem [54] used a flat D-dimensional Euclidean space, later generalized with independent orthogonal perturbations to any Riemannian manifold including non-positive signatures by Greene [55]. This choice of perturbations facilitates to obtain a differentiable smoothness of the embedding between the manifolds, which is a primary concern of Nash’s theorem and satisfies the Einstein–Hilbert principle, where the variation of the Ricci scalar is the minimum as possible. Accordingly, it guarantees that the embedded geometry remains smooth (differentiable) after smooth (differentiable) perturbations.

With all these concepts, let us consider a Riemannian geometry $V_4$ with a non-perturbed metric $\bar{g}_{\mu \nu }$ being locally and isometrically embedded in a D-dimensional Riemannian geometry $V_n$. The embedded space-time $V_4$ is endowed with the local coordinates $x^{\mu }=\{x^0,\ldots ,x^3\}$ whereas the extra-dimensions in the bulk space can be defined with the coordinates $x^{a}=\{x^4,\ldots ,x^{D-1}\}$ and $D=4+n$. Hence, the bulk local coordinates can be denoted by the set $\{x^{\mu }, x^a\}$. All these definitions allow us to construct a differentiable and regular map $\mathscr {X}: V_4 \rightarrow V_n$ satisfying the embedding equations

$$\begin{aligned}&\mathscr {X}^{A}_{,\mu } \mathscr {X}^{B}_{,\nu }\mathscr {G}_{AB}=\; \bar{g}_{\mu \nu }\;\;,\end{aligned}$$

(4)

$$\begin{aligned}&\mathscr {X}^{A}_{,\mu }\bar{\eta }^{B}_{a}\mathscr {G}_{AB}=\;0\;\;,\end{aligned}$$

(5)

$$\begin{aligned}&\bar{\eta }^{A}_{a}\bar{\eta }^{B}_{b}\mathscr {G}_{AB}=\;\bar{g}_{ab}\;\;, \end{aligned}$$

(6)

where the set of $\mathscr {X}^{A}(x^{\mu },x^a):\mathscr {X}^{A}=\{\mathscr {X}^{0}\ldots \mathscr {X}^{D-1}\}$ denotes the non-perturbed embedding function coordinates, the metric $\mathscr {G}_{AB}$ denotes the metric components of $V_D$ in arbitrary coordinates and $\bar{\eta }^{A}_{a}$ denotes a non-perturbed unit vector field orthogonal to $V_4$. Concerning notation, capital Latin indices run from 1 to n. Small case Latin indices refer to the extra dimension considered. All Greek indices refer to the embedded space-time counting from 1 to 4. Those sets of equations represent, respectively, the isometry condition in Eq. (4), the orthogonality between the embedding coordinates $\mathscr {X}$ and $\bar{\eta }$ in Eq. (5), and also, the vector normalization $\bar{\eta }^{A}_{a}$ and $\bar{g}_{ab} =\epsilon _a \delta _{ab}$ with $\epsilon _a = \pm 1$ in which the signs represent the signatures of the extra-dimensions. Hence, the integration of the system of equations in Eqs. (4), (5) and (6) assures a correct configuration of the embedding map $\mathscr {X}$.

The non-perturbed extrinsic curvature $\bar{k}_{\mu \nu }$ of $V_4$ is, by definition, the projection of the variation of $\bar{\eta }$ onto the tangent plane :

$$\begin{aligned} \bar{k}_{\mu \nu } = -\mathscr {X}^A_{,\mu }\bar{\eta }^B_{,\nu } \mathscr {G}_{AB}= \mathscr {X}^A_{,\mu \nu }\bar{\eta }^B \mathscr {G}_{AB}\;, \end{aligned}$$

(7)

where the comma denotes the ordinary derivative.

If one defines a geometric object $\bar{\omega }$ in $V_4$, its Lie flow for a small distance $\delta y$ is given by $\varOmega = \bar{\varOmega } + \delta y \pounds _{\bar{\eta }}{\bar{\varOmega }}$, where $\pounds _{\bar{\eta }}$ denotes the Lie derivative with respect to $\bar{\eta }$. In particular, the Lie transport of the Gaussian veilbein $\{\mathscr {X}^A_\mu , \bar{\eta }^A_a \}$, defined on $V_4$ gives straightforwardly the perturbed coordinate $\mathscr {Z}^A(x^{\mu },y^a):=\mathscr {Z}^A$ such as

$$\begin{aligned} \mathscr {Z}^A_{,\mu }= & {} X^{A}_{,\mu } + \delta y^a \;\pounds _{\bar{\eta }}{X^{A}_{,\mu }} = \mathscr {X}^{A}_{,\mu } + \delta y^a \; \bar{\eta }^{A}_{a,\mu }\;,\end{aligned}$$

(8)

$$\begin{aligned} \eta ^A_a= & {} \bar{\eta }^A_a + \delta y^b\;[\bar{\eta }_a, \bar{\eta }_b]^A \;= \;\bar{\eta }^A_a\;. \end{aligned}$$

(9)

It is worth mentioning that Eq. (9) shows that the normal vector $\eta ^A$ does not change under orthogonal perturbations. However, from Eq. (7), we note that in general $\eta _{,\mu } \ne \bar{\eta }_{,\mu }$. Hence, to describe the perturbed embedded geometry, we set a perturbed coordinates $\mathscr {Z}^A$ that are needed to satisfy the embedding equations similar to Eqs. (4), (5) and (6) as

$$\begin{aligned} \mathscr {Z}^A_{,\mu } Z^{B}_{,\nu }\mathscr {G}_{AB}=g_{\mu \nu },\;\mathscr {Z}^A_{,\mu } \eta ^B_b \mathscr {G}_{AB}= g_{\mu b}, \;\eta ^A_a\eta ^B_b , \mathscr {G}_{AB}=g_{ab}\;, \end{aligned}$$

(10)

where $g_{ab}=\epsilon _{a}\delta _{ab}$ with $\epsilon _a = \pm 1$.

If we take Eq. (10) and rewrite Eq. (5) as

$$\begin{aligned} g_{\mu b}=\;\mathscr {Z}^A_{,\mu } \eta ^B_b \mathscr {G}_{AB}=\;\delta y^a A_{\mu ab}\;. \end{aligned}$$

(11)

Then, Eq. (11) results from a generalization of the Gauss–Weingarten equations

$$\begin{aligned} \eta ^{A}_{a,\mu }=\;A_{\mu ac}g^{cb}\eta ^{A}_{b}-\bar{k}_{\mu \rho a}\bar{g}^{\rho \nu }\mathscr {Z}^{A}_{,\nu }\;, \end{aligned}$$

(12)

that leads to

$$\begin{aligned} A_{\mu ab}=\;\eta ^{A}_{a,\mu }\eta ^{B}_b\mathscr {G}_{AB}=\;\bar{\eta }^{A}_{a,\mu }\bar{\eta }^{B}_b\mathscr {G}_{AB}=\;\bar{A}_{\mu ab}\;. \end{aligned}$$

(13)

Likewise the unchanged normal vector in Eq. (9), it also happens that the torsion vector, $A_{\mu ab}$, does not change under orthogonal perturbations. In geometric language, the presence of a torsion potential tilts the embedded family of submanifolds with respect to the normal vector $\eta ^{A}_a$. If the bulk has certain killing vectors then $A_{\mu ab}$ transforms as a component of gauge fields under the group of isometries of the bulk [14, 27, 56]. It is worth noting that the gauge potential can only be present if the dimension of the bulk space is equal or greater than six ($n\ge 2$) in accordance with Eq. (13) since the torsion vector fields are antisymmetric under the exchange of extra coordinate a and b. Thus, with the Eq. (10) and using the definition from Eq. (7), one obtains the perturbed metric and extrinsic curvature of the new geometry written as

$$\begin{aligned} g_{\mu \nu }= & {} \;\bar{g}_{\mu \nu }-2y^a \bar{k}_{\mu \nu a} \nonumber \\&+\delta y^a \delta y^b\left[ \bar{g}^{\sigma \rho }\bar{k}_{\mu \sigma a}\bar{k}_{\nu \rho b}+g^{cd}A_{\mu ca}A_{\nu db}\right] , \end{aligned}$$

(14)

and the related perturbed extrinsic curvature

$$\begin{aligned} k_{\mu \nu a}=\;\bar{k}_{\mu \nu a}- \delta y^b \left( g^{cd}A_{\mu ca}A_{\nu db}+ \bar{g}^{\sigma \rho }\bar{k}_{\mu \sigma a}\bar{k}_{\nu \rho b}\right) \;. \end{aligned}$$

(15)

Taking the derivative of Eq. (14) with respect to y coordinate, one obtains Nash’s deformation condition

$$\begin{aligned} \bar{k}_{\mu \nu a}=\;-\frac{1}{2}\frac{\partial \bar{g}_{\mu \nu }}{\partial y^a}\;. \end{aligned}$$

(16)

The meaning of this expression is twofold. It can be understood in a pictorial view under the basic theory of curves, i.e., one gets a congruence of curves (or orbits) orthogonal to the embedded space $V_4$. Moreover, the parameter y is time-like or not, and it is irrelevant the sign of its signature. A similar expression was obtained years later in the context of the ADM formulation by Choquet-Bruhat and York [57]. In fact, the physical interpretation of Eq. (16) means that it localizes the matter in the embedded space-time imposing on it a geometrical confinement. In other words, it holds true for any perturbations resulting from n-parameter families of embedded submanifolds denoted by the set of $y^a$ coordinates, and the matter remains confined to the resulting perturbed metric that can bend and/or stretch without ripping the manifold (embedded space-time), which may be a valuable feature for a quantization process and cosmology [16].

In addition, the integrability conditions for equations in Eq. (10) are given by the non-trivial components of the Riemann tensor of the embedding space expressed in the Gaussian frame $\{\mathscr {Z}^A_{\mu }, \eta ^A_a\}$ known as the Gauss–Codazzi–Ricci equations. This guarantees to reconstruct the embedded geometry and to understand its properties from the dynamics of the four-dimensional embedded space-time. Consequently, we can define a Gaussian coordinate system in the new perturbed coordinates $\{\mathscr {Z}^A_{,\mu }, \eta ^{A}_a\}$ in the vicinity of $V_4$ that allows to write the metric of the bulk in a general way as

$$\begin{aligned} \mathscr {G}_{AB}= \left( \begin{array}{cc} g_{\mu \nu }+ g^{ab}A_{\mu a} A_{\nu b} &{} A_{\mu a} \\ A_{\nu b} &{} g_{ab} \\ \end{array} \right) , \end{aligned}$$

(17)

where the perturbed metric $g_{\mu \nu }$ is given by Eq. (14). The expression in Eq. (17) is the metric of the bulk with at least two extra-dimensions, i.e., $D\ge 6$. This resembles the non-Abelian Kaluza–Klein metric and the quantity $A_{\mu a}$ plays the role of the Yang–Mills potentials where $A_{\mu a}= x^b A_{\mu ab}$. We emphasize that for just one extra-dimension, the torsion vector does not exist and for two extra-dimensions it turns into the usual Maxwell field, which means that the non-Abelian part of $A_{\mu a}$ is lost in a six dimensional bulk. This means that the resulting force is the ordinary electromagnetic one in the case of two extra dimensions [17, 18, 27, 28].

As proposed in Refs. [14,15,16, 26, 29], one obtains the induced field covariant equations of motion taking Eq. (3) in the frame defined in Eq. (17) at background level. Thus, the background of a four-dimensional observer in the embedded space is set by the following equations

$$\begin{aligned} \bar{G}_{\mu \nu }+ \bar{Q}_{\mu \nu }= 8\pi G \bar{T}_{\mu \nu }\;, \end{aligned}$$

(18)

where the quantity $\bar{T}_{\mu \nu }$ denotes the stress energy tensors for ordinary intrinsic matter (including Yang–Mills fields). The second equation involves relations with extrinsic terms $\bar{k}_{\alpha \beta a}$ and $A_{\mu ab}$

$$\begin{aligned} \nabla _{\nu }^{*}\bar{k}_{a}- \nabla ^{*}_{\mu }\bar{k}^{\mu }_{a\nu }= 8\pi G \bar{T}_{a\nu }\;, \end{aligned}$$

(19)

where the term $\nabla _{\mu }^{*}\bar{k}_{\alpha \beta a}$ denotes $\nabla _{\mu }^{*}\bar{k}_{\alpha \beta a}:= \bar{k}_{\alpha \beta a;\mu }- A_{\mu ab} \bar{k}_{\alpha \beta }^b$ and the semicolon denotes the covariant derivative. Moreover, the third equation is denoted as

$$\begin{aligned} R+\bar{k}_{\mu \nu m} \bar{k}^{\mu \nu m} - \bar{k}_{a}\bar{k}^{a}= -16\pi G \eta _{ab} \bar{T}_{ab}\;, \end{aligned}$$

(20)

where $\eta _{ab}=\epsilon _a\delta _{ab}$ with $\epsilon _a=\pm 1$. The quantities G, $\bar{T}_{a\nu }$, $\bar{T}_{ab}$ denote the induced gravitational Newton’s constant, the stress energy tensors projections of the corresponding energy-momentum tensor of the bulk $T_{AB}$ on the cross and normal directions of the space-time, respectively. This set of equations results from the integrability conditions of the embedding given by the Gauss–Codazzi–Ricci equations. From the Nash-Greene theorem, the solutions of these equations were obtained by a differentiable process [14,15,16, 19, 21,22,23,24,25,26, 28]. The first of the two equations are known, respectively, by the gravi-tensor equation (a modified Einstein’s equations by the appearance of the extrinsic curvature) as in Eq. (18) and the gravi-vector equation as in Eq. (19). In summary, they reflect the meaning of a dynamical embedding: the pseudo-Riemann curvature of the embedding space acts as a reference for the pseudo-Riemann curvature of the embedded space-time. Moreover, the projection of the Riemann tensor of the embedding space along the normal direction is given by the tangent variation of the extrinsic curvature as shown by Eq. (19) that is the trace of the Codazzi equations composed by the extrinsic terms $\bar{k}_{\alpha \beta a}, A_{\mu ab}$. The last equation is known as gravi-scalar equation and serves as a constrain on the torsion vector fields $A_{\mu ab}$.

The quantity $\bar{Q}_{\mu \nu }$ is denoted by

$$\begin{aligned} \bar{Q}_{\mu \nu }= & {} \;\bar{g}^{cd}\left( \bar{g}^{\rho \sigma }\bar{k}_{\mu \rho c}\bar{k}_{\nu \sigma d}- \bar{k}_{\mu \nu d}\bar{g}^{\alpha \beta }\bar{k}_{\alpha \beta c} \right) \nonumber \\&-\frac{1}{2}\left( \bar{k}_{\lambda \phi c} \bar{k}^{\lambda \phi }_{\;d}\bar{g}^{\alpha \beta }\bar{k}_{\alpha \beta ^{d}}\bar{g}^{\gamma \delta }\bar{k}_{\gamma \delta ^{c}}\right) \bar{g}_{\mu \nu }\;, \end{aligned}$$

(21)

is an independently conserved quantity in the sense of Noether’s theorem with $Q_{\mu \nu \;;\nu }=0$. It means that this geometric new term does not exchange gravitational energy with ordinary matter. The conservation of $Q_{\mu \nu }$ also holds true for perturbed quantities of $g_{\mu \nu }$ and $k_{\mu \nu a}$.

2.2 The background cosmological model

To the present cosmological application, we consider a four-dimensional metric embedded in a five-dimensional bulk to make a proper comparison with the most common cosmological models in recent literature. In this framework, the set of field equations is quite simplified. The torsion vector $A_{\mu ab}$ does not exist in five-dimensions and Eq. (19) turns into a homogeneous equation. Moreover, Eq. (20) provides only a relation of consistence between Ricci scalar and extrinsic scalar quantities (no a priori information is gained).

To obtain the embedded four-dimensional equations, one can take Eq. (18) written in the Gaussian frame embedding veilbein $\{\mathscr {X}^{A}_{\mu }, \eta ^{A}\}$. This reference frame is composed by a regular and differentiable coordinate $\{\mathscr {X}^{A}_{\mu }\}$ and a unitary normal vector $\{\eta ^{A}\}$. Accordingly, one can obtain the set of the embedded four-dimensional field equations

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}R\bar{g}_{\mu \nu }+\bar{Q}_{\mu \nu }= 8\pi G \bar{T}_{\mu \nu }\;, \end{aligned}$$

(22)

$$\begin{aligned}&\bar{k}_{\mu ;\rho }^{\;\rho }-\bar{h}_{,\mu } =0\;, \end{aligned}$$

(23)

where the semi-colon denotes a covariant derivative. The $\bar{T}_{\mu \nu }$ tensor is the four-dimensional energy-momentum tensor of a perfect fluid, expressed in co-moving coordinates as

$$\begin{aligned} \bar{T}_{\mu \nu }=(\bar{p}+\bar{\rho })U_{\mu }U_{\nu }+\bar{p}\;\bar{g}_{\mu \nu },\;\;\;U_{\mu }=\delta _{\mu }^{4}\;, \end{aligned}$$

where $U_{\mu }$ is the co-moving four-velocity. Moreover, the non-perturbed deformation tensor $\bar{Q}_{\mu \nu }$ is now written as

$$\begin{aligned} \bar{Q}_{\mu \nu }=\bar{g}^{\rho \sigma }\bar{k}_{\mu \rho }\bar{k}_{\nu \sigma }- \bar{k}_{\mu \nu }\bar{h} -\frac{1}{2}\left( \bar{K}^2-\bar{h}^2\right) \bar{g}_{\mu \nu }\;, \end{aligned}$$

(24)

where we denote $\bar{h}= \bar{g}^{\mu \nu }\bar{k}_{\mu \nu }$ that gives the definition of the Gaussian mean curvature $\bar{h}^2$ by the product $\bar{h}^2=\bar{h}.\bar{h}$. The term $\bar{K}^{2}=\bar{k}^{\mu \nu }\bar{k}_{\mu \nu }$ denotes the related Gaussian curvature. Straightforwardly, it follows that the conservation of $\bar{Q}_{\mu \nu }$ holds, i.e.,

$$\begin{aligned} \bar{Q}^{\mu \nu }{}_{;\nu }=0\;. \end{aligned}$$

(25)

The related conservation equation for $\bar{T}_{\mu \nu }$ is given by

$$\begin{aligned} \bar{\rho } + 3H\left( \bar{\rho } + \bar{p}\right) =0\;, \end{aligned}$$

(26)

where $\bar{\rho }$ and $\bar{p}$ denote the non-perturbed matter density and pressure, respectively. Moreover, we work with a spatially Friedman–Lemaître–Robertson–Walker (FLRW) geometry with the line element expressed in coordinates $(r,\theta ,\phi ,t)$ in such a way

$$\begin{aligned} ds^2=\;-dt^2+a^2\left[ dr^2+f_{\kappa }^2(r)\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) \right] \;, \end{aligned}$$

(27)

where $f(r)_{\kappa }=\sin r$, r,$\sinh r$. Since the FLRW geometry can be locally embedded in five-dimensions, it can be regarded as a four-dimensional hypersurface dynamically evolving in a flat five-dimensional bulk whose Riemann tensor $\mathscr {R}_{ABCD}$ is

$$\begin{aligned} \mathscr {R}_{ABCD}=0\;, \end{aligned}$$

(28)

where $\mathscr {G}_{AB}$ denotes the bulk metric components in arbitrary coordinates. Hence, with a flat dimensional bulk, concerning our cosmological applications, we are not considering the appearance of the cosmological constant $\varLambda$.

In the following, we summarize the background results obtained in previous works [15, 19]. Using Eq. (27), one obtains a solution for Eq. (23) that is given by

$$\begin{aligned}&\bar{k}_{ij}=\frac{b}{a^2}\bar{g}_{ij},\;\;i,j=1,2,3, \;\;\;\; \bar{k}_{44}=\frac{-1}{\dot{a}}\frac{d}{dt}\frac{b}{a}, \end{aligned}$$

where the extrinsic bending function $b(t)=k_{11}$ is function of time. The dot symbol denotes an ordinary time derivative. This arbitrariness follows from the confinement of the four-dimensional gauge fields, which produces the homogeneous equation as shown in Eq. (23).

Denoting the usual Hubble parameter by $H = \dot{a}/a$ and the extrinsic parameter $B= \dot{b}/b$, one obtains

$$\begin{aligned}&\bar{k}_{ij}=\frac{b}{a^2}\bar{g}_{ij},\;\; \bar{k}_{44}=-\frac{b}{a^{2}}\left( \frac{B}{H}-1\right) , \end{aligned}$$

(29)

$$\begin{aligned}&\bar{K}^{2}=\frac{b^2}{a^4}\left( \frac{B^2}{H^2}-2\frac{B}{H}+4\right) , \;\;\, \bar{h}=\frac{b}{a^2}\left( \frac{B}{H}+2\right) ,\end{aligned}$$

(30)

$$\begin{aligned}&\bar{Q}_{ij}= \frac{b^{2}}{a^{4}}\left( 2\frac{B}{H}-1\right) \bar{g}_{ij},\;\bar{Q}_{44} = -\frac{3b^{2}}{a^{4}}, \end{aligned}$$

(31)

$$\begin{aligned}&\bar{Q}= -(\bar{K}^2 -\bar{h}^2) =\frac{6b^{2}}{a^{4}} \frac{B}{H}\;, \end{aligned}$$

(32)

where in Eq. (31), we have denoted $i,j=1\ldots 3$, with no sum in indices. For the sake of notation, we denote the expansion parameter as $a(t)=a$ and the bending function as $b(t)=b$.

Since the dynamics equations for the extrinsic curvature are not complete in five-dimensions, motivated by the lack of uniqueness of the function b(t), and being the extrinsic curvature independent rank-2 field, one can derive the Einstein–Gupta equations [19, 58] in a form

$$\begin{aligned} \mathscr {F}_{\mu \nu }=0\;, \end{aligned}$$

(33)

where they are defined as a copy (concerning its structure) of the usual Riemannian geometry. Hence, once can define a “f-Riemann tensor”

$$\begin{aligned}&\mathscr {F}_{\alpha \beta \mu \nu }= \;\partial _{\mu }\varUpsilon _{\alpha \nu \beta }- \;\partial _{\nu }\varUpsilon _{\alpha \mu \beta }+ \varUpsilon _{\alpha \mu \lambda }\varUpsilon _{\nu \beta }^{\lambda } -\varUpsilon _{\alpha \nu \lambda }\varUpsilon _{\mu \beta }^{\lambda }\;,\\&\quad \varUpsilon _{\mu \nu \sigma }=\;\frac{1}{2}\left( \partial _\mu \; f_{\sigma \nu }+ \partial _\nu \;f_{\sigma \mu } -\partial _\sigma \;f_{\mu \nu }\right) , \\&\quad \varUpsilon _{\mu \nu }{}^{\lambda }= f^{\lambda \sigma }\;\varUpsilon _{\mu \nu \sigma }.\; \end{aligned}$$

that were constructed from a “connection” associated with $k_{\mu \nu }$ and

$$\begin{aligned} f_{\mu \nu } = \frac{2}{K}k_{\mu \nu }, \;\; \text{ and } \;\;f^{\mu \nu } = \frac{2}{K}k^{\mu \nu }\;, \end{aligned}$$

(34)

in such a way that the normalization condition $f^{\mu \rho }f_{\rho \nu } =\delta ^\mu _\nu$ holds.

2.3 The modified Friedmann equation

From the results of Eqs. (22), (23) and (25) by means of calculating $Q^{\mu }_{\mu ,i}=0$, the Friedmann equation modified by the extrinsic curvature can be written as

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^2=\frac{8}{3}\pi G\bar{\rho }+\alpha _0a^{2\beta _0-4}e^{\gamma ^{\pm }(t)}\;\;, \end{aligned}$$

(35)

where $\alpha _0$ denotes an integration constant originated from the influence of the extrinsic curvature. We point out that when $\alpha _0\rightarrow 0$, we obtain the standard result of GR. Concerning the total energy $\bar{\rho }$, we denote $\bar{\rho } = \rho _{mat}+\rho _{rad}$, which is composed by the matter density $\rho _{mat}$ and the radiation energy density $\rho _{rad}$, respectively. The $\gamma$-exponent in the exponential function in Eq. (35) is defined as $\gamma ^{\pm }(t)=\pm \sqrt{|4\eta _0a^4 - 3|}\mp \sqrt{3}\arctan \left( \frac{\sqrt{3}}{3}\sqrt{|4\eta _0a^4 -3|}\right)$ and the relation of expansion scale factor with redshift is given by $a=\frac{1}{1+z}$. The parameter $\eta _0$ results from the information gained from Eq. (33) calculated in the spatially flat FLRW space-time given by the metric in Eq. (27). By means of background cosmography tests [22, 23, 25], it was shown that the parameter $\beta _0$ tunes the magnitude of the deceleration parameter q(z) and the parameter $\eta _0$ adjusts the width of the transition phase redshift from a decelerating to accelerating phase. Moreover, we can write Friedman equations as

$$\begin{aligned} H(z)=H_0\sqrt{\varOmega _{m}(z)+\varOmega _{rad}(z)+\varOmega _{ext}(z)e^{\pm \gamma (z)}}\;, \end{aligned}$$

(36)

where H(z) is the Hubble parameter in terms of redshift z and $H_0$ is the current value of the Hubble constant. The matter density parameter is denoted by $\varOmega _m(z)=\varOmega ^0_{m}(1+z)^3$, $\varOmega _{rad}(z)=\varOmega ^0_{rad} (1+z)^{4}$ with $\varOmega _{rad}^{0}=\varOmega _{m}^0z_{eq}$ and the term $\varOmega _{ext}(z)=\varOmega ^0_{ext}(1+z)^{4-2\beta _0}\tilde{\gamma }_0$ stands for the density parameter associated with the extrinsic curvature and $\tilde{\gamma }_0$ is an integration constant. The upper script “0” indicates the present value of any quantity. The equivalence number for the expansion factor $a_{eq}$ given by

$$\begin{aligned} a_{eq}= \frac{1}{1+z_{eq}}=\frac{1}{(1 + 2.5\times 10^4 \varOmega _m h^2 (T_{cmb}/2.7)^{-4})}\; \end{aligned}$$

(37)

where $z_{eq}$ is the equivalence redshift. As a reference, we adopt the value of the CMB temperature $T_{cmb} = 2.7255 K$ and the dimensionless Hubble parameter $h=0.672$.

The complete form for Hubble parameter as in Eq. (36) has been investigated in a sequence of studies [19, 21,22,23, 25] but at perturbation level, the Hubble function in Eq. (36) is not continuous for any arbitrary redshift z or, equivalently, for the expansion factor a. To obtain a stable solution, we analytically expand H(a) by using a Mclaurin-Puiseux series with $\eta _0\rightarrow 0$ for an asymptotic limit $a\rightarrow 0$ truncating at second order, i.e, $e^{\gamma (x(a))}\sim 1+\frac{\sqrt{3}}{3}x(a)^{3/2}+ \mathscr {O}(x^{5/2})$. Considering only the linear order, it gives roughly in terms of redshift $e^{\gamma (z)}\sim (z+1)^{-4}$. The convergence of $e^{\gamma (a)}$ is in compliance with the Walsh theorem on the convergence of analytic approximations [59]. For a flat space, the current “extrinsic contribution” $\varOmega ^0_{ext}$ is given by the normalization condition for redshift at $z=0$ that results in

$$\begin{aligned} \varOmega ^0_{ext}=\frac{2}{\eta _0}\left( 1-\varOmega ^0_{m}-\varOmega ^0_{rad}\right) \;. \end{aligned}$$

(38)

Hence, we can write the dimensionless Hubble parameter $E(z)=\frac{H(z)}{H_0}$ as

$$\begin{aligned} E^2(z)= & {} \varOmega ^0_{m}(1+z)^3+\varOmega ^0_{rad} (1+z)^{4} \nonumber \\&+\left( 1-\varOmega ^0_{m}-\varOmega ^0_{rad}\right) (1+z)^{-2\beta _0}\;. \end{aligned}$$

(39)

To facilitate referencing, we call, for short, the proposed model as $\beta$-model. We point out that when $\beta _0=0$, the expansion history are the same as that of the $\varLambda$CDM model, i.e., $H(z)_{\beta }=H(z)_{\varLambda CDM}$.

3 Matter evolution equations in conformal Newtonian gauge

In longitudinal conformal Newtonian gauge, the metric in Eq. (27) is given by

$$\begin{aligned} ds^2 = a^2 [(1+ 2\varPhi ) d\eta ^2 - ((1-2\varPsi )\delta _{ij} dx^i dx^j] \;, \end{aligned}$$

(40)

where $\varPhi =\varPhi (\mathbf {x},\eta )$ and $\varPsi =\varPsi (\mathbf {x},\eta )$ denote the Newtonian potential and the Newtonian curvature, respectively. The conformal time $\eta$ is related with physical time as $dt=a(\eta )d\eta$.

The perturbed field equations of Eqs. (22) and (23) can be written as

$$\begin{aligned} \delta G_{\mu \nu }+\delta Q_{\mu \nu }\;= & {} 8\pi G\delta T_{\mu \nu }\;, \end{aligned}$$

(41)

$$\begin{aligned} \delta k_{\mu \nu ;\rho }= & {} \delta k_{\mu \rho ;\nu }\;. \end{aligned}$$

(42)

To obtain the explicit form for perturbed field equations in Eqs.(41) and (42), we need to determine both perturbed metric $\delta g_{\mu \nu }$ and perturbed extrinsic curvature $\delta k_{\mu \nu }$. Using the main result of the Nash-Greene theorem [54, 55], one can use the relation

$$\begin{aligned} \delta g_{\mu \nu }= -2 \bar{k}_{\mu \nu }\delta y \;, \end{aligned}$$

(43)

where $\delta y$ denotes an infinitesimal displacement of the extra dimension y in the bulk space. Thus, the linear perturbations of a new geometry $g_{\mu \nu }$ is given by $g_{\mu \nu }=\;\bar{g}_{\mu \nu }+\delta g_{\mu \nu }$ that can be written as

$$\begin{aligned} g_{\mu \nu }=\;\bar{g}_{\mu \nu } - 2\delta y \bar{k}_{\mu \nu }\;, \end{aligned}$$

(44)

and the related perturbed extrinsic curvature

$$\begin{aligned} k_{\mu \nu }=\;\bar{k}_{\mu \nu }-2 \delta y\;\bar{g}^{\sigma \rho }\bar{k}_{\mu \sigma }\bar{k}_{\nu \rho }\;, \end{aligned}$$

(45)

where we can identify $\delta k_{\mu \nu }=\bar{g}^{\sigma \rho }\bar{k}_{\mu \sigma }\bar{k}_{\nu \rho }$. Using the Nash relation $\delta g_{\mu \nu }= -2 \bar{k}_{\mu \nu }\delta y$, we obtain

$$\begin{aligned} \delta {k}_{\mu \nu }=\;\bar{g}^{\sigma \rho }\bar{k}_{\mu \sigma }\delta g_{\nu \rho }\;. \end{aligned}$$

(46)

The perturbation of the deformation tensor $Q_{\mu \nu }$ can be made from its background form in Eq. (21) and the resulting $k_{\mu \nu }$ perturbations from Nash’s fluctuations in Eq. (46). Thus, one obtains

$$\begin{aligned} \delta Q_{\mu \nu }= -\frac{3}{2}(\bar{K}^2-\bar{h}^2)\delta g_{\mu \nu } \;. \end{aligned}$$

(47)

Likewise Eq. (25), the perturbed deformation tensor is independently conserved in a sense that $\delta Q_{\mu \nu ;\nu }=0$. It is worthy noting that due to the Nash fluctuations in Eq. (44), we notice that the Codazzi equations in Eq. (42) and the Einstein–Gupta equations in Eq. (33) are invariant under the Nash perturbations and also are confined to the background (in the sense that they maintain their same background form). Then using the background relations in Eqs. (29), (30), (31), and (32), we can determine the components of $\delta Q_{\mu \nu }$

$$\begin{aligned} \delta Q^{i}_{j}= & {} \gamma _0 a^{2\beta _0-2}\varPsi \delta ^i_j\;,\end{aligned}$$

(48)

$$\begin{aligned} \delta Q^{i}_{4}= & {} 0\;, \end{aligned}$$

(49)

$$\begin{aligned} \delta Q^{4}_{4}= & {} \gamma _0 a^{2\beta _0-2}\varPhi \delta ^4_4\;. \end{aligned}$$

(50)

where $\gamma _0$ is a constant term that merges all integration constants and also carries an extrinsic curvature constant from integration of the bending function b(t) which means that if $\gamma _0$ is zero, the usual GR configuration is restored if all terms originated from extrinsic curvature vanish accordingly.

For a perturbed fluid with pressure p and density $\rho$, one can write the perturbed components of the related stress-tensor

$$\begin{aligned} \delta T^4_4= & {} \delta \rho \;, \end{aligned}$$

(51)

$$\begin{aligned} \delta T^4_i= & {} \frac{1}{a}(\rho _0+p_0)\delta u_{\parallel i}\;, \end{aligned}$$

(52)

$$\begin{aligned} \delta T^i_j= & {} -\delta p\;\delta ^i_j\;, \end{aligned}$$

(53)

where $\delta u_{\parallel i}$ denotes the tangent velocity potential. Hereon, the quantities $\rho _0$ and $p_0$ denote the non-perturbed components of density and pressure, respectively.

Moreover, we adopt the simplest condition for perturbations $\varPsi =\varPhi$ and obtain the following set of equations in the wave-number k-space of Fourier modes as

$$\begin{aligned}&k^2\varPhi _k + 3 \mathscr {H} \left( \varPhi ^{'}_k + \varPhi _k \mathscr {H} \right) = -4\pi G a^2 \delta \rho _k + \gamma _0 a^{2\beta _0}\varPhi _k \;,\nonumber \\\end{aligned}$$

(54)

$$\begin{aligned}&(a\varPhi _{k})'= -4\pi G a^2(\rho _0+p_0) \theta \;,\end{aligned}$$

(55)

$$\begin{aligned}&\varPhi ^{''}_{k}\; + 3\mathscr {H}\varPhi '_k + (\mathscr {H}^2+2\mathscr {H}')\varPhi _k-\gamma _0 a^{2\beta _0}\varPhi _k \nonumber \\&\qquad = 4\pi G a^2 c^2_s \delta \rho _k \;, \end{aligned}$$

(56)

where the conformal Hubble parameter is $\mathscr {H}\equiv aH$, $c_s$ denotes the sound speed and $\theta = ik^j\delta u_{\parallel j}$ denotes the divergence of fluid velocity in k-space. Hence, from Eqs.(54), (55) and (56), one obtains the gravitational potential formula in k-space:

$$\begin{aligned}&\varPhi ^{''}_{k} + 3(1+c^2_s)\mathscr {H}\varPhi '_k + \left[ k^2c^2_s + (1+3c^2_s)\mathscr {H}^2\right] \varPhi _k \nonumber \\&\qquad = \gamma _0 a^{2\beta _0}(1+c^2_s)\varPhi _k-2\mathscr {H}' \varPhi _k \;. \end{aligned}$$

(57)

As a matter of consistence, we point out when $\gamma _0\rightarrow 0$ in Eq. (57), the standard GR correspondence is obtained. Thus, one recovers the subhorizon approximation with $k^2>>\mathscr {H}^2$ or $k^2>>a^2H^2$ and Eq. (57) turns the Newtonian formula $\varPhi _k\sim \frac{\delta \rho _k}{k^2}$.

After a Fourier transform, we perform the definition of the “contrast” matter density $\delta _m \equiv \frac{\delta \rho }{\rho _0}$. For a pressureless matter and a null anisotropic matter stress, we use Eq. (54) and obtain a relation of $\varPhi _k$ and $\delta _m$ given by

$$\begin{aligned} k^2 \varPhi _k= -4\pi G_{eff} a^2\rho _0 \delta _m\;, \end{aligned}$$

(58)

where $G_{eff}$ is the effective Newtonian constant and is given by

$$\begin{aligned} G_{eff}(a,k)=\frac{G}{1-\frac{\gamma _0}{k^2}a^{2\beta _0}}\;, \end{aligned}$$

(59)

where G is the Newtonian gravitational constant.

The corresponding equation of evolution of the contrast matter density $\delta _m(\eta )$ in conformal longitudinal Newtonian frame can be written as

$$\begin{aligned} \delta ''_m + \mathscr {H}\delta '_m - 4\pi G_{eff} a^2\rho _0 \delta _m=0\;, \end{aligned}$$

(60)

where the prime symbols denote derivatives with respect to conformal time $\eta$. And, in terms of the expansion factor a(t), we obtain the contrast matter density $\delta _m(a)$ accordingly

$$\begin{aligned} \ddot{\delta }_m(a)+\left( \frac{3}{a}+\frac{\dot{H}(a)}{H(a)}\right) \dot{\delta }_m(a)-\frac{3\varOmega _{m0}G_{eff}/G}{2(H^2(a)/H_0^2)}\delta _m(a)=0\;, \end{aligned}$$

(61)

where the dot symbols denote derivatives with respect to scale factor a.

4 Observational constraints: analysis and results

4.1 Cosmological data

The methodology used to handle the data relies on the Markov Chain Monte Carlo (MCMC) technique based on the Metropolis-Hasting algorithm with a modified version of the original available publicly Mathematica$^\mathrm{TM}$ code from refs. [37, 38]. We apply our $\chi ^2$-statistics to the joint likelihood of the 1107 data points. We have 1048 points from the Pantheon SNIa observations [39], 3 points from the CMB Planck 2018 release [1] and 15 points from BAO surveys [60]. Concerning specifically to BAO surveys, we point out that the BAO points of [42] were augmented by the $f\sigma _8$ points shown in Table 1 of [61] along with the full covariance matrix [42]. Moreover, the most up-to-date H(z) compilation is summarized in Table 1 from [40] resulting in 31 points added to the analysis and also the available independent $f\sigma _8$ values in Table 3 of Ref.[61] with 10 points of the growth-rate data. Moreover, we used the background parameter vectors for the $\beta$-model as $\{\varOmega _{m0}, \varOmega _{b0}h^2, \beta _0, h, \sigma _8\}$ and also for the $\varLambda$CDM and wCDM models as $\{\varOmega _{m0}, \varOmega _{b0}h^2, -1, h, \sigma _8\}$ and $\{\varOmega _{m0}, \varOmega _{b0}h^2, w, h, \sigma _8\}$, respectively. Specifically, the $\beta$-model priors were $\{(0.001, 1), (0.001, 0.08), (-0.3,1), (0.01, 0.5), (0.1,1.8)\}$. To implement the MCMC chains, the joint analysis is defined by the product of the particular likelihoods $\mathscr {L}$ for each data set

$$\begin{aligned} \mathscr {L}_{tot}= \mathscr {L}_{Pantheon}.\mathscr {L}_{BAO}.\mathscr {L}_{CMB}.\mathscr {L}_{H(z)}.\mathscr {L}_{Growth}\;, \end{aligned}$$

(62)

and the sum of individual $\chi ^2$ to get the related total $\chi ^2$

$$\begin{aligned} \chi ^2_{tot}= \chi ^2_{Pantheon} + \chi ^2_{BAO}+ \chi ^2_{CMB} + \chi ^2_{H(z)}+\chi ^2_{Growth}. \end{aligned}$$

(63)

For the growth analysis, we use the $\sigma _8$ parameter that measures the growth of r.m.s fluctuations on the scale of 8h$^{-1}$Mpc by defining the quantity

$$\begin{aligned} f\sigma _8(a) \equiv f(a).\sigma _8(a)\;, \end{aligned}$$

(64)

where $f(a)=\frac{\ln \delta }{\ln a}$ is the growth rate and the growth factor $\delta (a)$. The data dependence from the fiducial cosmology and another cosmological survey must be compatibilized. It can be done by rescaling the growth-rate data by the ratio r(z) of the Hubble parameter H(z) and the angular distance $d_A(z)$ by the relation

$$\begin{aligned} r(z) = \frac{H(z)d_A(z)}{H_f(z)D_fA(z)}\;, \end{aligned}$$

(65)

where the subscript “f” corresponds to a quantity of fiducial cosmology. Moreover, the angular distance $d_A(z)$ is defined as

$$\begin{aligned} d_A(z)= \frac{c}{(1 + z)}\int _{z}^{0}\frac{1}{H(z')} dz'\;. \end{aligned}$$

(66)

Likewise, the general regulation of the $\chi ^2$ statistics is given by

$$\begin{aligned} \chi ^2 (\varOmega _{m0},w,\beta _0,\sigma _8)= V^i C^{-1}_{ij}V_j \;, \end{aligned}$$

(67)

where $V^i\equiv f\sigma _{8,i} - r(z_i)f\sigma _8(z_i,\varOmega _{m0}, w,\beta _0,\sigma _8)$ denotes a set of vectors that goes up to ith-datapoints at redshift $z_i$ for each $i=1...N$. The term N is the total number of datapoints of a related collection of data and from theoretical predictions.

For the CMB data, we used the Planck 2018 release data [1] with $\chi ^2$ statistics

$$\begin{aligned} \chi _{CMB}^2=X_{Planck2018}^{T}C_{CMB}^{-1}X_{Planck2018}\;, \end{aligned}$$

(68)

where the covariant matrix for the parameters for $R, l_A, \varOmega _{b0} h^2$ is given by

$$\begin{aligned} X_{Plankc2018}= \left( \begin{array}{ccc} R-1.74451 \\ l_{A}-301.76918 \\ \omega _{b}-0.022483 \end{array} \right) \end{aligned}$$

(69)

where $\omega _{b}=\varOmega _{b0}h^{2}$. The quantities R and $l_A$ are the shift parameters defined as the scale distance and acoustic scale, respectively, as

$$\begin{aligned} R=\frac{\sqrt{\varOmega _{m0}}}{c}d_{A}(z_{CMB})(1+z_{CMB})\;, \end{aligned}$$

(70)

$$\begin{aligned} l_{A}=\frac{\pi {d_{A}}(z_{CMB})(1+z_{CMB})}{r_{s}(z_{CMB})}\;, \end{aligned}$$

(71)

where the angular distance $d_A$ is given by Eq. (66) and the related redshift at recombination $z_{cmb}$ is given by

$$\begin{aligned} z_{CMB}=1048[1+0.00124(\varOmega _{b0}h^2)^{-0.738}][1+g_1(\varOmega _{m0}h^2)^{g_2}]\;, \end{aligned}$$

(72)

and the parameters $(g_1,g_2)$ are defined as

$$\begin{aligned} g_1=\frac{0.0783(\varOmega _{b0}h^2)^{-0.238}}{1+39.5(\varOmega _{b0}h^2)^{0.763}};\,\,\,g_2=\frac{0.560}{1+21.1(\varOmega _{b0}h^2)^{1.81}}\;. \end{aligned}$$

(73)

Table 1 A compilation of 31 datapoints of the Hubble function H(z) data used in the current analysis as shown in Table 2 of [40]. The relative error points are denoted by the $\sigma _H$ column.

Table 2 A summary of best-fit values of the main cosmological parameters calculated by using MCMC chains. The $\chi _{bf}^2$ denotes the $\chi ^2$ best-fit values from MCMC chains of each individual model.

Table 3 A summary of the mean values of the main cosmological parameters calculated by using MCMC chains of each model.

The comoving sound horizon $r_s(z)$ is given by

$$\begin{aligned} r_s(z)=c\int _{z}^{\infty }\frac{c_s(z')}{H(z')}dz'\;, \end{aligned}$$

(74)

and the related sound speed $c_s$

$$\begin{aligned} c_s(z)=\frac{1}{\sqrt{3(1+\bar{R}_b/(1+z))}}\;, \end{aligned}$$

(75)

with $\bar{R}_b=31500\varOmega _{b0}h^2(T_{CMB}/2.7K)^{-4}$. Moreover, the inverse of the covariant matrix $C_{CMB}^{-1}$ for the parameters for $R,l_a,\varOmega _{b0} h^2$ is given by $C_{CMB}^{-1}= \sigma _i \sigma _j C$, with $\sigma _i$ = (0.093, 0.0051, 0.00016) for the normalized covariance matrix given by

$$\begin{aligned} C= 10^{-8} \left( \begin{array}{ccc} 2556.7782 &{} 23212.222 &{} -57.345815 \\ 23212.222 &{} 830122.02 &{} -628.56261 \\ -57.345815 &{} -628.56261&{} 2.5300094\\ \end{array} \right) \end{aligned}$$

(76)

The BAO datasets are summarized in Table 1 of ref. [61] from the conjunction of probes on BOSS DR12 [42], SDSS DR7 MGS [43], eBOSS DR14 [44], BOSS DR12 Ly$\alpha$ forest [45] and BOSS DR11 Ly$\alpha$ forest [46]. The total correlated BAO is given by

$$\begin{aligned} \chi _{BAO}^2=(d_{obs}-d_{th})C_{BAO}^{-1}(d_{obs}-d_{th})^{T}\;. \end{aligned}$$

(77)

where $d_{obs}$ denotes the observable distance and $d_{th}$ is theoretical distance, respectively. The full covariant matrix $C_{BAO}$ can be found in [42].

For the Pantheon supernova type Ia data the theoretical distance modulus $\mu _{th}(z)$ is given by

$$\begin{aligned} \mu _{th}(z) = 5 \log _{10}(d_L(z)) + \mu _0, \end{aligned}$$

(78)

where $\mu _0 = 42.38 - 5 \log _{10} \mathbf {h}$. The luminosity distance $d_L$ related to Hubble expansion rate is given by

$$\begin{aligned} d_L(z|s,\mu _0) = (1 + z) \int _{0}^{z} \frac{du}{E(u|s)}\;, \end{aligned}$$

(79)

where s denotes the model parameters. As a prior, we adopt the density parameter value of visible baryonic matter $\varOmega _{b0} = 2.236/100\mathbf {h}^2$. Accordingly, the $\chi ^2$ statistics is

$$\begin{aligned} \chi ^2_{SnIa}(s|\mu _0) =\sum _{i=1}^{n}\frac{\left[ \mu _{th,i}(s,\mu _0| z_i) - \mu _{obs,i}(z_i)\right] }{\sigma ^2_{\mu i}}\;, \end{aligned}$$

(80)

where $n = 1048$ is the number of events of the Pantheon SNIa data [39], the distance modulus obtained from observations is denoted by $\mu _{obs,i}(z_i)$, and $\sigma _{\mu i}$ is the total uncertainty of the observational data.

Fig. 1

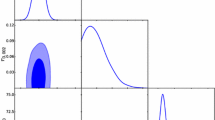
Contour regions at 1-$\sigma$, 2-$\sigma$ and 3-$\sigma$ at $68.3\%$, $95.4\%$ and $99.7\%$ C.L, respectively, of the $(\sigma _8-\varOmega _m)$ and $(\varOmega _{b0}h^2-\varOmega _{m})$ planes. The black points represent the mean values of the parameters in the MCMC chains of the $\beta$-model. The open circles represent the Planck 2018 data of TT,TE,EE+lowE on 68$\%$ interval with $\sigma _8=0.8120\pm 0.0073$ and $\varOmega _{b0}h^2=0.02236\pm 0.00015$.

Fig. 2

One-dimensional PDF likelihood of the main cosmological parameters for the $\beta$-model used in this study. The vertical dashed lines connote the values of CMB Planck 2018 of TT,TE,EE+lowE on 68$\%$ interval for $\varOmega _{m0},\varOmega _{b0}h^2,\sigma _8$. The last right panel also shows the degeneracies for the $\beta _0$ parameter.

Fig. 3

Numerical solutions of the matter density evolution of each model. The left panel shows the comparison between $\varLambda$CDM, wCDM and $\beta$-model with the mean values of each model calculated from the MCMC chains as summarized in Table 3. The right panel shows a better visualization in logarithm scale of the comparison with these models by the ratio $\delta _{m\;i}/\delta _{m \varLambda CDM}$.

4.2 Results and discussions

The results of the MCMC chains of each model were summarized in Tables 2 and 3, respectively. Error estimates were calculated from the Fisher Matrices around the related best-fit and mean values for each model. In Fig. 1, we present the obtained 3$\sigma$-contour plots for the $\beta$-model. The black points mark the obtained mean values from MCMC chains and the open circles connote the CMB Planck 2018 data of TT,TE,EE+lowE on 68$\%$ intervals for a flat $\varLambda$CDM model for the related cosmological parameters (Table 2 of Ref.([1])). The left panel presents a $(\sigma _8-\varOmega _m)$ contour that shows a persistence of the tension at 3-$\sigma$ in comparison with the 3-$\sigma$ tension from CMB Planck 2018 between low redshift data H(z) and the Planck probe. This tension is mildly reduced to 2-$\sigma$ contour when only considering TE+lowE at 68$\%$ limits. In the right panel, it is shown the $(\varOmega _{b0}h^2-\varOmega _m)$ plane that pinpoints a good accommodation of the baryonic luminous matter parameter with the values from Planck 2018 data within the 1-$\sigma$ contour. An important matter is shown in Fig. 2 that exhibits the PDF behaviour of the main considered cosmological parameters for the $\beta$-model. The vertical dashed lines indicate the values of CMB Planck 2018 of TT,TE,EE+lowE on 68$\%$ interval for $(\varOmega _{m0},\varOmega _{b0}h^2,\sigma _8)$. The degeneracies found in the marginalization of $\beta _0$ may decrease the obtained 3-$\sigma$ tension of $\sigma _8$ to 2-$\sigma$ contour.

Fig. 4

The percentage relative difference $\%$diff$(H_i-H_j)$ in linear (left panel) and logarithm (central panel) scales between the $\beta$-model, $\varLambda$CDM and wCDM models for their mean values as shown in Table 3. In the right panel, it is also shown Om(z) diagnosis.

In Fig. 3 is shown the behaviour of the growth-rate evolution of the $\beta$-model (Eq. 61) in comparison with the $\varLambda$CDM and wCDM models. The adopted values were extracted from the mean values of the MCMC chains for each model as shown in Table 3. In the left panel, it is shown that the resulting curves from the three models are indistinguishable. On the other hand, a relative comparison by ratio $\delta _{m\;i}/\delta _{m \varLambda CDM}(a)$ (where the index i denotes $i=\beta$-model, wCDM), between the models is shown the right panel that exhibits a clear difference on the behaviour of growth-rate of $\varLambda$CDM as compared with $\beta$-model and wCDM. Thus, $\delta _{m\;\beta -\text {model}}/\delta _{m \varLambda CDM}(a)$ (blue dotted line) shows a higher growth as compared with $\varLambda$CDM (black solid line) and the ratio $\delta _{m\;wCDM}/\delta _{m \varLambda CDM}(a)$. Also, both curves of $\delta _{m\;\beta -model}/\delta _{m \varLambda CDM}(a)$ and the ratio $\delta _{m\;wCDM}/\delta _{m \varLambda CDM}(a)$ start to deviate from $\varLambda$CDM around $a\sim 0.2-0.3$. This is corroborated in the following different analysis.

In the Fig. 4 we obtain the percentage relative difference between the aforementioned models in what concerns the evolution of Hubble function. In the left panel, it shows in linear scale that the percentage difference between the $\beta$-model with $\varLambda$CDM and wCDM. The percentage difference between $\beta$-model and wCDM reaches values lower than 1$\%$ in early times and tends to close equivalence in present time. In comparison with $\varLambda$CDM, the percentage difference is lesser (around $\sim 0.2 \%$) at early times but present a mild fluctuation around $a\sim 0.2-0.3$ and reaches a top $a\sim 0.6-0.8$ with $0.3\%$ of percentage difference. This fluctuation is clearer in the central panel with the spike in the black solid curve due to the degeneracies on the $\beta _0$ parameter that leads to a mild signature on the baryonic luminous matter. It is important to point out that these differences may be amplified when considering anisotropic matter stresses.

Moreover, to reinforce the phenomenological distances between the models, we apply the Om(z) diagnosis [49] as a null test, by using the formula

$$\begin{aligned} Om(z)= \frac{E(z)^2-1}{(1+z)^3-1}\;. \end{aligned}$$

(81)

The right panel shows in the black dashed line the same values for Om(z) for any redshift as expected for $\varLambda$CDM. The blue and red solid lines indicate Om(z) values higher ($\beta$-model) and lower (wCDM), respectively, like that of evolving dark energy models. The resulting Om(z) diagnosis is in compliance with the results of the MCMC chains and former H(z) percentage difference between the models exhibiting a close similarity at early universe with a departure that begins around $a\sim 0.2-0.3$. We expect that a large percentage difference may be obtained with higher orders of Mclaurin-Puiseux series to provide a control on growth-rate density.

Table 4 A summary of the obtained values of AIC for the studied models. The $\varLambda$CDM model is adopted as a reference.

Another useful tool to analyse the constraining on the parameters from MCMC chains for the model comparisons refers to the level of statistical correlation between competing models. Adopting the errors being as Gaussian, we use AIC systematic to classify the fit-to-data for small samples sizes [62, 63]

$$\begin{aligned} AIC= \chi ^2_{bf} + 2k+\frac{2k(k+1)}{N-k-1}\;, \end{aligned}$$

(82)

where $\chi ^2_{bf}$ is the best-fit $\chi ^2$ of a model, k represents the number of the free parameters and N is the number of the data point in the adopted dataset. The difference $|\varDelta AIC|= AIC_{model\;2}-AIC_{model\;1}$ obeys the Jeffreys’ scale [64] that measures the intensity of tension between two competing models due to the lost information from the related fitting. In general, the preferred model is that one with lesser values for AIC. In comparison, higher values of AIC denote a higher statistical distance and may indicate a statistically disfavoring model. In Jeffreys’ scale for $|\varDelta AIC\le 2|$ tells that the models are statistically consistent with a certain good level of empirical support. For $4< \varDelta AIC < 7$ indicates a positive tension against the model with a higher value of AIC. For $|\varDelta AIC \ge 10|$ defines a strong empirical evidence against a model with a higher AIC. Accordingly, we obtained the AIC and $\varDelta AIC$ values shown in Table 4 that indicates some weak evidence against $\beta$-model with a $\varDelta AIC$ roughly $\sim 2$. This result reinforces the previous ones and leads to the conclusion that the $\beta$-model is favored by its statistical consistency with $\varLambda$CDM and wCDM models at present time with mild fluctuations at perturbation level.

5 Remarks

In this paper, we discussed the dark energy problem with a proposal of a geometric model in a search of explanation of some aspects of the accelerated expansion. By construction, we used the Nash-Greene theorem to propose a geometric model with a resulting modified Friedman equation from the influence of the extrinsic curvature thought as a complement to Einstein’s gravity, and we call, for short, $\beta$-model. From background level, an asymptotic solution valid in the range $a=[0,1]$ was obtained using a Mclaurin-Puiseux series of the Hubble function H(z) of the model due to the fact the parameter $\eta _0\rightarrow 0$. At perturbation level, we obtained the perturbed equations in the longitudinal Newtonian gauge.

In this paper, the $\beta$-model was compared with the well-known models in the literature as the $\varLambda$CDM and wCDM models. With a different motivation, the $\beta$-model proposes a complement to the general concept of curvature adding an extrinsic Gaussian curvature to the Riemannian geometry. This was made by the embedding of geometries with the Nash-Greene theorem and as consequence we obtained a modification of the geometrical part of induced (embedded) Einstein equations. Hopefully, throughout this mechanism a new information may be added to Einstein’s gravity making, a priori, no necessity, e.g., of quintessence fields nor any modification of cosmic fluids to model the missing energy.

As a test, from the MCMC analysis of each considered models, we obtained the resulting contours for the $\beta _0$ model from the analysis on $(\sigma _8-\varOmega _m)$ plane that shows a persisting 3-$\sigma$ tension. In the $(\varOmega _{b0}h^2)-\varOmega _m$ plane, we obtained well accommodated points as compared with the Planck 2018 data of TT,TE,EE+lowE values. In addition, the related PDF 1-dimensional plot of the $\beta$-model parameters shows the degeneracies on the $\beta _0$ parameter and may improve the aforementioned $\sigma _8$ tension. Such possibility does not allow to happen in the $\varLambda$CDM and wCDM usual contexts. From numerical solutions on growth-rate and H(z) evolutions, it was shown a certain compatibility between the $\beta$-model with the $\varLambda$CDM and wCDM models with a percentage difference lower than 1$\%$ at early times. This small difference appears to be limited only to the second Maclaurin-Puiseux expansion order. Moreover, we applied the AIC classifiers that favour the $\varLambda$CDM model but with a statistical compatibility with $\beta$-model with $\varDelta AIC$ roughly $\sim 2$. We reinforce that these differences may be amplified when considering anisotropic matter stresses to the $\beta$-model perturbed equations. As future prospects, we intend to investigate how the $\beta$-model may inflict changes in the Integrated Sachs–Wolfe (ISW) contribution in comparison with the one as predicted to $\varLambda$CDM with a lower peak of the second CMB peak. Also, to investigate the behaviour of the viscosity parameter and growth index rate resulting from the $\beta$-model in a search of a more realistic context. This process is in due course and will be reported elsewhere.