1 Introduction

One of the fundamental properties of general relativistic wormhole geometry is that this spacetime is tunnel-like spacetime connecting two widely disconnected regions of a same universe or two different universes and supported by exotic matter, which can characterize by the stress–energy tensor of the spreading matter content in the wormhole that violates the null energy condition(NEC) \(T_{\mu \nu }v^\mu < 0\), where \(v^\mu \) is a null vector [1, 2]. Hochberg and Visser [3,4,5] showed that the wormhole generically violates the NEC after the wormhole throat and they also provided some striking theorems that generalized the Morris–Thorne seminal results on the exotic matter with the help of the theory of embedded hypersurfaces on the Riemann tensor and stress–energy tensor after the wormhole throat radius. The first wormhole solution, Einstein–Rosen bridge, was provided by Einstein and Rosen [6] and it was regarded as a mathematical product because of its non traversable property. Later in the year 1973, Ellis [7] provided a new spherically symmetric wormhole solution with a ghost massless scalar field. Moreover, these wormholes are traversable and neither have singularity nor horizon showed by Morris and Thorne [1]. Further, Shinkai and Hayward [8] showed that Ellis wormholes are unstable and this result ensures that Ellis wormholes are practically nonexistent. However, inter-universe travel is certainly possible with a stable traversable wormhole [9, 10].

The connecting and traveling characteristics of wormholes attract the theoretical research community and from the last few decades many researchers have intensively studied various aspects of traversable wormholes within Einstein gravity as well as in different theories of modified gravity [3, 11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55]. Further, in the last year, more different wormhole like geometries are found in the bumblebee gravity [56], Einstein–Cartan Garvity [57], exponential f(R, T) gravity [58], modified gravity with \(\rho (R, R')\) matter [59] and Novel Einstein-scalar-Gauss–Bonnet gravity [60].

It is well-known from the Standard Model of Cosmology that the universe contains only 5% ordinary matter and energy of the total mass–energy of the Universe. The remaining 95% matter and energy of total mass–energy are distributed into the dark sector, which is divided in dark matter (DM) and dark energy (DE). The unseen DM component is about roughly 27% of the dark sector and the DE, which is the main fuel that drives the current cosmic acceleration of the universe is about 68% of the dark sector. In the year 1933, astronomer Zwicky firstly concluded the existence of DM with the help of the Virial theorem, which is described as Dunkle Materie in the galaxy cluster [61, 62]. The presence of DM within the universe, particularly in the Milky Way, is established on the basis of sound observational grounds [63,64,65]. From the last few years [66, 67], the detailed descriptions of DM distribution in the galaxy are obtained by the tremendous numerical simulations. Further, several observables have used, namely, star counts, the motion of gas and stars or microlensing events in order to constrain Milky Way mass models. Applying microlensing observations and dynamical measurement concepts Iocco et al. [68] have showed that constraints can be set on the DM distribution, which provides complementary evidence for the existence of DM in the galaxy. The exitance of the DM in the galactic halo is also deduced from its gravitational impression on the rotational curve of a spiral galaxy [69,70,71].

In astronomy, the bulge is a tightly packed collection of celestial compact stars within a galaxy. The bulge exclusively refers to the central group of compact stars, which is found in most of the spiral galaxies. Nowadays, it is considered that there are at least two types of bulges: (i) Bulges that are elliptical like and (ii) Bulges that are like spiral. The common two scenarios for the bulge formation are: (i) the merging of the early disks and fragments, and (ii) the secular evolution of disks and bars. An enrich bulge component forms from a clump-unstable, star-bursting disk. Mamon et al. [72] studied the mass and shape of the galactic dark halo, the large-scale structure of the Milky Way and provided the evidence that the inner Galaxy is dominated by baryonic matter. They have also studied the bulge formation from clumpy, gas-rich disks, disk-like, enrich bulges similar to the galactic bulge. From the last few decades, several studies supposed from star count observations that the galaxy must contain a separate, new, flat long bar component, twisted relative to the barred bulge. Martinez-Valpuesta [73] has study the boxy bulge and planar long bar in MWG.

Inspired from the different studied of wormholes in different modified gravities, many researchers have gave attention to find the wormhole geometries in galactic level. From that attention wormhole solutions are found in the central region as well as the outer of the galactic halo supported by the exotic dark matter (DM). Rahaman et al. [74] have showed that DM supports the wormhole geometry in the outer region of the galactic halo. Moreover, the central region also contains the wormhole [75, 76]. Sarkar et al. [77] have found that wormhole also exists in the isothermal galactic halo and void supported by the DM. Moreover, Kuhfitting [78] has studied the gravitational lensing of wormholes in the galactic halo region.

Pando et al. [79] have proposed that topological defects are responsible for the structure formation of the galaxies. Nucamendi et al. [80] have suggested that the monopole (its energy density proportional to \(1/r^2\)) could be the galactic dark matter in the spiral galaxies. Thus it seems monopoles (one of the topological defects) take part an important contribution of the galaxy formations. In the year 2003, Nueamendi [81] has studied the static spherically symmetric spacetimes black holes with Global Monopole Charge. Very recently, the cosmic censorship hypothesis for the Reissner–Nordström anti-de-Sitter black holes with Global Monopole Charge have studied in Ref. [82].

In this article, we have obtained the traversable wormholes in the bulge of the MWG concerned with Global Monopole Charge. Here, we have considered the MacMillan [83, 84] DM density profile of the bulge of the MWG to generate our wormhole solutions. The content of this article has been designed as follows: we have set up the Einstein field equations with a Global Monopole Charge in Sect. 2. Section 3 is arranged for the wormhole formulation in the bulge of MWG into two subsections: Sect. 3.1 contains the details of our wormhole structure while Sect. 3.2 deals with the null energy condition(NEC) corresponding to three different redshift functions, Sect. 3.2.1: the tidal force redshift function, Sect. 3.2.2: the rational redshift function, and Sect. 3.2.3: the redshift function obtained from the flat rotational curve of the galactic halo. We have estimated embedding surface and proper radial distance of wormhole in Sect. 5 and Matched our reported solutions to the external Schwarzschild solution in Sect. 6. Finally, the discussion and conclusion of our work have been made in Sect. 8.

2 Einstein’s field equations with a Global Monopole Charge

In this section, we are going to compute the Einstein field equations with Global Monopole Charge which can obtain from the 3+1 dimensional action. In the gravitational unit(\(c = G = 1\)), the 3+1 dimensional action without a cosmological constant is given as

$$\begin{aligned} S=\int \sqrt{-g}\left( \mathcal {L}+\frac{\mathfrak {R}}{16\pi } \right) d^4x+S_m \end{aligned}$$
(1)
Fig. 1
figure 1

The density is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2}, \alpha = 0.5\) and \( r_0 = 2 ~kpc\)

Full size image

The Lagrangian density for a self-coupling scalar triplet \(\phi ^a\) can be written as [85]

$$\begin{aligned} \mathcal {L}=-\frac{\lambda }{4}(\phi ^2-\eta ^2)^2-\frac{1}{2}\sum _a g^{ij}\partial _i\phi ^a\partial _j\phi ^a \end{aligned}$$
(2)

where \(a = 1,~2,~3\) and \(\lambda \), \(\eta \) are the self-interaction term, scale of a gauge-symmetry breaking, respectively. The monopole describing field configuration can be represented as

$$\begin{aligned} \phi ^a=\frac{\eta }{r}f(r)x^a \end{aligned}$$
(3)

where \(x^a=(r\sin \theta \cos \phi ,~r\sin \theta \sin \phi ,~r\cos \theta )\) such that \(\sum _ax^ax^2 = r^2.\)

Now, we consider Morris–Thorne traversable wormhole space-time [1], which is given by the following line element

$$\begin{aligned} ds^2 = e^{2\Phi (r)}dt^2-\left( 1-\frac{b(r)}{r}\right) ^{-1}dr^2-r^2(d\theta ^2 + sin^2\theta d\phi ^2) \end{aligned}$$
(4)
Fig. 2
figure 2

The shape function b(r) is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~\beta = 0.8, ~r_{th} = 1~kpc\) and \( r_{0} = 2~kpc\)

Full size image

where \(\Phi (r)\) and b(r) are the functions of the radial coordinate r only and termed as the redshift function and shape function, respectively. The minimum radius \(r = r_{th}\) in the metric coefficient \(g_{rr}\) of the line element (4) is termed as the throat radius of the wormhole, where \(b(r_{th}) = r_{th}\) . Formation of an event horizon should be avoided in order for the wormhole to be traversable i.e. the redshift function \(\phi (r)\) should be finite everywhere. Again, from the fundamental definition of traversable wormhole, the shape function must satisfy the following conditions to presents wormhole solutions:

  1. (i)

    The redshift function \(\Phi (r)\) should be well-defined and regular for \(r \ge r_{th}\).

  2. (ii)

    The shape function b(r) should be well-defined for \(r > r_{th}\)

  3. (iii)

    The shape function b(r) should satisfy the condition \(\left( 1-\frac{b(r)}{r}\right) > 0\) for \(r > r_{th}\) i.e. \(\frac{b(r)}{r} < 1\) for \(r > r_{th}\).

  4. (iv)

    The shape function b(r) should satisfy the flare-out condition [86]: \([b(r)-rb'(r)]/b^2(r) > 0\) for \(r > r_{th}\) in which \(b^{\prime }(r_{th}) < 1\).

Now, in terms of f(r), the Lagrangian density express as

$$\begin{aligned} \mathcal {L}=-\frac{\eta ^2 f^2}{r^2}-\frac{\lambda \eta ^4}{4}(f^2-1)^2 -\left( 1-\frac{b(r)}{r}\right) \frac{\eta ^2(f^\prime )^2}{2} \end{aligned}$$
(5)

Also, the Euler–Lagrange equation for the field f yields

$$\begin{aligned}&\left( 1-\frac{b(r)}{r}\right) f^{\prime \prime } +\left\{ \left( \frac{b(r)-rb^\prime (r)}{2r^2}\right) +\frac{2}{r}\left( 1-\frac{b(r)}{r}\right) \right\} \nonumber \\&\quad \times f^\prime -\left\{ \frac{2}{r^2}+\lambda \eta ^2(f^2-1)\right\} f=0 \end{aligned}$$
(6)

From the Lagrangian density (2), the energy momentum tensor is obtaines as

$$\begin{aligned} \bar{T}_{ij}= \partial _i\phi ^a\partial _j\phi ^a-\frac{1}{2}g_{ij} g^{\mu \nu }\partial _\mu \phi ^a\partial _\nu \phi ^a-\frac{g_{ij}\lambda }{4}(\phi ^2-\eta ^2)^2 \end{aligned}$$
(7)

From Eq. (7), the individual expression of the components of energy–momentum are given as follows

$$\begin{aligned} \bar{T}_t^t= & {} -\eta ^2\left\{ \frac{f^2}{r^2} +\left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2} +\frac{\lambda \eta ^2}{4}(f^2-1)^2\right\} \end{aligned}$$
(8)
$$\begin{aligned} \bar{T}_r^r= & {} -\eta ^2\left\{ \frac{f^2}{r^2} -\left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2} +\frac{\lambda \eta ^2}{4}(f^2-1)^2\right\} \end{aligned}$$
(9)
$$\begin{aligned} \bar{T}_\theta ^\theta= & {} \bar{T_\phi ^\phi } =-\eta ^2\left\{ \left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2}+\frac{\lambda \eta ^2}{4}(f^2-1)^2\right\} .\nonumber \\ \end{aligned}$$
(10)

One can easily see that the Eq. (6) is a complicated equation, which cannot be solved exactly. To solve the Eq. (6), it is sufficient to take \(f(r)\rightarrow 1\) outside the wormhole. Therefore, for this choice of f(r), the components of energy–momentum reduce as

$$\begin{aligned} \bar{T}_t^t=\bar{T}_r^r\simeq -\frac{\eta ^2}{r^2},~~ \bar{T}_\theta ^\theta =\bar{T}_\phi ^\phi \simeq 0 . \end{aligned}$$
(11)
Fig. 3
figure 3

The ratio function b(r)/r is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~\beta = 0.8, ~r_{th} = 1~kpc\) and \( r_{0} = 2~kpc\)

Full size image

The Einstein field equations is written as

$$\begin{aligned} G_{ij}=R_{ij}-\frac{1}{2}g_{ij}R=8\pi \mathcal {T}_{ij}, \end{aligned}$$
(12)

where \(\mathcal {T}_{ij}\) is the total energy–momentum tensor of matter fluid and matter fields and it can be expressed as

$$\begin{aligned} \mathcal {T}_{ij}=T_{ij}^{(0)}+\bar{T}_{ij} \end{aligned}$$
(13)

Since the anisotropy plays a crucial role in the equilibrium of wormhole, so for our study we shall consider the anisotropic matter distribution. Later, we shall discuss the equilibrium for our reported wormholes. The components of energy–momentum tensor for anisotropic matter fluid is given as follows

$$\begin{aligned} {T_j^i}~^{(0)}=(-\rho (r), \mathcal {P}_r(r), \mathcal {P}_\theta (r), \mathcal {P}_\phi (r)). \end{aligned}$$
(14)
Fig. 4
figure 4

The function \([b(r)-rb'(r)]/b^2(r)\) is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\) and \(r_{0} = 2~kpc\)

Full size image

For the Morris–Thorne traversable wormhole metric (4), Einstein tensor components are

$$\begin{aligned} G_t^t= & {} -\frac{b^{\prime }(r)}{r^2}, \end{aligned}$$
(15)
$$\begin{aligned} G_r^r= & {} -\frac{b(r)}{r^3}+2\left( 1-\frac{b(r)}{r}\right) \frac{\Phi ^{\prime }}{r},\end{aligned}$$
(16)
$$\begin{aligned} G_\theta ^\theta= & {} \left( 1-\frac{b(r)}{r}\right) \Big \{\Phi ^{\prime \prime }+(\Phi ^{\prime })^2 -\frac{b^{\prime }r-b}{2r(r-b)}\Phi ^{\prime }\nonumber \\&-\frac{b^{\prime }r-b}{2r^2(r-b)}+\frac{\Phi ^{\prime }}{r}\Big \},\nonumber \\ G_\phi ^\phi= & {} G_\theta ^\theta . \end{aligned}$$
(17)

Finally, the Einstein field equations with the Global Monopole Charge are given as follows:

$$\begin{aligned} \rho (r)= & {} \frac{1}{8\pi }\left( \frac{b^\prime (r)}{r^2}-8\pi \eta ^2\right) , \end{aligned}$$
(18)
$$\begin{aligned} \mathcal { P}_r(r)= & {} \frac{1}{8\pi }\left[ \left( 1-\frac{b(r)}{r}\right) \left( \frac{1}{r^2}+\frac{2\phi ^\prime (r)}{r}\right) -\frac{1}{r^2}+\frac{8\pi \eta ^2}{r^2}\right] , \end{aligned}$$
(19)
$$\begin{aligned} \mathcal {P}_t(r)= & {} \frac{1}{8\pi } \left( 1-\frac{b(r)}{r}\right) \phi ^{\prime \prime }(r) +\left( 1-\frac{b(r)}{r}\right) {\phi ^\prime }^2(r)\nonumber \\&+\frac{1}{2}\left( \frac{b(r)}{r^2} -\frac{b^\prime (r)}{r}\right) \phi ^\prime (r)+\frac{1}{r} \left( 1-\frac{b(r)}{r}\right) \phi ^\prime (r)\nonumber \\&+\frac{1}{2r}\left( \frac{b(r)}{r^2} -\frac{b^\prime (r)}{r}\right) . \end{aligned}$$
(20)

where \(\prime \) stands for \(\frac{d}{dr}\).

3 Wormhole formulation in the bulge of Milky Way galaxy

Here, we are willing to obtain a new wormhole structure representing shape function with the help of a DM density profile of the bulge in MWG.

Fig. 5
figure 5

\(b^{\prime }(r_{th})\) is plotted with respect to \(\eta \) corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\) and \(r_{0} = 2~kpc\)

Full size image

3.1 Wormhole structure

We consider a DM density profile of the bulge in MWG as follows from the striking work of MacMillan [83, 84]

$$\begin{aligned} \rho (r)=\rho _0 \left( \frac{r_1}{r}\right) ^\alpha \exp \left[ -\left( \frac{r}{r_0}\right) ^\beta \right] \end{aligned}$$
(21)

where \(\alpha ,~\beta ,~r_1\) are the model dependent parameters and \(\rho _0,~r_0\) are the core density, radius of the bulge, respectively. For simplicity, we have considered \(r_0 = r_1\).

Motivation: Recently, several authors have studied the possible exitances of wormholes in outer, inner regions of galaxy and void with the help of the NFW, quasi-isothermal or Burkert and isothermal density profiles [74,75,76,77]. Consequently, all these studies effectively increase the interest among the theoretical researchers to study the wormhole structures in galactic level and encourage the scientific community to find the observational evidences. In this study, we consider the observationally verified MacMillan density profile (21) of the bulge to show the possible existence of wormhole in the bulge of MWG with Global Monopole Charge. The consideration of Global Monopole Charge is for generalization and to see the effect of Global Monopole Charge in wormhole formations, if we off the Global Monopole Charge we come to the Einstein gravity and the corresponding solutions are analyzed. Hopefully, our study may inspire the scientific community to search observational evidence of the presence of wormhole in the Milky Way bulge region.

The entire behavior of density profile (21) is displayed through graphical demonstration in Fig. 1 corresponding to the parameters \(\rho _0 = 0.004~ kpc^{-2}, ~ \alpha = 0.5, r_0 = 2 kpc\) and \(0.2 \le \beta \le 1\). Figure 1 ensures that the density profile is positively decreasing from inner region to outer region of the bulge.

Fig. 6
figure 6

\(\rho (r) + \mathcal {P}_r(r)\) is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\) and \(r_{0} = 2~kpc\)

Full size image
Fig. 7
figure 7

NEC is shown at the radial distance \(r = 1.5~kpc\) with respect to the Global Monopole Charge \(\eta \) corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\) and \(r_{0} = 2~kpc\)

Full size image

Now, on imposing the above density profile (21) in Eq. (18) and after using the condition \(b(r_{th}) = r_{th}\), we obtain the following shape function

$$\begin{aligned} b(r)&=\frac{8\pi r^3 }{3\beta }\left[ \beta \eta ^2-3 \rho _0\left( \frac{r_0}{r}\right) ^{\alpha } F(r)\right] +A \end{aligned}$$
(22)

whereas

$$\begin{aligned} F(r)= & {} E\left[ \frac{\alpha +\beta -3}{\beta },\left( \frac{r}{r_0}\right) ^\beta \right] \end{aligned}$$
(23)
$$\begin{aligned} A= & {} \frac{8 \pi \rho _0}{\beta } r_{th}^{3-\alpha } r_0^\alpha F(r_{th})-\frac{8}{3} \pi r_{th}^3 \eta ^2+r_{th} \end{aligned}$$
(24)

Here, E[m, x] is called as the exponential integral function, defined as

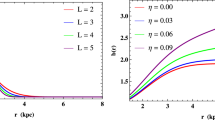
$$\begin{aligned} E[m,y]=\int _0^1 e^{-\frac{y}{\xi }}\xi ^{m-2}d\xi ;~~~y > 0 \end{aligned}$$
(25)

To explain the actual characteristic of the reported shape function we have explored some graphical demonstrations for that shape function in Figs. 2, 3, 4 and 5 with respect to the particular choice of parameters \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5~ \beta = 0.8, ~r_{th} = 1~kpc, r_{0} = 2~kpc\) and the Global Monopole Charge \(0 \le \eta \le 0.006\). Jusufi [87] has taken the value of Global Monopole Charge \(\eta = 10^{-5}\) in his study of wormhole with Global Monopole Charge. From this small value of \(\eta \), we have considered a small range of Global Monopole Charge \(0 \le \eta \le 0.006\) to generate our systems. Figure  2 shows the exact behavior of shape function against the radial coordinate r, it is well-defined and positively increasing in nature after the throat \(r = r_{th} = 1 kpc\). The obtained shape function is less than the radial coordinate r for \(r > r_{th}\), clear from Fig. 3. Figure 4 indicates that the flare-out condition is satisfied by our indicated shape function and moreover \(b'(r_{th}) < 1\) for \(0 \le \eta \le 0.006\), clear from Fig. 5. So, based on the DM density profile (21), the qualitative features meet all the requirements for the existence of a wormhole and consequently, the reported shape function is perfectly well-fitted to form a wormhole geometry in the bulge region of the MWG. Note that, for \(\eta = 0\) the solution will associate with the Einstein gravity without Global Monopole Charge.

3.2 Null energy condition

Here, we are going to be primarily concerned with the null energy condition (NEC) to complete our discussion on the possible formation of wormhole. The violation of NEC is an indispensable condition to hold a wormhole like geometry by the matter content contained in wormhole. In GTR, the NEC is given as \(T_{\mu \nu } v^\mu v^\nu \ge 0\), \(n^\nu \) is a null vector, its explicit form is \(\rho (r) + \mathcal {P}_r(r)\ge 0\). So the NEC is violated if \(\rho (r) + \mathcal {P}_r(r) < 0\). Now, to compute the exact expression of radial pressure \(\mathcal {P}_r(r)\) from Eq. (19) we need to know redshit function f(r). So, to fix the exact expression of the radial pressure \(\mathcal { P}_r(r)\) and check the NEC we shall consider three different redshift functions.

Fig. 8
figure 8

\(\rho (r) + \mathcal {P}_r(r)\) is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, \tau = 2.5\) and \(r_{0} = 2~kpc\)

Full size image

3.2.1 Redshift function \(\Phi (r) = 0\)

The redshift function \(\Phi (r) = 0\) [88] is known as tidal force and being finite it avoids event horizon. According to M. Cataldo etc [89], there does not exits wormhole solution sustained everywhere by an isotropic perfect fluid corresponding to the tidal force redshift function and hence our assumption of anisotropic matter distribution is appropriate. On imposing the redshift function \(\Phi (r) = 0 \) and the shape function given in Eq. (22) in Eq. (19) we obtain the following explicit expression of radial pressure

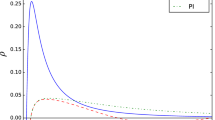
$$\begin{aligned} \mathcal {P}_r(r)=\frac{\rho _0}{\beta } F(r) \left( \frac{r_0}{r}\right) ^{\alpha }-\frac{A}{8 \pi r^3}+\frac{1}{3} \eta ^2 \left( \frac{3}{r^2}-1\right) \end{aligned}$$
(26)

Figure 6 ensures that \(\rho (r) + \mathcal {P}_r(r) < 0\) corresponding to the specific choice of parameters \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, r_{0} = 2~kpc\) and the Global Monopole Charge \(0 \le \eta \le 0.006\). So, our solution presenting DM content of the bulge violates NEC after the wormhole throat. This proves that the DM contained in the bulge gives fuel to sustain wormhole in the bulge region of the MWG. Moreover, it is clear from Fig. 7 that the Global Monopole Charge \(\eta \) reduces the probability of violation of NEC near the throat and hence our considered DM density profile and the Global Monopole Charge have the crucial effect on the violation of NEC.

3.2.2 Redshift function \(\Phi (r) = \frac{\tau }{r}\)

The redshift function \(\Phi (r) = \tau /r\) [88], \(\tau \) is non zero constnt, is always finite for \(r > 0\) i.e. it does not has any kind of event horizon after the throat radius of wormhole. Here, on the basis of this redshift function we obtain radial pressure from Eq. (19) as

$$\begin{aligned} \mathcal {P}_r(r)= & {} \frac{r_0^\alpha }{24 \pi \beta r^{4+\alpha }}\Big [24 \pi \rho _0 F(r) r^3 (r-2 \tau )+\beta \left( \frac{r}{r_0}\right) ^{\alpha }\nonumber \\&\times \big \{6 A \tau -3 r (A+2 \tau )-8 \pi \eta ^2 r^2 \left( r^2-2 \tau r-3\right) \big \}\Big ]\nonumber \\ \end{aligned}$$
(27)

Here, we also have \(\rho (r) + \mathcal {P}_r(r) < 0\), clear from Fig. 8 and hence the NEC is indeed violated by the wormhole containing DM candidate of the bulge. Consequently, the DM content supports wormhole structure. Here, the Global Monopole Charge \(\eta \) is also reducing the probability of violation of NEC near the throat (see Fig. 9).

Fig. 9
figure 9

NEC is shown at the radial distance \(r = 1.5~kpc\) with respect to the Global Monopole Charge \(\eta \) corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, \tau = 2.5\) and \(r_{0} = 2~kpc\)

Full size image
Fig. 10
figure 10

\(e^{2\Phi (r)}\) is plotted with respect to the radial coordinate r corresponding to the parameters \( C = 0.05, j = 1,~k = 1, ~\delta = 0.1\), and \(\gamma = 0.001\)

Full size image

3.2.3 Redshift Function \(\Phi (r)\) from the Flat Rotational Curve

One can know from the Refs. [90, 91] that for the circular stable geodesic motion in the equatorial plane the tangential velocity can be obtain from from the flat rotation curve as

$$\begin{aligned} v^{\phi }(r) = \sqrt{r\Phi ^\prime (r)} \end{aligned}$$
(28)

One can easily fit the flat rotational curve for DM on using Eq. (28). Rahaman et al. [75, 76] proposed a flat rotational curve profile in the region of the DM as

$$\begin{aligned} v^{\phi }(r)=\gamma (1-e^{-jr})+\beta r e^{-kr} \end{aligned}$$
(29)

where \(\gamma \), \(\delta \), k and j are positive parameters.

Fig. 11
figure 11

\(\rho (r) + \mathcal {P}_r(r)\) is plotted with respect to the radial coordinate r corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, C = 0.05,~ j = 1, ~k = 1, ~\delta = 0.1, ~\gamma = 0.001\) and \(r_{0} = 2~kpc\)

Full size image

Therefore the redshift function is obtained by imposing Eq. (29) in Eq. (28) as

$$\begin{aligned} \Phi (r)= & {} \gamma ^2\{ \ln (r)+2E[1,jr]-E[1,2jr]\}+C-\frac{\delta ^2e^{-2ir}}{2i }\nonumber \\&\times \left[ r+\frac{1}{2i}\right] -2\delta \gamma e^{-ir} \left[ \frac{1}{i}-\frac{1e^{-jr}}{(i+j) }\right] \end{aligned}$$
(30)

where E[x, y] is exponential integral function, defined in Eq. (25) and C is an integration constant. For the above redshift function (30), \(e^{2\Phi (r)}\) is depicted in Fig. 10. Similarly, for monitoring the NEC we shall compute the radial pressure from Eq. (19) using the above redshift function (30).

Now, Eq. (19) yields the explicit expression of radial pressure by using the redshift function (30) and the shape function, given in Eq. (22) as

$$\begin{aligned} \mathcal {P}_r(r)= & {} \frac{1}{24\pi r^3 k \beta } \bigg [24\pi r \eta ^2 k\beta -3k\beta A-8\pi r^3 k \chi _1(r)\nonumber \\&+2\delta e^{-2(j+k)r}\left( \frac{r_0}{r}\right) ^\alpha \bigg \{\chi _2(r)-2kr\gamma e^{(j+k)r} \nonumber \\&-r e^{2jr}(kr\delta -\delta -4k\gamma )\bigg \}\bigg \{24\rho _0 \pi r^3 F(r)\nonumber \\&-\beta (3(A-r)+8\pi r^3 \eta ^2)\left( \frac{r}{r_0}\right) ^\alpha \bigg \}\bigg ] \end{aligned}$$
(31)

whereas

$$\begin{aligned} \chi _1(r)= & {} \eta ^2 \beta -3\rho _0 F(r)\left( \frac{r_0}{r}\right) ^\alpha \end{aligned}$$
(32)
$$\begin{aligned} \chi _2(r)= & {} k\delta e^{2kr}(e^{2jr}-2e^{jr})+k\delta e^{2kr} \end{aligned}$$
(33)

Figure 11 evidently ensures that \(\rho (r) + \mathcal {P}_r (r)< 0\) i.e. the NEC is completely violated after the wormhole throat \(r_{th} = 1~ kpc\). Note that, here, we have taken following values of parameters \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5, ~\beta = 0.8, ~r_{th} = 1~kpc, C = 0.05, j = 1, k = 1, \delta = 0.1, \gamma = 0.001\) and \(r_{0} = 2~kpc\). So, the DM within the bulge sustains wormhole geometry nicely. Furthermore, the Global Monopole Charge has the same effect on NEC near the wormhole throat, clear from Fig. 12.

4 Average null energy condition violating matter

Here, we are willing to investigate how the total amount of averaged null energy condition (ANEC) violating matter in the spacetime of wormholes depends on the Global Monopole Charge \(\eta \). The total ANEC violating matter is quantified by the following integral [92]

$$\begin{aligned} I=\oint \{\rho (r)+\mathcal {P}_r(r)\}dV = 2\int _{r_{th}}^{\infty }4\pi r^2\{\rho (r)+\mathcal {P}_r(r)\}dr \end{aligned}$$
(34)

where, \(dV = r^2 \sin \theta dr d\theta d\phi \) and the factor 2 comes for the both mouths of wormhole.

Fig. 12
figure 12

NEC is shown at the radial distance \(r = 1.5~kpc\) with respect to the Global Monopole Charge \(\eta \) corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, C = 0.05,~ j = 1, ~k = 1, ~\delta = 0.1, ~\gamma = 0.001\) and \(r_{0} = 2~kpc\)

Full size image
Fig. 13
figure 13

The embedding diagram of z(r)

Full size image

The exact results of the above integral (34) can not be found explicitly for our solutions due to the presence of complicated forms of exponential and exponential integral functions within the solutions. It is obvious that the dependence of the integral (34) on \(\eta \) will follow the dependence of the factor \(r^2\{\rho (r)+\mathcal {P}_r(r)\}\) on \(\eta \) near the wormholes throat. For that reason, we will analyze the fact with respect to the factor \(r^2\{\rho (r)+\mathcal {P}_r(r)\}\). Now, interestingly, we obtain the same value of \(r^2\{\rho (r)+\mathcal {P}_r(r)\}\) for each of our wormhole solutions near the wormhole throat as

$$\begin{aligned} r^2\{\rho (r)+\mathcal {P}_r(r)\}|_{r \rightarrow r_{th}}= & {} \eta ^2-\frac{1}{8\pi }+\rho _0 r_{th}^2 \left( \frac{r_{0}}{r_{th}}\right) ^\alpha \nonumber \\&\times \exp \left[ -\left( \frac{r_{th}}{r_0}\right) ^\beta \right] \end{aligned}$$
(35)

The above result shows that it depends on the several parameters \(\rho _0,~r_0,~r_{th},~\alpha ,~\beta \) and the Global Monopole Charge \(\eta \). If we kept fixed the parameters \(\rho _0,~r_0,~r_{th},~\alpha ,~\beta \) then \(\eta \) plays a significant role in it and it will reduce for reducing values of \(\eta \). Consequently, the total amount of ANEC violating matter in the wormhole spacetime depends on \(\eta \) and can be reduced and minimized with reducing values of \(\eta \).

5 Embedding surface and proper radial distance of wormhole

The embedding surface of the wormhole is denoted by the function z(r) and given by the following differential equation [1]

$$\begin{aligned} \frac{dz(r)}{dr} = \pm \left( \frac{r}{b(r)}-1\right) ^{-\frac{1}{2}} \end{aligned}$$
(36)

It is noted that for the above equation dz(r)/dr does not converse at the throat of the wormhole as \(b(r_{th}) = r_{th}\) and it concludes that the embedding surface indeed becomes vertical at the wormhole throat. The differential equation (36) gives the following integral expression for the embedding surface z(r)

$$\begin{aligned} z(r) = \pm \int _{r_{th}^+}^r \left( \frac{r}{b(r)}-1\right) ^{-\frac{1}{2}} \end{aligned}$$
(37)
Fig. 14
figure 14

The diagram of proper radial length l(r)

Full size image

Also, the proper radial distance of wormhole is defined as

$$\begin{aligned} l(r) = \pm \int _{r_{th}^+}^r \left( 1-\frac{b(r)}{r}\right) ^{-\frac{1}{2}} \end{aligned}$$
(38)

where \(r_{th}^+\) is an arbitrary nearest distance of the throat from right hand side.

Now, one can see that our reported shape function given in Eq. (22) is complicated one due to the presence of exponential integral function E[x, y] in it. Therefore, we can not solve the above integrals provided in Eqs. (37) and (38) using the analytical technique. But to know the behavior of z(r) and l(r) we have performed the numerical technique on the integrals Eqs. (37) and (38) using the Mathematica software. Both the numerical integrations are done by fixing a particular value of lower limit \(r_{th}^+ = 1.1~ kpc\) and by changing the upper limit. The corresponding obtained values of z(r) and l(r) are provided in Table 1 for selected some upper limit of integration. The diagrams of embedding surface z(r) and radial proper distance l(r) of 4-dimensional wormhole have been depicted in Figs. 13 and 14, respectively. Note that, to draw the diagrams for z(r) and l(r) we have taken a very small step length of the integration. Now, if we rotted the embedding diagram of z(r) about the Z-axis then we get the full visualization picture of 4D wormhole. For our solution, the full visualization diagram of 4D wormhole is given in Fig. 15.

Fig. 15
figure 15

The full visual diagram of wormhole

Full size image

6 Matching to the external Schwarzschild solution

Matching concept is needed whenever wormhole is not asymptotically flat. For the asymptotical flat wormhole geometry \(b(r)/r\rightarrow 0\) and \(e^{2\Phi (r)}\) tends to unity as \(r\rightarrow \infty \). For the choice of the values of parameter \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc, r_{0} = 2~kpc\), we can see from the Fig. 3 that the b(r)/r tends to zero as \(r\rightarrow \infty \) for the zero Global Monopole Charge \(\eta \). More specifically, for those values of parameters we obtain the redshift function from Eq. (22) as \(b(r) = \frac{1}{r}[3.22628 - 0.177715 r^{2.5} E[-2.125, 0.574349 r^{0.8}]]\), which tends to zero as r tends to infinity(One can see using Mathematica software). Also, only for the first two choices of redshift functions \(e^{2\Phi (r)}\) tends to unity as \(r\rightarrow \infty \). So, only these two redshift functions associated with zero Global Monopole Charge provide asymptotically flat wormholes. But for positive values of \(\eta \), b(r)/r does not approach zero, clear from Fig. 3 and hence in this case wormhole is not asymptotically flat, also for third choice of \(\Phi (r)\) \(e^{2\Phi (r)}\) does not tend to unity as \(r\rightarrow \infty \) (see Fig. 10). The wormhole must, therefore, be cut off at some \(\mathcal {R}>r_s\), Schwarzschild radius and joined to the external Schwarzschild vacuum solution.

Now, let us consider the Schwarzschild line element

$$\begin{aligned} ds^2= & {} - \left( 1-\frac{2M}{r}\right) dt^2 +\left( 1-\frac{2M}{r}\right) ^{-1}dr^2\nonumber \\&+r^2(d\theta ^2 + \text {sin}^2\theta d\phi ^2), \end{aligned}$$
(39)

where M represents the mass of wormhole. Now, directly we get \(b(\mathcal {R})=2M\). Next, there is an arbitrary constant C in the expression of redshift function (30) and we have to choose the value of this constant C in such a way that \(\Phi (\mathcal {R})=\frac{1}{2}\ln (1-2M/\mathcal {R})\). This condition gives the value of C as

$$\begin{aligned} C= & {} \frac{1}{2}\ln (1-2M/\mathcal {R})+\frac{\delta ^2e^{-2i\mathcal {R}}}{2i }\left[ \mathcal {R}+\frac{1}{2i}\right] +2\delta \gamma \nonumber \\&\times e^{-i\mathcal {R}}\left[ \frac{1}{i}-\frac{1e^{-j\mathcal {R}}}{(i+j) }\right] -\gamma ^2\big \{ \ln (r)+2E[1,j\mathcal {R}]\nonumber \\&-E[1,2j\mathcal {R}]\big \} \end{aligned}$$
(40)

Then the wormhole representing line element becomes

$$\begin{aligned} ds^2= & {} - e^{2\Phi (r)}dt^2+\left( 1-\frac{b(r)}{r}\right) ^{-1}dr^2+r^2(d\theta ^2 \nonumber \\&+ \text {sin}^2\theta \,d\phi ^2), \quad \text {for}\quad r<\mathcal {R} \end{aligned}$$
(41)

and

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{b(\mathcal {R})}{r}\right) dt^2 +\left( 1-\frac{b(\mathcal {R})}{r}\right) ^{-1}dr^2\nonumber \\&+r^2(d\theta ^2 + \text {sin}^2\theta \,d\phi ^2), \quad \text {for}\quad r\ge \mathcal {R}. \end{aligned}$$
(42)
Fig. 16
figure 16

Two forces are plotted with respect to the radial coordinate r corresponding to the parameters \(\eta = 0.003\), \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\) and \(r_{0} = 2~kpc\)

Full size image
Fig. 17
figure 17

Three forces are plotted with respect to the radial coordinate r corresponding to the parameters \(\eta = 0.003, ~\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~ \beta = 0.8, ~r_{th} = 1~kpc\), \(r_{0} = 2~kpc\) along with \(\tau = 2.5\) and \(C = 0.05,~ j = 1, ~k = 1, ~\delta = 0.1, ~\gamma = 0.001\), respectively

Full size image

7 Equilibrium condition

The equilibrium position can be occurred by satisfying the generalized Tolman–Oppenheimer–Volkoff (TOV) equation. The generalized TOV equation is given as:

$$\begin{aligned} -\frac{M_g(r)(\rho +\mathcal {P}_r)}{r}e^{\{\nu (r)-\lambda (r)\}/ 2}-\frac{d\mathcal {P}_r}{dr}+\frac{2}{r}(\mathcal {P}_t-\mathcal {P}_r)=0, \end{aligned}$$
(43)

where \(\nu (r) = 2\Phi (r), ~\lambda (r) = -\log (1-b(r)/r)\) and \(M_g(r) \) stands for the effective gravitational mass from the throat of wormhole to some radius r and is obtained from Tolman-Whittaker formula and the Einstein field equations as:

$$\begin{aligned} M_g(r)=\frac{1}{2}re^{\{\lambda (r)-\nu (r)\}/2}~\nu '. \end{aligned}$$
(44)

The TOV equation (43) reduces on using the value of \(M_g(r)\) from Eq. (44) as

$$\begin{aligned} -\frac{\nu '(r)}{2}\{\rho (r)+\mathcal {P}_r(r)\}-\frac{d\mathcal {P}_r(r)}{dr}+\frac{2}{r}\{\mathcal {P}_t(r)-\mathcal {P}_r(r)\}=0. \end{aligned}$$
(45)

The above equation can also be represented as

$$\begin{aligned} F_g(r)+F_h(r)+F_a(r)=0, \end{aligned}$$
(46)

where \(F_g(r) = -\frac{\nu '(r)}{2}\{\rho (r)+\mathcal {P}_r(r)\}\) is termed gravitational force, \(F_h(r) = -\frac{d\mathcal {P}_r(r)}{dr}\), is termed as hydrostatics force and \(F_a(r) = \frac{2}{r}\{\mathcal {P}_t(r)-\mathcal {P}_r(r)\}\) is termed as anisotropic force. For the tidal force redshift function \(\Phi (r) = 0\), the gravitational force \(F_g(r)\) becomes zero and in this case, the equilibrium stage of the wormhole is achieved due to the combined effect of hydrostatic force and anisotropic force (see Fig. 16). Figure 17 ensures that the systems corresponding to the redshift functions \(\Phi (r) = \tau /r\) and obtained from flat rotational curve are balanced by the simultaneous action of \(F_g(r)\), \(F_h(r)\) and \(F_a(r)\). It is noted that, in the case of redshift functions obtained from the flat ration curve, the gravitational force \(F_g(r)\) is too small (see Fig. 17). Here, one can say that the anisotropic force within the anisotropic medium plays as a catalyst to achieve the equilibrium for each of reported wormhole systems.

Table 1 Some specific numerical values of the embedding surface z(r) and proper radial distance l(r) corresponding to the parameters \(\rho _0 = 0.004~kpc^{-2},~\alpha = 0.5,~ \beta = 0.8, ~r_{th}^+ = 1.1~kpc, r_{0} = 2~kpc\) along with \(\eta \) = 0, 0.003 and 0.006, respectively
Full size table

8 Discussions and conclusion

In this article, we have manifested the existence of wormhole in the bulge of the MWG on the basis of dark DM density profile and Global Monopole Charge. As have mentioned in introduction part that the possible existence wormholes in the galactic halo region has already been successfully discussed on the basis the NFW, Universal Rotation Curve, Isothermal and Void density profiles. In our study, we have considered an observationally motivated DM density profile of the bulge followed from MacMillan [83, 84] in the following form

$$\begin{aligned} \rho (r)=\rho _0 \left( \frac{r_0}{r}\right) ^\alpha \exp \left[ -\left( \frac{r}{r_0}\right) ^\beta \right] \end{aligned}$$
(47)

The behavior of this density profile is shown in Fig. 1 corresponding to the suitable values of parameters \(\rho _0 = 004~kpc^{-2}, ~ \alpha = 0.5, r_0 = 2 (kpc)\) and \(0.2 \le \beta \le 1\), which shows that this profile is positively decreasing against the radial coordinate r. The characteristic of our reported shape function corresponding to the above density profile is displayed in Figs. 2, 3, 4 and 5. Figure 2 ensures that the shape function positive and incresing in behavior while Fig. 3 indicates that the shape function is less than the radial coordinate r after the wormhole throat. Moreover, the shape function satisfies the flare-out condition, clear from Figs. 4 and 5. Therefore, our presenting shape function satisfies all the fundamental criterions to hold wormhole like geometry. It is well-known that the solution of Einstein field equations would sustain wormhole by violating of the null energy condition(NEC). Here, we have checked the NEC by considering three different redshift functions, a tidal force, a rational redshift functions and the redshift function obtained from the flat rotational curve. One can see that \(e^{\Phi (r)}\)s are finite for the first two choices of redshift functions and for third choice of redshift function of \(e^\Phi (r)\) is demonstrated in Fig. 10, which is regular for \(r \ge r_{th}\). Therefore, all these redshift functions fulfil the condition to present the traversable wormholes. For each of these redshift functions respective model violates the NEC(see Figs. 6, 8,  11). Consequently, the bulge DM content of MWG plays as the suitable candidate to harbor wormhole. Moreover, for each of respective considered redshift function, the probability of violation of NEC near the throat reduces whenever the Global Monopole Charge increases (see Figs. 7, 9 and 12) and hence our considered DM density profile and the Global Monopole Charge have the crucial effect on the violation of NEC. The total reducing amount of ANEC violating matter in the wormhole spacetime depends on the reducing values of Global Monopole Charge \(\eta \). The values of the embedding surface z(r) and proper radial distance l(r) are calculated by applying numerical technique corresponding to \(\rho _0 = 0.004~kpc^{-2},~ \alpha = 0.5,~\beta = 0.8, ~r_{th}^+ = 1.1~kpc, r_{0} = 2~kpc\) along with \(\eta \) = 0, 0.003 and 0.006, respectively and provided in Table 1. The sketches for z(r) and l(r) are shown in Figs. 13 and 14, respectively corresponding to \(\eta \) = 0, and 0.006. The full visualization diagram is obtained by rotating z(r) about the Z-axis, for our model it is shown in Fig. 15. The reported shape function satisfies all the essential conditions mentioned in Sect. 2 to present the traversable wormhole (see Figs. 2, 3, 4, 5). One can see that the first two choices of redshift functions are definitely well-defined and regular for \(r \ge r_{th}\) and third redshift function is also regular and well-defined, shown in Fig. 10. Consequently, the wormholes are traversable in nature. We want to mention here that for the first two choices of redshift functions our solutions present asymptotically flat wormholes on the absence of Global Monopole Charge \(\eta \) while positive \(\eta \) i.e. the presence of Global Monopole Charge provides non asymptotically flat wormhole like geometry (see Fig. 3). So, for our model, the Global Monopole Charge \(\eta \) plays an important role on the asymptotical flatness of wormhole. Moreover, the non asymptotically flat wormhole is matched with the external Schwarzschild vacuum solution at the certain radial distance \(r = \mathcal {R} > r_s\), Schwarzschild radius. The equilibrium positions are also analyzed for the reported solutions. The gravitational force \(F_g(r)\) becomes zero for the tidal force redshift function \(\Phi (r) = 0\), and in this case, the equilibrium stage of the wormhole is maintained due to the combined effect of hydrostatic force and anisotropic force, clear from Fig. 16. Figure 17 shows that the wormhole structures corresponding to the redshift functions \(\Phi (r) = \tau /r\) and obtained from flat rotational curve are balanced by the simultaneous action of three foreces \(F_g(r)\), \(F_h(r)\) and \(F_a(r)\). Moreover, for the redshift functions obtained from the flat ration curve, the gravitational force \(F_g(r)\) becomes too small (see Fig. 17). Here, one can see that the anisotropic force within the anisotropic medium plays as a catalyst to achieve the equilibrium for each of the wormhole structure. Recently, several proposals are suggested for observing wormholes. Event Horizon Telescope (EHT) has observed the black hole (BH) shadow that has opened a new direction of the tests of gravity in the strong field regime and that includes the probes of violations of the no-hair theorem [93]. It is argued that some black hole solutions was found to effectively mimic a wormhole and the BH shadow probes the geometry of space-time in the vicinity of the event horizon. The search of the iron K\(\alpha \) line profiles emitted from probable accretion disks nearby the traversable wormholes (using X-ray reflection spectroscopy) may a possible proof of the presence of astrophysical wormholes in active galactic nuclei [94]. It is known that a traversable wormhole easily connects two different spacetimes. De-Chang Dai et al. [95] proposed that the objects circulating in a neighborhood of a wormhole in one space should affect the objects propagating in the other space. In this way, wormholes may be observed.

Finally, we can say that our solution seems entirely possible existence of wormholes in the bulge of the Milky Way galaxy. So, our study may inspire the scientific community to search observational evidence of the presence of wormhole in the Milky Way bulge region.