1 Introduction

As an interdisciplinary area of general relativity, quantum mechanics, thermodynamics and statistical physics, particle physics and string theory, black hole physics plays a very important role in modern physics. The investigation of the thermal properties and the internal microstructure of black holes has always been one of the topics of interest to theoretical physicists. Recently, based on the study of the thermodynamic properties of black holes, some researchers have adopted Boltzmann’s profound idea, i.e., a black hole can change its temperature by absorbing and emitting matter. An object with a temperature has a microstructure. According to this view, the literature [1,2,3] proposes that black holes are also composed of valid molecules. They think that just as our rooms are filled with air molecules, the interior of a black hole is filled with a kind of “black hole molecule”. These black hole molecules, of course, give the number of microscopic states of a black hole in a statistical physical sense, and hence the entropy of a black hole. They believe that this internal entropy is equivalent to the “Bekenstein–Hawking entropy” of the black hole horizon, and that the black hole molecules themselves carry microscopic degrees of freedom of the black hole’s entropy. Based on this hypothesis, the concept of molecular density of black holes is introduced to obtain the phase transition of black holes. It is given by

$$\begin{aligned} m=\frac{1}{v} = \frac{1}{2l_\mathrm{p}^2 r_ +}, \end{aligned}$$
(1.1)

where \(l_\mathrm{p} \) is the Planck length, \(l_\mathrm{p} = \sqrt{\hbar G / c^3}\). One introduces \(m\equiv (m_{\mathrm{SBH}} - m_{\mathrm{LBH}} ) / m_\mathrm{c} \) with the aid of the critical molecules number density \(m_\mathrm{c} = 1 / (2\sqrt{6}Q)\). According to the research, the order parameter has a nonzero value when the system passes through the first-order phase transition of a small black hole and a large one. The value of the order parameter gradually decreases as the temperature increases, and it becomes zero at the critical point. To some extent, the microstructure of small black holes and large black holes will converge at the critical point. It is found that the variation of the molecular density of the black hole is the internal cause of the black hole phase transition. By studying the “black hole molecules” inside a black hole, their collective behavior can be compared to that of a fluid. In other words, these ‘black hole molecules’ are like a “fluid” inside the black hole. When a black hole is at a certain temperature, given the pressure of these black hole molecules (the cosmological constant), the black hole can undergo a phase transition, known as a “big black hole” and “small black hole” phase transition, in which the size of the black hole can change suddenly. For example, a large black hole can suddenly shrink in half its size and become a small black hole.

From the point of view of mathematics, one uses string theory and supersymmetry theory to explain the microstructure of black holes. From the perspective of thermodynamics, the hypothesis of “black hole molecules” and “space-time atoms” has been proposed to explore the microscopic behavior of black holes [4]. These two aspects of research have made some progress. The microscopic behavior of the thermal stable AdS black hole was studied completely from the thermodynamic point of view by Ruppeiner’s thermodynamic geometry method, combining the “black hole molecule” hypothesis and the concept of microscopic particle number density in [5,6,7,8], and one has given a natural explanation for the microscopic behavior of the black hole. It is pointed out that the interaction between black hole molecules in the black hole is mainly attractive, and the description of the molecular potential of the “black hole” was proposed for the first time. In addition, based on the proposed description of the molecular potential, the correction of the molecular potential to the equation of state of the black hole is calculated and the rationality of the correction term is analyzed.

Recent studies have shown that the RN-AdS black hole has similar thermodynamic critical characteristics to a van der Waals (vdW) system. The cosmological constant is interpreted as the pressure in the thermodynamic system [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. With these issues, the thermodynamic characteristics and critical phenomena of AdS and dS black holes are studied, and the first-order and second-order phase transitions of RN-AdS black holes are obtained [8, 9, 60]. However, a Schwarzschild–de Sitter black hole without charge has no phase transition like a vdW system [61]. Therefore, the charge of the black hole plays a key role in the phase transition, and the effect of the black hole charge on the phase transition must be considered in the microstructure theory of the black hole.

In the case of a vdW system, the microstructure of the system changes as the fluid undergoes a liquid–gas phase transition, and thus the physical properties of the system change [1,2,3]. It is well known from the study of the black hole system that when the system meets the requirement of thermodynamic equilibrium stability in isothermal or isobaric process, the P–V curve or T–S curve describing the change of the system is discontinuous, and the system has the latent heat of the phase transition when it crosses the two-phase coexistence curve. The system has different physical properties in the two phases and thus it has a different microstructure in the different phases. In the literature [62], the Maxwell equal-area law was used to discuss the critical behavior of the RN-AdS black hole, and it was found that the generation of the phase transition of the RN-AdS black hole was mainly determined by the electric potential at the event horizon of the black hole, rather than simply being determined by the size of the black hole. Recent observations showed that the dark energy is prevailing in our universe [64, 65]. The equation of state of dark energy approaches the cosmological constant or vacuum energy expressions [66]; however, dynamical dark energy is also possible [67], and quintessence could affect the black hole space-time [68].

It is showed that, in the presence of quintessence, the charged AdS black hole exhibits a small–large black hole phase transition, which is similar to the liquid–gas phase transition of vdW fluid. Near the critical point, the heat capacity will diverge. It also shares the critical phenomena and scaling laws [69, 71]. For we have the dark energy corresponding to the state parameter \(\alpha \) and the state equation \(p =\omega \rho \) with the corresponding parameter \(\omega \) in the charged AdS black holes with a cloud of strings and quintessence (charged AdSQ black hole). So, the study of the critical behavior of a charged AdSQ black hole must address the effect of \(\alpha \) and \(\omega \) on the phase transition. In order to make the conclusion universal, two groups of independent variables, P–V and T–S, were selected to discuss the critical behavior of the charged AdSQ black hole. The microscopic interpretation of the black hole phase transition and the critical exponential thermodynamic geometry method, as a unique perspective, played an important role in the study of the black hole phase transition. Ruppeiner’s clear physical picture makes it widely used [6,7,8, 72,73,74,75,76,77, 79, 80].

This paper is organized as follows. In Sect. 2, we give a brief review for the thermodynamic quantity of a charged AdSQ black hole. In Sect. 3, we choose different conjugate variables and use Maxwell’s equal-area law to study the phase transition of the charged AdSQ black hole, which is not a simple phase transition between a small black hole and a large black hole. The first-order phase transition of a black hole is a mutation for the potential \(\phi = \frac{Q}{r_ +}\) and the quintessence potential \(\Theta =\frac{3\alpha }{r_+^{3\omega +1}}\). On the other hand, this reflects that black holes produce first-order liquid–vapor phase transitions similar to vdW systems and have coexistence zones. Because the charged AdSQ black hole molecule is affected by an electric potential (electric field) and a quintessence potential, the black hole molecule produces orientation polarization and displacement polarization, which makes the black hole molecule have a certain orientation. Under the dual action of the quintessence potential and thermal motion, the orientation degree of the black hole molecules is different. The orientation degree of the black hole molecules determines the phase of the black hole. Guided by this thought, in Sect. 4, we analyze the influence of each parameter on the latent heat of the phase transition when the first-order phase transition occurred in charged AdSQ black hole. In Sect. 5, the electric potential and quintessence potential were selected as the order parameters for studying the black hole phase transition, and Landau continuous phase transition theory was used to analyze the continuous phase transition of the charged AdSQ black hole. In Sect. 6, we try to understand some properties of the microstructure of the black hole molecules by analyzing the influence of the value of x under different parameters (that is, taking different temperatures) on R. Section 7 is a summary. For simplicity, we adopt the units \(\hbar =c=k_\mathrm{B}=G=1\).

2 Charged AdS black hole

In the presence of quintessence, the line element of a charged AdS black hole is [63,64,65,66,67,68,69,70,71]

$$\begin{aligned} \mathrm{d}s^2 = - f(r)\mathrm{d}t^2 + f^{ - 1}\mathrm{d}r^2 + r^2\mathrm{d}\Omega _2^2 , \end{aligned}$$
(2.1)

where the metric function is given by

$$\begin{aligned} f(r) = 1 - \frac{2M}{r} + \frac{Q^2}{r^2} - \frac{\Lambda r^2}{3} - \alpha r^{ - 3\omega - 1}. \end{aligned}$$
(2.2)

Here the parameters M, Q and \(\Lambda \) are, respectively, related to the black hole mass, charge and cosmological constant. \(\omega \) is the state parameter for quintessence matter under the state equation \(p = \omega \rho \). If \(\omega \) satisfies \(-1<\omega <-1/3\), the quintessence will give the universe accelerated expansion. The parameter \(\alpha \) is related to the energy density of quintessence matter.

In the extended phase space, the cosmological constant is treated as a thermodynamic pressure,

$$\begin{aligned} P = - \frac{\Lambda }{8\pi }. \end{aligned}$$
(2.3)

Solving the equation \(f(r_+)=0\), one can obtain the event horizon radius \(r_+\), with which the mass of the black hole mass can be expressed as

$$\begin{aligned} M=\frac{r_ + }{2} + \frac{Q^2}{2r_ + } + \frac{4\pi P}{3}r_ + ^3 - \frac{\alpha }{2}r_ + ^{ - 3\omega }. \end{aligned}$$
(2.4)

According to the Bekenstein–Hawking entropy–area relation, the black hole entropy is

$$\begin{aligned} S = \frac{A}{4} = \pi r_ + ^2 . \end{aligned}$$
(2.5)

Treating the state parameter \(\alpha \) as a new thermodynamic quantity, the first law of the black hole is [69, 71]

$$\begin{aligned} \mathrm{d}M = T\mathrm{d}S + \phi \mathrm{d}Q + V\mathrm{d}P + \Theta \mathrm{d}\alpha . \end{aligned}$$
(2.6)

Employing it, we can obtain the thermodynamic quantities

$$\begin{aligned} T= & {} \frac{f'(r_ + )}{4\pi } = \frac{1}{4\pi r_ + }\left( {1 - \frac{Q^2}{r_ + ^2 } + 8\pi \mathrm{Pr}_ + ^2 + 3\omega \alpha r_ + ^{ - 3\omega - 1} } \right) , \nonumber \\ \phi= & {} \frac{Q}{r_ + }, \quad V = \frac{4}{3}\pi r_ + ^3 , \quad \Theta = - \frac{1}{2}r_ + ^{ - 3\omega } . \end{aligned}$$
(2.7)

It has the same critical behavior as that of the vdW fluid. Especially, when the parameter \(\omega =-2/3\), the analytical critical point can be obtained [69],

$$\begin{aligned} r_ + ^c = \sqrt{6} Q, \quad T_\mathrm{c} = \frac{\sqrt{6} }{18\pi Q} - \frac{\alpha }{2\pi }, \quad P_\mathrm{c} = \frac{1}{96\pi Q^2}. \end{aligned}$$
(2.8)

3 The equal-area law of the charged AdSQ black hole in extended phase space

Keeping Q, \(\alpha \) and \(\omega \) of the charged AdSQ black hole as constants, for Eq. (2.7), the equation of states of the charged AdSQ black hole is analogous to the simple system of the general thermodynamics system. The equation of states can be written in the form of \(f(T,P,V)=0\). First, we use the Maxwell equal-area law to study the condition of the phase transition occurs with Q, \(\alpha \) and \(\omega \) fixed and with the differential conjugate variables P–V and T–S.

3.1 The construction of equal-area law in P–V diagram

Taking Q, \(\alpha \) and \(\omega \) of the charged AdSQ black hole as constants, the temperature \(T_0\) (\(T_0 \le T_\mathrm{c} )\), \(T_\mathrm{c} \) is critical temperature. The horizontal axes of the two-phase coexistence region are \(V_2\) and \(V_1\), and the vertical axis is \(P_0\), which depends on the radius \(r_+\) of the black hole horizon. We can obtain the following expression by Maxwell’s equal-area laws:

$$\begin{aligned} P_0 (V_2 - V_1 ) = \int \limits _{V_1 }^{V_2 } {P\mathrm{d}V}=\int \limits _{r_1 }^{r_2 } {4 P(r)\pi r^2 \mathrm{d}r}. \end{aligned}$$
(3.1)

From Eq. (3.1), we can obtain

$$\begin{aligned} P_0= & {} \frac{T_0 }{2r_1 } - \frac{1}{8\pi r_1^2 } + \frac{Q^2}{8\pi r_1^4 } - \frac{3\omega \alpha }{8\pi }r_1^{ - 3\omega - 3} , \quad \nonumber \\ P_0= & {} \frac{T_0 }{2r_2 } - \frac{1}{8\pi r_2^2 } + \frac{Q^2}{8\pi r_2^4 } - \frac{3\omega \alpha }{8\pi }r_2^{ - 3\omega - 3}, \end{aligned}$$
(3.2)
$$\begin{aligned} 2P_0= & {} \frac{3T_0 (1 + x)}{2r_2 (1 + x + x^2)} - \frac{3}{4\pi r_2^2 (1 + x + x^2)} \nonumber \\&+ \frac{3Q^2}{4\pi r_2^4 x(1 + x + x^2)} - \frac{3\alpha (1 - x^{3\omega })}{4\pi r_2^{3\omega + 3} x^{3\omega }(1 - x^3)},\nonumber \\ \end{aligned}$$
(3.3)

where \(x = r_1 / r_2 \). From Eq. (3.2), we can obtain

$$\begin{aligned} 0= & {} T_0 - \frac{1}{4\pi r_2 x}(1 + x) + \frac{Q^2}{4\pi r_2^3 x^3}(1 + x^2)(1 + x) \nonumber \\&- \frac{3\omega \alpha (1 - x^{3\omega + 3})}{4\pi r_2^{3\omega + 2} x^{3\omega + 2}(1 - x)}, \end{aligned}$$
(3.4)
$$\begin{aligned} 2P_0= & {} \frac{T_0 }{2r_2 x}(1 + x) - \frac{1}{8\pi r_2^2 x^2}(1 + x^2) \nonumber \\&+ \frac{Q^2}{8\pi r_2^4 x^4}(1 + x^4) - \frac{3\omega \alpha (1 + x^{3\omega + 3})}{8\pi r_2^{3\omega + 3} x^{3\omega + 3}}. \end{aligned}$$
(3.5)

From Eqs. (3.3) and (3.5), we can obtain

$$\begin{aligned} \frac{1}{4\pi r_2 x}= & {} \frac{T_0 (1 + x)(1 - x)^2}{(1 + x - 4x^2 + x^3 + x^4)} \nonumber \\&+ \frac{Q^2[(1 + x^4)(1 + x + x^2) - 6x^3]}{4\pi r_2^3 x^3(1 + x - 4x^2 + x^3 + x^4)}\nonumber \\&- \frac{3\alpha \left[ {\omega (1 + x^{3\omega + 3})(1 - x^3) - 2x^3(1 - x^{3\omega })} \right] }{4\pi r_2^{3\omega + 2} x^{3\omega + 2}(1 - x)(1 + x - 4x^2 + x^3 + x^4)}.\nonumber \\ \end{aligned}$$
(3.6)

Form Eq. (3.4), we obtain

$$\begin{aligned} T_0= & {} \frac{(1 + x)}{4\pi r_2 x} - \frac{Q^2}{4\pi r_2^3 x^3}(1 + x)(1 + x^2) \nonumber \\&+ \frac{3\omega \alpha (1 - x^{3\omega + 3})}{4\pi r_2^{3\omega + 2} x^{3\omega + 2}(1 - x)}. \end{aligned}$$
(3.7)

Substituting Eq. (3.7) into (3.6), we get

$$\begin{aligned} r_2^2= & {} \frac{Q^2}{x^2}\frac{(1 + 2x - 6x^2 + 2x^3 + x^4)}{(1 - x)^2} \nonumber \\&+ \frac{3\alpha }{r_2^{3\omega - 1} x^{3\omega + 2}(1 - x)^3}\left[ \omega (1 - x^{3\omega + 3})(1 - x^2)(1 - x) \right. \nonumber \\&\left. - \omega (1 + x^{3\omega + 3})(1 - x^3) + 2x^3(1 - x^{3\omega }) \right] \nonumber \\= & {} Q^2f_1 (x) + \frac{3\alpha }{r_2^{3\omega - 1} }f_2 (x,\omega )\nonumber \\= & {} Q^2f_1 (x) - r_2^2\Theta _2 f_2(x,\omega ), \end{aligned}$$
(3.8)

where \(f_1 (x) = \frac{(1 + 4x + x^2)}{x^2}\), the quintessence potential of the black hole horizon \(\Theta _2 = \frac{3\alpha }{r_2^{3\omega + 1} }\),

$$\begin{aligned} f_2 (x,\omega ) = \frac{\omega (1 - x^{3\omega + 3})(1 - x^2)(1 - x) - \omega (1 + x^{3\omega + 3})(1 - x^3) + 2x^3(1 - x^{3\omega })}{x^{3\omega + 2}(1 - x)^3}. \end{aligned}$$

When \(\omega = - 2 / 3\), \(_{ }f_2 (x, - 2 / 3) = 0\), Eq. (3.8) can be written as \(r_2^2 = \frac{Q^2}{x^2}(1 + 4x + x^2) = Q^2f_1 (x)\), this result being identical with the one of the RN-AdS black hole [62]. When \(\omega \ne - 2 / 3\), \(r_1 = r_2 = r_\mathrm{c}\), from Eq. (3.8) we can find that the radius of the horizon \(r_\mathrm{c}\) of the critical point satisfies

$$\begin{aligned} r_\mathrm{c}^2= & {} 6Q^2 - \frac{9\omega \alpha }{2r_\mathrm{c}^{3\omega - 1} }(\omega + 1)(3\omega + 2) \\= & {} 6Q^2 + \frac{3r_\mathrm{c}^2 }{4\pi }B_\mathrm{c} (\omega + 1)(3\omega + 2), \end{aligned}$$

so

$$\begin{aligned} \frac{1}{6}= & {} \frac{Q^2}{r_\mathrm{c}^2 } + \frac{\rho _\mathrm{c} A_\mathrm{c} }{8\pi }(\omega + 1)(3\omega + 2) \nonumber \\= & {} \phi _\mathrm{c}^2 + \frac{B_\mathrm{c} }{8\pi }(\omega + 1)(3\omega + 2), \end{aligned}$$
(3.9)

where \(A_\mathrm{c} = 4\pi r_\mathrm{c}^2 \) is the area of the critical horizons, \(\rho _\mathrm{c} = - \frac{3\omega \alpha }{2r_\mathrm{c}^{3(\omega + 1)} }\) is the density of quintessence of the critical horizons, \(B_\mathrm{c} = \rho _\mathrm{c} A_\mathrm{c} = - \frac{6\omega \alpha \pi }{r_\mathrm{c}^{3\omega + 1}}\) is the quintessence of the unit thickness of the black hole horizon, \(\phi _\mathrm{c}\) is the charged potential of the critical horizon, \(r_\mathrm{c} \) is the radius of the horizon.

When \(B_\mathrm{c}\) and \(\omega \) is given, from Eq. (3.9) we can obtain \(\phi _\mathrm{c}\). When the charged Q is given, from \(\phi _\mathrm{c}\) we can get the critical radius \(r_\mathrm{c}\). According to Eq. (3.9), when the parameter \(\omega \) was set, there is a second phase transition for the charged AdSQ black hole. The sum \(B_\mathrm{c}\) of the electric potential \(\phi _\mathrm{c}\) and quintessence on the event horizon of the charged AdSQ black hole is a constant. Therefore, the position of the second-order phase transition point of the black hole is determined by the electric potential \(\phi _\mathrm{c}\) at the event horizon of the black hole and the sum of quintessence potential per unit thickness on the event horizon of the black hole. When \(\omega =-2/3\), the second phase transition position of the charged AdSQ black hole is only related to the electric potential, which is the same as a charged AdS black hole [62].

When \(x \rightarrow 1\), from Eq. (3.7) we can obtain the critical temperature \(T_\mathrm{c} \), which satisfies

$$\begin{aligned} T_\mathrm{c}= & {} \frac{1}{3\pi r_\mathrm{c} } - \frac{3\omega \alpha (3\omega - 1)(\omega + 1)}{4\pi r_\mathrm{c}^{3\omega + 2} } \nonumber \\= & {} \frac{1}{3\pi r_\mathrm{c} }\left( {1 + \frac{3B_\mathrm{c} (3\omega - 1)(\omega + 1)}{8\pi }} \right) . \end{aligned}$$
(3.10)

When \(x \rightarrow 1\), from Eq. (3.3) we can obtain the critical pressure \(P_\mathrm{c} \), which satisfies

$$\begin{aligned} P_\mathrm{c}= & {} \frac{1}{6\pi r_\mathrm{c}^2 } + \frac{Q^2}{8\pi r_\mathrm{c}^4 } - \frac{3\omega ^2\alpha (3\omega + 2)}{8\pi r_\mathrm{c}^{3\omega + 3} } \nonumber \\= & {} \frac{1}{6\pi r_\mathrm{c}^2 }\left( {1 + \frac{3}{4}\phi _\mathrm{c}^2 + \frac{3\omega B_\mathrm{c} (3\omega + 2)}{8\pi }} \right) . \end{aligned}$$
(3.11)
Fig. 1
figure 1

The simulated phase transition and the boundary of a two-phase coexistence on the base of isotherms in the P–V diagram for charged anti-de Sitter black holes. The temperature of isotherms decreases from top to bottom. The green line is the critical isotherm

Full size image

When \(\omega = -2/3 \), the critical position \(r_\mathrm{c}\), the critical temperature \(T_\mathrm{c}\) and the critical pressure return to the well-known values of the conclusion in [34, 69, 71]. Substituting Eq. (3.8) into Eq. (3.7), we get

$$\begin{aligned} T_0= & {} \frac{(1 + x)}{\pi r_2 x^2f_1 (x)} + \frac{3\alpha }{4\pi xr_2^{3\omega + 2} }\left[ \frac{(1 + x)(1 + x^2)f_2 (x,\omega )}{1 + 4x + x^2} \right. \nonumber \\&\left. + \frac{\omega (1 - x^{3\omega + 3})}{x^{3\omega + 1}(1 - x)} \right] . \end{aligned}$$
(3.12)

Taking \(T_0 = \chi T_\mathrm{c} = \frac{\chi }{3\pi r_\mathrm{c} } - \chi \frac{3\omega \alpha (3\omega - 1)(\omega + 1)}{4\pi r_\mathrm{c}^{3\omega + 2} }\), with \(0<\chi \le 1\), and substituting it into Eq. (3.12), we can obtain

$$\begin{aligned}&\frac{\chi }{3r_\mathrm{c} }\left( {1 + \frac{3B_\mathrm{c} (3\omega - 1)(\omega + 1)}{8\pi }} \right) = \frac{(1 + x)}{r_2 x^2f_1 (x)} \nonumber \\&\quad - \frac{B_\mathrm{c} r_\mathrm{c}^{3\omega + 1} }{8\pi \omega xr_2^{3\omega + 2} }\left[ \frac{(1 + x)(1 + x^2)f_2 (x,\omega )}{1 + 4x + x^2} \right. \nonumber \\&\quad \left. + \frac{\omega (1 - x^{3\omega + 3})}{x^{3\omega + 1}(1 - x)} \right] . \end{aligned}$$
(3.13)

For given \(\chi \), \(B_\mathrm{c}\), \(\omega \) and Q, substituting Eq. (3.8) into Eq. (3.13), we can obtain the value of x at a certain temperature. Substituting the obtained value x into Eq. (3.8), we can get \(r_2\), and we get \(r_1\) from \(r_1 = x r_2\).

From

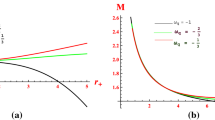
$$\begin{aligned} P = \frac{\chi T_\mathrm{c} }{2r_ + } - \frac{1}{8\pi r_ + ^2 } + \frac{Q^2}{8\pi r_ + ^4 } + \frac{B_\mathrm{c} r_\mathrm{c}^{3\omega + 1} }{16\pi ^2}r_ + ^{ - 3\omega - 3} , \end{aligned}$$
(3.14)

we can give the P–V graph for the temperature \(T_0 = \chi T_\mathrm{c} \), and constant Q, \(B_\mathrm{c}\) and \(\omega \ne -2/3\) in Fig. 1. The horizontal line in Fig. 1 is the region where the two phases coexist, and the intersection point of the horizontal line and the curve is the position of the first-order phase transition point of the black hole. To show the effect of the parameters \(B_\mathrm{c}\) and \(\omega \) on the phase transition point, at the same temperature, we draw the P–V curves of different \(B_\mathrm{c}\) and \(\omega \) in Fig. 2. As shown in Fig. 2, the pressure for the phase transition point increases, and the coexistence zone of the two phases decreases with the value of \(B_\mathrm{c}\) decrease at the same black hole temperature. The pressure for the phase transition point increases and the coexistence zone of the two phase decreases as the value of \(\omega \) decreases at the same black hole temperature.

Fig. 2
figure 2

The simulated phase transition and the boundary of a two-phase coexistence on the base of isotherms in the P–V diagram for charged anti-de Sitter black holes with differential \(B_\mathrm{c} \) and \(\omega \). The left figure shows \(Q = 1,\omega = - 1 / 2\), the right figure \(Q = 1,B_\mathrm{c} = 0.1\)

Full size image

3.2 The construction of equal-area law in T–S diagram

Taking the invariable cosmological constant l, the horizontal axes of the two-phase coexistence region are \(S_2\) and \(S_1\), respectively. The vertical axis is \(T_0 (T_0 \le T_\mathrm{c} )\) which depends on the radius \(r_+\) of the black hole event horizon. We can obtain by Maxwell’s equal-area laws

$$\begin{aligned} T_0 (S_2 - S_1 )= & {} \int \limits _{S_1 }^{S_2 } {T\mathrm{d}S_ + } \nonumber \\= & {} \int \limits _{r_1 }^{r_2 } {\frac{1}{2}\left( {1 + \frac{3r_ + ^2 }{l^2} - \frac{Q^2}{r_ + ^2 } + 3\omega \alpha r_ + ^{ - 3\omega - 1} } \right) \mathrm{d}r_ + } , \nonumber \\ \end{aligned}$$
(3.15)
$$\begin{aligned} T_0= & {} \frac{1}{4\pi r_2 }\left( {1 + \frac{3r_2^2 }{l^2} - \frac{Q^2}{r_2^2 } + 3\omega \alpha r_2^{ - 3\omega - 1} } \right) , \quad \nonumber \\ T_0= & {} \frac{1}{4\pi r_1 }\left( {1 + \frac{3r_1^2 }{l^2} - \frac{Q^2}{r_1^2 } + 3\omega \alpha r_1^{ - 3\omega - 1} } \right) .\nonumber \\ \end{aligned}$$
(3.16)

From Eq. (3.15) we can obtain

$$\begin{aligned} 2\pi T_0 r_2^2 (1 - x^2)= & {} r_2 (1 - x) + \frac{r_2^3 }{l^2}(1 - x^3)\nonumber \\&- Q^2\frac{1 - x}{r_2 x} + \frac{\alpha (1 - x^{3\omega })}{r_2^{3\omega } x^{3\omega * }}. \end{aligned}$$
(3.17)

From Eq. (3.16) we get

$$\begin{aligned} 0= & {} - \frac{1 - x}{r_2 x} + \frac{3r_2 }{l^2}(1 - x) + \frac{Q^2}{r_2^3 x^3}(1 - x^3) \nonumber \\&- \frac{3\omega \alpha (1 - x^{3\omega + 2})}{r_2^{3\omega + 2} x^{3\omega + 2}}, \end{aligned}$$
(3.18)
$$\begin{aligned} 8\pi T_0= & {} \frac{1 + x}{r_2 x} + \frac{3}{l^2}r_2 (1 + x) - \frac{Q^2}{r_2^3 x^3}(1 + x^3) \nonumber \\&+ \frac{3\omega \alpha (1 + x^{3\omega + 2})}{r_2^{3\omega + 2} x^{3\omega + 2}}. \end{aligned}$$
(3.19)

From Eqs. (3.17), (3.18) and (3.19) we can obtain

$$\begin{aligned} \frac{r_2^2 }{l^2}x= & {} 1 - \frac{Q^2(1 + x - 4x^2 + x^3 + x^4)}{r_2^2 x^2(1 - x)^2} \nonumber \\&+ \frac{3\omega \alpha (1 + x^{3\omega + 2})(1 - x^2) - 4\alpha x^2(1 - x^{3\omega })}{r_2^{3\omega + 1} x^{3\omega + 1}(1 - x)^3}.\nonumber \\ \end{aligned}$$
(3.20)

Substituting Eq. (3.18) into Eq. (3.20), we get

$$\begin{aligned} 1= & {} \frac{Q^2(1 + 2x - 6x^2 + 2x^3 + x^4)}{r_2^2 x^2(1 - x^2)} \nonumber \\&- \frac{3\alpha [\omega (1 - x)(1 + 2x + 2x^{3\omega + 2} + x^{3\omega + 3}) - 2x^2(1 - x^{3\omega })]}{r_2^{3\omega + 1} x^{3\omega + 1}(1 - x)^3},\nonumber \\ \end{aligned}$$
(3.21)

we find that Eq. (3.21) is equivalent to Eq. (3.8).

Fig. 3
figure 3

The simulated phase transition and the boundary of a two-phase coexistence on the base of isobaric in the T–S diagram for charged anti-de Sitter black holes with differential \(B_\mathrm{c} \) and \(\omega \). The left figure shows \(Q = 1,\omega = - 1 / 2\), the right figure \(Q = 1,B_\mathrm{c} = 0.1\)

Full size image

From Fig. 3, we find that at the same black hole pressure, the temperature decreases, and the region of coexistence increases as the transition point increases as the value of \(B_\mathrm{c}\) increases, the temperature decreases, and the region of coexistence increases. Meanwhile the temperature decreases and the coexistence zone of the two phases increases with the decrease of the value of \(\omega \).

According to Eqs. (3.8) and (3.13), if the temperature \(T_0\) and \(\omega \) are given, the location \(r_2 \) or \(r_1\) of the phase transition in a charged AdSQ black hole is related to the charge Q and \(\alpha \). Thus, the phase transition in the charged AdSQ black hole at a given temperature of \(T_0\) depends on the electric potential \(\phi _2\) and the quintessence potential \(\Theta _2\) at the event horizon of the black hole, or \(\phi _1\) and \(\Theta _1\). It is not simply related to the event horizon of the black hole \(r_2\) or \(r_1\).

For constant Q and \(\alpha \), at a given temperature \(T_0 (T_0<T_\mathrm{c})\), when the radius of the event horizon of the black hole is \(r_+ <r_1\), a charged AdSQ black hole corresponds to the liquid phase of the van der Waals system. When the event horizon radius of the black hole is \(r_+>r_2\), the charged AdSQ black hole corresponds to the vapor phase of the van der Waals system. When the event radius of the horizon of the black hole is \(r_1 \le r_+\le r_2\), the charged AdSQ black hole corresponds to the vapor–liquid coexistence region of the van der Waals system. Thus, according to the electric potential of three different states, we get a charged AdSQ black hole at a given temperature of \(T < T_\mathrm{c}\), the same pressure \(P_0\), and the same charge Q and \(\alpha \), corresponding to three different states; \(\phi \) and \(\Theta \) are, respectively, called high potential and high quintessence potential phase (referred to as high coefficient phase), middle potential and middle quintessence potential phase (referred to as medium coefficient phase) and low potential and low quintessence potential phase (referred to as low coefficient phase). They, respectively, correspond to the liquid phase, liquid-vapor coexistence phase, and vapor phase of a van der Waals system.

4 The latent heat of the phase transition of the charged AdSQ black hole

Due to the lack of complete knowledge of the chemical thermal potential of the ordinary thermodynamic systems, the phase diagram, which is the P–T curve when the two phases \(\alpha \) and \(\beta \) are in equilibrium, is determined directly by experiment. The slope of the P–T curve is determined by the Clapeyron equation

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}T} = \frac{L}{T(v^\beta - v^\alpha )} \end{aligned}$$
(4.1)

where \(L=T(s^\beta -s^\alpha )\), \(s^\alpha \) and \(s^\beta \) is the molar entropy of phase \(\alpha \) and \(\beta \), \(v^\alpha \) and \(v^\beta \) is the molar volume of phase \(\alpha \) and \(\beta \). For the general thermodynamic system, the Clapeyron equation is in good agreement with the experimental results, which provides a direct experimental verification for the correctness of thermodynamics point of view.

For the charged AdSQ black hole thermodynamic system, substituting Eq. (3.8) into Eq. (3.12) we get the latent heat L of the phase transition of the black hole,

$$\begin{aligned} L= & {} \pi T(1 - x^2)r_2^2\nonumber \\= & {} \pi (1 - x^2)r_2^2 \left[ \frac{(1 + x)}{\pi r_2 x^2f_1 (x)} + \frac{3\alpha }{4\pi xr_2^{3\omega + 2} }\right. \nonumber \\&\times \left. \left( {\frac{(1 + x)(1 + x^2)f_2 (x,\omega )}{1 + 4x + x^2} + \frac{\omega (1 - x^{3\omega + 3})}{x^{3\omega + 1}(1 - x)}} \right) \right] .\nonumber \\ \end{aligned}$$
(4.2)

Given Q, \(\omega \) and \(B_\mathrm{c} \), by Eqs. (3.8) and (4.2), the latent heat of the phase transition is a function of x. When \(Q= 1\), the effects of different \(\omega \) and \(B_\mathrm{c}\) on the latent heat of the phase transition are shown in Tables 1 and 2.

Table 1 The latent heat of the phase transition for different \(\omega \) with \(B_\mathrm{c}=0.10\)
Full size table
Table 2 The latent heat of the phase transition for different \(B_\mathrm{c}\) with \(\omega =-1/2\)
Full size table

From Tables 1 and 2, at the same value of \(B_\mathrm{c} \), the latent heat of the phase transition increases with the value of \(\omega \) increasing. At the same value of \(\omega \), the latent heat decreases with the increase of the value of \(B_\mathrm{}c\). As the value of x increases, the latent heat decreases. Tables 1 and 2 show that at the same temperature and pressure, the black hole from \(r_1\) to \(r_2\) through the two-phase coexistence zone needs to absorb heat—the latent heat of the phase transition, which means that the black hole molecules inside the black hole have different microstructures when they are in phase 1 and 2.

Fig. 4
figure 4

The \(\Psi (T) - x\) diagram for charged anti-de Sitter black holes with differential \(B_{\mathrm c}\) and \(\omega \). The left figure \(Q =1,\omega =-1/2\), the right figure \(Q=1,B_\mathrm{c}=0.1\)

Full size image

5 The microcosmic explanation of the phase transition for charged AdSQ black hole

According to Eqs. (3.8) and (3.13), given \(T_0\), \(B_c\) and \(\omega \), when the black hole system phase transition occurs, the molecular potential \(\phi = \frac{Q}{r_ +} \) and the quintessence potential \(\Theta = - \frac{B_\mathrm{c} r_\mathrm{c}^{3\omega + 1} }{2\omega \pi r_+ ^{3\omega + 1} }=\frac{3\alpha }{r_ + ^{3\omega + 1} }\) show a mutation, which reflects the inconsistent microstructures of the black hole molecules in different phases. When the temperature is fixed, the electric potential and quintessence potential of the two-phase system are, respectively, determined by

$$\begin{aligned} \phi _2= & {} \frac{Q}{r_2 }, \quad \Theta _2 = \frac{3\alpha }{r_2^{3\omega + 1} }, \quad \nonumber \\ \phi _1= & {} \frac{Q}{r_1 } = \frac{Q}{xr_2 }, \quad \Theta _1 = \frac{3\alpha }{x^{3\omega + 1}r_2^{3\omega + 1} }, \end{aligned}$$
(5.1)

where x is given by Eq. (3.13). When the temperature \(T_0 \le T_\mathrm{c} \), \(0 < x \le 1\), one takes the order parameter

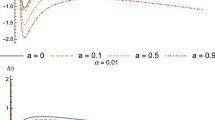
$$\begin{aligned} \Psi (T)= & {} \frac{\phi _1 - \phi _2 }{\phi _\mathrm{c} } + \frac{\Theta _1 - \Theta _2 }{\Theta _\mathrm{c} } = - \frac{\Delta \phi }{\phi _\mathrm{c} } - \frac{\Delta \Theta }{\Theta _\mathrm{c} } \nonumber \\= & {} \frac{r_\mathrm{c} (1 - x)}{r_2 x} + \frac{r_\mathrm{c}^{3\omega + 1} (1 - x^{3\omega + 1})}{r_2^{3\omega + 1} x^{3\omega + 1}}. \end{aligned}$$
(5.2)

When \(\chi \), \(B_\mathrm{c}\), \(\omega \), and Q are given, substituting Eq. (3.8) into Eq. (3.13), one can obtain the solution to x and \(r_2\) for the corresponding temperature. Substituting \(\chi \), x, \(r_2\), and \(r_\mathrm{c}\) into Eq. (5.2), we get \(\Psi (T)\) in Fig. 4 and we find that the curves are coincident with the differential \(B_\mathrm{c}\) and \(\omega \). In other words, the quintessence parameters \(B_\mathrm{c}\) and \(\omega \) have little effect on the order parameter.

Recently, the microstructure of the phase transition of black holes has been studied, and the phase transition between black holes of different sizes is caused by the different density of molecules of black holes with different sizes [1,2,3,4,5,6]. Considering the influence of charge and quintessence on the phase transition, we re-examined the physical mechanism of the phase transition in a charged AdSQ black hole.

The Landau theory of a continuous phase transition is characterized by changes in the degree of material order and the accompanying changes in the symmetry of matter. Since the black hole has the characteristics of ordinary thermodynamics, whether the phase transition of the black hole also shows the symmetry change similar to the phase transition of ordinary thermodynamics is a question that generally is paid attention to. According to the above discussion, we believe that the phase transition in a charged AdSQ black hole is also a symmetry change. When the temperature of the black hole is lower than the critical point temperature and the black hole molecule is at a high coefficient phase 1, the black hole molecule inside the black hole is subjected to a strong electric potential \(\phi \). The black hole molecule has a certain orientation under the action of the strong electric potential and the higher quintessence potential. The black hole molecules are in a relatively ordered state with low symmetry. At the same temperature, when the black hole molecule is in the low coefficient phase 2, the potentials \(\phi \) and \(\Theta \) that cause the orientation of the black hole molecule are weakened, and the order degree of the black hole molecule is relatively low and the symmetry is relatively high. With the increase of temperature, the thermal motion of the black hole molecules tends to weaken the order orientation. But the temperature is not too high, there are still some black hole molecules that have a certain orientation. When the temperature of the black hole is above the critical temperature, the thermal motion of the black hole molecules increases and the orientation of the black hole molecules tends to zero. The phase below the critical temperature has low symmetry, higher order and nonzero \(\Psi (T)\). The phase above the critical temperature has higher symmetry, lower order, and the order parameter \(\Psi (T)\) is zero. As the temperature decreases, the order parameter \(\Psi (T)\) continuously changes from zero to nonzero at the critical point.

In Landau’s idea, the order parameter \(\Psi (T)\) has a small value near the critical point \(T_\mathrm{c}\), and one can expand the Gibbs energy \(G(T,\phi )\) near \(T_\mathrm{c}\) as a power of \(\Psi (T)\). Considering that the phase transition of the system is due to the change of order degree of the black hole molecules inside the black hole, then the system is symmetric with respect to the transformation \(\phi \rightleftarrows -\phi \). When \(\Psi (T)\) can be taken as the order parameter and the thermodynamic quantity of the black hole \(G(T,\phi )\) is expanded according to the order parameter perturbation series, there is no odd power term of the order parameter, but only the even-order term of the order parameter. So

$$\begin{aligned} G(T,\phi ) = G_0 (T) + \frac{1}{2}a(T)\Psi ^2 + \frac{1}{4}b(T)\Psi ^4 + \cdots , \end{aligned}$$
(5.3)

where \(G_0(T)\) is the Gibbs function when \(\Psi (T)=0\). We determine the functional relationship between \(\Psi (T)\) and temperature T by using the minimum stable equilibrium Gibbs function at T, P constant. Note that the Gibbs function is written as \(G(T,\phi )\), where \(\Psi \) is not an independent variable. According to the requirement that G(T) has minimum value in a stable equilibrium state, \(\Psi \) should have three solutions:

$$\begin{aligned} \Psi = 0, \quad \Psi = \pm \sqrt{ - \frac{a}{b}}. \end{aligned}$$
(5.4)

This solution \(\Psi =0\) concerns the disordered state, corresponding to the temperature range \(T > T_\mathrm{c}\) at \(a>0\). This nonzero solution \(\Psi =\pm \sqrt{-\frac{a}{b}}\) represents an orderly state, corresponding to the \(T<T_c\) temperature range at \(a<0\).

The order parameter continues to shift from zero to nonzero at \(T_\mathrm{c}\), so we should have \(a=0\) at \(T=T_\mathrm{c}\). we can just take near the critical point

$$\begin{aligned} a = a_0 \left( {\frac{T - T_\mathrm{c} }{T_\mathrm{c} }} \right) = a_0 t, \quad a_0 > 0. \end{aligned}$$
(5.5)

Note that \(\Psi =\pm \sqrt{-\frac{a}{b}}\) is real. When \(T<T_\mathrm{c}\), \(a<0\), we give the constant \(b>0\). From this we can get

$$\begin{aligned} \Psi= & {} 0, \quad t > 0, \nonumber \\ \Psi= & {} \pm \left( {\frac{a_0 }{b}} \right) ^{1 / 2}( - t)^{1 / 2}, \quad t < 0. \end{aligned}$$
(5.6)

Various ferromagnetic systems have been found to obey the following cooperative experimental laws in the critical point field:

  • When \(t=\frac{t-t_\mathrm{c}}{T_\mathrm{c}} \rightarrow -0 \), the spontaneous magnetization follows the rules

    $$\begin{aligned} M \propto ( - t)^\beta , \quad t \rightarrow - 0. \end{aligned}$$
    (5.7)

  • The zero field magnetization of various ferromagnetic substances \(\chi = \left( {\frac{\partial M}{\partial H}} \right) _T \) is divergent at \(t \rightarrow \pm 0\). The change rule of \(\chi \) with t is

    $$\begin{aligned} \chi \propto t^{ - \gamma }, \quad t \rightarrow + 0; \quad \chi \propto ( - t)^{ - \gamma '}, \quad t \rightarrow - 0. \end{aligned}$$
    (5.8)

  • At \(t=0\) and very weak magnetic field, the relationship between the magnetization of M and the external magnetic field of H is

    $$\begin{aligned} M \propto H^{1 / \delta }. \end{aligned}$$
    (5.9)

  • At \(t\rightarrow \pm 0\), the zero field specific heat capacity of the ferromagnetic material, \(c_\mathrm{H}(H = 0)\), follows the law

    $$\begin{aligned} c_\mathrm{H} \propto t^{ - \bar{\alpha }}, \quad t > 0; \quad c_\mathrm{H} \propto ( - t)^{ - \bar{\alpha }'}, \quad t < 0. \end{aligned}$$
    (5.10)

The dependence of \(\Psi \) on t from Eq. (5.6) is the same as Eq. (5.7), with the critical index of \(\beta =1/2\). According to the method of the literature [62], we can obtain the critical exponent \(\bar{\alpha }=\bar{\alpha }'=0\), \(\gamma =\gamma '=1\), \(\delta =3\), and the entropy of the charged AdSQ black hole near the critical point.

Table 3 The Ruppeiner curvature scalar for different \(\omega \) with \(B_\mathrm{c}=0.10\)
Full size table
Table 4 The Ruppeiner curvature scalar for differential \(B_\mathrm{c}\) with \(\omega =-1/2\)
Full size table

The entropy of disordered phase is \(S=S_0\), and the entropy of the ordered phase is

$$\begin{aligned} S=S_0+\frac{a_0^2 t}{2bT_\mathrm{c}}. \end{aligned}$$
(5.11)

When \(t=0\), the entropy of the ordered phase is equal to the entropy of the disordered phase. It means that the entropy of the black hole is continuous at the critical point.

6 Thermodynamic geometry of the charged AdSQ black hole

From the discussion in Sect. 5, we find that Eq. (5.3) contains parameters of a and b related to specific system characteristics, but the critical exponent given above is irrelevant to a and b. And is well known there are similar problems in the general thermodynamic system. The cause is basically that when we discuss the continuous phase transition, we do not consider the strong fluctuation of the order parameters in the critical point domain. Fortunately, the famous Ruppeiner geometry comes from the thermodynamic fluctuation theory. The singularity of the curvature scalar of corresponding thermodynamic geometry is studied to reveal the phase transition of the black hole [72, 73]. Therefore, we can reveal the microstructure of the black hole molecules by studying the Ruppeiner geometry. We take a (S, P) fluctuation, with fixed Q, \(B_\mathrm{c}\) and \(\omega \). One can obtain the Ruppeiner curvature scalar (Ricci scalar) as

$$\begin{aligned} R= & {} \left( (8 P S+1) S^{\frac{3 (\omega +1)}{2}}-\pi Q^2 S^{\frac{1}{2} (3 \omega +1)}+3 \alpha S \pi ^{\frac{1}{2} (3 \omega +1)} \omega \right) \nonumber \\&\times \left( -2 \pi Q^2 (16 P S+3) S^{3 \omega +1}+2 (8 P S+1) S^{3 \omega +2} \right. \nonumber \\&+3 \alpha \pi ^{\frac{1}{2} (3 \omega +1)} \omega S^{\frac{3 (\omega +1)}{2}} (24 P S (\omega +1)+3 \omega +5) \nonumber \\&\left. +4 \pi ^2 Q^4 S^{3 \omega }-3 \alpha Q^2 \pi ^{\frac{3 (\omega +1)}{2}} \omega (3 \omega +7) S^{\frac{3 (\omega +1)}{2}}\right. \nonumber \\&\left. +27 \alpha ^2 S \pi ^{3 \omega +1} \omega ^2 (\omega +1)\right) /2 S^{3/2} \nonumber \\&\times \left( S^{3 \Omega /2} (-\pi Q^2 + S + 8 P S^2)+3 \alpha \pi ^{(1 + 3 \Omega )/2 } \sqrt{S} \Omega \right) ^3 .\nonumber \\ \end{aligned}$$
(6.1)

At the same temperature R is divided into two parts, one representative \(\phi _2 = \frac{Q}{r_2 }\), \(\Theta _2= - \frac{1}{2r_2^{3\omega } }\), another representative \(\phi _1 = \frac{Q}{r_1 } = \frac{Q}{xr_2 }\), \(\Theta _1 = - \frac{1}{2x^{3\omega }r_2^{3\omega } }\). Substitute Eqs. (3.5) and (3.7) into Eq. (6.1) and we get the value of R with fixed \(B_c\), \(\omega \) and Q.

From Tables 3 and 4, two curves of R will overlap at \(x = 1\) with differential \(B_\mathrm{c} \) and \(\omega \). For an anyon gas curvature scalar \(R > \)0 (or \(R <0\)) the average interaction between particles is repulsive or attractive, while the average interaction is zero as \(R =0\) [5,6,7,8, 78,79,80]. From Tables 3 and 4, we can find that \(0< R(r_2 ) < R(r_1)\), and we think that the average attraction between the black hole molecules of phase 2 in black holes is less than phase 1. According to Eq. (1.1) relating the number density of the black hole molecules and the position of the event horizon, the number density of the black hole molecules in phase 2 is less than that in phase 1. The number density of the black hole molecules decreases and mutual attraction decreases, which satisfies Lenard–Jones’ description of the interaction potential between particles. When the distance between particles increases, the interaction potential between particles decreases, that is, when the number density of particles decreases, the interaction potential decreases.

From Tables 3 and 4, for constant \(B_\mathrm{c} \), \(R(r_1)\) and \(R(r_2)\) will change as \(\omega \) and x change, \(R(r_1 )-R(r_2 )\) will increase with \(\omega \) increasing. When \(\omega \) is fixed \(R(r_1 )-R(r_2 )\) will increase with \(B_\mathrm{c} \) increasing. Whatever the values of \(B_\mathrm{c}\) and \(\omega \), \(R(r_1 )-R(r_2 )\) starts to increase as x increases until it reaches its maximum value at \(x=0.5\), then \(R(r_1 )-R(r_2 )\) starts to decrease, and finally \(R(r_1 )-R(r_2 )=0\) when \(x=1\). According to Eq. (2.7), the change of \(B_\mathrm{c}\) and \(\omega \) with the same temperature and pressure is accompanied by the change of the radius of the event horizon of the black hole. Therefore, the change of \(B_\mathrm{c}\) and \(\omega \) makes the number of the black hole molecule density change with the temperature and pressure fixed. So, we think that the charge Q, \(B_\mathrm{c} \) and \(\omega \) play two roles in the phase transition of black hole: on the one hand, they can change the order degree of the black hole molecules, on the other hand, they can change the number density of the black hole molecules. These two aspects are the main reasons for the phase transition of the thermodynamic system.

7 Discussion and summary

The investigation of the thermal properties and the internal microstructure of black holes has always been one of the topics of interest for theoretical physicists. Although the precise statistics description of the thermodynamic states corresponding to a black hole is unclear, the black hole thermodynamics as well as the critical phenomenon is still a popular topic. Since the discovery of the accelerated expansion of the universe, dark energy has become one of the topics that many physicists are interested in. Among the many dark energy models, quintessence is very influential.

In this paper, we choose different conjugate variables and use Maxwell’s equal-area law to study the phase transition of a charged AdSQ black hole. We find that the phase transition points which are obtained by choosing the conjugate variable (P, V) and (T, S), respectively, are the same for the same temperature. It was found that the charged AdSQ black hole had a phase transition similar to that of a vdW system when the temperature was below the critical temperature, and the charged AdSQ black hole had a phase transition similar to that of a vdW system under the same temperature and pressure. From Eq. (3.8), whether a black hole experiences a first-order phase transition depends on the electric potential at the event horizon \(\phi = \frac{Q}{r_ + }\) and the quintessence potential \(\Theta =-\frac{B_\mathrm{c} r_\mathrm{c}^{3\omega + 1} }{2\omega \pi r_ + ^{3\omega + 1} } = \frac{3\alpha }{r_ + ^{3\omega + 1} }\), not just the size of the black hole. It shows that the microstructure of black hole molecules will change under the action of electric potential and quintessence potential. Through the analysis in Sect. 4, we found that the charged AdSQ black hole had a phase transition latent heat similar to the vdW system in the phase transition of the first order.

From the microscopic point of view, a fluid is made up of fluid molecules, so it can be speculated that a black hole is also made up of black hole molecules, and black hole molecules themselves carry the microscopic degree of freedom of the black hole entropy [1,2,3, 5,6,7,8, 62]. We consider that the phase transition of the charged AdSQ black hole at a certain temperature and pressure is not simply a phase transition from a large black hole to a small black hole, but is determined by the electric potential and quintessence potential at the event horizon. The charge Q of the black hole, the dark energy state parameter \(\omega \) and the normalized factor \(\alpha \) related to the dark energy density play a key role in the phase transition, so we introduced the order parameter of the charged AdSQ black hole. In Sect. 5, Landau continuous phase transition theory is used to analyze the critical phenomenon of the black hole, and the critical index is obtained. In Sect. 6, we reveal the microstructure of the black hole molecules by studying the geometry of Ruppeiner of the black hole system. According to the standard curvature R and the statistical interpretation, curvature scalar \(R>0\) (or \(R <0\)) means that the average interaction between particles is repulsive or attractive, while the average interaction is zero as \(R =0\). According to the given conclusion, the average black hole molecules in the interior of the charged AdSQ black hole are attracted by each other. We have analyzed the influence of the dark energy state parameter \(\omega \) and the dark energy density related normalized factor \(\alpha \) on the phase transition and the latent heat of the phase transition.

This work revealed that the microstructure of the charged AdSQ black hole was similar to that of vdW system.These conclusions are helpful to explore the microstructure of black holes. The study of the black hole microstructure is the basis of quantum gravity theory and the bridge to understanding the relationship between quantum mechanics and gravity theory. In particular, the in-depth study of the black hole microstructure will help to understand the basic properties of black hole gravity, and it is of great significance to the establishment of quantum gravity.