1 Introduction

Polytropes are playing a very vital role to discuss the astronomical objects. In astrophysics many mathematicians and researchers have shown great interest in the study of polytropes. In this respect, different authors and researchers have used theory of polytropes. Chandrasekhar [2] introduced first time the basic concept of Newtonian polytropes by using the laws of thermodynamics. He calculated the density and mass of white dwrafs. Tooper [3] studied the solution of Einstein field equations for compressible fluid, which obeyed the polytropic equation of state. He also discussed the Lane–Emden equation in case of relativistic polytropes [4]. Kaplan and Lupanov [5] obtained a analytical relation between mass and density using polytropic sphere. Kaufmann [6] studied the static polytropic sphere and calculated the mass-radius relation for different values of polytropic index n. Occhionero [7] analyzed the rotation of structure by using the polytropes for \(n\ge 2\). Kovetz [8] put some divergences right in the theory of polytropes defined by Chandrasekhar [2].

Horedt [9] observed the instability of the model for the polytroic index \(n>3\), he also analyzed the physical attributes like mean density, mass, acceleration and gravitational potential of higher dimensional radially-symmetric polytropes by using gamma function [12]. Sharma [10] used Pade approximation to calculate the exact solution of field equation for spherical geometry. Abramowicz [11] used spherical, cylindrical and planer polytropes to develop the Lane–Emden equation. Pandey [13] studied in detail spherical symmertric structures with polytropic equation of state. Zhang et al. [14] verified that equation of hydrostatic equilibrium is satisfied by self-gravitating polytropes.

Herrera [15] discussed the relativistic polytropes with the help of effective variables. Herrera and Barreto [16] gave a generalized mathematical structure of anisotropic Newtonian stars with polytropic equation of state. They [17] also provided a general framework for anisotropic polytropes and discussed the stability by using Tolman mass. Herrera et al. [18] minimized the parameters in spherically anisotropic polytopic models by using the conformally flat condition and developed modified form of Lane–Emden equation. Herrera et al. [19] also used cracking method to discussed stability analysis of relativistic anisotropic polytropes.

Polytropes depend upon a relation between pressure and density of objects in which pressure depends on density. The generalized polytropes are usually defined by two equations of state.

  1. (i)

    Linear equation of state, defined as

    $$\begin{aligned} P_{r}=\alpha _{1}\mu _{o}, \end{aligned}$$
    (1)

    where \(P_{r}\) is radial pressure and \(\alpha _{1}\) is constant of proportionality.

  2. (ii)

    Polytropic equation of state, defined as

    $$\begin{aligned} P_{r}=K\mu ^{\gamma }_{o}=K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$
    (2)

    where \( \gamma \), n and K are called polytropic exponent, polytropic index and polytropic constant respectively.

Azam et al. [20] used generalized polytropic equation of state, which is a combination of the Eqs. (1) and (2) given as

$$\begin{aligned} P_{r}=\alpha _{1}\mu _{o} + K\mu ^{\gamma }_{o}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$
(3)

if \(\mu _{o}\) is changed by \(\mu \) then Eq. (3) takes the form

$$\begin{aligned} P_{r}=\alpha _{1}\mu + K\mu ^{1+\frac{1}{n}}. \end{aligned}$$
(4)

Azam et al. [21] discussed the relativistic charged polytropes using the generalized polytropic equation of state in the context of general relativity. They first time introduced the concept of general polytropic equation of state and also established the general frameworks of anisotropic cylindrical and spherical polytropes with modified form of polytropic equation of state. Stability analysis was carried out by Tolmann mass and cracking technique.

Herrera [1] first time introduced the concept of complexity factor in the vicinity of general theory of relativity by splitting the Riemann tensor \(R_{\alpha \gamma \beta \delta }\) into four structure scalars \(X_{T}, X_{TF}, Y_{T} \) and \( Y_{TF}\). One of them \(Y_{TF}\) named as complexity factor after this, he quantified it equal to zero and termed it as vanishing complexity factor. Sharif and Iqra [22] applied the vanishing complexity factor on charged spherical system and found that the electromagnetic field decreases complexity of the system.

The plan of this paper is as follows. In Sect. 2 we will discuss the Einstein field equation and generalized Tolman-Oppehheinar-Volkoff equation (TOV). In Sect. 3 relation of Riemann and Weyl tensor will be stuied. In Sect.  4 mass function and Weyl tensor will be discussed. We shall talk about the orthogonal splitting of Reimann tensor and complexity factor in Sects. 5 and 6. Section  7 will be devoted to study the generalized polytropes and the energy conditions. In Sect. 8 we shall discuss the graphs of generalized polytropes with complexity factor. In last section we shall summarized our discussion.

2 Einstein field equations

We consider static spherically symmetric distributions of fluid, bounded by a spherical surface \(\Sigma \). The line element is given as

$$\begin{aligned} ds^2=e^{\nu }dt^{2}-e^{\lambda }dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(5)

where \(\nu =\nu (r)\) and \(\lambda =\lambda (r)\). We number the coordinates: \(x^{0}=t, x^{1}=r, x^{2}=\theta , x^{3}=\phi \). The energy-momentum tensor for anisotropic fluid distribution is given by

$$\begin{aligned} T_{\mu \nu }=(\mu +P_{\perp })u_{\mu }u_{\nu }-P_{\perp }g_{\mu \nu }+(P_{r}-P_{\perp })s_{\mu }s_{\nu }, \end{aligned}$$
(6)

where \( P_{\perp }\) is the tangential pressure. The four velocity \(u_{\mu }\) and four vector \(s_{\mu }\) are given by the following equations respectively,

$$\begin{aligned} u^{\mu }=(e^{\frac{-\nu }{2}},0,0,0), \end{aligned}$$
(7)
$$\begin{aligned} s^{\mu }=(0,e^{\frac{-\lambda }{2}},0,0), \end{aligned}$$
(8)

with properties \(s^{\mu }u_{\mu }=0,\quad s^{\mu }s_{\mu }=-1\).

The Einstein field equations are

$$\begin{aligned} \mu= & {} -\frac{1}{8\pi } \left[ -\frac{1}{r^{2}}+e^{-\lambda }\left( \frac{1}{r^{2}}-\frac{\lambda '}{r}\right) \right] , \end{aligned}$$
(9)
$$\begin{aligned} P_{r}= & {} -\frac{1}{8\pi } \left[ \frac{1}{r^{2}}-e^{-\lambda }\left( \frac{1}{r^{2}}-\frac{\nu '}{r}\right) \right] , \end{aligned}$$
(10)
$$\begin{aligned} P_{\perp }= & {} \frac{1}{8\pi } \left[ \frac{e^{-\lambda }}{4} \left( 2\nu ''+\nu '^{2}-\lambda '\nu '+2\frac{\nu '-\lambda '}{r}\right) \right] , \end{aligned}$$
(11)

where primes indicate the derivatives w. r. t. ‘r’. From Eqs. (9-11) it is easy to write the hydrostatic equilibrium equation as

$$\begin{aligned} P^{'}_{r}=-\frac{\nu ^{'}}{2}(\mu +P_{r})+\frac{2(P_{\bot }-P_{r})}{r}. \end{aligned}$$
(12)

It is called generalized TOV equation for anisotropic fluid.

As another option is

$$\begin{aligned} \nu '=2\frac{m+4\pi P_{r}r^{3}}{r(r-2m)}, \end{aligned}$$
(13)

then we may write

$$\begin{aligned} P'_{r}=-\frac{(m+4\pi P_{r}r^{3})}{r(r-2m)}(\mu +P_{r})+\frac{2(P\bot -P_{r})}{r}, \end{aligned}$$
(14)

here m is the mass function given by

$$\begin{aligned} R^{3}_{232}=1-e^{-\lambda }=\frac{2m}{r}, \end{aligned}$$
(15)

alternatively

$$\begin{aligned} m=4\pi \int ^{r}_{0}{\overline{r}}^{2}\mu d{\overline{r}}. \end{aligned}$$
(16)

From four velocity vector Eq. (7) we can calculate the four acceleration, \(a^{a}=u^{\alpha }_{,\beta }u^{\beta }\), whose non-vanishing component is

$$\begin{aligned} a_{1}=-\frac{\nu '}{2}. \end{aligned}$$
(17)

It will be favorable to put down the energy-momentum tensor as

$$\begin{aligned} T_{\nu }^{\mu }=\mu u^{\mu }u_{\nu }-Ph_{\nu }^{\mu }+\Delta _{\nu }^{\mu }, \end{aligned}$$
(18)

with

$$\begin{aligned} \Delta _{\nu }^{\mu }= & {} \Delta (s^{\mu }s_{\nu }+\frac{1}{3}h_{\nu }^{\mu });\quad P = \frac{P_{r}+2P_{\perp }}{3}.\nonumber \\ \Delta= & {} P_{r}-P_{\perp };\quad h_{\nu }^{\mu }=\delta _{\nu }^{\mu }-u^{\mu }u_{\nu }. \end{aligned}$$
(19)

We take Schwarzschild space time for the exterior of the fluid distribution

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}dt^{2}\right) - \left( 1-\frac{2M}{r}\right) ^{-1}dr^{2}\nonumber \\&-r(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(20)

In order to match smoothly the two metrics Eqs. (5) and (20) on the boundary \(r=r_{\Sigma }=\)constant, we need the continuity of the first and second fundamental form as

$$\begin{aligned} e^{\nu _{\Sigma }}= & {} 1-\frac{2M}{r_{\Sigma }}, \end{aligned}$$
(21)
$$\begin{aligned} e^{-\lambda _{\Sigma }}= & {} 1-\frac{2M}{r_{\Sigma }}, \end{aligned}$$
(22)
$$\begin{aligned} P_{\Sigma }= & {} 0. \end{aligned}$$
(23)

3 The Riemann and Weyl Tensor

The Weyl tensor \(C^{\rho }_{\alpha \beta \mu }\), the Ricci tensor \(R_{\alpha }^{\beta }\) and the Ricci scalar R can be used to expressed the Riemann tensor as

$$\begin{aligned} R^{\rho }_{\alpha \beta \mu }=&C^{\rho }_{\alpha \beta \mu }+\frac{1}{2}R^{\rho }_{\beta g\alpha \mu }-\frac{1}{2}R_{\alpha \beta }\delta _{\mu }^{\rho }+\frac{1}{2}R_{\alpha \mu }\delta _{\beta }^{\rho }\nonumber \\&-\frac{1}{2}R_{\mu }^{\mu } g_{\alpha \beta }-\frac{1}{6}R(\delta _{\beta }^{\rho } g_{\alpha \mu }-g_{\alpha \beta }\delta _{\mu }^{\rho }). \end{aligned}$$
(24)

In the spherical symmetric case, magnetic part of the Weyl tensor vanishes and we can write Weyl tensor within its electric part \((E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta })\) as

$$\begin{aligned} C_{\mu \nu 8\pi \lambda }=(g_{\mu \nu \alpha \beta }g_{\kappa \lambda \gamma \delta }-\eta _{\mu \nu \alpha \beta }\eta _{\kappa \lambda \gamma \delta })u^{\alpha }u^{\gamma }E^{\beta \delta }, \end{aligned}$$
(25)

with \(g_{\mu \nu \alpha \beta }=g_{\mu \alpha }g_{\nu \alpha }\) and \(\eta _{\mu \nu \alpha \beta } \) denoting the Levi-Civita tensor. Note that \(E_{\alpha \beta }\) can also be expressed as

$$\begin{aligned} E_{\alpha \beta }=E(s_{\alpha }s_{\beta }+\frac{1}{3}h_{\alpha \beta }), \end{aligned}$$
(26)

with

$$\begin{aligned} E=-\frac{e^{-\lambda }}{4} \left[ \nu ''+\frac{\nu ^{'2}-\lambda '\nu '}{2}-\frac{\nu '-\lambda '}{r}+\frac{2(1-e^{\lambda })}{r^{2}}\right] ,\nonumber \\ \end{aligned}$$
(27)

satisfying the following properties:

$$\begin{aligned} E_{\alpha }^{\alpha }=0,\quad E_{\alpha \gamma }=E_{(\alpha \gamma )},\quad E_{\alpha \gamma }u^{\gamma }=0. \end{aligned}$$
(28)

4 The mass function

Now we shall bring in a widely used definition for the mass of a sphere interior to the surface and some relations between it and the Weyl tensor. Using Eqs. (9–11, 24, 26) and the mass function given in Eq. (15) or (16) we have

$$\begin{aligned} m=\frac{4\pi }{3}r^{3}(\mu +P_{\perp }-P_{r})+\frac{r^{3}E}{3}, \end{aligned}$$
(29)

and then we have

$$\begin{aligned} E=-\frac{4\pi }{r^{3}}\int _{0}^{r}{\overline{r}}^{3}\mu 'd{\overline{r}}+4\pi (P_{r}-P_\perp ). \end{aligned}$$
(30)

Finally, inserting Eq. (30) into Eq. (29) we have

$$\begin{aligned} m(r)=\frac{4\pi }{3}r^{3}\mu -\frac{4\pi }{3}\int _{0}^{r}{\overline{r}}^{3}\mu 'd{\overline{r}}. \end{aligned}$$
(31)

Equation (30) associates the Weyl tensor with the two physical attributes of the self gravitating fluid distribution, first density in homogeneity and second the anisotropy in pressure. Equation (31) expresses the mass function in terms of homogeneous energy density distribution, plus the change induced by density inhomogeneity.

5 The orthogonal splitting of the Riemann tensor

The Bel [23] first time introduced the orthogonal splitting of Riemann tensor. Thus according to Bel, we have

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(32)
$$\begin{aligned} Z_{\alpha \beta }= & {} ^{*}R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }=\frac{1}{2}\eta _{\alpha \gamma \epsilon \mu }R^{\epsilon \mu }_{\beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(33)
$$\begin{aligned} X_{\alpha \beta }= & {} ^{*}R^{*}_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }=\frac{1}{2}\eta _{\alpha \gamma }^{\epsilon \mu }R^{*}_{\epsilon \mu \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$
(34)

where \(*\) denote the dual tensor i.e. \(R^{*}_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }\; R_{\alpha \beta }^{\epsilon \mu }\). It is possible to show that the Riemann tensor can be expressed in terms of these tensors which is called orthogonal splitting of Riemann tensor [24]. Using the field equations, Eq. (24) may be written as

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=C^{\alpha \gamma }_{\beta \delta }+28\pi T_{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}+8\pi T\left( \dfrac{1}{3}\delta ^{\alpha \gamma }_{[\beta ^{\delta }\delta ]}-\delta _{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}\right) , \end{aligned}$$
(35)

we split the Riemann tensor by using Eq. (18) into Eq. (35)

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=R_{(I)\beta \delta }^{\alpha \gamma }+\beta _{(II)\beta \delta }^{\alpha \gamma }+R_{(III)\beta \delta }^{\alpha \gamma }, \end{aligned}$$
(36)

where

$$\begin{aligned} R_{(I)\beta \delta }^{\alpha \gamma }= & {} 16\pi \mu u^{[\alpha \gamma ]}u_{[\beta ^{\delta }\delta ]}-28\pi Ph^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}\nonumber \\&+8(\mu -3P) \left( \dfrac{1}{3}\delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}\right) -\delta ^{[\alpha \gamma ]_{[\beta ^{\delta }\delta ]}}, \end{aligned}$$
(37)
$$\begin{aligned} R_{(II)\beta \delta }^{\alpha \gamma }= & {} 16\pi \Delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}, \end{aligned}$$
(38)
$$\begin{aligned} R_{(III)\beta \delta }^{\alpha \gamma }= & {} 4u^{[\alpha \gamma ]}u_{[\beta ^{E}\delta ]}-\epsilon ^{\alpha \gamma }_{\mu }\epsilon _{\beta \delta \nu }E^{\mu \nu }=0, \end{aligned}$$
(39)

with

$$\begin{aligned} \epsilon _{\alpha \gamma \beta }=u^{\mu }\eta _{\mu \alpha \gamma \beta },\quad \epsilon _{\alpha \gamma \beta }u^{\beta }=0, \end{aligned}$$
(40)

and where the vanishing, due to the spherical symmetry of magnetic part of the Weyl tensor \((H_{\alpha \beta }=^{*}C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta })\) has been used.

With the help of above results, we can now find the explicit expressions for the three tensors \(Y_{\alpha \beta },\;Z_{\alpha \beta }\) and \(X_{\alpha \beta }\) in term of the phyisical variables, we have

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{4\pi }{3}(\mu +3P)h_{\alpha \beta }+4\pi \Delta _{\alpha \beta }+E_{\alpha \beta }, \end{aligned}$$
(41)
$$\begin{aligned} Z_{\alpha \beta }= & {} 0, \end{aligned}$$
(42)

and

$$\begin{aligned} X_{\alpha \beta }=\frac{8\pi }{3}\mu h_{\alpha \beta }+4\pi \Delta _{\alpha \beta }-E_{\alpha \beta }. \end{aligned}$$
(43)

These tensors, can be written in term of scalar functions, called structure scalars [25].

Fig. 1
figure 1

Graphs between \(\xi \) and v; for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =8\times 10^{-10}\)(curve d)

Full size image
Fig. 2
figure 2

Graphs between \(\xi \) and \(\psi _{o}\); for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =4\times 10^{-10}\)(curve d)

Full size image
Fig. 3
figure 3

Graphs between \(\xi \) and \(\Delta \); for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =4\times 10^{-10}\)(curve d)

Full size image

Using tensor \(X_{\alpha \beta }\) and \( Y_{\alpha \beta }\) we can define four scalars functions \(X_{T},\; X_{TF},\; Y_{T},\; Y_{TF}, \) and a fifth scalar related to the tensor \(Z_{\alpha \beta }\) vanishing in the static case. These scalars can be written as

$$\begin{aligned} X_{T}= & {} 8\pi \mu , \end{aligned}$$
(44)
$$\begin{aligned} X_{TF}= & {} 4\pi \Delta _{\alpha \beta } -E, \end{aligned}$$
(45)
$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3} \int _{0}^{r}\overline{r^3}\mu 'd{\overline{r}}, \end{aligned}$$
(46)
$$\begin{aligned} Y_{T}= & {} 4\pi (\mu +3P_{r}-2\Delta ), \end{aligned}$$
(47)
$$\begin{aligned} Y_{TF}= & {} 4\pi \Delta +E, \end{aligned}$$
(48)

or using Eq. (30)

$$\begin{aligned} Y_{TF}=8\pi \Delta -\frac{4\pi }{r^3}\int _{0}^{r}{\overline{r}}^3\mu 'd{\overline{r}}. \end{aligned}$$
(49)

From Eqs. (46) and (49) local anisotropy of pressure is given by

$$\begin{aligned} 8\pi \Delta =X_{TF}+Y_{TF}. \end{aligned}$$
(50)

6 Complexity factor and fluid distribution

Herrera in [1] introduced \(Y_{TF}\) as complexity factor. This complexity factor not only disappears for homogeneous isotropic fluid where two term of Eq. (49) vanishes, but also for all configurations where the two terms in Eq. (49) cancel each other. It also noticeable that contribution of the pressure anisotropy to \(Y_{TF}\) is local and contribution of the density energy inhomogeneity is not.

The Eqs. (9–11) form system three differential equations with five unknowns \((\lambda ,\mu ,\nu ,P_{\perp },P_{r})\). If we apply the condition \(Y_{TF}=0\) we shall still need one condition to solve system. From Eq. (58), vanishing complexity factor condition will be

$$\begin{aligned} \Delta = \frac{1}{2r^3}\int _{0}^{r}{\overline{r}}^3\mu 'd{\overline{r}}. \end{aligned}$$
(51)

From Eq. (51), it is noticeable that vanishing complexity factor condition implies either pressure isotropy and homogeneous energy density, or inhomogeneous energy density and pressure anisotropy.

7 Polytropes with Generalized Polytropic Equation of State

Now we consider the generalized polytropic equation of state for anisotropic fluid [20] as

Case1

$$\begin{aligned} P_{r}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$
(52)

the mass density \(\mu _{o}\) connected with total energy density \(\mu \) [18] as

$$\begin{aligned} \mu =\mu _{o}+nP_{r}. \end{aligned}$$
(53)

Let us consider the following assumption

$$\begin{aligned} \alpha= & {} \frac{P_{rc}}{\mu _{c}},\quad r=\frac{\xi }{A},\quad A^{2}=\frac{4\pi \mu _{c}}{\alpha (n+1)}. \end{aligned}$$
(54)
$$\begin{aligned} \psi _{o}= & {} \frac{P_{o}}{\mu _{oc}},\quad v(\xi )=\frac{m(r)A^{3}}{4\pi \mu _{c}}. \end{aligned}$$
(55)

Then TOV Eq. (13) becomes

$$\begin{aligned}&-v -[\xi {\psi _o}' (\xi -2 \alpha v ) ((n+1) {\psi _o} \beta _1\nonumber \\&\qquad +{\alpha _1} n (1-\alpha n))(v +\alpha \xi ^3 {\psi _o}^{n+1})]\Big /\nonumber \\&\quad [\alpha (n+1) {\psi _o} ((n+1) {\psi _o} \beta _1-(\alpha n-1) \nonumber \\&\qquad \beta _2(v +\xi ^3 {\psi _o}^n ({\alpha _1}+{\psi _o} \beta _1\nonumber \\&\qquad -\alpha {\alpha _1} n))] -\alpha \xi ^3 {\psi _o}^{n+1}+[2 \Delta {\psi _o}^{-n} (\xi -2 \alpha (n+1) v )\nonumber \\&\qquad (v +\alpha \xi ^3 {\psi _o}^{n+1})]\Big / [(n+1) {P_{rc}} ((n+1) {\psi _o} \nonumber \\&\qquad \beta _1-(\alpha n-1) \beta _2(v +\xi ^3 {\psi _o}^n ({\alpha _1}+{\psi _o} \beta _1-\alpha {\alpha _1}\nonumber \\&\qquad n))]=0, \end{aligned}$$
(56)

where \(\beta _1= \alpha -\alpha _1\alpha +\alpha \alpha _1n \), \(\beta _2=\alpha _1+\alpha _1n +1\) and prime indicates the derivative w. r. t. \(\xi \). From the definition of mass function Eqs. (15) and (9), we have

$$\begin{aligned} m'=4\pi r^{2}\mu , \end{aligned}$$
(57)

or using Eqs. (54, 55) we have

$$\begin{aligned} \dfrac{dv}{d\xi }=\xi ^2 {\psi _o}^n (n {\psi _o} (\alpha -{\alpha _1}+\alpha {\alpha _1} n)-(\alpha n-1) ({\alpha _1} n+1)).\nonumber \\ \end{aligned}$$
(58)

The boundary of surface of sphere is defined by \(\xi =\xi _{n}\) such that \(\psi _{o}(\xi _{n})=0\) and following boundary conditions are applied

$$\begin{aligned} \psi _{o}(\xi =0)=1\quad and \quad v(\xi =0)=0. \end{aligned}$$
(59)

Eqs. (56, 58) to gather give the Lane–Emden equation for generalized polytropic equation of state in this case

$$\begin{aligned}&\quad \Big [(2 n \alpha \Delta (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\beta _3-(n+1) \beta _4{\psi _o}) \\&\quad \times (\alpha \xi ^3 {\psi _o}^{n+1}+v )(\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}\\&\quad +\beta _4 {\psi _o}) {\psi _o}^n+v ) {\psi _o}'{\psi _o}^{1-n} -2 \alpha \Delta ((n \alpha -1)\beta _3\\&\quad -(n+1) \beta _4 {\psi _o})(\alpha \xi ^3 {\psi _o}^{n+1}+v )(\alpha \xi ^3 {\psi _o}^{n+1} \\&\quad +v )(\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n+v ) \\&\quad \times (1-2 (n+1) \alpha \xi ^2{\psi _o}^n (n \beta _4 {\psi _o}-(n \alpha -1)\\&\quad \times (n {\alpha _1}+1))) {\psi _o}^{2-n}-2 (n+1) \alpha \beta _4 \Delta (\xi \\&\quad -2 (n+1) \alpha v ) (\alpha \xi ^3 {\psi _o}^{n+1}+v )\\&\quad \times (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n +v ) {\psi _o}' {\psi _o}^{2-n}\\&\quad -{P_{rc}} \xi ^3 (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o}) \\&\quad \times (n (1-n \alpha ) {\alpha _1}+(n+1) \beta _4 {\psi _o}) (\alpha \xi ^3 {\psi _o}^{n+1}+v ) {\psi _o}'\\&\quad \times ((n+3) \beta _4 {\psi _o}^2 +((n+1) \beta _4 \xi {\psi _o}'-(n \alpha -1) \\&\quad \times ((n+3) {\alpha _1}+1)) {\psi _o}+n (1-n \alpha ) {\alpha _1} \xi \\&\qquad {\psi _o}') {\psi _o}^n+{P_{rc}} \xi ^3 (\xi -2 (n+1) \alpha v ) \\&\quad \times (n (1-n \alpha ) {\alpha _1}+(n+1) \beta _4 {\psi _o}) ((n \alpha -1)\beta _3\\&\quad -(n+1) \beta _4 {\psi _o}) (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n+v ) {\psi _o}' \\&\quad \times (-(n \alpha -1) (n {\alpha _1}+1)+((n+3)\alpha \\&\quad +n (n \alpha -1) {\alpha _1}) {\psi _o}+(n+1) \alpha \xi {\psi _o}') {\psi _o}^{n+1}\\&\quad +(n+1) {P_{rc}} \alpha \xi ^2 ((n \alpha -1)(n {\alpha _1}+1) -n \beta _4 {\psi _o}) \\&\quad \times ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o})^2 (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}\\&\quad +\beta _4 {\psi _o}){\psi _o}^n+v )^2 {\psi _o}^{n+2}-(n+1)^2 {P_{rc}} \alpha ^2 \xi ^3 ((n \alpha -1)\\&\qquad \beta _3-(n+1)\beta _4 {\psi _o})^2 (\xi ^3 (-n \alpha {\alpha _1} +{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n\\&\quad +v )^2 {\psi _o}' {\psi _o}^{n+2}-3 (n+1) {P_{rc}} \alpha ^2 \xi ^2 ((n \alpha -1)\beta _3 \\&\quad -(n+1) \beta _4 {\psi _o})^2 (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1} +\beta _4 {\psi _o}) {\psi _o}^n\\&\quad +v )^2 {\psi _o}^{n+3}-2 \alpha \Delta \xi ^2 (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\beta _3\\&\quad -(n+1) \beta _4 {\psi _o}) (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1} +\beta _4{\psi _o}){\psi _o}^n+v ) \\&\quad (-(n \alpha -1) (n {\alpha _1}+1)+((n+3) \alpha +n (n \alpha -1) \\&\qquad {\alpha _1}) {\psi _o}+(n+1) \alpha \xi {\psi _o}'){\psi _o}^2+(n+1) \\&\qquad {P_{rc}} \beta _4 \xi (\xi -2 (n+1) \alpha v ) (n (1-n \alpha ) {\alpha _1}+(n+1) \beta _4{\psi _o}) \\&\quad \times (\alpha \xi ^3 {\psi _o}^{n+1}+v ) {\psi _o}'^2 {\psi _o}+(n+1) {P_{rc}} \beta _4 \xi \\&\quad \times (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o}) \\&\quad \times (\alpha \xi ^3{\psi _o}^{n+1}+v ) (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n\\&\quad + v ) {\psi _o}'^2 {\psi _o}+{P_{rc}} (\xi -2 (n+1) \alpha v ) (n (1-n \alpha ){\alpha _1}\\&\quad +(n+1) \beta _4 {\psi _o}) ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o}) \\&\quad \times (\alpha \xi ^3 {\psi _o}^{n+1}+v )(\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n \end{aligned}$$
$$\begin{aligned}&\quad +v ){\psi _o}' {\psi _o}+{P_{rc}} \xi (n (1-n \alpha ){\alpha _1}+(n+1) \beta _4 {\psi _o}) \nonumber \\&\quad \times ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o}) (\alpha \xi ^3 {\psi _o}^{n+1}+v )\nonumber \\&\quad \times (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n+v ) (1-2 (n+1) \nonumber \\&\qquad \alpha \xi ^2 {\psi _o}^n (n \beta _4 {\psi _o}-(n \alpha -1)(n {\alpha _1}+1))) {\psi _o}' {\psi _o}\nonumber \\&\quad +2 \alpha \Delta \xi ^2 (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\nonumber \\&\qquad \beta _3-(n+1) \beta _4 {\psi _o}) (\alpha \xi ^3 {\psi _o}^{n+1}+v ) ((n+3) \beta _4 {\psi _o}^2 \nonumber \\&\quad +((n+1) \beta _4 \xi {\psi _o}'-(n \alpha -1) ((n+3) {\alpha _1}+1)) {\psi _o}\nonumber \\&\quad +n (1-n \alpha ) {\alpha _1} \xi {\psi _o}') {\psi _o}+{P_{rc}} \xi (\xi -2 (n+1) \alpha v )\nonumber \\&\quad \times (n (1-n \alpha ) {\alpha _1}+(n+1) \beta _4 {\psi _o}) ((n \alpha -1)\beta _3\nonumber \\&\quad -(n+1) \beta _4 {\psi _o}) (\alpha \xi ^3 {\psi _o}^{n+1}+v ) (\xi ^3 (-n \alpha {\alpha _1} \nonumber \\&\quad +{\alpha _1}+\beta _4 {\psi _o}){\psi _o}^n+v ) {\psi _o}'' {\psi _o} -{P_{rc}} \xi \nonumber \\&\quad \times (\xi -2 (n+1) \alpha v ) ((n \alpha -1)\beta _3 -(n+1) \beta _4 {\psi _o})\nonumber \\&\quad \times (n (1-n \alpha ) {\alpha _1}+(n+1) \beta _4 {\psi _o})(\alpha \xi ^3 {\psi _o}^{n+1}+v ) \nonumber \\&\quad \times (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n+v ) {\psi _o}'^2)\Big ] \Big / \nonumber \\&\quad \Big [((n+1) {P_{rc}} \alpha {\psi _o}^2 ((n \alpha -1)\beta _3-(n+1) \beta _4 {\psi _o})^2\nonumber \\&\quad \times (\xi ^3 (-n \alpha {\alpha _1}+{\alpha _1}+\beta _4 {\psi _o}) {\psi _o}^n+v )^2)\Big ]=0, \end{aligned}$$
(60)
Fig. 4
figure 4

Graphs between \(\xi \) and v; for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =8\times 10^{-10}\)(curve d)

Full size image
Fig. 5
figure 5

Graphs between \(\xi \) and \(\psi \); for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =8\times 10^{-10}\)(curve d)

Full size image
Fig. 6
figure 6

Graphs between \(\xi \) and \(\Delta \); for \(\alpha _{1}=.5\), \(n=1\) and \(\alpha =10^{-10}\) (curve a); \(\alpha =2\times 10^{-10}\)(curve b); \(\alpha =4\times 10^{-10}\)(curve c) and \(\alpha =8\times 10^{-10}\)(curve d)

Full size image

where \(\beta _3 = (n {\alpha _1}+{\alpha _1}+1) \) and \(\beta _4 =(n {\alpha _1} \alpha +\alpha -{\alpha _1})\).

Equations (56, 58, 60) become Eqs. (30, 32, 57) of Herrera [17], when \((\alpha _{1}\rightarrow 0)\) and then obviously, Eq. (60) becomes

$$\begin{aligned} \frac{d^{2}\psi _{o}}{d\xi ^{2}}+\frac{2}{\xi }\frac{d\psi _{o}}{d\xi }+\psi _{o}^{2}=0. \end{aligned}$$
(61)

in the Newtonian limit \((\alpha \rightarrow 0)\). Equation (61) is called classical Lane–Emden equation.

Case2

Another possibility can be consider [20] as

$$\begin{aligned} P_{r}=\alpha _{1}\mu +K\mu ^{1+\frac{1}{n}}, \end{aligned}$$
(62)

in this case mass density \(\mu _{o}\) is replaced by total energy density \(\mu \) in Eq. (53), and they are related to each other as [16]

$$\begin{aligned} \mu =\frac{\mu _{o}}{(1-K\mu _{o}^{1/n})^{n}}. \end{aligned}$$
(63)

Introducing \(\psi ^{n}=\frac{\mu }{\mu }_{o}\) we obtain TOV equation as

$$\begin{aligned}&\quad -v +\big [\xi \psi ' (2 \alpha (n+1) v -\xi ) ((n+1) (\alpha -{\alpha _1}) \psi \nonumber \\&\quad +{\alpha _1} n) (v +\alpha \xi ^3 \psi ^{n+1})\big ]\big / \big [\alpha (n+1) \psi ((\alpha -{\alpha _1}) \psi \nonumber \\&+{\alpha _1}+1) (v -\xi ^3 \psi ^n (({\alpha _1}-\alpha ) \psi -{\alpha _1}))\big ]\nonumber \\&\quad -\alpha \xi ^3 \psi ^{n+1}+\big [2 \Delta \psi ^{-n} (\xi -2 \alpha (n+1) v ) \nonumber \\&\quad \times (v +\alpha \xi ^3 \psi ^{n+1})\big ]\big / \big [(n+1) {P_{rc}} ((\alpha -{\alpha _1}) \psi +{\alpha _1}+1) \nonumber \\&\quad \times (v -\xi ^3 \psi ^n (({\alpha _1}-\alpha ) \psi -{\alpha _1}))\big ]=0, \end{aligned}$$
(64)

and from Eq. (57) we have

$$\begin{aligned} \frac{dv}{d\xi }=\xi ^{2}\psi ^{n}. \end{aligned}$$
(65)

Eqs. (64, 65) to gather give the generalized Lane-Emdan equation

$$\begin{aligned}&\big [-2 n \alpha \Delta (\xi -2 (n+1) \alpha v ) ({\alpha _1}+(\alpha -\alpha _1) \psi +1)\\&\quad \times (\alpha \xi ^3 \psi ^{n+1}+v ) (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi ' \psi ^{1-n}\\&\quad -2 \alpha \Delta (\alpha _1+(\alpha -\alpha _1)\psi +1) (1-2 (n+1) \alpha \xi ^2 \psi ^n)\\&\quad \times (\alpha \xi ^3 \psi ^{n+1}+v ) (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi ^{2-n}\\&\quad +2 \alpha (\alpha -\alpha _1) \Delta (\xi -2 (n+1) \alpha v ) (\alpha \xi ^3 \psi ^{n+1}+v )\\&\quad \times (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi ' \psi ^{2-n}-P_{rc} \xi ^3(\xi \\&\quad -2 (n+1) \alpha v ) (\alpha _1+(\alpha -\alpha _1) \psi +1) (n \alpha _1\\&\quad +(n+1)(\alpha -\alpha _1) \psi ) (\alpha \xi ^3 \psi ^{n+1}+v ) \\&\qquad \psi '(3 (\alpha -\alpha _1) \psi ^2+(3 \alpha _1+(n+1)\\&\quad \times (\alpha -\alpha _1) \xi \psi '+1) \psi +n \alpha _1 \xi \psi ') \psi ^n\\&\quad +P_{rc} \xi ^3 (\xi -2 (n+1) \alpha v )(\alpha _1+(\alpha -\alpha _1)\\&\qquad \psi +1) (n \alpha _1+(n+1) (\alpha -\alpha _1) \psi ) (v -\xi ^3 \psi ^n \\&\quad \times ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi '(3 \alpha \psi +(n+1) \alpha \xi \psi '+1) \psi ^{n+1}\\&\quad +(n+1) P_{rc} \alpha \xi ^2 (\alpha _1+(\alpha -\alpha _1) \psi +1)^2 ( v -\xi ^3 \psi ^n \\&\quad \times ((\alpha _1-\alpha ) \psi -\alpha _1))^2 \psi ^{n+2}+(n+1)^2 P_{rc} \alpha ^2 \xi ^3 \\&\quad \times (\alpha _1+(\alpha -\alpha _1) \psi +1)^2 (v -\xi ^3 \psi ^n \\&\quad \times ((\alpha _1-\alpha ) \psi -\alpha _1))^2 \psi ' \psi ^{n+2}+3 (n+1) P_{rc} \alpha ^2 \xi ^2 \\&\quad \times (\alpha _1+(\alpha -\alpha _1) \psi +1)^2 (v -\xi ^3 \psi ^n \\&\quad \times ((\alpha _1-\alpha ) \psi -\alpha _1))^2 \psi ^{n+3}+2 \alpha \Delta \xi ^2 (2 (n+1) \alpha v \\&\quad -\xi ) (\alpha _1+(\alpha -\alpha _1) \psi +1) (v -\xi ^3 \psi ^n ((\alpha _1\\&\quad -\alpha ) \psi -\alpha _1)) (3 \alpha \psi +(n+1) \alpha \xi \psi '+1) \\&\qquad \psi ^2+(n+1) P_{rc} (\alpha -\alpha _1) \xi (\xi -2 (n+1) \alpha v )\\&\quad \times (\alpha _1+(\alpha -\alpha _1) \psi +1) (\alpha \xi ^3 \psi ^{n+1}+v )\\&\quad \times (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi '^2 \psi -P_{rc}(\alpha -\alpha _1)\\&\qquad \xi (\xi -2 (n+1) \alpha v ) (n \alpha _1+(n+1) (\alpha -\alpha _1) \psi )(\alpha \xi ^3 \psi ^{n+1}\\&\quad +v ) (v -\xi ^3 \psi ^n((\alpha _1-\alpha ) \psi -\alpha _1)) \psi '^2 \psi \\&\quad +P_{rc} (\xi -2 (n+1) \alpha v ) (\alpha _1+(\alpha -\alpha _1) \psi \\&\quad +1) (n \alpha _1+(n+1) (\alpha -\alpha _1) \psi ) (\alpha \xi ^3 \psi ^{n+1}+v )\\&\quad \times (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi ' \psi +P_{rc} \xi (\alpha _1\\&\quad +(\alpha -\alpha _1) \psi +1)(n \alpha _1+(n+1) (\alpha -\alpha _1) \psi ) \\&\quad \times (1-2 (n+1) \alpha \xi ^2 \psi ^n) (\alpha \xi ^3 \psi ^{n+1}+v ) (v -\xi ^3 \psi ^n\\&\quad \times ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi ' \psi -2 \alpha \Delta \xi ^2 (2 (n+1)\\&\qquad \alpha v -\xi ) (\alpha _1+(\alpha -\alpha _1) \psi +1) (\alpha \xi ^3 \psi ^{n+1}+v ) \end{aligned}$$
$$\begin{aligned}&\quad \times (3 (\alpha -\alpha _1) \psi ^2+(3 \alpha _1+(n+1)\nonumber \\&\quad \times (\alpha -\alpha _1) \xi \psi '+1) \psi +n \alpha _1 \xi \psi ') \psi \nonumber \\&\quad +P_{rc} \xi (\xi -2 (n+1) \alpha v )(\alpha _1+(\alpha -\alpha _1) \psi +1)\nonumber \\&\quad \times (n \alpha _1+(n+1) (\alpha -\alpha _1) \psi ) (\alpha \xi ^3 \psi ^{n+1}+v ) \nonumber \\&\quad \times (v -\xi ^3 \psi ^n((\alpha _1-\alpha ) \psi -\alpha _1)) \psi '' \psi \nonumber \\&\quad - \xi (\xi -2 (n+1) \alpha v ) (\alpha _1+(\alpha -\alpha _1) \psi +1)\nonumber \\&\quad \times (n \alpha _1+(n+1) (\alpha -\alpha _1) \psi )\nonumber \\&\quad \times (\alpha \xi ^3 \psi ^{n+1}+v ) (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1)) \psi '^2\Big ]\Big / \nonumber \\&\qquad \Big [(n+1) P_{rc} \alpha \psi ^2 (\alpha _1+(\alpha -\alpha _1) \psi +1)^2\nonumber \\&\quad \times (v -\xi ^3 \psi ^n ((\alpha _1-\alpha ) \psi -\alpha _1))^2\Big ]=0. \end{aligned}$$
(66)

Eqs. (64, 66) become Eqs. (59, 60) of Herrera [17], when \((\alpha _{1}\rightarrow 0)\) and in this case Eq. (66) becomes Eq. (61) in Newtonian limit \((\alpha \rightarrow 0)\).

In general theory of relativity the energy conditions are derived to achieve maximal possible details without imposing a certain equation of state for energy. The energy conditions are used with the sense that energy density cannot be \(-ve\) and satisfied by all the models as [18]

$$\begin{aligned} \mu >0,\quad \frac{P_{r}}{\mu }\le 1, \quad \frac{P_{\perp }}{\mu }\le 1. \end{aligned}$$
(67)

For case 1 conditions (67) becomes as

$$\begin{aligned}&n\alpha +n\alpha _{1}(1-n\alpha )<1,\nonumber \\&\qquad \frac{\alpha \psi _{o}+\alpha _{1}(1-n\alpha )(1-\psi _{o})}{(1-n\alpha )(1+n\alpha _{1})+n(\alpha -\alpha _{1}+n\alpha \alpha _{1})\psi _{o}}\le 1,\nonumber \\&\qquad \frac{\frac{3v}{\xi ^{3}\psi _{o}^{n}}+\alpha \psi _{o}+\alpha _{1}(1-n\alpha )(1-\psi _{o})}{(1-n\alpha )(1+n\alpha _{1})+n(\alpha -\alpha _{1}+n\alpha \alpha _{1})\psi _{o}}-1\le 1,\nonumber \\ \end{aligned}$$
(68)

and for Case 2 these conditions (67) tern out to be as

$$\begin{aligned}&\mu >0,\quad \alpha \psi +\alpha _{1}(1-\psi )\le 1,\nonumber \\&\frac{3v}{\xi ^{3}\psi ^{n}}+\alpha \psi +\alpha _{1}(1-\psi )-1\le 1. \end{aligned}$$
(69)

It can be observed that conditions (68) and (69) become (31) and (35) of Herrera [18] when \((\alpha _{1}\rightarrow 0)\).

8 The generalized polytropes with vanishing complexity factor

8.1 Case No.1

The vanishing complexity factor \(Y_{TF}=0\), with the notation in Eqs. (54, 55), will be read as

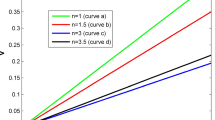
$$\begin{aligned}&\big [4 \xi ^2 (\xi {\psi _o} (2 \Delta ')+ {\mu _c} (-n) \xi {\psi _o}^n {\psi _o}' ((n+1){\psi _o} (\alpha \nonumber \\&\qquad -{\alpha _1}+\alpha {\alpha _1} n)-(\alpha n-1) ({\alpha _1} n+1))\nonumber \\&\qquad +6 \Delta {\psi _o})\big ]\big /\big [{\mu _c} {\psi _o}\big ]=0. \end{aligned}$$
(70)

Now Eqs. (56, 58, 70) form a system of first order differential equation with three unknown function v, \(\psi _{o}\) and \(\Delta \) depending on a triplet of parameters n, \(\alpha \) and \(\alpha _{1}\). This system is solved and the solution is depicted through graphs. Figures 1, 2 and 3 for different values of n, \(\alpha \) and \(\alpha _{1}=.5\) describe the behavior of v, \(\psi _{o}\) and \(\Delta \).

8.2 Case No.2

In this case the complexity factor will be read as

$$\begin{aligned} \frac{6\Delta }{n\mu _{c}}+\frac{2\xi }{n\mu _{c}}\frac{d\Delta }{2\xi }=\psi ^{n-1}\xi \frac{d\psi }{d\xi }. \end{aligned}$$
(71)

Eqs. (64, 65, 71) form a system of first order differential equation with three unknown function \(\psi \), v and \(\Delta \) depending on a triplet of parameters n, \(\alpha \) and \(\alpha _{1}\). This system is solved and the solution is shown through graphs in Figs. 4, 5 and 6.

9 Summary

In this work we have formed a framework to study the relativistic polytropes with generalized polytropic equation of state using vanishing complexity factor. For this purpose spherical symmetry is used for compact object with anisotropic inner fluid distribution. In order to discuss the relativistic polytropes we have developed the formalism to obtain the generalized Lane–Emden equation. The generalized polytropes have been studied in two different cases. The energy conditions for both cases have been developed. In case \(\mathbf (1) \) mass density is to be taken and in case \(\mathbf (2) \) energy density is to be considered. These cases led us to a system of two differential equations and these systems made consistent with the help of vanishing complexity factor.

In case \(\mathbf (1) \) the system of differential equations solved and solution were shown through graphs in Figs. 1, 2 and 3. Figure 1 shows the behavior of v for different value of parameters. The graphs in Fig. 1 depict that v is zero at center and gradually increase with the the increase of radius and it does not show any abnormal pattern. Graphs of Fig. 2 show that the value of \(\psi _{o}\) is minimum at center and increases with the increase of radius and it becomes maximum at the boundary surface. All four curves show normal behavior for different values of parameters. In Fig. 3 curves of graphs show that \(\Delta \) has maximum at center and continuously decreases with the increase of radius and it becomes zero at surface boundary. All four curves show normal pattern through out the graphs. In case \(\mathbf (2) \) graphs in Figs. 4, 5 and 6 have same pattern of the variables v, \(\psi _{o}\) and \(\Delta \) for different values of \(\xi \). They have minimum value at the center and gradually increase with the increase of radius and become maximum at the boundary surface. All the graphs of this case show no abnormal behavior.