1 Introduction

The ultra-relativistic nucleus–nucleus collisions at Relativistic Heavy-Ion Collider (RHIC) and Large Hadron Collider (LHC) have created a new type of matter, the so-called quark–gluon plasma (QGP). One of the novel features of QGP is jet quenching: when high-energy partons propagate through the hot and dense medium, the interaction between hard jets and the medium will lead to parton energy loss (see [1, 2] for recent reviews on this topic). On the other hand, much evidence implies that QGP does not behave as a weakly coupled gas of quarks and gluons, but rather as a strongly coupled fluid [3, 4]. Therefore, calculational tools for strongly coupled, real time QCD dynamics are required, such as gauge/gravity duality.

Gauge/gravity duality is a useful tool for the study of dynamics of strongly coupled non-Abelian plasmas. The best-studied example is the AdS/CFT correspondence [5,6,7]: a conjectured duality between type IIB string theory formulated on \(\hbox {AdS}_5\times S^5\) and \({\mathcal {N}}=4\) supersymmetric Yang–Mills theory (SYM) with an SU(N) gauge group in four dimensions. In the limit of a large number of colors, it allows us to study strongly coupled processes on the gauge theory side through classical (super)gravity calculations on the string theory side. Over the past two decades, this correspondence has yielded many important insights for studying different aspects of QGP (see [8] for a review). Already, the jet quenching of hard probes in such strongly coupled plasma has been explored. For example, the energy loss of heavy quarks has been studied by the drag force extracted from a trailing string moving in the dual geometry [9, 10]. Also, the energy loss of light quarks has been addressed based on various approaches, e.g., the jet quenching parameter [11, 12], falling string [13,14,15,16,17], and shooting string [18, 19] approaches.

In this paper we are interested in studying the effect of the gluon condensate on the energy loss of light quarks. The gluon condensate was originally introduced at zero temperature as a measure for nonperturbative physics in QCD [20]. Later, it was identified as an order parameter for (de)confinement and used to study the nonperturbative nature of QGP [21,22,23] (see [24] for the role of the gluon condensate in RHIC physics). On the other hand, lattice results at finite temperature show that the value of the gluon condensate suddenly drops near \(T_c\) (the critical temperature of the deconfinement transition) regardless of the number of quark flavors [25]. Similar results are obtained in [22]. Based on these results, it would be interesting to investigate the possible effects that the gluon condensate might have on various observables or quantities that are relevant to QGP. Already, there is some interesting research of this type. For instance, the effect of the gluon condensate on the heavy quark potential was discussed in [26] and it was shown that the potential becomes deeper as the value of the gluon condensate decreases in the deconfined phase, implying that the heavy quarkonium mass drops above the deconfinement transition. Also, the gluon condensate dependence of the jet quenching parameter and drag force was analyzed in [27] and it was found that the two quantities both decrease as the gluon condensate decreases in the deconfined phase, indicating that the energy loss decreases near \(T_c\). In the present work, we want to see whether the gluon condensate has the same effect on the energy loss of light quarks as with heavy quarks, and our conclusion is affirmative.

The organization of this paper is as follows. In the next section, we introduce the deformed AdS background with backreaction due to the gluon condensate. In Sects. 3 and 4, we study the effect of the gluon condensate on the energy loss of light quarks within the falling string and shooting string approaches, in turn. In the last section, we give a conclusion and suggest directions for future research.

2 Background geometry

The 5-dimensional (5D) gravity action in Minkowski spacetime with a dilaton coupled is given by [28]

$$\begin{aligned} I=\frac{1}{2\kappa ^2}\int d^5x\sqrt{g}\left( {\mathcal {R}}+\frac{12}{R^2} -\frac{1}{2}\partial _M\phi \partial ^M\phi \right) , \end{aligned}$$
(1)

where \(\kappa ^2\) is the 5D Newtonian constant. \({\mathcal {R}}\) denotes the Ricci scalar. R represents the AdS radius (for simplicity we set \(R=1\) for the rest of the paper). \(\phi \) stands for the dilaton and couples to the gluon operator. M runs from 0 to 4.

By solving the Einstein equations and the dilaton equation of motion, one can obtain two relevant solutions for the action (1). The first is the dilaton-wall solution, given by [29, 30]

$$\begin{aligned} \mathrm{d}s^2=\frac{1}{z^2}(\sqrt{1-c^2z^8}(\mathrm{d}\vec {x}^2-\mathrm{d}t^2)+\mathrm{d}z^2), \end{aligned}$$
(2)

with

$$\begin{aligned} \phi (z)=\sqrt{\frac{3}{2}}\log \left( \frac{1+cz^4}{1-cz^4}\right) +\phi _0, \end{aligned}$$
(3)

where \(\vec {x}=x^1,x^2,x^3\) are the boundary coordinates. z denotes the coordinate of the fifth dimension with \(z=0\) the boundary. \(\phi _0\) represents a constant. \(c=1/z_c^4\) where \(z_c\) is for the IR cutoff.

Another one is the dilaton black hole solution, given by [31, 32]

$$\begin{aligned} \mathrm{d}s^2=\frac{1}{z^2}[A(z)\mathrm{d}\vec {x}^2-B(z)\mathrm{d}t^2+\mathrm{d}z^2], \end{aligned}$$
(4)

with

$$\begin{aligned} \phi (z)=\frac{c}{f}\sqrt{\frac{3}{2}}\log \left( \frac{1+fz^4}{1-fz^4}\right) +\phi _0, \end{aligned}$$
(5)

where

$$\begin{aligned} A(z)= & {} (1+fz^4)^{(f+a)/{2f}}(1-fz^4)^{(f-a)/{2f}},\nonumber \\ B(z)= & {} (1+fz^4)^{(f-3a)/{2f}}(1-fz^4)^{(f+3a)/{2f}},\nonumber \\ f^2= & {} a^2+c^2, \end{aligned}$$
(6)

where a is related to the temperature by \(a=(\pi T)^4/4\).

Note that the dilaton black hole solution is well defined only in the range \(0<z<f^{-1/4}=z_f\), where f determines the position of the singularity and \(z_f\) behaves as an IR cutoff. For \(a=0\), it reduces to the dilaton-wall solution. Meanwhile, for \(c=0\), it becomes the Schwarzschild black hole solution. Also, for both solutions, expanding the dilaton profile near \(z=0\) will give

$$\begin{aligned} \phi (z)=\phi _0+\sqrt{6}cz^4+\cdots , \end{aligned}$$
(7)

and one sees that c is nothing but the gluon condensation. Thus, one could say that solution (2) describes the zero temperature with gluon condensation, while solution (4) refers to the finite temperature with gluon condensation. Moreover, as discussed in [32], there exists a Hawking–Page transition between the two solutions at some critical value of a. So the former is for the confined phase, while the latter describes the deconfined phase. For more details as regards the two solutions, we refer to [32].

3 Energy loss of light quarks in the dilaton black hole background

3.1 Falling string

In this subsection, we study the energy loss of light quarks using the falling string approach for the background metric (4). As previously mentioned, various authors [13,14,15,16,17] have used the AdS/CFT correspondence to evaluate the (maximum) stopping distance of massless, high-energy jets in a strongly \({\mathcal {N}}=4\) SYM plasma, in different ways, e.g., with and without the addition of fundamental-charge matter, specifying different initial conditions. But almost all of the analysis of the stopping distance traveled by such falling particles in an \(AdS_5\)–Schwarzschild model are consistent. Here we will follow the approach in [16, 17], where the authors study jets that carry an R-charged current, generated by a massless gauge field in dual gravity, and measure how far that charge travels before stopping and thermalizing. Specifically, the induced current is considered as an energetic jet passing through the medium, and when the wave packet of the massless field falls into the horizon of the dual geometry, the image jet on the boundary dissipates and thermalizes in the medium.

Fig. 1
figure 1

Left: \(x/x_a\) versus T with fixed c. Right: \(x/x_0\) versus c with fixed T. Here we take \(|\vec {q}|=0.99\omega \)

Full size image

In the WKB approximation, the wave packet of the gauge field in dual gravity is localized in the momentum space. Then the wave function of the gauge field could be factorized as

$$\begin{aligned} A_j(t,z)=exp\left[ \frac{i}{\hbar }\left( q_kx^k+\int \mathrm{d}zq_z\right) \right] {\tilde{A}}_j(t,z), \end{aligned}$$
(8)

where \(q_k\) denotes the 4-momentum, which is conserved, as the metric preserves the translational symmetry along the 4D spacetime. \(q_z\) represents the momentum along the bulk direction. j, k =0,1,2,3 are the 4D spacetime coordinates. \({\tilde{A}}_j(t,z)\) refers to the slow-varying field with respect to t and z.

Following [17], a null geodesic obeys

$$\begin{aligned} 0=(\mathrm{d}s^2)=\mathrm{d}x^ig_{ij}\mathrm{d}x^j+\mathrm{d}zg_{zz}\mathrm{d}z, \end{aligned}$$
(9)

and so

$$\begin{aligned} \frac{\mathrm{d}z}{\mathrm{d}\lambda }=\frac{1}{\sqrt{g_{zz}}}\left[ -g_{ij} \frac{\mathrm{d}x^i}{\mathrm{d}\lambda }\frac{\mathrm{d}x^j}{\mathrm{d}\lambda }\right] ^{1/2}, \end{aligned}$$
(10)

where \(\lambda \) is considered as an affine parameter for the trajectory. By the 4D translation invariance,

$$\begin{aligned} g_{ij}\frac{\mathrm{d}x^j}{\mathrm{d}\lambda }, \end{aligned}$$
(11)

is conserved and proportional to \(q_i\),

$$\begin{aligned} \frac{\mathrm{d}x^i}{\mathrm{d}\lambda } \propto g^{ij}q_j. \end{aligned}$$
(12)

Dividing (12) by (10), one arrives at the null geodesics in 5D space with 4D translation invariance,

$$\begin{aligned} \frac{\mathrm{d}x^i}{\mathrm{d}z}=\sqrt{g_{zz}}\frac{g^{ij}q_j}{(-q_kg^{kl}q_l)^{1/2}}; \end{aligned}$$
(13)

thus, the wave packet could be approximated as a massless particle and the null geodesic will yield a (maximum) stopping distance for an image jet on the boundary in the classical limit (\(\hbar \rightarrow 0\)).

Fig. 2
figure 2

Left: \((\mathrm{d}E/\mathrm{d}x)/(\mathrm{d}E/\mathrm{d}x)_a\) versus T with fixed c. Right: \((\mathrm{d}E/\mathrm{d}x)/(\mathrm{d}E/\mathrm{d}x)_0\) versus c with fixed T (here \(x=0.1fm\))

Full size image

To proceed, one takes the 3-momentum \(\vec {q}\) to point in one of \(\vec {x}\) directions, e.g., the \(x^1\) direction, and writes \(q_i=(-\omega ,|\vec {q}|,0,0)\), where \(\omega \) and \(\vec {q}\) are the energy and the spatial momentum of the particle, respectively. Then from (4), (5) and (13), one can obtain the total distance \(x^1\) traveled in falling from the boundary to the horizon (here we consider \(z_f\) as the “horizon”, similar to [26]),

$$\begin{aligned} x=\int _0^{z_f}\frac{\mathrm{d}z}{A(z)e^{-\phi (z)/2}(\frac{1}{B(z)} \frac{\omega ^2}{|\vec {q}|^2}-\frac{1}{A(z)})^{1/2}}, \end{aligned}$$
(14)

where we assumed that the particle carries the spatial momentum solely along the \(x^1\) direction. Moreover, one can check that in this computation the null geodesic in (13) remains unchanged even when one uses the Einstein frame.

Since analytic results for Eq. (14) are cumbersome and not very illuminating, we will mainly focus on the numerical results. Before numerical calculation, we discuss the values of some parameters. First, to compare with the implications of the experimental data, we choose T to be not far above the QCD phase transition (here we set \(T_c=170 MeV\) [33]). Also, we take \(0\le c\le 0.9 GeV^4\) and \(\phi _0=0\), as follows from [26, 27].

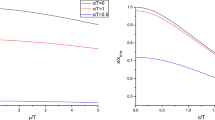
In the left panel of Fig. 1, we plot \(x/x_a\) as a function of T with fixed c, where \(x_a=x|_{T=170 MeV}\). From these curves, one can see that, at fixed c, increasing T leads to decreasing \(x/x_a\), implying that the stopping distance decreases with an increase in T. One step further, the energy loss increases with an increase in T, as expected.

In the right panel of Fig. 1, we plot \(x/x_0\) as a function of c with fixed T, where \(x_0=x|_{c=0}\). From these figures, one sees that, at fixed T, \(x/x_0\) decreases as c increases, which means that the inclusion of the gluon condensate decreases the stopping distance, thus enhancing the energy loss, in agreement with the findings of the jet quenching parameter and drag force [27]. Moreover, by comparing the three curves, one finds that the higher the temperature, the smaller the slope, indicating that the gluon condensate has a stronger effect on the stopping distance (or energy loss) at low temperature, in accord with [27].

3.2 Shooting string

In Refs. [18, 19], the authors proposed another formula for jet energy loss using finite-endpoint-momentum shooting strings. Therein, they considered a particular type of classical string motion: the string endpoint is close to the horizon initially and moves towards the boundary, carrying some energy and momentum which are gradually bled off into the rest of the string during its rise. So this motion is termed finite-endpoint-momentum shooting string motion (or shooting string motion for short).

Now we follow the approach in [18, 19] to study the effect of the gluon condensate on the energy loss of light quarks for the background (4). The instantaneous energy loss of light quarks has the following form:

$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}x}=-\frac{|L|}{2\pi \alpha ^\prime }G_{xx}(z), \end{aligned}$$
(15)

where L is the null geodesic that the endpoint follows. From the above equation one can see that a small z (or the endpoints starting close to the boundary) will yield a large energy loss, indicating the jets will be quenched in a short time and will not be observable. To avoid this, they need to start close to the horizon.

Here again, one considers the quark moving along the \(x^1\) direction. The energy and momentum of the quark are conserved,

$$\begin{aligned} E=-\frac{e^{\phi (z)/2}}{\eta }\frac{B(z)}{z^2}, \end{aligned}$$
(16)
$$\begin{aligned} p_{x_1}=\frac{e^{\phi (z)/2}}{\eta }\frac{A(z)}{z^2}\frac{\mathrm{d}x}{\mathrm{d}t}, \end{aligned}$$
(17)

with \(\eta \) the auxiliary field. Given that, the null geodesics becomes

$$\begin{aligned} L=\frac{E}{p_{x_1}}=-\frac{B(z)}{A(z)}\frac{\mathrm{d}t}{\mathrm{d}x}. \end{aligned}$$
(18)

The finite momentum endpoints will move along the null geodesics \(ds^2=0\), yielding

$$\begin{aligned} \left( \frac{\mathrm{d}x}{\mathrm{d}z}\right) ^2=\frac{B(z)}{A^2(z)L^2-A(z)B(z)}. \end{aligned}$$
(19)

If the endpoints follow the null geodesics, the denominator of (19) will vanish at \(z=z_*\), resulting in

$$\begin{aligned} L=-\sqrt{\frac{B(z_*)}{A(z_*)}}, \end{aligned}$$
(20)

then one gets

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}z}=\sqrt{\frac{B(z)A(z_*)}{A^2(z)B(z_*)-A(z)B(z)A(z_*)}}. \end{aligned}$$
(21)

Finally, one arrives at the energy loss for the dilaton black hole background,

$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}x}=-\frac{1}{2\pi \alpha ^\prime } \frac{A(z)e^{\phi (z)/2}}{z^2}\sqrt{\frac{B(z_*)}{A(z_*)}}. \end{aligned}$$
(22)

Before proceeding, we recall the results of \({\mathcal {N}}=4\) SYM theory [19],

$$\begin{aligned} \left( \frac{\mathrm{d}E}{\mathrm{d}x}\right) _{SYM}=-\frac{\pi \sqrt{\lambda }}{2}T^2(1+\pi Tx)^2, \end{aligned}$$
(23)

where \(T=r_h/\pi R^2\) and \(\lambda =g_{YM}^2N_c=\frac{R^4}{{\alpha ^\prime }^2}\). From (23), one finds that, for small, intermediate and large x, the energy loss looks like \(T^2\), \(xT^3\) and \(x^2T^4\), respectively.

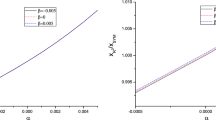
In the left panel of Fig. 2, we plot \((\mathrm{d}E/\mathrm{d}x)/(\mathrm{d}E/\mathrm{d}x)_a\) versus T with fixed c for two different values of x, where \((\mathrm{d}E/\mathrm{d}x)_a=(\mathrm{d}E/\mathrm{d}x)|_{T=170 MeV}\). One can see that increasing T leads to increasing energy loss. Also, for large x this effect is more pronounced, in agreement with that found in [19].

Also, in order to study the effect of the gluon condensate on the energy loss of light quarks, we plot \((\mathrm{d}E/\mathrm{d}x)/(\mathrm{d}E/\mathrm{d}x)_0\) as a function of c with fixed T in the right panel of Fig. 2, where \((\mathrm{d}E/\mathrm{d}x)_0=(\mathrm{d}E/\mathrm{d}x)|_{c=0}\). From these figures, one sees that at fixed T, the ratio increases as c increases, indicating that the inclusion of the gluon condensate increases the energy loss. Moreover, one finds that, as T increases, the slope of the curve decreases, implying that c has a stronger effect on the energy loss at low temperature, in agreement with the analysis of the stopping distance, and consistent with the findings of the drag force and jet quenching parameter [27].

4 Conclusion and discussion

The gluon condensate is a useful quantity to characterize the QCD deconfinement transition. Studying the effects of the gluon condensate on various observables may help us to understand some properties of QGP. In this work, we investigated the energy loss of light quarks traversing in a deformed AdS background with backreaction due to the gluon condensate. We performed the analysis using the falling string and shooting string approaches, respectively. For the former, we analyzed the stopping distance of a massless particle moving along the null geodesic, while, for the latter, we evaluated the instantaneous energy loss based on the finite-endpoint-momentum framework. For both cases, it is shown that increasing the gluon condensate leads to increasing the energy loss. Also, this effect is more pronounced at low temperature, in accord with the findings of the drag force and jet quenching parameter [27].

In addition, by comparing the results of this work with that of [27], one may conclude that the effects of the gluon condensate on the energy loss of light quarks and heavy quarks are consistent: the inclusion of the gluon condensate enhances the quark energy loss.

On the other hand, it was argued [25] that the value of the gluon condensate drops near the deconfinement transition. Also, Ref. [34] indicates that, at high temperatures, the gluon condensate becomes independent of T and \(\mu \) (the chemical potential), but when T is not very high, c strongly depends on T and \(\mu \). Taking all this together, one could infer that the energy loss decreases as c decreases in the deconfined phase, and at high temperature it is nearly not modified by c. However, we could not give a concrete conclusion on the energy loss at intermediate or low temperature. To solve this problem, one needs to investigate the competitive effects of c, \(\mu \), T (on the energy loss) as well as the correlation or relationship among those three. We leave this as a subject of further study.