1 Introduction

It is well known that the astrophysical compact objects are formed due to the gravitational collapse. These compact stars belong to three different groups like neutron stars, white dwarfs, and black holes. The arrangement of these stars is constructed according to their internal structure. The black hole is the densest stars in the universe. Till now, it is an open problem in astrophysics to know about the behavior, nature and exact configuration of these astrophysical compact objects which are more compact than the normal compact objects, therefore in recent days, it is still an active field of research. Based on the hypothesis of strange matter, the strange quark matter could be more stable than nuclear matter. Therefore, the neutron stars must essentially be composed of pure quark matter. The current expansion in a cosmological investigation has explained gradually the origin and distribution of substance and growth of compact objects in the Universe. Few of their assets, such as rotation frequencies, masses, and emission of radiation are computable. The measurements of the essential parameters decide the nature of compact objects which is still an observational challenge because these properties are not directly associated with the observations, such as the internal configuration of masses and radii that need the growth of hypothetical models. In view of theoretical computation, the mass and radii are calculated by solving the hydrostatic equilibrium equation that gives an equilibrium condition between the hydrostatic and gravitational force. In the case of Einstein general relativity, the Tolman–Oppenheimer–Volkoff (TOV) equations can represent the equilibrium condition for a spherical compact object. However, equation of state is necessary for describing the complete structure of these spherical compact objects. In the modern days, the experimental data shows the existence of such astrophysical objects which are observed at very high densities [1], and few of the astrophysical objects like Her X-1 (X-ray pulsar), PSR 0943+10, 4U 1820-30 (X-ray burster), 4U 1728-34, RX J185635-3754 (X-ray sources), and SAX J 1808.4-3658 (millisecond pulsar) extremely favor for the probability that these compact objects could essentially be strange stars. In further arguments, there is no any resilient confirmation to establish the mechanism for the understanding of astrophysical compact objects. According to the theoretical investigations, such compact objects are composed of a perfect fluid [2]. Mostly, the bag equation of state (EOS) and polytropic EOS (\(p=k\,\rho ^{\gamma }\)) have been extensively applied to describe less compact star and a white dwarf [3,4,5]. In this connection Herrera and Barreto [6] conveyed a general study on polytropic relativistic stars with anisotropic pressure while polytropic quark star models have been studied by Lai and Xu [7]. From a theoretical point of view, the impact of anisotropic compact objects was first introduced by Bowers and Liang [8]) and another study headed by Ruderman [9] revealed that nuclear matter may be composed of anisotropic pressure at a very high density which is the order of \(10^{15} \,\mathrm{g/cm}^3\). In this scenario the several objects have been discovered by the authors (see Refs. [10,11,12,13,14,15,16,17,18,19,20,21]). It has also been investigated that the pressure anisotropy can disturb the critical mass, compactness, and steadiness of the extremely dense relativistic compact objects. Recently Chaichian et al. [22], Ferrer et al. [23] have proposed that the pressure anisotropy can be produced by the action of the magnetic field on a Fermi gas. Recently, Maurya et al. [24,25,26,27,28,29] have discovered several charged and uncharged solution for the compact stars. The effect and role of anisotropy with and without equation of state (EOS) were proposed by Harko and Mak [30], Maurya et al. [31,32,33,34,35], Varela et al. [36]. On the other hand, Sharma and Maharaj [37] have obtained an analytical extended solution by taking a specific choice of mass function. In the current days, the embedding class one solution has much attraction towards the researchers. Many mathematicians and physicists have explained the concept of embedding that the curved spacetime can be embedded into higher dimensional flat spacetime. The Riemann proposed the innovative idea of Riemannian geometry by giving an exhaustive study of the geometric objects in 1850. Sudden after, some mathematicians proposed some concept that the Riemannian manifold can be embedded into Euclidian space of higher dimensional. This concept was known as the isometric embedding problem which was unproved for many years. The first time in 1871, the Schlaefli guessed the prospect of embedding the Riemannian manifold locally and isometrically into the higher-dimensional Euclidean space under some constraint. Later on this conjecture was proved and founded by Janet [38], Cartan [39] and Burstin [40]. They have proved that any l dimensional Riemannian space can always be locally embedded into any pseudo-Euclidean space of dimension \(L\ge l(l+1)/2\). In the case of symmetric, we need at least \(L=(l+1)\)-dimension of pseudo-Euclidian flat space for the embedding of l dimensional Riemannian geometry isometrically. This embedding theory has been also well explained by Stephani [41] and his collaborators in their pioneering work. In this concerns, the most popular work on embedding class one have been done by several authors [42,43,44,45,46,47,48,49,50,51,52,53,54,55].

In recent days, the technique of gravitational decoupling by minimal geometric deformation (MGD) has a great interest among the researchers. This is a powerful tool to extend any previously available solutions into a more complex form or provide more general new solutions. This effective minimal geometric deformation (MGD) mechanism and its extended case have been developed by Ovalle and his collaborators [56,57,58]. The MGD solutions in the context of Randall–Sundrum gravity have been discovered by Ovalle et al. [59,60,61]. Later on, Ovalle and Casadio et al. [62] have determined a new black hole solution by using this minimal geometric deformation (MGD) approach as well as they also explained that how the MGD introduce the anisotropy in the self-gravitating system and how spherically symmetric matter distribution changes the Schwarzschild vacuum solution. Using this MGD approach, several authors have obtained the solutions in a more complex forms, see Refs. [63,64,65,66,67,68,69,70,71,72,73,74,75,76]. Very recently, Singh and Maurya [77] have determined the first solution of embedding class one spacetime using the minimal geometric deformation (MGD) approach for anisotropic matter distribution. Now we are going to discuss how the MGD works in solving the Einstein field equation (EFE) which are the following: (I) First we choose the energy–momentum tensor \({T}_{\mu \nu }\) corresponding to already known solution. Then we can extend this known solutions of Einstein field equation into more complex form by joining of extra new stress tensor which will be introduced by MGD. Then the obtained new solution can be described by coupling of the \({T}_{\mu \nu }\) for the seed solution and new stress tensor through a non-dimensional coupling constant \(\alpha \) as:

$$\begin{aligned} T_{\mu \nu } \mapsto \tilde{T}^{(1)}_{\mu \nu }=T_{\mu \nu }+\alpha ^{(1)}\,\hat{T}^{(1)}_{\mu \nu } \end{aligned}$$
(1)

similarly we can extend the new energy momentum tensor \(\tilde{T}^{(1)}_{\mu \nu }\) as,

$$\begin{aligned} \tilde{T}^{(1)}_{\mu \nu } \mapsto \tilde{T}^{(2)}_{\mu \nu }=\tilde{T}^{(1)}_{\mu \nu }+\alpha ^{(2)}\,\hat{T}^{(2)}_{\mu \nu } \end{aligned}$$
(2)

and continue the same procedure as n times. In this process we can extend our simple initial solution of Einstein field equation connected with the source \(T_{\mu \nu }\) into more generalised form which is related to the source \(T_{\mu \nu }=\tilde{T}^{(n)}_{\mu \nu }\). It is important to mention that each different component for the source \({T}^{n}_{\mu \nu }\) is individually conserved,

$$\begin{aligned} \nabla _\mu \tilde{T}^{\mu \nu }=\nabla _\mu {T}^{(1){\mu \nu }} = \nabla _\mu {T}^{(2){\mu \nu }}= \cdots = \nabla _\mu {T}^{(n){\mu \nu }}=0.\nonumber \\ \end{aligned}$$
(3)

(II) On the other hand, this methodology can also work very well in reverse order to obtain the solution for compact objects. In order to proceed with this reverse methodology, first, we separate a more complex energy-momentum tensor \(\tilde{T}_{\mu \nu }\) into many different simpler energy tensor components like \({T}^{n}_{\mu \nu }\). After these separations, we will solve the Einstein field equation corresponding to each component of \({T}^{n}_{\mu \nu }\) for the compact object. In this process we will get multiple solutions that are connected with the above source \({T}^{n}_{\mu \nu }\). Finally the complete solution of the EFE for the original stress tensor \(\tilde{T}^{n}_{\mu \nu }\) can be obtained by joining of above each distinct solution. Moreover, we can describe this methodology by taking a particular example which can be given as: let us consider two gravitational sources namely \(S_1\) and \(S_2\) where \(S_1\) is a source connected standard Einstein’s equations while second source \(S_2\) corresponding to the quasi-Einstein equations. After specifying both sources, we solve both systems of equations individually. Finally, we join both solutions and find a solution for the complete system which is given as \(S_1\cup S_2\). Moreover, it is well known that Einstein’s field equations are highly nonlinear in nature. Therefore, the minimal geometric deformation (MGD) approach is a powerful methodology to solve the EFE.

The article is organised as follows: In Sect. 2, we defined the field equations for the charged matter distribution via gravitational decoupling (GD) and corresponding interior space-time. For this purpose, we divide this Sect. 2 into three Sects. 2.1, 2.2 and 2.3. In Sects. 2.1 and 2.2, we defined the action for two sources and corresponding field equations for both sources, respectively. The embedding class one condition is given in Sect. 2.3. We have obtained new solution for charged anisotropic matter distribution via GD in Sect. 3. In Sect. 4, we have performed the matching condition to determined the arbitrary constants and necessary parameters. The physical analysis has been presented in Sect. 4 which consist three subsections namely Sect. 5.1. Regularity of gravitational decoupling model, Sect. 5.2. Equilibrium condition for GD model, and Sect. 5.3. Stability of the stellar model via cracking. The mass-radius ratio and surface redshift are given in Sect. 6 where we discussed the gravitational and effective mass. The final section has been made for discussion and conclusion.

2 The field equations for the charged matter distribution via gravitational decoupling (GD) and corresponding interior space-time

2.1 The action for two sources

We define the action for the modified matter distribution by using the extra source as [58]

$$\begin{aligned} S=S_{EH}+S_{E}=\int \left[ {\frac{R}{16\pi }}+{\mathscr {L}}_M+{\mathscr {L}}_E\right] \sqrt{-g}~ d^4x \end{aligned}$$
(4)

where \({\mathscr {L}}_M\) and \({\mathscr {L}}_E\) represent corresponding the matter fields and additional Lagrangian matter density due to presence of the extra source. It is well defined notation as R represents a Ricci scalar while g is the determinant of the metric tensor \(g_{\mu \nu }\). Then the energy-momentum tensor corresponding to both Lagrangian matter distributions can be written as,

$$\begin{aligned} {T}_{\mu \nu }= & {} -\frac{2}{\sqrt{-g}}\,\frac{\delta (\sqrt{-g}\,{\mathscr {L}}_M)}{\delta g^{\mu \nu }}=-\frac{2\,\partial ({\mathscr {L}}_M)}{\partial g^{\mu \nu }}+g_{\mu \nu } {\mathscr {L}}_M \end{aligned}$$
(5)
$$\begin{aligned} \varTheta _{\mu \nu }= & {} -{2 \over \sqrt{-g}}~{\delta (\sqrt{-g}{\mathscr {L}}_E) \over \delta g^{\mu \nu }}=-2{\delta {\mathscr {L}}_E \over \delta g^{\mu \nu }}+g_{\mu \nu } {\mathscr {L}}_E. \end{aligned}$$
(6)

After varying the action (4) with respect to the metric tensor \(g^{\mu \nu }\), we obtain the general equations of motion for the extra stress tensor \(\varTheta _{\mu \nu }\) as

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu } R =-8\pi \,(T_{\mu \nu }+\,\varTheta _{\mu \nu })=T_{\mu \nu }^{\text {eff}}. \end{aligned}$$
(7)

Let us consider the spacetime being static and spherically symmetric that describes the interior of the compact object. This spacetime can be written in the following form as,

$$\begin{aligned} ds^{2} = e^{\nu (r) } \, dt^{2}-e^{\lambda (r)} dr^{2} +r^{2}\left( d\theta ^{2} -\sin ^{2} \theta \, d\phi ^{2}\right) . \end{aligned}$$
(8)

Now using Eqs. (7) and (8), we obtain Einstein’s equations for static spherically symmetric spacetime for the energy tensor \(T^{\text {eff}}_{\mu \nu }\) as ,

$$\begin{aligned}&8\pi (T^0_0+\varTheta ^{0}_{0})={\mathrm{e}^{-\lambda }}\left( {\frac{\lambda ^{{\prime }}}{r}}-\frac{1}{r^2}\right) +\frac{1}{r^2}, \end{aligned}$$
(9)
$$\begin{aligned}&-8\pi (T^1_1+\varTheta ^{1}_{1})={\mathrm{e}^{-\lambda }} \left( {\frac{\nu ^{{\prime }}}{r}}+\frac{1}{r^2}\right) -\frac{1}{r^2},\end{aligned}$$
(10)
$$\begin{aligned}&-8\pi (T^2_2+\varTheta ^{2}_{2})=\frac{\mathrm{e}^{-\lambda }}{4} \left( 2 \nu ^{{\prime \prime }}+\nu ^{\prime 2}+2{\frac{\nu ^{{\prime }}-\lambda ^{{\prime }}}{r}}-\nu ^{\prime }\lambda ^{\prime } \right) .\nonumber \\ \end{aligned}$$
(11)

Then the linear combination of Eqs. (9)–(11) satisfy the following conservation equation

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}\,({T}^0_{0}-{T}^1_{1})+ & {} ({T}^1_{1})^{\prime }-\frac{2}{r}\,({T}^2_{2}-{T}^1_{1})-\frac{\nu ^{\prime }}{2}(\varTheta ^{0}_{0}-\varTheta ^{1}_{1})\nonumber \\+ & {} (\varTheta ^{1}_{1})^{\prime }-\frac{2}{r}\,(\varTheta ^{2}_{2}-\varTheta ^{1}_{1})=0, \end{aligned}$$
(12)

Our next aim to write the field equations corresponding to both stress tensor and solve them separately using the minimal geometric deformation approach.

2.2 The field equations for \(T_{\mu \nu }\) and \(\varTheta _{\mu \nu }\) via MGD approach

In this approach, we will look that the system will be converted in such a way that the equation of motions associated with the stress tensor \(\varTheta _{\mu \nu }\) satisfy the effective “quasi-Einstein system”. However, the impact of the extra source \(\varTheta _{\mu \nu }\) on the energy tensor \(T_{\mu \nu }\) can be determined by the geometric deformations as,

$$\begin{aligned}&{{\xi }}\mapsto \nu = \xi +\alpha \, h(r) \end{aligned}$$
(13)
$$\begin{aligned}&e^{-{\mu }} \mapsto e^{-\lambda } = e^{-{\mu }}+\alpha \,f(r). \end{aligned}$$
(14)

where f(r) and h(r) denote the geometric deformation functions undergone by the radial and temporal metric component, respectively while the constant \(\alpha \) is a free parameter. These deformations are known as the complete geometric deformation (GD) or extended geometric deformation along the radial and temporal components of the line element. Now let us substitute the deformed metric function from Eqs. (10) and (14) in the field Eqs. (9)–(11) which separate the system into two sets namely: (a) first set as the standard Einstein field equations corresponding to energy–momentum tensor \(T_{\mu \nu }\) which is described by line element (8),

$$\begin{aligned}&8\pi T^0_0 = \frac{1-e^{-{\mu }}}{r^{2}}+\frac{e^{-{\mu }}{\mu }'}{r} \end{aligned}$$
(15)
$$\begin{aligned}&-8\pi T^1_1 = \frac{e^{-{\mu }}-1}{r^{2}}+\frac{e^{-{\mu }}{\xi }'}{r} \end{aligned}$$
(16)
$$\begin{aligned}&-8\pi T^2_2 = e^{-{\mu }}\left( \frac{{\xi }''}{2}+\frac{{\xi }'^{2}}{4}-\frac{{\xi }'{\mu }'}{4}+\frac{{\xi }'-{\mu }'}{2r} \right) . \end{aligned}$$
(17)

and (b) The second set gives the equation of motions for the source \(\varTheta _{\mu \nu }\), known as “quasi-Einstein equations”, which are given as,

$$\begin{aligned}&8\pi \varTheta ^0_0 = -{\alpha \,f' \over r}-{\alpha \,f\over r^2} \end{aligned}$$
(18)
$$\begin{aligned}&8\pi \varTheta ^1_1+\alpha \,F_1=-\alpha \,f\left( {{\nu }' \over r}+{1\over r}\right) \end{aligned}$$
(19)
$$\begin{aligned}&8\pi \varTheta ^2_2+\alpha \,F_2 {=} -{\alpha \,f \over 2}\left( {\nu }''{+}{{\nu }'^2 \over 2}{+}{{\nu }' \over r}\right) {-}{\alpha \,f' \over 2}\left( {{\nu }' \over 2}{+}{1\over r}\right) . \nonumber \\ \end{aligned}$$
(20)

where \(F_1\) and \(F_2\) can be defined as,

$$\begin{aligned} F_1= & {} \frac{e^{-\mu }\,h^{\prime }}{r},\\ F_2= & {} \frac{e^{-\mu }}{4}\,\left( 2\,h^{\prime \prime }+\alpha \,h^{{\prime }\,2}+\frac{2\,h^{\prime }}{r}+2\,\xi ^{\prime }\,h^{\prime }-\mu ^{\prime }\,h^{\prime }\right) . \end{aligned}$$

Along with the conservation equations for both systems,

$$\begin{aligned}&-\frac{\xi ^{\prime }}{2}\,({T}^0_{0}-{T}^1_{1})+({T}^1_{1})^{\prime }-\frac{2}{r}\,({T}^2_{2}-{T}^1_{1}) = 0, \end{aligned}$$
(21)
$$\begin{aligned}&-\frac{\nu ^{\prime }}{2}(\varTheta ^{0}_{0}-\varTheta ^{1}_{1}){+}(\varTheta ^{1}_{1})^{\prime }{-}\frac{2}{r}\,(\varTheta ^{2}_{2}{-}\varTheta ^{1}_{1})= \frac{\alpha \,h^{\prime }}{2} (T^0_0-T^1_1).\nonumber \\ \end{aligned}$$
(22)

Now by motivation of Ovalle [58], we define Maxwell energy–momentum tensor for a charged self-gravitating distribution which corresponds to the extra source \(\varTheta _{\mu \nu }\) in Eq. (7). Then electromagnetic field tensor \(\varTheta _{\mu \nu }\) can be written as,

$$\begin{aligned} \varTheta _{\mu \nu }=\frac{1}{4 \pi }\left( -F^{m}_{\mu }F_{\nu \,m} + \frac{1}{4}{g_{\mu \nu }} F_{\gamma \,n}F^{\gamma \,n}\right) . \end{aligned}$$
(23)

It is well known that the anti-symmetric electromagnetic field tensor \(F_{\mu \nu }\) in Eq. (23) satisfies the Maxwell field equations,

$$\begin{aligned}&\nabla _{v}\left[ (-g)^{1/2}\,F^{\mu \nu }\right] = 4\pi \, (-g)^{1/2}\,j^{\mu }, \end{aligned}$$
(24)
$$\begin{aligned}&F_{\mu \nu ,\gamma } + F_{\nu \gamma ,\mu }+F_{\gamma \mu , \nu }=0, \end{aligned}$$
(25)

where the electromagnetic four current vector \(j^i\) is defined as

$$\begin{aligned} J^{i}=\frac{\sigma }{\sqrt{g_{44}}}\,\frac{dx^i}{dx^4}=\sigma \,v^i, \end{aligned}$$
(26)

with charge density \(\sigma =e^{\nu /2}\,J^{0}(r)\). It is noted that only the non-vanishing component of the four-current is \(J^4\) for static matter distribution. Since in the case of spherical symmetry, the four-current component is only a function along radial direction ‘r’. Then corresponding non-zero components for electromagnetic field tensor are \(F^{01}\) and \(F^{10}\) that is related as \(F^{01}=-F^{10}\). These components describe the electric field along the radial vector r. From Eqs. (24)–(26), the expression of electric field component for spherically symmetric line element (8) can be written in the form of electric charge as,

$$\begin{aligned} F^{01} = - F^{10}=\frac{q}{r^2}\,e^{-(\nu +\lambda )/2} \end{aligned}$$
(27)

where q(r) describes the electric charge which is contained within the sphere of radius r. Then q(r) can be defined by using relativistic Gauss law and corresponding electric field E as,

$$\begin{aligned}&q(r)=4\,\pi \int ^{r}_{0}{\sigma \,r^2\,e^{\lambda /2} dr}=r^2\,\sqrt{-F_{10}\,F^{10}}, \end{aligned}$$
(28)
$$\begin{aligned}&E^2=-F_{10}\,F^{10}=\frac{q^2}{r^4}. \end{aligned}$$
(29)

In order to define \({T}_{\mu \nu }\), we consider the fluid matter inside of spherical body is completely filled by anisotropic fluid. In this case the energy momentum tensor \({T}_{\mu \nu }\) can be given as,

$$\begin{aligned} {T}_{\mu \nu }=({\rho }+{p_t})u_\mu u_\nu -{p_t}g_{\mu \nu }+\left( {p_r}-{p_t}\right) v_\mu v_\nu , \end{aligned}$$
(30)

where the covariant component \({u _{\nu }}\) denote the 4-velocity, fulfilling \(u_{\mu }u^{\mu }= -1\) and \({\nu ^{\mu }}u_{\mu }=0\). Here, \(\rho \), \({p}_{r}\) and \({p}_{t}\) represent the matter density and pressures (radial and tangential) for anisotropic matter distribution. Then the components for \(T^{\mu }_{\nu }\) and \(\varTheta ^{\mu }_{\nu }\) can be expressed as,

$$\begin{aligned} T^{0}_{0}= & {} \rho (r),\quad T^{1}_{1}=-p_r(r),\quad T^{2}_{2}=-p_t(r), \end{aligned}$$
(31)
$$\begin{aligned} \varTheta ^{0}_{0}= & {} \varTheta ^{1}_{1}=- \varTheta ^{2}_{2}=\frac{1}{8\pi }\,\frac{q^2(r)}{r^4}. \end{aligned}$$
(32)

By plugging the Eqs. (31) and (32) in the field equations (15)–(17) and (18)–(20) we obtain,

$$\begin{aligned}&8\pi \rho = \frac{1-e^{-{\mu }}}{r^{2}}+\frac{e^{-{\mu }}{\mu }'}{r} \end{aligned}$$
(33)
$$\begin{aligned}&8\pi p_r = \frac{e^{-{\mu }}-1}{r^{2}}+\frac{e^{-{\mu }}{\xi }'}{r} \end{aligned}$$
(34)
$$\begin{aligned}&8\pi p_t = e^{-{\mu }}\left( \frac{{\xi }''}{2}+\frac{{\xi }'^{2}}{4}-\frac{{\xi }'{\mu }'}{4}+\frac{{\xi }'-{\mu }'}{2r} \right) . \end{aligned}$$
(35)

and

$$\begin{aligned}&\frac{q^2}{r^4} = -{\alpha \,f' \over r}-{\alpha \,f\over r^2} \end{aligned}$$
(36)
$$\begin{aligned}&\frac{q^2}{r^4}+\alpha \,F_1=-\alpha \,f\left( {{\nu }' \over r}+{1\over r}\right) \end{aligned}$$
(37)
$$\begin{aligned}&{-}\frac{q^2}{r^4}{+}\alpha \,F_2 = {-}{\alpha \,f \over 2}\left( {\nu }''{+}{{\nu }'^2 \over 2}{+}{{\nu }' \over r}\right) {-}{\alpha \,f' \over 2}\left( {{\nu }' \over 2}{+}{1\over r}\right) .\nonumber \\ \end{aligned}$$
(38)

Then the Eqs. (21) and (22) yield the following conservation equations,

$$\begin{aligned}&-\frac{\xi ^{\prime }}{2}\,(\rho +p_r)-(p_r)^{\prime }+\frac{2}{r}\,(p_t-p_r) = 0, \end{aligned}$$
(39)
$$\begin{aligned}&\varPsi ^{\prime }+\frac{4}{r}\,\varPsi - \frac{\alpha \,h^{\prime }\,e^{-\mu }}{2r} \big (\xi ^{\prime }+\mu ^{\prime })=0, \end{aligned}$$
(40)

where \(\varPsi =\frac{q^2}{r^4}\).

2.3 Embedding class one condition associated with the geometry {\(T_{\mu \nu }\), \(\xi \), \(\mu \)}

If the space-time for \(T_{\mu \nu }\) satisfies the Karmarkar [78] condition, then

$$\begin{aligned} R_{1414}R_{2323} = R_{1212}R_{3434}+R_{1224}R_{1334} \end{aligned}$$
(41)

where the Karmarkar condition must satisfy the Pandey and Sharma condition [79] \(R_{2323}\ne 0\) to describe a class one solution. Then Eq. (41) provides an differential equation which relates both metric functions \(\xi \) and \(\mu \) as,

$$\begin{aligned} {{\mu }'~ {\xi }' \over 1-e^{{\mu }}} = {\mu }'~ {\xi }'-2\,{\xi }''-{\xi }'^2. \end{aligned}$$
(42)

If the space-time satisfy the above condition (41) then corresponding four dimensional space-time can be embedded into five dimensional pseudo-Euclidean space which describe an embedding class one space-time.

On integration of the Eq. (42) which yields

$$\begin{aligned} e^{{\xi }}=\left( A+B\int \sqrt{e^{{\mu }}-1}~dr\right) ^2\quad \text {or}\quad e^{{\mu }}=\left( 1{+}\frac{\xi ^{\prime \,2}}{4B}\,e^{\xi }\right) \nonumber \\ \end{aligned}$$
(43)

where A and B are constants of integration.

Using the definition of ansitropy in Eqs. (34) and (35) together with Eq. (43) we express the anisotropic factor, \(\varDelta (r)\) corresponding to energy–momentum tensor \({T}_{\mu \nu }\) by some manipulation [43] as

$$\begin{aligned} {\varDelta }(r) = {p}_t-{p}_r={{\xi }' \over 32 \pi e^{{\mu }}}\bigg [{2\over r}-{{\mu }' \over e^{{\mu }}-1}\bigg ] \bigg [{{\xi }' e^{{\xi }} \over 2\,r\,B^2}-1 \bigg ]. \nonumber \\ \end{aligned}$$
(44)

From Eq. (44) we see that if \(\varDelta =0\) then we can recover only two kinds of isotropic fluid solutions, namely Schwarzschild interior solution which can be obtained by taking the first factor in Eq. (44) to be zero while vanishing of the second factor in Eq. (44) gives a Kohlar–Chao solution. Both solutions are already discussed in the literature. Therefore, we choose energy-momentum tensor \({T}_{\mu \nu }\) for the anisotropic matter distribution to find a new solution for embedding class one space-time. Before proceeding to the next section we will mention some important comments here: (a) Initially we will solve the field Eqs. (33)-(35) via embedding class one condition to obtain a new solution for the anisotropic star. (b) Then we will solve of Maxwell Eqs. (36)–(38) (known as quasi-Einstein equations) together with conservation Eq. (40). After solving both systems we will determine the complete thermodynamic observable for the charged anisotropic model.

3 New embedding class one solution by gravitational decoupling

In this section, we will present the solutions for both systems. Firstly, we solve the field Eqs. (33)–(35) corresponding to energy-momentum tensor \({T}_{ij}\) which involves two unknown source functions, namely \(\mu \) and \(\xi \). Once both metric functions are specified then immediately we can obtain the complete thermodynamical observable \({\rho }\), \({p_r}\) and \({p_t}\) for stress tensor \(T_{ij}\). It is well known that according to the Lake algorithms, the source function \({\xi }(r)\) should be monotonic increasing and regular minimum at \(r=0\) which provides a physically viable static spherically symmetric perfect fluid solution of Einstein’s equations that is regular at \(r=0\) [80]. Therefore, we chose the source function \(e^{\xi }\) same as Durgapal-IV [81] solution,

$$\begin{aligned} e^{{\xi }}= C\,(1+a\,r^2)^4. \end{aligned}$$
(45)

where a and C are positive constants and the dimension of a is  \(length^{-2}\). The metric function \({\xi }(r)\) in Eq. (45) is regular at centre \(r=0\) and positive increasing throughout within the stellar compact object that gives a realistic compact star model. Now using the embedding class one condition by plugging the Eq. (45) in Eq. (43), we get a following expression for \(e^{\mu }\) of the form,

$$\begin{aligned} e^{{\mu }} = 1+D\,a r^2 (1+ar^2)^2 \end{aligned}$$
(46)

where \(D=16\,a\,C/B\). From Eq. (46) we note that the metric function \(e^{{\mu }}\) can be expressed in the form of \(e^{{\mu }}\rightarrow 1+O(r^2)\). This form provides a necessary condition to be a regular model at the origin. Therefore, the solution of the Einstein field Eqs. (33)–(35) can be given by following line element,

$$\begin{aligned} d\tilde{s}^2= & {} - \left[ 1+D\,a r^2 (1+ar^2)^2\right] \,dr^2 - r^2(d\theta ^2\nonumber \\&+ \sin ^2 \theta ~d\phi ^2) +C\,(1+ar^2)^4\, dt^2. \end{aligned}$$
(47)

Now we will determine electric field E and deformation functions f(r) and g(r) by solving of Maxwell Eqs. (36)–(38). The Eqs. (36)–(38) are containing especially three undermined unknowns namely q, h and f because \(\mu \) and \(\xi \) are already obtained in Eqs. (45) and (46). Now we solve the conservation Eq. (42) by taking a suitable form of deformation function h(r). As we see that the Eq. (42) is a first order ordinary differential equation which can be written in form of integral as,

$$\begin{aligned} \varPsi =\frac{\alpha }{2\,r^4}\int {{h^{\prime }\,e^{-\mu }} \big (\xi ^{\prime }+\mu ^{\prime })}\,r^3\,dr. \end{aligned}$$
(48)

Substituting the value of \(\xi \) and \(\mu \) from Eqs. (45) and (46) in above integral Eq. (48), we get

$$\begin{aligned} \varPsi =\frac{\alpha }{2\,r^4}\int {\frac{2\,a\,r^4\,\big [4 {+} D (1 {+} a r^2)^2\,(1 {+} 7 a r^2)\big ]\,{h^{\prime }}}{(1{+}a r^2)\,\big [1 {+} D(a r^2 {+} 2 a^2\,r^4 {+} a^3\,r^6)\big ]^2}}\,dr.\nonumber \\ \end{aligned}$$
(49)

Now the choice for h(r) depends upon three following facts: (i) The deformation function h(r) should be non singular at centre and monotonically increasing within compact object, (ii) The Eq. (49) should be integrable under the choice of h(r), (iii) The function \(\varPsi (r)=\frac{q^2}{r^4}\) in Eq. (49) must vanish at centre of the star and monotonically increasing (Fig. 1). By keeping these points, we choose the expression for deformation function \(h^{\prime }(r)\) as,

$$\begin{aligned} h^{\prime }(r)=2a\,r\,(1+a r^2)\,\big [1 + D(a r^2 + 2 a^2\,r^4 + a^3\,r^6)\big ]^2.\nonumber \\ \end{aligned}$$
(50)

On inserting the value of \(h^{\prime }(r)\) in Eq. (49) and the integrate w.r.t  r  we get,

$$\begin{aligned} \varPsi =\frac{q^2}{r^4}=\frac{\alpha \,a^2\, r^2\,}{12}\,\left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] .\nonumber \\ \end{aligned}$$
(51)
Fig. 1
figure 1

The behavior of electric charge q(r) verses radial coordinate r / R. For obtaining the trend of the charge inside the object we have taken mass-radius ratio \(M/R=0.2\) for different values of parameter \(\alpha \)

Full size image

Now substituting the Eq. (51) in Eq. (36) we obtain,

$$\begin{aligned} {(r\,f)^{\prime }}=-\frac{a^2\, r^4}{12}\,\left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] ,\nonumber \\ \end{aligned}$$
(52)

On integrating of Eqs. (50) and (52) which yield the deformation functions h(r) and f(r) as,

$$\begin{aligned} h(r){=}\frac{140 a\,r^2 (6 {+} h_ 1 (r)) {+} D\,a^4\,r^8 [84 (15{+}4 a r^2) {+} 5 D h_ 2 (r)]}{840}, \end{aligned}$$
(53)
$$\begin{aligned} f(r){=}-\frac{a^2 r^4\, [1232 {+} D (308 {+} 1485 a r^2 {+} 1540 a^2 r^4 {+} 490 a^3 r^6)]}{4620},\nonumber \\ \end{aligned}$$
(54)

where, \( h_ 1 (r) = 3 a (1 + 2 D) r^2 + 2 a^2 D (6 + D) r^4\), \(h_ 2 (r) = (210 + 336 a r^2 + 280 a^2 r^4 + 120 a^3 r^6 + 21 a^4 r^8)\).

Then the complete deformed metric potentials are given as,

$$\begin{aligned}&e^{\nu } = C\,(1+ar^2)^4\,e^{\alpha \, h(r)} \end{aligned}$$
(55)
$$\begin{aligned}&e^{\lambda } = \frac{[1+D\,ar^2\,(1+ar^2)^2]}{1+[1+D\,ar^2\,(1+ar^2)^2]\,\alpha \,f(r)}. \end{aligned}$$
(56)

and corresponding space-time can be expressed as,

$$\begin{aligned} ds^2= & {} \big [C\,(1+ar^2)^4\,e^{\alpha \,h(r)}\,\big ] dt^2- r^2(d\theta ^2 + \sin ^2 \theta ~d\phi ^2)\nonumber \\&+\bigg [\frac{[1+D\,ar^2\,(1+ar^2)^2]}{1+[1+D\,ar^2\,(1+ar^2)^2]\,\alpha \,f(r)}\bigg ] dr^2, \end{aligned}$$
(57)

where h(r) and f(r) are given by Eqs. (53) and (54). This deformed space-time (57) will provide a complete structure of the matter distribution for effective energy momentum tensor \(T^{\text {eff}}_{\mu \nu }\).

Fig. 2
figure 2

The behavior of deformations functions h(r) (top left) and |f(r)| (top right) while the deformed metric potentials \(e^{\nu (r)}\) (bottom left) and \(e^{\lambda (r)}\) (bottom right) verses radial coordinate r / R. For plotting of this figure we have taken the mass-radius ratio \(M/R=0.2\)

Full size image

Now the effective pressures and effective density can be written as,

$$\begin{aligned} 8\pi \,\rho ^{\text {eff}}= & {} 8\pi \,\rho +\frac{q^2}{r^4}, \end{aligned}$$
(58)
$$\begin{aligned} 8\pi \,p_r^{\text {eff}}= & {} 8\pi \,p_r-\frac{q^2}{r^4}, \end{aligned}$$
(59)
$$\begin{aligned} 8\pi \,p_t^{\text {eff}}= & {} 8\pi \,p_t+\frac{q^2}{r^4}. \end{aligned}$$
(60)

Then the corresponding expressions for \(\rho ^{\text {eff}}\), \(p_r^{\text {eff}}\) and \(p_t^{\text {eff}}\) can be given as,

$$\begin{aligned} \rho ^{\text {eff}}= & {} \frac{a D (1 {+} a r^2) [3 {+} 7ar^2 {+} D (ar^2 {+} 3a^2 r^4 {+} 3 a^3 r^6 {+} a^4 r^8)]}{8\pi \,[1{+}D (ar^2 {+} 2 a^2r^4 {+} a^3 r^6)]^2}\nonumber \\&{+}\frac{\alpha }{96\pi }\, a^2 r^2 \left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] , \end{aligned}$$
(61)
$$\begin{aligned} p_r^{\text {eff}}= & {} \frac{a\,[8{-}D\,(1{+}ar^2)^3]}{8\pi \,(1 {+} a r^2)\,[1{+}D\,ar^2\,(1{+}ar^2)^2]} \nonumber \\&{-}\frac{\alpha }{96\pi }\, a^2 r^2\left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] , \end{aligned}$$
(62)
$$\begin{aligned} p_t^{\text {eff}}= & {} \frac{a\,[8 {+} 16 a r^2 {+} D ({-}1 {+} a r^2) (1 {+} a r^2)^3]}{8\pi \,(1 {+} a r^2)^2\,[1 {+}D\,ar^2(1{+}ar^2)^2]} \nonumber \\&{+}\frac{\alpha }{96\pi }\, a^2 r^2 \left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] .\nonumber \\ \end{aligned}$$
(63)

Using Eqs. (62) and (63), we obtain effective anisotropy \(\varDelta ^\mathrm{eff}\) as

$$\begin{aligned} \varDelta ^{\text {eff}}= & {} \frac{a^2r^2\, [8 {-} 6 D (1 {+} a r^2)^3 {+} D^2 (1 {+} a r^2)^6]}{8\pi \,(1 {+} a r^2)^2\,[1 {+}D\,ar^2(1{+}ar^2)^2]^2}\nonumber \\&{+}\frac{\alpha }{48\pi \,}\, a^2 r^2 \left[ 16 {+} D (4 {+} 27 a r^2 {+} 36 a^2 r^4 {+} 14 a^3 r^6)\right] .\nonumber \\ \end{aligned}$$
(64)
Fig. 3
figure 3

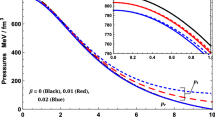
The variation of pressures \(p_r^{\text {eff}}\) (top left), \(p_t^{\text {eff}}\) (top right), energy density \(\rho ^{\text {eff}}\) (bottom left) and anisotropy \(\varDelta ^{\text {eff}}\) (bottom right) verses radial coordinate r / R. For finding the trend of physical thermodynamic observable we have used same mass-radius ratio \(M/R=0.2\)

Full size image

4 Matching conditions

For the study of stellar interiors, it is a necessary and important point that the interior spacetime geometry must join with the exterior spacetime geometry in a smooth way. For doing this, we will introduce the well known Israel–Darmois junction conditions [82, 83]. These junction conditions require the continuity of the gravitational potentials across the surface \(\varSigma \) boundary (defined by \(r=R\))

$$\begin{aligned} \left[ ds^{2}\right] _{\varSigma }=0, \end{aligned}$$
(65)

or equivalently

$$\begin{aligned} e^{\nu ^{-}(r)}|_{r=R}= & {} e^{\nu ^{+}(r)}|_{r=R}, \end{aligned}$$
(66)
$$\begin{aligned} e^{\lambda ^{-}(r)}|_{r=R}= & {} e^{\lambda ^{+}(r)}|_{r=R}. \end{aligned}$$
(67)

The above expressions are called as the first fundamental form. On the other hand, It is also required for a vanishing radial pressure at the boundary of the star as,

$$\begin{aligned} p_{r}(r)|_{r=R}=0 \mapsto p^{\text {eff}}_{r}(r)|_{r=R}=0. \end{aligned}$$
(68)

The above condition is known as the second fundamental form which determines the size of the compact object i.e the radius R. Moreover, since the compact object contains a charge, then the continuity of the electric charge q(r) on the surface of the compact object must be added to the first fundamental form,

$$\begin{aligned} q(r)|_{r=R}=Q, \end{aligned}$$
(69)

where Q is the total charge of the compact object. On the other hand, if the electric charge is a continuous function of the radial coordinates across the boundary then the electric field E(r) will also continuous across the boundary of the compact object. Then, it is observed that the Riemannian exterior manifold can be described by the well known Reissner–Nordström spacetime, which is given as,

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}+\frac{q^2}{r^2}\right) dt^{2} -\left( 1-\frac{2M}{r}+\frac{q^2}{r^2}\right) ^{-1}\,dr^{2} \nonumber \\&-r^{2} \left( d\theta ^{2}+\sin ^{2} \theta d\phi ^{2}\right) , \end{aligned}$$
(70)

we obtained the explicit expressions by matching of the first fundamental form as,

$$\begin{aligned}&\bigg [\frac{1{+}[1{+}D\,ar^2\,(1{+}ar^2)^2]\,\alpha \,f(r)}{[1{+}D\,ar^2\,(1{+}ar^2)^2]}\bigg ]=\bigg (1{-}{\frac{2M}{R}}{+}\frac{Q^2}{R^2}\bigg ), \end{aligned}$$
(71)
$$\begin{aligned}&C\,(1+aR^2)^4\,e^{\alpha \,h(R)}= \left( 1-{\frac{2M}{R}} +\frac{Q^2}{R^2}\right) . \end{aligned}$$
(72)

Here the parameter M represents the total mass containing within the compact star. By solving of the Eqs. (71) and (72) and second fundamental form given by (68) we get the expressions for the constant parameters D, M and C as,

$$\begin{aligned} D= & {} \frac{-D_1(R) {+} \sqrt{(1 {+} aR^2)^2\,[D_2(R) {+} D_3(R) {+} D_4(R)]}}{2\,\alpha \,a^2R^4\,(1 {+} aR^2)^3\, (4 {+} 27 aR^2 {+} 36 a^2R^4 {+} 14 a^3R^6)}, \end{aligned}$$
(73)
$$\begin{aligned} M= & {} \frac{R}{2}\,\bigg [\frac{\alpha \,a^2\,R^4}{12}\,M_1(R){+}\frac{D\,aR^2\,(1{+}aR^2)^2}{1{+}D\,aR^2\,(1{+}aR^2)^2}{-}\alpha \,f(R)\bigg ], \end{aligned}$$
(74)
$$\begin{aligned} C= & {} \frac{1+[1+D\,aR^2\,(1+aR^2)^2]\,\alpha \,f(R)}{(1+aR^2)^4\,[1+D\,aR^2\,(1+aR^2)^2]\,e^{\alpha \,h(R)}}. \end{aligned}$$
(75)

where,

$$\begin{aligned} M_1(R)= & {} [16 + D (4 + 27 a R^2 + 36 a^2 R^4 + 14 a^3 R^6)],\\ D_1(R)= & {} 4 (9 + \alpha ) aR^2 + (36 + 47 \alpha ) a^2R^4\\&+ 3 (4 + 37 \alpha ) A^3R^3\\&+ 98 \alpha A^4 R^8+ 30 \alpha a^5R^{10}+12,\\ D_2(R)= & {} 144 + 96 (6 + \alpha ) aR^2 + 8 (108\\&+ 345 \alpha + 2 \alpha ^2) a^2R^4,\\ D_3(R)= & {} 8 (72 + 1962 \alpha + 11 \alpha ^2) a^3R^6\\&+ 3 (48 + 9736 \alpha )\,a^4R^8 \\&+ 153 \alpha ^2\,a^4R^8 +24 \alpha (928 + 3 \alpha ) a^5R^{10}, \\ D_4(R)= & {} 4 (1524 - 7 \alpha ) \alpha a^6 R^{12}- 16 {\alpha }^2 a^7R^{14} + 4 \alpha ^2 a^8R^{16}. \end{aligned}$$

5 Physical analysis

5.1 Regularity of the gravitational decoupling model

For the physical acceptable model, the solution must be free from the geometrical and physical singularity i.e. the deformed gravitational potentials must be regular at the centre and throughout within the compact object. From Eqs. (55) and (56) we can easily observe that \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) fulfil the requirement of regularity at centre as,

$$\begin{aligned} e^{\nu (0)}=C,\quad e^{\lambda (0)}=1. \end{aligned}$$
(76)

Since the gravitational potentials must be positive within the compact object then the Eq. (76) provided that the constant C must be positive. The profile of gravitational potentials has been shown in Fig. 2 which is shows that the gravitational potentials are regular and positive throughout the fluid model. Moreover we have also determined the behavior of effective physical parameters such as density (\(\rho ^{\text {eff}}\)), radial pressures (\(p_r^{\text {eff}}\)) and tangential pressure (\(p_t^{\text {eff}}\)) within the self-gravitating stellar object. For the regular stellar model, the above physical parameters must be positive and decreasing outward as well as the maximum value must attains at the centre of the compact object (Fig. 3). For this purpose we determine the central value of these physical parameters to fix the range of the arbitrary constants which are as follows,

$$\begin{aligned}&\big (\rho ^{\text {eff}}\big )_{r=0}=\frac{3\,a\,D}{8\,\pi }~> 0 \Longrightarrow ~D>0~(\text {as}~ a~ \text {is~ positive}), \end{aligned}$$
(77)
$$\begin{aligned}&\big (p_r^{\text {eff}}\big )_{r=0}=\big (p_t^{\text {eff}}\big )_{r=0}=\frac{a\,(8-D)}{8\,\pi }~>0~\Longrightarrow ~ D<8.\nonumber \\ \end{aligned}$$
(78)

Now, the ratio of pressure and density should be less than unity that gives,

$$\begin{aligned} \bigg (\frac{p^{\text {eff}}}{\rho ^{\text {eff}}}\bigg )_{r=0} \le 1~~ \Longrightarrow ~~~D\ge 2. \end{aligned}$$
(79)

In addition to above the causality condition must satisfy everywhere within the star i.e. \(\text {v}^2_r<1\) and \(\text {v}^2_t<1\). Then we obtain the values of \((\text {v}^2_r)_{r=0}\) and \((\text {v}^2_t)_{r=0}\) as,

$$\begin{aligned}&(\text {v}_r^2)_{r=0}=\frac{-3 D^2 + 4 (6 + \alpha ) + D (30 + \alpha )}{15 D^2 - 4 \alpha - D (30 + \alpha )} < 1, \end{aligned}$$
(80)
$$\begin{aligned}&(\text {v}^2_t)_{r=0}=\frac{-6 D^2 + D (48 - \alpha ) - 4 k}{15 D^2 - 4 \alpha - D (30 + \alpha )} < 1. \end{aligned}$$
(81)

Since D is positive then from the Eqs. (80) and (81) we get,

$$\begin{aligned}&D>\frac{(2\,\alpha +60)+\sqrt{(2\alpha +60)^2+72\,(8\alpha +24)}}{36} , \end{aligned}$$
(82)
$$\begin{aligned}&D>\frac{78}{21} . \end{aligned}$$
(83)

Using the Eqs. (77)–(79) and (82), (83), we get the following inequality as,

$$\begin{aligned}&\frac{(2\,\alpha +60)+\sqrt{(2\alpha +60)^2+72\,(8\alpha +24)}}{36}~< D <~8 , \end{aligned}$$
(84)
$$\begin{aligned}&\frac{78}{21}~< D <~8. \end{aligned}$$
(85)

It can be easily verified that If the coupling parameter \(\alpha \) is very small as near to zero then the inequality (84) holds for D while the Eq. (85) will provide the restriction on D for the large values of \(\alpha \).

5.2 Equilibrium condition for GD model

In this section, we will discuss the equilibrium condition for the geometric deformation (GD) for decoupling source \(\varTheta _{\mu \nu }\) via generalised Tolman–Oppenheimer–Volkoff (TOV) equation. It is well known that the equilibrium condition can be described from the conservation equation of \(T^{\text {eff}}_{\mu \nu }\) as follows,

$$\begin{aligned} \nabla ^{\mu }T^{\text {eff}}_{\mu \nu }=0. \end{aligned}$$
(86)

The explicit form of the Eq. (86) can be described as,

$$\begin{aligned} ({T}^1_{1}+\varTheta ^1_1)^{\prime }- & {} \frac{\nu ^{\prime }}{2}\,\left( {T}^0_{0}-{T}^1_{1}+\varTheta ^0_0-\varTheta ^1_1\right) \nonumber \\- & {} \frac{2}{r}\,\left( {T}^2_{2}-{T}^1_{1}+\varTheta ^2_2-\varTheta ^1_1\right) =0. \end{aligned}$$
(87)

After substituting the components of \(T^{\mu }_{\nu }\) and \(\varTheta ^{\mu }_{\nu }\) from Eqs. (31) and (32) into Eq. (87) we get,

$$\begin{aligned} -p^{\prime }_r- & {} \frac{\xi ^{\prime }}{2}\,(\rho +p_r)+\frac{2}{r}\,(p_t-p_r) +\frac{2\,q\,q^{\prime }}{8\pi \,r^4}\nonumber \\- & {} \frac{\alpha \,h^{\prime }}{2}\,(\rho +p_r)=0. \end{aligned}$$
(88)

Now the Eq. (88) shows that the system is balanced under different forces as,

$$\begin{aligned}&\text {Hydrostatic force:} F_h=-\frac{d{p_r}}{dr},\end{aligned}$$
(89)
$$\begin{aligned}&\text {Gravitational force:} F_g=-\frac{\xi ^{\prime }}{2}\,({\rho }+{p_r}),\end{aligned}$$
(90)
$$\begin{aligned}&\text {Electric force:} F_e=\frac{2\,q\,q^{\prime }}{8\,\pi \,r^4},\end{aligned}$$
(91)
$$\begin{aligned}&\text {Anisotropic force:} F_a=\frac{2\,}{r}\,(p_t-p_r),\end{aligned}$$
(92)
$$\begin{aligned}&\text {Coupling force:} F_{\alpha }=- \frac{\alpha \,h^{\prime }}{2}\,(\rho +p_r). \end{aligned}$$
(93)
Fig. 4
figure 4

The behavior of different forces verses radial coordinate r / R. The description of the figures as follows: (i) top left for \(\alpha =0.0\), (ii) top right for \(\alpha =0.10\), (iii) bottom left for \(\alpha =0.25\), and (iv) bottom right for \(\alpha =0.50\). For plotting of this figure we have taken the mass-radius ratio \(M/R=0.2\)

Full size image

These above forces form the equilibrium of the system. The variation of these forces is intensely connected to the constant parameter \(\alpha \). Figure 4 shows that how we reached the equilibrium of the GD system under these different forces. Now we will focus on several points based on the different values taken for establishing the equilibrium stage. We have plotted the Fig. 4 for several values of \(\alpha \). The top left figure is plotted of \(\alpha =0.0\). As we see that the electric force (\(F_e\)) and extra coupling force (\(F_{\alpha }\)) have no effect to balance this mechanism however the gravitational force (\(F_g\)) is balanced by joint action of hydrostatic (\(F_h\)) and anisotropic (\(F_a\)) forces. On the other hand, the Figures top right, bottom left and bottom right have been plotted for \(\alpha =0.10\), \(\alpha =0.25\) and \(\alpha =0.50\), respectively. From these figures, it is interesting to note that the electric force \(F_{e}\) and coupling force \(F_{\alpha }\) have same values in magnitude within the star but they are acting in the opposite directions while \(F_g\) can be balanced by combining of \(F_a\) and \(F_h\). Therefore, the equilibrium is achieved for each different value of \(\alpha \).

5.3 Stability of the stellar model via cracking

Normally after analyzing of equilibrium condition of the system, it is necessary to determine the stability of the model. For this purpose, it is essential to examine whether the perturbation introduced by the pressure anisotropy yields a stable equilibrium system or not. To analyze this condition, we use Abreu’s criteria [84] which has been developed by Herrera’s cracking criterion [85]. The Abreu’s criteria for the stability analysis of the stellar compact objects can be described by the subliminal radial and tangential sound speeds as,

$$\begin{aligned}&-1\le v^{2}_{t}-v^{2}_{r}\le 1 \nonumber \\&\quad = \left\{ \begin{array}{ll} -1\le v^{2}_{t}-v^{2}_{r}\le 0,&{}\quad \mathrm {Potentially\ stable\ } \\ 0< v^{2}_{t}-v^{2}_{r}\le 1, &{}\quad \mathrm {Potentially\ unstable} \end{array} \right\} . \end{aligned}$$
(94)
Fig. 5
figure 5

The variation of radial (\(\text {v}^2_r\)) and tangential (\(\text {v}^2_t\)) speed of sound verses radial coordinate r / R. For plotting of this figure we have employed same data values as used in Fig. 4

Full size image

Clearly it can be observed that both radial and tangential subliminal speed of sound must fulfill the causality condition i.e. \(v^{2}_{r}<1\) and \(v^{2}_{t}<1\) everywhere inside the compact object (by taking the speed of light \(c=1\) in relativistic geometrized units). From the Fig. 5, it is clear that the obtained stellar model satisfies the causality condition. But we would mention an interesting point that for increasing value of \(\alpha \) the radial velocity behaves dual nature i.e. first it is decreasing and then start increasing when \(\alpha \ge 0.275\) while tangential velocity decreases throughout for all values of \(\alpha \). Now let us discuss the stability of the model through the cracking concept. Form the Fig. 6, we observe that stability factor \(\text {v}^2_t-\text {v}^2_r\) lies between \(-1\) and 0 and the factor \(\text {v}^2_r-\text {v}^2_t\) lies between 0 and 1. This shows that radial velocity is greater than the tangential velocity throughout the star as well as there is no cracking appears within the model. Therefore, the obtained self-gravitating model is stable.

Fig. 6
figure 6

The variation of stability factors \(\text {v}^2_t-\text {v}^2_r\) (top) and \(\text {v}^2_r-\text {v}^2_t\) (bottom) verses radial coordinate r / R. For plotting of this figure we have employed same data values as used in Fig. 4

Full size image

6 Mass-radius ratio and surface redshift

6.1 Gravitational and effective mass

To describe the structure of the compact object it is necessary to study the upper limit of the mass-radius ratio. It is well known that the upper limit of the mass-radius ratio for the isotropic matter distribution is given by Buchdahl’s [86]. This limit was founded in the context of perfect fluid which has a decreasing energy density outwards. The upper bound of mass-radius can be given as,

$$\begin{aligned} \frac{2M}{R}\le \frac{8}{9}, \end{aligned}$$
(95)

where M is the total mass of the perfect fluid sphere and R the radius of the star in Schwarzschild coordinates, which is determined by the vanishing of pressure on the boundary of the star. The above inequality has a significant implication, which gives the maximum limit of the surface redshift \(\text {z}_s\).

However, the Buchdahl’s limit is changed in the presence of electric charge. In this situation, the upper and lower limits are given by Andreasson [87] and Bohmer and Harko [88] as,

$$\begin{aligned} \frac{Q^{2}\left( 18R^{2}{+}Q^{2}\right) }{2R^{2}\left( 12R^{2}{+}Q^{2}\right) }\le \frac{M}{R}\le \frac{4R^{2}{+}3Q^{2}{+}2R\sqrt{R^{2}{+}3Q^{2}}}{9R^{2}}.\nonumber \\ \end{aligned}$$
(96)

Here we would like to mention that the mass M appears in the Eq. (96) is not the same as the total mass in (95). More clearly, we can say that the total mass in (95) describes the mass for an isotropic fluid sphere which is exactly equal to the gravitational and effective mass in case of the perfect fluid matter distribution. Explicitly it can be written as,

$$\begin{aligned} M=m(R)=4\pi \int ^{R}_{0}r^{2}\rho (r)dr=\frac{R}{2}\left[ 1-e^{-\lambda (R)}\right] . \end{aligned}$$
(97)

On the other hand, the mass M appears in expression (96) defines the gravitational mass for the charged compact object which is given as

$$\begin{aligned} M= & {} m(R)=4\pi \int ^{R}_{0}r^{2}\rho ^{\text {eff}}(r)dr\nonumber \\&+\frac{1}{2}\int ^{R}_{0}\frac{Q^{2}(r)}{r^{2}}dr+\frac{Q^{2}(R)}{2R}\nonumber \\= & {} \frac{R}{2}\left[ 1-e^{-\lambda (R)}+\frac{Q^{2}(R)}{R^{2}}\right] . \end{aligned}$$
(98)

From the Eqs. (97) and (98), it can be observed that the gravitational mass has more value in the case of electrically charged compact structures as compared to uncharged perfect fluid matter distribution. Therefore, the effective mass for the charged compact object can be given as,

$$\begin{aligned} M_{\text {eff}}= & {} m_{\text {eff}}(R)=4\pi \int _{0}^{R}\left( {\rho ^{\text {eff}}}+\frac{q^{2}}{8\pi \,r^4}\right) r^{2}dr\nonumber \\= & {} \frac{R}{2}\left[ 1-e^{-\lambda (R)}\right] . \end{aligned}$$
(99)

6.2 Surface and gravitational redshift

It was discussed in the above section that the mass-radius ratio plays an important role to decide the value of surface redshift \(Z_s\). Then the surface red-shift can be calculated as,

$$\begin{aligned} \text {z}_s= & {} \left( 1-2u\right) ^{-1/2}-1\nonumber \\= & {} e^{\lambda (R)/2}-1, \quad \text{ where } \quad u\equiv \frac{M_{\text {eff}}}{R}. \end{aligned}$$
(100)

while the gravitational redshift within the stellar models can be calculated by following formula,

$$\begin{aligned} \text {z}={e^{-\nu (r)/2}}-1. \end{aligned}$$
(101)

The variation of gravitational redshift within the stellar model is given in Fig. 7. From this figure, we predict that the gravitational redshift is maximum at centre and decreasing away from centre. The numerical values of surface redshift is given in Table 2 for different values of coupling parameter \(\alpha \).

Fig. 7
figure 7

The behavior of gravitational redshift (Z) verses radial coordinate r / R. We have used the same data values for plotting of this figure as given in Fig. 1

Full size image
Table 1 The numerical values of physical parameters and constants of the compact star of mass \(M=1.04M_{\odot }\) and radius \(R=7.67\) km for different values of \(\alpha \)
Full size table
Table 2 Comparative study of lower bound, mass-radius ratio, upper bound, compactness \((u=M_{\text {eff}}/R)\) and surface red-shift of the star for different values of \(\alpha \)
Full size table

7 Discussion and conclusions

Our study is dedicated to a new class of completely deformed solution for the spherically symmetric charged anisotropic compact stellar model. This completely deformed solution has been obtained by using the gravitational decoupling approach in the framework of embedding class one spacetime. In our investigations, we confirm that the ‘gravitational decoupling’ technique is a powerful mechanism to determine a more general solution of the Einstein field equations in the scenario of embedding class one spacetime. To be more specific, in this study first we define the action for the modified matter distribution via introducing another extra source. Then we write the general equation of motion by varying this action along with the metric tensor \(g^{\mu \nu }\). Next, we obtain the Einstein field equations of spherically symmetric metric corresponding to the above general equation of motion for effective energy-momentum tensor \(T^{\text {eff}}_{\mu \nu }\), which is the combination of two sources namely \(T_{\mu \nu }\) and \(\varTheta _{\mu \nu }\). By using gravitational decoupling \({{\xi }}~\mapsto ~ \nu = \xi +\alpha \ h(r)\) and \(e^{-{\mu }}~ \mapsto ~ e^{-\lambda } = e^{-{\mu }}+\alpha \,f(r)\), we separated the effective system into two separate systems as first corresponds to \(T_{\mu \nu }\) (known as Einstein field equations) and second for \(\varTheta _{\mu \nu }\) (Known as quasi-Einstein field equations). Now our aim is to solve both systems individually. As we see that the first system [Eqs. (33)–(35)] depend on two unknowns \(\xi \) and \(\mu \). To solve this system we chose a particular form of gravitational potential, \(\xi =C(1+ar^2)^4\), same as Durgapal IV solution which satisfies all the physical and mathematical requirements for a regular and well-behaved solution [89]. Then we apply the embedding class one condition to determine the solution for this system for anisotropic matter distribution. Now we will focus on second system which is given by the Eqs. (18)–(20). Before solving these equations, first we converted the quasi-Einstein Eqs. (18)–(20) into a Maxwell field Eqs. (36)–(38) by applying the Ovalle [58] approach. Now we see that field Eqs. (36)–(38) depend on mainly three unknowns as electric charge q, deformation functions h(r) and f(r). For determining the solution of this Maxwell system, we need to solve the conservation Eq. (40) which is a first-order ordinary differential (ODE) equation containing two unknown functions \(\varPsi \) and h(r), where (\(\varPsi ={q^2}/{r^4}\)). Therefore, we solve this ODE by taking a specific form of deformation function h(r) [which is non-singular at the center and increasing away from the centre, see Eqs. (50) and (53)], and then obtained a closed-form expression for electric field (Eq. 51). Then after we obtain an another deformation function f(r) [see Eq. (54)] by solving of the Eq. (36) together with Eq. (51). In this way, we have solved both systems completely and the obtained solution for this complete system is given by line element (57). Moreover, we also determined the effective quantities density, pressures (radial and tangential) and anisotropy factor to describe the structure of the charged compact object. To perform the graphical analysis we used the matching conditions and obtain all the arbitrary constants. The physical analysis of the solution for the charged compact object is given as follows:

The behavior of electric charge q is shown in Fig. 1 for different values of \(\alpha \) with respect to specific mass-radius ratio \(M/R=0.2\). From this figure we see that electric charge is zero at centre and increasing towards the boundary of star. We have also calculated the amount of charge on the boundary in Coulomb unit as: (i) \(Q=0.5593\times 10^{20} \text {C}\) for \(\alpha =0.10\), (ii) \(Q=0.8748\times 10^{20} \text {C}\) for \(\alpha =0.25\), (iii) \(Q=1.0278\times 10^{20} \text {C}\) for \(\alpha =0.35\), (iv) \(Q=1.2156\times 10^{20} \text {C}\) for \(\alpha =0.50\). This amount of charge shows that it is increasing as \(\alpha \) increases.

In Fig. 2, the variation of deformations function h(r) and f(r) are given by top (left and right) figures while the bottom (left and right) figures are corresponding to gravitational potentials, viz. \(e^{\lambda }\) and \(e^{\nu }\) for different \(\alpha \) and fixed \(M/R=0.2\). It can be clearly seen that for each different values of \(\alpha \), the both deformation functions and gravitational potential are free from singularity and increasing throughout within the compact stellar model. The such behavior of h(r), f(r), \(e^{\lambda }\) and \(e^{\nu }\) gives a physically well-behaved stellar model. The variation of effective matter distribution \(p^{\text {eff}}_r\) and \(p^{\text {eff}}_t\) against the radial coordinate r / R are given shown in top (left and right) of Fig. 3 while \(\rho ^{\text {eff}}\) and \(\varDelta ^{\text {eff}}\) are featured in bottom (left and right) of this Fig. 3. From this figure, we observe that effective pressures and density are maximum at the centre and decreasing outward. Also, the effective anisotropy is zero at the centre (i.e. radial and tangential pressure are equal at center) and positive throughout within in stellar model. This feature of anisotropy shows that the force due to anisotropy is directed outward which allows the construction of a more compact object. Moreover, the numerical values for central pressure, central and surface density are given in Table 1. The surface density of the present model lies between \(3.131\rho _s-3.112\rho _s\) which is higher than the normal nuclear density \(\rho _s\) [9, 90, 91]. The above range of surface density confirm that the obtained stellar structure is an appropriate candidate for the hypothetical ultradense compact object.

To check the equilibrium position of all forces, we have studied the generalized TOV equation for a gravitationally decoupled system. In Fig. 4, we have shown the distributions of all forces \(F_h\), \(F_a\), \(F_g\), \(F_e\) and \(F_{\alpha }\) for the coupling parameter \(\alpha =0.0\) (top left), \(\alpha =0.10\) (top right), \(\alpha =0.25\) (bottom left) and \(\alpha =0.50\) (bottom right). From these individual figures, we see that all forces achieve the equilibrium condition, which shows the stability of the system. In this gravitational decoupled system, a new kind of force \(F_{\alpha }\) is coming due to the geometric deformation in the gravitational potential source. For all values of \(\alpha >0\), this extra force \(F_{\alpha }\) acts along inward direction and behaves an attractive nature which is balanced by electric force \(F_e\) such that \(F_e +F_\alpha =0\), this yields an equilibrium condition for the extra source \(\varTheta _{\mu \nu }\). On the other hand, the gravitational force \(F_{g}\) is balanced by the joint action of hydrostatic force \(F_h\) and anisotropic force \(F_a\) such that \(F_g+F_h+F_a=0\), which provides the stable equilibrium for the matter distribution \(T_{\mu \nu }\). By combining of both equilibrium conditions, we get \(F_g+F_h+F_a+F_e +F_\alpha =0\). This last equation shows that our complete system is in equilibrium stage.

The causality and stability analysis of the model have been shown in Figs. 5 and 6, respectively. From Fig. 5, we observe that both velocities are satisfying the causality condition, i.e. \(0<\text {v}^2_r<1\) and \(0<\text {v}^2_t<1\), everywhere within the star. Moreover, it is interesting to see from this figure that the radial speed of sound (\(\text {v}^2_r\)) is decreasing throughout for \(0<\alpha <0.27\) while if \(\alpha \ge 0.27\), then \(\text {v}^2_r\) decreases first and reach the minimum level and then start increasing towards the boundary. This feature of the \(\text {v}^2_r\) shows that the solution is not well behaved for higher values of \(\alpha \) (Lake and Delgaty [89]). On the other hand, the tangential speed of sound is decreasing throughout the compact object for all values of \(\alpha \). Now we will focus on the stability of the model via Aberu criterion (known as Herrera cracking concept). For this purpose, we plotted the stability factors \(\text {v}^2_t-\text {v}^2_r\) (upper panel) and \(\text {v}^2_r-\text {v}^2_t\) (lower panel) against the radial coordinate r / R in Fig. 6. From this figure it can be clearly observed that both factors lie within the stability range i.e. \(0<\text {v}^2_r-\text {v}^2_t<1\) and \(-1<\text {v}^2_t-\text {v}^2_r<0\). This stability range shows that the radial velocity is always greater than the tangential velocity throughout the star. Therefore, the obtained stellar model is stable.

Now at last we discuss the most important physical features as gravitational and effective mass, and surface redshift of the present model. It is argued that the gravitational mass in always greater than effective mass in presence of electric charge within the matter distribution. However, both masses are same for the perfect or anisotropic fluid matter distribution i.e. only in absence of charge (see subsection 6.1 for complete details). In Table 2, the numerical values of the effective mass-radius ratio \(\big (\frac{M_{\text {eff}}}{R}\big )\) are given for different \(\alpha \) with fixed gravitational mass-radius ratio \(\big (\frac{M}{R}\big )\). From this table we have also noticed that the ratio \(\frac{M_{\text {eff}}}{R}\) is decreasing for increasing \(\alpha \). Since the surface redshift depends on the compactness \(\big (u=\frac{M_{\text {eff}}}{R}\big )\) then the surface redshift will also decrease if \(\alpha \) increases which can be seen in Table 2. The obtained surface redshift for different values of \(\alpha \) is given as follows: (i) \(\text {z}_s=0.2911\) for \(\alpha =0.0\), (ii) \(\text {z}_s=0.286885\) for \(\alpha =0.10\), (iii) \(\text {z}_s=0.280921\) for \(\alpha =0.25\), (iv) \(\text {z}_s=0.277152\) for \(\alpha =0.35\), and (v) \(\text {z}_s=0.271582\) for \(\alpha =0.50\). The Fig. 7 shows the behavior gravitational redshift inside the charged compact star, which is maximum at centre and decreasing towards the surface boundary, and attains minimum at surface. The above obtained surface redshift is compatible with the values proposed by Ivanov [2] and Bowers and Liang [8]. Finally, we would like to mention that the geometric deformation gravitational decoupling approach is a very effective technique to solve the Einstein field equations for a more complex system.