Naturalising the third family hypercharge model for neutral current $B{-}\hbox {anomalies}$

Abstract

We consider a deformation of the Third Family Hypercharge Model, which arguably makes the model more natural. Additional non-zero charges of the spontaneously broken, family-dependent $U(1)_F$ gauge symmetry are assigned to the second family leptons, and the third family leptons’ charges are deformed away from their hypercharges in such a way that the $U(1)_F$ gauge symmetry remains anomaly-free. Second family $U(1)_F$ lepton charges allow a $Z^\prime$ coupling to muons without having to assume large charged lepton mixing, which risks violating tight lepton flavour violation bounds. In this deformed version, only the bottom and top Yukawa couplings are generated at the renormalisable level, whereas the tauon Yukawa coupling is absent. The $Z^\prime$ mediates a beyond the Standard Model contribution to an effective $({\bar{b}} s) (\bar{\mu }\mu )$ vertex in the combination $C_9=-9C_{10}$ and is able to fit the apparent discrepancy between Standard Model predictions in flavour changing neutral-current $B-$meson decays and their measurements, whilst simultaneously avoiding current constraints from direct $Z^\prime$ searches and other measurements, when $0.8~\text {TeV}< M_{Z^\prime } < 12.5 ~\text {TeV}$.

1 Introduction

Various measurements of B meson decays are currently in tension with Standard Model predictions. For instance, the ratio of branching ratios

$$\begin{aligned} R_{K^{(*)}} \equiv BR(B \rightarrow K^{(*)} \mu ^+ \mu ^-) / BR(B \rightarrow K^{(*)} e^+ e^-) \end{aligned}$$

is predicted to be 1.00 in the Standard Model (SM), for lepton invariant mass squared bin $m_{ll}^2 \in [1.1,6]$ $\hbox {GeV}^2$. In this bin, LHCb measurements [1, 2] imply $R_K=0.846^{+0.060}_{-0.054}{}^{+0.016}_{-0.014}$ and $R_{K^{*}}=0.69^{+0.11}_{-0.07}\pm 0.05$. The branching ratio $B_s \rightarrow \mu ^+ \mu ^-$ [3,4,5,6] is also measured to be lower than the SM prediction, which is accurate at the percent level. Angular distributions in the $B \rightarrow K^{(*)} \mu ^+ \mu ^-$ decays have [7,8,9,10] a higher level of disagreement with SM predictions [11, 12], although theoretical uncertainties in the SM predictions are larger, at the ten(s) percent level. There are several other indications of disagreements between SM predictions and measurements involving the $({\bar{s}} b) ({\bar{\mu }} \mu )$ effective coupling. Henceforth, we shall collectively call these disagreements the Neutral Current $B-$Anomalies (NCBAs).

We begin with the effective Lagrangian pertinent to the NCBAs¹

$$\begin{aligned} {{\mathcal {L}}}_{bs\mu \mu }= & {} \frac{C_L}{(36 ~\text {TeV})^2} \left( \overline{s_L} \gamma _\rho b_L \right) \left( \overline{\mu _L} \gamma ^\rho \mu _L \right) \\&+\,\frac{C_R}{(36 ~\text {TeV})^2} \left( \overline{s_L} \gamma _\rho b_L \right) \left( \overline{\mu _R} \gamma ^\rho \mu _R \right) , \nonumber \end{aligned}$$

(1)

where we are currently neglecting a contribution from right-handed quarks because there is no strong evidence in its favour from the data. The dimensionful denominator in front of each effective coupling is equal to $4 \pi v^2/(V_{tb} V_{ts}^*\alpha )$, where $v=174$ GeV is the SM Higgs vacuum expectation value (VEV), $\alpha$ is the fine structure constant and $V_{tb}$ and $V_{ts}$ are Cabbibo-Kobayashi-Maskawa (CKM) matrix elements.² The SM contributes $C_L^{SM}=8.64$ and $C_R^{SM}=-\,0.18$ [13], the dominant contributions to each being from one-loop Feynman diagrams involving W bosons.

As discussed above, current data strongly favour a beyond the SM (BSM) contribution to $C_L$ and possibly $C_R$ [14,15,16,17,18,19]. One possibility to generate this at tree-level is by a heavy $Z^\prime$ vector boson that has flavour non-universal interactions including

(2)

Once the $Z^\prime$ is integrated out of the theory (such that the appropriate theory is the SM effective field theory SMEFT), one obtains the operators

$$\begin{aligned} {{\mathcal {L}}}_{bs\mu \mu }^{\mathrm {SMEFT}}= & {} \frac{g_{sb} g_{\mu _L}}{M_{Z^\prime }^2} (\overline{s_L} \gamma ^\rho b_L) (\overline{\mu _L} \gamma _\rho \mu _L) \\&+\frac{g_{sb} g_{\mu _R}}{M_{Z^\prime }^2} (\overline{s_L} \gamma ^\rho b_L) (\overline{\mu _R} \gamma _\rho \mu _R). \nonumber \end{aligned}$$

(3)

Matching Eq. 2 with Eq. 2 identifies $C_{L,R}=g_{sb} g_{\mu _{L,R}} (36 ~\text {TeV}/M_{Z^\prime })^2$.

Many models based on spontaneously broken flavour-dependent gauged U(1) symmetries [20, 21] have been proposed from which such $Z^\prime$s may result, for example from $L_\mu -L_\tau$ and related groups [20, 22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Some models also have several abelian groups [55] leading to multiple $Z^\prime$s. Some other models [56, 57] generate BSM contributions to $C_L$ and $C_R$ with loop-level penguin diagrams.

In Ref. [53], we introduced the Third Family Hypercharge Model (TFHM). This model is based on a spontaneously broken anomaly-free flavour-dependent $U(1)_F$ symmetry, namely gauged third family hypercharge, and has the following desirable properties:

• A $Z^\prime$ particle of several TeV in mass is predicted which can explain the NCBAs. The couplings $g_{sb}$ and $g_{\mu _L}$ are generated from the rotation between the weak and mass eigenstates.

• The $Z^\prime$ does not appreciably couple to first or second family quarks (except to the second family quarks through the coupling $g_{sb}$), which is hinted at by a number of experimental data; firstly, the absence of any similar neutral current anomalies in the semi-leptonic decays of lighter mesons such as kaons, pions, or charm-mesons; secondly, the absence of significant deviations with respect to the SM predictions for neutral meson mixing in the kaon and $B_d$ systems; and thirdly, the current absence of direct $Z^\prime$ production in pp collisions at the Large Hadron Collider (LHC), since the production cross-section would be enhanced by sizeable couplings of the $Z^\prime$ to valence quarks.

• The (3,3) entries of the up quark, down quark, and charged lepton Yukawa matrices were the only ones predicted to be non-zero at the renormalisable level. Small corrections to this picture are expected from non-renormalisable operators, but the model explains the hierarchical heaviness of the top and bottom quarks and the tau lepton. It also implies that the two CKM mixing angles involving the third family must be small, agreeing with current experimental measurements.

• The model is free of any gauge anomalies (including mixed or gravitational anomalies) without needing to introduce any additional chiral fermions beyond those of the SM (although sterile right-handed neutrinos may be added in order to provide a mechanism for neutrino mass generation).

The charge assignment of the TFHM is shown in Table 1. The most up-to-date experimental bounds on the parameter space of the TFHM are presented in Ref. [58].

Table 1 $U(1)_F$ charges of the fields in the original Third Family Hypercharge Model (TFHM), where $i \in \{1, 2\}$. All gauge anomalies, mixed gauge anomalies and mixed gauge-gravity anomalies cancel. Under the SM gauge symmetry $SU(3)\times SU(2)_L \times U(1)_Y$, the fields transform as $H \sim (1, 2, -1/2)$, ${Q_i}_L'\sim (3, 2, 1/6)$, ${L_i}_L'\sim (1, 2, -1/2)$, ${u_i}_R'\sim (3, 1, 2/3)$, ${d_i}_R'\sim (3, 1, -1/3)$, ${e_i}_R'\sim (1, 1, -1)$, $\theta \sim (1,1,0)$. $F_\theta$ is left undetermined

1.1 Motivation for extending the TFHM

Despite these virtues, there is a somewhat ugly feature arising in the charged lepton sector of the model, as follows. In order to transfer the $Z^\prime$ coupling from $\tau _L'$ to $\mu _L$ so that the NCBAs may be fit, the TFHM requires large mixing between the weak and mass eigenstates of these two fields [53]. However, individual lepton numbers, which are accidental symmetries of the SM, appear to be symmetries in Nature to a good approximation, since experiments place strong upper bounds on lepton flavour violating processes (e.g. in $\tau \rightarrow 3 \mu$ or $\mu \rightarrow e \gamma$). Thus, introducing a flavour-changing interaction through large charged lepton mixing is potentially dangerous from the point of view of these bounds. Indeed, experimental constraints on $BR(\tau \rightarrow 3 \mu )$ [59] place a tight bound on the coupling . This favours a mixing angle which is very close to $\pi /2$ between the second and third family left-handed charged leptons. Such a mixing angle implies the renormalisable (3,3) Yukawa coupling for charged leptons must in fact be highly suppressed with respect to the (2,3) and (3,2) Yukawa couplings (which, recall, can only arise from non-renormalisable operators given the charge assignment in the TFHM). The TFHM model as presented in Refs. [53, 58] has no explanation for this per se because the (3,3) charged lepton Yukawa coupling should be present at the renormalisable level and must therefore be set to be small without explanation. From the outset, the model appears less natural because of this; a deformed model which does not require large $\mu _L-\tau _L$ mixing in order to obtain $g_{\mu _L} \ne 0$ or $g_{\mu _R} \ne 0$ would be more natural. In this paper, we will construct such an anomaly-free deformation of the TFHM, in which the third family quarks and leptons and the second family leptons are charged under $U(1)_F$, which we shall see remedies the aforementioned ugly feature, while preserving the successes of the TFHM.

There is a second, albeit less troublesome, niggle in the TFHM setup. If we were to assume that CKM mixing came from down quarks only, the TFHM would obtain the wrong sign for $C_L \propto g_{sb} g_{\mu _L}$. Thus, additional CKM mixing (of the opposite sign and roughly double the magnitude) must be invoked in the TFHM between $t_L$ and $c_L$, allowing $g_{sb}$ to be of the correct sign and magnitude. This is another feature that will be remedied in our deformation of the TFHM, which will rather be compatible with purely down-quark CKM mixing (as well as the case where there is also a contribution from the up quarks).

The resulting model, which we call the Deformed Third Family Hypercharge Model (DTFHM), is in these ways a more natural explanation of the NCBAs than the TFHM. Interestingly, we shall see that the charge assignment in the DTFHM predicts contributions to both Wilson coefficients $C_L$ and $C_R$ (rather than just $C_L$, as predicted in the original TFHM example case), in the particular combination $C_L+\frac{4}{5}C_R$ (at least, in the most natural example case of the DTFHM). To our knowledge, no model has been suggested to explain the NCBAs with this particular ratio of Wilson coefficients. We find that such a combination of operators can indeed fit the NCBA data much better than the SM.

In Sect. 2, we shall construct the TFHM deformation, calculating the $Z^\prime$ couplings and the $Z-Z^\prime$ mixing therein. Then, in Sect. 3, we examine the phenomenology of an example case of the model (i.e. with various simplifying assumptions about fermion mixing). Firstly, the parameter space where the model fits the NCBAs is estimated. Then other phenomenological bounds are examined, notably from $B_s$ mixing and the measured lepton flavour universality of Z couplings. Direct $Z^\prime$ search constraints are calculated next, and we find that the model has parameter space which evades all bounds but which explains the NCBAs successfully. We summarise in Sect. 4. In Appendix A, we begin to sketch how some features of the example case might be predicted in a more complete and detailed model.

2 The deformed third family hypercharge model

We deform the TFHM by allowing $U(1)_F$ charges (in the weak eigenbasis) not only for the third family of SM fermions, but also for the second family leptons, thus coupling the $Z^\prime$ directly to muons so that charged lepton mixing, and the lepton flavour violation (LFV) that it induces, can be small. In the spirit of bottom-up model building we shall not invoke any additional fields beyond those of the SM, the $Z^\prime$, and a flavon field whose rôle is to spontaneously break $U(1)_F$ at the scale of a few TeV by acquiring a non-zero vacuum expectation value (VEV).

To constrain our $U(1)_F$ charges we shall, as in the TFHM, require anomaly cancellation. This avoids the complication of including appropriate Wess-Zumino (WZ) terms to cancel anomalies in an otherwise anomalous low-energy effective field theory (EFT). Moreover, even if a specific set of anomalies could be cancelled at high energies by new UV physics, such as a set of heavy chiral fermions (from which the WZ terms must emerge as low-energy remnants), it would be difficult to give these chiral fermions large enough masses in a consistent framework, without prematurely breaking $SU(2)_L$. Thus, we require that our charge assignment is anomaly-free.

2.1 Anomaly-free deformation

It turns out that the constraint of anomaly cancellation is strong enough to uniquely determine the charge assignment in our deformation of the TFHM up to a constant of proportionality. To derive this, we shall use the machinery developed in Ref. [21], albeit in an especially simple incarnation. We shall denote the $U(1)_F$ charge of field M under $U(1)_F$ by $F_M$, where $M \in \{ Q_i,L_i,e_i,u_i,d_i,H \}$ and the index $i \in \{1,2,3\}$ labels the family. In the DTFHM, non-zero charges are allowed only for $M \in \{ Q_3,u_3,d_3,L_2,L_3,e_2,e_3,H \}$. We shall for now normalise the gauge coupling $g_F$ such that all the $U(1)_F$ charges $F_M$, which are necessarily rational numbers,³ are taken to be integers.

There are six anomaly cancellation conditions (ACCs) which must hold, which guarantee the vanishing of all possible one-loop triangle diagrams involving at least one external $U(1)_F$ gauge boson, and two other external gauge bosons. Four of these equations are linear in the charges, and together these equations fix the third family quark charges to be proportional to their hypercharges as in the TFHM. This, along with a choice for the constant of proportionality, results in the charge assignments

$$\begin{aligned} F_{Q_3} = 1,\quad F_{u_3} = 4,\quad F_{d_3} = -2, \end{aligned}$$

(4)

and also enforce

$$\begin{aligned} F_{L_2} + F_{L_3} = -3, \quad F_{e_2} + F_{e_3} = -6. \end{aligned}$$

(5)

The remaining two ACCs are non-linear, one being quadratic and the other cubic. Following [21], we recast these two equations in terms of the variables $F_{L-} = F_{L_2} - F_{L_3}$ and $F_{e-} = F_{e_2} - F_{e_3}$. We find that with this prudent choice of variables, the cubic ACC necessarily vanishes, and the quadratic one becomes simply

$$\begin{aligned} F_{e-}^2 - F_{L-}^2 = 27. \end{aligned}$$

(6)

This equation is guaranteed to have at least one integer solution, because any odd number $2m+1$ can be written as the difference of two consecutive squares, since $2m+1=(m+1)^2-m^2$. Thus, we have the solution.

$$\begin{aligned} 14^2 - 13^2 = 27. \end{aligned}$$

(7)

Equation (6) has another integer solution, namely $6^2 - 3^2 = 27$. However, setting $F_{e-} = 6$ and $F_{L-} = 3$, together with Eq. (5), implies $F_{L_2} = F_{e_2} = 0$, and so this “trivial branch” of solution just returns us to the TFHM charge assignment. It is straightforward to check that there are no other solutions to Eq. (6) in which $F_{e-}$ and $F_{L-}$ are both integers. Thus, choosing $F_{e-} = 14$ and $F_{L-} = 13$, we deduce the lepton charges:

$$\begin{aligned} F_{L_2} = +5, \quad F_{L_3} = -8, \quad F_{e_2} = +4, \quad F_{e_3} = -10. \end{aligned}$$

(8)

Hence we see that, given our assumptions, enforcing anomaly cancellation does indeed fix a unique charge assignment.⁴

For the rest of the paper, we divide all the $F_M$ charges by 6, so that the quarks and Higgs doublet have their charges equal to the usual hypercharge assignment. The $U(1)_F$ charge assignment of the DTFHM, in the weak eigenbasis, is then listed in Table 2.

Table 2 $U(1)_F$ charges of the fields in the Deformed Third Family Hypercharge Model (DTFHM). All gauge anomalies, mixed gauge anomalies and mixed gauge-gravity anomalies cancel with this charge assignment, which has been previously listed in an ‘Anomaly-Free Atlas’ in Refs. [21, 60]. At this stage, $F_\theta$ is left undetermined

Before we proceed to flesh out the details of this model, let us make a few comments. Firstly, $F_{L_2}$ (and $F_{e_2}$) now have the same sign as $F_{Q_3}$. This means that we may assume the CKM mixing comes from the down quarks only, which would produce a coupling $g_{sb}\propto V_{tb} V_{ts}^*F_{Q_3'}$, and obtain $C_L \propto g_{sb}g_{\mu _L}<0$ (neglecting small imaginary parts in the CKM matrix elements), the correct sign for fitting the NCBAs. Secondly, the magnitude of the lepton charges are large compared with $F_{Q_3}$, which shall make the constraints from $B_s-\overline{B_s}$ mixing easier to satisfy while simultaneously providing a good fit to the NCBAs. Thirdly, as mentioned above, the $Z^\prime$ coupling to the muon is no longer left-handed, but is now proportional to $C_L + \frac{4}{5}C_R$.

Finally, let us discuss the implications of this new charge assignment for the Yukawa sector of the model. With the charge assignment in Table 2, the only renormalisable Yukawa couplings are

$$\begin{aligned} {{\mathcal {L}}}=-Y_t {\overline{{Q_3}_L'}} H t_R' - Y_b \overline{{Q_3'}_L} H^c b_R'+ H.c, \end{aligned}$$

(9)

where we suppress gauge indices and $H^c=(H^+,\ -{H^0}^*)^T$. In contrast to the TFHM, all Yukawa couplings for the charged leptons are now banned at the renormalisable level, even the (3,3) element. So there is no expectation for a heavy tauon in this theory, whose mass would therefore, like the first and second family fermions, arise from non-renormalisable operators. We find this palatable given $m_\tau \simeq 1.7\ \mathrm {GeV} \ll m_t$. Indeed, $m_\tau$ is closer to the charm mass, $m_c \simeq 1.3\ \mathrm {GeV}$ (which like other second family fermion masses must also arise at the non-renormalisable level) than it is to either of the third family quark masses.

In this model, one would still expect the bottom and top quarks to be hierarchically heavier than the lighter quarks, and expect small CKM angles mixing the first two families with the third. One would not necessarily expect the CKM mixing between the first two families to be small (as indeed it is not), given the approximate U(2) symmetry in the light quarks, as is also the case in the TFHM and many other models. We require a small renormalisable parameter $Y_b \sim 1/40$ in order to fit the bottom mass.

2.2 Neutrino masses

If we augment the SM fermion content by three right-handed sterile neutrinos $\nu ^\prime _{iR}$, $i\in \{1,2,3\}$, which are uncharged under all of $\hbox {SM}\times U(1)_F$, then, given the charge assignment in Table 2, one cannot write down any renormalisable Yukawa couplings for neutrinos. Nonetheless, just as for the charged leptons and the first and second family quarks, we expect effective Yukawa operators for the neutrinos, of the form $\overline{{L_i'}_L} H \nu '_{jR}$, to arise from higher-dimension operators, for example involving insertions of the flavon field. Moreover, once we include three right-handed sterile neutrinos, then we should also include a generic 3 by 3 matrix of Majorana mass terms in the Lagrangian, which correspond to super-renormalisable dimension-3 operators of the form $\overline{{\nu _i'}_R^c} \nu '_{jR}$, whose dimensionful mass parameters reside at some a priori decoupled heavy mass scale. Thus, employing the same coarse reasoning with which we discussed quark and lepton masses, it is natural to expect a spectrum of three light neutrinos within our model, together with three very heavy right-handed counterparts, arising from a see-saw mechanism.

In the remainder of this Section, we complete our description of this model by discussing first the neutral gauge boson mass mixing, which results from the Higgs being charged under both the electroweak symmetry and under $U(1)_F$, and second the coupling of the $Z^\prime$ to the fermion sector. These aspects are similar to the setup of the original TFHM, as described in Ref. [53].

2.3 Masses of gauge bosons and $Z-Z^\prime$ mixing

The mass terms for the neutral gauge bosons are of the form ${\mathcal {L}}_{N,\text {mass}} = \frac{1}{2}{{\varvec{A}}'_{\mu }}^T {\mathcal {M}}^2_N {{\varvec{A}}'_{\mu }}$, where ${{\varvec{A}}'_{{\varvec{\mu }}}}=(B_\mu ,W_\mu ^3,X_\mu )^T$,⁵ and

$$\begin{aligned} {\mathcal {M}}^2_N=\frac{v_F^2}{4}\left( \begin{array}{ccc} r^2 {g'}^2 &{} -r^2 gg' &{} r^2 g'g_F \\ -r^2 gg' &{} r^2g^2 &{} -r^2gg_F \\ r^2 g'g_F &{} -r^2gg_F &{} g_F^2(4 F_\theta ^2+r^2) \\ \end{array}\right) , \end{aligned}$$

(10)

where $r\equiv v/v_F\ll 1$ is the ratio of the VEVs, and $F_\theta$ is the $U(1)_F$ charge of the flavon $\theta$. The mass basis of physical neutral gauge bosons is defined via $(A_\mu ,Z_\mu ,Z^{\prime }_\mu )^T\equiv {{\varvec{A}}}_{{\varvec{\mu }}}=O^T {{\varvec{A}}'_{\mu }}$, where

$$\begin{aligned} O= \left( \begin{array}{ccc} \cos \theta _w &{} -\sin \theta _w \cos \alpha _z &{} \sin \theta _w \sin \alpha _z \\ \sin \theta _w &{} \cos \theta _w \cos \alpha _z &{} -\cos \theta _w \sin \alpha _z \\ 0 &{} \sin \alpha _z &{} \cos \alpha _z \\ \end{array}\right) , \end{aligned}$$

(11)

where $\theta _w$ is the Weinberg angle (such that $\tan \theta _w=g'/g$). In the (consistent) limit that $M_Z/M_Z^\prime \ll 1$ and $\sin \alpha _z \ll 1$, the masses of the heavy neutral gauge bosons are given by

$$\begin{aligned} M_Z\approx \frac{M_W}{\cos \theta _w}=v\frac{\sqrt{g^2+{g'}^2}}{2}, \qquad M_{Z^\prime }\approx g_F v_F F_\theta , \end{aligned}$$

(12)

where $M_W =gv/2$, and the $Z-Z^\prime$ mixing angle is

$$\begin{aligned} \sin \alpha _z \approx \frac{g_F}{\sqrt{g^2+{g'}^2}}\left( \frac{M_Z}{M_Z^\prime }\right) ^2. \end{aligned}$$

(13)

Recall that we expect $v_F \gg v$, so that the $Z^\prime$ is indeed expected to be much heavier than the electroweak gauge bosons of the SM.

2.4 $Z^\prime$ couplings to fermions

We begin with the couplings of the $U(1)_F$ gauge boson $X_\mu$ to fermions in the Lagrangian in the weak (primed) eigenbasis

(14)

where $g_F$ is the $U(1)_F$ gauge coupling. Writing the weak eigenbasis fields as 3-dimensional vectors in family space $\mathbf{u_R}'$, $\mathbf{Q_L}'=(\mathbf{u_L}',\ \mathbf{d_L}')$, $\mathbf{e_R}'$, ${{\varvec{d}}_R}'$, $\mathbf{L_L}'=({{{\varvec{\nu }}}_L}', \mathbf{e_L}')$, we define the 3 by 3 unitary matrices $V_P$, where $P \in \{u_R,\ d_L,\ u_L,\ e_R,\ u_R,\ d_R,\ \nu _L,\ e_L \}$ to transform between the weak eigenbasis and the mass (unprimed) eigenbasis⁶:

$$\begin{aligned} {\mathbf{P}'}^T = V_P \mathbf{P}^T. \end{aligned}$$

(15)

The CKM matrix is $V=V_{u_L}^\dag V_{d_L}$ and the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix is $U=V_{\nu _L}^\dag V_{e_L}$. Re-writing Eq. 14 in the mass eigenbasis,

(16)

up to small terms $\sim {{\mathcal {O}}}(M_Z^2/M_{Z^\prime }^2)$ induced by the $Z-Z^\prime$ mixing. We have defined the 3 by 3 matrices in family space $\Lambda ^{(P)}_\zeta = V_P^\dag \zeta V_P$, where $\zeta \in \{ \xi , \Omega , \Psi \}$ and

$$\begin{aligned} \xi = \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array}\right) , \qquad \Omega = \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} -\frac{8}{5} \\ \end{array}\right) , \qquad \Psi = \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} -\frac{5}{2} \\ \end{array}\right) .\nonumber \\ \end{aligned}$$

(17)

In order to make further progress with phenomenological analysis, we must fix the fermion mixing matrices $V_P$. The $Z^\prime$ boson couples to both left-handed and right-handed muons, as can be seen by reference to Eq. 16 and the non-zero (2,2) entries of $\Psi$ and $\Omega$. However, in order to fit the NCBAs, we require a coupling of the $Z^\prime$ to $\overline{s_L} b_L$. This implies that $(V_{d_L})_{23} \ne 0$. The $Z^\prime$ will then, once integrated out of the effective field theory, induce a $({\overline{s}} b) ({\bar{\mu }} \mu )$ effective operator which, we shall show below, can explain the NCBAs. The $Z^\prime$ also mediates other flavour-changing neutral currents, and so will be subject to various bounds upon its flavour-changing or flavour non-universal couplings. This will translate to bounds upon the various entries of the $V_P$.

2.5 Example case

We shall here construct an example of the set of $V_P$ that is not obviously ruled out a priori, for further phenomenological analysis. We shall assume that the currently measured CKM quark mixing is due to the down quarks, thus $V_{d_L}=V$, $V_{u_L}=1$. Explicitly, this yields the following matrix of couplings to down quarks

$$\begin{aligned} \Lambda ^{(d_L)}_{\xi } = \left( \begin{array}{ccc} |V_{td}|^2 &{} V_{td}^* V_{ts} &{} V_{td}^* V_{tb} \\ V_{td} V_{ts}^* &{} |V_{ts}|^2 &{} V_{ts}^* V_{tb} \\ V_{tb}^* V_{td} &{} V_{tb}^* V_{ts} &{} |V_{tb}|^2 \\ \end{array} \right) . \end{aligned}$$

(18)

We shall also assume that the observed PMNS mixing is due solely to the neutrinos, i.e. $V_{\nu _L}=U^\dagger$, $V_{e_L}=1$. We note that (in contrast to the original TFHM), despite there being no charged lepton mixing, there is a $Z^\prime$ coupling to muons. For simplicity and definiteness, we choose $V_{u_R}=1=V_{d_R}=V_{e_R}$. The assumed alignment of the charge lepton weak basis with the mass basis ensures no lepton flavour violation (LFV), which is very tightly constrained by experimental measurements (in particular $\tau \rightarrow 3\mu$, and $\mu \rightarrow e\gamma$). The example case corresponds to some strong (but reasonable) assumptions about the $V_P$, which may not hold in reality. In the future, we may perturb away from this particular example case, but it will suffice for a first study of viable parameter space and relevant direct $Z^\prime$ search limits from the LHC. In what follows, we shall refer to this example case of the DTFHM as the ‘DTFHMeg’.

The assumptions on the mixing matrices $\{V_P\}$ are rather strong, and one may ask what would be required of some more detailed model in order to obtain them. For example, to obtain $V_{u_L}=V_{u_R}=1$, we require that the predicted form of the up-quark Yukawa matrix be diagonal in the weak eigenbasis. In Appendix A, we sketch how this might be achieved in a more detailed Froggatt-Nielsen model.

3 Phenomenology of the example case

In this section, we will go through the most relevant phenomenological limits on the DTFHMeg in turn, concluding with a discussion of the combination of them all. The phenomenology that we discuss is only sensitive to $F_\theta$ and $v_F$ through $M_{Z^\prime }$ in Eq. 12. We shall leave each undetermined and use $M_{Z^\prime }$ as the independent variable instead.

3.1 NCBAs

From the global fit to $C_9$ and $C_{10}$ in Ref. [17] (the left-hand panel of Fig. 1), we extract the fitted BSM contributions from the $68\%$ CL ellipse

$$\begin{aligned} \left( \begin{array}{c} C_9 \\ C_{10} \end{array} \right) = \mathbf{c} + \frac{s_1}{\sqrt{2.3}} \mathbf{v_1}+ \frac{s_2}{\sqrt{2.3}} \mathbf{v_2}, \end{aligned}$$

(19)

where⁷ $\mathbf{c}=(-0.72,\ 0.40)^T$, $\mathbf{v_1}=(0.29,\ 0.15)^T$, $\mathbf{v_2}=(-0.08,\ 0.16)^T$ is orthogonal to $\mathbf{v_1}$ and $s_1$, $s_2$ are independent one-dimensional Gaussian probability density functions with mean zero and unit standard deviation. We are thus working in the approximation that the fit yields a 2-dimensional Gaussian PDF near the likelihood maximum. We plot our characterisation of the $68\%$ and $95\%$ error ellipses in Fig. 1 (left). Overlaying it on top of Fig. 1 of Ref. [17] shows that this is a good approximation in the vicinity of the best-fit point.

The best-fit point has a $\chi ^2$ of some 42.2 units less than the SM [17]. We have $C_9=C_L + C_R$ and $C_{10}=C_R - C_L$, so, for the DTFHMeg in which $C_L=\alpha$ and $C_R = 4/5 \alpha$, we have $(C_9,\ C_{10})=\mathbf{d}(\alpha ) \equiv \alpha (9 /5,\ -1/5)$. We may use the orthogonality of $\mathbf{v_1}$ and $\mathbf{v_2}$ to solve for

$$\begin{aligned} s_i(\alpha ) = \frac{\sqrt{2.3}}{|\mathbf{v_i}|^2}{} \mathbf{v_i}\cdot \left( \mathbf{d}(\alpha ) - \mathbf{c}\right) , \end{aligned}$$

(20)

where $i \in \{1,2\}$. The value of $\Delta \chi ^2$ that we extract from the fit is then the difference in $\chi ^2$ between our fit and the best fit point in $(C_9,\ C_{10})$ space:

$$\begin{aligned} \Delta \chi ^2(\alpha ) = s_1^2(\alpha )+s_2^2(\alpha ). \end{aligned}$$

(21)

The value of $\alpha$ which minimises this function ($\alpha _{\text {min}}$) is the best-fit value and the places where it crosses $\Delta \chi ^2(\alpha _{\text {min}})+1$ yield the $\pm 1\sigma$ estimate for its uncertainty under the hypothesis that the model is correct, i.e.

$$\begin{aligned} \alpha = -0.53 \pm 0.09. \end{aligned}$$

(22)

The SM lies at $\alpha =0$ and so the fit is $5.9\sigma$ away from it, of comparable quality to the two-parameter fit of $C_9$ and $C_{10}$ (which is $6.5\sigma$ away from the SM point). $\Delta \chi ^2(\alpha )$ is plotted in the vicinity of the minimum in Fig. 1 (right).

Fig. 1

Our digitisation of the fits of Ref. [17]. Left: The point shows the best-fit in $(C_9, C_{10})$ space, surrounded by $68\%$ (inner) and $95\%$ (outer) CL regions. The red dashed line shows the trajectory of our model, which predicts that $C_9 = -\,9 C_{10}$. We see that this ratio of Wilson coefficients is capable of fitting the NCBA data at the $1.5\sigma$ level. For reference, we also include (green dashed line) the trajectory of models corresponding to the same anomaly-free charge assignment, but with the lepton families permuted such that $F_{L_2\prime }$ and $F_{e_2\prime }$ are in the ratio $-2:1$ or $1:-2$. Such a model only offers a bad quality fit to the NCBAs, similar to the SM. Right: Shows $\Delta \chi ^2(\alpha )$ as a function of $\alpha$ along the red dashed line (i.e. $C_9=-\,9 C_{10}$). The horizontal dotted line shows $\Delta \chi ^2$ of unity above the best-fit value, and is used to calculate the 1$\sigma$ uncertainties on $\alpha$

This minimum is obtained at a higher $\Delta \chi ^2(\alpha _{\text {min}})=4.2$ as compared to the unconstrained fit to $(C_9,\ C_{10})$, for one parameter fewer, i.e. one additional degree of freedom. The model still constitutes a good fit to the NCBAs, having a best-fit $\chi ^2$ value 38.0 lower than the SM.

The couplings in the DTFHMeg relevant to a new physics contribution to the $({\bar{b}}s) ({\bar{\mu }} \mu )$ vertices are

(23)

where ‘$+H.c.$’ signifies that we are to add the Hermitian conjugate copies of all terms in the square brackets. By reference to Eqs. 2 and 23, we identify $g_{sb} = V_{ts}^*V_{tb} g_F/6$, $g_{\mu _L}=5g_F/6$ and $g_{\mu _R}=2g_F/3$. Using $V_{ts}^*V_{tb} \approx -0.04$ and matching $C_L$ to $\alpha$’s fit value in Eq. 22, we obtain

$$\begin{aligned} 0.22 \le g_F \frac{1 ~\text {TeV}}{M_{Z^\prime }} \le 0.31. \end{aligned}$$

(24)

as the two sigma ($95\%$ CL) fit to the NCBAs.

3.2 $Z^\prime$ width

The partial width of a $Z^\prime$ decaying into a massless fermion $f_i$ and massless anti-fermion ${\bar{f}}_j$ is $\Gamma _{ij}=C/(24 \pi ) |g_{ij}|^2 M_{Z^\prime }$, where $g_{ij}$ is the coupling of the $Z^\prime$ to $f_i {\bar{f}}_j$, and $C=3$ for coloured fermions ($C=1$ otherwise). In the limit that $M_{Z^\prime }$ is much larger than the top mass, we may approximate all fermions as being massless. Summing over all fermion species, we obtain that the total width $\Gamma$ satisfies $\Gamma /M_{Z^\prime }=5 g_F^2 / (12 \pi )$. The model is non-perturbative when this quantity approaches unity, i.e. $g_F \sim \sqrt{12 \pi /5}=2.7$. Eq. 24 implies that to avoid this non-perturbative régime requires $M_{Z^\prime } \lesssim 12.5$ TeV. The $Z^\prime$ in this model decays with the following branching ratios: $18\%$ into quarks of various flavours, $11\%$ into muons, $46\%$ into tauons, and $25\%$ into neutrinos.

We observe that these branching ratios are a significant departure from those in the original TFHM; in particular, the branching ratios into quark pairs (predominantly tops and bottoms) is much reduced, and the branching ratio into neutrinos and tauons is much enhanced in the DTFHM. This is because of the significantly larger lepton charges in this model (which, recall, were fixed by anomaly cancellation), and the fact that the coupling to left-handed tauons no longer needs to be transferred into a coupling to left-handed muons in the example case.

3.3 Neutral meson mixing

The most recent constraint coming from comparing $B_s$ mixing predictions from lattice data and sum rules [61] with experimental measurements [62] yields [63] $|g_{sb}| \le M_{Z^\prime }/(194~\text {TeV})$. $B_s$ mixing thus usually places a strong constraint upon $Z^\prime$ models that explain the NCBAs [64]. Substituting for $g_{sb}$, we obtain

$$\begin{aligned} g_F \frac{1 ~\text {TeV}}{M_{Z^\prime }} < 0.77, \end{aligned}$$

(25)

which we see is satisfied by the whole $2\sigma$ range favoured by a fit to the NCBAs in Eq. 24.

The flavour-changing couplings of the $Z^\prime$ to down quarks, given in Eq. 18 in our example case, also produce corrections beyond the Standard Model to the mixings of other neutral mesons, specifically to kaon and $B_d$ mixing. For the DTFHMeg, we compute the 95% CL bound from neutral kaon mixing to be $g_F \left( 1 ~\text {TeV}/M_{Z^\prime }\right) < 1.46$, while that from $B_d$ mixing is $g_F \left( 1 ~\text {TeV}/M_{Z^\prime }\right) < 0.82$, where in both cases we have used the constraints presented in Ref. [65]. Thus, the bound from $B_s$ mixing given above turns out to be the strongest of the three.

3.4 Z boson lepton flavour universality

Here, we follow Ref. [53] to compute the bound coming from lepton flavour universality measurements of Z boson couplings (with the difference that here, we must also include the contribution from $\mu _R$). The LEP measurement is:

$$\begin{aligned} R_{\text {LEP}} =0.999\pm 0.003, \qquad R\equiv \frac{\Gamma (Z\rightarrow e^+e^-)}{\Gamma (Z\rightarrow \mu ^+\mu ^-)}. \end{aligned}$$

(26)

We compute the prediction for this in our model by evaluating the following ratio of partial widths,

$$\begin{aligned} R_{\text {model}} = \frac{|g_Z^{e_L e_L}|^2+ |g_Z^{e_R e_R}|^2}{|g_Z^{\mu _L \mu _L}|^2+|g_Z^{\mu _R \mu _R}|^2}, \end{aligned}$$

(27)

where $g_Z^{ff}$ is the coupling of the physical Z boson to the fermion anti-fermion pair $f{\bar{f}}$. One can obtain the couplings $g_Z^{ff}$ in the DTFHMeg by first writing down the terms in the Lagrangian which couple the first and second family charged leptons to the neutral bosons B, $W^3$, and X:

(28)

and then inserting ${{\varvec{A}}_\mu }'=O {{\varvec{A}}_\mu }$ (where O is given in Eq. 11) to rotate to the mass basis. To leading order in $\sin \alpha _z$, we find

$$\begin{aligned} \begin{aligned} g_Z^{e_L e_L}&=-\frac{1}{2}g\cos \theta _w+\frac{1}{2}g'\sin \theta _w,\\ g_Z^{e_R e_R}&=g'\sin \theta _w,\\ g_Z^{\mu _L \mu _L}&=-\frac{1}{2}g\cos \theta _w+\frac{1}{2}g'\sin \theta _w+\frac{5}{6}g_F\sin \alpha _z,\\ g_Z^{\mu _R \mu _R}&= g'\sin \theta _w + \frac{2}{3}g_F\sin \alpha _z. \end{aligned} \end{aligned}$$

(29)

The SM prediction (i.e. $R=1$) is recovered by taking $\alpha _z$ to zero. Within our model, we may expand $R_{\text {model}}$ to leading order in $\sin \alpha _z$ to obtain

$$\begin{aligned} R_{\text {model}}= & {} 1 +\frac{2}{3}\frac{g_F(5g\cos \theta _w-13g'\sin \theta _w)\sin \alpha _z}{(g\cos \theta _w-g'\sin \theta _w)^2+4{g'}^2\sin ^2\theta _w} \nonumber \\= & {} 1+2.6 g_F^2 \left( \frac{M_Z}{M_{Z^\prime }}\right) ^2, \end{aligned}$$

(30)

having substituted in Eq. 13 for $\sin \alpha _z$, and the central experimental values $g=0.64$ and $g'=0.34$. Comparison with the upper LEP limit in Eq. 26, at the $95\%$ CL, yields the Z boson lepton flavour universality constraint from LEP (which we henceforth refer to as the LEP LFU bound):

$$\begin{aligned} g_F^2 \left( \frac{M_Z}{M_{Z^\prime }}\right) ^2< 0.0019 \Rightarrow g_F \frac{1~\text {TeV}}{M_{Z^\prime }} < 0.48, \end{aligned}$$

(31)

which is satisfied by the entire range favoured by current fits to NCBAs in Eq. 24.

One might have expected that, due to the enhanced $Z^\prime$ couplings to muons, the LEP LFU bound would be more aggressive in the DTFHM than in the TFHM. However, in the DTFHM, a partial cancellation occurs between the contributions to $R_{\text {model}}$ coming from $g_Z^{\mu _L \mu _L}$ and $g_Z^{\mu _R \mu _R}$. This does not occur in the original TFHM, in which the coupling of the $Z^\prime$ (and thus of the Z, after $Z-Z^\prime$ mixing) to muons is purely left-handed. Due to this partial cancellation, this constraint from LEP LFU in the DTFHMeg is somewhat less aggressive than it would be otherwise, ending up very close to that of the TFHM example case.

3.5 Invisible width of the Z Boson

$Z^\prime$ couplings contribute to the invisible width of the Z boson $\Gamma _{\text {inv}}$ beyond the SM via $Z-Z^\prime$ mixing and the $Z^\prime$ coupling to neutrinos. Experimental constraints upon it are [66]

$$\begin{aligned} {\Gamma }^{(\text {exp})}_{\text {inv}}=499.0 \pm 1.5 ~\text {MeV} , \end{aligned}$$

(32)

whereas the SM prediction from the decay into $\overline{\nu _e} \nu _e$, $\overline{\nu _\mu } \nu _\mu$ and $\overline{\nu _\tau } \nu _\tau$ is ${\Gamma }^{(\text {SM})}_{\text {inv}}=501.44$ MeV [59]. Thus, we may constrain any new physics contribution to be

$$\begin{aligned} \Delta \Gamma ^{(\text {exp})} = {\Gamma }^{(\text {exp})}_{\text {inv}} - {\Gamma }^{(\text {SM})}_{\text {inv}} = -2.5 \pm 1.5 ~\text {MeV}. \end{aligned}$$

(33)

The terms in the Lagrangian that couple the Z boson to neutrinos are, to leading order in $\sin \alpha _z \ll 1$,

(34)

In collider experiments the neutrinos are not observed and so their flavour is not measured. We may therefore compute $\Delta \Gamma _{\text {inv}}$ using the couplings to the weak eigenbasis fermion fields, as written in Eq. 34, because the mixing between the weak and mass eigenbases is unitary. We see from Eq. 34 that the Z boson coupling to electron neutrinos is unchanged from the SM, the coupling to muon neutrinos $g_{{\nu _L'}_\mu }$ is enhanced whereas the coupling to tauon neutrinos $g_{{\nu _L'}_\tau }$ is diminished. The partial width for each decay $Z \rightarrow \overline{{\nu _L'}_i} {\nu _L'}_i$ is $\Gamma _{\nu _i}=|g_{{\nu _i}'}|^2M_Z/(24 \pi )$. There is a partial cancellation between the muon neutrino and the tauon neutrino contributions. Working to first order in $\sin \alpha _z \ll 1$ and substituting for it using Eq. 13, we find that the prediction in the DTFHMeg is

$$\begin{aligned} \frac{\Delta \Gamma _{\text {inv}}^{\text {DTFHM}}}{M_Z} =- \frac{g_F^2}{48 \pi } \left( \frac{M_Z}{M_{Z^\prime }} \right) ^2. \end{aligned}$$

(35)

Comparing this to Eq. 33, we find that the DTFHM prediction for the sign is in accordance with the data and may fit the inferred invisible width of the Z boson some $1.7\sigma$ better than the SM.

Applying Eq. 33 as a constraint implies that, to the $95\%$ CL,

$$\begin{aligned} g_F \frac{1 ~\text {TeV}}{M_Z^{\prime }} < 1.05, \end{aligned}$$

(36)

which is again satisfied by the whole region of parameter space that fits the NCBAs in Eq. 24.

3.6 Direct $Z^\prime$ search constraints on parameter space

ATLAS has released 13 TeV 36.1 $\hbox {fb}^{-1}$ $Z^\prime \rightarrow t {\bar{t}}$ searches [67, 68], which impose $\sigma \times BR(Z^\prime \rightarrow t {\bar{t}})<10$ fb for large $M_{Z^\prime }$. There is also a search [69] for $Z^\prime \rightarrow \tau ^+ \tau ^-$ for 10 $\hbox {fb}^{-1}$ of 8 TeV data, which imposes $\sigma \times BR(Z^\prime \rightarrow \tau ^+ \tau ^-)<3$ fb for large $M_{Z^\prime }$. These searches constrain the DTFHMeg, but they produce less stringent constraints than an ATLAS search for $Z^\prime \rightarrow \mu ^+\mu ^-$ in 139 $\hbox {fb}^{-1}$ of 13 TeV pp collisions [70]. We shall therefore concentrate upon this search. The constraint is in the form of upper limits upon the fiducial cross-section $\sigma$ times branching ratio to di-muons $BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ as a function of $M_{Z^\prime }$. At large $M_{Z^\prime } \approx 6$ TeV, $\sigma \times BR(Z^\prime \rightarrow \mu ^+\mu ^-)<0.015$ fb [71], and indeed this will prove to be the most stringent $Z^\prime$ direct search constraint, being stronger than the others mentioned above.

In its recent $Z^\prime \rightarrow \mu ^+ \mu ^-$ search, ATLAS defines [70] a fiducial cross-section $\sigma$ where each muon has transverse momentum $p_T>30$ GeV and pseudo-rapidity $|\eta |<2.5$, and the di-muon invariant mass satisfies $m_{\mu \mu }>225$ GeV. No evidence for a significant bump in $m_{\mu \mu }$ was found, and so $95\%$ upper limits on $\sigma \times BR(\mu ^+ \mu ^-)$ were placed. Re-casting constraints from such a bump-hunt is fairly simple: one must simply calculate $\sigma \times BR(\mu ^+ \mu ^-)$ for the model in question and apply the bound at the relevant value of $M_{Z^\prime }$ and $\Gamma /M_{Z^\prime }$. Efficiencies are taken into account in the experimental bound and so there is no need for us to perform a detector simulation. Following Ref. [63], for generic $z \equiv \Gamma /M_{Z^\prime }$, we interpolate/extrapolate the upper bound $s(z, M_{Z^\prime })$ on $\sigma \times BR(\mu ^+ \mu ^-)$ from those given by ATLAS at $z=0$ and $z=0.1$. In practice, we use a linear interpolation in $\ln s$:

$$\begin{aligned} s(z,M_{Z^\prime }) = s(0,M_{Z^\prime }) \left[ \frac{s(0.1,M_{Z^\prime })}{s(0,M_{Z^\prime })}\right] ^{\frac{z}{0.1}}. \end{aligned}$$

(37)

Equation 37 is a reasonable fit [63] within the range $\Gamma /M_{Z^\prime } \in [0,0.1]$. We shall also use Eq. 37 to extrapolate out of this range.

Fig. 2

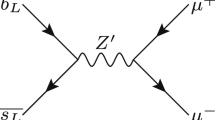
Feynman diagrams of tree-level $Z^\prime$ production in the LHC by the DTFHM followed by decay into muons, where $q_{i,j} \in \{ u,c,d,s,b \}$ are such that the combination ${q_i}_L \overline{{q_j}_L}$ or ${q_i}_R \overline{{q_j}_R}$ has zero electric charge. In the DTFHMeg, by far the dominant production mode is by $q_i=b_L$ and $q_j=b_L$

In order to use Eq. 37, we must calculate $\sigma \times BR(\mu ^+\mu ^-)$, and so we now detail the method of our calculation. For the DTFHMeg, we made a UFO file⁸ by using FeynRules [72, 73]. We use the MadGraph_2_6_5 [74] event generator to estimate $\sigma \times BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ for the tree-level production processes shown in Fig. 2, in 13 TeV centre of mass energy pp collisions. Five flavour parton distribution functions are used in order to re-sum the logarithms associated with the initial state b-quark [75].

Fig. 3

Constraints on parameter space of the DTFHMeg. The white region is allowed at $95\%$ CL. We show the region excluded at the $95\%$ CL by the fit to NCBAs, as well as the $95\%$ region excluded by the 13 TeV LHC 139 $\hbox {fb}^{-1}$ ATLAS search [70, 71] for $Z^\prime \rightarrow \mu ^+ \mu ^-$ (labelled by ‘ATLAS $\mu \mu$ excl’). Other constraints, such as from $B_s$ mixing, or lepton flavour universality of the Z boson’s coupling, are dealt with in the text and are less restrictive than those shown. The example point displayed in Table 3 is shown by the dot. Values of $\Gamma /M_{Z^\prime }$ label the dashed line contours

3.7 Combination of constraints

We display the resulting constraints upon the DTFHMeg in Fig. 3, with the allowed region shown in white. This allowed region extends out (beyond the range of the figure) to $M_{Z^\prime }=12.5$ TeV, where the model becomes non-perturbative. We see that there is plenty of parameter space where the NCBAs are fit and where current bounds are not contravened. Bounds from $B_s$ mixing and lepton flavour universality of Z couplings are much weaker than those shown, and do not impact on the domain of parameter space shown in the figure. The region to the right-hand side of the $\Gamma /M_{Z^\prime }=0.1$ contour in the figure is an extrapolation of the bounds in Eq. 37, rather than an interpolation. We should bear in mind therefore that the extrapolation may be less accurate the further we move toward the right, away from this contour. The branching ratio of $Z^\prime \rightarrow \mu ^+ \mu ^-$ is approximately constant over the parameter space shown for $M_{Z^\prime } > 0.8$ TeV. The shape of the excluded region then depends purely on $\sigma$, which happens to be close to the inferred search bound for the top excluded region around $M_{Z^\prime } \sim 3-4$ TeV. This is illustrated by Fig. 4.

Fig. 4

$\sigma \times BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ divided by its upper limit from the ATLAS direct search in the DTFHMeg. We do not plot any points where this ratio is larger than two, leading to the white regions on the left-hand side of the figure (which correspond to excluded parameter space)

Note that since the vertical axis is $\propto g_F/ M_{Z^\prime }$, and since $\sigma \propto g_F^4$, $\sigma \times BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ is non-monotonic with respect to $M_{Z^\prime }$ at constant $g_F/ M_{Z^\prime }$.

Table 3 Example point in the DTFHMeg parameter space, $(g_F,M_{Z^\prime })=(0.81,3\ \mathrm {TeV})$. We display the fiducial production cross-section times branching ratio into di-muons as $\sigma$. By far the dominant 13 TeV LHC production mode is $b {\bar{b}} \rightarrow Z^\prime$ (the next largest, $b {\bar{s}} + s {\bar{b}} \rightarrow Z^\prime$, yields $\sigma =6.1 \times 10^{-5}$ fb)

In Table 3, we display branching ratio information for an example parameter space point of the DTFHMeg which fits the NCBAs. The dominant production mode is via $b {\bar{b}} \rightarrow Z^\prime$. We see that decays into top quark pairs, tauon pairs and bottom quark pairs will also be targets for future searches for the DTFHMeg.

4 Summary

We have presented a model which explains the NCBAs whilst avoiding current constraints. The model explains some of the coarse features of the fermion mass spectrum, namely the hierarchical heaviness of the third family quarks and the smallness of CKM mixing angles. The model was obtained by deforming the TFHM in such a way as to retain its successes whilst remedying an ugly feature. The ugly feature involved strong assumptions that had to be made concerning the charged lepton Yukawa couplings, that were not motivated by the symmetries of the model. The deformed model remedies this by introducing additional charges, such that the $Z^\prime$ resulting from spontaneous breaking of an anomaly-free $U(1)_F$ symmetry couples directly to muons already in the weak eigenbasis (in contrast to the TFHM, where this had to be obtained by $\mu$-$\tau$ mixing). Another qualitative difference is in how $V_{ts}$ is generated. The $\overline{s_L}-b_L$ coupling of the $Z^\prime$, which is necessary to explain the NCBAs, is produced by left-handed strange-bottom mixing. In the TFHM, this implied that $V_{ts}$ had to be generated by a cancellation of $\overline{b_L}-s_L$ mixing and $\overline{t_L}-c_L$ mixing. In the deformed model, this is no longer necessarily the case.

We re-cast the most sensitive LHC Run II direct search constraint, a 139 $\hbox {fb}^{-1}$ ATLAS search for $Z^\prime \rightarrow \mu ^+ \mu ^-$, for our DTHFMeg model, following Ref. [63], where a similar analysis was performed for the TFHM (and two simplified models). The result is shown in Fig. 3, which, along with the definition of the model, is the central result of this paper. Previously, in Ref. [76], Run I di-jet and di-lepton resonance searches (and early Run II searches) were used to constrain simple $Z^\prime$ models that fit the NCBAs. The NCBA data have significantly changed since then, as have the search bounds. Also, since Ref. [76] was before the conception of the TFHM and the DTFHM, it didn’t explicitly constrain their parameter spaces.

In Refs. [54, 77], the sensitivity of future hadron colliders to $Z^\prime$ models that fit the NCBAs was estimated. A 100 TeV future circular collider (FCC) [78] would have sensitivity to the whole of parameter space for one simplified model (MDM) and the majority of parameter space for another (MUM). It will be interesting to calculate the future collider reach for both the DTFHM and the TFHM, which we suppose may cover the whole perturbative parameter space of each.

A Froggatt-Nielsen structure to obtain a diagonal up Yukawa matrix

In the example case that we chose to study, denoted the DTFHMeg, we made some specific choices for the mixing matrices $\{V_P\}$. In particular, we assumed $V_{u_L}=1$ and $V_{u_R}=1$ for simplicity, with the CKM mixing arising solely from the down-type quarks. This ‘up-alignment’ requires there be a sensible limit in which the effective up-type Yukawa matrix $Y_u$ is approximately diagonal. In this Appendix, we sketch how this might be obtained from a more detailed model utilising the Froggatt-Nielsen [79] mechanism. Evidently, such a model must ultimately break the U(2) flavour symmetry acting on the light up-type quarks, in order to suppress the $(Y_u)_{12}$ and $(Y_u)_{21}$ matrix elements with respect to their diagonal counterparts. There are presumably other ways of model building such detailed Yukawa structures, but our purpose here is only to provide an existence proof of such mechanisms, with more detailed model building being well beyond the scope of the present paper.

Froggatt-Nielsen models postulate the existence of heavy vector-like fermions in the same representations as the SM chiral fermions, but with independent charges under $U(1)_F$. We shall here denote such a heavy fermion by its SM counterpart field but with a tilde, i.e. ${\tilde{Q}}^{F}_{L,R} \sim (3, 2, 1/6, F)$, ${\tilde{L}}^{F}_{L,R} \sim (1, 2, -1/2, F)$, ${\tilde{e}}^{F}_{L,R} \sim (1, 1, -1, F)$, ${\tilde{d}}^{F}_{L,R} \sim (3, 1, -1/3, F)$, ${\tilde{u}}^{F}_{L,R} \sim (3, 1, 2/3, F)$. The idea is that their masses (denoted loosely and collectively as M) are larger than $v_F$, say five times larger or so. Then, after $U(1)_F$ breaking and integrating out the heavy fermions, the model generates $U(1)_F$-violating operators in the SM effective field theory, such as that depicted by the Feynman diagram in Fig. 5. Each such operator is suppressed by a power of $v_F/M$ that is set by the total $U(1)_F$ charge of the Yukawa operator in the SM effective field theory.

Fig. 5

Feynman diagram yielding an effective non-zero entry in $(Y_u)_{22}$. Each solid blob represents a mass insertion factor of 1 / M

Hereafter we assume that $F_\theta =1/6$. The coefficient of the effective operator in Fig. 5 would be equal to the product of four dimensionless coupling constants and a factor of $(v_F/M)^3$. The typical assumption in Froggatt-Nielsen models is then that the fundamental dimensionless coupling constants are all roughly equal to 1, and that all the heavy fermion fields have roughly the same mass, denoted by M, which would yield a prediction $(Y_u)_{22}\sim {\mathcal {O}}(v_F/M)^3$. It is by changing these strong assumptions that one may generate operators which are further suppressed for the off-diagonal entries of $Y_u$, and thus predict $V_{u_L}\approx V_{u_R} \approx 1$ as we assumed in the DTFHMeg. Such suppression may come from a suppression of some of the fundamental dimensionless coupling constants, which may be set by other symmetries or dynamics of the model.

To give an explicit realisation of this idea that is pertinent to the DTFHMeg, suppose that the effective coupling $(Y_u)_{22}$ is mediated by a ‘spaghetti diagram’ involving the ${\tilde{Q}}_{L,R}$ fields, as in Fig. 5, whereas the effective coupling $(Y_u)_{11}$ is mediated by the ${\tilde{u}}_{L, R}$ fields, as in Fig. 6. This could be achieved if the fundamental dimensionless couplings of $\overline{u_1} H {\tilde{Q}}^{+3}_L$ and $\overline{{\tilde{u}}^{+3}_R} H Q_2$ were zero or approximately zero for some reason (thus explicitly breaking the U(2) flavour symmetry that acts on light up-type quarks), but all other gauge invariant Yukawa couplings were of the same order. Then a mixing term such as $(Y_u)_{12}$ must be mediated by both $\tilde{u}_{L, R}$ and ${\tilde{Q}}_{L,R}$ fields, leading to an additional suppression because the dimensionality of the operator is higher than the diagonal entries. Thus, the off-diagonal effective couplings $(Y_u)_{12}$ and $(Y_u)_{21}$ would be heavily suppressed compared to $(Y_u)_{11}$ or $(Y_u)_{22}$.⁹ Similar methods can be employed to suppress other off-diagonal terms in the up-quark or charged lepton sectors, as required by the particular example case being explored.

Fig. 6

Feynman diagram yielding an effective non-zero entry in $(Y_u)_{11}$. Each solid blob represents a mass insertion of 1 / M