$U(1)_{B_3-L_2}$ explanation of the neutral current $B-$anomalies

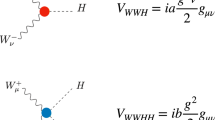
Abstract

We investigate a speculative short-distance force, proposed to explain discrepancies observed between measurements of certain neutral current decays of B hadrons and their Standard Model predictions. The force derives from a spontaneously broken, gauged $U(1)_{B_3-L_2}$ extension to the Standard Model, where the extra quantum numbers of Standard Model fields are given by third family baryon number minus second family lepton number. The only fields beyond those of the Standard Model are three right-handed neutrinos, a gauge field associated with $U(1)_{B_3-L_2}$ and a Standard Model singlet complex scalar which breaks $U(1)_{B_3-L_2}$, a ‘flavon’. This simple model, via interactions involving a TeV scale force-carrying $Z^\prime$ vector boson, can successfully explain the neutral current $B-$anomalies whilst accommodating other empirical constraints. In an ansatz for fermion mixing, a combination of up-to-date $B-$anomaly fits, LHC direct $Z^\prime$ search limits and other bounds rule out the domain 0.15 $\hbox {TeV}< M_{Z^\prime }<$ 1.9 TeV at the $95\%$ confidence level. For more massive $Z^\prime$s, the model possesses a flavonstrahlung signal, where pp collisions produce a $Z^\prime$ and a flavon, which subsequently decays into two Higgs bosons.

1 Introduction

Data from the first decade of running of Large Hadron Collider (LHC) experiments involving the decays of B hadrons show some discrepancies with Standard Model (SM) predictions. For example, measurements of the ratio of branching ratios $R_{K^{(*)}}=BR(B \rightarrow K^{(*)} \mu ^+ \mu ^-)/BR(B \rightarrow K^{(*)} e^+ e^-)$ [1, 2], $BR(B_s \rightarrow \mu ^+ \mu ^-)$ [3,4,5,6] and some angular distributions in $K^*\mu ^+ \mu ^-$ decays [7,8,9,10,11,12] all show some discrepancy (there are others). Each discrepant observable is only 1-4$\sigma$ away from SM predictions but collectively, they point to a roughly similar conclusion. Despite a recent flagship LHCb measurement of $R_{K}$ fluctuating somewhat toward its SM prediction (announced at the Moriond 2019 conference), the overall picture remains. Relative theoretical uncertainties, while taken into account in the number of sigma, vary from less than $1\%$ to $20\%$, depending on the particular observable in question. In summary, several measurements of B hadron decays are somewhat inconsistent with the SM prediction of the $({\bar{s}} b)({\bar{\mu }} \mu )$ effective coupling. We call these discrepancies the neutral current¹$B-$anomalies (NCBAs).

Several different fits to over a hundred $B-$observables [14,15,16,17,18,19,20] broadly agree: they favour a beyond the SM contribution to the weak effective theory operator

(1)

where ${{\mathcal {N}}}=1/(36\, \hbox {TeV})^2$ (in the present paper, $C_9 \ne 0$ means a contribution beyond the SM). We shall focus on one of the fits for definiteness: Ref. [17], where the result is that

$$\begin{aligned} C_9 = -0.97 \pm 0.15.\end{aligned}$$

(2)

The coefficient of the operator at the best-fit point has a pull of $5.9\sigma$ away from the SM value of 0 (taking the operator with $P_L$ inserted before the final $\mu$ field in (1) provides an even better, but comparable, fit, $6.6\sigma$ away from the SM value).

One possibility to generate such beyond the SM contributions is from the interactions of a new electrically neutral, massive, force carrying particle, dubbed a $Z^\prime$, which has family dependent interactions. In particular, in order to explain the $B-$anomalies, the Lagrangian density should include (with the possible inclusion or exclusion of the second term) the interaction terms

(3)

where $g_{sb}$, $g_{\mu _L}$ and $g_{\mu _R}$ are all dimensionless coupling constants. Once the $Z^\prime$ is integrated out, in the weak effective field theory, one obtains the Lagrangian density terms

$$\begin{aligned} {{\mathcal {L}}}_{WET}= & {} -\frac{g_{sb} g_{\mu _L}}{M_{Z^\prime }^2} (\overline{s_L} \gamma ^\rho b_L) (\overline{\mu _L} \gamma _\rho \mu _L) \nonumber \\&- \frac{g_{sb} g_{\mu _R}}{M_{Z^\prime }^2} (\overline{s_L} \gamma ^\rho b_L) (\overline{\mu _R} \gamma _\rho \mu _R) + H.c. \end{aligned}$$

(4)

These are precisely of the type that can explain the NCBAs: identifying (1) and (4) we see that

$$\begin{aligned} C_9= g_{sb}(g_{\mu _L}+g_{\mu _R}) (36\text {~TeV}/M_{Z^\prime })^2. \end{aligned}$$

(5)

Many models of flavoured $Z^\prime$ vector bosons have been invented based on spontaneously broken gauged U(1) flavour symmetries [21, 22], for example from $L_\mu -L_\tau$ and other groups [21, 23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Some models have several abelian groups in the extension [60], whilst some others [61,62,63] generate beyond the SM contributions with loop-level penguin diagrams. Some of the models are more ambitious than others, providing more or less detail toward ultra-violet completion.

In Refs. [43, 45] a gauged $U(1)_{B_3-L_2}$ symmetry was proposed to explain the neutral current $B-$anomalies. Both papers are quite detailed in their exposition, providing information about fermion mass model building through additional vector-like representations of the gauge group.

In Ref. [43], Alonso et al. introduce three additional SM-singlet scalar fields charged under $U(1)_{B_3-L_3}$ and² a vector-like fermion for each Weyl fermion of the SM (plus three right-handed neutrinos). It was shown how all SM fermion masses and mixings can originate via the Froggatt–Nielsen mechanism [64]. The Froggatt–Nielsen mechanism derives effective SM Yukawa couplings from renormalisable interactions which appear to be non-renormalisable from the low energy effective field theory point of view, once some heavy particles (the additional heavy vector-like fermions) are integrated out of the theory. It was shown by Alonso et al. how assumptions about hierarchies in their masses and further assumptions regarding the renormalisable couplings of the model translate into empirically feasible values of fermion masses and fermion mixing.

In Ref. [45], Bonilla et al. introduce two SM-singlet scalars that are charged under $U(1)_{B_3-L_2}$ along with a second Higgs doublet, also charged under $U(1)_{B_3-L_2}$. Two vector-like quark doublet representations are included. Once these scalar fields acquire vacuum expectation values (with various hierarchies between them assumed), a realistic pattern of neutrino masses and mixing can be achieved. In this model, Yukawa couplings leading to quark mixing are obtained already at the renormalisable level, without invoking the Froggatt-Nielsen mechanism.

The most robustly testable part of the phenomenology of the models of Alonso et al. and Bonilla et al. is that of the $Z^\prime$, since it is the interactions of the $Z^\prime$ that explain the NCBAs. Since the $Z^\prime$ contributes to processes other than those included in the NCBAs, compatibility with measurements of these other processes then provides constraints upon each model. In both analyses, contributions from the additional non-$Z^\prime$ states to the NCBAs and to other constraints were neglected by choosing parameters such that the additional states decouple.

It is our purpose here to examine the up-to-date collider phenomenology of similar models without worrying about the details of the physics that fixes the fermion mass data. To this end, we provide a simplified broad-brush formulation of a low energy effective field theory of a gauged, spontaneously broken $U(1)_{B_3-L_2}$ model and apply the latest bounds and fits, which have changed since the original analyses of Refs. [43, 45] due to a significantly increased integrated luminosity at the LHC. Since the original analyses, $Z^\prime$ constraints from direct searches have had an increase from 36 $\hbox {fb}^{-1}$ to 139 $\hbox {fb}^{-1}$ and the NCBA fits have changed due to the inclusion of further B meson decay data in some of the observables (the LHCb data set roughly doubling in size). In the effective field theory, we shall include the $Z^\prime$ boson as well as the flavon, a complex scalar field whose vacuum expectation value breaks $U(1)_{B_3-L_2}$. We shall neglect to specify other fields of the model, arguing that (along similar lines to Alonso et al. and Bonilla et al.) our analysis should capture the most pertinent features of the most currently relevant phenomenology, provided other states are sequestered from it either by sufficiently weak couplings or heavy masses. Thus, compared to Refs. [43, 45], we do not have as detailed a model of fermion masses but instead we have, in the back of our minds (such as through the Froggatt-Nielsen mechanism or through mixing with heavy vector-like fermion representations) an idea of how some small perturbations may be generated to correct the textures of Yukawa matrices that are predicted at the level of the renormalisable, unbroken $U(1)_{B_3-L_2}$ theory. However, the latest bounds and fits presented here will be applicable to all models where assumptions about the flavour mixing of the $Z^\prime$ couplings match ours and where other states are sufficiently decoupled.

Our paper proceeds as follows: in Sect. 2, we define the effective $U(1)_{B_3-L_2}$ model, examining the $Z^\prime$ couplings to fermions, which are of paramount importance for phenomenology. To specify a model for phenomenological study, it is necessary to make further assumptions about fermion mixing; these are made in Sect. 3. Then, in Sect. 4, we examine the current consistency of NCBA fits with the other experimental constraints. A novel signal process, flavonstrahlung, is identified. In Sect. 5, we provide a summary and discussion. Technical definitions of mixing matrices and fields are made available in Sect. 1.

2 $B_3-L_2$ Model

The gauge group of the model is $SU(3) \times SU(2)_L \times U(1)_Y \times U(1)_{B_3-L_2}$.

Table 1 $B_3-L_2$ charge assignments of fields. A prime denotes a weak eigenstate Weyl fermion. Under $SU(3) \times SU(2)_L \times U(1)_Y$, the fields have representation ${ Q_L'}_j\sim (3, 2, 1/6)$, ${ L_L'}_j\sim (1, 2, -1/2)$, ${ e_R'}_j\sim (1, 1, -1)$, ${ d_R'}_j\sim (3, 1, -1/3)$, ${ u_R'}_j\sim (3, 1, 2/3)$, ${ \nu _R'}_j\sim (1, 1, 0)$, $H=(H^+,\ H^0)^T \sim (1,2,1/2)$, respectively. $i \in \{ 1,2\},\ j \in \{1,2,3\}$ are family indices. The flavon, $\theta$, is a SM-singlet complex scalar field and $q_\theta$ is a non-zero rational real number

We display the charge assignments of the fields in the model under $U(1)_{B_3-L_2}$ in Table 1. The chiral fermions are all in vector-like representations with respect to $U(1)_{B_3-L_2}$ and so standard arguments imply that the symmetry is free from local perturbative anomalies, given that the SM plus three right-handed neutrinos is already free of local gauge anomalies under $SU(3) \times SU(2)_L \times U(1)_Y$.

At the renormalisable unbroken level, $U(1)_{B_3-L_2}$ predicts that the Yukawa matrices of SM fermions (see 1 for definitions and conventions) have the texture

$$\begin{aligned} Y_u \sim \left( \begin{array}{ccc} \times &{} \times &{} 0 \\ \times &{} \times &{} 0 \\ 0 &{} 0 &{} \times \\ \end{array} \right) , Y_d \sim \left( \begin{array}{ccc} \times &{} \times &{} 0 \\ \times &{} \times &{} 0 \\ 0 &{} 0 &{} \times \\ \end{array} \right) , Y_e \sim \left( \begin{array}{ccc} \times &{} 0 &{} \times \\ 0 &{} \times &{} 0 \\ \times &{} 0 &{} \times \\ \end{array} \right) , \end{aligned}$$

(6)

where $\times$ denotes an arbitrary dimensionless entry, which may be non-zero. From this prediction, we deduce that the Cabbibo–Kobayashi–Maskawa (CKM) matrix has zero entries for $V_{ub}$, $V_{cb}$, $V_{ts}$ and $V_{td}$. However, the $U(1)_{B_3-L_2}$ symmetry is spontaneously broken by the vacuum expectation value $\langle \theta \rangle$ of a flavon: a SM singlet scalar $\theta$ with non-zero $B_3-L_2$ charge $q_\theta$. This breaking will replace the zero entries in (6) by small corrections generated by non-renormalisable operators. The model then predicts that the magnitudes of the CKM matrix entries $V_{ub}$, $V_{cb}$, $V_{ts}$ and $V_{td}$ are suppressed from unity by some small factor. This qualitative expectation [43, 45] agrees with current experimental estimates: $|V_{cb}|=(41.0\pm 1.4) \times 10^{-3}$, $|V_{ub}|=(3.82\pm 0.24) \times 10^{-3}$, $|V_{td}|=(8.0\pm 0.3) \times 10^{-3}$, $|V_{ts}|=(38.8\pm 1.1) \times 10^{-3}$ [13]. We note that fermion mass data dictate that there should be hierarchies within the $\times$ symbols of each matrix in (6). A more complete ultra-violet theory could explain such hierarchies. The (33) entry of each matrix should not be suppressed, in order to explain the hierarchically large masses of third family fermions as compared to the other two families. Smaller corrections to the zeroes will then indeed predict small entries for the magnitudes of $V_{ub}$, $V_{cb}$, $V_{ts}$ and $V_{td}$.

Neutrinos acquire mass through the see-saw mechanism with an initial symmetric mass matrix (whose basis is defined in (A.4)):

(7)

where the entries marked are of order the electroweak scale multiplied by the neutrino Yukawa couplings $Y_\nu$ and we expect the entries marked $*$ to be much greater than , since the mass scale $*$ is not fixed to the electroweak scale by any symmetry. As it stands, (7) has two eigenvalues of order $*$, two of order and two of order . However, we expect some of the zeroes in (7) to be corrected by ‘small’ non-renormalisable corrections from the spontaneous breaking of $U(1)_{B_3-L_2}$: in particular, the bottom right-hand 3 by 3 sub-matrix will be corrected by terms of order $*$ times a small number. It is expected that such corrections will still be many orders of magnitude above . Depending on the value of $q_\theta$, some of the other entries may be corrected by terms of order $\langle \theta \rangle$. However, it is not our intention here to go into the minutæ of fermion mass model building for the model; instead we shall be content with the ‘broad-brush’ sketch expected of three very light neutrinos and three very heavy ones resulting from the expected small corrections and the see-saw mechanism.

We begin with the couplings of the $U(1)_{B_3-L_2}$ gauge boson $Z^\prime _\mu$ to fermions in the Lagrangian in the weak (primed) eigenbasis

(8)

where $g_Z^\prime$ is the $U(1)_{B_3-L_2}$ gauge coupling. $U(1)_{B_3-L_2}$ is broken by $\langle \theta \rangle \ne 0$ and so the $Z^\prime$ acquires a mass

$$\begin{aligned} M_{Z^\prime } = q_\theta g_F \langle \theta \rangle . \end{aligned}$$

(9)

We shall see below that a combination of LHC search bounds and NCBAs will imply that $M_{Z^\prime }$ is at least of order the TeV scale. We assume that the approximately right-handed neutrinos discussed above have a much higher mass than $M_{Z^\prime }$. The $Z^\prime$ boson ‘eats’ one real degree of freedom of $\theta$ via the Brout–Englert–Higgs mechanism [65, 66] to form its longitudinal polarisation mode. In the spontaneously broken theory, we expand $\theta = (\langle \theta \rangle + \vartheta )/\sqrt{2}$, in terms of the one real physical flavon degree of freedom, $\vartheta$. Its tree-level mass $m_{\vartheta }$, depends on free parameters in the $\theta$ potential, but barring special circumstances we may expect it to be of order $\langle \theta \rangle$.

Writing the weak eigenbasis fermionic fields as 3-dimensional vectors in family space $\mathbf{u_R}'$, $\mathbf{Q_L}'=(\mathbf{u_L}',\ \mathbf{d_L}')$, $\mathbf{e_R}'$, $\mathbf{d_R}'$, $\mathbf{L_L}'=({\varvec{\nu }_L}', \mathbf{e_L}')$, we define the 3 by 3 unitary matrices $V_P$, where $P \in \{u_R,\ d_L,\ u_L,\ e_R,\ u_R,\ d_R,\ \nu _L,\ e_L \}$. These transform between the weak eigenbasis and the mass (unprimed) eigenbasis³ as detailed in 1:

$$\begin{aligned} {\mathbf{P}'} = V_P \mathbf{P}. \end{aligned}$$

(10)

Re-writing (8) in the mass eigenbasis and using the quark and lepton mixing matrices V and U defined in (A.8)

(11)

We have defined the 3 by 3 dimensionless Hermitian coupling matrices

(12)

where $I \in \{ u_L, d_L, e_L, \nu _L, u_R, d_R, e_R, \nu _R \}$, $\alpha \in \{ \varXi , \varOmega \}$ and

$$\begin{aligned} \varXi := \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array}\right) , \qquad \varOmega := \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right) . \qquad \end{aligned}$$

(13)

Provided that $(V_{d_L})_{23} \ne 0$, (11) contains tree-level couplings of the $Z^\prime$ to $\overline{b_L} s_L$, $\overline{s_L} b_L$ and $\mu ^+ \mu ^-$. Thus, it shows promise to explain the NCBAs through processes such as the one in Fig. 1.

Fig. 1

Tree-level Feynman diagram of a process which contributes to the NCBAs

3 Example case

In order to specify the model further, we should detail the mixing matrices $V_I$. However, we have not constructed a detailed model for them. Here, we shall make a simple ansatz for fermion mixing matrices which is likely to not to be ruled out by other flavour bounds on flavour changing neutral currents but which is favourable from the point of view of the NCBAs. For example, in order to successfully describe the NCBAs, we require $(V_{d_L})_{23} \ne 0$. We shall examine the limit (which we call ‘$(B_3-L_2)\hbox {eg}$’) where

$$\begin{aligned} V_{d_L} = \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos \theta _{sb} &{} -\sin \theta _{sb} \\ 0 &{} \sin \theta _{sb}&{} \cos \theta _{sb} \\ \end{array}\right) , \end{aligned}$$

(14)

$V_{d_R}=1, V_{e_R}=1, V_{e_L}=1$ and $V_{u_R}=1$, meaning that $V_{u_L} = V_{d_L} V^\dag$, $V_{\nu _L}=U^\dag$, where U is the lepton mixing matrix defined in 1. Thus, the predicted tree-level flavour changing neutral currents are, aside from the $Z^\prime$ coupling to ${\bar{b}} s$ and ${\bar{s}} b$, relegated to the up quarks and neutrinos, where the bounds from experiment are significantly weaker. Our assumptions here are of course strong, but they merely constitute an example case for phenomenological study in order to assess viability. Extracting the couplings of the $Z^\prime$ relevant for the NCBAs, we have

(15)

Thus, by identifying (15) with (5), we have

$$\begin{aligned} g_{sb}=\frac{g_{Z^\prime }}{2} \sin 2 \theta _{sb}, \qquad g_{\mu _L}=g_{\mu _R}=- \frac{3g_{Z^\prime }}{2}. \end{aligned}$$

(16)

4 Phenomenology

We have now specified the $(B_3-L_2)\hbox {eg}$ enough to apply experimental constraints to it. We first bound its free parameters through the fit to the NCBAs and then go on to derive other pertinent bounds before considering predictions.

4.1 Fit to NCBAs

Fig. 2

$\sin 2 \theta _{sb}$ in the $(B_3-L_2)\hbox {eg}$ as constrained by a fit [17] to the NCBAs in (18). Central $C_9=-0.97$ and lower $C_9=-0.65$.

At energy scales far below $M_{Z^\prime }$, in the effective theory where the $Z^\prime$ is integrated out, (15) becomes

$$\begin{aligned} {{\mathcal {L}}} = \frac{3 {g_Z^\prime }^2}{2 M_{Z^\prime }^2} \sin 2 \theta _{sb} (\bar{s} \gamma ^\rho P_L b) ({\bar{\mu }} \gamma _\rho \mu ) + H.c., \end{aligned}$$

(17)

where $\gamma ^\rho$ are Dirac matrices, $P_L$ is a left-handed projection matrix and $\rho \in \{0,1,2,3\}$ is a space-time index. The fits prefer no sizeable contributions from the operator obtained by switching $P_L \rightarrow P_R$ in (17) [17] and indeed, since we have assumed $V_{d_R}=1$, we predict none (at tree level.⁴) Substituting $g_{sb}$, $g_{\mu _L}$ and $g_{\mu _R}$ from (16) into (5), we have

$$\begin{aligned} \sin 2 \theta _{sb} = -5.1 \times 10^{-4} \left( \frac{M_{Z^\prime }}{g_{Z^\prime } \text {TeV}}\right) ^2 C_9. \end{aligned}$$

(18)

Requiring that $\sin 2 \theta _{sb} \le 1$ implies that

$$\begin{aligned} g_{Z^\prime } \frac{\text {TeV}}{M_{Z^\prime }} \ge 0.023 \sqrt{C_9 / (-0.97)}. \end{aligned}$$

(19)

The $(B_3-L_2)$eg has three pertinent free parameters: $M_{Z^\prime }$, $\theta _{sb}$ and $g_{Z^\prime }$. It will suit us to adopt (18) with the empirically-fitted input for $C_9$ in order to reduce the number of free-parameters to two, so that the parameter space of the model can be captured and plotted in two dimensions. The central value of $C_9$ as extracted from fits to the NCBAs shown in (2) will be the ‘central $C_9$’ value of -0.97, however we will also refer to the ‘lower $C_9$’ value. This is the value of $C_9$ which is closest to the SM limit but still fits the relevant data to within $2\sigma$ (i.e. $C_9=-0.65$ [17]). We display the value of $\sin 2 \theta _{sb}$ for these two cases in Fig. 2.

4.2 $B_s - \overline{B_s}$ mixing

Fig. 3

Tree-level Feynman diagram of a beyond the SM contribution to $B_s - \overline{B_s}$ mixing

Since our $Z^\prime$ couples to bottom and strange (anti-)quarks, it induces a beyond the SM contribution to $B_s - \overline{B_s}$ mixing via the process in Fig. 3. The value of the bound depends on lattice data [67] which change the SM prediction. These have varied significantly over the last decade. We use a recent determination based on lattice data and sum rules [68] which implies that⁵$g_{Z^\prime } \sin 2 \theta _{sb}/2 \le M_{Z^\prime } / 194 \text {~TeV}$ [69]. Using (18), this implies the lower bound

$$\begin{aligned} g_{Z^\prime } \frac{\text {TeV}}{M_{Z^\prime }} \ge 0.048 \frac{C_9}{-0.97}. \end{aligned}$$

(20)

The fact that this is a lower bound might at first seem counter-intuitive, until one realises that, for lower values of $g_{Z^\prime } \text {TeV}/M_{Z^\prime }$, one can only fit the NCBAs with a larger value of $\sin 2 \theta _{sb}$, i.e. a larger $Z^\prime$ coupling to bottom and strange (anti-)quarks and therefore a larger contribution to $B_s-\overline{B_s}$ mixing.

4.3 Neutrino trident

$Z^\prime \hbox {s}$ which couple to muon neutrinos contribute to the process $\nu _\mu N \rightarrow \nu _\mu N \mu ^+ \mu ^-$, where N is a heavy nucleus, for example by the process depicted in Fig. 4 (there are other diagrams involving W bosons). In the heavy $Z^\prime$ limit, the predicted tree-level ratio of the $(B_3-L_2)$eg model cross-section to the SM one is [45]

$$\begin{aligned} \frac{\sigma _{(B_3-L_2)\text {eg}}}{\sigma _{SM}} = \frac{1+ (4 s_W^2 + 18 v^2 g_{Z^\prime }^2 / M_{Z^\prime }^2)^2}{1 + (1+4 s_W^2)^2}, \end{aligned}$$

(21)

where v is the SM Higgs vacuum expectation value and $s_W$ is the sine of the Weinberg angle. The measurement of the neutrino trident cross section by the CCFR collaboration yields the constraint $\sigma _{(B_3-L_2)\text {eg}}/\sigma _{SM}\le 1.38$ [70]. Using the central values $v=246.22$ GeV and $s_W^2=0.22337$ [13] in (21), this yields

$$\begin{aligned} g_{Z^\prime } \frac{\text {TeV}}{M_{Z^\prime }} \le 1.1. \end{aligned}$$

(22)

Fig. 4

Tree-level Feynman diagram of a beyond the SM contribution to the neutrino trident process

Fig. 5

Tree-level diagram of a new physics contribution to $Z\rightarrow 4 \mu$ decay

4.4 $Z^0 \rightarrow \mu ^+ \mu ^- Z^\prime$

For $Z^\prime$ particles whose mass is less than that of the $Z^0$ boson, i.e. $M_{Z^\prime }<M_Z$, a recent CMS search in 77.3 $\hbox {fb}^{-1}$ of 13 TeV pp collisions for $Z^0 \rightarrow \mu ^+ \mu ^- Z^\prime$ followed by $Z^\prime \rightarrow \mu ^+ \mu ^-$ provides constraints [71]. Stringent 95$\%$ upper bounds upon the product of branching ratios

$$\begin{aligned} R_{4\mu }=BR(Z^0 \rightarrow \mu ^+ \mu ^- Z^\prime )\times BR(Z^\prime \rightarrow \mu ^+ \mu ^-) \end{aligned}$$

at the level of $10^{-7}-10^{-8}$ are presented as a function of $M_{Z^\prime } \in [5 \text {~GeV},\ 70 \text {~GeV}]$. For a given value of $M_{Z^\prime }$ in the aforementioned range and a reference value of $g_{Z^\prime }$, we use MadGraph_2_6_5 [72] to calculate the value of $R_{4\mu }$. In the parameter range considered for which this decay is relevant, $BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ is independent of $g_{Z^\prime }$ to a very good approximation and so $R_{4\mu }$ is predicted to be proportional to $g_{Z^\prime }^2$. We can thus scale $g_{Z^\prime }$ to find its value at the 95$\%$ upper limit.

4.5 $Z^\prime$ width and perturbativity

The partial width of a $Z^\prime$ decaying into a Weyl fermion $f_i$ and and Weyl anti-fermion ${{\bar{f}}}_j$ is

$$\begin{aligned} \varGamma _{ij} = \frac{C}{24 \pi } |g_{ij}|^2 M_{Z^\prime }, \end{aligned}$$

(23)

where $g_{ij}$ is the coupling of the $Z^\prime$ boson to $f_i {\bar{f}}_j$ and C is the number of colour degrees of freedom of the fermions (here, 3 or 1). In the limit that $m_t / M_{Z^\prime } \rightarrow 0$, we may approximate all fermions as being massless. Summing over fermion species (it is simplest to do this in the weak eigenbasis), we obtain a total width $\varGamma$:

$$\begin{aligned} \frac{\varGamma }{M_{Z^\prime }} = \frac{13 g_{Z^\prime }^2}{8 \pi }. \end{aligned}$$

(24)

To remain in the perturbative régime such that we may trust our perturbative calculations, we should have $\varGamma /M_{Z^\prime }<1$, i.e. $g_{Z^\prime } < \sqrt{8 \pi /13}=1.4$. Substituting this into (20) yields an upper bound $M_{Z^\prime } \le 29 (-0.97/C_9)$ TeV from perturbativity, fits to NCBAs and $B_s-\overline{B_s}$ mixing measurements.

4.6 LHC $Z^\prime$ searches

The ATLAS experiment has performed various searches in pp collisions at the LHC for resonant $Z^\prime$ vector bosons decaying into different final states. None of them have found a significant signal to date and so lower limits are placed upon the production cross-sections times branching ratio as a function of the invariant mass of the final state. For example, a 36.1 $\hbox {fb}^{-1}$ 13 TeV search in $t {\bar{t}}$ imposes $\sigma \times BR(Z^\prime \rightarrow t {\bar{t}})<10$ fb for large $M_{Z^\prime }$ [73, 74]. A di-tau final state search from the 8 TeV run imposes $\sigma \times BR(Z^\prime \rightarrow \tau ^+ \tau ^-)<3$ fb for large $M_{Z^\prime }$ [75]. However, the most constraining channel to date for the $(B_3-L_2)\hbox {eg}$ is from a $Z^\prime \rightarrow \mu ^+\mu ^-$ in 139 $\hbox {fb}^{-1}$ of 13 TeV pp collisions [76], where, for $M_{Z^\prime }=6$ TeV, $\sigma \times BR(Z^\prime \rightarrow \mu ^+ \mu ^-)<0.015$ fb, where $\sigma$ is the fiducial $Z^\prime$ production cross-section. We shall therefore use this search to constrain the model.⁶ Feynman diagrams of example $Z^\prime$ production signal processes are shown in Fig. 6.

In this ATLAS di-muon resonance search, each muon is required to have a transverse momentum $p_T>30$ GeV, pseudo-rapidity magnitude $|\eta |<2.5$ and a di-muon invariant mass $m_{\mu \mu }>225$ GeV. ATLAS has already taken efficiencies into account in their published bounds so there is no need to simulate the detector. Upper bounds $s(M_{Z^\prime }, z)$ on $\sigma \times BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$ are published for $z:=\varGamma /M_{Z^\prime }$ values from 0 to 0.1 [77]. In Ref. [69], it was shown that a function

$$\begin{aligned} s(z,M_{Z^\prime }) = s(0,M_{Z^\prime }) \left[ \frac{s(0.1,M_{Z^\prime })}{s(0,M_{Z^\prime })} \right] ^{\frac{z}{0.1}} \end{aligned}$$

(25)

fits the given published bounds well in the given domain $z \in [0,0.1]$. We shall also use (25) to extrapolate slightly outside of this domain, but will delineate regions of parameter space where the bound is extrapolated rather than interpolated.

The $(B_3-L_2)\hbox {eg}$ model was encoded into UFO format via FeynRules [78, 79] for inclusion into an event generator. We calculate the fiducial cross-section $\sigma (pp \rightarrow Z^\prime \rightarrow \mu ^+ \mu ^-$ with the MadGraph_2_6_5 [72] event generator for a centre of mass energy of 13 TeV. We have added the possibility of producing an additional jet along with the $Z^\prime$ so that the second diagram of Fig. 6 is included in our estimate of the cross-section. We also use five flavour parton distribution functions to re-sum initial state $b-\hbox {quark}$ logarithms [80] and neglect interference with SM backgrounds.

Fig. 6

Example Feynman diagrams of tree-level $B_3-L_2$ inclusive $Z^\prime$ production at the LHC followed by decay into muons. $q_{i,j} \in \{ u,c,d,s,b \}$ are such that the combination ${q_i} \overline{{q_j}}$ has zero electric charge

Table 2 Example point in $(B_3-L_2)\hbox {eg}$ parameter space that fits the NBCAs (for central $C_9=-0.97$) and survives all constraints. We show the largest partonic contributions to the cross-section at the bottom of the table. For the last two rows, the CP conjugated process has been added to the cross-section contribution. ‘$(+j)$’ refers to the fact that the cross-section includes the addition of another jet in the final state

We display an allowed parameter space point ($M_{Z^\prime }=3$ TeV, $g_{Z^\prime }=0.15$) in Table 2. From the table, we can see that the dominant process is $b {\bar{b}} \rightarrow Z^\prime \rightarrow \mu ^+ \mu ^-$, the sub-dominant process is ($b g \rightarrow Z^\prime b \rightarrow \mu ^+ \mu ^- b$ plus the CP conjugated process). The other tree-level processes simulated make a negligible contribution to the cross-section.

Fig. 7

Constraints upon $(B_3-L_2)\hbox {eg}$ for $M_{Z^\prime }>300$ GeV. $\sin 2\theta _{sb}$ has been set as in (18) such that every point fits the NCBAs. The white region is currently allowed. The red and blue coloured regions show the $95\%$ excluded regions from a 13 TeV 139 $\hbox {fb}^{-1}$ ATLAS $Z^\prime \rightarrow \mu ^+ \mu ^-$ search [76] and from $B_s-\overline{B_s}$ mixing as in (20), respectively. The latter bound moves from the blue coloured region at lower $C_9=-0.65$ to the region below the dashed line for central $C_9=-0.97$. The magenta region in the top left-hand corner shows the region ruled out by the neutrino trident process. The direct search bound is extrapolated above the solid curve and interpolated between ATLAS data below it, according to (25)

In Fig. 7, we display constraints upon the $(B_3-L_2)$eg parameter space for $M_{Z^\prime }>300$ GeV. There is only a small region of parameter space where the ATLAS di-muon resonance search bounds have been extrapolated (slightly): above the solid curve. The white region of the figure is allowed by all constraints. We see that $M_{Z^\prime }>1.9$ TeV from these. The direct search constraint does not change by eye from the one shown in the figure when one chooses the central value of $C_9=-0.97$ from the NCBA fit or the lower value. We may understand this by the fact that $\sin 2 \theta _{sb}$ is small throughout the vast majority of the plot, whichever value of $C_9$ is used, in accordance with Fig. 2. The dominant $Z^\prime$ production amplitude is proportional to the $Z^\prime {\bar{b}} b$ coupling, which is proportional to $g_{Z^\prime } \cos 2 \theta _{sb}\approx g_{Z^\prime }$ and so loses the sensitivity⁷ that $\sin 2 \theta _{sb}$ has on $C_9$ through (18). The $B_s$ mixing bound is however sensitive to a change in $C_9$ (via its effect on $g_{sb}$) and the bound becomes the dashed line for central $C_9$. So: for central $C_9$, one concludes that $M_{Z^\prime }>2.2$ TeV. For either value of $C_9$ and throughout the allowed parameter space shown, $BR(Z^\prime \rightarrow \mu ^+ \mu ^-)$, $BR(Z^\prime \rightarrow {\bar{b}} b)$ and $BR(Z^\prime \rightarrow {\bar{t}} t)$ do not change (to the significant figure quoted) from the values in Table 2.

Fig. 8

Constraints upon $(B_3-L_2)$eg for $M_{Z^\prime }\le 300$ GeV. $\sin 2\theta _{sb}$ has been set as in (18) such that every point fits the NCBAs. The white region is currently allowed. The red and blue coloured regions show the $95\%$ excluded regions from a 13 TeV 36.1 $\hbox {fb}^{-1}$ ATLAS $Z^\prime \rightarrow \mu ^+ \mu ^-$ search [76] and from $B_s-\overline{B_s}$ mixing as in (20), respectively. The latter bound moves from the blue coloured region at lower $C_9=-0.65$ to the region below the dashed line for central $C_9=-0.97$. The magenta region shows the region ruled out by the neutrino trident process and the green region by a CMS search in 77.3 $\hbox {fb}^{-1}$ of 13 TeV pp collisions for $Z^0 \rightarrow \mu ^+ \mu ^- Z^\prime \rightarrow 4 \mu$ [71]. In the grey region at the bottom of the plot, the effect of the $Z^\prime$ on the NCBAs is too weak to fit them

Bonilla et al. showed that, in the model of Ref. [45], a region of parameter space with $M_{Z^\prime }<$300 GeV could pass all constraints. We now re-examine this lighter mass range; our analysis closely follows that of Bonilla et al., except for the fact that we constrain the parameter space to always fit the NCBAs and that we have updated the constraints from $Z \rightarrow \mu ^+ \mu ^- Z^\prime \rightarrow 4 \mu$ with a new search from CMS.

The ATLAS search for $Z^\prime \rightarrow \mu ^+\mu ^-$ used above provided no constraints for $M_{Z^\prime } \le 300$ GeV. Thus, we have used an earlier ATLAS search⁸ for $Z^\prime \rightarrow \mu ^+ \mu ^-$ in 36.1$^{-1}$ fb of 13 TeV pp collisions, which presented exclusions on generic⁹$Z^\prime \hbox {s}$ for $M_{Z^\prime } \ge 150$ GeV [81]. We calculate the acceptance (for muon transverse momenta $p_T>30$ GeV and muon pseudorapidities $|\eta |<2.5$) times cross section times branching ratio for $Z^\prime \rightarrow \mu ^+ \mu ^- (+ j)$ using MadGraph_2_6_5. We find that the region 150 $\hbox {GeV}< M_{Z^\prime } <300$ GeV is excluded by this search for the entire domain $0.001\le g_{Z^\prime } \le 0.2$. The available parameter space is shown in Fig. 8. We see that the $(B_3-L_2)\hbox {eg}$ may fit the NCBAs for $M_{Z^\prime }<150$ GeV while still passing other experimental constraints.

4.7 Flavonstrahlung

Fig. 9

Feynman diagram of flavonstrahlung process at a hadron collider. $q_{i,j} \in \{ u,c,d,s,b \}$ are such that the combination ${q_i} \overline{{q_j}}$ has zero electric charge

In the unbroken $U(1)_{B_3-L_2}$ theory, $\theta$ interacts with the Higgs boson via the Lagrangian density term $-\lambda _{\theta H} \theta \theta ^\dag H H^\dag$. Supposing that the dimensionless coefficient $\lambda _{\theta H} \ne 0$, the flavon $\vartheta$ will then decay into two physical Higgs bosons hh with approximately $100\%$ branching ratio. Moreover, the $\theta$ kinetic term leads to the Lagrangian density term $g_{Z^\prime }^2 q_\theta ^2 Z^{\prime }_\mu {Z^{\prime }}^\mu \langle \theta \rangle \vartheta$ after spontaneous symmetry breaking. Thus, if a proton-proton collider has sufficient energy and luminosity, it may produce $Z^\prime \vartheta$, leading to the spectacular signature of $\mu ^+ \mu ^- h h$, where $\mu ^+ \mu ^-$ have a resonance at an invariant mass of $M_{Z^\prime }$ and hh have one at the flavon mass $m_{\vartheta }$. This ‘flavonstrahlung’ process is depicted in Fig. 9. Flavonstrahlung would probably not be the first detection of beyond the SM physics in the model: $Z^\prime$ production followed by decay into $\mu ^+\mu ^-$ would most likely be the first, followed perhaps by $Z^\prime \rightarrow t {\bar{t}}$ and $b {\bar{b}}$. Flavonstrahlung is suppressed compared to exclusive $Z^\prime$ production because of its larger final-state phase space and kinematics, and would thus require significantly more luminosity and partonic energy to detect.

5 Discussion

Spontaneously broken $U(1)_{B_3-L_2}$ [43, 45] has parameter space that is consistent with contemporary direct search limits whilst fitting neutral current $B-$anomalies and passing other indirect bounds (the most constraining being those from measurements of $B_s-\overline{B_s}$ mixing).

We have provided a simple broad-brush formulation of the $U(1)_{B_3-L_2}$ model, similar to the one of the Third Family Hypercharge Model (TFHM) [54] and variants [82]. We then presented an example case for phenomenological study, the ‘$(B_3-L_2)\hbox {eg}$’. Figure 7 shows that in the $(B_2-L_2)\hbox {eg}$ the current empirical constraints imply that $M_{Z^\prime }>1.9$ TeV or $M_{Z^\prime }<150$ GeV. The fact that $M_{Z^\prime }<150$ GeV is currently allowed motivates further effort in order to push interpretations of LHC $\mu ^+ \mu ^-$ resonance searches to lower invariant masses where, admittedly, backgrounds are steeply increasing.

The constraints in Figs. 7 and 8 apply to any gauged, spontaneously broken $U(1)_{B_3-L_2}$ model where our assumptions about the $Z^\prime$ couplings detailed in Sect. 3 approximately hold. This is the case for the model of Alonso et al. [43], which found the weaker bound of $M_{Z^\prime } > 1.0$ TeV from the various predecessor constraint data and NCBA fits. The bound has moved to $M_{Z^\prime } > 1.9$ TeV with the latest fits and data. Alonso et al. did not consider $M_{Z^\prime }<300$ GeV, but our results in Fig. 8 show that $M_{Z^\prime }<150$ GeV is currently viable. The model of Bonilla et al. [45] does not match the pattern of $(B_3-L_2)\hbox {eg}$ $Z^\prime$ couplings to left-handed down quarks and so our results are not directly applicable to it.

The direct $Z^\prime \rightarrow \mu ^+ \mu ^-$ search constraints on the $(B_3-L_2)\hbox {eg}$ in Fig. 7 are comparable to those on similarly constructed TFHMeg models.¹⁰ In TFHMs though, the Higgs doublet is necessarily charged under the additional U(1) in order to allow a renormalisable top Yukawa coupling (which seems necessary, given that it is of order 1 and so is inconsistent with a small effective coupling induced by symmetry breaking). This leads to tree-level $Z-Z^\prime$ mixing, associated strong bounds from inferences of the $\rho$ parameter [83]: indeed, these entirely disallow the $M_{Z^\prime }\le 300$ GeV region for the TFHMs. The $U(1)_{B_3-L_2}$ model is not subject to these strong bounds, however, since the SM Higgs doublet is uncharged under $U(1)_{B_3-L_2}$.

In Sect. 4.7, we have identified a novel flavonstrahlung signal process, where pp collisions result in $Z^\prime$ plus flavon production, followed by $Z^\prime$ decay into $\mu ^+ \mu ^-$ and flavon decay into hh. This process will also be present in other similar NCBA-explaining U(1) extensions which are broken by a SM singlet, since the flavon field used to break the U(1) extension will generically have couplings with the SM Higgs doublet. Thus, for example, TFHMs also predict the possibility of flavonstrahlung.

Appendix A: Conventions and fermion mixing

Here, we detail the rotation of fermion fields to the mass basis in order to fix our conventions. We write

$$\begin{aligned} \mathbf{u_L'}= & {} \left( \begin{array}{c} u_L' \\ c_L' \\ t_L' \\ \end{array} \right) , \qquad \mathbf{d_L'}=\left( \begin{array}{c} d_L' \\ s_L' \\ b_L' \\ \end{array} \right) , \qquad {\varvec{\nu }_L'}=\left( \begin{array}{c} {\nu _e'}_L \\ {\nu _\mu '}_L \\ {\nu _\tau '}_L \\ \end{array} \right) , \nonumber \\ \mathbf{e_L'}= & {} \left( \begin{array}{c} e_L' \\ \mu _L' \\ \tau _L' \\ \end{array} \right) ,\qquad \mathbf{u_R'}=\left( \begin{array}{c} u_R' \\ c_R' \\ t_R' \\ \end{array} \right) , \qquad \mathbf{d_R'}=\left( \begin{array}{c} d_R' \\ s_R' \\ b_R' \\ \end{array} \right) , \nonumber \\ \mathbf{e_R'}= & {} \left( \begin{array}{c} e_R' \\ \mu _R' \\ \tau _R' \\ \end{array} \right) , \qquad {\varvec{\nu }_R'}=\left( \begin{array}{c} {\nu _e'}_R \\ {\nu _\mu '}_R \\ {\nu _\tau '}_R \\ \end{array} \right) , \end{aligned}$$

(A.1)

along with the SM fermionic electroweak doublets

$$\begin{aligned} \mathbf{Q_L'}_i=\left( \begin{array}{c} \mathbf{u_L'}_i \\ \mathbf{d_L'}_i \end{array} \right) ,\qquad \mathbf{L_L'}_i=\left( \begin{array}{c} {\varvec{\nu }_L'}_i \\ \mathbf{e_L'}_i \end{array} \right) . \end{aligned}$$

(A.2)

The fermions acquire their masses through the terms

(A.3)

where $Y_u$, $Y_d$ and $Y_e$ are dimensionless complex coupling constants, each written as a 3 by 3 matrix in family space. The matrix M is a 3 by 3 complex symmetric matrix of mass dimension 1, ${}^c$ denotes the charge conjugate of a field and ${{\tilde{H}}} = ({H^0}^*, -H^-)^T$. After electroweak symmetry breaking and the $W^\pm$ boson eating the electrically charged components of the Higgs doublet, we may write $H=(0,\ (v + h)/\sqrt{2})$, where h is the physical Higgs boson field and (A.3) includes the fermion mass terms

(A.4)

where

$$\begin{aligned} M_\nu = \left( \begin{array}{cc} 0 &{} m_{\nu _D} \\ m_{\nu _D}^T &{} M \\ \end{array} \right) , \end{aligned}$$

(A.5)

$V_{I_L}$ and $V_{I_R}$ are 3 by 3 unitary mixing matrices for each species I, $m_u:=v Y_u/\sqrt{2}$, $m_d:=v Y_d/\sqrt{2}$, $m_e:=v Y_e/\sqrt{2}$ and $m_{\nu _D}:=v Y_\nu /\sqrt{2}$. The final explicit term in (A.4) incorporates the see-saw mechanism via a 6 by 6 complex symmetric mass matrix. Since the elements in $m_{\nu _D}$ are much less than those in M, one performs a rotation to obtain a 3 by 3 complex symmetric mass matrix for the light neutrinos. To a good approximation, these coincide with the left-handed weak eigenstates ${\varvec{\nu }'_L}$, whereas three heavy neutrinos approximately correspond to the right-handed weak eigenstates ${\varvec{\nu }'_R}$. The neutrino mass term of (A.4) becomes, to a good approximation,

$$\begin{aligned} - {{\mathcal {L}}}_{\nu } = \frac{1}{2} {\overline{\varvec{\nu }_L'^c}} m_\nu {\varvec{\nu }_L'} + \frac{1}{2} {\overline{\varvec{\nu }_R'^c}} M {\varvec{\nu }_R'} + H.c., \end{aligned}$$

(A.6)

where $m_\nu := m_{\nu _D}^T M^{-1} m_{\nu _D}$ is a complex symmetric 3 by 3 matrix.

Choosing to be diagonal, real and positive for $I \in \{ u,d,e\}$, and $V_{{\nu }_L}^T m_\nu V_{{\nu }_L}$ to be diagonal, real and positive (all in increasing order of mass from the top left toward the bottom right of the matrix), we can identify the non-primed mass eigenstates

(A.7)

We may then find the CKM matrix V and the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix U in terms of the fermionic mixing matrices:

(A.8)