Parton showers and matching uncertainties in top quark pair production with Herwig 7

Abstract

We evaluate the theoretical uncertainties in next-to-leading order plus parton shower predictions for top quark pair production and decay in hadronic collisions. Our work is carried out using the Herwig  7 event generator and presents an in-depth study of variations in matching schemes with two systematically different shower algorithms, the traditional angular-ordered and alternative dipole shower. We also present all of the required extensions of the Herwig dipole shower algorithm to properly take into account quark mass effects, as well as its ability to perform top quark decays. The predictions are compared at parton level as well as to Large Hadron Collider data, including in the boosted regime. We find that the regions where predictions with a non-top-quark-specific tune differ drastically from data are plagued by large uncertainties which are consistent between our two shower and matching algorithms.

1 Introduction

Top quark pair production is an extremely important process at the Large Hadron Collider (LHC) due to its significant cross section. As the top quark decays before it can hadronize, top quark pair production provides us with a unique opportunity to study Quantum Chromodynamics (QCD) radiation and corrections involving massive particles. This includes measurements of the top quark mass, which is important to constrain the higher-order corrections in the electroweak sector of the Standard Model. Top quark pair production at hadron colliders has become a ‘standard candle’ due to the accurate calculation [1] and measurement of the total cross section. However, the large production rate also allows the measurement of an ever increasing range of kinematic quantities. This means that different kinematic reconstruction strategies for the top quark, and its mass in particular, including in the boosted regime, can be evaluated. It also means that we can study QCD in detail by comparing with less inclusive calculations and Monte Carlo event generators. The large production rate also means that top quark pair production, particularly with the presence of extra jets from QCD radiation, is often the main background to searches for physics Beyond the Standard Model. A number of measurements are available both extracting the top quark mass [2, 3], as well as a number of kinematic properties, e.g. [4].

Monte Carlo event generators [5,6,7] used for predictions of top quark pair production have seen several improvements, which mainly concentrated on combining next-to-leading order QCD corrections with subsequent parton shower algorithms [8,9,10,11], and the production of additional jets using multi-jet merging algorithms, e.g. unitarized schemes [12,13,14,15] as employed inside Herwig  7, or approaches which share a similar spirit [16]. Some of the matching algorithms have addressed off-shell effects in the calculation of the hard process [17], though none of the event generators yet features shower algorithms which properly take into account the effect of the finite width of the top quark and its interplay with the parton shower infrared cutoff.

As compared to indirect approaches based on total cross section measurements, these state-of-the-art simulations provide a very sophisticated description of kinematic properties and thus allow to extract the top quark mass from kinematic properties with an unprecedented precision through template fits. These fits determine the top quark mass parameter used by the event generator simulation. The question in what scheme this mass parameter needs to be interpreted, and what uncertainties need to be taken into account, is still subject to ongoing research [18,19,20], and for coherent parton shower evolution in $e^+e^-$ collisions first analytic and numeric insights have been gained on the role of the mass parameter, including measurements of the top quark mass from reconstruction of its decay products [21]. In Ref. [22] the authors consider predictions of observables that are sensitive to the top quark mass, including an evaluation of uncertainties due to scale variations similar to those considered in this paper. Some aspects of the hadronization effects in such observables have also recently been evaluated [23], however a comprehensive analysis of variations in parton shower evolution, and the impact of different paradigms to include higher order corrections has not yet been performed.

The present work is centred around a thorough investigation of how reliable predictions by established paradigms, namely scale variations in matched predictions, are across phase space. This question has not yet been answered by an in-depth comparison of similar, yet algorithmically very different, predictions and their associated variations which can be established to constitute a set of uncertainties when meeting well-defined constraints [24]. We do this particularly in the light of event generator predictions which are highly specialized in their parameter choices and thus might generate a wrong impression of how well theoretical understanding is under control, and the associated question of what improvements, specifically concerning multi-jet merging, are required.

We also use this study to introduce some improvements to both radiation from heavy quarks and the handling of their decays in the Herwig dipole shower module. These changes enable us to perform this study between different matching and shower algorithms in a consistent way, using the same hadronization and underlying event models and with control over shower starting scales and resummation in the hard emission region.

2 Outline of this work

In this study we use the most recent version, 7.1.4, of the Herwig event generator to make use of the various improvements to the simulation of heavy quarks in production, shower emissions and decays. The modelling of this physics will be discussed in detail in the following sections. In the version considered Herwig sets up the next-to-leading order (NLO) QCD corrections to the top quark pair production process using the automated facilities outlined in Ref. [10], using external libraries [25, 26] to evaluate the required amplitudes on a phase-space point by phase-space point basis. The production of top quark pairs has been validated against MCFM [27,28,29,30]. NLO corrections to the decays are included within a NLO matched parton shower simulation, while we neglect non-factorizable corrections which are beyond the leading contribution in the narrow-width approximation.

Matching the production process to the parton shower is possible within both the subtractive (MC@NLO-type  [8]) and the multiplicative (Powheg-type  [31]) matching paradigms, using the matching subtractions obtained by the Matchbox module along with the QCD corrections required. The matching of the decay to the parton shower is available within the multiplicative paradigm in both the QTilde¹ (angular-ordered) [32] and Dipole (Catani–Seymour [33, 34] dipole-type) [35] shower modules.

The details of the simulation inputs including the scale choices, parton distribution functions (PDFs), strong coupling running and analyses used to obtain results are included in the subsequent sections. The default electroweak parameters of Herwig  7.1 are used in all runs and for the decay corrections the top mass is used as the renormalization scale.

The remainder of this work is organized as follows. In Sect. 3 we consider QCD radiation from the top quark pair production process. In Sect. 4 the parton shower simulation of the decay stage is discussed in detail. We then proceed with an in-depth discussion of the NLO matching in Sect. 5. In Sect. 6 we discuss the parton shower hard scale. We use the framework to assess phenomenologically relevant uncertainties in the matched NLO+PS predictions, and present benchmarks and data comparisons together with a detailed analysis of our findings in Sect. 7. Finally we summarize and give an outlook in Sect. 8.

3 Radiation in production of heavy quarks

3.1 Generalities

For both parton shower algorithms used in the Herwig event generator, a colour flow is assigned to the hard process on the basis of the tree-level colour sub-amplitudes sq. This is a consequence of evaluating the colour correlations relevant to the soft radiation pattern in the limit of a large number of colour charges, $N_c\rightarrow \infty$. The chosen colour flow is used to set the initial conditions in both parton shower modules, in particular identifying which ‘dipole’-type systems radiate coherently. Radiation in both parton showers is also subject to a veto on hard emissions, as set by the hard shower scale, to be discussed in more detail in Sect. 7.

Since a comprehensive treatment of non-factorizable QCD effects which connect the production process and the decay beyond the narrow-width-approximation is not available both parton shower algorithms evolve the production process down to the infrared cutoff which, in the current version, is a cutoff on the relative transverse momentum of the emissions. Once the cutoff has been reached by the evolution of the hard process, the decay of the top quark(s) is performed, and further showering of the decay system is simulated as discussed in Sect. 4.

3.2 Angular-ordered shower

The improved angular-ordered shower used by default in Herwig is described in detail in Refs.  [6, 32]. Here we will only summarize the important details relevant for heavy quark production together with recent improvements not described in Refs.  [6, 32]. The momenta of the partons produced in the parton shower are decomposed in terms of the 4-momentum of the parton initiating the jet, p ($p^2=m^2$, the on-shell parton mass-squared), a light-like reference vector, n, in the direction of the colour partner of the parton initiating the jet and the momentum transverse to the direction of p and n. The four momentum of any parton produced in the evolution of the jet can be decomposed as

$$\begin{aligned} q_i = \alpha _i p + \beta _i n + q_{\perp i}, \end{aligned}$$

(1)

where $\alpha _i$ and $\beta _i$ are coefficients and $q_{\perp i}$ is the transverse four momentum of the parton ($q_{\perp i}\cdot p = q_{\perp i}\cdot n =0$). If we consider the branching of a final-state parton i to two partons j and k, i.e. $i\rightarrow j k$, the evolution variable is

$$\begin{aligned} {\tilde{q}}^2_i = \frac{q^2_i-m^2_i}{z_i(1-z_i)}, \end{aligned}$$

(2)

where $q^2_i$ is the square of the virtual mass developed by the parton i in the branching, $m_i$ is the physical mass of parton i, and $z_i$ is the momentum fraction of the parton j defined such that

$$\begin{aligned} \alpha _j = z_i \alpha _i, \quad \alpha _k = (1-z_i)\alpha _i. \end{aligned}$$

(3)

The transverse momenta of the partons produced in the branching are

$$\begin{aligned} q_{\perp j} = z_i q_{\perp i} + k_{\perp i}, \quad q_{\perp k} = (1-z_i)q_{\perp i} - k_{\perp i}, \end{aligned}$$

(4)

where $k_{\perp i}$ is the transverse momentum generated in the branching. In this case the virtuality of the parton i is

$$\begin{aligned} q_i^2 = \frac{p^2_{Ti}}{z(1-z)} + \frac{m_j^2}{z}+\frac{m_k^2}{1-z}, \end{aligned}$$

(5)

where $p_{Ti}$ is the magnitude of the transverse momentum produced in the branching defined such that $k_{\perp i}^2=-p^2_{Ti}$.

In this case the probability for a single branching to occur is

$$\begin{aligned} \mathrm{d} {\mathcal {P}} = \frac{\mathrm{d}{\tilde{q}}^2_i}{{\tilde{q}}^2_i}\frac{\alpha _S}{2\pi } \frac{\mathrm{d} \phi _i}{2\pi } \mathrm{d} z_i P_{i\rightarrow jk}(z,{\tilde{q}}), \end{aligned}$$

(6)

where $P_{i\rightarrow jk}(z,{\tilde{q}})$ is the quasi-collinear splitting function and $\phi _i$ is the azimuthal angle of the transverse momentum $k_{\perp i}$ generated in the splitting.

As described in Ref.  [32] this choice of evolution variable, including the mass of the radiating parton, together with the use of the quasi-collinear splitting functions gives a better treatment of radiation from the parton in the small-angle region. In this region we expect a suppression of soft radiation for angles $\theta \lesssim m/E$, where $\theta$ is the angle of emission, m and E the mass and energy of the radiating parton, respectively. The choices used in Herwig  7 give the expected smooth turn-off of soft radiation rather than the ‘dead-cone’² [36] used in HERWIG 6 [37].

The angular-ordered shower is simulated as a series of individual emissions, and only the shower variables (${\tilde{q}},z,\phi$) are calculated for each emission. Once the evolution has terminated, i.e. there is no phase space available for further emissions, the external particles are taken to be on-shell and the physical momenta reconstructed.

If we set $\alpha _i=1$ for final-state progenitors³ and $\alpha _i=x$, the light-cone momentum fraction, for initial-state progenitors then using Eq. (3) and the momentum conservation relation $\alpha _{i}=\alpha _{j}+\alpha _{k}$, all the $\alpha$ values can be iteratively calculated, starting from the hard process and working outward to the external legs. For final-state radiation the transverse momenta can be calculated in the same way using Eq. (4), whereas for initial-state radiation the transverse momentum is calculated iteratively assuming that the parton extracted from the proton as a result of the backward evolution has zero transverse momentum.⁴ The $\beta$ variables for the external partons can then be calculated using the on-shell condition and those for radiating partons using momentum conservation, i.e. $\beta _{i}=\beta _{j}+\beta _{k}$. The latter step may be iterated until the progenitor is reached giving all the $\beta$ coefficients.

As a result of the shower evolution all the progenitor partons, I, produced in the hard process gain a virtual mass, i.e. the progenitor partons, which initiated the jets, are no longer on mass shell, $q_{I}^{2}\ne m_{I}^{2}$. We need to restore momentum conservation in a way that disturbs the internal structure of the jet as little as possible. The easiest way to achieve this is by boosting each jet along its axis so that their momenta are rescaled, i.e. for every jet a Lorentz boost is applied such that

$$\begin{aligned} q_I=\left( {\mathbf {q}}_I;\sqrt{{\mathbf {q}}_I^{2}+q_I^{2}}\right) {\mathop {\longrightarrow }\limits ^{\mathrm{boost}}}q_I^{\prime }=\left( k_I {\mathbf {p}}_I;\sqrt{k^{2}{\mathbf {p}}_I^{2}+q_I^{2}}\right) ,\nonumber \\ \end{aligned}$$

(7)

where $k_I$ is the rescaling factor. The rescaling factors, and the choice of frame in which to apply the boosts, are determined by the choice of which kinematic variables we wish to preserve in the rescaling process. In Ref.  [32] an approach was suggested based on the colour connections between the partons initiating the jets:

• for colour-connected final-state partons the reconstruction was performed in the centre-of-mass frame of the partons and the momenta rescaled such that the centre-of-mass energy was conserved, i.e.

  $$\begin{aligned} \sum _{I=1}^{n}\sqrt{k^{2}{\mathbf {p}}_{I}^{2}+q_{J}^{2}}=\sqrt{s}, \end{aligned}$$

  (8)

  where $\sqrt{s}$ is the centre-of-mass energy and the same rescaling factor k is used for all the jets;

• for colour-connected initial-state partons the reconstruction is performed in the hadronic centre-of-mass frame and the partonic centre-of-mass energy is preserved. In order to fully specify the kinematics an additional constraint is required which in Ref.  [32] was chosen such that the rapidity of the partonic collision was preserved;

• for partons with a colour connection between the initial and final state, such as Deep Inelastic scattering (DIS), the system is reconstructed in the Breit frame of the partons such that the virtuality of the system is preserved.

As the majority of hadronic collisions cannot be decomposed into separate colour-singlet systems in early versions of Herwig++ hadronic collisions were all reconstructed by first using the procedure for colour-connected initial-state partons and then that for final-state partons. This was changed such that if possible the hard process was decomposed into separate colour-singlet systems,⁵ for example in $q{\bar{q}} \rightarrow t {\bar{t}}$, then the separate colour-singlet systems were reconstructed as described above.

In Herwig  7 we have adopted an approach which attempts to use as much information as possible on the colour structure of the hard process when performing the reconstruction. In order to achieve this we now consider all the partons in the hard process and commence the reconstruction with the parton which had the hardest, i.e. largest $p_T$, emission in the parton shower. The system formed by this parton and its colour partner is then reconstructed, with either a full reconstruction of the jet produced by the colour partner, the default, or optionally just using the partner to absorb the recoil leaving it on its partonic mass shell and not performing the reconstruction of the full jet. This procedure is repeated for the parton with the hardest shower emission which has not been reconstructed until all the kinematics of all the jets have been reconstructed. Together with an additional option of preserving the momentum fraction of the softer incoming parton in the hard process, for systems with colour connections between initial-state partons, this means that for a single emission the kinematics reduce to those of the Catani–Seymour [33, 34] dipoles making matching in the MC@NLO approach simpler.

3.3 Dipole shower

The dipole shower algorithm evolves singlet systems of colour connected dipoles, referred to chains [10], based on the colour flow information assigned to the hard process. For the massless case the details of the dipole shower algorithm in Herwig have been discussed in Refs.  [10, 35]. In this paper we focus on the generalization of the algorithm to radiation from heavy quarks, and radiation in the decays of coloured objects, to be covered in detail in Sect. 4. While the heavy quark treatment in Ref.  [38] has previously been based on Ref.  [39], an improved description is presented here which is in one-to-one correspondence to the massless case, and in particular adopts the transverse momentum relevant in the quasi-collinear limit [34], with a smooth massless limit. Throughout this work we use the terminology ‘massive dipole’ to refer to a dipole that includes at least one massive parton and/or splits to produce at least one massive parton.

Fig. 1

Diagrams of the massive dipoles

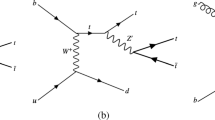
Splittings involving massive incoming partons are not currently implemented in the Herwig dipole shower. This means that there are three possible dipole configurations involving massive partons. These are shown diagrammatically in Fig. 1. Massive final–final (FF) dipoles, with final-state emitter and spectator, Fig. 1c, must include at least one massive outgoing parton before or after the splitting. Massive final–initial (FI) dipoles, Fig. 1a, consist of a massless incoming spectator and an outgoing emitter. At least one of the outgoing partons before or after the splitting must be massive. Massive initial–final (IF) dipoles, Fig. 1b, consist of a massless incoming emitter and massive final-state spectator.

Due to its large mass, parton shower emissions from top quarks are highly suppressed. This means that emissions from massive FI dipoles do not make a significant contribution in the parton shower. Similarly emissions from FF dipoles with a top quark emitter are highly suppressed, however emissions from FF dipoles with a massless emitter and top quark spectator are not suppressed in this way. Therefore both massive FF and IF dipole splittings make a significant contribution in the parton shower.

A detailed understanding of these radiation processes with full mass effects is therefore mandatory, and the main goal of this work is to formulate the relevant kinematic parametrization and evolution quantities in a similar way to the massless case, with emphasis on a covariant formulation and an evolution variable which reflects the transverse momentum relevant to the enhancements present for collinear radiation. We present the kinematics used for splittings of all massive dipoles in the following sections. The kernels used to describe the splittings are those given in Ref. [34].

For each dipole the kernels and kinematics used to describe a splitting are parametrized by two splitting variables and an azimuthal angle. In Herwig  7.1 we use spin-averaged dipole splitting kernels, therefore we randomly generate the azimuthal angle for each splitting according to a uniform distribution. The splitting variables used to parametrize the splitting for each dipole are those used in Ref. [34] and are given for each dipole in the following sections.

In the dipole shower in Herwig we actually generate the transverse momentum, $p_\perp$, and the light-cone momentum fraction, z, as used in the standard quasi-collinear Sudakov parametrization of the momenta following a splitting. This is the parametrization used in the angular-ordered shower [32], see Sect. 3.2. We choose a light-like vector n to define the collinear direction and for a splitting from a final-state emitter with momentum ${\tilde{p}}_{ij}$ we write the momentum, $q_j$, of the emitted parton as

$$\begin{aligned} q_j = (1-z){\tilde{p}}_{ij} + \frac{m_j^2 - (1-z)^2 m_{ij}^2 + p_\perp ^2}{2 {\tilde{p}}_{ij}\cdot n (1-z)} n - k_\perp , \end{aligned}$$

(9)

where m is the mass of the emitted parton and $m_{ij}$ is the mass of the emitter. The space-like vector $k_\perp$ satisfies $k_\perp \cdot {\tilde{p}}_{ij} = k_\perp \cdot n = 0$ and $k_\perp ^2 = - p_\perp ^2$ .

Similarly for a splitting from a massless incoming parton we write the momentum of the emitted parton as

$$\begin{aligned} q_j = (1-z)q_a + \frac{ p_\perp ^2}{2 q_a\cdot n (1-z)} n - k_\perp , \end{aligned}$$

(10)

where $q_a$ is the momentum of the parton incoming from the proton following the splitting and $k_\perp \cdot q_a = k_\perp \cdot n = 0$.

In view of these parametrizations, which are the ones relevant in the (quasi-)collinear limit, we choose to set up kinematic mappings for a dipole splitting including momentum conservation in a way that we express the resulting kinematics in terms of these physical variables, $p_\perp$ and z, rather than the ones which most conveniently allow the separation and integration over the phase space. This has been done in the massless case, and the mappings below generalize this to the massive case with a smooth massless limit.

3.3.1 Final–final dipoles

We consider the splitting process ${\tilde{p}}_{ij},{\tilde{p}}_k\rightarrow q_i,q_j,q_k$ where all momenta before and after the splitting are on-shell, ${\tilde{p}}_{ij}^2 = m_{ij}^2$, ${\tilde{p}}_{k}^2 = q_k^2 = m_k^2$, $q_{i,j}^2 = m_{i,j}^2$ and satisfy momentum conservation for the dipole considered, i.e. $Q={\tilde{p}}_{ij}+{\tilde{p}}_{k}=q_i+q_j+q_k$ with $s=Q^2$. Splittings from FF dipoles are conveniently parametrized by the splitting variables $z_i$ and $y_{ij,k}$ which are defined in terms of the physical momenta as

$$\begin{aligned} z_i= & {} \frac{q_i \cdot q_k}{ (q_i + q_j) \cdot q_k }\,, \end{aligned}$$

(11a)

$$\begin{aligned} y_{ij,k}= & {} \frac{q_i \cdot q_j}{q_i \cdot q_j + q_i \cdot q_k + q_j \cdot q_k}\,. \end{aligned}$$

(11b)

A fully consistent mapping from ${\tilde{p}}_{ij},{\tilde{p}}_k \rightarrow q_{i,j,k}$ written in terms of $z_i$ and $y_{ij,k}$ is presented in Appendix A.1, however we do not consider it further here. This is because, while this mapping and the corresponding mapping from $q_{i,j,k}\rightarrow {\tilde{p}}_{ij},{\tilde{p}}_k$ defined in Ref. [34] are formulated for arbitrary particle masses, the identification of the physical degrees of freedom relevant in the quasi-collinear limit [40] is not directly obvious.

For a massless spectator the relevant direction can be directly identified, however for a massive spectator we first need to map both of the massive dipole momenta prior to emission into light-like momenta $n_{ij}$ and $n_k$, which in general have $n_{ij}+n_k\ne Q$. We therefore define

$$\begin{aligned} (n_{ij}+n_k)^2= 2 n_{ij}\cdot n_k \equiv s_{ij,k}\ . \end{aligned}$$

(12)

We can write these light-like vectors in terms of the emitter and spectator momenta as

$$\begin{aligned} n_{ij}= & {} \frac{s_{ij,k}^2}{s_{ij,k}^2- m_{ij}^2 m_k^2} \left( {\tilde{p}}_{ij} - \frac{m_{ij}^2}{s_{ij,k}}{\tilde{p}}_k \right) , \end{aligned}$$

(13a)

$$\begin{aligned} n_k= & {} \frac{s_{ij,k}^2}{s_{ij,k}^2- m_{ij}^2 m_k^2} \left( {\tilde{p}}_{k} - \frac{m_{k}^2}{s_{ij,k}}{\tilde{p}}_{ij} \right) , \end{aligned}$$

(13b)

which gives

$$\begin{aligned}&s_{ij,k}= 2n_{ij}\cdot n_k \nonumber \\&\quad = \frac{1}{2} \left( s-m_{ij}^2-m_k^2 + \sqrt{(s-m_{ij}^2-m_k^2)^2-4 m_{ij}^2 m_k^2}\right) .\nonumber \\ \end{aligned}$$

(14)

The scaled emitter and spectator momenta can be parametrized as

$$\begin{aligned} q_{ij}= & {} x_{ij} n_{ij} + \frac{m_{ij}^2}{x_{ij}s_{ij,k}} n_k\,, \nonumber \\ q_{k}= & {} x_k n_{k} + \frac{m_{k}^2}{x_k s_{ij,k}} n_{ij}\,. \end{aligned}$$

(15)

The emitter and spectator momenta relevant in the quasi-collinear limit for the definition of z and $p_\perp$ are expressed as

$$\begin{aligned} q_i= & {} z q_{ij} + \frac{m_i^2-{z}^2 m_{ij}^2 - k_\perp ^2 }{x_{ij} s_{ij,k}z} n_k + k_\perp \,, \nonumber \\ q_j= & {} (1-z)\ q_{ij} + \frac{m_j^2-(1-z)^2 m_{ij}^2 - k_\perp ^2 }{x_{ij} s_{ij,k}(1-z)} n_k - k_\perp \,. \end{aligned}$$

(16)

Notice that the limit $m_k\rightarrow 0$ smoothly reproduces the parametrization where one works with a light-like collinear direction along the spectator. Comparison to Eq. (9) allows us to identify the physical branching variables $p_\perp$ and z, which relate to the propagator involved in the splitting as

$$\begin{aligned}&\frac{1}{z(1-z) }\left( p_\perp ^2 + z m_j^2 + (1-z) m_i^2 - z(1-z) m_{ij}^2 \right) \nonumber \\&\quad = \left[ (q_i+q_j)^2 -m_{ij}^2 \right] . \end{aligned}$$

(17)

The remaining details of this formulation, including expressions for the scaling variables $x_{ij}$ and $x_k$ and expressions for $z_i$ and $y_{ij,k}$ in terms of the variables $p_\perp$ and z, are provided in Appendix A.2. A formulation similar to that presented here is described in Ref. [41], however it differs in the definition of the momenta of the splitting products and the variables used.

The probability for a single branching to occur from a final–final dipole is

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}} = \frac{1}{(q_i + q_j)^2 - m_{ij}^2} \langle V_{i j, k} \left( z_i,y_{ij,k}\right) \rangle \mathrm {d} q_j \ , \end{aligned}$$

(18)

where $\langle V_{i j, k} \left( z_i,y_{ij,k}\right) \rangle$ is the spin-averaged dipole splitting kernel used to describe the branching of a final-state emitter into partons i and j with final-state spectator, k. The single-particle emission phase space, discussed in more detail in Appendix A.2, is denoted by $\mathrm {d}q_j$.

Finally, we show that this formulation of the splitting momenta is consistent with the definitions of the kernels and requirements in Ref. [34]. Following the splitting there are three momenta that must be determined, $(q_i,q_j,q_k)$, with no considerations this system contains twelve degrees-of-freedom. Given that we know the identity and therefore the mass of each parton, we can immediately remove three degrees-of-freedom. We are now left with nine degrees-of-freedom, namely the energy, $E_n$, polar angle, $\theta _n$, and azimuthal angle, $\phi _n$, for each parton n, i.e.

$$\begin{aligned}&q_i: \left\{ E_i, \theta _i, \phi _i \right\} , \nonumber \\&q_j: \left\{ E_j, \theta _j, \phi _j \right\} , \nonumber \\&q_k: \left\{ E_k, \theta _k, \phi _k \right\} \ . \end{aligned}$$

(19)

We choose to work in the rest frame of the dipole with ${\tilde{p}}_{ij}$ along the positive z-axis. Implicitly ${\tilde{p}}_{k}$ must lie along the negative z-axis and the mapping from $q_{i,j,k}\rightarrow {\tilde{p}}_{ij},{\tilde{p}}_k$ defined in Ref. [34] requires that, in this frame, the spectator only absorbs longitudinal momentum in the splitting. Therefore $\theta _k = \phi _k = 0$ which eliminates two degrees-of-freedom. Furthermore we require that the momentum Q is conserved in the splitting which eliminates a further four degrees of freedom. Finally we generate the azimuthal angle of the splitting $\phi = \phi _i = -\phi _j$, where the second equality follows from momentum conservation, according to a uniform distribution. We are now left with two degrees-of-freedom.

It is important to note that the above constraints on the degrees-of-freedom follow from the requirement of momentum conservation in the splitting and the requirements in Ref. [34]. We have also chosen to simplify the picture by working in a convenient frame which additionally defines the meaning of the azimuthal angle $\phi$. Therefore, given $\phi$, the momenta following the splitting must be fully constrained by two independent variables. Hence for a given $z_i$ and $y_{ij,k}$ the momenta are fully constrained. Therefore regardless of the variables we generate and the explicit covariant expressions that we use, so long as $z_i$ and $y_{ij,k}$ can be uniquely expressed in terms of the generated variables, the splitting momenta are uniquely defined. Importantly, we can use the splitting kernels and phase-space limits given in Ref. [34] with our covariant formulation of the splitting kinematics.

3.3.2 Final–initial dipoles

As the spectator in a FI dipole is necessarily massless, one can use the standard quasi-collinear parametrization of the kinematics to describe splittings from massive FI dipoles. In order to be consistent with the formulation used to describe splittings from IF dipoles, Sect. 3.3.3, we instead choose to provide a parametrization in terms of the dipole splitting variables. The four-momenta of the spectator and emitter prior to the splitting are ${\tilde{p}}_b$ and ${\tilde{p}}_{ij}$, respectively. The four-momenta of the spectator, emitter and emission following the splitting are $q_b$, $q_i$ and $q_j$, respectively. The mass of the emitter prior to the splitting and the masses of the emitter and emitted partons following the splitting are $m_{ij}$, $m_i$ and $m_j$, respectively.

Splittings from FI dipoles are parametrized by the splitting variables $z_i$ and $x_{ij,b}$ which are defined in terms of the physical momenta as

$$\begin{aligned} z_i= & {} \frac{q_i \cdot q_b}{(q_i + q_j)\cdot q_b},\, \end{aligned}$$

(20)

$$\begin{aligned} x_{ij,b}= & {} \frac{(q_i +q_j)\cdot q_b - q_i \cdot q_j + \frac{1}{2} \left( m_{ij}^2 - m_i^2 - m_j^2 \right) }{(q_i + q_j)\cdot q_b}.\nonumber \\ \end{aligned}$$

(21)

As the spectator is incoming and therefore massless, $z_i$ is identical to the generated variable z. We define the conserved momentum transfer

$$\begin{aligned} Q = {\tilde{p}}_{ij} - {\tilde{p}}_{b} = q_i + q_j - q_b\,, \end{aligned}$$

(22)

and for convenience the invariant

$$\begin{aligned} s_{ij,b}= 2 {\tilde{p}}_{ij} \cdot {\tilde{p}}_b\,. \end{aligned}$$

(23)

The momenta prior to the splitting are written in terms of the momenta following the splitting as

$$\begin{aligned} {\tilde{p}}_b= & {} x_{ij,b}\, q_b \ , \end{aligned}$$

(24)

$$\begin{aligned} {\tilde{p}}_{ij}= & {} q_i + q_j - (1-x_{ij,b})q_b \ . \end{aligned}$$

(25)

These expressions are satisfied by writing the momenta following the splitting as

$$\begin{aligned} q_i= & {} z_i{\tilde{p}}_{ij} +k_\perp + \left[ (1-z_i)\left( \frac{1-x_{ij,b}}{x_{ij,b}}\right) \right. \nonumber \\&\left. + \frac{1}{s_{ij,b}} \left( m_i^2 - m_j^2 + (1-2z_i)m_{ij}^2 \right) \right] {\tilde{p}}_b\,, \end{aligned}$$

(26a)

$$\begin{aligned} q_j= & {} (1-z_i){\tilde{p}}_{ij} - k_\perp + \left[ z_i\left( \frac{1-x_{ij,b}}{x_{ij,b}}\right) \right. \nonumber \\&\left. + \frac{1}{s_{ij,b}} \left( -m_i^2 + m_j^2 - (1-2z_i)m_{ij}^2 \right) \right] {\tilde{p}}_b\,, \end{aligned}$$

(26b)

$$\begin{aligned} q_b= & {} \frac{1}{x_{ij,b}} {\tilde{p}}_b\,. \end{aligned}$$

(26c)

We obtain an expression for the splitting variable $x_{ij,b}$ in terms of the generated variables $p_\perp$ and z by comparison with Eq. (9), giving

$$\begin{aligned} x_{ij,b}= \left[ 1 + \frac{p_\perp ^2 + (1-z) m_i^2 + z m_j^2 - z(1-z) m_{ij}^2}{ s_{ij,b}z(1-z)} \right] ^{-1}. \end{aligned}$$

(27)

The probability for a single branching to occur from a FI dipole is given by

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}}= & {} \frac{1}{(q_i+q_j)^2 - m_{ij}^2} \frac{1}{x_{ij,b}} \frac{f_b(x_s/x_{ij,b})}{f_b(x_s)}\nonumber \\&\times \langle V_{i j}^b \left( z_i, x_{ij,b}\right) \rangle \mathrm {d} q_j\,, \end{aligned}$$

(28)

where $\langle V_{i j}^b \left( z_i, x_{ij,b}\right) \rangle$ is the spin-averaged dipole splitting kernel used to describe the branching of a final-state emitter into the partons i and j with an initial-state spectator, b. The parton density function of the incoming spectator is $f_b(x)$ and $x_s$ is the proton momentum fraction carried by the spectator prior to the splitting, and $\mathrm {d}q_j$ denotes the single-particle emission phase space. A detailed description of the emission phase space is given in Appendix A.3.

3.3.3 Initial–final dipoles

The momenta of the incoming emitter and outgoing spectator prior to the splitting are ${\tilde{p}}_{aj}$ and ${\tilde{p}}_k$, respectively. The new emitter following the splitting is defined to be the parton incoming from the proton while the emitted particle is the emitted final-state parton. The momenta of the emitter, emitted particle and spectator following the splitting are $q_a$, $q_j$ and $q_k$, respectively. The mass of the spectator is $m_k$.

Splittings from IF dipoles are parametrized by the splitting variables $x_{jk,a}$ and $u_j$ which are defined in terms of the physical momenta as

$$\begin{aligned} x_{jk,a}= & {} \frac{q_a \cdot q_j + q_a \cdot q_k - q_j \cdot q_k}{(q_j + q_k) \cdot q_a}\,, \end{aligned}$$

(29)

$$\begin{aligned} u_j= & {} \frac{q_a \cdot q_j}{(q_j + q_k) \cdot q_a}\,. \end{aligned}$$

(30)

We define the conserved momentum transfer

$$\begin{aligned} Q ={\tilde{p}}_k -{\tilde{p}}_{aj} = q_j + q_k - q_a\,, \end{aligned}$$

(31)

and the invariant

$$\begin{aligned} s_{aj,k}= 2 {\tilde{p}}_{aj} \cdot {\tilde{p}}_k\,. \end{aligned}$$

(32)

The momenta prior to the splitting are written in terms of the momenta following the splitting as

$$\begin{aligned} {\tilde{p}}_{aj}= & {} x_{jk,a}\, q_a\,, \end{aligned}$$

(33a)

$$\begin{aligned} {\tilde{p}}_k= & {} q_j + q_k - (1-x_{jk,a})q_a\,. \end{aligned}$$

(33b)

These expressions are satisfied by writing the momenta following the splitting as

$$\begin{aligned} q_a= & {} \frac{1}{x_{jk,a}} {\tilde{p}}_{aj}\,, \end{aligned}$$

(34a)

$$\begin{aligned} q_j= & {} \left[ \left( \frac{1-x_{jk,a}}{x_{jk,a}} \right) (1-u_j) - u_j\frac{2 m_k^2}{s_{aj,k}} \right] {\tilde{p}}_{aj}\nonumber \\&{}+ u_j{\tilde{p}}_k - k_\perp \,, \end{aligned}$$

(34b)

$$\begin{aligned} q_k= & {} \left[ \left( \frac{1-x_{jk,a}}{x_{jk,a}} \right) u_j+ u_j\frac{2 m_k^2}{s_{aj,k}} \right] {\tilde{p}}_{aj}\nonumber \\&{}+ (1-u_j) {\tilde{p}}_k + k_\perp \,. \end{aligned}$$

(34c)

We need to write the splitting variables in terms of the variables generated in the parton shower, $p_\perp$ and z. We set $n = {\tilde{p}}_k - (m_k^2/s_{aj,k}) {\tilde{p}}_{aj}$ in Eq. (10) and equate this to Eq. (34b) giving

$$\begin{aligned} x_{jk,a}= & {} \frac{s_{aj,k}}{2r(s_{aj,k}-m_k^2)}(1-z+r) \nonumber \\&\times \, \left[ 1 - \sqrt{1 - \frac{4r(s_{aj,k}-m_k^2)}{s_{aj,k}}\frac{z(1-z)}{(1-z+r)^2}} \right] ,\nonumber \\ \end{aligned}$$

(35a)

$$\begin{aligned} u_j= & {} x_{jk,a}\left( \frac{r}{1-z} \right) \,, \end{aligned}$$

(35b)

where we have defined $r = p_\perp ^2 / s_{aj,k}$. These expressions again relate the backward-evolution, dipole picture recoil to the quantities involved in the physical forward branching process, Eq. 10.

The probability for a single branching to occur from an IF dipole is

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}}= & {} \frac{1}{2 q_j \cdot q_a} \frac{1}{x_{jk,a}} \frac{f_a(x_e/x_{jk,a})}{{\tilde{f}}_{aj}(x_e)}\nonumber \\&{}\times \langle V^{a j}_k \left( u_j, x_{jk,a}\right) \rangle \mathrm {d} q_j\,, \end{aligned}$$

(36)

where $\langle V^{a j}_k \left( u_j, x_{jk,a}\right) \rangle$ is the spin-averaged dipole splitting kernel used to describe the branching of an initial-state emitter ${\widetilde{aj}}$ into an initial-state parton a and a final-state parton j with a final-state spectator k. The parton density function of the incoming partons ${\widetilde{aj}}$ and a are ${\tilde{f}}_{aj}(x)$ and $f_a(x)$, respectively. The proton-momentum fraction carried by the parton ${\widetilde{aj}}$ is $x_e$ and $\mathrm {d}q_j$ denotes the single-particle emission phase space. A detailed description of the emission phase space is given in Appendix A.4.

4 Radiation in the decays of heavy quarks

In both Herwig parton showers the production and decay processes are showered independently, following a factorized approach. In the case of top quark pair production, the hard process, e.g. $pp \rightarrow t{\bar{t}}$, is first evolved down to the IR cutoff $\mu _\mathrm {IR} \approx 1 \text {GeV}$,⁶ as described in Sect. 3. This involves radiation from both the initial- and final-state partons, including the top quarks. When simulating predictions with unstable top quarks, these then undergo a perturbative decay, and further shower evolution from the decaying system, and possible further decay products, e.g. those originating form a hadronic W decay. The hard scale relevant for emissions from the decaying top quark is the mass of the top quark, and the evolution will preserve its four-momentum including the virtuality.

Matchbox is currently limited to generating hard processes with on-shell outgoing particles, because in the factorized approach a smearing of the mass with some input distribution consistently is only possible at leading order (LO), and poses major challenges at next-to-leading order unless one resorts to a complete off-shell calculation, which can in principle be handled by the framework. While the angular-ordered shower can handle off-shell coloured particles, the dipole shower can currently only deal with on-shell coloured particles, such that we do not consider a reconstructed resonance hierarchy from a full calculation as an input to the showers. This also implies that in the hard process the top width is set to zero, as we could otherwise not treat it as an on-shell particle at the level of the hard process. In this paper we therefore use a strict narrow-width-approximation, i.e. no mass smearing is applied and the top quark decay width is not included as a scale in the showering.

In Herwig by default top quarks, t, are decayed according to the 3-body matrix element to a bottom quark, b, and two fermions, f and $\bar{f^\prime }$, via an intermediate W-boson in order that off-shell effects are included for the W-boson. The decay system is then showered as described in Sect. 4.1 for the angular-ordered shower and Sect. 4.2 for the dipole shower, which presents a new development which we cover in detail.

In both cases we first shower the top-bottom-W-boson, tbW, system followed by the W-boson-fermion-antifermion, $Wf\bar{f^\prime }$, system. In the shower the tbW and $Wf\bar{f^\prime }$ systems are considered to be colour isolated from each other and the rest of the process. In this sense each decay system is showered independently from the rest of the process. This pattern of evolving ‘down’ decay trees, i.e. from the hard process towards the final-state particles, is true for all decays in Herwig  7.

In both parton showers we have the option of performing the first emission from the decay system according to the real-emission matrix element using the builtin Powheg decay correction [42] for all SM decay processes, including both the top quark and W-boson decay. In practice this is sufficient as the NLO virtual corrections only effect the calculation of the width and not the physical distributions. This is switched on by default in the dipole shower whereas the angular-ordered shower uses a matrix-element correction by default. The dipole shower does not currently include QED radiation. In the case of SM decays involving no coloured particles, for example a leptonic W-boson decay, QED radiation can be generated using the SOPHTY implementation in Herwig [43] which is switched on by default when the dipole shower is used. The angular-ordered shower does include QED radiation and the SOPHTY implementation is not used in this case.

4.1 Angular ordered shower

The improved angular-ordered shower used in Herwig proceeds in much the same way for decays as for hard processes. The main difference is the handling of radiation with a coloured decaying particle connected to one of the decay products, e.g. $t\rightarrow bW^+$. In order to cover the full soft phase-space region we must have radiation from both the decaying particle and the decay product [32].⁷ This can be seen in Fig. 2 where in order to cover the full phase-space region for soft emission, i.e. $x_g\rightarrow 0$, we need radiation in both the upper region, from $b\rightarrow b g$ branchings, and the lower region from $t\rightarrow t g$ branchings. As can be seen in Fig. 2 the shower approximation overestimates the leading-order real emission matrix element over all the filled phase space and the two results agree in the soft $x_g\rightarrow 0$ and collinear limit where $x_W$ tens to its maximum value. The angular-ordered shower has a ‘dead-zone’ where there is no emission from the parton shower, and a region at large $x_g$ which could in principle be filled by the parton shower. In this region the parton shower significantly underestimates the real emission matrix element and therefore as this region contains to soft or collinear enhancements we choose not to generate parton shower emissions in it. As described in detail in Refs. [6, 32] the recoil from any shower emissions in this case is absorbed such that any recoil perpendicular to the direction of the W boson in the top rest frame is absorbed by the bottom quark, while the remaining component parallel to the W boson direction is absorbed by the W boson.

As with Herwig 6 [44] in Herwig 7 we apply both a hard matrix-element correction, to fill the ‘dead-zone’ and unfilled shower region as well as a soft matrix element to correct the hardest-so-far emission in the parton shower regions, this is described in more detail in Ref.  [45]. This is the default option, however there is also an option to apply a Powheg correction to the decay [42] including the truncated shower.

Fig. 2

Dalitz plot for $t\rightarrow b W^+ g$ where the gluon is emitted by the angular-ordered parton shower. The energy fractions of the gluon and $W^+$ boson are $x_g=2E_g/m_{\mathrm{top}}$ and $x_W=2E_W/m_{\mathrm{top}}$, respectively. In the regions of allowed emission in the angular-ordered parton shower the plot shows the ratio of the leading-order matrix element result over the parton-shower approximation. The red region, the ‘dead-zone’, is not filled by the parton shower while the empty region for large $x_g$ could be filled by the parton shower, in practice the the shower provides a poor approximation in this region and it and the ‘dead-zone’ are filled using a hard matrix-element correction

4.2 Dipole shower

In a top quark decay a dipole is formed by the decaying top quark and the outgoing bottom quark. During showering the incoming top quark can also form dipoles with other partons outgoing from the decay. In the current implementation of the dipole shower in Herwig we include emissions from final–initial decay (FI-decay) dipoles only and do not include initial–final decay (IF-decay) dipoles. In other words we explicitly consider emissions from outgoing emitter partons only and do not explicitly include emissions from the incoming top quark. This choice is justified in Sect. 4.2.3.

The dipole splitting kernels for radiation from FI-decay dipoles including only massless final-state particles are given in Refs. [46, 47]. In Ref. [48] the dipole splitting kernel for photon radiation from a massive outgoing quark in a FI-decay dipole is presented. The extension to QCD radiation is used to produce the numerical results presented in that paper, however they do not give the explicit form of the splitting kernels used. In all of these works, the authors also decide to include emissions from FI-decay dipoles only.

In this section we describe in detail the treatment of coloured particle decays in the Herwig  7 dipole shower. The simulation of top quark decays is the primary motivation behind the new developments outlined in this section, therefore we follow the example of top quark decays throughout. These developments have been implemented such that they are applicable to general decays, including BSM processes. In particular the new technical developments in the implementation of the dipole shower, Sect. 4.2.1, and the kinematics for splittings from decay dipoles, Sect. 4.2.2, are independent of the identity of the particles involved.

4.2.1 Implementation

In each decay system the colour chains and dipoles are constructed and updated following each splitting using exactly the same procedure as for the showering of hard production processes [10]. The shower starting scale for each decay system is chosen to be the mass of the incoming decayed particle.

In the case of a top quark decay, with the default POWHEG correction, we attempt to produce the first emission from the tbW system using the exponentiated real-emission matrix element. Following this corrected real emission we shower the system starting from a scale equal to the transverse momentum of the emission. In the rare case that there is no POWHEG emission above the IR cutoff, we do not shower the system.

The $Wf\bar{f^\prime }$ system is a FF dipole, therefore we require no new kinematics or kernels to shower the system. On-the-other-hand the top quark decay introduces new complications. The momentum of the top quark is set, prior to its decay, in the production process and we must not change its momentum following its decay. Therefore in dipoles with the top quark as spectator we cannot use the top quark to absorb the recoil from the splitting. Instead we choose to apply a boost to the rest of the outgoing particles in the decay system to absorb the recoil. This is discussed in more detail in Sect. 4.2.2.

The tbW system is showered until no further emission above the IR cutoff can be generated. This is followed by a ‘reshuffling’ of the momenta of the particles outgoing from the decay in order to put all partons on their constituent mass-shell as required for hadronization. Momentum conservation is enforced in each splitting in the dipole shower and we must ensure that, following the reshuffling procedure, the sum of the outgoing momenta remains equal to the four-momentum of the decayed particle.

In the case where there are two or more outgoing partons, we simply rescale the masses and 3-momenta of each parton such that all partons are put on their constituent mass shell. In the rare case of no emission from a tbW system, we rescale the mass and 3-momentum of the bottom quark and the 3-momentum of the W-boson while keeping the virtuality of the W-boson unchanged.

Splittings from decay dipoles and the reshuffling procedure can modify the momentum of the W-boson from the value set in the 3-body decay of the top-quark. Therefore following the showering of the tbW system and the subsequent reshuffling, we must apply a boost to the decay products of the W-boson to ensure that momentum is conserved in the W-boson decay. This boost is applied prior to showering the $Wf\bar{f^\prime }$ system. In longer decay trees, following the showering of each decay, we work down the decay tree updating the momenta of decay products as appropriate.

4.2.2 Kinematics

As a colour partner of the emitter we refer to the incoming top quark as the ‘spectator’, however we wish to preserve the 4-momentum of the top quark as its momentum has been set, before its decay, in the showering of the production process. Therefore the top quark is not used to absorb the recoil in splittings. Instead the recoil is absorbed by all outgoing particles from the top decay system, except for the emitter and the new emission.

Figure 3 shows a diagram of a decay dipole. The momenta of the incoming decayed parton and the outgoing emitter prior to the splitting are $q_b$ and ${\tilde{p}}_{ij}$, respectively. The total momentum of all other outgoing particles in the decay system is ${\tilde{p}}_k$. Following the splitting the momenta of the new outgoing emitter and emission are $q_i$ and $q_j$, respectively and the total momentum of all other outgoing particles in the decay system is $q_k$. It is implicit from our definition of the recoil system as all particles outgoing from the decay except the emitter that the incoming parton momentum $q_b$ is the conserved dipole momentum

$$\begin{aligned} Q = q_b = {\tilde{p}}_{ij} + {\tilde{p}}_k = q_i + q_j + q_k\,. \end{aligned}$$

(37)

The splitting kinematics then exactly follow those for a splitting from a massive final–final dipole given in Sect. 3.3.1. The only difference is that for splittings from a decay dipole the recoil, ${\tilde{p}}_k \rightarrow q_k$, is absorbed through the application of an appropriate Lorentz transformation to the recoil system rather than by a single spectator parton. We note that the treatment described here is the same as that used in Ref. [48].

4.2.3 Decay Kernels

Fig. 3

The final–initial decay dipole

As stated in Sect. 4.2 we do not include explicit splittings from IF-decay dipoles. This is because the kernel for a gluon emission from the incoming top quark contains a negative term proportional to the top quark mass-squared which gives rise to a kernel that is almost always negative. We have therefore chosen to include the IF-decay splitting kernels in the FI-decay splitting kernels which are usually large enough to remain positive following the inclusion of the negative mass-squared term. With these considerations there are two possible dipoles and three possible splittings we must consider: the $t-q$ dipole where the final state quark emits a gluon and the $t-g$ dipole where the final state gluon can split into either a $q{\bar{q}}$-pair or a pair of gluons.

Following the discussion in Sect. 4.2.2 the notation used to express the kernels follows that used for splittings from FF dipoles given in Sect. 3.3.1. We denote the mass of the incoming decayed parton as $m_b$.

There is only one possible splitting from the $t-q$ FI-decay dipole, $q \rightarrow qg$, therefore we must include the entire contribution from the corresponding $t \rightarrow tg$ splitting in this kernel. We have used some discretion with regard to which finite pieces are included in the kernels. The kernel, $V_{q\rightarrow qg}$, used to describe splittings from a $t-q$ FI-decay dipole in Herwig  7.1 is given in Eq. (38a). Note that following the conventions of Ref. [34] there is a propagator factor of $1/q_i\cdot q_j$ taken out of the kernel. This is the origin of the factor $y_{ij,k}/(1-z_i(1-y_{ij,k}))$ in front of the $t\rightarrow tg$ piece of the kernel and correctly reproduces the eikonal formula that would otherwise be obtained by summing over all possible splittings and configurations for each dipole.

In order to be consistent with the kernels used for splittings from other massive dipoles, we follow the convention from Ref. [34] of multiplying certain terms in the kernels by a finite ratio of relative velocities. The explicit forms of these terms are given in Eq. (39a).

The $t-g$ dipole is more complicated because there are two possible splittings, $g\rightarrow gg$ and $g\rightarrow q{\bar{q}}$. The splitting kernels $V_{g\rightarrow gg}$ and $V_{g\rightarrow q{\bar{q}}}$ used to describe the $g \rightarrow gg$ and $g \rightarrow q{\bar{q}}$ splittings in Herwig  7.1 are given in Eq. (38b) and Eq. (38c), respectively.

The limits on $z_i$, $z_{i,\pm }$, and the relative velocity term $v_{ij,i}$ required to express these kernels are given explicitly in Eq. (39c) and Eq. (39d) respectively. We have followed the convention of Ref. [34] and used a parameter $\kappa$ to distribute finite pieces between the two kernels. In Herwig  7.1, $\kappa$ is set to zero in all dipole shower splitting kernels.

We include divergences arising from the IR limits of both $q_i$ and $q_j$ in $V_{g\rightarrow gg}$ such that $V_{g\rightarrow gg }$ is symmetric with regard to $q_i$ and $q_j$. This is because this splitting produces indistinguishable final-state gluons and it is consistent with the other $g \rightarrow gg$ kernels used in the parton shower.⁸

$$\begin{aligned}&{V_{q\rightarrow qg}= 8 \pi \alpha _S \mathrm {C}_\mathrm {F}} \end{aligned}$$

(38a)

$$\begin{aligned}&\quad \left\{ \right. \frac{2 \left( 2 m_i^2 + 2y_{ij,k}{\bar{s}} + {\bar{s}} \right) }{(1+y_{ij,k}){\bar{s}} - z_i(1-y_{ij,k}){\bar{s}}} - \frac{{\tilde{v}}_{ij,k}}{v_{ij,k}} \left( (1+z_i) + \frac{2 m_i^2}{y {\bar{s}}} \right) \nonumber \\&\qquad + \frac{y_{ij,k}}{1-z_i(1-y_{ij,k})} \left[ \frac{2 \left( 2 m_i^2 + 2y_{ij,k}{\bar{s}} + {\bar{s}} \right) }{(1+y_{ij,k}){\bar{s}} - z_i(1-y_{ij,k}){\bar{s}}} \right. \nonumber \\&\left. \left. \qquad - \frac{{\tilde{v}}_{ij,k}}{v_{ij,k}} \left( 2 + \frac{2 m_b^2}{\left( 1-z_i(1-y_{ij,k})\right) {\bar{s}}} \right) \right] \right\} , \nonumber \\&{V_{g\rightarrow gg} = 16 \pi \alpha _S \mathrm {C}_\mathrm {A} } \end{aligned}$$

(38b)

$$\begin{aligned}&\quad \left\{ \frac{1+2y_{ij,k}}{(1+y_{ij,k})-z_i(1-y_{ij,k})} \right. \nonumber \\&\qquad + \frac{1+2y_{ij,k}}{(1+y_{ij,k})-(1-z_i)(1-y_{ij,k})}\nonumber \\&\qquad \left. + \frac{1}{v_{ij,k}} \left[ z_i(1-z_i) - (1-\kappa )z_{i,+}z_{i,-}-2 \right] \right\} \nonumber \\&\qquad { +8 \pi \alpha _S \mathrm {C}_\mathrm {F}} \nonumber \\&\left\{ \right. \frac{y_{ij,k}}{1-z_i(1-y_{ij,k})} \left[ \frac{2(1+2y_{ij,k})}{(1+y_{ij,k})-z_i(1-y_{ij,k})} \right. \nonumber \\&\qquad \left. - \frac{{\tilde{v}}_{ij,k}}{v_{ij,k}} \left( 2 + \frac{ 2 m_b^2}{(1-z_i(1-y_{ij,k})){\bar{s}}} \right) \right] \nonumber \\&\qquad + \frac{y_{ij,k}}{1-(1-z_i)(1-y_{ij,k})} \left[ \frac{2(1+2y_{ij,k})}{(1+y_{ij,k})-(1-z_i)(1-y_{ij,k})}\right. \nonumber \\&\qquad \left. \left. - \frac{{\tilde{v}}_{ij,k}}{v_{ij,k}} \left( 2 + \frac{ 2 m_b^2}{(1-(1-z_i)(1-y_{ij,k})){\bar{s}}} \right) \right] \right\} ,\nonumber \\&{V_{g\rightarrow q {\bar{q}}} = 8 \pi \alpha _S \mathrm {T}_\mathrm {R}} \end{aligned}$$

(38c)

$$\begin{aligned}&\quad \left\{ 1 - 2\left( z_i(1-z_i) - (1-\kappa )z_{i,+}z_{i,-}- \frac{\kappa m_i^2}{2m_i^2 + {\bar{s}}y_{ij,k}} \right) \right\} \nonumber \\ \end{aligned}$$

(38d)

$$\begin{aligned} {\tilde{v}}_{ij,k}= & {} \frac{\sqrt{ \lambda \left( s, m_{ij}^2, m_k^2 \right) } }{s-m_{ij}^2-m_k^2}, \end{aligned}$$

(39a)

$$\begin{aligned} v_{ij,k}\nonumber \\= & {} \frac{ \sqrt{ \left[ 2 m_k^2 + \left( s - m_i^2 - m_j^2 - m_k^2 \right) \left( 1 - y_{ij,k}\right) \right] ^2 - 4 m_k^2 }}{ \left( s - m_i^2 - m_j^2 - m_k^2 \right) \left( 1 - y_{ij,k}\right) },\nonumber \\ \end{aligned}$$

(39b)

$$\begin{aligned} z_{i,\pm }= & {} \frac{ 2 m_i^2 + \left( s - m_i^2 - m_j^2 - m_k^2 \right) y_{ij,k}}{ 2 \left[ m_i^2 + m_j^2 + \left( s - m_i^2 - m_j^2 - m_k^2 \right) y_{ij,k}\right] } \nonumber \\&\left( 1 \pm v_{ij,i} v_{ij,k} \right) , \end{aligned}$$

(39c)

$$\begin{aligned} v_{ij,i}= & {} \frac{ \sqrt{ \left( s - m_i^2 - m_j^2 - m_k^2 \right) ^2 y_{ij,k}^2 - 4 m_i^2 m_j^2 }}{\left( s - m_i^2 - m_j^2 - m_k^2 \right) y_{ij,k}+ 2 m_i^2 }. \end{aligned}$$

(39d)

Finally we include a symmetry factor of $\frac{1}{2}$, which is not written explicitly here, in front of the $g\rightarrow gg$ pieces of $V_{g\rightarrow gg}$. With the inclusion of this symmetry factor the factors in front of the eikonal parts from the $g \rightarrow gg$ and $q \rightarrow qg$ pieces are consistent in the large-$\text {N}_\text {C}$ limit and we reproduce the correct eikonal expression.

4.2.4 Validation

We present results to validate the new decay kernels and kinematics in the dipole shower. We consider observables which depend primarily on the first, hardest, emission from the decay system and we compare results obtained with and without the real emission decay correction. This comparison directly evaluates how well $V_{q \rightarrow qg}$, Eq. (38a), reproduces the full real emission correction. As can be seen in Fig. 4 the kernel overestimates the leading-order matrix element over most of the phase space, apart from a small region near the lower phase-space boundary for $0.1<x_g<0.4$.

Our procedure for the following tests exactly follows that used in Refs. [44, 45, 51]. We generate $e^+ e^- \rightarrow t {\bar{t}}$ events at LO at a collision energy of 360 GeV. This collision energy is chosen to be close to the threshold energy for the process, i.e. $2 m_\mathrm {top}$, in order to reduce radiation from the production process. We work at parton level and include only dileptonic processes. All final-state quarks and gluons are clustered into three jets using the $k_\perp$ algorithm [52] implemented in FastJet [53] and we exclude events containing a jet with transverse energy less than 10 GeV. We additionally exclude events in which the minimum jet separation is less than $\varDelta R = 0.7$ where $\varDelta R^2 = \varDelta \eta ^2 + \varDelta \phi ^2$, where $\eta$ and $\phi$ denote pseudorapidity and azimuthal angle respectively.

Fig. 4

Dalitz plot for $t\rightarrow b W^+ g$ where the gluon is showing the ratio of the leading-order matrix element result over the dipole-shower approximation. The energy fractions of the gluon and $W^+$ boson are $x_g=2E_g/m_{\mathrm{top}}$ and $x_W=2E_W/m_\mathrm{top}$, respectively

Fig. 5

The distribution of (upper) the minimum jet separation and (lower) the jet measure $y_3$ in 3-jet $e^+ e^- \rightarrow t {\bar{t}}$ events. The distributions are shown for events showered using the dipole shower with (DS-PowhegCorr) and without (DS-NoCorr) the real emission decay correction. In addition we show the distributions obtained using the angular-ordered shower (QS) with the full matrix-element decay correction

We present results for two observables; the separation ${\varDelta R}_\mathrm {min}$ of the closest pair of jets in the event and the jet measure $y_3$, defined as the value of the jet resolution parameter at which the three jet event would be identified as a two jet event. This is given by

$$\begin{aligned} y_3 = \frac{2}{s} {\min }_{ij} \left( \min \left( E_i^2 , E_j^2 \right) (1-\cos \theta _{ij}) \right) , \end{aligned}$$

(40)

where s is the centre-of-mass energy squared of the collision, $E_i$ and $E_j$ are the energy of jets i and j respectively and $\theta _{ij}$ is the angular separation of jets i and j.

Figure 5 shows the distribution of the minimum jet separation for events showered with and without the real emission decay correction. In general a harder first emission will produce a greater separation of the two closest jets. Therefore, as we expect, the shower with the real emission decay correction produces more events with a larger minimum jet separation. We see that the results with and without the real emission decay correction agree well $(\sim 10\%)$ at small jet separations. Furthermore even at large minimum jet separations, where we do not expect the splitting kernel alone to give a good description of the emission, the results agree to within roughly $30\%$.

Figure 5 also shows the distribution of $y_3$ for events showered with and without the real emission decay correction. Again, a harder first emission will in general lead to a larger separation of the two closest jets and thus such 2-jet events can be resolved into 3-jet events at a larger value of $y_3$. As we would expect there is a skew towards larger values of $y_3$ for the results with the real emission-corrected decay versus the results without the correction. We see that the results at low $y_3$, corresponding to a softer first emission, are well described by the shower without the real emission decay correction. The log scale used for $y_3$ in Fig. 5 emphasises the limitations of the splitting kernel in describing hard emissions. This is evident from the increasing disagreement between the results with and without the real emission decay correction at larger values of $y_3$.

These results show that the kernel $V_{q\rightarrow qg}$ behaves well in the IR region as we require. It also performs reasonably well in the case of harder emissions but its limitations are apparent in the distribution of $y_3$ in Fig. 5. There is a major limitation to these tests in that they only directly probe the $q \rightarrow qg$ splitting kernel. The effects of subsequent emissions are small and it is difficult to create a test to probe $g \rightarrow gg$ and $g \rightarrow q {\bar{q}}$ emissions from decay dipoles directly.

As a further comparison we have also included the results from showering with the angular-ordered shower with the appropriate full matrix element correction to the decay in both figures. In all except the lowest bins we see a good agreement between the dipole shower with the real emission decay correction and the angular-ordered shower. This verifies that the corrections in the two showers produce the same behaviour, as we would expect. The disagreement in the lower bins is not a concern as there are numerous differences between the showers and we do not expect agreement to be exact in all regions of phase space.

5 NLO matching and scale choices

A major improvement to the simulation of top quark production and decay in the Herwig  7 event generator is the inclusion of NLO QCD corrections consistently combined with the subsequent parton shower evolution. NLO matching paradigms are typically less ambiguous than their merging counterparts and entirely driven by solving a matching condition such that the combination of a NLO cross section with a parton-shower evolution reproduces the NLO cross section exactly, plus higher-order terms. In the following we will elaborate on the basic matching algorithms available in Herwig  7 and their implementation, and will consider in detail the sources of uncertainty involved in matched predictions.

5.1 Hard process setup and NLO subtraction

The partonic cross section for the hard process at leading order can be written as

$$\begin{aligned} \sigma _{\text {LO}}[u] = \int \mathrm{d}\sigma _B(\phi _n) \mathrm{d}f\ u(\phi _n), \end{aligned}$$

(41)

where $\mathrm{d}\sigma _B$ is the Born cross section, $\mathrm{d}f$ denotes the partonic luminosity (parton distribution functions), and $u(\phi _n)$ represents a generic observable defined on the Born phase-space point $\phi _n=\{p_a,p_b\rightarrow p_1,...,p_n\}$. The Herwig  7 Matchbox module [10] identifies the possible subprocesses contributing to the cross section, and sets up a multi-channel phase-space generator to map the phase-space measure $\mathrm{d}\phi _n$, which includes the momentum conserving $\delta$-function as well as mass-shell constraints.

For a NLO calculation, which we carry out in the dipole subtraction formalism based on Catani–Seymour dipole subtraction [33, 34], real emission processes including an additional jet are then identified in the same way as for the leading-order cross section, and the NLO cross section is calculated as

$$\begin{aligned} \sigma _{\text {NLO}}[u]= & {} \sigma _{\text {LO}}[u] + \sigma _{V+A+C}[u]+\sigma _{R-A}[u]\ , \end{aligned}$$

(42)

with

$$\begin{aligned} \sigma _{R-A}[u]= & {} \int \Big [ \mathrm{d}\sigma _R(\phi _{n+1})u(\phi _{n+1}) \nonumber \\&- \sum _i \mathrm{d}\sigma _A^{(i)}(\phi _{n+1} )u(\varPhi ^{(i)}_{n}(\phi _{n+1})) \,\Big ]\mathrm{d}f \ . \end{aligned}$$

(43)

The first two terms in Eq. (42) contain the leading-order cross section, as well as the finite combination $\sigma _{V+A+C}=\sigma _{V+I+P+K}$ of virtual corrections, analytically integrated subtraction terms, as well as collinear counterterms, which are all defined over the Born phase-space point $\phi _n$ and handled accordingly. We have further introduced the dipole subtraction terms $\mathrm{d}\sigma _A(\phi _{n+1})^{(i)}$ and the real-emission contributions $\mathrm{d}\sigma _R(\phi _{n+1})$ which are all functions of the real-emission phase-space point $\phi _{n+1}$, and the index i runs over the possible dipole configurations, each of which is associated with a particular kinematic mapping $\varPhi ^{(i)}_{n}(\phi _{n+1})$ onto the so-called ‘tilde’ or underlying Born kinematics. The phase-space mappings trigger phase-space convolutions which can be cast into phase-space factorizations upon introducing suitably adapted parton distribution functions

$$\begin{aligned} \left. \mathrm{d}\phi _{n+1}\mathrm{d}f \right| _{\phi _{n+1}=\varPhi ^{(i)}_{n+1}(\phi _n,r)} = \mathcal{J}^{(i)}(\phi _n,r)\mathrm{d}\phi _{n}\mathrm{d}f^{(i)}\mathrm{d}r , \end{aligned}$$

(44)

where $\varPhi ^{(i)}_{n+1}(\phi _n,r)$ is the inverse mapping to the mapping $\varPhi ^{(i)}_{n}(\phi _{n+1})$, and r here refers to the collection of variables required to describe the additional emission, i.e. a scale of the emission, a momentum fraction, and an azimuthal variable. We can also associate the respective definitions as functions of the real emission variables, $R^{(i)}(\phi _{n+1})$, such that

$$\begin{aligned} \varPhi ^{(i)}_{n+1}(\varPhi ^{(i)}_n(\phi _{n+1}),R^{(i)}(\phi _{n+1})) = \phi _{n+1} . \end{aligned}$$

(45)

Matchbox uses diagrammatic information to deduce which subtraction terms need to be included, and automatically sets up a cross section in the form above.

5.2 Parton-shower action and matching

The parton-shower action can conveniently be described as

$$\begin{aligned} \sigma [u]\rightarrow \sigma [\mathrm{PS}_{\mu _{\text {IR}}}[u]], \end{aligned}$$

(46)

where the parton-shower operator up to the first emission is

$$\begin{aligned}&\mathrm{PS}_{\mu _{\text {IR}}}[u](\phi _n) = \prod _i\varDelta ^{(i)}(\phi _n,\mu _{\text {IR}})u(\phi _n) \nonumber \\&\quad +\sum _i \mathrm{d}P^{(i)}(\phi _n,r)\kappa (Q^{(i)}(\phi _{n}),p_\perp (r))\theta (q(r)-\mu _{\text {IR}})\ \nonumber \\&\quad \times \prod _j\varDelta ^{(j)}(\phi _n,\mu _{\text {IR}})u(\varPhi ^{(i)}_{n+1}(\phi _n,r)) . \end{aligned}$$

(47)

Here q(r) is the evolution variable which we have singled out only in the phase-space limits on the evolution, starting at a hard scale $Q^{(i)}(\phi _{n})$ and ending at the infrared cutoff $\mu _{\text {IR}}$. The differential splitting probability is the combination of the respective phase-space factors and a ratio of parton luminosities, and the Sudakov form factor starting at the hard configuration is

$$\begin{aligned}&-\ln \varDelta ^{(i)}(\phi _n,\mu _{\text {IR}})\nonumber \\&\quad = \int \mathrm{d}P^{(i)}(\phi _n,r)\kappa (Q^{(i)}(\phi _{n}),p_\perp (r))\theta (q(r)-\mu _{\text {IR}}).\nonumber \\ \end{aligned}$$

(48)

Notice that the constraint on the hard scale is in general not a sharp cutoff, but might be imposed in different ways, see [24] and the discussion below in Sects. 6.1 and 6.2. We have, not accidentally, chosen the same kinematic mapping as has been used for the dipole subtraction terms. Indeed, the kinematic reconstruction algorithm, and not least the kinematics used in the dipole shower and the Powheg correction to be discussed below, resemble, for one emission, exactly the dipole subtraction kinematics, such that we do not need to consider any additional Jacobian factors.

At this point we can expand the shower action to first order in $\alpha _S$ and subtract this contribution from the NLO cross section to set up the matched cross section. To this extent it is worth noting that we can recast both, the integrand of the Sudakov exponent as well as the emission rate multiplied by the Born cross section into another approximate cross section using the inverse of the kinematic mapping,

$$\begin{aligned}&\mathrm{d}\sigma ^{(i)}_{\text {PS}}(\phi _{n+1})\mathrm{d}f \equiv \left[ \mathrm{d}\sigma _B\mathrm{d}f^{(i)} \mathrm{d}P^{(i)}(\phi _n,r)\right. \ \nonumber \\&\quad \times \left. \kappa (Q^{(i)}(\phi _{n}),p_\perp (r))\right] _{\phi _{n} = \varPhi _{n}^{(i)}(\phi _{n+1}),r = R^{(i)}(\phi _{n+1})} \ . \end{aligned}$$

(49)

We have explicitly left out the infrared cutoff in this expression for reasons which will soon become clear. The NLO matching subtraction term is then

$$\begin{aligned}&\sigma ^{\text {PS}}_{R-A}[u]=\sum _i \int \mathrm{d}\sigma ^{(i)}_{\text {PS}}(\phi _{n+1})\mathrm{d}f\ \nonumber \\&\quad \times \theta (q^{(i)}(\phi _{n+1})-\mu _{\text {IR}}) \left( u(\phi _{n+1})-u(\varPhi _n^{(i)}(\phi _{n+1}))\right) ,\nonumber \\ \end{aligned}$$

(50)

with the shorthand $q^{(i)}(\phi _{n+1})=q(R^{(i)}(\phi _{n+1}))$. The NLO matched cross section is

$$\begin{aligned} \sigma ^{\text {matched}}_{\text {NLO}}[u] =\sigma _{\text {NLO}}[u] -\sigma ^{\text {PS}}_{R-A}[u]\ , \end{aligned}$$

(51)

such that $\sigma ^{\text {matched}}_{\text {NLO}}[\mathrm{PS}_{\mu _{\text {IR}}}[u]]=\sigma _{\text {NLO}}[u]+\text {h.o.}$ This can be conveniently combined with the dipole book keeping already employed for the fixed-order NLO calculation to yield two contributions to the NLO matched cross section:

$$\begin{aligned} \sigma ^{\text {matched}}_{\text {NLO}}[u] = \sigma _{S}[u]+\sigma _{H}[u]\ , \end{aligned}$$

(52)

with

$$\begin{aligned} \sigma _S[u]= & {} \sigma _{\text {LO}}[u] + \sigma _{V+I+P+K}[u] \nonumber \\&+ \sum _i \int \left( \mathrm{d}\sigma ^{(i)}_{\text {PS}}(\phi _{n+1})\theta (q^{(i)}(\phi _{n+1})-\mu _{\text {IR}}) \right. \nonumber \\&- \, \left. \mathrm{d}\sigma ^{(i)}_{A}(\phi _{n+1})\right) \mathrm{d}f\ u(\varPhi _n^{(i)}(\phi _{n+1}))\ , \end{aligned}$$

(53)

which constitutes Born-type configurations, also referred to as ${{\mathcal {S}}}$ events, as well as

$$\begin{aligned}&\sigma _H[u] = \int \Big ( \mathrm{d}\sigma _R(\phi _{n+1}) \nonumber \\&\quad - \sum _i \mathrm{d}\sigma ^{(i)}_{\text {PS}}(\phi _{n+1}) \theta (q^{(i)}(\phi _{n+1})-\mu _{\text {IR}})\Big )\mathrm{d}f\ u(\phi _{n+1}),\nonumber \\ \end{aligned}$$

(54)

to provide real-emission type configurations, also referred to as ${{\mathcal {H}}}$ events. We stress that these contributions cannot yet be used to generate events with finite weights owing to the presence of the infrared cutoff, which allows for configurations with divergent weights, even if the parton-shower approximated cross section would be able to reproduce the full singularity structure of the real emission. Instead, an additional auxiliary cross section

$$\begin{aligned}&\sigma _{X}[u] = \sum _i \int \mathrm{d}\sigma ^{(i)}_{X}(\phi _{n+1})\mathrm{d}f\ \nonumber \\&\quad \times \theta (\mu _{\text {IR}}-q^{(i)}(\phi _{n+1}))\left( u(\varPhi _n^{(i)}(\phi _{n+1}))-u(\phi _{n+1})\right) ,\nonumber \\ \end{aligned}$$

(55)

can be added to the matched cross section to eventually yield modified versions of $\sigma _S$ and $\sigma _H$, which can be employed to generate events. In practice, we use the dipole subtraction terms themselves to facilitate this, i.e. $\mathrm{d}\sigma _X=\mathrm{d}\sigma _A$. Note that, for infrared-safe observables u, $\sigma _{X}$ only adds power corrections below the infrared cutoff.

5.3 Matching variants

Both the angular-ordered and the dipole showers fit into the framework outlined above, which constitutes the subtractive, or MC@NLO-type, matching in Herwig  7, and the sole task is to determine the shower matching subtraction $\mathrm{d}\sigma ^{\text {PS}}_{R-A}$, which we have implemented in a process-independent way in the Matchbox module. These subtractions are indeed very similar to the dipole subtraction terms, but averaged over azimuthal orientation and for colour correlators evaluated in the large-$N_c$ limit. With the recent development of spin-correlation algorithms in both shower modules [54], spin correlations can be restored in these subtractions, and full colour correlations can be justified when using colour matrix-element corrections [50, 55], at least for the dipole shower algorithm.

Another choice is a multiplicative, or Powheg-type, matching for which we employ a hardest emission generator, which performs a shower emission using a modified splitting function, or matrix-element correction, determined from the real-emission and Born matrix elements as

$$\begin{aligned} P^{(i)}(\phi _n,r)\rightarrow & {} \frac{w^{(i)}(\varPhi ^{(i)}_{n+1}(\phi _n,r))}{\sum _j w^{(j)}(\varPhi ^{(j)}_{n+1}(\phi _n,r))}\nonumber \\&\times \frac{|\mathcal{M}_R(\varPhi ^{(i)}_{n+1}(\phi _n,r)|^2}{|{{{\mathcal {M}}}}_B(\phi _n)|^2}\ , \end{aligned}$$

(56)

for which no complications arise as the full divergent behaviour is reproduced by construction. An additional truncated, vetoed shower needs to be included if the hardest emission generated this way is not the first one to occur. In practice, for the $w^{(i)}$ we use dipole-type partitioned Eikonal factors to perform the weighting into the different singular channels i and use the ExSample library [56] to generate emissions according to the Sudakov form factor obtained from the matrix-element correction defined above.

6 Parton shower hard scale

6.1 Profile scale choices

The parton shower hard scale needs to be limited from above in order to avoid the summation of an unphysical tower of logarithms in the Sudakov exponent. To this extent, we have not chosen a fixed starting scale, but a profile scale function $\kappa (Q^{(i)}(\phi _n),p_\perp (r))$ [c.f. Eqs. (47) to (49)]. This function encodes the possibility that not all of the emission phase space should be available to the parton shower. From here on we will generically denote $Q^{(i)}(\phi _n)=Q_\perp$, i.e. we choose the (upper) hard scale $Q^{(i)}(\phi _n)$ manifest as a scale $Q_\perp$ which defines an upper limit on the transverse momentum available to shower emissions.

Several possible parameterizations of the profile scale choices were investigated for leading-order plus parton-shower predictions [24]. We first introduce a hard veto scale $Q_\perp$, which defines an upper limit on the transverse momentum available to shower emissions. By default this is chosen to be the hard process scale, $\mu _\mathrm {H}$, which in turn is typically set to the factorization and renormalization scale, but may also be chosen independently in Herwig  7. The profile scale choice $\kappa \left( Q_\perp , p_\perp \right)$ is a function of $Q_\perp$ and the transverse momentum $p_\perp$ of the splitting. For convenience, we define the quantity x as the ratio of these scales

$$\begin{aligned} x=\frac{p_\perp }{Q_\perp }\ . \end{aligned}$$

(57)

The default profile scale choice in Herwig  7 is the resummation profile

$$\begin{aligned} \kappa \left( Q_\perp , p_\perp \right) = {\left\{ \begin{array}{ll} 1&{},\ x \le 1-2\rho , \\ 1 - \frac{\left( 1-2\rho -x\right) ^2}{2\rho ^2}&{},\ x \in (1-2\rho ,\,1-\rho ] , \\ \frac{\left( 1-x\right) ^2}{2\rho ^2}&{},\ x \in (1-\rho ,\,1] , \\ 0&{},\ x > 1 , \end{array}\right. } \end{aligned}$$

(58)

where $\rho$ is a parameter which is set in Herwig  7.1.4 to $\rho =0.3$. The resummation profile is one for $p_\perp < (1 - 2 \rho ) Q_\perp$, zero for $p_\perp > Q_\perp$, and quadratically interpolates between these regions. It is expected to reproduce the correct towers of logarithms, and switches off the resummation smoothly towards the hard region.

We compare the resummation profile to the hfact profile, which is the damping factor used in PowhegBox [57]. The hfact profile is defined as

$$\begin{aligned} \kappa \left( Q_\perp , p_\perp \right) = \frac{1}{1+x^2}\ . \end{aligned}$$

(59)

The hfact profile tends to one in the resummation region, i.e. for $p_\perp < Q_\perp$, and to zero in the fixed-order region, i.e. for $p_\perp > Q_\perp$. Unlike the resummation profile the hfact profile does not produce the desired towers of logarithms, as it varies over too broad a range of scales around the hard veto scale. In particular it is not close enough to one in the Sudakov region, i.e. $p_\perp \ll Q_\perp$, and does not enforce a sufficiently effective cutoff on the shower emissions in the hard region, i.e. for $p_\perp \gg Q_\perp$.

In this paper (see Sect. 7.4.1) we investigate some of the impacts of the choice of the profile scale on the prediction of observables using MC@NLO-type matching. For a detailed discussion of the exact properties of the various profile scale choices available in Herwig  7 we refer the reader to Ref. [24].⁹

6.2 Hard veto scale choices

Both shower modules require an upper limit on the transverse momentum of emissions, which is set by a hard veto scale $Q_\perp$ (see previous section). This hard veto scale coincides with the starting scale for the $p_\perp$-ordered dipole shower, and is explicitly implemented as an additional veto for the angular-ordered shower. By default in Herwig  7, in leading-order events, i.e. Born-type events, $Q_\perp$ is chosen to be the hard process scale $\mu _\mathrm {H}$.

For NLO matched predictions, the generated ${{\mathcal {S}}}$ and ${{\mathcal {H}}}$ events (see Sect. 5.2) separately undergo showering. While ${{\mathcal {S}}}$ events constitute Born-type events and are treated as such, several complications arise for ${{\mathcal {H}}}$ events.

In MC@NLO-type matching there is no requirement of exact cancellation between the real-emission matrix element and the subtraction term in any region of phase space, as it is possible for the subtracted real-emission cross section still to contain power corrections in the regions where the real emission is soft or collinear. Correspondingly we expect to see a fraction of ${{\mathcal {H}}}$ events with a soft and/or collinear emission. In the case of such an ${{\mathcal {H}}}$ event it is unnatural to choose the hard veto scale to be of the order of the small transverse momentum of the real emission. Consider for example our case of $t{\bar{t}}$ production, and say we have an ${{\mathcal {H}}}$ event in which the real emission has a transverse momentum of $\sim 2$ GeV. Given the high energy scales involved in $t{\bar{t}}$ production, it would be unreasonable to veto all shower emissions with transverse momentum greater than that of the real emission. Instead we need to choose a hard veto scale which is more representative of the scales involved in the process.

In general, as with most scale choices there is no ‘correct’ choice and we have some freedom in choosing the hard veto scale. By default in Herwig  7 we choose $Q_\perp = \mu _\mathrm {H}$, for which we typically choose $\mu _\mathrm {H}=\mu _\mathrm {F}=\mu _\mathrm {R}$ with $\mu _\mathrm {F}$ and $\mu _\mathrm {R}$ denoting the factorization and renormalization scale respectively. The hard veto scale and the scale of the hard process may also be chosen independently. Overall, given our previous discussion, we desire to choose $Q_\perp$ to be representative of the scales of the objects outgoing from the hard process. In the case of a hard real emission, a hard veto scale that reflects the scale of the real emission should be used. Conversely in the case of a relatively low-scale real emission, a larger scale should be chosen.

Assume for now that we use $Q_\perp = \mu _\mathrm {H}$ and consider an ${{\mathcal {H}}}$ event. Common choices for $\mu _\mathrm {H}$ involve the transverse masses of the top quark and antiquark, often in a linear or quadratic sum. In the case of a very low-$p_\perp$ real emission, the transverse masses of the top quarks will be largely unaffected by the emission. Therefore we would shower such an event from a scale similar to that had there been no emission. Conversely a high-$p_\perp$ real emission on-average increases the sum of the transverse masses of the top quarks, and the presence of the hard real emission is reflected in the hard veto scale. There are choices for $\mu _\mathrm {H}$ that, while significantly affected by the scale of the real emission, are relatively large over a wide range of real emission scales. If $\mu _\mathrm {H}$ is large enough, the actual maximum scale for showering will be the maximum physically allowed scale, determined from the splitting kinematics, for the first shower emission. In this case, while $\mu _\mathrm {H}$ may be directly affected by the scale of the real emission, the scale of the real emission will have only a small impact on the subsequent showering.

In the case described above one should consider using an alternative choice for $Q_\perp$. We have introduced such a scale, which we denote as $\mu _\mathrm {a}$, in Herwig  7.1 for use in $t{\bar{t}}$ production

$$\begin{aligned} \mu _\mathrm {a} = \sqrt{ \frac{1}{n_\mathrm {out}} \sum _i m_{\perp ,i}^2 } \ , \end{aligned}$$

(60)

where $n_\mathrm {out}$ is the number of particles outgoing from the hard process prior to showering and the sum is over these outgoing particles. This is simply the quadratic mean of the transverse masses of the outgoing particles in the lab frame. In an ${{\mathcal {H}}}$ event with a hard real emission, the scale $\mu _\mathrm {a}$ is sensitive to the scale of this real emission. In the case of an ${{\mathcal {H}}}$ event with a low-$p_\perp$ real emission, $\mu _\mathrm {a}$ is much larger than the scale of the real emission and better reflects the scales in the process. We note that this scale is not smooth in the limit of a soft/collinear emission, i.e. the transition from ${{\mathcal {H}}}$ to ${{\mathcal {S}}}$ events. In the case of an ${{\mathcal {H}}}$ event with a low-$p_\perp$ real emission this returns a scale smaller than that in an ${{\mathcal {S}}}$ event by a factor $\sqrt{2/3}$ in the soft/collinear limit. We expect the effects of this discontinuity on results to be very small.

In this paper (see Sect. 7.4.2) we investigate some of the impacts of the choice of the hard veto scale on the prediction of observables using MC@NLO-type matching, and how the effects change depending on the choice for the hard process scale. To do this we compare, for each of three different choices for $\mu _\mathrm {H}$, results obtained using $Q_\perp = \mu _\mathrm {H}$ and $Q_\perp = \mu _\mathrm {a}$. The three choices for $\mu _\mathrm {H}$ that we compare are

$$\begin{aligned} \mu _1= & {} \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{2} , \end{aligned}$$

(61a)

$$\begin{aligned} \mu _2= & {} \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{4} , \end{aligned}$$

(61b)

$$\begin{aligned} \mu _3= & {} m_{t{\bar{t}}} , \end{aligned}$$

(61c)

where $m_{t{\bar{t}}}$ is the invariant mass of the $t{\bar{t}}$-pair.¹⁰

As always in discussions of scale choices there is no right or wrong choice. The aim of this discussion is to highlight that when we use MC@NLO-type matching we have to make a choice for the hard veto scale. We will show that, depending on the choice for $\mu _\mathrm {H}$, different choices for $Q_\perp$ can have differing and significant effects on our predictions for observables.

7 Uncertainty benchmarks and data comparisons

In order to estimate the uncertainty for the event generator predictions we pursue both, variations of the scales involved in the hard production process as well as the scales involved in the subsequent parton showering (see Sect. 7.3). We also consider the impact of different profile scale choices and of different choices for the hard veto scale, dependening on the scale of the hard process (see Sect. 7.4). We consider $t{\bar{t}}$ pair production in proton-proton (pp) collisions using both ‘parton-level’, or ‘production-level’, predictions for stable top quarks and ‘particle-level’ predictions for unstable top quarks.

Due to the manifold scale choices and variations in our study, we discuss the impact on the observable distributions in some more detail. As mentioned before, in this study we concentrate our efforst in particular on NLO matched predictions. Understanding matched predictions, in the context of systematically disecting the effects of varying all relevant scales as we do in our study, is a relevant prerequisite to understanding similarly systematic uncertainty estimates in more sophisticated setups, like multi-jet merging.¹¹

7.1 Production level

All parton-level, or production-level, simulations are done for a centre-of-mass energy of $13\ \mathrm{GeV}$ and use the ‘benchmark’ settings of Ref. [24]. Except for the variations of interest in each section, we use identical input settings for the parton showers and matching schemes in every run. Only QCD radiation is included in the simulations and the same infrared cutoff of $\mu _\mathrm {IR}=1$ GeV (implemented as the minimum transverse momentum cutoff on shower emissions) is used in both showers. We use a mass parameter of $m_t=174.2$ GeV in the hard process as well as in the subsequent showering algorithms and all other quarks are considered to be massless.

The factorization and renormalization scales are set to the same value $\mu _\mathrm {R} = \mu _\mathrm {F} \equiv \mu _\mathrm {H}$, where our default for the central hard process scale choice is

$$\begin{aligned} \mu _\mathrm {H}= \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{4} \,, \end{aligned}$$

(62)

i.e. half of the average transverse masses of the top and anti-top quarks, unless stated otherwise. This scale choice is motivated by the results of Ref. [59]. We use the default choice, $Q_\perp = \mu _\mathrm {H}$, for the hard veto scale in all runs apart from those in which this is the scale of interest. Similarly, the resummation profile scale is used in all runs unless otherwise stated.

We use the MMHT2014nlo68cl parton distribution functions (PDFs) along with a two-loop running of $\alpha _S$ with $\alpha _S(M_Z)=0.12$ both in the parton shower and the hard process.¹² All runs use a four-flavour scheme. All cross sections are rescaled to the NNLO cross section of 815.96 pb ¹³, calculated using Top++2.0  [60] assuming a top mass of 173.2 GeV and including soft-gluon resummation to next-to-next-to-leading-log order, as are the variations we consider and the envelopes resulting from these variations.

We use a purpose-built analysis written in Rivet [61] to analyse the simulated events. Our analysis considers objects with pseudo-rapidity $|\eta | < 5$, with transverse momentum ordered jets obtained from the anti-$k_\perp$ jet algorithm [53, 62] with a jet radius of $R=0.4$.

7.2 Particle level

In contrast to production-level simulations, particle-level simulations include top quark decays, hadronisation and hadronic decays, including tau-lepton decays. Particle-level predictions are used to compare our simulations to experimental data in order to quantify how the different algorithms and their intrinsic uncertainties compare to existing collider data. We use existing and publicly available Rivet analyses, for which the collision energy, $\sqrt{s}$, at which each experimental result was measured and the final-states included are summarised in the following text. Specific details of the experimental analyses are available in the references provided. All of the particle-level measurements presented in this section are taken in the ‘combined channel’, i.e. including both electron and muon final states. Unless otherwise stated, the hard process scale used to generate these events is

$$\begin{aligned} \mu _\mathrm {H}= \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{2} . \end{aligned}$$

(63)

This scale was chosen because it was found to give rise to reasonable predictions of several observables sensitive to jet activity using MC@NLO-type matching. In particular we compared predictions of several observables included in the publicly available Rivet analyses for Refs. [4, 63] obtained using $\mu _\mathrm {H}=\mu _{1,2,3}$, i.e. the three scales defined in Sect. 6.2. The resummation profile scale is used in all runs and we use the default choice, $Q_\perp = \mu _\mathrm {H}$, for the hard veto scale in all runs apart from those in which this is the scale of interest.

The default angular-ordered and dipole shower tunes of Herwig  7.1.1 are used in all particle-level runs with the respective showers. The PDF set used is again MMHT2014nlo68cl while $\alpha _S$ is defined separately by using the tuned value for each shower. We use a five-flavour scheme in the runs using the angular-ordered shower, with massless incoming bottom quarks, and the four-flavour scheme in runs using the dipole shower, which treats partons of a given flavour as having the same mass in both the initial and final states. The masses of the bottom quark and top quark are set to 4.2 GeV and 174.2 GeV, respectively, while all other quarks are considered to be massless.

All distributions that are not normalised to their integral are again scaled to the appropriate next-to-next-to-leading order cross section. The NNLO cross sections are $173.60\ \mathrm{pb}$ and $247.74\ \mathrm{pb}$ for $7\ \mathrm{TeV}$ and $8\ \mathrm{TeV}$ collisions, respectively.

7.3 Scale variations

In this section we discuss the parton shower and matching scheme uncertainties that arise from scale variations. We present results for chosen observables that probe various aspects of the simulation and compare with existing data where possible.

Following the approach used in Ref. [24], we estimate the uncertainty on the predictions by considering the variations of three scales:

• the factorization and renormalization scale in the hard process, i.e. the hard process scale $\mu _\mathrm {H}=\mu _\mathrm {R}=\mu _\mathrm {F}$;

• the boundary on the hardness of emissions in the shower, i.e. the hard veto scale $Q_\perp$;

• the argument of $\alpha _S$ and the PDFs in the parton shower, i.e. the shower scale $\mu _\mathrm {S}$.¹⁴

We apply multiplicative factors of 0.5, 1 and 2 to each of the corresponding central scales such that the full set of variations consists of 27 different scale combinations. The complete uncertainty envelope corresponding to this set of variations is shown in each plot. In addition, for each result, we include ratio plots that break down the uncertainties according to the individual scale variations. For each of the three scales considered we separately plot the envelope produced by the upward and downward variations of that scale about the central result, i.e. only two variations are included for each envelope in addition to the central result.

7.3.1 Production level

We first compare results generated with LO matrix elements plus parton shower simulations, using both the angular-ordered (PS) and dipole showers (DS). We use LO plus parton-shower results primarily to compare and contrast the two showers in addition to discussing the uncertainties on the predictions. This is followed by a discussion of results produced by NLO matrix elements matched to a parton shower, i.e. NLO matched simulations. In this discussion, in addition to considering the uncertainties, we focus on the differences between the results obtained using the MC@NLO and Powheg matching schemes.

Figure 6 shows the LO plus parton-shower predictions for the transverse momentum distribution of the top quark ($p_\perp (t)$), the transverse momentum distribution of the $t{\bar{t}}$-pair ($p_\perp (t{\bar{t}})$) the jet multiplicity ($n_\mathrm {jets}$), and the separation between the $t{\bar{t}}$-pair and the hardest jet in the event ($\varDelta R(t{\bar{t}},j_1)$).¹⁵ We find, as expected, that the two shower schemes give similar predictions in the infrared and collinear limits (e.g. at low transverse momentum of the $t{\bar{t}}$-pair) but can diverge in regions of high momentum emissions. For example the dipole-shower prediction of an increased number of high jet-multiplicity events can be understood by the larger phase space available to the dipole shower due to the fact that there are no angular-ordering restrictions. Nonetheless, in all bins the two predictions agree within the prescribed uncertainties. Furthermore the sizes and sources of uncertainties are similar in all bins for both showers.

The transverse momentum of the $t{\bar{t}}$-pair, and the number of jets in the event are both sensitive to the hardest emission, and therefore to the cutoff scale used in the shower. The number of jets is also impacted by the strong coupling used in the shower emissions and we see some sensitivity to the shower scale for this observable at high number of jets.

The separation between the $t{\bar{t}}$-pair and the leading jet is entirely driven by the parton shower since no jet is produced by the LO matrix element. With only one jet the separation must be greater than $\pi$, and so the cutoff scale is the dominant source of uncertainty in this region. Separations of less than $\pi$ are therefore controlled by subsequent jet emissions, which are impacted both by the scale of the hardest jet and the shower scale. Additionally the total uncertainty band, particularly in the region $\varDelta R < \pi$, is much larger than the sum in quadrature of the individual components. This demonstrates the fact that the various scales can have correlated effects on the observables which must be taken into account, and suggests the use of the full envelope as done in this paper rather than separate estimation of each of the component followed by combination in quadrature.

Fig. 6

Scale variations for the inclusive top $p_\perp$-spectrum, the top pair transverse momentum spectrum, inclusive jet multiplicities and R distance between the top pair and the hardest jet using LO plus ($\mathrm {LO}\oplus$) parton shower simulations at $13\ \mathrm{TeV}$. In each plot the upper ratio plot compares the envelopes of all variations for the angular-ordered ($\mathrm {PS}$) and dipole ($\mathrm {DS}$) showers, with a ratio to the central prediction of the angular-ordered shower. The bottom two ratio plots in each plot show, for the angular-ordered and dipole showers respectively, a breakdown of all variations into variations of the (factorization and renormalization) scale in the hard process ($\mu _\mathrm {H}$), of the arguments of the running coupling and PDFs in the shower ($\mu _\mathrm {S}$) and of the hard veto scale ($Q_\perp$)

Fig. 7

Transverse momenta of the top quark (upper row) and the top quark pair (lower row), comparing variations for NLO matched predictions at $13\ \mathrm{TeV}$ for the angular-ordered ($\mathrm {PS}$, left column) and dipole showers ($\mathrm {DS}$, right column). The top panels in each plot compare the central prediction and overall variation between the MC@NLO-type ($\mathrm {NLO} \oplus$) and Powheg-type ($\mathrm {NLO} \otimes$) matching. The first ratio plot in each plot allows to directly compare the overall variations in both matching variants, in a ratio to the central MC@NLO-type prediction, while the lower two ratio plots in each plot show a breakdown of the variations for both matching variants regarding the hard process scale($\mu _\mathrm {H}$), the shower scale ($\mu _\mathrm {S}$) as well as the hard veto scale ($Q_\perp$)

Figure 7 shows the NLO-matched predictions for the $p_\perp (t)$ (upper row), and $p_\perp (t{\bar{t}})$ (lower row) distributions obtained using the angular-ordered (PS, left column) and dipole showers (DS, right column). In an NLO-matched sample these observables are formally predicted with NLO and LO accuracy respectively. Any differences between the the MC@NLO-type (NLO$\oplus$, aka subtractive) and Powheg-type (NLO$\otimes$, aka multiplicative) matching schemes are due to higher-order effects. Accordingly we see good agreement between the matching schemes for both showers. It should be noted that in the highest-$p_\perp$ bin, where uncertainties appear somehwat larger the effect is likely due to statistical uncertainties on the predictions used to construct the uncertainty envelopes.

In the case of $p_\perp (t{\bar{t}})$ we see much smaller uncertainties in the NLO predictions as compared to the LO predictions in Fig. 6 now that the hardest jet is described by the matrix element calculation. Accordingly, $Q_\perp$ is no longer the dominant uncertainty. Instead the scale of the hard process is relevant for the production of the first jet, playing a significant role across the entire distribution and dominating the uncertainty above $p_\perp (t{\bar{t}}) \sim 100~\text {GeV}$.

Fig. 8

Same as Fig. 7, in this case showing the inclusive jet multiplicities and the R distance between the $t{\bar{t}}$-pair pair and the hardest jet. See the text for discussion

Figure 8 shows the NLO-matched predictions of the $n_\mathrm {jets}$, and $\varDelta R(t{\bar{t}},j_1)$ distributions using the angular-ordered and dipole showers. For jet multiplicities above one, and for $\varDelta R(t{\bar{t}},j_1) < \pi$ these distributions are still controlled largely by the shower. Therefore, they do not benefit from the same magnitude reduction of uncertainties as was seen for $p_\perp (t{\bar{t}})$. But in both cases $\mu _\mathrm {H}$ now plays a larger role in the overall uncertainty, being relevant for production of the leading jet. The effect of terms beyond NLO accuracy is clearly visible in the jet multiplicity distribution, where the MC@NLO-type matching predicts more high multiplicity events than the Powheg-type matching. This is related to the choice of the hard veto scale as discussed in more depth in Sect. 7.4. The large impact of the hard veto scale on the MC@NLO predictions is clearly seen in the uncertainty band ratio plots. More accurate jet multiplicity distributions can be achieved through the use of multi-jet merging algorithms. However, this is beyond the scope of the paper. Both distributions also clealy show the correlated impact of these scale choices with total uncertainty envelopes larger than the sum in quadrature of the individual components.

To summarize this section, for a meaningful uncertainty estimate one must consider which parts of each distribution are well predicted by the hard matrix element and which are filled largely or entirely by the parton shower and one should not expect identical predictions from different parton showers away from the soft and collinear limits. In Monte Carlo studies a thorough evaluation of shower and matching uncertainties is required to account for these differences. Whereas in this section we only considered the production level, in Sect. 7.3.2 we will consider the full particle level, and investigate the uncertainties due to scale variations in the prediction of distributions measured from experiment.

7.3.2 Particle level

In Sect. 7.3.1 we discussed the uncertainty on predictions of distributions in the production-level process due to scale variations in the simulation. In this section we complete this discussion by looking at the uncertainty on predictions of distributions in the full-process, including top quark decays and hadronization and comparing to available experimental data using publicly available Rivet analyses. We perform the same scale variations as in Sect. 7.3.1 and the reader is referred to that discussion for details. We highlight that the veto scale in the showering of decay processes is fixed at the mass of the decayed particle and is not varied.

We examine three observables to compare and contrast with the production-level discussion. Namely we consider the transverse momentum of the hadronic top quark, $p_\perp (t)$, the jet multiplicity $n_{\text {jets}}$, and the scalar sum of the transverse momenta $H_T$ (Figs. 9, 10 and 11 respectively). Here, $H_T$ is defined as the sum over all jets in the event.

$$\begin{aligned} H_\mathrm {T} = \sum _{\mathrm {jets}} p_{\perp , \mathrm {jet}} \ . \end{aligned}$$

(64)

The choice of a different hard process scale [c.f. Eq. (63)] as compared to Sect. 7.3.1 [c.f. Eq. (62)] leads to two noticeable differences in the distributions. Firstly, the LO prediction of the top quark $p_T$ is now sensitive to the shower veto scale variations (comparing Fig. 9 to Figs. 6 and 7). This is because the hard process scale is also used as the central hard veto scale. The increase in this scale allows for the emission of harder jets from the shower which can be hard enough to alter the top $p_T$ distribution. Secondly we note that for this scale choice the number of extra jets in the event predicted by the Powheg-type and MC@NLO-type showers display reasonable agreement for both showers. This is in contrast to the differences between the matching schemes observed in Fig. 8. We have checked that these differences arise from the choice of hard process scale, and not to other differences in the settings used for the full process simulations.

Fig. 9

The transverse momentum of the reconstructed hadronically decaying top quark measured by ATLAS in semileptonic $8\ \mathrm{TeV}$ $pp\rightarrow t{\bar{t}}$ events [64]. The top plots shows leading-order production with angular-ordered (PS) and dipole (DS) parton showers, the middle plot NLO production matched to the angular-ordered parton shower while the bottom plot shows NLO production matched to the dipole shower. Two NLO matching schemes, MC@NLO-type ($\mathrm {NLO} \oplus$) and Powheg-type ($\mathrm {NLO} \otimes$), are used

Fig. 10

The multiplicity distribution of jets with transverse momentum greater than 25 GeV, measured in semileptonic 7 TeV $pp\rightarrow t{\bar{t}}$ events by ATLAS [63]. The theoretical predictions are the same as those described in the caption of Fig. 9

Fig. 11

The $H_\mathrm {T}$ distribution measured in semileptonic 8 TeV $pp\rightarrow t{\bar{t}}$ events by CMS [65]. The theoretical predictions are the same as those described in the caption of Fig. 9

As already noted the less restricted phase-space available to the dipole-shower leads to differences between the two algorithms in some regions away from the infrared and collinear limits. In particular the increased $n_{\text {jets}}$ prediction as well as the larger sensitivity of the dipole shower to the hard veto scale can be understood as coming from the differences in available phase-space (comparing Fig. 10 to Figs. 6 and 8).

Lastly, we note that the $H_T$ distribution shows sensitivity to both the choice of showering algorith and matching scheme (Fig. 11). Furthermore differences between the Powheg-type and MC@NLO-type matching are pronounced only for the angular shower. This is an example of the correlations between matching scheme and showering algorithm, indicating that the effects cannot be perfectly factorized, similarly to correlations already observed in the scale choices.

Fig. 12

The effect of different profile scale choices for the two shower algorithms, angular ordered ($\mathrm {PS}$) and dipole ($\mathrm {DS}$), respectively when using MC@NLO-type ($\mathrm {NLO} \oplus$) matching. We compare predictions for the default resummation profile versus the broader hfact profile. From left to right, top to bottom, we present the $p_\perp$ spectrum of the hardest jet, the inclusive jet multiplicity at a threshold of $25\ \mathrm{GeV}$ and $80\ \mathrm{GeV}$, respectively, as well as the azimuthal angle distance between the top pair and the hardest jet

7.4 Profile scale and hard veto scale choices

7.4.1 Impact of profile scales

In this study we restrict ourselves to a simple investigation of the effects of the profile scale choice on the simulation of $t{\bar{t}}$ production using MC@NLO-type matching. To do this we compare results obtained using the two profile scale choices defined above (see Sect. 6.1). This is not intended to be a complete discussion of profile scales and the uncertainties that arise due to choosing a specific one. We simply wish to highlight some of the potential effects of the profile scale choice and present a small selection of observables in which these effects are important.

In Fig. 12 we present production-level results obtained with both the angular-ordered (PS) and dipole showers (DS) using the resummation and hfact profiles. The results shown are the transverse momentum distribution of the hardest jet, $p_\perp (j_1)$, in the upper-left plot, the jet multiplicity, $n_\mathrm {jet}$, distributions with a minimum jet-$p_\perp$ cut of 25 GeV and 80 GeV in the upper-right and lower-left plots, respectively, and the distribution of the azimuthal separation of the $t{\bar{t}}$ pair and the hardest jet, $\varDelta \phi (t{\bar{t}},j_1)$, in the lower-right plot. For clarity we include a separate ratio plot for each shower which, for each bin, shows the ratio of the result obtained using the hfact profile to the result obtained using the resummation profile.

While the hfact profile suppresses hard shower emissions, it does not apply a hard cut on such emissions as in the resummation profile. We therefore expect to see an increase in both the hardness of the hardest jets and in the number of high-$p_\perp$ jets in events.

Most of the results in Fig. 12 clearly display the expected behaviour, however the jet multiplicity with a minimum jet-$p_\perp$ cut of 25 GeV requires some interpretation. We find that the rate of events with high jet-multiplicities predicted using the hfact profile in the angular-ordered shower is lower than that predicted using the resummation profile. The opposite trend is observed in the results obtained using the dipole shower.

The requirement of angular-ordering in the angular-ordered shower effectively puts a cut on the hardness of shower emissions. Through this the hfact profile can increase the emission phase space only up to a maximum possible value such that the effects of the change from the resummation to hfact profile are expected to be somewhat less pronounced for the angular-ordered shower than the dipole shower. In the case of the angular-ordered shower the angular-ordering restriction and the suppression of soft emissions by the hfact profile lead to a reduction in the number of low-$p_\perp$ jets.

Fig. 13

The effect of different choices of the hard veto scale $Q_\perp$ for the two shower algorithms, angular ordered ($\mathrm {PS}$) and dipole ($\mathrm {DS}$), respectively when using MC@NLO-type matching. We compare predictions for different choices of the resummation and factorization scale choice $\mu _\mathrm {H}$, using two choices for the hard veto scale in each case. The scales are specified in the format $(\mu _\mathrm {H},Q_\perp )$ and each of the scale choices is defined in the text. From top to bottom, left to right, we present the $p_\perp$ spectra of the hardest and second hardest jets, produced with the angular-ordered and dipole shower respectively

Fig. 14

Top: $t{\bar{t}}$-pair transverse momentum measured by ATLAS in semileptonic 8 TeV $pp\rightarrow t{\bar{t}}$ events [64] and predicted using the angular-ordered (PS) and dipole (DS) parton showers, respectively. Bottom: The multiplicity distribution of jets with $p_\perp > 25\ \mathrm{GeV}$ measured by ATLAS in semileptonic 7 TeV $pp\rightarrow t{\bar{t}}$ events [63] and predicted using the angular-ordered and dipole parton showers, respectively

Fig. 15

Top: the gap fraction measured by ATLAS in dileptonic 7 TeV $pp\rightarrow t{\bar{t}}$ events [66], in veto region $|y |< 2.1$, and predicted using the angular-ordered (PS) and dipole (DS) parton showers, respectively. Bottom: combined lepton channel measurement of the $H_\mathrm {T}$ distribution by CMS in semileptonic $8\ \mathrm{TeV}$ $pp\rightarrow t{\bar{t}}$ events [65] and predicted using the angular-ordered and dipole parton showers, respectively

7.4.2 Impact of hard veto scales

Next we consider the effect of the choice for the hard veto scale, $Q_\perp$, on results obtained using MC@NLO-type matching. The role of the hard veto scale in MC@NLO-type matching was discussed in Sect. 6.2. In the following we discuss the predictions produced using each of the three options ($\mu _1$, $\mu _2$, $\mu _3$) for $\mu _\mathrm {H}$ separately, the three options being

$$\begin{aligned} \mu _1= & {} \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{2} , \end{aligned}$$

(65a)

$$\begin{aligned} \mu _2= & {} \frac{m_{\perp ,t} + m_{\perp ,{\bar{t}}}}{4} , \end{aligned}$$

(65b)

$$\begin{aligned} \mu _3= & {} m_{t{\bar{t}}} , \end{aligned}$$

(65c)

where $m_{t{\bar{t}}}$ is the invariant mass of the $t{\bar{t}}$-pair.

Given that $Q_\perp$ directly affects the showering of the production-level process, we expect to see the largest effects due to the choice of $Q_\perp$ (which is either $Q_\perp =\mu _\mathrm {H}$ or $Q_\perp =\mu _\mathrm {a}$) in distributions that reflect the jet activity in each event. In particular an increase in $Q_\perp$ should increase the jet activity in events.

Figure 13 shows the transverse momentum distributions of the hardest jet, $p_\perp (j_1)$, and second hardest jet, $p_\perp (j_2)$, in production-level events showered using the angular-ordered and dipole showers. These distributions are very sensitive to the hard veto scale as it sets the upper limit on the scale of the first shower emission and affects the available phase space for subsequent emissions. An increase in $Q_\perp$ should produce an increase in the $p_\perp (j_1)$ distribution, however above some scale we expect all distributions to agree regardless of the choice of $Q_\perp$ as the very hardest jets are produced as a NLO real emission in ${{\mathcal {H}}}$ events. The scale choices are specified in the format $(\mu _\mathrm {H},Q_\perp )$.

In Figs. 14 and 15 we show predictions of several observables measured in particle-level events obtained using the angular-ordered and dipole showers. We highlight that the hard veto scale is applied in the showering of the production process only. The veto scale applied in the showering of the decay process is simply the mass of the decayed particle, i.e. the top quark, and is not varied. We therefore expect the predictions that show the largest change due to the choice of $Q_\perp$ to be those for observables that have a direct dependence on radiation from the production process.

In Fig. 14 the two upper plots show the transverse momentum distribution of the $t{\bar{t}}$-pair, $p_\perp (t{\bar{t}})$, measured by ATLAS [64] in semileptonic $t{\bar{t}}$-events at $\sqrt{s} = 8\text { TeV}$ while the two lower plots show the jet-multiplicity distribution measured by ATLAS [63] in semileptonic $t{\bar{t}}$ events at $\sqrt{s} = 7\text { TeV}$. The $p_\perp (t{\bar{t}})$ distribution should closely reflect the behaviour observed in the $p_\perp (j_1)$ distribution while we expect an increase in $Q_\perp$ to produce an increase in the rate of events with high jet multiplicity.

The two upper plots in Fig. 15 show predictions of the gap fraction, $f(Q_\mathrm {sum})$, measured by ATLAS [66] in dileptonic $t{\bar{t}}$-events at $\sqrt{s} = 7\text { TeV}$. The gap fraction is a measure of additional jet activity in $t{\bar{t}}$-events, i.e. jets which originate from quark and gluon radiation in the event as opposed to the decay products themselves. The analysis used selects only events in the dilepton decay channel so that additional jets can be easily distinguished from the decay products, i.e. two leptons and two bottom-tagged jets. The gap fraction is defined as

$$\begin{aligned} f(Q_\mathrm {sum}) = \frac{n(Q_\mathrm {sum})}{N} \ , \end{aligned}$$

(66)

where N is the number of $t{\bar{t}}$ events that pass the analysis cuts and $n(Q_\mathrm {sum})$ is the number of these events in which the sum of the scalar transverse momenta of the additional jets in a given rapidity range is less than the scale $Q_\mathrm {sum}$. In particular we present results for additional jets in the rapidity range $|y |< 2.1$. A decrease in the gap fraction corresponds to an increase in jet activity.

Finally, the two lower plots in Fig. 15 show the $H_\mathrm {T}$ distribution, as defined in Eq. (64), measured by CMS [65] in semileptonic $t{\bar{t}}$-events at $\sqrt{s} = 8\text { TeV}$. $H_\mathrm {T}$, which measures the number and hardness of the jets outgoing from an event, is a sensitive probe of the jet activity in events.

We first consider the choice $\mu _\mathrm {H}= \mu _1$ and compare the results for $Q_\perp = \mu _1$ to those for $Q_\perp = \mu _\mathrm {a}$. In ${{\mathcal {S}}}$-events $\mu _1$ is identical to $\mu _\mathrm {a}$ and it is only in ${{\mathcal {H}}}$-events with the very hardest NLO emissions that $\mu _\mathrm {a}$ is significantly larger than $\mu _1$. It follows from the similarity of the two scales in most events that most of the distributions in Figs. 13, 14 and 15 indicate very limited difference in the jet activity due to the choice for $Q_\perp$. The change in the $p_\perp (j_2)$ distribution is due to the difference between $\mu _1$ and $\mu _\mathrm {a}$ in those ${{\mathcal {H}}}$-events with the very hardest NLO emissions.

Next we consider $\mu _\mathrm {H}= \mu _2$ for which $\mu _\mathrm {a} > \mu _\mathrm {H}$ in all events. In ${{\mathcal {S}}}$-events we have $\mu _\mathrm {a} = 2 \mu _2$ and in ${{\mathcal {H}}}$-events with a low-$p_\perp$ NLO first emission we have $\mu _\mathrm {a} \sim \sqrt{8/3}\ \mu _2$. All of the results indicate an increase in the predicted jet activity using $Q_\perp = \mu _\mathrm {a}$ compared to using $Q_\perp = \mu _2$ which agrees with our expectation.

As expected the $p_\perp (j_1)$ distribution displays a difference up to some scale, above which the distributions predicted using both choices for $Q_\perp$ come into agreement. The jet multiplicity distribution predicted using the angular-ordered shower displays a more limited difference due to the choice for $Q_\perp$ than the distribution predicted using the dipole shower. This is again due to the additional angular-ordering requirement in the angular-ordered shower.

Finally, we consider the results for $\mu _\mathrm {H}= \mu _3$, the invariant mass of the $t{\bar{t}}$ pair, which is a large scale compared to $\mu _1$ and $\mu _2$ and is larger than $\mu _\mathrm {a}$ in the vast majority of events. All of the results, other than the jet multiplicity distribution predicted using the angular-ordered shower, indicate a decrease in the jet activity predicted in events using $Q_\perp =\mu _\mathrm {a}$ compared to using $Q_\perp =\mu _3$. The difference in the jet multiplicity distribution is again due to the additional angular-ordering requirement in the angular-ordered shower.

To summarize this section, we have compared the effect of using $Q_\perp = \mu _\mathrm {H}$ and $Q_\perp = \mu _\mathrm {a}$ for three different choices of $\mu _\mathrm {H}$. We use $\mu _\mathrm {a}$ to reflect the transverse momenta of the objects outgoing from the hard process. As there is no first principles choice for the hard veto scale $Q_\perp$, the aim of this discussion is to highlight that when we use MC@NLO-type matching we have to make a choice for this scale. We have demonstrated that the choice of the hard veto scale used in MC@NLO-type matching can have a significant effect on the prediction of observables of interest in $t{\bar{t}}$ production at the LHC. We have shown that, in general, using a smaller hard veto scale reduces the predicted jet activity in an event, whereas using a larger hard veto scale generally increases the predicted jet activity. We leave further investigation of potential scale choices to future work.

As far as the corrections to the decay and similar variations therein are considered we cannot find any significant impact on the observables considered here, which are mostly insensitive to changes in the decay system.

7.5 Observables sensitive to the decay process

While the production of top quarks is sensitive to the three scales ($\mu _\mathrm {H}$, $\mu _\mathrm {S}$, $Q_\perp$) investigated in this paper, the decay of a given top quark is only directly impacted by the choice of shower scale. The other scales are fixed at the mass of the decaying particle for the decay process. While there is always some interplay between the production and decay process we consider here observables sensitive to the decay process. For these observables we use the same settings as for comparisons to data, including the full process simulation. First we consider jet substructure in boosted tops, followed by an examination of the separation of b-jets in ttbar events.

The energy and luminosity provided at the LHC allow studies of top quarks with transverse momenta much higher than the top mass. In such cases the decay products of the top quark are generally not well separated. The b quark, and decay products from the W boson are often collimated, forming a single large jet referred to as a ‘boosted’ top jet. This topology has several distinct difficulties compared to the lower momentum cases.

Fig. 16

The N-subjettiness ratios $\tau _{21}$ (top) and $\tau _{32}$ (middle and bottom) for the large-radius jet associated with the highest momentum top-quark in boosted $t{\bar{t}}$ events. The top and middle plots show comparisons of the angular-ordered ($\mathrm {PS}$) and dipole ($\mathrm {DS}$) showers with both the MC@NLO-type (NLO$\oplus$) and Powheg-type (NLO$\otimes$) matching schemes. The bottom plot shows the effects of scale variations on $\tau _{32}$ using the dipole shower with each of the NLO matching schemes

Firstly, large-radius jets originating from top quarks need to be discriminated from large-radius jets originating from other coloured particles or from the decays of W and Z bosons. This discrimination, referred to as tagging, typically makes use of the substructure of the large jet. The three pronged nature of the top-quark decay leaves a characteristically three-pronged structure within the large jet which is not usually found in boson decays or pure QCD jets. In practice many different techniques are used to tag large jets as originating from a top quark. Whether it is through machine learning applied directly to jet-algorithm inputs or techniques based directly on high-level observables designed to provide substructure information, these taggers all ultimately make use of the distribution of energy within a jet to perform tagging. The performance of taggers is often estimated from simulation and it is therefore important to understand the impact of the various choices made in the Monte Carlo simulation on the description of the substructure of large jets originating from boosted top quarks.

As a probe of the sensitivity of jet substructure to the Monte Carlo approach we examined the N-subjettiness  [67] of boosted top quarks produced with Herwig  7. N-subjettiness measures the degree to which the constituents of a subjet are collimated along its N primary axes. Ratios of N-subjettiness values for different values of N are often used to tag large-radius jets. The ratios of 2-subjettiness to 1-subjettiness ($\tau _{21}$) and 3-subjettiness to 2-subjettiness ($\tau _{32}$) were compared using different Herwig  7 settings as shown in Fig. 16. Variation of the shower scale, $\mu _s$, is found to make the largest contribution to the uncertainty envelope, whereas the contributions from the other scale variations are negligible as we expect for an observable mostly sensitive to the top-quark decay. The choice of matching scheme is also found to have very little impact, except for the lowest $\tau _{32}$ bin. On the other hand, comparing the dipole shower and angular-ordered shower algorithms shows more significant differences, comparable to the uncertainty envelopes produced by scale variations.

In Fig. 17 we show predictions of the separation of the two hardest b-tagged jets in semi-leptonic $pp\rightarrow t{\bar{t}}$ events at a centre-of-collision energy of $8\ \mathrm{TeV}$. The separation is defined as $\varDelta R ({j_b}_1, {j_b}_2) = \sqrt{{\varDelta \phi }^2 + {\varDelta \eta }^2}$, where $\varDelta \phi$ and $\varDelta \eta$ denote the difference in the azimuthal angle and pseudorapidity respectively of the hardest and second-hardest bottom-tagged jets. This observable is sensitive to both the simulation of the decay and to the direction of the top quarks that decay to produce the bottom quarks. We measure this distribution using a purpose-built analysis in which we require at least one final-state dressed lepton, electron or muon, with $p_\perp > 30\text {GeV}$ and $|\eta |< 4.2$. Dressed leptons are created by clustering each bare lepton with any photons within a cone of $\varDelta R = 0.1$ around the lepton. We also require at least two light-flavour jets and two bottom-tagged jets with $p_\perp > 30\text {GeV}$ and $|\eta |< 4.2$. Additionally we implement a minimum missing transverse energy cut of 30 GeV, where the transverse energy of each visible outgoing particle is defined as $E_\perp = E \sin (\theta )$ where E and $\theta$ denote the energy and polar angle of the particle respectively, measured in the lab frame.

Fig. 17

The $\varDelta R (b_1, b_2) = \sqrt{{\varDelta \phi }^2 + {\varDelta \eta }^2}$ distribution, described in the text, simulated for semileptonic $8\ \mathrm{TeV}$ $pp\rightarrow t{\bar{t}}$ events

The dominant source of uncertainty on the LO predictions in the region $\varDelta R < \pi$ is the variation of $Q_\perp$. This is because the relative orientation of the top quarks, and hence the separation of the bottom-tagged jets, is sensitive to hard radiation from the production process. The uncertainty envelopes on the NLO-matched predictions are in general smaller than those on the LO predictions, and there is no single dominant source of uncertainty. This is because the the hardest jet from the production process is simulated to LO, rather than parton-shower, accuracy. As we do not use the benchmark settings for the full-process simulation, which is intended for comparison to data, any conclusions about the effects of different shower or matching algorithms on these plots must be made with care. The uncertainty on this prediction due to scale variations is small and our findings suggest that most of the uncertainty is due to the sensitivity to the production process.

With relatively few experimental analyses that measure decay-process sensitive observables currently available, the evaluation of the uncertainty on predictions of such observables is an area for future investigation.¹⁶

8 Summary and outlook

In this work we have presented a detailed study of NLO plus parton shower matched predictions for top pair production at the LHC in the Herwig 7 event generator. We have considered various sources of uncertainty, including the matching algorithms themselves for which two options, a subtractive (MC@NLO-type) and multiplicative (Powheg-type) paradigm can be used within Herwig 7, as well as all scale choices involved. We have not only considered NLO corrections to the production process, but also in the decay process. Both shower modules in Herwig 7 are now able to handle radiation in both the production and the decay of top quarks, and we have used this paper as an opportunity to present a new treatment for radiation from heavy quarks in the dipole shower.

We have found that no single scale variation encompasses the entire set of independent variations, therefore all sources need to be considered to obtain a reliable estimate of the uncertainty on predictions. We have explicitly shown that NLO matching provides improvements over a LO plus parton shower simulation where expected. Higher jet multiplicities, however, do suffer from large uncertainties, even using NLO matching, a fact which should be considered when using tuned predictions. We have further considered boosted topologies, looking at observables that are sensitive to the decay process, focusing on N-subjettiness ratios which highlight the internal structure of the jets.

Particular attention has been paid to the choice of the hard veto scale and the profile scale. This is an ambiguity in matching algorithms which has not been addressed extensively in the literature (with some investigations presented in Ref. [11], and a more elaborate leading-order analysis presented in Ref. [24]) but plays an important role in the handling of real-emission corrections present in the NLO matching. Inappropriate choices can lead to artificially suppressed or enhanced radiation, and we have found that scales which identify the hard objects in the process provide the most reliable results.

The main purpose of this work is to highlight the uncertainties and ambiguities associated with NLO matching, which need to be compared between different shower and matching algorithms. The Herwig  7 event generator provides unique capabilities to quantify the differences between predictions obtained using different setups and to benchmark variations against each other. These sources of uncertainty should be taken into account when comparing predictions against data, also in view of an improved simulation based on multi-jet merging, which can more reliably predict higher jet multiplicities. Being beyond the scope of this paper, a multi-jet merged study, considering a similar set of variations, would thus be a logical follow-up for future work.

Appendices

Dipole shower kinematics

1.1 Alternative formulation for the final–final dipole kinematics

The physical momenta of the partons following a splitting from a massive final–final dipole, written in terms of the splitting variables $z_i$ and $y_{ij,k}$, are

$$\begin{aligned} q_i= & {} A_i Q + k_\perp + B_i v_{\parallel }, \end{aligned}$$

(67a)

$$\begin{aligned} q_j= & {} A_j Q - k_\perp + B_j v_{\parallel }, \end{aligned}$$

(67b)

$$\begin{aligned} q_k= & {} A_k Q + B_k v_{\parallel }, \end{aligned}$$

(67c)

where

$$\begin{aligned} A_i= & {} \frac{1}{s} \left[ m_i^2 + \frac{{\bar{s}}}{2} \left( y_{ij,k}+ z_i(1-y_{ij,k})\right) \right] , \end{aligned}$$

(68a)

$$\begin{aligned} A_j= & {} \frac{1}{s} \left[ m_j^2 + \frac{{\bar{s}}}{2} \left( 1-z_i(1-y_{ij,k}) \right) \right] ,\end{aligned}$$

(68b)

$$\begin{aligned} A_k= & {} \frac{1}{s} \left[ m_k^2 + \frac{{\bar{s}}}{2}(1-y_{ij,k}) \right] ,\end{aligned}$$

(68c)

$$\begin{aligned} B_i= & {} \frac{1}{B_k}\left( s A_i A_k - \frac{{\bar{s}}}{2}z_i(1-y_{ij,k}) \right) ,\end{aligned}$$

(68d)

$$\begin{aligned} B_j= & {} \frac{1}{B_k}\left( s A_j A_k- \frac{{\bar{s}}}{2}(1-z_i)(1-y_{ij,k}) \right) ,\end{aligned}$$

(68e)

$$\begin{aligned} B_k= & {} \sqrt{ \frac{1}{s} \left( m_k^2 + \frac{{\bar{s}}}{2}(1-y_{ij,k}) \right) ^2 - m_k^2 }\,, \end{aligned}$$

(68f)

and the 4-vector

$$\begin{aligned} v_\parallel = \sqrt{ \frac{4 s}{ \lambda \left( s, m_k^2, m_{ij}^2 \right) } } \left( {\tilde{p}}_k - \frac{Q \cdot {\tilde{p}}_k}{s} Q \right) , \end{aligned}$$

(69)

is expressed using the Kallen function

$$\begin{aligned} \lambda (x,y,z) = x^2 + y^2 + z^2 - 2xy -2xz - 2yz\,. \end{aligned}$$

(70)

Note that while it is trivial to write an expression $p_\perp = p_\perp (z_i,y_{ij,k})$, this expression is cubic in $y_{ij,k}$ which leads to a complicated analytic equation for $y_{ij,k}= y_{ij,k}(p_\perp ,z_i)$.

1.2 Final–final dipole kinematics

1.2.1 Completing the formulation

In order to complete our formulation of the splitting kinematics in Sect. 3.3.1 we require expressions for the scaling parameters $x_k$ and $x_{ij}$ in terms of the variables $p_\perp$ and z. We first write an expression for the virtuality of the emitter and emission produced in the splitting

$$\begin{aligned} Q_{ij}^2 = \left( q_i + q_j \right) ^2 = \frac{1}{z(1-z)}\left[ p_\perp ^2 + (1-z) m_i^2 + z m_j^2 \right] .\nonumber \\ \end{aligned}$$

(71)

Defining the variables $\lambda _{ij}$ and $\lambda _k$ as

$$\begin{aligned} \lambda _k = 1 + \frac{m_k^2}{s_{ij,k}}, \quad \lambda _{ij} = 1 + \frac{m_{ij}^2}{s_{ij,k}} \ , \end{aligned}$$

(72)

we derive the following expressions for the scaling parameters

$$\begin{aligned} x_{ij}= & {} 1-\frac{m_k^2}{s_{ij,k}}\frac{(1-x_k)}{x_k} \ , \end{aligned}$$

(73)

$$\begin{aligned} x_k= & {} \frac{1}{2\lambda _k} \left[ \left( \lambda _{ij}\lambda _k + \frac{m_k^2}{s_{ij,k}} - \frac{Q_{ij}^2}{s_{ij,k}} \right) \right. \nonumber \\&\qquad {} \pm \left. \sqrt{ \left( \lambda _{ij}\lambda _k + \frac{m_k^2}{s_{ij,k}} - \frac{Q_{ij}^2}{s_{ij,k}} \right) ^2 - 4 \lambda _{ij} \lambda _k \frac{m_k^2}{s_{ij,k}} } \, \right] .\nonumber \\ \end{aligned}$$

(74)

Finally we require expressions for the splitting variables $z_i$ and $y_{ij,k}$ in terms of the variables $p_\perp$ and z. We write $y_{ij,k}$ as

$$\begin{aligned} y_{ij,k}= \frac{1}{{\bar{s}} z(1-z)} \left[ p_\perp ^2 + (1-z)^2 m_i^2 + z^2 m_j^2 \right] \ , \end{aligned}$$

(75)

where the invariant quantity ${\bar{s}}$ is

$$\begin{aligned} {\bar{s}} = s - m_i^2 - m_j^2 - m_k^2 \ . \end{aligned}$$

(76)

In order to express $z_i$ in terms of $p_\perp$ and z we write

$$\begin{aligned} z_i= \frac{2 q_i \cdot q_k}{(1-y_{ij,k}) {\bar{s}}} \ , \end{aligned}$$

(77)

where the denominator can be written as

$$\begin{aligned}&(1-y_{ij,k}) {\bar{s}} = \frac{1}{z(1-z)}\nonumber \\&\left[ z(1-z) - (1-z)^2 m_i^2 - z^2 m_j^2 - p_\perp ^2 \right] ,\nonumber \\ \end{aligned}$$

(78)

and the numerator is given by the expression

$$\begin{aligned} 2 q_i \cdot q_k = z x_{ij} x_k s_{ij,k}+ \frac{m_k^2}{z x_{ij} x_k s_{ij,k}} \left( p_\perp ^2 + m_i^2 \right) \ . \end{aligned}$$

(79)

1.2.2 Phase-space limits

In order to allow us to efficiently generate values for $p_\perp$ and z according to the splitting kernels we need to express the single-particle emission phase space and the limits on it in terms of these variables.

The limits on the dipole splitting variables $z_i$ and $y_{ij,k}$ are given in Ref. [34] and we include them here to provide a complete reference,

$$\begin{aligned} y_{ij,k,-}= & {} \frac{2 m_i m_j}{{\bar{s}}} \ , \end{aligned}$$

(80)

$$\begin{aligned} y_{ij,k,+}= & {} 1 - \frac{2 m_k (\sqrt{s}-m_k)}{{\bar{s}}} \ , \end{aligned}$$

(81)

$$\begin{aligned} z_{i,\pm }(y_{ij,k})= & {} \frac{ 2 m_i^2 + {\bar{s}}y_{ij,k}}{2\left[ m_i^2 + m_j^2 + {\bar{s}}y_{ij,k}\right] } ( 1 \pm v_{ij,i}v_{ij,k} ) \ , \end{aligned}$$

(82)

where the relative velocities $v_{ij,k}$ and $v_{ij,i}$ are expressed as functions of $y_{ij,k}$,

$$\begin{aligned} v_{ij,k}= & {} \frac{ \sqrt{ \left[ 2 m_k^2 + {\bar{s}}(1-y_{ij,k}) \right] ^2 - 4 m_k^2 s }}{{\bar{s}}(1-y_{ij,k})} \ , \end{aligned}$$

(83)

$$\begin{aligned} v_{ij,i}= & {} \frac{\sqrt{ {\bar{s}}^2 y_{ij,k}^2 - 4 m_i^2 m_j^2 }}{{\bar{s}}y_{ij,k}+ 2 m_i^2} \ . \end{aligned}$$

(84)

The limits on $p_\perp$ and z follow from the inequality $y_{ij,k}< y_{ij,k,+}$,

$$\begin{aligned} p_{\perp ,\mathrm {max}} = \frac{1}{2(\sqrt{s}-m_k)} \sqrt{ \lambda \left( m_i^2, m_j^2, (\sqrt{s}-m_k)^2 \right) } \ , \end{aligned}$$

(85)

$$\begin{aligned} z_{\pm }= & {} \frac{1}{2 \left( \sqrt{s}-m_k \right) ^2} \left[ m_i^2 - m_j^2 + (\sqrt{s}-m_k)^2 \right. \end{aligned}$$

(86)

$$\begin{aligned}&\left. \pm \sqrt{ \lambda \left( m_i^2, m_j^2, (\sqrt{s}-m_k)^2 \right) } \sqrt{ 1 - \frac{p_\perp ^2}{p_{\perp , \mathrm {max}}^2}} \right] \ . \end{aligned}$$

(87)

1.2.3 The single-particle emission phase space

The single-particle emission phase space required to express the branching probability in Eq. (18) is written as

$$\begin{aligned} \mathrm {d}q_j = \frac{1}{16\pi ^2} \frac{ {\bar{s}}^2}{\sqrt{\lambda \left( s, m_{ij}^2, m_k^2 \right) }} \left( 1-y_{ij,k}\right) \mathrm {d}y_{ij,k}\mathrm {d}z_i\frac{\mathrm {d}\phi }{2\pi } \ . \end{aligned}$$

(88)

As we consider only spin-averaged kernels the azimuthal angle, $\phi$, is averaged over in the phase-space integration and we do not consider it explicitly in the following discussion.

Using the above expression for the single-particle phase space we express the branching probability as

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}}= & {} \frac{1}{16\pi ^2} \langle V_{i j, k} \left( z_i, y_{ij,k}\right) \rangle \frac{1}{ \left( 1 + \frac{ m_i^2 + m_j^2 - m_{ij}^2}{{\bar{s}}y_{ij,k}} \right) } \nonumber \\&\times \, \frac{{\bar{s}}}{\sqrt{\lambda \left( s, m_{ij}^2, m_k^2 \right) }} \left( 1-y_{ij,k}\right) \frac{\mathrm {d}y_{ij,k}}{y_{ij,k}} \mathrm {d}z_i,\nonumber \\ \end{aligned}$$

(89)

where we can express the phase-space integration in terms of the generated variables using the replacement

$$\begin{aligned}&\frac{\mathrm {d}y_{ij,k}}{y_{ij,k}} \mathrm {d}z_i\rightarrow \left[ \frac{p_\perp ^2}{p_\perp ^2 + (1-z)^2 m_i^2 + z^2 m_j^2 } \right] \nonumber \\&\qquad \times \, \left[ 1 - 2\frac{1}{{\bar{s}}(1-y_{ij,k})}\frac{m_k^2 Q_{ij}^2}{x_{ij} x_k s_{ij,k}} \right] \frac{\mathrm {d} p_\perp ^2}{p_\perp ^2} \mathrm {d}z \ . \end{aligned}$$

(90)

1.3 Final–initial dipole kinematics

1.3.1 Phase-space limits

The upper limit on $x_{ij,b}$ is,

$$\begin{aligned} x_{ij,b,+} = \frac{s_{ij,b}}{s_{ij,b}- m_{ij}^2 + (m_i + m_j)^2} \ . \end{aligned}$$

(91)

We can derive a lower limit on $x_{ij,b}$. We first write the momentum of the incoming proton as P and the proton momentum-fraction carried by the spectator prior to the splitting as $x_s$. We can write

$$\begin{aligned} q_b = \frac{1}{x_{ij,b}} {\tilde{p}}_{b} = \frac{1}{x_{ij,b}} \left( x_s P \right) < P \ , \end{aligned}$$

(92)

hence we require

$$\begin{aligned} x_{ij,b}> x_s \ . \end{aligned}$$

(93)

From the inequality in Eq. (93) we derive the following limits on the variables $p_\perp$ and z

$$\begin{aligned} p_{\perp ,\mathrm {max}}^2 = \frac{s_{ij,b}^\prime }{4} \lambda \left( 1, \frac{m_i^2}{s_{ij,b}^\prime }, \frac{m_j^2}{s_{ij,b}^\prime } \right) \ , \end{aligned}$$

(94)

$$\begin{aligned} z_\pm= & {} \frac{1}{2} \left[ 1 + \frac{m_i^2 - m_j^2}{s_{ij,b}^\prime } \right. \nonumber \\&\left. \pm \, \sqrt{ \lambda \left( 1, \frac{m_i^2}{s_{ij,b}^\prime }, \frac{m_j^2}{s_{ij,b}^\prime } \right) } \sqrt{1-\frac{p_\perp ^2}{p_{\perp ,\mathrm {max}}^2}} \right] \ , \end{aligned}$$

(95)

where $\lambda$ is the standard Kallen function and for convenience we have defined the modified invariant

$$\begin{aligned} s_{ij,b}^\prime = s_{ij,b}\left( \frac{1-x_s}{x_s}\right) + m_{ij}^2 \ . \end{aligned}$$

(96)

1.3.2 The single-particle emission phase space

The single-particle emission phase space required to express the branching probability in Eq. (28) is written as

$$\begin{aligned} \mathrm {d}q_j = \frac{1}{16 \pi ^2} 2{\tilde{p}}_{ij} \cdot q_b \mathrm {d}z_i\mathrm {d}x_{ij,b}\frac{\mathrm {d}\phi }{2\pi } \ . \end{aligned}$$

(97)

As we consider only spin-averaged kernels the azimuthal angle is averaged over in the phase space integration.

Using the above expression for the single-particle phase space we express the branching probability as

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}}= & {} \frac{1}{16\pi ^2} \frac{f_b(x_s/x_{ij,b})}{f_b(x_s)} \langle V_{i j}^b \left( z_i, x_{ij,b}\right) \rangle \nonumber \\&{} \times \frac{1}{x_{ij,b}(1-x_{ij,b})} \mathrm {d}z_i\mathrm {d}x_{ij,b}. \end{aligned}$$

(98)

Noting that $z_i= z$ we can express the phase-space integration in terms of the generated variables using the replacement

$$\begin{aligned} {l}&\frac{1}{x_{ij,b}(1-x_{ij,b})} \mathrm {d}z_i\mathrm {d}x_{ij,b}\nonumber \\&\quad \rightarrow \left[ \frac{p_\perp ^2}{ p_\perp ^2 + (1-z) m_i^2 + z m_j^2 - z(1-z) m_{ij}^2} \right] \frac{ \mathrm {d}p_\perp ^2 }{p_\perp ^2} \mathrm {d}z.\nonumber \\ \end{aligned}$$

(99)

1.4 Initial–final dipole kinematics

1.4.1 Phase-space limits

The lower and upper limits on $u_j$ are

$$\begin{aligned} u_{j,+}= & {} 0 \end{aligned}$$

(100)

$$\begin{aligned} u_{j,+}= & {} \frac{1 - x_{jk,a}}{1 - x_{jk,a}(1 - m_k^2/s_{aj,k})} \ , \end{aligned}$$

(101)

and the upper limit on $x_{jk,a}$ is

$$\begin{aligned} x_{jk,a,+} = 1. \end{aligned}$$

(102)

Following an analogous argument to that used to derive the inequality in Eq. (93) we derive a lower limit for $x_{jk,a}$

$$\begin{aligned} x_{jk,a}> x_e \ , \end{aligned}$$

(103)

where $x_e$ is the proton momentum-fraction carried by the emitter prior to the splitting.

From the inequality in Eq. (103) we derive the following limits on the variables $p_\perp$ and z

$$\begin{aligned} p_{\perp ,\mathrm {max}}^2= & {} \frac{{s_{aj,k}^\prime }^2}{4} \left[ \frac{1}{m_k^2 + {s_{aj,k}^\prime }} \right] \ , \end{aligned}$$

(104)

$$\begin{aligned} z_{\pm }= & {} \frac{1}{2} \left[ (1+x_e) \pm (1-x_e) \sqrt{1-\frac{p_\perp ^2}{p_{\perp ,\mathrm {max}}^2}} \right] \ , \end{aligned}$$

(105)

where for convenience we have defined the rescaled invariant

$$\begin{aligned} {s_{aj,k}^\prime }= s_{aj,k}\left( \frac{1-x_e}{x_e} \right) \ . \end{aligned}$$

(106)

1.4.2 The single-particle emission phase space

The single-particle emission phase space required to express the branching probability in Eq. (36) is written as

$$\begin{aligned} \mathrm {d}q_j = \frac{1}{16\pi ^2} 2 q_a\cdot {\tilde{p}}_k \mathrm {d}u_j\mathrm {d}x_{jk,a}\frac{\mathrm {d}\phi }{2\pi } \ . \end{aligned}$$

(107)

As we consider only spin-averaged kernels the azimuthal angle is averaged over in the phase-space integration.

Using the above expression for the single-particle phase space we express the branching probability as

$$\begin{aligned} \mathrm {d}{\mathcal {P}}_{\mathrm {branching}}= & {} \frac{1}{16\pi ^2} \frac{f_a(x_e/x_{jk,a})}{{\tilde{f}}_{aj}(x_e)} \langle V^{a j}_k \left( u_j, x_{jk,a}\right) \rangle \nonumber \\&\quad \times \frac{1}{u_j} \frac{1}{x_{jk,a}} \mathrm {d}u_j\mathrm {d}x_{jk,a}\ , \end{aligned}$$

(108)

where we can express the phase-space integration in terms of the generated variables using the replacement

$$\begin{aligned}&\frac{1}{u_j}\frac{1}{x_{jk,a}}\mathrm {d}u_j\mathrm {d}x_{jk,a}\rightarrow \nonumber \\&\quad \left[ u_j+ x_{jk,a}- u_jx_{jk,a}\left( 1-\frac{m_k^2}{s_{aj,k}}\right) \right] ^{-1} \frac{\mathrm {d} p_\perp ^2}{p_\perp ^2} \mathrm {d}z \ . \end{aligned}$$

(109)

Generation cut for boosted top analyses

A difficulty for high momentum top quark simulation is that of CPU time required to populate the high-$\text {p}_{\perp }$ region of phase space targeted by these analyses. Given the steeply falling $t{\bar{t}}$ cross-section as a function of the transverse momentum of the top quark, analyses targeting boosted topologies are typically targeting $\sim 1$% of the total phase space or less. Simulating the inclusive phase-space can therefore be very inefficient, requiring orders of magnitude more events to be fully simulated than are actually of interest. In order to reduce the resources required for simulation a simple cut mechanism is available in the Matchbox framework of Herwig  7. This mechanism makes several options available to improve the efficiency of producing high-$\text {p}_{\perp }$ top quarks.

We can use the existing cut infrastructure in Herwig 7 to implement a generation cut to enhance the production of events that include a boosted top quark or antiquark. We create a ‘MatchboxFactoryMatcher’ that identifies top quarks and antiquarks and associate this with the existing ‘JetFinder’ and ‘JetCuts’ objets. Then we assign the existing ‘FirstJet’ and ‘SecondJet’ objects to the ‘JetRegions’ of the ‘JetCuts’ object. As we have assigned the matcher of the ‘JetCuts’ object to be our new top quark matcher, the ‘FirstJet’ and ‘SecondJet’ actually identify top quarks. Therefore we can set transverse momentum and rapidity cuts on the top quarks by setting the cuts on the ‘FirstJet’ and ‘SecondJet’. The code snippet required to do this is included below.

Example runs with cuts on the transverse momentum of the leading top quark of 200, 300 and 600 GeV were performed to test the efficiency. They showed no significant change in the distributions of weights. For a centre-of-mass energy of 13 TeV kinematic bins well beyond the cut values increased their overall statistics by factors of $\sim 5$, $\sim 20$ and $\sim 500$ respectively for the same total number of events, and relative errors were reduced accordingly. No appreciable impact on the computing time per event was found, allowing a significant reduction in computing power to achieve the same or better statistical power.

A code snippet of an input card to produce similar cuts is given below.