Exponential cosmological solutions with two factor spaces in EGB model with $\Lambda = 0$ revisited

Abstract

We study exact cosmological solutions in D-dimensional Einstein–Gauss–Bonnet model (with zero cosmological term) governed by two non-zero constants: $\alpha _1$ and $\alpha _2$ . We deal with exponential dependence (in time) of two scale factors governed by Hubble-like parameters $H >0$ and h, which correspond to factor spaces of dimensions $m >2$ and $l > 2$, respectively, and $D = 1 + m + l$. We put $h \ne H$ and $mH + l h \ne 0$. We show that for $\alpha = \alpha _2/\alpha _1 > 0$ there are two (real) solutions with two sets of Hubble-like parameters: $(H_1, h_1)$ and $(H_2, h_2)$, which obey: $h_1/ H_1< - m/l< h_2/ H_2 < 0$, while for $\alpha < 0$ the (real) solutions are absent. We prove that the cosmological solution corresponding to $(H_2, h_2)$ is stable in a class of cosmological solutions with diagonal metrics, while the solution corresponding to $(H_1, h_1)$ is unstable. We present several examples of analytical solutions, e.g. stable ones with small enough variation of the effective gravitational constant G, for $(m, l) = (9, l >2), (12, 11), (11,16), (15, 6)$.

1 Introduction

Currently, the Einstein–Gauss–Bonnet (EGB) model and related theories, see [1,2,3,4,5,6,7,8,9,10,11,12] and Refs. therein, are under intensive studies in cosmology, aimed at explanation of accelerating expansion of the Universe [13, 14]. Here we study the EGB model with zero cosmological term in D dimensions ($D = n+1$). This model contains Gauss–Bonnet term, which arises in (super)string theory as a correction to the (super)string effective action (e.g. heterotic one) [15,16,17]. The model is governed by two nonzero constants $\alpha _1$ and $\alpha _2$ which correspond to Einstein and Gauss–Bonnet terms in the action, respectively. In this paper we continue our studies of the EGB cosmological model from Ref. [8]. We deal with diagonal metrics governed by $n >3$ scale factors and consider the following ansatz for scale factors $a_i(t)$ (t is synchronous time variable): $a_1(t) = \dots = a_m(t) = \exp (Ht)$ and $a_{m+1}(t) = \dots = a_{m+l}(t) = \exp (ht)$, where $n =m + l$, $m > 2$, $l > 2$. We put here $H >0$ in order to describe exponential accelerated expansion of 3d subspace with Hubble parameter H [18].

In contrary to our earlier publication [8], where a lot of numerical solutions with small enough value of variation of the effective gravitational constant G were found, here we put our attention mainly to the search of analytical exponential solutions with two factor spaces of dimensions m and l. Here we show that the anisotropic cosmological solutions under consideration with two Hubble-like parameters $H>0$ and h obeying restrictions $h \ne H$, $mH + l h \ne 0$ do exist only if $\alpha = \alpha _2/ \alpha _1> 0$. In this case we have two solutions with Hubble-like parameters: $(H_1 > 0, h_1<0)$ and $(H_2 > 0, h_2<0)$, respectively, such that $x_1 = h_1/H_1< - m/l < x_2 = h_2/H_2$. By using results of Refs. [10, 11] (see also approach of Ref. [9]) we show that the solutions with Hubble-like parameters $(H_2, h_2)$ are stable (in a class of cosmological solutions with diagonal metrics), while those corresponding to $(H_1, h_1)$ are unstable.

Here we also present examples of analytical solutions for: (i) $m =l$; (ii) $m=3$, $l =4$; (iii) $m = 9$, $l >2$; (iv) $m = 12$, $l = 11$; (v) $m=11$, $l=16$ and (vi) $m =15$, $l =6$. It should be noted that analytical solutions in cases (iii) and (iv) were considered numerically in Ref. [8] in a context of solutions with a small (enough) variation of G (in Jordan frame, see Ref. [20]), e.g. obeying the most severe restrictions on variation of G from Ref. [19]. The stable solutions with zero variation of G in cases (v) and (vi) were found earlier in [8], while the stability of these solutions was proved in Ref. [10].

2 The set up

We start with the following action of the model

$$\begin{aligned} S = \int _{M} d^{D}z \sqrt{|g|} \{ \alpha _1 R[g] + \alpha _2 \mathcal{L}_2[g] \}. \end{aligned}$$

(2.1)

Here $g = g_{MN} dz^{M} \otimes dz^{N}$ is the metric defined on the manifold M, ${\dim M} = D$, $|g| = |\det (g_{MN})|$, $\Lambda$ is the cosmological term, R[g] is scalar curvature,

$$\begin{aligned} \mathcal{L}_2[g] = R_{MNPQ} R^{MNPQ} - 4 R_{MN} R^{MN} +R^2 \end{aligned}$$

is the Gauss–Bonnet term and $\alpha _1$, $\alpha _2$ are nonzero constants.

We deal with warped product manifold

$$\begin{aligned} M = {\mathbb {R}}\times M_1 \times \cdots \times M_n \end{aligned}$$

(2.2)

with the (cosmological) metric

$$\begin{aligned} g= - dt \otimes dt + \sum _{i=1}^{n} e^{2\beta ^i(t)} dy^i \otimes dy^i, \end{aligned}$$

(2.3)

where $M_1, \dots , M_n$ are one-dimensional manifolds (either ${\mathbb {R}}$ or $S^1$) and $n > 3$.

Here we put

$$\begin{aligned} \beta ^i(t) = v^i t + \beta ^i_0, \end{aligned}$$

(2.4)

$i = 1, \dots , n$, where $v^i$ and $\beta ^i_0$ are constants.

The equations of motion for the action (2.1) give us the set of polynomial equations [4, 5]

$$\begin{aligned}&G_{ij} v^i v^j - \alpha G_{ijkl} v^i v^j v^k v^l = 0, \end{aligned}$$

(2.5)

$$\begin{aligned}&\left[ 2 G_{ij} v^j - \frac{4}{3} \alpha G_{ijkl} v^j v^k v^l \right] \nonumber \\&\quad \times \sum _{k =1}^n v^k - \frac{2}{3} G_{sj} v^s v^j = 0, \end{aligned}$$

(2.6)

$i = 1,\ldots , n$, where $\alpha = \alpha _2/\alpha _1$. Here we denote [4, 5]

$$\begin{aligned} G_{ij} = \delta _{ij} -1, \qquad G_{ijkl} = G_{ij} G_{ik} G_{il} G_{jk} G_{jl} G_{kl}. \end{aligned}$$

(2.7)

For the case $n > 3$ (or $D > 4$) we have a set of forth-order polynomial equations.

3 Solutions governed by two Hubble-like parameters

Here we study solutions to Eqs. (2.5), (2.6) with following set of Hubble-like parameters

$$\begin{aligned} v =\left( \underbrace{H,H,H}_{``our\text {''} \ space},\underbrace{\overbrace{H, \ldots , H}^{m-3}, \overbrace{h, \ldots , h}^{l}}_{internal \ space}\right) . \end{aligned}$$

(3.1)

where H is the Hubble-like parameter corresponding to an m-dimensional factor space with $m > 2$, while h is the Hubble-like parameter corresponding to an l-dimensional factor space, $l > 2$. The splitting in (3.1) was done just for cosmological applications. Here we split the m-dimensional factor space into the product of 3d subspace (“our” space) and $(m-3)$-dimensional subspace, which is a part of $(m-3 +l)$-dimensional “internal” space.

Keeping in mind a possible description of an accelerated expansion of a 3d subspace, we impose the following restriction

$$\begin{aligned} H > 0. \end{aligned}$$

(3.2)

Due to ansatz (3.1), the m-dimensional subspace is expanding with the Hubble parameter $H >0$. The behaviour of scale factor corresponding to l-dimensional subspace is governed by Hubble-like parameter h.

Here we use the results of Refs. [7, 11] which tell us that the imposing of two restrictions on H and h

$$\begin{aligned} m H + lh \ne 0, \qquad H \ne h, \end{aligned}$$

(3.3)

reduces (2.5) and (2.6) to the set of two (polynomial) equations

$$\begin{aligned} E= & {} m H^2 + l h^2 - (mH + lh)^2 \nonumber \\&-\, \alpha [m (m-1) (m-2) (m - 3) H^4 \nonumber \\&+\, 4 m (m-1) (m-2) l H^3 h \nonumber \\&+\, 6 m (m-1) l (l - 1) H^2 h^2 \nonumber \\&+\, 4 m l (l - 1) (l - 2) H h^3 \nonumber \\&+\, l (l - 1) (l - 2) (l - 3) h^4] = 0, \end{aligned}$$

(3.4)

$$\begin{aligned} Q= & {} (m - 1)(m - 2)H^2 + 2 (m - 1)(l - 1) H h \nonumber \\&+\, (l - 1)(l - 2)h^2 = - \frac{1}{2 \alpha }. \end{aligned}$$

(3.5)

Relation (3.5) implies for $m > 2$ and $l > 2$:

$$\begin{aligned} H = (- 2 \alpha \mathcal{P})^{-1/2}, \end{aligned}$$

(3.6)

where

$$\begin{aligned} \mathcal{P}= & {} \mathcal{P}(x,m,l) \equiv (m - 1)(m - 2) \nonumber \\&+\, 2 (m - 1)(l - 1) x + (l - 1)(l - 2)x^2, \end{aligned}$$

(3.7)

$$\begin{aligned} x= & {} h/H, \end{aligned}$$

(3.8)

and

$$\begin{aligned} \alpha \mathcal{P} < 0. \end{aligned}$$

(3.9)

We rewrite (3.3) as follows

$$\begin{aligned} x \ne x_d \equiv - m/l, \qquad x \ne x_a \equiv 1. \end{aligned}$$

(3.10)

The relation (3.9) lead us to inequality

$$\begin{aligned} \mathcal{P}(x,m,l) \ne 0. \end{aligned}$$

(3.11)

Using (3.4) and (3.6) we obtain

$$\begin{aligned} \lambda (x)= & {} \lambda (x,m,l) \nonumber \\\equiv & {} \frac{1}{4} (\mathcal{P}(x,m,l))^{-1} \mathcal{M}(x,m,l) \qquad \nonumber \\&+\, \frac{1}{8 }( \mathcal{P}(x,m,l))^{-2} \mathcal{R}(x,m,l) = 0, \end{aligned}$$

(3.12)

$$\begin{aligned} \mathcal{M}(x,m,l)\equiv & {} m + l x^2 -(m + l x)^2, \end{aligned}$$

(3.13)

$$\begin{aligned} \mathcal{R}(x,m,l)\equiv & {} m (m-1) (m-2) (m - 3) \nonumber \\&+\, 4 m (m-1) (m-2) l x \qquad \nonumber \\&+\, 6 m (m-1) l (l - 1) x^2 \nonumber \\&+\, 4 m l (l - 1) (l - 2) x^3 \qquad \nonumber \\&+\, l (l - 1) (l - 2)(l - 3) x^4 = 0. \end{aligned}$$

(3.14)

Here the following identity is valid

$$\begin{aligned} \lambda (x,m,l) = \lambda (1/x,l,m) \end{aligned}$$

(3.15)

for $x \ne 0$.

It follows from (3.11) that [21]

$$\begin{aligned} x\ne & {} x_{\pm } \equiv \frac{-(m - 1)(l - 1) \pm \sqrt{\Delta }}{(l - 1)(l - 2)}, \end{aligned}$$

(3.16)

$$\begin{aligned} \Delta\equiv & {} (m - 1)(l - 1)(m + l - 3), \end{aligned}$$

(3.17)

where $x_{\pm }(m,l)$ are roots of the quadratic equation $\mathcal{P}(x,m,l) =0$, obeying

$$\begin{aligned} x_{-}< x_{+} < 0. \end{aligned}$$

(3.18)

Using (3.9) we get

$$\begin{aligned} x_{-}< x < x_{+} \quad \mathrm{for} \ \alpha > 0, \end{aligned}$$

(3.19)

and

$$\begin{aligned} x< x_{-} \ \mathrm{or} \ x > x_{+} \quad \mathrm{for} \ \alpha < 0. \end{aligned}$$

(3.20)

For $\alpha < 0$ the following relation is valid

$$\begin{aligned} \lim _{x \rightarrow \pm \infty } \lambda (x,m,l) = \lambda _{\infty }(l) \equiv - \frac{l(l + 1)}{8 (l - 1)(l - 2)} < 0. \end{aligned}$$

(3.21)

Equation (3.12) may be rewritten in the following form

$$\begin{aligned} 2 \mathcal{P}(x,m,l) \mathcal{M}(x,m,l) + \mathcal{R}(x,m,l) = 0, \end{aligned}$$

(3.22)

or, equivalently,

$$\begin{aligned}&l(l-1)(l-2)(l-3)x^4 + 4ml(l-1)(l-2)x^3 \nonumber \\&\quad +\, 6 m(m-1)l(l-1)x^2 + 4m(m-1)(m-2)lx \nonumber \\&\quad +\, m(m-1)(m-2)(m-3) \nonumber \\&\quad +\, 2[(m-1)(m-2)+ 2(m-1)(l-1)x \nonumber \\&\quad +\, (l-1)(l-2)x^2 ][m+lx^2-(m+lx)^2] =0. \end{aligned}$$

(3.23)

This equation is of fourth order in x for any $l > 2$. One can solve the Eq. (3.23) in radicals for any $m > 2$ and $l > 2$. The general solution is presented in Appendix.

Here we use the following proposition from Ref. [21].

Proposition 1

[21] For $m > 2$, $l > 2$

$$\begin{aligned} \lambda (x,m,l) \sim B_{\pm } (x - x_{\pm })^{-2}, \end{aligned}$$

(3.24)

as $x \rightarrow x_{\pm }$, where $B_{\pm } < 0$ and hence

$$\begin{aligned} \lim _{x \rightarrow x_{\pm }} \lambda (x,m,l) = - \infty . \end{aligned}$$

(3.25)

In what follows we use the relations for the extremum points of the function $\lambda (x)$ ($\frac{\partial }{\partial x} \lambda (x,m,l) = 0$) from [21]:

$$\begin{aligned} x_a= & {} 1, \end{aligned}$$

(3.26)

$$\begin{aligned} x_b= & {} - \frac{m-1}{l-2} < 0, \end{aligned}$$

(3.27)

$$\begin{aligned} x_c= & {} - \frac{m-2}{l-1} < 0, \end{aligned}$$

(3.28)

$$\begin{aligned} x_d= & {} - \frac{m}{l} < 0, \end{aligned}$$

(3.29)

which follow from the identity [21]

$$\begin{aligned}&\frac{\partial }{\partial x} \lambda (x,m,l) = - f(x,m,l) (\mathcal{P}(x,m,l))^{-3}, \end{aligned}$$

(3.30)

$$\begin{aligned}&f(x,m,l) = (l-1)(m-1)(x-1)(lx+m) \nonumber \\&\quad \times [(l-2)x + m-1][(l-1)x + m-2], \end{aligned}$$

(3.31)

$x \ne x_{\pm }$.

Here $x_b < x_c$ and the points $x_b, x_c, x_d$ belong to the interval $(x_{-},x_{+})$ for all $m > 2$ and $l > 2$. The location of the point $x_d$ depends upon m and l [21]:

$$\begin{aligned}&(1) \ x_b< x_c< x_d \quad \text {for } l < m/2, \end{aligned}$$

(3.32)

$$\begin{aligned}&(2) \ x_b< x_d< x_c \quad \text {for } m/2< l < 2m, \end{aligned}$$

(3.33)

$$\begin{aligned}&(3) \ x_d< x_b < x_c \quad \text {for } l > 2m, \end{aligned}$$

(3.34)

and

$$\begin{aligned}&(1_0) \ x_b < x_c = x_d \quad \text {for } l = m/2, \end{aligned}$$

(3.35)

$$\begin{aligned}&(3_0) \ x_d = x_b < x_c \quad \text {for } l = 2m. \end{aligned}$$

(3.36)

The values $\lambda _i=\lambda (x_i,m,l)$, $i=a,b,c,d$, were calculated in [21]. They obey

$$\begin{aligned} \lambda _{\infty } = \lambda _{\infty }(l)< \lambda _a <0, \qquad \lambda _i>0, \end{aligned}$$

(3.37)

$i = b, c,d$.

First, we consider the case $\alpha > 0$ and $x_{-}< x < x_{+}$.

Fig. 1

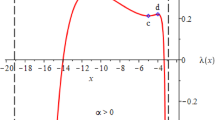
The function $\lambda (x)$ for $\alpha > 0$, $m=12$ and $l=3$ [21]

For $\alpha > 0$ in cases (1), (2) and (3) we have two points of local maximum and one point of local minimum among $x_b, x_c$ and $x_d$, see Fig. 1, while in cases $(1_0)$ and $(3_0)$ we have one point of local maximum and one point of inflection, see Fig. 2. Due to relations (3.30), (3.31) the function $\lambda (x)$ is monotonically increasing in the interval $(x_{-}, \mathrm{min}(x_b, x_c, x_d))$, and it is monotonically decreasing in the interval $(\mathrm{max}(x_b, x_c, x_d), x_{+})$.

Fig. 2

The function $\lambda (x)$ for $\alpha > 0$, $m =4$ and $l = 8$ [21]

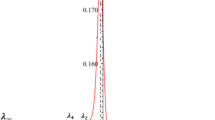
Now, let us consider the case $\alpha < 0$. We have: $x < x_{-}$ or $x > x_{+}$. Due to to the relations (3.21), (3.30) and Proposition 1, the function $\lambda (x)$ is monotonically decreasing in two intervals: (i) in the interval $(-\infty ,x_{-})$ from $\lambda _{\infty }$ to $- \infty$ and (ii) in the interval $(x_{a} = 1, +\infty )$ from $\lambda _{a}$ to $\lambda _{\infty }$. The function $\lambda (x)$ is monotonically increasing in the interval $(x_{+}, x_{a})$ from $- \infty$ to $\lambda _{a}$. Here $x_{a}= 1$ is a point of local maximum of the function $\lambda (x)$, which is excluded from the solution and $0> \lambda _{a} > \lambda _{\infty }$.

The functions $\lambda (x)/\alpha$ for $\alpha = +1, -1$, respectively, and $m = l =4$ are presented at Fig. 3.

Fig. 3

The functions $\Lambda (x) = \lambda (x)/\alpha$ for $\alpha = \pm 1$ and $m = l = 4$ [21]

By using the behaviour of the function $\lambda (x,m,l)$, which was considered above, one can readily prove the following proposition.

Proposition 2

For any $m > 2$, $l > 2$ there are only two real solutions $x_1, x_2$ to the master equation $\lambda (x) = \lambda (x,m,l) = 0$ (see (3.12)) for $\alpha > 0$. These solutions obey $x_{-}< x_1< - \frac{m}{l}< x_2< x_{+} < 0$ (see (3.16)). For $\alpha < 0$ the solutions to master equation are absent.

Proof

First, let us consider the case $\alpha < 0$. In this case it follows from our analysis above that $\lambda (x) < \lambda _{\infty }$ for $x < x_{-}$ and $\lambda (x) < \lambda _{a}$. Since $\lambda _{\infty }< \lambda _a < 0$, we get in the case $\alpha < 0$: $\lambda (x)< \lambda _{a} < 0$. Hence the equation $\lambda (x) = 0$ does not have solutions.

Now we consider the case $\alpha > 0$. We are seeking the solutions to equation $\lambda (x) = 0$ in the interval $(x_{-}, x_{+})$, where our function is smooth (and continuous). Let us denote: $x_{*} = \mathrm{min}(x_b, x_c, x_d)$ and $x_{**} =\mathrm{max}(x_b, x_c, x_d)$. The interval $[x_{*},x_{**}]$ should be excluded from our consideration since $\lambda (x) \ge \mathrm{min}(\lambda _a,\lambda _b,\lambda _c) > 0$ for $x \in [x_{*},x_{**}]$. (Here we use the fact that the smooth (e.g. continuous) function on the closed interval $[x_{*},x_{**}]$ has a minimum which should be equal to $\lambda (x_{*})$ or $\lambda (x_{**})$ or a value of the function in a point of local minimum (e.g. point of extremum) of the form $\lambda (x_{i})$, $i = b,c, d$. In any case this minimum coincides with $\lambda (x_{i})$ for some $i = b,c, d$.) Now we consider the interval $(x_{-},x_{*})$. The function $\lambda (x)$ is monotonically increasing in the interval $(x_{-},x_{*})$. Due to relation (3.21) there exists a point $x_{*,-} \in (x_{-},x_{*})$ such that $\lambda (x_{*,-}) < -1$ and hence any point x in the interval $(x_{-}, x_{*,-}]$ obey $\lambda (x) < -1$. Thus, we exclude the interval $(x_{-}, x_{*,-}]$ from our consideration. Now we consider the interval $[x_{*,-}, x_{*}]$, where $\lambda (x_{*,-}) < -1$ and $\lambda (x_{*}) > 0$. Due to intermediate value theorem there exists a point $x_1 \in (x_{*,-}, x_{*}) \subset (x_{-}, x_{*})$ such that $\lambda (x_{1}) = 0$. This point is unique since the function is monotonically increasing in this interval. By analogous arguments one can readily prove the existence of unique point $x_2 \in (x_{*}, x_{+})$ such that $\lambda (x_{2}) = 0$. By our definitions above we obtain $x_{-}<x_1< x_{*} \le x_d = - \frac{m}{l} \le x_{**}< x_2< x_{+} < 0$. This completes the proof of the proposition.

Thus, we are led to the following (physical) result: the anisotropic cosmological solutions under consideration with two Hubble-like parameters $H>0$ and h obeying restrictions (3.3) do exist only if $\alpha > 0$. In this case we have two solutions with Hubble-like parameters: $(H_1 > 0, h_1 <0)$ and $(H_2 > 0, h_2 <0)$ such that $h_1/H_1< - m/l< h_2/H_2< 0$. $\square$

4 Stability analysis and variation of G

Now, we consider the stability of cosmological solutions in a class of solutions with the metric (2.3)

$$\begin{aligned} g= - dt \otimes dt + \sum _{i=1}^{n} e^{2\beta ^i(t)} dy^i \otimes dy^i. \end{aligned}$$

(4.1)

In Ref. [21] we have proved the following proposition, which is valid for exponential solutions with two factor spaces and Hubble-like parameters obeying (3.2) and (3.3) in the EGB model with a $\Lambda$-term:

Proposition 3

[21] The cosmological solutions from [21], which obey $x = h/H \ne x_i$, $i = a,b,c,d$, where $x_a =1$, $x_b = - \frac{m -1}{l - 2}$, $x_c = - \frac{m-2}{l -1}$, $x_d = - \frac{m}{l}$, are stable, if (i) $x > x_d$ and unstable, if (ii) $x < x_d$.

Here it should be noted that our anisotropic solutions with non-static volume factor are not defined for $x= x_a$ and $x= x_d$. Meanwhile, they are defined when $x = x_b$ or $x = x_c$, if $x \ne x_d$.

Proposition 4

The cosmological solution under consideration for $\alpha >0$ corresponding to the big root of master equation $x_2$ is stable, while the solution corresponding to the small root $x_1$ is unstable.

Here we analyze the solutions by using the restriction on variation of the effective gravitational constant G (in the Jordan frame), which is inversely proportional to the volume scale factor of the (anisotropic) internal space (see [8] and references therein), i.e.

$$\begin{aligned} G = \mathrm{const } \exp {[- (m - 3) H t - l h t]}. \end{aligned}$$

(4.2)

By using (4.2) we get

$$\begin{aligned} \delta \equiv \frac{{\dot{G}}}{GH} = - (m - 3 + l x), \qquad x = h/H. \end{aligned}$$

(4.3)

Here we use, as in Ref. [8], the following bounds on the value of the dimensionless variation of the effective gravitational constant:

$$\begin{aligned} - 0.65 \cdot 10^{-3}< \frac{{\dot{G}}}{GH} < 1.12 \cdot 10^{-3}. \end{aligned}$$

(4.4)

They come from the most stringent bounds on G-dot (by the set of ephemerides) [19] ${\dot{G}}/G = (0.16 \pm 0.6) \cdot 10^{-13} \ year^{-1}$, which are allowed at 95% confidence (2-$\sigma$) level, and the value of the Hubble parameter (at present) [18] $H_0 = (67,80 \pm 1,54) \ km/s \ Mpc^{-1} = (6.929 \pm 0,157) \cdot 10^{-11} \ year^{-1}$, with 95% confidence level.

Let us consider the solution with x-parameter corresponding to dimensionless parameter of variation of G from (4.3). Then, we have

$$\begin{aligned} x = x_0(\delta ,m,l) \equiv - \frac{(m - 3 + \delta )}{l} \end{aligned}$$

(4.5)

and

$$\begin{aligned} x_0(\delta ,m,l) - x_d = \frac{ 3 - \delta }{l} > 0 \end{aligned}$$

(4.6)

for

$$\begin{aligned} \delta < 3. \end{aligned}$$

(4.7)

Let us consider a solution with a small enough parameter $\delta$, which satisfies restrictions (4.4). It obeys (4.7) and hence we obtain from (4.6) $x = x_2$ since $x_d < x_2$, while $x_1 < x_d$. Thus, this solution is stable due to Proposition 4. Hence, all solutions with small enough variation of G, which were obtained in Ref. [8], are stable. The stability two of them was proved in Ref. [10].

Remark

It follows from our consideration that a more wide class of solutions with $\delta < 3$ consists of stable solutions.

5 Examples of solutions

Here we present certain examples of analytical solutions in the model under consideration. These solutions may be readily verified by using Maple or Mathematica. They are given by $x = x_1, x_2$ and relations (3.6), (3.7), (3.8).

5.1 The solutions for $m=l$

For any $m = l > 2$ the master equation (3.22) was solved in fact in Ref. [22] (it was solved there for arbitrary $\Lambda$). The solution reads

$$\begin{aligned} \begin{aligned}&x(\nu ,m) = ((m+1)(m-2))^{-1} \left( - (m-1)^2 - \sqrt{2m^2-7m+7} \right. \\&\qquad \left. + \nu \sqrt{- (2 m^3- 11 m^2+15 m-4) + 2 (m-1)^2 \sqrt{2m^2-7m+7}} \right) , \end{aligned} \end{aligned}$$

$m > 2$, $\nu = \pm 1$. In our notations $x_1 = x(-1,m)$ and $x_2 = x(1,m)$.

For $m = 3,4,5$ we get:

$$\begin{aligned} x(\nu ,3) = \frac{1}{2} \left( - 3 + \nu \sqrt{5}\right) , \end{aligned}$$

(5.1)

see [12], and

$$\begin{aligned} x(\nu ,4)= & {} \frac{1}{10} \left( - 9 - \sqrt{11} + \nu \sqrt{ 18 \sqrt{11} - 8} \right) , \end{aligned}$$

(5.2)

$$\begin{aligned} x(\nu ,5)= & {} \frac{1}{18} \left( - 16 - \sqrt{22} + \nu \sqrt{ 32 \sqrt{22} - 46} \right) . \end{aligned}$$

(5.3)

5.2 The solution for $m=3$ and $l =4$

For the case $m= 3$, $l =4$ the master equation (3.22) has two real solutions

$$\begin{aligned} x(\nu )= & {} - \frac{1}{30} X^{-1/6} Y^{1/2} -3/5 \nonumber \\&+\, \frac{\nu }{2} \sqrt{ \frac{216}{25} X^{1/6} Y^{-1/2} - X^{1/3}+ \frac{7}{45} ( X^{-1/3}- 1)},\nonumber \\ \end{aligned}$$

(5.4)

$$\begin{aligned} X= & {} \frac{14 \sqrt{13}}{375 \sqrt{3}} + \frac{161}{3375}, \end{aligned}$$

(5.5)

$$\begin{aligned} Y= & {} 225 X^{2/3}-6 X^{1/3}-35, \end{aligned}$$

(5.6)

$\nu = \pm 1$. In our notations $x_1 = x(-1)$ and $x_2 = x(1)$. (Approximate values are following ones: $x_1 = -1,345775$ and $x_2 = - 0,258116$.)

5.3 The series of solutions for $m=9$ and $l > 2$

Now we consider the case $m=9$, $l > 2$. The master equation (3.22) in this case reads

$$\begin{aligned}&(l-2)(l-1)l(l+1) x^4 + 32(l-1)^2 lx^3 \nonumber \\&\quad +\,16(l-1)(25l-18)x^2 \nonumber \\&\quad +\, 2304(l - 1)x + 5040 = 0. \end{aligned}$$

(5.7)

It has two real solutions for any $l > 2$

$$\begin{aligned}&x(\nu ,l) = - \frac{1}{M} X^{-1/6} Y^{1/2} - R + \frac{\nu }{2} Z^{1/2}, \end{aligned}$$

(5.8)

$$\begin{aligned}&Z = P_Z X^{1/6} Y^{-1/2} - X^{1/3}+ Q_Z X^{-1/3}- R_Z, \end{aligned}$$

(5.9)

$$\begin{aligned}&Y = N_0 X^{2/3}- N_1 X^{1/3}- N_2, \end{aligned}$$

(5.10)

$$\begin{aligned}&X = P_X \sqrt{Q_X} + R_X, \end{aligned}$$

(5.11)

where $\nu = \pm 1$ and

$$\begin{aligned}&N_0 = 9(l-2)^2 (l-1)l^2(l+1)^2, \end{aligned}$$

(5.12)

$$\begin{aligned}&N_1 = 96(l-1)l(l^3+5l^2-56l+36), \end{aligned}$$

(5.13)

$$\begin{aligned}&N_2 = 64(l+9)(11l^2+34l+144), \end{aligned}$$

(5.14)

$$\begin{aligned}&R = \frac{8(l-1)}{(l-2)(l+1)}, \end{aligned}$$

(5.15)

$$\begin{aligned}&M = 6l(l-2)(l+1) \sqrt{l-1}, \end{aligned}$$

(5.16)

$$\begin{aligned}&P_Z = \frac{3072(l-1)^{1/2}(l^3+5 l^2-24l+36)}{(l-2)^2(l+1)^2}, \end{aligned}$$

(5.17)

$$\begin{aligned}&Q_Z = \frac{N_2}{N_0}, \end{aligned}$$

(5.18)

$$\begin{aligned}&R_Z = \frac{64 (l^3+5l^2-56l+36)}{3 l (l^2 - l - 2)^2} \end{aligned}$$

(5.19)

$$\begin{aligned}&P_X = \frac{512(l+9)}{(l-1)l^2(l-2)^3(l+1)^3} \end{aligned}$$

(5.20)

$$\begin{aligned}&Q_X = \frac{(l+6)(l+8)(5 l^2+4l+36)(9l^2+17l+72)}{3l(l-1)},\nonumber \\ \end{aligned}$$

(5.21)

$$\begin{aligned}&R_X = \frac{1024 (l+9)(49l^3+428l^2+900l+2592)}{27(l-2)^3(l-1)l^3 (l+1)^3}. \end{aligned}$$

(5.22)

Now, we study the behaviour of solutions $x_1 = x(-1,l)$ and $x_2 = x(1,l)$ for big values of l. By using (1 / l)-decomposition we get

$$\begin{aligned} x_1= & {} - \frac{10}{l} + o(l^{-1}), \end{aligned}$$

(5.23)

$$\begin{aligned} x_2= & {} - \frac{6}{l} + o(l^{-1}), \end{aligned}$$

(5.24)

for $l \rightarrow \infty$. These relations just follow from the formulae

$$\begin{aligned} X= & {} X_{\infty } l^{-6} ( 1 + o(l^{-1})), \end{aligned}$$

(5.25)

$$\begin{aligned} {\bar{Y}}\equiv & {} Y X^{-1/3} = 2^{12} l^{3} (1 + o(l^{-1})) \end{aligned}$$

(5.26)

as $l \rightarrow \infty$, where

$$\begin{aligned} X_{\infty } = 2^9 \left( \sqrt{15} + \frac{98}{27} \right) = \left( \frac{16 + 8 \sqrt{15} }{3} \right) ^3. \end{aligned}$$

(5.27)

The solutions $x_1 = x_1(l)$ give us unstable cosmological solutions (as $t \rightarrow \infty$), while $x_2 = x_2(l)$ lead us to stable ones.

Let us consider the second series of solutions. Here, one can obtain more subtle relation instead of (5.24)

$$\begin{aligned} x_2 = - \frac{6}{l} - \frac{3}{l^2} + o(l^{-2}), \end{aligned}$$

(5.28)

as $l \rightarrow \infty$. This relation implies the following asymptotic formula for the parameter of dimensionless variation of the effective gravitational constant in Jordan frame (see (4.2))

$$\begin{aligned} \delta = \frac{3}{l} + o(l^{-1}), \end{aligned}$$

(5.29)

as $l \rightarrow \infty$. Thus, we get

$$\begin{aligned} \delta = \delta (l) \rightarrow 0, \end{aligned}$$

(5.30)

for $l \rightarrow \infty$. The relation (5.30) was discovered numerically in Ref. [8].

5.4 The solutions for $m=12$ and $l = 11$

Let us consider the case $m=12$ and $l = 11$. We get

$$\begin{aligned} x(\nu )= & {} - \frac{1}{162} {\bar{Y}}^{1/2} - (55/54) + \frac{\nu }{2} Z^{1/2}, \end{aligned}$$

(5.31)

$$\begin{aligned} Z= & {} (5456/243) {\bar{Y}}^{-1/2} - X^{1/3}\nonumber \\&+ (299/6561)X^{-1/3}- (250/729), \end{aligned}$$

(5.32)

$$\begin{aligned} {\bar{Y}}= & {} 6561 X^{1/3}- 1125 - 299 X^{-1/3}, \end{aligned}$$

(5.33)

$$\begin{aligned} X= & {} (46/59049) \sqrt{1093} + 12673/531441, \end{aligned}$$

(5.34)

where $\nu = \pm 1$. Approximate numerical values for $x_1 = x(-1)$ and $x_2 = x(1)$ read

$$\begin{aligned} x_1= - 1.487006703, \qquad x_2 = - 0.818209536. \end{aligned}$$

(5.35)

The cosmological solution corresponding to $x_2$ is stable and gives the $\delta$-parameter (from (4.2))

$$\begin{aligned} \delta = -3.049 \times 10^{-4}, \end{aligned}$$

(5.36)

which obeys the bounds (4.4). The solution corresponding to $x_2$ was found numerically in Ref. [8].

5.5 The solutions for $m=11$ and $l = 16$

For $m=11$ and $l = 16$ we get two solutions. The first solution to the master equation, corresponging to unstable cosmological solution, reads

$$\begin{aligned} x_1= & {} X^{1/3} - (19967/509796) X^{-1/3} - 481/714, \end{aligned}$$

(5.37)

$$\begin{aligned} X= & {} \sqrt{28457}/(49(34)^{3/2})- 5656195/36399434, \end{aligned}$$

(5.38)

or numerically, $x_1 = - 0.871886679$. The second one was obtained in Ref. [8]:

$$\begin{aligned} x_2 = - 1/2. \end{aligned}$$

(5.39)

It gives a zero variation of the effective gravitational constant G in Jordan frame, i.e. $\delta = 0$. The stability of the corresponding cosmological solution was proved earlier in [10].

5.6 The solutions for $m=15$ and $l = 6$

Let us put $m=15$ and $l = 6$. We get two solutions. The first one corresponds to unstable cosmological solution. It reads

$$\begin{aligned} x_1= & {} X^{1/3} - (2/9) X^{-1/3} - 8/3, \end{aligned}$$

(5.40)

$$\begin{aligned} X= & {} \sqrt{187}/3^{3/2}-71/27, \end{aligned}$$

(5.41)

or numerically, $x_1 = - 4.278163073$. The second one was obtained in Ref. [8]:

$$\begin{aligned} x_2 = - 2. \end{aligned}$$

(5.42)

It leads to zero variation of G ($\delta = 0$). The stability of the corresponding cosmological solution was proved in [10].

6 Conclusions

We have considered the D-dimensional Einstein–Gauss–Bonnet (EGB) model with two non-zero constants $\alpha _1$ and $\alpha _2$. By using the ansatz with diagonal cosmological metrics, we have studied a class of solutions with exponential time dependence of two scale factors, governed by two Hubble-like parameters $H >0$ and h, corresponding to submanifolds of dimensions $m > 2$ and $l > 2$, respectively, with $D = 1 + m + l$. The equations of motion were reduced to the master equation $\lambda (x,m,l) = 0$ (see (3.12) or (3.23)), where the parameter $x = h/H$ obeys the restrictions: $x \ne 1$, $x \ne - m/l$ and $x \ne x_{\pm }$ ($x_{-}< x_{+} < 0$) are defined in (3.16). By using our earlier analysis from Ref. [21] we have proved that the master equation has real solutions only for $\alpha > 0$. In this case there are two solutions: $x_1$, $x_2$, which satisfy

$$\begin{aligned} x_{-}<x_1< - m/l< x_2< x_{+} < 0. \end{aligned}$$

The master equation may be solved in radicals, since it is equivalent to a polynomial equation of fourth order (for $l > 2$). See Appendix.

Any cosmological solution corresponding to $x_1$ or $x_2$ (for $\alpha > 0$) describes an exponential expansion of 3-dimensional subspace (“our” space) with the Hubble parameter $H > 0$ and anisotropic behaviour of $(m-3+ l)$-dimensional internal space: expanding in $(m-3)$ dimensions (with Hubble parameter H) and contracting in l dimensions (with Hubble-like parameter h).

By using our earlier results from Ref. [21] we have proved that the solution corresponding to $x_2$ is stable in a class of cosmological solutions with diagonal metrics, while the solution corresponding to $x_1$ is unstable.

We have presented several examples of exact solutions (in terms of $x = h/H$) in the following cases: (i) $m =l$; (ii) $m=3$, $l =4$; (iii) $m = 9$, $l >2$; (iv) $m = 12$, $l = 11$; (v) $m=11$, $l=16$ and (vi) $m =15$, $l =6$. In case (iii) we have also proved the asymptotical relation for variation of G: ${\dot{G}}/(GH) = 3/l + o(1/l)$, as $l \rightarrow \infty$, which is valid for stable solutions.

Appendix

The master equation (3.23) reads

$$\begin{aligned} F(x) = A x^4 + Bx^3 + Cx^2 + Dx + E = 0, \end{aligned}$$

(A.1)

where

$$\begin{aligned} A= & {} (l-2)(l-1)l(l+1), \end{aligned}$$

(A.2)

$$\begin{aligned} B= & {} 4(l-1)^2 l(m-1), \end{aligned}$$

(A.3)

$$\begin{aligned} C= & {} 2(l-1)(m-1)(3lm-2m-2l), \end{aligned}$$

(A.4)

$$\begin{aligned} D= & {} 4(l-1)(m-1)^2 m, \end{aligned}$$

(A.5)

$$\begin{aligned} E= & {} (m-2)(m-1)m(m+1). \end{aligned}$$

(A.6)

By making the substitution

$$\begin{aligned} X= & {} u + d, \nonumber \\ d= & {} - B/(4A) = - (l-1)(m-1)/( (l-2)(l+1)),\nonumber \\ \end{aligned}$$

(A.7)

we get

$$\begin{aligned} F (u + t) = (l-2)(l-1)l(l+1)(u^4 + a u^2 + b u + c), \end{aligned}$$

(A.8)

where for our values of A, B, C, D, E we have

$$\begin{aligned} a= & {} 2(m-1)(l^2 m-7 l m + 4m + l^3 - 4 l^2 + 7l)/\nonumber \\&( (l-2)^2 l(l+1)^2), \end{aligned}$$

(A.9)

$$\begin{aligned} b= & {} (8(m-1)^2(l^2m-3lm+4m+l^3-4l^2+3l))/\nonumber \\&( (l-2)^3 l (l+1)^3), \end{aligned}$$

(A.10)

$$\begin{aligned} c= & {} -(m-1)(l^4 m^3 -5 l^3 m^3 \nonumber \\&+\, 19 l^2 m^3-39l m^3+32 m^3 \nonumber \\&+\, 2 l^5 m^2-13 l^4 m^2+37 l^3 m^2\nonumber \\&-79 l^2 m^2 + 101 l m^2 -56 m^2 \quad \nonumber \\&+\, l^6 m-7 l^5 m+ 20 l^4 m - 48 l^3 m\nonumber \\&+\,107 l^2 m- 97 l m + 8m \quad \nonumber \\&+\, l^6-l^5-14l^4+38l^3-35l^2+11l)/ \nonumber \\&((l-2)^4 (l-1) l (l+1)^4). \end{aligned}$$

(A.11)

It may be readily verified that $b > 0$ for all $m > 2$ and $l > 2$.

Then, Eq. (A.1) reads as follows

$$\begin{aligned} u^4 + a u^2 + b u + c = 0. \end{aligned}$$

(A.12)

Solving the Eq. (A.12) by the well-known Ferrari method needs an arbitrary (real) solution to the cubic equation

$$\begin{aligned} y^4 + \frac{5}{2} a y^2 + ( 2 a^2 - c) u + \frac{1}{2} \left( a^3 - a c - \frac{1}{4} b^2\right) = 0, \end{aligned}$$

(A.13)

or another equation

$$\begin{aligned} v^3 + p v + q = 0, \end{aligned}$$

(A.14)

where

$$\begin{aligned} y = v - \frac{5}{6} a, \end{aligned}$$

(A.15)

and

$$\begin{aligned} p= & {} - \frac{1}{12} a^2 - c, \end{aligned}$$

(A.16)

$$\begin{aligned} q= & {} - \frac{1}{108} a^3 + \frac{1}{3} a c - \frac{1}{8} b^2. \end{aligned}$$

(A.17)

It follows from relations (A.9), (A.10), (A.11) that

$$\begin{aligned} p= & {} (2(m-1)(m+l)(lm^2+2m^2+l^2m \nonumber \\&-\,5lm-2m+2l^2-2l))/\nonumber \\&( 3(l-2)^2(l-1)l^2(l+1)^2), \end{aligned}$$

(A.18)

$$\begin{aligned} q= & {} (-4(m-1)^2 (m+l)(5lm^3+4m^3\nonumber \\&+\,10l^2m^2-42lm^2-4m^2 +5l^3 m \nonumber \\&-\, 42l^2 m+73lm+4l^3-4l^2))/\nonumber \\&( 27(l-2)^3(l-1) l^3(l+1)^3). \end{aligned}$$

(A.19)

It may be readily verified that $p > 0$ for all $m > 2$ and $l > 2$.

The real solution to cubic equation (A.13) has the following form

$$\begin{aligned} y = - \frac{5}{6} a - \frac{p}{3 U} + U, \end{aligned}$$

(A.20)

where

$$\begin{aligned} U = \root 3 \of { - \frac{q}{2} + \sqrt{\frac{q^2}{4} + \frac{p^3}{27}}} . \end{aligned}$$

(A.21)

Here $U > 0$ since $p > 0$.

The complex solutions to quartic equation (A.1) read as follows

$$\begin{aligned} x = d + \varepsilon _1 \frac{1}{2} \sqrt{a + 2y} + \varepsilon _2 \frac{1}{2} \sqrt{- \left( 3 a + 2y + \varepsilon _1 \frac{2b}{\sqrt{a + 2y}}\right) }, \end{aligned}$$

(A.22)

where $\varepsilon _1 = \pm 1$ and $\varepsilon _2 = \pm 1$ are two independent sign parameters.

Here $a + 2y > 0$, $b >0$ and we have two real roots which correspond to the following choice of sign

$$\begin{aligned} \varepsilon _1 = - 1. \end{aligned}$$

(A.23)