1 Introduction

It is well-known that HOMFLY-PT polynomials [1,2,3,4,5,6,7,8] possess evolution structure [9,10,11,12,13,14,15,16,17, 20, 21]. This has a simple explanation within the modernized Reshetikhin-Turaev (MRT) formalism [22,23,24,25,26,27], and the evolution eigenvalues are actually those of the \({\mathcal {R}}\)-matrix in the relevant representations. There is no known a priori reason to expect such structure in superpolynomials, defined in a very different way [28,29,30, 32,33,34,35,36,37] (see, however, [38, 41,42,43,44] and [45,46,47]). Still, in attempts to find a refined version of MRT, one can try to observe a similar structure for Khovanov polynomials empirically – and is immediately gratified: evolution was already proved to persist for the series of torus and twist knots [48,49,50,51]. For example, the n-dependence of reduced Khovanov invariant is of the form

$$\begin{aligned} \mathcal {X}^{\text {Torus}[2,n]} = C_1 \lambda _1^n + C_2 \lambda _2^n \end{aligned}$$
(1.1)

and for positive odd n it is actually

$$\begin{aligned}&\mathcal {X}^{\text {Torus}[2,n]} \sim \frac{1 -q^2T + q^4T^2}{1-q^2T} - \frac{(q^2T)^{n+1}}{1-q^2T} \nonumber \\&\quad = 1 + q^4T^2\cdot \frac{1-(q^2T)^{n-1}}{1-q^2T} \end{aligned}$$
(1.2)

i.e. an explicitly positive polynomial.

Switching to negative n makes this expression explicitly negative, and positivity is restored by insertion of additional overall factor \((-T)\). Additional simple modifications are needed for even n and for unreduced invariants, which might look like a minor issue and, indeed, in this particular example can be explained away by a simple requirement that invariants remain positive and minimal for all n. However, as one considers more and more general knot/link families it becomes increasingly clear that there is more to the story.

In this paper we look at a rather representative family of pretzel knots (see Sect. 2 for a definition), which includes the entire twist and double-twist series, but only 2-strand sub-family of torus knots. Their evolution at HOMFLY-PT and, partly, superpolynomial levels was described in detail in [9,10,11,12,13,14,15,16,17, 20, 21] and [52,53,54,55, 57]. Here we study the evolution of Khovanov polynomials for this family. We immediately see that parameter space has rich, even puzzling, chamber structure: transitions between the chambers (an analog of changing the sign or parity of evolution parameter in 2-strand torus case) cannot be fully explained by the positivity requirement (this line of thought, however, does not break completely, see Remarks 3.3 and 3.7). Before going into details we briefly outline what happens.

1.1 The problem

In the region where all winding parameters are positive, reduced Khovanov polynomials for pretzel knots (not links! – see Sect. 6) of genus g are given by the general formula

$$\begin{aligned} \boxed {\begin{aligned} \mathcal {X}_{n_i > 0}^{\text {knots}}&= \frac{q }{s^g [2]_{qt}} \frac{1}{[2]_{qt}^{g+1}} \left( \prod _{i=0}^g \Big ( 1 + {[3]_{qt}} {\left( q^2 T \right) }^{n_i}\Big ) \right. \\&\quad \left. + [3]_{qt} \prod _{i=0}^g \Big ( 1 - {\left( q^2 T \right) }^{n_i}\Big )\right) \end{aligned}} \end{aligned}$$
(1.3)

Here \(s = \sqrt{-T}\) and qt-numbers are \([n]_{qt} = \frac{(sq)^{n} - (sq)^{-n}}{sq - (sq)^{-1}}\sim \frac{1-(-q^2T)^n}{1+q^2T}\) (note that they are themselves not positive, but combine in an intricate way inside (1.3) to give a positive result – see Remarks 3.3 and 3.7). This formula, however, is too simple: modulo trivial normalization coefficient it can be obtained just by the change of variables \(q^2 \rightarrow (-T) \cdot q^2,\ A^2 \rightarrow (-T) \cdot q^4\) from the arborescent formula [52,53,54,55, 57,58,59,60,61] for the corresponding HOMFLY-PT polynomial – reflecting the fact that all knots in this region are homologically thin [62]. That is, the arborescent formula [58,59,60,61] survives in this case not only the generalization to superpolynomial, but also the reduction to Khovanov (\(N=2\)) polynomials, which are defined and calculated in an absolutely different way.

However, as one goes out of the positive octant, one immediately encounters discrepancies. The simplest example is provided by the pair of 3-strand torus knots, \(\text {Torus}[3,4]\) and \(\text {Torus}[3,5]\), which are still pretzels (there are no more torus pretzels except these two and the 2-strand series). Indeed, of the five terms in the reduced Khovanov polynomial

$$\begin{aligned}&\mathcal {X}{\left( \text {Torus}[3,4] \right) } \equiv \mathcal {X}{\left( \text {Pretzel}[3,3,-2] \right) } \nonumber \\&\quad = \ q^{13} T^6+q^9 T^4+q^7 T^3+q^7 T^2+q^3 T \end{aligned}$$
(1.4)

only three are reproduced by the formula (1.3), provided one multiplies it by an extra \((-T)\):

$$\begin{aligned} (1.3) \ \Longrightarrow \ q^{13} T^6+q^9 T^4+q^3 T \end{aligned}$$
(1.5)

And, as a rule, the discrepancy gets worse and worse as one moves away from the positive octant – the presented example is by no means unique.

Taken in isolation, this is not so big a problem and not even a surprise. Indeed, Poincare polynomials of differential complexes, of which Khovanov polynomial is an example, usually behave much worse than corresponding Euler characteristics. But if one remembers the context, which exists on \(T = -1\) level, then discrepancy (1.5) is very important. Indeed, at \(T = -1\), the analog of (1.3) has deep representation theory connections; it is made of so-called Racah matrix [73,74,75,76,77,78,79]. This immediately allows one to generalize (1.3\(_{T = -1}\)) to the colored case, simultaneously revealing its connection to Chern-Simons [87, 88] theory.

If one ever hopes to have similarly rich context at \(T \ne -1\) level, then understanding, or at least taming, this naive breakdown of (1.3) is crucial, and this is precisely what we do in the present paper.

Another point of interest is that proper description of the \(T \ne -1\) structure may shed some light on the use of the topological string formalism to calculate refined knot polynomials. So far, this was understood only in the example of double Hopf link [89].

1.2 The main results

In this paper we look at Khovanov polynomials for low genus pretzel knotsFootnote 1 and find the following loosely related structures:

1.2.1 Nimble evolution in exceptional regions

The abovementioned \(\text {Pretzel}[3,3,-2]\) is near the tip of a special region in the parameter space

$$\begin{aligned} n_g \le 0, \ \ n_i > -n_g, \ i = 0 \ ..\ g-1 \end{aligned}$$
(1.6)

where reduced Khovanov polynomials receive unsymmetric correction term

$$\begin{aligned} \boxed { \frac{q}{s^g} \frac{(1 + T)}{[2]_{qt}^{g}} \prod _{j = 0}^{g-1} {\left( 1 + [3]_{qt}(q^2 T)^{n_j + n_g} \right) } } \end{aligned}$$
(1.7)

in which \(n_g\) is distinguished and plays a special role. This term, of course, vanishes at \(T = -1\). There are a few regions, shaped similarly to (1.6), with more-or-less analogous kind of correction terms.

The most prominent feature of (1.7) is that the dependence on \(n_g\) is very different from dependence on other windings \(n_i\). \((q^2 T)^{n_g}\) occurs in each and every bracket. Cumulative effect of these extra eigenvalues in all the brackets is that in the preferred direction evolution occurs faster than would be naively expected. We call this phenomenon “nimble evolution”.

For arbitrary genus this is definitely not the whole story, but in Sect. 3 we present the details of what we understand so far.

For genera \(g=1\) and \(g=2\), however, this description of reduced Khovanov polynomials for knots is exhaustive and complete – the only deviation from (1.3) are correction terms (3.14) and (3.18), analogous to (1.7), appearing in “exceptional” regions, shaped by inequalities (3.15) and (3.17). Only in these exceptional regions does one encounter thick knots, i.e. such knots (as opposed to thin knots) whose Khovanov polynomial contains (q, T)-monomials that do not lie on the cricical diagonals of the Newton plane (see Sect. 1.1 in [70] and referenced therein). While for thin knots Khovanov polynomial can be obtained from the respective Jones polynomial by simple change of variables, for thick knots one cannot do it, and this is what makes thin-thick knot distinction so important.

1.2.2 Unreduced polynomials can be restored from reduced ones

For genus 2 the unreduced Khovanov polynomials can be recovered from reduced ones by adding simple corrections (see Sect. 4). They also change abruptly between strata, but inside each stratum they depend only on the planar diagram’s unorientability (see Sects. 4 and 5).

1.2.3 Link polynomials have similar structure

Unreduced Khovanov polynomials for links are not very much different from unreduced Khovanov polynomials for knots: they have simple extra correction terms that depend on the mutual linking numbers of the components and unorientability (see Sect. 5) of the planar diagram. Still, the structure of these terms is so different from arborescent structure (1.3) that joining links with different number of connected components into one evolution series (as was done in [51]) is more confusing than illuminating (see Sect. 6).

We completely leave the question of structures present in reduced Khovanov polynomials for links out of this paper. This is mainly because reduced Khovanov polynomials for links require a different point of view: to any given link one associates not just one, but the whole bunch of polynomials, one for each choice of marked connected component.

In this paper we present an interpretation of the extensive experimental data on Khovanov polynomials. Of course, what we really want in the future, is to do prediction: to write down formulas similar to (1.7) beforehand from some kind of guiding principle and then check that they indeed give Khovanov polynomials, calculated with help of their explicit definition.

We conclude by discussing the meaning and limitations of our results and pointing further directions in Sect. 8.

2 Pretzel knots

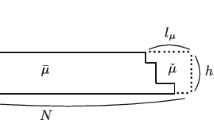
Recall that pretzel knot of genus g is a certain kind of knot that can be drawn on a genus g surface. It consists of \(g+1\) 2-strand braids, with winding numbers \(n_0\) through \(n_g\), respectively, which are joined, as shown on the picture.

(2.1)

In order to define framing (see Sect. 5), it is important to choose a particular planar projection, and for pretzel knots we always have in mind this one.

Depending on parities of windings \(n_i\), pretzel planar diagram (2.1) can be either a knot or a link. A diagram is a knot, when either:

  • one of the windings is even, and all the rest are odd

  • genus g is even and all the windings are odd

In the former case the “even” braid has to be antiparallel, while all “odd” braids are parallel. In the latter case all the braids are antiparallel

(2.2)

For the purposes of this paper we will call the former pretzel knots (that have exactly one antiparallel braid) charged and the latter pretzel knots neutral, since the former ones have non-zero unorientability (see Sect. 5), while the latter ones do not.

It is crucial to distinguish charged and neutral pretzel knots, since, as we shall see in Sect. 3, starting from genus \(g = 2\) in some regions evolution formulas for these two types of pretzel knots do differ.

3 Reduced Khovanov polynomials

In this section we present the evolution formulas for reduced Khovanov polynomials. We go incrementally, from the simpler formulas valid in some regions of the parameter space, to more and more complicated formulas.

Here, unless otherwise specified, index i runs from 0 to g, index J is some distinguised index (and in this case the region considered is the union of regions for all possible choices of J). Here, and in the following sections as well, \(\lambda \) is equal to \(q^2 T\):

$$\begin{aligned} \lambda := q^2 T \end{aligned}$$
(3.1)

The simplest possible formula is

$$\begin{aligned}&\mathcal {X}_{\text {bulk}_g}^{\text {knots}} = \frac{q (-T)}{(q^{-1} - q T)} \frac{1}{(q^{-1} - q T)^{g+1}}\nonumber \\&\quad \times {\left( \prod _{i=0}^g \Big ( 1 + {[3]_{qt}} {\left( q^2 T \right) }^{n_i}\Big ) + [3]_{qt} \prod _{i=0}^g \Big ( 1 - {\left( q^2 T \right) }^{n_i}\Big ) \right) }, \end{aligned}$$
(3.2)

which is valid in the region

$$\begin{aligned}&\text {bulk}_g \ : \ (n_i> 0) \text { or }(n_J = 0 \text { and }n_{i \ne J}> 0) \nonumber \\&\quad \text { or }(n_J = -1 \text { and }n_{i \ne J} > 1) \end{aligned}$$
(3.3)

The motivation behind the region’s name will become clear in a second. The formula (3.2) is straightforwardly obtained from the HOMFLY polynomial with help of change of variables \(q^2 \rightarrow (-T) \cdot q^2,\ A^2 \rightarrow (-T) \cdot q^4\). This is to be expected, since all the knots in this region are alternating and, hence, homologically thin (which precisely means they can be restored from respective HOMFLY with the substitution).

The formula (3.2) for sure cannot be true on the entire windings space, since, as one tries to apply it outside the \(\text {bulk}_g\) region, it stops giving positive answer (see Remarks 3.3 and 3.7).

The failure of positivity of (3.2) is, in fact, cured in a very easy way in a number of regions, which we denote \(\text {bulk}_a\), \(a = -g, -g + 2, \dots , g - 2, g\). The shape of these regions is, in general, complicated (at least so far we were unable to find a generic description of their shape by some inequalities), but one of the regions – \(\text {bulk}_{-g}\) – is the antipode of \(\text {bulk}_{g}\):

$$\begin{aligned}&\text {bulk}_{-g} \ : \ (n_i< 0) \text { or }(n_J = 0 \text { and }n_{i \ne J}< 0) \nonumber \\&\quad \text { or }(n_J = 1 \text { and }n_{i \ne J} < -1) \end{aligned}$$
(3.4)

The correct formula in bulk-regions is

$$\begin{aligned} \mathcal {X}_{\text {bulk}_a}^{\text {knots}} = (-T)^{\frac{a - g}{2}} \mathcal {X}_{\text {bulk}_g}^{\text {knots}} \end{aligned}$$
(3.5)

Remark 3.1

In \(g = 1\) case, there are just two regions \(\text {bulk}_1\) and \(\text {bulk}_{-1}\), which are larger than in general case, namely

$$\begin{aligned} \text {bulk}_1 \,&: \ n_0 + n_1 > 0\nonumber \\ \text {bulk}_{-1} \,&: \ n_0 + n_1 < 0 \end{aligned}$$
(3.6)

i.e. they span the whole parameter space (the diagonal \(n_0 = n_1\) contains only links). Note that there is no separate restriction on \(n_0\) and \(n_1\) – just on their sum, because for \(g=1\) it is easy to rewrite (3.2) to depend manifestly only on \(n_0 + n_1\).

Remark 3.2

Note that the mirror symmetry, which is a fundamental property of the Khovanov polynomials, presents here in the form

$$\begin{aligned}&\mathcal {X}(\text {Pretzel}[n_0,\ldots ,n_g])(q,T)\nonumber \\&\quad =q^2\mathcal {X}(\text {Pretzel}[-n_0,\ldots ,-n_g])(q^{-1},T^{-1}), \end{aligned}$$
(3.7)

where an extra factor of \(q^2\) is a due to the peculiarity of the definition of the reduced polynomials [63]. One can explicitly verify that (3.7) indeed relates the p and m versions of all our evolution formulas.

Remark 3.3

One can observe that all our evolution formulas are in fact assembled from the elementary factors of the three kinds,

$$\begin{aligned} f_n(\lambda )&=\lambda ^{-n}\frac{1-\lambda ^n}{1-\lambda }=\frac{\lambda ^{-n}-1}{1-\lambda },\nonumber \\ g_n(\lambda )&=(\lambda ^{-1}-1+\lambda )\lambda ^{n}f_n(\lambda )=\lambda ^{-1}-\lambda ^{n-1}\nonumber \\&\quad +\lambda \Big (\frac{1-\lambda ^{n-2}}{1-\lambda }+\lambda ^{n-2}+\lambda ^{n-1}\Big )\nonumber \\&= \lambda ^{-1}+\lambda ^{n-1}f_{n-2}(\lambda )+\lambda ^n,\nonumber \\ F_n(\lambda )&=\lambda ^{-n}\frac{1+[3]_{qT}\lambda ^n}{1-\lambda }=\frac{\lambda ^{-n}-\lambda ^{-1}+1-\lambda }{1-\lambda }\nonumber \\&=\lambda +\frac{\lambda ^{-n+1}-1}{1-\lambda } . \end{aligned}$$
(3.8)

These factors are (Laurent) polynomials in \(\lambda \) for any integer n. Moreover, \(F_n(\lambda )\) and \(f_n(\lambda )\) are positive (negative) polynomials for \(n>0\) (\(n<0\)), and \(g_n(\lambda )\) is a positive (negative) polynomials for \(n>1\) (\(n<-1\)). All these polynomials are almost proportional to ordinary quantum numbers \([n]_q\) with \(\lambda \) on the place of q (see the explicit examples in App. B). In addition, (3.8) satisfy certain relations (see App.  A) that allow one to rewrite the evolution formulas as explicitly positive polynomials.

In particular, one can rewrite \(g=1\) answer (3.2) in the form

$$\begin{aligned} \mathcal {X}^{n_0,n_1}&=q^4T\frac{\lambda ^{n_0+n_1}}{\lambda -1}\Big (F_{n_0}F_{n_1}-\lambda ^{-n_1}f_{n_0}g_{n_1}\Big )\nonumber \\&= q^2\lambda ^{n_0+n_1}F_{n_0+n_1}(\lambda ), \end{aligned}$$
(3.9)

so that it depends only on \(n_0+n_1\) (as it should) and literally coincides with the standard Khovanov polynomial (under the considerations from the beginning of Sect. 1.2) of the knot \(\text {Torus}[2,n_1+n_0]\sim \text {Pretzel}(n_0,n_1)\) [50].

Similarly, algebraic manipulations with (3.2) allow one to rewrite it as

$$\begin{aligned} \mathcal {X}_{\text {bulk}_2}^{\text {knots}}&= q^5T\frac{\lambda ^{n_0+n_1}}{1-\lambda }\Big (F_{n_0}(\lambda )F_{n_1}(\lambda )F_{n_2}(\lambda )\nonumber \\&\quad -f_{n_0}(\lambda )f_{n_1}(\lambda )\lambda ^{-n_2}g_{n_2}(\lambda )\Big ) \nonumber \\&=q^3\lambda ^{n_0+n_1}\Big (F_{n_0}(\lambda )F_{n_1}(\lambda )+F_{n_0}(\lambda )g_{n_2}(\lambda )\nonumber \\&\quad +f_{n_1}(\lambda )g_{n_2}(\lambda )\Big ). \end{aligned}$$
(3.10)

The last expression is an explicitly positive polynomial for \(n_0>1\), \(n_1>0\), and \(n_2>1\). Moreover, one can find several equivalent forms of (3.2) with their own domains of explicit positivity (or negativity), so that the union of these domains is exactly the union of all the \(\text {bulk}_a\) regions.

Analogues of (3.10) for other (not bulk-region) evolution formulas for \(g=2\) are presented below. The higher genera evolution formulas reveal very similar structures, but we postpone this for the upcoming work on systematic analysis of these cases.

For \(g > 1\) bulk-regions do not span the whole space, but they still do take a significant (say, greater than 1 / 2) fraction of its volume.

Remark 3.4

In the bulk-regions it doesn’t matter, whether knot is charged or neutral – formula (3.5) interpolates between both possibilities.

Formula (3.5) also does not provide correct answers on the whole parameter space. Already for \(g = 2\) one has torus knots \(\text {Torus}[3,4]\) and \(\text {Torus}[3,5]\) for which there is a discrepancy (typeset in bold)

$$\begin{aligned}&\mathcal {X}{\left( \text {Torus}[3,4] \right) } \equiv \mathcal {X}{\left( \text {Pretzel}[3,3,-2] \right) } \nonumber \\&\quad = q^{13} T^6+q^9 T^4+q^3 T+\varvec{q^7 T^3 + q^7 T^2} \nonumber \\&\mathcal {X}{\left( \text {Torus}[3,5] \right) } \equiv \mathcal {X}{\left( \text {Pretzel}[5,3,-2] \right) } \nonumber \\&\quad = q^{17} T^8 + q^{13} T^6 - q^5 T^2 + \varvec{q}^{\mathbf{11}} \varvec{T}^{\mathbf{5}} + \varvec{q}^{\mathbf{11}} \varvec{T}^\mathbf{{4}} \nonumber \\&\qquad + \varvec{q}^\mathbf{{7}} \varvec{T}^{\mathbf{3}} + \varvec{q}^{\mathbf{7}} \varvec{T}^{\mathbf{2}} + \varvec{q}^{\mathbf{5}} \varvec{T}^{\mathbf{2}} + \varvec{q}^{\mathbf{5}} \varvec{T} \end{aligned}$$
(3.11)

We see that in case of \(\text {Torus}[3,5]\) the mismatch is more severe: the naive bulk answer does not give sign-definite polynomial at all!

Nevertheless, extra bold terms in both \(\text {Torus}[3,4]\) and \(\text {Torus}[3,5]\) are successfully accounted for by the following corrected formulas

$$\begin{aligned}&\mathcal {X}_{\mathrm {bulk_\mathbf {-2}}}^{\text {Pretzel}[3,3,-2]} =\varvec{-T}\mathcal {X}_{\mathrm {bulk_\mathbf {2}}}^{\text {Pretzel}[3,3,-2]} =-q^7\varvec{T^3}\nonumber \\&\quad +Tq^3\big (1+q^4T^2\big )\big (1+q^6T^3\big ),\nonumber \\&\mathcal {X}^{\text {Pretzel}[3,3,-2]}=q^7\varvec{T^2}\nonumber \\&\quad +Tq^3\big (1+q^4T^2\big )\big (1+q^6T^3\big ), \end{aligned}$$
(3.12)

and

$$\begin{aligned}&\mathcal {X}_{\mathrm {bulk_{\mathbf {-2}}}}^{\text {Pretzel}([5,3,-2])} =\varvec{-T}\mathcal {X}_{\mathrm {bulk_{\mathbf {2}}}}^{\text {Pretzel}([5,3,-2])}\nonumber \\&\quad = -q^5\varvec{T^2}\big (1+q^2T+q^{6}T^3\big )\nonumber \\&\qquad +q^7T^3\big (1+q^4T^2\big )\big (1+q^6T^3\big ),\nonumber \\&\mathcal {X}^{\text {Pretzel}([5,3,-2])}\nonumber \\&\quad =q^5\varvec{T}\big (1+q^2T+q^{6}T^3\big )\nonumber \\&\qquad +q^7T^3\big (1+q^4T^2\big )\big (1+q^6T^3\big ). \end{aligned}$$
(3.13)

The bold type indicates above the T powers that are different in the bulk and actual evolution formulas. These factors are responsible for the bold terms in (3.11) and for the cancellation of the negative term for \(\text {Torus}[3,5]\).

Generally, the evolution formulas

$$\begin{aligned}&\mathcal {X}_{\text {pExceptCharged}}^{\text {knots}} = (-T) \mathcal {X}_{\text {bulk}_g}^{\text {knots}} \nonumber \\&\quad + q (1 + T) \frac{1}{(q^{-1} - q T)^g} \prod _{i \ne J} {\left( 1 + [3]_{qt}\lambda ^{n_i + n_J} \right) } \nonumber \\&\mathcal {X}_{\text {mExceptCharged}}^{\text {knots}} = (-T)^{-1} \mathcal {X}_{\text {bulk}_{-g}}^{\text {knots}} \nonumber \\&\quad + q (1 + T^{-1}) \frac{(-T)^g}{(q^{-1} - q T)^g} \prod _{i \ne J} {\left( 1 + [3]_{qt}\lambda ^{n_i + n_J} \right) }. \end{aligned}$$
(3.14)

are valid, respectively, in positive exceptional charged region and negative exceptional charged region, whose shape is

$$\begin{aligned} \left\{ \begin{array}{c} \text {positive} \\ \text {exceptional} \\ \text {charged} \end{array} \right\} \,&: \ n_J \text { is even} \text { and }n_J \le 0 \text { and }n_{i \ne J} > - n_J; \ \ \vec {n} \notin \text {bulk}_g \nonumber \\ \left\{ \begin{array}{c} \text {negative} \\ \text {exceptional} \\ \text {charged} \end{array} \right\} \,&: \ n_J \text { is even} \text { and }n_J \ge 0 \text { and }n_{i \ne J} < - n_J; \ \ \vec {n} \notin \text {bulk}_{-g} \end{aligned}$$
(3.15)

That is, each of the exceptional charged regions consists of \(g+1\) subregions, corresponding to the choice of special direction \(J = 0 \dots g+1\). Moreover, all the knots in the region are charged, since \(n_J\) is even, justifying the name of these regions.

Remark 3.5

Crucial feature of the evolution formulas (3.14) (and of the formulas (3.18) below) is that eigenvalue \(\lambda \) corresponding to the chosen preferred direction J enters all the brackets of the correction term, while eigenvalues corresponding to other, non-preferred, directions each enter precisely one bracket. Hence, if we consider evolution w.r.t just \(n_J\), with other \(n_i\) fixed, then it occurs faster (resulting in extra terms in (3.11)) than would be naively guessed. We call this nimble evolution and hope to study in the future how it manifests itself in the regions of the parameter space we haven’t covered so far.

Remark 3.6

The positive polynomial decomposition over elementary factors (3.8) in the case of \(g=2\), e.g., for the first of formulas (3.14) is

$$\begin{aligned} \mathcal {X}_{\text {pExceptCharged}}^{\text {knots}}{=}q^3 \lambda ^{n_0+n_1+n_2}\big (\lambda ^{n_2}F_{n_0+n_2}F_{n_1+n_2}{+}\varvec{T}F_{n_2}g_{n_2}\big ). \end{aligned}$$
(3.16)

Remarkably, bulk formula (3.2)\(\equiv \)(3.10) is recovered from (3.16) if one substitutes the bold \(\varvec{T}\) with \(-1\), just as we have seen in explicit Examples (3.12, 3.13).

The odd, or neutral, counterpart of the exceptional regions

$$\begin{aligned} \left\{ \begin{array}{c} \text {positive} \\ \text {exceptional} \\ \text {neutral} \end{array} \right\} \,&: \ {n_J \text { is odd} \text { and }n_J \le 1 \text { and }n_{i \ne J} > - n_J}; \ \ \vec {n} \notin \text {bulk}_g\\ \left\{ \begin{array}{c} \text {negative} \\ \text {exceptional} \nonumber \\ \text {neutral} \end{array} \right\} \,&: \ {n_J \text { is odd} \text { and }n_J \ge -1 \text { and }n_{i \ne J} < - n_J}; \ \ \vec {n} \notin \text {bulk}_{-g} \end{aligned}$$
(3.17)

requires for a more complicated description, which we present here only for \(g=2\),

$$\begin{aligned}&\mathcal {X}_{\text {pExceptNeutral}}^{\text {knots}} = (-T) \mathcal {X}_{\text {bulk}_2}^{\text {knots}} \nonumber \\&\quad + q (1 + T) \frac{[3]_{qt}}{(q^{-1} - q T)^2}{\left( 1 + \lambda ^{n_2+1} \right) }{\left( 1 + \lambda ^{n_2-1} \right) } \nonumber \\&\mathcal {X}_{\text {mExceptNeutral}}^{\text {knots}} = (-T)^{-1} \mathcal {X}_{\text {bulk}_{-2}}^{\text {knots}} \nonumber \\&\quad + q (1 + T)\frac{[3]_{qt}(-T)^2}{(q^{-1} - q T)^2}{\left( 1 + \lambda ^{n_2+1} \right) }{\left( 1 + \lambda ^{n_2-1} \right) }. \end{aligned}$$
(3.18)

On very shallow level, the structure of (3.18) is still similar to (3.14). That is, there is still one preferred direction J, and evolution in this direction is nimble. And the correction terms still vanish at \(T = -1\). But understanding the structure of (3.18) on a deeper level, as well as the systematic analysis of higher genera, is the subject for future research. In particular, for \(g > 2\) “bulk” and “exceptional” regions from above do not span the whole parameter space – there are additional regions, where the dependence of the Khovanov polynomial is still to be described.

Remark 3.7

Decomposition over positive polynomial (3.8), e.g., in the first case, is

$$\begin{aligned} \mathcal {X}_{\text {pExceptNeutral}}^{\text {knots}}&=q^3\lambda ^{n_0+n_1+n_2}\Big (\lambda ^{n_2}( F_{n_0+n_2}F_{n_1+n_2-1}\nonumber \\&\quad +\lambda ^{-1}F_{n_0+n_2})+\varvec{T}f_{n_2-1}g_{n_2+1}\Big ). \end{aligned}$$
(3.19)

Again, the substitution of \(-1\) for the bold \(\varvec{T}\) turns (3.19) into bulk formula (3.2)\(\equiv \)(3.10).

Remark 3.8

For \(g=2\) the regions \(\text {bulk}_{\pm 2}\), \(\text {bulk}_{0}\) and positive and negative exceptional charged and neutral regions span the entire space (the \(\text {bulk}_{0}\) is the complement of all other regions). Hence, for \(g=2\) formulas (3.5), (3.14) and (3.18) provide complete description for reduced Khovanov polynomials’ evolution.

Remark 3.9

The double-braid knots, instrumental in finding a relation between inclusive and exclusive Racah matrices [58,59,60,61, 72], are embedded into \(\text {bulk}_2\) region for \(g=2\) as \(\text {Pretzel}[n_0, -1, n_2]\). This is a weak hint that evolution formula (3.2) should be at the core of the (hypothetical) homological analog of the arborescent calculus.

Remark 3.10

While charged exceptional regions, indeed, contain only charged knots, the neutral exceptional regions contain both charged and neutral knots. Namely, they contain those charged knots for which the preferred direction J does not coincide with the direction, which has even winding. For instance, a charged pretzel knot \(\text {Pretzel}[5, -3, 4]\) belongs to positive exceptional neutral region with \(J = 1\) (the distinguished direction), while its only antiparallel braid corresponds to winding \(n_2 = 4\).

Remark 3.11

One may wonder whether choosing the preferred direction in exceptional regions is consistent with topological invariance. Note that topological invariance implies only invariance of the answers w.r.t cyclic permutation of the winding numbers, for example

$$\begin{aligned} \text {Pretzel}[5, -3, 4] = \text {Pretzel}[4, 5, -3] = \text {Pretzel}[-3, 4, 5] \end{aligned}$$
(3.20)

That is, to reproduce these answers one needs to use formula (3.18) with different \(J = 1\), 2 and 0, respectively.

4 Relation between reduced and unreduced Khovanov polynomials

It turns out that in each stratum of the parameter space unreduced polynomials can be recovered from the reduced ones. For genus 2 the description below is exhaustive, while for higher genera we don’t yet know what happens in some of the regions.

The relation betwen reduced (\(\mathcal {X}\)) and unreduced (X) polynomials is particularly simple in bulk-regions

$$\begin{aligned} X_{\text {bulk}_a}^{\text {knots}} = \frac{(1 + q^4 T)}{q^2 (1 + q^2 T)} \mathcal {X}_{\text {bulk}_a}^{\text {knots}} + \frac{q^a (1 + T)}{(1 + q^2 T)} \lambda ^{\text {unorientability}}, \end{aligned}$$
(4.1)

where \(\text {unorientability}\) is a simple combinatorial quantity associated to a planar diagram and is defined in Sect. 5.

In exceptional charged regions it is slightly more complicated, for instance,

$$\begin{aligned} X_{\text {pExceptCharged}}^{\text {knots}} =&\frac{(1 + q^4 T)}{q^2 (1 + q^2 T)} \mathcal {X}_{\text {pExceptCharged}}^{\text {knots}} \nonumber \\&+ \frac{q^{g-1} (1 + T)}{(1 + q^2 T)} \lambda ^{\text {unorientability}} \nonumber \\&+ \frac{q^{1-g} (1 + T)(1+q^4 T)}{(1 + q^2 T) T} \lambda ^{2 n_J} \lambda ^{\text {unorientability}} \end{aligned}$$
(4.2)

Though each individual correction term is very simple, their generic structure is not clear at the moment: more research is needed to clarify the issue.

Since we, in any case, don’t have a generic description, this section is very sketchy, but from what we observe so far, the jumps in unreduced and reduced Khovanov homology occur together – chambers for reduced and unreduced polynomials are the same.

5 Unorientability and framing

Unorientability is defined as follows. Consider checkerboard coloring of the planar diagram (where we’ve denoted colored regions with black circles):

Out of the two possible choices we choose the one that doesn’t contain an infinite region. Now, contributions of different types of crossings to the unorientability are

(5.1)

Throughout the paper, we use a very particular choice of framing (with respect to Bar-Natan’s conventions). This is needed in order to restore the symmetry between different windings \(n_i\), even though some of them correspond to parallel braids and others correspond to antiparallel braids. Namely, the required framing factor is simply \((T q^3)\) to the power of unorientability, which for pretzel knots is equal to sum of windings of parallel-oriented braids:

$$\begin{aligned} \left\{ \begin{array}{c} \text {framing} \\ \text {factor} \end{array} \right\} = {\left( T q^3 \right) }^{\text {unorientability}} = \prod _{i : \begin{array}{c} \text {parallel} \\ \text {braid} \end{array}} {\left( T q^3 \right) }^{n_i} \end{aligned}$$
(5.2)

6 Unreduced Khovanov polynomials for pretzel links

If we consider links, not just knots, and try to interpolate between different answers for unreduced Khovanov polynomials then for the \(\text {bulk}_g\) region we would get

$$\begin{aligned} X_{\text {bulk}_g}&= \frac{(1 + q^4 T) (-T)^{g/2}}{(1 + q^2 T)(1 - q^2 T)} \frac{1}{[2]_{qt}^{g+1}} \nonumber \\&\quad \times {\left( \prod _{i=0}^g {\left( 1 + [3]_{qt} \lambda ^{n_i} \right) } + [3]_{qt} \prod _{i=0}^g {\left( 1 - \lambda ^{n_i} \right) } \right) } \nonumber \\&\quad + \frac{(T + 1)}{2 (1 + q^2 T)} \left( \prod _{i = 0}^g {\left( \frac{q}{2} + \frac{q}{2}(-1)^{n_i} + q (q^2 T)^{n_i} \right) } \right. \nonumber \\&\quad \left. + \prod _{i = 0}^g {\left( \frac{q}{2} + \frac{q}{2}(-1)^{n_i} - q (q^2 T)^{n_i} \right) } \right) \nonumber \\&\quad + \frac{(T + 1)}{(1 + q^2 T)} \prod _{i = 0}^g {\left( -\frac{q}{2} + \frac{q}{2}(-1)^{n_i} \right) } \end{aligned}$$
(6.1)

It is clear that the answer changes abruptly when one changes the number of link components (i.e. the number of windings \(n_i\) that are even).

Namely, if we have an M-component link, then the correction w.r.t the naive arborescent answer is

$$\begin{aligned} \Delta X_{\text {bulk}_g} =&\ \frac{(T + 1)}{2 (1 + q^2 T)} q^{g+1} \lambda ^{\text {unorientability}} \nonumber \\&\quad \times \left( \prod _{C_i< C_j} (1 + \lambda ^{2 \ \text {lk}(C_i, C_j)}) \right. \nonumber \\&\quad \left. + (-1)^{g+1 - M} \prod _{C_i < C_j} (1 - \lambda ^{2 \ \text {lk}(C_i, C_j)}) \right) \nonumber \\&\quad + \frac{(T + 1)}{(1 + q^2 T)} (-q)^{g + 1} \delta _{M,1} \delta _{\text {unorientability},0}, \end{aligned}$$
(6.2)

where we’ve written it in the form that has a chance to generalize beyond the pretzel knots. Here unorientability of a planar diagram is as in Sect. 5, \(\text {lk}(C_i, C_j)\) is the linking number of the link components \(C_i\) and \(C_j\), and products \(\prod _{C_i < C_j}\) run over distinct pairs of link components.

Overall, we see that corrections (6.2) look very differently from the arborescent piece. Hence, rather than trying to find a formula that interpolates between knots and links (with varying number of components), it is much more fruitful to direct attention to formulas for links with fixed number of components. The main focus of the present paper was on knots, but, hopefully, this section shows that answers for links with other number of components are only a little bit more complicated.

7 Different approaches to similar problems

Here we briefly review different papers, that are in some way related to what we do in this paper.

7.1 Khovanov polynomials for genus 2 Prezel knots

An orthogonal research direction to our experimental approach consists in honest symbolic computation of Khovanov polynomials “by hands”, i.e. in honestly deriving formulas like (1.3) and (1.7), rather than getting them via interpolation.

The key point here is that the Khovanov’s complex for an open two strand braid has a simple and explicit description. Moreover, the complexes for the two strand braids can be multiplied (via the operation of so-called horizontal composition) so that a pretzel knot (or link) is obtained, and its Khovanov polynomial can be thus explicitly computed. This plan was gradually implemented for all genus two pretzel knots. Here are the relevant milestones.

Pioneering takes on the problem relied in an essential way on the exact skein sequence and the differential expansion (which substitute the skein relations and the quantum group structure, respectilely).

For quasi-alternating links, which constitute a large fraction of all links at genus two, this resulted in the general Theorem 4.5 of [90] for the unreduced polynomials.

The next step was the explicit computation of unreduced Khovanov polynomials for several infinite series of non-quasi-alternating genus 2 pretzel links [91,92,93]. All these polynomials proved to be homologically thin, and thus similar to the polynomials of the alternating links.

The remaining genus two pretzel links were captured in  [69]. The paper contains the general answer for the unreduced polynomial of a pretzel link. In particular, this answer explicitly shows that some families of the genus 2 pretzel links are homolgically thick, i.e., the corresponding Khovanov polynomials are not fully defined by other invariants.

Hence, this cooperated research provides the complete list of the explicit formulas for the unreduced Khovanov polynomials for genus 2 pretzel links. Yet, the evolution formulas were never presented in a condensed and consice form in these papers, as we do in the present paper. This, we hope, is one of our main contributions to this development, and hopefully will give a clue on how to extend explicit description to higher genera.

7.2 Evolution formulas for Khovanov(-Rozansky) polynomials

The focused study of the evolution of Khovanov–Rozansky polynomials at finite N, to the best of our knowledge, was started in [50]. There, the authors concentrated their attention on the case of torus knots, which, on one hand, allowed them to study Khovanov–Rozansky polynomials, and not just Khovanov (\(N = 2\)) ones, but on the other hand, concealed the full generality of the chamber structure – there the chamber structure took the form of the breaking of the mirror symmetry.

A very interesting aspect of the paper [50] is that the main role is played not by the KR-polynomials themselves, but rather by finite difference equations, that these polynomials satisfy. In the present paper we do not comment on this approach at all, but this dual point of view is a potential source of many new insights.

7.3 Evolution formulas for double-braid knots

Fourth of all, the present paper is the development of [51]. There, also, evolution for Khovanov polynomials (i.e. \(N=2\)) was studied for a concrete family of knots – the double-braid knots (which authors called “figure-eight-like”). The richness of the chamber structure for Khovanov polynomials was already observed there, moreover, answers were proven, not just guessed from computer experiments, as in the present paper. Pretzel knots, considered in the present paper, contain double braid ones, for example, as \(\text {Pretzel}[a,b,1]\). An interesting feature of [51] is that evolution formulas are written for knots and links jointly, which results in appearance of extra eigenvalue. Now, our analysis in Sect. 6 suggests that this point of view is more confusing that it is fruitful – it is much more instructive to consider links with different number of components as different evolution series.

7.4 Superpolynomials of torus knots

Other but closely related objects are superpolynomials for torus knots, studied in [38, 41,42,43,44].

Superpolynomials are, roughly speaking, “stable component” of the Khovanov–Rozansky polynomials. Namely, if one studies Khovanov–Rozansky polynomials for any given knot for different ranks N of the group, for \(N > N^*\) (where \(N^*\) depends on the knot) the dependence on N becomes analytic – polynomial stabilizes. In particular, at the level of superpolynomials evolution method works perfectly, what was further confirmed in the case of twist knots in [10, 11]. Chambers with abrupt changes between them appeared in these considerations, but these changes could be easily ignored in [10, 11] by saying that evolution smoothly connects pure positive polynomials with pure negative ones – what is true in the twist and torus cases. For the first time the seriousness of the chamber problem for superpolynomials was realized in the study of satellite knots in [71]. As we explain in the present paper, the problem is indeed very general, just in the case of pretzels it fully manifests itself for finite N. Thus chamber dependence can be considered as a kind of pronounced

non-perturbative phenomenon, which is strengthened beyond the large-N (loop) expansion – and this is what we study in the present paper.

There are, of course, many more papers that are related to the present work in one way or another. We do not pretend to make a comprehensive review here – we only mention results, which directly affected the motivations and content of the present paper.

8 Conclusion and further directions

In this paper we analyzed the explicit expressions for Khovanov polynomials for pretzel knots of low genera, obtained from computer experiments with the help of [65] (with our custom set of wrappers, which make our life more convenient, but are not necessarily easy to read [66]), and, partly, from direct computations of [70].

We were mainly interested in the fate of the evolution formulas. We observed that chamber structure is very rich for this family of knots. While for some knots (alternating and quasi-alternating) evolution is very simple and just follows from evolution for HOMFLY-PT polynomials, for other knots (the thick pretzel knots) there are non-trivial corrections. But, perhaps, the main surprise and good news is that our suggested formulas (3.14) and (3.18) are still of the shape that is comparable to naive answer (3.2). This gives a hope that some homological generalization of MRT-formalism, or even arborescent calculus, is, indeed, possible. Before, the only multiparametric family of knots, for which such generalization was constructed (on the level of superpolynomials [38, 41,42,43,44]) were torus knots, i.e. generalized was the celebrated Rosso-Jones formula [80,81,82,83,84,85,86].

Apart from generalizing our formulas to higher genera, another obvious research route would be to understand their quadruply-graded homology analogues [94, 95].

Finally, the study of (q,t)-deformed pretzel formulas may be helpful in developing explicit formulas for the Racah matrices (quantum 6j-symbols) themselves. So far even at \(T = -1\) their description is far from being complete (see [96, 97] for current state of art) and it well may be that some aspects become clearer as one goes to \(T \ne -1\).

So far the picture we present is complete only for genera 1 and 2, while already for genus 3 there are regions, where the form of the evolution is still obscure, hence, we can not insist that corrections are always as tame as (3.14) or (3.18). Something more wild is still not excluded. Our work is continuing in these directions.