1 Introduction

Observations made on the dynamics of galaxies indicate a discrepancy between the observed mass of galaxy from dynamics of galaxies and the mass inferred from the existence of luminous matter [1, 2]. It appears that a large part of the mass of the galaxies and thus universe as a whole universe is not visible, this non-luminous missing mass of the universe is known as dark matter [3, 4]. Several models have been proposed for the dark matter, such as axion [5], black holes [6], neutrino [7] and gravitino [8]. However, none of these dark matter models has been verified, and this has led to the development of alternative approaches to explain this discrepancy between the observed and measured rotation of galaxies. These approaches are motivated by a large distance modification of dynamics, such that this modified dynamics can resolve this discrepancy. In fact, it has been demonstrated that by modifying the Newtonian dynamics at galactic scales, it is possible to resolve this discrepancy, and this large distance correction to the Newtonian dynamics is called Modified Newtonian Dynamics (MOND) [9]. Even though the MOND explains the dynamics at galactic scale, it does not correct describe the dynamics at intra-galactic scale, and hence it cannot be used to analyze the clustering of galaxies [10,11,12].

It has also been argued that it is possible to have other modifications to gravity, such as modified theory of gravity (MOG), which do not have this problem, and can explain the clustering of galaxies [13, 14]. In MOG, the field content of general relativity are increased to include scalar, and vector fields, apart from the tensor field [15]. The dynamics of a test particle in MOG are modified by the inclusion of these additional fields. This is because the coupling of the metric to both the scalar and the vector fields, modifies the usual solution to the field equations for a point mass [16]. In fact, the rotation curves of galaxies in MOG have also been analyzed using a static spherically symmetric point mass solution derived from the field equations [17, 18]. The same procedure has been applied to the dynamics of globular clusters [19], clusters of galaxies [20], and the bullet cluster [21]. It has been observed that MOG can explain the dynamics at intra-galactic scales, and hence it can be used to analyze clustering of galaxies. In the weak field approximation, MOG produces the Newtonian potential with and a large distance correction to the Newtonian potential. The weak field approximation of the MOG has been used for analyzing such systems [22,23,24], so in this paper, we will also use the weak field approximation to MOG.

As the intra-galactic distances are much larger than the diameter of individual galaxies, we can approximate the individual galaxies as point particle [25]. So, such a system of galaxies interacting through a potential can be studied using standard techniques of statistical mechanics. In fact, such a system of galaxies interacting thought a Newtonian potential has already been studied using such techniques from statistical mechanics [26,27,28]. It has also been observed that for this system the gravitational clustering can evolve through a sequence of quasi-equilibrium state [26, 29]. Thus, the cosmological many body partition function has been obtained by using an ensemble of co-moving cells containing galaxies interacting through the usual Newtonian potential [30]. It has also been observed that if the cells is smaller than the correlation length, then each member of this ensemble is correlated gravitationally with other cells. So, for such cells, the correlations within a cell is greater than correlations among cells, so that extensivity is a good approximation to study such a system [30, 31]. The techniques of statistical mechanics can also used to analyze the clustering of different types of galaxies. In fact, the clustering of different kind of galaxies has been studied using a multi-component system [32,33,34]. The galaxies in this multi-component system were again assumed to interact through a Newtonian potential.

The clustering has also been studied using the large distance modification of Newtonian potential. It is possible to obtain large distance correction to the Newtonian potential in brane world models [35], and the clustering of galaxies has been studied using such a large distance correction to Newtonian potential [36]. The effects of of cosmological constant on clustering of galaxies has been analyzed, and the thermodynamics for such a system of galaxies has been studied [37]. The cluster of galaxies under the effect of dynamical dark energy has also been studied, and the gravitational partition function for this system has been constructed [38]. This gravitational partition function has been used to analyze the thermodynamics of this system. As the dark energy is dynamical in this model, the time evolution of the clustering parameter is studied using the time dependence of this dynamical dark energy. So, it is both interesting and important to analyze the large distance modification to the clustering of galaxies using standard techniques of statistical mechanics. As MOG produces an phenomenologically important large distance modification of Newtonian potential, in this paper, we will use this MOG modified Newtonian potential to analyze the clustering of galaxies.

2 Modified Newtonian potential

In this section, we obtain the MOG modified potential for a system of different types of galaxies. So, first we will review the weak field approximation of MOG [22,23,24], and then analyze the modification to that potential from the softening parameter which is used for studding the clustering of galaxies [26, 28, 30]. Apart from tensor field, MOG consists of massive vector field \(\phi _\mu \) and three scalar fields, Newton’s constant G, a vector field coupling constant \(\omega \). The mass of the vector filed \(\mu \) acts as scalar fields, and so the mass of the scalar field is a dynamical function in space-time. This theory also contains the self interacting potentials for various field, which can be denoted by \(V_\phi (\phi _\mu \phi ^\mu )\), \(V_G(G)\), \(V(\omega )\) and \(V_\mu (\mu )\). Now the action for MOG can be written as [15, 24],

$$\begin{aligned} S=S_G+S_\phi +S_S+S_M, \end{aligned}$$
(1)

where \(S_G\) is the original Einstein gravity action, \(S_\phi \) is the action of a massive vector field \(\phi \), \(S_S\) is the action of scalar fields, and \(S_M\) is the matter action, which can be considered as pressureless dust. These actions can be expressed as

$$\begin{aligned} S_G&=-\frac{1}{16\pi }\int \frac{1}{G}\left( { R}+2\Lambda \right) \sqrt{-g}~d^4x,\nonumber \\ S_\phi&=-\frac{1}{4\pi }\int \omega \left[ \frac{1}{4}\mathbf{ B^{\mu \nu }B_{\mu \nu }}-\frac{1}{2}\mu ^2\phi _\mu \phi ^\mu + V_\phi (\phi _\mu \phi ^\mu )\right] \sqrt{-g}~d^4x,\nonumber \\ S_S&=-\int \frac{1}{G}\nonumber \\&\times \left[ \frac{1}{2}g^{\alpha \beta }\biggl (\frac{\nabla _\alpha G\nabla _\beta G}{G^2} +\frac{\nabla _\alpha \mu \nabla _\beta \mu }{\mu ^2}\biggr ){+}\frac{V_G(G)}{G^2}{+}\frac{V_\mu (\mu )}{\mu ^2}\right] \sqrt{-g}~d^4x, \nonumber \\ S_M&= \int (- \rho \sqrt{u^\mu u_\mu } - \omega Q_5u^\mu \phi _\mu )\sqrt{-g} dx^4, \end{aligned}$$
(2)

where \(B_{\mu \nu }= \partial _\mu \phi _\nu - \partial _\nu \phi _\mu \), and \(\nabla _\nu \) is covariant derivative with respect to metric \(g_{\mu \nu }\). In matter action \(\rho \) is matter density, and \(Q_5\) is the source of the fifth force, and it is related to matter density as \(Q_5 = \kappa \rho \), where \(\kappa \) is a constant.

To make weak field approximation, we have considered fields as background plus perturbation. The indices (0) and (1) are background and perturbation respectively. Since, there is no gravitational source for vector field \(\phi _{\mu (0)}=0\), and \(\phi _{\mu (1)} \equiv \phi _{\mu }\), the equation of motion for G is given by

$$\begin{aligned} \nabla ^\mu \nabla _\mu G_{(1)} = -\frac{G_{(0)}}{16\pi } R_{(1)}, \end{aligned}$$
(3)

where \(R_{(1)}\) is the perturbation of the Ricci scalar in the forth order. Similarly, we get equation of motion varying the tensor component we get

$$\begin{aligned} R_{\mu \nu (1)} - \frac{1}{2} R_{(1)} \eta _{\mu \nu } = - 8\pi G_0 T_{\mu \nu (1)}^{(M)} - 8\pi G_0 T_{\mu \nu (1)}^{(\phi )} \end{aligned}$$
(4)

where we have considered only first order terms and \(T_{\mu \nu (1)}^{(\phi )}\) is the energy momentum tensor of the vector field

$$\begin{aligned} T_{\mu \nu }^{(\phi )}= & {} \frac{\omega }{4\pi }\left( B_\mu {}^{\alpha } B_{\nu \alpha } - \frac{1}{4} g_{\mu \nu }B^{\alpha \beta }B_{\alpha \beta }\right) \nonumber \\&- \frac{\mu ^2\omega }{4\pi }\left( \phi _\mu \phi _\nu - \frac{1}{2}\phi _\alpha \phi ^\alpha g_{\mu \nu }\right) . \end{aligned}$$
(5)

Here \(T_{\mu \nu (1)}^{(M)}\) is the tensor for matter. Now considering \(T_{\mu \nu (1)}^{(\phi )} \ll T_{\mu \nu (1)}^{(M)}\), we get

$$\begin{aligned} R_{(1)} = 8\pi G_0 T^\mu {}_{\mu (1)}^{(M)}. \end{aligned}$$
(6)

Since we are considering pressureless matter, the energy momentum tensor \(T^\mu {}_{\mu (1)}^{(M)} = \rho \). For the scalar field G, we have

$$\begin{aligned} \nabla ^2\biggl (\frac{G_{(1)}}{G_0}\biggr ) =\frac{1}{2}G_0\rho . \end{aligned}$$
(7)

Here, \(G_{(1)}/G_0\) is of the order of the gravitational potential, and is of the order \((v/c)^2\), where v is the internal velocity of the system. So, for clusters of galaxies, the deviation from the constant \(G_0\) is of the order of \(G_1/G_0\simeq 10^{-7}-10^{-5}\).

For (0, 0) component of first order perturbation of Ricci tensor can be written as

$$\begin{aligned} R_{00(1)} =\frac{1}{2}\nabla ^2 h_{00}, \end{aligned}$$
(8)

and so, the equation of motion is

$$\begin{aligned} \frac{1}{2}\nabla ^2( h_{00}) = -4\pi G_0 \rho . \end{aligned}$$
(9)

The equation of motion for massive vector field is

$$\begin{aligned} \nabla _\nu B^{\mu \nu } - \mu ^2 \phi ^\mu = -\frac{4\pi }{\omega } J^\mu . \end{aligned}$$
(10)

Assuming conservation of the vector matter current, \(\nabla _\mu J^\mu =0\), makes it possible to impose the gauge condition, \(\phi ^\mu {}_{,\mu } = 0\) in the weak field approximation. Thus, for the static case, we can write

$$\begin{aligned} \nabla ^2\phi ^0 -\mu ^2\phi ^0 = -\frac{4\pi }{\omega }J^0, \end{aligned}$$
(11)

and this has the solution,

$$\begin{aligned} \phi ^0(r ) = \frac{1}{\omega }\int \frac{e^{-\mu |\mathbf{r }-\mathbf{r '}|}}{|\mathbf{r }-\mathbf{r '}|}J^0(\mathbf{r '})d^3\mathbf{r '}. \end{aligned}$$
(12)

The field equation for an effective potential in the weak field approximation, can be obtained as follows,

$$\begin{aligned} \nabla \cdot \mathbf{a} - \frac{1}{2}\nabla ^2 h_{00} = - \omega \kappa \nabla ^2\phi ^0, \end{aligned}$$
(13)

where \(\mathbf{a}\) is acceleration of the test particle. An effective potential for the test particle can be defined and given by, \(\mathbf{a} = -\nabla \Phi _{eff}\), and relate it to matter distribution as follows,

$$\begin{aligned} \nabla \cdot (\nabla \Phi _{eff} - \kappa \omega \nabla \phi ^0) = 4\pi G_0\rho . \end{aligned}$$
(14)

The solution to the above Poisson equation, \(\Phi _N\) is given by

$$\begin{aligned} \Phi _{N} = \Phi _{eff} - \kappa \omega \phi ^{0}. \end{aligned}$$
(15)

So, the effective potential can be written as

$$\begin{aligned} \Phi _{eff}(\mathbf{r }) = - \int \frac{G_0 \rho (\mathbf{r '})}{|\mathbf{r }-\mathbf{r '}|}d^3\mathbf{r '} +\kappa ^2\int \frac{\mathrm{e}^{-\mu |\mathbf{r }-\mathbf{r '}|}}{|\mathbf{r }-\mathbf{r '}|}\rho (\mathbf{r '})d^3\mathbf{x'}. \end{aligned}$$
(16)

From the above relation it is clear that there is a repulsive Yukawa force term, in addition to attractive gravitational force. Using the Dirac-delta function \(\rho (\mathbf{r '})= M \delta ^3(\mathbf{r '})\), for a point massive particle the effective potential becomes,

$$\begin{aligned} \Phi _{eff}(r ) = - \frac{G_0 M}{r } + \kappa ^2\frac{M \mathrm{e}^{-\mu r }}{r }, \end{aligned}$$
(17)

where \(r =\vert \mathbf{r }\vert \). Expanding the exponential term for distances compared to \(\mu ^{-1}\), the effective potential becomes

$$\begin{aligned} \Phi _{eff}(r ) = - \frac{(G_0 - \kappa ^2)M}{r } - \mu \kappa ^2 M. \end{aligned}$$
(18)

The first term is the Newtonian gravitational contribution, \(G_0 - \kappa ^2 =G_N\). As at large distances, (\(\mu r \rightarrow \infty \)), we just have the first term of this equation, so \(G_0\) can be identified with the effective gravitational constant at infinity \(G_{\infty }\). The effective potential for an extended distribution of matter in MOG, can be written as [22,23,24]

$$\begin{aligned} \Phi _{eff}(\mathbf{r }) = - G_\infty \left[ \int \frac{\rho (\mathbf{r '})}{|\mathbf{r }-\mathbf{r '}|}\biggl (1 -\frac{G_\infty - G_N}{G_\infty }\mathrm{e}^{-\mu |\mathbf{r }-\mathbf{r '}|}\biggr )d^3\mathbf{r '} \right] . \end{aligned}$$
(19)

So, we can define \(\alpha = (G_\infty - G_N)/G_N\), and write the effective potential as

$$\begin{aligned} \Phi _{eff}(\vec r ) = - G_N \left[ \int \frac{\rho (\vec r ')}{|\vec r -\vec r '|}(1+\alpha -\alpha e^{-\mu |\vec r -\vec r '|})d^3r ' \right] . \end{aligned}$$
(20)

where \(\alpha \) and \(\mu \) can be treated as constant parameters, in the weak field approximation [22,23,24]. Now for a system of galaxies, the MOG modified Newtonian potential between two galaxies, can be written as [15],

$$\begin{aligned} \phi _{i,j}=-\frac{Gm^2}{r_{ij}}\biggl (1+\alpha -\alpha e^{-\mu r}\biggr ), \end{aligned}$$
(21)

It may be noted that, for the point masses, the partition function of galaxies interacting through usual Newtonian potential diverges at \(r_{ij}=0\). This divergence occurs due to the assumption that the galaxies are point like objects. However, this divergence can be removed by taking the extended nature of galaxies into account by introducing a softening parameter which takes care of the finite size of each galaxy [26, 28, 30]. Thus by incorporating the softening parameter the MOG modified interaction potential energy between galaxies can be represented as,

$$\begin{aligned} \phi _{i,j}=-\frac{Gm^2}{(r_{ij}^2+\epsilon ^2)^{1/2}} (1+\alpha -\alpha e^{-\mu {r_{ij}}}). \end{aligned}$$
(22)

This is the potential we will use for analyzing the clustering of galaxies, in this paper.

3 Gravitational partition function

In this section, we will first approximate galaxies as point particles, as the intra-galactic distances are much larger than the galactic scales. However, we will analyze this using a multi-component system as we can have different types of galaxies, with different parameters. The multi-component system has already been used to analyze different types of galaxies interacting though a Newtonian potential [32,33,34], and here we will analyze such a system of galaxies interacting through a MOG modified Newtonian potential. To analyze such a multi-component system, we will first explicitly analyze a three component system, which will consists of \(N_{1}\) galaxies of mass \(m_{1}\), \(N_2\) galaxies of mass \(m_2\) and \(N_3\) galaxies of mass \(m_3\). The partition function for such a system can be expressed as

$$\begin{aligned} Z_{N}(T,V)&= \frac{1}{\Lambda ^{3N}N!}\nonumber \\&\quad \times \int d^{3N_1}p_{i}d^{3N_1}rd^{3N_2}p_{j}d^{3N_2}r^\prime d^{3N_3}p_{k}d^{3N_3}r^{\prime \prime } \nonumber \\&\quad \times exp\biggl (-\biggl [\sum _{i=1}^{N}\frac{p_{i}^2}{2m_1} +\sum _{j=1}^{N}\frac{p_{j}^2}{2m_2}+\sum _{k=1}^{N}\frac{p_{k}^2}{2m_1} \nonumber \\&\quad +\Phi (r_{1},{\ldots }, r_{N_1},r_{1}^\prime ,{\ldots }, r_{N_2}^\prime r_{1}^{\prime \prime },{\ldots }, r_{N_3}^{\prime \prime })\biggr ] T^{-1}\biggr ), \end{aligned}$$
(23)

where N! takes the distinguish-ability of classical galaxies into account, and \(\Lambda \) is the normalization factor which results from integration over momentum space. Now, integrating the momentum space, we obtain the following expression

$$\begin{aligned} Z_{N}(T,V)&= \frac{1}{\Lambda ^{3N}N!}(2\pi m_{1}T)^{3N_{1}/2}(2\pi m_{2}T)^{3N_{2}/2}\nonumber \\&\quad \times (2\pi m_{3}T)^{3N_{3}/2} Q_{N}(N_1,N_2,N_3,T,V), \end{aligned}$$
(24)

where \(Q_{N}(N_1,N_2,T,V)\) is the configurational integral given by [30],

$$\begin{aligned}&Q_{N}(N_1,N_2,N_3,T,V)\nonumber \\&\quad =\int exp\biggl (-\Phi (r_{1},\dots , r_{N_1},r_{1}^\prime ,\dots , r_{N_2}^\prime ,r_{1}^{\prime \prime },\dots , r_{N_3}^{\prime \prime })\biggr ) \nonumber \\&\qquad \times d^{3N_1}rd^{3N_2}r^{\prime }d^{3N_3}r^{\prime \prime } \end{aligned}$$
(25)

where, after taking the softening parameter into account, we have

$$\begin{aligned} \phi _{i,j}=-\frac{Gm^2}{(r_{ij}^2+\epsilon ^2)^{1/2}} (1+\alpha -\alpha e^{-\mu {r_{ij}}}). \end{aligned}$$
(26)

We can use a two particle Mayer function \(f_{ij}=e^{-\Phi _{ij}/T}-1\), such that it vanishes in absence of interactions, and is non-zero only for interacting galaxies and the configurational integral can be expressed in terms of the MOG modified function \(f_{ij}\)

$$\begin{aligned} Q_{N}(T,V)= & {} \int ....\int ((1+f_{12})(1+f_{13})\dots ))\nonumber \\&\times d^{3}r_{1}\dots d^{3}r_{N_1}d^{3}r_{1}^\prime \dots d^{3}r_{N_2}^\prime d^{3}r_{1}^{\prime \prime } \dots d^{3}r_{N_3}^{\prime \prime }\nonumber \\ \end{aligned}$$
(27)

where we have used the MOG modified potential

$$\begin{aligned} f_{ij}=\frac{Gm_{1}m^\prime }{(r^2+\epsilon ^2)^{1/2}}\big (1+\alpha -\alpha e^{-\mu r}\big ). \end{aligned}$$
(28)

It may be noted that this configurational integral has been studied for usual Newtonian gravity [30], however, here we have analyzed the large distance modification to it from MOG. Here \(m^\prime \) can be \(m_{1}\) or \(m_{2}\), and so we can obtain,

$$\begin{aligned} Q_{3}(T,V)&= 4\pi V\int _{0}^{R_{1}}\biggl (1+\frac{Gm_{1}m_{2}}{T}\big [(1+\alpha ) \frac{r^{2}}{(r^{2}+\epsilon ^{2})^{1/2}}\nonumber \\&\quad -\alpha \frac{r^{2}e^{-\mu r}}{(r^{2}+\epsilon ^{2})^{1/2}}\bigr ]\biggr ) \nonumber \\&\quad \times \biggl (1+\frac{Gm_{1}m_{3}}{T}\bigg [(1+\alpha )\frac{r^{2}}{(r^{2} +\epsilon ^{2})^{1/2}}\nonumber \\&\quad -\alpha \frac{r^{2}e^{-\mu r}}{(r^{2} +\epsilon ^{2})^{1/2}}\bigg ]\biggr )drdr^{\prime }dr^{\prime \prime }. \end{aligned}$$
(29)

In order to calculate the integral containing exponential part, we further make an approximation that for small \(\epsilon \), we have \((r^2+\epsilon ^2)^{1/2}=r\), and obtain

$$\begin{aligned} Q_{3}(T,V){=}V^3\left( 1{+}(\alpha _{1}{+}\beta _{1})\frac{m_2}{m_1}x\right) \left( 1{+}(\alpha _{1}+\beta _{1})\frac{m_3}{m_1}x\right) , \end{aligned}$$
(30)

where \(x=\beta \rho T^{-3}\) with \(\beta =(3Gm_{1}^{2}/2)\). The values of \(\alpha _1\) and \(\beta _1\) are given by

$$\begin{aligned} \alpha _1= & {} (1+\alpha )\gamma _{1}, \end{aligned}$$
(31)
$$\begin{aligned} \beta _{1}= & {} -\alpha \gamma _{2}, \end{aligned}$$
(32)

where, we have

$$\begin{aligned} \gamma _{1}= & {} \left( \sqrt{1+\epsilon ^{2}/R_{1}^{2}}+\frac{\epsilon ^2}{R_{1}^2} ln{\frac{\epsilon /R_{1}}{1+\sqrt{1+\frac{\epsilon ^2}{R_{1}^{2}}}}}\right) , \end{aligned}$$
(33)
$$\begin{aligned} \gamma _{2}= & {} \frac{2}{R_{1}^2\mu ^2}(-e^{-\mu R_{1}}(\mu R_{1}+1)+1)). \end{aligned}$$
(34)

By using the scale invariance, \(\rho \rightarrow \lambda ^{-3}\rho \), \(T\rightarrow \lambda ^{-1}T\) and \(r\rightarrow \lambda r\), we obtain

$$\begin{aligned} \frac{3}{2}(Gm^2)^{3}\rho T^{-3}=\beta \rho T^{-3}. \end{aligned}$$
(35)

The general configurational integral for a three component system can be obtained by similar procedure, thus we write expression for general term as

$$\begin{aligned} Q_{N}(T,V)&=V^N\big (1+(\alpha _{1}+\beta _{1})x\big )^{N_1-1}\nonumber \\&\times \left( 1{+}(\alpha _{1}{+}\beta _{1})\frac{m_2}{m_1}x\right) ^{N_2}\! \left( \!1{+}(\alpha _{1}{+}\beta _{1})\frac{m_3}{m_1}x\right) ^{N_3}. \end{aligned}$$
(36)

For \(N_{1}>>1\), we can write the configurational integral as,

$$\begin{aligned} Q_{N}(T,V)&=V^N\big (1{+}(\alpha _{1}{+}\beta _{1})x\big )^{N_1}\nonumber \\&\times \left( 1{+}(\alpha _{1}{+}\beta _{1})\frac{m_2}{m_1}x\right) ^{N_2}\! \left( \!1{+}(\alpha _{1}{+}\beta _{1})\frac{m_3}{m_1}x\right) ^{N_3}. \end{aligned}$$
(37)

For a multi-component system i.e., the system containing \(N_{1}\) galaxies with mass \(m_{1}\), \(N_{2}\) galaxies with mass \(m_{2}\), \(N_{3}\) galaxies with mass \(m_{3}, \ldots ,\) the configurational integral can be generalized as,

$$\begin{aligned} Q_{N}(T,V)=V^N\prod _{l=1}^{s}\left( 1+(\alpha _{1}+\beta _{1})\frac{m_l}{m_1}x\right) ^{N_l}. \end{aligned}$$
(38)

Hence, the gravitational partition function for such a multi-component system given by,

$$\begin{aligned} Z_{N}(T,V)=\frac{1}{N!}\prod _{l}{N_{l}!Z_{N_{l}}}, \end{aligned}$$
(39)

where we can write

$$\begin{aligned} Z_{N_{l}}=\frac{V^{N_{l}}}{\Lambda ^{3N_{l}}N_{l}!}(2\pi m_{l})^{3N_{l}/2}\left( 1+\frac{m_l}{m_1}(\alpha _1+\beta _1)x\right) ^{N_{l}}.\nonumber \\ \end{aligned}$$
(40)

We will use partition function to study thermodynamics of the system.

4 Multi-component system of galaxies

It is possible to study clustering of different types of galaxies using the partition function of a multi-component system, as different types of galaxies can be modeled using a multi-component system [32,33,34]. So, such a partition function can now be used to calculate relevant thermodynamical quantities for the multi-component system of galaxies interacting with MOG potential. First of all, we can write the Helmholtz free energy using the following relation in the canonical ensemble,

$$\begin{aligned} F= & {} -T\ln Z_{N}(T,V) \nonumber \\= & {} -T\ln {\frac{1}{N!}\prod _{l}{N_{l}!Z_{N_{l}}}} \nonumber \\= & {} NT\ln N-NT-T\sum _l \ln N_l+\sum _{l}{F_{l}}. \end{aligned}$$
(41)

where

$$\begin{aligned} \sum _l F_{l}= & {} -\sum _{l}T\ln Z_{N_l}(T,V)\nonumber \\&-\sum _l \biggl (T\ln \biggl (\frac{1}{N_{l}!}\left( \frac{2\pi m_lT}{\Lambda ^2}\right) ^{3N_{l}/2}V^{N_{l}}\nonumber \\&\times \bigg (1+(\alpha _{1} +\beta _{1})\frac{m_l}{m_1}x\bigg )^{N_l}\biggr )\biggr ). \end{aligned}$$
(42)

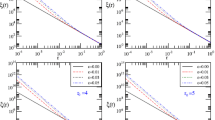
Here, we have made use of Stirling’s approximation, \( \ln N!\approx N\ln N -N. \) We can see behavior of the Helmholtz free energy in terms of temperature by Fig. 1. We assumed different values for \(N_{l}\), and find form the Fig. 1a that its value is important in behavior of F. For \(N_{l} = 3\), the Helmholtz free energy is completely negative. For \(N_{l}=4\), we can see some positive values of F, including a maximum, also a minimum for low temperature case (Fig. 1b). In the case of high temperature, we can find large value for the Helmholtz free energy. The value of the mentioned maximum of the Helmholtz free energy depends on number of components. Increasing number of components, increased value of the Helmholtz free energy at peak. There are some critical temperatures (\(T\approx 0.5\) and \(T\approx 5\) in the Fig. 1b), where the Helmholtz free energy of all multi-component systems are the same. Moreover, the Helmholtz free energy is zero at zero-temperature limit.

Fig. 1
figure 1

Typical behavior of the Helmholtz free energy in terms of T. (a) \(N_{l}=3\) (blue dash), \(N_{l}=4\) (red solid), \(N_{l}=5\) (green dash dot); \(l=1, 2, 3, 4, 5\). (b) \(N_{l}=4\); \(l=1, 2, 3\) (blue dash), \(l=1, 2, 3, 4\) (red solid), \(l=1, 2, 3, 4, 5\) (green dash dot); \(l=1, 2, 3, 4, 5, 6\) (orange dot)

Full size image

Also, the behavior of the Helmholtz free energy in terms of N is shown in Fig. 2. It is clear that the Helmholtz free energy is an increasing function of N. As before, we can see that by increasing number of components, value of the Helmholtz free energy is increased. We also find that the Helmholtz free energy is a decreasing function of \(\alpha \).

Fig. 2
figure 2

Typical behavior of the Helmholtz free energy in terms of N. \(N_{l}=5\); \(l=1, 2, 3\) (blue dash), \(l=1, 2, 3, 4\) (red solid), \(l=1, 2, 3, 4, 5\) (green dash dot); \(l=1, 2, 3, 4, 5, 6\) (orange dot)

Full size image

The entropy S can now be calculated from the Helmholtz free energy,

$$\begin{aligned} S= & {} -\biggl (\frac{\partial F}{\partial T}\biggr )_{N,V} \nonumber \\= & {} -N\ln N+N+\sum _l\ln N_l+\sum _{l}S_l, \end{aligned}$$
(43)

where, we have

$$\begin{aligned} \sum _l S_l&= \sum _l \biggl (N_l\ln \left( \frac{T^{3/2}}{\rho }\right) +N_{l}\ln \left( 1+(\alpha _{1}+\beta _{1})\frac{m_l}{m_1}x\right) \nonumber \\&\quad -3N_l\frac{(\alpha _{1}{+}\beta _{1})\frac{m_l}{m_1}x}{1{+}(\alpha _{1}{+}\beta _{1})\frac{m_l}{m_1}x} {+}\frac{5}{2}N_l+\frac{3}{2}N_l\ln \bigg (\!\frac{2\pi m_l}{\Lambda ^2}\bigg )\biggr ). \end{aligned}$$
(44)

In Fig. 3, we see typical behavior of the entropy. Figure 3a shows that the entropy may be negative at low temperature physics. It may be cause of some instability below a critical temperature. Also, at the critical temperature, all multi-component systems are the same. Figure 3b shows that value of the entropy increases by increasing number of components. Finally, Fig. 3c shows that the entropy is decreasing function of \(\alpha \), by the small variation linearly.

Fig. 3
figure 3

Typical behavior of the entropy in terms of a T, b N and c \(\alpha \). \(N_{l}=3\); \(l=1, 2, 3\) (blue dash), \(l=1, 2, 3, 4\) (red solid), \(l=1, 2, 3, 4, 5\) (green dash dot); \(l=1, 2, 3, 4, 5, 6\) (orange dot)

Full size image

Here, we define the multi-component clustering parameter as,

$$\begin{aligned} B_l=\sum _l\frac{(\alpha _{1}+\beta _{1})\frac{m_l}{m_1}x}{1+(\alpha _{1} +\beta _{1})\frac{m_l}{m_1}x}, \end{aligned}$$
(45)

We see the clustering parameter depends upon the masses of the interacting galaxies. This can be used to study the merging of galaxies. The internal energy \(U = F+TS\) of a multi-component system of galaxies, can now be expressed as,

$$\begin{aligned} U = \sum _l{\frac{3}{2}N_lT\big (1-2B_l\big )}, \end{aligned}$$
(46)

which is independent of N, and decreasing function of \(\alpha \). In the Fig. 4, we can see typical behavior of the internal energy with respect to the temperature. We can see a minimum of energy at low temperature, and large energy at high temperature. However, such minimum has negative internal energy, and negative entropy (Fig. 3b). Hence, we can see negative entropy and internal energy below a critical temperature (\(T_{c}\approx 1\) with fixed parameters as given by figures), which may be sign of thermodynamical instability.

Fig. 4
figure 4

Typical behavior of the internal energy in terms of T. \(N_{l}=5\); \(l=1, 2, 3\) (blue dash), \(l=1, 2, 3, 4\) (red solid), \(l=1, 2, 3, 4, 5\) (green dash dot); \(l=1, 2, 3, 4, 5, 6\) (orange dot)

Full size image

Similarly, we can write the pressure P and chemical potential \(\mu \) as follows,

$$\begin{aligned} P= & {} -\biggl (\frac{\partial F}{\partial V}\biggr )_{N,T} = \sum _l\frac{N_lT}{V}\big (1-B_l\big ), \end{aligned}$$
(47)
$$\begin{aligned} \frac{N\mu }{T}= & {} \biggl (\frac{F}{T}+\frac{PV}{T}\biggr )\nonumber \\= & {} \ln \frac{N!}{\prod N_{l}!}+\sum _l\frac{N_l\mu }{T}, \end{aligned}$$
(48)
$$\begin{aligned} \mu= & {} \frac{T}{N}\left[ N\ln N-N-\sum _l\ln N_l+\sum _l\frac{N_l\mu _{l}}{T}\right] , \end{aligned}$$
(49)

where

$$\begin{aligned} \sum _l\frac{N_l\mu _l}{T}= & {} \sum _l\biggl ( N_l \ln (\rho T^{-3/2}){-} N_l \ln \left( 1{+}(\alpha _{1}{+}\beta _{1})\frac{m_l}{m_1}x\right) \nonumber \\&- N_l \frac{3}{2}\ln \big (\frac{2\pi m_l}{\Lambda ^2}\big )- N_l B_l\biggr ). \end{aligned}$$
(50)

Now Fig. 5 show typical behavior of the chemical potential in terms of T, N, \(\alpha \) and V. In the Fig. 5a we can see that chemical potential is increasing function of the temperature. Also, increasing number of component increases value of the chemical potential. From the Fig. 5b we can see that chemical potential is decreasing function of N. Figure 5c shows that chemical potential is linearly decreasing function of N. Finally, Fig. 5d shows that chemical potential is decreasing function of V.

Fig. 5
figure 5

Typical behavior of the chemical potential in terms of a T, b N, c \(\alpha \) and d V. \(N_{l}=5\); \(l=1, 2, 3\) (blue dash), \(l=1, 2, 3, 4\) (red solid), \(l=1, 2, 3, 4, 5\) (green dash dot); \(l=1, 2, 3, 4, 5, 6\) (orange dot)

Full size image

The probability of finding N galaxies can be written as

$$\begin{aligned} F(N)=\frac{e^{\frac{N\mu }{T}}Z_{N}(V,T)}{Z_{G}(T,V,z)}, \end{aligned}$$
(51)

where \(Z_{G}=zZ_{N}\) and z is the activity.

Thus, for a multi-component system of gravitationally interacting galaxies of different species, we have,

$$\begin{aligned} F(N_1,N_2,\dots N_l)= & {} \prod _l \frac{Z_{N_l}e^{{\frac{N_l \mu }{T}}}}{e^{{{\bar{N}}}_l(1-B_l)}} \end{aligned}$$
(52)

where \(N=N_1+N_2+\dots N_l\). The general distribution of a multi-component system with MOG effect can be written as,

$$\begin{aligned} F(N)= & {} \frac{\bar{N_1}^{N_1}}{N_1!}\biggl (1{+}\frac{N_1}{{{\bar{N}}}_1} \frac{B_1}{(1-B_1)}\biggr )^{N_{1}-1}\biggl (1{+}\frac{B_1}{(1-B_1)}\biggr )^{-N_1} \nonumber \\&\times e^{(-N_1B_1-\bar{N_1}(1-B_1))} \nonumber \\&\times \prod _{2}^l\biggl (\frac{\bar{N_l}^{N_l}}{N_l!}\biggl (1{+}\frac{N_l}{{{\bar{N}}}_l} \frac{B_l}{(1-B_l)}\biggr )^{N_{l}}\biggl (1{+}\frac{B_l}{(1-B_l)}\biggr )^{-N_l} \nonumber \\&\times e^{(-N_lB_l-\bar{N_l}(1-B_l))}\biggr ) \end{aligned}$$
(53)

If all the galaxies are of same mass the result reduces to

$$\begin{aligned} F(N)= & {} \frac{{\bar{N}}^{N}}{N!}\biggl (1+\frac{N}{{{\bar{N}}}} \frac{B}{(1-B)}\biggr )^{N-1}\biggl (1+\frac{B}{(1-B)}\biggr )^{-N} \nonumber \\&\times e^{(-NB-{{\bar{N}}}(1-B))}, \end{aligned}$$
(54)

where, we have

$$\begin{aligned} B=\frac{(\alpha _{1}+\beta _{1})x}{1+(\alpha _{1}+\beta _{1})x}. \end{aligned}$$
(55)

We find that distribution function is increasing function of temperature, while it is a decreasing function of numbers. We also find that clustering parameter decreases value of the distribution function. In the next section the behavior of the above mentioned parameter for the multi-component system is discussed.

We can defined the clustering parameter between the galaxies of different mass components as follow,

$$\begin{aligned} B_l=\sum _l\frac{(\alpha _{1}+\beta _{1})\frac{m_l}{m_1}x}{1+(\alpha _{1} +\beta _{1})\frac{m_l}{m_1}x}, \end{aligned}$$
(56)

We see the clustering parameter depends upon the masses of the interacting galaxies. This can be used to study the merging of galaxies. We can express the parameter x, in terms of the number of galaxies as

$$\begin{aligned} x=\beta \rho T^{-3}=\beta (N_l/N_1){\bar{\rho }}T^{-3}=(N_l/N)y. \end{aligned}$$
(57)

Thus, we can write

$$\begin{aligned} B_l=\sum _l\frac{(\alpha _{1}+\beta _{1})\frac{m_l N_l}{m_1 N_1}y}{1+(\alpha _{1}+\beta _{1})\frac{m_l N_l}{m_1 N_1}y}, \end{aligned}$$
(58)

It may be noted that as, we can express the clustering parameter as

$$\begin{aligned} B_l=b\sum _l\biggl (\frac{1+\alpha (1-\frac{\gamma _{2}}{\gamma _{1}}) \frac{m_lN_l}{m_lN_l}}{1+ \alpha (1-\frac{\gamma _{2}}{\gamma _{1}})\frac{m_lN_l}{m_lN_l}b}\biggr ), \end{aligned}$$
(59)

So, for one component, we have

$$\begin{aligned} B=b\frac{1+\alpha (1-\frac{\gamma _{2}}{\gamma _{1}})}{1+\alpha (1 -\frac{\gamma _{2}}{\gamma _{1}})b}. \end{aligned}$$
(60)

where, b is given by

$$\begin{aligned} b=\frac{\gamma _{1}y}{1+\gamma _{1}y}, \end{aligned}$$
(61)

It is interesting to note that the effect of MOG modified potential enter into the distribution function only through the clustering parameter. Now for attractive potential, we have \(0\le B_l\le 1\). So, it is the deviation of distribution function, which can give an estimate of merging as well as multi-component clustering. Thus, it is possible to study the clustering of galaxies of different masses using a multi-component systems.

5 Conclusion and discussion

In this paper, we have studied the clustering of a system of galaxies interacting thought a MOG modified Newtonian potential. As it is possible for the system of galaxies to have different masses, we have analyzed this system using a multi-component systems. This MOG modified Newtonian potential can be obtained from the weak field approximation of MOG, and we have used it for calculating the partition function of this multi-component system. We compute the partition function, and studied the thermodynamics of this system using that partition function. We also analyzed the general clustering parameter for this multi-component system of galaxies interacting though MOG.

Indeed we have thermodynamical study of clustering of the multi-component systems of galaxies in modified gravity to see how MOG (also number of components) affect thermodynamics quantities. We have shown that clustering parameter decreased value of most important thermodynamics quantities, while number of components increase value of thermodynamics variables. Helmholtz free energy for multi-component system of galaxies is evaluated and the variation Helmholtz free energy F with temperature depends on the value of \(N_l\). When \(N_l = 3\), the F is negative for all values of temperature. For \(N_l = 5\) the Helmholtz free has high positive values and keeps increasing for higher temperatures. For \(N_l = 4\), F has positive values with a minima and a maxima, we notice that changing the values of l the maxima or peak shifts upwards with increasing values of l. We also study the variation of free energy as a function of N, which increases with the value of N, and by increasing the number of components the free energy curve shifts upwards. The entropy of multi-component system of galaxy is also studied, it is seen that it has negative values for low values of temperature, and further increasing the temperatures the entropy becomes positive and keeps increasing. The variation of entropy with N shows that the value of entropy increases initially as a function of N, and then decreases on further increasing the value of N. We also see that in entropy versus N plot, increasing the value of l from 3 to 6, and the over all entropy curve is shifted upwards. To check the dependency of entropy on the parameters \(\alpha \), we plot S as a function of \(\alpha \) and notice that S decreases linearly with increasing value of \(\alpha \). The study of the internal energy of multi-component system of galaxies shows that it depends on the the multi-component clustering parameter, \(B_l\). The behavior of internal energy with respect to temperature is studied, and it is seen that at low temperature the internal energy has a minima. However, as the temperature increases further it increases and takes large values. Chemical potential plays very important role in clustering of galaxies, and it depends on the temperature, \(\alpha \), N and volume, V. The variation of chemical potential with respect to temperature shows that as temperature increases the chemical potential increases and for higher values l, the chemical potential increases rapidly. With N the chemical potential initially drops rapidly for small values of N, and remains almost constant for higher values of N. Furthermore, we notice that, the rate at which \(\mu \) changes for large values of l is slower in comparison to small values of l. The chemical potential decreases linearly as the value of \(\alpha \) increases. The chemical potential decreases logarithmically as the volume of the multi-component system increases. We found that distribution function is increasing function of clustering parameter as well as temperature, while is decreasing function of numbers.