1 Introduction

The quark–gluon plasma (QGP) produced in the Relativistic Heavy-Ion Collider (RHIC) at Brookhaven National Laboratory and Large Hadron Collider (LHC) at CERN provides an opportunity to study the universe at the age of a few microseconds and the different phases of quantum chromodynamics (QCD). The observed QGP is seen to behave more like a near-perfect fluid (a tiny value of \(\eta /s\)) [1,2,3,4,5,6,7,8]. There have been proposed several indirect probes for the QGP in heavy-ion collisions. Among them, collective flow, jet quenching, quarkonia suppression and the suppression of high \(p_T\) hadrons are the most reliable ones indicating the creation of a QGP. The suppression of high \(p_T\) hadrons is mainly caused by the energy loss of moving heavy partons in the QGP medium [9,10,11,12,13,14]. This set the motivation for the present work.

Let us now discuss the current understanding of energy loss due to a fast charged particle in the interacting plasma medium. In classical electrodynamics, the energy loss of a fast-moving charged particle, passing through a plasma is of particular importance in which one can relate the stopping power to the dielectric permittivity of the medium [15]. In QCD, the analog of this problem is the energy loss of high energy partons moving in the hot QCD medium. The high energy partons/heavy quarks that are created in the initial hard scatterings, in ultra-relativistic heavy-ion collisions, pass through the hot and dense matter produced after the collision and lose their energy through various processes (collisions, radiation, etc). Some of the initial investigations primarily involve work by Bjorken, who studied the collisional energy loss suffered by the high energy partons due to the elastic scatterings off thermal quarks and gluons in the QCD plasma [16]. Later on, Thoma and Gyulassy developed a formalism [17] in which they obtained the collisional energy loss in terms of the longitudinal and transverse dielectric functions. In this approach, the infrared divergence is self-regulated due to the collective plasma effects. Within the finite temperature field theory approach, Braaten and Thoma [18, 19] had constructed a systematic framework of the energy loss for both soft and hard momentum transfers [20,21,22]. As the (momentum) anisotropy is present in all the stages of the system expansion, the authors in Refs. [23,24,25,26,27] have studied the anisotropic effects in the context of heavy quarks energy loss. Apart from that, there are several excellent articles in which authors have discussed the energy loss of heavy quarks either through radiative or collisional means [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. Recently, the polarization energy loss of heavy quarks, considering a hot viscous QGP, has also been studied by Jiang et al. [54, 55]. The heavy quarks’ collisional energy loss inside the QGP medium within the framework of the transport approach, employing the finite RTA, has been studied in Ref. [56]. The same with the BGK collisional kernel has been investigated in Ref. [57]. The energy loss of moving heavy quarks has also been studied considering the ADS/CFT approach in Refs. [58,59,60].

Here, we present the study of energy loss of bottom and charm quarks traversing through the isotropic collisional QGP within the effective transport theory approach. The collisions have been modeled using the BGK collisional kernel in the Boltzmann–Vlasov transport equation. Whenever a charged quark passes through the hot QCD medium, it induces the chromo-electric field that generates the Lorentz force which acts back on the moving quark. Hence, the incident quark loses its energy. The induced chromo-electric field is obtained in terms of the longitudinal and transverse parts of the medium’s dielectric permittivity, which, in turn, can be expressed in terms of the gluon selfenergy. The gluon selfenergy has been obtained using the transport theory approach in the Abelian limit. This matches with the one-loop results from the HTL effective theory [61,62,63]. In this limit, one needs to consider a high temperature, where the perturbation theory is relevant. To incorporate the non-ideal hot QCD medium interaction effects in the analysis, the effective fugacity quasi-particle model (EQPM) [64,65,66] is employed which has recently been studied in Refs. [67,68,69]. The results are then compared with those obtained on considering the ideal case (or leading order (LO)). A systematic comparison of the results as regards the energy loss of heavy quarks employing the BGK and RTA kernels (collisions) is presented here.

The paper is organized as follows. In Sect. 2, we shall discuss the energy loss of heavy quarks moving in the hot QCD medium. Here, we shall obtain its expression in terms of dielectric functions using the BGK kernel within a semi-classical transport theory approach. It is important to note that in our previous work [70], we have already calculated the gluon selfenergy using the BGK kernel within the same method. We shall use a few of the results directly from there. In Sect. 3, we shall discuss the various outcomes and provide a comparative analysis. Section 4 is dedicated to the summary and future possibilities of the present work.

2 Energy loss of a moving heavy parton

The motion of a classical color charged particle traversing through the chromodynamic field of a plasma can be described by Wong’s equations [26, 27, 71]. These equations are simply a set of classical equations of motion for a point-like particle interacting with a chromo-dynamical field, which is in the Lorentz covariant form given by

$$\begin{aligned} \frac{dx^{\mu }(\tau )}{d\tau }= & {} u^{\mu }(\tau ), ~~~~~~~\frac{dp^{\mu }(\tau )}{d\tau } =g q^{a}(\tau ) F^{\mu \nu }_{a}(x(\tau ))u_{\nu }(\tau ),\nonumber \\ \frac{dq^{a}(\tau )}{d\tau }= & {} -gf^{abc} u_{\mu }(\tau )A^{\mu }_{b}(x(\tau ))q_{c}(\tau ), \end{aligned}$$
(1)

where \(q^a(\tau )\) is the quark’s color charge, g is the coupling constant and \(F_{a}^{\mu \nu }\) is the chromodynamic field strength tensor. \(\tau \), \(x^{\mu }\) and \(p^{\mu }(\tau )\) are the proper time, trajectory and four momentum of the parton, respectively. The four velocity is \(u^{\mu }=\gamma (1,\mathbf{u})=\frac{p^{\mu }(\tau )}{m}\) (where m is the mass of the particle). Here, we have \(N_{c}^{2}-1\) chromo-electric/magnetic fields which belong to the \(SU(N_c)\) gauge group, \(A^{\mu }_{a}\) is the four potential. The expression of the energy loss can be obtained from Wong’s equations (given in Eq. (1)), following two assumptions. First, we consider the gauge condition \(u_{\mu }A^{\mu }_{a} = 0\) which says that \(q^{a}\) is independent of \(\tau \), and second the quark’s momentum and energy evolve in time without changing the magnitude of its velocity while interacting with the chromodynamic field. Now considering the zeroth component, \(\mu =0\), in the second Wong equation (Eq. (1)) one can obtain the energy loss per unit length:

$$\begin{aligned} -\frac{\text {dE}}{\text {d}\mathbf{x }}=g~q^a ~\frac{\mathbf{u}}{|\mathbf{u}|}\cdot \mathbf{E}^{a}(X). \end{aligned}$$
(2)

The QGP is, in fact, a statistical system and hence, the polarization (\(\mathbf{E}^{a}_{ind}(X)\) ) and fluctuating (\(\mathbf{E}_{fl}^{a}\)) chromo-electromagnetic fields produced at the same time when a heavy quark travels through the QGP. The \(\mathbf{E}^{a}_{ind}(X)\) relates to the external current of the moving heavy quark whereas the randomly fluctuating \(E_{fl}^{a}\) vanishes on the statistical averaging, i.e., \(\left\langle \mathbf{E}_{fl}^{a}\right\rangle =0\). Therefore, the main contribution to the energy loss comes from the polarization of the chromo-electric field that can be expressed as in [17, 22, 56, 57],

$$\begin{aligned} -\frac{\text {dE}}{\text {d}\mathbf{x }}=g~q^a~\frac{\mathbf{u}}{|\mathbf{u}|} \cdot \mathbf{E}_{ind}^{a}(X). \end{aligned}$$
(3)

It is to be noted that the other components (\(\mu =1,2,3\)) are also important to consider while doing the full analysis on the energy loss (such as energy loss due to fluctuations and correlations, etc.). Here, we mainly focus on the polarization energy loss. Therefore, it is sufficient to consider the zeroth component.

To obtain the induced chromo-electric field, we start with the classical Yang–Mills equation in the Lorentz covariant form given by

$$\begin{aligned} \partial _{\mu }F_{a}^{\mu \nu }(X) = J^{\nu }_{a, ind}(X) + J^{\nu }_{a, ext}(X). \end{aligned}$$
(4)

Rewriting the above equation in Fourier space, we obtain

$$\begin{aligned} -iK_{\mu } F'^{\mu \nu }_{a}(K) = J'^{\nu }_{a, ind}(K) + J'^{\nu }_{a, ext}(K), \end{aligned}$$
(5)

where \(K\equiv K^{\mu } =(\omega ,\mathbf{k })\). Now, the induced current, \(J'^{\mu }_{a, ind}(K)\), in the Fourier space can be obtained:

$$\begin{aligned} J'^{\mu }_{a, ind}(K) = \varPi ^{\mu \nu }(K)A'_{\nu , a}(K). \end{aligned}$$
(6)

Here \(\varPi ^{\mu \nu }(K)\) is the gluon selfenergy (or the gluon polarization tensor). Using Eqs. (5) and (6) we get

$$\begin{aligned} \bigg [K^{2} g^{\mu \nu } - K^{\mu } K^{\nu } + \varPi ^{\mu \nu }(K)\bigg ]A'_{\mu ,a}(K) = - J'^{\nu }_{a, ext}(K).\nonumber \\ \end{aligned}$$
(7)

Considering the temporal axial gauge defined by \(A_0=0\) (with \(A^{j}_{a} = \frac{E^{j}_{a}}{i\omega }\)), we can write Eq. (7) in terms of a chromo-electric field as

$$\begin{aligned} \bigg [(k^2-\omega ^2)\delta ^{ij} - k^{i} k^{j} + \varPi ^{ij}(k)\bigg ] E^{j}_{a}(K) = i \omega J'^{i}_{a, ext}(K).\nonumber \\ \end{aligned}$$
(8)

Rewriting the above equation, we have

$$\begin{aligned} {[}\varDelta ^{ij}(K)]^{-1} E^j_{a}(K) = i \omega J'^{i}_{a, ext}(K), \end{aligned}$$
(9)

or

$$\begin{aligned} E^{j}_{a}(K) = i \omega \, \varDelta ^{ij}(K) J'^{i}_{a,ext}(K), \end{aligned}$$
(10)

with

$$\begin{aligned} {[}\varDelta ^{ij}(K)]^{-1} = (k^2-\omega ^2)\delta ^{ij} - k^{i} k^{j} + \varPi ^{ij}(K), \end{aligned}$$
(11)

where \(\varDelta ^{ij}(k)\) is the gluon propagator for the isotropic hot QCD medium. It is important to note that the inclusion of collisions does not change the above expressions (only the form of \(\varPi ^{ij}(K)\) is modified with the effects of collisions as we shall discuss in the next section). The external current, \(\mathbf{J}_{ext}^a(X)\), of a color point charge is given by

$$\begin{aligned} \mathbf{J}_{ext}^a(X)= g~ q^a ~\mathbf{u}~\delta ^3 \left( \mathbf{x}-\mathbf{u}t\right) . \end{aligned}$$
(12)

In Fourier space \(\mathbf{J_{ext}}^a(X)\) reads

$$\begin{aligned} \mathbf{J'}_{ext}^{a}\left( K\right) =\frac{i~ g q^a ~\mathbf{u}}{\omega -\mathbf{k}.\mathbf{u}+i 0^+}. \end{aligned}$$
(13)

Here, we are considering a very near equilibrium situation. Therefore, all the collective modes are damped and the only stationary contribution comes from the pole of \(\mathbf{J'}_{ext}^{a}\left( K\right) \). Next, for the isotropic collisional case, the gluon selfenergy, \(\varPi ^{\mathrm{ij}}(K,\nu )\) relates with the dielectric permittivity, \(\varepsilon ^{ij}(K,\nu )\), thus:

$$\begin{aligned} \varepsilon ^{ij}(K,\nu )=\delta ^{ij}-\frac{1}{\omega ^2}\varPi ^{\mathrm{ij}}(K,\nu ), \end{aligned}$$
(14)

where \(\nu \) is the collision frequency.

The permittivity tensor can be expanded in terms of longitudinal and transverse components by

$$\begin{aligned} \varepsilon ^{\mathrm{ij}}(K,\nu )= A^{ij}~\varepsilon _T(K,\nu )+B^{ij}~\varepsilon _L(K,\nu ), \end{aligned}$$
(15)

with

$$\begin{aligned} A^{\mathrm{ij}}=\delta ^{\mathrm{ij}}-\frac{k^i k^j}{k^2}, ~~~~~B^{\mathrm{ij}}=\frac{k^i k^j}{k^2}. \end{aligned}$$
(16)

Using Eqs. (11), (14) and (15) in (10), and taking the inverse Fourier transformation, the induced chromo-electric field in the coordinate space is obtained:

$$\begin{aligned} \mathbf{E}^{a}_{ind}(X)= & {} -i\frac{gq^{a}}{\pi }\int {d}\omega {d}^3\mathbf{k} \frac{1}{\omega ~ k^2}\bigg [\mathbf{k}~(\mathbf{k}\cdot \mathbf{u}) \left( \varepsilon ^{-1}_L-1\right) \nonumber \\&+ \Big ({k}^2 \mathbf{u}-\mathbf{k}~(\mathbf{k}\cdot \mathbf{u})\Big ) \bigg \{\left( \varepsilon _T-\frac{k^2}{\omega ^{2}}\right) ^{-1}\nonumber \\&-\left( 1-\frac{k^2}{\omega ^2}\right) ^{-1}\bigg \}\bigg ] \frac{e^{ i(\mathbf{k}\cdot \mathbf{x}-\omega t)}}{\omega -\mathbf{k}\cdot \mathbf{u}+i 0^+}. \end{aligned}$$
(17)

Integrating over, \(\omega \) in Eqs. (17) and substituting in Eq. (3), we obtain the energy loss of a heavy parton moving in the hot QCD medium:

$$\begin{aligned} -\frac{\text {dE}}{\text {d}\,\mathbf{x}}= & {} \frac{C_F \alpha _s}{2 \pi ^2 |\mathbf{u}|} \int ^{k_\infty }_{k_0} d^3\mathbf{k}\frac{\omega }{k^2} \bigg \{\left( k^2 |\mathbf{u}|^2-\omega ^2\right) \text {Im}(\omega ^2 \varepsilon _T-k^2)^{-1}\nonumber \\&+\text {Im}\varepsilon ^{-1}_{L}\bigg \}_{\omega =\mathbf{k \cdot u}}, \end{aligned}$$
(18)

where \(\alpha _{s}(T)\) is the QCD running coupling constant at finite temperature [72] and \(C_F =4/3\) is the Casimir invariant in the fundamental representation of the SU(3).

Now to solve Eq. (18), we need to know the form of the transverse and longitudinal components of the dielectric permittivity. We shall discuss this while considering the collisional effects using the BGK kernel in the next subsection.

2.1 Dielectric permittivity in the presence of collisions

As mentioned earlier \(\varepsilon ^{ij}(K,\nu )\) can be obtained within the semi-classical transport theory approach. To do so, one first needs to calculate the gluon selfenergy, \(\varPi ^{ij}(K,\nu )\). The detailed calculations of \(\varPi ^{ij}(K,\nu )\) considering the BGK-collision kernel is provided in our previous work shown in Ref. [70]. There we have given a full calculation of gluon selfenergy for a collisional anisotropic hot QCD medium that can be easily transferred to the isotropic collisional case by equating the anisotropic parameter, \(\xi \) to zero. For the sake of completeness, we shall briefly provide its derivation. We begin with the consideration that the current is induced in the plasma due to a slight deviation, \(\delta f^a(\mathbf{p}, X)\) in the particles’ distribution function from the equilibrium distribution function, \(f^{0}(\mathbf{p})\) such that \( f^{0}(\mathbf{p}) \gg \delta f^a(\mathbf{p}, X)\). The induced current then could be obtained:

$$\begin{aligned} J^{\mu ,a}_{ ind}(X) = g \int \frac{d^{3}{} \mathbf{p}}{(2\pi )^{3}E} p^{\mu }\delta f^{a}(\mathbf{p},X), \end{aligned}$$
(19)

where

$$\begin{aligned} \delta f^{a}(\mathbf{p},X) = 2 N_{c} \delta f_{g}^{a}(\mathbf{p},X) + N_{f} (\delta f_{q}^{a}(\mathbf{p},X) - \delta f_{\bar{q}}^{a}(\mathbf{p},X)).\nonumber \\ \end{aligned}$$
(20)

Here \(\delta f_{g}^{a}(\mathbf{p},x)\), \(\delta f_{q}^{a}(\mathbf{p},x)\) and \(\delta f_{\bar{q}}^{a}(\mathbf{p},x)\) are the fluctuating parts of the gluon, the quark and anti-quark densities, respectively. In the Abelian limit, the fluctuation in the distribution function of each species in the medium can be understood from the Boltzmann–Vlasov [73,74,75,76] transport equation,

$$\begin{aligned} u^{\mu }\cdot \partial ^{X}_{\mu }\delta f_a^i(p,X) +g\theta _{i} u_{\mu }F^{\mu \nu }_a(X)\partial ^p_{\nu }f^{i}(p)=C^i_a(p,X),\nonumber \\ \end{aligned}$$
(21)

where the index i represents the plasma species (quark, anti-quark and gluon). \(\theta _{i}\in \{\theta _g,\theta _q,\theta _{\bar{q}}\}\) have the values \(\theta _{g}=\theta _{q}=1\) and \(\theta _{\bar{q}}=-1\). \(C^i_a(p,X)\) is the collisional kernel which describes the effects of collisions between hard particles in the hot QCD medium. Here, we initially focus on \(C^{i}_a(p,X)\) consiedred to be of BGK-type [73, 74, 77], which is defined by

$$\begin{aligned} C^{i}_a(p,X)=-\nu \left[ f^{i}_a(p,X)-\frac{N^{i}_a(X)}{N^{i}_{\text {eq}}}f^{i}_{\text {eq}}(|\mathbf {p}|)\right] \,, \end{aligned}$$
(22)

where \(\nu \) is the same collision frequency as mentioned earlier. The BGK collision term [77] describes the equilibration of the system, due to the collisions, in a time proportional to \(\nu ^{-1}\). Here, we assume \(\nu \) to be independent of the momentum and particle species. The collision term, \(C^{i}_a(p,X)\) in the special case, \(\frac{N^{i}_a(X)}{N^{i}_{\text {eq}}} \rightarrow 1\) with \(\nu =\frac{1}{\tau }\), \(\tau \) being the relaxation time, gives the form of the RTA kernel. BGK modeling is comparatively more reliable in the sense that it conserves the particle number instantaneously, which is absent in the RTA approach, i.e., while using the BGK kernel we have

$$\begin{aligned} \int \frac{d^{3}p}{(2\pi )^3}C^{i}_a(p,X)=0, \end{aligned}$$
(23)

where the particle number, \(N^{i}_a(X)\) and its equilibrium value, \(N^{i}_{\text {eq}}\) are defined as follows:

$$\begin{aligned}&N^{i}_a(X)=\int \frac{d^{3}p}{(2\pi )^3} f^{i}_a(p,X) , \end{aligned}$$
(24)
$$\begin{aligned}&N^{i}_{\text {eq}} =\int \frac{d^{3}p}{(2\pi )^3} f^{i}_{\text {eq}}(|\mathbf {p}|) = \int \frac{d^{3}p}{(2\pi )^3} f^{i}(\mathbf {p}). \end{aligned}$$
(25)
Fig. 1
figure 1

Energy loss of the charm quark (\(m=1.8~GeV\)) for various values of \(\nu \) at \(T = 2 T_c\) and different Equations of State (EoSs)

Full size image
Fig. 2
figure 2

Energy loss of the bottom quark (\(m=4.5~GeV\)) for various values of \(\nu \) at \(T = 2 T_c\) and different EoSs

Full size image

Next, solving Eq. (21) for \(\delta f^{a}_{q, {\bar{q}}, g}\) in Fourier space and using Eqs. (19) and (6), we obtain the spatial components of the gluon selfenergy, \(\varPi ^{ij}(K)\):

$$\begin{aligned} \varPi ^{ij}(K,\nu )= & {} m_D^2(T)\int \frac{d\varOmega }{4 \pi } u^{i} u^{l}\left\{ u^{j} k^{l}+\left( \omega -\mathbf{k} \cdot \mathbf{u}\right) \delta ^{lj}\right\} \nonumber \\&\times D^{-1}\left( K,\nu \right) , \end{aligned}$$
(26)

where

$$\begin{aligned} D\left( K,\nu \right)= & {} \omega +i \nu -\mathbf{k}\cdot \mathbf{u}. \end{aligned}$$
(27)

The Debye mass, \(m_D\), is given by

$$\begin{aligned} m_D^2= & {} -4 \pi \alpha _{s}(T) \bigg (2 N_c \int \frac{d^3 p}{(2 \pi )^3} \partial _p f_g (\mathbf{p})\nonumber \\&+ 2 N_f \int \frac{d^3 p}{(2 \pi )^3} \partial _p f_q (\mathbf{p})\bigg ). \end{aligned}$$
(28)

Here, we adopt the quasi-particle distribution functions considering the EQPM, \( f_{eq}\equiv \lbrace f_{g}, f_{q} \rbrace \), which describes the strong interaction effects in terms of effective fugacities, \(z_{g,q}\) [64,65,66],

$$\begin{aligned} f_{g/q}= \frac{z_{g/q}\exp [-\beta E_p]}{\bigg (1\mp z_{g/q}\exp [-\beta E_p]\bigg )}, \end{aligned}$$
(29)

where \(E_{p}=|\mathbf{p}|\) for the gluons and \(\sqrt{|\mathbf{p}|^2+m_q^2}\) for the quark degrees of freedom (\(m_q\) denotes the mass of the quarks). The fugacity parameter, \(z_{g/q}\rightarrow 0\), as temperature \(T\rightarrow \infty \). Since the model is valid only in the deconfined phase of QCD (beyond \(T_c\)), the mass of the light quarks can be neglected as compared to the temperature. Next, the \(\varPi ^{ij}(K,\nu )\) can be further decomposed (in the isotropic collisional case) in terms of its longitudinal and transverse parts:

$$\begin{aligned} \varPi ^{\mathrm{ij}}(K,\nu )= A^{ij}~P_T(K,\nu )+ B^{ij}P_L(K,\nu ), \end{aligned}$$
(30)

where the structure constants \(P_T(K,\nu )\) and \(P_L(K,\nu )\) for the isotropic collisional case can be obtained:

$$\begin{aligned} P_T(K,\nu )= & {} \frac{m_D^2~\omega }{4 k^3} \bigg [2 k (\omega +i \nu ) + \Big (k^2+(\nu -i \omega )^2\Big )\nonumber \\&\times \log \Big (\frac{\omega +i \nu +k }{\omega +i \nu -k }\Big )\bigg ], \end{aligned}$$
(31)
$$\begin{aligned} P_L(K,\nu ) =-\frac{\omega ^2 m_D^2 \left( 1-\frac{\omega +i \nu }{2 k} \log \left( \frac{\omega +i \nu +k }{\omega +i \nu -k }\right) \right) }{k^2 \left( 1-\frac{i \nu }{2 k} \log \left( \frac{\omega +i \nu +k }{\omega +i \nu -k }\right) \right) }. \end{aligned}$$
(32)

From Eqs. (14), (15) and (30), one can obtain the longitudinal and transverse part of the dielectric permittivity, respectively:

$$\begin{aligned}&\varepsilon _L(K,\nu )=1- \frac{P_L(K,\nu )}{\omega ^2}, \end{aligned}$$
(33)
$$\begin{aligned}&\varepsilon _T(K)=1- \frac{P_T(K,\nu )}{\omega ^2}, \end{aligned}$$
(34)

which can could be written

$$\begin{aligned} \varepsilon _L(K,\nu )=1+\frac{m_D^2 \left( 2 k-(\omega +i \nu ) \log \left( -\frac{k+i \nu +\omega }{k-i \nu -\omega }\right) \right) }{k^2 \left( 2 k-i \nu \log \left( -\frac{k+i \nu +\omega }{k-i \nu -\omega }\right) \right) }\nonumber \\ \end{aligned}$$
(35)

and

$$\begin{aligned} \varepsilon _T(K,\nu )= & {} 1-\frac{m_D^2}{2~ \omega ~k} \bigg [\frac{(\omega +i \nu )}{k} +\frac{1}{2}\left( 1-\frac{(\omega +i \nu )^2}{k^2}\right) \nonumber \\&\times \log \left( -\frac{k+i \nu +\omega }{k-i \nu -\omega }\right) \bigg ]. \end{aligned}$$
(36)

As mentioned earlier, the RTA kernel can be obtained from the BGK one (given in Eq. (22)) by considering \(\frac{N^{i}_a(X)}{N^{i}_{\text {eq}}}\rightarrow 1\) and \(\nu =\frac{1}{\tau }\), \(\tau \) being the relaxation time. We repeated the whole analysis using the RTA term in Eq. (22) and obtained the longitudinal and transverse part of the dielectric permittivity considering the hot QCD medium:

$$\begin{aligned} \varepsilon _L(K,\nu )=1+\frac{m_D^2~ \omega '}{k^2 \omega } \left( 1-\frac{\omega '}{2 k} \log \left[ \frac{\omega '+k}{\omega '-k}\right] \right) , \end{aligned}$$
(37)
$$\begin{aligned} \varepsilon _T(K,\nu )= & {} 71-\frac{m_D^2}{\omega ^2} \left( \frac{\omega ~ \omega '}{k^2} +\frac{\omega }{2 k} \left( 1-\frac{\omega '^2}{k^2}\right) \right. \nonumber \\&\times \left. \log \left[ \frac{\omega '+k}{\omega '-k}\right] \right) , \end{aligned}$$
(38)

where \(\omega '=\omega +i\nu \). Now, in both cases, using \(\varepsilon _L(K,\nu )\) and \(\varepsilon _T(K,\nu )\) in Eq. (18), one can obtain the energy loss for the heavy quarks (charm and bottom) moving in the isotropic collisional hot QCD medium. In the next section, we shall show and discuss the various plots regarding the energy loss of the charm and bottom quarks against their momenta at different collision frequencies.

3 Results and discussion

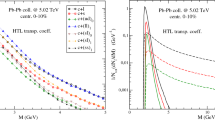
The energy loss of heavy quarks (charm and bottom) moving in the isotropic collisional hot QCD/QGP medium has been studied. In this context, Eq. (18) has been solved numerically. To perform the numerical integration, the lower and upper limits have, respectively, been taken as \(k^{EoSs}_{0}=0\) and \(k^{EoSs}_{\infty }\sim m^{EoSs}_{D}(T)\) for each Equation of State (EoS). The results obtained for the ideal case (or the leading order (LO)) are compared with the non-ideal cases (\((2+1)\) lattice EoS and 3-loop HTL EoS, denoted LB and \(HTL_{pt}\), respectively, in the plots). The different collision frequencies, \(\nu \), have been chosen to investigate their impact on the energy loss and also have been compared with the collision-less case \(\nu =0.0\). Little work considering the LO case using the BGK kernel is already available in the literature [57]. Our numbers for the LO are slightly different. The reason is that in the present case the coupling constant and the Debye mass are not fixed. Instead, they are temperature dependent. Here, we are working at temperature, \(T=2~T_c\) where \(T_c=0.17 ~GeV\).

Fig. 3
figure 3

Energy loss of the charm and bottom quarks at \(T =2 T_c\) and \(\nu =0.0~ \text {and}~ 0.1 m_{D}\) for the leading order case

Full size image

In Figs. 1 and 2, the energy loss of the charm and bottom quarks have been plotted for the collision-less case \(\nu =0\) (left), with collision frequency \(\nu =0.1~m_{D}\) (center) and \(\nu =0.3~m_{D}\) (right), respectively. We have noticed that the energy loss initially increases and then saturates with the increasing particle’s momentum, which matches with the results that are already present in the literature [57]. While considering the non-ideal EoSs (LB and \(HTL_{pt}\)) the energy loss (for both heavy quarks) have been found to be suppressed as compared to the ideal one (LO) at fixed collision frequency. An increase in the collision frequency causes a higher energy loss. In Fig. 3, we compare the energy loss of charm and bottom quarks at \(\nu =0.0 ~\text {and}~0.1~m_{D}\) for the leading order case and observed that the charm quark loses more energy at fixed momentum than the bottom quark. This supports the idea that a heavy particle loses less energy while moving in a medium than the lighter one, given the same conditions.

As mentioned earlier, we also obtained the results using the RTA-collisional kernel to have a comparative study with the BGK case. Mathematically, the difference occurs only in the expressions of the longitudinal and transverse part of the dielectric tensor. The energy loss of charm and bottom quarks using the RTA kernel has been plotted in Fig. 4 and we observed the same patterns as the BGK one at \(\nu = 0.1m_{D}\). In Fig. 5, a comparison between RTA and BGK results is shown for the charm quark (in the upper panel) and the bottom quark (in the lower panel) at \(\nu = 0.1m_{D}\). It has been observed that, given the same momentum and the collision frequency, the energy loss is seen to be higher in the RTA case than in the BGK case.

Fig. 4
figure 4

Energy loss of charm and bottom quark using the RTA kernel at \(\nu = 0.1 m_{D}\) and \(T = 2 T_c\)

Full size image
Fig. 5
figure 5

Comparison of energy loss of the charm and bottom quarks the using BGK and RTA kernels at \(\nu =0.1 m_{D}\) and \(T = 2 T_c\)

Full size image

4 Summary and future aspects

The energy loss of the heavy quarks moving through the isotropic collisional hot QCD medium produced in the relativistic heavy-ion collision experiments has been investigated. The expression of the energy loss is obtained in terms of the longitudinal and transverse part of the dielectric permittivity. Employing the effective kinetic theory in the high-temperature limit (considering the Abelian part) using the BGK kernel, the gluon selfenergy and the dielectric permittivity tensor have been obtained. We found that the energy loss increases initially with the momentum and then saturates. The energy loss also is found to be higher for higher collision frequency. Moreover, the bottom quark is found to lose less energy than the charm quark for the same collision frequency and momentum and, therefore, thermalizes late as compared to the charm quark. We also performed the same analysis considering the RTA kernel and provided a comparative study. It has been observed that the expression of the dielectric permittivity was modified and a slight deviation has been found in the results. Considering the same values of momentum and collision frequency, a higher energy loss is observed in the RTA case than in the BGK case.

We intend to incorporate the momentum anisotropy in the formalism in the near future. The inclusion of viscous effects by employing the effective quasi-particle picture will also be an immediate extension to the present work. In addition, \(R_{AA}\) would be another important quantity to investigate, as it is essential to relate the theoretical estimations with the experimental observations.