Stability of scalarized charged black holes in the Einstein–Maxwell–Scalar theory

Abstract

We analyze the stability of scalarized charged black holes in the Einstein–Maxwell–Scalar (EMS) theory with quadratic coupling. These black holes are labelled by the number of $n=0,1,2,\ldots$, where $n=0$ is called the fundamental black hole and $n=1,2,\ldots$ denote the n-excited black holes. We show that the $n=0$ black hole is stable against full perturbations, whereas the $n=1,2$ excited black holes are unstable against the $s(l=0)$-mode scalar perturbation. This is consistent with the EMS theory with exponential coupling, but it contrasts to the $n=0$ scalarized black hole in the Einstein–Gauss–Bonnet–Scalar theory with quadratic coupling. This implies that the endpoint of unstable Reissner-Nordström black holes with $\alpha >8.019$ is the $n=0$ black hole with the same q. Furthermore, we study the scalarized charged black holes in the EMS theory with scalar mass $m^2_\phi =\alpha /\beta$.

1 Introduction

A scalarization of the Reissner–Nordström (RN) black holes was obtained in the Einstein–Maxwell–Scalar (EMS) theory [1]. The EMS theory is a simple second-order theory providing three kinds of propagating modes of scalar, vector, and tensor around the black hole background. It is worth reminding that the appearance of the scalarized charged black holes is closely connected to the instability of the RN black hole [2]. We note that these black holes are denoted as the $n=0,1,2,\ldots$ black holes with $\alpha$ coupling constant.

All black hole solutions could be linearly tested to confirm that some solutions are selected as black holes in the curved spacetimes. Concerning the stability of scalarized black holes, it was firstly shown that the $n=0$ black hole is stable against $l=0(s$-mode) scalar perturbation, while $n=1,2,\ldots$ black holes are unstable against the s-mode scalar perturbation in the Einstein-Born-Infeld-Scalar theory [3]. As was mention in [4], a difference between exponential and quadratic couplings in the Einstein-Gauss-Bonnet-Scalar (EGBS) theory is that the $n=0$ black hole is stable against radial perturbations for the exponential coupling, while it is unstable for the quadratic coupling. This implies that the $n=0$ black hole could be regarded as the endpoint of the evolution of unstable Schwarzschild black hole for the exponential coupling, whereas this is not the case for the quadratic coupling. Recently, it is argued that the quadratic term controls the onset of the instability giving the $n=0$ black hole, while the higher-order terms including the exponential coupling control the stability of the $n=0$ black hole in the EGBS theory [5]. Very recently, the spontaneous scalarization of black holes and its stability in the EGBS theory were studied by including a massive scalar term for different couplings [6, 7].

For the stability of scalarized black holes in the EMS theory with exponential coupling [8], it is known that the $n=0$ black hole is stable against full perturbations, while $n=1,2$ black holes are unstable against the s-mode scalar perturbation. In this case, the endpoint of unstable RN black holes may be the stable $n=0$ black hole with the same q in the EMS theory with exponential coupling. Hence, it is curious to know the stability issue of the $n=0,1,2$ black holes in the EMS theory with quadratic coupling. In this respect, it is shown that the $n=0$ black hole may be stable in the EMS theory with quadratic coupling by mentioning the positive potentials [9].

In this work, we will study the $n=0,1,2$ scalarized charged black holes in the EMS theory with quadratic coupling by observing the potentials and computing quasinormal mode spectrum. Also, we wish to investigate the scalarized charged black holes in the EMS theory with scalar mass $m^2_\phi =\alpha /\beta$. The full tensor-vector-scalar perturbations will be adopted for the massless case. Observing the potentials around the $n=0,1,2$ black holes and together with computing quasinormal frequencies of the five physical modes, we show that the $n=0$ black hole is still stable against full perturbations, while $n=1,2$ black holes are unstable against the s-mode scalar perturbation in the EMS theory with quadratic coupling. This implies that the endpoint of unstable RN black holes with $\alpha >8.019$ and $q=Q/M=0.7$ may be the $n=0(\alpha \ge 8.019)$ scalarized charged black hole with the same q.

2 $n=0,1,2,\ldots$ black holes

We consider the action of EMS theory with quadratic coupling [1]

$$\begin{aligned} S_\mathrm{EMS}=\frac{1}{16 \pi }\int d^4 x\sqrt{-g}\Big [ R-2\partial _\mu \phi \partial ^\mu \phi -V_\phi -\left( 1+\alpha \phi ^2\right) F^2\Big ], \end{aligned}$$

(1)

where $\alpha$ is a Maxwell-scalar coupling constant and we choose $V_\phi =0$. If one considers a quadratic coupling of $\alpha \phi ^2$, one has to choose $\bar{\phi }=\mathrm{const}$ to obtain the RN black hole with a different charge $\tilde{Q}^2= \bar{\phi }^2 Q^2$. In order to make the analysis clear, here, we choose an equivalent coupling of $1+\alpha \phi ^2$ [9] together with $\bar{\phi }=0$ to give the same RN black hole.

From the action (1), the equations of motion are obtained as

$$\begin{aligned} G_{\mu \nu }=2\partial _\mu \phi \partial _\nu \phi -(\partial \phi )^2g_{\mu \nu }+2T_{\mu \nu } \end{aligned}$$

(2)

with $G_{\mu \nu }=R_{\mu \nu }-(R/2)g_{\mu \nu }$ and $T_{\mu \nu }=(1+\alpha \phi ^2)(F_{\mu \rho }F_{\nu }~^\rho -F^2g_{\mu \nu }/4)$, and the Maxwell equation takes the form

$$\begin{aligned} \nabla ^\mu F_{\mu \nu }-2\alpha \phi \nabla ^{\mu } (\phi )F_{\mu \nu }=0. \end{aligned}$$

(3)

The scalar equation is given by

$$\begin{aligned} \square \phi -\frac{\alpha F^2}{2} \phi =0 . \end{aligned}$$

(4)

We introduce the scalar perturbed equation $[(\bar{\square }+ \alpha Q^2/r^4) \delta \varphi = 0]$ on the RN black hole background

$$\begin{aligned} ds^2_\mathrm{RN}=-\tilde{N}(r)e^{-\tilde{\delta }(r)}dt^2+\frac{dr^2}{\tilde{N}(r)}+r^2\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) \end{aligned}$$

(5)

with

$$\begin{aligned} \tilde{N}(r)=1-\frac{2M}{r}+\frac{Q^2}{r^2},~ \tilde{\delta }(r)=0,~\tilde{\phi }(r)=0,~\tilde{A}_0=\frac{Q}{r}.\nonumber \\ \end{aligned}$$

(6)

We note that this RN background is surely independent of $\alpha$. Considering the separation of variables around the spherically symmetric RN background

$$\begin{aligned} \delta \varphi (t,r,\theta ,\varphi )=\frac{u(r)}{r}e^{-i\omega t}Y_{lm}(\theta ,\varphi ), \end{aligned}$$

(7)

and introducing a tortoise coordinate $r_*$ defined by $dr_*=dr/\tilde{N}(r)$, the perturbed scalar equation is given by

$$\begin{aligned} \frac{d^2u}{dr_*^2}+\Big [\omega ^2-V_\mathrm{ml}(r)\Big ]u(r)=0, \end{aligned}$$

(8)

where the massless potential takes the form

$$\begin{aligned} V_\mathrm{ml}(r)=\tilde{N}(r)\left[ \frac{2M}{r^3}+\frac{l(l+1)}{r^2}-\frac{2Q^2}{r^4}-\alpha \frac{Q^2}{r^4}\right] . \end{aligned}$$

(9)

Actually, (8) is suitable for analyzing the stability of RN black hole.

In order to obtain bifurcation points, one needs to solve the static perturbed equation for $\varphi (r)=u(r)/r$ as

$$\begin{aligned} \frac{1}{r^2}\frac{d}{dr}\left[ r^2 \tilde{N}(r)\frac{d\varphi (r)}{dr}\right] -\left[ \frac{l(l+1)}{r^2}-\frac{\alpha Q^2}{r^4}\right] \varphi (r)=0. \end{aligned}$$

(10)

Here, Eq. (10) describes an eigenvalue problem: for given $l=0$, requiring an asymptotically vanishing, smooth scalar selects a discrete set of the bifurcation points for scalarized solution as $\alpha _n(q=0.7)=\{8.019,~40.84,~99.89,\ldots \}$. In this case, the bifurcation points of the RN solution are the same as those of exponential coupling $e^{\alpha \phi ^2}$ [2, 8] because the static scalar perturbed equation takes the same form as in (10). In Fig. 1, these solutions are classified by the node number n for $\varphi (z)$ with $z=r/(2M)$. Furthermore, n will denote the order number for classifying different branches of scalarized black holes.

Fig. 1

Radial profiles of $\varphi (z)$ as function of $z=r/(2M)$ for the first three perturbed scalar solutions on the RN black hole with $q=0.7$. Here n represents the node number of $\varphi (z)$ and it will denote the order number for labelling different scalarized black holes

To obtain scalarized charged black holes, we have to introduce the spherically symmetric metric ansatz as

$$\begin{aligned} ds^2_\mathrm{SBH}= & {} \bar{g}_{\mu \nu }dx^\mu dx^\nu =-N(r)e^{-2\delta (r)}dt^2+\frac{dr^2}{N(r)}\nonumber \\&+r^2(d\theta ^2+\sin ^2\theta d\varphi ^2) \end{aligned}$$

(11)

with a metric function of $N(r)=1-2m(r)/r$, in addition to electric potential $\bar{A}_0=v(r)$ and scalar field $\bar{\phi }(r)$. We note that scalarized charged black holes could be obtained by restricting an allowable range for $\alpha$. The threshold of instability for the RN black hole is closely related to the appearance of the $n=0(\alpha \ge 8.019)$ black hole. Also, we emphasize that the static scalar perturbation around the RN black hole determines the appearance of $n=1,2\ldots$ black holes.

Plugging (11) into (2)–(4), one has the four equations

$$\begin{aligned}&\quad -2m'(r)+e^{2\delta (r)}\left[ 1+\alpha (\bar{\phi }(r))^2\right] r^2(v'(r))^2\nonumber \\&\quad \quad +[r^2-2rm(r)](\bar{\phi }'(r))^2=0, \end{aligned}$$

(12)

$$\begin{aligned}&\delta '(r)+r(\bar{\phi }'(r))^2=0, \end{aligned}$$

(13)

$$\begin{aligned}&v'(r)\left[ \phantom {\left. +\frac{2r\alpha \bar{\phi }(r)\bar{\phi }'(r)}{1+\alpha \bar{\phi }(r)^2}\right] }2+r\delta '(r)+\frac{2r\alpha \bar{\phi }(r)\bar{\phi }'(r)}{1+\alpha \bar{\phi }(r)^2}\right] +r v''(r)=0, \end{aligned}$$

(14)

$$\begin{aligned}&e^{2\delta (r)}r^2\alpha \bar{\phi }(r)(v'(r))^2+r[r-2m(r)]\bar{\phi }''(r)\nonumber \\&\quad -\left[ m(r)(2-2r\delta '(r))\right. \nonumber \\&\quad \left. +r(-2+r\delta '(r)+2m'(r))\right] \bar{\phi }'(r)=0, \end{aligned}$$

(15)

where the prime ($'$) denotes differentiation with respect to its argument.

Considering the existence of a horizon located at $r=r_+$, one suggests an approximate solution to equations in the near horizon

$$\begin{aligned} m(r)= & {} \frac{r_+}{2}+m_1(r-r_+)+\cdots , \end{aligned}$$

(16)

$$\begin{aligned} \delta (r)= & {} \delta _0+\delta _1(r-r_+)+\cdots , \end{aligned}$$

(17)

$$\begin{aligned} \bar{\phi }(r)= & {} \phi _0+\phi _1(r-r_+)+\cdots , \end{aligned}$$

(18)

$$\begin{aligned} v(r)= & {} v_1(r-r_+)+\ldots , \end{aligned}$$

(19)

where the four coefficients are given by

$$\begin{aligned} m_1= & {} \frac{Q^2}{2r_+^2\left( 1+\alpha \phi _0^2\right) },\nonumber \\ \phi _1= & {} \frac{\alpha \phi _0 Q^2}{r_+\left( \left( 1+\alpha \phi _0^2\right) Q^2-\left( 1+\alpha \phi _0^2\right) ^2r_+^2\right) },\nonumber \\ \delta _1= & {} -r_+\phi _1^2,\quad v_1=-\frac{e^{-\delta _0}Q}{r_+^2\left( 1+\alpha \phi _0^2\right) }. \end{aligned}$$

(20)

This approximate solution involves two parameters of $\phi _0=\phi (r_+)$ and $\delta _0=\delta (r_+)$, which will be found when matching (16)–(19) with the asymptotic solutions in the far region

$$\begin{aligned} m(r)= & {} M-\frac{Q^2+Q_s^2}{2r}+\cdots ,~\bar{\phi }(r)=\phi _\infty +\frac{Q_s}{r}+\cdots , \nonumber \\ \delta (r)= & {} \frac{Q_s^2}{2r^2}+\cdots ,~v(r)=\Phi +\frac{Q}{r}+\cdots , \end{aligned}$$

(21)

where $Q_s$ and $\Phi$ denote the scalar charge and the electrostatic potential, in addition to the ADM mass M and the electric charge Q. For simplicity, we choose $\phi _\infty =0$.

Fig. 2

A scalarized charged black hole solution with $\alpha =8.083$ located in the $n=0 (\alpha \ge 8.019)$ fundamental branch in the EMS theory. This is plotted as a function of $\ln r$ on and outside the horizon at $\ln r$= $\ln r_+=-0.154$

Fig. 3

Two similar graphs for scalar charge $Q_s/\alpha$ vs $M/\alpha$ for the $n=0$ black hole. The $M/\alpha$-axis represents the unstable RN black hole with $q=0.7$ for $0<M/\alpha <0.06$ and the stable RN black hole for $M/\alpha >0.06$. (Left) exponential coupling and (Right) quadratic coupling

Now, let us display a numerical solution with the coupling constant $\alpha = 8.083$ locating on the $n=0(\alpha \ge 8.019)$ fundamental branch in Fig. 2 by solving (12)–(15) together with $q=0.7$ numerically. It is worth noting that the $n=1(\alpha \ge 40.84)$, $2(\alpha \ge 99.89)$ black holes take the similar forms as the $n=0$ case. Actually, we need to obtain hundreds of numerical solution depending $\alpha$ to compute quasinormal modes for full perturbations to each scalarized black hole.

On the other hand, we solve Eq. (12) after replacing $e^{\alpha (\bar{\phi })^2}$ with $1+\alpha (\bar{\phi })^2$ and Eq. (15) after inserting $e^{\alpha (\bar{\phi })^2}$ at the first term to obtain the scalarized RN black holes in the EMS theory with exponential coupling. From Fig. 3, we find that the fundamental branch ($n=0$) of exponential coupling is nearly the same as that of quadratic coupling. Here, both the $n=0$ branches are defined from 0 to $\frac{M}{\alpha }=0.5/8.019\approx 0.06$ where the RN black holes are unstable. For $M/\alpha >0.06$, the scalar hair (scalar charge $Q_s$) disappears and the branch merges with the stable RN branch.

3 EMS theory with scalar mass term

Recently, it was shown that the introduction of a scalar mass term has a significant influence on the bifurcation points where the scalarized black holes branch out of the Schwarzschild black hole in the EGBS theory [6, 7]. In this section, we wish to explore how the introduction of a specific mass term of $V_\phi =2m^2_\phi \phi ^2$ in the EMS theory affects the bifurcation points where the scalarized charged black holes branch out of the RN black hole with $q=0.418$. In general, the presence of a massive scalar term affects significantly the stability of RN black hole and in turn the existence of scalarized charged black holes. A choice of scalar mass $m^2_\phi =\alpha /\beta$ is quite interesting because it does not belong to an independent mass term, but it is given by the combination of coupling parameter $\alpha$ and mass parameter $\beta$. This choice would provide a compact result on the stability.

As a first step, we have to analysis the stability of RN black hole in the EMS theory with mass term based on the perturbed scalar equation

$$\begin{aligned} \left( \bar{\square }-\frac{\alpha }{\beta }+ \frac{\alpha Q^2}{r^4}\right) \delta \varphi = 0 \end{aligned}$$

(22)

because two other linearized equations remain Einstein–Maxwell system for $\bar{\phi }=0$ case. In this case, a radial part of the scalar perturbed equation takes the form

$$\begin{aligned} \frac{d^2u}{dr_*^2}+\left[ \omega ^2-V(r)\right] u(r)=0. \end{aligned}$$

(23)

Here the scalar potential V(r) is given by

$$\begin{aligned} V(r)=\tilde{N}(r)\left[ \frac{2M}{r^3}+\frac{l(l+1)}{r^2}+ \frac{\alpha }{\beta }-\frac{2Q^2}{r^4}-\alpha \frac{Q^2}{r^4}\right] . \end{aligned}$$

(24)

We focus on the $l=0$ mode only since the $s(l=0)$-mode is allowed for the scalar perturbation and it plays the important role in testing the stability of the RN black hole. Also, we emphasize that $V(r) \rightarrow \alpha /\beta$ (positive) as $r\rightarrow \infty$, contrasting to the massless case of $V_\mathrm{ml}(r)\rightarrow 0$ in the EMS theory. This implies that we could not derive the sufficient condition for instability of $\int ^\infty _{r_+} dr V_\mathrm{ml}(r)/\tilde{N}(r)<0$ in the EMS theory because of $\int ^\infty _{r_+} dr V(r)/\tilde{N}(r)\rightarrow \infty$.

On the other hand, observing the potential (24) carefully, the positive definite potential without negative region (sufficient condition for stability) could be implemented by imposing the bound

$$\begin{aligned} \frac{V(r)}{\tilde{N}(r)} \ge 0 \rightarrow \beta \le g(r,\alpha )= \frac{\alpha r^4}{Q^2(\alpha +2)-2Mr}, \end{aligned}$$

(25)

which guarantees a stable RN black hole. This is so because $\tilde{N}(r)\le 0$ for $r\in [r_+,\infty ]$. In Fig. 4, we observe the behavior of $g(r,\alpha )$ function. Minimum value of $g(r,\alpha )$ appears ‘83’ around $r=r_+$ for $\alpha =20,000$. Explicitly, the stability bound can be obtained from $g(r,\alpha )$ and Fig. 4 as

$$\begin{aligned} \beta \le \frac{r_+^4}{Q^2}=83.217, \quad \mathrm{as}~\alpha \rightarrow \infty , \end{aligned}$$

(26)

where any scalarized charged black holes could not be obtained for any $\alpha$ because the appearance of the scalarized charged black holes is closely related to the instability of the RN black hole [2].

Fig. 4

A 3D graph of function $g(r,\alpha )$ for $r\in [r_+=1.995,200]$ and $\alpha \in [0.01,20,000]$. Its minimum stays near $r=r_+=1.9943$ as $\alpha$ increases. The gray strip along the r-axis indicates negative region of $g(r,\alpha )$ and so, it is excluded from consideration

Unfortunately, it is hard to obtain the instability bound from the potential (24) directly. First of all, we wish to find the negative region of potential outside the horizon because it may show a signal of instability. Guided by the stability condition (26), one expects that the negative region appears for $\beta >83.217$ and $\alpha <\infty$. However, some potentials with negative region near the horizon do not always imply the instability. A truly criterion to determine whether a black hole is stable or not against the massive scalar perturbation depends on whether the time-evolution of the perturbation is decaying or not. The linearized equation (23) around a RN black hole may allow for a growing (unstable) mode like $e^{\Omega t}(\Omega >0)$ of the scalar perturbation and thus, it indicates the instability of the black hole. Therefore, we solve (23) directly with appropriate boundary conditions. From Fig. 5, we read off the thresholds $\alpha _\mathrm{th}(\beta )$ of instability depending on $\beta$. Importantly, the instability bound is determined numerically by

$$\begin{aligned} \alpha (\beta ) \ge \alpha _\mathrm{th}(\beta ) \end{aligned}$$

(27)

where $\alpha _\mathrm{th}(\beta )=$174.22(200), 132.51(240), 102.29(300), 82.76(380), and 68.41(500) is exactly the same as the first bifurcation point $\alpha _{n=0}(\beta )$ which is determined when solving the static perturbed equation (23) with $\omega =0$. We find that $\alpha _{n=0}(\beta )$ decreases as $\beta$ increases. It is conjectured that $\alpha _{n=0}(\beta )\rightarrow \infty$, as $\beta \rightarrow 83.217$. In other words, we show that there is no unstable RN black holes for the case of $\beta \le 83.217$, where any scalarized charged black holes could not be found for any $\alpha$.

Fig. 5

Five graphs of $\Omega$ in $e^{\Omega t}$ vs $\alpha$ to determine the thresholds of instability [$\alpha _\mathrm{th}(\beta )$] which are the crossing points at $\alpha$-axis. We read off those as $\alpha _\mathrm{th}(\beta )$ = 174.22(200), 132.51(240), 102.29(300), 82.76(380), and 68.41(500)

Importantly, it is noted that the RN black hole is allowed for any value of $\alpha$, whereas a scalarized charged black hole solution may exist only for $\alpha (\beta )\ge \alpha _\mathrm{th}(\beta )$ for $\beta > 83.217$. A close connection always exists between the instability of a RN black hole and appearance of the $n=0$ scalarized charged black hole in the EMS theory with massive scalar term.

Now, let us derive the $n=0$ scalarized charged black hole which corresponds to the $q=0.418$ and $\alpha (\beta =200) \ge 174.22$ case. Adopting the metric ansatz (11), Eqs. (12)–(15) get modified to include a scalar mass term. The approximate solution in the near horizon is the same form as in (16)–(19) with the same coefficients as $\delta _1$ and $v_1$ in (20) and two different coefficients

$$\begin{aligned}&m_1=\frac{Q^2}{2r_+^2\left( 1+\alpha \phi _0^2\right) }+\frac{\alpha r_+^2\phi _0^2}{2\beta }, \end{aligned}$$

(28)

$$\begin{aligned}&\phi _1=\frac{\alpha \phi _0 Q^2-\alpha \left( 1+\alpha \phi _0^2\right) \phi _0r_+^4/\beta }{r_+(1+\alpha \phi _0^2)\left[ Q^2-r_+^2\left( 1+\alpha \phi _0^2\right) \left( 1-\alpha \phi _0^2r_+^2/\beta \right) \right] },\nonumber \\ \end{aligned}$$

(29)

which lead to (20) in the massless limit of $\beta \rightarrow \infty$.

On the other hand, the asymptotic solution in the far region takes the different form

$$\begin{aligned} m(r)= & {} M-\frac{Q^2}{2r}-\frac{Q_s^2e^{-2\sqrt{\frac{\alpha }{\beta }}r}}{2r^{1+2M\sqrt{\frac{\alpha }{\beta }}}}+\cdots ,\nonumber \\ v(r)= & {} \Phi +\frac{Q}{r}+\frac{e^{-2\sqrt{\frac{\alpha }{\beta }}r}}{r^{ 2M\sqrt{\frac{\alpha }{\beta }}}}\frac{QQ_s^2}{2\sqrt{\alpha \beta }r^4}+\cdots ,\nonumber \\ \delta (r)= & {} Q_s^2\left( 2\sqrt{\alpha /\beta }\right) ^{2+2M\sqrt{\alpha /\beta }}\Gamma \left[ \phantom {\left. -2M\sqrt{\alpha /\beta },2\sqrt{\alpha /\beta }r\right] }-2 \right. \nonumber \\&\quad \left. -2M\sqrt{\alpha /\beta },2\sqrt{\alpha /\beta }r\right] +\cdots , \nonumber \\ \phi (r)= & {} \frac{Q_se^{-\sqrt{\alpha /\beta }r}}{r^{1+M\sqrt{\alpha /\beta }}}+\cdots , \end{aligned}$$

(30)

which lead to (21) except $\bar{\phi }(r)$ in the massless limit of $\beta \rightarrow \infty$. This means that all asymptotic forms are changed under the inclusion of scalar mass term. We wish to display a numerical solution with $\alpha =198.34$ belonging to the $n=0$ fundamental branch in Fig. 6 by solving (12)–(15) together with mass term. Here we observe that N(r) and $\delta (r)$ are similar to those in Fig. 2 of the EMS theory, while $\bar{\phi }(r)$ shows a different asymptotic behavior from the scalar in the EMS theory.

Fig. 6

Plots of a scalarized charged black hole with $\alpha =198.34$ for the $n=0$ fundamental branch of $\alpha (\beta =200) \ge 174.22$ and $q=0.418$ in the EMS theory with massive scalar. These are plotted as a function of r on and outside the horizon at $r_+=1.9943$

4 Full linearized theory

We consider the full perturbed fields around the background quantities

$$\begin{aligned} g_{\mu \nu }= \bar{g}_{\mu \nu }+h_{\mu \nu },\quad A_\mu =\bar{ A}_\mu (r)+a_{\mu },\quad \phi = \bar{\phi }(r) +\delta \phi . \nonumber \\ \end{aligned}$$

(31)

Plugging (31) into Eqs. (2)–(4) leads to complicated linearized equations. Considering ten degrees of freedom for $h_{\mu \nu }$, four for $a_{\mu }$, and one for $\delta \phi$ initially, the EMS theory describing a massless scalar and massless vector-tensor propagations provides five (1 + 2 + 2 = 5) physically propagating modes on the scalarized black hole background. The stability analysis should be based on these physically propagating fields as the solutions to the linearized equations. In a spherically symmetric background (11), the perturbations can be decomposed into spherical harmonics $Y_{lm}(\theta ,\varphi )$ with multipole index l and azimuthal number m. This decomposition splits the tensor-vector perturbations into “axial (A) part” and “polar (P) part”.

We expand the metric perturbations in tensor spherical harmonics under the Regge-Wheeler gauge, providing six degrees of freedom. The axial part $h^\mathrm{A}_{\mu \nu }(t,r,\theta ,\varphi )$ is composed of two radial modes $h_0(r)$ and $h_1(r)$ and the polar part $h^\mathrm{P}_{\mu \nu }(t,r,\theta ,\varphi )$ takes four radial modes [$H_0(r),H_1(r),H_2(r),K(r)$] with time-dependence $e^{-i\omega t}$. Similarly, we decompose the vector perturbations into the axial vector $a^\mathrm{A}_{\mu }(t,r,\theta ,\varphi )$ with single mode $u_4(r)$ and the polar vector $a^\mathrm{P}_{\mu }(t,r,\theta ,\varphi )$ with two modes $u_1(r)$ and $u_2(r)$, giving three degrees of freedom. Lastly, we have a polar scalar perturbation as

$$\begin{aligned} \delta \phi (t,r,\theta ,\varphi )=\int d\omega e^{-i\omega t}\sum _{l,m}\delta \phi _1(r)Y_{lm}(\theta ,\varphi ). \end{aligned}$$

(32)

We note that the linearized equations could be split into axial and polar parts.

In general, the axial part is composed of two coupled equations for Maxwell $\hat{F}(u_4)$ and Regge–Wheeler $\hat{K}(h_0,h_1)$,

$$\begin{aligned} \left[ \frac{d^2}{dr_{*}^2}+\omega ^2\right] \hat{F}(r)= & {} V^\mathrm{A}_\mathrm{FF}(r)\hat{F}(r)+V^\mathrm{A}_\mathrm{FK}(r)\hat{K}(r), \end{aligned}$$

(33)

$$\begin{aligned} \left[ \frac{d^2}{dr_{*}^2}+\omega ^2\right] \hat{K}(r)= & {} V^\mathrm{A}_\mathrm{KK}(r)\hat{K}(r)+V^\mathrm{A}_\mathrm{KF}(r)\hat{F}(r), \end{aligned}$$

(34)

where the potentials are given by

$$\begin{aligned} V^\mathrm{A}_\mathrm{FF}(r)= & {} \frac{N}{r^2 e^{2\delta }}\left[ \phantom {\left. + \frac{\alpha rN\bar{\phi }'}{1+\alpha \bar{\phi }^2}\left( \frac{r\bar{\phi }'}{1+\alpha \bar{\phi }^2}-2\bar{\phi }\right) \right] }e^{2\delta }r^2\left( \phantom {\left. -\frac{\alpha ^2\bar{\phi }^2}{1+\alpha \bar{\phi }^2}\right) }4(1+\alpha \bar{\phi }^2)\right. \right. \nonumber \\&\left. -\frac{\alpha ^2\bar{\phi }^2}{1+\alpha \bar{\phi }^2}\right) (v')^2+l(l+1)\nonumber \\&\left. + \frac{\alpha rN\bar{\phi }'}{1+\alpha \bar{\phi }^2}\left( \frac{r\bar{\phi }'}{1+\alpha \bar{\phi }^2}-2\bar{\phi }\right) \right] , \nonumber \\ V^\mathrm{A}_\mathrm{FK}(r)= & {} V^\mathrm{A}_\mathrm{KF}(r)=-\frac{2\sqrt{1+\alpha \bar{\phi }^2}e^{-\delta }(l-1)(l+2)N v'}{r}, \nonumber \\ V^\mathrm{A}_\mathrm{KK}(r)= & {} \frac{N}{r^2 e^{2\delta }}\left[ (l-1)(l+2)-r N'+N(2+r\delta )\right] .\nonumber \\ \end{aligned}$$

(35)

Here the tortoise coordinate $r_*\in (-\infty ,\infty )$ is defined by the relation of $dr_*/dr= e^\delta /N$. At this stage, it is worth noting that in the limits of $\bar{\phi }=\delta =0$, $V^\mathrm{A}_\mathrm{FF}(r)$, $V^\mathrm{A}_\mathrm{FK}(r)$, and $V^\mathrm{A}_\mathrm{KK}(r)$ recovers those for the RN black hole in the Einstein–Maxwell theory [10]. Here, we will derive the quasinormal modes propagating around $n=0,1,2$ scalarized black holes by solving the two coupled equations directly.

On the other hand, the polar part is composed of six coupled equations for Zerilli (3), Maxwell (2), and scalar (1) as

$$\begin{aligned} K'(r)= & {} -\left( \frac{l(l+1)+2N+2r N'-2}{2r^2}+e^{2\delta }(1+\alpha \bar{\phi }^2)v'^2\right. \nonumber \\&\left. \phantom {\left( \frac{l(l+1)+2N+2r N'-2}{2r^2}+e^{2\delta }(1+\alpha \bar{\phi }^2)v'^2\right. }+N\bar{\phi }'(r)^2\right) H_1(r)\nonumber \\&+\frac{H_0(r)}{r}+\left( \frac{N'}{2N}-\frac{1}{r}-\delta '\right) K(r)-\frac{2\bar{\phi }'}{r}\delta \phi _1(r), \end{aligned}$$

(36)

$$\begin{aligned} H_1'(r)= & {} -\frac{4i(1+\alpha \bar{\phi }^2)v'}{\omega }f_{12}(r)-\frac{H_0(r)+K(r)}{N}\nonumber \\&+\left( \delta '-\frac{N'}{N}\right) H_1(r), \end{aligned}$$

(37)

$$\begin{aligned} H_0'(r)= & {} \left( \frac{1}{r}+2\delta '-\frac{N'}{N}\right) \Big [H_0(r)-K(r)\Big ]\nonumber \\&+\frac{4e^{2\delta }(1+\alpha \bar{\phi }^2)v'}{N}f_{02}(r)+\frac{2\bar{\phi }'}{r}\delta \phi _1(r) \end{aligned}$$

(38)

$$\begin{aligned}&+\left( \frac{e^{2\delta }\omega ^2}{N}-e^{2\delta }(1+\alpha \bar{\phi }^2)v'^2-N\bar{\phi }'^2 \right. \nonumber \\&\left. -\frac{l(l+1)}{2r^2}-\frac{N+rN'-1}{r^2}\right) H_1(r),\nonumber \\ f_{02}'(r)= & {} v'K(r)+\frac{2\alpha \bar{\phi }V'}{r(1+\alpha \bar{\phi }^2)}\delta \phi _1(r) \nonumber \\&+\left( \frac{l(l+1)ie^{-2\delta }N}{r^2\omega }-i\omega \right) f_{12}(r), \end{aligned}$$

(39)

$$\begin{aligned} f_{12}'(r)= & {} -\frac{i\omega e^{2\delta }}{N^2}f_{02}(r)+\left( \delta '-\frac{2\alpha \bar{\phi }\bar{\phi }'}{1+\alpha \bar{\phi }^2}-\frac{N'}{N}\right) f_{12}(r), \end{aligned}$$

(40)

$$\begin{aligned} \delta \phi ''_1(r)= & {} \left[ \frac{e^{2\delta }\alpha (-1+3\alpha \bar{\phi }^2)v'^2}{N(1+\alpha \bar{\phi }^2)}\right. \nonumber \\&+\frac{l(l+1)}{r^2N}-\frac{e^{2\delta }\omega ^2}{N^2}\nonumber \\&+\left. \frac{N'+N(-\delta '+4r\bar{\phi }'^2)}{rN}\right] \delta \phi _1(r)\nonumber \\&+\left( \delta '-\frac{N'}{N}\right) \delta \phi '_1(r)+\frac{2il(l+1)\alpha \bar{\phi }v'}{r\omega }f_{12}(r)\nonumber \\&+\frac{4e^{2\delta }(1+\alpha \bar{\phi }^2)r v'\bar{\phi }}{N}f_{02}(r)\nonumber \\&-\frac{r\left( e^{2\delta }\alpha \bar{\phi }v'^2+(N'-2N\delta ')\bar{\phi }'\right) }{N}H_0(r)\nonumber \\&+\frac{2re^{2\delta }\alpha \bar{\phi }v'^2}{N}K(r) \end{aligned}$$

(41)

with $H_2(r)=H_0(r)$ and $f_{01}(r)=i\omega f_{12}(r)+f'_{02}(r)$. Interestingly, these coupled equations describe three physically propagating modes.

5 Stability Analysis of $n=0,1,2$ black holes

First of all, we wish to mention briefly why the $n=0$ black hole is stable (unstable) against radial perturbations for the exponential (quadratic) coupling in the EGBS theory by providing two kinds of potentials. It is well known that the radial perturbations for $l=0,1$-modes are equivalent to the full perturbations for the same modes. However, this is not true for higher modes of $l=2,3,4,\ldots$ which are necessary to introduce the full perturbations. The EGBS theory [11] is given by

$$\begin{aligned} S_\mathrm{EGBS}=\frac{1}{16 \pi }\int d^4 x\sqrt{-g}\Big [ R-2\partial _\mu \phi \partial ^\mu \phi +\lambda ^2f(\phi )\mathcal{R}^2_\mathrm{GB}\Big ], \end{aligned}$$

(42)

where $\lambda$ is the Gauss-Bonnet coupling constant and $f(\phi )$ is the coupling function defined as

$$\begin{aligned}&\mathrm{exponential:} f(\phi )=\frac{1}{12}(1-e^{-6\phi ^2}); \nonumber \\&\quad \mathrm{quadratic:} f(\phi )=\frac{1}{2}\phi ^2. \end{aligned}$$

(43)

When solving two linearized scalar equations with static ansatz, one obtains a discrete spectrum of parameter $\lambda$ as $M/\lambda = \{0.587, 0.226, 0.140\ldots \}$, which describes the $n=0,1,2,\cdots$ scalarized black holes [12]. From Fig. 7, we observe that the fundamental branch of $n=0$ black hole is a finite region of $0<M/\lambda <0.587$ in the exponential coupling, while it is just a band with bandwidth of $0.587<M/\lambda <0.636$ for quadratic coupling [4, 13]. It is important to note that the latter locates on the stable Schwarzschild black hole bound (outside the fundamental branch for exponential coupling). This points out one of differences between exponential and quadratic couplings in the EGBS theory. Introducing radial (spherically symmetric) perturbations around the scalarized black holes as

$$\begin{aligned} ds^2_\mathrm{EGBS}= & {} -N(r)e^{-2\delta (r)}\left( 1+\epsilon H_0\right) dt^2\nonumber \\&+\frac{dr^2}{N(r)\left( 1 +\epsilon H_1\right) }+r^2\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) ,\nonumber \\ \phi= & {} \bar{\phi }(r)+\epsilon \delta \phi , \end{aligned}$$

(44)

a decoupling process makes a single second order equation for scalar perturbation [4, 14]

$$\begin{aligned} g(r)^2\frac{\partial ^2\delta \phi }{\partial t^2}-\frac{\partial ^2\delta \phi }{\partial r^2} +C_1\frac{\partial \delta \phi }{\partial r}+U(r)\delta \phi =0, \end{aligned}$$

(45)

where g(r), $C_1(r)$ and U(r) are functions of N(r), $\delta (r)$ and $\bar{\phi }(r)$ [4]. Considering a further separation of perturbed scalar $\delta \phi (t,r)=\delta \phi (r)e^{-i\omega t}$, we obtain the Schrödinger equation for scalar perturbation

$$\begin{aligned} \frac{d^2Z}{d r_*^2}=\Big [V(r)-\omega ^2\Big ]Z, \end{aligned}$$

(46)

where $r_*$ is the tortoise coordinate and a redefined scalar perturbation Z(r) reads as

$$\begin{aligned} r_*=\int _{r_+}^\infty g(r) dr,\quad Z(r)=\frac{\delta \phi (r)}{C_0(r)}. \end{aligned}$$

(47)

Fig. 7

Two different graphs of scalar charge $Q_s/\lambda$ vs $M/\lambda$ for the $n=0$ black hole with $r_+=1.174$. The $M/\lambda$-axis represents the unstable Schwarzschild black hole for $0<M/\lambda <0.587$ and and the stable Schwarzschild black hole for $M/\lambda >0.587$ [12]. (Left) exponential coupling has a finite region of $0<M/\lambda <0.587$ which is the unstable bound for Schwarzschild black hole, while (Right) quadratic coupling has a band with bandwidth of 0.587$<M/\lambda<$0.636 which exits within the stable bound for Schwarzschild black hole

Fig. 8

Two scalar potential graphs of $V_0(r,\lambda )$ for s-mode scalar around the $n=0$ black hole with horizon radius $r_+=1.174$. (Left) exponential coupling. (Right) quadratic coupling. The magnification of the enclosed region shows the specific potential behaviors just outside the horizon, indicating negative-positive-negative regions

Importantly, the potential is given by

$$\begin{aligned} V(r)= & {} \frac{U(r)-C_1'(r)}{g(r)^2}+\frac{C_1g'(r)+g''(r)}{g(r)^3}-\frac{2g'(r)^2}{g(r)^4}.\nonumber \\ \end{aligned}$$

(48)

In Fig. 8, we plot the potentials $V_0(r,\lambda )$ for $l=0$-scalar mode around the $n=0$ black hole in the EGBS theory with exponential and quadratic couplings. It is obvious that the potential for exponential coupling is positive outside the horizon, while the potential for quadratic coupling develops negative-positive-negative regions outside the horizon, leading to $\int _{r_+}^\infty V_0(r)g(r)dr<0$ [sufficient condition for instability]. This is the other of differences between exponential and quadratic couplings. Thus, the endpoint of unstable Schwarzschild black holes may be the stable $n=0$ black hole in the EGBS theory with exponential coupling only.

Now let us turn to the stability analysis for the $n=0,1,2$ black holes in the EMS theory. The stability analysis may be performed by getting quasinormal frequency of $\omega =\omega _{r}+i\omega _i$ in $e^{-i\omega t}$ when solving the linearized equations with appropriate boundary conditions at the outer horizon: ingoing waves and at infinity: purely outgoing waves. We will compute the lowest quasinormal modes of the scalarized black holes by making use of a reasonable numerical background and the linearized equations (33)–(34) for axial part and the linearized equations (36)–(41) for polar part. To compute the quasinormal modes, we use a direct-integration method [15].

Usually, a positive definite potential V(r) without any negative region guarantees the stability of black hole. On the other hand, a sufficient condition for instability is given by $\int ^{\infty }_{r_+} dr [e^\delta V(r)/N(r)] <0$ [16] in accordance with the existence of unstable modes. However, some potentials with negative region near the outer horizon whose integral is positive ($\int ^{\infty }_{r_+} dr [e^\delta V(r)/N(r)] >0$) may not imply a definite instability. To determine the instability of the $n=0,1,2$ black holes clearly, one has to solve all linearized equations for physical perturbations numerically. Accordingly, the criterion to determine whether a black hole is stable or not against the physical perturbations is whether the time evolution $e^{-i\omega t}$ of the perturbation is decaying or not. If $\omega _i<0(>0)$, the black hole is stable (unstable), irrespective of any value of $\omega _r$. However, it is not an easy task to carry out the stability of scalarized charged black holes because these black holes comes out as not an analytic solution but numerical solutions. To have a reasonable numerical background, it needs to obtain hundreds of numerical solutions in the each branch. It is convenient to classify the linearized equations according to multiple index of $l=0,1,2,\ldots$ because l determines number of physical fields at the axial and polar sectors.

5.1 $l=0$ case: $n=0,1,2$ black holes

For $l=0$(s-mode), the linearized equation obtained from the polar part is given entirely by a scalar equation $\left( S^\mathrm{P}_0=r \delta \phi _1\right)$

$$\begin{aligned} \left[ \frac{d^2}{dr_{*}^2}+\omega ^2\right] S^\mathrm{P}_0-V^\mathrm{P}_{0}(r,\alpha )S^\mathrm{P}_0=0, \end{aligned}$$

(49)

where the potential $V^\mathrm{P}_\mathrm{0}(r,\alpha )$ is given by [9]

$$\begin{aligned} V^\mathrm{P}_\mathrm{0}(r,\alpha )= & {} \frac{N}{e^{2\delta }r^2}\left[ \phantom {\left. \quad +1-N-2r^2(\bar{\phi }')^2\right] }(N+r(N'-N\delta ')-1)\right. \nonumber \\&\times \Bigg (2r^2\bar{\phi }'^2-\frac{4\alpha \bar{\phi }\bar{\phi }'r^2}{1+\alpha \bar{\phi }^2}\nonumber \\&\quad \left. -\frac{1+\alpha +\alpha \bar{\phi }^2(2-3\alpha +\alpha \bar{\phi }^2)}{(1+\alpha \bar{\phi }^2)^2}\right) \nonumber \\&\left. \quad +1-N-2r^2(\bar{\phi }')^2\right] , \end{aligned}$$

(50)

which is the same form as that obtained by taking radial perturbations [9]. We display three scalar potentials $V^\mathrm{P}_\mathrm{0}(r,\alpha )$ in Fig. 9 for $l=0$ case around the $n=0$ black hole. The whole potentials are positive definite except that the $\alpha =8.65$ case has negative region near the horizon. It does not represent instability because this is near the threshold of instability. Actually, the $n=0$ black hole is stable against the $l=0$ scalar perturbation. We confirm it from Fig. 10 that the imaginary frequency is negative for $\alpha \ge 8.019$, implying a stable $n=0$ black hole. This means that the endpoint of unstable RN black holes with $\alpha >8.019$ is the $n=0(\alpha \ge 8.019)$ scalarized charged black hole with the same q. This is one of our main results.

Now let us turn to the stability issue of the $n=1,2$ black holes. We observe from Fig. 11 that $\int ^{\infty }_{r_+} dr [e^\delta V(r)/N(r)] <0$ for the $n=1$ black hole, while the whole potentials are negative definite for the $n=2$ black hole. This implies that the $n=1,2$ black holes are unstable against the $l=0$ scalar perturbation. Clearly, the instability could be found from Fig. 10 because their imaginary frequencies are positive. Here the red curve denotes the unstable RN black holes as a function of $\alpha >8.091$. Hereafter, we will perform the stability analysis for higher multipoles on the $n=0$ black hole only because the $n=1,$ 2 black holes turned out to be unstable against the $l=0$ scalar perturbation. In other words, it seems meaningless to carry out a further stability analysis for the unstable $n=1,$ 2 black holes.

Fig. 9

Three scalar potential graphs $V^\mathrm{P}_0(r,\alpha )$ for $l=0$ mode around the $n=0(\alpha \ge 8.019)$ black hole. The whole potentials are positive definite except that the $\alpha =8.65$ case having negative region near the horizon does not imply instability

Fig. 10

The negative imaginary frequency $\omega _i$ ($\omega _r=0$) as function of $\alpha$ appears for the $l=0$ scalar around the $n=0$ black hole, implying the stability. Two positive imaginary frequencies $\omega _i$ ($\omega _r=0$) are as functions of $\alpha$ for the $l=0$ scalar around the $n=1,2$ black holes, indicating the instability. A red solid curve with $q=0.7$ represents the quasinormal frequency of $l=0$ scalar mode as function of $\alpha$ around the RN black hole [2], showing the unstable RN black holes for $\alpha >8.019$

Fig. 11

Three scalar potential graphs $V^\mathrm{P}_0(r,\alpha )$ for $l=0$ scalar around (Left) $n=1(\alpha \ge 40.84)$ black hole and (Right) $n=2 (\alpha \ge 99.89)$ black hole

5.2 $l=1$ case: $n=0$ black hole

In this case, we have three physical modes propagating around the $n=0$ black hole. For $l=1$ case, the axial linearized equation around the $n=0$ black hole is given by

$$\begin{aligned} \left[ \frac{d^2}{dr_{*}^2}+\omega ^2\right] Z^\mathrm{A}_1-V^\mathrm{A}_1(r,\alpha )Z^\mathrm{A}_1=0, \end{aligned}$$

(51)

where the potential takes the form

$$\begin{aligned} V^\mathrm{A}_1(r,\alpha )= & {} -\frac{e^{-2\delta } N}{r^2}\Big [N\Big (4-\alpha ^2\bar{\phi }^2+\alpha r(\bar{\phi }^2)'\nonumber \\&-r^2(\alpha -4+2\alpha ^2\phi ^2)(\bar{\phi }')^2\Big )\nonumber \\&-6+4r N'+\alpha ^2\bar{\phi }^2(1-r N')\Big ] \end{aligned}$$

(52)

We find that all potentials are positive definite for the $n=0(\alpha \ge 8.019)$ black hole. This means that the $n=0$ black hole is stable against the axial $l=1$ vector perturbation. We confirm it by showing that $\omega _i$ is negative, indicating a stable black hole.

Finally, we obtain the vector-led and scalar-led modes propagating around the n=0 black hole by solving the polar $l=1$ linearized equations (36)–(41). We find that $\omega _i$ of vector-led mode around the $n=$0 is negative, implying a stable black hole. Also, it is found that $\omega _i$ of scalar-led mode around the $n=0$ black hole is negative, implying a stable black hole.

5.3 $l=2$ case: $n=0$ black hole

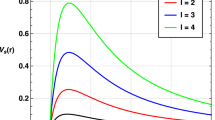
First of all, we consider the axial part because of its simplicity. The axial $l=2$ linearized equations are given by two coupled equations for Regge-Wheeler-Maxwell system as shown in (33)–(34). Solving these coupled equation with boundary conditions leads to negative quasinormal frequencies $\omega _i$ for $l=2$ vector-led mode around the $n=0$ black hole, implying stable black hole. Also, we find that the $n=0$ black hole is stable against the $l=2$ gravitational-led mode.

Finally, the polar $l=2$ linearized equations are given by Eqs. (36)–(41) with $l=2$. Here we have three modes: vector-led, gravitational-led, and scalar-led modes. We find that all $\omega _i$ of these modes are negative, implying the stable $n=0$ black hole.

6 Summary and discussions

First of all, it was shown in the EGBS theory that the $n=0$ black hole is stable against radial perturbations for the exponential coupling, while it is unstable for the quadratic coupling. In the former case, the $n=0$ black hole could be regarded as the endpoint of the evolution of unstable Schwarzschild black hole, whereas this is not the case for the latter. We wish to point out the differences between exponential and quadratic couplings for the $n=0$ black hole (fundamental blanch) in the EGBS theory. We observe from Fig. 7 that the fundamental branch of $n=0$ black hole is a finite region of $0<M/\lambda <0.587$ in the exponential coupling, while it is just a band with bandwidth of $0.587<M/\lambda <0.636$ for quadratic coupling where locates within the stable Schwarzschild black hole bound (beyond the fundamental branch for exponential coupling). This is one difference between exponential and quadratic couplings in the EGBS theory. Also, it is shown from Fig. 8 that the potential for exponential coupling is positive outside the horizon, while the potential for quadratic coupling develops negative-positive-negative regions outside the horizon, leading to $\int _{r_+}^\infty V_0(r)g(r)dr<0$ [sufficient condition for instability]. This corresponds to the other difference between exponential and quadratic couplings for the $n=0$ black hole in the EGBS theory.

Concerning the EMS theory with scalar mass $m^2_\phi =\alpha /\beta$, there is no unstable RN solution with $q=0.418$ for $\beta \le 83.217$ as $\alpha \rightarrow \infty$. This implies that for $\beta \le 83.217$, any scalarized charged black holes could not found for any $\alpha$. On the other hand, we may develop the $n=0,1,2,\ldots$ scalarized charged black holes for the case of $\beta > 83.217$ without limitation on number of bifurcation points even though the mass term changes significantly the location of bifurcation points. We have found the $n=0$ scalarized charged black hole solution from the EMS theory with scalar mass term whose metric functions are similar to those in the $n=0$ scalarized black hole obtained from the EMS theory. It is emphasized that the scalar is different from that found in the EMS theory. However, the stability analysis of the $n=0$ scalarized charged black hole in the EMS theory with scalar mass term seems to be a difficult and complicated task and thus, we could not report its result on this work. This is mainly due to difficulty in handling the asymptotic boundary conditions.

We have shown that the $n=1(\alpha \ge 40.84),2(\alpha \ge 99.89)$ excited black holes are unstable against against the $l=0$ scalar perturbation, while the $n=0(\alpha \ge 8.019)$ fundamental black hole is stable against all scalar-vector-tensor perturbations in the EMS theory with quadratic coupling. In the latter, we found all negative quasinormal frequencies ($\omega _i<0$) of $9=1(l=0)+3(l=1)+5(l=2)$ physical modes around the $n=0$ black hole. In other words, we could not find any unstable modes from the $l=0,1,2$ scalar-vector-tensor perturbations around the $n=0$ black hole. Even though we have carried out the stability analysis on the $n=0$, 1, 2 black holes, we expect from Fig. 10 that the other higher excited ($n=$3, 4, 5, $\ldots$) black holes are unstable against the $s(l=0)$-mode scalar perturbation because their frequencies may exist as further branches along the unstable RN black holes. This is consistent with those for the EMS theory with exponential coupling [8], but it contrasts to the $n=0$ scalarized black hole found in the ESGB theory with quadratic coupling when making use of radial perturbations [4]. Actually, the $n=0$ black hole found in the ESGB theory with exponential coupling has a similar property found in the EMS theory with exponential and quadratic couplings (See Figs. 3, 7). This implies that the endpoint of unstable RN black holes with $\alpha >8.019$ is the $n=0$ scalarized black hole with the same $q=0.7$ in the EMS theory with quadratic and exponential couplings.