Three-quark force effect in proton–proton scattering at 7, 8 and 13 TeV

Abstract

Considering that the proton has an outer pion cloud of radius $\sim 0.87$ fm and an inner core of radius $\sim 0.44$ fm where the valence three quarks are confined and in the framework of optical limit approximation of Glauber, the proton–proton elastic scattering differential cross section, total cross section, the ratio of real part to imaginary part of elastic scattering amplitude in the forward direction, the total elastic and inelastic cross sections are calculated for LHC energy at $\sqrt{s}=7,\;8,\;13$ TeV. The three-quark force is included. A good agreement is obtained with the experimental data at LHC energy 7, 8 and 13 TeV of last measurements of TOTEM Collaborations. Only for the differential cross section a disagreement is obtained for $q^{2}>1\;(\mathrm{GeV}/c)^{2}$, where the complete Glauber polynomial is needed. We tried to confirm the results of radii of two- and three-quark force and the gluon quant energy which were obtained before at ISR energy.

1 Introduction

The results of measurements of proton–proton elastic scattering data at 7, 8, 13 TeV by TOTAM and ATLAS Collaboration [1,2,3,4,5,6,7,8,9,10] are in the focus of attention of researcher at the last few years. Different models with different basis and different degree of agreement with the experimental data of LHC energy [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] were suggested and used. Therefore, we need more studies at this range of energy.

Since in the previous our work [26] we obtained a good agreement with p–p elastic scattering data of ISR energy at $\sqrt{s}=19.42-53$ GeV by using optical limit approximation of Glauber theory [27], we try to use the same approximation to discuss the results of TOTEM measurements of LHC energy at $\sqrt{s}=7,\;8,\;13$ TeV [1,2,3,4,5,6,7,8]. In the present paper we will calculate the p–p elastic scattering differential cross section $d\sigma /dq^{2}$, total cross section $\sigma _t$, the ratio $\rho$ of real part to imaginary part of elastic scattering amplitude in the forward direction, the total elastic and inelastic cross sections $\sigma _{el}$ and $\sigma _{in}$, respectively. In these calculations, the three-quark force is considered using the same approach in [26]. We try to confirm the results of the radii of two- and three-quark force and the gluon quant energy which were obtained at ISR energy.

2 The model

We consider that the proton consists of an outer pion cloud of radius $\sim 0.87\ \hbox {fm}$ and an inner core of radius $\sim 0.44\, \hbox {fm}$ where the valence three quarks are confined [28]. Therefore, proton–proton elastic scattering amplitude can be written as

$$\begin{aligned} T({{\varvec{q}}})=T_0 ({{\varvec{q}}})+F({{\varvec{q}}}), \end{aligned}$$

(1)

where ${{\varvec{q}}}$ is the momentum transfer vector, $T_0 ({{\varvec{q}}})$ represents the incident cloud–target cloud interaction and is given by a phenomenological formula [29], in dimensionless variable ${{\varvec{q}}}_{{\varvec{0}}} =R_0 {{\varvec{q}}}$,

$$\begin{aligned} {{\varvec{T}}}_{{\varvec{0}}} ({{\varvec{q}}})={\textit{iR}}_0^2 (s)B_0 \exp \{-c_0 q_0^2 /2\} \end{aligned}$$

(2)

where $c_0$ and $B_0$ are dimensionless constants and $R_0$ is the inelastic radius of proton [30]. The second term $F({{\varvec{q}}})$ represents core-core scattering amplitude as composite systems of three quarks for each. In this work, we represent this amplitude in terms of quark–quark interaction in the framework of optical limit approximation [31]. Thus,

$$\begin{aligned} F({{\varvec{q}}})=\frac{iR_0^2 (s)}{2\pi }\int {d{{\varvec{b}}}_{{\varvec{0}}} \exp \{i{{\varvec{q}}}_{{\varvec{0}}}\,.\,{{\varvec{b}}}_{{\varvec{0}}} \}} [1-\exp \{i\chi _{opt} ({{\varvec{b}}}_{{\varvec{0}}} )\}],\nonumber \\ \end{aligned}$$

(3)

where ${{\varvec{b}}}$ is the two-dimensional impact vector between the mass centres of the two protons, and ${{\varvec{b}}}_{{\varvec{0}}} ={{\varvec{b}}}/R_0$. Considering the three-quark force, the total optical phase shift $\chi _{{\textit{opt}}}({{\varvec{b}}}_{{\varvec{0}}})$ is given by [26, 32]

$$\begin{aligned} \chi _{{\textit{opt}}} ({{\varvec{b}}}_{{\varvec{0}}} )=\sum _{j,k} {\chi _{jk}^t ({{\varvec{b}}}_0)} +\sum _{\begin{array}{c} j,m,k \\ j\ne m \end{array}} {\chi _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_0)} +\sum _{ \begin{array}{c} j,k,l \\ k\ne l \end{array}} \chi _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_0) ,\!\!\!\nonumber \\ \end{aligned}$$

(4)

where $\chi _{{\textit{jk}}}^t({{\varvec{b}}}_0)$ is the two-quark force phase shift, $\chi _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_0)$ and $\chi _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_0)$ are the three-quark force corrections. In the used approach, $({\textit{jm}})k$ means that the incident quark j interacts with the target quark k and, at the same time, the incident quark j interacts with another quark m in the incident proton. Also, $j({\textit{kl}})$ means that the incident quark j interacts with the target quark k and, at the same time, the target quark k interacts with another target quark l.

In terms of profile functions of interactions $\varGamma _{{\textit{jk}}}^t ({{\varvec{b}}}_0)$, $\Gamma _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{{\varvec{t}}}}{'}_{0{\textit{kl}}})$ and $\Gamma _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{\varvec{t}}}_{0\ {\textit{jm}}})$ of two-quark force and three-quark forces, respectively, the phase shifts $\chi _{{\textit{jk}}}^t ({{\varvec{b}}}_0)$, $\chi _{j({\textit{kl}})}^{{\textit{th}}}({{\varvec{b}}}_0)$ and $\chi _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_0)$ are given by [26, 32]

$$\begin{aligned}&\chi _{jk}^t ({{\varvec{b}}}_0)\nonumber \\&=i\int {d{\varvec{\rho }} _{{\varvec{0}}} d{{\varvec{r}}}_{{\varvec{0}}} d{{\varvec{\rho }}}'_{{\varvec{0}}} d{{{\varvec{r}}}}'_{{\varvec{0}}} \left| { \varphi _{{I}} ({\varvec{\rho }} _{{\varvec{0}}} ,{{\varvec{r}}}_{{\varvec{0}}} )\varphi _{\textit{T}} ({{\varvec{\rho }} }'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}} )} \right| } ^{2}\Gamma _{{\textit{jk}}}^t ({{\varvec{b}}}_{0\ {\textit{jk}}} ), \end{aligned}$$

(5)

$$\begin{aligned}&\chi _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_0 )\nonumber \\&=i\int {d{\varvec{\rho }}_{{\varvec{0}}} d{{\varvec{r}}}_{{\varvec{0}}} d{{\varvec{\rho }} }'_{{\varvec{0}}} d{{{\varvec{r}}}}'_{{\varvec{0}}} \left| { \varphi _{{I}} ({\varvec{\rho }} _{{\varvec{0}}} ,{{\varvec{r}}}_{{\varvec{0}}} )\varphi _{{T}} ({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}} )} \right| } ^{2}\Gamma _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{{\varvec{t}}}}'_{0\ {\textit{kl}}} ), \nonumber \\ \end{aligned}$$

(6)

$$\begin{aligned}&\chi _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_0 )\nonumber \\&=i\int {d{\varvec{\rho }} _{{\varvec{0}}} d{{\varvec{r}}}_{{\varvec{0}}} d{{\varvec{\rho }}}'_{{\varvec{0}}} d{{{\varvec{r}}}}'_{{\varvec{0}}} \left| { \varphi _{{I}} ({\varvec{\rho }} _{{\varvec{0}}} ,{{\varvec{r}}}_{{\varvec{0}}} )\varphi _{{T}} ({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}} )} \right| } ^{2}\Gamma _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{\varvec{t}}}_{0\ {\textit{jm}}}),\nonumber \\ \end{aligned}$$

(7)

where $\varphi _{{I}}({\varvec{\rho }} _{{\varvec{0}}} ,{{\varvec{r}}}_{{\varvec{0}}} )$ and $\varphi _{{T}}({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}} )$ are the wave functions of the relative motion of the incident and target proton, respectively, with dimensionless variables $({\varvec{\rho }} _{{\varvec{0}}} ,{{\varvec{r}}}_{{\varvec{0}}})$ and $({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}})$, respectively. If ${{\varvec{r}}}_1 ,\;{{\varvec{r}}}_2$ and ${{\varvec{r}}}_3$ are the position vectors of the quarks inside the proton, then, ${\varvec{\rho }}=R_{{\textit{0}}} {\varvec{\rho }} _{{\varvec{0}}} = {{\varvec{r}}}_3 -({{\varvec{r}}}_1 +\;{{\varvec{r}}}_2 )/2$, ${{\varvec{r}}}=R_{\textit{0}} {{\varvec{r}}}_{{\varvec{0}}} ={{\varvec{r}}}_1 -\; {{\varvec{r}}}_2$ are the relative coordinates of quarks. The independent variables of profile functions are

$$\begin{aligned}&{{\varvec{b}}}_{0\ {\textit{jk}}} ={{\varvec{b}}}_0 -{{\varvec{t}}}_{0\ j} +{{{\varvec{t}}}}{'}_{0\ k} , \quad {{\varvec{t}}}_{0\ jm} ={{\varvec{t}}}_{0\ j} -{{\varvec{t}}}_{0m} , \\&{{\varvec{t}}}_{01} =\frac{2}{3}{{\varvec{\rho }}}_{{{\varvec{0}}}\bot } , \quad {{\varvec{t}}}_{02} =-\frac{1}{3}{\varvec{\rho }} _{{{\varvec{0}}}\bot } +\frac{1}{2}{{\varvec{r}}} _{{{\varvec{0}}}\bot }, \\&\quad {{\varvec{t}}}_{03} =-\frac{1}{3}{\varvec{\rho }} _{0\bot } -\frac{1}{2}{{\varvec{r}}}_{0\bot } \end{aligned}$$

where the sign $\bot$ means that the projection is on the impact plane. For the target proton we have the same formulas with dashes.

The profile functions $\varGamma _{{\textit{jk}}}^t ({{\varvec{b}}}_0)$, $\Gamma _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{{\varvec{t}}}}{'} _{0{\textit{kl}}})$ and $\Gamma _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{\varvec{t}}}_{0\ {\textit{jm}}})$ of two-quark force [29] and three-quark forces [26, 32, 33], respectively, are taken as follows

$$\begin{aligned}&\Gamma _{{\textit{jk}}}^t ({{\varvec{b}}}_{0\ {\textit{jk}}} ) =\frac{A_{0\ {\textit{jk}}} }{9}\frac{(1-i\varepsilon _{{\textit{jk}}} )}{4\pi \beta _{0\ {\textit{jk}}} }\exp \left\{ -\frac{1}{2\beta _{0\ {\textit{jk}}} }{{\varvec{b}}}_{0\ {\textit{jk}}}^2 \right\} , \end{aligned}$$

(8)

$$\begin{aligned}&\Gamma _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{{\varvec{t}}}}{'}_{0\ {\textit{kl}}} )\nonumber \\&=(A_{j({\textit{kl}})} +iB_{j({\textit{kl}})})\exp \left\{ -\frac{1}{\gamma _{0}}\left( {{\varvec{b}}}_{0\ {\textit{jk}}}^{2} +{{\varvec{t}}}{'}_{0{\textit{kl}}}^{2}\right) \right\} , \end{aligned}$$

(9)

$$\begin{aligned}&\Gamma _{({\textit{jm}})k}^{th} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{\varvec{t}}}_{0\ {\textit{jm}}} )\nonumber \\&=(A_{({\textit{jm}})k} +iB_{({\textit{jm}})k} )\exp \left\{ -\frac{1}{\gamma _0 }\left( {{\varvec{b}}}_{0\ {\textit{jk}}}^2 +{{\varvec{t}}}_{0\ {\textit{jm}}}^2 \right) \right\} \end{aligned}$$

(10)

For knowledge only, the corresponding quark–quark elastic scattering amplitudes of the profile functions (8), (9) and (10) are obtained by inverse Fourier transformations

$$\begin{aligned}&f_{{\textit{jk}}}^t ({{\varvec{q}}})=\frac{i}{2\pi }\;\int d{{\varvec{b}}}_{0\ {\textit{jk}}} e^{i{{\varvec{q}}_0}.{{\varvec{b}}}_{0\ {\textit{jk}}} }\Gamma ^{t}_{\textit{jk}}) ({{\varvec{b}}}_{0\ {\textit{jk}}}) \nonumber \\&= \frac{A_{0\ {\textit{jk}}}}{9}\frac{(i+\varepsilon _{{\textit{jk}}} )}{4\pi }\exp \left\{ -\beta _{0\ {\textit{jk}}} {{\varvec{q}}}^{2}_0/2\right\} \end{aligned}$$

(11)

$$\begin{aligned}&f_{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{q}}}{} \mathbf{,}{{{\varvec{q}}}}') \nonumber \\&=\frac{i}{2\pi }\;\int {d{{\varvec{b}}}_{0\ {\textit{jk}}} d{{{\varvec{t}}}}{'}_{0{\textit{kl}}} e^{i{{\varvec{q}}_0}.{{\varvec{b}}}_{0\ {\textit{jk}}} +\mathrm{i}{{{\varvec{q}}_0}}'.{{{\varvec{t}}}}'_{0\ {\textit{kl}}}} \Gamma _{j({\textit{kl}})}^{{\textit{th}}} ({{\varvec{b}}}_{0 {\textit{jk}}} ,{{{\varvec{t}}}}{'}_{0\ {\textit{kl}}} )} \nonumber \\&= \frac{i\pi \gamma _0^2 }{2}(A_{j({\textit{kl}})} +iB_{j({\textit{kl}})}) \exp \{-\gamma _0 ({{\varvec{q}}}^{2}+{{{\varvec{q}}}}'^{2})/4\}\end{aligned}$$

(12)

$$\begin{aligned}&f_{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{q}}}{} \mathbf{,}{{{\varvec{q}}}}') \nonumber \\&=\frac{i}{2\pi }\;\int {d{{\varvec{b}}}_{0\ {\textit{jk}}} d{{\varvec{t}}}_{0\ {\textit{jm}}} e^{i{{\varvec{q}}_0}.{{\varvec{b}}}_{0 {\textit{jk}}} +\mathrm{i}{{{\varvec{q}}_0}}'.{{\varvec{t}}}_{0\ {\textit{jm}}}} \Gamma _{({\textit{jm}})k}^{{\textit{th}}} ({{\varvec{b}}}_{0\ {\textit{jk}}} ,{{\varvec{t}}}_{0\ {\textit{jm}}} )} \nonumber \\&=\frac{i\pi \gamma _0^2 }{2}(A_{({\textit{jm}})k} +iB_{({\textit{jm}})k}) \exp \left\{ -\gamma _0 ({{\varvec{q}}}^{2}_0+{{{\varvec{q}}}}{'}^{2}_0)/4\right\} \end{aligned}$$

(13)

The used transformation in Eqs. (12) and (13) are suggested by Hassan et al. [33]. $A_{0 _{{\textit{jk}}}} ,\varepsilon _{{\textit{jk}}}$ and $\beta _{0\ {\textit{jk}}}$ are two-quark force dimensionless parameters. The quantity $\varepsilon _{{\textit{jk}}}$ is the ratio of the real to imaginary parts of the quark–quark amplitude in the forward direction and $\beta _{0\ {\textit{jk}}}$ is the slope parameter and is related to the radius of two-quark interaction. From the profile function $\varGamma _{{\textit{jk}}}^t ({{\varvec{b}}}_{0\ {\textit{jk}}})$, we can consider $r_t =\sqrt{2\beta _{{\textit{jk}}}}$ as a radius of quark–quark interaction, where $\beta _{{\textit{jk}}} =\beta _{0\ {\textit{jk}}} R_0^2$. The parameters $A_{j({\textit{kl}})} ,B_{j({\textit{kl}})} ,\;A_{({\textit{jm}})k} ,B_{({\textit{jm}})k}$ and $\gamma _0$ are the three-quark force dimensionless parameters. Also, $r_{{\textit{th}}} =\sqrt{\gamma }$, where $\gamma =\gamma _0 R_0^2$, could be considered as the three-quark force radius [26]. From the uncertainty relation of energy and time, we know that $r_{{\textit{th}}} =\frac{1}{2}r_t$. Therefore, we can write $\sqrt{\gamma }=\frac{1}{2}\sqrt{2\beta _{{\textit{jk}}}}=\sqrt{\frac{\beta _{{\textit{jk}}}}{2}}$. Thus, we can take $\gamma =\frac{\beta _{{\textit{jk}}}}{2}$. If we represent the uncertainty relation in the form $\Delta {t}\Delta E\ge \hbar$ we have $\Delta E\ge \frac{\hbar }{\Delta t}=\frac{\hbar c}{\Delta r}$. If we consider $\Delta r$ is a radius of a certain force, then, $\Delta E$ can be considered as the quant energy of the mediator of this force, approximately.

The wave functions of incident and target protons are taken in the form

$$\begin{aligned} \phi _I({\varvec{\rho }} _0 ,{{\varvec{r}}}_0 )=\sqrt{\frac{\alpha _0^3}{3^{3/2}\pi ^{3}}}e^{{-\frac{\alpha _0 }{2}\left( \frac{2}{3}{\varvec{\rho }} _0^2 +\frac{1}{2}{{\varvec{r}}}_0^2 \right) }}, \end{aligned}$$

(14)

With $({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}})$ we have the same form for the wave function $\phi _{{T}} ({{\varvec{\rho }}}'_{{\varvec{0}}} ,{{{\varvec{r}}}}'_{{\varvec{0}}})$ of the target proton. The parameter $\alpha _0=R_0^2 \alpha$, where $\alpha$ is related to the root mean square radius $\left\langle {r^{2}} \right\rangle _p^{1/2}$ of proton by the relation $\alpha =\frac{1}{\left\langle {r^{2}} \right\rangle _p}$ [34].

In this study, we take $A_{0\ {\textit{jk}}} = A_0$, $\varepsilon _{{\textit{jk}}} =\varepsilon$ and $\beta _{0\ {\textit{jk}}} =\beta _0$ for all j and k. Also, we take $A_{j\left( {{\textit{kl}}}\right) } =A_{\left( {{\textit{jm}}} \right) k} =A$ and $B_{j\left( {{\textit{kl}}} \right) } =B_{\left( {{\textit{jm}}}\right) k} =B$ for all j, k, l and m as previously [26]. Thus, the total proton–proton optical phase shift $\chi _{{\textit{opt}}}$ is given by [26]

$$\begin{aligned} \chi _{{\textit{opt}}} ({{\varvec{b}}}_0 )= & {} \chi _{{\textit{opt}}}^t ({{\varvec{b}}}_0 ) +\chi _{{\textit{opt}}}^{{\textit{th}}} ({{\varvec{b}}}_0 ) \nonumber \\= & {} \frac{9\alpha _0 A_0 \left( {i+\varepsilon } \right) }{12 \pi \left( {2 +3 \alpha _0 \beta _0 } \right) }\exp \left\{ -[3 \alpha _0 /(4+6 \alpha _0 \beta _0 )] {{\varvec{b}}}_0^2 \right\} \nonumber \\&+\frac{108\alpha _0^2 \gamma _0^2 (iA- B)}{5+10 \alpha _0 \gamma _0 + 3 \alpha _0^2 \gamma _0^2 }\nonumber \\&\times \exp \left\{ -\frac{3 \alpha _0 \left( {2 +\alpha _0 \gamma _0 } \right) }{{ 5}+{ 10} \alpha _0 \gamma _0 + { 3} \alpha _0^2 \gamma _0^2 }b_0^2 \right\} . \end{aligned}$$

(15)

Therefore, the elastic scattering amplitude $F({{\varvec{q}}})$, Eq. (3), is obtained in the form

$$\begin{aligned} F({{\varvec{q}}})&=-\;iR_0^2 (s)\sum _{n=1}^\infty \sum _{m=0}^n \frac{i^{n}}{(n-m) !\; m !} G(m,n)\nonumber \\&\quad \times \exp \left\{ -H(m,n) {{\varvec{q}}}_{{\varvec{0}}}^{{\varvec{2}}} \right\} , \end{aligned}$$

(16)

where

$$\begin{aligned} G(m,n)= & {} \frac{(9\alpha _0 A_0 ( {i+\varepsilon } ))^{m}(2+3 \alpha _0 \beta _0 )^{1-m}\;(108\alpha _0^2 \gamma _0^2 (iA- B))^{n-m}\left( 5+10 \alpha _0 \gamma _0 + 3 \alpha _0^2 \gamma _0^2 \right) ^{1-n+m}}{(12 \pi )^{m} 3\alpha _0 \left( m (5+10 \alpha _0 \gamma _0 + 3 \alpha _0^2 \gamma _0^2 ) + (n-m) (2 +\alpha _0 \gamma _0 ) (4+6 \alpha _0 \beta _0 )\right) }, \end{aligned}$$

(17)

$$\begin{aligned} H(m,n)= & {} \frac{(2+3 \alpha _0\beta _0)\;(5+10 \alpha _0 \gamma _0+ 3 \alpha _0^2 \gamma _0^2 )}{6\alpha _0 (m (5+10 \alpha _0 \gamma _0 + 3 \alpha _0^2 \gamma _0^2 ) + (n-m) (2 +\alpha _0 \gamma _0) (4+6 \alpha _0 \beta _0 ))} \end{aligned}$$

(18)

Table 1 The dimensionless values of $\alpha _0=R_0^2/\left\langle {r^{2}} \right\rangle _p$, two-quark force parameters $A_0$, $\varepsilon$ and $\beta _0$, three-quark force parameters A, B and $\gamma _0$ and cloud parameters $B_0$ and $c_0$. $R_0^2 (s)=\sigma _{{\textit{in}}} (s)/\pi$ and the experimental value of $\sigma _{{\textit{in}}} (s)$ of proton–proton scattering are taken from [1, 3, 5] for 7, 8 and 13 TeV, respectively

The proton–proton elastic scattering differential cross section is given by

$$\begin{aligned} \frac{d\sigma }{dq^{2}}=\pi \left| {T_0 (q)+F(q)} \right| ^{2}. \end{aligned}$$

(19)

For the proton–proton total cross section we will use

$$\begin{aligned} \sigma _t (s)=4\pi \hbox { Im}(T_0 (0)+F(0)). \end{aligned}$$

(20)

The ratio $\rho$ of real part to imaginary part of proton–proton elastic scattering amplitude in the forward direction is given by

$$\begin{aligned} \rho =\frac{\hbox {Re}(T_0 (0)+F(0))}{\hbox {Im}(T_0 (0)+F(0))}. \end{aligned}$$

(21)

To calculate the total cross section of elastic scattering, we will use the relation

$$\begin{aligned} \sigma _{{\textit{el}}} =\int \limits _0^\infty {\frac{d\sigma }{dq^{2}}} \;dq^{2}=\pi \int \limits _0^\infty {\left| {T_0 (q)+F(q)} \right| ^{2}dq^{2}} \end{aligned}$$

(22)

By using Eqs. (2) and (16) we get

$$\begin{aligned} \sigma _{{\textit{el}}}= & {} \pi \;R_0^2 (s)\; \left[ \frac{B_0^2 }{c_0 } -\sum _{n=1}^\infty \sum _{m=0}^n \frac{i^{n}}{(n-m) !\; m !} \frac{B_0 G(m,n)}{H(m,n) +c_0 /2}\right. \nonumber \\&\left. -\sum _{j=1}^\infty \;\sum _{k=0}^j \frac{(-i)^{j}}{(j-k) !\; k !}\frac{B_0 G^{*}(k,j)}{H(k,j)+c_0 /2} \right. \nonumber \\&\left. +\sum _{j=1}^\infty \sum _{k=0}^j \sum _{n=1}^\infty \sum _{m=0}^n \frac{(-i)^{j}}{(j-k) !\; k !} \frac{i^{n}}{(n-m) !\; m !} \frac{G^{*}(k,j)\;G(m,n)}{H(k,j)+H(m,n)}\right] \nonumber \\ \end{aligned}$$

(23)

The inelastic total cross section is given by

$$\begin{aligned} \sigma _{{\textit{in}}} =\sigma _t -\sigma _{{\textit{el}}}. \end{aligned}$$

(24)

3 Results and discussion

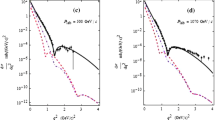
The results of $\frac{d\sigma }{{\textit{dq}}^{2}}$ calculations at the energies 7, 8, 13 TeV are presented in the Figs. 1, 2 and 3, respectively. The fitting quark–quark parameters of two- and three-quark forces and the values of parameters of pion-cloud part are given in the Table 1. In these calculations, the value of root mean square radius of proton is $\left\langle {r^{2}}\right\rangle _p^{1/2}=0.868\hbox { fm}$, noting that the experimental value of proton radius is $r_p =0.84-0.87\hbox { fm}$ [35]. The data at 7, 8 and 13 TeV is taken from the Refs. [1, 4, 6,7,8], respectively. A complete set of 7 TeV data with statistical and systematic errors is given in [1] for $q^{2}$ up to $2.44(\mathrm{GeV}/c)^{2}$, while the data at 8 and 13 TeV are preliminary and the statistical and systematic errors are given only up to $0.2(\mathrm{GeV}/c)^{2}$. Therefore, to show the extent of agreement of the calculations with the data the quantities $\chi ^{2}/NDF=[\sum \nolimits _{\mathrm{i=1}}^{\mathrm{n}} (\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2} )_{\mathrm{exp.}}$ $-\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2})_{\mathrm{theo.}} )^{{2}}/\hbox {error}_\mathrm{i}^{2} ] /\hbox {n}$, $[\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2})_{\mathrm{exp.}} -\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2} )_{\mathrm{theo.}} ]/\sqrt{{\mathrm{error}}_{\mathrm{stat.}}^{2} +\hbox {error}_{\mathrm{syst.}}^{2}}$ and $[\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2})_{\mathrm{exp.}} -\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2})_{\mathrm{theo.}} ]/\hbox {(d}\upsigma /\hbox {dq}_\mathrm{i}^{2})_{\mathrm{theo.}}$ are calculated for 7 TeV as in the Ref. [18], see Fig. 1. For the other two energies where the statistical and systematic errors are not available for us, the last quantity is only calculated, see Figs. 2 and 3. A good agreement is obtained with two-, three-quark forces and pion-cloud effects up to $q^{2}\approx 1(\mathrm{GeV}/c)^{2}$. In fact, the pion-cloud effect has a contribution in the forward direction for $q^{2}\le 0.5 (\mathrm{GeV}/c)^{2}$ and it decreases with increasing the energy $\sqrt{s}$ and $q^{2}$, see Figs. 1, 2 and 3. The pion-cloud contribution is not enough to obtain an agreement with the experimental data. Only with three-quark force contribution we have a good agreement for $q^{2}\le 1\;(\mathrm{GeV}/c)^{2}$ . The disagreement for $q^{2}>1\;(\mathrm{GeV}/c)^{2}$ may be related to the absence of multi-scattering terms in the optical limit approximation. This is because the actual effects of the multi-scattering terms are in this region. This conclusion is related to many published works in the framework of complete polynomial of Glauber approximation at ISR energy [29, 34, 36], where, with a simple correction, the agreement with the differential cross section was obtained up to $q^{2}=10\;(\mathrm{GeV}/c)^{2}$. Since, the first minimum and second maximum are coming from the interference of the single- and double scattering terms, we need to interpret the agreement with the data at these regions without the double scattering terms. Since, the scattering processes with three-quark force correction are considered as processes of many particle together (three quarks), we believe that these processes play, partially at least, the same role of multi-scattering processes.

Using the same parameter values of Table 1, we calculate the total cross section $\sigma _t$ and the ratio $\rho$ of proton–proton scattering at 7, 8, and 13 TeV. The obtained results are given in the Table 2, where the experimental data of $\sigma _t$ are taken from [1, 3, 5] for 7, 8, and 13 TeV, respectively. The $\rho$ values of the COMPETE preferred-model extrapolation at 7 and 8 TeV [37] are presented in the last column, as well as the measured value of $\rho$ at 13 TeV [6]. A good agreement with the experimental data of $\sigma _t$ and the values of $\rho$ [6, 37] means that the used model with three-quark force correction can describe well the data at these very high energies. The contributions of the pion-cloud in the total cross section $\sigma _t$ and the ratio $\rho$ is clear, see the Table 2.

Fig. 1

The p–p elastic scattering differential cross section at 7 TeV. The dashed, dot-dashed and solid curves represent the results of (two-quark force) only, (two-quark force $+$ pion cloud effect), and (two-+three-quark force+ pion-cloud effect), respectively. The experimental data are taken from [1]

Fig. 2

Same as Fig. 1 for 8 TeV. The experimental data are taken from [4, 8]

Fig. 3

Same as Fig. 1 for 13 TeV. The experimental data are taken from [6,7,8]

To ensure this conclusion, we calculate the total cross section of elastic scattering $\sigma _{{\textit{el}}}$ and the total cross section of inelastic scattering $\sigma _{{\textit{in}}}$. The results with all corrections are given in the Table 3. The good agreement with the experimental data indicates that the model is physically accepted to describe the data and the three-quark force is important.

Although, the model has a limited range of applicability that extends approximately up to the first diffractive minimum and maximum, and due to this reason the model gives reasonable description of $\sigma _t,\sigma _{el},\sigma _{\textit{in}}$ and $\rho$, that are sensitive to the low values of $q^{2}$ but are not sensitive to elastic scattering data at large values of $q^{2}$. However, we expect a good agreement over a wide range of $q^{2}$ if we use the complete polynomial of Glauber theory [27].

From all above results of $\frac{d\sigma }{{\textit{dq}}^{2}}$, $\rho$, $\sigma _t,\sigma _{el},\sigma _{\textit{in}}$ we can trust the seriousness of the parameter values in Table 1. Therefore, using the relations $r_{t}=\sqrt{2\beta }, r_{\textit{th}}=\sqrt{\gamma }$ and $E_g \ge \frac{\hbar c}{r_t}$ for two-quark interaction radius, three-quark force radius and the quant energy of force mediator (gluon), respectively, these quantities are calculated. These quantities were calculated in previous work [26] at ISR energy, their values, in average, were $r_t=0.738\,{\textit{fm}}$, $r_{{\textit{th}}} =0.364\,{\textit{fm}}$ and $E_g\approx 271.695MeV$, respectively. The results at 7, 8, 13 TeV are given in Table 4. In average, we have $r_t =0.826\,{\textit{fm}}, r_{{\textit{th}}} =0.411\,{\textit{fm}}$ and $E_g \approx 238.946MeV$. It is clear that, the values of $r_t$ and $r_{{\textit{th}}}$ are still less than the radius of proton, 0.87 fm, and the radius of core, 0.44 fm, respectively. Note that, from Table 4, each of these quantities has the same order at different LHC energies as in the case of ISR energy, [26], where the same order at energy $\sqrt{s}$ in the range 19.42–53 GeV. The values of radii $r_{\textit{th}}$ and $r_{t}$ at LHC energy are greater than their values at ISR energy by 12%, approximately. This leads to decreasing the energy of mediator by 12%, approximately. However, we can consider the values of the radii and energy of gluon at ISR and LHC energies of the same order, approximately.

Table 2 Total cross section with (two-quark force, $\sigma _t^t$), with (two-quark force +pion cloud, $\sigma _t^{t+c}$) and with (two-quark force +pion cloud+three-quark force, $\sigma _t^{t+c+{\textit{th}}}$). The ratio of real to imaginary parts of p–p elastic scattering amplitude in the forward direction with(two-quark force, $\rho ^{t}$), with (two-quark force +pion cloud, $\rho ^{t+c}$) and with (two-quark force +pion cloud + three-quark force, $\rho ^{t+c+{\textit{th}}}$). The experimental data of total cross sections at 7, 8 and 13 TeV are taken from [1, 3, 5], respectively. The values of ratio $\rho$ in the last column are taken from [37] for 7 and 8 TeV and from [6] at 13 TeV

As in the previous work [26], we try to evaluate residue energy to know the field particle of the external strong field of proton. The residual energy of proton is defined as [26]

$$\begin{aligned} E_{\textit{res}}&={\textit{proton}}\, {\textit{mass}}- ({\textit{mass}}\, {\textit{of}}\, {\textit{three}}\, {\textit{quarks}}\\&\quad + {\textit{sum}}\, {\textit{of}} \,{\textit{gluons}}\ {\textit{of}}\, {\textit{two}}- {\textit{quark}}\, {\textit{interactions}})\\&= m_p-\left( {\textit{mass}}\, {\textit{of}}\, {\textit{three}}\, {\textit{quarks}}+E_{\textit{guu}}+E_{\textit{gud}}+E_{\textit{gud}}\right) \end{aligned}$$

Taking $E_{{\textit{guu}}} =E_{{\textit{gud}}} =E_g \approx 238.946\;\hbox {MeV}$, $m_{p}=938.27$ MeV and the current mass of three valence quarks of proton together is about 9.95 MeV [38] we have

$$\begin{aligned} E_{{\textit{res}}} =938.27-(9.95+3\times 238.946)=211.482\;\hbox {MeV} \end{aligned}$$

Table 3 The total cross section of proton–proton elastic scattering $\sigma _{el}$ and inelastic scattering $\sigma _{in}$. The experimental data are taken from [1, 3, 5] for 7, 8 and 13 TeV, respectively

Table 4 The values of $r_{\textit{th}}$ and $r_t$. $E_{2g}$ and $E_{g}$ are the two-gluon exchange and one-gluon exchange energy

This value of $E_{{\textit{res}}}$ is greater than the mass of $\pi -$ meson of order 140 MeV which is considered as the mediator of proton strong force. The increment of order 71 MeV. From the uncertainty relation of time and energy, we conclude that the radius of strong force out the proton at the LHC energy is of order 1fm. At the same time, with the mass of $\pi -$ meson of order 140 MeV we have this radius of value 1.414 fm. In the previous work [26], where $E_{{\textit{res}}} =135.66\;\hbox {MeV}$, we have the radius of proton strong force is 1.454 fm. Regarding these results, we can consider that the strength of proton field is related to the energy of the proton and its field at LHC energy is stronger than its field at ISR energy with smaller radius.

We must remember that the first determinations of quark masses were performed using quark models. The resulting masses only make sense in the limited context of a particular quark model, and cannot be related to the quark current masses. In order to discuss the current quark masses, definitions based on quantum field theory were used. The picture of the proton in our calculations, is based on an effective field theory model [28]. Therefore, the current masses of quarks are used in our calculations of $E_{{\textit{res}}}$.

It is well known that the proton mass (938.27 MeV), the sum of current masses of three quarks (9.95 MeV) and the mass of $\pi -\hbox {meson}$, the particle of proton strong field (139.57 MeV). Also, we can consider that the residual mass $E_{{\textit{res}}}$ equals to the mass of $\pi -\hbox {meson}$. Therefore, regardless of the proton incident energy and optical limit calculations, we can calculate the gluon energy $E_g$ by using the relation

$$\begin{aligned} E_{g}= & {} \frac{1}{3}\left\{ m_p -(\hbox {mass}\;\hbox {of}\;\hbox {the}\;\hbox {three}\;\hbox {quarks} +E_{{\textit{res}}})\right\} \\= & {} \frac{1}{3}\left\{ 938.27-(9.95+139.57)\right\} =262.917\;\hbox {MeV} \end{aligned}$$

With this $E_g$ value, the quark–quark interaction radius $r_t$ is 0.75 fm and the three-quark force radius $r_{{\textit{th}}}$ is 0.375 fm. It is clear that, these values of $E_g$, $r_t$ and $r_{{\textit{th}}}$, are consistent, approximately, with the obtained values of these quantities in our previous work [26] and this work.

Fig. 4

a and b Represent the proton picture with $R_q$, $R_d$, and $R_{{\textit{qd}}}$ values of [15, 18], respectively

Finally, it is useful to note that the optical limit results of the elastic scattering differential cross section have a shoulder where $1.5<q^{2}<2\;(\mathrm{GeV}/c)^{2}$ and this shoulder does not exist in the experimental data of the differential cross section at ISR and LHC energies. Since the second minimum in Glauber formalism is coming from the interference of double and triple scattering terms which take place with the composite particles of three or more constituents, the proton picture as two constituent’s system is suggested in [39]. Bialas and Bzdak proposed a model of nucleons interaction at ISR energy for small momentum transfer where the nucleon was considered as a quark and diquark system [14, 15]. In this model the interaction between quarks and diquarks is assumed to be purely absorptive, therefore the forward scattering amplitude of the Bialas and Bzdak model has no real part. With this assumption the results of [16] at ISR energis ($\sqrt{s}=23.5-62.5\;\hbox {GeV})$ and LHC (TOTEM) energy of $\sqrt{s}=7\;\hbox {TeV}$ have a good agreement with the experimental data except at the minimum region, where a singular point was obtained due to the zero real part of amplitude. At the same energies, with nonzero real part of parton-parton scattering amplitude the results of Bialas–Bzdak model describe well the dip region of the differential cross-section where the singularity is deleted [17, 18].

However, in Bialas–Bzdak model, at ISR energy, for example, the values of quark radius $R_q$, diquark radius $R_d$ and the distance between the centres of quark and diquark $R_{{\textit{qd}}}$, in the proton, approximately, are 0.28, 0.76 and 0.32 fm, respectively, [15]. These values at 7 TeV are 0.45, 0.94 and 0.32 fm, respectively, [18]. Since, the radius of proton is 0.87 fm, we cannot separate quark and diquark into two entities, i.e., we cannot consider that quark and diquark are two independent constituents. Both quark and diquark occupy spaces that cannot be separated. In other words, if we consider the quark and diquark as spheres, then the quark takes a place inside the diquark at any time. Thus, with these values of $R_q$, $R_d$, and $R_{{\textit{qd}}}$, and the proton radius $R_p$ of the same order of diquark radius $R_d$, we can consider the proton is the diquark with one constitute quark inside it, see Fig. 4. The increasing of the total cross section is not enough to accept this physical picture of proton and we need more studies in this concern.

At the same time, in the framework of multiple scattering theory of Glauber, Wakazumi [29] studied p–p scattering in terms of quark–quark amplitude for number of constitutes $\hbox {n}=2, 3, 4,{\ldots }$, to determine the number of constituents of proton. He found that this number equals 3 constituents, see Fig. 3 in [29]. Also, many works with three quark assumption at ISR and LHC energies and with good agreement with the experimental data can be found.

4 Conclusions

In conclusion, the three-quark force is important to obtain a good agreement with proton–proton elastic scattering data at LHC energies 7, 8, 13 TeV in the framework of optical limit approximation. Only we need to use the complete polynomial of Glauber model to obtain a good fit with the differential cross section for $q^{2}>1\;(\mathrm{GeV}/c)^{2}$. Since the total cross section and ratio are calculated at $q^{2}=0$, their results with complete polynomial of Glauber model are not affected and will be the same as in optical limit approximation. Also, the effect on the elastic and inelastic total cross sections will be small due to that the effect of multi-scattering terms are in general small. The obtained values for the radii of two-quark and three-quark forces are consistent with the radii of proton and core of proton, respectively. Finally, we need a physical interpretation for the values of the residual energy representing the strong field outside the proton.