1 Introduction

At zero temperature, Bloch and Nordsieck [1] were among the first to study the infra-red (IR) behaviour of fermionic QED. Later, it was shown [2] that the cross section for the bremsstrahlung of very low energy quanta in elementary particle collisions has an IR divergence:

$$\begin{aligned} \sigma _{\mathrm{brems}} = \frac{\sigma _0}{k} + \sigma _1 + k \sigma _2 + \ldots ~, \end{aligned}$$
(1)

where k is the energy of the photon and \(\sigma _j\) have appropriate dimensions. It was further shown that \(\sigma _0\) and \(\sigma _1\) can be calculated from the corresponding elastic amplitude for both scalar and spinor cases at the leading order in perturbation theory, calculated up to \({{\mathcal {O}}}(k)\). This was later extended [3] for pure fermionic QED where it was shown that the (logarithmic) IR divergences cancel to all orders (rendering the total cross section IR finite) when both virtual and real photon emission corrections are included. Such soft real emissions need to be included due to finite detector resolution since they cannot be distinguished from the virtual lower order process. Some of the technical shortcomings of Ref. [3] such as translational and gauge-invariance were addressed in a subsequent paper by Grammer and Yennie [4].

Many clarifications and simplifications occurred over the next decades, including [5] the question about whether a charge particle exists relativistically due to the IR structure of gauge theories where the Green functions for charged matter have no poles but a branch cut. This implies a soft cloud always surrounds each physical charge. This question was addressed (positively) in Refs. [6, 7] where they used velocity-superselection rules inspired by heavy quark effective theory for abelian theories to obtain on-shell Green’s functions that are IR finite to all orders in perturbation theory. Specifically, they used scalar QED for simplicity, since Low [2] had shown that the electron spin structure does not affect the IR divergence as long as the matter fields are massive. (The spin structure of massless QED makes its asymptotic dynamics richer; for instance, collinear divergences turn on.) Scalar QED has also been studied recently [8] in the context of its asymptotic symmetries and relation to Weinberg’s soft photon theorem.

Many papers have also addressed the IR finite remainder in such scalar theories. For instance, in Refs. [9,10,11], the factorisation and exponentiation of IR divergences is shown in a translation and gauge-invariant way, using order-by-order agreement with Operator Product Expansion (OPE) before summation and by requiring that the exponentiation of all factorisable parts is done before the integrations are carried out. Then the IR finite remainder is defined in terms of correlations with respect to the photon momenta in the integrands. This involves an all order generalisation of Low’s theorem and also includes a calculation of both soft and hard photon contributions.

In the case of thermal field theory, there are additional linear divergences owing to the nature of the thermal photon propagator. The infra-red finiteness of such thermal QED with purely charged fermions has been shown [12, 13] to all orders in the theory. In particular, both absorption and emission of photons with respect to the heat bath are required [12, 14] in order to cancel the linear divergences as well as the logarithmic subdivergences.

In the first of this set of two papers we address the proof of the infrared finiteness, to all orders, of a thermal field theory of pure charged scalars, referred to as scalar QED. In the second paper, we apply these results, and the earlier results on the IR finiteness of thermal fermionic QED, to address the issue of IR finiteness of thermal models of dark matter, thereby extending the results obtained in Ref. [15] at NLO to all orders. The analysis is an extension of that presented in Ref. [12] which was based on the approach developed by Grammer and Yennie (GY) [4] and is motivated by the results of Ref. [15]. The crux of this paper is the identification of the correct set of terms that allows the factorisation and exponentiation of the IR divergent terms to all orders for thermal scalar fields.

In contrast to fermionic QED, we now have not only the 3-point scalar–photon–scalar vertex, but also 4-point (2-scalar-2-photon) ones. These contribute through both seagull and tadpole diagrams; see vertex diagrams in Appendix A. While the result we obtain is similar to that obtained in the usual fermionic QED, the inclusion of the seagull and tadpole diagrams give rise to additional terms that are essential in order to achieve the exponentiation and cancellation of IR divergent terms between real and virtual contributions.

In the next paper, Paper II, we apply our results to show the IR finiteness of the corresponding thermal field theory of dark matter to all orders. This result is, thus, a generalisation of Ref. [12] to include both charged fermions and scalars. Again, the key fact used in the proof is that both photon absorption and emission diagrams are required to cancel the linear sub-divergences. As mentioned earlier, this was also noticed in the NLO calculation in Ref. [15], where the finite term has also been calculated to NLO.

In Sect. 2, we briefly review the propagator and vertex structure of the relevant thermal field theory; details are given in Appendix A. We also review the approach of Grammer and Yennie (GY) to address the IR behaviour of such field theories. In Sect. 3, we analyse the photon–scalar interactions using the approach motivated by GY: by rearranging the polarisation sums of the inserted virtual photons into so-called K-photon and G-photon parts (see Eq. 4). This was used by GY to establish the IR finiteness of fermionic QED to all orders. As in the case of fermionic QED, the K-photon contributions are divergent; however, in scalar QED, they can be factorised and exponentiated only on inclusion of the additional vertices. In particular, the \({\mathcal O}(k^2)\) IR finite contribution from the tadpole diagrams cancels a similar contribution from the 3-particle interaction terms and enables the factorisation. As far as we are aware, this observation of the need for inclusion of the IR finite tadpole contributions in order to achieve the factorisation and subsequent exponentiation of the IR divergent parts, has not been pointed out in the literature before. The G-photon contributions are finite, again, as was shown to be the case for fermionic QED. Proof of IR finiteness of the G-photon insertions is non-trivial due to the presence of both 4-point vertices as well as thermal indices and is the second main contribution of this work. In Sect. 3, the corresponding analysis for insertion of real photons is also considered. A similar rearrangement of the polarisation sums of real photons into \({\widetilde{K}}\) and \({\widetilde{G}}\) enables the IR divergent parts to be collected into the \({\widetilde{K}}\) contribution. We show that the IR divergent parts will cancel between the virtual and real diagrams, that is, between the K and \({\widetilde{K}}\) contributions, when they are added, order by order, in the theory. This is achieved only when both real photon emission into, and absorption from, the heat bath is taken into account. This establishes the infrared finiteness to all orders for scalar thermal QED. We end with some remarks and discussion in Sect. 4. Many technical details are relegated to the appendices.

Appendix A lists the relevant Feynman rules while Appendix B lists some useful generalised Feynman identities of use in the thermal field theoretic analysis. The details of the calculation for the insertion of a virtual K photon into a lower order graph is found in Appendix C where it is shown that the total contribution from all possible virtual K photon insertions into an nth order graph is a single term proportional to the lower order matrix element itself (and is also IR divergent). Details of the result for the insertion of a virtual G photon in all possible ways into an nth order graph is found in Appendix D; it is shown that all such virtual G photon contributions are IR finite.

2 Real-time formulation of thermal field theory

We review briefly the real-time formulation of thermal (scalar and photon) fields in equilibrium with a heat bath at temperature T. In the case of such a thermal field theory, there is an additional complication which can be understood in a real-time formulation [16, 17] where the integration in the complex time plane is over a contour that includes the temperature, chosen so that correct thermal averages of the S-matrix elements [18] are obtained. The fields satisfy periodic boundary conditions,

$$\begin{aligned} \varphi (t_0) = \varphi (t_0 - i \beta )~, \end{aligned}$$
(2)

where \(\beta = 1/T\), with T being the temperature of the heat bath. This results in the well-known field-doubling, so that fields are of type-1 (physical) or type-2 (ghosts), with propagators acquiring \(2 \times 2\) matrix forms. Only type-1 fields can occur on external legs (as mandated by unitarity) while fields of both types can occur on internal legs, with the off-diagonal elements of the propagator allowing for conversion of one type into another.

Both scalar and photon field propagators assume matrix forms (see Appendix A for details) with the (11) and (22) terms having both \(T=0\) and finite temperature contributions. In particular, the photon propagator corresponding to a momentum k can be expressed (in the Feynman gauge) as,

$$\begin{aligned} i \mathcal{D}^{ab}_{\mu \nu } (k)&= - i g_{\mu \nu } \, D^{ab} (k)~, \end{aligned}$$
(3)

where the information on the field type is contained in \(D^{ab} (k)\); see Appendix A for its definition.

Finally, the vertices, both 3-point and 4-point ones, are modified in the thermal theory. Details are again in Appendix A; we only note here that all the fields at a given vertex must be of the same type.

2.1 The GY approach to study the IR behaviour

Several methods can be adopted to prove all-order finiteness. For example, one may consider propagators dressed with arbitrary coherent states. We shall, instead, adopt a simpler method that lends itself more readily to an understanding of the issues involved. The approach of GY, which we use here, addressed the IR finiteness of fermionic QED at zero temperature, and we extend this to a theory of charged scalars in contact with a heat bath. GY started with an nth-order graph with n photon–fermion vertices and considered the effect of adding an additional real or virtual photon to it. Since the photon is a boson, all symmetric permutations, i.e., all possible insertions, must be considered. In particular, for the virtual photon insertion, they found it useful to express the photon propagator as,

$$\begin{aligned} -i \frac{g_{\mu {\nu }}}{k^2+i\epsilon }&= \frac{-i}{k^2+i\epsilon } \, \left[ \left( g_{\mu \nu } - b_k (p_f, p_i)k_\mu k_\nu \right) \right. \nonumber \\&\quad \left. + \left( b_k (p_f, p_i) k_\mu k_\nu \right) \right] ~, \nonumber \\&\equiv \frac{-i}{k^2+i\epsilon } \, \left[ G_{\mu \nu } + K_{\mu \nu } \right] ~. \end{aligned}$$
(4)

Here, \(b_k\) depends on the momenta \(p_f\), \(p_i\), where the final and initial vertices are inserted [and also implicitly on the momentum k of the inserted \((n+1)\)th photon], and is defined such that the so-called G-photon terms in the matrix element with \((n+1)\) photons are IR finite (in both the \(T=0\) and \(T\ne 0\) cases for fermionic QED) and the K-photon terms contain all the IR divergent terms:

$$\begin{aligned} b_k(p_f,p_i)&= \frac{1}{2} \Bigg [ \frac{(2p_f-k) \cdot (2p_i-k)}{((p_f-k)^2-m^2)((p_i-k)^2-m^2)}\nonumber \\&\quad + (k \leftrightarrow -k) \Bigg ]~. \end{aligned}$$
(5)

Note that, on account of its k dependence, \(b_k\) does not represent a gauge transformation.

On expressing the \((n+1)\)th virtual photon contribution in this way, the K photon contribution turns out to be proportional to the matrix element of the underlying graph with n-photon vertices and has a simple structure. The object of this paper is to obtain an analogous result for a theory of thermal charged scalars.

Note that the factor \(g_{\mu \nu }\) occurs in all components of the thermal photon propagator, enabling a separation into K- and G-type photons, just as before, with the sameFootnote 1 definition for \(b_k\) as in Eq. (5). We can therefore apply the technique of GY to the case of thermal fields in equilibrium with a heat bath at temperature T. There are two major differences in this case, firstly, that the relevant part of the thermal photon propagator is proportional to,

$$\begin{aligned} i \mathcal{{D}}^{ab} (k) \sim&\left[ \frac{i}{k^2+i\epsilon } \delta ^{ab} \pm 2 \pi \delta (k^2) N(\vert k^0 \vert ) D^{ab}_{T} \right] ~, \end{aligned}$$
(6)

where the first term corresponds to the \(T=0\) contribution and the second to the finite temperature part. The bosonic number operator in the second term contributes an additional power of k in the denominator in the soft limit, since

$$\begin{aligned} N(\vert k^0 \vert ) \equiv \frac{1}{\hbox {exp}[|k^0|/T] - 1} \; {\mathop {\longrightarrow }\limits ^{k \rightarrow 0}} \; \frac{T}{\vert k^0 \vert }~. \end{aligned}$$
(7)

Hence, it can be seen that the leading IR divergence in the finite temperature part is linear rather than logarithmic as was the case at zero temperature. Consequently, there is a residual logarithmic subdivergence that must also be shown to cancel at finite temperatures, thus making the generalisation to the thermal case non-trivial.

Secondly, it turns out that the inclusion of thermal matter fields adds another layer of complexity to the analysis, since not only is the propagator structure now different from the zero temperature case, but, in contrast to the case of fermions, the number operator corresponding to charged scalars is bosonic and hence can potentially give rise to divergences as well.

In summary, the major differences between this and the earlier works are as follows.

  1. 1.

    The scalar theory has additional vertices, including the 4-point seagull vertices; see Fig. 11 in Appendix A. This contributes additional terms to both the K and G photon insertions compared to the thermal theory with fermions only.

  2. 2.

    The thermal theory has additional field types; in particular, the thermal charged scalar legs add more complications compared to the results with thermal fermions.

We consider both modifications when analysing the IR behaviour of thermal scalar QED in the next section.

3 The IR behaviour of thermal scalar QED

In view of the discussion in the preceding section, we begin by considering pure scalar QED, discounting quartic scalar self-couplings.Footnote 2 Thus, it behoves us to start with the fundamental hard scattering process here, viz. \(\gamma ^{(*)} + \phi ^{(*)} \rightarrow \phi ^{(*)}\) where any of the three lines could represent either an on-shell or an off-shell particle. Higher order contributions would arise from the inclusion of both virtual as well as soft real photons.

We begin by considering insertions on an n-photon graph with trilinear (scalar–scalar–photon) vertices alone so that the n vertices imply n scalar–photon interactions (with the understanding that both vertices of an internal line are counted). We will, subsequently, extend the analysis to graphs with an arbitrary admixture of 3-point and 4-point vertices.

The (n)th order graph has n trilinear vertices with s vertices on the final scalar leg with 4-momentum \(p'\) and \(r \, (= n - s)\) vertices on the initial scalar leg with 4-momentum p (see Fig. 1). For reasons that will become clear later, these vertices are already symmetrised. The photons carry away momentum \(l_q, \, q = 1, \ldots , s\), from the vertex q on the \(p'\)-leg and momentum \(-t_q, \, q = 1, \ldots , r\), from the vertex q on the p leg. The notation is arbitrary since the momenta may be entering or leaving the vertex and the corresponding photon may be a real or virtual one.

Hence the momentum of the particle to the right of the qth vertex on the p leg is \((p + \textstyle \sum _{i=1}^q t_i)\) while the momentum corresponding to the particle line to the left of the qth vertex on the \(p'\) leg is \((p' + \textstyle \sum _{i=1}^q l_i)\).

In contrast to the fermionic case, which has only three-point vertices, scalar QED admits of 4-point vertices as well, so that an additional photon can be inserted at a new vertex (giving rise to a new 3-point vertex) or at an already existing 3-point vertex, thus converting it to a 4-point vertex. Thus the consideration of charged scalars requires consideration of both types of insertions. This is true for both real and virtual photon insertions.

We begin by considering insertion of an additional virtual photon. Adopting the expression of \(g_{\mu \nu }\) in the photon propagator in terms of \(K_{\mu \nu }\) and \(G_{\mu \nu }\) (as in Eq. 4), we start with the insertion of virtual K-photons (which are expected to contain the IR divergent contributions) leaving the inclusion of the G-photons (expected to give IR finite contributions) until later.

3.1 Insertion of virtual K photons

Consider the insertion of one of the virtual K photon vertices, say \(\mu \), on an external line. As per the Feynman rules listed in Appendix A, there can be two types of vertices, with one or two photon lines at each vertex, corresponding to 3-point or 4-point vertices respectively. (In addition, these fields carry a thermal index, \(t_a (=1,2)\), depending on the field type at the ath vertex). Hence, there are two types of K photon insertions possible; one where the insertion is at a new vertex, forming a new 3-point vertex, or one where the \((n+1)\)th K photon is inserted on an already existing vertex, thus forming a 4-point vertex. The total set of all possible insertions of the \((n+1)\)th K photon on the \(p'\) line can be grouped into sets having the new \(\mu \) vertex as a 3-point or 4-point vertex, as shown in Figs. 2 and 3 respectively. In contrast, note that only the set of graphs shown in Fig. 2 contributes if the \(p'\)-leg is a fermion line.

It is convenient to group 3- and 4-point vertices to obtain “circled vertices”: for instance, consider the insertion of the \(\mu \) vertex to the right of a generic vertex q or at the vertex q. The corresponding two diagrams are shown in Fig. 4 and the contribution from the sum of these is shown in the figure as a circled vertex and denoted by \({}_q\mu \).

In the thermal case, the propagators contain more than just the \(1/(P^2-m^2)\) part and appear more complex. However, they satisfy generalised identities, analogous to the zero temperature case, as shown in Appendix B, which can be used to simplify and factor these contributions to obtain a similar result. Retaining only the \(k_\mu \) factor in the \((b_k k_\mu k_\nu )\) part of the K photon propagator (the \(k_\nu \) factor will be similarly included when the other vertex \(\nu \) is inserted on the p leg, and \(b_k\) is an overall factor), and omitting the other terms in the photon propagator for clarity, we have (denoting a scalar propagator from the vertex \(\mu _b\) of thermal type \(t_b\) to the vertex \(\mu _a\) having fields of thermal type \(t_a\) as \(i{\mathcal {S}}^{t_at_b}(p'+\sum _{i=1}^q l_i,m) \equiv i S^{ab}_{p'+\sum _q})\),

$$\begin{aligned} {\mathcal {M}}_{n+1}^{q~\mathrm{to~left~of~}\mu }&= e^{s+1}(-1)^{(\sum _{i=1}^s t_i)+s} \cdots (-1)^{t_\mu +1}\nonumber \\&\quad \times \left[ S^{q-1,\mu }_{p'+\sum _{q-1}} \times ((2p'+2\Sigma _{q-1}+k)\cdot k) \right. \nonumber \\&\quad \left. \times S^{\mu ,q}_{p'+\sum _{q-1}+k} \right] \left( 2p'+2\Sigma _{q-1}+2k+l_q\right) _{\mu _q}\nonumber \\&S^{q,q+1}_{p'+\sum _q+k}\cdots , \nonumber \\&\quad = e^{s+1}(-1)^{(\sum _{i=1}^s t_i)+s} \nonumber \\&\qquad \cdots \left[ S^{q-1,q}_{p'+\sum _{q-1}} \delta _{t_\mu ,t_q} - S^{q-1,q}_{p'+\sum _{q-1}+k} \delta _{t_\mu ,t_{q-1}} \right] \cdots ~, \end{aligned}$$
(8)
$$\begin{aligned} {\mathcal {M}}_{n+1}^{q=\mu }&= e^{s+1} (-1)^{(\sum _{i\ne q}^s t_i)+s-1} \cdots (-1)^{t_\mu +1}\nonumber \\&\quad \times \left[ S^{q-1,\mu }_{p'+\sum _{q-1}} (-2k_{\mu _q}) \delta _{t_\mu ,t_q} \times S^{q,q+1}_{p'+\sum _q+k} \right] \cdots ~; \nonumber \\&= e^{s+1}(-1)^{(\sum _{i=1}^s t_i)+s}\nonumber \\&\quad \cdots \left[ S^{q-1,q}_{p'+\sum _{q-1}} \delta _{t_\mu ,t_q} (-2k_{\mu _q}) S^{q,q+1}_{p'+\sum _q+k} \right] \cdots ~. \end{aligned}$$
(9)

Here, \(t_i (=1,2)\) denote the thermal indices of the inserted photons and \(t_\mu \) is the thermal indexFootnote 3 of the inserted photon at the vertex \(\mu \). Notice that all the thermal powers of \((-1)^{t_i+1}\) match and there is no sign ambiguity between the relative contributions of the two terms, which is independent of the thermal field type. Hence the two can be combined to give the total contribution to Fig. 4 as a difference of two terms, viz.,

$$\begin{aligned} \mathcal{M}_{n+1}^{q\mu ,\mathrm{tot}}&= e^{s+1} (-1)^{(\sum _{i=1}^s t_i)+s} \nonumber \\&\quad \cdots \left[ S^{q-1,q}_{p'+\sum _{q-1}} \delta _{t_\mu ,t_q} \left( 2p'+ 2\Sigma _{q-1}+l_q\right) _{\mu _q} \right. \nonumber \\&\quad \left. - S^{q-1,q}_{p'+\sum _{q-1}+k} \delta _{t_\mu ,t_{q-1}} \left( 2p'+2\Sigma _{q-1}+2k+l_q\right) _{\mu _q} \right] \nonumber \\&\quad S^{q,q+1}_{p'+\sum _q+k} \cdots ~. \end{aligned}$$
(10)

This is the thermal generalisation of the corresponding result obtained by GY for the fermionic case at \(T=0\). This combination of differences of terms from K photon insertion helps in pair-wise cancellation and hence simplification and factorisation of the IR divergent part even at finite temperature. Note that due to the absence of 4-point vertices, the corresponding thermal result for the insertion of a thermal virtual K photon into a fermion line was much simpler [12]:

$$\begin{aligned}&\mathcal{M}_{n+1}^{q\mu ,\mathrm{fermion}} = e^{s+1} (-1)^{(\sum _{i=1}^s t_i)+s} \nonumber \\&\quad \left[ S^{q-1,q}_{p'+\sum _{q-1}} \delta _{t_\mu ,t_q} - S^{q-1,q}_{p'+\sum _{q-1}+k} \delta _{t_\mu ,t_{q-1}} \right] ~ S^{q,q+1}_{p'+\sum _q+k} \cdots ~, \end{aligned}$$
(11)

where the propagators are now fermionic.

Fig. 1
figure 1

Schematic of an nth order graph of \(\gamma ^* \phi \rightarrow \phi \), with s vertices on the \(p'\) leg and r on the p leg, \(r+s=n\). V labels the special but arbitrary hard photon–scalar vertex

Full size image
Fig. 2
figure 2

Set of \((s+1)\) diagrams showing all possible trilinear insertions of a virtual photon at vertex \(\mu \) on the \(p'\) leg of a scalar/fermion

Full size image
Fig. 3
figure 3

Set of s diagrams showing all possible insertions of a virtual photon at vertex \(\mu \) which is one of the already existing s vertices on the \(p'\) leg of a scalar particle, thus giving rise to a 4-point vertex. Analogous diagrams for fermions do not exist

Full size image
Fig. 4
figure 4

Combining the two possible sets of insertions (as in Figs. 2 and 3) of the \((n+1)\)th virtual K photon at the vertex \(\mu \) on the \(p'\) leg to give a single circled vertex, \({}_q\mu \); see text for details. The photon lines have been suppressed for clarity

Full size image

We now apply this simplification to all sets of diagrams. We have the following possibilities:

  1. 1.

    The inserted K photon vertices are on different external lines, in-coming and out-going.

  2. 2.

    The two vertices of the inserted K photon are on the same lines.

We will address them one by one.

3.1.1 K photon insertions on different lines

The case where the vertices are on different lines is straightforward. Start with a lower order diagram that contains only 3-point vertices; we will relax this condition later. Consider the insertion of the \(\mu \) vertex of the \((n+1)\)th K photon in all possible ways on the \(p'\) leg. In terms of the circled vertices, these can be expressed in terms of the graphs shown in Fig. 5.

Fig. 5
figure 5

The graphs in Figs. 2 and 3 can be combined into the s circled vertex graphs and an \((s+1)\)th graph with the inserted \(\mu \) vertex to the left of all the other s vertices on the \(p'\) leg, as shown above

Full size image
Fig. 6
figure 6

The diagrams with all circled vertices that belong to set I

Full size image

Since the relevant term in the K photon propagator is \((b_k k_\mu k_\nu )\), we compute the contribution to the part of the matrix element, \(\mathcal{{M}}_{n+1}^{\mu ,p'\mathrm{leg}}\), from an insertion \(\mu \) on the \(p'\) leg. The contribution from each of the first s graphs in Fig. 5, retaining only the \(k_\mu \) term in the photon propagator, and omitting overall constants including a factor of \(e^{s+1} (-1)^{(\sum _{i=1}^s t_i)+s}\), can be written from inspecting the result in Eq. (10) (see the corresponding graphs in Fig. 4),

$$\begin{aligned}&\mathcal{{M}}_{n+1}^{\mu ,p',s} \propto \left\{ 0 + \delta _{t_\mu ,t_1} (2p'+l_1)_{\mu _1} S^{t_1,t_2}_{p'+\sum _1+k}\right. \nonumber \\&\qquad \left. (2p'+2\Sigma _1+2k+l_2)_{\mu _2} \cdots (V) \cdots \right\} \nonumber \\&\qquad + \left\{ (2p'+l_1)_{\mu _1} \left[ S^{t_1,t_2}_{p'+\sum _1} \delta _{t_\mu ,t_2} (2p'+2\Sigma _1+l_2)_{\mu _2} \right. \right. \nonumber \\&\qquad \left. \left. -S^{t_1,t_2}_{p'+\sum _1+k} \delta _{t_\mu ,t_1} (2p'+2\Sigma _1+2k+l_2)_{\mu _2} \right] \cdots (V) \cdots \right\} \nonumber \\&\qquad + \left\{ \cdots \right\} \nonumber \\&\qquad + \left\{ (2p'+l_1)_{\mu _1} S^{t_1,t_2}_{p'+\sum _1} \cdots \left[ S^{t_{s-1},t_s}_{p'+\sum _{s-1}} \delta _{t_\mu ,t_s} (2p'+2\Sigma _{s-1}+l_s)_{\mu _s} \right. \right. \nonumber \\&\qquad \left. \left. - S^{t_{s-1},t_s}_{p'+\sum _{s-1}+k} \delta _{t_\mu ,t_{s-1}} (2p'+2\Sigma _{s-1}+2k+l_s)_{\mu _s} \right] \cdots (V) \cdots \right\} ~, \nonumber \\&\quad = \left\{ 0 + M_1 \right\} + \left\{ M_2 - M_1 \right\} + \left\{ \cdots \right\} + \left\{ M_s - M_{s-1} \right\} ~. \end{aligned}$$
(12)

Here (V) denotes the (arbitrary) vertex that separates the \(p'\) and p legs, and the first term vanishes since \(p'\) is on-shell. It can be seen that the terms now cancel, just as happened in the \(T=0\) case for GY, leaving only the last term, \(M_s\). The contribution from the unpaired \((s+1)\)th term which is the last graph shown in Fig. 2 is

$$\begin{aligned}&\mathcal{{M}}_{n+1}^{\mu ,p',s+1} \propto (2p'+l_1)_{\mu _1} S^{t_1,t_2}_{p'+\sum _1} \nonumber \\&\qquad \cdots \left[ S^{t_s,t_V}_{p'+\sum _s} \delta _{t_\mu ,t_V} - S^{t_s,t_V}_{p'+\sum _s+k} \delta _{t_\mu ,t_s} \right] \, (V) \cdots ~, \nonumber \\&\quad = \left\{ M_{s+1} - M_s\right\} ~. \end{aligned}$$
(13)

Hence the second term of Eq. (13) cancels the contribution of the previous s terms in Eq. (12), so that the total contribution from the insertion of the \(\mu \) vertex of the \((n+1)\)th K photon in all possible ways on the \(p'\) leg gives a contribution that is independent of the inserted momentum, k, as in the case with fermions. That is, the result of adding the contributions of inserting both A and B types of vertices in all possible ways on the \(p'\) leg is,

$$\begin{aligned} \mathcal{{M}}_{n+1}^{\mu ,p',tot}&\propto (2p'+l_1)_{\mu _1} S^{t_1,t_2}_{p'+\sum _1} \cdots S^{t_s,t_V}_{p'+\sum _s} \left[ \delta _{t_\mu ,t_V} \right] \times \nonumber \\&(V) \cdots ~. \end{aligned}$$
(14)

Note the presence of the delta-function, \(\delta _{t_\mu ,t_V}\), arising from matching the field types at the vertex. Since the hard photon is observable, \(t_V=1\) and hence \(t_\mu =1\) as well.

Inclusion of the 4-point vertex

The calculation can be extended to the case when there are both 3- and 4-point vertices in the n-photon graph. Graphs with the same number of photons rather than the same number of vertices are grouped together, so that the overall charge factors (powers of \(\alpha \)) are the same for the entire set of diagrams. Hence the corresponding n-photon graph may have fewer than n vertices, and in fact will have \((m/2 + (n-m))\) vertices if m of the n photons participate in a 4-point vertex. For such diagrams there is an additional constraint since it is obvious that the additional \((n+1)\)th photon cannot be added at an already existing 4-point vertex.

Fig. 7
figure 7

The diagrams with only \(\mu \) vertices circled that belong to set II

Full size image
Fig. 8
figure 8

The diagrams with only \(q=\nu \) vertices circled that belong to set III

Full size image
Fig. 9
figure 9

The diagrams with \({}_\nu \mu \) circled vertices that belong to set IV. The last term corresponds to the self energy diagram and is to be omitted on the p leg to avoid double counting

Full size image

Two photons, say \(l_q\) and \(l_r\), are at vertex q. No more photons can be added at this vertex, and in fact, the vertex factor for this vertex is proportional to \(g_{qr}\delta _{t_q,t_r}\), with no momentum dependence. As before, any \(q=\mu \) vertex (that is, the new photon forms a 4-point vertex) contributes a term with a factor \((-2k_{\mu _q})\) in the numerator which cancels a similar term from a 3-point \(\mu \) vertex as shown in Fig. 4. The terms cancel diagram by diagram, similar to that shown in Eq. (12). The \(g_{qr} \delta _{t_q,t_r}\) factor gets carried along and does not spoil the re-grouping and cancelling of terms when an additional \((n+1)\)th K-photon vertex \(\mu \) is added.

A similar result is obtained when the \(\nu \) vertex of the virtual K photon is inserted on the p (distinct) leg, with pair-wise cancellations, leaving a single term containing \(\delta _{t_\nu ,t_V}\). Putting back the factors of \(b_k(p',p)\) as well as the rest of the photon propagator, the total contribution from the insertion in all possible ways of an \((n+1)\)th K-photon (contributing a factor \((b_k(p',p) k_\mu k_\nu )\)) into a set of graphs with n photons containing an arbitrary number of 3- or 4-point vertices, is given by,

$$\begin{aligned} \mathcal{M}^{p'p,K\gamma }_{n+1}&= -ie^2 \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \, \delta _{t_\mu ,t_V} \, \delta _{t_\nu ,t_V} b_k(p',p) D^{t_\mu ,t_\nu } (k) \nonumber \\&\quad \times \mathcal{M}_n~, \end{aligned}$$
(15)

and hence is proportional to the lower order matrix element \(\mathcal{M}_n\).

The major difference between the \(T=0\) case and the thermal case is the presence of the thermal indices. Crucially, there are additional delta functions, \(\delta _{t_\mu ,t_V}\) and \(\delta _{t_\nu ,t_V}\), arising from matching the field types at the special (hard) scalar–photon vertex V. Since the hard photon is observable, \(t_V=1\) so \(t_\mu \), \(t_\nu =1\) as well; hence the K photon thermal propagator is constrained to be of type \(D^{11}\) alone. This is a crucial requirement for the cancellation to occur between real and virtual photon contributions to the lower order diagram, as we shall see below.

3.1.2 Both K photon insertions on the \(p'\) leg alone

The case where both vertices of the \((n+1)\)th K photon are inserted on the \(p'\) leg is more complex due to the presence of a large number and type of diagrams as well as the presence of the additional 4-point vertices. While only seagull 4-point vertices contribute in the previous case (of independent insertions of \(\mu \) and \(\nu \) on different legs), tadpole diagrams also contribute when both vertices are inserted at the same point on the same leg. Double-counting is avoided by insisting that the \(\mu \) vertex is always to the right of the \(\nu \) vertex.

As before, the case with only 3-point vertices in the lower order graph is first considered; this condition is then relaxed to prove the general case. The diagrams obtained when the \((n+1)\)th K photon is inserted in all possible ways can be grouped into sets labelled set I, set II, set III, and set IV, as shown in Figs. 6, 7, 8 and 9. While set I (Fig. 6) has circled vertices at both \(\mu \) and \(\nu \) insertions, set II (Fig. 7) has circled vertices only at \(\mu \), with \(\nu \) to the right of the special V vertex. Set III (Fig. 8) has all 4-point vertex insertions at \(\nu \), with \(\mu \) immediately adjacent to \(\nu \). Finally, set IV (Fig. 9) is a set of \({}_\nu \mu \) circled vertices that includes all tadpole insertions, \(\mu =\nu \), as shown in Fig. 10.

Fig. 10
figure 10

A typical tadpole diagram where the vertices \(\mu \), \(\nu \) of the \((n+1)\)th K photon have been inserted between the vertices q and \(q-1\)

Full size image

In order to simplify the analysis, we first consider only the \(T=0\) contribution which is logarithmically divergent in the IR/soft limit. We will show that various contributions can be combined so that the term-by-term cancellation is more easily seen. This analysis also highlights the role of the tadpole contributions in factorising the IR divergent parts. We will then use the understanding acquired in this analysis to consider the entire finite temperature contribution which contains linear divergences and logarithmic subdivergences that must be factorised as well.

K photon insertions with both vertices on the \(p'\) leg: \(T=0\) Tadpole diagrams are proportional to \(g_{\mu \nu }\) as per the Feynman rules in Appendix A. (Note the presence of an additional symmetry factor of 1 / 2 with respect to the seagull vertex factor shown here.) Hence the K photon insertions of tadpoles on the \(p'\) leg contribute terms proportional to \(k^2\) and are IR finite. Thus, it appears at first sight that tadpole diagrams can be neglected when discussing the IR behaviour of scalar QED. However, this is not so, since the contributions from these tadpoles are crucial in obtaining the factorisation and subsequent exponentiation of the IR divergent terms from the K photon insertions. We show this result by first considering the (simpler) \(T=0\) case without tadpoles. The contributing diagrams are sets I–IV, excluding the tadpole contributions in set IV, which we name as set IV\('\).

In Appendix  C we show that the contributions from various contributing diagrams from Sets I to IV\('\) can be expressed as a term proportional to the lower order matrix element, \(\mathcal{{M}}_n\), as required, as well as terms linear and quadratic in k:

$$\begin{aligned}&{\mathcal {M}}_{n+1}^{\mu \nu ,p'p'} (T=0) \propto \left[ \left\{ (2p'+l_1)_{\mu _1} \frac{1}{(p'+\mathcal {S}_1)^2}\right. \right. \nonumber \\&\quad \left. \left. \cdots \frac{1}{(p'+\mathcal {S}_s)^2} (V) \cdots \right\} \right] \nonumber \\&\quad -\left[ \left\{ (2p'+l_1)_{\mu _1} \frac{1}{(p'+\mathcal {S}_1)^2} \cdots \frac{1}{(p'+\mathcal {S}_{s-1})^2} (-2k)_{\mu _s}\right. \right. \nonumber \\&\quad \left. \frac{1}{(p'+\mathcal {S}_s)^2} (V) \cdots \right\} + \Bigg \{ \cdots \Bigg \} \nonumber \\&\quad + \left\{ (2p'+l_1)_{\mu _1} \frac{1}{(p'+\mathcal {S}_1)^2} \cdots {(2p'+2\Sigma _{q-1} + l_q)_{\mu _q}}\right. \nonumber \\&\quad \left. \frac{1}{(p'+\mathcal {S}_q)^2} (-2 k)_{\mu _q} \cdots (V) \cdots \right\} + \left. \Bigg \{ \cdots \Bigg \} \right] +\left[ \Bigg \{ \cdots \Bigg \} \right. \nonumber \\&\quad + \left\{ (2p'+l_1)_{\mu _1} \frac{1}{(p'+\mathcal {S}_1)^2} \cdots (2p'+2\Sigma _{q-1}+l_q)_{\mu _q} \right. \nonumber \\&\quad \times \left\{ \frac{1}{(p'+\mathcal {S}_q)^2} {(2 k \cdot (p'+ \sum _q) + k^2)} \frac{1}{(p'+\mathcal {S}_q)^2} \right\} \nonumber \\&\quad \times (2p'+2{\sum }_q+l_{q+1})_{\mu _{q+1}} \cdots \nonumber \\&\quad \left. \frac{1}{(p'+\mathcal {S}_s)^2} (V) \cdots \right\} + \left. \Bigg \{ \cdots \Bigg \} \right] ~. \end{aligned}$$
(16)

Here the zero temperature propagator of a scalar with momentum \(p'+\sum _q\) is \(i/((p'+\sum _q)^2-m^2)\), which we have represented as \(i/(p'+\mathcal{{S}}_q)^2\). It can be seen that apart from the first term in Eq. (16) which is proportional to the lower order matrix element, \(\mathcal{{M}}_n\), the remaining terms are proportional to \((-2k)_{\mu _q}\), \(2k \cdot P\), and \(k^2\), with no other k dependence in the denominators. Since \(b_k\) is even in k (by definition), the terms proportional to either of \((-2k)_{\mu _q}\) and \(2 k \cdot P\) vanish on integration, leaving only the term proportional to \(\mathcal{{M}}_n\) and terms proportional to \(k^2\). Recall that the \(T=0\) contribution is logarithmically divergent in the soft photon limit while the finite T contribution has both linear (\(\mathcal{{O}}(1)\)) and logarithmic (\(\mathcal{{O}}(k)\)) divergences; consequently, terms proportional to \(k^2\) are IR finite. While these \(\mathcal{{O}}(k^2)\) terms do not spoil the IR finiteness of the theory, they also do not allow the \((n+1)\)th matrix element to be expressed as purely proportional to the lower nth order matrix element, which would have enabled the IR divergent pieces to be factorised and exponentiated to all orders, eventually cancelling with the corresponding IR divergent parts from the real photon contributions.

A straightforward calculation of the contribution of the hitherto neglected tadpole diagrams in set IV (see Appendix C shows that this contribution exactly cancels these \(\mathcal{{O}}(k^2)\) terms left over in Eq. (16) above; hence the total contribution from inserting a virtual K photon in all possible ways such that both vertices are on the \(p'\) leg is simply a term proportional to the lower order matrix element, as required. With the understanding that the tadpole contributions are crucial in achieving this result, we now go on to consider the finite temperature case of interest.

K photon insertions with both vertices on the \(p'\) leg: finite T We use the insight we have gained from the zero temperature case to complete the calculation for the general thermal case when both the K photon vertices are inserted into the same leg. The same diagrams contribute; we consider each set in turn and make use of the generalised thermal identities discussed in Appendix B since the propagators are no longer simple and have a \(2 \times 2\) matrix form. Generalised identities are used to get term by term cancellations; as in the zero temperature case, there are many left-over terms due to the presence of the additional 4-point vertices, in contrast to the fermionic case. This is the most complex of the calculations, and most of the details are relegated to Appendix C. The grouping of terms in order to cancel them is made easier by the understanding gained from considering the zero temperature case.

As in the zero temperature case, there are many terms contributing to the various sets. It is shown in Appendix C that left-over terms of sets \((I+II+III)\) cancel against corresponding terms in set IV, leaving behind a term proportional to the lower order matrix element \(\mathcal{M}_n\), as required, and towers of terms linear in k. The cancellation occurs as follows. The contribution from set IV can be expressed as,

$$\begin{aligned}&\mathcal{{M}}_{n+1}^{\mu \nu ,p'p', IV} \propto \left\{ \left[ A_s - B_s + C_s \right] \right\} + \left\{ \cdots \right\} \nonumber \\&\qquad + \left\{ \left[ A_1 - B_1 + C_1 \right] \right\} + \left\{ \left[ -B_0 + C_0 \right] \right\} ~, \end{aligned}$$
(17)

where

$$\begin{aligned} A_q&= (2p'+l_1)_{\mu _1} S^{12}_{p'+\sum _1} (2p'+2\Sigma _1+l_2)_{\mu _2} \nonumber \\&\quad \cdots \left[ S^{q-1,q}_{p'+\sum _{q-1}+k} \delta _{t_\mu ,t_{q-1}} \delta _{t_\nu ,t_q} \right] \cdots (\hbox {no } k) ~, \nonumber \\ B_q&= (2p'+l_1)_{\mu _1} S^{12}_{p'+\sum _1} (2p'+2\Sigma _1+l_2)_{\mu _2} \nonumber \\&\quad \cdots \left[ S^{q-1,q}_{p'+\sum _{q-1}} \delta _{t_\mu ,t_{q-1}} \delta _{t_\nu ,t_{q-1}} \right] \cdots (\hbox {no } k) ~, \nonumber \\ C_q&= (2p'+l_1)_{\mu _1} S^{12}_{p'+\sum _1} (2p'+2\Sigma _1+l_2)_{\mu _2} \nonumber \\&\;\cdots \left[ S^{\nu ,q}_{p'+\sum _{q}} (2p'{+}2\Sigma _{q-1})\cdot k \, \delta _{t_\mu ,t_\nu } S^{\nu ,q}_{p'+\sum _q} \right] \cdots (\hbox {no } k) ~, \end{aligned}$$
(18)

where “no k” indicates that the remaining terms do not have any k dependence. Here the term \((-B_0+C_0)\) arises from self-energy corrections on the \(p'\) leg, with \(B_i\) proportional to \(\mathcal{M}_n\). Note that all \(C_i\) are odd in k.

Details of the calculation for sets I, II, and III are given in Appendix C. Combining sets I, II and III, we have,

$$\begin{aligned} \mathcal{{M}}_{n+1}^{\mu \nu ,p'p', I+II+III}&= \left[ \sum _{q=1}^s B_q - \sum _{q=0}^s A_q + Y\right] \end{aligned}$$
(19)

where Y is defined in Eq. (C.12) in Appendix C and each term in Y is proportional to \((-2k)_{\mu _q}\). Hence both the contributions of \(C_q\) and Y have linear powers of k in the numerator, and no other dependence on k apart from the overall factors such as \(b_k\), etc. Hence these terms are odd in \(k \leftrightarrow -k\) and vanish. We see that the \(A_q\) terms cancel between the contributions of set IV in Eq. (C.11) and sets (\(I+II+III)\) in Eq. (C.12), as also all the \(B_q\) except for \(-B_0\) which remains as the only left over piece when all sets are combined and we further recall that this term is proportional to the lower order matrix element, as in the \(T=0\) case.

Note that the \(\mathcal{O} (k^2)\) terms are present in the two contributing graphs corresponding to each term in the typical circled vertices of set IV and exactly cancel against one another. While the \(\mathcal{O} (k^2)\) terms, and hence, the tadpole contributions are IR finite and do not pose any problems for the theory, it is not just simply a preference that these be included with the IR finite G photon contributions; \(b_k\) was designed to isolate the IR singular terms and resum them; hence the presence of such \(\mathcal{O} (k^2)\) terms in addition to the term proportional to the lower order matrix element, precludes the factorisation and resummation of the K photon contributions to all orders; hence it is a matter of satisfaction that such \(\mathcal{O} (k^2)\) terms cancel exactly.

The sum of the contributions from all four sets of diagrams with all possible insertions of the \((n+1)\)th K photon, with both vertices on the \(p'\) leg, is therefore a term that contains the IR divergence and is proportional to the lower order matrix element with no additional finite contributions, as is the case with the zero temperature theory and fermionic QED. Putting back the overall factors, we have,

$$\begin{aligned} \mathcal{M}^{p'p', K\gamma }_{n+1}= & {} +ie^2 \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \, \delta _{t_\mu ,t_1} \, \delta _{t_\nu ,t_1} \nonumber \\&\times b_k(p',p') \, D^{t_\mu ,t_\nu } (k)~\mathcal{M}_n~. \end{aligned}$$
(20)

Since \(t_1=1\) necessarily, it depends only on the \(D^{11}\) photon propagator, as before.

3.1.3 Both K photon insertions on the p leg alone

A similar analysis can be done for the case when both the vertices of the inserted \((n+1)\)th K photon are on the p leg. As discussed in GY, the outermost self energy insertion graph is neglected here to compensate for wave function renormalisation, due to which the sum of contributions for all possible insertions on the p leg adds up to zero. As shown in Appendix C, the term \((-B_0 + C_0)\) arises from self-energy corrections on the \(p'\) leg. A similar contribution occurs when the virtual K photon is inserted on the p leg. Hence when we remove the self-energy correction on the p leg to account for wave function renormalisation, we remove the term corresponding to \((-B_0 + C_0)\). (The contribution of \(C_0\) is in any case zero since it is odd in k.) The total contribution for the insertion of a virtual K photon in all possible ways on the \(p'\) leg added up to \(-B_0\). When this is removed to account for wave function renormalisation for insertions on the p leg, we find that the total contribution vanishes.

Since this compensation could have been included in either of the legs, we symmetrise over the two possibilities, thus giving us the contributions:

$$\begin{aligned} \mathcal{M}^{p'p', K\gamma }_{n+1}&= +ie^2 \frac{1}{2}\, \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \nonumber \\&\quad \delta _{t_\mu ,t_1} \, \delta _{t_\nu ,t_1} \, b_k(p',p') \, D^{t_\mu ,t_\nu } (k)~\mathcal{M}_n~,\nonumber \\ \mathcal{M}^{pp, K\gamma }_{n+1}&= +ie^2 \frac{1}{2} \, \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \nonumber \\&\delta _{t_\mu ,t_1} \, \delta _{t_\nu ,t_1} \, b_k(p,p) \, D^{t_\mu ,t_\nu } (k)~\mathcal{M}_n~. \end{aligned}$$
(21)

The contribution is once more proportional to the lower order matrix element and depends on the \(D^{11}\) part of the inserted photon propagator alone.

3.1.4 Inclusion of ‘disallowed diagrams’

Certain ‘disallowed diagrams’ may contribute at higher orders. For instance, the outermost self-energy insertion graph is removed at a certain order to account for wave function renormalisation. However, while making K or G photon insertions at the next higher order, these lower order diagrams must be included, as these can give rise to allowed graphs at the next order. As in the case of the zero temperature theories, these terms add to zero. There is an additional disallowed diagram in the thermal case that must be similarly included: these are lower order graphs with ‘outermost’ vertices next to the \(p'\) or p external legs that are of thermal unphysical type with \(t_1=2\). A calculation shows that these diagrams also do not contribute at the next higher order.

3.1.5 The total K photon contribution

The total contribution from the insertion of the \((n+1)\)th virtual K photon therefore is,

$$\begin{aligned}&\mathcal{{M}}_{n+1}^{K\gamma ,\mathrm{tot}} = \frac{ie^2}{2} \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \, \left\{ \delta _{t_\mu ,t_1} \, \delta _{t_\nu ,t_1} \right. \nonumber \\&\qquad \times D^{t_\mu ,t_\nu } (k) \, \left[ b_k(p',p') + b_k(p,p) \right] \nonumber \\&\qquad +\left. \delta _{t_\mu ,t_V} \, \delta _{t_\nu ,t_V} \, D^{t_\mu ,t_\nu } (k) \, \left[ -2b_k(p',p) \right] \right\} \mathcal{{M}}_{n}~, \nonumber \\&\quad \equiv \left[ B \right] \mathcal{{M}}_{n}~, \end{aligned}$$
(22)

where

$$\begin{aligned} B&= \frac{ie^2}{2} \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \, D^{11} (k)\nonumber \\&\quad \, \left[ b_k(p',p') - 2 b_k(p',p) + b_k(p,p) \right] ~, \nonumber \\&\equiv \frac{ie^2}{2} \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \, D^{11} (k) \, \left[ J^2(k) \right] ~. \end{aligned}$$
(23)

In Eq. (23) we have used the fact that the thermal types of the hard/external vertices must be type-1; \(t_1=t_V =1\), so that each term is proportional to the (11) component of the photon contribution. This will be crucial to achieve the cancellation between virtual and real photon insertions, as we show below.

Hence the structure of the contribution from virtual K photon insertion is the same as in the \(T=0\) case; however, note that, due to the thermal contributions in the photon propagator, there are both linear and logarithmic divergences in these terms. Demonstration of the cancellation of the linear divergences follows the same route as that of GY at \(T=0\); the demonstration of cancellation of the logarithmic subdivergences is discussed separately later.

3.2 Insertion of virtual G photons

In GY, it was shown that insertion of a virtual G photon into the n vertex graph with only 3-point vertices gives finite contributions. The key point was that the G photon contribution at \(T=0\) was proportional to

$$\begin{aligned} \mathcal{{M}}_{n+1}^{G\gamma ;T=0}&\propto \left\{ g_{\mu \nu } - b_k(p_f,p_i) k_\mu k_\nu \right\} \times p_f^\mu \, p_i^\nu ~, \nonumber \\&= 0 + \mathcal{{O}}(k)~. \end{aligned}$$
(24)

Since the leading divergence for the \(T=0\) theory is a logarithmic one, terms proportional to powers of k in the numerator are IR finite; hence the G photon contribution was IR finite.

At finite temperatures, there are two major modifications: one due to the thermal part of the photon propagator and the other due to the thermal part of the scalar propagator. We start by considering the contribution due to the thermal part of the photon propagator. Although there are different types of thermal fields and hence four different photon propagators, \(\mathcal{D}^{ab}_{\mu \nu }\), all of them have the same leading IR behaviour: the divergence is a linear one due to the presence of the term in the photon propagator that is proportional to

$$\begin{aligned} 2\pi \delta (k^2) N(\vert k^0 \vert ) \equiv 2\pi \delta (k^2) \frac{1}{\exp ^{\vert k^0 \vert /T} - 1}~. \end{aligned}$$
(25)

This is cancelled for the G photons in exactly the same way as the \(T=0\) case. However, there is also a logarithmic subdivergence arising from terms linear in k in the numerator whereas these terms are IR finite in the \(T=0\) case. Proving the IR finiteness of these contributions is the central result of this paper. A detailed case-by-case analysis can be found in Appendix D.

We start by ignoring the \(T=0\) parts of the propagators and concentrate on the thermal parts alone. Since the thermal part of the photon propagator includes an overall \(\delta (k^2)\), there are two simplifications that result. First, the coefficient factor \(b_k(p_f,p_i)\) simplifies to

$$\begin{aligned} b^{T\ne 0}_k(p_f,p_i) = \frac{p_f \cdot p_i}{p_f \cdot k \; \; p_i \cdot k}~. \end{aligned}$$
(26)

In addition, we can ignore \(k^2\) terms in the scalar propagators. The complete structure of this matrix element can be written as,

$$\begin{aligned}&\mathcal{M}^{G\gamma }_{n+1} \sim \int d^4 k \left[ \frac{i}{k^2+i\epsilon } \delta _{t_\mu ,t_\nu } \pm 2 \pi \delta (k^2) N(\vert k \vert ) D^{t_\mu ,t_\nu }_T \right] \nonumber \\&\quad \times \left[ g^{\mu \nu } - b_k k^\mu k^\nu \right] \, \left[ \mathrm{scalar} \right] _{\mu \nu }, \end{aligned}$$
(27)

where the terms in the first two square brackets correspond to terms in the definition of the G photon propagator, with the relative sign in the first being determined by the thermal field indices, \(t_\mu , t_\nu \). The last term represents the contribution from the \(\mu \) and \(\nu \) virtual G photon insertions on the scalar legs, p and \(p'\), and are products of the vertex and propagator factors. Combining the second term in Eq. (27) with the vertex factors at only the \(\mu \) and \(\nu \) vertices (assuming them to be 3-point for now) in the third term, we get,

$$\begin{aligned}&\left[ g^{\mu \nu } - b_k k^\mu k^\nu \right] \, \left\{ S^{q-1,\mu }_{p_f+\sum _{q-1}}\left[ (2p_f+ 2\Sigma _{q-1}+k)_\mu \right. \right. \nonumber \\&\qquad \left. \left. \times S^{\mu ,q}_{p_f+\sum _{q-1}+k} (2p_f+ 2\Sigma _{q-1}+2k+l_q)_{\mu _q}\right] \right\} \nonumber \\&\qquad \times \left\{ S^{m+1,\nu }_{p_i+\sum _{m}+k} \left[ (2p_i+ 2\Sigma _{m}+k)_\nu \, S^{\nu ,m}_{p_f+\sum _{m}}\right. \right. \nonumber \\&\qquad \left. \left. \times (2p_i+ 2\Sigma _{m-1}+l_m)_{\mu _m}\right] \right\} \nonumber \\&\quad = \left[ 4 P_f \cdot P_i + 2 (P_f+P_i) \cdot k - 4 b_k P_f \cdot k \,P_i \cdot k \right] \nonumber \\&\qquad \times \left[ S^{q-1,\mu } S^{\mu ,q} S^{m+1,\nu } S^{\nu ,m} (\cdots )_{\mu _q} (\cdots )_{\mu _m} \right] ~,\nonumber \\&\quad = \left[ 0 (p_f \cdot p_i) + 2 (p_f + p_i) \cdot k \right] \cdots ~, \end{aligned}$$
(28)

where we have used \(P_f = p_f + \sum _{i=1}^{q-1}l_i\) and \(P_i = p_i + \sum _{i=1}^{m-1}l_i\). In the soft limit, replacing \(P_f \rightarrow p_f\), \(P_i \rightarrow p_i\), and substituting for \(b_k\) from Eq. (26), we get the last line of Eq. (28). We see that the leading \((p_f \cdot p_i)\) term vanishes (indeed, \(b_k\) was chosen for this very reason) and the term in the square brackets is exact with no further corrections. The ellipses refer to the contribution from the remaining vertices and propagators, some of which (the set of vertices and propagators that lie between the \(\mu \) and \(\nu \) vertices) also depend on k. Substituting this back in Eq. (27), we have,

(29)

where the slashes on \(\mu \) and \(\nu \) indicate that the contribution from these vertices have been removed and simplified as per Eq. (28) and,

(30)

where we have indicated the powers of k in the numerator of the matrix element from the scalar contribution above.

We know that the \(T=0\) part is logarithmically divergent while the leading thermal divergence is linear. The factor \(b_k\) is so chosen so that the \((p_f \cdot p_i) \times [\mathcal{O}(1)]\) term, obtained by combining Eqs. (29) and (30), vanishes. Note that this term gives rise to the leading log divergence at \(T=0\) (from the \(1/(k^2+ i\epsilon )\) term in the photon propagator) as well as the leading linear divergence at \(T\ne 0\) (from the \(\delta (k^2) N(\vert k \vert )\) term). The remaining \(T=0\) part is IR finite since any power of k in the numerator renders the term finite.

At \(T \ne 0\), in addition, the logarithmic subdivergence arising from the \((p_f \cdot p_i) \times [\mathcal{O}(k)]\) term from Eqs. (29) and (30), also vanishes since the coefficient of this term is zero. But there is a term arising from the \(((p_f + p_i) \cdot k) \times [\mathcal{O}(1)]\) factor in the thermal part, that appears to be a logarithmic subdivergence. We however observe that the \([\mathcal{O}(1)]\) terms in the scalar part are symmetric under the interchange \((k \leftrightarrow -k)\); since the term \(((p_f + p_i) \cdot k)\) is linear in k, the entire contribution is odd under this interchange, so that this potential subdivergent log contribution vanishes. Higher order terms arising from even powers of k in the integrand are IR finite. Hence the G photon insertions are IR finite.

We have implicitly assumed that there are no divergences associated with the photon momenta \(l_i\) in the lower order graphs (that is, from \(\mathcal{M}_n\)). This is not necessarily true; divergences can potentially arise from any of the soft photons in the graph. Here, the procedure, as shown by GY, is to separate out the photon momenta into groups that cause an IR divergence and those that do not. It is then possible to ignore the latter group and construct so-called “skeletal graphs” where the divergence arises only when each of the controlling momenta, \(l_i, i=1,\ldots ,m\), simultaneously vanish. It was shown in Refs. [4, 12] that G photon insertions are finite with respect to all such controlling momenta for a theory of charged fermions at zero and finite temperature. In Appendix D we show that this holds for scalars at finite temperature as well.

This result also holds when we extend the analysis to include the possibility that the \(\mu \) and \(\nu \) vertex insertions are of 4-point type, or even that some or all of the vertices in the lower order graph are of 4-point type as well; each of these cases is dealt with in detail in Appendix D. The final generalisation is when we include thermal effects in the scalar propagator as well (those in the vertices are quite trivial to deal with). We discuss this below.

3.2.1 Effect of including thermal scalars

When the scalar field is also thermal, it is not sufficient to consider the \(1/(P^2 -m^2)\) part of the scalar propagator. There are factors of the scalar number operator, \(N_S\), that can cause a potential divergence since the scalar fields are bosons with,

$$\begin{aligned} N_S(\vert P^0 \vert ) = \frac{1}{\exp [\vert P^0 \vert /T] -1} \; {\mathop {\longrightarrow }\limits ^{P^0 \rightarrow 0}} \; \frac{1}{\vert P^0 \vert }~, \end{aligned}$$
(31)

in contrast to the fermionic case where the number operator is finite, \(N_f \rightarrow 1/2\), as \(\vert P^0 \vert \rightarrow 0\); so we need to check that this result holds when the scalars are thermal as well. We begin as usual by considering graphs with only 3-point vertices.

The numerator factors arising from the scalar–photon vertices acquire only irrelevant modifications when temperature effects are included; hence the structure of the vertices, that were crucial in obtaining the cancellation of the leading divergence of the G photon contributions between the \(g_{\mu \nu }\) and \(b_k k_\mu k_\nu \) terms in Eq. (28), still holds. We need to consider only the terms linear in k that can give rise to subleading logarithmic divergences as discussed above.

We, therefore, examine the finite temperature dependence of the scalar propagators. In contrast to the case of thermal photons, the momentum \(p_f\) (or \(p_i\)) flows through all the scalar lines and this controls the behaviour in the soft limit. The pure \(L_0(l_i) \sim 1/(l_i^2-m^2)\) dependence at \(T=0\) is replaced by a sum of \(L_0(l_i)\) and \(L_T(l_i) \sim \delta (l_i^2 - m^2)\) terms. Hence, none, some, or all the scalar propagators can have thermal contributions. The case where all scalar propagators correspond to \(L_0\) is the case that we have studied so far.

While the two propagators have the same dimensional dependence on k, \(L_T(l_i = P+k)\) contains a delta-function \(\delta ((P+k)^2-m^2)\) dependence which either makes the term finite or else leads to a constraint where \(k^0\) is related to combinations of the remaining (controlling) momenta and hence there is no (logarithmic sub)divergence associated with this term. This holds even when more than one of the scalar propagators is a thermal \(L_T\) type. The detailed analysis for adding a G photon to a lower order graph with thermal electrons, and having one or more momenta in the controlling set, can be found in Ref. [12] and applies to the case of charged scalars as well. Hence the G photon insertion is IR finite when we consider the entire thermal structure of the theory, both for charged scalars and photons, and even if the charged particles are fermions. More details are found in Appendix D. Finally, the cases when some of the vertices are K photons or real photon vertices is also discussed in Appendix D.

As before, we have to verify that when we “flesh out” skeletal graphs and include self-energy or other terms, the graph remains IR finite; this is also shown in Appendix D. This concludes the proof that the entire virtual G photon insertions of the full finite temperature theory (with both charged fermions and scalars) are in general IR finite.

3.3 The final matrix element for virtual photons

We have obtained the familiar result that the (IR divergent) contribution of the K photon insertions is proportional to the lower order matrix element, \(\mathcal{M}_n\) while the G photon insertions are finite. We proceed as in the case of \(T=0\) scalar QED or thermal fermionic QED and consider the contribution of the nth order graph with \(n_K\) virtual K photons and \(n_G\) virtual G photons. Hence \(n=n_K+n_G\) and there are at most n vertices (since some can be seagulls or tadpoles). As a consequence of the Bose symmetry for the n photons, each distinct graph can arise in \(n!/n_K!\,n_G!\) ways, so that the total matrix element can be expressed as a sum of all possible individual contributions,

$$\begin{aligned} \frac{1}{n!}\, \mathcal{M}_n = \sum _{n_K=0}^{n} \frac{1}{n_K!} \frac{1}{n - n_K!} \mathcal{M}_{{n_G},{n_K}}~. \end{aligned}$$
(32)

Summing over all orders, we get

$$\begin{aligned} \sum _{n=0}^{\infty } \frac{1}{n!} \mathcal{M}_n&= \sum _{n=0}^{\infty } \sum _{n_K=0}^{n} \frac{1}{n_K!} \frac{1}{n - n_K!} \mathcal{M}_{{n_G},{n_K}}~, \nonumber \\&= \sum _{n_K=0}^\infty \sum _{n_G=0}^{\infty } \frac{1}{n_K!} \frac{1}{n_G!} \mathcal{M}_{{n_G},{n_K}}~, \end{aligned}$$
(33)

and we use the result that the K photon contribution is proportional to the lower order matrix element to obtain:

$$\begin{aligned} \mathcal{M}_{{n_G},{n_K}}&= (B)^{n_K} M_{n_G,0} \equiv (B)^{n_K} M_{n_G}~, \end{aligned}$$
(34)

where B as defined in Eq. (23) is the contribution from each K-photon insertion and can be isolated and factored out, leaving only the IR finite G-photon contribution, \(\mathcal{M}_{n_G}\). Re-sorting and collecting terms, we obtain the requisite exponential IR divergent factor:

$$\begin{aligned} \sum _{n=0}^\infty \frac{1}{n!} \mathcal{M}_n&= \sum _{n_K=0}^\infty \frac{(B)^{n_K}}{n_K!} \sum _{n_G=0}^{\infty } \frac{1}{n_G!} \mathcal{M}_{n_G}~, \nonumber \\&= \mathrm{e}^{B} \sum _{n_G=0}^\infty \frac{1}{n_G!} \mathcal{M}_{n_G}~. \end{aligned}$$
(35)

Again we highlight that this factorisation was made possible since the K-photon insertions gave precisely one term and no additional pieces, IR-finite or otherwise; this occurred due to the presence of both 3-point and 4-point vertices in the theory. The resulting cross section including only the virtual photon contributions to all orders is,

$$\begin{aligned} \sigma ^{\mathrm{virtual}}&\propto \int \mathrm{d}\phi _{p'} (2\pi )^4 \delta ^4(p+q-p') \left| \sum _{n=0}^\infty \frac{1}{n!} \mathcal{M}_n \right| ^2~, \nonumber \\&= \int \mathrm{d}\phi _{p'} (2\pi )^4 \delta ^4(p+q-p') ~\vert Z \vert ^2 ~ \sigma ^{\mathrm{virtual}}_G~, \end{aligned}$$
(36)

where \(\mathrm{d}\phi _{p'}\) is the phase space factor corresponding to the final state scalar with momentum \(p'\) and a(n irrelevant) flux factor in the denominator has been suppressed. The IR-finite part is contained in the last term and the IR divergent part is contained in the exponent,

$$\begin{aligned} \vert Z \vert ^2&\equiv \exp \left( B + B^* \right) ~, \end{aligned}$$
(37)

and will be shown below to cancel against a corresponding contribution from real (soft) photon emission/absorption with respect to the heat bath, thus indicating that thermal scalar electrodynamics is also IR finite at all orders.

3.4 Emission/absorption of real photons

There is a major difference in the thermal case: real photons can be emitted into or absorbed from the heat bath. Again, the real photon vertex can be either on the p or \(p'\) leg, and the contributions of the two can be independently calculated. The insertion can be a 3-point vertex (photon inserted on the p or \(p'\) leg at a new vertex \(\mu \)) or a 4-point vertex (photon inserted on an already existing vertex, giving seagull but not tadpole diagrams since a real photon is actually emitted/absorbed).

Unlike the virtual photon insertions, physical momentum is carried away or brought in by the real photon. Without loss of generality, this can be accounted for by retaining the momenta of the external scalar legs to be p and \(p'\) and adjusting the momentum at the special vertex V to maintain energy-momentum conservation. Hence the factors are somewhat different from the virtual photon case: when the \((n+1)\)th photon is emitted from the p leg, the momentum of the scalar/fermion to the right of the insertion \(\mu \) is \((p + \sum _{i=1}^q l_i -k)\) where q is the vertex immediately to the left of \(\mu \); here \(l_i\) are the photon momenta emitted/absorbed at the ith vertex. Similarly, for an emission from the \(p'\) leg, the momentum of the scalar/fermion to the left of \(\mu \) is \((p' + \sum _{i=1}^q l_i+k)\), where q is the vertex immediately to the right of \(\mu \). If the photon is absorbed rather than emitted, the sign of k is reversed.

Since the real photon insertions contribute to \(\vert \mathcal{{M}} \vert ^2\), that is, to the cross section, we need to consider thermal modifications to the phase space. The thermal phase space element corresponding to the ith real photon with momentum \(k_i\) is given by,

$$\begin{aligned} \mathrm{d}\phi _i&= \frac{\mathrm{d}^4k_i}{(2\pi )^4} \, 2\pi \delta (k_i^2) \, \left[ \theta (k_i^0) + N(\vert \varvec{k_i} \vert ) \right] ~. \end{aligned}$$
(38)

Here emission of photons corresponds to \(k_i^0 > 0\) and absorption to \(k_i^0 < 0\), thus giving the correct statistical factors of \(N\!+\!1\) for photon emission into, and N for photon absorption from, the heat bath at temperature T. Again, the presence of the thermal number operator worsens the divergence in the case of real photon emission/absorption as well, giving a leading IR dependence that is linear, since \(N \sim 1/k\) in the soft limit. Note that the presence of the same term acts as an UV cut off when \(k \rightarrow \infty \).

We proceed as in GY, re-writing the polarisation sum in the cross section and separating it into a \({\widetilde{K}}\) part that potentially contains the entire IR divergent part and an IR finite \({\widetilde{G}}\) photon part:

$$\begin{aligned} \sum _{\mathrm{pol}} \epsilon ^*_\mu (k)\,\epsilon _\nu (k) = - g_{\mu \nu }~, \end{aligned}$$
(39)

with

$$\begin{aligned} g_{\mu \nu }&= \left\{ \left[ g_{\mu \nu } - {\tilde{b}}_k(p_f,p_i) k_\mu k_\nu \right] + \left[ {\tilde{b}}_k(p_f,p_i) k_\mu k_\nu \right] \right\} ~, \nonumber \\&\equiv \left\{ \left[ {\widetilde{G}}_{\mu \nu }\right] + \left[ {\widetilde{K}}_{\mu \nu }\right] \right\} ~, \end{aligned}$$
(40)

where the tildes have been used to distinguish the real from the virtual photon contributions. Since \(k^2=0\) for both real photon emission and absorption, we define,

$$\begin{aligned} {\tilde{b}}_k(p_f, p_i) = b_k(p_f, p_i)\Big |_{k^2 = 0} = \frac{p_f \cdot p_i}{ k\cdot p_f\; k\cdot p_i}~, \end{aligned}$$
(41)

where \(p_i\) (\(p_f\)) corresponds to the initial (final) momentum of the hard scalar in \(\mathcal{{M}}\) (\(\mathcal {M}^*\)) where the real photon of momentum k is inserted.

3.4.1 Emission/absorption of real \({\widetilde{K}}\) photons

The proof that the contribution from \({\widetilde{K}}\) photons is IR divergent and can be factored is much simpler than the corresponding case of virtual photons. The key point to note is that real photons, whether emitted or absorbed, correspond to thermal type 1 photons, so that the inserted vertex (either \(\mu \) or \(\nu \)) is of type 1 alone. This is critical in obtaining a cancellation against the virtual photon contribution and the significance of this virtual contribution being proportional to \(D^{11}\) alone, as shown in Eqs. (15) and (21), is now clear.

The calculation for photon emission proceeds exactly as in the case of virtual photon vertex insertion on a p or \(p'\) leg (see diagrams shown in Fig. 5). Again, there is a term-by-term cancellation, leading to a factor proportional to the matrix element of the n photon diagram, \(\mathcal{{M}}_n\). Similar insertions on the p leg give a result proportional to \(-\mathcal{{M}}_n\); the difference in sign with the case of insertion of \(b_k (p',p)\) virtual K photons is due to the fact that the real photon momentum is always out-going for emitted photons; while the virtual momentum enters/leaves at the \(\nu /\mu \) vertex. The overall sign is reversed in the case of photon absorption; however, this is irrelevant and unobserved in the cross section. Adding the two terms and squaring gives the contribution of the real \({\widetilde{K}}\) photon insertion to be an overall factor multiplying the nth order cross section, proportional to,

$$\begin{aligned} \left| \mathcal{{M}}_{n+1}^{{\widetilde{K}}\gamma ,\mathrm{tot}} \right| ^2&\propto -e^2 \left[ {\tilde{b}}_k(p,p) -2 {\tilde{b}}_k(p',p) + {\tilde{b}}_k(p',p') \right] ~, \nonumber \\&\equiv -e^2 {\widetilde{J}}^2(k)~. \end{aligned}$$
(42)

The result holds even when some vertices of the lower order graph are 4-point ones, or correspond to virtual photon insertions as well; this follows from the arguments given for the virtual K photon insertions in Appendix C.

Before discussing the cross section, we will first complete the discussion on insertions of real \({\widetilde{G}}\) photons, which, as expected, will be IR finite.

3.4.2 Emission/absorption of real \({\widetilde{G}}\) photons

The proof of IR finiteness of the real \({\widetilde{G}}\) photon cross section follows from the same argument as for the virtual G-photon insertion and is not repeated here in detail. Specifically, the case where the insertions are on different legs (\(p'\) and p) is relevant for the real photon insertions. All the cases such as including both 3- and 4-point vertices, including thermal effects in both photon and scalar propagators, etc., hold here; there are no tadpole diagrams in this case and also no quadratic \(\mathcal{O}(k^2)\) contribution that needs to be cancelled.

The key point to note here is the k-dependence of the thermal part. The leading divergence (logarithmic in the zero temperature case and linear in the finite temperature case) cancels as before, between the \(g_{\mu \nu }\) and the \({\tilde{b}}_k k_\mu k_\nu \) parts of \({\widetilde{G}}\), owing to the definition of \({\tilde{b}}_k\). We are thus concerned only with terms with powers of k in the numerator which potentially give logarithmic subdivergences.

The main difference between virtual and real photon insertion is that the phase space factor is not symmetric under \(k \leftrightarrow -k\) because of the presence of the theta function, as seen from Eq. (38). However, the finite temperature part of the phase space is symmetric under this exchange since it includes both photon emission and absorption. These are anyway the only contributions of interest since any powers of k in the numerator are finite with respect to the \(T=0\) part. This symmetry enables us to symmetrise the integrand with respect to \(k \leftrightarrow -k\) and obtain the analogous result that real \({\widetilde{G}}\) photon insertions are IR finite. Notice that application of the symmetry requires the presence of both soft photon emission and absorption terms.

Again, the result holds when one of the photons with momentum \(k_l\) contributes through its \(T=0\) part; in this case, its corresponding momentum cannot be flipped since its phase space is not symmetric under this exchange. We apply the same logic as with skeletal graphs in the virtual photon case: if this photon is not a part of the controlling set, there is no divergence associated when it vanishes and this gives us no trouble. If it is a part of the controlling set, then the sub-divergence occurs only when all (including this) momenta vanish simultaneously; however, any power of \(k_l\) in the numerator renders the contribution finite since it contributes through its \(T=0\) part and so again its contribution is finite. The analysis holds when arbitrary number of these photons contribute through their \(T=0\) parts; also when some of these are virtual photons, since their contribution is always symmetric in the loop momentum.

Hence, \({\widetilde{G}}\) photon emissions give a finite contribution to the cross section.

3.4.3 The total cross section from real photon emission/absorption

Consider an nth order graph with an arbitrary number of \({\widetilde{K}}\) and \({\widetilde{G}}\) photon insertions. Now \(n_K\) \({\widetilde{K}}\) and \(n_G\) \({\widetilde{G}}\) real photon emission/absorption can occur in \(n!/n_K!n_G!\) ways; \(n=n_K+n_G\), and each real photon carries away/brings in a physical momentum \(k_l\) from/to the process. Dividing by n! due to n identical photons in the final state, to this order, we have,

$$\begin{aligned} \mathrm{d}\sigma ^{\mathrm{real}}_n&= \sum _{n_K=0}^{n} \int \frac{1}{n_K!} \left[ \prod _{i=1}^{n_K} \mathrm{d}\phi _i \left\{ -e^2 {\widetilde{J}}^2(k_i) \right\} \right] \nonumber \\&\quad \times \frac{1}{n_G!} \left[ \prod _{j=n_K+1}^{n} \mathrm{d}\phi _j \left\{ - {\widetilde{G}}_{\mu \nu } \left| \mathcal{M}^{\mu \nu , {\tilde{G}}\gamma ,tot}_{n_G} \right| ^2 \right\} \right] \nonumber \\&\quad \times (2\pi )^4 \delta ^4\left( p+q-p'-\sum _{l=1}^{n} (-1)^{l} k_l \right) ~, \end{aligned}$$
(43)

where the factor \((-1)^l\) corresponds to \(\pm 1\) depending on whether the photon with momentum \(k_l\) is emitted/absorbed. Here the phase space factor is given by Eq. (38) and the factor \({\widetilde{J}}(k_i)\) contains the IR divergent part. The \(k_i\) dependence in the energy-momentum conserving delta function is removed by the usual trick of redefining the delta-function:

$$\begin{aligned}&(2\pi )^4 \delta ^4\left( p+q-p'-\sum _{l=1}^{n} (-1)^l k_l \right) \nonumber \\&\quad = \int \mathrm{d}^4x \exp \left[ -i(p+q-p')\cdot x \right] \prod _l \exp (\pm i\,k_l \cdot x)~, \nonumber \\ \end{aligned}$$
(44)

where the sign of \(k_l\) in the last term depends on whether the real photon was emitted or absorbed; furthermore, we separate out the \({\widetilde{K}}\) photon contribution in the last term:

$$\begin{aligned} \prod _{l=1}^n \exp \left[ \pm i\,k_l \cdot x \right]= & {} \prod _{k=1}^{n_K} \exp \left[ \pm i\,k_k \cdot x \right] \nonumber \\&\times \prod _{g=n_K+1}^{n} \exp \left[ \pm i\,k_g \cdot x \right] . \end{aligned}$$
(45)

The terms that depend on the \(k_k\) \({\widetilde{K}}\) photon momenta are then combined with the (common) factor for every \({\widetilde{K}}\) insertion. Then the total contribution from each \({\widetilde{K}}\) photon is:

$$\begin{aligned} {\widetilde{B}}(x) = -e^2 \int {\widetilde{J}}^2(k_k) \mathrm{d}\phi _k \exp \left[ {\pm i\, k_k \cdot x}\right] . \end{aligned}$$
(46)

The total contribution from \({\widetilde{K}}\) real photons in Eq. (43) can now be factored as,

$$\begin{aligned} \mathrm{d}\sigma ^{\mathrm{real, {\widetilde{K}}}}_n&\propto \sum _{n_K=0}^{n} \frac{1}{n_K!} \left( {\widetilde{B}}(x) \right) ^{n_K}~, \end{aligned}$$
(47)

and hence can be exponentiated as \(n \rightarrow \infty \). We will use this factor and compute the total cross section for the process to all orders.

3.5 The total cross section to all orders

The all-order corrections to the tree-level cross section for \(\gamma ^{(*)}\phi \rightarrow \phi \) arising from both virtual and real (soft) photon insertions yields the total cross section for this process:

$$\begin{aligned} \mathrm{d}\sigma ^{\mathrm{tot}}&= \int \mathrm{d}^4x \, e^{-i(p+q-p')\cdot x} \mathrm{d}\phi _{p'} \exp \left[ B+B^* \right] \exp \left[ {\widetilde{B}} \right] \nonumber \\&\quad \times \sum _{n_G=0}^{\infty } \frac{1}{n_G!} \prod _{j=0}^{n_G} \times \int \mathrm{d}\phi _j e^{\pm i k_j \cdot x} \left[ -G_{\mu \nu } \mathcal{M}_{n_G}^{\dagger \mu } \mathcal{M}_{n_G}^\nu \right] ~,\nonumber \\&= \int \mathrm{d}^4x \, e^{-i(p+q-p')\cdot x}\, \mathrm{d}\phi _{p'} \exp \left[ B+B^*+{\widetilde{B}} \right] \, \sigma ^{\mathrm{finite}} (x)~, \end{aligned}$$
(48)

where \(\sigma ^{\mathrm{finite}}\) contains the finite G and \({\widetilde{G}}\) photon contributions from both virtual and real photons. The IR divergent parts of both the virtual and real photon contributions exponentiate and combine to give an IR finite sum, as can be seen by studying their small-k behaviour:

$$\begin{aligned} (B+B^*) + {\widetilde{B}}&= e^2 \int \mathrm{d}\phi _k \left[ J(k)^2\left\{ 1+2N(\vert k^0 \vert )\right\} \right. \nonumber \\&\quad \left. -{\widetilde{J}}(k)^2 \left\{ \left( 1+N(\vert k^0 \vert )\right) e^{i k\cdot x} + N(\vert k^0 \vert )e^{-i k\cdot x} \right\} \right] \nonumber \\&\quad {\mathop {\longrightarrow }\limits ^{k \rightarrow 0}} ~0 + \mathcal{O}(k^2)~. \end{aligned}$$
(49)

Notice that the cancellation occurs between virtual and real contributions only when photon absorption terms [last term in Eq. (49) above] are also included. This is the all-order proof of IR finiteness of the thermal scalar field theory, analogous to that obtained for the thermal field theory of fermions in Ref. [12].

4 Summary and discussion

Corrections to typical hard scattering processes from virtual and real (soft) photon emission combine so that the infra-red (IR) divergences cancel order by order to all orders in perturbation theory. The IR finiteness of pure scalar QED at finite temperature was explicitly shown here to all orders in perturbation theory using the technique of Grammer and Yennie. The explicit IR finiteness of the corresponding zero temperature result was also established along the way. Although the IR behaviour of such theories are expected to be independent of their spin structure, it was instructive to calculate the details of the scalar case in order to understand the key role of the (IR finite) 4-point vertex contributions which enabled the soft terms to be factorised and exponentiated for the all-order case. In particular, it was shown that the presence of the IR finite tadpole contributions was crucial in factorising and exponentiating the IR divergent terms for virtual photon insertions.

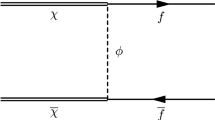
Along with the results of Ref. [12] where the IR finiteness of thermal fermionic QED was proven to all orders, the present results now allow the calculation to be extended to the interesting case of the interaction of dark matter with thermal fermion and scalar fields at finite temperature. Such results are of importance in precision estimates of higher order contributions to dark matter interactions such as \(\chi + \mathcal{{F}} \rightarrow \chi + \mathcal{{F}}\), where the interaction of the dark matter particle, \(\chi \), with fermions \(\mathcal{{F}}\) is mediated by charged scalars. Emission and absorption of soft photons from the heat bath in the early Universe can significantly alter these cross sections. We address the issue of the IR finiteness of such models of bino-like dark matter in the companion paper [19].