Study of $B^-\rightarrow \Lambda \bar{p}\eta ^{(')}$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda }\eta ^{(')}$ decays

Abstract

We study the three-body baryonic $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$ decays with M representing the $\eta$ or $\eta '$ meson. Particularly, we predict that $\mathcal{B}(B^-\rightarrow \Lambda \bar{p}\eta ,\Lambda \bar{p}\eta ') =(5.3\pm 1.4,3.3\pm 0.7)\times 10^{-6}$ or $(4.0\pm 0.7,4.6\pm 1.1)\times 10^{-6}$, where the errors arise from the non-factorizable effects as well as the uncertainties in the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ and $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transition form factors, while the two different results are due to overall relative signs between the form factors, causing the constructive and destructive interference effects. For the corresponding baryonic $\bar{B}_s^0$ decays, we find that $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ,\Lambda \bar{\Lambda } \eta ') =(1.2\pm 0.3,2.6\pm 0.8)\times 10^{-6}$ or $(2.1\pm 0.6,1.5\pm 0.4)\times 10^{-6}$ with the errors similar to those above. The decays in question are accessible to the experiments at BELLE and LHCb.

1 Introduction

In association with the QCD anomaly, the b and c-hadron decays with $\eta ^{(\prime )}$ as the final states have drawn lots of theoretical and experimental attentions, where the $\eta$ and $\eta ^\prime$ mesons are in fact the mixtures of the singlet $\eta _1$ and octet $\eta _8$ states, with $\eta _{1,8}$ being decomposed as $\eta _n=(u\bar{u}+d\bar{d})/\sqrt{2}$ and $\eta _s=s\bar{s}$ in the FKS scheme [1, 2]. In addition, the two configurations of $b\rightarrow s n\bar{n}\rightarrow s\eta _n$ ($n=u$ or d) and $b\rightarrow s\bar{s} s\rightarrow s\eta _s$ have been found to be the causes of the dramatic interferences between the $B\rightarrow K^{(*)}\eta$ and $B\rightarrow K^{(*)}\eta ^{\prime }$ decays, that is, $\mathcal{B}(B\rightarrow K\eta )\ll \mathcal{B}(B\rightarrow K\eta ')$ and $\mathcal{B}(B\rightarrow K^*\eta )\gg \mathcal{B}(B\rightarrow K^*\eta ')$ [3]. Note that the theoretical prediction gives $\mathcal{B}(\bar{B}^0_s\rightarrow \eta ^{(\prime )}\eta ^\prime )\gg \mathcal{B}(\bar{B}^0_s\rightarrow \eta \eta )$ [4], while the only observation is $\mathcal{B}(\bar{B}^0_s\rightarrow \eta ^\prime \eta ^\prime )=(3.3\pm 0.7)\times 10^{-5}$ [5]. On the other hand, with the dominant $b\rightarrow s\bar{s} s\rightarrow s\eta _s$ transition, the theoretical calculations result in $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta )\simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ')$ [6, 7], which has not been confirmed by the the current data [8]. For the dominant tree-level decay modes, the theoretical results indicate that $\mathcal{B}(B\rightarrow \pi \eta )\simeq \mathcal{B}(B\rightarrow \pi \eta ')$ [4] and $\mathcal{B}(\Lambda _c^+\rightarrow p\eta )\simeq \mathcal{B}(\Lambda _c^+\rightarrow p\eta ')$ [9,10,11]. Nonetheless, the observed values of $\mathcal{B}(B\rightarrow \pi \eta ,\pi \eta ')$ show a slight tension with the predictions. Experimentally, there are more to-be-measured decays with $\eta ^{(\prime )}$, such as the B decays of $\bar{B}^0_s\rightarrow \eta \eta ,\eta \eta '$ and $\Lambda _c^+$ decays of $\Lambda _c^+\rightarrow p\eta ^\prime ,\Sigma ^+\eta ^\prime$.

Although the charmless three-body baryonic B decays ($B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$) have been abundantly measured [3], and well studied with the factorization [12,13,14,15, 17,18,19,20,21,22,23,24], neither theoretical calculation nor experimental measurement for $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ has been done yet. We note that the prediction of $\mathcal{B}(B^-\rightarrow \Lambda \bar{p}\phi ) =(1.5\pm 0.3)\times 10^{-6}$ [21] based on the factorization method is slightly larger than the recent BELLE data of $(0.818\pm 0.215\pm 0.078)\times 10^{-6}$ [25]. In $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$, the threshold enhancement has been observed as a generic feature [26,27,28,29,30,31], which is shown as the peak at the threshold area of $m_{{\mathbf{B}}\bar{\mathbf{B}}'}\simeq m_\mathbf{B}+m_\mathbf{B'}$ in the spectrum, with $m_{{\mathbf{B}}\bar{\mathbf{B}}'}$ denoted as the invariant mass of the di-baryon. With the threshold effect, one expects that $\mathcal{B}(B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )})\sim 10^{-6}$, being accessible to the BELLE and LHCb experiments. Furthermore, with $b\rightarrow sn\bar{n}\rightarrow s\eta _n$ and $b\rightarrow s\bar{s} s\rightarrow s\eta _s$, it is worth to explore if $B^-\rightarrow \Lambda \bar{p}\eta ^{(')}$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda }\eta ^{(')}$ have the interference effects for the branching ratios, which can be useful to improve the knowledge of the underlying QCD anomaly for the $\eta -\eta '$ mixing. In this report, we will study the three-body baryonic B decays with one of the final states to be the $\eta$ or $\eta '$ meson state, where the possible interference effects from the $b\rightarrow s n\bar{n}\rightarrow s\eta _n$ and $b\rightarrow s\bar{s} s\rightarrow s\eta _s$ transitions can be investigated.

2 Formalism

Fig. 1

The short-distance pictures for $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$ through the three quasi-two-body decays, where a–c correspond to the collinearly moving $M\mathbf{B}$, $M{\bar{\mathbf{B}}'}$ and ${{\mathbf{B}}\bar{\mathbf{B}}'}$, respectively

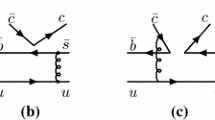
Unlike the two-body mesonic $B\rightarrow MM$ decays, the $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$ decays require two additional quark pairs for the $\mathbf{B}\bar{\mathbf{B}}'$ formation. This is in accordance with the short-distance pictures depicted in Fig. 1 [31, 32], where $q_1\bar{q}_1$ and $q_2\bar{q}_2$ are connected by the gluons $g_{1,2}$, respectively. In Fig. 1a(b), the meson and (anti)baryon move collinearly, with $g_1$ for a collinear quark pair. By connecting to a back-to-back $q_2\bar{q}_2$ pair, $g_2$ is far off the mass shell, such that it is a hard gluon, resulting in the suppression with the factor of order $\alpha _s/q^2$. There remain the resonant contributions observed to be small, which correspond to the suppression due to the short-distance pictures. For example, one has $\mathcal{B}(B^-\rightarrow p\Theta (1710)^{--},\Theta (1710)^{--}\rightarrow \bar{p} K^-)<9.1\times 10^{-8}$ and $\mathcal{B}(\bar{B}^0\rightarrow p\Theta (1540)^-, \Theta (1540)^-\rightarrow \bar{p} K_s^0)<5\times 10^{-8}$ [3]. Moreover, $B^-\rightarrow \Lambda (1520)\bar{p},\Lambda (1520)\rightarrow p K^-$ is observed with $\mathcal{B}\sim 10^{-7}$ [33, 34].

On the other hand, the baryon pair in Fig. 1c moves collinearly, so that $g_{1,2}$ are both close to the mass shell, causing no suppression. Besides, the amplitudes can be factorized as $\mathcal{A}_1\propto \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|J_a|0\rangle \langle M|J_b|B\rangle$ and $\mathcal{A}_2\propto \langle M|J_a|0\rangle \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|J_b|B\rangle$.

Fig. 2

Feynman diagrams for $B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )}$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}$decays through a–d $B\rightarrow \eta ^{(\prime )}$ transitions with $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ productions and e–g $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transitions with the recoiled $\eta ^{(\prime )}$

Accordingly, the Feynman diagrams for the three-body baryonic $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ decays with the short-distance approximation are shown in Fig. 2. In our calculation, we use the generalized factorization as the theoretical approach. The non-factorizable effects are included by the effective Wilson coefficients [35,36,37]. In terms of the effective Hamiltonian for the $b\rightarrow sq\bar{q}$ transitions [38], the decay amplitudes of $B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )}$ by the factorization can be derived as [13,14,15, 18, 19, 22, 23, 37]

(1)

where $n=u$ or d, $G_F$ is the Fermi constant, and $\mathcal{A}_{1}$ and $\mathcal{A}_{2}$ correspond to the two different decaying configurations in Fig. 2. Similarly, the amplitudes of $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}$ are given by

$$\begin{aligned} \mathcal{A}\left( \bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}\right)= & {} \mathcal{A}_1\left( \bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}\right) + \mathcal{A}_2\left( \bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}\right) ,\nonumber \\ \mathcal{A}_1\left( \bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}\right)= & {} \frac{G_F}{\sqrt{2}}\bigg \{ \bigg [ \langle \Lambda \bar{\Lambda } |\bar{n}\gamma _\mu (\alpha _2^+ -\alpha _2^-\gamma _5) n|0\rangle \nonumber \\&+ \left\langle \Lambda \bar{\Lambda } |\bar{s}\gamma _\mu (\alpha _3^+ -\alpha _3^-\gamma _5) s |0\right\rangle \bigg ]\nonumber \\&\times \left\langle \eta ^{(\prime )}|\bar{s} \gamma _\mu (1-\gamma _5) b|\bar{B}^0_s\right\rangle \nonumber \\&+\alpha _6^s\left\langle \Lambda \bar{\Lambda } |\bar{s}(1+\gamma _5) s|0\right\rangle \left\langle \eta ^{(\prime )}|\bar{s}(1-\gamma _5) b|\bar{B}^0_s\right\rangle \bigg \},\nonumber \\ \mathcal{A}_2\left( \bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}\right)= & {} \frac{G_F}{\sqrt{2}}\bigg \{ \bigg [\beta _2\langle \eta ^{(\prime )}|\bar{n}\gamma _\mu \gamma _5 n|0\rangle + \beta _3\langle \eta ^{(\prime )}|\bar{s} \gamma _\mu \gamma _5 s|0\rangle \bigg ]\nonumber \\&\left\langle \Lambda \bar{\Lambda } |\bar{s} \gamma _\mu (1-\gamma _5) b|\bar{B}^0_s\right\rangle \nonumber \\&+ \beta _6\left\langle \eta ^{(\prime )}|\bar{s}\gamma _5 s|0\rangle \langle \Lambda \bar{\Lambda } |\bar{s}(1-\gamma _5) b|\bar{B}^0_s\right\rangle \bigg \}\;. \end{aligned}$$

(2)

The parameters $\alpha _i$ and $\beta _i$ in Eqs. (1) and (2) are defined as

$$\begin{aligned} \alpha _1= & {} V_{ub}V_{us}^* a_1-V_{tb}V_{ts}^*(a_4+a_{10}),\nonumber \\ \alpha _2^\pm= & {} V_{ub}V_{us}^* a_2-V_{tb}V_{ts}^* \left( 2a_3\pm 2a_5\pm \frac{a_7}{2}+\frac{a_9}{2}\right) ,\nonumber \\ \alpha _3^\pm= & {} -V_{tb}V_{ts}^*\left( a_3+a_4\pm a_5\mp \frac{a_7}{2}-\frac{a_9}{2}-\frac{a_{10}}{2}\right) ,\nonumber \\ \alpha _6= & {} V_{tb}V_{ts}^*2(a_6+a_8),\nonumber \\ \alpha _6^s= & {} V_{tb}V_{ts}^*2\left( a_6-\frac{a_8}{2}\right) ,\nonumber \\ \beta _2= & {} -\alpha _2^-,\beta _3=-\alpha _3^-,\beta _6=\alpha _6^s, \end{aligned}$$

(3)

where $V_{ij}$ the CKM matrix elements, and $a_i=c^{eff}_i+c^{eff}_{i\pm 1}/N_c$ for $i=$odd (even) with $N_c$ the effective color number in the generalized factorization approach, consisting of the effective Wilson coefficients $c_i^{eff}$ [37]. The matrix elements in Eq. (1) for the $\eta ^{(\prime )}$ productions read [39]

$$\begin{aligned}&\langle \eta ^{(\prime )}|\bar{n}\gamma _\mu \gamma _5 n|0\rangle = -\frac{i}{\sqrt{2}}f^n_{\eta ^{(\prime )}} q_\mu ,\nonumber \\&\quad \langle \eta ^{(\prime )}|\bar{s}\gamma _\mu \gamma _5 s|0\rangle =-if^s_{\eta ^{(\prime )}} q_\mu ,\nonumber \\&\quad 2m_s \langle \eta ^{(\prime )}|\bar{s}\gamma _5 s|0\rangle =-ih^s_{\eta ^{(\prime )}}, \end{aligned}$$

(4)

with $f^{n,s}_{\eta ^{(\prime )}}$ and $h^s_{\eta ^{(\prime )}}$ the decay constants and $q_\mu$ the four-momentum vector. The $\eta$ and $\eta '$ meson states mix with $|\eta _n\rangle =(|u\bar{u}+d\bar{d}\rangle )/\sqrt{2}$ and $|\eta _s\rangle =|s\bar{s}\rangle$ [1, 2], in terms of the mixing matrix:

$$\begin{aligned} \left( \begin{array}{c} \eta \\ \eta ' \end{array}\right) = \left( \begin{array}{cc} \cos \phi &{}-\sin \phi \\ \sin \phi &{}\cos \phi \end{array}\right) \left( \begin{array}{c} \eta _n\\ \eta _s \end{array}\right) , \end{aligned}$$

(5)

with the mixing angle $\phi =(39.3\pm 1.0)^\circ$. Therefore, $f^n_{\eta ^{(\prime )}}$ and $f^s_{\eta ^{(\prime )}}$ actually come from $f_n$ and $f_s$ for $\eta _n$ and $\eta _s$, respectively. In addition, $h^s_{\eta ^{(\prime )}}$ receive the contributions from the QCD anomaly [39]. The matrix elements of the $B\rightarrow \eta ^{(\prime )}$ transitions are parameterized as [40,41,42]

$$\begin{aligned} \langle \eta ^{(\prime )}| \bar{q} \gamma ^\mu b|B\rangle&{=}&\bigg [(p_B+p_{\eta ^{(\prime )}})^\mu {-}\frac{m^2_B-m^2_{\eta ^{(\prime )}}}{t}q^\mu \bigg ] F_1^{B\eta ^{(\prime )}}(t)\nonumber \\&+\frac{m^2_B-m^2_{\eta ^{(\prime )}}}{t}q^\mu F_0^{B\eta ^{(\prime )}}(t), \end{aligned}$$

(6)

with $q=p_B-p_{\eta ^{(\prime )}}=p_\mathbf{B}+p_{\bar{\mathbf{B}}'}$ and $t\equiv q^2$, where the momentum dependences are expressed as [43]

$$\begin{aligned} F^{B\eta ^{(\prime )}}_1(t)= & {} \frac{F^{B\eta ^{(\prime )}}_1(0)}{(1-\frac{t}{M_V^2}) \left( 1-\frac{\sigma _{11} t}{M_V^2}+\frac{\sigma _{12} t^2}{M_V^4}\right) },\;\nonumber \\ F^{B\eta ^{(\prime )}}_0(t)= & {} \frac{F^{B\eta ^{(\prime )}}_0(0)}{1-\frac{\sigma _{01} t}{M_V^2}+\frac{\sigma _{02} t^2}{M_V^4}}. \end{aligned}$$

(7)

According to the mixing matrix in Eq. (5), one has

$$\begin{aligned} (F^{B\eta },F^{B\eta '})= & {} (F^{B\eta _n}\cos \phi ,F^{B\eta _n}\sin \phi ),\nonumber \\ (F^{B_s\eta },F^{B_s\eta '})= & {} (-F^{B_s\eta _s}\sin \phi ,F^{B_s\eta _s}\cos \phi ), \end{aligned}$$

(8)

for the $B^-$ and $\bar{B}^0_s$ transitions to $\eta ^{(\prime )}$, respectively, where $F^{B\eta ^{(\prime )}}$ represent $F^{B\eta ^{(\prime )}}_{1,0}(0)$.

The matrix elements in Eq. (1) for the baryon-pair productions are parameterized as [14, 15]

$$\begin{aligned} \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|(\bar{q}q')_V|0\rangle= & {} \bar{u}\bigg [F_1\gamma _\mu +\frac{F_2}{m_\mathbf{B}+m_{\bar{\mathbf{B}}'}}i\sigma _{\mu \nu }q^\nu \bigg ]v,\nonumber \\ \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|(\bar{q}q')_A|0\rangle= & {} \bar{u}\bigg [g_A\gamma _\mu +\frac{h_A}{m_\mathbf{B}+m_{\bar{\mathbf{B}}'}}q_\mu \bigg ]\gamma _5 v,\nonumber \\ \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|(\bar{q}q')_S|0\rangle= & {} f_S\bar{u}v,\nonumber \\ \langle {{\mathbf{B}}\bar{\mathbf{B}}'}|(\bar{q}q')_P|0\rangle= & {} g_P\bar{u} \gamma _5 v, \end{aligned}$$

(9)

with $(\bar{q}q')_{V,A,S,P}= (\bar{q}\gamma _\mu q',\bar{q}\gamma _\mu \gamma _5q',\bar{q}q',\bar{q}\gamma _5 q')$, where u(v) is the (anti-)baryon spinor, and $(F_{1,2},g_A,h_A,f_S,g_P)$ are the timelike baryonic form factors. Meanwhile, the matrix elements of the $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transitions are written to be [13, 18]

(10)

with $p_\mu =(p_B-q)_\mu$, where $g_i(f_i)$ $(i=1,2, ...,5)$ and $\bar{g}_j(\bar{f}_j)$ $(j=1,2,3)$ are the $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transition form factors. The momentum dependences of the baryonic form factors in Eqs. (9) and (10) depend on the approach of perturbative QCD counting rules, given by [13, 18, 44, 46],

$$\begin{aligned}&F_1=\frac{\bar{C}_{F_1}}{t^2},\quad g_A=\frac{\bar{C}_{g_A}}{t^2},\quad f_S=\frac{\bar{C}_{f_S}}{t^2},\quad g_P=\frac{\bar{C}_{g_P}}{t^2},\quad \nonumber \\&f_i=\frac{D_{f_i}}{t^3},\quad g_i=\frac{D_{g_i}}{t^3},\quad \bar{f}_i=\frac{D_{\bar{f}_i}}{t^3},\quad \bar{g}_i=\frac{D_{\bar{g}_i}}{t^3}, \end{aligned}$$

(11)

where $\bar{C}_i=C_i [\text {ln}({t}/{\Lambda _0^2})]^{-\gamma }$ with $\gamma =2.148$ and $\Lambda _0=0.3$ GeV. Compared to the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ form factors, the $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ ones have an additional 1 / t, which is for a gluon to speed up the slow spectator quark in B. Due to $F_2=F_1/(t\text {ln}[t/\Lambda _0^2])$ in [47], derived to be much less than $F_1$, and $h_A=C_{h_A}/t^2$ [48] that corresponds to the smallness of $\mathcal{B}(\bar{B}^0\rightarrow p\bar{p})\sim 10^{-8}$ [49, 50], we neglect $F_2$ and $h_A$. Under the SU(3) flavor and SU(2) spin symmetries, the constants $C_i$ can be related, given by [14, 24, 44]

$$\begin{aligned}&(C_{F_1},C_{g_A},C_{f_S},C_{g_P})= \sqrt{\frac{3}{2}}\left( C_{||},C_{||}^*,-\bar{C}_{||},-\bar{C}_{||}^*\right) ,\;\;\;\nonumber \\&\quad \text {(for }\langle \Lambda \bar{p}|\left( \bar{s} u)_{V,A,S,P}|0\rangle \right) \nonumber \\&\left( C_{F_1},C_{g_A},C_{f_S},C_{g_P}\right) = \left( C_{||},C_{||}^*,-\bar{C}_{||},-\bar{C}_{||}^*\right) ,\;\;\;\nonumber \\&\quad \text {(for }\langle \Lambda \bar{\Lambda } |(\bar{s} s)_{V,A,S,P}|0\rangle )\nonumber \\&\left( C_{F_1},C_{g_A}\right) =\frac{1}{2}\left( C_{||}+C_{\overline{||}},C_{||}^*-C_{\overline{||}}^*\right) ,\;\;\; \text {(for }\langle \Lambda \bar{\Lambda } |(\bar{n} n)_{V,A}|0\rangle )\nonumber \\ \end{aligned}$$

(12)

with $C_{||(\overline{||})}^*\equiv C_{||(\overline{||})}+\delta C_{||(\overline{||})}$ and $\bar{C}_{||}^*\equiv \bar{C}_{||}+\delta \bar{C}_{||}$, where $\delta C_{||(\overline{||})}$ and $\delta \bar{C}_{||}$ are added to account for the broken symmetries, indicated by the large and unexpected angular distributions in $\bar{B}^0\rightarrow \Lambda \bar{p}\pi ^+$ and $B^-\rightarrow \Lambda \bar{p}\pi ^0$ [27]. With the same symmetries [13, 18, 19, 22, 23], $D_i$ are related by

$$\begin{aligned} \langle \Lambda \bar{p}|(\bar{s} b)_{V,A}|B^-\rangle \!:\;\; D_{g_1}= & {} D_{f_1}=\sqrt{\frac{3}{2}}D_{||},\;\nonumber \\ D_{g_{4,5}}= & {} -D_{f_{4,5}}=-\sqrt{\frac{3}{2}}D_{||}^{4,5}, \nonumber \\ \langle \Lambda \bar{p}|(\bar{s} b)_{S,P}|B^-\rangle \!:\;\; D_{\bar{g}_1}= & {} -D_{\bar{f}_1}=\sqrt{\frac{3}{2}}\bar{D}_{||},\;\nonumber \\ D_{\bar{g}_{2,3}}= & {} D_{\bar{f}_{2,3}}=-\sqrt{\frac{3}{2}}\bar{D}_{||}^{2,3}, \nonumber \\ \langle \Lambda \bar{\Lambda } |(\bar{s} b)_{V,A}|\bar{B}^0_s\rangle \!:\;\; D_{g_1}= & {} D_{f_1}=D_{||},\;\nonumber \\ D_{g_{4,5}}= & {} -D_{f_{4,5}}=-D_{||}^{4,5}, \nonumber \\ \langle \Lambda \bar{\Lambda } |(\bar{s} b)_{S,P}|\bar{B}^0_s\rangle \!:\;\; D_{\bar{g}_1}= & {} -D_{\bar{f}_1}=\bar{D}_{||},\;\nonumber \\ D_{\bar{g}_{2,3}}= & {} D_{\bar{f}_{2,3}}=-\bar{D}_{||}^{2,3}, \end{aligned}$$

(13)

where the ignorances of $D_{g_{2,3}}$ and $D_{f_{2,3}}$ correspond to the derivations of $f_M p^\mu \bar{u} (\sigma _{\mu \nu } p^\nu )v=0$ for $g_2(f_2)$ and $f_M p^\mu \bar{u} p_\mu v\propto m_M^2$ for $f_3(g_3)$ in the amplitudes. For the integration over the phase space in the three-body decay, we refer the general equation of the decay width in the PDG, given by [3]

$$\begin{aligned} \Gamma =\int _{m_{12}^2}\int _{m_{23}^2} \frac{1}{(2\pi )^3}\frac{|{\bar{\mathcal{A}}}|^2}{32M^3_B}dm_{12}^2 dm_{23}^2, \end{aligned}$$

(14)

with $m_{12}=p_\mathbf{B}+p_{\bar{\mathbf{B}}'}$ and $m_{23}=p_\mathbf{B}+p_{\eta ^{(\prime )}}$, where $|{\bar{\mathcal{A}}}|^2$ represents the amplitude squared with the total summations of the baryon spins. On the other hand, we can also study the partial decay rate in terms of the the angular dependence, given by [18]

$$\begin{aligned} {d\Gamma \over d\cos \theta } = \int _t \frac{\beta _t^{1/2}\lambda ^{1/2}_t}{(8\pi m_B)^3}|{\bar{\mathcal{A}}}|^2\;dt, \end{aligned}$$

(15)

where $t\equiv m_{12}^2$, $\beta _t=1-(m_\mathbf{B}+m_{\bar{\mathbf{B}}'})^2/t$, $\lambda _t=[(m_B+m_M)^2+t][(m_B-m_M)^2+t]$, and $\theta$ is the angle between the moving directions of $\mathbf B$ and M.

3 Numerical analysis

Table 1 The values of $\alpha _i$ and $\beta _i$ with $N_c=2,\,3$, and $\infty$

Table 2 Numerical results for $\mathcal{B}(B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )})$ and $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )})$, with $\mathcal{B}_\pm =\mathcal{B}_1+\mathcal{B}_2\pm \mathcal{B}_{1\cdot 2}$, where $(\mathcal{B}_1, \mathcal{B}_2, \mathcal{B}_{1\cdot 2})$ are denoted as the partial branching ratios from the amplitudes $\mathcal{A}_1$, $\mathcal{A}_2$ and the interferences, while the errors come from the non-factorizable effects and form factors, respectively

Fig. 3

The kinematical allowed regions of I, II, IIIa and IIIb (left panel) and Dalitz plot distribution (right panel) in the plane of $m_{\Lambda \bar{p}}$ and $m_{\Lambda \eta }$ for $B^-\rightarrow \Lambda \bar{p}\eta$

In the numerical analysis, we use the Wolfenstein parameters for the CKM matrix elements:

$$\begin{aligned}&V_{ub}=A\lambda ^3(\rho -i\eta ),\,V_{tb}=1,\nonumber \\&V_{us}=\lambda ,\,V_{ts}=-A\lambda ^2, \end{aligned}$$

(16)

with $\lambda$, A, $\rho =\bar{\rho }/(1-\lambda ^2/2)$ and $\eta =\bar{\eta }/(1-\lambda ^2/2)$, given by [3]

$$\begin{aligned} \lambda= & {} 0.22453{\pm } 0.00044, A = 0.836\pm 0.015, \nonumber \\ \bar{\rho }= & {} 0.122^{+0.018}_{-0.017}, \bar{\eta }=0.355^{+0.012}_{-0.011}. \end{aligned}$$

(17)

In the adoption of the effective Wilson coefficients $c_i^{eff}$ in Ref. [37], the values of $\alpha _i$ and $\beta _i$ in Eqs. (1), (2) and (3) are given in Table 1 with $N_c=(2,3,\infty )$ to estimate the non-factorizable effects. For the $0\rightarrow (\eta ,\eta ^\prime )$ productions and $B\rightarrow (\eta ,\eta ^\prime )$ transitions, one gets [39, 43, 51]

$$\begin{aligned}&(f^n_{\eta },f^n_{\eta ^\prime },f^s_{\eta },f^s_{\eta ^\prime })= (0.108,\,0.089,-0.111,\,0.136)\,\text {GeV},\nonumber \\&(h^s_{\eta },h^s_{\eta ^\prime })=(-0.055,\,0.068)\,\text {GeV}^3,\nonumber \\&(F^{B\eta _n},\sigma _{11},\sigma _{12},\sigma _{01},\sigma _{02}) =(0.33,\,0.48,\,0,\,0.76,\,0.28),\nonumber \\&(F^{B_s\eta _s},\sigma _{11},\sigma _{12},\sigma _{01},\sigma _{02}) =(0.36,\,0.60,\,0.20,\,0.80,\,0.40),\nonumber \\ \end{aligned}$$

(18)

with $M_V=5.32$ GeV, resulting in $(F^{B\eta },F^{B\eta '})=(0.26,0.21)$ and $(F^{B_s\eta },F^{B_s\eta '})=(-0.23,0.28)$ by Eq. (8).

To extract the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ baryonic form factors, the minimal $\chi ^2$ fitting method has been used to fit with 20 data points, where 11 of them are from the branching ratios of $D_s^+\rightarrow p\bar{n}$, $\bar{B}^0_{(s)}\rightarrow p\bar{p}$, $B^-\rightarrow \Lambda \bar{p}$, $\bar{B}^0\rightarrow n\bar{p} D^{*+}(\Lambda \bar{p} D^{(*)+})$, $\bar{B}^0(B^-)\rightarrow \Lambda \bar{p}\pi ^{+(0)}$, $B^-\rightarrow \Lambda \bar{p} \rho ^0$ and $B^-\rightarrow \Lambda \bar{\Lambda } K^-$, 4 the angular distribution asymmetries of $\bar{B}^0\rightarrow \Lambda \bar{p} D^{(*)+}$, $\bar{B}^0(B^-)\rightarrow \Lambda \bar{p}\pi ^{+(0)}$ and 5 the angular distribution in $\bar{B}^0\rightarrow \Lambda \bar{p}\pi ^+$ [27]. This presents a reasonable fit with $\chi ^2/d.o.f\simeq 2.3$, where d.o.f stands for the degree of freedom. Hence, we adopt the fitted values to be [22,23,24]

$$\begin{aligned}&(C_{||},\,\delta C_{||})=(154.4\pm 12.1,\,19.3\pm 21.6)\;\mathrm{GeV}^{4},\nonumber \\&(C_{\overline{||}},\,\delta C_{\overline{||}})=(18.1\pm 72.2,\,-477.4\pm 99.0)\;\mathrm{GeV}^{4},\nonumber \\&(\bar{C}_{||},\,\delta \bar{C}_{||})=(537.6\pm 28.7,\,-342.3\pm 61.4)\;\mathrm{GeV}^{4}. \end{aligned}$$

(19)

Here, we have assumed that the timelike baryonic form factors are real. In general, they can be complex numbers if some resonances are involved with un-calculable strong phases. However, these phases are believed to be negligible. For the $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transition ones, the extractions depend on 28 data points with 7 from the branching ratios of $B^-\rightarrow p\bar{p} (K^-,\pi ^-)$, $B^-\rightarrow p\bar{p} e^-\bar{\nu }_e$ and $\bar{B}^0\rightarrow p\bar{p} (K^{(*)0},D^{(*)0})$, 3 the CP violating asymmetries of $B^-\rightarrow p\bar{p} (K^{(*)-},\pi ^-)$ and 2 the angular distribution asymmetries of $B^-\rightarrow p\bar{p} (K^-,\pi ^-)$, together with 16 data points from the angular distributions in $B^-\rightarrow p\bar{p} (K^-,\pi ^-)$ [29], resulting in $\chi ^2/d.o.f\simeq 0.8$ for a reasonable fit also. The values of $D_i$ are given by [22, 23]

$$\begin{aligned} D_{||}= & {} (45.7\pm 33.8)\;\mathrm{GeV}^{5},\nonumber \\ \left( D_{||}^4,D_{||}^5\right)= & {} (6.5\pm 18.1,-147.1\pm 29.3)\;\mathrm{GeV}^{4},\nonumber \\ \left( \bar{D}_{||},\bar{D}_{||}^2,\bar{D}_{||}^3\right)= & {} (35.2\pm 4.8,-22.3\pm 10.2, 504.5\pm 32.4)\;\mathrm{GeV}^{4}.\nonumber \\ \end{aligned}$$

(20)

With the theoretical inputs in Eqs. (19) and (20), one has well explained the observations of $\mathcal{B}(\bar{B}^0_s\rightarrow \bar{p}\Lambda K^+ +p\bar{\Lambda } K^-)$ and $\mathcal{B}(B\rightarrow p\bar{p} MM)$ [23, 24].

Fig. 4

Decay spectra versus $m_{{\mathbf{B}}\bar{\mathbf{B}}'}$ (left) and $m_{\mathbf{B}\eta ^{(\prime )}}$ (right) of the three-body $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ decays, where the solid (dash) curves for $B^-\rightarrow \Lambda \bar{p}\eta$ with the constructive (destructive) interfering effects correspond to the kinematical regions in the left panel of Fig. 3, while those for $B^-\rightarrow \Lambda \bar{p}\eta ^\prime$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}$ are similarly presented

Since the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ and $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ baryonic transition form factors are separately extracted from the data, it is possible to have overall positive or negative signs between C and D in Eqs. (19) and (20), causing two different scenarios for the interferences. In Table 2, we present the results for $\mathcal{B}(B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )})$ and $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )})$ with $\mathcal{B}_{\pm }\equiv \mathcal{B}_1+\mathcal{B}_2\pm \mathcal{B}_{1\cdot 2}$, where the notations of “±” are due to the undetermined relative signs, and $(\mathcal{B}_1, \mathcal{B}_2, \mathcal{B}_{1\cdot 2})$ are denoted as the partial branching ratios from the amplitudes $\mathcal{A}_1$, $\mathcal{A}_2$ and the interferences, respectively. Note that the errors in Table 2 arise from the estimations of the non-factorizable effects in the generalized factorization with $N_c=2,3,\infty$ for the parameters in Table 1, and the uncertainties in the form factors of the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ productions and $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transitions in Eqs. (19) and (20). On the other hand, the uncertainties from the CKM matrix elements in Eq. (17) have been computed to be negligibly small.

Fig. 5

Angular distributions of $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ versus $\cos \theta$ with $\theta$ being the angle between the baryon and meson moving directions, where the solid (dash) curves correspond to the constructive (destructive) interference effects

In Table 2, we have used the central values of $(\mathcal{B}_1,\mathcal{B}_2,\mathcal{B}_{1\cdot 2})= (2.92,1.73,0.65)\times 10^{-6}$ and $(\mathcal{B}'_1,\mathcal{B}'_2,\mathcal{B}'_{1\cdot 2})= (1.71,2.24,-0.61)\times 10^{-6}$ for $B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )}$. Clearly, the results of $|\mathcal{B}_{1\cdot 2}^{(\prime )}|\sim { O}(10^{-6})$ indicate sizable interferences. As shown in the table, we find that $\mathcal{B}_{1\cdot 2}^{(\prime )}$ causes a constructive (destructive) interfering effect in $\mathcal{B}_+(B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )})$, and a destructive (constructive) interfering one in $\mathcal{B}_-(B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )})$. Besides, the inequalities of $\mathcal{B}_1>\mathcal{B}'_1$ and $\mathcal{B}_2<\mathcal{B}'_2$ are due to $F^{B\eta }>F^{B\eta '}$ and $|h^s_{\eta }|<|h^s_{\eta ^\prime }|$, respectively. Similarly, one has that $(\mathcal{B}_{s1},\mathcal{B}_{s2},\mathcal{B}_{s1\cdot s2})=(1.33,0.33,-0.46)\times 10^{-6}$ for $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta$ and $(\mathcal{B}'_{s1},\mathcal{B}'_{s2},\mathcal{B}'_{s1\cdot s2})=(1.73,0.29,0.57)\times 10^{-6}$ for $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{\prime }$, which present that $\mathcal{B}_{s1\cdot s2}^{(\prime )}$ has a destructive (constructive) interfering effect in $\mathcal{B}_+(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )})$, and a constructive (destructive) interfering one in $\mathcal{B}_-(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )})$. As a result, in terms of $|\mathcal{B}_{(s)1\cdot (s)2}^{(\prime )}|\sim { O}(10^{-6})$ being traced back to the interferences between the two decaying configurations in Fig. 2, we conclude that $B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )}$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}$ are like $B\rightarrow K^{(*)}\eta ^{(\prime )}$ to have large values from the interferences, in comparison with $\mathcal{B}(\Lambda _b\rightarrow \Lambda \eta )\simeq \mathcal{B}(\Lambda _b\rightarrow \Lambda \eta ')$ [6, 7] and $\mathcal{B}(\Lambda _c^+\rightarrow p\eta )\simeq \mathcal{B}(\Lambda _c^+\rightarrow p\eta ')$ [9,10,11], which show less important interferences.

By following Refs. [52, 53], we present the kinematical allowed regions and Dalitz plot distribution in the plane of $m_{\Lambda \bar{p}}$ and $m_{\Lambda \eta }$ for $B^-\rightarrow \Lambda \bar{p}\eta$ in Fig. 3 to illustrate the generic features in $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}M$. As shown in the left panel in the figure, the allowed area can be divided into four different regions, denoted as I, II, IIIa and IIIb, respectively. In Region I, $\mathbf{B}$ and ${\bar{\mathbf{B}}'}$ can move collinearly, with the recoiled M in the opposite direction. In Region II, $\mathbf B$, $\bar{\mathbf{B}}'$ and M all have large energies, so that none of any two final states can be back-to-back. In Region IIIa(b), M and $\mathbf{B}({\bar{\mathbf{B}}'}$) move collinearly, with $\bar{\mathbf{B}}'$ ($\mathbf B$) being energetic and separated from the meson-(anti)baryon system. Since the collinear moving di-baryon in Region I and meson-(anti)baryon in Region IIIa(b) cause different kinds of quasi-two-body decays, the t and s (u)-channel contributions should be dominant, respectively, where $t\equiv (p_\mathbf{B}+p_{\bar{\mathbf{B}}'})^2$, $s\equiv (p_\mathbf{B}+p_{M})^2$ and $u\equiv (p_{\bar{\mathbf{B}}'}+p_M)^2$ are the Mandelstam variables. In Region II, the three channels are supposed to contribute with $(s,t,u)\sim m_B^2/3$.

Although Regions I, II and IIIa(b) have distinct dynamic properties, we assume that the expressions of Eqs. (1) and (2) for the di-baryon threshold effect in Region I can be extended to the other regions. In fact, the extension has been demonstrated to be able to describe the $\bar{B}^0\rightarrow p\bar{p} D^0$ spectra at different energy ranges [54,55,56], where the data points for the spectrum vs. $m_{Dp}$ are measured at the range of $m_{p\bar{p}}>2.29$ GeV, which correspond to the regions II and III of Fig. 3. In order that the extension of the amplitudes in Eqs. (1) and (2) can be tested by the future observations, we present the spectra versus $m_{{\mathbf{B}}\bar{\mathbf{B}}'}$ and $m_{\mathbf{B}\eta ^{(\prime )}}$ in the three-body $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ decays in Fig. 4 for the different kinematic regions in the Dalitz plots. Besides, we show the angular distributions with $m_{{\mathbf{B}}\bar{\mathbf{B}}'}>2.5-2.7$ GeV in Fig. 5, to be compared to the future measurements. Note that $\cos \theta \simeq 0$ with $\theta \simeq 90^\circ$ corresponds to the central area of Region II for the Dalitz plots.

Like the $B\rightarrow K^{(*)}\eta ^{(\prime )}$ decays, it is possible that $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ can help to improve the knowledge of the underlying QCD anomaly for the $\eta -\eta '$ mixing. Provided that the decays of $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}\eta ^{(\prime )}$ are well measured, the experimental values to be inconsistent with the theoretical calculations will hint at some possible additional effects to the $\eta -\eta '$ mixing, such as the $\eta$-$\eta '$-G mixing with G denoting the pseudoscalar glueball state [57]. Moreover, the gluonic contributions to the $B(\bar{B}_s^0)\rightarrow \eta ^{(\prime )}$ transition form factors [58] could also lead to visible effects.

4 Conclusions

We have studied the three-body baryonic B decays of $B^-\rightarrow \Lambda \bar{p}\eta ^{(\prime )}$ and $\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ^{(\prime )}$. Due to the interference effects between $b\rightarrow s n\bar{n}\rightarrow s\eta _n$ and $b\rightarrow s\bar{s} s\rightarrow s\eta _s$, which can be constructive or destructive, we have predicted that $\mathcal{B}(B^-\rightarrow \Lambda \bar{p}\eta ,\Lambda \bar{p}\eta ')=(5.3\pm 1.4,3.3\pm 0.7)\times 10^{-6}$ or $(4.0\pm 0.7,4.6\pm 1.1)\times 10^{-6}$, to be compared to the searching results by LHCb and BELLE. We have also found that $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda \bar{\Lambda } \eta ,\Lambda \bar{\Lambda } \eta ') =(1.2\pm 0.3,2.6\pm 0.8)\times 10^{-6}$ or $(2.1\pm 0.6,1.5\pm 0.4)\times 10^{-6}$. In our calculations, the errors came from the estimations of the non-factorizable effects in the generalized factorization, together with the uncertainties from the form factors of the $0\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ productions and $B\rightarrow {{\mathbf{B}}\bar{\mathbf{B}}'}$ transitions, which are due to the fit with the existing data for the baryonic B decays. Due to the fact that the contributions from Region II and the resonant meson-baryon pairs in Regions III in Fig. 3 are not considered properly, our results just provide an order of magnitude estimation on branching ratios.