$\Lambda _b$ decays into $\Lambda _c^*\ell \bar{\nu }_\ell$ and $\Lambda _c^*\pi ^-$ $[\Lambda _c^*=\Lambda _c(2595)$ and $\Lambda _c(2625)]$ and heavy quark spin symmetry

Abstract

We study the implications for $\Lambda _b \rightarrow \Lambda _c^*\ell \bar{\nu }_\ell$ and $\Lambda _b \rightarrow \Lambda _c^*\pi ^-$ $[\Lambda _c^*=\Lambda _c(2595)$ and $\Lambda _c(2625)]$ decays that can be deduced from heavy quark spin symmetry (HQSS). Identifying the odd parity $\Lambda _c(2595)$ and $\Lambda _c(2625)$ resonances as HQSS partners, with total angular momentum–parity $j_q^P=1^-$ for the light degrees of freedom, we find that the ratios $\Gamma (\Lambda _b\rightarrow \Lambda _c(2595)\pi ^-)/\Gamma (\Lambda _b\rightarrow \Lambda _c(2625)\pi ^-)$ and $\Gamma (\Lambda _b\rightarrow \Lambda _c(2595) \ell \bar{\nu }_\ell )/ \Gamma (\Lambda _b\rightarrow \Lambda _c(2625) \ell \bar{\nu }_\ell )$ agree, within errors, with the experimental values given in the Review of Particle Physics. We discuss how future, and more precise, measurements of the above branching fractions could be used to shed light into the inner HQSS structure of the narrow $\Lambda _c(2595)$ odd-parity resonance. Namely, we show that such studies would constrain the existence of a sizable $j^P_q=0^-$ component in its wave-function, and/or of a two-pole pattern, in analogy to the case of the similar $\Lambda (1405)$ resonance in the strange sector, as suggested by most of the approaches that describe the $\Lambda _c(2595)$ as a hadron molecule. We also investigate the lepton flavor universality ratios $R[\Lambda _c^*] = \mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \tau \,\bar{\nu }_\tau )/\mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \mu \,\bar{\nu }_\mu )$, and discuss how $R[\Lambda _c(2595)]$ may be affected by a new source of potentially large systematic errors if there are two $\Lambda _c(2595)$ poles.

1 Introduction

Nowadays much attention is payed to the spectroscopy of heavy hadrons in order to investigate the symmetries of Quantum Chromodynamics (QCD). As pointed out in Refs. [1,2,3], in the infinite quark mass limit ($m_Q\rightarrow \infty$), the spectrum of hadrons containing a heavy quark should show a SU(2)–pattern, because of the symmetry that QCD acquires in that limit under arbitrary rotations of the spin of the heavy quark. This is known as heavy quark spin symmetry (HQSS) in the literature. In that case, the total angular momentum $j_q$ of the brown muck, which is the subsystem of the hadron apart from the heavy quark, is conserved and hadrons with $J=j_q\pm 1/2$ form a degenerate doublet. This is because the one gluon exchange chromomagnetic interaction between the heavy quark and the brown muck is suppressed by the infinitely large mass of the quark.

Table 1 Masses and widths of the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ resonances (MeV units). Thresholds (MeV) of some possible $S-$wave decay channels are also given. In addition, the thresholds of the three-body channels, after the $P-$wave decay of the $\Sigma _c^{(*)}$ resonances, are $M(\Lambda _c+\pi ^++\pi ^-)= 2565.60 \pm 0.14$ MeV and $M(\Lambda _c+\pi ^0+\pi ^0)= 2556.41 \pm 0.14$ MeV. Data taken from the Review of Particle Physics (RPP) [12]

Constituent quark models (CQMs) predict a nearly degenerate pair of $P-$wave $\Lambda _c^*$ excited states, with spin–parity $J^P=1/2^-$ and $3/2^-$, whose masses are similar to those of the isoscalar odd-parity $\Lambda _c(2595)$ and $\Lambda _c(2625)$ resonances [4,5,6,7,8]. In the most recent of these CQM studies [8], two different types of excitation-modes are considered: The first one, $\lambda -$mode, accounts for excitations between the heavy quark and the brown muck as a whole, while the second one, $\rho -$mode, considers excitations inside the brown muck. When all quark masses are equal, $\lambda -$ and $\rho -$modes are degenerate [8]. However for singly-heavy baryons, the typical excitation energies of the $\lambda -$mode are smaller than those of the $\rho -$mode. This is because for singly charm or bottom baryons, the interactions between the heavy quark and the brown muck are more suppressed than between the light quarks [8, 9]. Thus, one should expect the $\lambda$ excitation modes to become dominant for low-lying states of singly heavy-quark baryons. Within this picture, the $\Lambda ^\mathrm{CQM}_c(2595)$ and $\Lambda ^\mathrm{CQM}_c(2625)$ resonances would correspond to the members of the HQSS–doublet associated to $(\ell _\lambda =1,\ell _\rho =0)$, with total spin $S_q=0$ for the light degrees of freedom (ldof), leading to a spin-flavor-spatial symmetric wave-function for the light isoscalar diquark subsystem inside of the $\Lambda _c^*$ baryon. The total spins of these states are the result of coupling the orbital-angular momentum $\ell _\lambda$ of the brown muck – with respect to the heavy quark – with the spin ($S_Q$) of the latter. Thus both $\Lambda ^\mathrm{CQM}_c(2595)$ and $\Lambda ^\mathrm{CQM}_c(2625)$ states are connected by a simple rotation of the heavy-quark spin, and these resonances will be degenerate in the heavy-quark limit.¹

Since the total angular momentum and parity of the ldof in the $S-$wave $\pi \Sigma _c$ and $\pi \Sigma ^*_c$ pairs are $1^-$, as in the CQM $\Lambda _c(2595)$ and $\Lambda _c(2625)$ resonances, the $\Lambda ^\mathrm{CQM}_c(2595) \rightarrow \pi \Sigma _c \rightarrow \pi \pi \Lambda _c$ and $\Lambda ^\mathrm{CQM}_c(2625) \rightarrow \pi \Sigma ^*_c \rightarrow \pi \pi \Lambda _c$ decays respect HQSS, and hence one should expect sizable widths for these resonances, unless these transitions are kinematically suppressed. This scenario seems plausible, as can be inferred from the masses and thresholds compiled in Table 1. Indeed, the recent works of Refs. [10, 11] find widths for the CQM $(\ell _\lambda =1,\ell _\rho =0)$ states ($j_q^P=1^-$) predicted in [8] consistent with data.

A different mechanism to explain the small width of the $\Lambda _c (2595)$ would be that its wave-function had a large $j_q^P=0^-$ ldof component.² This is because the transition of this $j_q^P=0^-$ term of the $\Lambda _c(2595)$ to the final $\pi \Sigma _c$ state will be suppressed by HQSS. This new mechanism will act in addition to any possible kinematical suppression. As we will see in the next section, it turns out that some of the approaches that describe the $\Lambda _c(2595)$ as a hadron-molecule predict precisely a significant $j_q^P=0^-$ component for the inner HQSS structure of this resonance. These models generate also the existence of a second, broad, resonance in the region of the $\Lambda _c(2595)$, with a large $j_q^P=1^-$ ldof component, that could be naturally identified to the HQSS partner of the $\Lambda _c(2625)$, since both states will have the same brown muck configuration in the heavy-quark limit.³

In this work, we will derive HQSS relations between the $\Lambda _b$ decays into $\Lambda _c^*\pi ^-$ and $\Lambda _c^*\ell \bar{\nu }_\ell$ $[\Lambda _c^*=\Lambda _c(2595)$ and $\Lambda _c(2625)]$, supposing firstly that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ form the lowest-lying $j_q^P=1^-$ HQSS doublet. We will also discuss how measurements of the ratio of branching fractions $\Gamma [\Lambda _b\rightarrow \Lambda _c(2595)]/\Gamma [\Lambda _b\rightarrow \Lambda _c(2625)]$ can be used to constrain the existence of a sizable $j^P_q=0^-$ ldof component in the $\Lambda _c(2595)$ wave-function, and/or of a second pole, in analogy to the case of the similar $\Lambda (1405)$ resonance.

Exclusive semileptonic $\Lambda _b$ decays into excited charmed $\Lambda _c(2595)$ and $\Lambda _c(2625)$ baryons have been studied using heavy quark effective theory (HQET), including order $\Lambda _{\text {QCD}}/m_Q$ corrections [13, 14], and non-relativistic and semi-relativistic CQMs [15], always assuming a single pole structure for the first of these resonances and a dominant $j^P_q=1^-$ configuration. Recently, it has also been suggested that measurements of these decays by LHCb could be used to perform precise lepton flavor universality (LFU) tests [16, 17], comparing branching fractions with $\tau -$ or $\mu -$leptons in the final state. The analyses of Refs. [16, 17] assumed that both excited charmed baryons form a doublet under HQSS, and therefore it neither contemplated the possibility that the narrow $\Lambda _c(2595)$ might not be the HQSS partner of the $\Lambda _c(2625)$, nor that it could contain a non-negligible $j_q^P=0^-$ component, as it occurs in most of the molecular descriptions of this resonance. It is therefore timely and of the utmost interest to test the HQSS doublet assumption for the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ with the available data.

A first step in that direction was given in Refs. [18, 19]. In these two works, the semileptonic $\Lambda _b \rightarrow \Lambda _c^*$ transitions, together with the $\Lambda _b$ decays into $\Lambda _c^*\pi ^-$ and $\Lambda _c^*D_s^-$ were studied. It was found that the ratios of the rates obtained for $\Lambda _c(2595)$ and $\Lambda _c(2625)$ final states are very sensitive to the couplings of these resonances to the $D^*N$ channel, which also becomes essential to obtain agreement with the available data. Following the claims of Refs. [18, 19], these results seem to give strong support to the molecular picture of the two $\Lambda _c^*$ states, and the important role of the $D^*N$ component in their dynamics.⁴ As we will discuss in the next section, the $\Lambda _c(2595) D^*N$ and $\Lambda _c(2625) D^*N$ couplings, together with those to the DN and $\pi \Sigma _c^{(*)}$ pairs, can also be used to obtain valuable information on the inner HQSS structure of these resonances.

Within a manifest Lorentz and HQSS invariant formalism [21,22,23], we will re-examine here some of the results obtained in Refs. [18, 19], and will connect the findings of these two works with the quantum numbers of the ldof in the $\Lambda _c(2595)$ wave function. Specifically, we will discuss how future accurate measurements of the different ratios of branching fractions proposed in [18, 19] may be used to constrain or discard (i) a sizable $j^P_q=0^-$ component in the $\Lambda _c(2595)$ wave-function, and (ii) the existence of a second pole, analog to the second (broad) $\Lambda (1405)$ resonance [12]. The study will also shed some light on the validity of some of the most popular hadron-molecular interpretations of the odd-parity lowest-lying $\Lambda _c^*$ states.

This work is structured as follows. After this introduction, in Sect. 2 we critically review different molecular descriptions of the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ baryons, and discuss in detail the main features of those models that predict a two-pole pattern for the $\Lambda _c(2595)$. Next in Sect. 3, we study the semileptonic $\Lambda _b \rightarrow \Lambda _c^*\ell \bar{\nu }_\ell$ decays and the constrains imposed by HQSS to these processes. We derive a scheme that preserves spin-symmetry in the $b-$quark sector and that leads to simple and accurate expressions for the differential widths, including $\mathcal{O}(1/m_c)$ corrections and full finite-lepton mass contributions that are necessary for testing LFU. Semileptonic decays to molecular $\Lambda _c^\mathrm{MOL}$ states are addressed in Sect. 3.3, and the pion mode is examined in Sect. 4. The numerical results of this work are presented in Sect. 5. First in Sect. 5.1, we discuss the semileptonic ($\mu ^- \bar{\nu }_\mu$ or $e^- \bar{\nu }_e$) and pion $\Lambda _b\rightarrow \Lambda _c^*$ decays, and present $m_Q\rightarrow \infty$, $\mathcal{O}(1/m_Q)$ HQET and molecular-model predictions for the ratios of branching fractions studied in [18, 19]. Next in Sect. 5.2, we show results for $\Lambda _b$ semileptonic decays with a $\tau$ lepton in the final state that can be of interest for LFU tests. Finally, we outline the main conclusions of this work in Sect. 6.

2 HQSS structure of the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ states in hadron-molecular approaches

In this section, we will discuss the most important common features and results obtained from approaches where the $\Lambda _c(2595)$ and $\Lambda _c (2625)$ are described as hadron-molecules. These studies are motivated by the appealing similitude of these resonances to the $\Lambda (1405)$ and $\Lambda (1520)$ in the strange sector. In particular the two isoscalar S-wave $\Lambda (1405)$ and $\Lambda _c(2595)$ resonances have several features in common. The mass of the former lies in between the $\pi \Sigma$ and $\bar{K} N$ channel thresholds, to which it couples strongly [24,25,26]. In turn, the $\Lambda _c(2595)$ lies below the DN and just slightly above the $\pi \Sigma _c$ thresholds, and substituting the c quark by a s quark, one might expect the interaction of DN to play a role in the dynamics of the $\Lambda _c(2595)$ similar to that played by $\bar{K}N$ in the strange sector.

The hadronic molecular interpretation of the $\Lambda (1405)$ provides a good description of its properties. Actually, the dynamics of this resonance is mostly governed by the leading order (LO) SU(3) chiral Weinberg–Tomozawa (WT) meson–baryon interaction. The resonance is dynamically generated from the interaction of the mesons of the $0^-$ octet (Goldstone bosons) with the $1/2^+$ octet of ground state baryons [27,28,29,30,31,32,33,34] (see also the most recent works of Refs. [35, 36] and references therein for further details and other related studies on the $\Lambda (1405)$). One of the distinctive features of this resonance is its two-pole structure [29, 31,32,33,34,35,36], that have found experimental confirmation [37, 38] as discussed in Ref. [39]. This two-pole pattern⁵ is by now widely accepted by the community (see f.i. the mini review on this issue in the RPP by the Particle Data Group [12]).

On the other hand, many works have been also devoted to the study of dynamically generated $J^P=3/2^-$ states in the SU(3) sector [40,41,42,43,44,45,46,47,48,49,50,51]. Early works considered only the chiral interaction of pseudoscalar $0^-$ mesons with the baryons of the $3/2^+$ decuplet, but more recently, vector-mesons degrees of freedom have also been incorporated in the coupled-channel approach, using different schemes (see for instance the discussion in [51]). In these approaches, the $\Lambda (1520)$ is dynamically generated mostly from the $S-$wave $\pi \Sigma ^*-\bar{K}^* N$ coupled-channels dynamics, appearing it slightly above the $\pi \Sigma ^*$ threshold. It has a non-vanishing width, since the $\pi \Sigma ^*$ channel is open. In clear analogy, one might naturally think of a similar mechanism to generate the $\Lambda _c(2625)$ from the $\pi \Sigma ^*_c-D^* N$ dynamics, though the major difference is that the charm-resonance is located around 30-25 MeV below the $\pi \Sigma ^*_c$ threshold.

2.1 Molecular models

The general scheme consists of taking some $S-$wave interactions as kernel of a Bethe-Salpeter equation (BSE), conveniently ultraviolet (UV) renormalized, and whose solutions fulfill exact elastic unitarity in coupled-channels. In this context, bound and resonant states appear as poles in the appropriate Riemann-sheets,⁶ and the residues provide the coupling of the dynamically generated states to the different channels considered in the approach.

The resemblance of the physics in the odd-parity charm $C=1$ baryon sector to the phenomenology seen in $\bar{K} N-\pi \Sigma$ dynamics was first exploited in the works of Refs. [52, 53]. These first two works had some clear limitations. In the first one, the $J^P= 1/2^-$ sector is studied using the scattering of Goldstone bosons off $1/2^+$ heavy-light baryon resonances. Despite the interactions were fully consistent with chiral symmetry, neither the DN, nor the $D^*N$ channels were considered [52]. The work of Ref. [53] also studied the $\Lambda _c(2595)$ and there, the interactions were obtained from chirally motivated Lagrangians upon replacing the s quark by the c quark. Though in this way, the DN channel was accounted for, the HQSS counterpart $D^*N$ was not considered.

The subsequent works of Refs. [54,55,56] for the $J^P=3/2^-$ sector, introduced some improvements on the schemes of Refs. [52, 53]. Namely, the BSE interaction kernels were obtained from t-channel exchange of vector mesons between pseudoscalar mesons and baryons, in such a way that chiral symmetry is preserved in the light meson sector. Besides, the universal vector meson coupling hypothesis [Kawarabayashi–Suzuki–Fayyazuddin–Riazudden (KSFR) [57, 58]] was modified to take into account the reduction of the interaction strength provoked by the mass of the $t-$channel exchanged meson. In this way, some SU(4) flavor-symmetry breaking corrections, additional to those induced by the use of the physical masses, were considered. Similar qualitative findings were obtained in the work of Ref. [59], where some finite range effects were explored.

A detailed treatment of the interactions between the ground-state singly charmed and bottomed baryons and the pseudo-Nambu-Goldstone bosons, discussing also the effects of the next-to-leading-order chiral potentials, was carried out in [60]. However, channels not involving Goldstone bosons, like DN or $D^*N$, were again not considered. In this reference, several aspects related to the renormalization procedure were also critically discussed.⁷

In all cases, the $\Lambda _c(2595)$, or the $\Lambda _c(2625)$ if studied, could be dynamically generated after a convenient tuning of the renormalization constants. However, none of these works were consistent with HQSS since none of them considered the $D^*N$ [66]. Heavy pseudoscalar and vector mesons should be treated on equal footing, since they are degenerated in the heavy quark limit, and are connected by a spin-rotation of the heavy quark that leaves unaltered the QCD Hamiltonian in that limit. This is to say the D and $D^*$ mesons form a HQSS-doublet.

The first molecular description of the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ resonances, using interactions fully consistent with HQSS, was derived in Refs. [66, 67]. In these works a consistent $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ extension of the WT $\pi N$ Lagrangian –where “lsf” stands for light-spin-flavor symmetry–, is implemented, although the adopted renormalization scheme (RS) [54, 56] might not respect HQSS (see the discussion below). Within such scheme, two states are dynamically generated in the region of 2595 MeV. The first one, identified with the $\Lambda _c(2595)$ resonance, is narrow and it strongly couples to DN and especially to $D^*N$, with a small coupling to the open $\pi \Sigma _c$ channel. The second state is quite broad since it has a sizable coupling to this latter channel. On the other hand, a $J^P=3/2^-$ state is generated mainly by the $(D^*N-\pi \Sigma _c^*)$ coupled-channel dynamics. It would be the charm counterpart of the $\Lambda (1520)$, and could be identified with the $\Lambda _c(2625)$ resonance. The same $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ scheme also dynamically generates the $\Lambda _b(5912)$ and $\Lambda _b(5920)$ narrow resonances, discovered by LHCb in 2012 [68], which turn out to be HQSS partners, naturally explaining in this way their approximate mass degeneracy [69]. The extension of the model to the hidden charm sector was carried out in [70], and more recently, it was shown [71] that some (probably at least three) of the narrow $\Omega _c^*$ states recently observed by LHCb [72] in the $\Xi _c^+K^-$ spectrum in pp collisions can be also dynamically generated within the same scheme.

Several $\Lambda _c^*$ poles were also obtained in the approach followed in Ref. [73]. There, the interaction of DN and $D^*N$ states, together with their coupled channels are considered by using an extension to four flavours of the SU(3) local hidden gauge formalism from the light meson sector [74,75,76]. The scheme also respects LO HQSS constraints [77] and, as in Refs. [66, 67], a two-pole structure for the $\Lambda _c(2595)$ was also found, with the $D^*N$ channel playing a crucial role in its dynamics. This is a notable difference to the situation in the strange sector, where the analog $\bar{K}^*N$ channel is not even considered in most of the studies of the $\Lambda (1405)$, because of the large $\bar{K}^*-\bar{K}$ mass splitting. (See also the discussion carried out in Ref. [78]).

The beauty $\Lambda _b(5912)$ and $\Lambda _b(5920)$ states were also studied in the extended local hidden gauge (ELHG) approach in Ref. [79], while the the predictions of this scheme referred to the LHCb $\Omega _c^*$ states can be found in [80]. These latter states were also addressed in Ref. [81] using a model constructed out of the SU(4)-flavor t-channel exchange of vector mesons. There, the original model of Ref. [54] is revisited, and after taking an appropriate regularization scheme with physically sound parameters, two of the LHCb $\Omega _c^*$ resonances could be accommodated.

2.2 HQSS structure of the $\Lambda _c(2595)$ and $\Lambda _c (2625)$ hadron-molecules

To make more transparent the inner HQSS structure of the $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$, $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ and $\Lambda _c^\mathrm{MOL}(2625)$ states found in molecular (MOL) scenarios [(n) and (b) refer to the narrow and broad resonances that form the two-pole structure of the $\Lambda _c(2595)$ in these schemes], we perform a change of basis. We pass from $S-$wave states where the meson and baryon spins are defined, to other ones, where the total angular momentum of the ldof is well determined. In both set of states, the total angular momentum of the meson–baryon pair is defined. The two basis are related by a Racah rotation [77], which is straightforward to obtain in the present case, where the discussion is restricted to $S-$wave meson–baryon pairs. Thus for instance, we find (the rotation is independent of the isospin of the meson–baryon pair)

$$\begin{aligned} |S_Q^P= & {} 1/2^+\, j_q^P=1^-; J^P = 3/2^- \rangle _1 \nonumber \\= & {} |\pi \Sigma _c^*; J^P = 3/2^- \rangle \end{aligned}$$

(1)

$$\begin{aligned} |S_Q^P= & {} 1/2^+\, j_q^P=1^-; J^P = 3/2^- \rangle _2 \nonumber \\= & {} |D^* N; J^P = 3/2^- \rangle \end{aligned}$$

(2)

$$\begin{aligned} |S_Q^P= & {} 1/2^+\, j_q^P=1^-; J^P = 1/2^- \rangle _1 \nonumber \\= & {} |\pi \Sigma _c; J^P = 1/2^- \rangle \end{aligned}$$

(3)

$$\begin{aligned} |S_Q^P= & {} 1/2^+\, j_q^P=1^-; J^P = 1/2^- \rangle _2 \nonumber \\= & {} \frac{\sqrt{3}}{2} |D N; J^P = 1/2^- \rangle + \frac{1}{2} |D^* N; J^P = 1/2^- \rangle \end{aligned}$$

(4)

$$\begin{aligned} |S_Q^P= & {} 1/2^+\, j_q^P=0^-; J^P = 1/2^- \rangle _2 \nonumber \\= & {} -\frac{1}{2} |D N; J^P = 1/2^-\rangle + \frac{\sqrt{3}}{2} |D^* N; J^P = 1/2^- \rangle \nonumber \\ \end{aligned}$$

(5)

where we have used that the total angular momentum and parity of the ldof in the $\Sigma _c^{(*)}$ and $D^{(*)}$ ground states are $j_q^P=1^+$ and $1/2^-$, respectively. Besides, the sub-indices 1 and 2 on the states in the left-hand side of the equations distinguish if the meson is a Goldstone or a charmed heavy-light boson. In this context, the approximate HQSS of QCD leads to meson–baryon interactions V satisfying (kinetic terms respect HQSS)

$$\begin{aligned} _\alpha \langle S_Q^P= & {} 1/2^+\, j_q^P; J^P | V | S_Q^P=1/2^+\, \hat{j}_q^{P'}; \hat{J}^{P'} \rangle _\beta \nonumber \\= & {} \delta _{j_q^P \hat{j}_q^{P'}} \delta _{J^P \hat{J}^{P'}}\langle \alpha || V || \beta \rangle _{j_q^P}, \quad \alpha ,\beta =1,2 \end{aligned}$$

(6)

where $\mathcal{O}(\Lambda _\mathrm{QCD}/m_Q)$ corrections have been neglected. The reduced matrix elements depend only on the configuration of the ldof, because QCD dynamics is invariant under spin rotations of the heavy quark in the infinite mass limit. Note that quantum numbers like isospin or strangeness ..., are conserved by QCD, and that for simplicity, such trivial dependencies are not explicitly shown in Eq. (6), though the $\langle \alpha || V || \beta \rangle _{j_q^P}$ elements obviously depend on these additional properties needed to define the ldof. Finally, just mention that, in principle, the orthogonal $|{j_q^P=1^-; J^P} \rangle _1$ and $|{j_q^P=1^-; J^P} \rangle _2$ states can be connected by an interaction respecting HQSS. For instance, in the context of models based on the exchange of vector mesons, these contributions necessarily involve a $D^*$, instead of a $\rho -$meson, that will induce the transfer of charm between the baryon-baryon and meson-meson vertices.

2.2.1 $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$

To illustrate the discussion on the HQSS structure of the $\Lambda _c(2595)$ and $\Lambda _c (2625)$ within molecular descriptions, we will focus on the model derived in Refs. [66, 67]. There, the isoscalar interaction, $\widehat{V}$, used as kernel of the BSE in the $J^P=1/2^-$ and $J^P=3/2^-$ sectors respects HQSS (Eq. (6)) and it leads to⁸

$$\begin{aligned} \langle 1 || \widehat{V}|| 1 \rangle _{1^-}= & {} -4f(s), \quad \langle 2 || \widehat{V} || 2 \rangle _{1^-} = 0, \quad \nonumber \\ \langle 1 || \widehat{V} || 2 \rangle _{1^-}= & {} \sqrt{2}f(s), \quad \langle 2 ||\widehat{V} || 2 \rangle _{0^-} = -12f(s), \end{aligned}$$

(7)

when the coupled-channels space is truncated to that generated by the $\pi \Sigma ^{(*)}_c$ and $D^{(*)}N$ pairs. Besides, f(s) is a function of the meson–baryon Mandelstam variable s. Note that $\langle 1 || \widehat{V}|| 1 \rangle _{1^-}$ is determined by the isoscalar $\pi \Sigma _c^{(*)}\rightarrow \pi \Sigma _c^{(*)}$ transition, which is approximated in  [66, 67] by the LO WT chiral interaction. This fixes f(s) to

$$\begin{aligned} f(s)= \frac{\sqrt{s}-M}{2f^2_\pi }\, \frac{E+M}{2M} \end{aligned}$$

(8)

using the normalizations of these works. In the above equation, M(E) is the common mass [center-of-mass energy] of the $\Sigma _c^{(*)}$ baryons and $f_\pi \sim 92$ MeV is the pion decay constant.⁹ Coming back to Eq. (7), we see a large attraction for the $j_q^P=0^-$ ldof configuration, which is constructed out of the DN and $D^*N$ pairs, since the ldof in the $S-$wave $\pi \Sigma _c$ channel can be only $j_q^P=1^-$. Indeed, the $j_q^P=0^-$ eigenvector of the matrix $\widehat{V}$ is

$$\begin{aligned} v_0^\mathrm{atr}\equiv |S_Q^P=1/2^+\, j_q^P=0^-; J^P = 1/2^- \rangle _2 \, . \end{aligned}$$

(9)

On the other hand, diagonalizing $\widehat{V}$ in the $j_q^P=1^-$ ldof subspace, we find additional attractive and slightly repulsive eigenvalues $\lambda _1^\mathrm{atr}=-2-\sqrt{6}\sim -4.45$ and $\lambda _1^\mathrm{rep}=-2+\sqrt{6}\sim 0.45$, respectively, to be compared to $\lambda _0=-12$ obtained in the $j_q^P=0^-$ sector. The corresponding eigenvectors are $v_1^\mathrm{atr}\sim (1,\sqrt{2}-\sqrt{3})$ and $v_1^\mathrm{rep}\sim (\sqrt{3}-\sqrt{2}, 1)$ in the $|j_q^P=1^- \rangle _\alpha ,\, \alpha =1, 2$ basis. Taking normalized vectors, we find for $J^P=1/2^-$

$$\begin{aligned} ||v_1^\mathrm{atr}||^2_{1/2^-}= & {} \underbrace{0.91}_{\pi \Sigma _c}+\underbrace{0.07}_{DN}+\underbrace{0.02}_{D^*N}\,, \quad \nonumber \\ ||v_1^\mathrm{rep}||^2 _{1/2^-}= & {} \underbrace{0.09}_{\pi \Sigma _c}+\underbrace{0.68}_{DN}+\underbrace{0.23}_{D^*N}\, ,\quad \nonumber \\ ||v_0^\mathrm{atr}||^2_{1/2^-}= & {} \underbrace{0.25}_{DN}+\underbrace{0.75}_{D^*N}\, , \end{aligned}$$

(10)

while for $J^P=3/2^-$, we have

$$\begin{aligned} ||v_1^\mathrm{atr}||^2_{3/2^-} = \underbrace{0.91}_{\pi \Sigma _c^*}+\underbrace{0.09}_{D^*N}\, , \quad ||v_1^\mathrm{rep}||^2 _{3/2^-}= \underbrace{0.09}_{\pi \Sigma _c^*}+\underbrace{0.91}_{D^*N} \end{aligned}$$

(11)

In light of these results, we could easily explain some features of the results found in Refs. [66, 67] for the lowest-lying odd-parity $\Lambda _c^*$ states. There, a narrow $J^P=1/2^-$ $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$ resonance ($\Gamma \sim 1$ MeV) is reported, mostly generated from the extended WT $DN-D^*N$ coupled-channels dynamics. The modulus square of the couplings of this resonance to DN and $D^*N$ are approximately in the ratio 1 to 2.4, which does not differ much from the 1 to 3, that one would expect from the decomposition of $||v_0^\mathrm{atr}||^2_{1/2^-}$ in Eq. (10). Besides, this state has a small coupling to the $\pi \Sigma _c$ channel, which further supports a largely dominant $0^-$ ldof attractive configuration in its structure. Moreover, the detailed analysis carried out in [67] reveals that this narrow resonance stems from a $\mathbf{21}$ $\mathrm SU(6)_{ lsf}$ irreducible representation (irrep), where the light quarks –three quarks and anti-quark– behave (do not behave) as an isoscalar spin-singlet (triplet) diquark–symmetric spin-flavor state–.

The RS adopted in Refs. [66, 67], proposed in [54, 56], plays an important role in enhancing the influence of the $D^*N$ channel in the dynamics of the narrow $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$ state. Furthermore, this RS also produces a reduction in the mass of the resonance of around 200 MeV, which thus appears in the region of 2.6 GeV, instead of in the vicinity of the DN threshold. The RS establishes that all loop functions are set to zero at a common point [$\mu = \sqrt{m_\mathrm{th}^2+M_\mathrm{th}^2}$, where $(m_\mathrm{th}+M_\mathrm{th})$ is the mass of the lightest hadronic channel], regardless of the total angular moment J of the sector. However, we should point out that such RS might not be fully consistent with HQSS.

In addition, there appears a second $J^P=1/2^-$ pole [$\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$] in the 2.6 GeV region [66, 67]. Although it is placed relatively close to the $\pi \Sigma _c$ threshold, this resonance is broad ($\Gamma \sim 70-90$ MeV) thanks to its sizable coupling to this open channel, which in this case is larger than those to DN and $D^*N$. The study of Ref. [67] associates this isoscalar resonance to a $\mathbf{15}$ $\mathrm SU(6)_{ lsf}$ irrep, where the ldof effectively behave as an isoscalar spin-triplet diquark (antisymmetric spin-flavor configuration). Thus, it is quite reasonable to assign a dominant $j_q^P=1^-$ configuration to the ldof in this second pole. However, the ratios of $\pi \Sigma _c, DN$ and $D^*N$ couplings of this second resonance do not follow the pattern inferred from $||v_1^\mathrm{atr}||^2 _{1/2^-}$ in Eq. (10) as precisely as in the case of the narrow state. Actually, the couplings of this broad state to the DN and $D^*N$ pairs, though smaller, turn out to be comparable (absolute value) in magnitude to the $\pi \Sigma _c$ one (1.6, 1.4 and 2.3, respectively [67]). This points to the possibility that this second pole might also have a sizable component of the $1^-$ repulsive configuration, for which we should expect DN and $D^*N$ couplings much larger than the $\pi \Sigma _c$ one (likely in proportion 9 to 1 for the squares of the absolute values, just opposite to what is expected from the $1^-$ attractive eigenvector in Eq. (10)). Indeed, the fact that the $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ is located above the $\pi \Sigma _c$ threshold reinforces this picture, where there would be a significant mixing among the attractive and repulsive $1^-$ configurations, provoked by the flavor breaking corrections incorporated in the model of Refs. [66, 67]. These symmetry breaking terms affect the kernel f(s) of the BSE, the meson–baryon loops and the renormalization of the UV behaviour of the latter to render finite the unitarized amplitudes. The large difference between the actual $\pi \Sigma _c$ and $D^{(*)}N$ thresholds, which are supposed to be degenerate to obtain the results of Eq. (10), should certainly play an important role. The mass breaking effects were less relevant for the narrow $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$ resonance, because in that case i) the $\pi \Sigma _c$ channel had little influence in the dynamics of the state, and ii) the dominant DN and $D^*N$ thresholds turn out to be relatively close, thanks to HQSS. In addition, other higher channels like $\eta \Lambda _c$, $K \Xi ^{(\prime )}_c$, $D_s \Lambda$, $\rho \Sigma _c, \ldots$ which are considered in [66, 67], have not been included here in the simplified analysis that leads to the results of Eq. (10). Finally, one should neither discard a small $0^-$ ldof component in the $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ wave-function that will also change the couplings of this broad state to the different channels.

Note that the total angular momentum and parity of the ldof are neither really conserved in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model, nor in the real physical world because the charm quark mass is finite. Hence, both the narrow and broad $\Lambda _{c\, (n,b)}^\mathrm{MOL}(2595)$ resonances reported in [66, 67] will have an admixture of the $0^-$ and $1^-$ configurations¹⁰ in their inner structure. More importantly, the physical $\Lambda _c(2595)$ and the second resonance, if it exists, will also contain both type of ldof in their wave-function. As stressed in the Introduction, a non-negligible $0^-$ component in the $\Lambda _c(2595)$ or a double-pole structure have not been considered in the theoretical analyses of the exclusive semileptonic $\Lambda _b$ decays into $\Lambda _c(2595)$ carried out in Refs. [13, 14, 16]. One of the main objectives of this work is precisely the study of how these non-standard features affect the $\Lambda _b\rightarrow \Lambda _c^*$ transitions.

Finally, the lowest-lying $J^P=3/2^-$ isoscalar resonance found in Refs. [66, 67] is clearly the HQSS partner of the broad $J^P=1/2^-$ $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ state, with quantum number $j_q^P=1^-$ for the ldof. It is located above the $\pi \Sigma ^*_c$ threshold, with a width of around 40–50 MeV, and placed in the $\mathbf{15}$ $\mathrm SU(6)_{ lsf}$ irrep [67], as the broad $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ resonance. Moreover, the complex coupling of this $J^P=3/2^-$ pole to the $\pi \Sigma _c^*$ channel is essentially identical to that of the $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ to $\pi \Sigma _c$. In turn, the square of the absolute value of its coupling to $D^*N$ compares reasonably well with the sum of the squares of the couplings of the $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ to DN and $D^*N$, as one would expect from Eqs. (10) and (11). This $J^P=3/2^-$ isoscalar resonance is identified with the $D-$wave $\Lambda _c(2625)$ in Refs. [66, 67]. In these works, it is argued that a small change in the renormalization subtraction constant could easily move the resonance down by 40 MeV to the nominal position of the physical state, and that in addition, this change of the mass would considerably reduce the width, since its position would get much closer to the threshold of the only open channel $\pi \Sigma _c^*$.

Thus, within the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model, the $\Lambda _c(2625)$ turns out to be the HQSS partner of the second broad $\Lambda _{c\, (b)}^\mathrm{MOL}(2595)$ pole instead of the narrow $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$ resonance, as commonly assumed in the theoretical analyses of the exclusive semileptonic $\Lambda _b$ decays into $\Lambda _c(2595)$. This picture clearly contradicts the predictions of the CQMs where first, there is no a second 2595 pole, and second, the $\Lambda _c(2625)$ and the narrow $\Lambda _c(2595)$ are HQSS siblings, produced by a $\lambda -$mode excitation of the ground $1/2^+$ $\Lambda _c$ baryon.

2.2.2 Extended local hidden gauge (ELHG)

Within the model of Ref. [73], the dynamics of the lowest-lying odd-parity $\Lambda _c^*$ is mostly governed by the DN, $D^*N$ and $\pi \Sigma _c$ interactions ($V^\mathrm{HG}$). They are constructed using an SU(4) extension of the local hidden gauge formalism derived for the light meson sector [74,75,76], that in a first stage respects HQSS. It gives rise to reduced matrix elements

$$\begin{aligned} \langle 1 || V^\mathrm{HG}|| 1 \rangle _{1^-}= & {} -4f(s), \quad \langle 2 || V^\mathrm{HG} || 2 \rangle _{1^-} = -3f(s), \quad \nonumber \\ \langle 1 || V^\mathrm{HG} || 2 \rangle _{1^-}= & {} 0, \quad \langle 2 ||V^\mathrm{HG} || 2 \rangle _{0^-} = -3f(s), \end{aligned}$$

(12)

in the isoscalar sector. The flavor symmetry of the WT function f(s) is broken in the meson–baryon space by the use of physical masses. At first, $D^*-$exchange driven interaction terms connecting $|{j_q^P=1^-; J^P} \rangle _1$ and $|{j_q^P=1^-; J^P} \rangle _2$ states are neglected, as well as $DN\rightarrow D^*N$ coupled-channel interactions in the $J^P=1/2^-$ sector.

In a second stage, some additional contributions driven by the $D^*D\pi$ coupling, that formally vanish in the infinitely heavy quark mass limit, are considered in the kernels (potentials) of the BSE. These new terms provide:

• First, $DN\rightarrow \pi \Sigma _c$ transitions in the $J^P=1/2^-$ sector, which would give rise to $\quad \langle 1 || V^\mathrm{HG} || 2 \rangle _{1^-} = \sqrt{2}f(s)/4$. The factor 1 / 4 roughly accounts for the ratio $(m_\rho /m_{D^*})^2$, which one would expect to suppress the diagrams induced by the $t-$channel exchange of charmed vector mesons compared to those mediated by members of the light $\rho -$octet [55]. This assumes a universal KSFR vector-meson coupling. However, the effects due to $\quad \langle 1 || V^\mathrm{HG} || 2 \rangle _{1^-}\ne 0$ are, inconsistently with HQSS, not considered in the $J^P=3/2^-$ sector, and thus $D^*N$ and $\pi \Sigma _c^*$ channels are not connected¹¹ in the formalism of Ref. [73]. Actually, the isoscalar $\pi \Sigma _c^*$ pair is separately treated as a single channel. We will come back to this point below.

• Second, $D^{(*)}N\rightarrow D N$ transitions in the $J^P=1/2^-$ sector obtained from box diagrams, which also generate contributions to the $DN\rightarrow DN$ and $D^*N\rightarrow D^*N$ diagonal interaction-terms. In the $J^P=3/2^-$ sector, modifications of the $D^*N\rightarrow D^*N$ potential induced by box-diagrams constructed out, in this case, of the anomalous $D^*D^*\pi$ coupling are also taken into account in  [73].

In addition, other higher channels like $\eta \Lambda _c$, $\rho \Sigma _c, \ldots$ are considered in [73], though they have a little influence in the lowest-lying $\Lambda _c^*$ states. After fine tuning some UV cutoffs to reproduce the masses of the experimental narrow $\Lambda _c(2595)$ and $\Lambda _c(2625)$, the authors of Ref. [73] found that the latter resonance is essentially a $D^*N$ state, while the former one couples strongly both to DN and $D^*N$ and has a quite small coupling to $\pi \Sigma _c$. In addition, a state at 2611 MeV and a width of around 100 MeV, which couples mostly to $\pi \Sigma _c$ is also dynamically generated, confirming the double pole structure predicted in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model of Refs. [66, 67]. Note also that the narrow $\Lambda _c(2595)$ state found in [73] has similar DN and $D^*N$ couplings, from where one can conclude that it should have an important $0^-$ ldof configuration.

On the other hand, in the $J^P=3/2^-$ sector the isoscalar $\pi \Sigma _c^*$ is treated as a single channel in [73]. It gives rise to a further broad state ($\Gamma \sim$ 100 MeV) in the region of 2675 MeV, which is not related to the $\Lambda _c(2625)$ in that reference.

Finally, we should mention that the box-diagrams interaction terms evaluated in this ELHG model break HQSS at the charm scale, and it becomes difficult to identify any HQSS resonance doublet among the results reported in [73].

2.2.3 SU(4) flavor t-channel exchange of vector mesons

As already mentioned in this kind of models  [54, 55], the BSE potentials are calculated from the zero-range limit of $t-$channel exchange of vector mesons between pseudoscalar mesons and baryons. Chiral symmetry is preserved in the light meson sector, while the interaction is still of the WT type. Thus, the $J=1/2$ lowest-lying odd-parity $\Lambda _c^*$ resonances are mostly generated from $DN, \pi \Sigma _c$ coupled-channels dynamics. SU(4) flavor symmetry is used to determine the $DN\rightarrow DN$ and $DN\rightarrow \pi \Sigma _c$ interactions, which could be also derived assuming that the KSFR coupling relation holds also when charm hadrons are involved. The flavor symmetry is broken by the physical hadron masses, and in particular the large mass of the $D^*$ suppresses the off diagonal matrix element $DN\rightarrow \pi \Sigma _c$, as compared to the diagonal ones that are driven by $\rho -$meson exchange (see also the discussion in the previous subsection about the factor 1/4 included in the ELHG approach of Ref. [73]). These approaches do not include the $D^*N\rightarrow D^*N, DN, \pi \Sigma _c$ transitions, and therefore are not consistent with HQSS. Nevertheless, a $J^P = 1/2^-$ narrow resonance close to the $\pi \Sigma _c$ threshold, which can be readily identified with the $\Lambda _c(2595)$, is generated. It couples strongly to DN, and its nature is therefore very different from those obtained in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ and in the ELHG models, for which the $D^*N$ channel plays a crucial role. The reason why these SU(4) models can generate the $\Lambda _c(2595)$ is that the lack of the $D^*N$ in the $J^P=1/2^-$ sector is compensated by the enhanced strength in the DN channel. For instance, the DN coupling in the approaches of Refs. [54, 55] turned out to be of the same magnitude as that of the narrow $\Lambda _{c\, (n)}^\mathrm{MOL}(2595)$ to $D^*N$ in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model of Refs. [66, 67]. On the other hand, the $\pi \Sigma _c$ coupling, though still small, was found twice larger in Refs. [54, 55]. By construction, the resonance described in [54, 55] will mix $j_q^P=0^-$ and $1^-$ ldof configurations. The gross features of this dynamically generated state are similar to those of the the resonance reported in Ref. [53], where the similarity between the DN and $\bar{K} N$ systems, once the strange quark in the later is replaced by a charm quark, was exploited.

In addition, the models based on the t-channel exchange of vector mesons, when the unitarized amplitudes are renormalized as suggested in [54, 56], produce also a second $J^P=1/2^-$ broad resonance ($\Gamma \sim 100$ MeV) above 2600 MeV, with $\pi \Sigma _c$ (largest) and DN couplings similar to those found in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ and in the ELHG approaches (see Table XIV of Ref. [66] and the related discussion for an update of the results of the model used in [55]). Therefore, this type of molecular models might also predict a double pole structure for the $\Lambda _c(2595)$, in analogy with what happens in the unitary chiral descriptions of the $\Lambda (1405)$. We should, however, note that this second broad state is not generated when a RS based on an UV hard-cutoff is used [55, 59].

In the isoscalar $J^P=3/2^-$ sector, the chiral $\pi \Sigma _c^*$ WT interaction, driven by $\rho -$exchange, leads to a resonance with some resemblances to that reported in Refs. [66, 67], and that it is identified in [56] with the $\Lambda _c(2625)$, despite being located above 2660 MeV and having a width of the order of 50 MeV. Actually, this pole corresponds to that found in the single channel $\pi \Sigma _c^*$ analysis of Ref. [73], where it was, however, not associated to the physical $\Lambda _c(2625)$ state.

Fig. 1

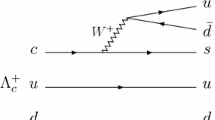
Left: Diagrammatic representation of the $\Lambda _b \rightarrow \Lambda _c^*\ell \bar{\nu }_\ell$ decay. Right: Hadronization creating $q\bar{q}$ pairs, together with the pictorial representation of the mechanism to produce a $\Lambda ^*_c$ resonance, through an intermediate propagation of DN and $D^*N$ pairs

2.2.4 Chiral isoscalar $\pi \Sigma ^{(*)}_c$ molecules

The chiral interactions between the ground-state singly charmed baryons and the Goldstone bosons lead to scenarios [52, 56, 60] where $\pi \Sigma _c$ and $\pi \Sigma ^*_c$ isoscalar molecules naturally emerge in the $J^P=1/2^-$ and $J^P=3/2^-$ sectors, respectively. These states will form a $1^-$ HQSS doublet, whose masses and widths depend on the details of the used RS. The works of Refs. [52, 56] found $J^P=1/2^-, 3/2^-$ resonances of around 50 MeV of width and masses in the 2660 MeV region using a RS, inspired in the success of Refs. [30, 34, 40] to describe the chiral SU(3) meson–baryon $J^P=1/2^-$ and $J^P=3/2^-$ sectors, later also employed in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model of Refs. [66, 67].¹² The $\pi \Sigma _c^*$ pole found in the ELHG scheme followed in [73] clearly matches the results of Ref. [56], though it was not identified with the $\Lambda _c(2625)$ in the work of Ref. [73].

In sharp contrast, subtraction constants or UV cutoffs were fine-tuned in Ref. [60] in such a way that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ experimental masses were reproduced, leading to weakly $\pi \Sigma _c$ and $\pi \Sigma _c^*$ bound states. Thus, the needed UV cutoffs turned out to be slightly higher than expected, 1.35 and 2.13 GeV, respectively. This could indicate some degrees of freedom that are not considered in the approach, such that CQM states or $D^{(*)}N$ components, and that could play a certain role, being their effects effectively accounted for the fitted real parts of the unitarity loops [82, 83].

2.3 Weinberg compositeness condition

In recent years, the compositeness condition, first proposed by Weinberg to explain the deuteron as a neutron-proton bound state [84, 85], has been advocated as a model independent way to determine the relevance of hadron-hadron components in a molecular state. With renewed interests in hadron spectroscopy, this method has been extended to more deeply bound states, resonances, and higher partial waves [86,87,88,89,90,91,92,93,94,95,96,97]. However, we should mention that the compositeness analysis proposed by Weinberg [84, 85] is only valid for bound states. For resonances, it involves complex numbers and, therefore, a strict probabilistic interpretation is lost as pointed out in Ref. [91].

For the particular case of the $\Lambda _c(2595)$, the situation is a bit unclear. For instance, it was shown in Ref. [98] that the $\Lambda _c(2595)$ is not predominantly a $\pi \Sigma _c$ molecular state using the effective range expansion. A similar conclusion was reached in Ref. [99], using a generalized effective range expansion including Castillejo-Dalitz-Dyson pole contributions. In this latter work, the effects of isospin breaking corrections are also taken into account and the extended compositeness condition for resonances developed in Ref. [100] was applied to calculate the component coefficients. Furthermore, although in the unitary approaches, the $\Lambda _c(2595)$ is found to be of molecular nature [52,53,54,55, 60, 66, 67, 73], there is no general agreement on its dominant meson–baryon components yet.

In general, one can conclude that the compositeness of the $\Lambda _c(2595)$ depends on the number of considered coupled channels, and on the particular regularization scheme adopted in the unitary approaches and, therefore, would be model dependent [61].

3 Semileptonic $\Lambda _b \rightarrow \Lambda _c^*\ell \bar{\nu }_\ell$ decays

The differential decay width for the semileptonic $b\rightarrow c$ transition shown in Fig. 1 is given by

$$\begin{aligned} \frac{d\Gamma }{d\omega }= & {} \Gamma _0 \frac{96\,M_{\Lambda _c^*}^3}{\pi \,M_{\Lambda _b}^5} \sqrt{\omega ^2-1}\, \mathcal{L}^{\alpha \beta }(q) \mathcal{H}_{\alpha \beta }(P,P')\,, \qquad \nonumber \\ \Gamma _0= & {} |V_{cb}|^2 \frac{G_F^{\,2}M_{\Lambda _b}^5}{192\pi ^3} \end{aligned}$$

(13)

where $|V_{cb}|$ is the modulus of the Cabibbo–Kobayashi–Maskawa (CKM) matrix element for the $b\rightarrow c$ transition, $G_F= 1.16638 \times 10^{-11}$ MeV$^{-2}$ is the Fermi decay constant, $P^\mu ,M_{\Lambda _b}$ ($P^{\prime \mu },M_{\Lambda _c^*}$) are the four-momentum and mass of the initial (final) baryon, $q^\mu =P^\mu -P^{\prime \mu }$ and $\omega$ is the product of the baryons four-velocities $[P^{(\prime )\mu }/M_{\Lambda _{b,c}^{(*)}}]$, $\omega =v\cdot v^\prime =\frac{M_{\Lambda _b}^2+M_{\Lambda _c^*}^2-q^2}{2M_{\Lambda _b}M_{\Lambda _c^*}}$. In the decay, $\omega$ ranges from $\omega =1$, corresponding to zero recoil of the final baryon, to a maximum value given, neglecting the antineutrino mass, by $\omega =\omega _\mathrm{max}= \frac{M_{\Lambda _b}^2 + M_{\Lambda _c^*}^2-m_\ell ^2}{2M_{\Lambda _b}M_{\Lambda _c^*}}$, where $m_\ell$ is the final charged lepton mass. In addition, $\mathcal{L}^{\alpha \beta }(q)$ is the leptonic tensor after integrating in the lepton momenta

$$\begin{aligned} \mathcal{L}^{\alpha \beta }(q)= & {} \int \frac{d^3k}{2|\vec {k}\,|} \frac{d^3k'}{2\sqrt{m^2_{\ell }+\vec {k}'^2}}\left( k'^\alpha k^\beta +k'^\beta k^\alpha - g^{\alpha \beta } k\cdot k^\prime \right. \nonumber \\&\left. + \mathrm{i} \epsilon ^{\alpha \beta \rho \sigma }k'_{\rho }k_\sigma \right) \delta ^4(q-k-k')\nonumber \\= & {} -\frac{\pi }{6 q^2}(q^2-m^2_\ell )\left\{ \left( q^2-\frac{m_\ell ^2}{2}-\frac{m_\ell ^4}{2q^2}\right) \,g^{\alpha \beta }\right. \nonumber \\&\left. - \left( q^2+m_\ell ^2-2\frac{m_\ell ^4}{q^2}\right) \,\frac{q^\alpha q^\beta }{q^2}\right\} \end{aligned}$$

(14)

where k and $k'$ are the four-momenta of the outgoing antineutrino and charged lepton [in our convention, we take $\epsilon _{0123}=+1$ and the metric $g^{\mu \mu }=(+,-,-,-)$]. Besides, $\mathcal{H}_{\alpha \beta }(P,P')$ is the hadronic tensor given by

$$\begin{aligned} \mathcal{H}^{\alpha \beta }(P,P')= & {} \frac{1}{2} \sum _{r,r'} \big \langle \Lambda _c^{*}, r'\ \vec {P}^{\,\prime }\big | J_{bc}^\alpha (0)\big | \Lambda _b, r\ \vec {P} \big \rangle \ \nonumber \\&\times \big \langle \Lambda _c^{*}, r'\ \vec {P}^{\,\prime }\big |J_{bc}^\beta (0) \big | \Lambda _b, r\ \vec {P} \big \rangle ^* \end{aligned}$$

(15)

with $\big |\Lambda _b, r\ \vec P\big \rangle \, \left( \big |\Lambda _c^{*}, r'\ \vec {P}\,'\big \rangle \right)$ the initial (final) baryon state with three-momentum $\vec P$ ($\vec {P}\,'$) and helicity r ($r'$), and normalized such that

$$\begin{aligned} \big \langle B, r'\ \vec {P}'\, |\,B, r \ \vec {P} \big \rangle \!=\! (2\pi )^3 \frac{E}{M} \,\delta _{rr'}\, \delta ^3 (\vec {P}-\vec {P}^{\,\prime }), \quad B\!=\! \Lambda _b, \Lambda _c^{*} \end{aligned}$$

(16)

with E and M, the baryon energy for three-momentum $\vec P$ and its mass, respectively. Finally, $J_{bc}^\mu (0)$ is the $b\rightarrow c$ charged weak current

$$\begin{aligned} J_{bc}^\mu (0)=\bar{\Psi }_{c}(0)\gamma ^\mu (1-\gamma _5)\Psi _b(0) \end{aligned}$$

(17)

with $\Psi _{b,c}$, Dirac fields, with dimensions of mass to the 3/2. Hadronic matrix elements can be parameterized in terms of form factors [14]. For $\frac{1}{2}^+ \rightarrow \frac{1}{2}^-$ transitions the form factor decomposition reads

$$\begin{aligned}&\big \langle \Lambda _c^{*1/2^-}, r'\ \vec {P}^{\,\prime }\left| \, J_{bc}^\mu (0)\, \right| \Lambda _b, r\ \vec {P} \big \rangle \nonumber \\&\quad = {\bar{u}}^{\Lambda _c^*}(\vec {P}^{\,\prime }, r')\Big \{ \gamma ^\mu \left[ F_1\gamma _5- G_1\right] + v^\mu \left[ F_2\gamma _5 -G_2\right] \nonumber \\&\qquad +v'^\mu \left[ F_3\gamma _5- G_3 \right] \Big \}u^{\Lambda _b}(\vec {P}, r \,) \end{aligned}$$

(18)

The $u_{r}$ are dimensionless Dirac spinors (${\bar{u}}_{r'} u_r = \delta _{r r'}$), $v^\mu$, $v'^\mu$ are the four velocities of the initial and final baryons and the three vector (axial) $F_1,\,F_2,\,F_3$ ($G_1,\,G_2,\,G_3$) form factors are functions of $\omega$ or equivalently of $q^2$. For $\frac{1}{2}^+ \rightarrow \frac{3}{2}^-$ decays we write

$$\begin{aligned}&\big \langle \Lambda _c^{*3/2^-},r'\vec P'\,|\,J_{bc}^\mu (0) \,|\,\Lambda _b,r\, \vec P\,\big \rangle \nonumber \\&\quad = ~\bar{u}^{\Lambda _c^*}_{\alpha }(\vec {P}', r')\,\Gamma ^{\alpha \mu }\, u^{\Lambda _b}(\vec {P}, r\,) \nonumber \\ \Gamma ^{\alpha \mu }= & {} v^\alpha \Big \{ \gamma ^\mu \left[ l_{V_1}-l_{A_1}\gamma _5\right] + v^\mu \left[ l_{V_2}-l_{A_2}\gamma _5\right] \nonumber \\&\qquad + v'^\mu \left[ l_{V_3}-l_{A_3}\gamma _5\right] \Big \}+ g^{\alpha \mu } \left[ l_{V_4}-l_{A_4}\gamma _5\right] . \end{aligned}$$

(19)

Here $u^{\Lambda _c^*}_{\alpha \,r'}$ is the Rarita-Schwinger spinor of the final spin 3/2 baryon normalized such that $(\bar{u}_{\alpha \,r'}^{B'}) u^{B'\,\alpha }_r = -\,\delta _{rr'}$, and we have four vector ($l_{V_{1,2,3,4}}(\omega )$) and four axial ($l_{A_{1,2,3,4}}(\omega )$) form factors.

3.1 Infinite heavy quark mass limit

The single heavy baryon and heavy quark velocities are equal in the $m_Q\rightarrow \infty$ limit. The heavy baryon can be viewed as a freely propagating point-like color source (the heavy quark), dressed by strongly interacting brown muck bearing appropriate color, flavor, baryon number, energy, angular momentum and parity to make up the observed physical state. Since an infinitely massive heavy quark does not recoil from the emission and absorption of soft $(E\sim \Lambda _\mathrm{QCD})$ gluons, and since chromomagnetic interactions of such a quark are suppressed as $1/m_Q$, neither its mass (flavor) nor its spin affect the state of the light degrees of freedom. This results in a remarkable simplification of the description of transitions in which a hadron containing a heavy quark, with velocity $v^\mu$, decays into another hadron containing a heavy quark of a different flavor. To the heavy quark, this looks like a free decay (up to pertubative QCD corrections), in which the light dressing plays no role. The brown muck, on the other hand, knows only that its point-like source of color is now recoiling at a new velocity $v'^{\mu }$, and it must rearrange itself about it in some configuration [23]. Hence, in the $m_Q\rightarrow \infty$ limit, the weak matrix elements must become invariant under independent spin rotations of the c and b quarks. This is easily shown in the brick wall frame ($\vec {v}=-\vec {v}\,'$, $v^0=v'^0$) by quantizing the angular momentum of the ldof (brown muck) about the spatial axis defined by $\vec {v}$. It follows that neither the initial and final heavy baryons, nor the c and b quarks have orbital angular momentum about this decay axis. Thus, in the Isgur-Wise (IW) limit, the spins of c and b are decoupled from the light quanta, and the component of the ldof total angular momentum along the decay axis is conserved [23, 101].

This large spin invariance in the $m_Q\rightarrow \infty$ limit leads to considerable simplifications [21, 102]. In particular, the semileptonic decay of the ground state $\Lambda _b$ into either $\Lambda _c^*$ in the $j_q^P= 1^-$ heavy doublet is described by an universal form-factor [9]. In this limit, the bottom quark carries all of the angular momentum of the $\Lambda _b$, where the ldof are coupled to $j_q^P=0^+$. Within the tensor representation of the heavy baryon states [23], the $\Lambda _b$ is accounted by a Dirac spinor $u_b(v)$, with v the velocity of the $\Lambda _b$ (and of its heavy point-like constituent), satisfying the subsidiary condition $\not vu_b(v)=u_b(v)$. The charm $j_q^P= 1^-$ doublet of baryons, with four velocity $v'$, are represented by the multiplet-spinor $\mathcal{U}^\mu _c(v')$

$$\begin{aligned} \mathcal{U}^\mu _c(v') = u^{3/2\mu }_c(v') + \frac{1}{\sqrt{3}}(\gamma ^\mu + v'^\mu )\gamma _5 u^{1/2}_c(v') \end{aligned}$$

(20)

where the Dirac $u^{1/2}_c(v')$ and the Rarita-Schwinger spinors $u^{3/2\mu }_c(v')$ stand for the spin 1/2 and spin 3/2 members of this doublet, respectively. The multiplet-spinor in Eq. (20) satisfies $\not v'\mathcal{U}^\mu _c(v')=\mathcal{U}^\mu _c(v')$, and $v'_\mu \mathcal{U}^\mu _c(v')=0$. Note also that $\gamma _\mu u^{3/2\mu }_c=0$ [23].

Under a Lorentz transformation, $\Lambda$, and b and c quark spin transformations $\widehat{S}_b$ and $\widehat{S}_c$, the above spinor wave functions transform as $S(\Lambda )\,u_b,\, \Lambda ^\mu _\nu S(\Lambda )\, \mathcal{U}^\nu _c$ and $\widehat{S}_b\, u_b$ and $\widehat{S}_c \,\mathcal{U}^\mu _c$, respectively, with $S(\Lambda )=\exp \{-i\sigma _{\mu \nu }S^{\mu \nu }/4\}$, the usual spinor representation. Note that $\widehat{S}_b$ and $\widehat{S}_c$ are also of the form $S(\hat{\Lambda })$, but with $\hat{\Lambda }$ restricted to spatial rotations and affecting only to the heavy quark spinor.

In addition in the $m_Q\rightarrow \infty$ limit, under heavy quark spin rotations, the $b\rightarrow c$ flavor changing current transforms as $J^\mu _{bc} \rightarrow \widehat{S}_c J^\mu _{bc} \widehat{S}_b^\dagger$. With all these ingredients, the most general form for the matrix element respecting HQSS is [9, 14]

$$\begin{aligned}&\big \langle \Lambda _c^{*1/2^-,\,3/2^-}; j_q^P=1^-\left| \, J_{bc}^\mu (0)\, \right| \Lambda _b\big \rangle \nonumber \\&\quad = \sigma (\omega ) v_\lambda \, \bar{\mathcal{U}}^\lambda _c(v') \gamma ^\mu (1-\gamma _5) u_b(v) + \mathcal{O}(1/m_{b,c})\,, \end{aligned}$$

(21)

Here $\sigma (\omega )$ is the (real) dimensionless leading IW function for the transition to this excited doublet. It follows $\sqrt{3}\,F_1/(\omega -1)=\sqrt{3}\,G_1/(\omega +1)=-\sqrt{3}\,F_2/2=-\sqrt{3}\,G_2/2=l_{V_1}=l_{A_1}=\sigma$ and $F_3=G_3=l_{V_{2,3,4}}=l_{A_{2,3,4}}=0$. In Ref. [14], $\sigma (\omega )$ was predicted in the large $N_c$ limit,

$$\begin{aligned} \sigma (\omega ) = 1.2 \left[ 1-1.4(\omega -1)\right] \end{aligned}$$

(22)

where subleading $1/N_c$ corrections are neglected.

The matrix element in Eq. (21) vanishes at zero recoil, where $v=v'$, and it trivially leads to¹³

$$\begin{aligned}&\mathcal{H}^{\alpha \beta }_{3/2^-}[j_q^P=1^-] = 2 \mathcal{H}^{\alpha \beta }_{1/2^-} [j_q^P=1^-]= \frac{2\sigma ^2(\omega )}{3} (\omega ^2-1)\, \nonumber \\&\quad \times \left( v^\alpha v'^\beta +v^\beta v'^\alpha -\omega g^{\alpha \beta } -i \epsilon ^{\alpha \beta \rho \sigma }v_\rho v'_\sigma \right) + \mathcal{O}(1/m_{b,c}) \nonumber \\ \end{aligned}$$

(23)

the antisymmetric term does not contribute to $d\Gamma /d\omega$ since the leptonic tensor, after integrating in the lepton momenta, becomes symmetric. Thus in the $m_Q\rightarrow +\infty$ limit, $d\Gamma _{\Lambda _c^{*3/2}}/d\omega = 2 d\Gamma _{\Lambda _c^{*1/2}}/d\omega$ since both members of the $j^P_q= 1^-$ doublet are degenerate. Furthermore, one easily deduces that $\Lambda _b$ decays to excited $\Lambda _c^{*3/2^-}$ with helicity $\pm 3/2$ are forbidden by HQSS in the IW limit, since the component of the ldof total angular momentum along the decay axis is conserved, and equal to zero.

On the other hand, for the ground-state $\Lambda _b$ transition to the $J^P=1/2^-$ charmed baryon with $j_Q^P=0^-$ ldof, one can use for the latter a spinor $u_c(v')$, but the form-factors must be pseudoscalar and therefore involve a Levi-Civita tensor [22]. At leading order in the $1/m_Q$ expansion, there are not enough vectors available to contract with the indices of the epsilon tensor so these unnatural¹⁴ parity matrix elements vanish [13, 14].

A different way to understand why the $\Lambda _b[1/2^+, j_q^P=0^+] \rightarrow \Lambda _c^*[1/2^-, j_q^P=0^-]$ is forbidden in the IW limit is adopting the picture introduced in Refs. [18, 19]. In the heavy-quark limit, the weak transition occurs on the b quark, which turns into a c quark and a $W^-$ boson, as shown in the left panel of Fig. 1. Since we will have a $1/2^-$ or $3/2^-$ state at the end, and the u, d quarks are spectators, remaining in a $0^+$ spin-parity configuration, the final charm quark must carry negative parity and hence must be in an $L = 1$ level. This corresponds to an orbital angular momentum excitation between the heavy quark and the isoscalar u, d diquark as a whole, which maintains the same spin-parity quantum numbers, $0^+$, as in the initial $\Lambda _b$, leading to a non-zero ldof wave-function overlap. Within this picture, the total angular momentum and parity of the light subsystem will be $j_q^P=1^-\,[= 0^+\otimes (L=1)]$, and the transition will be described by the matrix element in Eq. (21), that will go through $P-$wave, giving rise to the $(\omega ^2-1)$ factor in Eq. (23). In sharp contrast, the $(j_q^P=0^-,J^P=1/2^-)$ final baryon contains a $P-$wave excitation inside the brown muck and a realignment of the light quarks spins to construct a spin triplet state. That requires going beyond the spectator approximation of Fig. 1, involving dynamical changes in the QCD dressing of the heavy baryon during the transition, which are $1/m_Q-$ suppressed. Thus in the heavy quark limit, the initial and final ldof overlap for the unnatural $0^+\rightarrow 0^-$ transition vanishes. It would be parametrized by a pseudoscalar form-factor, involving the Levi-Civita tensor. As mentioned above, at leading order in the $1/m_Q$ expansion, there are not enough vectors available to contract with the indices of the epsilon tensor.

3.2 $\mathcal{O}(\Lambda _\mathrm{QCD}/m_c)$ corrections

Corrections of order $1/m_Q$ to $d\Gamma (\Lambda _b\rightarrow \Lambda _c^{*3/2}[j^P_q=1^-])/d\omega$ and $d\Gamma (\Lambda _b\rightarrow \Lambda _c^{*1/2}[j^P_q=1^-])/d\omega$ distributions were studied in [14] and shown to be quite large, specially in the $J^P=1/2^-$ case (see Fig. 1 of that reference).

Neglecting $\mathcal{O}(\Lambda _\mathrm{QCD}/m_b)$ terms, this is to say keeping still the invariance of the weak matrix element under arbitrary $b-$quark spin rotations, the general forms of the semileptonic matrix elements are

$$\begin{aligned}&\big \langle \Lambda _c^{*1/2^-}\left| \, J_{bc}^\mu (0)\, \right| \Lambda _b\big \rangle \nonumber \\&\quad = \frac{1}{\sqrt{3}} \bar{u}_c(v')\left[ (\not v-\omega ) \Delta _1-\Delta _2\right] \nonumber \\&\qquad \times \gamma ^\mu (1-\gamma _5) u_b(v) + \mathcal{O}(1/m_{b})\,, \end{aligned}$$

(24)

$$\begin{aligned}&\big \langle \Lambda _c^{*3/2^-}\left| \, J_{bc}^\mu (0)\, \right| \Lambda _b\big \rangle \nonumber \\&\quad = \bar{u}_c^\lambda (v')v_\lambda \left[ \Omega _1-(\not v-\omega )\Omega _2\right] \nonumber \\&\qquad \times \gamma ^\mu (1-\gamma _5) u_b(v) + \mathcal{O}(1/m_{b})\,, \end{aligned}$$

(25)

where $\Delta _{1,2}$ and $\Omega _{1,2}$ are form factors function of $\omega$ that are used to construct independent linear combinations of the identity and $\not v$ matrices. For semileptonic transitions to $\Lambda _c^{*1/2^-}$, we find $\sqrt{3} F_1= (\omega -1)\Delta _1+\Delta _2$, $\sqrt{3} G_1=(\omega +1)\Delta _1+\Delta _2$, $F_2=G_2=-2\Delta _1/\sqrt{3}$ and $F_3=G_3=0$. Similarly for $\Lambda _c^{*3/2^-}$, we find $l_{V_1}= \Omega _1+(\omega +1)\,\Omega _2$, $l_{A_1}= \Omega _1+(\omega -1)\,\Omega _2$, $l_{V_2}= l_{A_2}= -2\,\Omega _2$ and $l_{V_{3,4}}= l_{A_{3,4}}=0$.

If $\Delta _1= \Omega _1= \sigma$ and $\Delta _2=\Omega _2=0$, the IW limit of Eq. (23) is recovered for transitions to $\Lambda _c^{*3/2^-,\, 1/2^-}\,[j_q^P=1^-]$ states.¹⁵

The differential decay widths deduced from the general matrix elements of Eqs. (24) and  (25) are given by

$$\begin{aligned}&\frac{d\Gamma [\Lambda _b\rightarrow \Lambda _c^*(J^P)]}{d\omega }\nonumber \\&\quad = C_J \frac{8\,\Gamma _0}{3}\left( \frac{M_{\Lambda _c^*}}{M_{\Lambda _b}}\right) ^3\left( 1-\frac{m^2_\ell }{q^2}\right) ^2(\omega ^2-1)^J\,\nonumber \\&\qquad \times \left\{ \alpha _J^2\left[ 3\omega \frac{q^2+m_\ell ^2}{M_{\Lambda _b}^2} + 2\frac{M_{\Lambda _c^*}}{M_{\Lambda _b}}(\omega ^2-1)\left( 1+\frac{2m^2_\ell }{q^2}\right) \right] \right. \nonumber \\&\qquad +2\,(\omega ^2-1)\,\left[ \alpha _1(\omega )\alpha _2(\omega )\right] _J \nonumber \\&\qquad \left. \times \left[ \frac{2q^2+ m_\ell ^2}{M_{\Lambda _b}^2} + \left( 1-\frac{M^2_{\Lambda _c^*}}{M_{\Lambda _b}^2}\right) \left( 1+\frac{2m^2_\ell }{q^2}\right) \right] \right\} \nonumber \\&\qquad + \mathcal{O}(1/m_{b})\,, \end{aligned}$$

(26)

with $J^P= 1/2^-, \, 3/2^-$, $C_J = \left( 2J+1\right)$ and

$$\begin{aligned} \alpha _{J=1/2}^2(\omega )= & {} \Delta _2^2(\omega )+(\omega ^2-1)\Delta _1^2(\omega ), \qquad \nonumber \\ \left. \alpha _{1}(\omega )\,\alpha _{2}(\omega )\,\right| _{J=1/2}= & {} \Delta _1(\omega )\,\,\Delta _2 (\omega )\end{aligned}$$

(27)

$$\begin{aligned} \alpha _{J=3/2}^2(\omega )= & {} \Omega _1^2(\omega )+(\omega ^2-1)\Omega _2^2(\omega ), \qquad \nonumber \\ \left. \alpha _{1}(\omega )\,\alpha _{2}(\omega )\,\right| _{J=3/2}= & {} \Omega _1(\omega )\,\,\Omega _2(\omega ) \end{aligned}$$

(28)

At order $\mathcal{O}(\Lambda _\mathrm{QCD}/m_Q)$, there are corrections originating from the matching of the $b\rightarrow c$ flavor changing current onto the heavy quark effective theory and from order $\Lambda _\mathrm{QCD}/m_Q$ corrections to the effective Lagrangian [3, 13, 14, 103, 104]. Following the discussion of Ref. [14], for $\Lambda _b$ decays, they have a quite different physiognomy depending on the total angular momentum and parity of the ldof in the daughter charm excited baryon. In particular,

• $j_q^P= 1^-$: Neglecting $1/m_b$ corrections and QCD short-range logarithms [14],

  $$\begin{aligned} \Delta _1(\omega )= & {} \sigma (\omega ) + \frac{1}{2m_c}\left( \phi _\mathrm{kin}^{(c)}(\omega ) - 2 \phi _\mathrm{mag}^{(c)}(\omega )\right) ,\quad \nonumber \\ \Delta _2(\omega )= & {} \frac{1}{2m_c} \left( 3(\omega \bar{\Lambda }'-\bar{\Lambda })\sigma (\omega )\right. \nonumber \\&\left. +2(1-\omega ^2)\sigma _1(\omega ) \right) \end{aligned}$$

  (29)
  $$\begin{aligned} \Omega _1(\omega )= & {} \sigma (\omega ) + \frac{1}{2m_c}\left( \phi _\mathrm{kin}^{(c)}(\omega ) + \phi _\mathrm{mag}^{(c)}(\omega )\right) ,\quad \nonumber \\ \Omega _2(\omega )= & {} \frac{\sigma _1(\omega )}{2m_c} \end{aligned}$$

  (30)

  with $m_c\sim 1.4$ GeV, the charm quark mass, and $\bar{\Lambda }\sim 0.8$ GeV [$\bar{\Lambda }'\sim (1 \pm 0.1$ GeV)] the energy of the ldof in the $m_Q\rightarrow \infty$ limit in the $\Lambda _b$ [$\Lambda _c^*\,(j_q^P=1^-)$] baryon. The $\sigma _1(\omega )$ form-factor determines, together with $\bar{\Lambda }$ and $\bar{\Lambda }'$, the $1/m_c$ corrections stemming from the matching of the QCD and effective theory currents. This sub-leading IW function is unknown and in Ref. [14], it was varied in the range $\pm 1.2 \left[ 1-1.6(\omega -1)\right]$ GeV. In addition, $\phi _\mathrm{kin}^{(c)}$ and $\phi _\mathrm{mag}^{(c)}$ account for the time ordered product of the dimension-five kinetic energy and chromomagnetic operators in the effective Lagrangian. The chromomagnetic term is neglected in [14], because it is argued that it should be small relative to $\Lambda _\mathrm{QCD}$. In addition, the kinetic energy correction is estimated in the large $N_c$ limit, $\phi _\mathrm{kin}^{(c)} = -\frac{\bar{\Lambda }}{8}\sqrt{\frac{\bar{\Lambda }^3}{\kappa }}\left( \omega ^2-1\right) \sigma (\omega )$, with $\kappa =(0.411\,\mathrm{GeV})^3$ [14].

  The Eqs. (29) and (30) can be re-derived from

  $$\begin{aligned}&\big \langle \Lambda _c^{*1/2^-,\,3/2^-}; j_q^P=1^-\left| \, J_{bc}^\mu (0)\, \right| \Lambda _b\big \rangle \nonumber \\&= \bar{\mathcal{U}}^\lambda _c(v')\, \left\{ v_\lambda [\beta _1+(\omega -\not v)\beta _2]+ \gamma _\lambda \beta _3/3\right\} \nonumber \\&\qquad \times \gamma ^\mu (1-\gamma _5) u_b(v) + \mathcal{O}(1/m_{b})\,, \end{aligned}$$

  (31)

  where the $\mathcal{O}(1/m_c)$ $\beta _2$ and $\beta _3$ form-factors and the sub-leading term of $\beta _1$ depend on J. Thus, we have

  $$\begin{aligned} \beta _1(\omega )|_J= & {} \sigma (\omega ) + \frac{1}{2m_c}\left( \phi _\mathrm{kin}^{(c)}(\omega ) +c_J \phi _\mathrm{mag}^{(c)}(\omega )\right) \nonumber \\ \beta _2(\omega )|_J= & {} \frac{c_J}{2m_c}\, \sigma _1(\omega )\, ,\quad \nonumber \\ \beta _3(\omega )= & {} 3\,\frac{(\omega \bar{\Lambda }'-\bar{\Lambda })}{2m_c}\,\sigma (\omega ) \end{aligned}$$

  (32)

  with $c_{J=1/2}= -2$ and $c_{J=3/2}= 1$, which correspond to the eigenvalues of the operator $2\, \vec {S}_c \cdot \vec {j}_q$

  $$\begin{aligned} c_J= J\,(J+1)-\frac{1}{2}\,\left( \frac{1}{2}+1\right) -1\,(1+1)\,, \end{aligned}$$

  (33)

  for $j_q= 1$ and $S_c=1/2$, and

  $$\begin{aligned}&\Omega _1 = \beta _1(\omega )|_{J=3/2}, \quad \Delta _1 = \beta _1(\omega )|_{J=1/2}, \quad \nonumber \\&\Omega _2 = \beta _2(\omega )|_{J=3/2}, \nonumber \\&\Delta _2 = \beta _3(\omega )+\beta _2(\omega )|_{J=1/2}. \end{aligned}$$

  (34)

  The $1/m_b$ contributions, not taken into account, are much smaller than the theoretical uncertainties induced by the errors on $(\bar{\Lambda }-\bar{\Lambda }')$ and the $\sigma _1(\omega )$ form-factor. Hence, the form-factors of Eqs. (29) and (30) provide an excellent approximation to the results reported in Ref. [14].

  Two final remarks to conclude this discussion: (i) The $(\omega \bar{\Lambda }'- \bar{\Lambda })$ difference in $\Delta _2$ [$\gamma _\lambda$ form-factor in Eq. (31)] provides a $S-$wave $W^-\Lambda _c^* (1/2^-)$ term that should scale as $\sqrt{\omega ^2-1}$, and hence should dominate this differential rate at zero recoil. ii) The kinetic operator correction is the only $1/m_c$ term that does not break HQSS.

• $j_q^P= 0^-$: For the case of this unnatural transition, the matrix elements of the $1/m_Q$ current and kinetic energy operator corrections are zero for the same reason that the leading form factor vanished [14]. The time ordered products involving the chromomagnetic operator lead to non-zero contributions, which however vanish at zero recoil [14] and can be cast in a $\Delta _1-$type form factor. At order $1/m_Q$ the corresponding $\Delta _2$ form-factor is zero.

  From the above results, we conclude that the $\Lambda _b$ semileptonic decay to a $J^P=1/2^--$daughter charm excited baryon with a $j_q^P= 0^-$ ldof–configuration can be visible only if HQSS is severely broken and higher $\left( 1/m_Q\right) ^n$ corrections are sizable.

3.3 Decays to molecular $\Lambda _c^\mathrm{MOL}$ states

Following the spectator image of Fig. 1, the c quark created in the weak transition must carry negative parity and hence must be in a relative $P-$wave. The parity and total angular momentum of the final resonance are those of the intermediate system before hadronization. Since the molecular $\Lambda _c^\mathrm{MOL}$ states come from meson–baryon interaction in our picture, we must hadronize the final state including a $q\bar{q}$ pair with the quantum numbers of the vacuum ($^{2S+1}L_J=^3P_0$). This is done following the work of Refs. [18, 19], and thus we include $u\bar{u}+d\bar{d} + s\bar{s}$ as in the right panel of Fig. 1. The c quark must be involved in the hadronization, because it is originally in an $L = 1$ state, but after the hadronization produces the $D^{(*)}N$ state, and the c quark in the $D^{(*)}$ meson is in an $L = 0$ state. Neglecting hidden-strange contributions, the hadronization results in isoscalar $S-$wave DN and $D^*N$ pairs, but does not produce $\pi \Sigma _c^{(*)}$ states [18, 19].

The production of $J^P=1/2^-, 3/2^-$ resonances ($R_J$) is done after the created DN and $D^*N$ in the first step couple into the resonance, as shown in the right panel of Fig. 1. The transition matrix, $t_{R_J}$, for such mechanism leads to

$$\begin{aligned}&\overline{\sum }\sum |t_{R_J}|^2 \nonumber \\&\quad = \sum _M \mathcal{C} \left( \frac{1}{2} 1 J| M 0 M\right) ^2 \, |\varphi (\omega )\,|^2 \,\nonumber \\&\qquad \times \left| C_J^{DN}\,g_{R_J}^{DN}\, G_{DN} + C_J^{D^*N}\,g_{R_J}^{D^*N}\, G_{D^*N} \right| ^2, \end{aligned}$$

(35)

where the sums are over the spins of the initial and final particles, and the bar over the sum denotes the average over initial spins. The Clebsch-Gordan coefficient accounts for the coupling of spin and orbital angular momentum of the $c-$quark to the total angular momentum J of the intermediate system, composed by the charm quark and the spectator isoscalar $0^+$ ud diquark (see Fig. 1). Because angular momentum conservation, the spin of the resonance, produced after hadronization and meson–baryon re-scattering, will be J as well. The important point is that the third component of the orbital angular momentum of the $c-$quark must be zero [23, 101] (see also the discussion at the beginning of Sect. 3.1). Let us note for future purposes that $\mathcal{C}(\frac{1}{2} 1 \frac{3}{2}| M 0 M)^2\,/\, \mathcal{C}(\frac{1}{2} 1 \frac{1}{2} | M 0 M)^2 = 2, \, M= \pm 1/2$.

The function $\varphi (\omega )$ accounts for some $\omega$ dependences induced by the hadronization process and by the matrix element between the initial $S-$wave $b-$quark, the outgoing $W-$plane wave and the $P-$wave $c-$quark created in the intermediate hadronic state. This latter factor should scale like $|\vec {q}\,| \propto \sqrt{\omega ^2-1}$ close to zero recoil [18, 19]. In the heavy quark limit assumed in the mechanism depicted in Fig. 1, one expects $\varphi (\omega )$ to be independent of the angular momentum, J, of the final resonance.

The $C_J^{D^{(*)}N}$ coefficients account for different overlaps between DN and $D^*N$ $S-$wave pairs and the intermediate hadronic state, whose wave-function is determined by a excitation among the heavy quark and the brown muck (ldof) as a whole. This is a $\lambda -$excited state in the framework of CQM’s, and it has $j_q^P=1^-$ quantum-numbers for the brown muck. The values of $C_J^{D^{(*)}N}$ can be readily obtained from Eq. (5),

$$\begin{aligned} C_J^{D^{(*)}N} = \langle D^{(*)} N; J\,|\,S_Q^P=1/2^+\, j_q^P=1^-; J \rangle _2 \end{aligned}$$

(36)

Finally, $G_{D^{(*)}N}$ is the loop function for the $D^{(*)}N$ propagation¹⁶ and $g_{R_J}^{D^{(*)}N}$ is the dimensionless coupling of the resonance $R_J$ to the $D^{(*)} N$ channel in isospin zero. They are defined for instance in Eqs. (15) and (18) of Ref. [66], and we compute them at the resonance position in the complex plane. Note that the couplings $g_{R_J}^{D^{(*)}N}$, obtained from the residues of the coupled-channels meson–baryon $T-$matrix, contain effects from intermediate $\pi \Sigma _c^{(*)}$ loops.

With all these ingredients close to zero recoil, we find

$$\begin{aligned}&\left. \frac{d\Gamma /d\omega [\Lambda _b\rightarrow \Lambda _c^*(1/2^-)]}{d\Gamma /d \omega [\Lambda _b\rightarrow \Lambda _c^*(3/2^-)]}\right| _\mathrm{MOL} \nonumber \\&\quad = \frac{1}{2} \,\frac{\left| \frac{\sqrt{3}}{2}\,g_{R_{J=1/2}}^{DN}\, G_{DN} + \frac{1}{2} \,g_{R_{J=1/2}}^{D^*N}\, G_{D^*N} \right| ^2}{\left| g_{R_{J=3/2}}^{D^*N}\, G_{D^*N}\right| ^2} \end{aligned}$$

(37)

where the factor 1 / 2 comes from the ratio of Clebsch-Gordan coefficients. In this way, we recover the main result of Ref. [18]. It shows that the above ratio of differential decay widths is very sensitive to the couplings of the $\Lambda _c^*$ resonances to the DN and $D^*N$ channels. We could expect Eq. (37) to hold also in good approximation for the ratio of integrated rates since the available phase space is quite small

In the infinite heavy quark mass limit, the degeneracy of the D and $D^*$ masses implies $G_{DN}=G_{D^*N}$. In addition for $1^-$ and $0^-$ ldof quantum numbers, the couplings of DN and $D^*N$ to $\Lambda _c^*$ are related

$$\begin{aligned} j_q^P= 1^-\Rightarrow & {} \frac{2}{\sqrt{3}}\, g_{\Lambda _c^*(1/2^-)}^{DN}=2g_{\Lambda _c^*(1/2^-)}^{D^*N}=g_{\Lambda _c^*(3/2^-)}^{D^*N} \end{aligned}$$

(38)

$$\begin{aligned} j_q^P= 0^-\Rightarrow & {} \sqrt{3}\,g_{\Lambda _c^*(1/2^-)}^{DN}=-g_{\Lambda _c^*(1/2^-)}^{D^*N}\,, \end{aligned}$$

(39)

as inferred from Eq. (5). Hence, we re-obtain the $m_Q\rightarrow \infty$ results of Sect. 3.1,

$$\begin{aligned}&\frac{d\Gamma /d\omega [\Lambda _b\rightarrow \Lambda _c^*(1/2^-)]_{j^p_q =1^-}}{d\Gamma /d\omega [\Lambda _b\rightarrow \Lambda _c^*(3/2^-)]_{j^p_q =1^-}} = \frac{1}{2},\quad \nonumber \\&\frac{d\Gamma /d\omega [\Lambda _b\rightarrow \Lambda _c^*(1/2^-)]_{j^p_q =0^-}}{d\Gamma /d\omega [\Lambda _b\rightarrow \Lambda _c^*(3/2^-)]_{j^p_q =1^-}} = 0. \end{aligned}$$

(40)

For molecular states, we might have deviations from the above IW limit predictions, and in particular visible widths for a charm $J^P=1/2^-$ excited baryon with significant $0^-$ ldof components. This could happen if the meson–baryon interactions, which generate the molecular state, induce important $\left( 1/m_Q\right) ^n$ corrections, bigger than would be expected from the discussion in Subsec. 3.2.

4 $\Lambda _b \rightarrow \Lambda _c^* \pi ^-$ decay

Looking again at the diagram depicted in the left panel of Fig. 1, the $\Lambda _b \rightarrow \Lambda _c^* \pi ^-$ decay could proceed through the mechanism of external emission [105], where the gauge $W^-$ boson couples to $\pi ^-$ instead of to the $(\ell ^-\bar{\nu }_{\ell })$ lepton pair. This is the factorization approximation, which should be accurate for processes that involve a heavy hadron and multiple light mesons in the final state, provided the light mesons are all highly collinear and energetic [106]. Actually for $\Lambda _b \rightarrow \Lambda _c^* \pi ^-$ decay, corrections are expected to be of the order $\Lambda _\mathrm{QCD}/E_\pi$, with $E_\pi$ the energy of the pion in the center of mass frame. There exist also some small strong coupling logarithmic corrections stemming from the matching of full QCD with the effective heavy quark theory. The $\Lambda _b \rightarrow \Lambda _c^* \pi ^-$ width is related to the differential decay rate $d\Gamma _\mathrm{sl}/d\omega$ at $q^2=m_\pi ^2$ [$\omega =(M_{\Lambda _b}^2 + M_{\Lambda _c^*}^2-m_\pi ^2)/2M_{\Lambda _b}M_{\Lambda _c^*}$] for the analogous semileptonic decay [14],

$$\begin{aligned} \Gamma _\pi [\Lambda _b \rightarrow \Lambda _c^* \pi ^-] \propto |V_{ud}|^2\,f_\pi ^2 \left. \frac{d\Gamma _\mathrm{sl}[\Lambda _b \rightarrow \Lambda _c^* e^-\bar{\nu }_e]}{d\omega }\right| _{q^2=m_\pi ^2} \end{aligned}$$

(41)

with $m_\pi$ and $f_\pi$, the pion mass and decay constant, respectively. In the case of decays into $\Lambda _c^*$ molecular states, we find again that the ratio of gG factors of Eq. (37) provides an estimate for $\left. \frac{\Gamma _\pi [\Lambda _b\rightarrow \Lambda _c^*(1/2^-)]}{\Gamma _\pi [\Lambda _b\rightarrow \Lambda _c^*(3/2^-)]}\right| _\mathrm{MOL}$. However, the kinematics now is significantly different to that of zero recoil. In the $M_{\Lambda _b}$ rest frame, the recoil three momentum is of the order of 2.2 GeV, even larger than the charm quark mass. Hence, the approximation of neglecting the effects of operators like $\vec {S}_c \cdot \vec {j}_q$ in the weak transition becomes inappropriate, since factors proportional to $|\vec {q}\,|/m_c$ can be large in this kinematics [$(\omega ^2-1)\sim 0.7$]. This type of operators couples the charm quark spin and the angular momentum of the ldof and induces dependences on J, the total angular momentum of the created hadron. In this situation, it can not be guarantied that the function $\varphi (\omega )$, introduced in Eq. (35), is independent of J. In fact, in Ref. [19] and in addition to the quotient of gG coefficients, a factor $(\vec {q}^{\,2}+E_\pi ^2)/E_\pi ^2\sim 2$ was found that increased the value of the $\left. \frac{\Gamma _\pi [\Lambda _b\rightarrow \Lambda _c^*(1/2^-)]}{\Gamma _\pi [\Lambda _b\rightarrow \Lambda _c^*(3/2^-)]}\right| _\mathrm{MOL}$ ratio. We will also use here this result, with some precautions, and we will multiply by a factor of 2 the estimates for the latter ratio deduced from the gG factors.

5 Results

5.1 Semileptonic ($\mu ^- \bar{\nu }_\mu$ or $e^- \bar{\nu }_e$) and pion $\Lambda _b\rightarrow \Lambda _c^*$ decays

Table 2 Ratios of semileptonic ($\mu ^- \bar{\nu }_\mu$ or $e^- \bar{\nu }_e$) and pion $\Lambda _b$ decays into odd parity $J=1/2$ and 3 / 2 charm baryons. We show predictions obtained from the molecular schemes of Refs. [66, 67] ($\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$) and [73] (ELHG), together with the $m_Q\rightarrow \infty$ limit (IW$_\infty$) ratios, and those found including the subleading corrections [IW$_{\mathcal{O}(1/m_Q)}$] derived in Ref. [14] for the case of a $j_q^P=1^-$ HQSS doublet. The ELHG results for the narrow $\Lambda _c(2595)$ are taken from Refs. [18, 19]. In the case of molecular approaches, the gG factors that enter in Eq. (37) are compiled in Table 3. The ranges quoted for the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ pion-mode ratios account for the factor of two introduced at the end of Sect. 4, suggested by the findings of Ref. [19]. We also show in the last column experimental estimates for these ratios obtained from branching fractions given in the RPP [12]. See the text for more details

Table 3 Values (MeV) of the factors $g_{R_J}^{D^{(*)}N}\, G_{D^{(*)}N}$ from Ref. [66] ($\mathrm{SU(6)}_\mathrm{lsf} \times$ $\mathrm{SU(2)}_\mathrm{HQSS}$) and [73] (ELHG). The signs of $g_{R_J=1/2}^{D^*N}\, G_{D^*N}$ are changed with respect to Ref. [73], as discussed in [19]. The values quoted for the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ $g_{R_J=1/2}^{D^*N}\,G_{D^*N}$ take into account the order meson–baryon used in this work to couple the spins (see footnote 8)

In Table 2, we show results for the ratios of semileptonic ($\mu ^- \bar{\nu }_\mu$ or $e^- \bar{\nu }_e$) and pion $\Lambda _b$ decays into odd parity $J=1/2$ and 3 / 2 charm baryons, obtained within the molecular schemes of Refs. [66, 67] ($\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$) and [73] (ELHG). As commented in Sect. 2.2, a double pole structure for the $\Lambda _c(2595)$ is found in these approaches, with clear similarities to the situation for the $\Lambda (1405)$, and hence we give results for both, the narrow (n) and (b) broad $\Lambda _c^\mathrm{MOL}(2595)$ states. In Table 2, we also show experimental estimates for these ratios deduced from branching fractions given in the RPP [12]. We have considered that the reconstructed $\Lambda _c(2595)$ resonance observed in the decays corresponds to the molecular narrow resonance. In addition, $m_Q\rightarrow \infty$ limit results (IW$_\infty$) and predictions obtained incorporating the subleading corrections (IW$_{\mathcal{O}(1/m_Q)}$) discussed in Ref. [14] are also shown in Table 2. In this latter work, it is assumed that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ form the lowest-lying $j_q^P=1^-$ HQSS doublet, and the values quoted in the table follow mostly from Eqs. (2.26) and (2.28) of that reference. To the error budget deduced from these equations, we have added in quadrature the effects due to the uncertainty ($\pm 0.1$ GeV) on the $\bar{\Lambda }'$ parameter in Eq. (29), which produces variations in the ratios of about 25%–30% [14]. The errors on the IW$_{\mathcal{O}(1/m_Q)}$ ratios are largely dominated by the uncertainties on the subleading $\sigma _1$ form-factor. It leads to opposite effects for $\Lambda _c(2595)$ or $\Lambda _c(2625)$ final states [14], as can be inferred here from Eqs. (32) and (33). The biggest (smallest) $\Gamma ^{\Lambda _{1/2}}_\mathrm{sl,\pi }/ \Gamma ^{\Lambda _{3/2}}_\mathrm{sl,\pi }$ values correspond to $\sigma _1(1)=-1.2$ (+1.2) GeV, while the central values are obtained for $\sigma _1(\omega )=0$. The $\Gamma ^{\Lambda _{1/2}}_\mathrm{sl}$ rate, depending on $\sigma _1$, could be significantly enhanced (around a factor 2.5 for $\sigma _1=0$) compared to the infinite mass prediction ($\sim 0.020\,\Gamma _0)$, while $1/m_Q$ effects are much smaller for $\Gamma ^{\Lambda _{3/2}}_\mathrm{sl}$. Predictions for the pion decay widths depend on $d\Gamma _\mathrm{sl}/d\omega$ at $q^2=m_\pi ^2$, and turn out to be quite uncertain due to $\sigma _1$. We see that IW$_{\mathcal{O}(1/m_Q)}$ predictions and experimental estimates for the $\Gamma ^{\Lambda _{1/2}}/ \Gamma ^{\Lambda _{3/2}}$ ratios agree, within errors, for both semileptonic and pion $\Lambda _b$ decay modes. A certain tendency is observed in the central values, for which the theoretical estimations are greater than the experimental ones, in particular in the semileptonic mode. However, it would not be really significant due to the great uncertainties.

In what respects to the ELHG ratios for the narrow molecular $\Lambda _c(2595)$ state, we give in Table 2 the ranges quoted in the original works of Refs. [18, 19]. The lowest ratios can be found using the gG coefficients compiled in Table 3, while the highest values account for corrections due to the contribution of hidden-strange ($D^{(*)}_s\Lambda$) channels in the hadronization. Within the ELHG scheme the broad $\Lambda _c(2595)$ ratios are negligible. This is because in this approach, the $J^P=3/2^-$ $\Lambda _c(2625)$ is a quasi-bound $D^*N$ state with a large coupling to this channel, whose absolute value is around five times bigger than that of the broad $\Lambda _c(2595)$ resonance to $D^*N$ or DN [19]. The narrow ELHG $\Lambda _c(2595)$ molecule has DN and $D^*N$ couplings (in absolute value) similar to $g_{\Lambda _c(2625)}^{D^*N}$, and its $\Gamma ^{\Lambda _{1/2}}_\mathrm{sl,\pi }/ \Gamma ^{\Lambda _{3/2}}_\mathrm{sl,\pi }$ ratios are larger and about 0.4 and 0.8, respectively, compatible within errors with the experimental expectations. It should be also noted that after renormalization, the DN loop function is almost a factor of two smaller than the $D^*N$ one, which produces a significant source of HQSS breaking in the ELHG approach of Ref. [19].

Finally, we see that the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ ratios for the narrow molecular $\Lambda _c(2595)$ resonance, though small ($0.14-0.28$), are neither negligible, nor totally discarded by the available data. As we expected, they are suppressed because within this approach this state has a large $j_q^P=0^-$ ldof component. Semileptonic decays into the broad $\Lambda _c(2595)$ resonance are about a factor of three larger, but the $\Gamma ^{1/2 (b)}_{sl,\,\pi }/ \Gamma ^{3/2}_{sl,\,\pi }$ ratios are still below 1/2, the $m_Q\rightarrow \infty$ prediction, and well below the IW$_{\mathcal{O}(1/m_Q)}$ central values obtained in [14] (see Fig. 2). Both sets of results point to important $\left( 1/m_Q\right) ^n$ corrections, induced by the meson–baryon interactions that generate the molecular states. On the other hand, we do not expect large variations from the consideration of hidden strange channels as intermediate states. From the couplings reported in Refs. [66, 67], only $\Lambda \, D_s$ and $\Lambda \, D_s^*$ might be important through their coupling to the narrow $\Lambda _c(2595)$ state, but the respective thresholds are located (around 3.1 and 3.2 GeV) well above the resonance position, and it is not reasonable to claim for large effects produced by these high energy physics contributions. Actually, we have checked that the ratios given in Table 2 for the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model hardly change if the large number of coupled-channels used in Refs. [66, 67] is reduced only to $D^{(*)}N$ and $\pi \Sigma _c^{(*)}$.

The predictions for the ratios in molecular schemes are very sensitive to the interference and relative weights of the DN and $D^*N$ contributions [18, 19], and thus future accurate measurements of these ratios will shed light on the nature of the $\Lambda _c(2595)$, allowing us to address issues as the existence of two poles or the importance of the $D^*N$ channel in the formation of the resonance(s). Such studies will also help to understand the interplay between CQM and hadron-scattering degrees of freedom [107,108,109,110,111,112] in the dynamics of the $\Lambda _c(2595)$ and $\Lambda _c(2625)$.

Note that in other molecular schemes, like the SU(4) flavor t-channel exchange of vector mesons of Refs. [54, 55, 59] or those based on the chiral isoscalar $\pi \Sigma ^{(*)}_c$ interactions [52, 56, 60], where the $D^*N$ channel is not included, the $\Gamma _\mathrm{sl}[\Lambda _b \rightarrow \Lambda _c(2625)]$ and $\Gamma _\mathrm{\pi }[\Lambda _b \rightarrow \Lambda _c(2625)]$ widths will be zero or highly suppressed. This is because the $\pi \Sigma _c^*$ pair, that dynamically generates the $\Lambda _c(2625)$ resonance in these models, can be only produced by going beyond the spectator approximation implicit in the mechanism of Fig. 1. This places an additional limitation on the validity of these approaches, which already have some problems to describe the mass and width of the $\Lambda _c(2625)$ (see the related discussion in Sects. 2.2.3 and 2.2.4).

Fig. 2

Differential $\Lambda _b \rightarrow \Lambda _c^*(1/2^-)\, \tau \, \bar{\nu }_\tau$ (solid blue line) and $\Lambda _b \rightarrow \Lambda _c^*(1/2^-)\, e\, \bar{\nu }_e$ rates calculated using different approaches. The black dashed and solid lines, together with the error bands of the latter, are taken from Fig.1a of Ref. [14], where the final baryon is treated as the $J^P=1/2^-$ member of the lowest-lying $j_q^P=1^-$ HQSS doublet. The dashed line shows the $m_Q\rightarrow \infty$ prediction, Eqs. (22) and (23), while the solid line include $1/m_Q$ effects for $\sigma _1(\omega )=0$. The bands account for the changes in the differential decay rate when $\sigma _1(1)$ is varied in the range $[-1.2, 1.2]$ GeV. The spectrum of the $\tau -$mode, which ends around $\omega \sim 1.2$, is calculated using Eq. (26) with $\Delta _{1,2}$ given in Eq. (29), and taking $\sigma _1(\omega )=0$. (Further details on the $\mathcal{O}(1/m_c)$ corrections for $\tau -$decays can be found in Table 4). On the other hand, the lowest dotted and dashed-dotted curves, together with the error bands of the latter, stand for the decay into the broad $[\Lambda _{c\, (b)}^\mathrm{MOL}(2595)]$ and narrow $[\Lambda _{c\, (n)}^\mathrm{MOL}(2595)]$ molecular resonances found in the $\mathrm{SU(6)}_\mathrm{lsf} \times \mathrm{SU(2)}_\mathrm{HQSS}$ model of Refs. [66, 67]. These differential rates have been obtained multiplying the corresponding molecular gG ratios given in Table 2 by the $\mathcal{O}(1/m_Q)$ improved $\Lambda _b \rightarrow \Lambda _c^*(3/2^-[j_q^P=1^-])\, e\, \bar{\nu }_e$ distribution displayed in Fig.1b of Ref. [14]. Central values have been evaluated using the black solid line of this latter figure. The bands, depicted for the decay into the narrow $\Lambda _c(2595)$ molecular state, show the impact in the spectrum of the uncertainties on the $\mathcal{O}(1/m_Q)$ corrections, and have been calculated using the shaded region shown in Fig.1b of Ref. [14]

Table 4 Semileptonic decay widths $\Gamma [\Lambda _b \rightarrow \Lambda _c^*\,\ell \,\bar{\nu }_\ell$] (in $\Gamma _0/100$ units) for $\mu$ and $\tau$ modes. The rates are calculated using Eq. (26), with form-factors given in Eqs. (29) and (30) or equivalently in Eq. (32). They contain the subleading $\mathcal{O}(1/m_c)$ corrections derived in Ref. [14], assuming that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ form the lowest-lying $j_q^P=1^-$ HQSS doublet. We also show the $\tau /\mu -$semileptonic ratios for both final baryon states, and $\Gamma _\mathrm{sl}[\Lambda _b \rightarrow \Lambda _{c}(2595)]/\Gamma _\mathrm{sl}[\Lambda _b \rightarrow \Lambda _c(2625)]$ for the $\tau \,\bar{\nu }_\tau$ semileptonic mode. Errors are derived from the uncertainties on the $\sigma _1$ form-factor and the $\bar{\Lambda }'$ parameter, and are added in quadrature for the ratios shown in the last three columns. Central values are obtained for $\sigma _1(\omega )=0$ in all cases. Results from Ref. [17] are taken from TABLE II

Table 5 Semileptonic $\Lambda _b \rightarrow \Lambda _c (1/2^+)$ LFU ratios, $R[\Lambda _c]$, obtained in the works of Refs. [17, 118,119,120,121,122]

5.2 $\Lambda _b \rightarrow \Lambda _c(2595)\tau \,\bar{\nu }_\tau$ and $\Lambda _b \rightarrow \Lambda _c(2625)\tau \,\bar{\nu }_\tau$ decays

Let us now pay attention to $\Lambda _b$ semileptonic decays with a $\tau$ lepton in the final state. At the LHC, a large number of ground-state $\Lambda _b$ baryons are produced [113], and its decays into charmed baryons can be used to constrain violations of LFU. These decays are of interest in light of the $R(D^{(*)})$ puzzle in the semileptonic $\bar{B} \rightarrow D^{(*)}\tau \,\bar{\nu }_\tau$ decays (see for instance the discussion in [114], and references therein). Decays involving the ground state charmed baryon, $\Lambda _c$, have been already studied in lattice QCD [115] and beyond the Standard Model [116]. On the other hand, the LHCb collaboration has reported large samples of $\Lambda _c(2595)$ and $\Lambda _c(2625)$ baryons in $\Lambda _b$ semileptonic decays [117], which makes meaningful to investigate the LFU ratios [16, 17]

$$\begin{aligned} R[\Lambda _c^*] = \frac{\mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \tau \,\bar{\nu }_\tau )}{\mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \mu \,\bar{\nu }_\mu )} \end{aligned}$$

(42)

with $\Lambda _c^*= \Lambda _c(2595)$ or $\Lambda _c(2625)$, due to the good prospects that LHCb can measure them in the short term. Results are shown in Table 4.

We have used Eq. (26) to compute $\Gamma [\Lambda _b \rightarrow \Lambda _c(2595)\tau \,\bar{\nu }_\tau ]$ and $\Gamma [\Lambda _b \rightarrow \Lambda _c(2625)\tau \,\bar{\nu }_\tau ]$, assuming that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ form the lowest-lying $j_q^P=1^-$ HQSS doublet, and have taken the $\mathcal{O}(1/m_c)$ improved form factors given in Eq. (32). Therefore, spin symmetry in the $b-$quark sector is conserved, which implies neglecting terms of order $\Lambda _\mathrm{QCD}/m_b$. This is an excellent approximation, and we reproduce within a 5% the $\Lambda _c(2595)$ differential and integrated rates reported in Ref. [14]. The approximation works even better for the $\Lambda _c(2625)$, and moreover it leads to simple expressions for the $\omega -$differential widths, including full finite-lepton mass contributions that are necessary for testing LFU. Note that the calculations of Ref. [14] were made in the $m_\ell \rightarrow 0$ limit.

Predictions for semileptonic $\tau -$decays are relatively stable against the uncertainties on the $\mathcal{O}(1/m_c)$ corrections, because in this case $\omega _\mathrm{max}\sim 1.2$, and the largest contributions to the integrated width come from regions relatively close to zero recoil (see blue solid line of Fig. 2). However, there are still some uncertainties associated with the lack of information about the form factor $\sigma _1(\omega )$, although they are significantly smaller than those shown in Table 2 for the case of massless leptons. The $\sigma _1$ term produces, also for $\tau -$decays, opposite effects for $\Lambda _c(2595)$ or $\Lambda _c(2625)$ final states (see Eqs. (32) and (33)). Uncertainties partially cancel in the $R[\Lambda _c(2595)]$ and $R[\Lambda _c(2625)]$ ratios, which are predicted in Table 4 with moderate errors. We expect these ratios to be comprised in the intervals [0.10, 0.15] and [0.10, 0.13], respectively. These estimates compare rather well with those obtained in the covariant confined quark model employed in Ref. [17].

Next we discuss the $\Gamma ^{1/2}_\mathrm{sl;\, \tau }/ \Gamma ^{3/2}_\mathrm{sl;\, \tau }$ ratio, for which theoretical errors are larger. The central value of this ratio compares rather well with that quoted in Table 2 for light leptons ($\mu$ or e), though its errors for the $\tau$ mode are slightly smaller.

The $\Gamma ^{1/2}_\mathrm{sl;\, \tau }/ \Gamma ^{3/2}_\mathrm{sl;\, \tau }$ ratio would drastically change if the final charmed baryons turned out to be predominantly hadronic molecules. In that situation, we would obtain the same values as in Table 2 from the gG factors compiled in Table 3. We should point out that because the available phase space is smaller for the $\tau$ mode, the decay most likely occurs near the zero-recoil point where the approximations that lead to the quotient of gG factors in Eq. (37) are more precise. The predicted ratios would depend on the molecular scheme, and on the member of the double pole structure of the $\Lambda _c(2595)$ involved in the decay. However, in all cases, we would obtain values below 0.5, at least one-sigma away from the predictions collected in Table 4, based on the hypothesis that the $\Lambda _c(2595)$ and $\Lambda _c(2595)$ form the lowest-lying $1^-$ HQSS multiplet of excited charm-baryons. This latter picture also discards the existence of a second $J^P=1/2^-$ (broad) resonance in the 2.6 GeV region.

It is not clear how the $R[\Lambda _c(2595)]$ and $R[\Lambda _c(2625)]$ ratios would be affected if any of the resonances has a large molecular component, since this will also affect the decay widths into light leptons that appear in the denominators of these ratios. Therefore, one might think that they would not be significantly modified with respect to the values given in Table 4, that mostly account for the reduction of phase space. Nevertheless, it is difficult to be more quantitative. However, $R[\Lambda _c(2595)]$ may be affected by a new source of potentially large systematic errors, if in the $\tau$ and $\mu$ or e modes, the same $\Lambda _c(2595)$ molecular state is not observed. This confusion would produce large numerical variations that would suggest false violations of LFU.

Finally, in Table 5 we collect several predictions [17, 118,119,120,121,122] of the LFU ratios for the $\Lambda _b$ semileptonic decay into the ground-state $\Lambda _c$ $(1/2^+)$. Comparing the ratios of Tables 4 and 5, we see that $R[\Lambda _c]$ is predicted to be significantly larger than $R[\Lambda _c^*]$. (Note, however, that the result of Ref. [122] is considerably smaller than those given by the other authors.)

6 Summary

In this work, we have studied the $\Lambda _b \rightarrow \Lambda _c^*\ell \bar{\nu }_\ell$ and $\Lambda _b \rightarrow \Lambda _c^*\pi ^-$ $[\Lambda _c^*=\Lambda _c(2595)$ and $\Lambda _c(2625)]$ decays, paying special attention to the implications that can be derived from HQSS. We have critically reviewed different molecular descriptions of these charm excited baryons, and have discussed in detail the main features of those schemes that predict a two-pole pattern for the $\Lambda _c(2595)$, in analogy to the case of the similar $\Lambda (1405)$ resonance in the strange sector.

We have calculated the ratios $\Gamma (\Lambda _b\rightarrow \Lambda _c(2595)\pi ^-)/\Gamma (\Lambda _b\rightarrow \Lambda _c(2625)\pi ^-)$ and $\Gamma (\Lambda _b\rightarrow \Lambda _c(2595)\, \ell \,\bar{\nu }_\ell )/ \Gamma (\Lambda _b\rightarrow \Lambda _c(2625)\, \ell \,\bar{\nu }_\ell )$, and have shown that molecular schemes are very sensitive to the interference and relative weights of the DN and $D^*N$ contributions, as firstly pointed out in Refs. [18, 19]. Actually, we have re-derived some of the results of these latter works using a manifest Lorentz and HQSS invariant formalism. In this context, we have argued that future accurate measurements of the above ratios will shed light on the nature of the $\Lambda _c(2595)$, allowing us to address issues as the existence of two poles or the importance of the $D^*N$ channel in the formation of the resonance(s).

We have also investigated the LFU ratios $R[\Lambda _c^*] = \mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \tau \,\bar{\nu }_\tau )/\mathcal{B}(\Lambda _b \rightarrow \Lambda _c^* \mu \,\bar{\nu }_\mu )$. We have computed $\Gamma [\Lambda _b \rightarrow \Lambda _c(2595)\tau \,\bar{\nu }_\tau ]$ and $\Gamma [\Lambda _b \rightarrow \Lambda _c(2625)\tau \,\bar{\nu }_\tau ]$ assuming that the $\Lambda _c(2595)$ and $\Lambda _c(2625)$ form the lowest-lying $j_q^P=1^-$ HQSS doublet, and have taken $\mathcal{O}(1/m_c)$ improved form factors [14]. We have used a scheme that preserves spin-symmetry in the $b-$quark sector, which implies neglecting corrections of order $\Lambda _\mathrm{QCD}/m_b$. This is an excellent approximation that leads to simple expressions for the $\omega -$differential widths, including full finite-lepton mass contributions that are necessary for testing LFU.

Finally, we have pointed out that the $R[\Lambda _c(2595)]$ ratio may be affected by a new source of potentially large systematic errors if there are two $\Lambda _c(2595)$ poles.

At the LHC, a large number $\Lambda _b$ baryons are produced, and the LHCb collaboration has reported large samples of $\Lambda _c(2595)$ and $\Lambda _c(2625)$ baryons in its semileptonic decays. Hence, there are good prospects that LHCb can measure in the near future some of the ratios discussed in this work.