Nonlinear stability analysis of the Schwarzschild thin-shell wormholes

Abstract

Eric Poisson and Matt Vissert in their 1995 paper studied the linear stability of the Schwarzschild thin-shell wormholes (STSW). It was shown that for a generic equation of state (EoS) of the form $p=p\left( \sigma \right)$ on the throat of the wormhole the regions of stability are independent of the explicit form of the surface energy density $\sigma$ and the EoS. Here in this work, the nonlinear version of their stability analysis is presented. To do so, three specific EoSs namely a linear, a quadratic and a power law barotropic EoS are considered. For every EoSs, the analytic function of the effective potential is obtained. Finally, the possible motions of the STSW within the corresponding effective potentials are studied.

1 Introduction

Thin-shell wormhole was introduced by Matt Visser in [1, 2]. The initial idea was to minimize the exotic matter needed to support a traversable Lorentzian wormholes [3,4,5]. The dynamics of such wormhole was studied in [2] where a general stability analysis is presented. Further investigation on the linear stability of the Schwarzschild thin-shell wormhole (STSW), however, was studied by Poisson and Visser in Ref. [6]. The idea was so practical which attracted intensive attentions from the gravity community. This can be seen from the papers published on the stability of the TSWs in different bulk spacetimes [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In spite of the fact that the linear stability formalism gives a reasonable solution about the local stability of the STSW but a relevant point has not received enough attentions. The point is that in must of the papers where the linear stability analysis has been employed, the actual form of the potential that the TSW undergoes, has been ignored. In Ref. [2], however, the picture is different, i.e., some explicit EoSs have been studied with their effects on the stability (not linear) of the considered TSWs. This missing point may be explained and justified in the framework of the linear stability analysis where by linearizing the actual effective potential, some of the information, mainly related to the motion in a larger scale, are discarded.

Furthermore, in the linear stability analysis it is assumed that a static equilibrium radius exists where $a_{0}=\dot{a}_{0}=\ddot{a}_{0}=0$. Naturally, investigating the stability status of the TSW at its equilibrium point i.e.,  $a=a_{0}$ requires a perturbation upon which the TSW becomes a dynamic system. The linear equation of motion of the system is the result of the linear approximation of the perturbation. Now, if one assumes that the perturbation is of the form of an initial kinetic energy, then its initial velocity can not be zero, i.e., $\dot{a}_{0}\ne 0.$ As we will show in this paper, assuming a very small initial velocity i.e., $\dot{a}_{0}^{2}\ll 1$, the results of the linear stability analysis are verified. However, for a greater values for the initial velocity, it is natural to expect some modifications in the results of the linear stability. The aim of this study is to consider the dynamic of the STSW in a large scale where the actual shape of the effective potential becomes relevant. Also the initial values of the motion will be assumed in accordance with the kinetic energy perturbation such that $\dot{a}_{0}=v_{0}\ne 0$. As we shall see in the paper, in order to find a larger picture of the motion of the STSW after the perturbation, one needs to consider an equation of state (EoS) for the fluid matter presented on the STSW. Hence, three different barotropic EoS will be considered and consequently the effective potential and the status of the stability for the initial equilibrium point will be investigated. The approach presented in this study is not the same as the standard linear stability analysis and therefore it will be refereed as the nonlinear stability analysis.

The organization of the paper is as follow. In Sect. 2, the details of the cut and paste formalism for the construction of a STSW are given [6, 15]. In Sect. 3, the linear stability analysis of STSW is presented. The nonlinear stability analysis is introduced in Sect. 4. The paper is concluded with some closing remarks in Sect. 5.

2 Construction of the STSW

Following [1, 2], let’s consider the Schwarzschild black hole solution of the Einstein’s equations with the line element

$$\begin{aligned} ds^{2}=-f\left( r\right) dt^{2}+\frac{dr^{2}}{f\left( r\right) }+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) \end{aligned}$$

(1)

in which

$$\begin{aligned} f\left( r\right) =1-\frac{2M}{r} \end{aligned}$$

(2)

and M is the mass of the black hole. From the manifold (1) we cut out the region $r<a\left( t\right)$ where $a\left( t\right) >2M$ and make two identical copies, namely $\mathcal {M}^{\pm }{=}$ $\{ x^{\mu ( \pm ) }{=}( t^{( \pm ) },r^{( \pm ) },\theta ^{( \pm ) },\varphi ^{( \pm ) }) |r^{( \pm ) }\ge a\} .$ Finally we glue the two copies at the timelike hyperplane $\Sigma :=r-a=0$ and make a complete manifold defined by $\mathcal {M}=\mathcal {M}^{+}\cup \mathcal {M}^{-}.$ Here the hyperplane $\Sigma$ is called the throat of the wormhole which joins the two spacetimes. The throat is a thin-shell and the spacetime is known as the Schwarzschild thin-shell wormhole (STSW). At the throat the Israel junction conditions have to be satisfied. The first condition implies that the induced metric on the throat should be continuous across the throat. The induced metric is defined as

$$\begin{aligned} ds_{w}^{2\left( \pm \right) }=h_{ij}^{\left( \pm \right) }dy^{i\left( \pm \right) }dy^{j\left( \pm \right) } \end{aligned}$$

(3)

in which

$$\begin{aligned} h_{ij}^{\left( \pm \right) }=g_{\alpha \beta }^{\left( \pm \right) }\frac{ \partial x^{\alpha \left( \pm \right) }}{\partial y^{i\left( \pm \right) }} \frac{\partial x^{\beta \left( \pm \right) }}{\partial y^{j\left( \pm \right) }}. \end{aligned}$$

(4)

Note that, $y^{i\left( \pm \right) }=\left( t^{\left( \pm \right) },\theta ^{\left( \pm \right) },\varphi ^{\left( \pm \right) }\right)$ and the induced metrics are

$$\begin{aligned} ds_{w}^{\left( \pm \right) 2}= & {} -\left( f^{\left( \pm \right) }\left( a\right) -\frac{a^{\prime \left( \pm \right) 2}}{f^{\left( \pm \right) }\left( a\right) }\right) dt^{\left( \pm \right) 2}\nonumber \\&+a^{2}\left( d\theta ^{\left( \pm \right) 2}+\sin ^{2}\theta ^{\left( \pm \right) }d\varphi ^{\left( \pm \right) 2}\right) . \end{aligned}$$

(5)

To satisfy the first Israel junction condition, one may set, $\theta ^{\left( \pm \right) }=\theta ,\varphi ^{\left( \pm \right) }=\varphi$ and $\left( f^{\left( \pm \right) }\left( a\right) -\frac{a^{\prime \left( \pm \right) 2}}{f^{\left( \pm \right) }\left( a\right) }\right) dt^{\left( \pm \right) 2}=d\tau ^{2}$ in which $\tau$ is defined as the proper time on the throat $\Sigma$ and $a^{\prime \left( \pm \right) }=\frac{da}{dt^{\left( \pm \right) }}$. In short, one finds

$$\begin{aligned} ds_{w}^{\left( \pm \right) 2}=-d\tau ^{2}+a^{2}\left( \tau \right) \left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) \end{aligned}$$

(6)

and upon using $f^{\left( +\right) }\left( a\right) =f^{\left( -\right) }\left( a\right) =1-\frac{2M}{a}$, one finds

$$\begin{aligned} -f\left( a\right) \dot{t}^{\left( \pm \right) 2}+\frac{\dot{a}^{2}}{f\left( a\right) }=-1 \end{aligned}$$

(7)

where an over-dot stands for the derivative with respect to $\tau .$ The second Israel junction condition implies ($G=1$)

$$\begin{aligned} \left[ K_{i}^{j}\right] -\delta _{i}^{j}\left[ K\right] =-8\pi S_{i}^{j} \end{aligned}$$

(8)

in which $S_{i}^{j}=diag\left( -\sigma ,p,p\right)$ is the energy momentum tensor on the throat, $\left[ Z\right] =Z^{+}-Z^{-}$,

$$\begin{aligned} K_{i}^{j\left( \pm \right) }=-n_{\gamma }^{\left( \pm \right) }\left( \frac{ \partial ^{2}x^{\gamma }}{\partial y^{i}\partial y^{j}}+\Gamma _{\alpha \beta }^{\gamma }\frac{\partial x^{\alpha }}{\partial y^{i}}\frac{\partial x^{\beta }}{\partial y^{j}}\right) ^{\left( \pm \right) } \end{aligned}$$

(9)

with the spacelike unit normal

$$\begin{aligned} n_{\gamma }^{\left( \pm \right) }=\pm \frac{1}{\sqrt{\Delta }}\frac{\partial \Sigma }{\partial x^{\gamma \left( \pm \right) }} \end{aligned}$$

(10)

and $K=K_{i}^{i}.$ Also, $n_{\gamma }^{\left( \pm \right) }n^{\gamma \left( \pm \right) }=1$ which yields

$$\begin{aligned} \Delta =g^{\left( \pm \right) \alpha \beta }\frac{\partial \Sigma }{\partial x^{\alpha \left( \pm \right) }}\frac{\partial \Sigma }{\partial x^{\beta \left( \pm \right) }}. \end{aligned}$$

(11)

A detail calculation reveals

$$\begin{aligned} \sigma =-\frac{1}{2\pi a}\sqrt{1-\frac{2M}{a}+\dot{a}^{2}} \end{aligned}$$

(12)

and

$$\begin{aligned} p=-\frac{\sigma }{2}+\frac{a^{2}\ddot{a}+M}{4\pi a^{2}\sqrt{1-\frac{2M}{a}+ \dot{a}^{2}}}. \end{aligned}$$

(13)

Furthermore, the energy conservation i.e., $S_{;j}^{ij}=0$ for $i=\tau$, reveals that $\sigma$ and p are not independent and they satisfy

$$\begin{aligned} \frac{d\sigma }{da}+\frac{2}{a}\left( \sigma +p\right) =0. \end{aligned}$$

(14)

Traditionally, one assumes that there exists a static equilibrium radius for the STSW where $a=a_{0}$ and $\dot{a}=\ddot{a}=0$. The static components of the energy-momentum tensor, hence, are obtained to be

$$\begin{aligned} \sigma _{0}=-\frac{1}{2\pi a_{0}}\sqrt{1-\frac{2M}{a_{0}}} \end{aligned}$$

(15)

and

$$\begin{aligned} p_{0}=-\frac{\sigma _{0}}{2}+\frac{M}{4\pi a_{0}^{2}\sqrt{1-\frac{2M}{a_{0}}} }. \end{aligned}$$

(16)

Now, we have a static equilibrium thin-shell wormhole whose throat is located at $a=a_{0}$ with $\dot{a}=\ddot{a}=0$ and $\sigma _{0}$ and $p_{0}$ are given above. The next step is to investigate the stability of the static equilibrium of the STSW. To do so one has to perturb the thin-shell wormhole from its static equilibrium and then study the behavior of the throat. Here in this study from the perturbation we mean an initial kinetic energy or an initial velocity i.e., $\dot{a}_{0}=v_{0}.$ Hence, the initial value of the surface energy density and angular pressure are no longer of the form given in the Eqs. (15) and (16) and instead they read as

$$\begin{aligned} \tilde{\sigma }_{0}=-\frac{1}{2\pi a_{0}}\sqrt{1-\frac{2M}{a_{0}}+v_{0}^{2}} \end{aligned}$$

(17)

and

$$\begin{aligned} \tilde{p}_{0}=-\frac{\tilde{\sigma }_{0}}{2}+\frac{M}{4\pi a_{0}^{2}\sqrt{1- \frac{2M}{a_{0}}+v_{0}^{2}}}. \end{aligned}$$

(18)

Note that $0\le v_{0}^{2}\le 1$ and $\tilde{\sigma }_{0}$ and $\tilde{p} _{0}$ are the initial values of $\sigma$ and p after the kinetic energy perturbation. In the sequel I study the linear and nonlinear stability of the STSW.

3 Linear stability analysis

Fig. 1

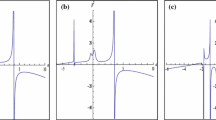
$V_{I}$ and $\sigma _{I}$ in terms of a for $a_{0}=2.5M$, $\beta _{0}^{2}=16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. The arising zero of $V_{I}$ where $V_{I}^{\prime }\ne 0$ is a turning point of the motion. The value of the surface energy density is negative in the region where the motion is physically possible. The stable STSW corresponding to the linear stability analysis, becomes unstable with $v_{0}^{2}>0$

Fig. 2

Plots of $V_{I}$ and $\sigma _{I}$ against a for $a_{0}=3M$, $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. We note that in linear stability analysis (corresponding to $v_{0}=0$) with $M=1$, $a_{0}=3M$ is the radius where the STSW is unstable irrespective of the value of $\beta _{0}^{2}.$ The effect of $v_{0}\ne 0$ can be seen in the shape of the potential

Fig. 3

Plots of $V_{I}$ and $\sigma _{I}$ against a for $a_{0}=5M$, $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. Similar to Fig. 1, the nonlinear analysis reveals that the well stable STSW in the framework of the linear perturbation, becomes unstable with large enough $v_{0}$

The equation of motion of the STSW after the perturbation is given by the Eqs. (12) or (13) provided one knows the closed form of the surface energy density $\sigma$ and the angular pressure p. On the other hands, for any type of fluid matter presented on the STSW, one may consider an equation of states (EoS). In this work, following the Ref. [6], we consider a generic EoS of the form $p=p\left( \sigma \right)$ such that

$$\begin{aligned} \left. \frac{dp}{d\sigma }\right| _{a=a_{0}}=\left. \frac{\partial p}{ \partial \sigma }\right| _{a=a_{0}}=\beta _{0}^{2}. \end{aligned}$$

(19)

Upon considering the energy conservation equation and the EoS one, in principle, is able to find the closed form of $\sigma$ and p which will result in two dependent equations of motion namely (12) and (13). Consequently, one of the equations may be considered, which traditionally is the equation of $\sigma$ which, in its rearranged form, reads as

$$\begin{aligned} \dot{a}^{2}+V\left( a\right) =0 \end{aligned}$$

(20)

where

$$\begin{aligned} V\left( a\right) =1-\frac{2M}{a}-\left( 2\pi a\sigma \left( a\right) \right) ^{2}. \end{aligned}$$

(21)

For a linear stability / perturbation analysis, we make a Taylor expansion of the potential about $a=a_{0}$ to obtain

$$\begin{aligned} V\left( a\right)\simeq & {} V\left( a_{0}\right) +V^{\prime }\left( a_{0}\right) \left( a-a_{0}\right) +\frac{1}{2}V^{\prime \prime }\left( a_{0}\right) \left( a-a_{0}\right) ^{2}\nonumber \\&+\mathcal {O}\left( \left( a-a_{0}\right) ^{3}\right) . \end{aligned}$$

(22)

As of the assumption of the linear perturbation, we assume that $v_{0}^{2}\simeq 0$ (but not zero) which yields $V\left( a_{0}\right) =-v_{0}^{2}\simeq 0,$ $V^{\prime }\left( a_{0}\right) =0$ and

$$\begin{aligned} V^{\prime \prime }\left( a_{0}\right) =\frac{24\left[ \beta _{0}^{2}\left( \frac{1}{6}\left( 1+v_{0}^{2}\right) x\left( \left( 1+v_{0}^{2}\right) x-5\right) +1\right) +\frac{1}{4}+\frac{1}{12}\left( -3+\left( 1+v_{0}^{2}\right) x\right) \left( 1+v_{0}^{2}\right) x\right] }{ M^{2}x^{3}\left( 2-x\left( 1+v_{0}^{2}\right) \right) } \end{aligned}$$

(23)

in which $x=a_{0}/M.$ With the linear perturbation / stability analysis, as we mentioned above, $v_{0}^{2}\ll 1$ and therefore $V^{\prime \prime }\left( a_{0}\right)$ approximately becomes

$$\begin{aligned} V^{\prime \prime }\left( a_{0}\right) \simeq \frac{24\left[ \beta _{0}^{2}\left( \frac{1}{6}x\left( x-5\right) +1\right) +\frac{1}{4}+\frac{1}{ 12}\left( -3+x\right) x\right] }{M^{2}x^{3}\left( 2-x\right) }. \end{aligned}$$

(24)

Clearly, a stable STSW needs $V^{\prime \prime }\left( a_{0}\right) \ge 0$. Upon (24), in terms of $\beta _{0}^{2}$ and $x=a_{0}/M,$ the regions of stability of STSW can be found (see Fig. 1 of Ref. [6]). Referring to the STSW, in Refs. [2, 6], $a_{0}=3M$ has been reported as a critical radius for the STSW at which the wormhole is definitely unstable irrespective of the value of $\beta _{0}^{2}.$ Also, for $a_{0}>3M$ and $a_{0}<3M$ there are different conditions for $\beta _{0}^{2}$ to be satisfied in order to have a stable STSW (see the Eqs. (31) and (32) of Ref. [6]). Hence, for a stable STSW

$$\begin{aligned} \left\{ \begin{array}{cc} \beta _{0}^{2}>-\frac{x^{2}-3x+3}{2\left( x-2\right) \left( x-3\right) } &{}2<x<3 \\ \beta _{0}^{2}<-\frac{x^{2}-3x+3}{2\left( x-2\right) \left( x-3\right) } &{} x>3 \end{array}\right. \end{aligned}$$

(25)

which are found from (24).

Fig. 4

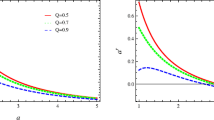
$V_{II}$ and $\sigma _{II}$ in terms of a for $a_{0}=2.5M$ , $\beta _{0}^{2}=16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. This figure is in analogy with Fig. 1 and the potential’s shape changes due to the effects of $v_{0}\ne 0.$ Such effects are not trivial but nonlinear

Fig. 5

$V_{II}$ and $\sigma _{II}$ in terms of a for $a_{0}=3M$, $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. With $v_{0}=0.0$, $a_{0}$ is clearly an unstable equilibrium point, however, a very small perturbation to the positive direction makes the STSW oscillating about a new stable point. This stability is a new observation which has not been detected before in linear stability analysis

Fig. 6

Plots of $V_{II}$ and $\sigma _{II}$ against a for $a_{0}=5M$, $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0

It is remarkable to observe that, having a generic EoS in [6] implies that the stability region becomes independent of the explicit form of the EoS and consequently $\sigma$.

4 Nonlinear stability analysis

Let’s recall that the exact equation of motion of the STSW has been reduced to (20) with the potential given in (21). Unlike the linear stability analysis, in a nonlinear stability analysis one has to know the function of $\sigma \left( a\right)$. This, however, requires a given EoS. Here in this section three specific barotropic EoSs, namely a linear, a quadratic and a power-law, are considered in order to calculate the corresponding surface energy densities and potentials. Consequently, we study the behavior of the perturbed STSW. Furthermore, any constraint on the initial velocity of the STSW is removed such that $v_{0}^{2}\in \left[ 0,1\right] .$

4.1 Linear and quadratic barotropic EoSs

First let’s consider the following linear and quadratic barotropic EoSs:

$$\begin{aligned} \left\{ \begin{array}{cc} \text {Case I:} &{} \quad p_{I}=\beta _{0}^{2}\left( \sigma \left( a\right) -\tilde{ \sigma }_{0}\right) +\tilde{p}_{0} \\ \text {Case II:} &{} \quad p_{II}=\frac{\beta _{0}^{2}}{2\sigma _{0}}\left( \sigma ^{2}\left( a\right) -\tilde{\sigma }_{0}^{2}\right) +\tilde{p}_{0} \end{array}\right. . \end{aligned}$$

(26)

Please note that these models are the simplest form of the barotropic EoS which satisfy the necessary conditions i.e., $p_{I,II}\left( a_{0}\right) = \tilde{p}_{0}$ and Eq. (19). The Case I, was also studied by Visser in [2]. Using the energy conservation equation (14), the explicit form of the surface energy densities are obtained as

$$\begin{aligned} \left\{ \begin{array}{cc} \text {Case I:} &{} \quad \sigma _{I}\left( a\right) =\frac{1}{\beta _{0}^{2}+1}\left[ \left( \tilde{\sigma }_{0}+\tilde{p}_{0}\right) \left( \frac{a}{a_{0}}\right) ^{-2\left( \beta _{0}^{2}+1\right) }+\beta _{0}^{2}\tilde{\sigma }_{0}-\tilde{ p}_{0}\right] \\ \text {Case II:} &{} \quad \sigma _{II}\left( a\right) =\frac{\tilde{\sigma }_{0}}{ \beta _{0}^{2}}\left[ \frac{\sqrt{\Lambda }}{\tilde{\sigma }_{0}}\tanh \left( \frac{\sqrt{\Lambda }}{\tilde{\sigma }_{0}}\ln \left( \frac{a}{a_{0}}\right) +\tan ^{-1}\left( \frac{\tilde{\sigma }_{0}\left( \beta _{0}^{2}+1\right) }{ \sqrt{\Lambda }}\right) \right) -1\right] \end{array}\right. \nonumber \\ \end{aligned}$$

(27)

in which

$$\begin{aligned} \Lambda =\left( \beta _{0}^{2}\tilde{\sigma }_{0}-\tilde{p}_{0}\right) ^{2}+ \tilde{\sigma }_{0}^{2}-\tilde{p}_{0}^{2}. \end{aligned}$$

(28)

Having $\sigma \left( a\right)$ in each Case, the corresponding potential is found using the Eq. (21). Referring to the critical radius of the STSW in the linear stability analysis i.e., $a_{0}=3M,$ we consider three different configurations: (1) $a_{0}=2.5M<3M$ with $\beta _{0}^{2}=16$, (2) $a_{0}=3M$ with $\beta _{0}^{2}=-16$ and (3) $a_{0}=5M>3M$ with $\beta _{0}^{2}=-16$. For all three cases the mass M behaves as a scale factor and without any loss of generality we may assume $M=1$. Let’s recall that, in the linear stability, the STSW is stable in cases (i) and (iii) while in case (ii) it is unstable irrespective of the value of $\beta _{0}^{2}$.

Figures. 1, 2, and 3 display the potential $V_{I}\left( a\right)$ and $\sigma _{I}\left( a\right)$ against a in accordance with the first, second and third configurations and various values of $v_{0}.$ In these figures the $v_{0}=0$-curve (the uppermost) corresponds to the potential used in the linear stability analysis. It is remarkable to observe from Fig. 1 that, having $v_{0}\ne 0$ not only shifts the potential to the negative region but also its shape is getting changed significantly. In other words the potential of the STSW depends on how it is perturbed. This becomes more interesting if we note that any intersection of the potential with the $a-$axis is a turning point for the motion of the STSW. Hence, for instance with $v_{0}$ very small there are two turning points which implies that the STSW oscillates between the two turning points. But for larger $v_{0}$ up to a certain $v_{0}$ there is only one turning point located to the left of $a=a_{0}$ which indicates that the STSW expands to infinity and is unstable. For large enough $v_{0}$ the only turning point disappears and depending on the direction of the initial velocity the STSW may either collapse into a black hole or expands to an evaporation. In Fig. 2, similar to Fig. 1 the shape of the potential is changed significantly such that although with $v_{0}=0$ the wormhole is unstable from both directions (i.e., it may collapse or evaporate) but with $v_{0}\ne 0$ the wormhole faces a barrier such that it can not penetrate to infinity and indeed collapses. Knowing that even for the linear stability one has to apply a non-zero initial velocity, Fig. 2 suggests that the such STSW definitely collapses to a black hole. Let’s comment that for very small velocity there is a different scenario which we shall come back later. Fig. 3 shows that the STSW which appearently is stable with $v_{0}=0$ and small $v_{0},$ may not be stable for large enough $v_{0}$ and collapses to form a black hole. In Figs. 1, 2, and 3, in the right column, we plot also the surface energy density using the same configurations. Here, it is observed that, in any possible motion of the STSW, its energy density is negative and the matter source remains exotic.

In Figs. 4, 5, and 6 we plot $V_{II}\left( a\right)$ and $\sigma _{II}\left( a\right)$ in terms of a for the same three different configurations as of the Figs. 1, 2, and 3. Although the general appearance of $V_{II}\left( a\right)$ and $\sigma _{II}\left( a\right)$ are different from $V_{I}\left( a\right)$ and $\sigma _{I}\left( a\right)$ but the effects of $v_{0}\ne 0$ are almost the same. In addition to that, there is a new observation in the shape of the potential in Fig. 5. It is seen that although with $v_{0}\simeq 0$ the wormhole is locally unstable at $a=a_{0},$ for a positive but very small velocity, it falls into a potential well and oscillates ever after. This means that a STSW which under the linear perturbation is considered to be unstable at $a_{0}=3M$, apparently, is stable. We should add that this new stability is not static stability at $a=a_{0}$ but a dynamic stability about a radius grater than $a=a_{0}$. The same argument as of Figs. 1, 2, and 3 is valid for the corresponding surface densities in Figs. 4, 5, and 6 as well.

Fig. 7

$V_{III}$ and $\sigma _{III}$ in terms of a for $a_{0}=2.5M$, $\beta _{0}^{2}=16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0

Fig. 8

$V_{III}$ and $\sigma _{III}$ in terms of a for $a_{0}=3M$ , $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0. See the caption of Figs. 2 and 5

Fig. 9

Plots of $V_{III}$ and $\sigma _{III}$ against a for $a_{0}=5M$, $\beta _{0}^{2}=-16$, $M=1$ and from above $v_{0}=0.0,0.2,0.4,0.6,0.8$ and 1.0

4.2 A power-law barotropic EoS

Beside the two EoSs which I have employed in the previous section, here I introduce a third form for the EoS whose structure is different. Let’s introduce

$$\begin{aligned} \text {Case III: }p_{III}=\tilde{p}_{0}\left( \frac{\sigma \left( a\right) }{ \tilde{\sigma }_{0}}\right) ^{\alpha } \end{aligned}$$

(29)

in which

$$\begin{aligned} \alpha =\frac{\tilde{\sigma }_{0}}{\tilde{p}_{0}}\beta _{0}^{2}. \end{aligned}$$

(30)

After applying the energy conservation equation (14) one finds

$$\begin{aligned} \sigma _{III}\left( a\right) =\left( \frac{\tilde{\sigma }_{0}}{\left( \frac{a }{a_{0}}\right) ^{2\left( \alpha -1\right) }\left( \tilde{\sigma }_{0}+\tilde{ p}_{0}\right) -\tilde{p}_{0}}\right) ^{\frac{1}{\alpha -1}}\tilde{\sigma } _{0}. \end{aligned}$$

(31)

We note that, $\sigma _{III}\left( a_{0}\right) =\tilde{\sigma }_{0}$, $p_{III}\left( a_{0}\right) =\tilde{p}_{0}$ and $\left. \frac{dp_{III}}{ d\sigma }\right| _{a=a_{0}}=\beta _{0}^{2}$ as are expected. Using Eq. (21) the corresponding effective potential is also obtained. Finally, $V_{III}\left( a\right)$ and $\sigma _{III}\left( a\right)$ are plotted in Figs. 7, 8, and 9 using the same configuration as in Figs. 1, 2, and 3 and Figs. 1, 2, 3, 4, 5, and 6. These three figures for the Case III, manifest the same facts as the other two cases. In particular, Fig. 7 shows that the linear stable STSW may not be stable after the nonlinear perturbation. This means that while for the smaller initial velocity the STSW remains stable around $a=a_{0},$ for a larger initial velocity, at first it may only blow to infinity and than for greater velocity it may collapse or evaporate depends on the direction of the initial velocity. Figs. 8 and 9 are strongly support our observations in the other two cases as well.

Fig. 10

A closer look at the potentials $V_{I},V_{II}$ and $V_{III}$ with very small initial velocity i.e., $v_{0}\ll 1$ and $a=3M$, $M=1$ and $\beta _{0}^{2}=16,-16$ and $-16$ for $V_{I},V_{II}$ and $V_{III}$ respectively. For all three potentials the value of the initial velocity varies from 0.0010 (the leftmost curve) to 0.0000 (the rightmost curve) with steps equal to 0.0002. Hence, $v_{0}=0.0000,0.0002,0.0004,0.0006,0.0008$ and 0.0010 correspond to the brown, red, green, gray, black and blue curve respectively

5 Closing remarks

The nonlinear stability analysis of the STSW has been presented. In this line, we studied the equation of motion of the STSW after a kinetic energy perturbation in the form of an initial velocity $v_{0}$. Having $v_{0}\ne 0$ , modifies the initial surface energy density and angular pressure. Hence, the effective potential is found to be depending on $v_{0}.$ For a linear stability analysis, one has to assume either $v_{0}=0$ or very close to zero i.e., $v_{0}^{2}\ll 1$. We employed three different EoSs and using the energy conservation equation, found the closed form of the surface energy density for each EoS. The corresponding effective potential, hence, has been obtained separately for each EoS. Finally, we plot the effective potential and the surface energy density in terms of the radius of the STSW for different configurations. Our numerical plots revealed that the stability of the STSW not only depends on the parameters such as a and $\beta _{0}^{2}$ , but also the initial velocity in a nonlinear manner. Specifically, the shape of the potential changes significantly with the different values of $v_{0}$. This shape-change is accompanied with a shift toward the negative region of the potential too. In Fig. 10 we plot again the potentials $V_{I},V_{II}$ and $V_{III}$ in terms of a with the equilibrium radius $a_{0}=3M$ and $M=1$ but for small initial speed. This radius is specifically important as it is the radius of the definite instability of the STSW in the formalism of the linear stability analysis. It is observed from this figure that although $a_{0}=3M$ is a local instability radius for the STSW, a very small perturbation as an initial speed in the positive radial direction, pushes the STSW to fall into a potential well with two turning points. Consequently, the STSW oscillates around a new stability radius which is greater than $a_{0}=3M$. Such a STSW experiences a new stability which is not static and instead we shall call it dynamic stability. The final point regarding to the Fig. 10 is that for the quadratic EoS, the potential i.e., $V_{II}$ in this figure, behaves the same even for $v_{0}=0$ . In other worlds, the potential $V_{II}$ suggests that $a_{0}=3M$ with $v_{0}=0$ is not a local stable equilibrium point. However, this does not necessarily mean that the STSW evaporates or collapses. It may become stable after a perturbation with a small initial velocity toward the positive radial direction. This behavior has not been noticed before in the context of the linear stability analysis.