1 Introduction

In the last decades, the ideas underlying the anti de-Sitter/conformal field theory (AdS/CFT) correspondence have been applied to get a better understanding of phenomena that occur in the condensed matter physics as the quantum Hall effect, the superconductivity or the superfluidity, see e.g. [1, 2]. As a significative example, we can mention the case of charged hairy black holes with a planar horizon that may be relevant to describe the behavior of unconventional superconductors [3]. In this scenario, the nonzero condensate behavior of the unconventional superconductors is mimicked by the existence of a hair at low temperature that must disappear in the high temperature regime [3]. Nevertheless, finding black holes with such features is a highly nontrivial problem that is rendered even more difficult by the various no-hair theorems with scalar fields existing in the current literature, see e.g. [4]. Fortunately, the precursor works of Refs. [5, 6] have established that scalar fields nonminimally coupled seem to be an excellent laboratory in order to escape the standard scalar no-hair theorems. Indeed, as shown independently in Refs. [5, 6], conformal scalar field nonminimally coupled to Einstein gravity can support black hole configuration with a nontrivial scalar field. These black hole solutions have been dubbed BBMB solution in the current literature. However, the BBMB solution suffers from some pathology essentially because of the divergence of the scalar field at the event horizon. This inconvenient makes its physical interpretation and the problem of its stability a subject of debate. A way of circumventing this pathology consists in introducing a cosmological constant whose effect is to precisely push the singularity behind the horizon, and as a direct consequence, the scalar field becomes well-defined at the event horizon [7]. It is important to stress that for the BBMB solution or its extensions with cosmological constant dubbed as the MTZ solution [7, 8], the parameter \(\xi \) that couples nonminimally the scalar field to the curvature is always the conformal one in four dimensions, namely \(\xi =\frac{1}{6}\), and the horizon topology of the black hole solutions is either spherical or hyperbolic depending on the sign of the cosmological constant. There also exist examples of black hole solutions with the conformal coupling \(\xi =\frac{1}{6}\) but with a potential term that breaks the conformal invariance of the matter source, see e.g. [9, 10]. Nevertheless, charged black holes with planar horizon topology for a scalar field nonminimally coupled to Einstein gravity with or without a cosmological constant are not known.Footnote 1 It seems that extra matter source is needed in order to sustain planar charged black hole with a nonminimal scalar field. This intuition is based on the works done in [14, 15] where a planar version of the MTZ solution was rendered possible thanks to the introduction of two 3-forms that were originated from two Kalb-Raimond potentials. Interestingly enough, this construction was also extended for arbitrary nonminimal coupling in [16]. Very recently, it has also been shown that (charged) planar AdS black holes can arise as solutions of General Relativity with a source composed by a conformal scalar field together with two axionic fields depending linearly on the coordinates of the planar base manifold [17]. The existence of these planar black holes is mainly due to the presence of the axionic scalar fields which, in addition of inducing an extra scale, allow the planar solutions to develop an event horizon. More precisely, as proved in [17], the black hole mass is related to the parameter associated to the axionic fields, and hence these axionic (charged) black branes can be interpreted as extremals in the sense that all their Noetherian charges are fixed in term term of the axionic intensity parameter. Many other interesting features are inherent to the presence of axionic fields for planar solutions. Among others, axionic fields depending linearly on the coordinates of the planar base manifold provide a very simple mechanism of momentum dissipation [18]. From an holographic point of view, this feature has a certain interest since, as established in Refs. [19, 20], the computation of the DC conductivities can be uniquely expressed in term of the black hole horizon data. Mainly because of these results, the study of axionic black hole configurations in different contexts has considerably grow up the last time, see e.g. [21,22,23,24,25,26,27,28].

In the present, we plan to extend the work done in the conformal situation [17] to the case of a four-dimensional scalar field with an arbitrary nonminimal coupling with two axionic fields. The model also involves a parameter b that enters in the scalar potential and in the function that minimally couples the scalar and the axionic fields, see below (2.3a–2.3b). The range of this extra parameter will be fixed by some reality conditions as well as by demanding the solutions to have positive entropy. Asymptotically AdS planar dyonic black hole solutions will be presented with axionic fields homogeneously distributed along the orthogonal planar coordinates of the base manifold for a priori any positive value of the nonminimal coupling parameter \(\xi \). However, the positive entropy condition will considerably reduce the range of the permissible values of the nonminimal coupling parameter. As in the conformal case [17], the solutions only contain an integration constant denoted by \(\omega \). Interestingly enough, the location of the event horizon can be at two different positions depending on the sign of the parameter \(\omega \). Moreover, for \(\omega <0\), the range of permissible values of the nonminimal coupling parameter is discrete, and the solution is shown to be extremal since its has zero temperature. Finally, the full DC conductivities associated to the charged black brane solutions will be computed following the recipes given in [19, 20]. One of our motivations is precisely to identify the impact on the conductivities of the nonminimal coupling parameter.

The plan of the paper is organized as follows. In the next section, we present the model which consists of the Einstein gravity action with a negative cosmological constant with a source given by a self-interacting and nonminimally scalar field coupled to two axionic fields. In Sect. 3, the asymptotically AdS planar dyonic solutions are presented. In Sect. 4, a detailed analysis of the thermodynamic properties of the solutions through the Hamiltonian method is provided allowing to identify correctly the mass of the dyonic solutions. In the next section, following the perturbative method presented in [19, 20], the full DC conductivities of the (non) extremal solutions are computed and the effects of the nonminimal coupling parameter are analyzed. The last section is devoted to our conclusions.

2 Model, field equations and black brane solutions

We consider a four-dimensional Einstein-Maxwell model with a negative cosmological constant, a nonminimally coupled and self-interacting scalar field \(\phi \) together with two axionic fields \(\psi _i \) for \(i=1, 2\) whose action is given by

$$\begin{aligned} S= & {} \int d^4x \sqrt{-g} \left( \kappa (R - 2\Lambda ) - \frac{1}{4} F_{\mu \nu }F^{\mu \nu } - \dfrac{1}{2}\partial _{\mu }\phi \partial ^{\mu }\phi \right. \nonumber \\&\left. - \dfrac{\xi }{2}R\phi ^2 - U_b(\phi ) - \dfrac{\varepsilon _b(\phi )}{2} \sum _{i=1}^{2} \partial _{\mu } \psi _i\ \partial ^{\mu } \psi _i \right) . \end{aligned}$$
(2.1)

Here the Maxwell field strength is \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\), the nonminimal coupling parameter is denoted by \(\xi \) while the potential \(U_b\) and the coupling \(\varepsilon _b\) will be given below. For latter convenience, we shall opt for the following parametrization of the nonminimal coupling parameter \(\xi \)

$$\begin{aligned} \xi =\frac{n-1}{4n}, \end{aligned}$$
(2.2)

which maps the region \(\xi >0\) to \(n\in \mathbb {R} {\setminus } [0,1]\).Footnote 2 Note that the particular value \(\xi =\frac{1}{4}\) which corresponds to the limit \(n\rightarrow \infty \) will be treated separately. The potential \(U_b(\phi )\) and the coupling \(\varepsilon _b(\phi )\) associated to the axionic fields depend on a positive constant denoted by b whose range will be conditioned by some reality conditions as shown below

$$\begin{aligned} U_b(\phi )= & {} \dfrac{1-n}{8n\left( 1-b\phi ^{\frac{2}{n-1}}\right) ^4} \Big ( 4b^3(n- 3)(n-4)\phi ^{\frac{2n+4}{n-1}}\nonumber \\&-3b^2(n-4)(3n-7)\phi ^{\frac{2n+2}{n-1}}+ \ 6b(n-3)^2\phi ^{\frac{2n}{n-1}} \nonumber \\&- (n-3)(n-4)\phi ^{2} - \ 6b^{5-n}\phi ^{\frac{8}{n-1}} \Big ), \end{aligned}$$
(2.3a)
$$\begin{aligned} \varepsilon _b(\phi )= & {} 1 + \dfrac{n-1}{8n\kappa }\nonumber \\&\times \ \left( \dfrac{(n-2)\phi ^2- (n-3)b\phi ^{\frac{2n}{n-1}}- b^{3-n}\phi ^{\frac{4}{n-1}}}{(1-b\phi ^{\frac{2}{n-1}})^2} \right) . \nonumber \\ \end{aligned}$$
(2.3b)

It is also important to stress that in order to ensure a mechanism of momentum dissipation as well as a correct sign for the axionic kinetic term, the minimal coupling function \(\varepsilon _b(\phi )\) must be strictly positive everywhere. Before proceeding, we would like to stress that the minimal case \(\xi =0\) or equivalently \(n=1\) which has been fully treated in [18] is clearly excluded from our analysis because of the form of the expressions \(U_b(\phi ) \) and \(\varepsilon _b(\phi )\). Also, we may note that for the conformal situation \(\xi =\frac{1}{6}\) or equivalently \(n=3\), the potential vanishes identically and the axionic minimal coupling \(\varepsilon _b(\phi )=1\), and this situation corresponds to the case already studied in [17].

The field equations obtained by varying the action (2.1) with respect to the metric, the Maxwell field \(A_{\mu }\), the scalar field \(\phi \) and the axionic fields \(\psi _i\) read respectively

$$\begin{aligned}&\kappa (G_{\mu \nu } + \Lambda g_{\mu \nu }) = \frac{1}{2} T^{\phi }_{\mu \nu } + \frac{1}{2}T^{\psi }_{\mu \nu } + \frac{1}{2}T^{\text {em}}_{\mu \nu },\nonumber \\&\nabla _{\mu } F^{\mu \nu } = 0,\nonumber \\&\square \phi = \dfrac{n-1}{4n} R\phi + \dfrac{dU_b}{d\phi } + \dfrac{1}{2}\dfrac{d\varepsilon _b}{d\phi } \sum _{i=1}^{2} g^{\mu \nu }\partial _{\mu }\psi _{i}\partial _{\nu }\psi _{i},\nonumber \\&\nabla _{\alpha } \left( \varepsilon _b(\phi )\nabla ^{\alpha }\psi _{i} \right) = 0,\quad i=1,2, \end{aligned}$$
(2.4)

where the different energy–momentum tensors are given by

$$\begin{aligned} T^{\phi }_{\mu \nu }= & {} \partial _{\mu }\phi \partial _{\nu } \phi - g_{\mu \nu }\left( \dfrac{1}{2}\partial _{\alpha } \phi \partial ^{\alpha }\phi + U_b(\phi ) \right) \\&+ \dfrac{n-1}{4n} \left( g_{\mu \nu }\square - \nabla _{\mu }\nabla _{\nu } + G_{\mu \nu }\right) \phi ^2, \\ T^{\psi }_{\mu \nu }= & {} \varepsilon _b(\phi )\sum _{i=1}^{2}\left( \partial _{\mu }\psi _{i}\partial _{\nu }\psi _{i} - \dfrac{1}{2} g_{\mu \nu }\partial _{\alpha }\psi _{i}\partial ^{\alpha }\psi _{i} \right) ,\\ T^{\text {em}}_{\mu \nu }= & {} F_{\mu \sigma }F_{\nu }^{\ \sigma } - \frac{1}{4}g_{\mu \nu }F_{\rho \sigma }F^{\rho \sigma }. \end{aligned}$$

Dyonic black brane solutions of the field equations for \(\Lambda =- \ 3\) and with axionic fields homogeneously distributed along the two-dimensional planar base manifold can be found, and are given by

$$\begin{aligned}&ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2(dx^2+dy^2),\nonumber \\&f(r)=\frac{1}{r^2} \left( r-\dfrac{3\omega }{\sqrt{12\kappa }}\right) \left( r + \dfrac{\omega }{\sqrt{12\kappa }} \right) ^3,\nonumber \\&\psi _1(x) = \omega x, \quad \psi _2(y)= \omega y\nonumber \\ \nonumber \\&\phi (r)=\Bigg [\frac{\omega }{b\left( \sqrt{12\kappa }r+\omega \right) }\Bigg ]^{\frac{n-1}{2}}, \nonumber \\&A_{\mu } dx^{\mu } =-\dfrac{q_e}{r} dt + \dfrac{q_m}{2}(x\ dy - y\ dx), \end{aligned}$$
(2.5)

where the intensity of the axionic fields \(\omega \) is tied to the electric and magnetic charges by the relation

$$\begin{aligned} \omega =\pm \Big (\frac{96\,b^{n-1}\, n\,\kappa ^2(q_e^2+q_m^2)}{n-1-8\, n\,\kappa \,b^{n-1}}\Big )^{\frac{1}{4}}. \end{aligned}$$
(2.6)
Table 1 Range of the permissible values of the nonminimal coupling parameter \(\xi \) depending on the sign of the axionic parameter \(\omega \) ensuring a real solution
Full size table

We will now be as exhaustive as possible to enumerate the properties of these dyonic black brane solutions. For a nonminimal coupling parameter \(\xi \) as parameterized by (2.2), we have to distinguish between the case \(n>1\) corresponding to \(\xi \in ]0,\frac{1}{4}[\), and the case \(n<0\), i.e. \(\xi \in ]\frac{1}{4},\infty [\). For \(n>1\), in order to deal with a real constant \(\omega \) as defined by (2.6), the parameter b of the model must belong to the interval \(b\in \,]0, b_0[\) with

$$\begin{aligned} b_0=\left( \frac{n-1}{8n\kappa }\right) ^{\frac{1}{n-1}}, \end{aligned}$$
(2.7)

while for \(n<0\), one must have \(b\in \,]b_0,\infty [\). Also, the constraint (2.6) allows both sign for the intensity of the axionic fields \(\omega \). This remark has an interesting consequence concerning the location of the horizon \(r_{+}\) since for \(\omega >0\), we have \(r_{+}=\frac{3\omega }{\sqrt{12\kappa }}\) while for \(\omega <0\), the event horizon is located at \(r_{+}=-\frac{\omega }{\sqrt{12\kappa }}\). In this latter case, because of the form of the metric function (2.5), the temperature of the solution vanishes identically and the black brane configuration can be interpreted as an extremal solution. It remains to ensure that the scalar field (2.5) is well-defined in the region outside the horizon, namely for \(r\in [r_{+},\infty [\). For \(\omega >0\), the scalar field is regular everywhere in the region \(r>0\). On the other hand, for a negative axionic intensity parameter \(\omega <0\), the reality condition on the scalar field on the region \(r\in [r_{+}=-\frac{\omega }{\sqrt{12\kappa }},\infty [\) restricts the parameter n to be an odd negative integer \(n=1-2k\) with \(k\in \mathbb {N}{\setminus }\{0\}\) or equivalently the nonminimal coupling parameters is forced to take the discrete values given by \(\xi =\frac{k}{2(2k-1)}\). All these details are summarized in the Table 1. It is also interesting to stress that for \(\omega <0\), even if the scalar field vanishes at the horizon, the expressions of the potential (2.3a) and the coupling (2.3b) remain finite once evaluated on the solution at the horizon, i.e.

$$\begin{aligned}&U_b(\phi )|_{r_{+}}=\frac{3(n-1)b^{1-n}}{4n},\nonumber \\&\varepsilon _b(\phi )|_{r_{+}}=1-\frac{(n-1)b^{1-n}}{8n\kappa }. \end{aligned}$$
(2.8)

This remark will be of importance for the finiteness of the DC conductivities of the extremal solutions. Finally, we would like to make a comment concerning the neutral configuration \(q_e=q_m=0\). In this case, the reality condition on \(\omega \) given by Eq. (2.6) is replaced by a constraint on b given by \(b=b_0\) where \(b_0\) is defined in (2.7).

To conclude this section, we briefly report the solution for the special coupling \(\xi =\frac{1}{4}\) which was excluded from the previous study. In contrast with the other couplings, the black brane solution can not be charged, and the neutral solution is given by

$$\begin{aligned} ds^2= & {} -\left( r^2 - \dfrac{\omega ^2}{2\kappa } - \dfrac{\omega ^3}{2\kappa r} \right) dt^2 \nonumber \\&+ \dfrac{dr^2}{\left( r^2 - \dfrac{\omega ^2}{2\kappa } - \dfrac{\omega ^3}{2\kappa r}\right) } + r^2(dx^2 +dy^2), \end{aligned}$$
(2.9)
$$\begin{aligned} \phi (r)= & {} e^{\frac{r}{\omega }},\quad \psi _1(x) = \omega x,\quad \psi _2(y) = \omega y, \end{aligned}$$
(2.10)

for a potential U and a coupling \(\varepsilon \) free of any couplings that read

$$\begin{aligned} U(\phi )= & {} \dfrac{\phi ^2}{4\kappa \ln (\phi )} ( 2\kappa \ln (\phi )^3 \nonumber \\&+ 6\kappa \ln (\phi )^2 + (3\kappa - 1)\ln (\phi ) -2 ), \end{aligned}$$
(2.11)
$$\begin{aligned} \varepsilon (\phi )= & {} 1 - \dfrac{\phi ^2}{4\kappa }(\ln (\phi ) + 2 ). \end{aligned}$$
(2.12)

One can easily see that for \(\omega >0\), the metric solution admits a single root located at \(r_{+}\in ]\frac{\omega ^2}{3\kappa },\infty [\).

3 Thermodynamics of the solutions by means of the Hamiltonian method

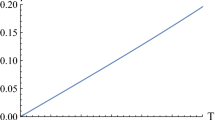
We now study the thermodynamic properties of the non-extremal solution (2.5) with \(\omega >0\) whose event horizon is located at \(r_{+}=\frac{3\omega }{\sqrt{12\kappa }}\) with \(n\in \mathbb {R} {\setminus } [0,1]\) or equivalently \(\xi \in ]0,\frac{1}{4}[\cup ]\frac{1}{4},\infty [\). In order to achieve this task, we will proceed using the Euclidean approach where the time is imaginary and periodic with period \(\beta = T^{-1}\). Here, T stands for the temperature which is fixed by requiring regularity at the horizon. The temperature of the non-extremal solution (2.5) reads

$$\begin{aligned} T = \dfrac{16\omega }{9\pi \sqrt{12\kappa }}. \end{aligned}$$
(3.1)

The Euclidean action \(I_{\tiny {Euc}}\) is related to the Gibbs free energy \(\mathcal {F}\) by

$$\begin{aligned} I_{\tiny {Euc}} = \beta \mathcal {F} = \beta \left( \mathcal {M} - T\mathcal {S} - \sum _i \mu _i \mathcal {Q}_i\right) , \end{aligned}$$

where \(\mathcal {M}\) is the mass, \(\mathcal {S}\) the entropy and \(\mu _i\) are the extra potentials with their corresponding charges \(\mathcal {Q}_i\) [29].

In order to construct a well-defined Euclidean action, we will consider a mini superspace where the metric is static and given by

$$\begin{aligned} ds^2 = N(r)f(r) d\tau ^2 + \dfrac{dr^2}{f(r)} + r^2(dx^2 + dy^2), \end{aligned}$$

with \(\tau \in [0, \beta ]\). The radial coordinate r ranges from the horizon to infinity, i.e. \(r \ge r_{+}\), and the planar coordinates both are assumed to belong to a compact set, that is \(x\in \Omega _x\) and \(y\in \Omega _y\) with \(\int dx\,dy=\Omega _x \Omega _y\). We also assume a specific ansatz for the scalar, axionic and electromagnetic fields, i.e. \(\phi = \phi (r)\), \(A_{\mu }dx^{\mu } = A_{\tau }(r)d\tau + A_{x}(y)dx + A_{y}(x)dy\), and \( \psi _1=\psi _{1}(x)\), and \(\psi _{2}= \psi _{2}(y)\). In doing so, the reduced Euclidean action takes the form

$$\begin{aligned} I_{\tiny {Euc}}= \int d^4x (N\mathcal {H} + A_\tau p' ) + B, \end{aligned}$$
(3.2)

where B is a boundary term that will be properly fixed below. Here p is the conjugate momentum of \(A_{\tau }\), \(p = -\dfrac{ r^2}{N(r)}A_{\tau }(r)'\), and the reduced Hamiltonian \(\mathcal {H}\) is given by

$$\begin{aligned} \mathcal {H}= & {} (2\kappa - \xi \phi (r)^2)(r f'(r) + f(r)) -\dfrac{1}{2}f(r)r^2\\&\times \ (-1+4\xi )\phi '(r)^{2} -r\xi \phi (r) (rf'(r) + 4f(r))\phi '(r)\\&- \ 2r^2f(r)\xi \phi (r)\phi ''(r) + \dfrac{\varepsilon _b(\phi )}{2} \sum _{i=1}^{2} (\partial _{i} \psi _i)^2 \\&+ \dfrac{ (\partial _x A_y - \partial _y A_x)^2}{2r^2}+ \dfrac{2p^2}{r^2} + r^2U_b(\phi ) + 2\kappa r^2 \Lambda . \end{aligned}$$

The boundary term B is fixed by requiring that the reduced action has an extremum, that is \(\delta I_{\tiny {Euc}} =0\), yielding to

$$\begin{aligned} \delta B= & {} \Bigg [ ( -A_{\tau }\delta p - N(r) [ (2r\kappa - r\xi \phi (r)^2 r^2\xi \phi (r)\phi '(r)) \delta f \nonumber \\&- \ r^2( f'(r)\xi \phi (r) + f(r)\phi '(r) - 2f(r)\xi \phi '(r)) \delta \phi \nonumber \\&+ \ 2r^2 f(r)\xi \phi (r) \delta \phi ' ] )_{r_{+}}^{R} \nonumber \\&- \int _{r_{+}}^{R}dr\ \varepsilon _b(\phi (r)) \left\{ \left[ \int _{\Omega _y}dy\ \partial _{x}\psi _{1} \delta \psi _1 \right] _{x\in \Omega _x} \right. \nonumber \\&\left. + \left[ \int _{\Omega _x}dx\ \partial _{y}\psi _{2} \delta \psi _2 \right] _{y\in \Omega _y} \right\} \nonumber \\&- \int _{r_{+}}^{R}dr\ \dfrac{N(r)}{r^2} \left\{ \left[ \int _{\Omega _x}dx\ (\partial _y A_x - \partial _x A_y)\delta A_x \right] _{y\in \Omega _y}\right. \nonumber \\&\left. - \left[ \int _{\Omega _y}dy\ (\partial _y A_x - \partial _x A_y)\delta A_y \right] _{x\in \Omega _x} \right\} \Bigg ]{\beta \Omega _x\Omega _y},\nonumber \\ \end{aligned}$$
(3.3)

where this expression has to be evaluated at the limit \(R\rightarrow \infty \). The field equations obtained from varying the Euclidean action (which do not depend on the boundary term B) imply that N is a constant, and this latter can be chosen without any loss of generality to be \(N(r)=1\). On the other hand, Gauss law implies that \(p=cst= q_e\). For the axionic fields, we note that their contribution strongly depends on the integral \(\int _{r_{+}}^{r} \varepsilon _b(\phi (r))\ dr\), which in our case can be computed yielding to

$$\begin{aligned} \int _{r_{+}}^{r} \varepsilon _b(\phi (r))dr= & {} r - \dfrac{(n-1)b^{1-n}}{96\kappa ^2 nr} \left( \omega ^{n-1}(\sqrt{12\kappa }r \right. \nonumber \\&\left. + \ \omega )^{3-n}- \omega ^2 \right) - (r \longleftrightarrow r_{+}). \end{aligned}$$
(3.4)

The final variation of \(\delta B\) at the infinity is finite and given by

$$\begin{aligned} \delta B (\infty )= & {} \beta \Omega _x\Omega _y \left( \dfrac{4\omega ^2}{\sqrt{12\kappa }} \right. \\&\left. + \ \eta \dfrac{(n-3)(n-1)\sqrt{12\kappa } b^{1-n}\omega ^2}{48n\kappa ^2} \right) , \end{aligned}$$

where \(\eta \) is defined as

$$\begin{aligned} \eta =\delta _n^2+\delta _n^{-k},\quad \text{ where } k\in \mathbb {N}{\setminus }\{0\}. \end{aligned}$$
(3.5)

The emergence of this extra contribution proportional to \(\eta \) which is effective only for \(n=2\) and for any nonzero negative integer can be explained from the fact that the “binomial” expression appearing between the large brackets in (3.4) will contribute with a linear term in the radial coordinate only for integer values \(n\in \mathbb {N}\) less or equal to three.Footnote 3 Working in the grand canonical ensemble, where \(\beta \) and all the potentials are fixed, the boundary term at the infinity can be integrated as

$$\begin{aligned} B (\infty )= & {} \beta \Omega _x\Omega _y \left( \dfrac{4\omega ^3}{3\sqrt{12\kappa }} \right. \nonumber \\&\left. + \ \eta \dfrac{(n-3)(n-1)\sqrt{12\kappa } b^{1-n}\omega ^3}{144n\kappa ^2} \right) . \end{aligned}$$
(3.6)

For the contribution at the horizon of the Euclidean action, we require the following variations

$$\begin{aligned}&\delta f\left| _{r_{+}} = -f'(r_{+})\delta r_{+}, \right. \quad \delta \phi \left| _{r_{+}}= \delta (\phi (r_{+})) - \phi '(r_{+})\delta r_{+} \right. \\&\delta p\left| _{r_{+}} = \delta q_e, \right. \quad \delta A_y \left| _{r_{+}}= \dfrac{x}{2} \delta q_m, \quad \delta A_x\left| _{r_{+}} = -\dfrac{y}{2} \delta q_m \right. \right. \\&\delta \psi _1\left| _{r_{+}} = x \delta \omega , \quad \delta \psi _2\left| _{r_{+}} = y\delta \omega \right. \right. \end{aligned}$$

For reason that will become clear, see below Eq. (3.10b), we define

$$\begin{aligned} \tilde{G} = \dfrac{1}{16\pi \kappa - \dfrac{2(n-1)}{n}\pi \phi (r_+)^2}, \end{aligned}$$
(3.7)

and we finally get

$$\begin{aligned} \delta B(r_{+})= & {} \delta \left( \dfrac{A_{+}}{4\tilde{G}} \right) + \beta [\Phi _e \delta q_e \nonumber \\&+ \ \Phi _m \delta q_m - \Phi _1 \delta \omega - \Phi _2 \delta \omega ]\Omega _x\Omega _y, \end{aligned}$$
(3.8)

where \(A_{+} = \Omega _x\Omega _y r_{+}^2\) is the horizon area, \(\Phi _e = \dfrac{q_e}{r_{+}}\), \(\Phi _m = \dfrac{q_m}{r_{+}}\) and \(\Phi _1\) and \(\Phi _2\) correspond to the axionic potentials, defined as \(\omega \) times the horizon term of (3.4), i.e.,

$$\begin{aligned} \Phi _1= & {} \Phi _2 \equiv \omega \left( r_{+} - \dfrac{(n-1)b^{1-n}}{96\kappa ^2 nr_{+}} \left( \omega ^{n-1}(\sqrt{12\kappa }r_{+}\right. \right. \\&\left. \left. + \ \omega )^{3-n}- \omega ^2 \right) - \eta \dfrac{(n-3)(n-1)\sqrt{12\kappa } b^{1-n}\omega }{96n\kappa ^2} \right) . \end{aligned}$$

Therefore, the boundary term at the horizon is

$$\begin{aligned} B(r_{+})= & {} \dfrac{A_{+}}{4\tilde{G}} + \beta \left[ \Phi _e q_e + \Phi _m q_m - \Phi _1 \omega \right. \nonumber \\&\left. - \ \Phi _2 \omega \right] \Omega _x\Omega _y. \end{aligned}$$
(3.9)

Plugging (3.6) and (3.9) we obtain our boundary term, \(B = B(\infty ) - B(r_{+})\). The relation between the boundary term and the Gibbs free energy allows us to identify the mass \(\mathcal {M}\), the entropy \(\mathcal {S}\), the electric charge \(\mathcal {Q}_e\), the magnetic charge \(\mathcal {Q}_m\) and the axionic charges \(\mathcal {Q}_1\) and \(\mathcal {Q}_2\),

$$\begin{aligned} \mathcal {M}= & {} \Omega _x\Omega _y \left( \dfrac{4\omega ^3}{3\sqrt{12\kappa }} \right. \nonumber \\&\left. + \ \eta \dfrac{(n-3)(n-1)\sqrt{12\kappa } b^{1-n}\omega ^3}{144n\kappa ^2} \right) , \end{aligned}$$
(3.10a)
$$\begin{aligned} \mathcal {S}= & {} \dfrac{A_{+}}{4\bar{G}}, \end{aligned}$$
(3.10b)
$$\begin{aligned} \mathcal {Q}_e= & {} \Omega _x\Omega _y q_e, \quad \mathcal {Q}_m = \Omega _x\Omega _y q_m,\nonumber \\ \mathcal {Q}_1= & {} \mathcal {Q}_2 = - \ \Omega _x\Omega _y \omega . \end{aligned}$$
(3.10c)

It is reassuring to check that in the conformal case \(n=3\), these thermodynamic quantities reduce to those obtained in [17]. On the other hand, even if the first law is satisfied by means of the constraint (2.6), the signs of the entropy and the mass must be analyzed carefully. Firstly, the positivity of the entropy imposes a lower bound for the parameter b; this is because the constant \(\tilde{G}\) as defined by (3.7) must be strictly positive, and this leads to

$$\begin{aligned}&b>\dfrac{1}{4} \left( \dfrac{n-1}{8n\kappa } \right) ^{\frac{1}{n-1}}=\frac{1}{4}\,b_0,\\&\quad \text{ for } n>1,\quad \text{ and }\quad b<\frac{1}{4}b_0, \quad \text{ for } n<0. \end{aligned}$$

Referring to the Table 1, one can see that the reality condition imposed by (2.6) for \(\omega >0\) make possible to deal with solutions with positive entropy only if \(n>1\) or equivalently \(\xi \in ]0,\frac{1}{4}[\) and the range of the parameter b must then be reduced to \(b\in ]\frac{1}{4}b_0, b_0[\). For the other values of the nonminimal coupling parameter \(n<0\) or equivalently \(\xi >\frac{1}{4}\), the entropy of the solutions turns out to be always negative because of the reality condition (2.6). Concerning the mass, it is interesting to note that the mass is always positive for \(\eta =0\) as defined by (3.5) or for the conformal case \(n=3\). On the other hand, for \(n=2\), the positivity of the mass requires \(b>\frac{1}{2}b_0\), and hence our static solution with \(n=2\) can have positive entropy and mass by demanding the parameter b to belong to the set \(b \in ]\frac{1}{2}b_0, b_0[\). Finally, for the remaining values for which \(\eta =1\), namely \(n=-1, -2,\ldots \), the solutions will always have negative mass and entropy.

For the extremal solution corresponding to \(\omega <0\) and \(\xi \) taking discrete values (cf. Table 1) with a scalar field vanishing at the horizon \(\phi (r_{+})=0\), it is not safe to consider the Euclidean approach since the inverse of the temperature is infinite. Nevertheless, one can compute the entropy of the extremal solution by means of the Wald’s formula [30] yielding

$$\begin{aligned} \mathcal {S}_{{\tiny \text{ extremal }}} = 4\pi \kappa \,\Omega _x\, \Omega _y\, r_{+}^2. \end{aligned}$$
(3.11)

It is interesting to note that this result matches with the non extremal expression (3.10b) with (3.7) by taking \(\phi (r_{+})=0\). In addition, as it can be seen from Eq. (3.11), the entropy of the extremal solution is always positive and given by the Hawking formula, \(S=\frac{{\text{ Area }}}{4 G}\), after restoring correctly the value of \(\kappa \) in term of the Newton gravitational constant, i.e. \(\kappa =\frac{1}{16\pi G}\). On the other hand, the mass of the extremal solution is given by

$$\begin{aligned} \mathcal {M}_{{\tiny \text{ extremal }}}= & {} \Omega _x\Omega _y \left( \dfrac{4\omega ^3}{3\sqrt{12\kappa }} \right. \nonumber \\&\left. + \dfrac{(n-3)(n-1)\sqrt{12\kappa } b^{1-n}\omega ^3}{144n\kappa ^2} \right) , \end{aligned}$$
(3.12)

and it is easy to see that for the permissible discrete values of the nonminimal coupling parameters \(n=1-2k\) with \(k\in \mathbb {N}{\setminus }\{0\}\) this expression is always positive for \(b>b_0\) (cf. Table 1) even if \(\omega <0\).

Table 2 Signs of the entropy and mass of the dyonic solutions whose reality conditions are fixed by Table 1 and where \(b_0=\left( \frac{n-1}{8n\kappa }\right) ^{\frac{1}{n-1}}\)
Full size table

4 Holographic DC conductivities

In Refs. [19, 20], it was established that the full DC conductivities for black holes enjoying a momentum dissipation can be computed in terms of the black hole horizon data. The main idea is to construct some conserved currents independent of the holographic radial coordinate r. To that end, we follow the prescription as described in Refs. [19, 20], and we first turn on the following relevant perturbations on the black brane solution (2.5)

$$\begin{aligned} \delta A_{x}= & {} -E_{x}t + a_x(r), \quad \delta A_{y} = -E_{y}t + a_y(r)\\ \delta g_{tx}= & {} r^2 h_{tx}(r),\quad \delta g_{rx} = r^2h_{rx}(r), \\ \delta g_{ty}= & {} r^2 h_{ty}(r), \quad \delta g_{ry} = r^2h_{ty}(r)\\ \delta \psi _1= & {} \chi _1(r),\quad \delta \psi _2 = \chi _2(r), \end{aligned}$$

where \(E_{x}, E_{y}\) are two constants. Consequently, the two perturbed Maxwell equations read

$$\begin{aligned}&f'a'_{x} + f a''_{x} + q_e h'_{tx} + q_m (f'h_{ry} + fh'_{ry}) = 0,\\&f'a'_{y} + f a''_{y} + q_e h'_{ty} - q_m (f'h_{rx} + fh'_{rx}) = 0, \end{aligned}$$

which allow to define the following two conserved currents,

$$\begin{aligned} J_{x}:= & {} - fa'_{x} - q_eh_{tx} - q_m fh_{ry}, \end{aligned}$$
(4.1a)
$$\begin{aligned} J_{y}:= & {} - fa'_{y} - q_eh_{ty} + q_m fh_{rx}. \end{aligned}$$
(4.1b)

According to the AdS/CFT correspondence, the holographic DC conductivities are determined by the conserved currents in the asymptotic boundary, and since the expressions obtained above (4.1a) and (4.1b) are independent of the radial coordinate, we can evaluate them at the horizon \(r_{+}\). The next step is to impose boundary conditions on the linearized perturbations at the black hole horizon. In order to achieve this task, it is convenient to use the Eddington-Finkelstein coordinates (v, r) such that \(v = t + \int \frac{dr}{f(r)}\). In this case, the gauge field will be well-defined by demanding

$$\begin{aligned} a_{x} = -E_{x}\int \dfrac{dr}{f(r)}, \quad a_{y} = -E_{y}\int \dfrac{dr}{f(r)}, \end{aligned}$$
(4.2)

while we will require the axionic fields to be constant near the horizon, and for the metric perturbations we will need to impose

$$\begin{aligned} h_{rx} = \dfrac{h_{tx}}{f(r)}, \quad h_{ry} = \dfrac{h_{ty}}{f(r)}. \end{aligned}$$
(4.3)

All the previous conditions can be substituted into the rx and ry components of the linearized Einstein equations, obtaining a system of equations for \(h_{tx}(r_{+})\) and \(h_{ty}(r_{+})\), whose solutions are given by

$$\begin{aligned}&h_{tx} = \left. \dfrac{-E_{y}q_m^3 - q_m\varepsilon _b(\phi )\omega ^2 r^2E_{y} - q_e\varepsilon _b(\phi )\omega ^2 r^2E_{x}- q_e^2q_mE_{y}}{16\alpha ^2 q_m^4 + 2 q_m^2 \varepsilon _b(\phi )\omega ^2 r^2 + \varepsilon _b(\phi )^2 \omega ^4r^4 + 16\alpha ^2 q_e^2 q_m^2} \right| _{r=r_{+}}, \end{aligned}$$
(4.4a)
$$\begin{aligned}&h_{ty} = \left. \dfrac{ q_e^2q_mE_{x} + q_m^3E_{x}- q_e\varepsilon _b(\phi )\omega ^2r^2 E_{y}+4\alpha q_m\varepsilon _b(\phi )\omega ^2 r^2E_{x}}{ q_m^4 +2q_m^2 \varepsilon _b(\phi )\omega ^2 r^2 + \varepsilon _b(\phi )^2 \omega ^4r^4 + Q_e^2 q_m^2} \right| _{r=r_{+}}. \end{aligned}$$
(4.4b)

Since the DC conductivities depend on the location of the horizon, we will first consider the non extremal case \(\omega >0\) where the horizon is at \(r_{+}=\frac{3\omega }{\sqrt{12\kappa }}\) while the extremal situation \(\omega <0\) and \(r_{+}=-\frac{\omega }{\sqrt{12\kappa }}\) will be treated at the end of the section. Hence, the final step is to insert (4.2–4.4b) into (4.1a), (4.1b) to obtain the conductivities through

$$\begin{aligned} \sigma _{xx}= & {} \dfrac{\partial J_{x}}{\partial E_{x}} \nonumber \\= & {} \dfrac{\tilde{\varepsilon _b}\omega ^4 (12 (q_e^2 + q_m^2)\kappa +9 \tilde{\varepsilon _b}\omega ^4)}{16 q_m^2 (q_e^2 + q_m^2)\kappa ^2 + 24 q_m^2 \tilde{\varepsilon _b}\omega ^4 \kappa + 9 \tilde{\varepsilon _b}^2 \omega ^8}, \nonumber \\ \sigma _{xy}= & {} \dfrac{\partial J_{x}}{\partial E_{y}} \nonumber \\= & {} \dfrac{q_eq_m \kappa (64 (q_e^2 + q_m^2)\kappa + 96\tilde{\varepsilon _b}\omega ^4)}{64 q_m^2 (q_e^2 + q_m^2)\kappa ^2 + 96 q_m^2 \tilde{\varepsilon _b}\omega ^4 \kappa + 36 \tilde{\varepsilon _b}^2 \omega ^8},\nonumber \\ \sigma _{yx}= & {} \dfrac{\partial J_{y}}{\partial E_{x}} = - \sigma _{xy}, \quad \sigma _{yy} = \dfrac{\partial J_{y}}{\partial E_{y}} = \sigma _{xx}, \end{aligned}$$
(4.5)

where we have defined

$$\begin{aligned} \tilde{\varepsilon }_b\equiv & {} \varepsilon _b(\phi (r_{+})) = 1 \nonumber \\&+ \dfrac{(n-1)(4^{2-n}(3n-5)-1)b^{1-n}}{72n\kappa }. \end{aligned}$$
(4.6)

The conductivity matrix is antisymmetric in accordance with the invariance under the SO(2) symmetry. The purely electric DC conductivity \(\sigma _{DC}\) is given by

$$\begin{aligned} \sigma _{DC}\equiv & {} \sigma _{xx}(q_m=0) = 1+\frac{4 q_e^2\kappa }{3\tilde{\varepsilon }_b \omega ^4} \nonumber \\= & {} 1 + \dfrac{(n-1)-8n\kappa b^{n-1}}{72n\kappa b^{n-1} + (n-1)(4^{2-n}(3n-5)-1)},\nonumber \\ \end{aligned}$$
(4.7)

where we have explicitly used the constraint (2.6). We are now in position to analyze the effects of the parameter b and the nonminimal coupling parameter n on the electrical DC conductivity. We also recall that the parameter b is subjected to some reality conditions (cf. Table 1) corresponding to the mathematical range of b but also to physical constraints that ensure the positivity of the mass and entropy (cf. Table 2) that we will refer as the physical range of b.

Fig. 1
figure 1

The conductivity \(\sigma _{DC}\) in term of the parameter b for nonminimal couplings \(0<\xi <\frac{1}{4}\)

Full size image

Firstly, it is straightforward to prove that there exists a value of the nonminimal coupling parameter \(n_0\approx 3.4681\) corresponding to \(\xi _0\approx 0.1779\) (2.2) such that for each \(n>n_0\), there exists a precise value of the parameter b denoted by \(b_1\) with \(\frac{b_0}{4}<b_1<b_0\) (cf. Table 2) such that the DC conductivity is strictly positive for \(b\in ]b_1, b_0[\) and \(\sigma _{DC}\) becomes infinite at \((n, b_1)\). In other words, this means that for any coupling greater than \(n_0\), one can always choose a parameter \(b\in ]b_1, b_0[\) of the theory that yields to well-defined physical solutions, namely solutions with positive mass and entropy and having a positive conductivity. Additionally, for the choice \(b=b_1\), the DC conductivity becomes infinite at the point \((n, b_1)\) with \(n>n_0\). This is due to the fact that the minimal coupling function \(\varepsilon _b(\phi )\) evaluated at the horizon vanishes at this point. This is not surprising since in order to ensure the mechanism of momentum dissipation yielding to finite conductivity, the coupling function \(\varepsilon _b(\phi )\) must not vanish.

Now, in order to visualize the influence on the electric DC conductivity of the parameters b and n, we will plot the graphics of \(\sigma _{DC}\) in function of b and n. In Fig. 1, we plot the conductivity vs the parameter b for two distinct values of the nonminimal coupling parameter, namely \(n=2<n_0\) and \(n=4>n_0\). The graphic given by Fig. 1a for \(n=2\) is in fact representative of all the cases \(1<n\le n_0\). One can see that for the physical range of b, namely \(b\in ]\frac{1}{4}b_0, b_0[\) or \(b\in ]\frac{1}{2}b_0, b_0[\) for \(n=2\) (cf. Table 2), the conductivity is strictly positive and finite.Footnote 4 In fact, the positivity of the conductivity is always ensured even for the full mathematical range of b, i.e. \(b\in ]0, b_0[\). On the other hand, the graphic represented in Fig. 1b for \(n=4\) will be similar for any value \(n>n_0\). In this case, as mentioned before, one can see the existence of a a vertical asymptote at \(b=b_1\) (for \(n=4\) we have \(b_1\approx 0.66534\)) where the conductivity becomes infinite. Nevertheless, in contrast with the previous case, the conductivity is positive only for \(b\ge b_1\), and hence part of the physical range, namely \(b\in ]\frac{1}{4}b_0, b_1[\) yields to negative conductivity. We also include a plot of the non extremal situation for \(n<0\) or equivalently \(\xi >\frac{1}{4}\), see Fig. 2. The mathematical range of b is located at the right of the blue line while its physical range is at the left of the dotted line. One can see that for a mathematically well-defined solution, the electric conductivity is always positive even if it has negative mass and entropy. We can also appreciate the influence of the nonminimal coupling parameter on \(\sigma _{DC}\) by drawing the graphics of this latter in function of n, see Fig. 3. In order to achieve this task, we must be careful with the election of b since its range of permissible values depends explicitly on n, see Tables 1 and 2 where we have defined \(b_0\) in (2.7). As explained before, one can see that for \(n\le n_0\), the electric conductivity is positive while for \(n>n_0\), one has \(\sigma _{DC}<0\). Finally, we would like to mention that as in the conformal case [17], the DC conductivity is temperature-independent. To be more precise, on one hand we have seen that the temperature depends on the axionic parameter \(\omega \). On the other hand, in order to have solutions that respect the AdS symmetry at the boundary, the axionic charge must be related with the electric and magnetic charges through the relation (2.6). It is important to stress that this particular relation is due to the fact that the fall off of the nominally coupled scalar modifies the asymptotic behavior of our solutions. Moreover this relation makes our thermodynamic analysis integrable. However, as one uses the relation (2.6) in the conductivity matrix, we notice that \(\omega \)-dependence disappears as it can be appreciated in the expression (4.7).

Fig. 2
figure 2

\(\sigma _{DC}\) vs b for any nonminimal couplings \(n<0\) or equivalently \(\xi >\frac{1}{4}\)

Full size image
Fig. 3
figure 3

Influence of the nonminimal coupling parameter n on the electric conductivity

Full size image

The remaining DC conductivities namely the thermoelectric and the heat conductivities can also be obtained by turning on a more general time-dependent perturbationFootnote 5

$$\begin{aligned} \delta A_x= & {} t\left( -E+\zeta a(r)\right) +a_x(r), \\ \delta g_{tx}= & {} -t\zeta f(r)+r^2 h_{tx}(r), \quad \delta g_{rx}=r^2h_{rx},\quad \delta \psi _i=\chi (r), \end{aligned}$$

where \(\zeta \) can be shown to parameterize a time dependent source for the heat current. As a consequence, in addition to the conserved current \(J_x\), the following quantity

$$\begin{aligned} Q_x=f(r)^2 (f(r)r^2 h_{tx} )^{\prime }-a J_x \end{aligned}$$

is also conserved along the radial coordinate [19]. Hence, the thermoelectric conductivities \(\alpha \) and \(\bar{\alpha }\) as well as the heat conductivity \(\bar{\kappa }\) can be computed yielding

$$\begin{aligned} \alpha= & {} \beta \frac{\partial Q_x}{\partial E}=\frac{4\pi q_e}{\omega ^2\tilde{\varepsilon }_b },\quad \bar{\alpha }=\beta \frac{\partial J_x}{\partial \zeta }=\frac{4\pi q_e}{\omega ^2\tilde{\varepsilon }_b }\nonumber \\ \bar{\kappa }= & {} \beta \frac{\partial Q_x}{\partial \zeta }=\frac{64\pi \omega }{3\tilde{\varepsilon }_b \kappa \sqrt{12\kappa }}, \end{aligned}$$
(4.8)

where \(\beta \) as usual is the inverse of the temperature.

Finally, for the extremal solutions, namely \(\omega <0\) (cf. Tables 1, 2), the analysis is completely analogue. This is due to the fact that, even if the scalar field vanishes at the event horizon, the minimal coupling function \(\tilde{\varepsilon }_b\) remains finite at the horizon (2.8). As a direct consequence, the expressions derived previously remain valid with the difference that in the extremal case, the horizon is located at \(r_{+}=-\frac{\omega }{\sqrt{12\kappa }}\). Interestingly enough, the conductivity matrix becomes an antisymmetric matrix given by

$$\begin{aligned} \sigma =\left( \begin{array}{c@{\quad }c} 0&{} -\frac{q_m}{q_e}\\ \frac{q_m}{q_e} &{} 0 \end{array} \right) . \end{aligned}$$
(4.9)

It is somehow appealing that for the extremal solution, the conductivity matrix has a Hall effect-like behavior with a Hall conductivity that looks like that \(B/\rho \) instead of \(\rho /B\), (here \(\rho \) is the density of charge and B the orthogonal magnetic field). Indeed, in the AdS/CFT dictionary, \((3+1)\)-dimensional AdS dyonic black holes are conjectured to be dual to a \((2+1)\) CFT. In this picture, the electric bulk gauge field does not have a counterpart in the dual field theory but instead it fixes the electric charge density \(\rho \) to be proportional to the electric charge of the black hole, i.e. \(\rho \propto q_e\). On the other hand, the magnetic bulk gauge field is in correspondence with an external magnetic field in the CFT side with a field strength \(B\propto q_m\). Hence, the Hall conductivity in our case (4.9) is proportional to the ratio between the magnetic field and the electric charge density, i.e. \(\sigma _{xy}\propto \frac{B}{\rho }\). As a final comment, one can notice that in the purely electric case \(q_m=0\), the DC conductivity for the extremal solution vanishes identically reproducing in turn an insulator behavior.

5 Conclusion

Here, we have considered a self-interacting scalar field nonminimally coupled to the four-dimensional Einstein gravity with a negative cosmological constant. The matter source is also supplemented by the Maxwell action with two axionic fields minimally coupled to the scalar field. Our model is specified from the very beginning by two parameters that are the nonminimal coupling parameter denoted \(\xi \) or equivalently n (2.2) and the constant b that enters in the minimal coupling as well as in the potential. For this model, we have obtained dyonic planar black holes with axionic fields depending linearly on the coordinates of the planar base manifold. We have noticed that these charged solutions depend on a unique integration constant denoted by \(\omega \) and the horizon can be located at two different positions depending on the sign of \(\omega \). Surprisingly, for \(\omega <0\), the temperature of the solution vanishes identically and hence one can interpret the solution as an extremal black brane. We have also shown that some reality conditions (cf. Table 1) supplemented by the requirement of having solutions with positive entropy and mass restrict considerably the permissible values of the nonminimal coupling parameter and of the parameter b, see Table 2. For a positive \(\omega >0\), the set of physically acceptable values of the nonminimal coupling parameter is given by \(\xi \in ]0,\frac{1}{4}[\) while for the extremal solution corresponding to \(\omega <0\), only discrete values of the nonminimal coupling parameter given by \(\xi =\frac{k}{2(2k-1)}\) with \(k\in \mathbb {N}{\setminus }\{0\}\) yield to solutions with positive mass and entropy. These restrictions on the nonminimal coupling parameter are to be expected since, even for purely scalar field nonminimally coupled to Einstein gravity, black hole configurations have been shown to be ruled out for \(\xi <0\) and \(\xi \ge \frac{1}{2}\), see Ref. [31].

In the last part of this work, we have taken advantage of the momentum dissipation ensured by the axionic fields to compute the different conductivities by means of the recipes given in Refs. [19, 20]. Many interesting results can be highlighted from the study of the holographic DC conductivities inherent to these dyonic solutions. For the non extremal solutions, we have shown that for \(n\le n_0\approx 3.4681\) or equivalently \( \xi \le \xi _0\approx 0.1779\), the dyonic solutions always enjoy a positive conductivity for any mathematically permissible value of b. On the other hand, for \(n>n_0\), the positive conductivity condition restricts the interval of b to be \(]b_1,b_0[\) with \(b_1>\frac{1}{4}b_0\). In other words, this means that the physical solutions (in the sense of having positive mass and entropy) for \(n>n_0\) with \(b\in ]\frac{1}{4}b_0, b_1[\) will have a negative conductivity. Also, we have shown that for \(n>n_0\) there always exist a value of the parameter b denoted by \(b_1\) which restores the translation invariance, in the sense that \(\sigma _{DC}(n, b_1)\rightarrow \infty \). Finally, for the extremal solution, we have shown that the diagonal elements of the conductivity matrix precisely vanish and its off-diagonal elements are similar to those inherent to the Hall effect.

An interesting extension of our model will be to consider an additional k-essence term for the axionic part of the action and to analyze the effects on the conductivities of the nonminimal coupling parameter \(\xi \) conjugated with the k-essence parameter, see Ref. [24]. In the same lines a natural generalization of these solutions would be the extension to higher dimensional scenarios following the lines of [32].

Finally, it will be very interesting to explore more deeply some of the properties of our solutions such as the extremality, the perfect conductivity or the Hall effect-like behavior of the extremal solutions. With this respect, in Ref. [33], it was shown that the Reissner-Nordstrom at the extremal limit experiences a sort of Meissner effect in the sense that the magnetic flux lines are expelled. Hence, a work to be done consists precisely in investigating the extremal solutions found here can exhibit a kind of Meissner effect.