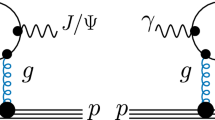$J/{\psi }$ production in hadron scattering: three-pomeron contribution

Abstract

In this paper we discuss the inclusive $J/\psi$ production in proton–proton collisions from fusion of three pomerons. We demonstrate that this mechanism gets dominant contribution from the region which can be theoretically described by CGC/saturation approach. Numerically, it gives a substantial contribution to the $J/\psi$ production, and is able to describe the experimentally observable shapes of the rapidity, momenta and multiplicity distributions. The latter fact provides a natural explanation of the experimentally observed enhancement of multiplicity distribution in $J/\psi$ production.

1 Introduction

The description of the charmonium hadroproduction remains one of the long-standing puzzles since its discovery. The large mass $m_{c}$ of the charm quark inspired applications of perturbative methods and consideration in the formal limit of infinitely heavy quark mass [1]. However, in reality the coupling $\alpha _{s}\left( m_{c}\right) \sim 1/3$ is not very small, so potentially some mechanisms suppressed in the large-$m_{c}$ limit, numerically might give a sizeable contribution.

The Color Singlet Model (CSM) [2,3,4] assumes that the dominant mechanism of charmonia production is the gluon-gluon fusion supplemented by emission of additional gluon. Early evaluations in the collinear factorization framework did not agree with the experimental data at large transverse momenta $p_{T}$ by several orders of magnitude. The failure of the expansion over $\alpha _{s}$ due to milder suppression of higher order terms at large $p_{T}$ [5, 6] and co-production of additional quark pairs [7, 8] motivated introduction of the phenomenological Color Octet contributions [9, 10]. The modern NRQCD formulation [11,12,13,14,15] constructs a systematic expansion over the Long Distance Matrix Elements (LDMEs) of different charmonia states which can be extracted from fits of experimental data. However, at present extracted matrix elements depend significantly on the technical details of the fit [14, 16, 17], which contradicts expected universality of the extracted LDMEs. At the same time, it is known that at large $p_{T}$, a sizeable contribution might come from other mechanisms, like for example gluon fragmentation into $J/\psi$ or co-production together with other hadrons [18,19,20,21]. The latter findings are partially supported by experimental data on multiplicity of co-produced charged particles [22,23,24,25,26] which suggest that $J/\psi$ production might get sizeable contribution from this mechanism.

Fig. 1

a Two parton showers contribution to $J/\psi$ production in hadron-hadron collisions. b Production of $J/\psi$ and even number of soft (non-perturbative) gluons.

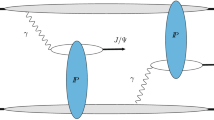
In this paper we analyze $J/\psi$ in the CGC/saturation approach, which incorporates the leading-log contributions from hadron production in the small-x kinematics, and takes into account saturation effects in the region of very small-x [39, 94]. We focus on the mechanism of $J/\psi$ production shown in the diagram (a) of the Fig. 1, when the production of $J/\psi$ occurs from fusion of three gluons, accompanied by the production of two parton showers.¹ In order to emphasize the role of co-production of other particles associated with $J/\psi$, below we will follow the terminology used in some BFKL papers and refer to this mechanism as “two-parton shower” contribution. This mechanism differs from the so-called “single-shower” mechanism shown in the diagram (b) of the Fig. 1. The latter corresponds to gluon-gluon fusion with emission of additional (soft) gluon in collinear and $k_{T}$-factorization approaches, and is a counterpart of CSM mechanism in BFKL framework. We expect that the two-parton shower mechanism should be dominant for the events with large multiplicities, exceeding the average multiplicity ${\bar{n}}$ of the gluon production in the inclusive process. This mechanism is similar to mechanisms studied earlier in the literature for proton–proton collisions [27, 28] and for proton–nucleus and nucleus–nucleus scattering [29,30,31]. For collisions involving heavy nuclei, the two parton shower mechanism inside heavy nuclei with atomic number A is dominant due to factor $\sim A^{1/3}$, and, because of this, has been comprehensively discussed during the past decade [32,33,34,35,36,37]. On the other hand, for proton–proton scattering we found only one paper which considers this process in the $k_{T}$-factorization approach [38].

At first sight, the two parton showers mechanism should be suppressed in comparison with the production of $J/\psi$ in one parton shower shown in the diagram (b) of the Fig. 1b: in contrast to $\alpha _{s}$ coupling which appears in the shower-quark vertex, the emission of soft gluon in Fig. 1b is not suppressed by any hard scale and thus does not bring a smallness proportional to ${\bar{\alpha }}_{S}$. In the DGLAP approach, it is expected that such diagrams are of higher twist and are (at least formally) suppressed by additional powers of hard scale. However, at high energy this suppression is compensated by enhanced contribution of the second parton shower (see [39] for review). For typical $\langle r\rangle \,\sim \,1\,\mathrm{GeV}^{-1}$ we get ${\bar{\alpha }}_{S}\left( 4/r^{2}\right) \approx 0.2$ so ${\bar{\alpha }}_{S}G^{\mathrm{BFKL}}\left( s,\dots \right) \,\propto {\bar{\alpha }}_{S}\,s^{\Delta _{\small \mathrm{BFKL}}}\ge 1$ at high energies, where $\Delta _{\mathrm{BFKL}}=4\ln 2{\bar{\alpha }}_{S}$ is the intercept of the BFKL Pomeron [40,41,42,43,44] and $G^{\mathrm{BFKL}}\left( s,\dots \right)$ is the Green function of the BFKL Pomeron. The numerical estimates of Ref. [38] suggests that the considered mechanism yields about one third of the experimental cross section in the $k_{T}$ factorization approach, though the final estimate suffers significantly from the uncertainty in digluon PDF modeling, namely the choice of value of the parameter $\sigma _{\mathrm{eff}}$(“effective double parton cross-section”). On the other hand, the diagram (b) in the Fig. 1 at high energies gets additional suppression due to growth of the saturation scale $Q_{s}$, which decreases the average dipole size and suppresses the emission of the extra gluons leading to $\alpha _{S}(Q_{s})$ suppression.

The main motivation of this paper is to re-visit the estimates of the contribution of the mechanism of Fig. 1a in the CGC/saturation framework and check if it can reproduce the observed multiplicity distributions. We demonstrate that: (i) this mechanism can be calculated in CGC/saturation approach (see Ref. [94] for a review) since the main contribution comes from the vicinity of the saturation scale, where we know theoretically the scattering amplitude, and (ii) it on its own gives a significant contribution to experimentally observable cross sections. In contrast to Ref. [38], we use a CGC/saturation framework, and in order to avoid uncertainties related to digluon distributions, we relate the cross-sections of the $J/\psi$ production to the diffractive production cross-section known from DIS.

The paper is organized as follows. In the next Sect. 2 we evaluate the contribution of the suggested mechanism in the CGC/saturation framework. We re-write this contribution in the coordinate representation and relate it to the gluon double densities. In Sect. 3 we discuss the interrelation of the suggested process with the diffractive production of $J/\psi$ in DIS. In the Sect. 4 we make phenomenological estimates and compare results with experimental data. The Sect. 4.1 is dedicated to the estimates of the total cross section of the process. In this subsection we point out the differences with Ref. [38]. In Sects. 4.2, 4.3 and 4.4 we consider the momenta, rapidity and multiplicity distributions of the differential cross-sections. Finally, in the Sect. 5 we draw conclusions.

Fig. 2

The cross-section corresponding to the first diagram of the Fig. 1 in the BFKL Pomeron calculus..The vertical wavy lines of different colors and shape passing through unitarity cut are BFKL Pomerons [described by the Green functions $G_{\mathbb {P}}\left( y,\,{\varvec{k}}_{T}\right)$ in Eq. (2)], helical lines correspond to the gluons

2 Charmonia production in the BFKL approach

At present, the effective theory of QCD at high energies exists in two forms: the CGC/saturation approach [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] and the BFKL Pomeron calculus [40,41,42,43,44,45, 64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80]. It has been proven that in general these two approaches are equivalent in a limited region of the rapidities [81,82,83,84]. The interpretation of processes at high energy appears quite different in each approach, since they have different structural elements.

The CGC/saturation approach, being more microscopic, describes the high energy interactions in terms of colorless dipoles, their density, distribution over impact parameters, evolution in energy, etc. The distinctive feature of this approach is the appearance of saturation effects which affect the dynamics for parton momenta comparable to some saturation scale $Q_{s}$, a new dimensional parameter. The studies of $J/\psi$ production in this approach may be found in [36] and by construction include all possible multishower contributions, although with additional model-dependent assumptions.

The BFKL Pomeron calculus works with BFKL Pomerons and their interactions, and phenomenologically is similar to the old Reggeon theory [85]. This approach is suitable for describing diffractive physics and correlations in multi-particle production, so we can use the Mueller diagram technique [86]. The relation between different processes at high energy are very often more transparent in this approach, since in addition to the Mueller diagram technique we can use the AGK cutting rules [87, 88], which are useful in spite of the restricted region of their application [89,90,91,92,93]. In this paper for the sake of definiteness we use the BFKL Pomeron calculus as a framework for evaluations.

In the framework of the BFKL Pomeron calculus, the cross-section of the process shown in the diagram (a) of the Fig. 1 is described by the exchange of two BFKL Pomerons as shown in Fig. 2. Since we are interested in inelastic $J/\psi$ production, the Pomerons in Fig. 2 are cut Pomerons in which all gluons are produced. From the unitarity constraints for the elastic amplitude $N^{\mathrm{BFKL}}$ of the dipole of size r, rapidity Y and at the impact parameter b, we have [94]

$$\begin{aligned} N_{\mathrm{cut}}^{\mathrm{BFKL}}\left( Y,\,r,\,b\right) \,\,\equiv \ 2\,N^{\mathrm{BFKL}}\left( Y,\,r,\,b\right) \end{aligned}$$

(1)

Its contribution to the total cross section for $J/\psi$ production² is equal to

$$\begin{aligned}&\frac{d^{2}\sigma \left( Y,q_{T}\right) }{dy\,d^{2}q_{T}} \nonumber \\&\quad =\frac{4\,C_{F}^{3}{\bar{\alpha }}_{S}^{3}}{(2\pi )^{6}}\int d^{2}k_{T}\,d^{2}p_{T}\,d^{2}Q_{T}\,G_{\mathbb {P}}^{\mathrm{cut}}\left( Y-y,\,{\varvec{p}}_{T},\,0\right) \nonumber \\&\qquad \times I\left( {\varvec{k}}_{T},{\varvec{q}}_{T}\right) \,I \left( {\varvec{k}}'_{T},{\varvec{q}}_{T}\right) G_{{\mathbb {P}}}^{\mathrm{cut}}\left( y,\,{\varvec{k}}_{T}+\frac{1}{2}{\varvec{q}}_{T}, {\varvec{Q}}_{T}\right) \nonumber \\&\qquad \times G_{{\mathbb {P}}}^{\mathrm{cut}}\left( y,\,-{\varvec{k}}_{T} +\frac{1}{2}{\varvec{q}}_{T},{\varvec{Q}}_{T}\right) \end{aligned}$$

(2)

where ${\bar{\alpha }}_{s}=N_{c}\alpha _{s}(m_{c})/\pi$, the notation $G_{\mathbb {P}}^{\mathrm{cut}}$ is used for the Green functions of the cut pomerons (it is related to elastic amplitudes $N_{\mathrm{cut}}^{\mathrm{BFKL}}$ by Fourier transform), the gluon momenta ${\varvec{k}}_{T},\,{\varvec{p}}_{T},\,{\varvec{q}}_{T}$, are defined in the Fig. 2, ${\varvec{Q}}_{T}\,=\,{\varvec{k}}_{T}\,-\,{\varvec{k}}'_{T}$, and

$$\begin{aligned} I\left( {\varvec{k}}_{T},{\varvec{q}}_{T}\right)= & {} \int _{0}^{1}dz\int d^{2}r\,\Big (e^{i\frac{1}{2}{\varvec{q}}_{T} \cdot {\varvec{r}}}\,\,-\, e^{i{\varvec{k}}_{T} \cdot {\varvec{r}}}\Big ) \nonumber \\&\times \Psi _{g}\left( p_{T},\, r;\,z\right) \,\Psi _{J/\psi }\left( r;\,z\right) \nonumber \\= & {} F\left( \frac{1}{2} {\varvec{q}}_{T}\right) \,-\,F\left( {\varvec{k}}_{T}\right) \end{aligned}$$

(3)

(the evaluation of the factor $I\left( {\varvec{k}}_{T},{\varvec{q}}_{T}\right)$ is discussed in more detail in Appendix 1). The additional factor 4 in Eq. (8) which comes from two sources: 2 from the AGK cutting rules [87, 88] and 2 from the fact that gluon that produces $c{\bar{c}}$-pair can come from another proton. In Eq. (3) $\Psi _{g}\left( p_{T},\,r\right)$ stands for the wave function of gluon with virtuality $p_{T}$, transverse quark–antiquark separation r and the light-cone fraction of the quark z, while $\Psi _{J/\psi }$ is the wave function of $J/\psi$ meson. The amplitude of the BFKL Pomeron $G_{{\mathbb {P}}}^{\mathrm{cut}}\left( y,\,{\varvec{k}}_{T}\pm \frac{1}{2}{\varvec{q}}_{T},\,{\varvec{Q}}_{T}\right)$ can be simplified if we take into account that the ${\varvec{Q}}_{T}$ dependence of the BFKL Pomeron is determined by the size of the largest of the interacting dipoles,³ and accounting for Eq. (1), may be written as

$$\begin{aligned}&G_{{\mathbb {P}}}^{\mathrm{cut}}\left( y,\,{\varvec{k}}_{T}\pm \frac{1}{2} {\varvec{q}}_{T},\,{\varvec{Q}}_{T}\right) \nonumber \\&\quad \approx \,\,2G_{\mathbb {P}}^{\mathrm{BFKL}}\left( y,\,{\varvec{k}}_{T}\pm \frac{1}{2} {\varvec{q}}_{T},\,{\varvec{Q}}_{T}=0\right) \,S_{h}\left( Q_{T}\right) \end{aligned}$$

(5)

The dependence on $Q_{T}$ is described by $S_{h}\left( Q_{T}\right)$ in Eq. (5), which has the non-perturbative origin and has to be taken from the experiment. Using Eq. (5) we can re-write Eq. (2) in the form

$$\begin{aligned} \frac{d\sigma \left( Y,\,Q^{2}\right) }{dy\,d^{2}q_{T}}\,\,= & {} \,\,\frac{4\,C_{F}^{3}\,{\bar{\alpha }}_{S}^{3}}{(2\pi )^{4}}\,\int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,S_{h}^{2}\left( Q_{T}\right) \nonumber \\&\times \int d^{2}k_{T}d^{2}p_{T}\,\,G_{\mathbb {P}}^{\mathrm{cut}}\left( Y-y,\, p_{T},\,0\right) \, \nonumber \\&\times \, I^{2}\left( {\varvec{k}}_{T},\,{\varvec{q}}_{T}\right) \, G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y;\,{\varvec{k}}_{T} +\frac{1}{2}{\varvec{q}}_{T},\,0\right) \nonumber \\&\times \, G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y,-{\varvec{k}}_{T}+\frac{1}{2}{\varvec{q}}_{T},\,0\right) . \end{aligned}$$

(6)

As we can see from (6), the dependence in $S\left( Q_{T}\right)$ only enters as a constant multiplicative factor $\sim \int d^{2}Q_{T}\,S_{h}^{2}\left( Q_{T}\right)$, which only affects the normalization of the cross-sections. In what follows, we will fix the normalization from the charmonia photoproduction data, and for this reason do not need to model the $Q_{T}$-dependence of $S_{h}\left( Q_{T}\right)$. For further evaluations it is very convenient to introduce momenta ${\varvec{p}}_{1,2,T}=\pm {\varvec{k}}_{T}+\frac{1}{2}{\varvec{q}}_{T}$, which allow to rewrite Eq. (6) as

$$\begin{aligned}&\frac{d\sigma \left( Y,\,Q^{2}\right) }{dy\,d^{2}q_{T}} \nonumber \\&\quad = \,\,\frac{4\,C_{F}^{3}\,{\bar{\alpha }}_{S}^{3}}{(2\pi )^{4}}\, \int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,S_{h}^{2}\left( Q_{T}\right) \, x_{g}G\left( x_{g},\,M_{J/\psi }\right) \nonumber \\&\qquad \times \int d^{2}p_{1,T}d^{2}p_{1,T}\,\delta ^{(2)} \left( {\varvec{p}}_{1,T}+{\varvec{p}}_{2,T}-{\varvec{q}}_{T} \right) \nonumber \\&\qquad \times I^{2}\left( {\varvec{p}}_{1,T},{\varvec{p}}_{2,T}\right) \, G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y;{\varvec{p}}_{1,T},\,0\right) \nonumber \\&\qquad \times G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y,{\varvec{p}}_{2,T},\,0\right) \end{aligned}$$

(7)

where we took the integral over ${\varvec{p}}_{T}\in \left( 0,\,2m_{c}\right)$ using $G_{\mathbb {P}}^{\mathrm{cut}} \left( Y-y,\,{\varvec{p}}_{T}, \,0\right) \,\, =\,\,d\,x\,G\left( x,\,p_{T}^{2} \right) \big /dp_{T}^{2}$, $x_{g}G\big (x_{g},M_{J/\psi }\big )$ is the gluon structure function, $x_{g}=\sqrt{M_{J/\psi }^{2}+q_{T}^{2}}e^{y}/\sqrt{s}$, and $Y-y\equiv \ln \left( 1/x_{g}\right)$. There is a freedom in the choice of the factorization scale $\mu _{F}$ (upper limit of integration over ${\varvec{p}}_{T}$) in gluon PDFs, and the physical observables should not depend on it (provided the evolution of gluon PDFs and loop corrections to hard coefficient functions are taken in the same order over $\alpha _{s}$). Our choice of the fixed scale $\mu _{F}=M_{J/\psi }$ is motivated by simplicity: for $p_{T}\lesssim M_{J/\psi }$ we may disregard the $p_{T}$-dependence of the gluon-$J/\psi$ transition form factor $I\left( {\varvec{p}}_{T},\,{\varvec{k}}_{T}\right)$ and thus the integration over $p_{T}$ leads to the standard collinear PDFs at factorization scale $M_{J/\Psi }$. In contrast, if we used the scale $\mu _{F}^{(k_{T})}=\sqrt{M_{J/\psi }^{2}+q_{T}^{2}}$ common in $k_{T}$-factorization approach, for larger $p_{T}\gtrsim M_{J/\psi }$ the transition gluon-$J/\psi$ form factor would start to decrease, violating the log integration over $p_{T}$ which are summed by the DGLAP evolution equation. Since the $q_{T}$-integrated observables obtain the main contribution from the region of small $q_{T}$, we expect that the $q_{T}$-integrated observables should not depend on this choice.

The choice of the factorization scale $\mu _{F}=\sqrt{M_{J/\psi }^{2}+q_{T}^{2}}$ does not work in our case since the production of $J/\Psi$ at large $q_{T}$ occurs due to large momentum transferred in scattering amplitudes (see Fig. 2). However, there is another contribution with $p_{T}\approx q_{T}$ at large values of $q_{T}$. In this contributions the value of $p_{T}$ of the lower two gluons are small and the $q_{T}$ dependence turns out to be similar to the one parton shower mechanism. We do not consider this possibility in the paper, leaving it to the further publication.

Making a Fourier transform, we may rewrite Eq. (7) in the coordinate space as

$$\begin{aligned}&\frac{d\sigma \left( Y,\,Q^{2}\right) }{dy\,d^{2}q_{T}} \nonumber \\&\quad =\,4\, \int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,S_{h}^{2}\left( Q_{T}\right) \,\,\, x_{g}G\left( x_{g},\,M_{J/\psi }\right) \,\, \nonumber \\&\qquad \times \,\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi } \,\frac{d^{2}r'}{4\pi }\,d^{2}b\,\,e^{-i{\varvec{q}}_{T}\cdot \left( {\varvec{b}}+\frac{1}{2}({\varvec{r}}-{\varvec{r}}') \right) } \nonumber \\&\qquad \times \, \langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\psi } \left( r,z\right) \rangle \,\langle \Psi _{g}\left( r',z'\right) \, \Psi _{J/\psi }\left( r',z'\right) \rangle \nonumber \\&\qquad \times \,\Bigg (N\left( y;\,{\varvec{b}}\right) \,+\,N\left( y;\, {\varvec{b}}+{\varvec{r}}-{\varvec{r}}'\right) \nonumber \\&\qquad -\,N\left( y;\, {\varvec{b}}+{\varvec{r}}\right) \,-\,N\left( y;{\varvec{b}}- {\varvec{r}}'\right) \Bigg )^{2}\nonumber \\&\quad =\,4\,\int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,S_{h}^{2}\left( Q_{T} \right) \,\,\,x_{g}G\left( x_{g},\,M_{J/\psi }\right) \,\,\nonumber \\&\qquad \times \,\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi } \,\frac{d^{2}r'}{4\pi }\,d^{2}b\,\,e^{-i{\varvec{q}}_{T}\cdot \left( {\varvec{b}}\right) } \nonumber \\&\qquad \times \langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\psi }\left( r,z\right) \rangle \,\langle \Psi _{g} \left( r',z'\right) \,\Psi _{J/\psi }\left( r',z'\right) \rangle \,\nonumber \\&\qquad \times \,\Bigg (N\left( y;\,{\varvec{b}}-\frac{1}{2} \left( {\varvec{r}}-{\varvec{r}}'\right) \right) +N\left( y;\, {\varvec{b}}+\frac{1}{2}\left( {\varvec{r}}-{\varvec{r}}' \right) \right) \nonumber \\&\qquad -\,N\left( y;\,{\varvec{b}}+\frac{1}{2}\left( {\varvec{r}} +{\varvec{r}}'\right) \right) \nonumber \\&\qquad -\,N\left( y;\,{\varvec{b}} -\frac{1}{2}\left( {\varvec{r}}+{\varvec{r}}'\right) \right) \Bigg )^{2} \end{aligned}$$

(8)

where the amplitudes $N\left( y;\,{\varvec{r}}_{i}\right)$ are related to the solutions of the BK equation as $N\left( y;\,{\varvec{r}}_{i}\right) =\int d^{2}b'\,N\left( y;\,{\varvec{r}}_{i},\,{\varvec{b}}'\right)$, and the variable ${\varvec{b}}$ is a Fourier conjugate of momentum ${\varvec{p}}_{1,T}+ {\varvec{p}}_{2,T}-{\varvec{q}}_{T}.$ In what follows, we will also need an expression for the $q_{T}$-integrated cross-section, which takes a simpler form

$$\begin{aligned} \frac{d\sigma \left( Y,\,Q^{2}\right) }{dy}= & {} 16\, \int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,S_{h}^{2}\left( Q_{T}\right) \,\,\,x_{g}G\left( x_{g},\,m_{c}\right) \,\, \nonumber \\&\times \,\,\,\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi }\, \frac{d^{2}r'}{4\pi } \nonumber \\&\times \left\langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\psi }\left( r,z\right) \right\rangle \,\left\langle \Psi _{g}\left( r',z'\right) \,\Psi _{J/\psi }\left( r',z'\right) \right\rangle \nonumber \\&\times \,\,\Bigg (\,N\left( y;\,\frac{\vec {r}+\vec {r}'}{2}\right) \,- \,N\left( y;\,\frac{\vec {r}-\vec {r}'}{2}\right) \Bigg )^{2} \end{aligned}$$

(9)

Finally, we would like to mention that the expressions presented in this section implicitly assume that each parton cascade is emitted independently, namely that parton correlations are negligible. In more general case with nonzero parton correlations, the expression (6) should be replaced with

$$\begin{aligned} \frac{d\sigma \left( Y,Q^{2}\right) }{dy\,d^{2}q_{T}}= & {} \,\,\frac{4\,C_{F}^{3}\,{\bar{\alpha }}_{S}^{2}}{(2\pi )^{4}} \nonumber \\&\times \int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,\int d^{2}k_{T}d^{2}p_{T}\,\,G_{\mathbb {P}}^{\mathrm{cut}}\left( Y-y,\,p_{T},\,0\right) \,\nonumber \\&\times I^{2}\left( {\varvec{k}}_{T},{\varvec{q}}_{T}\right) \, \rho ^{(2)} \nonumber \\&\times \left( y;{\varvec{k}}_{T}+\frac{1}{2}{\varvec{q}}_{T}; \,y,-{\varvec{k}}_{T}+\frac{1}{2}{\varvec{q}}_{T}; \,{\varvec{Q}}_{T}\right) \end{aligned}$$

(10)

where we replaced the product of pomeron propagators with the double transverse momentum densities $\rho ^{(2)}$ defined as

$$\begin{aligned}&\rho ^{(2)}\left( x_{1},{\varvec{p}}_{1,T};x_{2}, {\varvec{p}}_{2,T},{\varvec{Q}}_{T}\right) \nonumber \\&\quad = \,\left\langle P\left| \Bigg \{ a^{+}\left( x_{1}, {\varvec{p}}_{1,T}+\frac{1}{2}{\varvec{Q}}_{T};b\right) \right. \right. \nonumber \\&\qquad \qquad a^{+}\left( x_{2},{\varvec{p}}_{2,T}-\frac{1}{2}{\varvec{Q}}_{T} ;c\right) \nonumber \\&\qquad \qquad a\left( x_{2},{\varvec{p}}_{2,T}+\frac{1}{2}{\varvec{Q}}_{T} ;c\right) \nonumber \\&\qquad \qquad \left. \left. a\left( x_{1},{\varvec{p}}_{1,T}-\frac{1}{2}{\varvec{Q}}_{T} ;b\right) \Bigg \}\right| P\right\rangle \end{aligned}$$

(11)

Fig. 3

Two main contributions to the diffractive production of $J/\Psi$ meson. The elastic contribution (a) contributes mainly to production of hadrons with small total mass, while the inelastic contribution (b) is the source of hadrons with large total mass

where $\left( x_{1},p_{1,T}\right)$ and $\left( x_{2},p_{2,T}\right)$ are the light-cone and transverse momenta of the partons in the cascade,⁴ $|P\rangle$ is the Fock state of colliding hadrons, $a^{+}$ and a denote the creation and annihilation operators for gluons that have longitudinal momentum $x_{i}$ and transverse momentum $p_{i,T}$, $c_{i}$ are the color indexes. However, at present there is no experimental evidence that such correlations are large, for this reason in what follows we will use a simpler expressions (6). Similarly, in coordinate space the Eq. (8) can be extended as

$$\begin{aligned} \frac{d\sigma \left( Y,Q^{2}\right) }{dy\,d^{2}q_{T}}= & {} 4 \,\int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\,\,x_{g}G\left( x_{g},2\,m_{c} \right) \,\, \nonumber \\&\times \,\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi }\, \frac{d^{2}r'}{4\pi }\,d^{2}b\,\,e^{-i{\varvec{q}}_{T}\cdot {\varvec{b}}}, \nonumber \\&\times \langle \Psi _{g}\left( r,\,z\right) \,\Psi _{J/\psi } \left( r,\,z\right) \rangle \,\langle \Psi _{g}\left( r',\,z\right) \, \Psi _{J/\psi }\left( r',\,z\right) \rangle \nonumber \\&\times \,\Bigg (\rho ^{(2)}\left( y;{\varvec{b}}-{\varvec{r}}_{d} ;y;{\varvec{b}}-{\varvec{r}}_{d},Q_{T}\right) \,\nonumber \\&+\,\rho ^{(2)} \left( y;{\varvec{b}}+{\varvec{r}}_{d},y;{\varvec{b}}+ {\varvec{r}}_{d},Q_{T}\right) \, \nonumber \\&+\,\rho ^{(2)} \left( y;{\varvec{b}} +{\varvec{r}}_{s},y;{\varvec{b}}+{\varvec{r}}_{s},Q_{T}\right) \nonumber \\&\,+\,\rho ^{(2)}\left( y;{\varvec{b}}-{\varvec{r}}_{s},y; {\varvec{b}}-{\varvec{r}}_{s},Q_{T}\right) \nonumber \\&+\,2\,\rho ^{(2)} \left( y;{\varvec{b}}-{\varvec{r}}_{d},y;{\varvec{b}}+ {\varvec{r}}_{s},Q_{T}\right) \,-\,2\,\rho ^{(2)} \nonumber \\&\times \left( y; {\varvec{b}}+{\varvec{r}}_{d},y;{\varvec{b}}+{\varvec{r}}_{s}, Q_{T}\right) \,\nonumber \\&-\,\rho ^{(2)}\left( y;{\varvec{b}}-{\varvec{r}}_{d},y; {\varvec{b}}-{\varvec{r}}_{s},Q_{T}\right) \nonumber \\&-\,2\,\rho ^{(2)} \left( y;{\varvec{b}}+{\varvec{r}}_{d},y;{\varvec{b}}+ {\varvec{r}}_{s},Q_{T}\right) \nonumber \\&-\,2\,\rho ^{(2)}\left( y; {\varvec{b}}+{\varvec{r}}_{d},y;{\varvec{b}}-{\varvec{r}}_{s}, Q_{T}\right) \,\nonumber \\&+\,2\,\rho ^{(2)}\left( y;{\varvec{b}}+{\varvec{r}}_{s},y; {\varvec{b}}-{\varvec{r}}_{s},Q_{T}\right) \Bigg ) \end{aligned}$$

(12)

where $\rho ^{(2)}\left( x,\,{\varvec{r}};\,x,\,{\varvec{r}}';\,{\varvec{Q}}_{T}\right)$ is the double parton density in the coordinate representation, ${\varvec{r}}_{s}\,=\,\frac{1}{2}({\varvec{r}}+{\varvec{r}}')$ and ${\varvec{r}}_{d}\,=\,\frac{1}{2}({\varvec{r}}-{\varvec{r}}')$.

While for numerical estimates we could use parameterizations of the amplitude N available from the literature, we would like to minimize dependence on parameterization and make a few model-independent estimates. One of the important parameters for understanding the small-x dynamics is the saturation scale $Q_{s}$ and its product on characteristic size of the dipoles $\langle r\rangle$ in the process. The saturation has a mild dependence on energy [96] and in the kinematics of interest for our studies ($\sqrt{s}\in \left( 1.9,\,7\right)$ TeV) its values are $Q_{s}^{2}=0.7-0.9\,\mathrm{GeV}^{2}$. The typical size of the dipole essential in our process might be estimated as⁵

$$\begin{aligned} \left\langle r^{2}\right\rangle= & {} \frac{\int _{0}^{1}dz\int \,\frac{d^{2}r}{4\pi }\,\,\,r^{2}\left\langle \Psi _{g}\left( r,\,z\right) \,\Psi _{J/\psi }\left( r,\,z\right) \right\rangle }{\int _{0}^{1}dz\int \frac{d^{2}r}{4\pi }\,\,\,\left\langle \Psi _{g}\left( r,\,z\right) \,\Psi _{J/\psi }\left( r,\,z\right) \right\rangle } \nonumber \\\approx & {} 0.76\,\mathrm{GeV}^{-2} \end{aligned}$$

(13)

so the product $\tau \,\,\equiv \,\,\left\langle r^{2}\right\rangle \,Q_{s}^{2}\approx 0.5\,\ldots \,0.7$. Contrary to the large-$m_{c}$ expectations, this number is not very small and corresponds to the dynamics in the vicinity of the saturation scale [37, 98]. The scattering amplitude is well known in this region (see (15) below), so this implies minimal model-dependence in our estimates.

3 Interrelation with the diffractive $J/\psi$ production in DIS

The cross-section of the $J/\psi$ production in the small-x kinematics is closely related to the diffractive $J/\Psi$ production in DIS, and this relationship is useful to fix the unknown non-perturbative factor $\sim \int d^{2}Q_{T}\,S_{h}^{2}(Q_{T})$ which appears in (7, 8). In the BFKL picture, there are elastic and inelastic contributions to diffractive $J/\psi$ production, shown in the left and right panels of the Fig. 3. Taking into account approximate equality of the elastic and inelastic contributions [99, 100], we may focus on evaluation of the diagram (a) of the Fig. 3. For fixing the prefactor $\sim \int d^{2}Q_{T}\,S_{h}^{2}(Q_{T})$, it is sufficient to consider only the $q_{T}$-integrated cross-section $d\sigma _{\mathrm{diff}}/dy$, which is given by (see Fig. 3):

$$\begin{aligned}&\frac{d\sigma _{\mathrm{diff}}\left( y,\,Q^{2},\,\sqrt{s_{\gamma ^{*}p}} \right) }{dy} \nonumber \\&\quad =\,\,\,\int \frac{d^{2}Q_{T}}{(2\pi )^{2}} \,S_{h}^{2}\left( Q_{T}\right) \int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi }\,\frac{d^{2}r'}{4\pi } \nonumber \\&\qquad \times \left\langle \Psi _{\gamma ^{*}}\left( r,z\right) \,\Psi _{J/\psi }\left( r,z\right) \right\rangle \nonumber \\&\qquad \times \left\langle \Psi _{\gamma ^{*}}\left( r',z'\right) \,\Psi _{J/\psi }\left( r',z'\right) \right\rangle \nonumber \\&\qquad N\left( y,\,r^{2}\right) \,N\left( y,\,r'^{2}\right) . \end{aligned}$$

(14)

In the vicinity of the saturation scale, which gives the dominant contribution, the CGC/saturation approach predicts that the amplitude N has a form

$$\begin{aligned} N\left( y,\,r^{2},\,0\right) \approx \mathrm{Const}_{s}\left( r^{2}\,Q_{s}^{2}(x)\right) ^{{\bar{\gamma }}}, \end{aligned}$$

(15)

where ${\bar{\gamma }}\approx 0.63$ [94], $x\approx M_{J/\psi }e^{-y}/\sqrt{s}$, and $Q_{s}^{2}(x)$ is the saturation scale. The Eq. (14) in this case takes the form

$$\begin{aligned}&\frac{d\sigma _{\mathrm{diff}}\left( y,\,Q^{2},\,\sqrt{s_{\gamma ^{*}p}} \right) }{dy} \nonumber \\&\quad =\text{ Const }_{\mathrm{s}}^{2}\,\,\,\int \frac{d^{2}Q_{T}}{(2\pi )^{2}} \,S_{h}^{2}\left( Q_{T}\right) \int _{0}^{1}dz\int _{0}^{1}dz' \int \frac{d^{2}r}{4\pi }\,\frac{d^{2}r'}{4\pi }\, \nonumber \\&\qquad \times \,\,\left\langle \Psi _{\gamma ^{*}}\left( r,\,z\right) \, \Psi _{J/\psi }\left( r,\,z\right) \right\rangle \,\left\langle \Psi _{\gamma ^{*}}\left( r',\,z'\right) \,\Psi _{J/\psi }\left( r', \,z'\right) \right\rangle \nonumber \\&\qquad \times \left( Q_{s}^{2}\left( x\right) \,r^{2}\right) ^{{\bar{\gamma }}}\,\,\left( Q_{s}^{2} \left( x\right) \,r'^{2}\right) ^{{\bar{\gamma }}}, \end{aligned}$$

(16)

which allows to factorize all the energy- and rapidity dependence,

$$\begin{aligned} \frac{d\sigma _{\mathrm{diff}}\left( y,\,Q^{2},\,\sqrt{s_{\gamma ^{*}p}}\right) }{dy} \sim \,\left[ Q_{s}^{2}\left( x\right) \right] ^{2{\bar{\gamma }}} \end{aligned}$$

(17)

and in this way facilitate scaling from HERA to Tevatron and LHC energies. Similarly, for the gluon induced elastic $J/\psi$ production in the vicinity of the saturation scale (see Ref. [37]) we may simplify (9) to

$$\begin{aligned}&\frac{d\sigma \left( y,\,Q^{2},\,\sqrt{s_{\gamma ^{*}p}}\right) }{dy}\, \nonumber \\&\quad =\,16\,\,\,\text{ Const }_{\mathrm{s}}^{2}\int \frac{d^{2}Q_{T}}{(2\pi )^{2}}\, S_{h}^{2}\left( Q_{T}\right) \,\,\,x_{g}G\left( x_{g},\, M_{J/\Psi }\right) \,\, \nonumber \\&\qquad \times \,C_{F}^{2}\,\,\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi }\,\frac{d^{2}r'}{4\pi } \nonumber \\&\qquad \times \left\langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\psi }\left( r,z\right) \right\rangle \,\left\langle \Psi _{g}\left( r',z'\right) \,\Psi _{J/\psi }\left( r',z'\right) \right\rangle \nonumber \\&\qquad \times \Bigg \{\left( \int d^{2}b\,Q_{s}^{2}\left( x,\,b\right) \right) ^{2{\bar{\gamma }}} \nonumber \\&\qquad \times \left( \left( \frac{\vec {r}+\vec {r}'}{2} \right) ^{2\,{\bar{\gamma }}}\,-\,\left( \frac{\vec {r}- \vec {r}'}{2}\right) ^{2\,{\bar{\gamma }}}\right) ^{2}\Bigg \} \end{aligned}$$

(18)

which also has a factorizable dependence on energy and rapidity,

$$\begin{aligned} \frac{d\sigma \left( y,\,Q^{2}\right) }{dy}\sim x_{g}\,G \left( x_{g}\,M_{J/\psi }\right) \,\left[ Q_{s}^{2} \left( x\right) \right] ^{2{\bar{\gamma }}}. \end{aligned}$$

(19)

Taking into account that the wave functions of the proton and gluon are proportional to each other in the leading order of pQCD [35],

$$\begin{aligned} \Psi _{\gamma ^{*}}\left( r,\,z\right) \,\,=\,\,\frac{\sqrt{2N_{c}}}{g} \frac{2}{3}eN_{c}\Psi _{g}\left( r,\,z\right) \end{aligned}$$

(20)

we may expect the proportionality of the diffractive and inclusive cross-sections

$$\begin{aligned}&\frac{d\sigma \left( y,\,Q^{2}\right) /dy}{d\sigma _{\mathrm{diff}} \left( y,\,Q^{2}\right) /dy}\Bigg |_{Q=m_{J/\psi },y\rightarrow Y_{0}} \nonumber \\&\quad \approx \frac{9}{2}\,x_{g}G\left( x_{g},\,M_{J/\psi } \right) \,{\mathcal {R}}\,C_{F}^{2}\,\frac{\alpha _{S}}{\alpha _{\mathrm{e.m,.}}N_{c}^{3}} \end{aligned}$$

(21)

where

$$\begin{aligned} {\mathcal {R}}&=I_{1}/I_{2}\approx 1.27, \end{aligned}$$

(22)

$$\begin{aligned} I_{1}&=4\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi } \int \frac{d^{2}r'}{4\pi } \nonumber \\&\quad \times \left\langle \Psi _{\gamma ^{*}}\left( r,z\right) \, \Psi _{J/\psi }\left( r,z\right) \right\rangle \,\left\langle \Psi _{\gamma ^{*}}\left( r',z'\right) \, \Psi _{J/\psi }\left( r',z'\right) \right\rangle \nonumber \\&\quad \times \left[ \left( \frac{\vec {r}+\vec {r}'}{2}\right) ^{2{\bar{\gamma }}}- \left( \frac{\vec {r}-\vec {r}'}{2}\right) ^{2{\bar{\gamma }}}\right] ^{2}, \end{aligned}$$

(23)

$$\begin{aligned} I_{2}&=\int _{0}^{1}dz\int _{0}^{1}dz'\int \frac{d^{2}r}{4\pi } \int \frac{d^{2}r'}{4\pi } \nonumber \\&\quad \times \left\langle \Psi _{\gamma ^{*}}\left( r,z\right) \,\Psi _{J/\psi }\left( r,z\right) \right\rangle \nonumber \\&\quad \times \left\langle \Psi _{\gamma ^{*}}\left( r',z'\right) \,\Psi _{J/\psi }\left( r',z'\right) \right\rangle \left( r^{2}r'^{2}\right) ^{{\bar{\gamma }}} \end{aligned}$$

(24)

and for estimates of parameter ${\mathcal {R}}$ we used the parameterizations of the wave functions given in Appendix 1. The data on diffractive production are available from H1 and ZEUS experiments [99,100,101,102], and they show that in HERA kinematics the elastic and inelastic contributions (diagrams a and b in the Fig. 3, respectively) are approximately equal. As a consequence, for $W\equiv \sqrt{s}\approx 30\,\mathrm{GeV}$ ($x_{g}\approx 0.01$) the diffractive cross-section

$$\begin{aligned} \frac{d\sigma _{\mathrm{diff}}}{dy}\Bigg |_{Q=M_{J/\psi },y\rightarrow Y_{0}}\sim 20\,\mathrm{nb}. \end{aligned}$$

This allows to use Eq. (21) for estimate of the hadroproduction cross-section at $\sqrt{s}\approx 30$ GeV,

$$\begin{aligned} \left. \frac{d\sigma }{dy}\right| _{x_{g}\approx 10^{-2}}\approx 0.83\,\mathrm{\mu b}. \end{aligned}$$

(25)

In the next section we will extrapolate it with the help of the small-x evolution up to LHC energies.

4 Phenomenological estimates

4.1 Total $J/\Psi$ production cross section

As we demonstrated in Sect. 2, the typical size $\langle r\rangle$ of $Q{\bar{Q}}$ dipole is small when the saturation scale $Q_{s}(x)\lesssim m_{c}$ (see Eq. (13)), and for this reason from (18) we expect that the cross-section at central rapidities should scale with energy as

$$\begin{aligned} \left. \frac{d\sigma }{dy}\right| _{y=0}\sim x_{g}G\left( x_{g},\,M_{J/\psi } \right) \left( Q_{s}^{2}\left( x\right) \right) ^{2{\bar{\gamma }}}. \end{aligned}$$

(26)

For numerical estimates we assume that the saturation scale $Q_{s}^{2}$ scales as [98]

$$\begin{aligned} Q_{s}^{2}\left( x\right) =Q_{s}^{2}\left( x_{0}\right) \, \left( \frac{x_{0}}{x}\right) ^{\lambda }. \end{aligned}$$

(27)

with $\lambda \approx 0.2-0.3$ [106,107,108] and $x\approx \sqrt{M_{J/\psi }^{2}+q_{T}^{2}}e^{-y}/\sqrt{s}$. In case of Tevatron and LHC kinematics, this leads to the cross-section estimates given in the Table 1. In these estimates we use that the evolution does not change the ratio between the elastic and inelastic contributions which correspond to two terms in the solution to the evolution equation for $\rho ^{(2)}$ (see Appendix B and Fig. 9).

As we can see, the suggested mechanism gives a significant contribution to the total cross-section, though in view of inherent uncertainties of the CGC/saturation approach we cannot make more accurate estimate about the fraction of charmonia produced via this mechanism.

Table 1 Comparison of the theoretical estimates with experimental data for the cross-section $d\sigma /dy$ at central rapidities. Theoretical estimates correspond to values of parameter $\lambda \in (0.2,\,0.3)$ (lower and upper values respectively). In the last column we’ve quoted the data on prompt $J/\psi$ production. The cross-section $d\sigma /dy$ at Tevatron was extracted dividing the total cross-section $\sigma _{\mathrm{tot}}(|y|<0.6)$ by the width of the bin $\Delta y\sim 1.2$

As we have mentioned earlier, our estimates exceed the result of Ref. [38], where similar contribution was found approximately twice smaller. Below we would like to analyze the reasons which might be responsible for this discrepancy. It was assumed in [38] that the digluon distribution is proportional to a direct product of independent gluon distributions, with a phenomenological multiplicative prefactor usually described by the so-called effective cross-section $\sigma _{\mathrm{eff}}$. In the CGC/saturation picture, each gluon effectively is replaced by a pomeron, so the factorized model would correspond to the diagram (a) in the Fig. 3. As we discussed earlier, the inelastic contributions (diagram (b) in the same Figure) yields a numerically comparable contribution which would correspond to corrections breaking the factorized form. This additional inelastic contribution might be one of the reasons of the strong channel dependence of the phenomenological effective cross-section $\sigma _{\mathrm{eff}}.$⁶ In our approach, we fix the the only unknown constant $\int d^{2}Q_{T}\,S^{2}\left( Q_{T}\right)$ from experimental data at HERA and evolve the cross-section as prescribed by small-x evolution, thus taking into account both diagrams of the Fig. 3. The main source of uncertainty in this procedure is the energy dependence of the saturation scale $Q_{s}^{2}(x)$, namely the choice of coefficient $\lambda$ in (27). Theoretical estimates of this parameter significantly depend on the choice of the scale in the running coupling constant ${\bar{\alpha }}_{s}$, and lead to estimates $\lambda \approx 0.3-0.4$ [109], whereas phenomenological estimates of this parameter restrict it to the range $\lambda \in (0.2,\,0.3)$ [94]. We can see that it results in up to fifty per cent uncertainty in the theoretical estimates shown in the Table 1.

4.2 Transverse momentum distribution

Qualitatively the main features of $q_{T}$-distribution may be understood from (8). For small momenta $\frac{1}{2}q_{T}\lesssim Q_{s}\left( x\right)$, we can safely use the behaviour of the Pomeron Green function in the vicinity of the saturation momentum [98]

$$\begin{aligned}&G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y;\,{\varvec{k}}_{T}\,\pm \, \frac{1}{2}{\varvec{q}}_{T},\,{\varvec{Q}}_{T}=0\right) \nonumber \\&\quad \approx \mathrm{const}\left( \frac{Q_{s}^{2}\left( x\right) }{\left( {\varvec{k}}_{T}\,\pm \,\frac{1}{2}{\varvec{q}}_{T} \right) ^{2}}\right) ^{{\bar{\gamma }}},\quad \mathrm{small}\,{\varvec{q}}_{T}. \end{aligned}$$

(28)

In the kinematic region $\frac{1}{2}q_{T}\gtrsim k_{T}$ the scattering amplitude becomes sensitive to dynamics at shorter distances, which is described in perturbative QCD. In this region we may use a parameterization (15), which is a BFKL prediction for small dipoles with $r\lesssim Q_{s}^{-1}\left( x\right)$ [94].

The two approaches are valid for different values of $q_{T}$ and thus complement each other. The choice of the threshold scale $q_{0}$ between them is somewhat arbitrary, yet we expect that $q_{0}$ should be of order $\sim (1-2)\,M_{J/\psi }$.

Fig. 4

Solid green line corresponds to the shape of the $q_{T}$ distribution of produced $J/\psi$ at central rapidities described in the text. The threshold scale $q_{0}$ is chosen as $q_{0}\sim$5  GeV. Dashed and dotted brown lines correspond to an asymptotic form $\sim 1/\left( q_{T}^{2}+\Lambda _{c}^{2}\right) ^{2+2{\bar{\gamma }}}$discussed in the text, with parameter $\Lambda _{c}\approx (1-2)\,M_{J/\psi }$ The experimental data are taken from Refs. [110, 111]

In Fig. 4 we compare model predictions for the shape of the $q_{T}$-dependence with experimental data from [110, 111]. In order to avoid the above-mentioned global uncertainty in normalization, we consider the normalized ratio $\left( d^{2}\sigma /dy\,dq_{T}\right) /\left( d\sigma /dy\right)$. The cusp on the curve near the threshold scale $q_{T}=q_{0}$ can be smoothed out by more relaxed conditions.

The asymptotic behaviour of the cross-section might be understood from analysis of the cross-section (8). In this problem we have several relevant scales, however for asymptotic behavior we need to compare each variable $|{\varvec{b}}|,\,|{\varvec{r}}|,\,|\varvec{r'}|$ with $1/q_{T}$. In what follows we will analyze kinematics $q_{T}\gg m_{c}\sim Q_{s}(x)$. The region

$$\begin{aligned} |{\varvec{b}}|\sim |{\varvec{r}}|\sim |\varvec{r'}|\sim 1/q_{T} \end{aligned}$$

(29)

gives an asymptotically suppressed contribution which follows directly from the third line of (8)

$$\begin{aligned} \frac{d^{2}\sigma ^{(29)}}{d^{2}q_{T}}\,\sim \frac{1}{q_{T}^{6+4{\bar{\gamma }}}}\sim \frac{1}{q_{T}^{8.5}}. \end{aligned}$$

(30)

It should be noted that factor $1/q_{T}^{4}$ stems from the behaviour of the form factors for gluon-$J/\psi$ transition.

The regions

$$\begin{aligned} |{\varvec{b}}|&\sim |\varvec{{\varvec{r}}}+{\varvec{r}}'|\sim 1/q_{T}, \quad |{\varvec{r}}|\sim |\varvec{r'}|\sim m_{c}^{-1}\gg q_{T}^{-1} \end{aligned}$$

(31)

$$\begin{aligned} |{\varvec{b}}|&\sim |\varvec{{\varvec{r}}}-{\varvec{r}}'|\sim 1/q_{T}, \quad |{\varvec{r}}|\sim |\varvec{r'}|\sim m_{c}^{-1}\gg q_{T}^{-1} \end{aligned}$$

(32)

give the asymptotic contribution

$$\begin{aligned} \frac{d^{2}\sigma ^{(31,\, 32)}}{d^{2}q_{T}}\, \sim \frac{1}{q_{T}^{4+4{\bar{\gamma }}}}. \end{aligned}$$

(33)

Such behaviour in the momentum representation (7) comes from the integration region $k_{T}\lesssim M_{J/\psi }$: the $q_{T}$ dependence comes only from the Pomeron Green functions so the cross-section has an asymptotic behaviour $d^{2}\sigma /d^{2}q_{T}\,\propto \,\Bigg (G_{{\mathbb {P}}}^{\mathrm{BFKL}}\left( y,{\varvec{q}}_{T}/2,\,0\right) \Bigg )^{2}\,\propto \,1/(q_{T})^{4+4{\bar{\gamma }}}$. This contribution describes two gluons that are emitted from different quarks in the quark loop in Fig. 2. They are scattered at the same value of the momentum transfer and this contribution does not depend on the form factor of the gluon-$J/\Psi$ transition (the second term in (3)).

In preasymptotic regime, the behaviour (33) is regularized at smaller $q_{T}$ as

$$\begin{aligned} \frac{d^{2}\sigma ^{(31,\, 32)}}{d^{2}q_{T}} \sim \frac{1}{\left( q_{T}^{2}+\Lambda _{c}^{2}\right) ^{2+2{\bar{\gamma }}}} \end{aligned}$$

(34)

where the parameter $\Lambda _{c}\approx (1-2)\,M_{J/\psi }$. As we can see from the Fig. 4, the behaviour (34) agrees reasonably well with the data at large $p_{T}$. In our estimates of the $p_{T}$ dependence we considered leading order evaluation, and as was explained in Sect. 2, the coupling constant $\alpha _{s}$ in the gluon wave function $\Psi _{g}$ in (8) is taken at scale $\sim m_{c}$.

Now we would like to comment briefly on different $q_{T}$-dependence found in this section and in the $k_{T}$-factorization approach [38]. The working formulas in that approach have a structure similar to (2), provided Green functions are replaced with unintegrated gluon densities. The prefactor of (2) includes a common factor $\alpha _{s}^{2}\left( \mu _{F}\right)$, with the $k_{T}$-factorization scale prescription $\mu _{F}\sim q_{T}$. The use of running coupling leads to stronger observed suppression at larger $q_{T}$. However, since the latter is the next-to-leading order effect, a complete analysis of the NLO corrections is needed in this kinematics for analysis of $q_{T}$ dependence. Note, that these factors $\sim \left( \alpha _{s}(q_{T})\right) ^{2}$ have been included in the dipole scattering amplitude in our approach (see (8)) and finally have been absorbed in the definition of the saturation momenta in (15). Another crucial assumption which affects the large-$q_{T}$ slope of the cross-section is the value of the parameter ${\bar{\gamma }}$, as could be seen from (34). There is some uncertainty in the value of this parameter, and phenomenological fits [106, 108] frequently prefer slightly higher values of paramater ${\bar{\gamma }}$ than the theoretical value ${\bar{\gamma }}\approx 0.63$ used in our estimates. Potentially this also leads to stronger suppression at large $q_{T}$. These two effects explain the discrepancy between our result and findings of [38] in the $k_{T}$-factorization approach, and signal that in the large-$q_{T}$ kinematics the theoretical uncertainty might be significant.

Fig. 5

Rapidity distribution of produced $J/\psi$. The ratio $R_{J/\psi }(y)$ is defined as $R_{J/\psi }=\left( d\sigma _{J/\psi }/dy\right) /\left( d\sigma _{J/\psi }/dy\right) _{y=0}$. The dashed curve corresponds to Eq. (35) with BFKL-style parameterization 37 for gluon densities, the solid line takes into account $\sim (1-x)^{5}$-endpoint factors as described in the text. The data are taken from Ref. [111]

Fig. 6

Multiplicities in the $J/\psi$ production, accompanied by two parton showers

Fig. 7

Left plot: comparison of the multiplicity distribution with the experiment [22]. Solid line: result of evaluations with (9) using CGC parameterization for the dipole amplitude and saturation scale adjusted according to (38). The upper band marked “2-showers” stands for the estimates with approximate expression (39) and values of ${\bar{\gamma }}$ varied in the range ${\bar{\gamma }}\in \left( 0.67,\,0.76\right)$, as implemented in phenomenological parameterizations. Similarly, the lower color band marked with label “1-shower” stands for multiplicity distribution evaluated in single-shower mechanism shown in the Fig. 1b. Right plot: large-multiplicity extension of the solid curve from the left plot (result of evaluations with (9) using CGC parameterization)

4.3 Rapidity distribution

For numerical estimates in the previous sections we used the leading log approximation (LLA) for the BFKL Pomeron Green function, assuming additionally that mass $m_{c}$ is large, so that we could use a small-r approximation. The shape of the rapidity distribution in this approximation has a very simple form, which follows directly from Eq. (18):

$$\begin{aligned} \frac{d\sigma _{J/\psi }\left( y\right) /dy}{d\sigma _{J/\psi }\left( y\right) /dy |_{y=0}}&=\underbrace{\Bigg (\frac{Q_{s}^{2}\left( y^{*}-y\right) \left( Q_{s}^{2}\left( y^{*}+y\right) \right) ^{2}}{Q_{s}^{2} \left( y^{*}\right) \left( Q_{s}^{2}\left( y^{*}\right) \right) ^{2}} \Bigg )^{{\bar{\gamma }}}}_{\mathrm{Fig.~6{\text {-}}a}} \nonumber \\&\qquad +\,\, \underbrace{\Bigg (\frac{Q_{s}^{2}\left( y^{*}+y\right) \left( Q_{s}^{2} \left( y^{*}-y\right) \right) ^{2}}{Q_{s}^{2}\left( y^{*}\right) \left( Q_{s}^{2}\left( y^{*}\right) \right) ^{2}}\Bigg )^{{\bar{\gamma }}}}_{\mathrm{Fig.~6{\text {-}}b}} \nonumber \\&\quad =\,\,\cosh \left( \lambda {\bar{\gamma }}y\right) , \end{aligned}$$

(35)

$$\begin{aligned} y^{*}&=\,\,-\,\ln \left( \sqrt{\frac{M_{{J/\psi }}^{2}+q_{T}^{2}}{s}} \right) , \end{aligned}$$

(36)

since all dependence on rapidity is concentrated in the energy dependence of the saturation scale (27) which contributes to the cross-section (18) multiplicatively, and the gluon density in prefactor. The latter in the small-x kinematics is expected to have a simple power-like behaviour

$$\begin{aligned} x_{g}G\left( x_{g},\,M_{J/\psi }^{2}\right) \,\propto \,\left( Q_{s}^{2} \left( x_{g}\right) /M_{J/\psi }^{2}\right) ^{{\bar{\gamma }}}. \end{aligned}$$

(37)

However, such simple parameterization is valid only at central rapidities (near $y=0$), and as could be seen from the Fig. 5, outside this region ($|y|\gtrsim 1$) mismatches the experimental cross-section even on the qualitative level. This happens because at very forward or very backward kinematics we should add in (35) additional factor

$$\begin{aligned} \sim \left( 1-x\right) ^{5},\qquad x\,=\,e^{-y^{*}\pm y} \end{aligned}$$

per each gluon/pomeron in order to have correct endpoint behaviour of the gluon densities in the $x\rightarrow 1$ limit [112]. As we can see from the Fig. 5, the model gives a reasonable description of the rapidity dependence, which might be interpreted as confirmation of the applicability of the small-r approximation.

4.4 Multiplicity dependence

The $J/\psi$ production accompanied by two parton showers occurs in the events with larger multiplicity than the average multiplicity ${\bar{n}}$ in the inclusive hadron production  [22, 26]. The mechanism suggested in this paper provides a natural explanation of this enhancement. The cross-section includes contributions of additional parton shower as shown in Fig. 6a, b, which enhances the observed multiplicity. Technically, the dependence on multiplicity n of the produced particles affects the cross-section through the increase of the number of the particles in a parton shower and change of the value of the saturation scale, which is proportional to the density of produced gluons (see [39, 113,114,115] for more details). Assuming that for hadron-hadron collisions the area of interaction does not depend on multiplicity, the saturation scale is linearly proportional to the number of particles in the shower [116],

$$\begin{aligned} Q_{s}^{2}\left( y,\,n\right) \,\,=Q^{2}\left( y,\,{\bar{n}}\right) \frac{n}{{\bar{n}}}, \end{aligned}$$

(38)

where ${\bar{n}}$ is the average multiplicity at $y^{*}=0$ (${\bar{n}}\approx 6.5$ at $W=13\,\mathrm{TeV}$ [117]). As we discussed earlier, the product of dipole size on saturation scale $\left\langle r^{2}\right\rangle Q^{2}\left( y,\,{\bar{n}}\right)$ is close to one, for this reason the multiplicity events with $n/{\bar{n}}\gg 1$ probe a deep saturation regime, where approximation (18) is not valid, and we should use (9) with phenomenological parameterization of the dipole amplitude N.

In the Fig. 7 we plot the self-normalized multiplicity distribution evaluated with (9), using CGC parameterization for the dipole amplitude and saturation scale adjusted according to (38). We can see that agreement with experimental data from ALICE [22] is reasonable. At sufficiently small multiplicities, $dN_{J/\psi }/dy$ is increasing as a function of $dN_{\mathrm{ch}}/d\eta$, however, as can be seen from the right plot, at larger multiplicities in deep saturation regime it starts decreasing. This behaviour might be understood from the structure of the last line in (9): the dipole amplitude N saturates (approaches asymptotically a constant) [118], for this reason the difference $\left[ N\left( y;\,\frac{\vec {r}+\vec {r}'}{2},\,0\right) \,-\,N\left( y;\,\frac{\vec {r}-\vec {r}'}{2},\,0\right) \right] ^{2}$ gets suppressed. For the sake of completeness in the left panel of the Fig. 7 we also plotted the ratio evaluated with the simplified parameterization (15). Taking into account that contributions of left and right diagrams in the Fig. 6 contribute with relative weights $\sim \left( Q_{s}^{2}\left( y,n\right) \right) ^{2{\bar{\gamma }}}$ and  $\sim \left( Q_{s}^{2}\left( y,n\right) \right) ^{{\bar{\gamma }}}$ respectively, we may obtain for the self-normalized multiplicity dependence of contribution in Fig. 6 a simple expression

$$\begin{aligned} \frac{\frac{d\sigma _{J/\Psi }}{dy}\Big |_{\small \mathrm{fixed\,n}}\,\,\,\,\,}{\langle \frac{d\sigma _{J/\Psi }}{dy}\rangle \Big |_{\small \mathrm{sum\,over\,n}}}\,\,=\,\,\frac{1}{1+\kappa }\Bigg (\kappa \left( \frac{n}{{\bar{n}}} \right) ^{{\bar{\gamma }}}+\,\,\left( \frac{n}{{\bar{n}}}\right) ^{2\,{\bar{\gamma }}} \Bigg ) \end{aligned}$$

(39)

where the coefficient $\kappa =\left( Q_{s}^{2}\left( Y-y\right) /Q_{s}^{2}\left( y\right) \right) ^{{\bar{\gamma }}}\approx \,\,e^{{\bar{\gamma }}\,\lambda \left( Y-2y\right) }$ reflects the relative suppression of the contribution of the right diagram in the Fig. 6 with respect to the left diagram for different rapidities (at central rapidities used for comparison with data $\kappa \approx 1$). While the LO CGC/saturation predicts a value ${\bar{\gamma }}\approx 0.63$ , the phenomenological fits [106, 108] favor slightly higher values of ${\bar{\gamma }}$, for this reason we varied this parameter in the range ${\bar{\gamma }}\in \left( 0.67,\,0.76\right) .$ We also plotted the estimates of single-shower mechanism shown in the right part of the Fig. 1. Within model uncertainty, we can see that the experimental data support the main hypothesis of the paper that the $J/\psi$ production accompanied by the production of two parton showers gives a significant contribution.

5 Conclusions

In this paper we analyzed in the CGC/saturation framework the $J/\psi$ hadroproduction, accompanied by production of two parton showers. We demonstrated that this mechanism gives a large contribution to the total cross section of $J/\psi$ production, as well as to the transverse momenta and multiplicity distribution of produced $J/\psi$. The experimental data [22] on multiplicity distributions of produced $J/\psi$ seem to favor this hypothesis (compared to conventional mechanisms estimated in the CGC/saturation approach). This mechanism has no suppression of the order of ${\bar{\alpha }}_{S}$ at high energies compared to one parton shower contribution. We show that it alone can describe the shape of the $p_{T}$- and rapidity dependence of the cross section. As we commented in detail in Sect. 5, our results are approximately twice larger than similar evaluation of Ref. [38] and for this reason give a significant contribution to the experimental data. However, inherent uncertainties of the CGC/saturation approach preclude more precise estimates of its fraction. Since the main contribution to the cross section of this process stems from the vicinity of the saturation scale, the behaviour of the scattering amplitude in this region is largely under theoretical control, and thus has minor dependence on phenomenological parameterizations of the dipole amplitude.

We believe that our studies will bring attention to the contribution of multiparton densities in production of $J/\psi$.

Appendices

Appendix A: Evaluation of the factor $I\left( {\varvec{p}}_{1,T},{\varvec{p}}_{2,T}\right)$

In this section we would like to comment briefly the evaluation of the function $I\left( {\varvec{k}}_{T},{\varvec{q}}_{T}\right)$ in (3) in the light cone perturbative QCD [39] (Fig. 8).

Fig. 8

The diagram for $I\left( {\varvec{p}}_{1,T},{\varvec{p}}_{2,T}\right)$

We choose the polarization vectors of gluons $\epsilon _{\mu }^{\lambda }(p)$ in the light-cone gauge as

$$\begin{aligned}&\epsilon _{\mu }^{\alpha }(p)\,\,=\,\,\Bigg (0,\,\frac{2\, \varvec{\epsilon }_{\perp }^{\alpha }\cdot {\varvec{p}}_{T}}{\eta \cdot p},\,\varvec{\epsilon }_{\perp }^{\alpha }\Bigg );~~~~~\eta \,=\,(0,1,0,0)~~~~~~\text{ and } \nonumber \\&\varvec{\epsilon }_{\perp }^{\pm } \,\,=\,\,\frac{1}{\sqrt{2}}(\pm 1,i) \end{aligned}$$

(A1)

so according to the general rules of light cone perturbation theory (LCPT) [39, 86] the wave function of the ${\bar{Q}}Q$ pair after interaction with a pair of gluons with momenta ($y_{1,2},\,{\varvec{p}}_{1,2;\,T}$) is given by

$$\begin{aligned}&\Psi ^{(1,1)}\left( {\varvec{q}}_{T},z;{\varvec{p}}_{1,T},y_{1}; {\varvec{p}}_{2,T},y_{2}\right) \,\nonumber \\&\quad =\,g^{2}\lambda ^{a}\lambda ^{b}\frac{{\varvec{p}}_{1,T}\cdot \varvec{\epsilon }_{1}^{\alpha }}{p_{1,T}^{2}} \frac{{\varvec{p}}_{2,T}\cdot \varvec{\epsilon }_{2}^{\alpha }}{p_{2,T}^{2}} \nonumber \\&\qquad \times \Bigg (\Psi _{g}\left( {\varvec{l}}_{T},z\right) - \Psi _{g}\left( {\varvec{l}}_{T}+{\varvec{p}}_{1,T},z\right) \nonumber \\&\qquad \quad -\, \Psi _{g}\left( {\varvec{l}}_{T}+{\varvec{p}}_{2,T},z\right) \nonumber \\&\qquad \quad +\,\Psi _{g}\left( {\varvec{l}}_{T}+{\varvec{p}}_{1,T}+ {\varvec{p}}_{2,T},z\right) \Bigg ) \end{aligned}$$

(A2)

where $\lambda ^{a}$ is the Gell–Mann matrix, $\varvec{\epsilon }^{\alpha }$ is the polarization vector of the gluon with the helicity $\alpha$, and $\Psi _{g}\left( {\varvec{l}}_{T},\,z\right)$ is the wave function of ${\bar{Q}}Q$ pair formed after gluon splitting into quark–antiquark pair with transverse momentum ${\varvec{l}}_{T}$ and light-cone fraction z.

In the coordinate space the convolution of (A2) with the wave function of $J/\psi$ yields

$$\begin{aligned} I\left( {\varvec{p}}_{1,T},{\varvec{p}}_{2,T}\right)= & {} \int _{0}^{1}dz\,\int d^{2}r\left\langle \Psi _{g}\left( r,\,z\right) \,\Psi _{J/\Psi }\left( r,z\right) \right\rangle \nonumber \\&\times e^{-\frac{1}{2}{\varvec{q}}_{T}\cdot {\varvec{r}}} \Bigg (1\,\,-\,\,e^{i{\varvec{p}}_{1,T}\cdot {\varvec{r}}}\Bigg ) \Bigg (1\,\,-\,\,e^{i{\varvec{p}}_{2,T}\cdot {\varvec{r}}}\Bigg )\nonumber \\ \end{aligned}$$

(A3)

which agrees with (3) if we change notations of momenta to ${\varvec{p}}_{1,2\,T}=\frac{{\varvec{q}}_{T}}{2}\pm {\varvec{k}}_{T}$. In view of the heavy mass of the charm quark, in what follows we will use leading order perturbative results for the gluon wave functions $\Psi _{g}$ , as well as phenomenological parameterization of the $J/\psi$ wave function available from the literature [97], so the convolution of the two objects explicitly takes the form

$$\begin{aligned}&\left\langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\Psi }\left( r,z\right) \right\rangle _{T} \nonumber \\&\quad = \frac{g}{\pi \sqrt{2\,N_{c}}}\frac{1}{z(1-z)} \nonumber \\&\qquad \times \left( m_{c}^{2}\,K_{0} \left( \epsilon \,r\right) \,\phi _{T}\left( r,z\right) \right. \nonumber \\&\qquad \left. -\,\, \left( z^{2}+\left( 1-z\right) ^{2}\right) \,\epsilon \,K_{1} \left( \epsilon \,r\right) \partial _{r}\phi _{T}\left( r,z\right) \,\right) ; \end{aligned}$$

(A4)

$$\begin{aligned}&\left\langle \Psi _{g}\left( r,z\right) \,\Psi _{J/\Psi }\left( r,z\right) \right\rangle _{L} \nonumber \\&\quad =\, \frac{g}{\pi \sqrt{2\,N_{c}}}2p_{T}z(1-z)\,K_{0}\left( \epsilon \,r\right) \nonumber \\&\qquad \times \left( m_{J/\Psi }\phi _{L}(r,z)\,\,+\,\,\frac{m_{c}^{2}-\nabla _{r}^{2}}{m_{J/\Psi }\,z\,(1-z)}\phi _{L}(r,z)\right) \,; \end{aligned}$$

(A5)

$$\begin{aligned}&\phi _{T,L}(r,z) = \,\,N_{T,L}\,z(1-z) \nonumber \\&\qquad \times \exp \Bigg (-\frac{m_{c}^{2}\,\mathcal{R}^{2}}{8\,z\,(1-z)}\,-\,\frac{2\,z\,(1-z)\,r^{2}}{\mathcal{R}^{2}}\,\,+\,\,\frac{m_{c}^{2}\,\mathcal{R}^{2}}{2}\Bigg );\nonumber \\&\epsilon ^{2} = \,p_{T}^{2}\,z\,(1-z)\,\,+\,\,m_{c}^{2} \end{aligned}$$

(A6)

Appendix B: Evolution equation for the double gluon density

In Ref. [119] it is proven that the evolution equations for all partonic densities $\rho ^{(n)}\left( \{\vec {r}_{i},\vec {b}_{i}\}\right)$ are the linear BFKL evolution equations. The non-linear corrections are essential for the scattering amplitude (see, for example, the Balitsky–Kovchegov equation for dipole scattering amplitude [49,50,51] with nuclei) but they do not give a contribution to the evolution equation for multi-gluon densities. Referring our reader to Ref. [119] for the proof and details, we present here the resulting evolution equation for $r_{1}^{2}\,r_{2}^{2}\,\int d^{2}b\,\rho _{A}^{(2)} \left( x,\vec {r};x,\vec {r}';\vec {b}_{T}\right) \,=\,{\tilde{\rho }}^{(2)}\left( Y-Y_{0},\vec {r}_{1},\vec {r}_{2}\right)$:

$$\begin{aligned}&\frac{\partial \,{\tilde{\rho }}^{(2)}(Y-Y_{0};\vec {r}_{1},\vec {r}_{2})}{{\bar{\alpha }}_{S}\,\partial \,Y} =\,\sum _{i=1}^{2}\int \frac{d^{2}r'}{2\pi }\frac{1}{\left( \vec {r}_{i}- \vec {r}'\right) ^{2}} \nonumber \\&\quad \times \Bigg \{2{\tilde{\rho }}^{(2)}(Y-Y_{0};\vec {r}', \vec {r}_{i+1})\,-\,\frac{r_{1}^{2}}{r'^{2}}{\tilde{\rho }}^{(2)}(Y-Y_{0}; \vec {r}_{1},\vec {r}_{2})\Bigg \} \nonumber \\&\quad +\,\,{\tilde{\rho }}^{(1)}\left( Y-Y_{0}, \vec {r}_{1}+\vec {r}_{2}\right) \end{aligned}$$

(B1)

where $\left( \vec {r}_{1}+\vec {r}_{2}\right) ^{2}\int d^{2}b\,\rho ^{(1)}\left( Y-Y_{0},\vec {r}_{1}+ \vec {r}_{2},\,\vec {b}\right) \,\, =\,\,{\tilde{\rho }}^{(1)} \left( Y-Y_{0},\vec {r}_{1}+\vec {r}_{2}\right)$. The two terms in Eq. (B1) have clear physical meaning: the first one is the evolution of two parton showers, while the second describes the production of two gluon in one parton shower (see Fig. 9).

Fig. 9

Graphical illustration of the solution (B2). The diagram a with the exchange of two BFKL Pomerons (denoted by wavy lines) corresponds to the first term containing ${\tilde{\rho }}_{\mathrm{in}}^{(2)}\left( \gamma _{1},\gamma _{2}\right)$; the diagram b which includes the triple Pomeron vertex $\Gamma _{3{\mathbb {P}}}$ corresponds to the second term containing ${\tilde{\rho }}_{\mathrm{in}}^{(1)}\left( \gamma _{1}+\gamma _{2}\right)$. Helicoidal lines denote gluons

The solution takes the following form (see Ref. [37] and references therein):

$$\begin{aligned}&\rho ^{(2)}\left( Y,r_{1},Y,r_{2}\right) \nonumber \\&\quad =\,\, \int _{\epsilon -i\infty }^{\epsilon +i\infty }\frac{d\gamma _{1}}{2\pi i}\int _{\epsilon -i\infty }^{\epsilon +i\infty }\frac{d\gamma _{2}}{2\pi i}\,e^{\gamma _{1}\xi _{1}\,+\,\gamma _{2}\xi _{2}} \nonumber \\&\qquad \Bigg \{\underbrace{{\tilde{\rho }}_{\mathrm{in}}^{(2)}\left( \gamma _{1},\gamma _{2}\right) e^{{\bar{\alpha }}_{S} \left( \chi \left( \gamma _{1}\right) \,+\,\chi \left( \gamma _{2}\right) \right) \,Y}}_{Fig.~9{\text {-}}a} \nonumber \\&\qquad +\,\,\underbrace{h\left( \gamma _{1},\gamma _{2}\right) \, {\tilde{\rho }}_{\mathrm{in}}^{(1)}\left( \gamma _{1}+\gamma _{2}\right) \,\int _{0}^{Y}dy'e^{{\bar{\alpha }}_{S}\left( \chi \left( \gamma _{1} \right) +\chi \left( \gamma _{2}\right) \right) \,\left( Y-y'\right) \,\, +\,\,{\bar{\alpha }}_{S}\chi \left( \gamma _{1}+\gamma _{2}\right) \,y'}}_{Fig.~9{\text {-}}b}\Bigg \}\nonumber \\ \end{aligned}$$

(B2)

where [39,40,41,42,43,44] $\xi _{1}\,=\,\ln \left( r_{1}^{2}\right)$, $\xi _{2}\,=\,\ln \left( r_{2}^{2}\right)$ and

$$\begin{aligned} \chi \left( \gamma \right)= & {} 2\psi \left( 1\right) \,-\, \psi \left( \gamma \right) \,-\,\psi \left( 1-\gamma \right) \, ~~~~~~~~~\text{ where } \nonumber \\ \psi (z)= & {} \frac{d\,\ln \Gamma (z)}{dz}. \end{aligned}$$

(B3)

The functions ${\tilde{\rho }}_{\mathrm{in}}^{(2)}\left( \gamma _{1},\gamma _{2}\right)$ and ${\tilde{\rho }}_{\mathrm{in}}^{(1)}\left( \gamma _{1}+\gamma _{2}\right)$ are determined by the initial condition for the two and one parton shower productions (see Fig. 9). The explicit form of the function $h\left( \gamma _{1},\,\gamma _{2}\right)$ can be found in Ref. [37]. Different contributions in the solution (B2) might be visualized as shown in the Fig. 9.