Study of the quasi-two-body decays $B^{0}_{s} \rightarrow \psi (3770) (\psi (3686))\pi ^+\pi ^-$ with perturbative QCD approach

Abstract

In this note, we study the contributions from the S-wave resonances, $f_{0}(980)$ and $f_{0}(1500)$, to the $B^{0}_{s}\rightarrow \psi (3770)\pi ^ {+}\pi ^{-}$ decay by introducing the S-wave $\pi \pi$ distribution amplitudes within the framework of perturbative QCD approach. Both the resonant and the non-resonant contributions are contained in the scalar form factor in the S-wave distribution amplitude $\Phi ^S_{\pi \pi }$. Since the vector charmonium meson $\psi (3770)$ is a S–D wave mixed state, we calculate the branching ratios of S-wave and D-wave, respectively, and the results indicate that $f_{0}(980)$ is the main contribution of the considered decay, and the branching ratio of the $\psi (2S)$ mode is in good agreement with the experimental data. We also take the S–D mixed effect into the $B^{0}_{s}\rightarrow \psi (3686)\pi ^ {+}\pi ^{-}$ decay. Our calculations show that the branching ratio of $B^{0}_{s}\rightarrow \psi (3770)(\psi (3686))\pi ^ {+}\pi ^{-}$ can be at the order of $10^{-5}$, which can be tested by the running LHCb experiments.

1 Introduction

In the present decade, the B mesons’ three-body hadronic decays have drawn a lot of attention on both the experimental and the theoretical sides, since they can test the standard model (SM) and help us to have a better understanding of the scheme of QCD dynamics. The three-body decays of B mesons are more complicated than the two-body cases because they include both resonant and non-resonant contributions. We have two-gluon exchange in the decay amplitude within our framework of theoretical calculation, which will lead to a hard kernel that involves three bodies, and we may introduce possible final-state interactions [1,2,3,4]. So just as stated in Ref. [5], because of the interference between the resonance and non-resonance, it is difficult to make a direct calculation of the resonance and non-resonance contributions separately.

The Heavy Flavor Averaging Group [6] have collected lots of world averages of measurements of B-hadron properties from LHCb [7,8,9,10,11,12,13,14], Belle [15] and BaBar [16,17,18] and other collaborations, in which the LHCb Collaboration have measured sizable direct CP asymmetries in kinematic regions. Due to the progress of the experiments, three-body decays have been analyzed by different methods, which were based on symmetry principles and factorization theorems; however, the theoretical studies are still at an early stage. Many authors have studied the three-body decays with improved QCD factorization [19,20,21,22,23,24,25,26,27] and perturbative QCD (pQCD) factorization approaches [28,29,30,31,32,33,34,35,36,37,38,39]. The contribution studies within non-resonance have been performed by using a heavy meson chiral perturbative theory approach in Refs. [5, 27, 40] and in the references therein, and the resonance contributions were treated using the isobar model [41] within the Breit–Wigner formalism [42].

In the pQCD approach which is based on the $k _{T}$ factorization theorem, the three-body decay can be simplified into a two-body case by bringing in two-hadron distribution amplitudes [43, 44], which contain the information of both resonance and non-resonance. The dominant contributions come from the region where the pair of two light mesons move parallel with an invariant mass below $O (\bar{\Lambda }M_{B})$, where $\bar{\Lambda }=M_{B}-m_{b}$ is the mass difference of the B meson and b-quark. Therefore, one can express the typical pQCD factorization formula of the B meson’s three-body decay amplitude as [35, 36]

$$\begin{aligned} \mathcal{A}=\mathcal{H}\otimes \phi _{B} \otimes \phi _{h_{3}} \otimes \phi _{h_{1}h_{2}}, \end{aligned}$$

(1)

where the hard decay kernel $\mathcal{H}$ describes the contribution from the region with only a one gluon exchange diagram at leading order, which can be calculated in perturbation theory. The terms $\phi _{B}$, $\phi _{h_{1}h_{2}}$ and $\phi _{h_{3}}$, which can be extracted from experiment or calculated by several nonperturbative approaches, and can be regarded as nonperturbative input, are the distribution amplitude of the B meson, the $h_1h_2$ pair and $h_3$, respectively.

The $B^{0}_{s} \rightarrow \psi (2S)\pi ^{+}\pi ^{-}$ decay was first observed by the LHCb Collaboration [7]; the data was displayed based on the integrated luminosity of 1 $fb^{-1}$ in the pp collisions at a center-of-mass energy of $\sqrt{s}=7$ TeV. It is found that $f_{0}(980)$ is the main source of the decay rate by a method called the $sPlot$ technique. The $B^{0}_{s} \rightarrow \psi (3770)\pi ^{+}\pi ^{-}$ decay has not been observed yet, so it is desirable to make a theoretical prediction for the branching ratios of this decay mode, for testing the three-body decay’s mechanism and the mixing scheme of $\psi (3770)$ as well. In this work, we will calculate the branching ratio of the quasi-two-body decay mode $B^{0}_{s} \rightarrow \psi (3770) \pi ^+\pi ^-$. Since the vector charmonium meson $\psi (3770)$, the lowest-lying charmonium state just above the $D\bar{D}$ threshold, is mainly regarded as a S–D mixture, we will take the S-wave and D-wave contribution into account, respectively. Here, $\psi (2S)$ is the first radially excited charmonium meson, and the pure 1D state indicates the principal quantum number $n=1$ and the orbital quantum number $l=2$. The S–D mixing angle $\theta$ can be obtained from the ratio of the leptonic decay widths of $\psi (3686)$ and $\psi (3770)$ [45]. In Ref. [46], the authors make tentative calculations for different mixing solutions of the B meson exclusive decay $B \rightarrow \psi (3770)K$ with the QCD factorization, and they drew the conclusion that when taking account of higher-twist effects and adopting the S–D mixing angle $\theta =-(12\pm 2)^{\circ }$ (which the widely accepted value), the branching ratio of the decay $B \rightarrow \psi (3770)K$ can fit the experimental data well. Also, in Refs. [47,48,49], the authors provided two sets of mixing schemes within the nonrelativistic potential model: $\theta =-(12\pm 2)^{\circ }$ or $\theta =(27\pm 2)^{\circ }$. Here, the charmonium mesons $\psi (3686)$ and $\psi (3770)$ may in a good approximation be described as [47,48,49,50]

$$\begin{aligned} \begin{aligned} \psi (3686)=\cos \theta |c\bar{c}(1D)\rangle +\sin \theta |c\bar{c}(2S)\rangle ,\\ \psi (3770)=\cos \theta |c\bar{c}(1D)\rangle -\sin \theta |c\bar{c}(2S)\rangle . \end{aligned} \end{aligned}$$

(2)

The contents of this paper is as follows. After the introduction, we describe the theoretical framework and the wave function of the excited charmonium mesons $\psi (2S)$ and $\psi (1D)$ in Sect. 2. In Sect. 3, we list the decay amplitude of the considered decay modes. The numerical results and analysis as regards the results we have got are presented in Sect. 4. Finally we will finish this paper with a brief summary.

2 The theoretical framework and the wave function

For the quasi-two-body $B^{0}_{s} \rightarrow \psi f_{0}(\rightarrow \pi ^{+}\pi ^{-})$ decays, the relevant weak effective Hamiltonian can be written as [51]

$$\begin{aligned} \mathcal{H}_\mathrm{eff}= & {} \frac{G_\mathrm{F}}{\sqrt{2}}\bigg \{V^*_\mathrm{cb}V_\mathrm{cs}[C_{1}(\mu )O_{1}(\mu )+C_{2}(\mu )O_{2}(\mu )] \nonumber \\&\quad -V^*_\mathrm{tb}V_\mathrm{ts}[\sum ^{10}_{i=3}C_{i}(\mu )O_{i}(\mu )]\bigg \}+\mathrm{H.c.}, \end{aligned}$$

(3)

where $V^*_\mathrm{cb}V_\mathrm{cs}$ and $V^{*}_\mathrm{tb}V_\mathrm{ts}$ are Cabibbo–Kobayashi–Maskawa (CKM) factors, $O_{i}(\mu )$ is a local four-quark operator and $C_{i}(\mu )$ is the corresponding Wilson coefficient.

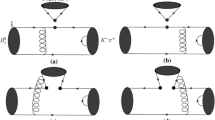
It is convenient for us to choose the light-cone coordinates for simplicity. In these coordinates, we choose the $B^0_{s}$ meson at rest, and let the $\pi \pi$ meson pair and $\psi (2S,1D)$ meson move along with the direction of $n=(1,0,0_{\top })$ and $v=(0,1,0_{\top })$, respectively, and the Feynman diagrams are described in Fig. 1. So the momenta of the $B^0_{s}$ ($p_{B}$), $\pi \pi$ (p), and $\psi (2S,1D)$ ($p_{3}$) are written as

$$\begin{aligned} \begin{aligned} p_{B}&=\frac{M_{B^{0}_{s}}}{\sqrt{2}}(1,1,0_{\top }), \\ p&=\frac{M_{B^{0}_{s}}}{\sqrt{2}}(1-r^2,\eta ,0_{\top }), \\ p_{3}&=\frac{M_{B^{0}_{s}}}{\sqrt{2}}(r^2,1-\eta ,0_{\top }). \end{aligned} \end{aligned}$$

(4)

Fig. 1

The lowest order Feynman diagrams for the $B^{0}_{s} \rightarrow \psi f_{0}(\rightarrow \pi ^{+}\pi ^{-})$ decays

Meanwhile, the corresponding light quark’s momentum in each meson reads as follows:

$$\begin{aligned} \begin{aligned} k_{B}&=\left( 0,\frac{M_{B^{0}_{s}}}{\sqrt{2}}{x _{B}},k_{B\top }\right) ,\\ k&=\left( \frac{M_{B^{0}_{s}}}{\sqrt{2}}{} z (1-r^2),0,k_{\top }\right) ,\\ k_{3}&=\left( \frac{M_{B^{0}_{s}}}{\sqrt{2}}r^2x _{3},\frac{M_{B^{0}_{s}}}{\sqrt{2}}(1-\eta )x _{3},k_{3\top }\right) , \end{aligned} \end{aligned}$$

(5)

where $M_{B^{0}_{s}}$ is the mass of $B^{0}_{s}$, and $r=\frac{M_\psi }{M_{B^{0}_{s}}}$ is the corresponding mass ratio. $M_{\psi }$ denotes the $\psi (2S,1D)$ mesons mass. We have the variable $\eta =\omega ^2/({M_{B^{0}_{s}}^2}-{M_\psi }^2)$, where the pion-pair invariant mass $\omega ^2$ and its momentum p satisfy the relation $\omega ^2=p^2$ and $p=p_{1}+p_{2}$. The quantities $x _{1}$, $z$, and $x _{3}$ indicate the momentum fractions of the spectator quark inside the meson; they are in the range of $0\sim 1$. By introducing the kinematic variables, $\zeta$, of the pion pair, we define $\zeta =p^+_{1}/p^+$ as the $\pi ^+$ meson momentum fraction; the other component’s kinematic variables of the pion pair can be expressed as

$$\begin{aligned} p^-_{1}= & {} \frac{M_{B^{0}_{s}}}{\sqrt{2}}(1-\zeta )\eta , \nonumber \\ p^+_{2}= & {} \frac{M_{B^{0}_{s}}}{\sqrt{2}}(1-\zeta )(1-r^2),\\ p^-_{2}= & {} \frac{M_{B^{0}_{s}}}{\sqrt{2}}\zeta \eta .\nonumber \end{aligned}$$

(6)

In our calculations, the hadron $B^{0}_{s}$ is usually treated as a heavy–light system, and the wave function of which can be found in Refs. [52,53,54]. We have

(7)

where the distribution amplitude (DA) ${\phi _{B_{s}}({x _{B},b _{B}})}$ of the $B^{0}_{s}$ meson is written in the form mostly used, which is

$$\begin{aligned}&\phi _{B_{s}}(x _{B},b _{B})=N _{B}{{x _{B}}^2}(1-{x _{B}})^2 \nonumber \\&\quad \times \exp \left[ -\frac{M^2_{B^{0}_{s}}{{x _{B}}^2}}{2\omega ^2_{B_{s}}}-\frac{1}{2}(\omega _{B_{s}}{b _{B}})^2\right] , \end{aligned}$$

(8)

the normalization factor $N _{B}$ can be calculated by the normalization relation $\int ^{1}_{0}{\mathrm{d}x}\phi _{B_{s}}(x _{B},b _{B}=0)=f _{B^{0}_{s}}/({2}{\sqrt{{2}{N }_\mathrm{c}}})$ with $N _\mathrm{c}=3$ being the number of colors. Here, we choose the shape parameter $\omega _{B_{s}}=0.50\pm 0.05$ GeV [55].

The vector charmonium meson $\psi (3770)$, as mentioned above, is commonly regarded as a S-wave and D-wave mixing state. We adopt the wave function form of this vector charmonium meson on the basis of a harmonic-oscillator potential, which has been applied to the charmonium state successfully, such as $J/\psi$, $\psi (2S)$, $\psi (3S)$ and so on [50, 56,57,58]. The theoretical results agree well with the measured experimental data, which indicates the reasonableness of adopting this form of the function. For the wave function of the pure 2S state, $\psi (2S)$, and the pure 1D state, $\psi (1D)$, the longitudinal polarized component is defined as [57, 58]

(9)

where $p_{3}$ is the momentum of the charmonium mesons $\psi (2S)$ and $\psi (1D)$, with the longitudinal polarization vector $\epsilon _{L}=\frac{M_{B^0_{s}}}{\sqrt{2} M_{\psi }}(-{r^2},(1-\eta ),0_{\top })$. $M_{\psi }$ is the corresponding mass. Here the $\psi ^{L }$ and $\psi ^{t }$ correspond to twist-2 and twist-3 distribution amplitudes (DAs). The explicit forms are [50, 57]

$$\begin{aligned}&\psi ^{L }(x _{3},b _{3})= \frac{f _{(2S,1D)}}{2\sqrt{2N _\mathrm{c}}}N^{L }{} x _{3}\overline{x }_{3} \mathcal{I}(x _{3})e^{-x _{3}\overline{x }_{3}\frac{m _c}{\omega } \left[ \omega ^2b _{3}^2+\left( \frac{x _{3}-\overline{x }_{3}}{2x _{3}\overline{x }_{3}}\right) ^2\right] }, \nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned}&\psi ^{t }(x _{3},b _{3})= \frac{f _{(2S,1D)}}{2\sqrt{2N_\mathrm{c}}}N^{t } ({x _{3}-\overline{x }_{3}})^2\mathcal{I}(x _{3})e^{-x _{3}\overline{x }_{3}\frac{m _c}{\omega } \left[ \omega ^2b _{3}^2+\left( \frac{x _{3}-\overline{x }_{3}}{2x _{3}\overline{x }_{3}}\right) ^2\right] },\nonumber \\ \end{aligned}$$

(11)

with $\mathcal{I}(x _{3})=1-4{m _c}\omega {x _{3}\overline{x }_{3}}{} b _{3}^2+\frac{m _c(1-2x _{3})^2}{\omega x _{3}\overline{x }_{3}}$ for $\psi (2S)$ and $\mathcal{I}(x _{3})=(\frac{1}{x _{3}\overline{x }_{3}}-m _\mathrm{c}\omega b _{3}^2)(6x _{3}^4-12x _{3}^3+7 x _{3}^2-x _{3})-\frac{m _c(1-2x _{3})^2}{4\omega x _{3}\overline{x }_{3}}$ for $\psi (1D)$. For the shape parameter $\omega _{1D}$ in the DAs of the $\psi (1D)$, we choose $\omega _{1D}=0.5\pm 0.05$ GeV, for the reason we have discussed in Ref. [50], and $\omega _{2S}=0.2\pm 0.1$ GeV [57]. $N^{i }(i=L,t)$ is the normalization constant, which satisfies the normalization conditions:

$$\begin{aligned} \int ^1_0 \psi ^{i }(x _{3},b _{3}=0){\text {d}}{x _{3}}= \frac{f _{(2S,1D)}}{2\sqrt{2N _\mathrm{c}}}, \end{aligned}$$

(12)

and the decay constants of the radially excited state $\psi (2S)$ and the angular excitation state $\psi (1D)$ are given in Table 1. Both the wave functions of Eq. (10) and of Eq. (11) are symmetric under $x \leftrightarrow \overline{x }$.

In the light of Refs. [59, 60], we adopt the distribution amplitudes for the S-wave pion pair as

$$\begin{aligned} \Phi ^{S}_{\pi \pi }= & {} \frac{1}{\sqrt{2 N _\mathrm{c}}}[\not {p}\phi ^{I=0}_{v\nu =-}(z ,\zeta ,\omega ^2)+\omega \phi ^{I=0}_{s}(z ,\zeta ,\omega ^2)\nonumber \\&\quad +\omega (\not {n}\not {v}-1)\phi ^{I=0}_{t\nu =+}(z ,\zeta ,\omega ^2)]. \end{aligned}$$

(13)

For simplicity, we put $\phi ^{I=0}_{v\nu =-}(z ,\zeta ,\omega ^2)$, $\phi ^{I=0}_{s}(z ,\zeta ,\omega ^2)$ and $\phi ^{I=0}_{t\nu =+}(z ,\zeta ,\omega ^2)$, abbreviated to $\phi _{0}$, $\phi _{s}$, and $\phi _{\sigma }$, respectively. The relevant DAs and time-like scalar form factor can be found in Refs. [34, 61, 62].

The differential branching ratios for the $B^{0}_{s} \rightarrow \psi (2S,1D) \pi ^+\pi ^-$ decay in the $B^{0}_{s}$ meson rest frame can be written as [63]

$$\begin{aligned} \frac{\mathrm{d}\mathcal {B}}{\mathrm{d}\omega }=\frac{\tau _{B^0_{s}}\omega \mid {\overrightarrow{p_{1}}} \mid \mid {\overrightarrow{p_{3}}} \mid }{32(\pi M_{B^0_{s}})^3} \mid \mathcal{A} \mid ^2, \end{aligned}$$

(14)

with $p_{1}=\frac{1}{2} \sqrt{\omega ^2-4 m^2_{\pi ^{\pm }}}$ and $p_{3}=\frac{1}{2\omega } \sqrt{[M^2_{B^0_{s}}-(\omega +M_{\psi })^2][M^2_{B^0_{s}}-(\omega -M_{\psi })^2]}$ in the pion-pair center-of-mass system and with the $B^0_{s}$ meson lifetime $\tau _{B^0_{s}}$.

3 The decay amplitudes

In the pQCD factorization approach, the $B^{0}_{s} \rightarrow \psi (2S)\pi ^+\pi ^-$ decay amplitude $\mathcal {A}$ can be expressed in form of

$$\begin{aligned} \mathcal{{A}}= & {} V^*_\mathrm{cb}V_\mathrm{cs}(F ^{(V-A)(V-A)}\nonumber \\&+M ^{(V-A)(V-A)})-V^*_\mathrm{tb}V_\mathrm{ts}(F ^{'(V-A)(V-A)}\nonumber \\&+F ^{(V-A)(V+A)}+M ^{'(V-A)(V-A)}+M ^{(S-P)(S+P)}), \nonumber \\ \end{aligned}$$

(15)

where the explicit forms of $F ^{(V-A)(V-A)}$, $F ^{'(V-A)(V-A)}$, $F ^{(V-A)(V+A)}$, and $M ^{(V-A)(V-A)}$, $M ^{'(V-A)(V-A)}$, $M ^{(S-P)(S+P)}$ are listed in the following formula, and $F$, $M$ denote the factorization and non-factorization contribution, respectively. $(V-A)(V-A)$ and $(V-A)(V+A)$ are the weak vertices of the operators, and $(S-P)(S+P)$ denotes the Fierz transformation of $(V-A)(V+A)$. We have

$$\begin{aligned} {F }^{(V-A)(V-A)}&=8\pi C _{F }f_{\psi }M^{4}_{B^0_{s}}\nonumber \\&\quad \times \int ^{1}_{0}\mathrm{d}{} x _{B}\mathrm{d}{} z \int ^\infty _{0}{} b _{B}{} b \mathrm{d}{} b _{B}\mathrm{d}{} b \phi _{B_{s}}(x _{B},b_{B})\nonumber \\&\quad \times \{[(\overline{\eta } (1+z (1-2r^2))-r^2) \phi _{0}\nonumber \\&\quad + \sqrt{\eta (1-r^2)}[((1-2z (1-r^2)) \overline{\eta }-r^2) \nonumber \\&\quad \times ( \phi _{s}+ \phi _{\sigma })+2r^2 \phi _{\sigma }]] \nonumber \\&\quad \times \alpha _{s}(t_{a})a _{1}(t_{a})h_{a}(x _{B}, z , b _{B}, b )\nonumber \\&\quad \times S_{t}(z )\exp [-S_{B^{0}_{s}}(t_{a})-S_{M}(t_{a})]\nonumber \\&\quad +[(r^2-1)[\overline{\eta }\eta +r^2(x _{B}-\eta )]\phi _{0}\nonumber \\&\quad +2\sqrt{\eta (1-r^2)}[\overline{\eta }-r^2(1-x _{B})]\phi _{s}] \nonumber \\&\quad \times \alpha _{s}(t_{b})a _{1}(t_{b})h_{b}(x _{B}, z , b _{B}, b )\nonumber \\&\quad \times S_{t}(|x _{B}-\eta |)\exp [-S_{B^{0}_{s}}(t_{b})-S_{M}(t_{b})]\}, \end{aligned}$$

(16)

$$\begin{aligned} {F }^{'(V-A)(V-A)}&={F }^{(V-A)(V-A)}|_{a _{1}\rightarrow a _{2}}, \end{aligned}$$

(17)

$$\begin{aligned} {F }^{(V-A)(V+A)}&={F }^{(V-A)(V-A)}|_{a _{1}\rightarrow a _{3}}, \end{aligned}$$

(18)

$$\begin{aligned} {M }^{(V-A)(V-A)}&=\frac{-32\pi C _{F }M^{4}_{B^{0}_{s}}}{\sqrt{2N _\mathrm{c}}}\nonumber \\&\quad \times \int ^{1}_{0}\mathrm{d}{} x _{B}\mathrm{d}{} z \mathrm{d}{} x _{3}\int ^\infty _{0}{} b _{B}{} b _{3}\mathrm{d}{} b _{B}\mathrm{d}{} b _{3}\phi _{B_{s}}(x _{B},b_{B})\nonumber \\&\quad \times \{[(\overline{\eta }-r^2)[((1-x _{3}-x _{B})(1-r^2)\nonumber \\&\quad +\eta (x _{3}(1-2r^2) \nonumber \\&\quad -(1-r^2)(1-z )+r^2))\psi ^{L}(x _{3}, b _{3})\nonumber \\&\quad +r r_\mathrm{c}\overline{\eta }\psi ^{t}(x _{3}, b _{3})]\phi _{0} \nonumber \\&\quad +\sqrt{\eta (1-r^2)}[\overline{\eta }(z (1-r^2)\nonumber \\&\quad +2r^2(1-x _{3})-r^2x _{B})\phi _{\sigma }\nonumber \\&\quad -(z \overline{\eta }(1-r^2)+r^2x _{B})\phi _{s}]\psi ^{L}(x _{3}, b _{3})]\nonumber \\&\quad \times \alpha _{s}(t_{c})C _{2}(t_{c})h_\mathrm{c}(x _{B}, z , x _{3}, b _{B}, b _{3})\nonumber \\&\quad \times \exp [-S_{B^{0}_{s}}(t_{c})-S_{M}(t_{c})-S_{\psi }(t_{c})]\nonumber \\&\quad +[(\overline{\eta }-r^2)[(x _{B}-z (1-r^2)\nonumber \\&\quad -x _{3}(\overline{\eta }+r^2))\psi ^{L}(x _{3}, b _{3})\nonumber \\&\quad +r r_\mathrm{c} \overline{\eta }\psi ^{t}(x _{3}, b _{3})]\phi _{0}\nonumber \\&\quad -\sqrt{\eta (1-r^2)}[((r^2x _{B}-\overline{\eta }(2r^2 x _{3}\nonumber \\&\quad +z (1-r^2)))\psi ^{L}(x _{3}, b _{3})+4r r_\mathrm{c}\overline{\eta }\psi ^{t}(x _{3}, b _{3}))\phi _{\sigma }\nonumber \\&\quad -(r^2x _{B}+z \overline{\eta }(1-r^2))\phi _{s}\psi ^{L}(x _{3}, b _{3})]]\nonumber \\&\quad \times \alpha _{s}(t_{d})C _{2}(t_{d})h_{d}(x _{B}, z , x _{3}, b _{B}, b _{3})\nonumber \\&\quad \times \exp [-S_{B^{0}_{s}}(t_{d})-S_{M}(t_{d})-S_{\psi }(t_{d})]\}, \end{aligned}$$

(19)

$$\begin{aligned} {M }^{'(V-A)(V-A)}=\,&{M }^{(V-A)(V-A)}|_{C _{2}\rightarrow a _{4}}, \end{aligned}$$

(20)

$$\begin{aligned} {M }^{(S-P)(S+P)}=\,&\frac{32\pi C _{F }M^{4}_{B^{0}_{s}}}{\sqrt{2N _\mathrm{c}}}\nonumber \\&\quad \times \int ^{1}_{0}\mathrm{d}{} x _{B}\mathrm{d}{} z \mathrm{d}{} x _{3}\nonumber \\&\quad \times \int ^\infty _{0}{} b _{B}{} b _{3}\mathrm{d}{} b _{B}\mathrm{d}{} b _{3}\phi _{B_{s}}(x _{B},b_{B})\nonumber \\&\quad \times \{[(\overline{\eta }-r^2)[((1-x _{3})(\overline{\eta }+r^2)\nonumber \\&\quad +z (1-r^2)-x _{B})\psi ^{L}(x _{3}, b _{3})\nonumber \\&\quad -r r_\mathrm{c}\overline{\eta }\psi ^{t}(x _{3}, b _{3})]\phi _{0} \nonumber \\&\quad +\sqrt{\eta (1-r^2)}[(\overline{\eta }{} z (r^2-1)\nonumber \\&\quad -r^2x _{B})\phi _{s}\psi ^{L}(x _{3}, b _{3}) \nonumber \\&\quad +[(\overline{\eta }(z (r^2-1)-2r^2(1-x _{3}))\nonumber \\&\quad +r^2x _{B})\psi ^{L}(x _{3}, b _{3})+4r r_\mathrm{c}\overline{\eta }\psi ^{t}(x _{3}, b _{3})]\phi _{\sigma }]] \nonumber \\&\quad \times \alpha _{s}(t_{c})a _{5}(t_{c})h_\mathrm{c}(x _{B}, z , x _{3}, b _{B}, b _{3})\nonumber \\&\quad \times \exp [-S_{B^{0}_{s}}(t_{c})-S_{M}(t_{c})-S_{\psi }(t_{c})] \nonumber \\&\quad +[(\overline{\eta }-r^2)[((1-r^2)(x _{B}-z \eta )\nonumber \\&\quad +x _{3}(r^2(\overline{\eta }-\eta )-\overline{\eta }))\psi ^{L}(x _{3}, b _{3})\nonumber \\&\quad -r r_{c} \overline{\eta }\psi ^{t}(x _{3}, b _{3})]\phi _{0} \nonumber \\&\quad +\sqrt{\eta (1-r^2)}[(z \overline{\eta }(1-r^2)+r^2x _{B})\phi _{s}\nonumber \\&\quad +(\overline{\eta }(z (r^2-1)-2r^2x _{3})+r^2x _{B})\phi _{\sigma }]\psi ^{L}(x _{3}, b _{3})] \nonumber \\&\quad \times \alpha _{s}(t_{d})a _{5}(t_{d})h_{d}(x _{B}, z , x _{3}, b _{B}, b _{3})\nonumber \\&\quad \times \exp [-S_{B^{0}_{s}}(t_{d})-S_{M}(t_{d})-S_{\psi }(t_{d})]\}, \end{aligned}$$

(21)

with $r_{c}=\frac{m_{c}}{M_{B^{0}_{s}}}$. $C_{F}=\frac{4}{3}$ is the group factor of the $SU(3)_{c}$ gauge group. The $S_{B^{0}_{s}}(t)$, $S_{M}(t)$, $S_{\psi }(t)$ used in the decay amplitudes, the hard functions $h_{i}(i=a, b, c, d)$, and the hard scales $t_{i}$ are collected in the appendix.

In our work, we also take vertex corrections into account in the factorization diagrams, and the Wilson coefficients are combined in the NDR scheme [64,65,66] as follows:

$$\begin{aligned}&a _{1}=C _{1}+\frac{C _{2}}{N_{c}}+\frac{\alpha _{s}}{9\pi }{} C _{2} \nonumber \\&\quad \qquad \times [-18-12\ln (\mu /m_{b})+f_{I}+g_{I}(1-r^2)],\nonumber \\&a _{2}=C _{3}+\frac{C _{4}}{N_{c}}+C _{9}+\frac{C _{10}}{N_{c}}+\frac{\alpha _{s}}{9\pi }\nonumber \\&\quad \qquad \times (C _{4}+C _{10}) \times [-18-12\ln (\mu /m_{b})+f_{I}+g_{I}(1-r^2)], \nonumber \\&a _{3}=C _{5}+\frac{C _{6}}{N_{c}}+C _{7}+\frac{C _{8}}{N_{c}}+\frac{\alpha _{s}}{9\pi }\nonumber \\&\quad \qquad \times (C _{6}+C _{8}) [6+12\ln (\mu /m_{b})-f_{I}-g_{I}(1-r^2)],\nonumber \\&a _{4}=C _{4}+C _{10}, \nonumber \\&a _{5}=C _{6}+C _{8}. \end{aligned}$$

(22)

The hard scattering functions $f_{I}$ and $g_{I}$ are given in Ref. [67], the renormalization scale $\mu$ is chosen at the order of $m_{b}$.

For the $B^{0}_{s} \rightarrow \psi (1D)\pi ^+\pi ^-$ decay, the amplitude is similar to the decay amplitude of $B^{0}_{s} \rightarrow \psi (2S)\pi ^+\pi ^-$, just replacing the DAs of $\psi (2S)$ with the corresponding DAs of $\psi (1D)$ in Eq. (15).

As for the decay amplitude of the $B^{0}_{s} \rightarrow \psi (3770) (\psi (3686))\pi ^+\pi ^-$ decay, we give the expression based on the idea of the S–D mixing scheme:

$$\begin{aligned}&\mathcal{A}(B^{0}_{s}\rightarrow \psi (3770)\pi ^{+}\pi ^{-})=\cos \theta \mathcal{A}(B_{s}\rightarrow \psi (1D)\pi ^+\pi ^-) \nonumber \\&\quad - \sin \theta \mathcal{A}(B_{s}\rightarrow \psi (2S)\pi ^+\pi ^-). \end{aligned}$$

(23)

$$\begin{aligned}&\mathcal{A}(B^{0}_{s}\rightarrow \psi (3686)\pi ^{+}\pi ^{-})=\cos \theta \mathcal{A}(B_{s}\rightarrow \psi (1D)\pi ^+\pi ^-) \nonumber \\&\quad +\sin \theta \mathcal{A}(B_{s}\rightarrow \psi (2S)\pi ^+\pi ^-). \end{aligned}$$

(24)

4 Numerical results and discussions

In our numerical calculation, the input parameters are listed in Table 1, where the masses of the involved mesons, the lifetime of meson and the Wolfenstein parameters are obtained from the 2018 PDG [63]. The decay constant of $\psi (2S)$ is calculated by the leptonic decay process $\psi (2S)\rightarrow \mathrm{e}^{+}\mathrm{e}^{-}$ [58] and the decay constant of $\psi (1D)$ was calculated in Ref. [68]. The masses of the b quark and c quark are running masses which are calculated under the modified minimal subtraction scheme at the renormalization scale $\mu$, which is equal to the quark mass.

Table 1 The input parameters of the $B^{0}_{s} \rightarrow \psi (2S,1D)\pi ^+\pi ^-$ decay

By using the differential branching ratio formula Eq. (14), first we make predictions of the branching ratios of the decay mode $B^{0}_{s} \rightarrow \psi (2S)\pi ^+\pi ^-$ for different intermediate states, including the $f_0(980)$ and $f_0(1500)$ resonances, and the numerical results are listed as follows:

$$\begin{aligned}&\mathcal{B}(B^{0}_{s} \rightarrow \psi (2S) f_{0}(980) \rightarrow \psi (2S)\pi ^+\pi ^-)\nonumber \\&\quad =[7.2^{+1.0+0.1+0.2}_{-0.7-0.0-0.0}]\times 10^{-5}, \end{aligned}$$

(25)

$$\begin{aligned}&\mathcal{B}(B^{0}_{s} \rightarrow \psi (2S) f_{0}(1500) \rightarrow \psi (2S)\pi ^+\pi ^-)\nonumber \\&\quad =[8.8^{+1.0+0.4+0.4}_{-1.5-0.0-0.1}]\times 10^{-7}, \end{aligned}$$

(26)

where the three main errors come from the shape parameter $\omega _{B_{s}}$ of the wave function of $B^{0}_{s}$ meson, the hard scale t, which varies from $0.9t\sim 1.1t$ (not changing $1/b_{i}$, $i=1,2,3$), and the Gegenbauer moment $a_{2}=0.2\pm 0.2$ [11] in the $\pi \pi$ distribution amplitude, respectively. The other errors from the uncertainty of the input parameters, for example, the decay constants of the $B^0_{s}$ and charmonium mesons and the Wolfenstein parameters, are tiny and can be neglected safely. We see that the input parameter $\omega _{B_{s}}$ of the $B^{0}_{s}$ meson is the primary source of the uncertainties, which range approximately in 9.7–17.1%, and then the Gegenbauer moment and the hard scale t, which characterizes the size of the next-leading-order contribution. When we consider the total S-wave contributions of the $f_{0}(980)$ and $f_{0}(1500)$, we can get

$$\begin{aligned} \mathcal{B}(B^{0}_{s} \rightarrow \psi (2S)(\pi ^+\pi ^-)_{S})=\left[ 7.6^{+0.9+0.1+0.1}_{-0.6-0.0-0.1}\right] \times 10^{-5}, \end{aligned}$$

(27)

which is in agreement with the new experiment data $(7.1\pm 1.3)\times 10^{-5}$ within the allowed errors [63]. Comparing with previous work [39], we find that our calculation of the branching ratio of the $B^{0}_{s} \rightarrow \psi (2S)\pi ^+\pi ^-$ is closer to the latest experimental results, for which the main reason is that we adopt the new input parameters in 2018 PDG, and the latest parameters lead to our uncertainties being smaller.

Fig. 2

The S-wave differential branching ratio of the $B^{0}_{s} \rightarrow \psi (2S)\pi ^{+}\pi ^{-}$ decay

From the numerical results, we can see that $f_0(980)$ is the principal contribution, which reaches a percentage of $94.7\%$, just as the experiment observed, and the $f_0(1500)$ is $1.2\%$, while the constructive interference between these two resonances can contribute nearly $4.1\%$ to the total branching ratio.

In experiment, the calculated ratio of the branching fraction has been given in Ref. [7], which is

$$\begin{aligned} \begin{aligned} \frac{\mathcal{B}({B^0_{s}\rightarrow \psi (2S)\pi ^+\pi ^-})}{\mathcal{B}({B^0_{s}\rightarrow J/\psi \pi ^+\pi ^-})}&=0.34\pm 0.04(\mathrm{stat})\\&\pm 0.03(\mathrm{syst})\pm 0.01(\mathrm{\mathcal {B}}). \end{aligned} \end{aligned}$$

(28)

By using the previous prediction as regards the branching ratio of the decay mode ${B^0_{s}\rightarrow J/\psi (\pi ^+\pi ^-)_{S}}$ [34], we obtain the ratio ${\mathcal{B}({B^0_{s}\rightarrow \psi (2S)\pi ^+\pi ^-})}/{\mathcal{B}({B^0_{s}\rightarrow J/\psi \pi ^+\pi ^-})}=0.46^{+0.16}_{-0.18}$, which is consistent with the experiment’s measurement, and which indicates that the harmonic-oscillator wave function for excited charmonium is applicable and reasonable. Besides the decay mode $B^{0}_{s} \rightarrow \psi (2S)\pi ^+\pi ^-$, we make a calculation for the part of 1D, and we consider similar contributions from the containing S-wave resonance state, $f_{0}(980)$ and $f_{0}(1500)$. The reason is that these two resonances masses are also within the scope of the $\pi \pi$ invariant mass spectra, which is ${2 m_{\pi }}< \omega < {M_{B_{s}^{0}}-M_{\psi }}$. After taking the integral over $\omega$, the results are

$$\begin{aligned}&\mathcal{B}(B^{0}_{s} \rightarrow \psi (1D) f_{0}(980) \rightarrow \psi (1D)\pi ^+\pi ^-)\nonumber \\&\quad =\left[ 1.2^{+0.1+0.0+0.8}_{-0.2-0.1-0.9}\right] \times 10^{-5}, \end{aligned}$$

(29)

$$\begin{aligned}&\mathcal{B}(B^{0}_{s} \rightarrow \psi (1D) f_{0}(1500) \rightarrow \psi (1D)\pi ^+\pi ^-)\nonumber \\&\quad =\left[ 4.6^{+0.3+0.0+1.5}_{-0.2-0.5-2.1}\right] \times 10^{-7}. \end{aligned}$$

(30)

Also, the total S-wave contribution of the $B^0_{s}\rightarrow \psi (1D)\pi ^+\pi ^-$ decay is

$$\begin{aligned} \mathcal{B}(B^{0}_{s} \rightarrow \psi (1D)(\pi ^+\pi ^-)_{S})=\left[ 1.3^{+0.1+0.0+0.8}_{-0.1-0.0-0.6}\right] \times 10^{-5}. \end{aligned}$$

(31)

In Figs. 2a and 3, we plot the differential branching ratio of the $B^{0}_{s} \rightarrow \psi (2S,1D)\pi ^{+}\pi ^{-}$ decay as a function of the $\pi \pi$ invariant mass $\omega$, in which we can clearly see that the peak arises from $f_{0}(980)$, while $f_{0}(1500)$ is unsharp, which also makes a contribution to the decay. For comparison, at the same time, we present the experiment data from LHCb [7] in Fig. 2b, which shows a basic agreement with our predictive results. Comparing the results of $\psi (2S)$ and $\psi (1D)$, it is easy to see that the results of $\psi (1D)$ are more sensitive to the Gegenbauer moment, $a_{2}=0.2\pm 0.2$. This means that, although the value is in good agreement with many decay modes, there is still a necessity to explore more accurate data to facilitate a better understanding of the nonperturbative hadron dynamics. In the $\psi (2S)$ and $\psi (1D)$ modes, since the $f_{0}(1500)$ mass is near the maximum of the $\pi \pi$ invariant mass, the corresponding contributions are very small compared to the total contributions of the S-wave. We note that the branching ratio of the $\psi (1D)$ is smaller than that of the $\psi (2S)$, which should be attributed to the dependence of the corresponding wave function and the decay constant.

Fig. 3

The S-wave differential branching ratio of the $B^{0}_{s} \rightarrow \psi (1D)\pi ^{+}\pi ^{-}$ decay

Furthermore, we calculate the branching fraction of the mode $B^{0}_{s}\rightarrow \psi (3770)(\psi (3686))\pi ^{+}\pi ^{-}$ based on the S–D mixing scheme, whose two sets of mixing angles have been introduced in Sect. 1, and we list the computational results in Table 2.

Table 2 Branching ratios of the quasi-two-decay $B^{0}_{s}\rightarrow \psi (3686, 3770)f_{0}(\rightarrow \pi ^ {+}\pi ^{-})$ in the pQCD approach based on two sets of S–D mixing angles, where the uncertainties are similar to the previous ones except the last one, which shows dependence of the mixing angle

Comparing with the pure D-wave state, we can notice that the branching ratio of the S–D mixing state for $B^{0}_{s}\rightarrow \psi (3770)\pi ^{+}\pi ^{-}$ will be increased approximately by a factor 2 when the mixing angle is $-12^{\circ }$; the reason is mainly the small decay constant of $\psi (1D)$, which is compatible with the summaries in Refs. [46, 49, 68,69,70]. Moreover, we can observe that the results of the $B^{0}_{s}\rightarrow \psi (3686)\pi ^{+}\pi ^{-}$ change a little comparing with the pure 2S mode when taking the mixing effect into account, so $\psi (3686)$ may be regarded as $\psi (2S)$ state. Considering the size of the data collected in LHCb, we may expect the measurement of this decay mode to come in the near future; this will help us to understand the structure of $\psi (3770)$ and the three-body decay mechanism.

5 Summary

In this work, we have calculated the contributions from the S-wave resonances, $f_{0}(980)$ and $f_{0}(1500)$, to the $B^{0}_{s}\rightarrow \psi (3770)(\psi (3686))\pi ^ {+}\pi ^{-}$ decay by introducing the S-wave $\pi \pi$ distribution amplitudes within the framework of the perturbative QCD approach. Due to the 2S–1D mixing scheme character of $\psi (3770)$, we calculate the branching ratios of S-wave and D-wave, respectively, and the results indicate that $f_{0}(980)$ is the main contribution of the considered decay, and the differential result of the $\psi (2S)$ mode is in good agreement with the experimental data. We also analyzed the theoretical uncertainties in this paper, to find that the result of $\psi (1D)$ is sensitive to the Gegenbauer coefficient, because of which we need more accurate data to understand the nonperturbative hadron dynamics. Finally, by introducing the mixing angle $\theta =-12^{\circ }$ and $\theta =27^{\circ }$, we make a further calculation of $B^{0}_{s}\rightarrow \psi (3770)(\psi (3686))\pi ^ {+}\pi ^{-}$, and our calculations show that the branching ratio may be of the order of $10^{-5}$ based on the small mixing angle $\theta =-12^{\circ }$, which will be tested by the running LHCb experiments.

Appendix: Formulas for the calculation used in the text

In this section, we list the explicit form of the formulas used above. The Sudakov exponents are defined by

$$\begin{aligned} \begin{aligned}&S_{B^0_{s}}=s(x _{B}p^+_{1},b _{B})+\frac{5}{3}\int ^{t}_{1/b _{B}}\frac{\mathrm{d}{\bar{\mu }}}{\bar{\mu }}\gamma _{q}(\alpha _{s}({\bar{\mu }})),\\&S_{M}=s(z p^{+},b )+s(\bar{z }p^+,b )+2\int ^{t}_{1/b }\frac{\mathrm{d}{\bar{\mu }}}{\bar{\mu }}\gamma _{q}(\alpha _{s}({\bar{\mu }})),\\&S_{\psi }=s(x _{3}p^{-}_{3},b _{3})+s(\bar{x }_{3}p^-_{3},b _{3})+2\int ^{t}_{1/b _{3}}\frac{\mathrm{d}{\bar{\mu }}}{\bar{\mu }}\gamma _{q}(\alpha _{s}({\bar{\mu }})), \end{aligned} \end{aligned}$$

(A.1)

where the Sudakov factor s(Q, b) results from the resummation of double logarithms; it can be found in Ref. [71]. $\gamma _{q}=-\alpha _{s}/\pi$ is the anomalous dimension of the quark. The hard scattering kernel function $h_{i}(i=a, b, c, d)$ arises from the Fourier transform of the virtual quark and gluon propagators and are written as follows:

$$\begin{aligned}&h_{a}(x _{B}, z , b _{B}, b )= K_{0}(M_{B_{s}}{} b _{B}\sqrt{x _{B}{} z (1-r^2)}) \nonumber \nonumber \\&\quad \times [\theta (b -b _{B})K_{0}(M_{B_{s}}{} b \sqrt{z (1-r^2)})I_{0}(M_{B_{s}}{} b _{B}\sqrt{z (1-r^2)}) \nonumber \\&\quad +(b _{B}\leftrightarrow b )], \nonumber \\&h_{b}(x _{B}, z , b _{B}, b )= K_{0}(M_{B_{s}}{} b \sqrt{x _{B}{} z (1-r^2)}) \nonumber \\&\quad \times \left\{ \begin{array}{ll} {[}\theta (b \!-\!b _{B})K_{0}(M_{B_{s}}{} b \sqrt{\kappa })I_{0}(M_{B_{s}}{} b _{B}\sqrt{\kappa })\\ +(b _{B}\leftrightarrow b )], &{} {\kappa \!\!\ge \! 0},\\ {[}\frac{i {\pi }}{2} \theta (b \!-\!b _{B})H^{(1)}_{0}(M_{B_{s}}{} b \sqrt{|\kappa |})J_{0}(M_{B_{s}}{} b _{B}\sqrt{|\kappa |})\\ +(b _{B}\leftrightarrow b )], &{} {\kappa \!\!<\! 0},\\ \end{array}\right. \nonumber \\&h_{c}(x _{B}, z , x _{3}, b _{B}, b _{3}) \nonumber \\&\quad =[\theta (b_{3}-b _{B})K_{0}(M_{B_{s}}{} b _{3}\sqrt{x _{B}{} z (1-r^2)}) \nonumber \\&I_{0}(M_{B_{s}}{} b _{B}\sqrt{x _{B}{} z (1-r^2)})+(b _{B}\leftrightarrow b _{3})] \nonumber \\&\quad \times \left\{ \begin{array}{ll} K_{0}(M_{B_{s}}{} b _{3}\sqrt{\beta }), &{} {\beta \ge 0},\\ \frac{i {\pi }}{2} H^{(1)}_{0}(M_{B_{s}}{} b _{3}\sqrt{|\beta |}), &{} {\beta < 0},\\ \end{array}\right. \nonumber \\&h_{d}(x _{B}, z , x _{3}, b _{B}, b _{3})=h_{c}(x _{B}, z , \bar{x }_{3}, b _{B}, b _{3}), \end{aligned}$$

(A.2)

with the $\kappa =(1-r^2)(x _{B}-\eta )$, $\beta =r^2_{c}-(z (1-r^2)+r^2\bar{x }_{3})(\bar{\eta }\bar{x }_{3}-x _{B})$, where $J_{0}$ is the Bessel function and $K_{0}$, $I_{0}$ are modified Bessel function with $H^{(1)}_{0}(x)=J_{0}(x)+iY_{0}(x)$. The threshold resummation factor $S_{t}(x)$ has been parameterized in [72],

$$\begin{aligned} S_{t}(x)=\frac{2^{1+2c}\Gamma (\frac{3}{2}+c)}{\sqrt{\pi }\Gamma (1+c)}[x(1-x)]^{c}, \end{aligned}$$

(A.3)

with the parameter $c=0.04Q^2-0.51Q+1.87$ and $Q^2=M_{B}^2(1-r^2)$ [73].

For killing the large logarithmic radiative corrections, the hard scales $t_{i}$ in the amplitudes are chosen as

$$\begin{aligned} \begin{aligned}&t_{a}=\mathrm {max}\{M_{B_{s}}\sqrt{z (1-r^2)}, 1/b , 1/b _{B}\},\\&t_{b}=\mathrm {max}\{M_{B_{s}}\sqrt{|\kappa |}, 1/b , 1/b _{B}\},\\&t_{c}=\mathrm {max}\{M_{B_{s}}\sqrt{x _{B}{} z (1-r^2)}, M_{B_{s}}\sqrt{|\beta |}, 1/b _{B}, 1/b _{3}\},\\&t_{d}=t_{c}|_{x _{3} \rightarrow \bar{x }_{3}}. \end{aligned} \end{aligned}$$

(A.4)