1 Introduction

The thermodynamics of black holes has been investigated intensively for over four decades. This area of research is considered to bring to light some links between general relativity and quantum mechanics and might be very useful for the verification of different approaches to quantum gravity [1]. It is supposed that all the approaches in the quasiclassical limit should lead to the same thermodynamic behaviour of black holes and to be in agreement with the laws of black hole mechanics [2] which were developed without any knowledge about the underlying theory of quantum gravity. It might be treated as a theory that allows one to correct or even get rid of some deficit approaches to quantum gravity. But it should be noted that such different approaches to quantum gravity as String Theory [3] and Loop Quantum Gravity [4] give rise to the same expression for the black hole entropy–area relation given by the celebrated Bekenstein–Hawking formula.

New great interest in thermodynamics of black holes has arisen in the past decade. This revival of activity can be explained by the fact that in recent work one proposed to extend the complex of thermodynamic variables which had been used in black holes’ theory and consider the cosmological constant as one of those thermodynamic values [5,6,7,8,9,10]. It was suggested that for a gravitational system for example for a black hole such a standard notion of thermodynamics as pressure can be introduced, being proportional to the cosmological constant. In the case of a Reissner–Nordstrom–AdS (RN-AdS) black hole one has a simple relation between the thermodynamic pressure and the cosmological constant: \(P=-\Lambda /8\pi \) [5,6,7,8]. Since the cosmological constant here is supposed to be a variable it changes the identification of the black hole mass in thermodynamics. In contrast to the well-established treatment of the mass as the black hole’s internal energy, in the extended approach it is considered to be like the thermodynamic enthalpy, namely: \(M=H=U+PV\). The second point that is strongly related to the introduced notion of the pressure is the definition of its thermodynamically conjugate value, namely it is the volume which can be introduced by the derivative, \(V=(\partial H/\partial P)_S\). The extended (enlarged) thermodynamic phase space allowed one to examine the phase behaviour of black holes, namely it was shown that a charged black hole possesses a phase transition that is completely analogous to Van der Waals liquid–gas phase transition and below the critical point it has a phase transition of the first order [9]. It should be noted that a richer thermodynamic behaviour appears in the case of a more general setting, namely for Born–Infeld theory or for black holes in a space of higher dimensions. For example, a reentrant phase transition appears [10, 11] or a tricritical (triple) point was observed [12, 13]. The facts mentioned stimulated deep interest and prolific investigations in this area of research which obtained the special name: black hole chemistry, and this name reflects the similarity in thermodynamic behaviour of black holes and ordinary condensed matter systems such as gases, liquids, multicomponent fluid systems. An overview of recent developments and possible future directions of this subfield of black hole thermodynamics is given in [14].

General Relativity is a very successful theory in the explanation of various phenomena from planetary up to cosmological scales. But nonetheless, different approaches to quantum gravity, namely String Theory, are supposed to modify the gravitational Einstein term replacing it with a sum of ones which takes into account higher orders corrections of curvature. In the low energy limit of the String Theory the standard Einstein term plus a nonminimally coupled dilaton field can be obtained [15]. It is worth stressing that dilaton field minimally coupled to Einstein’s gravity appears as a result of a dimensional reduction of the standard General Relativity in higher dimensions onto a space of lower dimension. Thus, such a low energy limit of the String Theory can be considered as Einstein gravity with an additional dilaton field. This model has attracted considerable attention in the past two decades, namely different types of black holes/strings solutions were investigated [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. We point out that in most of this work static solutions were studied, whereas the rotating solutions were examined for some particular choice of the dilaton coupling parameter [36,37,38,39,40,41,42,43,44]. It should be noted that special interest has been given to the investigation of Einstein-dilaton black holes with an additional dilaton potential of a so called Liouville-type form [21, 22, 24, 27, 29, 45,46,47,48,49,50,51]. The Liouville-type potential allows one to introduce terms which can be treated as a generalization of the known cosmological constant term. This fact can be used for examination of possible extensions of the AdS–CFT correspondence. It was also supposed that linear dilaton spacetime, which appears as a near horizon limit of a dilatonic black hole, might possess some holographic properties [52]. On the other side new black hole solutions which are not asymptotically flat nor of AdS-type (or dS-type) might be a good laboratory for application or testing of methods developed for the above-mentioned types of black hole solutions. The interest in the dilatonic black holes with Liouville dilaton potential was quite great; namely, black hole solutions with different types of nonlinear electromagnetic field coupled to a dilaton field were obtained [53,54,55,56,57,58]. Considerable attention was paid to the investigation of thermodynamic properties of the corresponding dilatonic black holes. It should be noted that the standard approach and the extended technique were applied for the study of their thermodynamics [47, 54, 57, 59,60,61,62,63,64,65,66,67,68,69].

In our work we examine a slowly rotating Einstein–Maxwell-dilaton black hole with a linear Maxwell field and electromagnetic–dilaton coupling. We also take into account a dilaton potential of the Liouville form which consists of two terms; in particular one of these is supposed to be a kind of generalization of a cosmological constant term. We also consider the thermodynamics of given black hole solution. For the first, assuming that the corresponding cosmological constant is fixed we obtain temperature and heat capacity. Secondly, using the modern technique where the thermodynamic pressure is introduced we obtain the equation of state and derive the Gibbs potential and investigate the critical behaviour.

This work is organized in the following way. In Sect. 2 the slowly rotating black hole is obtained and examined. Section 3 is devoted to the thermodynamics of the black hole; relations for the temperature and heat capacity are investigated. In Sect. 4 the equation of state and the Gibbs potential for the black hole are obtained and investigated. Section 5 is devoted to the derivation of critical exponents. Finally, Sect. 6 contains some conclusions.

2 Field equations and their solution

We consider \(n+1\)-dimensional gravity (\(n\ge 3\)) with dilaton and linear Maxwell fields. The action integral for this system can be written in the form

$$\begin{aligned} S= & {} \frac{1}{16\pi }\int _{\mathcal{M}} \mathrm{d}^{n+1}x\sqrt{-g}\nonumber \\&\times \,\left( R-\frac{4}{n-1}\nabla ^{\mu }\Phi \nabla _{\mu }\Phi -V(\Phi )-e^{-4\alpha \Phi /(n-1)}F_{\mu \nu }F^{\mu \nu }\right) \nonumber \\&-\frac{1}{8\pi }\int _{\partial \mathcal{M}}\mathrm{d}^{n}x\sqrt{-\gamma }\Theta (\gamma ) \end{aligned}$$
(1)

where R is the scalar curvature, \(\Phi \) is the dilaton field, \(V(\Phi )\) denotes the potential which depends on the dilaton field, \(\alpha \) denotes the dilaton–electromagnetic coupling parameter and \(F_{\mu \nu }\) is the electromagnetic field tensor, which is defined in the standard way, namely \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) and here \(A_{\mu }\) is a component of the electromagnetic potential. The second term in the action (1) corresponds to the so-called Gibbons–Hawking boundary term, which makes the variation of the action well defined and allows us to obtain conserved quantities. \(\partial \mathcal{M}\) denotes the boundary of the manifold \(\mathcal{M}\), \(\gamma _{ab}\) is the metric on the boundary and \(\Theta \) is the trace of the extrinsic curvature tensor \(\Theta _{ab}\) on the boundary.

Varying the action integral (1) with respect to the gravitational field, represented by the metric tensor \(g_{\mu \nu }\), dilaton field \(\Phi \) and the electromagnetic potential \(A_{\mu }\), one obtains field equations which can be written in the following form:

$$\begin{aligned} R_{\mu \nu }= & {} \frac{g_{\mu \nu }}{n-1}\left( V(\Phi )-e^{-4\alpha \Phi /(n-1)}F_{\rho \sigma }F^{\rho \sigma }\right) \nonumber \\&+\frac{4}{n-1}\partial _{\mu }\Phi \partial _{\nu }\Phi +2e^{-4\alpha \Phi /(n-1)} F_{\mu \sigma }F_{\nu }^{\sigma }; \end{aligned}$$
(2)
$$\begin{aligned}&\nabla _{\mu }\nabla ^{\mu }\Phi =\frac{n-1}{8}\frac{\partial V}{\partial \Phi }-\frac{\alpha }{2}e^{-4\alpha \Phi /(n-1)}F_{\rho \sigma }F^{\rho \sigma }; \end{aligned}$$
(3)
$$\begin{aligned}&\nabla _{\mu }(e^{-4\alpha \Phi /(n-1)}F^{\mu \nu })=0. \end{aligned}$$
(4)

We are interested in the solution of the field equations which represents a slowly rotating black hole, so we should make some choice as regards the supposed form of the metric. To find this solution we represent the metric in the form

$$\begin{aligned} \text {d}s^2= & {} -W(r)\text {d}t^2+\frac{\text {d}r^2}{W(r)}-2af(r)\sin ^2{\theta }\text {d}t\text {d}\varphi \nonumber \\&\quad +r^2R^2(r)(\text {d}\theta ^2+\sin ^2{\theta } \text {d}\varphi ^2+\cos ^2{\theta }\text {d}\Omega ^2_{n-3}) \end{aligned}$$
(5)

and here the metric functions W(r), f(r) and R(r) are supposed to depend on the radial coordinate r only; the parameter a is related to the angular momentum (or angular velocity) of the black hole. It is worth noting that a similar problem was considered in [50], but here we make a bit different choice of the dilaton potential \(V(\Phi )\). It should also be pointed out that a higher dimensional Einstein–Maxwell-dilaton black hole with multiple rotational parameters was considered in [51]. As pointed out in [48], the only term in the metric that appears due to slow rotation is the \(g_{t\varphi }\), term which is of the order of \(\mathcal{O}(a)\) and this fact motivates the choice of the third term in the metric (5). An infinitesimal rotation does not affect the dilaton field \(\Phi \) and the electromagnetic potential acquires a \(A_{\varphi }\) term which is also of the order if \(\mathcal{O}(a)\). In the limit \(a\rightarrow 0\) the static solution is recovered.

From Eq. (4) one can easily obtain the components of the gauge field tensor. The leading term of the electromagnetic field tensor takes the form

$$\begin{aligned} F_{tr}=\frac{qe^{4\alpha \Phi /(n-1)}}{r^{n-1}R^{n-1}} \end{aligned}$$
(6)

and here the constant of integration q is related to the electric charge of the black hole, which will be calculated below. As noted before, even the slow rotation we consider adds an “angular” component \(A_{\varphi }\) to the electromagnetic field potential, which can be chosen in the form [48]

$$\begin{aligned} A_{\varphi }=aqh(r)\sin ^2{\theta } \end{aligned}$$
(7)

and h(r) is a function of the radial coordinate; the evident form of this function can be obtained from the field equations (2)–(4). The other components of the electromagnetic field tensor would be proportional to the parameter a and as a result the term \(F_{\mu \nu }F^{\mu \nu }\) would be proportional to the parameter \(a^2\) and we do not take these terms into consideration in the field equations (2)–(4).

The dilaton potential \(V(\phi )\) is taken in the so-called Liouville form:

$$\begin{aligned} V(\Phi )=\Lambda _0 e^{\lambda _0\Phi }+\Lambda e^{\lambda \Phi }. \end{aligned}$$
(8)

To obtain a solution of the field equations (2)–(4) the following ansatz for the function R(r) can be used [47, 48]:

$$\begin{aligned} R(r)=e^{2\alpha \Phi /(n-1)}. \end{aligned}$$
(9)

Having used the latter ansatz we can solve the field equations (2)–(4) and obtain the metric functions W(r), f(r), the dilaton field \(\Phi (r)\) and the function h(r):

$$\begin{aligned} W(r)= & {} -mr^{1+(1-n)(1-\gamma )}\nonumber \\&+\frac{(n-2)(1+\alpha ^2)^2}{(1-\alpha ^2)(\alpha ^2+n-2)}b^{-2\gamma }r^{2\gamma }\nonumber \\&-\,\frac{\Lambda (1+\alpha ^2)^2}{(n-1)(n-\alpha ^2)}b^{2\gamma }r^{2(1-\gamma )}\nonumber \\&+\frac{2q^2(1+\alpha ^2)^2}{(\alpha ^2+n-2)(n-1)}b^{2(2-n)\gamma }r^{-2(n-2)(1-\gamma )},\nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned} f(r)= & {} \frac{m(\alpha ^2+n-2)}{(n-2)(1+\alpha ^2)}b^{(n-1)\gamma }r^{1+(1-n)(1-\gamma )}\nonumber \\&+\frac{\Lambda (1+\alpha ^2)}{(n-1)(n-2)}\times \frac{(n+\alpha ^2-2)}{(n-\alpha ^2)}b^{(n-1)\gamma }r^{2(1-\gamma )}\nonumber \\&-\frac{2q^2(1+\alpha ^2)}{(n-1)(n-2)}b^{(1-n)\gamma }r^{2(2-n)(1-\gamma )}, \end{aligned}$$
(11)
$$\begin{aligned} \Phi (r)= & {} \frac{\alpha (n-1)}{2(1+\alpha ^2)}\ln {\left( \frac{b}{r}\right) }, \end{aligned}$$
(12)
$$\begin{aligned} h(r)= & {} \frac{1}{n-2}r^{-1+(3-n)(1-\gamma )}, \end{aligned}$$
(13)

where the parameter m is an integration constant related to the black hole’s mass (as will be shown below) and \(\gamma =\alpha ^2/(1+\alpha ^2)\). We should pay special attention to the parameter b which appears in Eqs. (10)–(12), which is also an integration constant. However, it does not have a direct physical meaning; considering Eq. (12) we can treat it as a “scaling” parameter for the dilation field, but the physical meaning of this parameter is unclear. Since we have just assumed that the parameter b is a “scaling” one, we might perform a coordinate transformation, namely \({\bar{r}}=r/b\), to simplify Eqs. (10)–(12), but it is easy to check that such a rescaling does not simplify the mentioned relations and possibly requires the corresponding rescaling of the mass m and charge q parameters and of the parameter \(\Lambda \); this is not convenient and has no advantages. Since the parameter b is arbitrary we can set it equal to unity (\(b=1\)) for simplicity, but in what follows we keep it as it is in order to make our relations easily comparable with results previously obtained, namely in [48]. The obtained functions coincide with corresponding functions given in [48] when the parameter \(\Lambda \) is set to zero (\(\Lambda =0\)). It is worth stressing that the parameters \(\lambda _0\), \(\lambda \) and \(\Lambda _0\) are not arbitrary, whereas there is no restriction on the parameter \(\Lambda \), which can be treated as an effective cosmological constant that appears due to the specifically chosen form of the dilaton potential (8). To fully obey the system of equations (2)–(4) the parameters mentioned above should be taken in the following form:

$$\begin{aligned} \Lambda _0= & {} \frac{\alpha ^2(n-1)(n-2)}{b^2(\alpha ^2-1)},\nonumber \\ \lambda _0= & {} \frac{4}{\alpha (n-1)},\nonumber \\ \lambda= & {} \frac{4\alpha }{(n-1)}. \end{aligned}$$
(14)

Equation (10) describes a multitude of causal structures of the dilatonic black hole. The obtained metric functions (10)–(12) show that in general the solution is not asymptotically flat nor (anti)-de Sitterian. It can be shown that the Kretschmann scalar \(R_{\mu \nu \lambda \sigma }R^{\mu \nu \lambda \sigma }\) diverges only when \(r\rightarrow 0\) and is finite for \(r\ne 0\). It leads to the conclusion that the only physical singularity of the metric is located at the point \(r=0\). We remark that the black hole solution is not well defined when \(\alpha =1\). This is the so-called string singularity and there is another singularity of the metric when \(\alpha =\sqrt{n}\). Due to the similarity of the obtained metric function (10) to the corresponding metric function obtained in [47] the analysis of the causal structure would be the same as it was performed in the publication mentioned above.

In the limit when the dilaton parameter \(\alpha \) is set to zero it follows from the equations written above for the metric functions W(r) and f(r) that

$$\begin{aligned} W(r)= & {} 1-mr^{2-n}-\frac{\Lambda }{n(n-1)}r^2\nonumber \\&+\frac{2q^2}{(n-1)(n-2)}r^{2(2-n)}, \end{aligned}$$
(15)
$$\begin{aligned} f(r)= & {} mr^{2-n}+\frac{\Lambda }{n(n-1)}r^2\nonumber \\&-\frac{2q^2}{(n-1)(n-2)}r^{2(2-n)}. \end{aligned}$$
(16)

Thus we obtain the metric functions for a (n+1)-dimensional slowly rotating charged Kerr–AdS black hole [70].

Fig. 1
figure 1

Mass parameter m as a function of horizon radius \(r_+\) for several values of parameter \(\alpha \) (the left graph) or cosmological constant \(\Lambda \) (the right one). Namely, for the left graph the correspondence is the following: the solid curve corresponds to \(\alpha =0.1\), the dotted curve corresponds to \(\alpha =0.5\) and the dash-dotted one to \(\alpha =0.7\), for all the curves here \(\Lambda =-1\). On the right graph the correspondence is as follows: the solid, dotted and dash-dotted curves correspond to \(\Lambda =-1\), \(\Lambda =-2\) and \(\Lambda =-3\), respectively, for all the lines \(\alpha =0.3\). All the other parameters are held fixed for both graphs (\(n=3\), \(b=1\), \(q=0.1\))

Full size image

To obtain the black hole’s mass we use the quasilocal concept [71]. Following the mentioned work of Brown and York [71] to derive the quasilocal mass (or other quasilocal quantities) one should use an ADM decomposition of the spacetime manifold \(\mathcal{M}\) into a spacelike hypersurface evolving in time, \(\Sigma _t\), times the real time interval \({\mathbb {R}}\) (\(\mathcal{M}=\Sigma _t\times {\mathbb {R}}\)). Since our spacetime \(\mathcal{M}\) has boundary \(\partial \mathcal{M}\), the evolving hypersurface \(\Sigma _t\) also has a boundary, which we denote \(\mathcal{B}\). This boundary plays an important role in the calculation of quasilocal quantities. Namely, according to the quasilocal concept to derive the mass of the black hole one should use the following relation:

$$\begin{aligned} M=\frac{1}{8\pi }\int _{\mathcal{B}}d^{n-1}\chi \sqrt{\sigma } N(k-k_0); \end{aligned}$$
(17)

we point out here that the latter integral is taken over the boundary \(\mathcal{B}\) and k is a trace of extrinsic curvature of the hypersurface \(\mathcal{B}\) in the embedding manifold \(\Sigma _t\), \(k_0\) denotes the trace of the extrinsic curvature of a reference (background) metric, \(\sigma \) is the determinant of the metric on the spacelike hypersurface \(\mathcal{B}\) and N denotes the lapse function in the ADM decomposition of the spacetime metric mentioned above. As a result the black hole’s mass can be represented in the following form:

$$\begin{aligned} M=\frac{(n-1)b^{(n-1)\gamma }\omega _{n-1}}{16\pi (1+\alpha ^2)}m, \end{aligned}$$
(18)

where \(\omega _{n-1}\) is the surface area of a \(n-1\)-dimensional unit hypersphere. We point out that, since we consider a non-asymptotically flat spacetime, the concept of quasilocal energy might be applied here to calculate the black hole’s mass and angular momentum and the use of the quasilocal concept allows one to obtain the first law of thermodynamic similar to asymptotically flat black holes [72, 73]. It should be noted that the relation obtained above for the black hole’s mass (18) completely coincides with the corresponding relation calculated with the help of the Abbott–Deser method [74]. We also point out that the notion of a quasilocal energy (and mass) is not unique; there are several various notions of it and any of them is useful for some particular problems of gravity and might have serious drawbacks when one tries to analyze some different problems [75].

The electric charge of the black hole can be calculated via the relation (Gauss law)

$$\begin{aligned} Q=\frac{1}{4\pi }\int \exp \{-4\alpha \Phi /(n-1)\}*F \end{aligned}$$
(19)

and here \(*F\) denotes the form dual to the electromagnetic field form. It should be noted that the integration is performed over a closed spacelike hypresurface enclosing the black hole. Having used the previous relation we get

$$\begin{aligned} Q=\frac{\omega _{n-1}}{4\pi }q. \end{aligned}$$
(20)

The mass parameter can be rewritten in terms of the radius of black hole’s horizon:

$$\begin{aligned} m(r_+)= & {} (1+\alpha ^2)^2r_+^{(n-1)(1-\gamma )-1}\nonumber \\&\times \,\left( \frac{(n-2)}{(1-\alpha ^2)(\alpha ^2+n-2)}b^{-2\gamma }r_+^{2\gamma }\right. \nonumber \\&-\frac{\Lambda }{(n-1)(n-\alpha ^2)}b^{2\gamma }r_+^{2(1-\gamma )}\nonumber \\&\left. +\frac{2q^2}{(\alpha ^2+n-2)(n-1)}b^{2(2-n)\gamma }r_+^{2(2-n)(1-\gamma )}\right) .\nonumber \\ \end{aligned}$$
(21)

The behaviour of the mass parameter as a function of the horizon radius is represented in Fig. 1. All the plots show that the mass parameter, and as a consequence the black hole’s mass, has a point of minimal mass, which corresponds to some specific value of the horizon \(r_+\). Decrease or increase of the horizon radius leads to the increase of the mass. This fact is not a specific peculiarity of the dilatonic black holes, we have a similar situation for a charged black hole in an anti-de Sitter universe. The nonmonotonic behaviour of the mass can be explained by the competition between the terms corresponding to electromagnetic and nonelectromagnetic parts. For small \(r_+\) the electromagnetic part becomes dominant, which leads to a decreasing of the mass with the decrease of the horizon radius \(r_+\), whereas for large values of \(r_+\) the other term becomes leading which gives an increase of the mass when the horizon radius grows.

Since the black hole we consider is a rotating one it is important to calculate its angular momentum. To find the angular momentum, the quasilocal formalism can be used again [71]. It should be noted that the mentioned approach works for Einsteinian general relativity with an arbitrary matter field which should be coupled to gravity without derivative. The angular momentum is supposed to be a conserved quantity and its value can be obtained from the information as regards the behaviour of gravitational field on the boundary of a n-dimensional hypersurface evolving in time. Namely this information is encoded in the boundary term of the action (1). Similar to [48] one can write the boundary stress-energy tensor:

$$\begin{aligned} T_{ab}=\Theta _{ab}-\gamma _{ab}\Theta , \end{aligned}$$
(22)

which results from the variation of the action integral (1) with respect to the boundary metric \(\gamma _{ab}\). To proceed, one writes the boundary metric in ADM form:

$$\begin{aligned} \gamma _{ab}dx^{a}dx^{b}= & {} -N^2dt^2+\sigma _{ij}\nonumber \\&\times \,\left( d\varphi ^i+V^idt\right) \left( d\varphi ^j+V^jdt\right) ; \end{aligned}$$
(23)

the coordinates \(\varphi ^i\) parametrize the boundary hypersurface of constant r. N and \(V^i\) are the lapse and shift, respectively. As a result the quasilocal angular momentum can be represented in the following form [48, 71]:

$$\begin{aligned} J=\frac{1}{8\pi }\int _\mathcal{B}d^{n-1}\chi \sqrt{\sigma }T_{ab}n^{a}\xi ^b. \end{aligned}$$
(24)

It is worth of note that this integral is taken over a spacelike hypersurface \(\mathcal{B}\) of the boundary \(\partial \mathcal{M}\). In the integral (24) we have the following notation: \(\sigma \) is the determinant of the metric \(\sigma _{ij}\), \(n^a\) is the unit normal on the boundary \(\mathcal{B}\) and \(\xi ^a\) is the rotational Killing vector \((\xi ^{a}=\partial /\partial \varphi )\). The hypersurface \(\mathcal{B}\) is taken in such a way that it contains the orbits of the rotational Killing vector \(\xi ^a\). Having used Eq. (24) we obtain the evident form of the angular momentum:

$$\begin{aligned} J=\frac{(n+\alpha ^2-2)(n-\alpha ^2)}{8\pi n(n-2)(1+\alpha ^2)^2}b^{2(n-2)\gamma }\omega _{n-1}am. \end{aligned}$$
(25)

We note that the obtained relation for the angular momentum coincides with the corresponding relation calculated in [48] where a similar slowly rotating black hole, but without the cosmological constant \(\Lambda \), was examined. So, we conclude that in a linear approximation in terms of the parameter a the angular momentum of the black hole (25) does not have any imprint of the cosmological constant \(\Lambda \). This conclusion is in perfect agreement with the situation for the slowly rotating Kerr–Newmann–AdS black hole, where the angular momentum does not depend on \(\Lambda \) in the case when one restricts oneself to the linear approximation as regards the parameter a.

3 Thermodynamics of the black hole

In this section the thermodynamics of the given above black hole will be considered. To obtain the temperature we use the standard definition of the black hole’s surface gravity [2]:

$$\begin{aligned} \kappa ^2=-\frac{1}{2}\nabla _a\xi _b\nabla ^a\xi ^b \end{aligned}$$
(26)

where \(\xi ^{\mu }\) is a Killing vector which is null on the horizon. Since the black hole is considered in linear approximation over the rotation parameter a it can easily be shown that the black hole’s temperature takes the following form:

$$\begin{aligned} T= & {} \frac{\kappa }{2\pi }=\frac{W^{\prime }{}(r_+)}{4\pi }=-\frac{(\alpha ^2+n-2)}{4\pi (1+\alpha ^2)}mr_+^{(1-n)(1-\gamma )}\nonumber \\&+\frac{2(n-2)(1+\alpha ^2)}{4\pi (1-\alpha ^2)}b^{-2\gamma }r_+^{2\gamma -1}\nonumber \\&-\frac{2\Lambda (1+\alpha ^2)}{4\pi (n-\alpha ^2)}b^{2\gamma }r_+^{1-2\gamma }; \end{aligned}$$
(27)

here \(r_+\) is the radius of the black hole’s horizon. It is worth of note that here we have used the relation for the mass parameter (21) and expressed the charge parameter q in terms of the mass parameter m, the horizon radius \(r_+\) and the cosmological constant \(\Lambda \) with the following substitution of the relation obtained for the charge parameter into the relation for the temperature. We also point out that the expression given above for the temperature coincides with the corresponding expression obtained for the static solution [47]; in the limit when \(\Lambda =0\) one can arrive at the expression for the temperature of a slowly rotating black hole but without the cosmological constant term [48].

The mass parameter of the black hole m can be expressed in terms of the horizon radius \(r_+\), the cosmological constant \(\Lambda \) and the charge q and this representation is very convenient from the point of view of thermodynamics, because the mass of the black hole is identified with the internal energy, the horizon radius \(r_+\) might be represented as a function of entropy and the parameters q and \(\Lambda \) also can be treated as thermodynamic values. Now we rewrite the previous relation for the temperature taking into account the described above remark and as a result we arrive at the relation

$$\begin{aligned} T= & {} \frac{(1+\alpha ^2)}{4\pi }\left( \frac{n-2}{1-\alpha ^2}b^{-2\gamma }r^{2\gamma -1}_+\right. \nonumber \\&\left. -\frac{\Lambda }{n-1}b^{2\gamma }r_+^{1-2\gamma }-\frac{2q^2}{n-1}b^{2(2-n)\gamma }r_+^{2(2-n)(1-\gamma )-1}\right) .\nonumber \\ \end{aligned}$$
(28)

We note that the relation written above for the temperature (28) is more in the spirit of thermodynamics than Eq. (27), because the black hole entropy, which we are going to obtain below, would be a monotonous function of the horizon radius and this means that an inverse relation where the horizon radius is a function of the entropy is well defined and the two other parameters q and \(\Lambda \), as has already been mentioned, can be considered as thermodynamic quantities. The obtained dependence of the temperature T on the radius of the horizon \(r_+\) is rather complicated. To make it more transparent we represent it graphically for several different values of the coupling constant \(\alpha \) and the cosmological constant \(\Lambda \). Figure 2 shows the multiplicity of behaviours of the temperature for different values of the parameter \(\alpha \). But nevertheless, there are several features shared by all the variants represented here. Firstly, for some small value of the horizon radius \(r_+\) the temperature becomes negative and, as will be shown below, from the analysis of heat capacity it follows that the black hole is unstable in the domain where \(T<0\). Secondly, here we have two extrema, specifically points of minimal and maximal temperature. The maximal temperature is higher when the parameter \(\alpha \) is greater and the minimum of the temperature becomes lower when this parameter decreases. We also note that when the horizon radius becomes large enough the temperature also increases but the temperature grows slowly for larger parameter \(\alpha \). Going a bit further we remark that the extrema points are the points of the discontinuity of heat capacity, as investigated below.

Fig. 2
figure 2

Temperature as a function of horizon radius \(r_+\) for several different values of the dilaton coupling constant \(\alpha \) in assumption that cosmological constant is fixed (\(\Lambda =-1\)). The correspondence of the curves is as follows: the solid curve represents the case \(\alpha =0.1\), the dashed curve corresponds to the choice \(\alpha =0.3\), the dash-dotted curve represents the choice \(\alpha =0.5\) and finally the dotted curve corresponds to the case \(\alpha =0.7\). We also note that the other parameters in Eq. (28) are held fixed, namely \(n=3\), \(b=1\) and \(q=0.1\)

Full size image

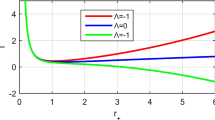
The second graph (Fig. 3) shows the T–\(r_+\) dependence for several values of the cosmological constant \(\Lambda \) when parameter \(\alpha \) is kept constant. Inspecting Fig. 3 one can conclude that the increase (in absolute values) of the cosmological constant gives rise to an increase of the black hole temperature. The second important point is the fact that when the cosmological constant is large enough (in absolute values) the extrema points that we have mentioned above disappear and it would be the only point which changes the character of the growth of the temperature, namely from fast growth to a regime of moderate increase.

Fig. 3
figure 3

Temperature as a function of horizon radius \(r_+\) for several different values of the cosmological constant \(\Lambda \). The solid, dashed, dash-dotted and dotted curves correspond to the cases \(\Lambda =0\), \(\Lambda =-1\), \(\Lambda =-2\) and \(\Lambda =-4\), respectively. The other parameters are held fixed, namely \(n=3\), \(\alpha =0.5\), \(b=1\) and \(q=0.1\)

Full size image

To consider thermodynamics we should have the entropy of the black hole. The entropy of the black hole is defined as a quarter of its horizon area:

$$\begin{aligned} S=\frac{\omega _{n-1}}{4}b^{\gamma (n-1)}r^{(n-1)(1-\gamma )}_+ \end{aligned}$$
(29)

Using Eqs. (18) and (20) it can easily be verified that

$$\begin{aligned} dM=TdS+\Phi dQ; \end{aligned}$$
(30)
$$\begin{aligned} T= & {} \left( \frac{\partial M}{\partial S}\right) _Q, \nonumber \\ \Phi= & {} \left( \frac{\partial M}{\partial Q}\right) _S, \end{aligned}$$
(31)

are the temperature and electric potential, respectively. We point out here that the first law of black hole thermodynamics for a rotating black hole usually contains an additional term \(\Omega _+ \text {d}J\), where \(\Omega _+\) is the angular velocity of the black hole and \(\text {d}J\) denotes a variation (differential) of the angular momentum, but this additional term would be of the order \({\sim }a^2\), whereas the metric we consider (5) takes into account only a \({\sim }a\) term, thus in linear approximation in the parameter a the first law of black hole thermodynamics (30) does not include a contribution from the angular momentum. As a result in a linear approximation in terms of the parameter a all the following thermodynamic relations also do not have any contribution from angular momentum.

To investigate thermal stability, the heat capacity should be calculated:

$$\begin{aligned} C_Q=T\left( \frac{\partial S}{\partial r_+}\right) _Q\left( \frac{\partial T}{\partial r_+}\right) ^{-1}_Q \end{aligned}$$
(32)

Having substituted the expression for the temperature (28) into the previous relation and performing partial differentiation we obtain

$$\begin{aligned} C_Q= & {} \frac{(n-1)\omega _{n-1}}{4}b^{\gamma (n-1)}r^{(n-1)(1-\gamma )-1}_+\nonumber \\&\times \,\left( \frac{n-2}{1-\alpha ^2}b^{-2\gamma }r^{2\gamma -1}_+-\frac{\Lambda }{n-1}b^{2\gamma }r_+^{1-2\gamma }\right. \nonumber \\&\left. -\frac{2q^2}{n-1}b^{2(2-n)\gamma }r_+^{2(2-n)(1-\gamma )-1}\right) \nonumber \\&\times \left( -(n-2)b^{-2\gamma }r^{2(\gamma -1)}_+-\frac{\Lambda (1-\alpha ^2)}{n-1}b^{2\gamma }r_+^{-2\gamma }\right. \nonumber \\&\left. -\frac{2q^2(3-2n-\alpha ^2)}{n-1}b^{2(2-n)\gamma }r_+^{2((2-n)(1-\gamma )-1)}\right) ^{-1}.\nonumber \\ \end{aligned}$$
(33)

As we have mentioned before, in the cases when the temperature (28) has two extrema (namely minimal and maximal temperature) the heat capacity (33) possesses the points of discontinuity for the same values of the horizon radius \(r_+\). Thus, these points can be treated as the very same points as allow us to separate stable and unstable configurations. To comprehend the behaviour of the heat capacity \(C_Q\) better we show plots of the heat capacity as a function of the horizon radius \(r_+\) (see Fig. 4). As one can see, between the points of discontinuity the heat capacity is negative and it tells us that the system is unstable whereas for the domains with positive heat capacity the system is stable. The discontinuity of the heat capacity means that the system has a phase transition of the second order. It is worth to emphasize that the heat capacity becomes negative in the region of negative temperature. This feature can be explained directly from the general relation (32), namely when the temperature is negative, but it grows with increasing of radius of horizon \(r_+\) (which we have in our case); it means that the derivative \((\partial T/\partial r_+)_Q\) and its inverse as we have in Eq. (32) both are positive, and the other derivative \((\partial S/\partial r_+)_Q\) is always positive. As a result we arrive at the conclusion that the heat capacity in this domain is always negative; thus the black hole is thermodynamically unstable.

Fig. 4
figure 4

Heat capacity \(C_Q\) as a function of horizon radius \(r_+\) when the other parameters are fixed (\(n=3\), \(\alpha =0.5\), \(b=1\), \(q=0.1\) and \(\Lambda =-1\)). The left graph represents the heat capacity near the first point of discontinuity and the right one shows the heat capacity near the second discontinuity point

Full size image

When the cosmological constant \(\Lambda \) exceeds in absolute value some critical one, namely when the two extrema disappear, the heat capacity would not have a discontinuity. The behaviour of the heat capacity in this case is shown on Fig. 5. We can conclude that when the cosmological constant goes up in absolute value the points of the discontinuity become closer to each other and for some specific (critical) value of \(\Lambda \) they merge and the following increase of \(\Lambda \) gives rise to a transformation of the merged discontinuity into a peak of a finite height.

Fig. 5
figure 5

Heat capacity \(C_Q\) as a function of horizon radius \(r_+\) when discontinuity disappears (\(n=3\), \(\alpha =0.5\), \(b=1\), \(q=0.1\)). The solid curve corresponds to the value \(\Lambda =-7.4\), the dashed curve corresponds to \(\Lambda =-8.5\) and finally the dotted line is related to \(\Lambda =-10\)

Full size image

The further increase of the absolute value of \(\Lambda \) leads to a decrease of the peak of the heat capacity and its subsequent disappearance. Thus, we can conclude that when the absolute value of \(\Lambda \) is large enough the heat capacity \(C_Q\) is positive for all values of \(r_+\) greater than the boundary value mentioned above when the temperature T (28) equals zero; as a result the system is thermodynamically stable for all these values of \(r_+\).

4 Extended thermodynamics

For a long time it has been supposed that black hole thermodynamics should be considered in a “fixed” background, which means that for the theories with cosmological constant, namely for AdS-type black holes, the cosmological constant is held fixed. An extension of standard thermodynamic phase space has been proposed recently. It was supposed that the cosmological constant might be varied [5]. It leads to interesting physical consequences and implications. As emphasized earlier, the extended thermodynamic phase space might bring about a better understanding of the black hole thermodynamics from a broader point of view and it allows one to reveal new ties with the thermodynamics of real systems, namely liquid–gas systems which are described by the Van der Waals equation of state [9, 10]. It was also noted that the variation of the cosmological constant allows one to solve some important problems in black hole thermodynamics, namely in the extended phase space the Smarr relation can be recovered. It was also pointed out that the extended thermodynamics which introduces the notion of a thermodynamic volume of a black hole satisfies the inverse isoperimetric inequality [6].

To develop the extended thermodynamics it was supposed that the cosmological constant defines the pressure due to the relation

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }. \end{aligned}$$
(34)

It was noted that matter fields which give rise to other black hole solutions might modify the latter relation. In the presence of a dilaton field the relation for the pressure takes the following form:

$$\begin{aligned} P=-\frac{\Lambda }{16\pi }\left( \frac{b}{r}\right) ^{2\gamma }. \end{aligned}$$
(35)

It was pointed out that in the case of extended thermodynamics the black hole’s mass should not be identified with the thermodynamic internal energy but rather with the enthalpy \(M=H\). Having used the well-known relation for the enthalpy one might obtain the thermodynamic volume:

$$\begin{aligned} V=\left( \frac{\partial H}{\partial P}\right) _T. \end{aligned}$$
(36)

Utilizing the previous relation we obtain the thermodynamic volume which takes the form

$$\begin{aligned} V=\frac{\omega _{n-1}(1+\alpha ^2)}{n-\alpha ^2}b^{(n-1)\gamma }r_+^{(n-1)(1-\gamma )+1}. \end{aligned}$$
(37)

The thermodynamic volume is supposed to be positive and from the relation given above a restriction on the parameter \(\alpha \) can be obtained, namely \(\alpha <\sqrt{n}\). The restriction imposed on the parameter \(\alpha \) can be explained by the fact that when \(\alpha >\sqrt{n}\) the third term in the function (10) changes sign and as a consequence it changes the asymptotic behaviour of the metric for large values of radius r. As a result it drastically affects the thermodynamics. It is easy to verify that in the limit \(\alpha =0\) the volume of a ball with radius \(r=r_+\) in n-dimensional space is recovered (which is supposed to be a geometrical volume of a slowly rotating charged black hole):

$$\begin{aligned} V_{\alpha =0}=\frac{\omega _{n-1}}{n}r_+^{n}. \end{aligned}$$
(38)

We also point out that both given definitions of the pressure can be used here – they change the resulting expression for the thermodynamic volume but this does not affect the conclusions which will be derived from the following analysis.

The equation of state for the black hole can be obtained due to Eqs. (28), (35) and (37) and takes the following form:

$$\begin{aligned} P= & {} \frac{(n-1)}{4(1+\alpha ^2)}\frac{T}{r_+}\nonumber \\&-\frac{(n-1)}{16\pi }\left( \frac{n-2}{1-\alpha ^2}b^{-2\gamma }r_+^{2(\gamma -1)}\right. \nonumber \\&\left. -\frac{2q^2}{n-1}b^{2(2-n)\gamma }r^{2((2-n)(1-\gamma )-1)}_{+}\right) . \end{aligned}$$
(39)

To obtain a “physical” equation of state a transformation from the “geometrical” values of pressure and temperature are usually replaced by “physical” ones:

$$\begin{aligned}{}[P]=\frac{\hbar c}{l^{n-1}_{Pl}}P, \quad [T]=\frac{\hbar c}{k}T, \end{aligned}$$
(40)

where \(l_{Pl}\) is the Planck length for the n-dimensional case. To make the analogy with Van der Waals equation more transparent in this equation of state the horizon radius times \(l^{n-1}_{Pl}\) is replaced by some specific volume.

In the following we will use geometric units for P, T but instead of the horizon radius \(r_+\) we introduce the specific “volume” v in the following manner:

$$\begin{aligned} v=\frac{4(1+\alpha ^2)}{n-1}r_+. \end{aligned}$$
(41)

Having used the introduced above parameter we rewrite the equation of state (39) in the form

$$\begin{aligned} P= & {} \frac{T}{v}-\frac{(n-2)(1+\alpha ^2)}{4\pi (1-\alpha ^2)}\kappa ^{2\gamma -1}b^{-2\gamma }v^{2(\gamma -1)}\nonumber \\&+\frac{q^2}{8\pi }\kappa ^{2((2-n)(1-\gamma )-1)}b^{2(2-n)\gamma }v^{2((2-n)(1-\gamma )-1)}\nonumber \\ \end{aligned}$$
(42)

where \(\kappa =(n-1)/(4(1+\alpha ^2))\).

It is easy to verify that the equation of state (42) has an inflection point for the temperatures below some critical value \(T_c\). In order to examine this critical behaviour further the standard relations for the inflection point are used:

$$\begin{aligned}&\left( \frac{\partial P}{\partial v}\right) _T=0, \nonumber \\&\left( \frac{\partial ^2 P}{\partial v^2}\right) _T=0. \end{aligned}$$
(43)

Having used the latter relations we obtain the critical specific volume \(v_c\) and critical temperature \(T_c\):

$$\begin{aligned}&v_c=\left( \frac{2q^2(n+\alpha ^2-1)(2n+\alpha ^2-3)}{(n-1)(n-2)}\kappa ^{2((2-n)(1-\gamma )-\gamma )}b^{2(3-n)\gamma }\right) ^{1/(2(\gamma -(2-n)(1-\gamma )))}, \end{aligned}$$
(44)
$$\begin{aligned} T_c= & {} \frac{(n-2)(n+\alpha ^2-2)}{\pi (1-\alpha ^2)(2n+\alpha ^2-3)}\kappa ^{2\gamma -1}b^{-2\gamma }v_c^ {2\gamma -1}, \end{aligned}$$
(45)

and for the critical pressure one arrives at the relation

$$\begin{aligned} P_c=\frac{(n-2)(n+\alpha ^2-2)}{4\pi (n+\alpha ^2-1)}\kappa ^{2\gamma -1} b^{-2\gamma }v_c^{2(\gamma -1)}. \end{aligned}$$
(46)

Having utilized the written above relations we obtain the critical ratio in the form

$$\begin{aligned} \rho _c=\frac{P_cv_c}{T_c}=\frac{(1-\alpha ^2)(2n+\alpha ^2-3)}{4(n+\alpha ^2-1)}. \end{aligned}$$
(47)

It is worth emphasizing that the critical value we have obtained depends on two parameters only, namely on the dimension of space (or spacetime) and the dilaton parameter \(\alpha \), which is given in the general action integral (1). We can conclude that the critical ratio represents some universal behaviour which does not depend on the particular solution of the equations of motion obtained from the action (1). We also emphasize that the relation obtained above for the critical ratio (47) coincides with corresponding relation for a static Einstein–Maxwell-dilaton black hole given in [60]. It should be noted that in order to have a conventional thermodynamic behaviour we have some restrictions on the dilaton parameter, namely from the previous relation for the critical temperature and critical ratio we obtain \(\alpha ^2<1\).

When the dilaton parameter \(\alpha =0\), the well-known critical ratio for a Van der Waals gas in \(n+1\)-dimensional space is recovered:

$$\begin{aligned} \left. \frac{P_cv_c}{T_c}\right| _{\alpha =0}=\frac{2n-3}{4(n-1)}. \end{aligned}$$
(48)

As has been mentioned above in the extended approach to thermodynamics the black hole’s mass is identified with the enthalpy, so one can perform a Legendre transformation for this thermodynamic function and obtain the Gibbs free energy, which is more suitable for analyzing of thermodynamic properties of systems with inherent critical behaviour. The Gibbs free energy reads

$$\begin{aligned} G(T,P)= & {} M-TS=\frac{\omega _{n-1}(1+\alpha ^2)b^{(n-1)\gamma }}{16\pi }\nonumber \\&\times \,\left( \frac{n-2}{\alpha ^2+n-2}b^{-2\gamma }r_+^{(n-1)(1-\gamma )+2\gamma -1}\right. \nonumber \\&-\frac{16\pi (1-\alpha ^2)P}{(n-1)(n-\alpha ^2)}r_+^{(n-1)(1-\gamma )+1}\nonumber \\&\left. +\frac{2q^2(\alpha ^2+2n-3)}{(n-1)(\alpha ^2+n-2)}b^{2(2-n)\gamma }r_+^{(3-n)(1-\gamma )-1}\right) .\nonumber \\ \end{aligned}$$
(49)

It is worth emphasizing that the Gibbs free energy is a function of temperature T and pressure P so in the previous relation the parameter \(r_+\) should be treated as a function of T and P through the equation of state (39). In the limit \(\alpha =0\) the relation written above leads to the Gibbs free energy for an \(n+1\)-dimensional RN-AdS black hole [10],

$$\begin{aligned} G(T,P)=\frac{\omega _{n-1}}{16\pi }\left( r_+^{n-2}{-}\frac{16\pi P}{n(n-1)}r_+^n{+}\frac{2q^2(2n-3)}{(n-1)(n-2)}r_+^{2-n}\right) .\nonumber \\ \end{aligned}$$
(50)

The behaviour of the Gibbs free energy (49) as a function of temperature for fixed values of the pressure is represented in Fig. 6. One can see that for small values of the dilaton parameter \(\alpha \) the Gibbs free energy shows swallowtail behaviour (in our case \(\alpha =0.1\)), which is typical for a Van der Waals system and for the RN-AdS black hole [10]. This swallowtail behaviour of the Gibbs free energy means that the system has a phase transition of the first order.

Fig. 6
figure 6

Gibbs free energy as a function of temperature for different values of pressure for \(n=3\), \(\alpha =0.1\) (left graph), \(\alpha =0.5\) (right graph), \(b=1\), \(q=0.1\). A solid curve corresponds to the value \(P=P_c\), a dashed curve corresponds to the value \(P=P_c/2\), a dash-dotted line corresponds to the value \(P=P_c/3\) and finally a dotted curve corresponds to the pressure \(P=3P_c/2\)

Full size image

For larger values of the dilaton parameter (for example, to make this new effect visible, we have chosen \(\alpha =0.5\)) the behaviour of the Gibbs potential is qualitatively different for the RN-AdS black hole, namely for the critical isobar (\(P=P_c\)) a specific maximum appears. For the pressures below the critical one a unique loop forming domain appears which does not happen in the case without dilaton parameter. Then, for some isobar (\(P_l<P_c\)), a closed loop is formed and for the pressures below that new characteristic value \(P<P_l\) one has a self-intersecting part of graph which consists of a swallowtail piece followed by some closed loop. Similar to other systems where the thermodynamics is described by a Van der Waals-like equation of state for the isotherms (or isobars) below the critical one we have a domain of instability which is characterized by a negative value of the isothermal compressibility \(\kappa _{T}\). The general form of the isothermal compressibility is as follows:

$$\begin{aligned} \kappa _T=-\frac{1}{V}\left( \frac{\partial V}{\partial P}\right) _T. \end{aligned}$$
(51)

For our equation of state (42) we can write

$$\begin{aligned}&\kappa _T=\frac{n+\alpha ^2}{1+\alpha ^2} \left( P-\frac{n-2}{4\pi }\kappa ^{2\gamma -1}b^{-2\gamma }v^{2(\gamma -1)}\right. \nonumber \\&\quad \left. +\frac{q^2}{8\pi }\frac{2n+\alpha ^2-3}{1+\alpha ^2}\kappa ^{2((2-n)(1-\gamma )-1)}b^{2(2-n)\gamma }v^{2((2-n)(1-\gamma )-1)}\right) ^{-1}.\nonumber \\ \end{aligned}$$
(52)

It is well known that the isothermal compressibility (52) should be considered as a function of temperature T and pressure P. To do so, one should use the equation of state (42) and express the volume v in terms of the thermodynamic variables mentioned above, but due to the complicated form of Eq. (42) it is impossible to perform in the general case. It can be checked easily that Eq. (52) gives rise to the conclusion that for the isobars above the critical one (\(P>P_c\)) the parameter \(\kappa _T\) is always positive, which means that the system is stable. Similarly, one can talk about the thermodynamic stability of the system for all the isotherms above the critical one (\(T>T_c\)). At the critical point (\(P=P_c\), \(T=T_c\)) we have a standard phase transition of the second order, which is typical for other Van der Waals systems at the critical point.

For isobars in the region \(P_l<P<P_c\) when a loop is forming we have a domain of instability (\(\kappa _T<0\)), but because the loop is not formed yet we have a domain of discontinuity of the Gibbs free energy. Quite recently it has been pointed out that due to the discontinuity of the Gibbs free energy one has a novel phase transition of the zeroth order in that region [69]. For the isobars below the characteristic one (\(P<P_l\)) when the loop is formed the phase transition becomes of the first order without discontinuity of the Gibbs free energy. To make this fact more transparent let us look at Fig. 7. It shows the transformation from the phase transition of the zeroth order into the phase transition of the first one when the pressure is decreasing. The right curve corresponds to the pressure in the region (\(P_l<P<P_c\)) when a closed loop has not formed yet and the dashed part of the curve represents the instable domain. The middle curve corresponds to the specific pressure \(P_l\) when a closed loop has just formed and the zeroth order phase transition turns into the first order phase transition. The left curve corresponds to the pressure \(P<P_l\) with a swallowtail part and an additional loop, and in this case we have a typical first order phase transition.

Fig. 7
figure 7

Gibbs free energy as a function of temperature for several values of pressure for \(n=3\), \(\alpha =0.5\), \(b=1\), \(q=0.1\) which demonstrates instability region. Instability domains are represented by red dashed parts of the curves

Full size image

It is well known that the Gibbs potential is constant during the first order phase transition. This fact helps us to obtain the coexistence curve for two phases. To do so we use Maxwell’s equal area law. On an isotherm with the temperature \(T<T_c\) two points with parameters \((P_0,v_1)\) and \((P_0,v_2)\) satisfy Maxwell’s equal area law:

$$\begin{aligned} P_0(v_2-v_1)=\int ^{v_2}_{v_1}P\mathrm{d}v. \end{aligned}$$
(53)

Having substituted in the right hand side of this relation the equation of state (42) and performing the integration we obtain

$$\begin{aligned}&P_0(v_2-v_1)=T\ln {\left( \frac{v_2}{v_1}\right) }+\frac{1+\alpha ^2}{1-\alpha ^2}A\left( v^{2\gamma -1}_2-v^{2\gamma -1}_1\right) \nonumber \\&\quad +\frac{1+\alpha ^2}{3-2n-\alpha ^2}B\left( v^{2(2-n)(1-\gamma )-1}_2-v^{2(2-n)(1-\gamma )-1}_1\right) \nonumber \\ \end{aligned}$$
(54)

where we denote

$$\begin{aligned} A= & {} \frac{(n-2)(1+\alpha ^2)}{4\pi (1-\alpha ^2)}\kappa ^{2\gamma -1}b^{-2\gamma },\nonumber \\ B= & {} \frac{q^2}{8\pi }\kappa ^{2((2-n)(1-\gamma )-1)}b^{2(2-n)\gamma }. \end{aligned}$$
(55)

From the equation of state (42) we derive

$$\begin{aligned}&T\left( \frac{1}{v_2}-\frac{1}{v_1}\right) -A\left( v^{2(\gamma -1)}_2-v^{2(\gamma -1)}_1\right) \nonumber \\&\quad +B\left( v^{2((2-n)(1-\gamma )-1)}_2-v^{2((2-n)(1-\gamma )-1)}_1\right) =0. \end{aligned}$$
(56)

To find the coexistence relation we introduce the new parameter x as the ratio of two volumes: \(x=v_1/v_2\) (\(0<x<1\)). Using the introduced parameter we rewrite Eq. (56) in the following way:

$$\begin{aligned} T= & {} \frac{x}{x-1}\left( Av^{2\gamma -1}_2\left( 1-x^{2(\gamma -1)}\right) \right. \nonumber \\&\left. -Bv^{2(2-n)(1-\gamma )-1}_2\left( 1-x^{2((2-n)(1-\gamma )-1)}\right) \right) . \end{aligned}$$
(57)

Taking into account Eqs. (54) and (57) we can find the relation for the volume of one phase as a function of parameter x:

$$\begin{aligned}&v^{2(\gamma -(2-n)(1-\gamma ))}_2\nonumber \\&=\frac{B}{A}\left( \frac{\frac{x}{x-1}\ln {x}(1-x^{2((2-n)(1-\gamma )-1)})+\frac{2(n+\alpha ^2-1)}{3-2n-\alpha ^2}\left( 1-x^{2(2-n)(1-\gamma )-1}\right) }{\frac{x}{x-1}\ln {x}(1-x^{2(\gamma -1)})-\frac{2}{1-\alpha ^2}\left( 1-x^{2\gamma -1}\right) }\right) .\nonumber \\ \end{aligned}$$
(58)

Having used the relation for temperature (57) we can rewrite the equation of state (42) as a function of x:

$$\begin{aligned} P= & {} \frac{1}{x-1}\left( Av^{2(\gamma -1)}_2\left( 1-x^{2\gamma -1}\right) \right. \nonumber \\&\left. -Bv^{2((2-n)(1-\gamma )-1)}_2\left( 1-x^{2(2-n)(1-\gamma )-1}\right) \right) . \end{aligned}$$
(59)

We point out that when we set \(x=1\) in Eqs. (57), (58) and (59) we recover the critical values for temperature \(T_c\) (45), volume \(v_c\) (44), and pressure \(P_c\) (46), respectively. These three equations allow one to obtain the coexistence curve between two phases. It should be noted that these equations give rise to the coexistence relation (P–T diagram) just for the region where the first order phase transition takes place (\(P<P_l\), \(T<T_l\)). In the region \(P_l<P<P_c\) and \(T_l<T<T_c\) the coexistence curve can be approximated by a line joining the points (\(T_l,P_l\)) and (\(T_c,P_c\)). Analyzing the behaviour of the coexistence curve (see Fig. 8) one can conclude that the domain where the zeroth order phase transition takes place extends with increasing dilaton parameter \(\alpha \). The end points of these curves represent the points of the second order phase transition, similar to other Van der Waals systems. It was pointed out [69] that, for dilaton parameter \(\alpha =0\), the zeroth order phase transition disappears and the coexistence curve is typical for Van der Waals systems where the first order phase transition’s domain terminates at the critical point of the second order phase transition.

Fig. 8
figure 8

P–T diagram (coexistence curve) for two phases for \(n=3\), \(\alpha =0.5\) (the left graph) or \(\alpha =0.7\) (the right one), \(b=1\), \(q=0.1\). The solid parts of the curves represent the domains where the first order phase transition takes place and the dotted parts of the curves represent the range where the zeroth order phase transition is found

Full size image

The slope of the coexistence curve can be calculated with the help of the Clapeyron equation:

$$\begin{aligned} \frac{\text {d}P}{\text {d}T}=\frac{L}{T(v_2-v_1)}, \end{aligned}$$
(60)

where \(L=T(s_2-s_1)\) is the latent heat of the phase change and \(s_1\) and \(s_2\) represent the corresponding entropies for the first and the second phases, respectively. In our case these two phases represent the black holes of different sizes, namely the so-called small and large black holes [10, 64, 66]; the latent heat represents the gain or loss of the mass of the black hole during the phase transition [77]. From the previous equation one can obtain the relation for the latent heat of the phase change:

$$\begin{aligned} L=T\frac{\text {d}P}{\text {d}T}(v_2-v_1)=v_2(1-x)T(x)\frac{\text {d}P}{\text {d}x}\frac{\text {d}x}{\text {d}T} \end{aligned}$$
(61)

Taking into account Eqs. (57), (58) and (59) one can represent the latent heat of the phase change as a function of temperature T but due to the complicated relation that appears here we show the graphical dependence only.

Fig. 9
figure 9

The left graph represents the latent heat L as a function of temperature T for different values of \(\alpha \) when n is fixed, namely \(n=3\) (in particular \(b=1\), \(q=0.1\) for both graphs) and \(\alpha =0.1\) (solid curve), \(\alpha =0.3\) (dashed curve) and \(\alpha =0.5\) (dash-dotted curve). The right graph demonstrates the L–T dependence for fixed \(\alpha =0.3\) and several values of n, namely \(n=3\) (dashed curve), \(n=4\) (dash-dotted curve), \(n=6\) (solid curve)

Full size image

Figure 9 represents the two types of possible changes. The left graph shows the dependence for fixed value of n and for several different values of the parameter \(\alpha \). One can see that for smaller values of \(\alpha \) the \(L=L(T)\) dependence is nonmonotonic with some specific maximum point and then decreasing to zero. Increasing of the parameter \(\alpha \) gives rise to the shift of the maximum point to lower temperatures. At the same time increasing of dimension n when \(\alpha \) is fixed leads to increase of the absolute value of the latent heat L with corresponding shift of the maximum point to higher temperatures. It should be pointed out that for the domain where we have the phase transition of the zeroth order it is not possible to calculate the latent heat with the help of Eq. (60), because this formula is obtained under the assumption that the Gibbs potential is continuous, which does not hold for the phase transition of the zeroth order. But reaching the critical temperature the phase transition transforms into a phase transition of the second order where the latent heat is equal to zero, so any of the represented curves should be continued by a sort of other curve reaching zero latent heat at the critical temperature corresponding to the very same parameters as n, \(\alpha \), b and q, which represent the given curve.

5 Critical exponents

Since the system possesses a critical point it is interesting to investigate the behaviour of the system in the domain close to the critical point. In general we follow the approach developed in Refs. [9, 10].

To obtain the critical exponent \(\alpha \) one should utilize the relation for the entropy (29) and represent it as a function of the temperature T and thermodynamic volume V (37):

$$\begin{aligned}&S(T,V)=\frac{\omega _{n-1}}{4}b^{(n-1)\gamma }\nonumber \\&\quad \times \,\left[ \frac{(n-\alpha ^2)}{\omega _{n-1}(1+\alpha ^2)}b^{-(n-1)\gamma }V\right] ^{(n-1)(1-\gamma )/((n-1)(1-\gamma )+1)}.\nonumber \\ \end{aligned}$$
(62)

The written relation shows that the entropy does not depend on the temperature T explicitly, thus the heat capacity \(C_V=0\) and as a result the corresponding critical exponent \({\bar{\alpha }}=0\). We point out here that this critical parameter is usually denoted by \(\alpha \), but in our work the letter \(\alpha \) already is used for the coupling parameter.

To find the other critical exponents we rearrange the Van der Waals equation introducing reduced variables:

$$\begin{aligned} p=\frac{P}{P_c}, \quad \tau =\frac{T}{T_c}, \quad \nu =\frac{v}{v_c}, \end{aligned}$$
(63)

where \(P_c\), \(T_c\) and \(v_c\) are the corresponding critical values given by Eqs. (46)–(44). As a result the equation of state (42) can be represented in the form

$$\begin{aligned} p= & {} \frac{4(n+\alpha ^2-1)}{(1-\alpha ^2)(2n+\alpha ^2-3)}\frac{\tau }{\nu }\nonumber \\&-\frac{(1+\alpha ^2)(n+\alpha ^2-1)}{(1-\alpha ^2)(n+\alpha ^2-2)}\nu ^{2(\gamma -1)}\nonumber \\&+\frac{(1+\alpha ^2)}{(n+\alpha ^2-2)(2n+\alpha ^2-3)}\nu ^{2((2-n)(1-\gamma )-1)}.\nonumber \\ \end{aligned}$$
(64)

In the limit \(\alpha =0\) one arrives at

$$\begin{aligned} p= & {} \frac{4(n-1)}{(2n-3)}\frac{\tau }{\nu }-\frac{n-1}{n-2}\nu ^{-2}\nonumber \\&+\frac{1}{(n-2)(2n-3)}\nu ^{2(1-n)}. \end{aligned}$$
(65)

This equation coincides with the corresponding equation of state obtained in Ref. [10].

Equation (64) can be rewritten in the form

$$\begin{aligned} p=\frac{1}{\rho _c}\frac{\tau }{\nu }+h(\nu ) \end{aligned}$$
(66)

where \(\rho _c\) is the critical ratio given by Eq. (47) and \(h(\nu )\) might be even more general than in Eq. (64). In the neighbourhood of the critical point (\(\tau =1,\nu =1\)) one can represent

$$\begin{aligned} \tau =1+t, \quad \nu =(1+\omega )^{1/z} \end{aligned}$$
(67)

and it should be noted that \(z>0\). Taking into account the definition of the critical point one can expand the right hand side of Eq. (64) into the series and as a consequence we arrive at the relation

$$\begin{aligned} p=1+At-Bt\omega -C\omega ^3+\mathcal{O}(t\omega ^2,\omega ^4) \end{aligned}$$
(68)

where

$$\begin{aligned} A= & {} \frac{1}{\rho _c}, \quad B=\frac{1}{z\rho _c}, \nonumber \\ C= & {} \frac{1}{z^3}\left( \frac{1}{\rho _c}-\frac{1}{6}h^{(3)}(1)\right) . \end{aligned}$$
(69)

We assume that \(C>0\). Differentiating Eq. (68) with respect to \(\omega \) we obtain

$$\begin{aligned} \mathrm{d}P=-P_c\left( Bt+3C\omega ^2\right) \mathrm{d}\omega . \end{aligned}$$
(70)

Having used Maxwell’s area law and denoting \(\omega _l\) and \(\omega _s\) the “volumes” of large and small black holes, respectively, we obtain

$$\begin{aligned} p=1+At-Bt\omega _l-C\omega ^3_l=1+At-Bt\omega _s-C\omega ^3_s.\nonumber \\ \end{aligned}$$
(71)

The previous equation gives us the nontrivial solution

$$\begin{aligned} \omega _s=-\omega _l=\sqrt{-\frac{Bt}{C}}. \end{aligned}$$
(72)

As a result we obtain

$$\begin{aligned} \eta =V_c\left( \omega _l-\omega _s\right) =2V_c\omega _l \sim (-t)^{1/2}. \end{aligned}$$
(73)

From this equation it immediately follows that

$$\begin{aligned} \beta =\frac{1}{2}. \end{aligned}$$
(74)

To calculate the exponent \({\bar{\gamma }}\) we use again Eq. (53) (we point out that similar to the critical exponent \({\bar{\alpha }}\) we use another notation for the critical exponent usually denoted as \(\gamma \)). One can write

$$\begin{aligned} \kappa _T=-\frac{1}{V}\left( \frac{\partial V}{\partial P}\right) _T\sim \frac{1}{P_cBt} , \quad \Rightarrow \quad {\bar{\gamma }}=1. \end{aligned}$$
(75)

Now it follows from the “critical isotherm” (\(t=0\)) that

$$\begin{aligned} p-1=-C\omega ^3, \quad \Rightarrow \quad \delta =3. \end{aligned}$$
(76)

One can see that the obtained critical exponents are the same as for the RN-AdS black hole, so we can conclude that the presence of the dilaton field, having a serious influence on the thermodynamics and critical behaviour, does not change the values of the critical exponents.

6 Conclusions

In our work we have considered a slowly rotating black hole in the framework of Einstein–Maxwell-dilaton theory. In this theory an additional dilaton potential term of the so-called Liouville form is taken into account and this form allows us to obtain a cosmological constant term. A similar problem was examined in [48, 50] but in the first reference of these the cosmological constant term is not taken into account, while in the second work this term takes a slightly different form. We have obtained the solution of the corresponding Einstein and field equations, which is in a perfect agreement with the results of the work of [47, 48, 50]. In the limit when the dilaton parameter goes to zero the slowly rotating Kerr–Newmann solution is recovered [70]. It should be pointed out that the solution obtained here can be treated as a generalization of the corresponding solution in [48]. We note that the obtained solution possesses a complicated causal structure, which in general respects is analogous to a nonrotating dilaton black hole [47].

We have investigated the black hole thermodynamics making the assumption that the cosmological constant is held fixed. Firstly, it was shown that, for negative cosmological constant, the temperature shows a nonmonotonous behaviour as a function of the horizon radius \(r_+\). It is shown that for small radius \(r_+\) the temperature (28) becomes negative and it gives rise to the conclusion that a black hole with such a small radius would be unstable. It is also demonstrated that the point when the temperature becomes equal to zero is the very same point as when the heat capacity \(C_Q\) changes sign from positive to negative, and this fact confirms the thermodynamic instability of the black hole. The heat capacity was shown to have two points of discontinuity which separate stable and unstable domains. But for cosmological constant large enough in absolute value the points of discontinuity merge with each other and finally disappear, transforming into a high peak, which diminishes with the following increasing of the cosmological constant (Fig. 5). It means that when the cosmological constant is large in absolute value we have a black hole which might be stable for an arbitrarily small radius of the horizon, which peculiarity, to the best of our knowledge, has not been paid attention to in previous work.

We also examined the thermodynamics using the extended technique. It was shown that the obtained black hole solution allows one to obtain a equation of state of Van der Waals type; see Eq. (39) (or (42)). Similar to recently obtained results of [69] our system possesses a domain of the first as well as of the zeroth order phase transitions. The appearance of the zeroth order phase transition is directly related to the existence of dilaton-Maxwell fields’ coupling, which is described by the parameter \(\alpha \). The main conclusion we should point out here is the fact that with increasing of the coupling the domain where the zeroth order phase transition takes place becomes wider. For small enough \(\alpha \) this domain, where a zeroth order phase transition happens, is negligibly small and it is hardly visible on the graph (see the left graph of Fig. 6), but when the coupling parameter \(\alpha \) increases this domain drastically increases and becomes notable on the graph. We also note that the zeroth order phase transition takes place also for other systems with dilaton–electromagnetic coupling with a different type of electromagnetic field action; see [76], but in that work it was pointed out that the discontinuity of the Gibbs potential which gives rise to the zeroth order phase transition is related not only to the dilaton–electromagnetic field coupling constant \(\alpha \). In our case we can state that the existence of the zeroth order phase transition is completely caused by the coupling between the fields. In the case this coupling disappears and the zeroth order transition would not occur. Using the equation of state and Maxwell’s equal area law we also obtained the coexistence relation for the system in the domain where the first order phase transition takes place. Having used the Clapeyron equation the latent heat was calculated numerically, and we note that these calculations are valid on the very same domain. Finally, we calculated the critical exponents. They are shown to be the same as for an Einstein–Maxwell black hole.